Grafika 2D. Animacja Zmiany Kształtu. opracowanie: Jacek Kęsik
|
|
|
- Fabian Zając
- 8 lat temu
- Przeglądów:
Transkrypt
1 Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik
2 Wykład przedstawia podstawy animacji zmiany kształtu - morfingu
3 Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving) łączenie dwóch obrazów poprzez płynne przejście - uśrednianie Wstawianie (tweening) proces sekwencyjnej interpolacji obrazów pośrednich między dwoma stanami kluczowymi w celu uzyskania wrażenia płynnego przejścia między nimi Deformowanie (warping) zniekształcanie obrazu uzależnione od obszaru tego obrazu, matematyczny odpowiednik nadruku na elastycznej powierzchni (rozciąganej i ściskanej w różnych miejscach) Przekształcanie (morphing) jest kombinacją powyższych
4 Na postawie pracy dr Stevena Seitza (University of Washington)
5 Czym jest morphing? Próba znalezienia stanu pośredniego pomiędzy dwoma obiektami NIE stan pośredni między dwoma obrazami obiektów tylko obraz obiektu pośredniego
6 Próba znalezienia stanu pośredniego pomiędzy dwoma obiektami Animacja wiąże się ze znalezieniem ważonych stanów pośrednich zależnych od czasu t Jak wygląda obiekt pośredni? Nie mamy pojęcia Ale możemy sfingować coś sensownego
7 Morphing jest kombinacją zlewania, wstawiania i deformowania Czasem wystarczy tylko zlewanie(uśrednianie) i wstawianie Obraz pośredni = (1-t)*Obraz 1 + t*obraz 2 Najczęściej 0 < t < 1
8 Jak znaleźć wartość pośrednią między P i Q? v = Q - P P Q Interpolacja liniowa dowolny punkt pośredni ap + bq, Zdefiniowany tylko gdy a+b = 1 więc ap+bq = ap+(1-a)q P + 0.5v = P + 0.5(Q P) = 0.5P Q P + 1.5v = P + 1.5(Q P) = -0.5P Q (ekstrapolacja) P i Q dowolne wartości: Punkty w 2D lub 3D Kolory RGB, HSV (3D) Całe obrazy (m-na-n D)
9 Metoda filmowa nazywana zlewanie / przenikanie Ale co gdy obrazy nie są dopasowane do siebie?
10 Najpierw dopasowanie potem przenikanie Dopasowanie wykorzystuje przekształcenie globalne (najczęściej rzut/przekrzywienie)
11 Co gdy obiekty różnią się kształtem? Przenikanie nie działa Globalne dopasowanie nie działa Ani żadna globalna transformacja (np. afiniczna)
12 Rozwiązanie: Dopasowywanie szczegółów Ogon do ogona, oko do oka... Wprowadzamy tym samym zniekształcenia lokalne (nie parametryczne)
13 Procedura morphingu dla każdego t, 1. Znajdź kształt pośredni każdego z obrazów Lokalne zniekształcenia 2. Interpoluj kolory pikseli z tych 2 obrazów pośrednich przenikanie
14 Konieczność zdefiniowana bardziej złożonego przekształcenia Przekształcenia globalne były funkcjami kilku parametrów Przekształcenia lokalne u(x,y) i v(x,y) mogą być zdefiniowane niezależnie dla każdej pozycji x,y! (każdego szczegółu) Gdy znamy zbiór wektorów przekształceń u,v możemy łatwo przekształcić każdy piksel (przekształcenie odwrotne + interpolacja)
15 Punkty kontrolne określają krzywe zniekształcenia Krzywe zapewniają gładkość zbioru wektorów przekształceń
16 Jak określić przekształcenie? Zdefiniować punkty kontrolne odpowiadających sobie krzywych Interpolacja reszty pozycji by uzyskać pełne przekształcenie Ale nie chcemy definiować całej siatki a tylko kilka punktów
17 Jak określić przekształcenie? Zdefiniować odpowiadające sobie punkty kontrolne Interpolacja reszty pozycji by uzyskać pełne przekształcenie Ale jak? Jak zdefiniować przejście od punktów kontrolnych do pikseli?
18 Rozwiązanie - siatka trójkątów 1. Oznaczenie odpowiadających sobie punktów w kluczowych obszarach obiektów
19 Rozwiązanie - siatka trójkątów 2. Zdefiniowanie siatki trójkątów, rozpiętej na tych punktach Ta sama siatka na obu obrazach Siatki określają odpowiadające sobie trójkąty na obrazach
20 Rozwiązanie - siatka trójkątów 3. Każdy trójkąt jest przekształcany osobno od wyglądu początkowego do końcowego Ale jak zbudować taką siatkę?
21 Podział otoczki wypukłej zestawu punktów na powierzchni na trójkąty jest nazywany Triangularyzacją. Punkty znajdują się tylko i wyłącznie w wierzchołkach trójkątów Istnieje wiele wyników triangularyzacji zestawu punktów
22 Algorytm triangularyzacji o złożoności O(n 3 ) Powtarzaj tak długo jak możliwe Wybierz 2 wierzchołki Jeśli linia je łącząca nie przecina poprzednich linii zapisz ją
23 Jakość triangularyzacji Niech (T) = ( 1, 2,.., 3t ) będzie wektorem kątów triangularyzacji T Triangularyzacja T 1 będzie lepsza od T 2 jeśli (T 1 ) > (T 2 ) leksykograficznie Najlepsza triangulacja maksymalizuje najmniejsze kąty (Delaunay triangulation) dobrze źle
24 Poprawianie triangularyzacji W każdym czworokącie wypukłym możliwe jest odwrócenie krawędzi wewnętrznej. Jeśli poprawia to lokalną jakość triangularyzacji, poprawia również jakość triangularyzacji globalnej Jeśli odwrócenie krawędzi poprawia triangularyzację, poprzednia krawędź jest nazywana nielegalną
25 Naiwny algorytm Delaunay Rozpocznij z dowolną triangularyzacją Odwracaj kolejno nielegalne krawędzie, tak długo jak występują Może pracować bardzo długo
26 algorytm Delaunay (Delone) Wykorzystuje podział płaszczyzny na komórki Woronoja (dla danego zbioru n punktów, dzieli się płaszczyznę na n obszarów, w taki sposób, że każdy punkt w dowolnym obszarze znajduje się bliżej określonego punktu ze zbioru n punktów niż do pozostałych n 1 punktów ) Łącząc punkty z sąsiadujących ze sobą obszarów uzyskujemy triangularyzację Delaunay Złożoność zredukowana do O(nlogn)
27 Wiemy już jak przekształcić jeden obiekt w drugi ale jak stworzyć animowaną sekwencję morfingu? 1. Utworzyć kształty pośrednie (interpolacja siatek) 2. Przekształcić do nich oba obrazy 3. Wykonać zlanie kolorów obu przekształconych obrazów
28 Obraz źródłowy Siatka źródłowa Siatka pośrednia Obraz pośredni 1 Obraz pośredni 2 Obraz połączony Siatka docelowa Obraz docelowy f 0 1 czas 0 n Przekształć obraz źródłowy zgodnie z siatką Morf = f P+(1-f)Q Przekształć obraz docelowy godnie z siatką
29 Dla siatki trójkątnej Uzyskanie siatki pośredniej w chwili t t = [0,1] Liniowa interpolacja dla każdej pary szczegółów np. (1-t)*p1+t*p0 dla odpowiedników p0 i p1
30 Ograniczenie dla morfingu 2D Możliwość wystąpienia złożenia trójkątów Pojawia się w przypadku zmiany kolejności punktów kontrolnych na obrazie Z reguły w przypadku próby wykonania przekształcenia pseudo 3D Działa poprawnie tylko z danymi 3D Za pomocą ekstrapolacji można osiągnąć ciekawe efekty - karykatury
31 Morfing można wykonać również na obrazach dynamicznie zmienianych
32 Morfing widoku view morphing Morfowaniu podlega pozycja wirtualnej kamery
33 Morfing widoku view morphing Metoda i efekt Kamery rejestrujące ten sam obiekt w tej samej chwili Tworzą zgrubną ścieżkę ruchu wokół obiektu Płynny ruch kamery wokół obiektu uzyskany dzięki morfowaniu pozycji wirtualnej kamery pomiędzy poszczególnymi rzeczywistymi kamerami w ścieżce
34 That s all folks
Grafika 2D. Animacja Zmiany Kształtu. Wykład przedstawia podstawy animacji zmiany kształtu - morfingu. opracowanie: Jacek Kęsik
 Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu 1 Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu 1 Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Grafika 2D. Animacja Zmiany Kształtu. opracowanie: Jacek Kęsik
 Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Metody animacji komputerowych
 Metody animacji komputerowych Definicja Animacja jest procesem automatycznego generowania serii obrazów, gdy kolejny obraz przedstawia pewną zmianę w stosunku do poprzedniego. Pojęcie to obejmuje zmiany
Metody animacji komputerowych Definicja Animacja jest procesem automatycznego generowania serii obrazów, gdy kolejny obraz przedstawia pewną zmianę w stosunku do poprzedniego. Pojęcie to obejmuje zmiany
KSMM PG. Definicja. Pojęcie to obejmuje zmiany pozycji w czasie (dynamika ruchu), kształtu, barwy, przezroczystości,
 Metody animacji KSMM PG Definicja Animacja jest procesem automatycznego generowania serii obrazów, gdy kolejny obraz przedstawia pewną zmianę w stosunku do poprzedniego. Pojęcie to obejmuje zmiany pozycji
Metody animacji KSMM PG Definicja Animacja jest procesem automatycznego generowania serii obrazów, gdy kolejny obraz przedstawia pewną zmianę w stosunku do poprzedniego. Pojęcie to obejmuje zmiany pozycji
Grafika 2D. Animacja - wstęp. Wykład obejmuje podstawowe pojęcia związane z animacja komputerową. opracowanie: Jacek Kęsik
 Grafika 2D - wstęp opracowanie: Jacek Kęsik Wykład obejmuje podstawowe pojęcia związane z animacja komputerową 1 podstawowe pojęcia Scena Rodzaje animacji Symbole Bardzo szybkie wyświetlanie sekwencji
Grafika 2D - wstęp opracowanie: Jacek Kęsik Wykład obejmuje podstawowe pojęcia związane z animacja komputerową 1 podstawowe pojęcia Scena Rodzaje animacji Symbole Bardzo szybkie wyświetlanie sekwencji
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Ćwiczenia nr 7. TEMATYKA: Krzywe Bézier a
 TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
1. Prymitywy graficzne
 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
 Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Techniki animacji komputerowej
 Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Autodesk 3D Studio MAX Animacja komputerowa i praca kamery
 Autodesk 3D Studio MAX Animacja komputerowa i praca kamery dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 5 maja 2017 1 / 22 Plan
Autodesk 3D Studio MAX Animacja komputerowa i praca kamery dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 5 maja 2017 1 / 22 Plan
Przygotowanie grafiki 3D do gier komputerowych
 Grafika Komputerowa i Wizualizacja Przygotowanie grafiki 3D do gier komputerowych Rafał Piórkowski Plan wykładu 1. Ogólne wiadomości 2. Modelowanie high poly 3. Rzeźbienie 4. Modelowanie low poly 5. Model
Grafika Komputerowa i Wizualizacja Przygotowanie grafiki 3D do gier komputerowych Rafał Piórkowski Plan wykładu 1. Ogólne wiadomości 2. Modelowanie high poly 3. Rzeźbienie 4. Modelowanie low poly 5. Model
Synteza i obróbka obrazu. Modelowanie obiektów 3D
 Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
1. Wykład NWD, NWW i algorytm Euklidesa.
 1.1. NWD, NWW i algorytm Euklidesa. 1. Wykład 1 Twierdzenie 1.1 (o dzieleniu z resztą). Niech a, b Z, b 0. Wówczas istnieje dokładnie jedna para liczb całkowitych q, r Z taka, że a = qb + r oraz 0 r< b.
1.1. NWD, NWW i algorytm Euklidesa. 1. Wykład 1 Twierdzenie 1.1 (o dzieleniu z resztą). Niech a, b Z, b 0. Wówczas istnieje dokładnie jedna para liczb całkowitych q, r Z taka, że a = qb + r oraz 0 r< b.
1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych
 1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych (2,0), (5,6) narysowany przy wykorzystaniu algorytmu Bresenhama
1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych (2,0), (5,6) narysowany przy wykorzystaniu algorytmu Bresenhama
WYKŁAD 3 WYPEŁNIANIE OBSZARÓW. Plan wykładu: 1. Wypełnianie wieloboku
 WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
 Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Rok akademicki: 2017/2018 Kod: JFM s Punkty ECTS: 7. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym.
 Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym. Po uruchomieniu Geogebry (wersja 5.0) Pasek narzędzi Cofnij/przywróć Problem 1: Sprawdź co się stanie, jeśli połączysz
Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym. Po uruchomieniu Geogebry (wersja 5.0) Pasek narzędzi Cofnij/przywróć Problem 1: Sprawdź co się stanie, jeśli połączysz
INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA
 INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA LITERATURA: R. Reinhardt, S. Dowd, Adobe Flash Professional. Biblia. D. Hirmes, JD Hooge, K. Jokol, FLASH. AKADEMIA MATEMATYCZNYCH SZTUCZEK ZASTOSOWANIA ANIMACJI
INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA LITERATURA: R. Reinhardt, S. Dowd, Adobe Flash Professional. Biblia. D. Hirmes, JD Hooge, K. Jokol, FLASH. AKADEMIA MATEMATYCZNYCH SZTUCZEK ZASTOSOWANIA ANIMACJI
Photoshop. Podstawy budowy obrazu komputerowego
 Photoshop Podstawy budowy obrazu komputerowego Wykład 1 Autor: Elżbieta Fedko O czym dzisiaj będziemy mówić? Co to jest grafika komputerowa? Budowa obrazu w grafice wektorowej i rastrowej. Zastosowanie
Photoshop Podstawy budowy obrazu komputerowego Wykład 1 Autor: Elżbieta Fedko O czym dzisiaj będziemy mówić? Co to jest grafika komputerowa? Budowa obrazu w grafice wektorowej i rastrowej. Zastosowanie
10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu.
 Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
Opis krzywych w przestrzeni 3D. Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH
 Opis krzywych w przestrzeni 3D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W przypadku tych krzywych wektory styczne w punkach końcowych są określane bezpośrednio
Opis krzywych w przestrzeni 3D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W przypadku tych krzywych wektory styczne w punkach końcowych są określane bezpośrednio
Plan wykładu. Akcelerator 3D Potok graficzny
 Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Gramatyki grafowe. Dla v V, ϕ(v) etykieta v. Klasa grafów nad Σ - G Σ.
 Gramatyki grafowe Def. Nieskierowany NL-graf (etykietowane wierzchołki) jest czwórką g = (V, E, Σ, ϕ), gdzie: V niepusty zbiór wierzchołków, E V V zbiór krawędzi, Σ - skończony, niepusty alfabet etykiet
Gramatyki grafowe Def. Nieskierowany NL-graf (etykietowane wierzchołki) jest czwórką g = (V, E, Σ, ϕ), gdzie: V niepusty zbiór wierzchołków, E V V zbiór krawędzi, Σ - skończony, niepusty alfabet etykiet
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II
 Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
Graficzne modelowanie scen 3D. POV-Ray. Wykład 3
 POV-Ray Wykład 3 Krzywa Beziera Krzywa Beziera to krzywa wielomianowa trzeciego stopnia, czyli taka która może być definiowana za pomocą trzech wielomianów z pewnym parametrem t (odpowiednio dla współrzędnych
POV-Ray Wykład 3 Krzywa Beziera Krzywa Beziera to krzywa wielomianowa trzeciego stopnia, czyli taka która może być definiowana za pomocą trzech wielomianów z pewnym parametrem t (odpowiednio dla współrzędnych
Projektowanie graficzne. Wykład 2. Open Office Draw
 Projektowanie graficzne Wykład 2 Open Office Draw Opis programu OpenOffice Draw OpenOffice Draw umożliwia tworzenie prostych oraz złożonych rysunków. Posiada możliwość eksportowania rysunków do wielu różnych
Projektowanie graficzne Wykład 2 Open Office Draw Opis programu OpenOffice Draw OpenOffice Draw umożliwia tworzenie prostych oraz złożonych rysunków. Posiada możliwość eksportowania rysunków do wielu różnych
Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
 Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
3. Macierze i Układy Równań Liniowych
 3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Programowanie liniowe
 Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań
 Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań Przekształcenia liniowe, diagonalizacja macierzy 1. Podano współrzędne wektora v w bazie B. Znaleźć współrzędne tego wektora w bazie B, gdy: a) v = (1,
Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań Przekształcenia liniowe, diagonalizacja macierzy 1. Podano współrzędne wektora v w bazie B. Znaleźć współrzędne tego wektora w bazie B, gdy: a) v = (1,
Obrót wokół początku układu współrzędnych o kąt φ można wyrazić w postaci macierzowej następująco
 Transformacje na płaszczyźnie Przesunięcie Przesunięcie (translacja) obrazu realizowana jest przez dodanie stałej do każdej współrzędnej, co w postaci macierzowej można przedstawić równaniem y'] = [ x
Transformacje na płaszczyźnie Przesunięcie Przesunięcie (translacja) obrazu realizowana jest przez dodanie stałej do każdej współrzędnej, co w postaci macierzowej można przedstawić równaniem y'] = [ x
Tworzenie prezentacji w MS PowerPoint
 Tworzenie prezentacji w MS PowerPoint Program PowerPoint dostarczany jest w pakiecie Office i daje nam możliwość stworzenia prezentacji oraz uatrakcyjnienia materiału, który chcemy przedstawić. Prezentacje
Tworzenie prezentacji w MS PowerPoint Program PowerPoint dostarczany jest w pakiecie Office i daje nam możliwość stworzenia prezentacji oraz uatrakcyjnienia materiału, który chcemy przedstawić. Prezentacje
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Oświetlenie obiektów 3D
 Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Ćwiczenia z grafiki komputerowej 4 PRACA NA WARSTWACH. Miłosz Michalski. Institute of Physics Nicolaus Copernicus University.
 Ćwiczenia z grafiki komputerowej 4 PRACA NA WARSTWACH Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 14 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadania
Ćwiczenia z grafiki komputerowej 4 PRACA NA WARSTWACH Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 14 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadania
Techniki wstawiania tabel
 Tabele w Wordzie Tabela w Wordzie to uporządkowany układ komórek w postaci wierszy i kolumn, w które może być wpisywany tekst lub grafika. Każda komórka może być formatowana oddzielnie. Możemy wyrównywać
Tabele w Wordzie Tabela w Wordzie to uporządkowany układ komórek w postaci wierszy i kolumn, w które może być wpisywany tekst lub grafika. Każda komórka może być formatowana oddzielnie. Możemy wyrównywać
Modelowanie dłoni. 1. Obraz referencyjny
 Modelowanie dłoni 1. Obraz referencyjny Obrazy referencyjne ustawiamy na panelach Properties (uaktywnienie/dezaktywacja klawiszem N), w zakładce Backgraund Images. Należy zaznaczyć opcje wyświetlania obrazu
Modelowanie dłoni 1. Obraz referencyjny Obrazy referencyjne ustawiamy na panelach Properties (uaktywnienie/dezaktywacja klawiszem N), w zakładce Backgraund Images. Należy zaznaczyć opcje wyświetlania obrazu
Analiza obrazu. wykład 4. Marek Jan Kasprowicz Uniwersytet Rolniczy 2009
 Analiza obrazu komputerowego wykład 4 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Filtry górnoprzepustowe - gradienty Gradient - definicje Intuicyjnie, gradient jest wektorem, którego zwrot wskazuje
Analiza obrazu komputerowego wykład 4 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Filtry górnoprzepustowe - gradienty Gradient - definicje Intuicyjnie, gradient jest wektorem, którego zwrot wskazuje
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
GRK 2. dr Wojciech Palubicki
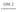 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
Analiza obrazu. wykład 1. Marek Jan Kasprowicz Uniwersytet Rolniczy Marek Jan Kasprowicz Analiza obrazu komputerowego 2009 r.
 Analiza obrazu komputerowego wykład 1 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Plan wykładu Wprowadzenie pojęcie obrazu cyfrowego i analogowego Geometryczne przekształcenia obrazu Przekształcenia
Analiza obrazu komputerowego wykład 1 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Plan wykładu Wprowadzenie pojęcie obrazu cyfrowego i analogowego Geometryczne przekształcenia obrazu Przekształcenia
Elementarna analiza statystyczna
 MatLab część V 1 Elementarna analiza statystyczna W standardowym pakiecie MatLab-a istnieją jedynie podstawowe funkcje analizy statystycznej. Bardziej zaawansowane znajdują się w pakiecie statystycznym
MatLab część V 1 Elementarna analiza statystyczna W standardowym pakiecie MatLab-a istnieją jedynie podstawowe funkcje analizy statystycznej. Bardziej zaawansowane znajdują się w pakiecie statystycznym
10. Wstęp do Teorii Gier
 10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Luty 2001 Algorytmy (4) 2000/2001
 Mając dany zbiór elementów, chcemy znaleźć w nim element największy (maksimum), bądź najmniejszy (minimum). We wszystkich naturalnych metodach znajdywania najmniejszego i największego elementu obecne jest
Mając dany zbiór elementów, chcemy znaleźć w nim element największy (maksimum), bądź najmniejszy (minimum). We wszystkich naturalnych metodach znajdywania najmniejszego i największego elementu obecne jest
Funkcje analityczne. Wykład 4. Odwzorowania wiernokątne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2016/2017) dla każdego s = (s.
 Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2016/2017) 1 Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2016/2017) 1 Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Modelowanie krzywych i powierzchni
 3 Modelowanie krzywych i powierzchni Modelowanie powierzchniowe jest kolejną metodą po modelowaniu bryłowym sposobem tworzenia części. Jest to też sposób budowy elementu bardziej skomplikowany i wymagający
3 Modelowanie krzywych i powierzchni Modelowanie powierzchniowe jest kolejną metodą po modelowaniu bryłowym sposobem tworzenia części. Jest to też sposób budowy elementu bardziej skomplikowany i wymagający
Wprowadzenie do programu 3ds Max THEBRAIN
 Szkolenie obejmuje zapoznanie się z interface m programu oraz zagadnieniami związanymi z modelowaniem w programie 3Ds Max. W trakcie szkolenia uczestnik będzie przyswajał wiedzę poprzez wykonywanie ćwiczeń,
Szkolenie obejmuje zapoznanie się z interface m programu oraz zagadnieniami związanymi z modelowaniem w programie 3Ds Max. W trakcie szkolenia uczestnik będzie przyswajał wiedzę poprzez wykonywanie ćwiczeń,
Kolorowanie płaszczyzny, prostych i okręgów
 Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
Interpolacja i modelowanie krzywych 2D i 3D
 Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
Autodesk 3D Studio MAX Podstawy modelowania 3D
 Autodesk 3D Studio MAX Podstawy modelowania 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 23 Plan Wykładu
Autodesk 3D Studio MAX Podstawy modelowania 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 23 Plan Wykładu
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył
 Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
GRAFIKA KOMPUTEROWA. Plan wykładu. 1. Początki grafiki komputerowej. 2. Grafika komputerowa a dziedziny pokrewne. 3. Omówienie programu przedmiotu
 GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
GRK 4. dr Wojciech Palubicki
 GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
Funkcje analityczne. Wykład 4. Odwzorowania wiernokątne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2017/2018)
 Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) 1. Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) 1. Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Ćwiczenie 1 Automatyczna animacja ruchu
 Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
(1,10) (1,7) (5,5) (5,4) (2,1) (0,0) Grafika 3D program POV-Ray - 73 -
 Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
OpenGL przezroczystość
 OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Grafika Komputerowa Materiały Laboratoryjne
 Grafika Komputerowa Materiały Laboratoryjne Laboratorium 14 Blender, podstawy animacji Wstęp Zagadnienie tworzenia animacji 3D w Blenderze jest bardzo szerokie i wiąże się z wieloma grupami rozwiązao.
Grafika Komputerowa Materiały Laboratoryjne Laboratorium 14 Blender, podstawy animacji Wstęp Zagadnienie tworzenia animacji 3D w Blenderze jest bardzo szerokie i wiąże się z wieloma grupami rozwiązao.
GIMP - Filtr Deformowanie (IWarp) r
 Poradnik Przegląd GIMP - Filtr Deformowanie (IWarp) 10-12-2015r Obraz oryginalny Zastosowanie filtra Deformacja Rysunek 1. Przykład zastosowania filtra Deformacja Filtr pozwala deformować interaktywnie
Poradnik Przegląd GIMP - Filtr Deformowanie (IWarp) 10-12-2015r Obraz oryginalny Zastosowanie filtra Deformacja Rysunek 1. Przykład zastosowania filtra Deformacja Filtr pozwala deformować interaktywnie
Przegląd metod optymalizacji wielowymiarowej. Funkcja testowa. Funkcja testowa. Notes. Notes. Notes. Notes. Tomasz M. Gwizdałła
 Przegląd metod optymalizacji wielowymiarowej Tomasz M. Gwizdałła 2012.12.06 Funkcja testowa Funkcją testową dla zagadnień rozpatrywanych w ramach tego wykładu będzie funkcja postaci f (x) = (x 1 1) 4 +
Przegląd metod optymalizacji wielowymiarowej Tomasz M. Gwizdałła 2012.12.06 Funkcja testowa Funkcją testową dla zagadnień rozpatrywanych w ramach tego wykładu będzie funkcja postaci f (x) = (x 1 1) 4 +
Algorytmy stochastyczne Wykład 12, Uczenie parametryczne w sieciach bayesowskich
 Algorytmy stochastyczne Wykład 2, Uczenie parametryczne w sieciach bayesowskich Jarosław Piersa 204-05-22 Zagadnienie uczenia sieci bayesowskich Problem mamy strukturę sieci bayesowskiej węzły, stany i
Algorytmy stochastyczne Wykład 2, Uczenie parametryczne w sieciach bayesowskich Jarosław Piersa 204-05-22 Zagadnienie uczenia sieci bayesowskich Problem mamy strukturę sieci bayesowskiej węzły, stany i
Młodzieżowe Uniwersytety Matematyczne. dr Michał Lorens
 Młodzieżowe Uniwersytety Matematyczne Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ODLEGŁOŚĆ NA POWIERZCHNI WIELOŚCIANU dr Michał Lorens 28.04.2012 Projekt
Młodzieżowe Uniwersytety Matematyczne Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ODLEGŁOŚĆ NA POWIERZCHNI WIELOŚCIANU dr Michał Lorens 28.04.2012 Projekt
Przekształcanie równań stanu do postaci kanonicznej diagonalnej
 Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 2 2 Problemy algorytmiczne Klasy problemów algorytmicznych Liczby Fibonacciego Przeszukiwanie tablic Największy
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 2 2 Problemy algorytmiczne Klasy problemów algorytmicznych Liczby Fibonacciego Przeszukiwanie tablic Największy
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Elastyczne projektowanie produktu w ZW3D. ZW3D CAD/CAM Biała księga
 Elastyczne projektowanie produktu w ZW3D Wprowadzenie Doświadczenie użytkownika wraz z efektem wizualnym zawsze było bardzo istotną częścią ZW3D. Ludzie wolą produkty z kształtami rzucającymi się w oczy,
Elastyczne projektowanie produktu w ZW3D Wprowadzenie Doświadczenie użytkownika wraz z efektem wizualnym zawsze było bardzo istotną częścią ZW3D. Ludzie wolą produkty z kształtami rzucającymi się w oczy,
Grafika Komputerowa Materiały Laboratoryjne
 Grafika Komputerowa Materiały Laboratoryjne Laboratorium 10 Blender, podstawy Wstęp Blender jest rozbudowanym narzędziem do tworzenia i edycji obiektów, scen i animacji 3D. Poznanie go na przyzwoitym poziomie
Grafika Komputerowa Materiały Laboratoryjne Laboratorium 10 Blender, podstawy Wstęp Blender jest rozbudowanym narzędziem do tworzenia i edycji obiektów, scen i animacji 3D. Poznanie go na przyzwoitym poziomie
Grafika Komputerowa Materiały Laboratoryjne
 Grafika Komputerowa Materiały Laboratoryjne Laboratorium 7b Teksturowanie Wstęp W poprzednim laboratorium poprawiliśmy kształt domku w trybie edycyjnym. Zmianom podlegał układ powierzchni obiektu ale nie
Grafika Komputerowa Materiały Laboratoryjne Laboratorium 7b Teksturowanie Wstęp W poprzednim laboratorium poprawiliśmy kształt domku w trybie edycyjnym. Zmianom podlegał układ powierzchni obiektu ale nie
Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA
 Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA Polecenie 3DWYRÓWNAJ umożliwia precyzyjne przemieszczanie bryły 3D w przestrzeni projektowej Przykład poniżej pokazuje jak z pomocą poleceń - 3DWYRÓWNAJ
Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA Polecenie 3DWYRÓWNAJ umożliwia precyzyjne przemieszczanie bryły 3D w przestrzeni projektowej Przykład poniżej pokazuje jak z pomocą poleceń - 3DWYRÓWNAJ
Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30
 Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30 2.3. Model rastrowy Rastrowy model danych wykorzystywany jest dla gromadzenia i przetwarzania danych pochodzących ze skanowania istniejących
Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30 2.3. Model rastrowy Rastrowy model danych wykorzystywany jest dla gromadzenia i przetwarzania danych pochodzących ze skanowania istniejących
Teoria grafów II. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
Przetwarzanie obrazów wykład 7. Adam Wojciechowski
 Przetwarzanie obrazów wykład 7 Adam Wojciechowski Przekształcenia morfologiczne Przekształcenia podobne do filtrów, z tym że element obrazu nie jest modyfikowany zawsze lecz tylko jeśli spełniony jest
Przetwarzanie obrazów wykład 7 Adam Wojciechowski Przekształcenia morfologiczne Przekształcenia podobne do filtrów, z tym że element obrazu nie jest modyfikowany zawsze lecz tylko jeśli spełniony jest
Technologie Informacyjne
 Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
Spis treści. Księgarnia PWN: Roland Zimek - SWiSH Max2 i SWiSH Max3. Wprowadzenie... 9
 Księgarnia PWN: Roland Zimek - SWiSH Max2 i SWiSH Max3 Spis treści Wprowadzenie... 9 1. Opis programu i instalacja... 13 1.1. Nowości w SWiSH Max2... 13 1.1.1. Wygląd okna programu... 13 1.1.2. Język skryptowy...
Księgarnia PWN: Roland Zimek - SWiSH Max2 i SWiSH Max3 Spis treści Wprowadzenie... 9 1. Opis programu i instalacja... 13 1.1. Nowości w SWiSH Max2... 13 1.1.1. Wygląd okna programu... 13 1.1.2. Język skryptowy...
Bartosz Bazyluk SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok
 SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
TWORZENIE TORU KOLEJOWEGO DLA LOKOMOTYWY - ZABAWKI. W tym przewodniku stworzymy tor kolejowy pasujący do zabawki.
 TWORZENIE TORU KOLEJOWEGO DLA LOKOMOTYWY - ZABAWKI W tym przewodniku stworzymy tor kolejowy pasujący do zabawki. Wymiary twojej zabawki mogą być inne niż ta, więc musisz zacząć od zmierzenia jej wymiarów.
TWORZENIE TORU KOLEJOWEGO DLA LOKOMOTYWY - ZABAWKI W tym przewodniku stworzymy tor kolejowy pasujący do zabawki. Wymiary twojej zabawki mogą być inne niż ta, więc musisz zacząć od zmierzenia jej wymiarów.
Maskowanie i selekcja
 Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Programy CAD Modelowanie geometryczne
 Programy CAD Modelowanie geometryczne Komputerowo wspomagane projektowanie CAD Narzędzia i techniki wspomagające prace w zakresie: projektowania, modelowania geometrycznego, obliczeniowej analizy FEM,
Programy CAD Modelowanie geometryczne Komputerowo wspomagane projektowanie CAD Narzędzia i techniki wspomagające prace w zakresie: projektowania, modelowania geometrycznego, obliczeniowej analizy FEM,
Struktury Danych i Złożoność Obliczeniowa
 Struktury Danych i Złożoność Obliczeniowa Zajęcia 2 Algorytmy wyszukiwania, sortowania i selekcji Sortowanie bąbelkowe Jedna z prostszych metod sortowania, sortowanie w miejscu? Sortowanie bąbelkowe Pierwsze
Struktury Danych i Złożoność Obliczeniowa Zajęcia 2 Algorytmy wyszukiwania, sortowania i selekcji Sortowanie bąbelkowe Jedna z prostszych metod sortowania, sortowanie w miejscu? Sortowanie bąbelkowe Pierwsze
Animowana grafika 3D Laboratorium 3
 3DStudio MAX teksturowanie modelu budynku dla potrzeb gry 3D W ćwiczeniu tym zakładamy, że mamy już ukończony model naszego budynku. Składa się on z wielu elementów: ścian, okien, drzwi, dachu itp. W teorii
3DStudio MAX teksturowanie modelu budynku dla potrzeb gry 3D W ćwiczeniu tym zakładamy, że mamy już ukończony model naszego budynku. Składa się on z wielu elementów: ścian, okien, drzwi, dachu itp. W teorii
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 10 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Zastosowania informatyki w geologii ćwiczenia 1,2 INKSCAPE 1
 INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),
INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),

