Wykład 5. Map, MapAt, MapThread, Outer, Inner,Thread, Applay. Map, MapAll. Funkcje Map, MapAt, Inner, Outer, etc.
|
|
|
- Gabriela Romanowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Wykład 5 Funkcje Map, MapAt, Inner, Outer, etc. In[1]:= ClearAll["Global`*"] wyczyść wszystko Map, MapAt, MapThread, Outer, Inner,Thread, Applay Map, MapAll In[2]:= g =. In[3]:=? Map Map[ f, expr] or f /@ expr applies f to each element on the first level in expr. Map[ f, expr, levelspec] applies f to parts of expr specified by levelspec. Map[ f] represents an operator form of Map that can be applied to an expression. In[4]:= Map[Funkcja, {K1, K2, {L1, L2}}] zastosuj do Out[4]= {Funkcja(K1), Funkcja(K2), Funkcja({L1, L2})} In[5]:= Funkcja /@ {K1, K2, {L1, L2}} Out[5]= {Funkcja(K1), Funkcja(K2), Funkcja({L1, L2})} In[6]:= Map[ff, {a, b, {c, d}, g}] zastosuj do Out[6]= {ff(a), ff(b), ff({c, d}), ff(g)}
2 2 wyklad5_2017_notes.nb In[7]:= {a, b, {c, d}, g} // TreeForm w formie drzewka List Out[7]//TreeForm= a b List g c d In[8]:= Map[ff, {a, b, {c, d}, g}, 2] zastosuj do Out[8]= {ff(a), ff(b), ff({ff(c), ff(d)}), ff(g)} In[9]:= Map[ff, {a, b, {c, d}, g}, {2}] zastosuj do Out[9]= {a, b, {ff(c), ff(d)}, g} In[10]:= f /@ {a, b, {c, d}, g} Out[10]= {f (a), f (b), f ({c, d}), f (g)} In[11]:= Out[11]= Reverse /@ {{a, b}, {c, d}, {e, f}} odwróć kolejność b a d c f e In[12]:= Lista = {a, b, {c, d}, g} Out[12]= {a, b, {c, d}, g} In[13]:= Lista[[3, 1]] Out[13]= c
3 wyklad5_2017_notes.nb 3 In[14]:= Array[ LegendreP[#, x] + HermiteH[#, x] &, 10]; tablic funkcja P Legendre'a wielomian H Hermite'a Total@% // oblicz sumę GRA /@ % Map[GRA, %%, {2}] zastosuj do Simplify // uprość Map[GRA, %%%, {3}] zastosuj do Expand rozszerz Out[15]= x x x x x x x x x x Out[16]= GRA x x7 GRA x3 GRA GRA + GRA + GRA x x x x8 + GRA GRA + GRA x x4 + GRA x GRA Out[17]= GRA GRA x10 + GRA 128 GRA x GRA - GRA x GRA - GRA x 7 + GRA GRA GRA x GRA - GRA x 4 + GRA - GRA GRA x 2 + GRA GRA(x) GRA x GRA x Out[18]= GRA(x) GRA 2 - GRA(x) GRA 3 - GRA(x) GRA GRA(x) GRA 5 + GRA(x) GRA 6 - GRA(x) GRA x GRA(x) GRA GRA(x)GRA 9 + GRA(x) GRA In[19]:= Map[f, {a, {b, G}, c}] zastosuj do Out[19]= {f (a), f ({b, G}), f (c)} In[20]:= f /@ {a, {b, G}, c} Out[20]= {f (a), f ({b, G}), f (c)} In[21]:=? MapAll MapAll[ f, expr] or f //@ expr applies f to every subexpression in expr.
4 4 wyklad5_2017_notes.nb In[22]:= MapAll[f, {a, {b, G}, c}] zastosuj do wszystkich Out[22]= f ({f (a), f ({f (b), f (G)}), f (c)}) In[23]:= f //@ {a, {b, G}, c} Out[23]= f ({f (a), f ({f (b), f (G)}), f (c)}) In[24]:= fff /@ h[p[a, b, c], d[g, f, h]] Out[24]= h(fff( p(a, b, c)), fff(d(g, f, h))) In[25]:= Sin /@ h[p[a, b, c], d[g, f, h]] sinus Out[25]= h(sin( p(a, b, c)), sin(d(g, f, h))) In[26]:= Log //@ h[p[a, b, c], d[g, f, h]] logarytm Out[26]= log(h(log( p(log(a), log(b), log(c))), log(d(log(g), log( f ), log(h))))) In[27]:= 10 x^20-2 x^3 + 4 Log //@ % logarytm Out[27]= 10 x 20-2 x Out[28]= log log (log(2) + i π) log log log 3 (x) + log log(10) log log log 20 (x) + log(4) In[29]:= Map[f, h[p[a, b, c], d[g, f, h]], {2}] (* na drugim poziomie *) zastosuj do Out[29]= h(p(f (a), f (b), f (c)), d(f (g), f (f ), f (h))) Jeśli ustawimy Heads -> True In[30]:= Map[FF, h[p[a, b, c], d[g, f, h]], {2}, zastosuj do Heads -> głowy True] prawda Out[30]= h(ff(p)(ff(a), FF(b), FF(c)), FF(d)(FF(g), FF(f ), FF(h))) In[31]:= Map[FF, h[p[a, b, c], d[g, f, h]], {2}] zastosuj do Out[31]= h( p(ff(a), FF(b), FF(c)), d(ff(g), FF( f ), FF(h)))
5 wyklad5_2017_notes.nb 5 In[32]:= 2 (x - y)^2 + A CC Plus[-A, #] & /@ % suma Times 1 2, # & /@ % mnożenie Out[32]= A + 2 (x - y) 2 CC Out[33]= 2 (x - y) 2 CC - A Out[34]= (x - y) 2 CC - A 2 MapAt In[35]:=? MapAt MapAt[ f, expr, n] applies f to the element at position n in expr. If n is negative, the position is counted from the end. MapAt[ f, expr, {i, j, }] applies f to the part of expr at position {i, j, }. MapAt[ f, expr, {{i 1, j 1, }, {i 2, j 2, }, }] applies f to parts of expr at several positions. MapAt[ f, pos] represents an operator form of MapAt that can be applied to an expression. In[36]:=? Lista Global`Lista Lista = {a, b, {c, d}, g} In[37]:= MapAt[ff, Lista, {{1}, {3, 1}}] zastosuj w danym miejscu Out[37]= {ff(a), b, {ff(c), d}, g} MapThread In[38]:=? MapThread MapThread[ f, {{a 1, a 2, }, {b 1, b 2, }, }] gives { f[a 1, b 1, ], f[a 2, b 2, ], }. MapThread[ f, {expr 1, expr 2, }, n] applies f to the parts of the expr i at level n. In[39]:= MapThread[f, {{a, b}, {x, y}}] zastosuj w wątku Out[39]= {f (a, x), f (b, y)} Zobacz różnice
6 6 wyklad5_2017_notes.nb In[40]:= Map[f, {{a, b}, {x, y}}] zastosuj do Out[40]= {f ({a, b}), f ({x, y})} In[41]:= MapThread[#1 + #2 &, {{a, b}, {x, y}}] zastosuj w wątku Out[41]= {a + x, b + y} Outer In[42]:=? Outer Outer[ f, list 1, list 2, ] gives the generalized outer product of the list i, forming all possible combinations of the lowest-level elements in each of them, and feeding them as arguments to f. Outer[ f, list 1, list 2,, n] treats as separate elements only sublists at level n in the list i. Outer[ f, list 1, list 2,, n 1, n 2, ] treats as separate elements only sublists at level n i in the corresponding list i. In[43]:= Outer[f, {a, b}, {x, y, z}] zewnętrzny Out[43]= f (a, x) f (a, y) f (a, z) f (b, x) f (b, y) f (b, z) In[44]:= Out[44]= Outer[ Times, {a, b, c}, {x, y, z}] zewnę mnożenie a x a y a z b x b y b z c x c y c z In[45]:= Outer[ Times, Array[a, 4], zewnę mnoże tablica wielow Array[b, 4]] // tablica wielowymia MatrixForm postać macierzy Out[45]//MatrixForm= a(1) b(1) a(1) b(2) a(1) b(3) a(1) b(4) a(2) b(1) a(2) b(2) a(2) b(3) a(2) b(4) a(3) b(1) a(3) b(2) a(3) b(3) a(3) b(4) a(4) b(1) a(4) b(2) a(4) b(3) a(4) b(4) In[46]:= Map[FFF, %] zastosuj do Out[46]= {FFF({a(1) b(1), a(1) b(2), a(1) b(3), a(1) b(4)}), FFF({a(2) b(1), a(2) b(2), a(2) b(3), a(2) b(4)}), FFF({a(3) b(1), a(3) b(2), a(3) b(3), a(3) b(4)}), FFF({a(4) b(1), a(4) b(2), a(4) b(3), a(4) b(4)})}
7 wyklad5_2017_notes.nb 7 In[47]:= Map[FFF, %%, {2}] zastosuj do Out[47]= FFF(a(1) b(1)) FFF(a(1) b(2)) FFF(a(1) b(3)) FFF(a(1) b(4)) FFF(a(2) b(1)) FFF(a(2) b(2)) FFF(a(2) b(3)) FFF(a(2) b(4)) FFF(a(3) b(1)) FFF(a(3) b(2)) FFF(a(3) b(3)) FFF(a(3) b(4)) FFF(a(4) b(1)) FFF(a(4) b(2)) FFF(a(4) b(3)) FFF(a(4) b(4)) Inner In[48]:=? Inner Inner[ f, list 1, list 2, g] is a generalization of Dot in which f plays the role of multiplication and g of addition. In[49]:= Inner[f, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }] uogólniony iloczyn skalarny Out[49]= f (a 1, b 1 ) + f (a 2, b 2 ) + f (a 3, b 3 ) In[50]:= Inner[ Times, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }] uogól mnożenie Out[50]= a 1 b 1 + a 2 b 2 + a 3 b 3 In[51]:= Inner[ Plus, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }] uogól suma Out[51]= a 1 + a 2 + a 3 + b 1 + b 2 + b 3 In[52]:= Inner[f, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }, G] uogólniony iloczyn skalarny Out[52]= G(f (a 1, b 1 ), f (a 2, b 2 ), f (a 3, b 3 )) In[53]:= Inner[ Plus, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }, Times] uogól suma mnożenie Out[53]= (a 1 + b 1 ) (a 2 + b 2 ) (a 3 + b 3 ) In[54]:= Inner[ Times, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }, Plus] uogól mnożenie suma Out[54]= a 1 b 1 + a 2 b 2 + a 3 b 3 In[55]:= Inner[ Times, {a 1, a 2, a 3 }, {b 1, b 2, b 3 }, Power] uogól mnożenie potęga Out[55]= (a 1 b 1 ) a a3 b3 2 b 2
8 8 wyklad5_2017_notes.nb Thread In[56]:=? Thread Thread[ f[args]] "threads" f over any lists that appear in args. Thread[ f[args], h] threads f over any objects with head h that appear in args. Thread[ f[args], h, n] threads f over objects with head h that appear in the first n args. In[57]:= Thread[f[a, b]] nawlecz Out[57]= f (a, b) In[58]:= Thread[f[{a, b}, {c, f}]] nawlecz Out[58]= {f (a, c), f (b, f )} In[59]:= a b // FullForm pełna forma Out[59]//FullForm= Rule[a, b] In[60]:= Thread[ Rule[{a, b}, {c, f}]] nawlecz reguła Out[60]= {a c, b f }
9 wyklad5_2017_notes.nb 9 In[61]:= Array[a # &, 100] tablica wielowymiarowa Array[b # &, 100]; tablica wielowymiarowa Thread[ Rule[%%, %]] nawlecz reguła Out[61]= {a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9, a 10, a 11, a 12, a 13, a 14, a 15, a 16, a 17, a 18, a 19, a 20, a 21, a 22, a 23, a 24, a 25, a 26, a 27, a 28, a 29, a 30, a 31, a 32, a 33, a 34, a 35, a 36, a 37, a 38, a 39, a 40, a 41, a 42, a 43, a 44, a 45, a 46, a 47, a 48, a 49, a 50, a 51, a 52, a 53, a 54, a 55, a 56, a 57, a 58, a 59, a 60, a 61, a 62, a 63, a 64, a 65, a 66, a 67, a 68, a 69, a 70, a 71, a 72, a 73, a 74, a 75, a 76, a 77, a 78, a 79, a 80, a 81, a 82, a 83, a 84, a 85, a 86, a 87, a 88, a 89, a 90, a 91, a 92, a 93, a 94, a 95, a 96, a 97, a 98, a 99, a 100 } Out[63]= {a 1 b 1, a 2 b 2, a 3 b 3, a 4 b 4, a 5 b 5, a 6 b 6, a 7 b 7, a 8 b 8, a 9 b 9, a 10 b 10, a 11 b 11, a 12 b 12, a 13 b 13, a 14 b 14, a 15 b 15, a 16 b 16, a 17 b 17, a 18 b 18, a 19 b 19, a 20 b 20, a 21 b 21, a 22 b 22, a 23 b 23, a 24 b 24, a 25 b 25, a 26 b 26, a 27 b 27, a 28 b 28, a 29 b 29, a 30 b 30, a 31 b 31, a 32 b 32, a 33 b 33, a 34 b 34, a 35 b 35, a 36 b 36, a 37 b 37, a 38 b 38, a 39 b 39, a 40 b 40, a 41 b 41, a 42 b 42, a 43 b 43, a 44 b 44, a 45 b 45, a 46 b 46, a 47 b 47, a 48 b 48, a 49 b 49, a 50 b 50, a 51 b 51, a 52 b 52, a 53 b 53, a 54 b 54, a 55 b 55, a 56 b 56, a 57 b 57, a 58 b 58, a 59 b 59, a 60 b 60, a 61 b 61, a 62 b 62, a 63 b 63, a 64 b 64, a 65 b 65, a 66 b 66, a 67 b 67, a 68 b 68, a 69 b 69, a 70 b 70, a 71 b 71, a 72 b 72, a 73 b 73, a 74 b 74, a 75 b 75, a 76 b 76, a 77 b 77, a 78 b 78, a 79 b 79, a 80 b 80, a 81 b 81, a 82 b 82, a 83 b 83, a 84 b 84, a 85 b 85, a 86 b 86, a 87 b 87, a 88 b 88, a 89 b 89, a 90 b 90, a 91 b 91, a 92 b 92, a 93 b 93, a 94 b 94, a 95 b 95, a 96 b 96, a 97 b 97, a 98 b 98, a 99 b 99, a 100 b 100 } In[64]:= /. a x_ b x_ In[64]:= a b // FullForm pełna forma Out[64]//FullForm= Equal[a, b] In[65]:= v1 = {a, b, c} v2 = {x, y, z} Out[65]= {a, b, c} Out[66]= {x, y, z} In[67]:= v1 v2 Out[67]= {a, b, c} {x, y, z} In[68]:= Thread[ Equal[v1, v2]] nawlecz równe Out[68]= {a x, b y, c z}
10 10 wyklad5_2017_notes.nb Apply In[69]:=? Apply Apply[ f, expr] or expr replaces the head of expr by f. Apply[ f, expr, {1}] or expr replaces heads at level 1 of expr by f. Apply[ f, expr, levelspec] replaces heads in parts of expr specified by levelspec. Apply[ f] represents an operator form of Apply that can be applied to an expression. In[70]:= Apply[f, {A, B, Cc}] zastosuj Out[70]= f (A, B, Cc) In[71]:= {A, B, C} stał Out[71]= f (A, B, C) In[72]:= {A, {B, C}, {x, {G, {y, {z}}}}} stała Out[72]= f (A, {B, C}, {x, {G, {y, {z}}}}) In[73]:= H[A, {B, C}, {x, {G, {y, {z}}}}] stała Out[73]= f (A, {B, C}, {x, {G, {y, {z}}}}) In[74]:= H[A, {B, C}, {x, {G, {y, {z}}}}] /. H F stała Out[74]= F(A, {B, C}, {x, {G, {y, {z}}}}) In[75]:= Sin x^2 + y Sin c + d ^3 sinus sinus % %% /. Sin f sinus Out[75]= sin y sin (c + d) 3 + x 2 Out[76]= f y sin (c + d) 3 + x 2 Out[77]= f y f (c + d) 3 + x 2 In[78]:= {A, B, C, DD, g, h} suma stała Out[78]= A + B + C + DD + g + h
11 wyklad5_2017_notes.nb 11 Ale In[79]:= Plus {A, B, { C, DD}, {g, {h}}} suma stała Out[79]= {A + B + C + g, {A + B + DD + h}} In[80]:= {A, B, { C, DD}, {g, {h}}} // FullForm stała pełna forma Out[80]//FullForm= List[A, B, List[C, DD], List[g, List[h]]] In[81]:= F[x, y, z] lista Out[81]= {x, y, z} In[82]:= {A, B, { C, DD}, {g, {h}}} stała Out[82]= f (A, B, {C, DD}, {g, {h}}) Zatem w przypadku Plus@@{A,B,{C,DD},{g,{h}}}, zastąpił Head List przez Plus, ale potem dodał do siebie dwie listy? In[83]:= A + B + { C, DD} + {g, {h}} stała Out[83]= {A + B + C + g, {A + B + DD + h}} In[84]:= { C, DD} + {g, {h}} stała A + B % + %% Out[84]= {C + g, {DD + h}} Out[85]= A + B Out[86]= {A + B + C + g, {A + B + DD + h}} In[87]:= A + B + { C, DD} stała {g, {h}} % + %% Out[87]= {A + B + C, A + B + DD} Out[88]= {g, {h}} Out[89]= {A + B + C + g, {A + B + DD + h}}
12 12 wyklad5_2017_notes.nb UWAGA działa jak Total In[90]:= Array[# &, 100] tablica wielowymiarow oblicz sumę Out[90]= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100} Out[91]= 5050 In[92]:= Total[{{A, b, {c, d}}, e, {f, {g}}}] oblicz sumę Total: Lists of unequal length in {{A, b, {c, d}}, e, {f, {g}}} cannot be added. Out[92]= Total[{{A, b, {c, d}}, e, {f, {g}}}] Zastosowania Niech będzie dana lista: L={{a[1],b[1],c[1]},{a[2],b[2],c[2]},...,{a[100],b[100],c[100]}} a) Napisz dwie funkcje/procedury, które generują listę L. b) Niech będzie dana funkcja F[x1,...,x100], napisz trzy różne funkcje/procedury, które działając na listę L zwracają {F[a[1],...,a[100]],F[b[1],...,b[100]],F[c[1],...,c[100]]}. c) Zmodyfikuj funkcję F, tak aby gdy liczba jej argumentów wynosi jeden zwracała Sin. d) Napisz funkcję/procedurę, która działając na L zwraca: L={{a[1],Sin[b[1]],c[1]},{a[2],Sin[b[2]],c[2]},...,{a[100],Sin[b[100]],c[100]}} UWAGA nie używaj funkcji For, Table, Array, Do, While... e) Napisz trzy różne funkcje, które zamieniają w każdej trójce symboli listy L element pierwszy z drugim. f) Wygeneruj listę {a[1],...,a[100]} i napisz prostą procedurę zwracającą F[a[1],...,a[100]]. Rozwiązanie a) Napisz dwie funkcje/procedury, które generują listę L. In[93]:= Table[{a[k], b[k], c[k]}, {k, 1, 100}]; tabela
13 wyklad5_2017_notes.nb 13 In[94]:= Table[{a[k], b[k], c[k]}, {k, 1, #}] &[100]; tabela In[95]:= Array[a, 100], transpozycja tablica wielowymi Array[b, 100], tablica wielowymi Array[c, 100]}; tablica wielowymiarow In[96]:= Array[#, 100] & {a, b, c} ; transpozycja tablica wielowymiarowa In[97]:= Clear[i] wyczyść Lista = {}; For[i = 1, i < 101, i++, AppendTo[Lista, {a[i], b[i], c[i]}]] dla dołącz na końcu do wartości zmiennej Lista; Dygresja In[101]:= a[x_] := ToExpression@ "a" <> ToString[x] zamień na wyrażenie przemień na ciąg z In[102]:= b[x_] := ToExpression@ StringJoin["b", ToString[x]] zamień na wyra połącz ciągi znaków przemień na ciąg z In[103]:= c[x_] := ToExpression@ StringJoin["c", ToString[x]] zamień na wyra połącz ciągi znaków przemień na ciąg z In[104]:= a[100] Out[104]= a100 In[105]:= Array[a # &, 100] tablica wielowymiarowa Out[105]= {a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9, a 10, a 11, a 12, a 13, a 14, a 15, a 16, a 17, a 18, a 19, a 20, a 21, a 22, a 23, a 24, a 25, a 26, a 27, a 28, a 29, a 30, a 31, a 32, a 33, a 34, a 35, a 36, a 37, a 38, a 39, a 40, a 41, a 42, a 43, a 44, a 45, a 46, a 47, a 48, a 49, a 50, a 51, a 52, a 53, a 54, a 55, a 56, a 57, a 58, a 59, a 60, a 61, a 62, a 63, a 64, a 65, a 66, a 67, a 68, a 69, a 70, a 71, a 72, a 73, a 74, a 75, a 76, a 77, a 78, a 79, a 80, a 81, a 82, a 83, a 84, a 85, a 86, a 87, a 88, a 89, a 90, a 91, a 92, a 93, a 94, a 95, a 96, a 97, a 98, a 99, a 100 } In[106]:= a[xxx] axxx Out[106]= True In[107]:= Clear[a] wyczyść Rozwiązanie b) Niech będzie dana funkcja F[x1,...,x100], napisz trzy różne funkcje/procedury, które działając na
14 14 wyklad5_2017_notes.nb listę L zwracają {F[a[1],...,a[100]],F[b[1],...,b[100]],F[c[1],...,c[100]]}. In[108]:= MapThread[F, Lista] zastosuj w wątku Out[108]= {F(a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8), a(9), a(10), a(11), a(12), a(13), a(14), a(15), a(16), a(17), a(18), a(19), a(20), a(21), a(22), a(23), a(24), a(25), a(26), a(27), a(28), a(29), a(30), a(31), a(32), a(33), a(34), a(35), a(36), a(37), a(38), a(39), a(40), a(41), a(42), a(43), a(44), a(45), a(46), a(47), a(48), a(49), a(50), a(51), a(52), a(53), a(54), a(55), a(56), a(57), a(58), a(59), a(60), a(61), a(62), a(63), a(64), a(65), a(66), a(67), a(68), a(69), a(70), a(71), a(72), a(73), a(74), a(75), a(76), a(77), a(78), a(79), a(80), a(81), a(82), a(83), a(84), a(85), a(86), a(87), a(88), a(89), a(90), a(91), a(92), a(93), a(94), a(95), a(96), a(97), a(98), a(99), a(100)), F(b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15, b16, b17, b18, b19, b20, b21, b22, b23, b24, b25, b26, b27, b28, b29, b30, b31, b32, b33, b34, b35, b36, b37, b38, b39, b40, b41, b42, b43, b44, b45, b46, b47, b48, b49, b50, b51, b52, b53, b54, b55, b56, b57, b58, b59, b60, b61, b62, b63, b64, b65, b66, b67, b68, b69, b70, b71, b72, b73, b74, b75, b76, b77, b78, b79, b80, b81, b82, b83, b84, b85, b86, b87, b88, b89, b90, b91, b92, b93, b94, b95, b96, b97, b98, b99, b100), F(c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12, c13, c14, c15, c16, c17, c18, c19, c20, c21, c22, c23, c24, c25, c26, c27, c28, c29, c30, c31, c32, c33, c34, c35, c36, c37, c38, c39, c40, c41, c42, c43, c44, c45, c46, c47, c48, c49, c50, c51, c52, c53, c54, c55, c56, c57, c58, c59, c60, c61, c62, c63, c64, c65, c66, c67, c68, c69, c70, c71, c72, c73, c74, c75, c76, c77, c78, c79, c80, c81, c82, c83, c84, c85, c86, c87, c88, c89, c90, c91, c92, c93, c94, c95, c96, c97, c98, c99, c100)} In[109]:= # & /@ Transpose[Lista] transpozycja Out[109]= {F(a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8), a(9), a(10), a(11), a(12), a(13), a(14), a(15), a(16), a(17), a(18), a(19), a(20), a(21), a(22), a(23), a(24), a(25), a(26), a(27), a(28), a(29), a(30), a(31), a(32), a(33), a(34), a(35), a(36), a(37), a(38), a(39), a(40), a(41), a(42), a(43), a(44), a(45), a(46), a(47), a(48), a(49), a(50), a(51), a(52), a(53), a(54), a(55), a(56), a(57), a(58), a(59), a(60), a(61), a(62), a(63), a(64), a(65), a(66), a(67), a(68), a(69), a(70), a(71), a(72), a(73), a(74), a(75), a(76), a(77), a(78), a(79), a(80), a(81), a(82), a(83), a(84), a(85), a(86), a(87), a(88), a(89), a(90), a(91), a(92), a(93), a(94), a(95), a(96), a(97), a(98), a(99), a(100)), F(b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15, b16, b17, b18, b19, b20, b21, b22, b23, b24, b25, b26, b27, b28, b29, b30, b31, b32, b33, b34, b35, b36, b37, b38, b39, b40, b41, b42, b43, b44, b45, b46, b47, b48, b49, b50, b51, b52, b53, b54, b55, b56, b57, b58, b59, b60, b61, b62, b63, b64, b65, b66, b67, b68, b69, b70, b71, b72, b73, b74, b75, b76, b77, b78, b79, b80, b81, b82, b83, b84, b85, b86, b87, b88, b89, b90, b91, b92, b93, b94, b95, b96, b97, b98, b99, b100), F(c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12, c13, c14, c15, c16, c17, c18, c19, c20, c21, c22, c23, c24, c25, c26, c27, c28, c29, c30, c31, c32, c33, c34, c35, c36, c37, c38, c39, c40, c41, c42, c43, c44, c45, c46, c47, c48, c49, c50, c51, c52, c53, c54, c55, c56, c57, c58, c59, c60, c61, c62, c63, c64, c65, c66, c67, c68, c69, c70, c71, c72, c73, c74, c75, c76, c77, c78, c79, c80, c81, c82, c83, c84, c85, c86, c87, c88, c89, c90, c91, c92, c93, c94, c95, c96, c97, c98, c99, c100)}
15 wyklad5_2017_notes.nb 15 In[110]:= % - %% Out[110]= {0, 0, 0} In[111]:= Thread[F[ Transpose[Lista]]] nawlecz transpozycja Out[111]= {F({a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8), a(9), a(10), a(11), a(12), a(13), a(14), a(15), a(16), a(17), a(18), a(19), a(20), a(21), a(22), a(23), a(24), a(25), a(26), a(27), a(28), a(29), a(30), a(31), a(32), a(33), a(34), a(35), a(36), a(37), a(38), a(39), a(40), a(41), a(42), a(43), a(44), a(45), a(46), a(47), a(48), a(49), a(50), a(51), a(52), a(53), a(54), a(55), a(56), a(57), a(58), a(59), a(60), a(61), a(62), a(63), a(64), a(65), a(66), a(67), a(68), a(69), a(70), a(71), a(72), a(73), a(74), a(75), a(76), a(77), a(78), a(79), a(80), a(81), a(82), a(83), a(84), a(85), a(86), a(87), a(88), a(89), a(90), a(91), a(92), a(93), a(94), a(95), a(96), a(97), a(98), a(99), a(100)}), F({b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15, b16, b17, b18, b19, b20, b21, b22, b23, b24, b25, b26, b27, b28, b29, b30, b31, b32, b33, b34, b35, b36, b37, b38, b39, b40, b41, b42, b43, b44, b45, b46, b47, b48, b49, b50, b51, b52, b53, b54, b55, b56, b57, b58, b59, b60, b61, b62, b63, b64, b65, b66, b67, b68, b69, b70, b71, b72, b73, b74, b75, b76, b77, b78, b79, b80, b81, b82, b83, b84, b85, b86, b87, b88, b89, b90, b91, b92, b93, b94, b95, b96, b97, b98, b99, b100}), F({c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12, c13, c14, c15, c16, c17, c18, c19, c20, c21, c22, c23, c24, c25, c26, c27, c28, c29, c30, c31, c32, c33, c34, c35, c36, c37, c38, c39, c40, c41, c42, c43, c44, c45, c46, c47, c48, c49, c50, c51, c52, c53, c54, c55, c56, c57, c58, c59, c60, c61, c62, c63, c64, c65, c66, c67, c68, c69, c70, c71, c72, c73, c74, c75, c76, c77, c78, c79, c80, c81, c82, c83, c84, c85, c86, c87, c88, c89, c90, c91, c92, c93, c94, c95, c96, c97, c98, c99, c100})} Rozwiązanie c) Zmodyfikuj funkcję F, tak aby gdy liczba jej argumentów wynosiła jeden zwracała Sin. In[112]:= F[x_] := Sin[x] sinus Rozwiązanie d) Napisz funkcję/procedurę, która działając na L zwraca: L={{a[1],Sin[b[1]],c[1]},{a[2],Sin[b[2]],c[2]},...,{a[100],Sin[b[100]],c[100]}} UWAGA nie używaj funkcji For, Table, Array, Do, While... In[113]:= MapAt[ Sin, #, 2] & /@ Lista zasto sinus a(1) sin(b1) c1 a(2) sin(b2) c2 a(3) sin(b3) c3 a(4) sin(b4) c4 a(5) sin(b5) c5 a(6) sin(b6) c6 a(7) sin(b7) c7 a(8) sin(b8) c8 a(9) sin(b9) c9 a(10) sin(b10) c10 11 sin b11 c11
16 16 wyklad5_2017_notes.nb Out[113]= a(11) sin(b11) c11 a(12) sin(b12) c12 a(13) sin(b13) c13 a(14) sin(b14) c14 a(15) sin(b15) c15 a(16) sin(b16) c16 a(17) sin(b17) c17 a(18) sin(b18) c18 a(19) sin(b19) c19 a(20) sin(b20) c20 a(21) sin(b21) c21 a(22) sin(b22) c22 a(23) sin(b23) c23 a(24) sin(b24) c24 a(25) sin(b25) c25 a(26) sin(b26) c26 a(27) sin(b27) c27 a(28) sin(b28) c28 a(29) sin(b29) c29 a(30) sin(b30) c30 a(31) sin(b31) c31 a(32) sin(b32) c32 a(33) sin(b33) c33 a(34) sin(b34) c34 a(35) sin(b35) c35 a(36) sin(b36) c36 a(37) sin(b37) c37 a(38) sin(b38) c38 a(39) sin(b39) c39 a(40) sin(b40) c40 a(41) sin(b41) c41 a(42) sin(b42) c42 a(43) sin(b43) c43 a(44) sin(b44) c44 a(45) sin(b45) c45 a(46) sin(b46) c46 a(47) sin(b47) c47 a(48) sin(b48) c48 a(49) sin(b49) c49 a(50) sin(b50) c50 a(51) sin(b51) c51 a(52) sin(b52) c52 a(53) sin(b53) c53 a(54) sin(b54) c54 a(55) sin(b55) c55 a(56) sin(b56) c56 a(57) sin(b57) c57 a(58) sin(b58) c58 a(59) sin(b59) c59 a(60) sin(b60) c60 a(61) sin(b61) c61 a(62) sin(b62) c62 a(63) sin(b63) c63 a(64) sin(b64) c64 a(65) sin(b65) c65 a(66) sin(b66) c66 a(67) sin(b67) c67 a(68) sin(b68) c68 a(69) sin(b69) c69 a(70) sin(b70) c70
17 wyklad5_2017_notes.nb 17 a(70) sin(b70) c70 a(71) sin(b71) c71 a(72) sin(b72) c72 a(73) sin(b73) c73 a(74) sin(b74) c74 a(75) sin(b75) c75 a(76) sin(b76) c76 a(77) sin(b77) c77 a(78) sin(b78) c78 a(79) sin(b79) c79 a(80) sin(b80) c80 a(81) sin(b81) c81 a(82) sin(b82) c82 a(83) sin(b83) c83 a(84) sin(b84) c84 a(85) sin(b85) c85 a(86) sin(b86) c86 a(87) sin(b87) c87 a(88) sin(b88) c88 a(89) sin(b89) c89 a(90) sin(b90) c90 a(91) sin(b91) c91 a(92) sin(b92) c92 a(93) sin(b93) c93 a(94) sin(b94) c94 a(95) sin(b95) c95 a(96) sin(b96) c96 a(97) sin(b97) c97 a(98) sin(b98) c98 a(99) sin(b99) c99 a(100) sin(b100) c100 Rozwiązanie e) Napisz trzy różne funkcje, które zamieniają w każdej trójce symboli listy L element pierwszy z drugim. In[114]:= {#[[2]], #[[1]], #[[3]]} & /@ Lista b1 a(1) c1 b2 a(2) c2 b3 a(3) c3 b4 a(4) c4 b5 a(5) c5 b6 a(6) c6 b7 a(7) c7 b8 a(8) c8 b9 a(9) c9 b10 a(10) c10 b11 a(11) c11 b12 a(12) c12 b13 a(13) c13 b14 a(14) c14 b15 a(15) c15 b16 a(16) c16 b17 a(17) c17 b18 a(18) c18 b19 a(19) c19 b20 a(20) c20
18 18 wyklad5_2017_notes.nb Out[114]= b21 a(21) c21 b22 a(22) c22 b23 a(23) c23 b24 a(24) c24 b25 a(25) c25 b26 a(26) c26 b27 a(27) c27 b28 a(28) c28 b29 a(29) c29 b30 a(30) c30 b31 a(31) c31 b32 a(32) c32 b33 a(33) c33 b34 a(34) c34 b35 a(35) c35 b36 a(36) c36 b37 a(37) c37 b38 a(38) c38 b39 a(39) c39 b40 a(40) c40 b41 a(41) c41 b42 a(42) c42 b43 a(43) c43 b44 a(44) c44 b45 a(45) c45 b46 a(46) c46 b47 a(47) c47 b48 a(48) c48 b49 a(49) c49 b50 a(50) c50 b51 a(51) c51 b52 a(52) c52 b53 a(53) c53 b54 a(54) c54 b55 a(55) c55 b56 a(56) c56 b57 a(57) c57 b58 a(58) c58 b59 a(59) c59 b60 a(60) c60 b61 a(61) c61 b62 a(62) c62 b63 a(63) c63 b64 a(64) c64 b65 a(65) c65 b66 a(66) c66 b67 a(67) c67 b68 a(68) c68 b69 a(69) c69 b70 a(70) c70 b71 a(71) c71 b72 a(72) c72 b73 a(73) c73 b74 a(74) c74 b75 a(75) c75 b76 a(76) c76 b77 a(77) c77 b78 a(78) c78 b79 a(79) c79 b80 (80) c80
19 wyklad5_2017_notes.nb 19 b80 a(80) c80 b81 a(81) c81 b82 a(82) c82 b83 a(83) c83 b84 a(84) c84 b85 a(85) c85 b86 a(86) c86 b87 a(87) c87 b88 a(88) c88 b89 a(89) c89 b90 a(90) c90 b91 a(91) c91 b92 a(92) c92 b93 a(93) c93 b94 a(94) c94 b95 a(95) c95 b96 a(96) c96 b97 a(97) c97 b98 a(98) c98 b99 a(99) c99 b100 a(100) c100 In[115]:= Lista /. a temp /. b a /. temp b b1 b1 c1 b2 b2 c2 b3 b3 c3 b4 b4 c4 b5 b5 c5 b6 b6 c6 b7 b7 c7 b8 b8 c8 b9 b9 c9 b10 b10 c10 b11 b11 c11 b12 b12 c12 b13 b13 c13 b14 b14 c14 b15 b15 c15 b16 b16 c16 b17 b17 c17 b18 b18 c18 b19 b19 c19 b20 b20 c20 b21 b21 c21 b22 b22 c22 b23 b23 c23 b24 b24 c24 b25 b25 c25 b26 b26 c26 b27 b27 c27 b28 b28 c28 b29 b29 c29 b30 b30 c30 b31 b31 c31 b32 b32 c32 b33 b33 c33 b34 b34 c34 b35 b35 c35
20 20 wyklad5_2017_notes.nb Out[115]= b36 b36 c36 b37 b37 c37 b38 b38 c38 b39 b39 c39 b40 b40 c40 b41 b41 c41 b42 b42 c42 b43 b43 c43 b44 b44 c44 b45 b45 c45 b46 b46 c46 b47 b47 c47 b48 b48 c48 b49 b49 c49 b50 b50 c50 b51 b51 c51 b52 b52 c52 b53 b53 c53 b54 b54 c54 b55 b55 c55 b56 b56 c56 b57 b57 c57 b58 b58 c58 b59 b59 c59 b60 b60 c60 b61 b61 c61 b62 b62 c62 b63 b63 c63 b64 b64 c64 b65 b65 c65 b66 b66 c66 b67 b67 c67 b68 b68 c68 b69 b69 c69 b70 b70 c70 b71 b71 c71 b72 b72 c72 b73 b73 c73 b74 b74 c74 b75 b75 c75 b76 b76 c76 b77 b77 c77 b78 b78 c78 b79 b79 c79 b80 b80 c80 b81 b81 c81 b82 b82 c82 b83 b83 c83 b84 b84 c84 b85 b85 c85 b86 b86 c86 b87 b87 c87 b88 b88 c88 b89 b89 c89 b90 b90 c90 b91 b91 c91 b92 b92 c92 b93 b93 c93 b94 b94 c94 b95 b95 c95
21 wyklad5_2017_notes.nb 21 b95 b95 c95 b96 b96 c96 b97 b97 c97 b98 b98 c98 b99 b99 c99 b100 b100 c100 In[116]:= Lista /. {aa_, bb_, cc_} {bb, aa, cc} Out[116]= b1 a(1) c1 b2 a(2) c2 b3 a(3) c3 b4 a(4) c4 b5 a(5) c5 b6 a(6) c6 b7 a(7) c7 b8 a(8) c8 b9 a(9) c9 b10 a(10) c10 b11 a(11) c11 b12 a(12) c12 b13 a(13) c13 b14 a(14) c14 b15 a(15) c15 b16 a(16) c16 b17 a(17) c17 b18 a(18) c18 b19 a(19) c19 b20 a(20) c20 b21 a(21) c21 b22 a(22) c22 b23 a(23) c23 b24 a(24) c24 b25 a(25) c25 b26 a(26) c26 b27 a(27) c27 b28 a(28) c28 b29 a(29) c29 b30 a(30) c30 b31 a(31) c31 b32 a(32) c32 b33 a(33) c33 b34 a(34) c34 b35 a(35) c35 b36 a(36) c36 b37 a(37) c37 b38 a(38) c38 b39 a(39) c39 b40 a(40) c40 b41 a(41) c41 b42 a(42) c42 b43 a(43) c43 b44 a(44) c44 b45 a(45) c45 b46 a(46) c46 b47 a(47) c47 b48 a(48) c48 b49 a(49) c49 b50 a(50) c50
22 22 wyklad5_2017_notes.nb Out[116]= b51 a(51) c51 b52 a(52) c52 b53 a(53) c53 b54 a(54) c54 b55 a(55) c55 b56 a(56) c56 b57 a(57) c57 b58 a(58) c58 b59 a(59) c59 b60 a(60) c60 b61 a(61) c61 b62 a(62) c62 b63 a(63) c63 b64 a(64) c64 b65 a(65) c65 b66 a(66) c66 b67 a(67) c67 b68 a(68) c68 b69 a(69) c69 b70 a(70) c70 b71 a(71) c71 b72 a(72) c72 b73 a(73) c73 b74 a(74) c74 b75 a(75) c75 b76 a(76) c76 b77 a(77) c77 b78 a(78) c78 b79 a(79) c79 b80 a(80) c80 b81 a(81) c81 b82 a(82) c82 b83 a(83) c83 b84 a(84) c84 b85 a(85) c85 b86 a(86) c86 b87 a(87) c87 b88 a(88) c88 b89 a(89) c89 b90 a(90) c90 b91 a(91) c91 b92 a(92) c92 b93 a(93) c93 b94 a(94) c94 b95 a(95) c95 b96 a(96) c96 b97 a(97) c97 b98 a(98) c98 b99 a(99) c99 b100 a(100) c100 In[117]:= Table[{#[[j, 2]], #[[j, 1]], #[[j, 3]]}, {j, 1, Length[#]}] tabela długość b1 a(1) c1 b2 a(2) c2 b3 a(3) c3 b4 a(4) c4 b5 a(5) c5
23 wyklad5_2017_notes.nb 23 Out[117]= b6 a(6) c6 b7 a(7) c7 b8 a(8) c8 b9 a(9) c9 b10 a(10) c10 b11 a(11) c11 b12 a(12) c12 b13 a(13) c13 b14 a(14) c14 b15 a(15) c15 b16 a(16) c16 b17 a(17) c17 b18 a(18) c18 b19 a(19) c19 b20 a(20) c20 b21 a(21) c21 b22 a(22) c22 b23 a(23) c23 b24 a(24) c24 b25 a(25) c25 b26 a(26) c26 b27 a(27) c27 b28 a(28) c28 b29 a(29) c29 b30 a(30) c30 b31 a(31) c31 b32 a(32) c32 b33 a(33) c33 b34 a(34) c34 b35 a(35) c35 b36 a(36) c36 b37 a(37) c37 b38 a(38) c38 b39 a(39) c39 b40 a(40) c40 b41 a(41) c41 b42 a(42) c42 b43 a(43) c43 b44 a(44) c44 b45 a(45) c45 b46 a(46) c46 b47 a(47) c47 b48 a(48) c48 b49 a(49) c49 b50 a(50) c50 b51 a(51) c51 b52 a(52) c52 b53 a(53) c53 b54 a(54) c54 b55 a(55) c55 b56 a(56) c56 b57 a(57) c57 b58 a(58) c58 b59 a(59) c59 b60 a(60) c60 b61 a(61) c61 b62 a(62) c62 b63 a(63) c63 b64 a(64) c64 b65 a(65) c65
24 24 wyklad5_2017_notes.nb b65 a(65) c65 b66 a(66) c66 b67 a(67) c67 b68 a(68) c68 b69 a(69) c69 b70 a(70) c70 b71 a(71) c71 b72 a(72) c72 b73 a(73) c73 b74 a(74) c74 b75 a(75) c75 b76 a(76) c76 b77 a(77) c77 b78 a(78) c78 b79 a(79) c79 b80 a(80) c80 b81 a(81) c81 b82 a(82) c82 b83 a(83) c83 b84 a(84) c84 b85 a(85) c85 b86 a(86) c86 b87 a(87) c87 b88 a(88) c88 b89 a(89) c89 b90 a(90) c90 b91 a(91) c91 b92 a(92) c92 b93 a(93) c93 b94 a(94) c94 b95 a(95) c95 b96 a(96) c96 b97 a(97) c97 b98 a(98) c98 b99 a(99) c99 b100 a(100) c100 Rozwiązanie f) Podpunkt f) Wygeneruj listę {a[1],...,a[100]} i napisz prostą procedurę zwracającą F[a[1],...,a[100]].
25 wyklad5_2017_notes.nb 25 In[118]:= Array[a, 100] tablica wielowymiar % Out[118]= {a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8), a(9), a(10), a(11), a(12), a(13), a(14), a(15), a(16), a(17), a(18), a(19), a(20), a(21), a(22), a(23), a(24), a(25), a(26), a(27), a(28), a(29), a(30), a(31), a(32), a(33), a(34), a(35), a(36), a(37), a(38), a(39), a(40), a(41), a(42), a(43), a(44), a(45), a(46), a(47), a(48), a(49), a(50), a(51), a(52), a(53), a(54), a(55), a(56), a(57), a(58), a(59), a(60), a(61), a(62), a(63), a(64), a(65), a(66), a(67), a(68), a(69), a(70), a(71), a(72), a(73), a(74), a(75), a(76), a(77), a(78), a(79), a(80), a(81), a(82), a(83), a(84), a(85), a(86), a(87), a(88), a(89), a(90), a(91), a(92), a(93), a(94), a(95), a(96), a(97), a(98), a(99), a(100)} Out[119]= F(a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8), a(9), a(10), a(11), a(12), a(13), a(14), a(15), a(16), a(17), a(18), a(19), a(20), a(21), a(22), a(23), a(24), a(25), a(26), a(27), a(28), a(29), a(30), a(31), a(32), a(33), a(34), a(35), a(36), a(37), a(38), a(39), a(40), a(41), a(42), a(43), a(44), a(45), a(46), a(47), a(48), a(49), a(50), a(51), a(52), a(53), a(54), a(55), a(56), a(57), a(58), a(59), a(60), a(61), a(62), a(63), a(64), a(65), a(66), a(67), a(68), a(69), a(70), a(71), a(72), a(73), a(74), a(75), a(76), a(77), a(78), a(79), a(80), a(81), a(82), a(83), a(84), a(85), a(86), a(87), a(88), a(89), a(90), a(91), a(92), a(93), a(94), a(95), a(96), a(97), a(98), a(99), a(100)) Generator liczb losowych Liczby losowe a raczej pseudolosowe In[120]:=? RandomReal RandomReal[] gives a pseudorandom real number in the range 0 to 1. RandomReal[{x min, x max }] gives a pseudorandom real number in the range x min to x max. RandomReal[x max ] gives a pseudorandom real number in the range 0 to x max. RandomReal[range, n] gives a list of n pseudorandom reals. RandomReal[range, {n 1, n 2, }] gives an n 1 n 2 array of pseudorandom reals. In[121]:=? RandomInteger RandomInteger[{i min, i max }] gives a pseudorandom integer in the range {i min, i max }. RandomInteger[i max ] gives a pseudorandom integer in the range {0,, i max }. RandomInteger[] pseudorandomly gives 0 or 1. RandomInteger[range, n] gives a list of n pseudorandom integers. RandomInteger[range, {n 1, n 2, }] gives an n 1 n 2 array of pseudorandom integers.
26 26 wyklad5_2017_notes.nb In[122]:=? RandomComplex RandomComplex[] gives a pseudorandom complex number with real and imaginary parts in the range 0 to 1. RandomComplex[{z min, z max }] gives a pseudorandom complex number in the rectangle with corners given by the complex numbers z min and z max. RandomComplex[z max ] gives a pseudorandom complex number in the rectangle whose corners are the origin and z max. RandomComplex[range, n] gives a list of n pseudorandom complex numbers. RandomComplex[range, {n 1, n 2, }] gives an n 1 n 2 array of pseudorandom complex numbers. In[123]:= RandomInteger[10] losowa liczba całkowita RandomInteger[10] losowa liczba całkowita RandomInteger[10] losowa liczba całkowita RandomInteger[10] losowa liczba całkowita Out[123]= 5 Out[124]= 4 Out[125]= 1 Out[126]= 2 In[127]:= SeedRandom[5] ziarno generatora liczb los RandomInteger[10] losowa liczba całkowita SeedRandom[5] ziarno generatora liczb los RandomInteger[10] losowa liczba całkowita SeedRandom[5] ziarno generatora liczb los RandomInteger[10] losowa liczba całkowita SeedRandom[5] ziarno generatora liczb los RandomInteger[10] losowa liczba całkowita Out[128]= 0 Out[130]= 0 Out[132]= 0 Out[134]= 0
27 wyklad5_2017_notes.nb 27 In[135]:= RandomReal[{0, 1}, 12] losowa liczba rzeczywista Out[135]= { , , , , , , , , , , , } Przykład In[136]:=? Line Line[{p 1, p 2, }] represents the line segments joining a sequence for points p i. Line[{{p 11, p 12, }, {p 21, }, }] represents a collection of lines. In[137]:=? Point Point[p] is a graphics and geometry primitive that represents a point at p. Point[{p 1, p 2, }] represents a collection of points. In[138]:= RandomReal[{-1, 1}, 2] losowa liczba rzeczywista Out[138]= { , }
28 28 wyklad5_2017_notes.nb In[139]:= L =. L = {}; Array[ tablica wielowymiarowa AppendTo[L, { RGBColor[ RandomReal[{0, 1}, 3]], RandomReal[{-1, 1}, 2]}] &, 400]; dołącz na końc kolor RGB losowa liczba rzeczywista losowa liczba rzeczywista Map[{ PointSize[ Large], zast rozmiar kro duży Graphics /@ %; grafika ListAnimate[%] animuj liste First@#, pierwszy Point[#[[2]]]} &, %, {2}]; punkt Out[144]= Funkcja dopasowująca: Fit Fit In[145]:=? Fit Fit[data, funs, vars] finds a least-squares fit to a list of data as a linear combination of the functions funs of variables vars.
29 wyklad5_2017_notes.nb 29 In[146]:= czas = Table[i, {i, 0, 9}] tabela Out[146]= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} In[147]:= odleglosc = {0, 1.5, 6.0, 13.5, 24.0, 37.5, 54.0, 73.5, 96.0, 121.5} Out[147]= {0, 1.5, 6., 13.5, 24., 37.5, 54., 73.5, 96., 121.5} In[148]:= Options[ TableForm] opcje w formie tabeli Out[148]= {TableAlignments Automatic, TableDepth, TableDirections Column, TableHeadings None, TableSpacing Automatic} In[149]:= vwdata = TableForm[%,, w formie tabeli Transpose[{czas, odleglosc}] transpozycja TableHeadings { None, { "Czas", "Odległość"}}] nagłówki tabeli żaden Out[149]= Out[150]//TableForm= Czas Odległość
30 30 wyklad5_2017_notes.nb In[151]:= TeXForm[%] zapis w TeX-u Out[151]//TeXForm= \left( \begin{array}{cc} 0 & 0 \\ 1 & 1.5 \\ 2 & 6. \\ 3 & 13.5 \\ 4 & 24. \\ 5 & 37.5 \\ 6 & 54. \\ 7 & 73.5 \\ 8 & 96. \\ 9 & \\ \end{array} \right) In[152]:= ListPlot[vwdata] wykres danych z listy Out[152]= Chop In[153]:= wynik = Fit[vwdata, {1, t, t^2, t^3}, t] dopasuj Out[153]= t t t In[154]:=? Chop Chop[expr] replaces approximate real numbers in expr that are close to zero by the exact integer 0. In[155]:= Chop 10^ -10 // N zamiana bardzo małej przybliże Out[155]=
31 wyklad5_2017_notes.nb 31 In[156]:= Chop[wynik] zamiana bardzo małej liczby na zero Out[156]= 1.5 t 2 In[157]:= Show[ ListPlot[vwdata], Plot[ Chop[wynik], {t, 0, 10}]] pokaż wykres danych z listy wyk zamiana bardzo małej liczby na zero Out[157]=
32 32 wyklad5_2017_notes.nb Dopasowanie do punktów In[158]:= hnew[x_] := Sin[2 π x] 1 + RandomVariate[ NormalDistribution[0, 0.5]] ; sinus próba losowa rozkład normalny {#, hnew[#]} & /@ {0.1, 0.2, 0.4, 0.5, 0.7, 0.9}; {#, hnew[#]} & /@ {0.15, 0.6, 1.1}; MapThread[ Function[ ListPlot[#1, PlotStyle {#2, PointSize[ Large]}, zastosuj w funkcja wykres danych styl grafiki rozmiar kro duży PlotRange {{0, 1.5}, {-0.5, 2}}]], {{%%, %}, { Pink, Blue}}] zakres wykresu różowy niebieski line[n_] := Fit %%%%, Array x^ # - 1 &, n, x ; dopasuj tablica wielowymiarowa {line[6], line[5], line[3]}; obraz1 = Show[ First[%%%], Plot[%, {x, 0, 1.2}, pokaż pierwszy wykres PlotStyle {{ Blue, Thick}, { Black, Thick}, { Orange, Thick}}]] styl grafiki niebi gruby czarny gruby pomara gruby Export["obraz1.eps", %]; eksportuj Show[%%, Last[%%%%%]] pokaż ostatni Export["obraz2.eps", %]; eksportuj obraz3 = Show[%%, pokaż Export["obraz3.eps", %]; eksportuj Plot[ Sin[2 π x], {x, 0, 1.5}, PlotStyle { Pink, Thick}]] wykres sinus styl grafiki różowy gruby Out[161]= ,
33 wyklad5_2017_notes.nb Out[164]= Out[166]= Out[168]= In[170]:= Clear[data, datanew] wyczyść Użyte funkcje In[171]:=? Export Export[" file.ext", expr] exports data to a file, converting it to the format corresponding to the file extension ext. Export[ file, expr, " format"] exports data in the specified format. Export[ file, exprs, elems] exports data by treating exprs as elements specified by elems.
34 34 wyklad5_2017_notes.nb In[172]:=? Show Show[graphics, options] shows graphics with the specified options added. Show[g 1, g 2, ] shows several graphics combined. In[173]:=?? RandomVariate RandomVariate[dist] gives a pseudorandom variate from the symbolic distribution dist. RandomVariate[dist, n] gives a list of n pseudorandom variates from the symbolic distribution dist. RandomVariate[dist, {n 1, n 2, }] gives an n 1 n 2 array of pseudorandom variates from the symbolic distribution dist. Attributes RandomVariate = {Protected} Options RandomVariate = Method Automatic, WorkingPrecision Automatic In[174]:=? NormalDistribution NormalDistribution[μ, σ] represents a normal (Gaussian) distribution with mean μ and standard deviation σ. NormalDistribution[] represents a normal distribution with zero mean and unit standard deviation. In[175]:= Plot[ Table[ PDF[ NormalDistribution[0, σ], x], {σ, {.75, 1, 2}}] // Evaluate, wyk tabela fu rozkład normalny oblicz {x, -6, 6}, Filling Axis] wypełnienie oś Out[175]= Obwody Elektryczne In[176]:= WolframAlpha["Gustav Kirchhoff"] zapytaj WolframAlpha Input interpretation: Gustav Kirchhoff (physicist) Basic information:
35 wyklad5_2017_notes.nb 35 full name date of birth place of birth date of death place of death Gustav Robert Kirchhoff Friday, March 12, 1824 (193 years ago) Konigsberg, Bavaria, Germany Monday, October 17, 1887 (age: 63 years) (130 years ago) Berlin, Berlin, Germany Image: Out[176]= Timeline: Gustav Kirchhoff Include today Scientific contributions: Physics: Kirchhoff's current law Kirchhoff's voltage law Ohm's law Wikipedia summary: Gustav Robert Kirchhoff (12 March October 1887) was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black body radiation by heated objects. Full entry» Wikipedia page hits history: Log scale (in hits per day) (based on weekly averages of daily hits to English-language "Gustav Kirchhoff" page)
36 36 wyklad5_2017_notes.nb Pierwsze Prawo Kirchhoffa In[177]:= WolframAlpha["Kirchhoff's current law"] zapytaj WolframAlpha Input interpretation: Kirchhoff's current law (physical principle) Description: At any node in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node. Alternate names: KCL Kirchhoff's first rule Kirchhoff's junction rule Out[177]= Kirchhoff's nodal rule Kirchhoff's point rule History: formulation date formulator 1845 (172 years ago) Gustav Kirchhoff Associated equation: n I k 0 k=1 Classes: Kirchhoff's rules laws of physics
37 wyklad5_2017_notes.nb 37 Drugie Prawo Kirchhoffa In[178]:= WolframAlpha["Kirchhoff's voltage law"] zapytaj WolframAlpha Input interpretation: Kirchhoff's voltage law (physical principle) Description: The signed sum of the voltages around any closed circuit must be zero. Alternate names: Kirchhoff's loop rule Kirchhoff's mesh rule Kirchhoff's second rule Out[178]= KVL History: formulation date formulator 1845 (172 years ago) Gustav Kirchhoff Associated equation: n V k 0 k=1 Classes: Kirchhoff's rules laws of physics Prawo Ohma In[179]:= WolframAlpha["Georg Ohm"] zapytaj WolframAlpha Input interpretation: Georg Ohm (physicist)
38 38 wyklad5_2017_notes.nb Basic information: full name date of birth place of birth date of death place of death Georg Simon Ohm Monday, March 16, 1789 (228 years ago) Erlangen, Bavaria, Germany Thursday, July 6, 1854 (age: 65 years) (163 years ago) Munich, Bavaria, Germany Image: Timeline: Georg Ohm Include today Out[179]= Familial relationships: Parents: Johann Wolfgang Ohm Maria Elizabeth Beck Siblings: Martin Ohm Elizabeth Barbara Ohm Scientific contributions: Physics: Ohm's law Watt's law for electrical power Wikipedia summary: Georg Simon Ohm (16 March July 1854) was a German physicist and mathematician. As a school teacher, Ohm began his research with the new electrochemical cell, invented by Italian scientist Alessandro Volta. Using equipment of his own creation, Ohm found that there is a direct proportionality between the potential difference (voltage) applied across a conductor and the resultan electric current. This relationship is known as Ohm's law. Full entry» Wikipedia page hits history: Log scale
39 wyklad5_2017_notes.nb (in hits per day) (based on weekly averages of daily hits to English-language "Georg Ohm" page) In[180]:= WolframAlpha["Ohm's law"] zapytaj WolframAlpha Assuming Ohm's law is referring to a physical principle Use as a formula instead Input interpretation: Ohm's law (physical principle) Description: The current through a conductor is directly proportional to the voltage across the conductor and inversely proportional to its resistance. Alternate description: A generalization also sometimes known as Ohm's law (but actually due to Kirchhoff) states the the current density is proportional to the product of conductivity and electric field strength. Out[180]= History: More formulation date formulator 1827 (190 years ago) Georg Ohm additional people involved Henry Cavendish Gustav Kirchhoff Associated equations: I V/R J σe Class: laws of physics
40 40 wyklad5_2017_notes.nb Rozwiązanie obwodu z prądem Wyznacz natężenia prądu na opornikach R 1, R 2, R 3, R 4, R 5, R 6, znając napięcie U. R 5 R 6 I 5 I 6 I 4 R 4 I 2 I 3 R1 I 1 R 2 R 3 U i 1 - i 2 - i 5 = 0 i 6 - i 4 - i 5 = 0 i 2 - i 3 - i 4 = 0 -i 5 R 5 + i 4 R 4 + i 2 R 5 = 0 -i 4 R 4 - i 6 R 6 + i 3 R 3 = 0 -i 2 R 2 - i 3 R 3 + U - i 1 R 1 = 0 In[181]:=? Solve Solve[expr, vars] attempts to solve the system expr of equations or inequalities for the variables vars. Solve[expr, vars, dom] solves over the domain dom. Common choices of dom are Reals, Integers, and Complexes. In[182]:= rownania =. rownania = {i1 - i2 - i5 == 0, i6 - i4 - i5 0, i2 - i3 - i4 0, -i5 R5 + i4 R4 + i2 R5 0, -i4 R4 - i6 R6 + i3 R3 0, -i2 R2 + i3 R3 + U - i1 R1 0} Out[183]= {i1 - i2 - i5 0, -i4 - i5 + i6 0, i2 - i3 - i4 0, i2 R5 + i4 R4 - i5 R5 0, i3 R3 - i4 R4 - i6 R6 0, -i1 R1 - i2 R2 + i3 R3 + U 0}
41 wyklad5_2017_notes.nb 41 In[184]:= Clear[i1, i2, i3, i4, i5, i6, R1, R2, R3, R4, R5, R6, rozwiazanie] wyczyść Solve[rownania, rozwiąż równanie {i1, i2, i3, i4, i5, i6} ] // Simplify uprość rozwiazanie = Flatten@% spłaszcz Out[185]= {{i1 -((U (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i2 -((U (R3 R5 + R4 (R5 + R6) + R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i3 (U (R4 (R5 + R6) + 2 R5 R6))/(R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) + R2 (R3 R5 + R4 (R5 + R6) + R5 R6) - R3 (R4 (R5 + R6) + 2 R5 R6)), i4 (R5 U (R6 - R3))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)), i5 -((U (R3 (R4 + R5) + R5 (R4 + R6)))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i6 -((U (R3 (R4 + 2 R5) + R4 R5))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)))}} Out[186]= {i1 -((U (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i2 -((U (R3 R5 + R4 (R5 + R6) + R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i3 (U (R4 (R5 + R6) + 2 R5 R6))/(R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) + R2 (R3 R5 + R4 (R5 + R6) + R5 R6) - R3 (R4 (R5 + R6) + 2 R5 R6)), i4 (R5 U (R6 - R3))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)), i5 -((U (R3 (R4 + R5) + R5 (R4 + R6)))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), i6 -((U (R3 (R4 + 2 R5) + R4 R5))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)))} Programy obliczeniowe (symboliczne) często mają błędy, sprawdźmy wynik In[187]:= rownania /. rozwiazanie // Simplify uprość Out[187]= {True, True, True, True, True, True} Załóżmy, że wszystkie oporniki charakteryzują sie tą samą impedancją In[188]:= rozwiazanie /. {R1 R, R2 R, R3 R, R4 R, R5 R, R6 R} Out[188]= i1 U R, i2 U 2 R, i3 U U, i4 0, i5 2 R 2 R, i6 U 2 R
42 42 wyklad5_2017_notes.nb Rysujemy wartości natężeń In[189]:= Prady[U_, {R1_, R2_, R3_, R4_, R5_, R6_}] := Evaluate[{i1, i2, i3, i4, i5, i6} /. rozwiazanie] oblicz In[190]:= Prady[10, {1, 1, 1, 1, 1, 1}] Out[190]= {10, 5, 5, 0, 5, 5} In[191]:= DiscretePlot[Prady[10, {1, 1, 1, 1, 1, 1}][[i]], {i, Array[# &, 6]}, ExtentSize 0.5] wykres dyskretny tablica wielowymia wielkość zakresu Out[191]= In[192]:= Out[192]= Array[{ StringJoin["i", ToString[#]], #} &, 6] tablica połącz ciągi znaków przemień na ciąg znaków i1 1 i2 2 i3 3 i4 4 i5 5 i6 6 In[193]:= Out[193]= Array[{"i" <> ToString[#], #} &, 6] tablica wielowy przemień na ciąg znaków i1 1 i2 2 i3 3 i4 4 i5 5 i6 6 In[194]:= 5 4 // Out[194]//FullForm= FullForm pełna forma Subscript[5, 4]
43 wyklad5_2017_notes.nb 43 In[195]:= DiscretePlot[Prady[10, {1, 1, 1, 1, 1, 1}][[i]], {i, Array[# &, 6]}, wykres dyskretny tablica wielowymiarowa ExtentSize 0.5, wielkość zakresu Ticks { Array[{#, znaczki n tablica wie Subscript["i", #]} &, 6], indeks dolny Automatic}] automatyczny Out[195]= 2 1 i 1 i 2 i 3 i 4 i 5 i 6 In[196]:= {i1, i2, i3, i4, i5, i6} /. rozwiazanie /. {R1 #, R2 -> #, R3 #, R4 #, R5 #, R6 #} &@10 Out[196]= U 10, U 20, U 20, 0, U 20, U 20 In[197]:= {i1, i2, i3, i4, i5, i6} /. rozwiazanie /. {R1, R2, R3, R4, R5, R6} &@10 ReplaceAll: {R1, R2, R3, R4, R5, R6} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing. Out[197]= {-((U (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), -((U (R3 R5 + R4 (R5 + R6) + R5 R6))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), (U (R4 (R5 + R6) + 2 R5 R6))/(R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) + R2 (R3 R5 + R4 (R5 + R6) + R5 R6) - R3 (R4 (R5 + R6) + 2 R5 R6)), (R5 U (R6 - R3))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)), -((U (R3 (R4 + R5) + R5 (R4 + R6)))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6))), -((U (R3 (R4 + 2 R5) + R4 R5))/(-R1 (R3 (R4 + 2 R5) + R4 (2 R5 + R6) + 2 R5 R6) - R2 (R3 R5 + R4 (R5 + R6) + R5 R6) + R3 (R4 (R5 + R6) + 2 R5 R6)))} /. {R1, R2, R3, R4, R5, R6} In[198]:= Outer[ Rule, {R1, R2, R3, R4, R5, R6}, {10}] zewnę reguła Out[198]= {{R1 10}, {R2 10}, {R3 10}, {R4 10}, {R5 10}, {R6 10}}
44 44 wyklad5_2017_notes.nb In[199]:= Outer[ Rule, {R1, R2, R3, R4, R5, R6}, {10}] spłaszcz zewnę reguła Out[199]= {R1 10, R2 10, R3 10, R4 10, R5 10, R6 10} In[200]:= {i1, i2, i3, i4, i5, i6} /. rozwiazanie /. Outer[ Rule, {R1, R2, R3, R4, R5, R6}, {10}] spłaszcz zewnę reguła Out[200]= U 10, U 20, U 20, 0, U 20, U 20 In[201]:= Manipulate[ zmieniaj DiscretePlot[Prady[10, {r1, r2, r3, r4, r5, r6}][[i]], wykres dyskretny {i, Array[# &, 6]}, tablica wielowymia Ticks { Array[{#, znaczki n tablica wie ExtentSize 0.5, wielkość zakresu PlotRange zakres wykresu Subscript["i", #]} &, 6], indeks dolny All, wszystko Automatic}], automatyczny {r1, , 10, 1}, {r2, , 10, 1}, {r3, , 10, 1}, {r4, , 10, 1}, {r5, , 10, 1}, {r6, , 10, 1}, {U, 0, 10}] r1 r2 r3 r4 r5 r6 U Out[201]= i 1 i 2 i 3 i 4 i 5 i 6
45 wyklad5_2017_notes.nb 45 In[202]:= Manipulate[ zmieniaj DiscretePlot[Prady[10, {r1, r2, r3, r4, r5, r6}][[i]], wykres dyskretny {i, Array[# &, 6]}, tablica wielowymia ExtentSize 0.5], {r1, , 10}, {r2, , 10}, wielkość zakresu {r3, , 10}, {r4, , 10}, {r5, , 10}, {r6, , 10}] r1 r2 r3 r4 r5 r6 Out[202]=
Wykład 6. Prawo Hooke a. Robert Hooke
 Wykład 6 Równania różniczkowe, funkcje DSolve oraz NDSolve. Wykres fazowy. Prawo Hooke a, drgania sprężyn. Ruch z oporem powietrza. In[1]:= ClearAll["Global`*"] wyczyść wszystko Prawo Hooke a Robert Hooke
Wykład 6 Równania różniczkowe, funkcje DSolve oraz NDSolve. Wykres fazowy. Prawo Hooke a, drgania sprężyn. Ruch z oporem powietrza. In[1]:= ClearAll["Global`*"] wyczyść wszystko Prawo Hooke a Robert Hooke
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Sin[Pi / 4] Log[2, 1024] Prime[10]
![Sin[Pi / 4] Log[2, 1024] Prime[10] Sin[Pi / 4] Log[2, 1024] Prime[10]](/thumbs/64/50895785.jpg) In[1]:= (* WSTĘP DO PAKIETU MATHEMATICA *) (* autorzy: Łukasz Płociniczak,Marek Teuerle*) (* Składnia: nazwy funkcji z wielkiej litery a argumenty w kwadratowych nawiasach. Wywołujemy wartość SHIFT+ENTER
In[1]:= (* WSTĘP DO PAKIETU MATHEMATICA *) (* autorzy: Łukasz Płociniczak,Marek Teuerle*) (* Składnia: nazwy funkcji z wielkiej litery a argumenty w kwadratowych nawiasach. Wywołujemy wartość SHIFT+ENTER
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Kurs Komputerowy S System Symboliczny Mathematica
 Kurs Komputerowy S System Symboliczny Mathematica Obliczenia numeryczne Dokladnosc i precyzja Precision[wartosc] SetPrecision[wartosc, precyzja] Accuracy[wartosc] SetAccuracy[wartosc, dokladnosc] MachinePrecision
Kurs Komputerowy S System Symboliczny Mathematica Obliczenia numeryczne Dokladnosc i precyzja Precision[wartosc] SetPrecision[wartosc, precyzja] Accuracy[wartosc] SetAccuracy[wartosc, dokladnosc] MachinePrecision
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
SzeregFouriera-Legendre a
 SzeregFouriera-Legendre a Szereg Fouriera-Legendre a : n=0 P n (t) f n Współczynniki f n = Pn (t) f (t) dt - Pn (t) 2 dt - = 2 n + Pn 2 - (t) f (t) dt Pn - (t) 2 dt = 2 2 n + Zadanie Policz kwadrat normy
SzeregFouriera-Legendre a Szereg Fouriera-Legendre a : n=0 P n (t) f n Współczynniki f n = Pn (t) f (t) dt - Pn (t) 2 dt - = 2 n + Pn 2 - (t) f (t) dt Pn - (t) 2 dt = 2 2 n + Zadanie Policz kwadrat normy
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Matematyka 3. Suma szeregu. Promień zbieżności szeregu. Przykład 1: Przykład 2: GenerateConditions
 Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y. 2. Współczynnik korelacji Pearsona
 KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Wykaz linii kolejowych, które są wyposażone w urzadzenia systemu ETCS
 Wykaz kolejowych, które są wyposażone w urzadzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
Wykaz kolejowych, które są wyposażone w urzadzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
Kurs Komputerowy S System Symboliczny Mathematica
 Kurs Komputerowy S System Symboliczny Mathematica Dodatek Struktura FullForm[] TreeForm[] Timing[] Apply[] In[4]:= w 3 x^2 5 x 4 Out[4]= 4 5 x 3 x 2 In[5]:= FullForm w Out[5]//FullForm= Plus 4, Times 5,
Kurs Komputerowy S System Symboliczny Mathematica Dodatek Struktura FullForm[] TreeForm[] Timing[] Apply[] In[4]:= w 3 x^2 5 x 4 Out[4]= 4 5 x 3 x 2 In[5]:= FullForm w Out[5]//FullForm= Plus 4, Times 5,
Steeple #3: Gödel s Silver Blaze Theorem. Selmer Bringsjord Are Humans Rational? Dec RPI Troy NY USA
 Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Wykaz linii kolejowych, które są wyposażone w urządzenia systemu ETCS
 Wykaz kolejowych, które są wyposażone w urządzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
Wykaz kolejowych, które są wyposażone w urządzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH
 POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
SG-MICRO... SPRĘŻYNY GAZOWE P.103
 SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
Pobieranie argumentów wiersza polecenia
 Pobieranie argumentów wiersza polecenia 2. Argumenty wiersza polecenia Lista argumentów Lista argumentów zawiera cały wiersz poleceń, łącznie z nazwą programu i wszystkimi dostarczonymi argumentami. Przykłady:
Pobieranie argumentów wiersza polecenia 2. Argumenty wiersza polecenia Lista argumentów Lista argumentów zawiera cały wiersz poleceń, łącznie z nazwą programu i wszystkimi dostarczonymi argumentami. Przykłady:
Raport bieżący: 44/2018 Data: g. 21:03 Skrócona nazwa emitenta: SERINUS ENERGY plc
 Raport bieżący: 44/2018 Data: 2018-05-23 g. 21:03 Skrócona nazwa emitenta: SERINUS ENERGY plc Temat: Zawiadomienie o zmianie udziału w ogólnej liczbie głosów w Serinus Energy plc Podstawa prawna: Inne
Raport bieżący: 44/2018 Data: 2018-05-23 g. 21:03 Skrócona nazwa emitenta: SERINUS ENERGY plc Temat: Zawiadomienie o zmianie udziału w ogólnej liczbie głosów w Serinus Energy plc Podstawa prawna: Inne
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
DM-ML, DM-FL. Auxiliary Equipment and Accessories. Damper Drives. Dimensions. Descritpion
 DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Inverse problems - Introduction - Probabilistic approach
 Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Z-ZIP Równania Różniczkowe. Differential Equations
 MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo
 POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
Zmiany techniczne wprowadzone w wersji Comarch ERP Altum
 Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
Polska Szkoła Weekendowa, Arklow, Co. Wicklow KWESTIONRIUSZ OSOBOWY DZIECKA CHILD RECORD FORM
 KWESTIONRIUSZ OSOBOWY DZIECKA CHILD RECORD FORM 1. Imię i nazwisko dziecka / Child's name... 2. Adres / Address... 3. Data urodzenia / Date of birth... 4. Imię i nazwisko matki /Mother's name... 5. Adres
KWESTIONRIUSZ OSOBOWY DZIECKA CHILD RECORD FORM 1. Imię i nazwisko dziecka / Child's name... 2. Adres / Address... 3. Data urodzenia / Date of birth... 4. Imię i nazwisko matki /Mother's name... 5. Adres
Tematyka do egzaminu ustnego z matematyki. 3 semestr LO dla dorosłych
 Tematyka do egzaminu ustnego z matematyki 3 semestr LO dla dorosłych I. Sumy algebraiczne 1. Dodawanie i odejmowanie sum algebraicznych 2. Mnożenie sum algebraicznych 3. Wzory skróconego mnożenia - zastosowanie
Tematyka do egzaminu ustnego z matematyki 3 semestr LO dla dorosłych I. Sumy algebraiczne 1. Dodawanie i odejmowanie sum algebraicznych 2. Mnożenie sum algebraicznych 3. Wzory skróconego mnożenia - zastosowanie
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Lecture 18 Review for Exam 1
 Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
OBWIESZCZENIE MINISTRA INFRASTRUKTURY. z dnia 18 kwietnia 2005 r.
 OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD I PSPICE
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
Arrays -II. Arrays. Outline ECE Cal Poly Pomona Electrical & Computer Engineering. Introduction
 ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
Podstawowe I/O Liczby
 Podstawowe I/O Liczby Informatyka Jolanta Bachan Implementacja algorytmów, cd. I/O: Keyboard in, screen out, no loops Jolanta Bachan 2 Implementacja algorytmów, cd. I/O: Keyboard in, screen out, no loops
Podstawowe I/O Liczby Informatyka Jolanta Bachan Implementacja algorytmów, cd. I/O: Keyboard in, screen out, no loops Jolanta Bachan 2 Implementacja algorytmów, cd. I/O: Keyboard in, screen out, no loops
METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
YKXS, YKXSżo 0,6/1 kv. Kable elektroenergetyczne z izolacją XLPE. Norma IEC :2004. Konstrukcja. Zastosowanie. Właściwości
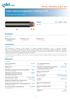 Kable elektroenergetyczne z izolacją XLPE Power cables with XLPE insulation YKXS, YKXSżo 0,6/1 kv Norma Standard IEC - 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca miedziana Copper Izolacja
Kable elektroenergetyczne z izolacją XLPE Power cables with XLPE insulation YKXS, YKXSżo 0,6/1 kv Norma Standard IEC - 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca miedziana Copper Izolacja
YAKXS, YAKXSżo 0,6/1 kv. Kable elektroenergetyczne z izolacją XLPE. Norma IEC :2004. Konstrukcja. Zastosowanie.
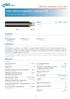 Kable elektroenergetyczne z izolacją XLPE Power cables with XLPE insulation YKXS, YKXSżo 0,6/1 kv Norma Standard IEC - 60502-1:04 3 2 1 Konstrukcja Construction Żyła przewodząca aluminiowa luminium Izolacja
Kable elektroenergetyczne z izolacją XLPE Power cables with XLPE insulation YKXS, YKXSżo 0,6/1 kv Norma Standard IEC - 60502-1:04 3 2 1 Konstrukcja Construction Żyła przewodząca aluminiowa luminium Izolacja
Machine Learning for Data Science (CS4786) Lecture 24. Differential Privacy and Re-useable Holdout
 Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
 !850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
!850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to students
 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI FUNKCJE KWADRATOWE PARAMETRY
 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI FUNKCJE KWADRATOWE PARAMETRY 1 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI ZADANIE 1 Wyznacz wzór funkcji f (x) = 2x
www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI FUNKCJE KWADRATOWE PARAMETRY 1 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI ZADANIE 1 Wyznacz wzór funkcji f (x) = 2x
Has the heat wave frequency or intensity changed in Poland since 1950?
 Has the heat wave frequency or intensity changed in Poland since 1950? Joanna Wibig Department of Meteorology and Climatology, University of Lodz, Poland OUTLINE: Motivation Data Heat wave frequency measures
Has the heat wave frequency or intensity changed in Poland since 1950? Joanna Wibig Department of Meteorology and Climatology, University of Lodz, Poland OUTLINE: Motivation Data Heat wave frequency measures
Surname. Other Names. For Examiner s Use Centre Number. Candidate Number. Candidate Signature
 A Surname _ Other Names For Examiner s Use Centre Number Candidate Number Candidate Signature Polish Unit 1 PLSH1 General Certificate of Education Advanced Subsidiary Examination June 2014 Reading and
A Surname _ Other Names For Examiner s Use Centre Number Candidate Number Candidate Signature Polish Unit 1 PLSH1 General Certificate of Education Advanced Subsidiary Examination June 2014 Reading and
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Wstęp do programowania
 Wstęp do programowania Programowanie funkcyjne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. XIV Jesień 2013 1 / 25 Paradygmaty programowania Programowanie imperatywne Program
Wstęp do programowania Programowanie funkcyjne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. XIV Jesień 2013 1 / 25 Paradygmaty programowania Programowanie imperatywne Program
YAKY, YAKYżo 0,6/1 kv. Kable elektroenergetyczne z izolacją PVC. Norma IEC - 60502-1:2004. Konstrukcja. Zastosowanie. Właściwości
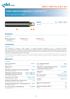 Kable elektroenergetyczne z izolacją PVC Power cables with PVC insulation YKY, YKYżo 0,6/1 kv Norma Standard IEC - 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca aluminiowa luminium Izolacja
Kable elektroenergetyczne z izolacją PVC Power cables with PVC insulation YKY, YKYżo 0,6/1 kv Norma Standard IEC - 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca aluminiowa luminium Izolacja
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Liczby zespolone to (uporządkowane) pary liczb rzeczywistych, dla których dodawanie i mnożenie jest określone wzorami:
 Przytaczając definicję liczb zespolonych, wyznacznika, wypowiedź twierdzenia Cramera oraz Kroneckera-Capelliego, korzystałem z I tomu wykładów Prof. Andrzeja Staruszkiewicza dla fizyków: ALGEBRA I GEOMETRIA,
Przytaczając definicję liczb zespolonych, wyznacznika, wypowiedź twierdzenia Cramera oraz Kroneckera-Capelliego, korzystałem z I tomu wykładów Prof. Andrzeja Staruszkiewicza dla fizyków: ALGEBRA I GEOMETRIA,
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Formularz recenzji magazynu. Journal of Corporate Responsibility and Leadership Review Form
 Formularz recenzji magazynu Review Form Identyfikator magazynu/ Journal identification number: Tytuł artykułu/ Paper title: Recenzent/ Reviewer: (imię i nazwisko, stopień naukowy/name and surname, academic
Formularz recenzji magazynu Review Form Identyfikator magazynu/ Journal identification number: Tytuł artykułu/ Paper title: Recenzent/ Reviewer: (imię i nazwisko, stopień naukowy/name and surname, academic
BULLETIN 2 II TRAINING CAMP POLISH OPEN MTBO CHAMPIONSHIPS 19-22.06.2014 MICHAŁOWO 23-29.06.2014 TRAINING CAMP WORLD MTB ORIENTEERING CHAMPIONSHIPS
 BULLETIN 2 II TRAINING CAMP POLISH OPEN MTBO CHAMPIONSHIPS 19-22.06.2014 MICHAŁOWO 23-29.06.2014 TRAINING CAMP WORLD MTB ORIENTEERING CHAMPIONSHIPS MASTERS WORLD MTB ORIENTEERING CHAMPIONSHIPS MTB ORIENTEERING
BULLETIN 2 II TRAINING CAMP POLISH OPEN MTBO CHAMPIONSHIPS 19-22.06.2014 MICHAŁOWO 23-29.06.2014 TRAINING CAMP WORLD MTB ORIENTEERING CHAMPIONSHIPS MASTERS WORLD MTB ORIENTEERING CHAMPIONSHIPS MTB ORIENTEERING
PLSH1 (JUN14PLSH101) General Certificate of Education Advanced Subsidiary Examination June 2014. Reading and Writing TOTAL
 Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials Section Mark Polish Unit 1 Reading and Writing General Certificate of Education Advanced Subsidiary
Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials Section Mark Polish Unit 1 Reading and Writing General Certificate of Education Advanced Subsidiary
Cracow University of Economics Poland
 Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:.
 ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX
 UNIWERSYTETU BIBLIOTEKA IEGO UNIWERSYTETU IEGO Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX 1. Make a new connection Open the System Preferences by going to the Apple menu
UNIWERSYTETU BIBLIOTEKA IEGO UNIWERSYTETU IEGO Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX 1. Make a new connection Open the System Preferences by going to the Apple menu
Wstęp do informatyki Ćwiczenia. Piotr Fulmański
 Wstęp do informatyki Ćwiczenia Piotr Fulmański Piotr Fulmański 1 e-mail 1: fulmanp@math.uni.lodz.pl Wydział Matematyki i Informatyki, Uniwersytet Łódzki Banacha 22, 90-238, Łódź Polska Data ostaniej modyfikacji:
Wstęp do informatyki Ćwiczenia Piotr Fulmański Piotr Fulmański 1 e-mail 1: fulmanp@math.uni.lodz.pl Wydział Matematyki i Informatyki, Uniwersytet Łódzki Banacha 22, 90-238, Łódź Polska Data ostaniej modyfikacji:
YKY, YKYżo 0,6/1 kv. Kable elektroenergetyczne z izolacją PVC. Norma. 10 mm² PN-HD 603 S1:3G >10 mm² IEC :2004. Konstrukcja.
 Kable elektroenergetyczne z izolacją PVC Power cables with PVC insulation YKY, YKYżo 0,6/1 kv Norma Standard 10 ² PN-HD 603 S1:3G >10 ² IEC 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca
Kable elektroenergetyczne z izolacją PVC Power cables with PVC insulation YKY, YKYżo 0,6/1 kv Norma Standard 10 ² PN-HD 603 S1:3G >10 ² IEC 60502-1:2004 3 2 1 Konstrukcja Construction Żyła przewodząca
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Wydział Fizyki, Astronomii i Informatyki Stosowanej Uniwersytet Mikołaja Kopernika w Toruniu
 IONS-14 / OPTO Meeting For Young Researchers 2013 Khet Tournament On 3-6 July 2013 at the Faculty of Physics, Astronomy and Informatics of Nicolaus Copernicus University in Torun (Poland) there were two
IONS-14 / OPTO Meeting For Young Researchers 2013 Khet Tournament On 3-6 July 2013 at the Faculty of Physics, Astronomy and Informatics of Nicolaus Copernicus University in Torun (Poland) there were two
THE RAIL RATES valid from 1st October 2015
 RAIL TARIFF This Rail Tariff is an integral part of intermodal transport arrangement service provided by PCC Intermodal S.A. and therefore it cannot be used as a standalone offer, only in combination with
RAIL TARIFF This Rail Tariff is an integral part of intermodal transport arrangement service provided by PCC Intermodal S.A. and therefore it cannot be used as a standalone offer, only in combination with
MAGNESY KATALOG d e s i g n p r o d u c e d e l i v e r
 MAGNESY KATALOG design produce deliver MAGNET 0,4 / 0,75MM owal, prostokąt, koło, kwadrat od 50 sztuk Flexible magnet 0.4 = strength example: able to hold one A4 sheet. 0.75 = strength example: able to
MAGNESY KATALOG design produce deliver MAGNET 0,4 / 0,75MM owal, prostokąt, koło, kwadrat od 50 sztuk Flexible magnet 0.4 = strength example: able to hold one A4 sheet. 0.75 = strength example: able to
Wyk lad 8: Leniwe metody klasyfikacji
 Wyk lad 8: Leniwe metody Wydzia l MIM, Uniwersytet Warszawski Outline 1 2 lazy vs. eager learning lazy vs. eager learning Kiedy stosować leniwe techniki? Eager learning: Buduje globalna hipoteze Zaleta:
Wyk lad 8: Leniwe metody Wydzia l MIM, Uniwersytet Warszawski Outline 1 2 lazy vs. eager learning lazy vs. eager learning Kiedy stosować leniwe techniki? Eager learning: Buduje globalna hipoteze Zaleta:
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A03 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Dany jest ciąg arytmetyczny (a
Arkusz A03 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Dany jest ciąg arytmetyczny (a
HAPPY ANIMALS L01 HAPPY ANIMALS L03 HAPPY ANIMALS L05 HAPPY ANIMALS L07
 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L07 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K ZW W8 W7 Ø x 6 szt. / pcs Ø7 x 70 Narzędzia / Tools DO MONTAŻU POTRZEBNE
HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L07 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K ZW W8 W7 Ø x 6 szt. / pcs Ø7 x 70 Narzędzia / Tools DO MONTAŻU POTRZEBNE
HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08
 HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K O G ZW W8 W4 20 szt. / pcs 4 szt. / pcs 4 szt. / pcs 4 szt. / pcs
HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K O G ZW W8 W4 20 szt. / pcs 4 szt. / pcs 4 szt. / pcs 4 szt. / pcs
MS Visual Studio 2005 Team Suite - Performance Tool
 MS Visual Studio 2005 Team Suite - Performance Tool przygotował: Krzysztof Jurczuk Politechnika Białostocka Wydział Informatyki Katedra Oprogramowania ul. Wiejska 45A 15-351 Białystok Streszczenie: Dokument
MS Visual Studio 2005 Team Suite - Performance Tool przygotował: Krzysztof Jurczuk Politechnika Białostocka Wydział Informatyki Katedra Oprogramowania ul. Wiejska 45A 15-351 Białystok Streszczenie: Dokument
Rev Źródło:
 KAmduino UNO Rev. 20190119182847 Źródło: http://wiki.kamamilabs.com/index.php/kamduino_uno Spis treści Basic features and parameters... 1 Standard equipment... 2 Electrical schematics... 3 AVR ATmega328P
KAmduino UNO Rev. 20190119182847 Źródło: http://wiki.kamamilabs.com/index.php/kamduino_uno Spis treści Basic features and parameters... 1 Standard equipment... 2 Electrical schematics... 3 AVR ATmega328P
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
photo graphic Jan Witkowski Project for exhibition compositions typography colors : +48 506 780 943 : janwi@janwi.com
 Jan Witkowski : +48 506 780 943 : janwi@janwi.com Project for exhibition photo graphic compositions typography colors Berlin London Paris Barcelona Vienna Prague Krakow Zakopane Jan Witkowski ARTIST FROM
Jan Witkowski : +48 506 780 943 : janwi@janwi.com Project for exhibition photo graphic compositions typography colors Berlin London Paris Barcelona Vienna Prague Krakow Zakopane Jan Witkowski ARTIST FROM
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
RECREATION ZONE Fall-Winter
 www.centremeredith.ca RECREATION ZONE Fall-Winter 2017-2018 Program Sports program Cultural program Day camp $10 /person 6 New! Semi Private Learn to Skate Lessons: Adults Interested in learning how
www.centremeredith.ca RECREATION ZONE Fall-Winter 2017-2018 Program Sports program Cultural program Day camp $10 /person 6 New! Semi Private Learn to Skate Lessons: Adults Interested in learning how
Bazy danych Ćwiczenia z SQL
 Bazy danych Ćwiczenia z SQL W ćwiczeniach wykorzystano przyk adowy schemat bazy danych dostarczany z Personal Oracle 8 Definicję schematu i dane tabel zawiera plik bdemobld sql (c) 2001 Katedra Informatyki
Bazy danych Ćwiczenia z SQL W ćwiczeniach wykorzystano przyk adowy schemat bazy danych dostarczany z Personal Oracle 8 Definicję schematu i dane tabel zawiera plik bdemobld sql (c) 2001 Katedra Informatyki
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Admission to the first and only in the swietokrzyskie province Bilingual High School and European high School for the school year 2019/2020
 Rekrutacja do pierwszego i jedynego w województwie świętokrzyskim Dwujęzycznego Liceum Ogólnokształcącego oraz Europejskiego Liceum Ogólnokształcącego na rok szkolny 2019/2020 Admission to the first and
Rekrutacja do pierwszego i jedynego w województwie świętokrzyskim Dwujęzycznego Liceum Ogólnokształcącego oraz Europejskiego Liceum Ogólnokształcącego na rok szkolny 2019/2020 Admission to the first and
ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM
 1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Instalacja Pakietu R
 Instalacja Pakietu R www.r-project.org wybór źródła wybór systemu operacyjnego: Download R for Windows opcja: install R for the first time opcja: Download R 3.3.3 for Windows uruchomienie R-3.3.3-win MAGDA
Instalacja Pakietu R www.r-project.org wybór źródła wybór systemu operacyjnego: Download R for Windows opcja: install R for the first time opcja: Download R 3.3.3 for Windows uruchomienie R-3.3.3-win MAGDA
HemoRec in Poland. Summary of bleeding episodes of haemophilia patients with inhibitor recorded in the years 2008 and 2009 04/2010
 HemoRec in Poland Summary of bleeding episodes of haemophilia patients with inhibitor recorded in the years 2008 and 2009 04/2010 Institute of Biostatistics and Analyses. Masaryk University. Brno Participating
HemoRec in Poland Summary of bleeding episodes of haemophilia patients with inhibitor recorded in the years 2008 and 2009 04/2010 Institute of Biostatistics and Analyses. Masaryk University. Brno Participating
Sargent Opens Sonairte Farmers' Market
 Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Cracow University of Economics Poland. Overview. Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005
 Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Python. Wprowadzenie. Jolanta Bachan
 Python Wprowadzenie Jolanta Bachan Zainstaluj i przetestuj Pythona https://www.python.org/downloads/ print 'Hello world!' operatory numeryczne: + - * / // % ** operatory porównania: ==!= > < >=
Python Wprowadzenie Jolanta Bachan Zainstaluj i przetestuj Pythona https://www.python.org/downloads/ print 'Hello world!' operatory numeryczne: + - * / // % ** operatory porównania: ==!= > < >=
Wprowadzenie do Pakietu R dla kierunku Zootechnika. Dr Magda Mielczarek Katedra Genetyki Uniwersytet Przyrodniczy we Wrocławiu
 Wprowadzenie do Pakietu R dla kierunku Zootechnika Dr Magda Mielczarek Katedra Genetyki Uniwersytet Przyrodniczy we Wrocławiu Instalacja Pakietu R www.r-project.org wybór źródła wybór systemu operacyjnego:
Wprowadzenie do Pakietu R dla kierunku Zootechnika Dr Magda Mielczarek Katedra Genetyki Uniwersytet Przyrodniczy we Wrocławiu Instalacja Pakietu R www.r-project.org wybór źródła wybór systemu operacyjnego:
