Fotometria i kolorymetria
|
|
|
- Franciszek Adamczyk
- 7 lat temu
- Przeglądów:
Transkrypt
1 13. x,y,y. Jednowymiarowe skale barw (długość fali dominującej i czystość bodźca; temperatura barwowa). Iluminanty i źródła normalne CIE. Układ CIE 1960 (u,v). Przestrzeń barw CIE 1964 (UVW). Układ CIE 1976 (u,v ). Układy CIELUV i CIELAB. Miary różnicy barw. Miejsce i termin konsultacji (zima 013/014): pokój 18/11 bud. A-1
2 Układ x,y,y Przedstawiony poprzednio układ CIE X,Y,Z to układ przestrzenny. Układ x,y to jego projekcja na płaszczyźnie. Ze względu na fakt, że informacja o całkowitej luminancji zawarta jest w składowej Y (ze względu na położenie punktów x i z na alychne, cała luminancja siedzi w Y!) używa się układu zwanego x,y,y. Określanie barwy przez podanie jej współrzędnych trójchromatycznych x,y oraz składowej Y jest częściej stosowane niż podawanie składowych X,Y,Z. Współrzędne x,y wyznaczają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje całe promieniowanie widmowe. Barwa ta ma czystość pobudzenia (patrz niżej) zerową, jest więc całkowicie nienasycona. Barwa monochromatyczna, widmowa, jest w pełni nasycona, ale formalnie ma jasność Y=0!
3 Układ x,y,y GAMUT zakres (paleta) barw możliwych do odwzorowania przez dane urządzenie.
4 Jednowymiarowe skale barw Określenie barwności (chromatyczności) wymaga dwóch parametrów dwóch współrzędnych chromatyczności lub odpowiedników odcienia i nasycenia. Jeżeli jednak zmienia się tylko odcień, to do określenia barwności wystarczy jeden parametr. Istnieje wiele takich skal barwy. Nie są one uniwersalne, ale upraszczają czynności klasyfikacyjne związane z wieloma zagadnieniami praktycznymi w produkcji i handlu. Przykład: określanie stężenia roztworu o znanym składzie, ale niewiadomej zawartości składnika. Konieczne jest sporządzenie wzorców barwnych o dużej trwałości.
5 Długość fali dominującej (dopełniającej) i czystość bodźca Każdy punkt na wykresie chromatyczności CIE 1931 można uznać za odpowiadający mieszaninie dwóch bodźców, w których jednym jest bodziec przyjęty umownie za achromatyczny, a drugim bodziec odpowiadający punktowi obwiedni pola barw fizycznych (spectrum locus). Istotnie, wszystkie bodźce uzyskane przez zmieszanie w różnych stosunkach promieniowania monochromatycznego z idealnie achromatycznym miałyby taki sam odcień, a zmieniałoby się tylko nasycenie.
6 Długość fali dominującej (dopełniającej) i czystość bodźca Pierwszy parametr: Długość fali dominującej λ d gdy punkt barwy czystej leży na krzywej barw widmowych lub powyżej trójkąta purpur; Długość fali dopełniającej gdy punkt ten leży na podstawie lub wewnątrz trójkąta purpur. Drugi parametr: Czystość pobudzenia (czystość kolorymetryczna): Czystość pobudzenia ma być liczona z tego z dwóch wzorów, którego licznik ma większą wartość: p e y y d y y w w lub czystość kolorymetryczna zaś: p e x x d x x w w p c p e yd y
7 Długość fali dominującej (dopełniającej) i czystość bodźca Zalety parametrów d i p e : - charakteryzują chromatyczność odpowiednikami psychofizycznymi cech subiektywnych barwy: odcienia i nasycenia (łatwiejsze kojarzenie nawet przez osoby nieznające zasad kolorymetrii); - ze znaku i wartości = d - d ( nowa barwa) można określić, który z odcieni jest w nadmiarze lub którym należy uzupełnić barwę produktu; ze znaku i wartości p=p e -p e z kolei można określić, w jakim stopniu i kierunku trzeba zmienić nasycenie barwnika.
8 PRZYPOMNIENIE! Skala temperatury barwowej Stosowana w kolorymetrii do określania chromatyczności promieniowania źródeł umownie achromatycznych, a w szczególności iluminantów i źródeł kolorymetrycznych normalnych. Skala ta jest oparta na ścisłej zależności pomiędzy temperaturą ciała czarnego i jego chromatycznością. Promieniowanie elektromagnetyczne składa się z mieszaniny fal elektromagnetycznych o różnej długości. Max Planck (1900) podał wzór na energię, przypadającą (w określonej temperaturze) na poszczególne długości fal promieniowania, emitowaną przez jednostkę powierzchni ciała doskonale czarnego w jednostce czasu: E, T 5 C1 C exp T 1
9 Skala temperatury barwowej Jeżeli zatem dowolne promieniowanie ma chromatyczność identyczną z jedną z tych, które są zawarte w gamie barw ciała czarnego, to barwa takiego promieniowania może być określona temperaturą odpowiadającą tej samej chromatyczności ciała czarnego temperaturą barwową. Widmowy względny rozkład określonego promieniowania może być przy tym zgodny z rozkładem ciała czarnego (nazywamy wtedy temperaturę barwową temperaturą rozkładu) lub odmienny (w wyniku metameryzmu). Temperaturę barwową podaje się w skali bezwzględnej (K) oraz w miredach (1 mired = 1 microreciprocal degree = 10 6 K -1 ).
10 Skala temperatury barwowej Temperaturę barwową podaje się w skali bezwzględnej (K) oraz w miredach (1 mired = 1 microreciprocal degree = 10 6 K -1 ). Takie odwrotności temperatur barwowych są rozmieszczone równomiernie na wykresie u,v CIE. 1 mired odpowiada bowiem ściśle, w zakresie całej skali od 0 do 1000 miredów, najmniejszej dostrzegalnej różnicy chromatyczności.
11 Skala temperatury barwowej Określenie temperatury barwowej źródła o względnym rozkładzie widmowym promieniowania odbiegającym znacznie od rozkładu widmowego ciała czarnego nie zawsze jest możliwe. Punkt chromatyczności takiego ciała może leżeć pod lub nad krzywą ciała czarnego, można zatem określić tylko przybliżoną zgodność barw. Pojęcie temperatury barwowej ma szeroki zastosowanie w technice źródeł światła (produkcja i oznaczanie wyrobów). Daje ono dostatecznie ścisłe określenie barwy światła źródeł lub różnic między barwami świateł dwóch źródeł odmiennych. Natomiast do porównania między sobą tzw. własności oddawania barw pojęcie to może mieć zastosowanie tylko wtedy, gdy porównywane źródła mają również zbliżony krzywych rozkładu widmowego promieniowania.
12 Iluminanty i źródła Iluminanty i źródła normalne CIE Iluminant promieniowanie o widmowym względnym rozkładzie energii określonym w zakresie długości fal zdolnych do wywierania wpływu na postrzeganie barw ciała (bo później wprowadzano inne iluminanty, niekoniecznie realizowane w postaci źródła fizycznego). CIE wprowadziła w 1931 r. trzy normalne źródła światła, oznaczone jako A, B i C, określone rozkładami widmowymi względnymi promieniowania oraz cechami fizycznymi i chemicznymi. Później uzupełniono zestaw iluminantów o serię D. Według zaleceń CIE do ogólnego stosowania w kolorymetrii powinny wystarczyć iluminanty A i D 65.
13 Iluminanty i źródła Iluminanty i źródła normalne CIE Iluminant A odpowiada światłu promiennika zupełnego w temperaturze bezwzględnej 856K. Realizacja: żarówka gazowana ze skrętką wolframową (dla nadfioletu: bańka kwarcowa). Iluminant B odpowiada światłu słonecznemu dziennemu o temperaturze barwowej najbliższej 4874K. Realizacja: źródło A z filtrem z dwóch roztworów (podany skład chemiczny!). Iluminant C odpowiada przeciętnemu światłu dziennemu o temperaturze barwowej 6774K. Realizacja: źródło A z filtrem z dwóch innych roztworów (skład chemiczny podany!). Iluminant D 65 odpowiada fazie światła dziennego o temperaturze barwowej najbliższej 6504K. Podano też przepis na stworzenie innych iluminantów D: ich chromatyczność, względny rozkład mocy, sposób prowadzenia obliczeń.
14 Iluminanty i źródła
15 Iluminanty i źródła
16 Iluminanty i źródła
17 Różnica barw Różnica bodźców W wielu zagadnieniach kolorymetrycznych potrzebne jest określenie w pewnej skali różnicy między bodźcami (np. między barwą odtworzoną a barwą wzorca) lub ustalenie tolerancji na te różnice. Narzucająca się tendencja do określenia wielkości: x y jako miary różnicy barw nie stanowi psychofizycznego odpowiednika wrażenia różnicy barw i nie ma w ogóle fizjologicznego znaczenia. Badania Judda, Mac Adama i in. wykazały, że miejsca geometryczne punktów wykresu chromatyczności leżących w odległości progowej od danego punktu są krzywymi podobnymi do elips.
18 Różnica barw x y? Późniejsze badania Wrighta, Mac Adama, Stilesa i in. oparte na liczniejszych próbkach potwierdziły te wyniki: kształt krzywych na wykresie (x,y), silne uzależnienie progów od położenia punktu na wykresie i kierunku zmiany chromatyczności oraz duże rozciągnięcie części zielonej i ściśnięcie niebieskopurpurowej.
19 Różnica barw Elipsy Stilesa Regularności te występują wyraźnie na wykresie Stilesa opartym na doświadczeniach nad postrzegalnością zmian barwy wywołanych dodawaniem światła o dużej chromatyczności do światła o chromatyczności odmiennej. Stiles zredukował uzyskane wartości dla usunięcia wpływu zmian luminancji zachodzących przy dodawaniu świateł, czego nie robili inni.
20 Równomierny wykres chromatyczności CIE 1960 (u,v) Podjęto próby takiego przekształcenia wykresu chromatyczności, aby odstępy progowe od każdego punktu barwy zakreślały krzywe bardziej zbliżone do kół i aby promienie tych kół stały się podobne. Prace takie podjęli m.in.: Juss, Wyszecki, Mac Adam, Breckenridge- Schaub, Hunter, Farnsworth, Neugebauer, OSA, Sugiyama-Fukuda. Większość z tych układów bazowała na pierwowzorze Judda stanowiły one jego przekształcenia dla uzyskania zgodności z układem Munsella.
21 Równomierny wykres chromatyczności CIE 1960 (u,v) Mac Adam dowiódł, że żadne z przekształceń wykresu chromatyczności (nawet nieliniowe) nie przeistoczy elips w doskonałe koła o jednakowym promieniu. Ponadto, gdyby nawet taki idealny wykres mógł być zrealizowany, tolerancje techniczne (np. utrzymanie jednorodności produkcji) nie zawsze mogłyby być utrzymane. Dodatkowo przyjęto założenie o równorzędności progu różnicy nasycenia i progu różnicy odcienia (nie zawsze prawdziwe). Samo określenie wartości progowej różnicy barwy jest obarczone dużą dowolnością (różnice międzyosobnicze i wahania u tych samych osób!). W1960 r. CIE przyjęła wykres Mac Adama (jako najlepszy) za nowy równomierny wykres chromatyczności CIE 1960 (w literaturze anglosaskiej używa się tez nazwy: UCS CIE 1960 Uniform Color Scale).
22 Równomierny wykres chromatyczności CIE 1960 (u,v)
23 Równomierny wykres chromatyczności CIE 1960 (u,v) Wykres ten powstał poprzez projekcję wykresu (x,y), opisaną wzorami: u X 4X 15Y 3Z v X 6Y 15Y 3Z (X,Y,Z składowe trójchromatyczne). Ten sam wykres można uzyskać poprzez transformacje: u x 4x 1y 3 v x 6y 1y 3 (x,y współrzędne trójchromatyczne).
24 Równomierny wykres chromatyczności CIE 1960 (u,v) Rozmieszczenie barw, jakie daje ten wykres chromatyczności uznano za percepcyjnie bliższe do równomiernego niż wykres (x,y) CIE przy obserwacji próbek mających pomijalną różnicę luminancji. Wykres ten jest przeznaczony do stosowania przy porównywaniu różnic między barwami ciał tego samego kształtu i rozmiarów, oglądanych w identycznym otoczeniu od białego do średnioszarego, przez obserwatora przystosowanego fotopowo do pola o chromatyczności niezbyt różniącej się od chromatyczności przeciętnego światła dziennego.
25 Równomierny wykres chromatyczności CIE 1960 (u,v) Aby ułatwić obliczenia kolorymetryczne przygotowano tablice, zawierające składowe trójchromatyczne widmowe i odpowiadające im współrzędne u v w u v w wyprowadzone z normalnych składowych trójchromatycznych widmowych: u 3 x v y 1 w x 3y z
26 Równomierny wykres chromatyczności CIE 1960 (u,v) Czemu nie wycofano wykresu (x,y) po wprowadzeniu nowego? Zaletą wykresu (x,y) jest równomierne rozmieszczenie barw, podczas gry wykres (u,v) jest ściśnięty w części zbliżonej do krzywej barw widmowych zawierającej promieniowanie o dłuższej fali, a rozszerzony w pozostałej.
27 Równomierny wykres chromatyczności CIE 1960 (u,v) Równomierny wykres chromatyczności (u,v) CIE 1960 może znaleźć zastosowanie tylko wtedy, gdy różnica luminancji obu próbek jest pomijalnie mała. W wielu przypadkach znaczące różnice luminancji uniemożliwiają użycie wykresu równomiernego lub jakiegokolwiek płaskiego i zmuszają do określania odstępów między barwami w przestrzeni trójwymiarowej. Dodanie trzeciego wymiaru i stworzenie przestrzeni barw (U,V,W) nie zapewniłoby rozkładu barw dostatecznie równomiernego.
28 Przestrzeń barw (U V W) CIE 1964 Dokonano więc kolejnego nieliniowego przekształcenia układu przestrzennego, zaleconego przez CIE w 1964r. W 5Y U 13W u u V 13W v v 0 0 dla 1 Y 100 Y jest współczynnikiem luminancji L/L max gdzie u 0 i v 0 są wartościami zmiennych dla bodźca umownie achromatycznego, umieszczonego w początku układu (U,V,W). W układzie CIE UVW składowa W reprezentuje jasność światła, a składowe U, V określają tzw. wektor barwności. Początek tego wektora odpowiada światłu achromatycznemu.
29 Układ CIE 1976 (u, v ) Kolejne przybliżenie w próbach stworzenia układu równomiernego. Wykres ten powstał poprzez projekcję wykresu (x,y), opisaną wzorami: u' X 4X 15Y 3Z v' X 9Y 15Y 3Z (X,Y,Z składowe trójchromatyczne) Ten sam wykres można uzyskać poprzez transformacje: 4x 9y u' v ' x 1y 3 x 1y 3 (x,y współrzędne trójchromatyczne) Czyli: u' u v' 1, 5 v
30 Układ CIE 1976 (u, v ) W układzie tym wprowadzono nowy sposób wyrażania luminancji, zachowany również w późniejszych układach CIE Luv i CIE Lab. Jest on bardziej fizjologiczny jednakowym różnicom liczbowym luminancji odpowiadają jednakowe różnice luminancji odczuwane przez obserwatora. 1 3 L Y Y dla 0, Y Y n n Y Y L 903 dla 0, Y n gdzie Y jest całką iloczynów składowych trójchromatycznych, mocy promieniowania i współczynnika transmisji po długości fali: Y y r d a y d 100 Y n Y n
31 Układ CIE 1976 (u, v ) Układ cylindryczny barw jest bardziej naturalny od układu kartezjańskiego. Jego środek W pokrywa się z punktem światła białego (np. D 65 ). Kąt chromatyczności barwy określa wzór: h uv v arctg u a jej nasycenie: v u n n s uv 13 [( u un) ( v vn ) ] 1/
32 Układy CIELUV (Luv, Luv) Naturalną ewolucją układu CIE 1976, zmierzającą do uzyskania równomiernej przestrzeni barw, jest układ Luv (MacAdam). Jest to układ trójwymiarowy występujący w dwóch wariantach: 1) prostokątny, kartezjański L u v, ze środkiem w punkcie iluminantu białego (np. D 65 ), osią u skierowaną równolegle do dawnej osi u, prostopadłą do niej osią v i pionową osią luminancji L, która przyjmuje wartości od 1 do 100;
33 Układy CIELUV (Luv, Luv) Struktura układu współrzędnych L u v przypomina układ Munsella. Jest więc pionowa oś luminancji L, ale jej maksymalna wartość nie wynosi 10 lecz 100. Płaszczyzny o jednakowej barwie są rozłożone na promieniu koła (cylindra), Miarą nasycenia s u,v jest odległość od osi L. Rozkład kolorów na obwodzie jest przeciwny. W porównaniu z układem Munsella dochodzi jeszcze jedna wielkość określająca barwę. Jest nią chromatyczność C określona jako iloczyn luminancji i nasycenia.
34 Układy CIELUV (Luv, Luv) Luminancję określają wzory przeniesione z CIE 1976: L 116 Y Y n Y n dla Y Y n 0, Y Y L 903 dla 0, Y n Współrzędne barwy u i v definiuje się następująco: u v 13L 13L ( u ( v u v n n ) ),
35 Układy CIELUV (Luv, Luv) Drugi wariant układu Luv: - cylindryczny L,C,h, ma jako współrzędne promień C (chromatyczność), nasycenie s uv oraz jako kąt chromatyczności kolor h uv : C s uv h uv 1 ( u v ) L suv 13 [( u un ) ( v vn arctg v u ( Jak widać, kolor h uv jest taki, jak kolor u układzie CIE 1976: ). ) ] 1/ h uv v arctg u v u n n v arctg u
36 Układy CIELUV (Luv, Luv)
37 Układy CIELUV (Luv, Luv)
38 Układy CIELUV (Luv, Luv)
39 Układy CIELUV (Luv, Luv)
40 Różnica barw Różnica barw w układzie CIELUV Skoro układ Luv jest układem o równomiernym rozkładzie barw, można w nim zdefiniować jednakowo odczuwalne przez człowieka różnice barw. Wielkość ta ma bardzo duże znaczenie w przemyśle farbiarskim i tekstylnym oraz przy badaniu wzroku. Różnicę barw w układzie kartezjańskim określa wzór: E uv [( L ) ( u ) ( v ) ] 1/ W układzie cylindrycznym różnicę barw wyznacza się ze wzoru: E uv [( L ) ( H ) ( C ) ] 1/ H h uv uv C1 C sin( ) gdzie: albo: H s s, uv uv1 uv
41 Układy CIE 1976 Lab (CIELAB, Lab) Układ bazuje na przestrzeni Huntera L,a,b (1948). Gwiazdki ( ) użyto w oznaczeniach dla odróżnienia układu od oryginalnej koncepcji układu trójchromatycznego α,β, opracowanego przez Huntera (194,1948). Układ α,β jest związany z (x,y) CIE zależnościami:,466x 1,0000x 1,3631y,633y 0,314 1,1054 0,5710x 1,0000x 1,447y,633y 0,5708 1,1054
42 Układy CIE 1976 Lab (CIELAB, Lab) L reprezentuje luminancję (0 to czarny, 100 to biały); a odpowiada za pozycję barwy pomiędzy zielonym (-) i czerwonym/magentą (+); b to wybór pomiędzy niebieskim (-) i żółtym (+). Układ CIE Lab jest bardzo rozpowszechniony w zastosowaniach profesjonalnych. Jego zaletą, podobnie jak układu Luv, jest możliwość obliczania różnicy barw. W układzie tym nie ma wielkości określanej w układach CIE 1976 oraz Luv nasyceniem barwy. Jest tylko chromatyczność. Barwy w układzie CIE Lab można również wyrażać w układzie kartezjańskim Lab lub cylindrycznym L, C, h.
43 Układy CIE 1976 Lab (CIELAB, Lab)
44 Układy CIE 1976 Lab (CIELAB, Lab)
45 Układy CIE 1976 Lab (CIELAB, Lab)
46 Układy CIE 1976 Lab (CIELAB, Lab) Współrzędne kartezjańskie układu Lab L 116f a 500 b 00 f f Y X Y Y n X Y 16 n f Y Y n f Z n Z n f t t dla 9 6 t t Uwaga: dla wszystkich iluminantów Y n =100. Poza tym: - dla iluminantu A: - dla iluminantu C: - dla iluminantu D 65 : X n 109,847, Z n X n 98,0705, Zn X n 94,87, Zn 35, ,46 107,414
47 Układy CIE 1976 Lab (CIELAB, Lab) Współrzędne cylindryczne: - kolor (kąt chromatyczności): h ab b arctg( a ) - chromatyczność: C ab ( a b ) 1 (hmmm, a gdzie jest trzecia współrzędna? Układ cylindryczny jest wszakże 3D )
48 Różnica barw Różnica barw w układzie CIELAB Różnica barw w układzie kartezjańskim Lab jest zwykłą odległością euklidesową pomiędzy dwoma punktami w przestrzeni trójwymiarowej: E ab [( L ab ) ( a ) ( b ) ] 1/. Obliczanie różnicy barw w układzie cylindrycznym: E ab [( L ) ( H ab ) ( C ab ) ] 1/. H h ab ab C1 C sin( )
49 Różnica barw Różnica barw w układzie CIELUV E ab [( L ab ) ( a ) ( b ) ] 1/. Można przyjąć, że standardowy obserwator zauważa różnicę barw następująco: 0 <ΔE < 1 - nie zauważa różnicy, 1 <ΔE < - zauważa różnicę jedynie doświadczony obserwator, <ΔE < 3,5 - zauważa różnicę również niedoświadczony obserwator, 3,5 <ΔE < 5 - zauważa wyraźną różnicę barw, 5 < ΔE - obserwator odnosi wrażenie dwóch różnych barw.
50 Różnica barw Miara różnicy barw Konsekwencją wprowadzenia równomiernej przestrzeni barw (UVW) było uznanie za miarę wielkości wrażenia różnicy dwóch obserwowanych barw odległości między odpowiadającymi im punktami wzoru na różnicę barw (CIE 1964): E CIE U 1 U V1 V W1 W 1
51 Różnica barw Miara różnicy barw Zebranie danych pomiarowych w kolejnych latach pozwoliło na zaproponowanie innych zależności na różnicę barw: 1) Wzór pierwiastka sześciennego: (było, przy Lab) E a 1 a b1 b L1 L gdzie: L 5,9G 18, 38 a ,0 R G R 1,1084X 0,085Y 0, 1454Z G X Y 0, 0004Z b ,34 G B 3 B 0,006X 0,0394Y 0, 819Z
52 Różnica barw Miara różnicy barw Wzór renotacji Munsella: E f s 1 1 cos3,6 H1 H C1 C 16 f C C V V h 1 1 w którym H, V i C są to odpowiednio: odcień (Hue), wartość (Value) i Chroma; (H 1 -H ) jest różnicą odcieni w procentach obwodu a 3,6(H 1 -H ) to ten sam kąt różnicy odcienia wyrażony w stopniach; f h jest czynnikiem wagi odcienia a f s jest czynnikiem otoczenia. Przy barwie otoczenia równej w przybliżeniu przeciętnej dwóch barw porównywalnych: f h =1 i f s =3. Dla otoczenia od białego do średnioszarego: 1 f 4 15 C 16V Vs f h s 1 3 cos3,6 H1 H 5 C 16V Vs V s jest zaś wartością Munsella dla otoczenia szarego lub białego. V C 1 1 V 1 C 1 V C
53 Różnica barw E Miara różnicy barw Opracowana przez Judda została oparta szeroko stosowana w USA jednostka NBS (National Bureau of Standarts). Jednostkę NBS wyrazić można w układzie trójchromatycznym, opracowanym przez Huntera. Różnicę barw można zapisać wtedy jako: f g Y k Y 1 1 Y 1 Y Y 1 1 Y 1 Y 1 Y f g to stała, która uwzględnia maskujący wpływ połysku powierzchniowego na wykrywanie różnicy barwy. W Y f g typowych warunkach kontroli: Y, 5 k to stała uwzględniająca wpływ różnic jasności na postrzeganie różnic barwy; jeżeli obie powierzchnie się stykają wzdłuż ostrej linii podziału, przyjmuje się k=1; przy rozsunięciu: k=3 lub k=4.
54 Różnica barw Miara różnicy barw Inna szeroko rozpowszechniona przy wyrażaniu tolerancji barwników jednostka różnicy barwy Mac Adama: s g 11 x g 1 x y g y g 33 Y Y Stałe g 11, g 1, g zależą od chromatyczności próbek i odczytuje się je ze specjalnych wykresów; stałą g 33 ustala się w zależności od warunków obserwacji (przy polu i ostrej linii granicznej miedzy próbkami: g 33 =1).
55 Różnica barw Miara różnicy barw Zdaniem Wrighta metrologii różnicy barwy nie można wyrazić prostymi zależnościami algebraicznymi. Czynnikami utrudniającymi są tu: zależność wartości ledwie dostrzegalnej różnicy i względnego znaczenia różnic luminancji i chromatyczności zależnej od warunków obserwacji, nieliniowość zależności między różnicą barwy a luminancją i (najważniejsze) nieaddytywności różnic barw, a więc zatracanie się nierówności dwóch drobnych różnic barwy przy ich podwojeniu. Każdy z podanych wzorów zawiera pewnie element empiryczny, żaden nie daje wyników odpowiadających ściśle wrażeniom wzrokowym. Wybór wzoru spośród podanych uzależnia się raczej od większej łatwości jego stosowania w praktycznych obliczeniach niż od zalet merytorycznych.
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy.
 Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
PODSTAWY BARWY, PIGMENTY CERAMICZNE
 PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
Fotometria i kolorymetria
 12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
Fotometria i kolorymetria
 13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
Fotometria i kolorymetria
 10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
Kolorymetria. Akademia Sztuk Pięknych Gdańsk październik Dr inŝ. Paweł Baranowski
 Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Janusz Ganczarski CIE XYZ
 Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
Luminancja jako jednostka udziału barwy składowej w mierzonej:
 Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
BARWA. Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle;
 BARWA Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle; Barwa psychofizyczna scharakteryzowanie bodźców świetlnych, wywołujących wrażenie barwy; ODRÓŻNIENIE BARW KOLORYMETR
BARWA Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle; Barwa psychofizyczna scharakteryzowanie bodźców świetlnych, wywołujących wrażenie barwy; ODRÓŻNIENIE BARW KOLORYMETR
Fotometria i kolorymetria
 11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
WYKŁAD 14 PODSTAWY TEORII BARW. Plan wykładu: 1. Wrażenie widzenia barwy. Wrażenie widzenia barwy Modele liczbowe barw
 WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
Kolorymetria. Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą.
 Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
WYKŁAD 11. Kolor. fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony
 WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Pojęcie Barwy. Grafika Komputerowa modele kolorów. Terminologia BARWY W GRAFICE KOMPUTEROWEJ. Marek Pudełko
 Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Dzień dobry. Miejsce: IFE - Centrum Kształcenia Międzynarodowego PŁ, ul. Żwirki 36, sala nr 7
 Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
PODSTAWY TEORII BARW
 WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 WYDZIAŁ Podstawowych Problemów Techniki Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim..fotometria i kolorymetria. Nazwa w języku angielskim.photometry and colorimetry. Kierunek studiów
WYDZIAŁ Podstawowych Problemów Techniki Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim..fotometria i kolorymetria. Nazwa w języku angielskim.photometry and colorimetry. Kierunek studiów
PROBLEMATYKA DOBORU KOLORÓW
 PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
Układy współrzędnych
 Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
Co to jest współczynnik oddawania barw?
 Co to jest współczynnik oddawania barw? Światło i kolor Kolory są wynikiem oddziaływania oświetlenia z przedmiotami. Różne źródła światła mają różną zdolność do wiernego oddawania barw przedmiotów Oddawanie
Co to jest współczynnik oddawania barw? Światło i kolor Kolory są wynikiem oddziaływania oświetlenia z przedmiotami. Różne źródła światła mają różną zdolność do wiernego oddawania barw przedmiotów Oddawanie
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ
 KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Technika świetlna. Przegląd rozwiązań i wymagań dla tablic rejestracyjnych. Dokumentacja zdjęciowa
 Technika świetlna Przegląd rozwiązań i wymagań dla tablic rejestracyjnych. Dokumentacja zdjęciowa Wykonał: Borek Łukasz Tablica rejestracyjna tablica zawierająca unikatowy numer (kombinację liter i cyfr),
Technika świetlna Przegląd rozwiązań i wymagań dla tablic rejestracyjnych. Dokumentacja zdjęciowa Wykonał: Borek Łukasz Tablica rejestracyjna tablica zawierająca unikatowy numer (kombinację liter i cyfr),
Barwy przedmiotów są wynikiem działania na oko promieniowania, które się od tych przedmiotów odbija lub jest przez nie przepuszczane.
 Barwy przedmiotów są wynikiem działania na oko promieniowania, które się od tych przedmiotów odbija lub jest przez nie przepuszczane. Skład promieniowania padającego na barwną substancję może być różny,
Barwy przedmiotów są wynikiem działania na oko promieniowania, które się od tych przedmiotów odbija lub jest przez nie przepuszczane. Skład promieniowania padającego na barwną substancję może być różny,
Fotometria i kolorymetria
 9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Wstęp. Ruch po okręgu w kartezjańskim układzie współrzędnych
 Wstęp Ruch po okręgu jest najprostszym przypadkiem płaskich ruchów krzywoliniowych. W ogólnym przypadku ruch po okręgu opisujemy równaniami: gdzie: dowolna funkcja czasu. Ruch odbywa się po okręgu o środku
Wstęp Ruch po okręgu jest najprostszym przypadkiem płaskich ruchów krzywoliniowych. W ogólnym przypadku ruch po okręgu opisujemy równaniami: gdzie: dowolna funkcja czasu. Ruch odbywa się po okręgu o środku
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
K O L O R Y M E T R I A
 K O L O R Y M E T R I A dr inż. Krzysztof Wandachowicz, / studenci/pomoce.html pok. 807, tel. 6652585, 0602 655505, Literatura: 1. Żagan W.: Podstawy techniki świetlnej. Oficyna Wydawnicza Politechniki
K O L O R Y M E T R I A dr inż. Krzysztof Wandachowicz, / studenci/pomoce.html pok. 807, tel. 6652585, 0602 655505, Literatura: 1. Żagan W.: Podstawy techniki świetlnej. Oficyna Wydawnicza Politechniki
Graficzne opracowanie wyników pomiarów 1
 GRAFICZNE OPRACOWANIE WYNIKÓW POMIARÓW Celem pomiarów jest bardzo często potwierdzenie związku lub znalezienie zależności między wielkościami fizycznymi. Pomiar polega na wyznaczaniu wartości y wielkości
GRAFICZNE OPRACOWANIE WYNIKÓW POMIARÓW Celem pomiarów jest bardzo często potwierdzenie związku lub znalezienie zależności między wielkościami fizycznymi. Pomiar polega na wyznaczaniu wartości y wielkości
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM PODSTAWOWY. Etapy rozwiązania zadania
 Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ
 KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
Analiza składowych głównych. Wprowadzenie
 Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
Akwizycja obrazów. Zagadnienia wstępne
 Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
Fotometria i kolorymetria
 1. Wprowadzenie (treść wykładu, literatura, warunki zaliczenia) Zadania radio- i fotometrii Podstawy fizjologiczne fotometrii (budowa oka ludzkiego; prawa fizjologiczne ważne dla fotometrii) http://www.if.pwr.wroc.pl/~wozniak/
1. Wprowadzenie (treść wykładu, literatura, warunki zaliczenia) Zadania radio- i fotometrii Podstawy fizjologiczne fotometrii (budowa oka ludzkiego; prawa fizjologiczne ważne dla fotometrii) http://www.if.pwr.wroc.pl/~wozniak/
Wyznaczanie zależności współczynnika załamania światła od długości fali światła
 Ćwiczenie O3 Wyznaczanie zależności współczynnika załamania światła od długości fali światła O3.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie zależności współczynnika załamania światła od długości fali
Ćwiczenie O3 Wyznaczanie zależności współczynnika załamania światła od długości fali światła O3.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie zależności współczynnika załamania światła od długości fali
Dźwięk. Cechy dźwięku, natura światła
 Dźwięk. Cechy dźwięku, natura światła Fale dźwiękowe (akustyczne) - podłużne fale mechaniczne rozchodzące się w ciałach stałych, cieczach i gazach. Zakres słyszalnej częstotliwości f: 20 Hz < f < 20 000
Dźwięk. Cechy dźwięku, natura światła Fale dźwiękowe (akustyczne) - podłużne fale mechaniczne rozchodzące się w ciałach stałych, cieczach i gazach. Zakres słyszalnej częstotliwości f: 20 Hz < f < 20 000
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Wektory, układ współrzędnych
 Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Modele i przestrzenie koloru
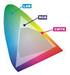 Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Poniżej przedstawiony został podział wymagań na poszczególne oceny szkolne:
 Prosto do matury klasa d Rok szkolny 014/015 WYMAGANIA EDUKACYJNE Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające
Prosto do matury klasa d Rok szkolny 014/015 WYMAGANIA EDUKACYJNE Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej
 Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło widzialne jest to promieniowanie elektromagnetyczne (zaburzenie poła elektromagnetycznego rozchodzące
Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło widzialne jest to promieniowanie elektromagnetyczne (zaburzenie poła elektromagnetycznego rozchodzące
Rys. 1. Zakres widzialny fal elektromagnetycznych dla widzenia w ciągu dnia i nocy.
 Pomiary natężenia oświetlenia Możliwości percepcyjne, a przez to stan psychofizyczny człowieka zależą w bardzo dużym stopniu od środowiska, w jakim aktualnie przebywa. Bodźce świetlne są decydującymi czynnikami
Pomiary natężenia oświetlenia Możliwości percepcyjne, a przez to stan psychofizyczny człowieka zależą w bardzo dużym stopniu od środowiska, w jakim aktualnie przebywa. Bodźce świetlne są decydującymi czynnikami
BADANIE INTERFEROMETRU YOUNGA
 Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli
 Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Przenośne urządzenia pomiarowe...59. Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64
 Barwa - wprowadzenie...55 Przenośne urządzenia pomiarowe...59 Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64 Wyposażenie do przenośnych urządzeń pomiarowych...66
Barwa - wprowadzenie...55 Przenośne urządzenia pomiarowe...59 Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64 Wyposażenie do przenośnych urządzeń pomiarowych...66
Laboratorium Grafiki Komputerowej Przekształcenia na modelach barw
 Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Analiza spektralna i pomiary spektrofotometryczne
 Analiza spektralna i pomiary spektrofotometryczne Zagadnienia: 1. Absorbcja światła. 2. Współrzędne trójchromatyczne barwy, Prawa Gassmana. 3. Trójkąt barw. Trójkąt nasyceń. 4. Rozpraszanie światła. 5.
Analiza spektralna i pomiary spektrofotometryczne Zagadnienia: 1. Absorbcja światła. 2. Współrzędne trójchromatyczne barwy, Prawa Gassmana. 3. Trójkąt barw. Trójkąt nasyceń. 4. Rozpraszanie światła. 5.
MODELE KOLORÓW. Przygotował: Robert Bednarz
 MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejkę z kodem szkoły dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdającego 1 Sprawdź, czy arkusz egzaminacyjny zawiera 15
Miejsce na naklejkę z kodem szkoły dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdającego 1 Sprawdź, czy arkusz egzaminacyjny zawiera 15
Ćwiczenie Nr 11 Fotometria
 Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 11 Fotometria Zagadnienia: fale elektromagnetyczne, fotometria, wielkości i jednostki fotometryczne, oko. Wstęp Radiometria (fotometria
Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 11 Fotometria Zagadnienia: fale elektromagnetyczne, fotometria, wielkości i jednostki fotometryczne, oko. Wstęp Radiometria (fotometria
Układ współrzędnych dwu trój Wykład 2 "Układ współrzędnych, system i układ odniesienia"
 Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Matematyka licea ogólnokształcące, technika
 Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Kształcenie w zakresie podstawowym. Klasa 2
 Kształcenie w zakresie podstawowym. Klasa 2 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
Kształcenie w zakresie podstawowym. Klasa 2 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/
 Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/ MATEMATYKA Klasa III ZAKRES PODSTAWOWY Dział programu Temat Wymagania. Uczeń: 1. Miara łukowa kąta zna pojęcia: kąt skierowany, kąt
Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/ MATEMATYKA Klasa III ZAKRES PODSTAWOWY Dział programu Temat Wymagania. Uczeń: 1. Miara łukowa kąta zna pojęcia: kąt skierowany, kąt
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II
 ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
Marcin Wilczewski Politechnika Gdańska, 2013/14
 Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Kolor w grafice komputerowej. Światło i barwa
 Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Wprowadzenie do cyfrowego przetwarzania obrazów
 Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE
 OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb
 Współzależność Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb (x i, y i ). Geometrycznie taką parę
Współzależność Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb (x i, y i ). Geometrycznie taką parę
MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ. programowej dla klas IV-VI. programowej dla klas IV-VI.
 MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ TEMAT LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ UWAGI. LICZBY I DZIAŁANIA 6 h Liczby. Rozwinięcia
MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ TEMAT LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ UWAGI. LICZBY I DZIAŁANIA 6 h Liczby. Rozwinięcia
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski 12 październik 2009 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 2 1/21 Plan wykładu Promieniowanie ciała doskonale czarnego Związek temperatury
Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski 12 październik 2009 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 2 1/21 Plan wykładu Promieniowanie ciała doskonale czarnego Związek temperatury
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony
 Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony Uczeń realizujący zakres rozszerzony powinien również spełniać wszystkie wymagania w zakresie poziomu podstawowego. Zakres
Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony Uczeń realizujący zakres rozszerzony powinien również spełniać wszystkie wymagania w zakresie poziomu podstawowego. Zakres
OCENA PRZYDATNOŚCI FARBY PRZEWIDZIANEJ DO POMALOWANIA WNĘTRZA KULI ULBRICHTA
 OCENA PRZYDATNOŚCI FARBY PRZEWIDZIANEJ DO POMALOWANIA WNĘTRZA KULI ULBRICHTA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki WPROWADZENIE Całkowity
OCENA PRZYDATNOŚCI FARBY PRZEWIDZIANEJ DO POMALOWANIA WNĘTRZA KULI ULBRICHTA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki WPROWADZENIE Całkowity
MATeMAtyka 3. Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych. Zakres podstawowy i rozszerzony. Zakres podstawowy i rozszerzony
 MATeMAtyka 3 Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych Zakres podstawowy i rozszerzony Zakres podstawowy i rozszerzony Wyróżnione zostały następujące wymagania programowe: konieczne
MATeMAtyka 3 Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych Zakres podstawowy i rozszerzony Zakres podstawowy i rozszerzony Wyróżnione zostały następujące wymagania programowe: konieczne
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Fizyka elektryczność i magnetyzm
 Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
2) R stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
 ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
LABORATORIUM OPTYKA GEOMETRYCZNA I FALOWA
 LABORATORIUM OPTYKA GEOMETRYCZNA I FALOWA Instrukcja do ćwiczenia nr 4 Temat: Wyznaczanie współczynnika sprawności świetlnej źródła światła 1 I. Wymagania do ćwiczenia 1. Wielkości fotometryczne, jednostki..
LABORATORIUM OPTYKA GEOMETRYCZNA I FALOWA Instrukcja do ćwiczenia nr 4 Temat: Wyznaczanie współczynnika sprawności świetlnej źródła światła 1 I. Wymagania do ćwiczenia 1. Wielkości fotometryczne, jednostki..
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki.
 Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki. 1. Równanie soczewki i zwierciadła kulistego. Z podobieństwa trójkątów ABF i LFD (patrz rysunek powyżej) wynika,
Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki. 1. Równanie soczewki i zwierciadła kulistego. Z podobieństwa trójkątów ABF i LFD (patrz rysunek powyżej) wynika,
Złudzenia optyczne. . Złudzenia optyczne dzieli się na cztery kategorie:
 ZŁUDZENIA OPTYCZNE Złudzenia optyczne Złudzenie optyczne - błędna interpretacja obrazu przez mózg pod wpływem kontrastu, cieni, użycia kolorów, które automatycznie wprowadzają mózg w błędny tok myślenia.
ZŁUDZENIA OPTYCZNE Złudzenia optyczne Złudzenie optyczne - błędna interpretacja obrazu przez mózg pod wpływem kontrastu, cieni, użycia kolorów, które automatycznie wprowadzają mózg w błędny tok myślenia.
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, shortinst Wstęp do astrofizyki I,
Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, shortinst Wstęp do astrofizyki I,
Ćwiczenie nr 1. Temat: BADANIE OSTROŚCI WIDZENIA W RÓŻNYCH WARUNKACH OŚWIETLENIOWYCH
 Grupa: Elektrotechnika, sem 3., wersja z dn. 03.10.2011 Podstawy Techniki Świetlnej Laboratorium Ćwiczenie nr 1. Temat: BADANIE OSTROŚCI WIDZENIA W RÓŻNYCH WARUNKACH OŚWIETLENIOWYCH Opracowanie wykonano
Grupa: Elektrotechnika, sem 3., wersja z dn. 03.10.2011 Podstawy Techniki Świetlnej Laboratorium Ćwiczenie nr 1. Temat: BADANIE OSTROŚCI WIDZENIA W RÓŻNYCH WARUNKACH OŚWIETLENIOWYCH Opracowanie wykonano
BIAŁOŚĆ WYROBÓW ELEWACYJNYCH - ZASADY POMIARU
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 2 (122) 2002 BUILDING RESEARCH INSTITUTE - QUARTERLY No 2 (122) 2002 ARTYKUŁY - REPORTS Małgorzata Prokop* BIAŁOŚĆ WYROBÓW ELEWACYJNYCH - ZASADY POMIARU
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 2 (122) 2002 BUILDING RESEARCH INSTITUTE - QUARTERLY No 2 (122) 2002 ARTYKUŁY - REPORTS Małgorzata Prokop* BIAŁOŚĆ WYROBÓW ELEWACYJNYCH - ZASADY POMIARU
Wymagania z matematyki KLASA VII
 Wymagania z matematyki KLASA VII Wymagania na ocenę dopuszczającą: -porównywanie liczb wymiernych (łatwiejsze -zaznaczanie liczb wymiernych na osi liczbowej - zamiana ułamka zwykłego na dziesiętny i odwrotnie
Wymagania z matematyki KLASA VII Wymagania na ocenę dopuszczającą: -porównywanie liczb wymiernych (łatwiejsze -zaznaczanie liczb wymiernych na osi liczbowej - zamiana ułamka zwykłego na dziesiętny i odwrotnie
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP. V. Obliczenia procentowe. Uczeń: 1) przedstawia część wielkości jako procent tej wielkości;
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP Liczby. TEMAT Rozwinięcia dziesiętne liczb wymiernych. Zaokrąglanie liczb. Szacowanie wyników. Dodawanie i odejmowanie liczb dodatnich. Mnożenie i dzielenie
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP Liczby. TEMAT Rozwinięcia dziesiętne liczb wymiernych. Zaokrąglanie liczb. Szacowanie wyników. Dodawanie i odejmowanie liczb dodatnich. Mnożenie i dzielenie
Kurs grafiki komputerowej Lekcja 2. Barwa i kolor
 Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
7. Wyznaczanie poziomu ekspozycji
 7. Wyznaczanie poziomu ekspozycji Wyznaczanie poziomu ekspozycji w przypadku promieniowania nielaserowego jest bardziej złożone niż w przypadku promieniowania laserowego. Wynika to z faktu, że pracownik
7. Wyznaczanie poziomu ekspozycji Wyznaczanie poziomu ekspozycji w przypadku promieniowania nielaserowego jest bardziej złożone niż w przypadku promieniowania laserowego. Wynika to z faktu, że pracownik
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
Ćwiczenie 42 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ. Wprowadzenie teoretyczne.
 Ćwiczenie 4 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ Wprowadzenie teoretyczne. Soczewka jest obiektem izycznym wykonanym z materiału przezroczystego o zadanym kształcie i symetrii obrotowej. Interesować
Ćwiczenie 4 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ Wprowadzenie teoretyczne. Soczewka jest obiektem izycznym wykonanym z materiału przezroczystego o zadanym kształcie i symetrii obrotowej. Interesować
Dr Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach
 Dr Kazimierz Sierański kazimierz.sieranski@pwr.edu.pl www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach Forma zaliczenia kursu: egzamin końcowy Grupa kursów -warunkiem
Dr Kazimierz Sierański kazimierz.sieranski@pwr.edu.pl www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach Forma zaliczenia kursu: egzamin końcowy Grupa kursów -warunkiem
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
Wymagania edukacyjne z matematyki - klasa I (poziom podstawowy) wg programu nauczania Matematyka Prosto do matury
 LICZBY RZECZYWISTE Na poziomie wymagań koniecznych - na ocenę dopuszczającą (2) uczeń potrafi: zamieniać ułamek zwykły na ułamek dziesiętny podać przykłady liczb niewymiernych podać przybliżenie dziesiętne
LICZBY RZECZYWISTE Na poziomie wymagań koniecznych - na ocenę dopuszczającą (2) uczeń potrafi: zamieniać ułamek zwykły na ułamek dziesiętny podać przykłady liczb niewymiernych podać przybliżenie dziesiętne
SPIS TREŚCI WSTĘP... 8 1. LICZBY RZECZYWISTE 2. WYRAŻENIA ALGEBRAICZNE 3. RÓWNANIA I NIERÓWNOŚCI
 SPIS TREŚCI WSTĘP.................................................................. 8 1. LICZBY RZECZYWISTE Teoria............................................................ 11 Rozgrzewka 1.....................................................
SPIS TREŚCI WSTĘP.................................................................. 8 1. LICZBY RZECZYWISTE Teoria............................................................ 11 Rozgrzewka 1.....................................................
Temat ćwiczenia: Zasady stereoskopowego widzenia.
 Uniwersytet Rolniczy w Krakowie Wydział Inżynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Zasady stereoskopowego widzenia. Zagadnienia 1. Widzenie monokularne, binokularne
Uniwersytet Rolniczy w Krakowie Wydział Inżynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Zasady stereoskopowego widzenia. Zagadnienia 1. Widzenie monokularne, binokularne
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Wymagania edukacyjne z matematyki w klasie III gimnazjum
 Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
