Laboratorium Grafiki Komputerowej Przekształcenia na modelach barw
|
|
|
- Seweryn Domański
- 8 lat temu
- Przeglądów:
Transkrypt
1 Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi w grafice komputerowej i konwersją danych pomiędzy nimi 2 Wprowadzenie Istnieje bardzo wiele modeli barw. W zależności od potrzeb konkretnego zastosowania należy wybrać odpowiednią metodę reprezentacji barwy. Tu zostanie przedstawionych tylko kilka. 2. Model W grafice komputerowej najczęściej stosowanym modelem jest model. Wywodzi się on z trójchromatycznej teorii widzenia. Jego geometrycznym odwzorowaniem jest sześcian o boku o długości, jeśli przyjmie się że każda z wartości, i będzie z zakresu 0.. (rys. ). Wszystkie możliwe do uzyskania w tym modelu kolory znajdują się wewnątrz tego sześcianu. C W K M ysunek : Model Jego wierzchołkami są punkty odpowiadające podstawowym barwom w tym modelu (czerwona, zielona i niebieska ) przy maksymalnej ich wartości oraz ich kombinacjom przy takim samym warunku (magneta M, żółta, cyjan C oraz biały W). Ostatnim wierzchołkiem jest punkt odpowiadający brakowi wszystkich składowych (czerń K). Na głównej przekątnej sześcianu (KW) znajdują się poziomy szarości. Niestety model ten nie odzwierciedla całego zbioru barw widzialnych, w szczególności ograniczona jest odwzorowywana maksymalna jasność. Przestrzeń wyznaczana przez ten model nie jest jednorodna pod względem percepcji barw, co oznacza, że jednakowe przesunięcia wewnątrz sześcianu w różnych jego miejscach nie powodują jednakowych zmian w odbiorze barwy przez człowieka. Zaletą jest to iż można
2 w prosty sposób zrealizować fizyczny pomiar wartości, i. Dla addytywnego mieszania barw (gdy jest to mieszanina świateł barw podstawowych) ten model nadaje się bardzo dobrze. 2.2 Model CM Model CM, podobnie jak model, tworzy przestrzeń barw w kształcie sześcianu (rys. 2). óżnicę stanowią barwy podstawowe w tym modelu: C cyjan (zielono-niebieska), M magenta (purpurowa) i żółta oraz zamienione miejscami barwa biała (W) i czarna (K). W modelu tym, w przeciwieństwie do modelu, mieszanie barw odbywa się substraktywnie (składowe barw podstawowych w świetle odbitym od kolorowego obiektu; czyli ze światła białego odfiltrowane są składowe, które nie występują w badanym kolorze). Z takim efektem mamy do czynienia w przypadku materiałów drukowanych, dlatego przy ich tworzeniu często wykorzystuje się ten model przestrzeni barw. arwę czarną w tym modelu tworzą wszystkie trzy składowe przyjmujące wartości maksymalne. Dla uproszczenia procesu drukowania i polepszenia jakości wydruków najczęściej podstawowe składowe uzupełnia się barwą czarną i jest to tzw. model CMK (zob 2.). K M W C ysunek 2: Model CM Zależności pomiędzy parametrami modelu CM i : 2. Model CMK C M = = C M () (2) Model CMK bazuje na modelu CM i powstał z myślą o stosowaniu go przy reprodukcji barw na trwałych nośnikach, np. papierze. Prócz składowych występujących w modelu CM dodano jeszcze jedną oznaczającą kolor czarny (K). Wynika to z tego, że teoretycznie złożenie składowych C, M i o maksymalnej wartości powinno dać w efekcie kolor czarny, a w przypadku rzeczywistych barwników często nie jest to prawdą. W literaturze można spotkać dwie metody przeliczania składowych CM na model CMK. Pierwsza z nich ([4]) bazuje na bezwzględnym obliczaniu różnic przy wyliczaniu składowych C, M i. Dla regulacji kontrastu stosuje się dodatkowy współczynnik kɛ < 0; >, przy czym najczęściej k =. Konwersję tę przedstawiają wzory ([4]): C = C k min(c, M, ) M = M k min(c, M, ) ()
3 = k min(c, M, ) K = k min(c, M, ) zaś konwersję z modelu CMK na model CM można dokonać następująco: C = C + K M = M + K (4) = + K a konwersję bezpośrednio z modelu można obliczyć: C = ( ) k min(,, ) M = ( ) k min(,, ) (5) = ( ) k min(,, ) K = k min(,, ) i w z powrotem: = C + K = M + K (6) = + K W drugim przypadku składowe obliczane są w sposób względny ([]): C = (C min(c, M, ))/( min(c, M, )) M = (M min(c, M, ))/( min(c, M, )) (7) = ( min(c, M, ))/( min(c, M, )) K = min(c, M, ) oraz w drugim kierunku: C = min(, C ( K) + K) M = min(, M ( K) + K) (8) = min(, ( K) + K) lub bezpośrednio z modelu ([]): C = ( min(,, ))/( min(,, )) M = ( min(,, ))/( min(,, )) (9) = ( min(,, ))/( min(,, )) K = min(,, ) oraz z powrotem: = min(, C ( K) + K) = min(, M ( K) + K) (0) = min(, ( K) + K)
4 2.4 Model HSV Model HSV opracował w 978 roku Alvey ay Smith. arwa w tym modelu opisana jest poprzez trzy parametry: odcień (Hue H), nasycenie (Saturation S) oraz wartość (Value V). Pewną odmianą modelu HSV jest model HSI, w którym ostatni parametr nazywany jest intensywnością (Intensity I) oraz model HS, w którym jest on jasnością (rightness ). eometrycznym odwzorowaniem tego modelu jest ostrosłup o podstawie sześciokąta foremnego rys.. Odcień barwy jest reprezentowany jako wartość kąta, przy czym za kąt zerowy przyjęto kąt odpowiadający barwie czerwonej. Nasycenie jest interpretowane jako odległość od osi ostrosłupa, zaś parametrowi intensywności odpowiada odległość od wierzchołka bryły. W tak utworzonej bryle podstawowym kolorom nasyconym odpowiadają: czerwonemu, żółtemu, zielonemu, cyjanowi, niebieskiemu i magnecie odpowiednio wierzchołki podstawy, które są przesunięte względem punktu zerowego (kolor czerwony) o 0Π, Π, 2Π, Π, 4Π, 5Π i 2Π. arwie białej odpowiada środek środek podstawy, barwie czarnej wierzchołek bryły, a na osi bryły znajdują się punkty reprezentujące poszczególne stopnie szarości. Każdy przekrój prostopadły do osi bryły odpowiada odpowiedniemu podsześcianowi w modelu. Przy tym modelu odcień przyjmuje wartości 0..2Π ( 60 ), a parametry nasycenia i wartości są z zakresu 0... ysunek : Model HSV Konwersja danych z modelu do modelu HSV odbywa się przy zastosowaniu wzorów (opracowane wg [4], [] i [2]): v = max(r, g, b) s = h = 0 dla v = 0 max(r,g,b) min(r,g,b) max(r,g,b) dla v 0 UNDEF dla v = min(r, g, b) g b dla v = r r min(r,g,b) 2 + b r dla v = g g min(r,g,b) 4 + r g dla v = b b min(r,g,b) ()
5 a z powrotem: (r, g, b) = (v, v, v) dla h = UNDEF (v, v ( (s ( h))), v ( s)) dla 0 h < (v ( (s ( h ))), v, v ( s)) dla h < 2 (v ( s), v, v ( (s ( h)))) dla 2 h < (v ( s), v ( (s ( h ))), v) dla h < 4 (v ( (s (5 h))), v ( s), v) dla 4 h < 5 (v, v ( s), v ( (s ( h 5)))) dla 5 h < 2 (2) 2.5 Model HLS W modelu HLS opracowanym przez firmę Tektronix barwa jest opisana trzema parametrami: odcieniem (H Hue), jasność (L Luminance) i nasyceniem (S Saturation). Jego przestrzeń reprezentują dwa stożki stykające się ze sobą podstawami. Na obwodzie stykających się podstaw stożków są rozmieszczone barwy nasycone na takiej samej zasadzie jak w modelu HSV. Osie brył tworzą oś L przy czym na wierzchołku jednego stożka parametr ten przyjmuje wartość 0 (i punkt ten reprezentuje barwę czarną), a na wierzchołku drugiego stożka wartość (punkt ten reprezentuje barwę białą). Zasadniczą różnicą w porównaniu z modelem HSV jest wartość jasności, dla której barwy przyjmują maksymalne nasycenie: w modelu HSV przyjmuje ona wartość, a w tym modelu wynosi 0,5. Konwersji z modelu można dokonać wg wzorów: l = max(r,g,b)+min(r,g,b) 2 s = h = max(r,g,b) min(r,g,b) max(r,g,b)+min(r,g,b) dla l < 0.5 max(r,g,b) min(r,g,b) 2 max(r,g,b) min(r,g,b) dla l 0.5 UNDEF dla r = g = b g b dla max(r, g, b) = r r min(r,g,b) 2 + b r dla max(r, g, b) = g g min(r,g,b) 4 + r g dla max(r, g, b) = b b min(r,g,b) () oraz w drugą stronę: (r, g, b) = { (l, l, l) dla h = UNDEF (val(h + 2 ), val(h), val(h 2 )) dla 0 h < 2 (4) gdzie: zaś val(x) = n + (n2 n) h dla 0 h < n2 dla h < n + (n2 n) ( 4 h) dla h < 4 n dla 4 h < 2 n2 = { l + l s dla 0 l 0.5 l + s l s dla 0.5 < l n = 2 l n2 (5) (6)
6 Program ćwiczenia. Zapoznać się z programem do konwersji formatów graficznych oraz dostępnymi kompilatorami. 2. Napisać funkcje konwersji pomiędzy zadanymi przez prowadzącego modelami barw.. Wykorzystując napisane funkcje konwersji modeli barw napisać program generujący następujące obrazki dla zadanej przez prowadzącego barwy: prostokąt o jednolitej barwie dla każdej współrzędnej przestrzeni barw prostokąt, którego barwa będzie się zmieniać w poziomie lub w pionie w całym dostępnym zakresie tej współrzędnej i zawierać zadaną barwę Np. dla zadanej barwy czerwonej o współrzędnych =(,0,0) i dla przestrzeni HSV powinny powstać następujące obrazy: czerwony prostokąt o barwie =(,0,0) zmiana parametru H: zmiana odcieni od czerwonego poprzez całe koło odcieni do czerwonego zmiana parametru S: zmiana nasycenia od barwy achromatycznej do pełnego nasycenia czerwieni zmiana parametru V: zmiana jasności od ciemnej do jasnej czerwieni, przy stałym nasyceniu wynikającym z konwersji parametrów do przestrzeni HSV 4. W sprawozdaniu zamieścić: stronę tytułową treść zadania Literatura wydruk napisanych funkcji i programu (z komentarzami!!!) uwagi i wnioski [] D. ourgin. Color spaces faq. [2] J. urkardt. Colors color conversion. colors/colors.html, 200. [] M. Jankowski. Elementy grafiki komputerowej. Wydawnictwa Naukowo-Techniczne, Warszawa, 990. [4] J. Zabrodzki, editor. rafika komputerowa. Wydawnictwa Naukowo-Techniczne, Warszawa, 994.
Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw.
 Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
MODELE KOLORÓW. Przygotował: Robert Bednarz
 MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
Pojęcie Barwy. Grafika Komputerowa modele kolorów. Terminologia BARWY W GRAFICE KOMPUTEROWEJ. Marek Pudełko
 Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
WYKŁAD 11. Kolor. fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony
 WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
Kurs grafiki komputerowej Lekcja 2. Barwa i kolor
 Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Marcin Wilczewski Politechnika Gdańska, 2013/14
 Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Adam Korzeniewski p Katedra Systemów Multimedialnych
 Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych Zastosowania grafiki komputerowej Światło widzialne Fizjologia narządu wzroku Metody powstawania barw Modele barw
Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych Zastosowania grafiki komputerowej Światło widzialne Fizjologia narządu wzroku Metody powstawania barw Modele barw
WYKŁAD 14 PODSTAWY TEORII BARW. Plan wykładu: 1. Wrażenie widzenia barwy. Wrażenie widzenia barwy Modele liczbowe barw
 WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
Kolor, mat. pomoc. dla technologia inf. (c) M. Żabka (12 listopada 2007) str. 1
 Kolor, mat. pomoc. dla technologia inf. (c) M. Żabka (12 listopada 2007) str. 1 Kolor (barwa) 1 Modele RBG i CMY(K) Kolor każdego punktu, linii lub powierzchni (oraz inne cechy wyglądu) jest wyznaczony
Kolor, mat. pomoc. dla technologia inf. (c) M. Żabka (12 listopada 2007) str. 1 Kolor (barwa) 1 Modele RBG i CMY(K) Kolor każdego punktu, linii lub powierzchni (oraz inne cechy wyglądu) jest wyznaczony
PODSTAWY BARWY, PIGMENTY CERAMICZNE
 PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
GRAFIKA RASTROWA GRAFIKA RASTROWA
 GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
Fotometria i kolorymetria
 12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Grafika komputerowa. Dla DSI II
 Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Przetwarzanie obrazów Grafika komputerowa. dr inż. Marcin Wilczewski 2016/2017
 Przetwarzanie obrazów Grafika komputerowa dr inż. Marcin Wilczewski 216/217 1 Zagadnienia, wykład, laboratorium Wykład: Reprezentacja danych multimedialnych na przykładzie obrazów cyfrowych oraz wideo.
Przetwarzanie obrazów Grafika komputerowa dr inż. Marcin Wilczewski 216/217 1 Zagadnienia, wykład, laboratorium Wykład: Reprezentacja danych multimedialnych na przykładzie obrazów cyfrowych oraz wideo.
PODSTAWY TEORII BARW
 WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
Modele i przestrzenie koloru
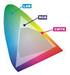 Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Fotometria i kolorymetria
 13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
Teoria koloru Co to jest?
 Teoria koloru Teoria koloru Co to jest? Dział wiedzy zajmujący się powstawaniem u człowieka wrażeń barwnych oraz teoretycznymi i praktycznymi aspektami czynników zewnętrznych biorących udział w procesie
Teoria koloru Teoria koloru Co to jest? Dział wiedzy zajmujący się powstawaniem u człowieka wrażeń barwnych oraz teoretycznymi i praktycznymi aspektami czynników zewnętrznych biorących udział w procesie
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ
 INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
Janusz Ganczarski CIE XYZ
 Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach
 TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Spis treści Spis treści 1. Model CMYK Literatura
 Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
Anna Barwaniec Justyna Rejek
 CMYK Anna Barwaniec Justyna Rejek Wstęp, czyli czym jest tryb koloru? Tryb koloru wyznacza metodę wyświetlania i drukowania kolorów danego obrazu pozwala zmieniać paletę barw zastosowaną do tworzenia danego
CMYK Anna Barwaniec Justyna Rejek Wstęp, czyli czym jest tryb koloru? Tryb koloru wyznacza metodę wyświetlania i drukowania kolorów danego obrazu pozwala zmieniać paletę barw zastosowaną do tworzenia danego
Temat: Kolorowanie i przedstawianie zespolonej funkcji falowej w przestrzeni RGB
 Spis treści 1 Model przestrzeni kolorów RGB 1 1.1 Rzutowanie z R 2 na przestrzeń RGB................ 2 Temat: Kolorowanie i przedstawianie zespolonej funkcji falowej w przestrzeni RGB Podstawa: Folley
Spis treści 1 Model przestrzeni kolorów RGB 1 1.1 Rzutowanie z R 2 na przestrzeń RGB................ 2 Temat: Kolorowanie i przedstawianie zespolonej funkcji falowej w przestrzeni RGB Podstawa: Folley
Percepcja obrazu Podstawy grafiki komputerowej
 Percepcja obrazu Podstawy grafiki komputerowej Światło widzialne wycinek szerokiego widma fal elektromagnetycznych 1 Narząd wzroku Narząd wzroku jest wysoko zorganizowanym analizatorem zmysłowym, którego
Percepcja obrazu Podstawy grafiki komputerowej Światło widzialne wycinek szerokiego widma fal elektromagnetycznych 1 Narząd wzroku Narząd wzroku jest wysoko zorganizowanym analizatorem zmysłowym, którego
Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji wizualnej i modeli barw
 Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji i modeli barw Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 38 Wprowadzenie do
Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji i modeli barw Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 38 Wprowadzenie do
Pełny raport kalibracyjny projektora:
 Pełny raport kalibracyjny projektora: BenQ W2000 Posiadasz taki lub inny projektor? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080
Pełny raport kalibracyjny projektora: BenQ W2000 Posiadasz taki lub inny projektor? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080
Pełny raport kalibracyjny telewizora:
 Pełny raport kalibracyjny telewizora: Samsung JS9000 Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080 434
Pełny raport kalibracyjny telewizora: Samsung JS9000 Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080 434
Ćwiczenie 6. Transformacje skali szarości obrazów
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Grafika Komputerowa. Percepcja wizualna i modele barw
 Grafika Komputerowa. Percepcja wizualna i modele barw Aleksander Denisiuk Polsko-Japońska Akademia Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk denisjuk@pja.edu.pl 1
Grafika Komputerowa. Percepcja wizualna i modele barw Aleksander Denisiuk Polsko-Japońska Akademia Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk denisjuk@pja.edu.pl 1
Pełny raport kalibracyjny telewizora:
 Pełny raport kalibracyjny telewizora: LG 55" EG910V Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080 434
Pełny raport kalibracyjny telewizora: LG 55" EG910V Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080 434
Luminancja jako jednostka udziału barwy składowej w mierzonej:
 Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Grafika komputerowa. Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Żółty
 Grafika komputerowa Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Czerwony czopek
Grafika komputerowa Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Czerwony czopek
PROBLEMATYKA DOBORU KOLORÓW
 PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 1 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Wprowadzenie do cyfrowego przetwarzania obrazów
 Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
KOLORY KOMPLEMENTARNE
 BARWY W DRUKU KOŁO (BARW) KOLORÓW KOLORY KOMPLEMENTARNE PODWÓJNE DOPEŁNIENIE DOPEŁNIENIE TRÓJDZIELNE KOLORY SĄSIADUJĄCE MIESZANIE BARW Synteza addytywna - polega na nakładaniu się na siebie świateł trzech
BARWY W DRUKU KOŁO (BARW) KOLORÓW KOLORY KOMPLEMENTARNE PODWÓJNE DOPEŁNIENIE DOPEŁNIENIE TRÓJDZIELNE KOLORY SĄSIADUJĄCE MIESZANIE BARW Synteza addytywna - polega na nakładaniu się na siebie świateł trzech
Wyznaczanie długości fali świetlnej metodą pierścieni Newtona
 Politechnika Łódzka FTIMS Kierunek: Informatyka rok akademicki: 2008/2009 sem. 2. grupa II Termin: 26 V 2009 Nr. ćwiczenia: 412 Temat ćwiczenia: Wyznaczanie długości fali świetlnej metodą pierścieni Newtona
Politechnika Łódzka FTIMS Kierunek: Informatyka rok akademicki: 2008/2009 sem. 2. grupa II Termin: 26 V 2009 Nr. ćwiczenia: 412 Temat ćwiczenia: Wyznaczanie długości fali świetlnej metodą pierścieni Newtona
BADANIE INTERFEROMETRU YOUNGA
 Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Laboratorium Programowanie Obrabiarek CNC. Nr H04
 Politechnika Poznańska Instytut Technologii Mechanicznej Laboratorium Programowanie Obrabiarek CNC Nr H04 Programowanie zarysów swobodnych FK Opracował: Dr inŝ. Wojciech Ptaszyński Poznań, 06 stycznia
Politechnika Poznańska Instytut Technologii Mechanicznej Laboratorium Programowanie Obrabiarek CNC Nr H04 Programowanie zarysów swobodnych FK Opracował: Dr inŝ. Wojciech Ptaszyński Poznań, 06 stycznia
Przykładowe pytania na teście teoretycznym
 Przykładowe pytania na teście teoretycznym Przedmiot: Informatyka I Rok akademicki: 2014/2015 Semestr : zimowy Studia: I / Z W grafice wektorowej obraz reprezentowany jest: przez piksele przez obiekty
Przykładowe pytania na teście teoretycznym Przedmiot: Informatyka I Rok akademicki: 2014/2015 Semestr : zimowy Studia: I / Z W grafice wektorowej obraz reprezentowany jest: przez piksele przez obiekty
Grafika komputerowa Wykład 11 Barwa czy kolor?
 Grafika komputerowa Wykład 11 czy kolor? Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 2 3 Mieszanie addytywne barw
Grafika komputerowa Wykład 11 czy kolor? Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 2 3 Mieszanie addytywne barw
Grafika 2D. Pojęcia podstawowe. opracowanie: Jacek Kęsik
 Grafika 2D Pojęcia podstawowe opracowanie: Jacek Kęsik Obraz - przedmiot, przeważnie płaski, na którym za pomocą plam barwnych i kreski, przy zastosowaniu różnych technik malarskich i graficznych autor
Grafika 2D Pojęcia podstawowe opracowanie: Jacek Kęsik Obraz - przedmiot, przeważnie płaski, na którym za pomocą plam barwnych i kreski, przy zastosowaniu różnych technik malarskich i graficznych autor
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli
 Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
Dostosowuje wygląd kolorów na wydruku. Uwagi:
 Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów informują o sposobach wykorzystania funkcji drukarki w celu zmiany ustawień wydruków kolorowych i dostosowania ich według potrzeby. Menu jakości
Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów informują o sposobach wykorzystania funkcji drukarki w celu zmiany ustawień wydruków kolorowych i dostosowania ich według potrzeby. Menu jakości
Przestrzenie barw. 1. Model RGB
 Przestrzenie barw Przeciętny człowiek, nie posiadający zaburzeń wzorku, potrafi dostrzec i opisać otaczające go barwy. Co prawda ilość rozpoznawanych odcieni kolorów bywa różna (wiek, płeć, indywidualne
Przestrzenie barw Przeciętny człowiek, nie posiadający zaburzeń wzorku, potrafi dostrzec i opisać otaczające go barwy. Co prawda ilość rozpoznawanych odcieni kolorów bywa różna (wiek, płeć, indywidualne
Przetwarzanie obrazów wykład 1. Adam Wojciechowski
 Przetwarzanie obrazów wykład 1 Adam Wojciechowski Teoria światła i barwy Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe
Przetwarzanie obrazów wykład 1 Adam Wojciechowski Teoria światła i barwy Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe
I V X L C D M. Przykłady liczb niewymiernych: 3; 2
 1 LICZBY Liczby naturalne: 0; 1; 2; 3;.... Liczby całkowite:...; -3; -2; -1; 0; 1; 2; 3;.... Liczbą wymierną nazywamy każdą liczbę, którą można zapisać w postaci ułamka a b, gdzie a i b są liczbami całkowitymi,
1 LICZBY Liczby naturalne: 0; 1; 2; 3;.... Liczby całkowite:...; -3; -2; -1; 0; 1; 2; 3;.... Liczbą wymierną nazywamy każdą liczbę, którą można zapisać w postaci ułamka a b, gdzie a i b są liczbami całkowitymi,
Opis funkcji programu AnaRIP mpower v.2.0
 Opis funkcji programu AnaRIP mpower v.2.0 Funkcja podglądu działa zgodnie z zasadą WYSWIG, czyli zmiany jakiegokolwiek parametru wydruku powoduje zmianę podglądu. Dzięki temu możemy zobaczyć na komputerze
Opis funkcji programu AnaRIP mpower v.2.0 Funkcja podglądu działa zgodnie z zasadą WYSWIG, czyli zmiany jakiegokolwiek parametru wydruku powoduje zmianę podglądu. Dzięki temu możemy zobaczyć na komputerze
Kolor w grafice komputerowej. Światło i barwa
 Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Newton Isaac ( ), fizyk, matematyk, filozof i astronom angielski.
 Pierwsze wyjaśnienie bogactwa barw w świecie zawdzięczamy geniuszowi Newtona. Oto jak opisuje on jedno ze swych doświadczeń: W roku 1666 sporządziłem sobie trójkątny pryzmat szklany, aby za jego pomocą
Pierwsze wyjaśnienie bogactwa barw w świecie zawdzięczamy geniuszowi Newtona. Oto jak opisuje on jedno ze swych doświadczeń: W roku 1666 sporządziłem sobie trójkątny pryzmat szklany, aby za jego pomocą
Chemia Procesu Widzenia
 Chemia Procesu Widzenia barwy H.P. Janecki Miłe spotkanie...wykład 11 Spis treści Światło Powstawanie wrażenia barwy Barwa Modele barw 1. Model barw HSV 2. Model barw RGB 3. Sprzętowa reprezentacja barwy
Chemia Procesu Widzenia barwy H.P. Janecki Miłe spotkanie...wykład 11 Spis treści Światło Powstawanie wrażenia barwy Barwa Modele barw 1. Model barw HSV 2. Model barw RGB 3. Sprzętowa reprezentacja barwy
Scenariusz zajęć pozalekcyjnych w ramach Innowacyjnej Szkoły Zawodowej
 Scenariusz zajęć pozalekcyjnych w ramach Innowacyjnej Szkoły Zawodowej Szkoła Zespół Szkół Rolniczych w Namysłowie Prowadzący mgr inż. Andrzej Kazimierczyk Liczba godzin - 3 1. Klasa II oraz IV technikum
Scenariusz zajęć pozalekcyjnych w ramach Innowacyjnej Szkoły Zawodowej Szkoła Zespół Szkół Rolniczych w Namysłowie Prowadzący mgr inż. Andrzej Kazimierczyk Liczba godzin - 3 1. Klasa II oraz IV technikum
Grenlandia się topi badanie rozkładu kątów pomiędzy strumykami na lądolodzie na podstawie analizy obrazu
 Grenlandia się topi badanie rozkładu kątów pomiędzy strumykami na lądolodzie na podstawie analizy obrazu Małgorzata Bąk, Marcin Byra, Filip Chudzyński, Marcin Osiekowicz Opiekun: dr hab. Piotr Szymczak
Grenlandia się topi badanie rozkładu kątów pomiędzy strumykami na lądolodzie na podstawie analizy obrazu Małgorzata Bąk, Marcin Byra, Filip Chudzyński, Marcin Osiekowicz Opiekun: dr hab. Piotr Szymczak
ZADANIE 1 (5 PKT) ZADANIE 2 (5 PKT) Oblicz objętość czworościanu foremnego o krawędzi a.
 ZADANIE 1 (5 PKT) Czworościan foremny o krawędzi a rozcięto płaszczyzna prostopadła do jednej z krawędzi, przechodzac a w odległości 0, 25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
ZADANIE 1 (5 PKT) Czworościan foremny o krawędzi a rozcięto płaszczyzna prostopadła do jednej z krawędzi, przechodzac a w odległości 0, 25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
Graniastosłupy mają dwie podstawy, a ich ściany boczne mają kształt prostokątów.
 GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
SCENARIUSZ LEKCJI CHEMII Z WYKORZYSTANIEM FILMU Kolory nie istnieją. SPIS TREŚCI: I. Wprowadzenie. II. Części lekcji.
 SCENARIUSZ LEKCJI CHEMII Z WYKORZYSTANIEM FILMU Kolory nie istnieją SPIS TREŚCI: I. Wprowadzenie. II. Części lekcji. 1. Część wstępna. 2. Część realizacji. 3. Część podsumowująca. III. Zasady BHP. IV.
SCENARIUSZ LEKCJI CHEMII Z WYKORZYSTANIEM FILMU Kolory nie istnieją SPIS TREŚCI: I. Wprowadzenie. II. Części lekcji. 1. Część wstępna. 2. Część realizacji. 3. Część podsumowująca. III. Zasady BHP. IV.
Jaki kolor widzisz? Doświadczenie pokazuje zjawisko męczenia się receptorów w oku oraz istnienie barw dopełniających. Zastosowanie/Słowa kluczowe
 1 Jaki kolor widzisz? Abstrakt Doświadczenie pokazuje zjawisko męczenia się receptorów w oku oraz istnienie barw Zastosowanie/Słowa kluczowe wzrok, zmysły, barwy, czopki, pręciki, barwy dopełniające, światło
1 Jaki kolor widzisz? Abstrakt Doświadczenie pokazuje zjawisko męczenia się receptorów w oku oraz istnienie barw Zastosowanie/Słowa kluczowe wzrok, zmysły, barwy, czopki, pręciki, barwy dopełniające, światło
WSTĘP DO GRAFIKI KOMPUTEROWEJ
 WSTĘP DO GRAFIKI KOMPUTEROWEJ Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 44 Plan wykładu Światło, kolor, zmysł wzroku Obraz: fotgrafia, poligrafia, grafika
WSTĘP DO GRAFIKI KOMPUTEROWEJ Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 44 Plan wykładu Światło, kolor, zmysł wzroku Obraz: fotgrafia, poligrafia, grafika
Wyższa Szkoła Informatyki Stosowanej i Zarządzania
 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa IZ06TC01, Zespół 3 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr 5 Temat: Modelowanie koloru, kompresja obrazów,
Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa IZ06TC01, Zespół 3 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr 5 Temat: Modelowanie koloru, kompresja obrazów,
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 13 Teoria stereometria
 1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
Jak posługiwać się kartą testową BM_Test_Gradation.pdf?
 Jak posługiwać się kartą testową BM_Test_Gradation.pdf? Wprowadzenie. Wiele nowoczesnych i zaawansowanych drukarek laserowych i atramentowych posiada w swoim menu możliwość wydrukowania z pamięci własnej
Jak posługiwać się kartą testową BM_Test_Gradation.pdf? Wprowadzenie. Wiele nowoczesnych i zaawansowanych drukarek laserowych i atramentowych posiada w swoim menu możliwość wydrukowania z pamięci własnej
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE
 OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
Wykonawca: PIOTR DOMALEWSKI. Termin oddania sprawozdania: 30.08
 SPRAWOZDANIE Z LABORATORIUM Przedmiot: KOMUNIKACJA CZŁOWIEK KOMPUTER Temat ćwiczenia: ZNACZENIE BARWY W PROJEKTOWANIU INTERFEJSU UŻYTKOWNIKA Kierunek: Informatyka Tryb / semestr: Zaoczne / VI Termin wykonania
SPRAWOZDANIE Z LABORATORIUM Przedmiot: KOMUNIKACJA CZŁOWIEK KOMPUTER Temat ćwiczenia: ZNACZENIE BARWY W PROJEKTOWANIU INTERFEJSU UŻYTKOWNIKA Kierunek: Informatyka Tryb / semestr: Zaoczne / VI Termin wykonania
Opracowanie tablic: Adam Konstantynowicz, Anna Konstantynowicz, Kaja Mikoszewska
 Opracowanie tablic: Adam Konstantynowicz, Anna Konstantynowicz, Kaja Mikoszewska Redaktor serii: Marek Jannasz Ilustracje: Magdalena Wójcik Projekt okładki: Teresa Chylińska-Kur, KurkaStudio Projekt makiety
Opracowanie tablic: Adam Konstantynowicz, Anna Konstantynowicz, Kaja Mikoszewska Redaktor serii: Marek Jannasz Ilustracje: Magdalena Wójcik Projekt okładki: Teresa Chylińska-Kur, KurkaStudio Projekt makiety
3. ZJAWISKO BARWY W SZKŁACH. Rodzaje POSTRZEGANIA
 3. ZJAWISKO BARWY W SZKŁACH Rodzaje POSTRZEGANIA Wyróżniamy trzy rodzaje POSTRZEGANIA: a) Skotopowe opiera się na czynności samych pręcików; duża czułośd na kontrast; brak widzenia barw; dostrzegane kontury
3. ZJAWISKO BARWY W SZKŁACH Rodzaje POSTRZEGANIA Wyróżniamy trzy rodzaje POSTRZEGANIA: a) Skotopowe opiera się na czynności samych pręcików; duża czułośd na kontrast; brak widzenia barw; dostrzegane kontury
Wszystkie zdjęcia użyte w niniejszym dokumencie służą wyłącznie do celów szkoleniowych.
 Nadruk CMYK na kubkach reklamowych to narzędzie o ogromnych możliwościach. Nie oznacza to jednak, że technologia ta może być wykorzystywana w każdym przypadku. Nadruki te posiadają bowiem szereg ograniczeń,
Nadruk CMYK na kubkach reklamowych to narzędzie o ogromnych możliwościach. Nie oznacza to jednak, że technologia ta może być wykorzystywana w każdym przypadku. Nadruki te posiadają bowiem szereg ograniczeń,
Multimedia i grafika komputerowa
 Część pierwsza Grafika komputerowa wprowadzenie Autor Roman Simiński Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie zawiera skrót treści wykładu, lektura tych materiałów nie zastąpi
Część pierwsza Grafika komputerowa wprowadzenie Autor Roman Simiński Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie zawiera skrót treści wykładu, lektura tych materiałów nie zastąpi
Fotometria i kolorymetria
 9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
Jakość koloru. Menu Jakość. Strona 1 z 7
 Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów stanowią pomoc w poznawaniu, jak za pomocą dostępnych funkcji drukarki można zmieniać ustawienia kolorowych wydruków i dostosowywać je do
Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów stanowią pomoc w poznawaniu, jak za pomocą dostępnych funkcji drukarki można zmieniać ustawienia kolorowych wydruków i dostosowywać je do
Środowisko pracy grafików
 atedra Informatyki Stosowanej Politechniki Łódzkiej Projekt do druku - Agnieszka owalska-owczarek Środowisko pracy grafików Użyteczność modeli łączenia barw w projektach przeznaczonych do wyświetlania
atedra Informatyki Stosowanej Politechniki Łódzkiej Projekt do druku - Agnieszka owalska-owczarek Środowisko pracy grafików Użyteczność modeli łączenia barw w projektach przeznaczonych do wyświetlania
1. Rozwój grafiki użytkowej i jej rola we współczesnym świecie Pismo oraz inne środki wyrazu wchodzące w skład pojęcia,,sztuka graficzna
 Estetyka druku 1. Rozwój grafiki użytkowej i jej rola we współczesnym świecie 1.1. Pismo oraz inne środki wyrazu wchodzące w skład pojęcia,,sztuka graficzna Początki sztuk plastycznych w historii prymitywnych
Estetyka druku 1. Rozwój grafiki użytkowej i jej rola we współczesnym świecie 1.1. Pismo oraz inne środki wyrazu wchodzące w skład pojęcia,,sztuka graficzna Początki sztuk plastycznych w historii prymitywnych
ZASADY STOSOWANIA LOGO 2 WERSJA PODSTAWOWA 3 WERSJA CZARNA I BIAŁA 4 POLE OCHRONNE 5 MINIMALNA WIELKOŚĆ 6 KOLORY 7 TYPOGRAFIA
 ZASADY STOSOWANIA LOGO 2 WERSJA PODSTAWOWA 3 WERSJA CZARNA I BIAŁA 4 POLE OCHRONNE 5 MINIMALNA WIELKOŚĆ 6 KOLORY 7 TYPOGRAFIA WERSJA PODSTAWOWA Logo składa się z trzech liter nazwy firmy. Ich krój, kolor,
ZASADY STOSOWANIA LOGO 2 WERSJA PODSTAWOWA 3 WERSJA CZARNA I BIAŁA 4 POLE OCHRONNE 5 MINIMALNA WIELKOŚĆ 6 KOLORY 7 TYPOGRAFIA WERSJA PODSTAWOWA Logo składa się z trzech liter nazwy firmy. Ich krój, kolor,
GRAFIKA. Rodzaje grafiki i odpowiadające im edytory
 GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 13 Zadania stereometria
 1 TEST WSTĘPNY 1. (1p) Graniastosłup ma 12 wierzchołków. Liczba krawędzi tego graniastosłupa to: A. 12 B. 18 C. 24 D. 36 2. (1p) Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu
1 TEST WSTĘPNY 1. (1p) Graniastosłup ma 12 wierzchołków. Liczba krawędzi tego graniastosłupa to: A. 12 B. 18 C. 24 D. 36 2. (1p) Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu
1 Podstawowe pojęcia i definicje
 1 Podstawowe pojęcia i definicje J a c e k Ta r a s i u k 1.1 Grafika wektorowa i rastrowa grafika rastrowa grafika bitmapowa grafika wektorowa Rysunek 1.1 Przykładowa grafika rastrowa (bitmapa) W grafice
1 Podstawowe pojęcia i definicje J a c e k Ta r a s i u k 1.1 Grafika wektorowa i rastrowa grafika rastrowa grafika bitmapowa grafika wektorowa Rysunek 1.1 Przykładowa grafika rastrowa (bitmapa) W grafice
Makijaż zasady ogólne
 Makijaż Makijaż zasady ogólne -relatywizm barw, -światłocień, -perspektywa barwna, -podział kolorów, -technika monochromatyczna, -zasada kontrastu (kolory dopełniające się). relatywizm barw relatywizm
Makijaż Makijaż zasady ogólne -relatywizm barw, -światłocień, -perspektywa barwna, -podział kolorów, -technika monochromatyczna, -zasada kontrastu (kolory dopełniające się). relatywizm barw relatywizm
Fotometria i kolorymetria
 11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
Środowisko pracy grafików
 Katedra Informatyki Stosowanej Politechniki Łódzkiej Środowisko pracy grafików - Agnieszka Kowalska-Owczarek Środowisko pracy grafików Użyteczność modeli łączenia barw w projektach przeznaczonych do wyświetlania
Katedra Informatyki Stosowanej Politechniki Łódzkiej Środowisko pracy grafików - Agnieszka Kowalska-Owczarek Środowisko pracy grafików Użyteczność modeli łączenia barw w projektach przeznaczonych do wyświetlania
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
5. ZJAWISKO BARWY PERCEPCJA (WRAŻENIE) BARWY
 5. ZJAWISKO BARWY Barwa pochodzi od światła. Światło jest przenoszone przez fale elektromagnetyczne o określonych długościach. Widzialne długości fal można zaobserwować pomiędzy 380 a 780 nm. (1 nanometr
5. ZJAWISKO BARWY Barwa pochodzi od światła. Światło jest przenoszone przez fale elektromagnetyczne o określonych długościach. Widzialne długości fal można zaobserwować pomiędzy 380 a 780 nm. (1 nanometr
PODSTAWY KOREKTY KOLORU
 PODSTAWY KOREKTY KOLORU Barwa / Nasycenie Kolor selektywny Polecenie Replace Color (Wymień kolor) Polecenie Channel Mixer (Mieszanie kanałów) Korekta koloru w praktyce Naprawa zeskanowanego materiału Funkcja
PODSTAWY KOREKTY KOLORU Barwa / Nasycenie Kolor selektywny Polecenie Replace Color (Wymień kolor) Polecenie Channel Mixer (Mieszanie kanałów) Korekta koloru w praktyce Naprawa zeskanowanego materiału Funkcja
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy.
 Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Ustawienia materiałów i tekstur w programie KD Max. MTPARTNER S.C.
 Ustawienia materiałów i tekstur w programie KD Max. 1. Dwa tryby własności materiału Materiał możemy ustawić w dwóch trybach: czysty kolor tekstura 2 2. Podstawowe parametry materiału 2.1 Większość właściwości
Ustawienia materiałów i tekstur w programie KD Max. 1. Dwa tryby własności materiału Materiał możemy ustawić w dwóch trybach: czysty kolor tekstura 2 2. Podstawowe parametry materiału 2.1 Większość właściwości
Skrypt 19. Bryły. 14. Zastosowanie twierdzenia Pitagorasa do obliczania pól powierzchni ostrosłupów
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 19 Bryły 11. Ostrosłupy - rozpoznawanie,
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 19 Bryły 11. Ostrosłupy - rozpoznawanie,
Zmysły. Wzrok 250 000 000. Węch 40 000 000. Dotyk 2 500 000. Smak 1 000 000. Słuch 25 000. Równowaga?
 Zmysły Rodzaj zmysłu Liczba receptorów Wzrok 250 000 000 Węch 40 000 000 Dotyk 2 500 000 Smak 1 000 000 Słuch 25 000 Równowaga? Fale elektromagnetyczne Wzrok Informacje kształt zbliżony do podstawowych
Zmysły Rodzaj zmysłu Liczba receptorów Wzrok 250 000 000 Węch 40 000 000 Dotyk 2 500 000 Smak 1 000 000 Słuch 25 000 Równowaga? Fale elektromagnetyczne Wzrok Informacje kształt zbliżony do podstawowych
Czy pamiętasz? Zadanie 1. Rozpoznaj wśród poniższych brył ostrosłupy i graniastosłupy.
 1. Bryły Tradycyjna futbolówka jest zszyta z 3232 kawałków. Gdybyśmy ją rozcięli, ujrzelibyśmy siatkę dwudziestościanu ściętego. Kulisty kształt piłka otrzymuje dzięki wypełnieniu sprężonym powietrzem.
1. Bryły Tradycyjna futbolówka jest zszyta z 3232 kawałków. Gdybyśmy ją rozcięli, ujrzelibyśmy siatkę dwudziestościanu ściętego. Kulisty kształt piłka otrzymuje dzięki wypełnieniu sprężonym powietrzem.
Rodzaje skanerów. skaner ręczny. skaner płaski. skaner bębnowy. skaner do slajdów. skaner kodów kreskowych
 Skaner Rodzaje skanerów skaner ręczny skaner płaski skaner bębnowy skaner do slajdów skaner kodów kreskowych Skaner ręczny Skaner płaski Przetwornik CCD CCD (ang. Charge Coupled Device) technologia stosowana
Skaner Rodzaje skanerów skaner ręczny skaner płaski skaner bębnowy skaner do slajdów skaner kodów kreskowych Skaner ręczny Skaner płaski Przetwornik CCD CCD (ang. Charge Coupled Device) technologia stosowana
Rok akademicki: 2013/2014 Kod: JIS s Punkty ECTS: 5. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Podstawy grafiki komputerowej Rok akademicki: 2013/2014 Kod: JIS-1-505-s Punkty ECTS: 5 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Informatyka Stosowana Specjalność: - Poziom studiów:
Nazwa modułu: Podstawy grafiki komputerowej Rok akademicki: 2013/2014 Kod: JIS-1-505-s Punkty ECTS: 5 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Informatyka Stosowana Specjalność: - Poziom studiów:
Posiadasz taki lub inny TV?
 Pełny raport kalibracyjny telewizora: Panasonic 55" DX700 Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080
Pełny raport kalibracyjny telewizora: Panasonic 55" DX700 Posiadasz taki lub inny TV? Umów się na kalibrację by oglądać materiały wideo w takiej formie w jakiej widział je reżyser filmu! Telefon: 510 080
KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM. Etap Wojewódzki
 Kod ucznia - - pieczątka WKK Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM Etap Wojewódzki Drogi Uczniu, witaj na III etapie konkursu matematycznego. Przeczytaj uważnie
Kod ucznia - - pieczątka WKK Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM Etap Wojewódzki Drogi Uczniu, witaj na III etapie konkursu matematycznego. Przeczytaj uważnie
Podstawy grafiki komputerowej
 Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Wymagania edukacyjne na poszczególne stopnie szkolne klasa III
 Wymagania edukacyjne na poszczególne stopnie szkolne klasa III Rozdział 1. Bryły - wie, czym jest graniastosłup, graniastosłup prosty, graniastosłup prawidłowy - wie, czym jest ostrosłup, ostrosłup prosty,
Wymagania edukacyjne na poszczególne stopnie szkolne klasa III Rozdział 1. Bryły - wie, czym jest graniastosłup, graniastosłup prosty, graniastosłup prawidłowy - wie, czym jest ostrosłup, ostrosłup prosty,
ROZDZIAŁ 1 Podstawowe pojęcia i definicje
 ROZDZIAŁ 1 Podstawowe pojęcia i definicje W tym rozdziale omówiono: Grafikę wektorową i rastrową Pojęcie rozdzielczości Powiększenie obrazu Podstawową reprezentację barw Modele barw Kanały alfa Obrazy
ROZDZIAŁ 1 Podstawowe pojęcia i definicje W tym rozdziale omówiono: Grafikę wektorową i rastrową Pojęcie rozdzielczości Powiększenie obrazu Podstawową reprezentację barw Modele barw Kanały alfa Obrazy
WYTYCZNE DOTYCZĄCE PROMOCJI
 Unia Europejska Europejski Fundusz Rozwoju Regionalnego Załącznik nr 12 do PRZEWODNIKA BENEFICJENTA RPO WP 2007-2013 WYTYCZNE DOTYCZĄCE PROMOCJI PROJEKTÓW UE DLA BENEFICJENTÓW REGIONALNEGO PROGRAMU OPERACYJNEGO
Unia Europejska Europejski Fundusz Rozwoju Regionalnego Załącznik nr 12 do PRZEWODNIKA BENEFICJENTA RPO WP 2007-2013 WYTYCZNE DOTYCZĄCE PROMOCJI PROJEKTÓW UE DLA BENEFICJENTÓW REGIONALNEGO PROGRAMU OPERACYJNEGO
Geometria. Hiperbola
 Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
