Adam Korzeniewski p Katedra Systemów Multimedialnych

Transkrypt

1 Adam Korzeniewski p Katedra Systemów Multimedialnych

2 Operacja na dwóch funkcjach dająca w wyniku modyfikację oryginalnych funkcji (wynikiem jest iloczyn splotowy). Jest działaniem przemiennym (podobnie jak mnożenie)

3 Algorytm FFT jest tak bardzo skuteczny, że w przypadku obliczania splotu kołowego y n x n h n 2 ( N mnożeń i N 1 2 dodawań) opłaca się obliczyć FFT FFT widma sygnałów x n X k, h H k, pomnożyć widma Y k k H k i obliczyć odwrotne przekształcenie Y k y n. X IFFT

4 Ten sposób obliczania splotu nazywa się szybkim splotem, gdyż obliczenia trwają krócej już od N = 32 w przypadku splatania sygnałów zespolonych i od N = 64 w przypadku splatania sygnałów rzeczywistych. Korzystne jest to, że w tym zastosowaniu FFT nie ma potrzeby przenumerowywania próbek. Dodatkowe korzyści odnosi się w typowej sytuacji, gdy splot jest obliczany dla różnych sygnałów x[n] przy tej samej funkcji h[n]. Wystarczy wtedy obliczyć przekształcenie tylko jeden raz.

5 x FFT x h y x h ş X k H k Y k X k H k IFFT y FFT h

6 Jeżeli sygnał wejściowy x[n] jest bardzo długi (czy wręcz nieskończony, tak jak to jest przy przetwarzaniu w czasie rzeczywistym sygnałów dźwiękowych, czy obrazów ruchomych), to jego splatanie z odpowiedzią impulsową filtru h[n] o długości K jest rozbijane na sumę szybkich splotów.

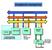
7 Sygnał wejściowy należy rozbić na sumę bloków, każdy o długości M. Splot liniowy dwóch sygnałów o długościach M i K daje sygnał o długości M + K - 1. Splot kołowy powinien mieć taką właśnie długość N = M + K - 1, aby równał się splotowi liniowemu. Dlatego przed wykonaniem splotu kołowego sygnał h[n] jest uzupełniany M-1 zerami do N oraz blok sygnału wejściowego x i [n] jest uzupełniany K-1 zerami do N. Wyniki kolejnych splotów kołowych y i [n] są sumowane na zakładkę o długości K-1, stąd metoda ma angielską nazwę overlap-add.

8 x K h N M + K 1 M 1 0 Uzupełnienie zerami M M M M K 1 0 x 1 y 1 M K 1 + Uzupełnienie zerami M K 1 0 x 2 y 2 M K 1 + Uzupełnienie zerami M K 1 0 x 3 y 3 M L K 1

9 Równoważny sposób postępowania polega na zapamiętaniu K-1 końcowych próbek z poprzedniego bloku x i-1 [n] i uzupełnieniu tymi próbkami początku następnego bloku x i [n]. Tym razem splot kołowy daje K-1 początkowych próbek fałszywych (różniących się od wyniku splotu liniowego) i są one odrzucane z sygnału wyjściowego.

10 x K h K 1 0 Uzupełnienie zerami K 1 Odrzuć to N M + K 1 M 1 0 Uzupełnienie zerami M M M x 1 M y 1 M K 1 K 1 Odrzuć to Zapamiętaj i przenieś x 2 y 2 M M K 1 K 1 Odrzuć to Zapamiętaj i przenieś x 3 y 3 M M L

11 Liczba kolejnych bloków próbek sygnału wejściowego x[n] może być nieskończenie wielka. Ten sposób wprowadzania może być stosowany w procesorach sygnałowych przetwarzających sygnały cyfrowe w czasie rzeczywistym. Kolejne próbki ze źródła sygnału (mikrofon, kamera telewizyjna) są wprowadzane do odbiorczego bufora kołowego, a wyniki są wyprowadzane do nadawczego bufora kołowego.

12 Wykonanie programu komputerowego, to wykonanie sekwencji instrukcji. Instrukcję można przedstawić jako 5 bloków (stopni), każdy wykonywany w 1 cyklu zegara. Bloki oznaczymy literami F, D, E, A, S (pierwsze litery nazw w języku angielskim).

13 E F D ALU A S pobranie instrukcji z pamięci (ang. instruction fetch) dekodowanie instrukcji (ang. instruction decode) wykonanie instrukcji (ang. instruction execute) otwarcie dostępu do pamięci (ang. memory access) zapisanie wyniku wykonania instrukcji (ang. store, write back)

14 W zwykłym (niepotokowym) przetwarzaniu najpierw wykonuje się bloki pierwszej instrukcji, następnie drugiej instrukcji, itd. Wyniki wykonania kolejnych instrukcji są zapisywane co 5 cykli zegara. Przetwarzanie niepotokowe Clock cycle Instr. 1 F1 D1 E1 A1 S1 Instr. 2 F2 D2 E2 A2 S2

15 Procesor sygnałowy ma logikę przystosowaną do wykonywania wszystkich bloków jednocześnie, dzięki czemu jest możliwe przetwarzanie potokowe. Począwszy od 5-go cyklu zegara wykonywanych jest 5 bloków jednocześnie, każdy dla innej, kolejnej instrukcji. Wyniki S1, S2,... są dostępne w kolejnych cyklach zegara (5-tym, 6-tym, itd.), a nie po co 5-tym cyklu zegara, jak to było w przetwarzaniu niepotokowym.

16 Potencjalnie jest możliwe 5-cio krotne zwiększenie prędkości obliczeń. Niestety trzeba z góry przewidzieć sytuacje konfliktowe, hazard (w literaturze naukowej wymienia się kilkadziesiąt takich sytuacji). Na przykład w przypadku instrukcji skoku, w najgorszym przypadku trzeba wycofać instrukcje, które następowały po instrukcji skoku i rozpocząć zapełnianie potoku od adresu, do którego nastąpił skok.

17 Clock cycle Przetwarzanie potokowe Instr. 1 F1 D1 E1 A1 S1 Instr. 2 F2 D2 E2 A2 S2 Instr. 3 F3 D3 E3 A3 S3 Instr. 4 F4 D4 E4 A4 S4 Instr. 5 F5 D5 E5 A5 S5 Instr. 6 F6 D6 E6 A6 S6

18 KONIEC