Complex Analysis Theorems
|
|
|
- Maciej Małek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Complex Analysis Theorems Chapter : Complex Numbers Proposition. (Basic Identities and Inequalities). Let z, z, z 2, z 3 C. Let z = x + iy = r(cos θ + i sin θ) and z k = x k + iy k = r k (cos θ k + i sin θ k ). z = z = zz = z 2 = zz Re z = (z + z) 2 Im z = (z z) 2i z + z 2 = z + z 2 (conjugation is a field automorphism) z z 2 = z z 2 z z 2 = z z 2 z + z 2 z + z 2 (triangle inequality) z + z z n z + z z n (generalized triangle inequality) z z 2 z z 2 z + z z + z 2 2 = 2 ( z 2 + z 2 2) (parallelogram equality) z z 2 = r r 2 ( cos(θ + θ 2 ) + i sin(θ + θ 2 ) ) arg z = arg(z ) = arg z z n = r n (cos nθ + i sin nθ) for n Z (De Moivre s Formula) ( z /n = r /n cos θ + 2πk + i sin θ + 2πk ) for n N and k = 0,,..., n n n Proposition.2. Let z, z 2 C \ {0}. Then they are positive multiples of each other if and only if z z 2 is real and positive. Proposition.3. Let p(x) be a polynomial with real coefficients. If p(z) = 0 for some z C, then p(z) = 0. (That is, the Galois group of C/R is just Z/2Z, the identity and complex conjugation.) Proposition.4. Let z C \ {}. Then n k=0 z k = + z + z z n = zn+ z Proposition.5. The sum of the nth roots of equals zero for n 2.
2 2 Chapter 2: Complex Differentiation Proposition 2. (Basic Properties of Complex Differentiation). Let f and g be complexvalued functions defined on an open set G.. If f is differentiable at z 0, then f is continuous at z (Leibniz rule) If f and g are differentiable at z 0, then f + g and fg are differentiable at z 0, and (f + g) (z 0 ) = f (z 0 ) + g (z 0 ) and (fg) (z 0 ) = f (z 0 )g(z 0 ) + f(z 0 )g (z 0 ). 3. If f and g are differentiable at z 0 and g(z 0 ) 0, then f/g is differentiable at z 0. (There is a quotient rule, but just apply the product rule to f g.) 4. (Chain rule) If f is differentiable at z 0 and g is differentiable at f(z 0 ), then the composition g f is differentiable at z 0 and (g f) (z 0 ) = g (f(z 0 ))f (z 0 ). Proposition 2.2. Polynomial functions are holomorphic. Proposition 2.3. Rational functions are holomorphic everywhere that their denominator is nonzero. Proposition 2.4 (Cauchy-Riemann Equations). Let f(z) = f(x + iy) = u(x, y) + iv(x, y) be a complex function defined on an open set G containing z 0. Then f is differentiable at z 0 if and only if u, v are differentiable at z 0 and u x (z 0) = v y (z 0) and u y (z 0) = v x (z 0) In that case, f (z 0 ) = u x (z 0) + i v x (z 0) = v y (z 0) i u y (z 0) Proposition 2.5. In polar form, the Cauchy-Riemann equations are r u r = v θ u θ = r v r Proposition 2.6. Let the complex-valued function f = u + iv be defined in the open subset G C, and assume that u and v have first partial derivatives in G. Then f is differentiable at each point where those partial derivatives are continuous and satisfy the Cauchy-Riemann equations. Proposition 2.7. Let f be holomorphic in an open disk D. If any of the following hold for all z D, then f is constant in D: f (z) = 0, f(z) R, f = c, arg f = c. Proposition 2.8. Let f be holomorphic on the open set G. Then f(z) is holomorphic on {z : z G}. Proposition 2.9. A function f is differentiable at z 0 if and only if z (z 0) = 0. Proposition 2.0. If f is differentiable at z 0, then f (z 0 ) = f z (z 0). 2
3 Proposition 2.. Let f be holomorphic on an open set G and let : I G be a curve such that is differentiable at t 0, and let z 0 = (t 0 ). Then the curve f : I f(g) is differentiable at t 0 and (f ) (t 0 ) = f ((t 0 )) (t 0 ) = f (z 0 ) (t 0 ) Proposition 2.2 (Holomorphic Maps are Conformal where Derivative is Nonzero). Let f be holomorphic on an open set G and let z 0 G such that f (z 0 ) 0. Let, 2 be curves such that (t ) = 2 (t 2 ) = z 0, and j is regular at t j. Then the angle between f and f 2 is equal to the angle between and 2. Proposition 2.3 (Conformal implies Holomorphic). Let f : G C where G C is open, and suppose that Re f and Im f have continuous first partial derivatives. If f is conformal at each z 0 G, then f is holomorphic and f 0 in G. Proposition 2.4. Let f : G C. imaginary parts are harmonic. Then f is holomorphic if and only if its real and Proposition 2.5. Holomorphic functions are harmonic. Proposition 2.6. Let u, v : G C where G C is open and suppose u, v are of class C 2. Then u, v are harmonic conjugates if and only if u + iv is holomorphic. 3 Chapter 3: Linear Fractional Transformations Proposition 3.. The map CP C given by [z, z 2 ] z z 2 (The RHS is taken to be when z 2 = 0.) is well-defined, and is a bijection. Proposition 3.2. A linear fractional transformation gives a bijection C C. Proposition 3.3. Linear fractional transformations form a group under function composition. That is, LFTs are closed under composition and the inverse of a linear fractional transformation is a linear fractional transformation. Proposition 3.4. Let φ, φ 2 be linear fractional transformations induced by matrices M, M 2 respectively. Then φ φ 2 is induced by M M 2. If φ is a linear fractional transformation induced by M, then φ is induced by M. That is, the map [ ] ( a b z az + b ) c d cz + d from GL(2, C) to the group of LFTs is a group homomorphism. The kernel is H = {λi 2 : λ C \ {0}} where I 2 is the identity of GL(2, C). Thus the LFT group is isomorphic to GL(2, C)/H 3
4 Proposition 3.5. Every linear fractional transformation can be written as a product of a dilation, rotation, translation, and inversion. That is, the dilations, rotations, translations, and the inversion map generate the group of linear fractional transformations. Proposition 3.6. Linear fractional transformations are conformal. Consequently, they are holomorphic and have a first derivative that never vanishes. The next lemma seems very out of place, since it is purely topological. However, it is very useful when dealing with linear fractional transformations. Lemma 3.7. Let X be a topological space, and A X. Let φ : X X be a homeomorphism so that φ(a) = A and φ A : A A is a homeomorphism. Then φ( A) = A and φ A : A A is a homeomorphism. Corollary 3.8. Let φ be a linear fractional transformation, and let C be a clircle dividing C into two disconnected regions X, Y. Since φ(c) is a clircle, it divides C into two disconnected regions X, Ỹ. Then φ X is a bijection X X or a bijection X Ỹ. Intuitively speaking, the above result says that a linear fractional transformation that maps a given clirlce to another clircle must map one side of the clircle in the domain to one side of the image clircle. (Where side refers to the inside/outside if it is a circle, and side refers to top/bottom or right/left if it is a line.) Proposition 3.9. A linear fractional transformation has exactly one or two fixed points. Proposition 3.0. Let z, z 2, z 3 be distinct poins in C, and w, w 2, w 3 be distinct points in C. There is a unique linear fractional transformation φ so that φ(z i ) = w i. Proposition 3.. Let z, z 2, z 3, z 4 be distinct points in C and φ a linear fractional transformation. Then (φz, φz 2 ; φz 3, φz 4 ) = (z, z 2 ; z 3, z 4 ) Proposition 3.2. All translations except for translation by zero are mutually conjugate. Proposition 3.3. Let f be a fractional linear transformation with a unique fixed point at. Then f is a translation. Proposition 3.4. A linear fractional transformation with exactly one fixed point is conjugate to a translation. Proposition 3.5. The image of a clircle under a linear fractional transformation is a clircle. Proposition 3.6. Let z, z 2, z 3, z 4 be distinct points in C. They all lie on a clircle if and only if the cross ratio (z, z 2 ; z 3, z 4 ) is real. Proposition 3.7. A clircle is uniquely determined by three points. 4
5 4 Chapter 4: Elementary Functions Proposition 4.. Let z, z 2 C. Then e z e z 2 = e z +z 2. Proposition 4.2. The complex exponential is holomorphic. Its derivative is itself. Proposition 4.3. If f : C C is holomorphic and f = f, then f is a constant multiple of e z. Proposition 4.4. All complex trigonometric and hyperbolic functions are holomorphic everywhere they are defined. Proposition 4.5. Let z C. Then cos z = cosh iz sin z = i sinh iz Proposition 4.6. Let z C \ {0}. If w is a logarithm of z, then w = ln z + i arg z. Proposition 4.7. If f is holomorphic on a disk containing z 0 and f(z 0 ) 0, then there is a branch of log f on a disk containing z 0. Proposition 4.8. Let G be an open connected subset of C \ {0}. There exists a branch of arg in G if and only if there exists a branch of log in G. Proposition 4.9. If α is a branch of arg z in G, then α + 2πn is another branch for any n Z. Conversely, if α, α 2 are branches of arg in G, then they differ by an integer mulitple of 2π. Proposition 4.0. If l is a branch of log z in G, then l + 2πin is another branch for any n Z. Conversely, any two branches of l in G differ by an integer multiple of 2πi. Proposition 4.. Let l be a branch of log z in the open connected set G. holomorphic and l (z) =. z Then l is Proposition 4.2. If there is a branch of log f in G, then it is a holomorphic function and its derivative is f f. Proposition 4.3. If h is a branch of f /n, then h is holomorphic and h h = f nf. 5 Chapter 5: Power Series Proposition 5.. If n=0 c n converges then lim n c n = 0. Proposition 5.2. Let z C. The geometric series n=0 zn converges to diverges for z. Proposition 5.3. If n=0 c n converges, then c n n=0 c n n=0 z if z < and 5
6 Proposition 5.4. If a series converges absolutely, then it converges. Proposition 5.5. A series of functions converges uniformly on S if and only if it is uniformly Cauchy on S. Proposition 5.6. Let g n be a sequence of complex valued functions that converges uniformly on G. Then g n converges uniformly on any subset of G. Proposition 5.7. Let n=0 a n(z z 0 ) n be a power series. The region of convergence is either {z 0 }, C, or an open disk z z 0 < R, possibly including points on the boundary of that disk. If it converges on the disk z z 0 < R, then it converges absolutely and locally uniformly. Proposition 5.8. Let n=0 a nz n and n=0 b n be power series with respective radii of convergence R, R 2. If there exists M > 0 so that a n M b n for all but finitely many n, then R R 2. Proposition 5.9. Let a n be a sequence of real numbers. Then lim a n exists if and only if lim sup a n = lim inf a n. If it exists, then lim a n = lim sup a n = lim inf a n. Proposition 5.0. Let a n, b n be real sequences. Then lim sup(a n + b n ) lim sup a n + lim sup b n provided the sum on the right is well-defined (that is, it isn t ). If either sequence converges, then we get equality. Proposition 5.. Let a n, b n be positive real sequences. Then lim sup(a n b n ) (lim sup a n )(lim sup b n ) as long as the product on the right is meaningful (i.e. not 0 ). If either sequence converges, we get equality. Proposition 5.2 (Cauchy-Hadamard Theorem). The radius of convergence of n=0 a n(z z 0 ) n is lim sup n a n /n Proposition 5.3. Let n=0 a nz n and n=0 b n be power series with respective radii of convergence R, R 2. The radius of convergence of n=0 (a n + b n )z n is at least min(r, R 2 ). The radius of convergence of n=0 a nb n z n is at least R R 2 (as long as R R 2 isn t 0 ). Proposition 5.4. A power series n=0 a nz n and its termwise derivative n= na nz n have the same radius of convergence. Proposition 5.5 (Ratio Test). If lim a n+ a n n exists, then the above limit is the radius of convergence of n=0 a n(z z 0 ) n. 6
7 Proposition 5.6. Suppose that the power series n=0 a n(z z 0 ) n has positive radius of convergence R. Then the function f represented by the above power series in the disk z z 0 < R is holomorphic, and f is represented in the same disk by the termwise derivative n= na n(z z 0 ) n. Proposition 5.7. A function represented by a power series in a disk z z 0 < R is infinitely differentiable on that disk. Proposition 5.8. The power series has infinite radius of convergence, and represents the function e z on all of C. n=0 Proposition 5.9. Let n=0 a n(z z 0 ) n and n=0 b n(z z 0 ) n be power series with the same center, both with positive radii of convergence R, R 2 respectively. Then their Cauchy product converges in the disk z z 0 < min(r, R 2 ). The function represented by the Cauchy product is the product of functions represented by the original series. That is, ( n ) ( ) ( ) a k b n k (z z 0 ) n = a n (z z 0 ) n b n (z z 0 ) n n=0 k=0 n=0 6 Chapter 6: Complex Integration Proposition 6. (Linearity of Complex Integral). Let φ, φ 2 : [a, b] C be piecewise continuous and let c, c 2 C. Then b a z n n! n=0 b b c φ (t) + c 2 φ 2 (t)dt = c φ (t)dt + c 2 φ 2 (t)dt Proposition 6.2 (Fundamental Theorem of Calculus). Let φ : [a, b] C be piecewise C. Then b a φ (t)dt = φ(b) φ(a) Proposition 6.3. Let φ : [a, b] C be piecewise continuous. Then b a a b φ(t)dt φ(t) dt Proposition 6.4 (Linearity of Complex Line Integral). Let G, G 2 C and f : G C and f 2 : G 2 C. Let : [a, b] G G 2 be piecewise C, and c, c 2 C. Then c f (z) + c 2 f 2 (z)dz = c f (z)dz + c 2 f 2 (z)dz a a 7
8 Proposition 6.5 (Partitioning of Curves of a Line Integral). Let G C and f : G C. Let : [a, c] G be piecewise C, and let b [a, c]. Define = [a,b] and 2 = [b,c]. Then f(z)dz = f(z)dz + f(z)dz 2 Proposition 6.6. Let G C be open, and let f : G C be holomorphic, and assume that f is continuous. Let : [a, b] G be a piecewise C curve. Then f (z)dz = f((b)) f((a)) In particular, if is a closed curve, then the above integral is zero. Proposition 6.7. Let z 0 C and r > 0. Define : [0, 2π] C by (t) = z 0 + re it. (Note that parametrizes the circle z z 0 = r traversed once clockwise.) Then { (z z 0 ) dz = 2πi n = n 0 n Proposition 6.8. Let G C be open and f : G C and let : [a, b] G be piecewise C. Let = β be a reparametrization of. Then f(z)dz = f(z)dz Because of this equality, when speaking of an integral of a function over a curve, one is free to choose a convenient parametrization to compute the integral. (Note: Reversing the direction of a curve is NOT a reparametrization.) Proposition 6.9. Reversing the direction of a curve changes the sign of the integral over that curve. That is, f(z)dz = f(z)dz Proposition 6.0. Let G C and f : G C be continuous. Let : [a, b] G be piecewise C. Let M be the maximum of f on, that is, M = max{ f((t)) : t [a, b]} Note that M exists by the extreme value theorem becase the trace of is compact. Then f(z)dz ML() where L() is the length of. Proposition 6. (Passing a Limit through an Integral). Let G C and let f n : G C be a sequence of continuous functions. Let : [a, b] G, and suppose that f n converges uniformly to f on ([a, b]). Then lim n f n (z)dz = WARNING: Uniform convergence is necessary! lim f n(z) = f(z)dz n 8
9 7 Chapter 7: Core Versions of Cauchy s Theorem Proposition 7. (Cauchy s Theorem for Triangles). Let G C be open, and let f : G C be holomorphic. Let T be a triangle in C such that T and its interior are contained in G. Then f(z)dz = 0 T Note that this is subsumed by later, more general, versions of Cauchy s Theorem. Proposition 7.2 (Cauchy s Theorem for a Star-Shaped Region). Let G C be star shaped and open. Let f : G C be holomorphic. Let : [a, b] G be a piecewise C curve. Then f(z)dz = 0 Note that this is subsumed by later, more general, versions of Cauchy s Theorem. Proposition 7.3. Let G C be open and star shaped, and let f : G C be holomorphic. Then f has a primitive in G. (Later, we will only need G to be simply connected.) Proposition 7.4 (Cauchy s Formula for a Circle). Let C be a counterclockwise oriented circle and let f be holomorphic on an open set containing C and its interior. Then f(z) = f(w) 2πi w z dw for z in the interior of C. (That is, we can recover the value of f at the center of a circle from the values on the circle.) Proposition 7.5 (Mean Value Property). Let f be holomorphic in the disk z z 0 < R. Then for 0 < r < R, f(z 0 ) = 2π f(z 0 + re it )dt 2π 0 That is, the value of f at the center of the circle z z 0 = r is the average of the values along the circle. Proposition 7.6 (Mean Value Property, 2). Let f be holomorphic in the disk z z 0 < R. Then for 0 < r < R, f(z 0 ) = f(z) da πr 2 z z 0 <r That is, the value of f at the center of the disk z z 0 < r is equal to the average of the values of f on that disk. Proposition 7.7 (Holomorphic functions have local power series representations). Let f be be holomorphic on an open set containing the disk z z 0 < r. Then there is a power series n=0 a n(z z 0 ) n representing f in that disk. In particular, f is represented by its Taylor C series: on z z 0 < R. f(z) = n=0 f (n) (z 0 ) (z z 0 ) n n! 9
10 Proposition 7.8 (Cauchy Integral Formula). The derivative of a holomorphic function is holomorphic. In particular, if f is holomorphic on G, then for z z 0 < r < dist(z 0, G c ) we have f (n) (z) = n! f(w) dw 2πi (w z) n+ Consequently, if f has the local power series representation n=0 a n(z z 0 ) n, then a n = f (n) (z 0 ) = f(w) dw n! 2πi C r (w z 0 ) n+ C r Proposition 7.9 (Converse of Goursat s Lemma, sometimes called Morera s Theorem). Let f be a continuous complex valued function on an open subset G of C. If f(z)dz = 0 for T every triangle T with interior contained in G, then f is holomorphic. Proposition 7.0 (Morera s Theorem for Rectangles). Let f be a continuous complex valued function on an open subset G of C. If f(z)dz = 0 for every rectangle R with interior R contained in G, then f is holomorphic. Proposition 7. (Liouville s Theorem). If f is entire and bounded, then it is constant. Proposition 7.2 (Fundamental Theorem of Algebra). Every nonconstant polynomial with complex coefficients can be factored over C into linear factors. Proposition 7.3. Let f : G C be holomorphic, and let z 0 G be a zero of order m. Then the Taylor series of f centered at z 0 is a n (z z 0 ) n n=m Proposition 7.4. Zeroes of finite order of holomorphic functions are isolated. That is, if z 0 is a zero of order m of a holomorphic function f, then there exists r > 0 so that f(z) 0 for z B(z 0, r). Proposition 7.5. If f : G C has a zero of infinite order at z 0, then f is the zero function on the connected component of G containing z 0. Proposition 7.6. Let f : G C be holomorphic with G connected, with f not the zero function. Then each zero of f is of finite order, and f (0) has no limit points in G. Proposition 7.7. Let f : G C be holomorphic and have a zero of order m at z 0. Then there is a branch of f m in a disk centered at z 0. Proposition 7.8 (Identity Principle). Let f, g : G C be holomorphic with G connected. If f(z) = g(z) for all z in a subset of G that has a limit point in G, then f = g. Proposition 7.9 (Weierstrass Convergence Theorem). Let G C be open and let {f k } k= be a sequence of holomorphic functions in G that converges locally uniformly in G to the function f. Then f is holomorphic, and for each n N, the sequence {f (n) k } k= converges locally uniformly to f (n). That is, the locally uniform limit of holomorphic functions is holomorphic. 0
11 Proposition 7.20 (Maximum Modulus Principal). Let f be a nonconstant holomorphic function in the open connected set G C. Then f does not attain a local maximum in G. As a consequence, if K G is compact, then f attains its maximum over K only at points on the boundary of K. Proposition 7.2. Let f be a nonconstant holomorphic function in the connected open subset G C. Then f can attain a local minimum only at a zero of f. Proposition 7.22 (Schwarz s Lemma). Let f be a holomorphic map of the open unit disk to itself so that f(0) = 0. Then f(z) z for all z in the disk. The inquality is strict at all points except 0, unless f is a rotation, i.e. f(z) = λz where λ =. Proposition 7.23 (Existence of a Harmonic Conjugate on a Convex Set). Let u be a realvalued harmonic function in the convex open subset G C. Then there is a holomorphic function g : G C so that u = Re g. The function g is unique up to addition of an imaginary constant. (That is, Im g is a harmonic conjugate to u.) Proposition Harmonic functions are infinitely differentiable. Proposition 7.25 (Mean Value Property for Harmonic Functions). Let u : G C be harmonic with G C open. Let z 0 G. Then u(z 0 ) = 2π u(z 0 + re it )dt 2π 0 for 0 < r < dist(z 0, G c ). Proposition 7.26 (Identity Principle for Harmonic Functions). Let G C be open and connected. Let u, v : G C be harmonic functions that agree on a nonempty open subset of G. Then u = v. Proposition 7.27 (Maximum Modulus Priniple for Harmonic Functions). Let G C be open an connected. Let u : G R be a nonconstant harmonic function. Then u does not attain a local maximum in G. 8 Laurent Series and Isolated Singularities Note: Prof Schenker presented this material in a different order in class, giving a different definition for singularities, but it all turns out to be logically equivalent. Proposition 8. (Generalized Cauchy-Hadamard Theorem). Consider the Laurent series n= a n(z z 0 ) n and let R = lim sup a n /n R 2 = n lim sup n a n /n If R < R 2, then the Laurent series converges absolutely and locally uniformly in the annulus R < z z 0 < R 2.
12 Proposition 8.2. Consider the Laurent series n= a n(z z 0 ) n and let R = lim sup a n /n R 2 = n lim sup n a n /n For z such that R < z z 0 < R 2 define f(z) = n= a n(z z 0 ) n. Then f is holomorphic on the annulus. In addition, for r satsifying R < r < R 2, let C r denote the circle z z 0 = r, then a n = 2πi C r f(z) dz (z z 0 ) n+ Proposition 8.3 (Cauchy s Theorem for Concentric circles). Let f be holomorphic in the annulus R < z z 0 < R 2, and for R < r < R 2 let C r be the circle z z 0 = r oriented counterclockwise. Then C r f(z)dz is independent of r (for R < r < R 2.) Proposition 8.4 (Cauchy s Formula for an Annulus). Let f be holomorphic in the annulus R < z z 0 < R 2, and for R < r < R 2 let C r be the circle z z 0 = r oriented counterclockwise. If R < r < w w 0 < r 2 < R 2, then f(w) = 2πi C r2 f(z) z w dz 2πi C r f(z) z w dz Proposition 8.5. Let f be holomorphic in the annulus R < z z 0 < R 2. Then f has a Laurent series representation on that annulus. Proposition 8.6 (Criterion for a Removable Singularity). Let f be holomorphic with an isolated singularity at z 0. Then f is bounded in some punctured disk with center z 0 if and only if z 0 is a removable singularity. Proposition 8.7 (Criterion for a Pole). Let f be holomorphic with an isolated singularity at z 0. If lim z z 0 f(z) = then z 0 is a pole of f. Proposition 8.8 (Casorati-Weierstrass Theorem). Let f : G C be holomorphic with an essential isolated singularity at z 0. Then for any w C, there is a sequence (z n ) n= in G so that lim n z n = z 0 lim f(z n ) = w n The above proposition says that functions behave very badly near essential singularities. It says that not only does not limit as z z 0 of f(z) not exist, it actually can take ANY value in C, for a suitably chosen path. The following result was not proven in our class, but is included in the book for interest s sake. Proposition 8.9 (Picard s Theorem). Let f be holomorphic with an essential isolated singularity at z 0. Then in any punctured disk centered at z 0, the range of f includes every complex value infinitely many times, with possibly one exception. 2
13 Proposition 8.0. Let f, g be holomorphic on an open set containing z 0 and suppose g has f a simple zero at z 0. Then res = f(z 0). z0 g g (z 0 ) Proposition 8. (Computing a Residue at a Pole). Let f be holomorphic on an open set containing z 0 and let f have a pole of order k at z 0. Then res z0 f = In particular, if z 0 is a simple pole, (k = ), then (k )! lim d k [ (z z0 ) k f(z) ] z z 0 dz k res z0 f = lim z z0 (z z 0 )f(z) Proposition 8.2 (Baby Residue Theorem). Let f be holomorphic with an isolated singularity at z 0. Let C be a counterclockwise oriented circle centered at z 0 so that f is holomorphic on the punctured interior of C. Then f(z)dz = 2πi res z0 f We can rewrite this as 9 Cauchy s Theorem C res z 0 f = f(z)dz 2πi C Proposition 9.. Let φ : [a, b] C \ {0} be continuous. Then there is a continuous ψ : [a, b] C \ {0} so that φ = e ψ. Furthermore, ψ is unique up to addition integer multiples of 2πi. Proposition 9.2. Let φ : [a, b] C \ {0} be piecewise C. Let c be a value of log φ(a). Then define ψ : [a, b] C \ {0} by Then ψ is continuous and φ = e ψ. ψ(t) = c + t a φ (s) φ(s) dx Proposition 9.3. Let : [a, b] C be a piecewise C curve and f holomorphic on an open set containing and nonvanishing on. Then f (z) (log f, ) = f(z) dz Proposition 9.4. Let : [a, b] C be a piecewise C closed curve, and let z 0 be a point not in the trace of. Then ind (z 0 ) = dz 2πi z z 0 Since the RHS is a continuous function of z 0, and integer valued, it is constant on each connected component of C \ ([a, b]). In particular, the index must be zero on the unbounded component. 3
14 Proposition 9.5. Let Γ = j n j j be a contour. Then ind Γ (z 0 ) = dz 2πi Γ z z 0 Proposition 9.6 (The Separation Lemma). Let G C be open, and let K G be compact. Then there is a simple contour Γ in G \ K such that K int Γ G, and such that if f is holomorphic in G, then f(z 0 ) = 2πi Γ f(z) z z 0 dz Proposition 9.7 (Cauchy s Theorem). Let G C be open and let Γ be a contour with interior contained in G, and let f : G C be holomorphic. Then f(z)dz = 0 (Keep in mind that Γ doesn t wind around anything outside G.) Γ Proposition 9.8. Let φ : [0, ] [0, ] C \ {0} be continuous. Then there is a continuous ψ : [0, ] [0, ] C such that φ = e ψ. The function ψ is unique up to addition of integer multiples of 2πi. Proposition 9.9 (Homotopic Loops give Same Winding Number). Let G C be open. Let 0, be closed piecewise C curves in G that are homotopic in G. Then ind 0 (z) = ind (z) for z C \ G. (Note that it is important that z G.) Proposition 9.0 (Homotopy Version of Cauchy s Theorem). Let G C be open and let f : G C be holomorphic. Let 0, be closed piecewise C curves in G that are homotopic in G. Then f(z)dz = 0 f(z)dz 0 Residue Theorem and Riemann Mapping Theorem Proposition 0.. Every star shaped domain is simply connected. Proposition 0.2 (Winding Number Criterion). Let G C be a domain. Then G is simply connected if and only if every contour Γ in G has winding number zero around every point in C \ G. Proposition 0.3 (Cauchy s Theorem for Simply Connected Domains). Let G C be a simply connected domain, and let f : G C be holomorphic, and let Γ be a contour in G. Then f(z)dz = 0 Note that this is a special case of the Residue Theorem. Γ 4
15 Proposition 0.4 (Existence of Primitive Criterion). Let G C be a domain. Then G is simply connected if and only if every holomorphic function f : G C has a primitive. Proposition 0.5 (Existence of Logarithms). Let G C be a simply connected domain, and let f : G C \ {0} be holomorphic. Then there is a branch of log f in G. Proposition 0.6 (Existence of Harmonic Conjugates). Let G C be a simply connected domain, and let u : G R be harmonic. Then u has a harmonic conjugate in G, which is unique up to an additive constant. Proposition 0.7 (Partial Equivalence of Definitions of Simply Connected). Let G C be a domain. If every closed curve in G is nullhomotopic, then G is simply connected. (The converse is also true, but proven later, using the Riemann Mapping Theorem.) Proposition 0.8 (Residue Theorem). Let G C be a domain, and let Γ be a contour with interior contained in G. Let f be holomorphic in G except for isolated singularities z,..., z p, none of which lies on Γ. Then Γ f(z)dz = 2πi p ind Γ (z k ) res zk (f) k= Proposition 0.9 (Cauchy Integral Formula). Let G C be a domain, and let f : G C be holomorphic, and let Γ be a simple contour with interior in G. Then f(z 0 ) = f(z) dz 2πi z z 0 for z 0 int Γ. More generally, for z 0 int Γ. f (n) (z 0 ) = n! 2πi Γ Γ f(z) dz (z z 0 ) n+ Proposition 0.0 (Argument Principle). Let G C be a domain and let Γ be a simple contour with interior contained in G. Let f : G C be holomorphic and nonvanishing on the trace of Γ. Then the number of zeroes of f in the interior of Γ (counting multiplicities) is 2πi Γ f (z) f(z) dz Proposition 0. (Rouche s Theorem). Let G C be a domain, and let K G be compact. Let f, g : G C be holomorphic such that f(z) g(z) < f(z) z K Then f, g have the same number of zeroes in the interior of K (counting multiplicities). 5
16 Proposition 0.2 (Hurwtiz s Theorem). Let (f n ) n= be a sequence of holomorphic functions on a domain G converging locally uniformly in G to a nonconstant function f. If f has at least m zeroes in G, then all but finitely many f n have at least m zeroes in G. Consequently, if infinitely many f n are univalent (injective), then f is univalent. Proposition 0.3 (Local Mapping Theorem). Let f be a nonconstant holomorphic function in the domain G. Let z 0 G and let w 0 = f(z 0 ). Let m be the order of the zero of f w 0 at z 0. For every sufficiently small δ > 0, there exists ɛ > 0 such that every value w satisfying 0 < w w 0 < ɛ is assumed by f at exactly m distinct points in the punctured disk 0 < z z 0 < δ, with multiplicity at each of those points. Proposition 0.4 (Open Mapping Theorem). Let G be a domain, and let f : G C be holomorphic. Then f is an open map. Proposition 0.5 (Local Inverses). If f is holomorphic and f (z 0 ) 0, then there is a disk centered at z 0 on which f is univalent. Proposition 0.6. A univalent holomorphic function has a nowhere vanishing derivative. Proposition 0.7. The inverse of a univalent holomorphic function is holomorphic. Proposition 0.8 (Stieltjes-Osgood Theorem). A locally uniformly bounded sequence of holomorphic functions (on a domain in C) has a locally uniformly convergent subsequence. (That is, it is a normal family.) Proposition 0.9 (Arzela-Ascoli Theorem). Let X be a compact metric space, and let C(X) be the space of continuous functions f : X R. Then F C(X) is equicontinuous and pointwise bounded if and only if it is a normal family. Proposition If a domain is conformally equivalent to a simply connected domain, then it is simply connected. Proposition 0.2 (Riemann Mapping Theorem). Every simply connected domain in C except for C itself is conformally equivalent to the unit disk. (That is to say, if G C is not equal to C, then there is a univalent holomorphic function f : D G, where D is the open unit disk.) 6
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Unitary representations of SL(2, R)
 Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Stability of Tikhonov Regularization Class 07, March 2003 Alex Rakhlin
 Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Rachunek lambda, zima
 Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Mixed-integer Convex Representability
 Mixed-integer Convex Representability Juan Pablo Vielma Massachuse=s Ins?tute of Technology Joint work with Miles Lubin and Ilias Zadik INFORMS Annual Mee?ng, Phoenix, AZ, November, 2018. Mixed-Integer
Mixed-integer Convex Representability Juan Pablo Vielma Massachuse=s Ins?tute of Technology Joint work with Miles Lubin and Ilias Zadik INFORMS Annual Mee?ng, Phoenix, AZ, November, 2018. Mixed-Integer
harmonic functions and the chromatic polynomial
 harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
CS 6170: Computational Topology, Spring 2019 Lecture 09
 CS 6170: Computtionl Topology, Spring 2019 Lecture 09 Topologicl Dt Anlysis for Dt Scientists Dr. Bei Wng School of Computing Scientific Computing nd Imging Institute (SCI) University of Uth www.sci.uth.edu/~beiwng
CS 6170: Computtionl Topology, Spring 2019 Lecture 09 Topologicl Dt Anlysis for Dt Scientists Dr. Bei Wng School of Computing Scientific Computing nd Imging Institute (SCI) University of Uth www.sci.uth.edu/~beiwng
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Dupin cyclides osculating surfaces
 Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
adasalai.org POWERS OF IMAGINARY UNIT = i i 2001 Division algorithm : n = 4(q) + r
 .COMPLEX NUMBERS Pai POWERS OF IMAGINARY UNIT i =, i = i, i 4 = Division algorithm : n = 4(q) + r i n = (i) 4q+r = (i) 4q (i) r = (i 4 ) q (i) r if r = 0, i n = ; if r =, i n = i; if r =, i n = ; if r
.COMPLEX NUMBERS Pai POWERS OF IMAGINARY UNIT i =, i = i, i 4 = Division algorithm : n = 4(q) + r i n = (i) 4q+r = (i) 4q (i) r = (i 4 ) q (i) r if r = 0, i n = ; if r =, i n = i; if r =, i n = ; if r
O przecinkach i nie tylko
 O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
Title: On the curl of singular completely continous vector fields in Banach spaces
 Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Steeple #3: Gödel s Silver Blaze Theorem. Selmer Bringsjord Are Humans Rational? Dec RPI Troy NY USA
 Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Previously on CSCI 4622
 More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Chapter 1: Review Exercises
 Chpter : Review Eercises Chpter : Review Eercises - Evlute the following integrls:..... 6. 8. ( + ) 9. +.. ( + ). ( ). 8. 9....... 6. 7. (csc + + ) sin tn 6. ( )( + ) 7. ) 8.. + ( + )( ). ( ) sin sin sec
Chpter : Review Eercises Chpter : Review Eercises - Evlute the following integrls:..... 6. 8. ( + ) 9. +.. ( + ). ( ). 8. 9....... 6. 7. (csc + + ) sin tn 6. ( )( + ) 7. ) 8.. + ( + )( ). ( ) sin sin sec
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
Counting quadrant walks via Tutte s invariant method
 Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
1. Liczby zespolone Zadanie 1.1. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone (1) 1 i (2) (5)
 . Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
. Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
SubVersion. Piotr Mikulski. SubVersion. P. Mikulski. Co to jest subversion? Zalety SubVersion. Wady SubVersion. Inne różnice SubVersion i CVS
 Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Roland HINNION. Introduction
 REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
Lecture 20. Fraunhofer Diffraction - Transforms
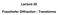 Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Standardized Test Practice
 Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Some Linear Algebra. Vectors operations = =(,, ) =( 1 + 2, 1 + 2, ) λ =(λ,λ,λ ) Addition. Scalar multiplication.
 Basic Geometry Vectors operations Some Linear Algebra Addition + 2 =( 1 + 2, 1 + 2, 1 + 2 ) =(,, ) + Scalar multiplication λ =(λ,λ,λ ) Norm = 2 + 2 + 2 2 Scalar Product Commutative Linear Orthogonally
Basic Geometry Vectors operations Some Linear Algebra Addition + 2 =( 1 + 2, 1 + 2, 1 + 2 ) =(,, ) + Scalar multiplication λ =(λ,λ,λ ) Norm = 2 + 2 + 2 2 Scalar Product Commutative Linear Orthogonally
Lecture 18 Review for Exam 1
 Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
F-Theory duals of heterotic K3 orbifolds
 F-Theory duals of heterotic K3 orbifolds Fabian Ruehle Deutsches Elektronensynchrotron DESY Hamburg String Pheno 2014 07/08/2014 Based on Ludeling, Ruehle: [1405.2928] T 4 /Z 2 Orbifold 2 2 2 2 2 2 2 2
F-Theory duals of heterotic K3 orbifolds Fabian Ruehle Deutsches Elektronensynchrotron DESY Hamburg String Pheno 2014 07/08/2014 Based on Ludeling, Ruehle: [1405.2928] T 4 /Z 2 Orbifold 2 2 2 2 2 2 2 2
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
 Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów
 Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
OBWIESZCZENIE MINISTRA INFRASTRUKTURY. z dnia 18 kwietnia 2005 r.
 OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
17-18 września 2016 Spółka Limited w UK. Jako Wehikuł Inwestycyjny. Marek Niedźwiedź. InvestCamp 2016 PL
 17-18 września 2016 Spółka Limited w UK Jako Wehikuł Inwestycyjny InvestCamp 2016 PL Marek Niedźwiedź A G E N D A Dlaczego Spółka Ltd? Stabilność Bezpieczeństwo Narzędzia 1. Stabilność brytyjskiego systemu
17-18 września 2016 Spółka Limited w UK Jako Wehikuł Inwestycyjny InvestCamp 2016 PL Marek Niedźwiedź A G E N D A Dlaczego Spółka Ltd? Stabilność Bezpieczeństwo Narzędzia 1. Stabilność brytyjskiego systemu
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Agnostic Learning and VC dimension
 Agnostic Learning and VC dimension Machine Learning Spring 2019 The slides are based on Vivek Srikumar s 1 This Lecture Agnostic Learning What if I cannot guarantee zero training error? Can we still get
Agnostic Learning and VC dimension Machine Learning Spring 2019 The slides are based on Vivek Srikumar s 1 This Lecture Agnostic Learning What if I cannot guarantee zero training error? Can we still get
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Bergman Kernel and Kobayashi Pseudodistance in Convex Domains
 Bergman Kernel and Kobayashi Pseudodistance in Convex Domains Zbigniew B locki Uniwersytet Jagielloński, Kraków, Poland http://gamma.im.uj.edu.pl/ blocki (Joint work with W lodzimierz Zwonek) NORDAN Reykjavík,
Bergman Kernel and Kobayashi Pseudodistance in Convex Domains Zbigniew B locki Uniwersytet Jagielloński, Kraków, Poland http://gamma.im.uj.edu.pl/ blocki (Joint work with W lodzimierz Zwonek) NORDAN Reykjavík,
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
First-order logic. Usage. Tautologies, using rst-order logic, relations to natural language
 First-order logic. Usage Tautologies, using rst-order logic, relations to natural language A few important tautologies 1 x(ϕ ψ) ( xϕ xψ); A few important tautologies 1 x(ϕ ψ) ( xϕ xψ); 2 xϕ ϕ, o ile x
First-order logic. Usage Tautologies, using rst-order logic, relations to natural language A few important tautologies 1 x(ϕ ψ) ( xϕ xψ); A few important tautologies 1 x(ϕ ψ) ( xϕ xψ); 2 xϕ ϕ, o ile x
4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4.
![4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4. 4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4.](/thumbs/99/139565186.jpg) Lecture 4 & 5 4 4.1 Riemnn t f(t) [, b] (Riemnn ) f(t)dt [, b] n 1 t 1,...,t n 1 t 0
Lecture 4 & 5 4 4.1 Riemnn t f(t) [, b] (Riemnn ) f(t)dt [, b] n 1 t 1,...,t n 1 t 0
Sargent Opens Sonairte Farmers' Market
 Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Wprowadzenie do programu RapidMiner, część 5 Michał Bereta
 Wprowadzenie do programu RapidMiner, część 5 Michał Bereta www.michalbereta.pl 1. Przekształcenia atrybutów (ang. attribute reduction / transformation, feature extraction). Zamiast wybierad częśd atrybutów
Wprowadzenie do programu RapidMiner, część 5 Michał Bereta www.michalbereta.pl 1. Przekształcenia atrybutów (ang. attribute reduction / transformation, feature extraction). Zamiast wybierad częśd atrybutów
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku
 Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Camspot 4.4 Camspot 4.5
 User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
Modern methods of statistical physics
 Modern methods of statistical physics František Slanina Institute of Physics, Academy of Sciences of the Czech Republic, Prague slanina@fzu.cz www.fzu.cz/ slanina Ising model Renormalisation group Modern
Modern methods of statistical physics František Slanina Institute of Physics, Academy of Sciences of the Czech Republic, Prague slanina@fzu.cz www.fzu.cz/ slanina Ising model Renormalisation group Modern
Wybrzeze Baltyku, mapa turystyczna 1: (Polish Edition)
 Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
How to translate Polygons
 How to translate Polygons Translation procedure. 1) Open polygons.img in Imagine 2) Press F4 to open Memory Window 3) Find and edit tlumacz class, edit all the procedures (listed below) 4) Invent a new
How to translate Polygons Translation procedure. 1) Open polygons.img in Imagine 2) Press F4 to open Memory Window 3) Find and edit tlumacz class, edit all the procedures (listed below) 4) Invent a new
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
Machine Learning for Data Science (CS4786) Lecture 24. Differential Privacy and Re-useable Holdout
 Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
7.1. Lecture 8 & 9. f(x)dx =lim f(x)dx (7.1) I = f(x)dx (7.3) f(z), z (0 argz π), zf(z) 0. f(z)dz = I R := f(z)dz = f(re iθ )ire iθ dθ (7.
 Lecture 8 & 9 7, r f(x) =lim f(x) (7.) r r f(x) =lim f(x) +lim f(x) (7.) r r r 7. f(z) I = f(x) (7.) f(z), z ( argz π), zf(z) [ R, R], : z = R Jordan C f(z). C f(z)dz = R R f(x) + f(z)dz =πi i Res z=zi
Lecture 8 & 9 7, r f(x) =lim f(x) (7.) r r f(x) =lim f(x) +lim f(x) (7.) r r r 7. f(z) I = f(x) (7.) f(z), z ( argz π), zf(z) [ R, R], : z = R Jordan C f(z). C f(z)dz = R R f(x) + f(z)dz =πi i Res z=zi
Fuss-Catalan numbers in noncommutative probability
 Fuss-Catalan numbers in noncommutative probability Wojciech M lotkowski (Wroc law) Bielefeld, 28.08.2018 Wojciech M lotkowski Fuss-Catalan numbers 28.08.2018 1 / 35 Abstract The generalized Fuss-Catalan
Fuss-Catalan numbers in noncommutative probability Wojciech M lotkowski (Wroc law) Bielefeld, 28.08.2018 Wojciech M lotkowski Fuss-Catalan numbers 28.08.2018 1 / 35 Abstract The generalized Fuss-Catalan
Egzamin maturalny z języka angielskiego na poziomie dwujęzycznym Rozmowa wstępna (wyłącznie dla egzaminującego)
 112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz
![[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz](/thumbs/101/148499235.jpg) [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
Funkcje Analityczne, ćwiczenia i prace domowe
 Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Mathematics A Brief Guide for Engineers and Technologists. Chapter 2. Second. Properties. S is a vector space. Note
 Mathematics A Brief Guide for Engineers and Technologists Dział. Drugi Chapter 2. Second. Dystrybucje wolnorosnące.. Przestrzeń funkcji testowych S S = S (IR n ) to wszystkie funkcje klasy C (IR n ) malejące
Mathematics A Brief Guide for Engineers and Technologists Dział. Drugi Chapter 2. Second. Dystrybucje wolnorosnące.. Przestrzeń funkcji testowych S S = S (IR n ) to wszystkie funkcje klasy C (IR n ) malejące
n [2, 11] 1.5 ( G. Pick 1899).
![n [2, 11] 1.5 ( G. Pick 1899). n [2, 11] 1.5 ( G. Pick 1899).](/thumbs/98/135090138.jpg) 1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych. mgr inż. Paweł Koszut
 Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych mgr inż. Paweł Koszut Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych Zamiast wstępu : Inspiracja GSM w Grecji
Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych mgr inż. Paweł Koszut Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych Zamiast wstępu : Inspiracja GSM w Grecji
Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo
 POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION
 Glasgow Math. J.: page 1 of 12. C Glasgow Mathematical Journal Trust 2012. doi:10.1017/s0017089512000353. EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION SEAN SATHER-WAGSTAFF Mathematics Department,
Glasgow Math. J.: page 1 of 12. C Glasgow Mathematical Journal Trust 2012. doi:10.1017/s0017089512000353. EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION SEAN SATHER-WAGSTAFF Mathematics Department,
Prices and Volumes on the Stock Market
 Prices and Volumes on the Stock Market Krzysztof Karpio Piotr Łukasiewicz Arkadiusz Orłowski Warszawa, 25-27 listopada 2010 1 Data selection Warsaw Stock Exchange WIG index assets most important for investors
Prices and Volumes on the Stock Market Krzysztof Karpio Piotr Łukasiewicz Arkadiusz Orłowski Warszawa, 25-27 listopada 2010 1 Data selection Warsaw Stock Exchange WIG index assets most important for investors
Permutability Class of a Semigroup
 Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2)
 Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
THICK SETS IN BANACH SPACES AND THEIR PROPERTIES
 Quaestiones Mathematicae 29(2005), 59 72. c 2005 NISC Pty Ltd, www.nisc.co.za THICK SETS IN BANACH SPACES AND THEIR PROPERTIES Olav Nygaard Department of Mathematics, Agder University College, Servicebox
Quaestiones Mathematicae 29(2005), 59 72. c 2005 NISC Pty Ltd, www.nisc.co.za THICK SETS IN BANACH SPACES AND THEIR PROPERTIES Olav Nygaard Department of Mathematics, Agder University College, Servicebox
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
