APPLICATION OF THE HAAR AND B-SPLINE WAVELETS TO APPROXIMATE SOLUTION OF THE BOUNDARY PROBLEMS
|
|
|
- Maksymilian Sikorski
- 6 lat temu
- Przeglądów:
Transkrypt
1 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2011 Seria: MATEMATYKA STOSOWANA z. 1 Nr kol Anna KORCZAK Institute of Mathematics Silesian University of Technology APPLICATION OF THE HAAR AND B-SPLINE WAVELETS TO APPROXIMATE SOLUTION OF THE BOUNDARY PROBLEMS Summary. This paper presents an application of the wavelet theory to function approximation and to approximate solutions of chosen differentialequations.thereareconsideredthefunctionsofclassl 2 (R)andthe first and the second order linear differential equations in interval[0, 1] with appropriate boundary conditions. Haar wavelet and linear B-spline wavelet were applied to approximate these functions and solving these problem. ZASTOSOWANIE FALEK HAARA I B-SPLAJNOWEJ W PRZYBLIŻONYM ROZWIĄZYWANIU ZAGADNIEŃ BRZEGOWYCH Streszczenie. W artykule przedstawiono zastosowanie teorii falek w aproksymacji funkcji oraz w aproksymacji rozwiązań wybranych równań różniczkowych.rozważanesąrównieżfunkcjeklasyl 2 (R)orazrównania różniczkowe liniowe rzędów pierwszego i drugiego, określone na przedziale [0, 1], z odpowiednimi warunkami brzegowymi. Do aproksymacji wyżej wymienionych funkcji oraz równań zostały zastosowane falka Haara oraz falka B-splajnowa liniowa Mathematics Subject Classification: 80M99, 65M99. Wpłynęło do Redakcji(received): r.
2 150 A. Korczak 1. Introduction Wavelettheoryisarespectivelynewfieldofmathematics.Ithasbeenveryintensively developed since eighties and is promising in usage to various applications. Wavelets find an application in many different problems like analyzing acoustic emission pulses[1], technical diagnostics[4], local images filtering[6], finite elements method[3]. Their popularity is caused by the combination of theoretical and applied mathematics represented by this approach. WaveletisakindoffunctionΨ(x) L 2 (R)suchthattheset B Ψ ={2 j/2 Ψ(2 j x k);j Z,k Z} (1) isabaseinspacel 2 (R)[2].FamillyB Ψ iscalledthewaveletbase. Previousdefinitionimpliesthatanyfunctionf(x) L 2 (R)canbeshowedas linearcombinationofbasefunctionsψ jk =2 j/2 Ψ(2 j x k)(ifψisawavelet). Thatmeansthatfunctionfcanbewrittenasthefollowingseries f(x)= f jk Ψ jk (x), (2) j Zk Z wheref jk arethefouriercoefficientsdefinedasfollows f jk = f(x),ψ jk (x) = f(x)ψ jk (x)dx. 2. Haar wavelet ThesimplestexampleofwaveletistheHaarwaveletwhichisdefinedasfollows 1, x [0, 1 2 ), H(x)= 1, x [ 1 2,1), 0, x/ [0,1). Function H(x) is connected with the set B H ={2 j/2 H(2 j k);j Z,k Z}. (3) FunctionsH jk (x) B H (forfixedjandk)havetheform 2 j/2, x [k2 j,(k+ 1 2 )2 j ), H jk (x)= 2 j/2, x [(k+ 1 2 )2 j,(k+1)2 j ), 0, x/ [k2 j,(k+1)2 j ). (4)
3 Application of the Haar and B-spline wavelets ThesupportoffunctionH jk (x)istheinterval supph jk (x)= [ k2 j,(k+1)2 j]. (5) BasicpropertyoftheHaarwaveletistheorthogonalityofbaseH jk H j1k 1,H j2k 2 =0 for j 1 j 2 k 1 k 2. (6) AnyfunctionH jk isobtainedbytranslatingandscalingofthehaarwavelet Haar wavelet approximation Function f(x) belonging to the appropriate function space can be approximatedbyusingthehaarwaveletandthebaseb H associatedwithit. Weapproximatefunctionfonlyininterval[ 2 m,2 m ],outofitwetake value0.moreover,wedefinethevaluer Z,whichisthemaximumapproximation (resolution) level of function f. Forfixedmandrtheapproximationoffunctionfisasfollows f(x)=f m (x)+ r j=m 2 j m 1 k= 2 j m f jk H jk (x). (7) where,forj<m,wehave f m (x)= 2 m 2 m 0 f(x)dx, x [ 2 m,0), 0 2 m f(x)dx, x [0,2 m ). 2 m Example 2.1 In this example, we will approximate function f(x), defined as follows { sinx+0.5, x [0,1), f(x)= 0, x/ [0,1). Functionf(x)istheelementofspaceL 2 (R)andcanbeapproximatedbyusing the Haar wavelet. Forthefollowingapproximationlevels:r=1,2,3,4,Figure1illustratesthe comparisons of function f(x) and its approximations. Whereas, the error of approximationsforlevels:r=1,2,3,4,aredisplayedinfigure2.basingonthe
4 152 A. Korczak r=1 r= r= r= Fig. 1. Comparison of function f(x) and its approximations Rys. 1. Porównanie przebiegu funkcji f(x) i jej aproksymacji presented diagrams we can say that the increase of approximation level causes the double decrease of the approximation error. Calculatingtheapproximationerrorinpointsx i = i 10 fori=0,1,2,...,10 the efficiency of function approximation can be compared for different wavelets. Errorsinpointsx i forthehaarwaveletareshownintable1. WaveletbaseB H givesanopportunitytoapproximatethesolutionsoflinear differential equations. We consider differential equation of the form forx [0,1],withtheinitialcondition y +f(x)y=g(x), (8) y(0)=y 0, wheretheunknownfunctiony=y(x)andthegivenfunctionsf(x)ig(x)belong totheappropriateclassin[0,1].byusingwaveletbaseb H wearelookingforthe solution having the following form ỹ r (x)=a+ r 2 j 1 j=0k=0 a jk H jk (x), (9)
5 Application of the Haar and B-spline wavelets r=1 r= r= r= Fig. 2. Error of the function approximation Rys. 2. Błąd aproksymacji funkcji Functionỹ r dependsonparametersaanda jk,whichareunknownandneedto befound.thisfunctionisconstantineachofintervals [ i2 r 1,(i+1)2 r 1), i=0,...,2 r+1 1[2]. Example 2.2 ByusingthewaveletbaseB H wewillfindtheapproximatesolutionofthe following differential equation of the first order y (x)+y(x)=x 2 sinx, x [0,1], (10) with initial condition y(0)=1. Exact solution of this equation is the following y(x)= 1 2 e x ( 3+e x cosx 2e x xcosx+e x x 2 cosx+e x sinx e x x 2 sinx).(11)
6 154 A. Korczak Table 1 Function approximation error x i r=1 r=2 r=3 r= By using described algorithm of finding approximate solution we obtain the approximate solution in points x i =(i+ 1 2 )2 r 1 fori=0,...,2 r+1 1. Forthefollowingapproximationlevels:r=1,2,3,4,Figure3illustratescomparison of the exact solution of considered problem and its approximations. Whereas, the approximation errors for these levels are illustrated in Figure 4. Basing on the presented diagrams we can say that the increase of approximation level causes the decrease of approximation error. InthenextexampleofwaveletbaseB H applicationthreeboundaryproblems for linear differential equation of the second order will be considered. Let us consider the equation y (x)+f(x)y (x)+g(x)y(x)=h(x), x [0,1], (12) with the following boundary conditions: { y(0)=y 0, y (0)=y 0, (13)
7 Application of the Haar and B-spline wavelets r=1 r= r= r= Fig. 3. Comparison of the exact and approximate solution of differential equation(10) Rys. 3. Porównanie przebiegu rozwiązania dokładnego równania różniczkowego i jego aproksymacji(10) { { y(0)=y 0, y(1)=y 1, y (0)=y 0, y(1)=y 1. (14) (15) Theunknownfunctiony=y(x)andthegivenfunctionsf(x),g(x)ih(x)belong to the appropriate class. Solutionofthisproblemissoughtasthesum(9).Similarlylikeincaseofthe firstorderequationtheunknownelementsareaanda jk. Example 2.3 ByusingthewaveletbaseB H wewillfindtheapproximatesolutionofthe following linear differential equation of the second order y (x)+y(x)= cosxe x, x [0,1], (16)
8 156 A. Korczak r= r= r= r= Fig. 4. Error of approximate solution of differential equation(10) Rys. 4. Błąd aproksymacji rozwiązania równania różniczkowego(10) with the boundary conditions of the second type y(0)=0 and y(1)=0. Exact solution of this equation is the following: y(x) = 1 10 (2cosx 2ex cosxcos2x+5esinx 5e x sinx+ecos2sinx 2ctg1sinx+2ecos2ctg1sinx+2esin2sinx ectg1sin2sinx +e x cosxsin2x 2e x sinxsin2x). By applying the proposed approach we obtain the approximated solution in points x i =(i+ 1 2 )2 r 1 fori=0,...,2 r+1 1.Forthefollowingapproximationlevels:r=1,2,3,4,Figure 5 shows the comparison of the exact and approximate solution of the considered
9 Application of the Haar and B-spline wavelets r=1 0 r= r= r= Fig. 5. Comparison solution of differential equation(16) and its approximation Rys. 5. Porównanie przebiegu rozwiązania równania różniczkowego(16) i jego aproksymacji problem. Whereas, approximation errors for levels: r = 1, 2, 3, 4, are illustrated in Figure 6. According to the presented diagrams we can say that with the increase of approximation level the approximation error decreases. 3. B-spline wavelet B-spline wavelet is often defined by means of the scaling functions[7]. Scaling function of the m-order B-spline wavelet is defined as the following convolution: φ m (t)=(φ m 1 φ 1 (t))= φ m 1 (t x)φ 1 (x)dx= 1 0 φ m 1 (t x)dx. (17) Moreover, the m-order B-spline wavelet can be defined as the linear combination of scaling functions: Ψ m (x)= 3m 2 k=0 q k φ m (2x k), (18)
10 158 A. Korczak r=1 r= r= r= Fig. 6. Error of approximate solution of differential equation(16) Rys. 6. Błąd aproksymacji rozwiązania równania różniczkowego(16) where q k =( 1) k 2 1 m m l=0 ( ) m φ 2m (k+1 l). (19) l ItisworthtonoticethatthefirstorderB-splinewaveletistheHaarwavelet. Scaling function of the linear B-spline wavelet is defined by the formula x, x [0,1), φ 2 (x)= 2 x, x [1,2), (20) 0, x/ [0,2). Furtherscalingfunctionform=2isdenotedasφ(x).Then,thetwo-scalerelation for this function is the following x j k, x [k2 j,(k+1)2 j ), φ j,k (x)= 2 (x j k), x [(k+1)2 j,(k+2)2 j ), (21) 0, x/ [k2 j,(k+2)2 j ), wherex j =2 j x k.
11 Application of the Haar and B-spline wavelets m=1 2.0 m= m= m= Fig.7. Scalingfunctionsform=1,2,3,4 Rys.7. Funkcjeskalującedlam=1,2,3,4 Functionφ j,k (x)isdefinedasthescaledandtransformedfunctionφ(x)by usingparametersjandk.functionsφ j,k (x)arehelpfulinformingthefunctions approximation. Linear B-spline wavelet is defined by the formula: x 6, x [0,1 2 ), Ψ 2 (x)= 1 6 ( 7x+4), x [1 2,1), 1 6 (16x 19), x [1,3 2 ), 1 6 ( 16+29), x [3 2,2), 1 6 (7x 17), x [2,5 2 ), 1 6 ( x+3), x [5 2,3), 0, x/ [0,3). (22)
12 160 A. Korczak m= m= m= m= Fig.8. B-splinewaveletsoforder1,2,3,4 Rys.8. FalkiB-splajnowerzędu1,2,3,4 Ψ 2 (x)waveletisassociatedwiththewaveletbase[5](x j =2 j x k): ψ j,k (x)= x j 2 j/2 6, x [k2 j,(k+ 1 2 )2 j ), ( 7x j +4) 2j/2 6, x [(k+1 2 )2 j,(k+1)2 j ), (16x j 19) 2j/2 6, x [(k+1)2 j,(k+ 3 2 )2 j ), ( 16x j +29) 2j/2 6, x [(k+3 2 )2 j,(k+2)2 j ), (7x j 17) 2j/2 6, x [(k+2)2 j,(k+ 5 2 )2 j ), ( x j +3) 2j/2 6, x [(k+5 2 )2 j,(k+3)2 j ), 0, x/ [k2 j,(k+3)2 j ]. (23) Similarly like in case of the Haar wavelet, parameter j is responsible for scaling andparameterkisresponsiblefortranslatingthefunctionψ jk.
13 Application of the Haar and B-spline wavelets Linear B-spline wavelet approximation[5] Foranyfixedpositiveintegerr N,thefunctionf(x)definedover[0,1]may be represented by the B-spline scaling functions in the following way where s k = 1 0 f(x)= 2 r+1 1 k= 1 s k φ r+1,k (x), (24) f(x) φ r+1,k (x)dx, k= 1,0,...,2 r+1 1. (25) Functions φ r+1,k (x)arethedualfunctionsforφ r+1,k (x)givenbytherelation 1 0 Φ r+1 Φ r+1 dx=i, (26) whereφ r+1 =[φ r+1, 1,φ r+1,0,...,φ r+1,2 r+1 1] T andiistheidentitymatrixof dimension.(2 r+1 +1) (2 r+1 +1) Let From(26)and(27)weget P r+1 = 1 0 Φ r+1 Φ T r+1dx. (27) Φ r+1 =(P r+1 ) 1 Φ r+1. (28) Example 3.1 In this example we approximate the function f(x) defined as follows { sinx+0.5, x [0,1), f(x)= 0, x/ [0,1). For the first approximation level the comparison of function f(x) and its approximationisshowninfigure9.
14 162 A. Korczak Fig.9. Comparisonoffunctionf(x)anditsapproximationforr=1 Rys.9. Porównanieprzebiegufunkcjiijejaproksymacjidlar=1 r= r= r= r= Fig. 10. Error of the function approximation Rys. 10. Błąd aproksymacji funkcji Diagramoff(x)anditsapproximationarepracticallythesame,evenforfirst approximation level which confirms the good precision of approximation. Error analysis for the successive levels gives the opportunity to compare efficiency of approximation. Approximation errors for levels: r = 1, 2, 3, 4, are illustrated in Figure10.Basingonthepresenteddiagramswecansaythattheincreaseof
15 Application of the Haar and B-spline wavelets Error of the approximate solution Table 2 x i r=1 r=2 r=3 r= approximation level causes the decrease of approximation error. Errors in points x i fortheb-splinewaveletareshownintable B-spline wavelet approximation[5] Let us consider the linear differential equation of the first order y (x)+f(x)y=g(x), (29) with the initial condition y(0)=y 0, (30) wheref(x),g(x)arethegivenfunctionsofclassl 2 [0,1],y 0 isthegivenreal numberandy(x)istheunknownfunction.thedifferentiationofthevectorsφ r+1 andψcanbeexpressedinfollowingway Φ r+1 =D ΦΦ r+1, Ψ =D Ψ Ψ, (31) whered Φ andd Ψ denotethe(2 r+1 +1) (2 r+1 +1)operationalmatricesof derivative for B-spline scaling functions and wavelet.
16 164 A. Korczak Approximation of the function f(x) can be expressed y(x)=c T Ψ(x), (32) wherecisanunknownvectorofdimension2 r+1 +1.From(32)weobtain y (x)=c T Ψ (x)=c T D Ψ Ψ(x). (33) Using(29)and(33)wehave C T D Ψ Ψ+f(x)C T Ψ=g(x). (34) From(30)and(32)weget C T Ψ(0)=y 0. (35) Tofindthesolutiony(x)firstwecollocateequality(34)inx i = 2i 1 2 r+1 2,for i=1,2,...,2 r+1 1.Theresultingequationwithinitialcondition(35)generates 2 r+1 +1linearequations.SolutionoftheseequationsisvectorCwhichcanbeset into(32) and gives the approximation(29). Example 3.2 ByusingwaveletbaseΨ j,k,wewillfindtheapproximatesolutionofthefollowing differential equation y (x)+y(x)=x 2 sinx, x [0,1] (36) with the initial condition y(0)=1. Diagramoff(x)anditsapproximationarepracticallythesameevenforfirst approximation level(figure 11) what means the good precision of approximation. Error analysis at the successive levels gives opportunity to compare the efficiency ofapproximations.approximationerrorsforlevels:r=1,2,3,4,aredisplayedin Figure12.Basingonthepresenteddiagramswecansaythatwiththeincreaseof approximation level the approximation error decreases. We consider now the second order linear differential equation with the boundary condition y (x)+f(x)y +g(x)y(x)=h(x), (37) y(0)=y 0, y(1)=y 1, (38)
17 Application of the Haar and B-spline wavelets Fig. 11. Comparison of the solution of differential equation and its approximation for r=1 Rys. 11. Porównanie przebiegu rozwiązania równania różniczkowego i jego aproksymacji dlar=1 r=1 r= r= r= Fig. 12. Error of approximate solution of the differential equation Rys. 12. Błąd aproksymacji rozwiązania równania różniczkowego wheref(x),g(x),h(x)arethegivenfunctionsofclassl 2 [0,1],y 0 andy 1 arethe given real numbers and y(x) is the unknown function.
18 166 A. Korczak Tofindtheapproximationoffunctiony(x)weproceedasincaseofthefirst order linear differential equation. We substitute into equation(37) the following functions y(x)=c T Ψ(x), y (x)=c T Ψ (x)=c T D Ψ Ψ(x), (39) y (x)=c T DΨ 2Ψ(x). We obtain: From(38)and(39)wehave: C T D 2 ΨΨ+f(x)C T D Ψ Ψ+g(x)C T Ψ=h(x). (40) C T Ψ(0)=y 0, C T Ψ(1)=y 1. (41) Tofindthesolutiony(x)firstwecollocateequation(40)inpointsx i = 2i 1 2 r+1 2, fori=1,2,...,2 r+1 1.Theresultingequationwithboundaryconditions(38) generates2 r+1 +1linearequations.SolutionoftheseequationsisvectorCwhich canbesetinto(39)andgivestheapproximation(37). Example 3.3 ByusingwaveletbaseΨ j,k,wewillfindtheapproximatesolutionofthefollowing differential equation y (x)+y(x)= cosxe x, x [0,1] (42) with the boundary conditions and y(0)=0 y(1)=0. Diagramoff(x)anditsapproximationarepracticallythesameevenforfirstapproximation level(figure 13) which confirms the good precision of approximation. Error analysis at the successive levels gives opportunity to compare the efficiency of approximation. Approximation errors for levels: r = 1, 2, 3, 4, are illustrated infigure14.basingonpresenteddiagramswecansaythatwiththeincreaseof approximation level the approximation error decreases.
19 Application of the Haar and B-spline wavelets Fig. 13. Comparison of the exact solution of differential equation and its approximation forr=1 Rys. 13. Porównanie przebiegu dokładnego rozwiązania równania różniczkowego i jego aproksymacjidlar=1 r=1 r= r= r= Fig. 14. Error of approximate solution of the differential equation Rys. 14. Błąd aproksymacji rozwiązania równania różniczkowego 4. Conclusions This paper presents the comparison of Haar s wavelet and linear B-spline wavelet with regard to the efficiency in function approximations and in approximate
20 168 A. Korczak solutions of the first and second order differential equations. Presented examples prove that linear B-spline wavelet gives better results in functions approximation and in finding the approximate solutions of differential equations than Haar wavelet. Approximation errors calculated for each level of B-spline wavelet are much smaller than for Haar wavelet. Moreover, the examples show that errors for the Haar wavelet approximation counted for particular levels of approximation decrease much faster than approximation errors generated by using the B-spline wavelet. References 1. Boczar T.: Application of signal processing elements for the characteristics of acoustic emission pulses generated by partial discharges. Phys. Chem. Solid State 8(2007), Grzymkowski R., Zielonka A.: Application of the wavelets theory in the boundary problems. WPKJS, Gliwice 2004(in Polish). 3. Jiawei X., Xuefeng Ch., Zhengjia H., Yinghong Zh.: A new wavelet-based thin plate element using B-spline wavelet on the interval. Comput. Mech. 41(2008), Katunin A., Korczak A.: The possibility of application of B-spline family wavelets in diagnostic signal processing. Acta Mech. Autom. 3(2009), Lakestani M., Razzaghi M., Dehghan M.: Semiorthogonal spline wavelets approximation for Fredholm integro-differential equations. Math. Probl. Eng (2006), Samavati F., Mahdavi-Amiri N.: A filtered B-spline models of scanned digital images. J. Sci. 10(2000), Ueda M., Lodha S.: Wavelets: an elementary introduction and examples. University of California at Santa Cruz, Santa Cruz Omówienie W niniejszym artykule dokonano porównania falki Haara i falki B-splajnowej liniowej pod względem efektywności aproksymacji funkcji oraz rozwiązań równań różniczkowych rzędów pierwszego i drugiego. Falka Haara jest najstarszą falką, zdefiniowaną już w 1910 roku, dobrze poznaną i obecnie powszechnie stosowaną w wielu dziedzinach. Falka Haara należy do grupy falek ortogonalnych i ze względu
21 Application of the Haar and B-spline wavelets na jej prostą postać funkcyjną jej użycie nie wymaga skomplikowanych algorytmów. Natomiast falka B-splajnowa liniowa nieco bardziej skomplikowana jest falką biortogonalną, co daje szersze możliwości zastosowania jej w wielu dziedzinach nauki. Analizując przykłady zawarte w tym artykule można zauważyć, że falka B-splajnowa liniowa daje dużo lepsze rezultaty w aproksymacji rozpatrywanych funkcji oraz rozwiązań równań różniczkowych. Na każdym z poziomów rozdzielczości błędy aproksymacji, liczone dla falki B-splajnowej liniowej, były mniejsze, aniżeli liczone dla falki Haara. W wybranych przykładach można również zaobserwować, że w przypadku falki Haara błąd liczony na poszczególnych poziomach aproksymacji spada dużo szybciej niż w przypadku falki B-splajnowej. Należy podkreślić, że teoria falek B-splajnowych jest teorią stosunkowo nową, intensywnie rozwijaną przez liczne ośrodki naukowe na całym świecie. Obecnie ze względu na swoje ciekawe własności i zastosowania jest tematem wielu prac naukowych.
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM
 1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Z-ZIP Równania Różniczkowe. Differential Equations
 MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y
 Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM
 Zbigniew ZDZIENNICKI Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe Struktury równoległe układów niezawodnościowych,
Zbigniew ZDZIENNICKI Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe Struktury równoległe układów niezawodnościowych,
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
WAVELET TRANSFORM OF SELECTED SIMULATION SIGNALS USING DETAILS AS INFORMATION SOURCE
 TRANSPORT PROBLEMS 9 PROBLEMY TRANSPORTU Volume 4 Issue 3 Part Izabela JÓZEFCZYK Warsaw University of Technology, Engineering, Mechanics and Petrochemistry Department, Technical and Social Science School
TRANSPORT PROBLEMS 9 PROBLEMY TRANSPORTU Volume 4 Issue 3 Part Izabela JÓZEFCZYK Warsaw University of Technology, Engineering, Mechanics and Petrochemistry Department, Technical and Social Science School
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Krytyczne czynniki sukcesu w zarządzaniu projektami
 Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
LOKALNA APROKSYMACJA POCHODNYCH Z UŻYCIEM NIEREGULARNIE ROZMIESZCZONYCH WĘZŁÓW LOCAL APPROXIMATION OF DERIVATIVES USING SCATTERED NODES
 ARTUR KROWIAK LOKALNA APROKSYMACJA POCHODNYCH Z UŻYCIEM NIEREGULARNIE ROZMIESZCZONYCH WĘZŁÓW LOCAL APPROXIMATION OF DERIVATIVES USING SCATTERED NODES S t r e s z c z e n i e A b s t r a c t W artykule
ARTUR KROWIAK LOKALNA APROKSYMACJA POCHODNYCH Z UŻYCIEM NIEREGULARNIE ROZMIESZCZONYCH WĘZŁÓW LOCAL APPROXIMATION OF DERIVATIVES USING SCATTERED NODES S t r e s z c z e n i e A b s t r a c t W artykule
WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA CIEPŁA
 39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
RESONANCE OF TORSIONAL VIBRATION OF SHAFTS COUPLED BY MECHANISMS
 SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji
 Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji Marek A. Kowalski Uniwersytet Kardynała Stefana Wyszyńskiego
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji Marek A. Kowalski Uniwersytet Kardynała Stefana Wyszyńskiego
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Tadeusz SZKODNY. POLITECHNIKA ŚLĄSKA ZESZYTY NAUKOWE Nr 1647 MODELOWANIE I SYMULACJA RUCHU MANIPULATORÓW ROBOTÓW PRZEMYSŁOWYCH
 POLITECHNIKA ŚLĄSKA ZESZYTY NAUKOWE Nr 1647 Tadeusz SZKODNY SUB Gottingen 217 780 474 2005 A 3014 MODELOWANIE I SYMULACJA RUCHU MANIPULATORÓW ROBOTÓW PRZEMYSŁOWYCH GLIWICE 2004 SPIS TREŚCI WAŻNIEJSZE OZNACZENIA
POLITECHNIKA ŚLĄSKA ZESZYTY NAUKOWE Nr 1647 Tadeusz SZKODNY SUB Gottingen 217 780 474 2005 A 3014 MODELOWANIE I SYMULACJA RUCHU MANIPULATORÓW ROBOTÓW PRZEMYSŁOWYCH GLIWICE 2004 SPIS TREŚCI WAŻNIEJSZE OZNACZENIA
QUANTITATIVE AND QUALITATIVE CHARACTERISTICS OF FINGERPRINT BIOMETRIC TEMPLATES
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
ANALIZA TRÓJELEMENTOWEGO OBWODU MEMRYSTOROWEGO NIECAŁKOWITEGO RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 77 Electrical Engineering 4 Mikołaj BUSŁOWICZ* ANALIZA TRÓJELEMENTOWEGO OBWODU MEMRYSTOROWEGO NIECAŁKOWITEGO RZĘDU W pracy rozpatrzono szeregowy
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 77 Electrical Engineering 4 Mikołaj BUSŁOWICZ* ANALIZA TRÓJELEMENTOWEGO OBWODU MEMRYSTOROWEGO NIECAŁKOWITEGO RZĘDU W pracy rozpatrzono szeregowy
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Matematyka Stosowana na Politechnice Wrocławskiej. Komitet Matematyki PAN, luty 2017 r.
 Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
PORTFOLIO Próbki tekstu składanego systemem L A TEX
 PORTFOLIO Próbki tekstu składanego systemem L A TEX Autor: Spis treści Wstęp. Wprowadzenie...................................... Warunki korzystania z usługi............................ Przykładowe próbki
PORTFOLIO Próbki tekstu składanego systemem L A TEX Autor: Spis treści Wstęp. Wprowadzenie...................................... Warunki korzystania z usługi............................ Przykładowe próbki
STANISŁAW KĘPIŃSKI (1867 1908) AND HIS PAPERS IN THE FIELD OF DIFFERENTIAL EQUATIONS
 TECHNICAL TRANSACTIONS FUNDAMENTAL SCIENCES CZASOPISMO TECHNICZNE NAUKI PODSTAWOWE -NP/015 JAN KOROŃSKI* STANISŁAW KĘPIŃSKI (1867 1908) AND HIS PAPERS IN THE FIELD OF DIFFERENTIAL EQUATIONS STANISŁAW KĘPIŃSKI
TECHNICAL TRANSACTIONS FUNDAMENTAL SCIENCES CZASOPISMO TECHNICZNE NAUKI PODSTAWOWE -NP/015 JAN KOROŃSKI* STANISŁAW KĘPIŃSKI (1867 1908) AND HIS PAPERS IN THE FIELD OF DIFFERENTIAL EQUATIONS STANISŁAW KĘPIŃSKI
Liczbę 29 możemy zaprezentować na siedem różnych sposobów:
 Numeryczna analiza rozkładu liczb naturalnych na określoną sumę liczb pierwszych Świerczewski Ł. Od blisko 200 lat matematycy poszukują odpowiedzi na pytanie zadane przez Christiana Goldbacha, który w
Numeryczna analiza rozkładu liczb naturalnych na określoną sumę liczb pierwszych Świerczewski Ł. Od blisko 200 lat matematycy poszukują odpowiedzi na pytanie zadane przez Christiana Goldbacha, który w
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
 Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
APPLICATION OF THE CLONAL SELECTION ALGORITHM FOR RECONSTRUCTION OF THE THIRD KIND BOUNDARY CONDITION
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2012 Seria: MATEMATYKA STOSOWANA z. 2 Nr kol. 1874 Edyta HETMANIOK, Adam ZIELONKA, Damian SŁOTA Institute of Mathematics Silesian University of Technology APPLICATION
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2012 Seria: MATEMATYKA STOSOWANA z. 2 Nr kol. 1874 Edyta HETMANIOK, Adam ZIELONKA, Damian SŁOTA Institute of Mathematics Silesian University of Technology APPLICATION
Matematyka 3. Suma szeregu. Promień zbieżności szeregu. Przykład 1: Przykład 2: GenerateConditions
 Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION
 Mirosław GUZIK Grzegorz KOSZŁKA PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION W artykule przedstawiono niektóre
Mirosław GUZIK Grzegorz KOSZŁKA PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION W artykule przedstawiono niektóre
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016
 Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016 Paweł Lula Cracow University of Economics, Poland pawel.lula@uek.krakow.pl Latent Dirichlet Allocation (LDA) Documents Latent
Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016 Paweł Lula Cracow University of Economics, Poland pawel.lula@uek.krakow.pl Latent Dirichlet Allocation (LDA) Documents Latent
II wariant dwie skale ocen II alternative two grading scales
 Kryteria przeliczania uzyskanych przez kandydata ocen na punkty do listy rankingowej University Criteria for converting candidates grades into the points for the Ranking List Wymagane przedmioty : fizyka,
Kryteria przeliczania uzyskanych przez kandydata ocen na punkty do listy rankingowej University Criteria for converting candidates grades into the points for the Ranking List Wymagane przedmioty : fizyka,
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
The Lorenz System and Chaos in Nonlinear DEs
 The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
Stany związane. Andrzej Baran 18 stycznia 2017 UMCS
 Stany związane Andrzej Baran 18 stycznia 2017 UMCS Macierzowy algorytm Numerowa Algorytm macierzowy Numerowa I Algorytm Numerowa dla równania ψ (x) = f(x)ψ(x), (1) (dla równania Schroedingera f(x) = 2m(E
Stany związane Andrzej Baran 18 stycznia 2017 UMCS Macierzowy algorytm Numerowa Algorytm macierzowy Numerowa I Algorytm Numerowa dla równania ψ (x) = f(x)ψ(x), (1) (dla równania Schroedingera f(x) = 2m(E
Innowacje społeczne innowacyjne instrumenty polityki społecznej w projektach finansowanych ze środków Europejskiego Funduszu Społecznego
 Zarządzanie Publiczne, 2(18)/2012, s. 33 45 Kraków 2012 Published online September 10, 2012 doi: 10.4467/20843968ZP. 12.009.0533 Innowacje społeczne innowacyjne instrumenty polityki społecznej w projektach
Zarządzanie Publiczne, 2(18)/2012, s. 33 45 Kraków 2012 Published online September 10, 2012 doi: 10.4467/20843968ZP. 12.009.0533 Innowacje społeczne innowacyjne instrumenty polityki społecznej w projektach
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: MATEMATYKA STOSOWANA II 2. Kod przedmiotu: Ma2 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Zastosowanie informatyki
I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: MATEMATYKA STOSOWANA II 2. Kod przedmiotu: Ma2 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Zastosowanie informatyki
H γ0 - the standard enthalpy of g phase. H β γ - the transition enthalpy of b to g
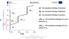 H α0 - the standard enthalpy of a phase H β0 - the standard enthalpy of b phase H γ0 - the standard enthalpy of g phase H α β - the transition enthalpy of a to b phase at T t1 H β γ - the transition enthalpy
H α0 - the standard enthalpy of a phase H β0 - the standard enthalpy of b phase H γ0 - the standard enthalpy of g phase H α β - the transition enthalpy of a to b phase at T t1 H β γ - the transition enthalpy
PRZEWODNIK PO PRZEDMIOCIE. Negotiation techniques. Management. Stationary. II degree
 Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Selection of controller parameters Strojenie regulatorów
 Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
DOBÓR FUNKCJI WŁASNEJ PRZEMIESZCZENIA UKŁADÓW DRGAJĄCYCH GIĘTNIE W RUCHU UNOSZENIA
 MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s. 7-34, Gliwice 007 DOBÓR FUNKCJI WŁASNEJ PRZEMIESZCZENIA UKŁADÓW DRGAJĄCYCH GIĘTNIE W RUCHU UNOSZENIA ANDRZEJ BUCHACZ, SŁAWOMIR ŻÓŁKIEWSKI Instytut Automatyzacji
MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s. 7-34, Gliwice 007 DOBÓR FUNKCJI WŁASNEJ PRZEMIESZCZENIA UKŁADÓW DRGAJĄCYCH GIĘTNIE W RUCHU UNOSZENIA ANDRZEJ BUCHACZ, SŁAWOMIR ŻÓŁKIEWSKI Instytut Automatyzacji
MODEL RACHUNKU OPERATORÓW DLA RÓŻ NICY WSTECZNEJ PRZY PODSTAWACH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
A Zadanie
 where a, b, and c are binary (boolean) attributes. A Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty a (maks) (2) (2) (2) (2) (4) F(6) (8) T (8) (12) (12) (40) Nazwisko i Imiȩ: c Uwaga: ta część zostanie wypełniona
where a, b, and c are binary (boolean) attributes. A Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty a (maks) (2) (2) (2) (2) (4) F(6) (8) T (8) (12) (12) (40) Nazwisko i Imiȩ: c Uwaga: ta część zostanie wypełniona
Zdzisław Kamont ( )
 Zdzisław Kamont (1942-2012) Zdzisław Kamont urodził się 1 listopada 1942 roku we wsi Leśniki w obecnym województwie podlaskim. Był absolwentem Liceum Pedagogicznego w Białymstoku. W 1961 roku zdał egzamin
Zdzisław Kamont (1942-2012) Zdzisław Kamont urodził się 1 listopada 1942 roku we wsi Leśniki w obecnym województwie podlaskim. Był absolwentem Liceum Pedagogicznego w Białymstoku. W 1961 roku zdał egzamin
Nauka Przyroda Technologie
 Nauka Przyroda Technologie ISSN 1897-7820 http://www.npt.up-poznan.net Dział: Rolnictwo Copyright Wydawnictwo Uniwersytetu Przyrodniczego w Poznaniu 2010 Tom 4 Zeszyt 4 ALICJA SZABELSKA 1, MICHAŁ SIATKOWSKI
Nauka Przyroda Technologie ISSN 1897-7820 http://www.npt.up-poznan.net Dział: Rolnictwo Copyright Wydawnictwo Uniwersytetu Przyrodniczego w Poznaniu 2010 Tom 4 Zeszyt 4 ALICJA SZABELSKA 1, MICHAŁ SIATKOWSKI
1 Wartości własne oraz wektory własne macierzy
 Szymon Toruńczyk Wartości własne oraz wektory własne macierzy Niech A będzie kwadratową macierzą n n Wówczas A wyznacza przekształcenie liniowe przestrzeni R n w siebie Niech v R n będzie pewnym niezerowym
Szymon Toruńczyk Wartości własne oraz wektory własne macierzy Niech A będzie kwadratową macierzą n n Wówczas A wyznacza przekształcenie liniowe przestrzeni R n w siebie Niech v R n będzie pewnym niezerowym
INSPECTION METHODS FOR QUALITY CONTROL OF FIBRE METAL LAMINATES IN AEROSPACE COMPONENTS
 Kompozyty 11: 2 (2011) 130-135 Krzysztof Dragan 1 * Jarosław Bieniaś 2, Michał Sałaciński 1, Piotr Synaszko 1 1 Air Force Institute of Technology, Non Destructive Testing Lab., ul. ks. Bolesława 6, 01-494
Kompozyty 11: 2 (2011) 130-135 Krzysztof Dragan 1 * Jarosław Bieniaś 2, Michał Sałaciński 1, Piotr Synaszko 1 1 Air Force Institute of Technology, Non Destructive Testing Lab., ul. ks. Bolesława 6, 01-494
Zaawansowane metody programowania. Algorytmy
 Zaawansowane metody programowania Dr Zbigniew Kozioł - wykład Mgr Mariusz Woźny - laboratorium Wykład IV Algorytmy Drzewa, grafy, etc... Najpierw o algorytmach General Feldmarschall Albrecht Theodor Emil
Zaawansowane metody programowania Dr Zbigniew Kozioł - wykład Mgr Mariusz Woźny - laboratorium Wykład IV Algorytmy Drzewa, grafy, etc... Najpierw o algorytmach General Feldmarschall Albrecht Theodor Emil
P R A C A D Y P L O M O W A
 POLITECHNIKA POZNAŃSKA Wydział Maszyn Roboczych i Transportu P R A C A D Y P L O M O W A Autor: inż. METODA Ε-CONSTRAINTS I PRZEGLĄDU FRONTU PARETO W ZASTOSOWANIU DO ROZWIĄZYWANIA PROBLEMU OPTYMALIZACJI
POLITECHNIKA POZNAŃSKA Wydział Maszyn Roboczych i Transportu P R A C A D Y P L O M O W A Autor: inż. METODA Ε-CONSTRAINTS I PRZEGLĄDU FRONTU PARETO W ZASTOSOWANIU DO ROZWIĄZYWANIA PROBLEMU OPTYMALIZACJI
OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA
 Politechnika Poznańska Wydział Maszyn Roboczych i Transportu Inż. NATALIA LEMTIS OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA Promotor: DR INŻ. MARCIN KICIŃSKI Poznań, 2016
Politechnika Poznańska Wydział Maszyn Roboczych i Transportu Inż. NATALIA LEMTIS OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA Promotor: DR INŻ. MARCIN KICIŃSKI Poznań, 2016
OPISYWANIE IZOTERM SORPCJI WYBRANYMI RÓWNANIAMI Z WYKORZYSTANIEM PROGRAMU EXCEL
 Inżynieria Rolnicza 5(13)/28 OPISYWANIE IZOTERM SORPCJI WYBRANYMI RÓWNANIAMI Z WYKORZYSTANIEM PROGRAMU EXCEL Zbigniew Zdrojewski, Stanisław Peroń Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy
Inżynieria Rolnicza 5(13)/28 OPISYWANIE IZOTERM SORPCJI WYBRANYMI RÓWNANIAMI Z WYKORZYSTANIEM PROGRAMU EXCEL Zbigniew Zdrojewski, Stanisław Peroń Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Gradient Coding using the Stochastic Block Model
 Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent
 Piotr Olczak 1, Agata Jarosz Politechnika Krakowska 2 Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent Wprowadzenie Autorzy niniejszej pracy dokonali porównania
Piotr Olczak 1, Agata Jarosz Politechnika Krakowska 2 Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent Wprowadzenie Autorzy niniejszej pracy dokonali porównania
Cracow University of Economics Poland
 Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
Metody numeryczne rozwiązywania równań różniczkowych
 Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
The Overview of Civilian Applications of Airborne SAR Systems
 The Overview of Civilian Applications of Airborne SAR Systems Maciej Smolarczyk, Piotr Samczyński Andrzej Gadoś, Maj Mordzonek Research and Development Department of PIT S.A. PART I WHAT DOES SAR MEAN?
The Overview of Civilian Applications of Airborne SAR Systems Maciej Smolarczyk, Piotr Samczyński Andrzej Gadoś, Maj Mordzonek Research and Development Department of PIT S.A. PART I WHAT DOES SAR MEAN?
harmonic functions and the chromatic polynomial
 harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR. Wojciech Zieliński
 PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
Inverse problems - Introduction - Probabilistic approach
 Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
WYZNACZANIE KOSZTÓW TRANSPORTU Z WYKORZYSTANIEM OCTAVE 3.4.3
 PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 111 Transport 2016 Joanna Szkutnik-, Wojskowa Akademia Techniczna, W WYZNACZANIE KOSZTÓW TRANSPORTU Z WYKORZYSTANIEM OCTAVE 3.4.3 : maj 2016 Streszczenie: samochodowej.
PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 111 Transport 2016 Joanna Szkutnik-, Wojskowa Akademia Techniczna, W WYZNACZANIE KOSZTÓW TRANSPORTU Z WYKORZYSTANIEM OCTAVE 3.4.3 : maj 2016 Streszczenie: samochodowej.
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
TRANSFORMATA FALKOWA WYBRANYCH SYGNAŁÓW SYMULACYJNYCH
 1-2013 PROBLEMY EKSPLOATACJI 27 Izabela JÓZEFCZYK, Romuald MAŁECKI Politechnika Warszawska, Płock TRANSFORMATA FALKOWA WYBRANYCH SYGNAŁÓW SYMULACYJNYCH Słowa kluczowe Sygnał, dyskretna transformacja falkowa,
1-2013 PROBLEMY EKSPLOATACJI 27 Izabela JÓZEFCZYK, Romuald MAŁECKI Politechnika Warszawska, Płock TRANSFORMATA FALKOWA WYBRANYCH SYGNAŁÓW SYMULACYJNYCH Słowa kluczowe Sygnał, dyskretna transformacja falkowa,
Uniwersytet Rzeszowski
 Seminarium z Równań Różniczkowych 21 marca 2017 r., godz. 12:15, sala 270 (B2): mgr Grzegorz Głowa, mgr Jarosław Napora, wykorzystaniem języka R, cz.2 Analizy statystyczne z 7 marca 2017 r., godz. 12:15,
Seminarium z Równań Różniczkowych 21 marca 2017 r., godz. 12:15, sala 270 (B2): mgr Grzegorz Głowa, mgr Jarosław Napora, wykorzystaniem języka R, cz.2 Analizy statystyczne z 7 marca 2017 r., godz. 12:15,
APROKSYMACJA DANYCH RÓŻNYMI FUNKCJAMI PRZY OBLICZENIACH DEFORMACJI TERENU
 Stanisław KOWALIK Politechnika Śląska, Gliwice APROKSYMACJA DANYCH RÓŻNYMI FUNKCJAMI PRZY OBLICZENIACH DEFORMACJI TERENU Streszczenie. W pracy dokonano aproksymacji danych liczbowych dotyczących przemieszczeń
Stanisław KOWALIK Politechnika Śląska, Gliwice APROKSYMACJA DANYCH RÓŻNYMI FUNKCJAMI PRZY OBLICZENIACH DEFORMACJI TERENU Streszczenie. W pracy dokonano aproksymacji danych liczbowych dotyczących przemieszczeń
NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ SERII NORM PN-EN ISO 3740
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH
 ELEKTRYKA 4 Zeszyt (9) Rok LX Andrzej ZAWADZKI, Maciej WŁODARCZYK Politechnika Świętokrzyska w Kielcach ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH Streszczenie.
ELEKTRYKA 4 Zeszyt (9) Rok LX Andrzej ZAWADZKI, Maciej WŁODARCZYK Politechnika Świętokrzyska w Kielcach ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH Streszczenie.
PRACA DYPLOMOWA Magisterska
 POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM
 Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Opis Przedmiotu Zamówienia oraz kryteria oceny ofert. Część nr 8
 Załącznik nr 1 do Ogłoszenia Opis Przedmiotu Zamówienia oraz kryteria oceny ofert Część nr 8 Wydział Prawa Kanonicznego Przedmiotem zamówienia jest realizacja wykładów dla studentów Uniwersytetu Kardynała
Załącznik nr 1 do Ogłoszenia Opis Przedmiotu Zamówienia oraz kryteria oceny ofert Część nr 8 Wydział Prawa Kanonicznego Przedmiotem zamówienia jest realizacja wykładów dla studentów Uniwersytetu Kardynała
Discretization of continuous signals (M 19) Dyskretyzacja sygnałów ciągłych
 SILESIAN UNIVESITY OF TECHNOLOGY FACULTY OF ENERGY AND ENVIRONMENTAL ENGINEERING INSTITUTE OF POWER ENGINEERING AND TURBOMACHINERY POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT
SILESIAN UNIVESITY OF TECHNOLOGY FACULTY OF ENERGY AND ENVIRONMENTAL ENGINEERING INSTITUTE OF POWER ENGINEERING AND TURBOMACHINERY POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT
Warsztaty Ocena wiarygodności badania z randomizacją
 Warsztaty Ocena wiarygodności badania z randomizacją Ocena wiarygodności badania z randomizacją Każda grupa Wspólnie omawia odpowiedź na zadane pytanie Wybiera przedstawiciela, który w imieniu grupy przedstawia
Warsztaty Ocena wiarygodności badania z randomizacją Ocena wiarygodności badania z randomizacją Każda grupa Wspólnie omawia odpowiedź na zadane pytanie Wybiera przedstawiciela, który w imieniu grupy przedstawia
Wykaz linii kolejowych, które są wyposażone w urządzenia systemu ETCS
 Wykaz kolejowych, które są wyposażone w urządzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
Wykaz kolejowych, które są wyposażone w urządzenia W tablicy znajdującej się na kolejnych stronach tego załącznika zastosowano następujące oznaczenia: - numer kolejowej według instrukcji Wykaz Id-12 (D-29).
Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych
 Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki Politechnika Śląska, Gliwice Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych Algorytm SWMEB. Część
Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki Politechnika Śląska, Gliwice Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych Algorytm SWMEB. Część
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
XII International PhD Workshop OWD 2010, 23 26 October 2010. Metodyka pozyskiwania i analizy wyników badań symulacyjnych ścieżek klinicznych
 XII International PhD Workshop OWD 2010, 23 26 October 2010 Metodyka pozyskiwania i analizy wyników badań symulacyjnych ścieżek klinicznych Methodology of Acquiring and Analyzing Results of Simulation
XII International PhD Workshop OWD 2010, 23 26 October 2010 Metodyka pozyskiwania i analizy wyników badań symulacyjnych ścieżek klinicznych Methodology of Acquiring and Analyzing Results of Simulation
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to students
 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016
 PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016 Krzysztof Rokicki 1 GPS AND OBD DATA IN TESTING OF THE VEHICLE DYNAMICS 1. Introduction Previously to determine the speed of the vehicle during dynamic
PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016 Krzysztof Rokicki 1 GPS AND OBD DATA IN TESTING OF THE VEHICLE DYNAMICS 1. Introduction Previously to determine the speed of the vehicle during dynamic
