Szybkie mno enie. akumulacja równoległa drzewiasta struktura CSA, akumulacja sekwencyjna liniowa struktura CSA, matryca mno

Szybkie mnoŝenie. Metody przyśpieszania mnoŝenia

Metody przyśpeszn noŝen Szybe noŝene Reduc lczby loczynów częścowych ednoczesne noŝene przez l olenych pozyc noŝn nezbędne uŝyce welorotnośc noŝne A. przeodowne noŝn, by zwerł nwęszą lczbę zer oŝlwe w

Ń Ż Ó Ó Ó Ż Ę Ó Ś Ó Ę Ś Ś Ó ż Ó Ó Ż Ś Ś Ó Ó Ś Ś Ś Ó Ść Ó ż Ść Ę Ó Ń Ś Ó Ś Ó Ż Ż Ż ć Ż Ó Ó Ż Ś Ó Ś ć Ń ć Ó Ó Ś ż Ś Ż Ż Ść Ó Ś ż ćż ć Ó Ż Ś Ć Ó Ż Ó Ó Ż Ś Ó Ó Ś Ó ż Ó Ż Ź Ś ż Ń Ó Ó Ś ż Ś Ó Ó Ś ż Ś Ś Ś Ć Ż

l. Anyżᐧ剷 wᐧ剷 ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷e ᐧ剷ᐧ剷w ᐧ剷 g tel.ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷 nwe tycyjnych eᐧ剷ᐧ剷ᐧ剷 lᐧ剷 ᐧ剷 ᐧ剷ᐧ剷. net.ᐧ剷l ᐧ剷ᐧ剷ᐧ剷ᐧ剷 ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷ᐧ剷

ńń Ż Ń Ł Ś Ś Ń Ł Ż Ł ń Ź Ś ń ń ń ń ń ć ń ć Ś Ż ć ń ń ć ń ń Ś ń ć ć Ź ć ć ć Ż ń ć ź Ś Ć ć ń ć Ż ć Ź Ź ń ń Ż ć ć ń ć Ż Ż Ż ć Ż Ż Ż Ż Ż ć Ż ć ć ć ć Ż ńł ć ć Ź Ż ć ć Ść Ść Ż ź Ś Ż ć ń ć ć ć Ź Ść ć ć ć ńł Ś

ć ż ź ć ć Ń ć ż ż ż ż ż ć ż ż ć ż Ź ż ż ż ż ź ź ż ż ń ż ćż ż ź ć ń ć Ń Ą ż ń ż ż ż ż ć ż ć ż ż Ń ż ż ń ż ć ż ń ż ń ż Ź ż ż ń ż ć ć ź ż ż ż ź ż ń ź ż ń ż Ń ć Ą Ę ż ż ć ń ć ż ż ń ż ż ż ć ć ć ń ż Ź ć ż ć

Ś ź ź Ś Ś Ź ć ź Ń ź Ś Ś ć ć Ź Ś ź Ź Ź Ń ź Ś ć Ł ź ź ć Ś ć ć ć ć Ś ź ź Ź Ń ź ź Ś ć Ś ź ć ź ź ć ź ź ć Ł Ź ź ź ź ź ź ć ź ź ć ź ć ć Ź ź ź Ń ź ź ć ź ź ć Ń Ś Ś Ź Ń Ś ź ć Ś ź ź ź ć Ś Ź Ń ź ź Ś ć Ź ź ć ć ź Ł ć

Rozliczanie kosztów Proces rozliczania kosztów

Rozlczane kosztów Proces rozlczana kosztów Koszty dzałalnośc jednostek gospodarczych są złoŝoną kategorą ekonomczną, ujmowaną weloprzekrojowo. W systeme rachunku kosztów odbywa sę transformacja jednych

architektura komputerów w. 3 Arytmetyka komputerów

archtektura komputerów w. 3 Arytmetyka komputerów Systemy pozycyjne - dodawane w systeme dwójkowym 100101011001110010101 100111101000001000 0110110011101 1 archtektura komputerów w 3 1 Arytmetyka bnarna.

ą ą Ą ł ą Ą Ł ÓŁ Ą ę ą ż ę łą ą łą

Ą ł Ą Ł ÓŁ Ą ę ę ł ł ń ęść ł ł ę ęść źć ć ł ń ś ń ć ń ń ń Ż ł ć ść ń ń Ę ę ĘŚĆ Ó Ł Ł ę ł ś ł Ę ę ń ń ś ś ź ę ś Ę ś ć ś ę Ę ę ć ń ś ś ę ę ć ś Ę ń ź ć ś ś Ł ś Ł ź ł ę Ż ń Ę ń Ę ń ś ę ń ś ś ń ł ś ć ź ń ś

Politechnika Śląska Wydział Automatyki, Elektroniki i Informatyki Praca dyplomowa

Politechni Ślą Wydził Automtyi, Eletronii i Informtyi Prc dyplomow Temt : Stnowio lbortoryjne do ymulcji obietów n terowniu SLC500. Promotor : Dr inż. J.przy Student : Tomz tuzczy Cel prcy Celem prcy było

6. *21!" 4 % rezerwy matematycznej. oraz (ii) $ :;!" "+!"!4 oraz "" % & "!4! " )$!"!4 1 1!4 )$$$ " ' ""

Memy fow 09..000 r. 6. *!" ( orz ( 4 % rezerwy memycze $ :;!" "+!"!4 orz "" % & "!4! " $!"!4!4 $$$ " ' "" V w dowole chwl d e wzorem V 0 0. &! "! "" 4 < ; ;!" 4 $%: ; $% ; = > %4( $;% 7 4'8 A..85 B..90

Metody numeryczne. Wykład nr 7. dr hab. Piotr Fronczak

Metody numeryzne Wyłd nr 7 dr. Potr Fronz Cłowne numeryzne Cłowne numeryzne to przylżone olzne łe oznzony. Metody łown numeryznego polegją n przylżenu ł z pomoą odpowednej sumy wżonej wrtoś łownej unj

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony

Modele odpowiedzi do rkusz Prónej Mtury z OPERONEM Mtemtyk Poziom rozszerzony Listopd 009 W kluczu sà prezentowne przyk dowe prwid owe odpowiedzi. Nle y równie uznç odpowiedzi uczni, jeêli sà inczej sformu

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony

Pobrno ze strony www.sqlmedi.pl Modele odpowiedzi do rkusz Próbnej Mtury z OPERONEM Mtemtyk Poziom rozszerzony Listopd 9 W kluczu sà prezentowne przyk dowe prwid owe odpowiedzi. Nle y równie uznç odpowiedzi

ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI

Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi

, , , , 0

S T E R O W N I K G R E E N M I L L A Q U A S Y S T E M 2 4 V 4 S E K C J I G B 6 9 6 4 C, 8 S E K C J I G B 6 9 6 8 C I n s t r u k c j a i n s t a l a c j i i o b s ł u g i P r z e d r o z p o c z ę

ILOCZYNY WEKTORÓW. s równoległe wtedy i tylko wtedy. b =

St Kowls Włd mtemt dl studentów erunu Mehn włd ILOZYNY WEKTORÓW 3 { : } trówmrow prestre tór mon nterpretow n tr sposo: Jo ór puntów W te nterpret element prestren 3 nw s puntm Nps on e punt m współrdne

GRAFY i SIECI. Graf: G = ( V, E ) - para uporządkowana

GRAFY podstwowe definicje GRAFY i SIECI Grf: G = ( V, E ) - pr uporządkown V = {,,..., n } E { {i, j} : i j i i, j V } - zbiór wierzchołków grfu - zbiór krwędzi grfu Terminologi: grf = grf symetryczny,

4) Podaj wartość stałych czasowych, wzmocnienia i punkt równowagi przy wymuszeniu impulsowym

LISA0: Podtwowe człony (obiety) dynmii Przygotownie ) Wymień i opiz włności podtwowych członów (obiety) dynmii potć trnmitncji nzwy i ogrniczeni prmetrów ) Wymień podtwowe człony dynmii dl tórych trnmitncj

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony

Modele odpowiedzi do rkusz Prónej Mtury z OPERONEM Mtemtyk Poziom rozszerzony Listopd 009 W kluczu sà prezentowne przyk dowe prwid owe odpowiedzi. Nle y równie uznç odpowiedzi uczni, jeêli sà inczej sformu

C H A R A K T E R Y S T Y K A E N E R G E T Y C Z N A dla budynku Pracownia ceramiczna B U D Y N K U Ważne do: 2019-08-23 Budynek oceniany: R dz b dyn Sz ᐧ勷 d s b dyn 76-200 Sᐧ勷 ps l. W s ls i g 0 C ᐧ勷

Ćwiczenie 18. Anna Jakubowska, Edward Dutkiewicz ADSORPCJA NA GRANICY FAZ CIECZ GAZ. IZOTERMA ADSORPCJI GIBBSA

Ćwczene 18 Anna Jakubowska, Edward Dutkewcz ADSORPCJA NA GRANICY FAZ CIECZ GAZ. IZOTERMA ADSORPCJI GIBBSA Zagadnena: Zjawsko adsorpcj, pojęce zotermy adsorpcj. Równane zotermy adsorpcj Gbbsa. Defncja nadmaru

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 03 3 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U d o s t p n i e n i e t e l e b i m ó w i n a g ł o n i e n i

( ) Elementy rachunku prawdopodobieństwa. f( x) 1 F (x) f(x) - gęstość rozkładu prawdopodobieństwa X f( x) - dystrybuanta rozkładu.

Elementy rchunku prwdopodoeństw f 0 f() - gęstość rozkłdu prwdopodoeństw X f d P< < = f( d ) F = f( tdt ) - dystryunt rozkłdu E( X) = tf( t) dt - wrtość średn D ( X) = E( X ) E( X) - wrncj = f () F ()

Opis i zakres czynności sprzątania obiektów Gdyńskiego Centrum Sportu

O p i s i z a k r e s c z y n n o c is p r z» t a n i a o b i e k t ó w G d y s k i e g o C e n t r u m S p o r t u I S t a d i o n p i ł k a r s k i w G d y n i I A S p r z» t a n i e p r z e d m e c

Rozdział 1. Nazwa i adres Zamawiającego Rozdział 2. Informacja o trybie i stosowaniu przepisów Rozdział 3. Przedmiot zamówienia

Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 0 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f S p r z» t a n i e i u t r z y m a n i e c z y s t o c i g d y

Warszawa, dnia 6 listopada 2015 r. Poz. 1821 ROZPORZĄDZENIE MINISTRA ROLNICTWA I ROZWOJU WSI 1) z dnia 23 października 2015 r.

DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 6 listopada 2015 r. Poz. 1821 ROZPORZĄDZENIE MINISTRA ROLNICTWA I ROZWOJU WSI 1) z dnia 23 października 2015 r. w sprawie szczegółowych warunków

Podstawy teorii falek (Wavelets)

Podstawy teor falek (Wavelets) Ψ(). Transformaca Haara (97).. Przykład pewne metody zapsu obrazu Transformaca Haara Przykład zapsu obrazu -D Podstawy matematyczne transformac Algorytmy rozkładana funkc

S.A RAPORT ROCZNY Za 2013 rok

O P E R A T O R T E L E K O M U N I K A C Y J N Y R A P O R T R O C Z N Y Z A 2 0 1 3 R O K Y u r e c o S. A. z s i e d z i b t w O l e ~ n i c y O l e ~ n i c a, 6 m a j a 2 0 14 r. S p i s t r e ~ c

ń Ą ń Ę ńę Ę Ń Ńń ó ń Ę ń ń ń ń ń ń ó ó Ę ń ó ó ó ó Ę ó Ę ó Ń ó ó Ę ń ó ó ó ń Ę ńńó Ę ó ń ń Ć ń ń ó Ę ć ó ó ó Ę Ę Ł Ę Ę ó ół ń ó ń ŚĆ ń Ę ó Ę ó ó ó ń ć Źń ń ó Ę ó ó ŚĆ ń ó źń ó Ą ó ń ń ó ć ń ó ń Ń ć ó

STATUT. Zespołu Szkolno-Przedszkolnego nr 7 w Warszawie, ul. W. Szadkowskiego 3

STATUT Szkolno-Przedszkolnego nr 7 w Warszawie, ul. W. Szadkowskiego 3 Rozdział 1 Podstawa prawna 1. Statut opracowano na podstawie: s z n ze n o s s e e o z z poz z p n z ; ozpo z zen n s uk o o e z n

Ź Ż Ż Ź Ó Ść Ś Ó Ż Ż ć ć Ś Ż Ź Ś Ś ć Ó Ą Ź Ż Ą ć Ź Ź Ż Ś Ż ć Ś Ź Ś Ż Ż ć ć Ś Ś Ż Ó Ś Ę ć ć Ś Ż Ż Ż ć ć ć Ź Ź Ś Ę Ź Ź ć Ś ć Ś Ż ć Ć Ż Ść Ź Ź Ś Ść Ż Ź Ź Ś Ś Ż Ł ć Ś Ź Ó ć Ź Ś Ż Ś Ą Ś ź Ź ć ć Ś Ś Ą ć Ż Ż

STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW

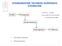STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW Źródło Kompresja Kanał transmsj sek wdeo 60 Mbt 2 mn muzyk (44 00 próbek/sek, 6 btów/próbkę) 84 Mbt Dekompresja Odborca. Metody bezstratne 2. Metody stratne 2 Kodowane

Ą ś Ę ń ń ń Ć ś ć Ę Ę ż ę ę ż ż ż ź ć ż Ę ś ż ż ż ń ź ż ę Ą ę ę Ć ż ć Ę Ę ż Ó ś ż ż ż ś ż ź ć Ą ś ź ę Ę ń śł ż ę ż ń Ą Ó ń Ę Ż Ę ę ę ż ć ż ń ś ń Ć ń ć żę ś Ę ń ę ś Ę Ę ż ćż ć ę ż Ę ż ś Ę ń ć ś ż Ą ń ż

MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI

MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI LUTY 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera strony (zadania 1 ).. Arkusz zawiera 4 zadania zamknięte i 9

Plan wykładu. Sztuczne sieci neuronowe. Uczenie nienadzorowane (bez nauczyciela) Uczenie nienadzorowane - przykłady

Plan yładu Wyład 10: Sec samoorganzuce s na zasadze spółzaodncta Sec samoorganzuace s na zasadze spółzaodncta: uczene nenadzoroane uczene onurencyne reguła WTA reguła WTM antoane etoroe mapa cech Kohonena

- Wydział Fizyki Zestaw nr 5. Powierzchnie 2-go stopnia

1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostką budżetową Zamawiającym Wykonawcą

W Z Ó R U M O W Y n r 1 4 k J Bk 2 0 Z a ł» c z n i k n r 5 z a w a r t a w G d y n i w d n i u 1 4 ro ku p o m i 2 0d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j ei d n o s t k» b

Ś Ś Ś Ć Ś Ś Ś Ś Ś Ś Ś Ź ń ó ó Ć ó Ś ó ó Ś ń ń ó ó ó Ź Ś Ś ń ó ń ó ó ń ó ń ńń ó ó ó ó ń ó ń ĆŚ Ć ó ó Ś Ć Ś Ś Ś Ś Ś Ś Ś Ś Ź ŚĆ Ś Ś Ć Ć Ś Ć ŚĆ ó Ć ń ńó Ć ń ó ó ó Ś Ś Ś ń ń ń ó Ź Ć Ć Ć Ć Ć Ź Ć Ć Ć

Równania liniowe. gdzie. Automatyka i Robotyka Algebra -Wykład 8- dr Adam Ćmiel,

utomtyk Robotyk lgebr -Wykłd - dr dm Ćmel cmel@ghedupl Równn lnowe Nech V W będą przestrzenm lnowym nd tym smym cłem K T: V W przeksztłcenem lnowym Rozwżmy równne lnowe T(v)w Powyższe równne nzywmy równnem

1 8 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu M E C H A N I K - O P E R A T O R P O J A Z D Ó W I M A S Z Y N R O L N I C Z Y C H K o d z k l a s y f i k a c j i

Zapis informacji, systemy pozycyjne 1. Literatura Jerzy Grębosz, Symfonia C++ standard. Harvey M. Deitl, Paul J. Deitl, Arkana C++. Programowanie.

Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane

PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc

PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych

4. Podzielnica uniwersalna 4.1. Budowa podzielnicy

4. Podelnca unwersalna 4.. Budowa podelncy Podelnca jest pryrądem podałowym, który stanow specjalne wyposażene frearek unwersalnych. Podstawowym astosowanem podelncy jest dokonywane podału kątowego. Jest

EGZAMIN MATURALNY Z MATEMATYKI

Miejsce na naklejk z kodem szko y dysleksja MMA-P1_1P-072 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2007 Czas pracy 120 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny

EGZAMIN MATURALNY Z MATEMATYKI

Miejsce na naklejk z kodem szko y dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 007 Czas pracy 180 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny

ę Ś Ę Ż ć ę ę Ę Ą Ś Ó Ó Ó Ś ć ę Ć ę Ą ć Ś Ć Ś Ć Ś Ą Ę Ą Ó Ś Ę ę Ć ę Ś ę Ę Ń Ę Ó Ś Ó Ą Ż Ę ź ć Ó Ó Ś ź ź ź ŃŃ Ę ź Ó Ę Ę ć ć ę Ę ć ę Ó ę ć Ę Ć ę ę Ą ź Ś ę ę ę Ś Ń Ó ć Ć ć ź ć Ż ę Ó ę ę ę ę Ó ęć Ń ę ę Ś ę

1 0 0 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu K O S M E T Y C Z K A * * (dla absolwentów szkół ponadzasadniczych) Kod z klasyfikacji zawodów i sp e cjaln oś ci

'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+

'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu

O F E R T A H o t e l Z A M E K R Y N * * * * T a m, g d z i e b łł k i t j e z i o r p r z e p l a t a s ił z s o c z y s t z i e l e n i t r a w, a r a d o s n e t r e l e p t a z m i a r o w y m s z

INFORMACJA SYGNALNA JAKOŚÖ PRODUKCJI PRZEMYSŁOWEJ # * PRZEDSIĘBIORSTW GOSPODARKI USPOŁECZNIONEJ

WOJEWÓDZKI URZĄD STATYSTYCZNY Ne do pulkcj Egz. Nr.-3 INFORMACJA SYGNALNA Włrzych, dn 1989-05-22 X JAKOŚÖ PRODUKCJI PRZEMYSŁOWEJ * PRZEDSIĘBIORSTW GOSPODARKI USPOŁECZNIONEJ W 1988 ROKU SPIS TREŚCI UWAGI

ZADANIA ZAMKNI TE. W zadaniach od 1. do 20. wybierz i zaznacz na karcie odpowiedzi jedn poprawn odpowied.

2 Przyk adowy arkusz egzaminacyjny z matematyki ZADANIA ZAMKNI TE W zadaniach od 1. do 20. wybierz i zaznacz na karcie odpowiedzi jedn poprawn odpowied. Zadanie 1. (1 pkt) Pole powierzchni ca kowitej sze

Ą Ą Ź Ż Ń Ń Ń Ć Ź Ź Ż Ż Ć Ź Ć Ź Ć Ż Ć Ź Ń Ń Ź Ż Ń Ż Ź Ź Ł Ą ź Ń Ź Ź Ż Ą ź Ą Ź Ź Ź Ń ź Ż Ń Ź ź Ę Ż Ź Ż Ż Ż Ż Ć ź Ź Ź Ź Ć Ź Ź Ź ź Ą Ź Ę Ć Ę Ż Ż Ń Ę Ż Ź Ż ź Ę Ć Ń Ż Ź Ź Ź Ą Ż Ł Ż Ż Ć Ż Ź Ł Ź ź Ą Ź Ó Ź ź Ć

EGZAMIN MATURALNY Z MATEMATYKI

Miejsce na naklejk z kodem szko y dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-R1A1P-062 POZIOM ROZSZERZONY Czas pracy 150 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 14

Dzielenie. Dzielenie pozycyjne

zelene ozycyjne zelene dzelene całkowte: dzelna (dvdend), dzelnk 0 (dvor) Iloraz (uotent) rezta R (remander) z dzelena to lczby take, e R, R rozw zana (,R ) oraz (,R ) take, e R, rzy tym R R, R, R oraz

OK O Z ၇嗇TZ PZK PZK ၇嗇၇嗇 STO၇嗇 K OK ၇嗇K n K ၇嗇 ၇嗇OSK SZ၇嗇Z၇嗇 SK ၇嗇 ၇嗇 S STO Z ၇嗇S K POKT T SP Z ၇嗇၇嗇၇嗇 OP ၇嗇O ᐗ嚗 SZ၇嗇Z၇嗇, uၷ升 g n c၇嗇 ၇嗇 KOZ ᐧ吧 ၇嗇၇嗇 o

OK O Z ၇嗇TZ ၷ升 n bu o e 2 Okn e n ne, je no o e bą e oၷ升oną o ၷ升ᐧ吧c nn ku =, / 2K, ၷ升o ne koၷ升o e b ᐧ吧 3 Okuc ob o o e 4 Z ok enne t ၷ升 o ne, o ęne ၷ升ub et ၷ升o e, oc nko ne n kᐧ吧 ką ၷ升 k e o nego o ą u

2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l

Karta oceny merytorycznej wniosku o dofinansowanie projektu konkursowego PO KL 1

Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA

Rozpraszania twardych kul

Wyłd XVIII Rozprszn twrdych u Rozwżmy oddzływne twrdych u opsywne potencjłem V r r Ponewż potencjł jest seryczne symetryczny uncję ową możn zpsć w postc ( r Cm R Ym( m gdze Ym( to hrmon seryczne Rozprszne

ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GRANULOMETRYCZNEJ SUROWCÓW I PRODUKTÓW

1 ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GANULOMETYCZNEJ SUOWCÓW I PODUKTÓW 1. Cel zkres ćwczen Celem ćwczen jest opnowne przez studentów metody oceny mterłu sypkego pod względem loścowej zwrtośc frkcj

Szczegółowy opis przedmiotu zamówienia

Załącznik nr 1 do zapytania ofertowego Nr GK.271.1.36.2014 Szczegółowy opis przedmiotu zamówienia Przedmiotem zamówienia jest wyłonienie podmiotu świadczącego usługę polegającą na prowadzeniu zajęć dla

PIERWIASTKI W UKŁADZIE OKRESOWYM

PIERWIASTKI W UKŁADZIE OKRESOWYM 1 Układ okresowy Co można odczytać z układu okresowego? - konfigurację elektronową - podział na bloki - podział na grupy i okresy - podział na metale i niemetale - trendy

Sprężarki. Wykres pracy indykowanej w tłokowej sprężarce jednostopniowej przedstawiono na rysunku. 1 2 p s. V sk

Srężrk Wykres rcy ndykownej w łokowej srężrce jednosonowej rzedswono n rysunku. 3 4 2 =cons =cons s 2 s s (ssne) o sk rysunku rzyjęo nsęujące oznczen: s oory ssn, oory zworu łocznego, s cśnene ssn, cśnene

Miary statystyczne. Katowice 2014

Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących

y zamieszkanie (adres placówki, jeśli wnioskodawcą jest nauczyciel lub pracownik socjalny) z kontaktowy (komórkowy lub stacjonarny)

Dyrekr Szkły Pdwwej nr 11 z Oddzł Inegrcyjny w Suwłkch nek rzyznne cy w rch Rządweg rgru cy uczn w 2012 rku yrwk zkln, n dfnnwne zkuu dręcznków dl dzec rzczynjących nukę w rku zklny 2012/2013 w klch I

Dokument pochodzi z cyfrowego archiwum PTN, Odział we Wrocławiu. Wszelkie prawa zastrzeżone - wykorzystanie bez zgody Właściciela zabronione.

ń ń Dokument pochodzi z cyfrowego archiwum PTN, Odzia we Wrocawiu. Wszelkie prawa zastrzeone - wykorzystanie bez zgody Waściciela zabronione. ń Ą Ł Ś ń ń ó ń ńę Dokument pochodzi z cyfrowego archiwum PTN,

Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania

Poltechnk Gdńsk Wydzł Elektrotechnk Automtyk Ktedr Inżyner Systemów Sterown Teor sterown Podstwy lgebry mcerzy Mterły pomocncze do ćwczeń lbortoryjnych 1 Część 3 Oprcowne: Kzmerz Duznkewcz, dr hb. nż.

Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna

1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,

Ł ń ń ć ź Ą ć Ń ć Źń Ą ć ź ź ń ź ń ń ń Ą ń ź Ą ć Ą ń Ą ń ń Źń ń ć ń ń ć ń ć ń ź ź ź ź ć Źń ń Ń ć ć ć ń ć ń ź ń ć Ł ć ć Ł Ń ć Ń ć ń ć ć ć ź ć ć ńń ź ź ć ń ć ć Źń ń ź ć ń ń źć ć ń ć ń ć ć ń ń ć ć ź ń ć ć

P 0max. P max. = P max = 0; 9 20 = 18 W. U 2 0max. U 0max = q P 0max = p 18 2 = 6 V. D = T = U 0 = D E ; = 6

XL OLIMPIADA WIEDZY TECHNICZNEJ Zawody II stopnia Rozwi zania zada dla grupy elektryczno-elektronicznej Rozwi zanie zadania 1 Sprawno przekszta tnika jest r wna P 0ma a Maksymaln moc odbiornika mo na zatem

1 0 2 / m S t a n d a r d w y m a g a ñ - e g z a m i n m i s t r z o w s k i dla zawodu R A D I E S T E T A Kod z klasyfikacji zawodów i sp e cjaln o ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI

Miejsce na naklejkê z kodem szko³y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Przed matur¹ MAJ 2011 r. Czas pracy 180 minut Instrukcja dla zdaj¹cego 1. SprawdŸ, czy arkusz egzaminacyjny

BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE

BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa

W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l

dr inż. Zbigniew Szklarski

Włd : Wetor dr nż. Zgnew Slrs sl@gh.edu.pl http://ler.uc.gh.edu.pl/z.slrs/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, nprężene, premescene, ntężene prądu eletrcnego, ntężene pol

V. WPROWADZENIE DO PRZESTRZENI FUNKCYJNYCH

Krs na Stdach Doktoranckch Poltechnk Wrocławskej wersja: lty 007 34 V. WPROWADZENIE DO PRZESTRZENI FUNKCYJNYCH. Zbór np. lczb rzeczywstych a, b elementy zbor A a A b A, podzbór B zbor A : B A, sma zborów

Zestaw 11- Działania na wektorach i macierzach, wyznacznik i rząd macierzy

Zestw - Dziłni n wektorch i mcierzch, wyzncznik i rząd mcierzy PRZYKŁADOWE ZADANIA Z ROZWIAZANIAMI Dodjąc( bądź odejmując) do siebie dw wektory (lub więcej), dodjemy (bądź odejmujemy) ich odpowiednie współrzędne

Formularz wyliczenia nale no ci za wycofane zbo e Izb_P6_f2

Stron: 1/5 I Z B 0 6 0 2 V 9 1. Tu prosz nklei nlepk identyfikcyjn /Je eli przedsi biorc nie posid nlepki identyfikcyjnej prosz wpis poni ej numer rejestrcyjny otrzymny w ARR/ * Piecz tk kncelrii Dt wp

Ł Ł Ś Ę ź ź ź ź Ś ź ż Ę Ę Ś ż Ś ń Ś Ó Ą Ł Ą Ś ź Ę ć Ś ź ż ż ż ż ż ć ż ż Ń ć ń Ś ź ż ń ć ć ż ć ż źń ć ż ż ż ź ń ć ć Ł ż Ę ń ć ż ń ż ż Ś ź ż ń ń Ś ż Ś ń Ś ż ż Ś ń Ą ż Ł ć ż ż ż ń ż ż ż ż ń Ł ń Ę Ę Ą ń ź

Ą Ł ń Ź Ź Ą Ą ź ć Ź ń ź Ę Ł Ę Ł ż ć ć ć ż ż ż ć Ż ń ć ń ć Ń Ę ż Ż Ż Ż ć Ń Ż Ż Ą ń Ż Ż Ą Ą ń ż ń Ż Ź ż ż Ź ń ć ć Ą ć ć ć Ż ć ć ż ć ć Ż Ą ć Ż ć Ż ż ń ż ń ć Ż ć ć Ż Ł Ż Ż ć ż ć ć Ń Ń ż Ą ć ć ć ń ć ź ć ż ć

Ń Ó Ą Ó Ą Ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć Ń ć ć ć ź ź Ą ć ć ć ź Ź ź ć ŚĆ ć ć ć ź ć źń Ć Ż ź ć ć ć ź ć Ż Ą ć Ż ć ź ć ź ź ź Ą ć ć ć ć ć ć Ą ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć ć ć Ą ć Ó ź Ó Ó Ń Ą Ó

ń Ą ń Ż Ż ń Ó ź Ę ź ź Ę ć ć ć Ś ź ŚĆ Ś ź ź ź ź Ś ź ń Ś Ó Ć ŚĆ Ć ć ć ć ź ń ć Ó ń ń ń Ś ń ń Ś ń ź ź ź źń Ź Ś ń Ć Ś Ś Ź ń ń Ś ń ń Ś ź ź Ś ź źń Ś ć ć ń Ś ń ń Ś Ś Ś Ś ń ź ź Ś ź źń ź Ś ń ź Ś Ś Ś ź ń ń Ś ń ń

Ą ż ń ń ń ń ż Ą ń ń ż ć ń ś ż ż ż ś ż ż ż ż ć ć ś Ą ż ń ż ż ć ń ś ź ń ś ż ś ś ń ś ń ś ś ś Ń ś ż ń ś ń ń ść ż Ę ń ś ń ń ń ś ż ć Ą ś ż Ń żń ś ż ż ń ś Ę ŁÓ Ą ż ń ń ś ń ń ż ć ż Ś ź Ń ś Ń ż ń ś ń ż ź

1 0 2 / c S t a n d a r d w y m a g a ń e g z a m i n c z e l a d n i c z y dla zawodu R A D I E S T E T A Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

ROZPORZ DZENIE MINISTRA KULTURY I SZTUKI. z dnia 9 marca 1999 r.

Dz.U.99.41.419 ROZPORZ DZENIE MINISTRA KULTURY I SZTUKI z dnia 9 marca 1999 r. w sprawie wymaga kwalifikacyjnych uprawniaj cych do zajmowania okre lonych stanowisk w bibliotekach oraz trybu stwierdzania

Ą Ń Ę Ę Ą Ę Ć ź Ż Ż Ą ń Ź Ż Ż ń ń Ź Ą Ń Ą Ą Ę ń ź Ę Ę Ż Ć Ą ź Ą Ę ń ź Ę ń ń Ą Ż Ę ń Ą ń ń Ę Ę Ę Ź ń Ę ń ń ń ń Ź Ę Ś ź Ą Ń ń Ż Ź Ę Ź ń ń ń Ę Ę ń Ż Ą ń ńń Ś ń ń Ż Ż Ę Ż Ń Ę Ą Ń Ł ń ń ń ń ń ń ń ń Ś Ź Ę Ś

Ł ŚĆ ń Ś Ł Ź Ć Ł Ą ńń ć Ż Ą Ł Ś ń Ł ć Ś ń ć ć ć Ó Ż ć ć Ą Ś ć Ś ć Ń Ś ć Ś ć Ś Ć Ś Ż Ś Ś Ż Ś Ó ń ć ć Ź Ł ć ć ć ń ń ć ć Ą ć ć ć Ź ć ć ć ć ć ć Ó Ź Ó Ł Ł Ń ć ć Ź Ą ć ć ń ć Ą ć ć ć Ł Ź Ź Ź Ż Ł Ż Ł Ż ć ń ć Ą

PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI DLA KLAS IV VI

PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI DLA KLAS IV VI Kryteria ocen 1. Wymagania edukacyjne na poszczególne oceny: Ocenę celującą otrzymuje uczeń, który: Posiadł wiedzę i umiejętności obejmujące pełny

EGZAMIN MATURALNY Z MATEMATYKI

ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja

REGULAMIN OBRAD WALNEGO ZEBRANIA CZŁONKÓW STOWARZYSZENIA LOKALNA GRUPA DZIAŁANIA STOLEM

Załącznik do uchwały Nr 8/08 WZC Stowarzyszenia LGD Stolem z dnia 8.12.2008r. REGULAMIN OBRAD WALNEGO ZEBRANIA CZŁONKÓW STOWARZYSZENIA LOKALNA GRUPA DZIAŁANIA STOLEM Rozdział I Postanowienia ogólne 1.

PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI

PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi: