Wykorzystanie systemu Velocity w COI Gliwice. Jacek Wendykier
|
|
|
- Edward Filipiak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Wykorzystanie systemu Velocity w COI Gliwice Jacek Wendykier
2 Wykorzystanie rzeczywiste - Dose Deformation Deformacja/transformacja deformacyjna rozkładu dawki z jednego badania CT na inne. stare CT + dawka na stare CT + nowe CT Transformacja deformacyjna ma miejsce między bryłami (badaniami CT), po czym obliczana jest deformacja starej dawki na nową bryłę i jej transformacja (resample), aby uzyskać nowy (stary) rozkład dawki. Na wyjściu transformacja deformacyjna między bryłami oraz nowy (stary) rozkład dawki na nowszą bryłę. Velocity User Manual, PD0001_USM, rev /24/2016
3 Volume Resampling Wszystkie operacje na objętościach (volume resampling), czyli tworzenie nowych, operacje na zbiorach, skalowanie i sumowanie dawek etc. opierają się tak naprawdę na przenoszeniu punktów z jednego do drugiego układu współrzędnych. Najczęściej zachowywane są właściwości geometryczne tych operacji, czyli na przykład zachowana jest objętość, ale same wartości wokseli są najczęściej zmieniane w procesie interpolacji. Używana jest do tego interpolacja liniowa w trzech wymiarach (trilineal interpolation) wagowana odległością. Najbardziej widoczne jest to przy obiektach typu PET, DOSE oraz NM, ponieważ mają one relatywnie duże woksele. Velocity User Manual, PD0001_USM, rev /24/2016
4 Dose Deformation zmiana liczby wokseli
5 Volume Resampling przykład 1 u x = k=0 N k=0 N w k (x)u k w k (x) 1 w k x = d(x, x k ) p _Sheparda Velocity User Manual, PD0001_USM, rev /24/2016 3? = = 4
6 Volume Resampling/Trilinear Interpolation ? = = 8? 7.5 5? = = =
7 Volume Resampling przykład 2 Kolejny przykład to sztywna transformacja jednego CT w inne; wtedy nie ma zmian objętości wokseli. Możliwe za to jest przesunięcie wokseli między oryginalnym i nowym CT (w poniższym przypadku jest to przesunięcie o ¼). Wtedy w efekcie takiej transformacji wartość nowego woksela będzie interpolowaną przy użyciu uśredniania wagowanego odległością. Z reguły transformowane CT ma mniejsze wartości maksymalne wokseli w odniesieniu do oryginalnego CT. Velocity User Manual, PD0001_USM, rev /24/2016
8 Dose Deformation przykładowy pacjent
9 Dose Deformation przykładowy pacjent
10 Dose Deformation przykładowy pacjent
11 QA ocena wizualna Lawson JD, et al. Quantitative evaluation of a cone-beam computed tomography planning computed tomography deformable image registration method for adaptive radiation therapy, Journal of Applied Clinical Medical Physics, 2007; 8(4):
12 QA - Deformable Wrap Map
13 QA - Deformable Wrap Map
14 QA - jakobian ciemnoniebieski i czarny zmniejszenie objętości (0 < j < 1) czerwony wzrost objętości (j > 1) Velocity User Manual, PD0001_USM, rev /24/2016
15 Dose Deformation trudny przypadek
16 Dose Deformation trudny przypadek
17 Velocity User Manual, PD0001_USM, rev /24/2016 Wykorzystanie potencjalne
18 Wykorzystanie potencjalne - BED oraz EQD2 Dose Scaling Przed zsumowaniem dawek pochodzących z różnych rodzajów frakcjonowania lub rodzajów terapii, można najpierw przeskalować dawki fizyczne na zarówno dawkę skuteczną biologicznie (Biological Effective Dose, BED), jak i na równoważną radiobiologicznie dawce frakcyjnej równej 2 Gy (EQD2). Nie można sumować dawki fizycznej z biologiczną; jeśli jedna z nich jest przeskalowana, to druga też musi być dawką biologiczną. CT + dawka fizyczna [+ struktury] Do przeliczania dawki są stosowane odpowiednie równania. Liczba frakcji wpisywana ręcznie lub z planu. Należy tylko zaznaczyć wybrane struktury i zadać im odpowiednie wartości α/β. Tkanki nieokreślone również muszą mieć zadaną wartość α/β. Velocity User Manual, PD0001_USM, rev /24/2016
19 Wykorzystanie potencjalne - BED oraz EQD2 Dose Scaling Na wyjściu nowy plik dawki biologicznej oraz dokument zawierający szczegóły przeliczenia (równanie, liczba frakcji, α/β dla struktur oraz ostrzeżenia o ich nakładaniu) Z tak uzyskanymi dawkami można zrobić to wszystko, co z dawkami fizycznymi: wyświetlenie izodoz, ich zamiana na struktury, deformację na bryłę lub sumę dawek z innymi dawkami efektywnymi. Velocity User Manual, PD0001_USM, rev /24/2016
20 Biological Effective Dose (BED) Scaling Dla skali minutowej skali czasu użyte jest zwykłe równanie liniowokwadratowe (LQ), bez czynnika czasu, jako opis związku między niszczeniem DNA komórki (lethal lesions) a dawką fizyczną: uszkodzenia śmiertelne = αd + βd 2 gdzie D jest dawką. Przy niskiej dawce parametr liniowy, α, opisuje zdarzenie jonizacyjne, które skutkuje podwójnym pęknięciem łańcucha DNA i śmiercią komórki. Przy wyższych dawkach, parametr kwadratowy, β, opisuje oddzielne zdarzenia jonizacyjne, dające razem efekt podwójnego pęknięcia łańcucha DNA każde ze zdarzeń daje pęknięcie pojedynczego łańcucha, ale są one oddalone tylko o kilka par zasad i pojawiają się przed naprawą DNA. Wartości α oraz β są charakterystyczne dla danej tkanki, a ich iloraz α/β wskazuje wartość dawki fizycznej, dla której te dwa typy śmierci komórki mają taki sam udział. Jednostką ilorazu jest Gy. Velocity User Manual, PD0001_USM, rev /24/2016
21 Biological Effective Dose (BED) Scaling W skali makroskopowej, równanie LQ ma znaczenie kliniczne w odniesieniu do kontroli guza i późnych efektów komplikacji tkanek prawidłowych. Przyjmując rozkład Poissona zdarzeń śmiertelnych między komórkami, frakcja przeżywająca (surviving fraction, SF) jest opisana jako: SF = e (αd+βd2 ) BED skaluje dawkę fizyczną na frakcję (d) za pomocą charakterystycznych dla danej tkanki ilorazów α/β i liczby frakcji (n). Skalowanie BED może być użyte do porównania różnych planów leczenia przy użyciu punktu widzenia opartego na hipotezie log-kill komórek. To ujęcie nie uwzględnia re-proliferacji komórek guza w czasie napromieniania lub przerw między seansami. BED = nd 1 + d α β Velocity User Manual, PD0001_USM, rev /24/2016
22 Biological Effective Dose (BED) Scaling Na podstawie: Fowler JF, The radiobiology of prostate cancer including new aspects of fractionated radiotherapy, Acta Oncologica, 44(3):265:276, 2005 przyjęte zostały takie wartości:
23 Biological Effective Dose (BED) Scaling
24 Biological Effective Dose (BED) Scaling Dla dawek frakcyjnych 2 Gy (BEQD2) można powyższe równanie znormalizować: nd 1 + α d β BEQD 2 = α β Velocity User Manual, PD0001_USM, rev /24/2016
25 Biological Effective Dose (BED) Scaling
26 Biological Effective Dose (BED) Scaling
27 Biological Effective Dose (BED) Scaling
28 Biological Effective Dose (BED) Scaling
29 Biological Effective Dose (BED) Scaling α/β rectum = 6 Gy α/β bladder = 4 Gy α/β rectum = 10 Gy α/β bladder = 15 Gy
30 Biological Effective Dose (BED) Scaling α/β rectum = 6 Gy α/β bladder = 4 Gy α/β rectum = 10 Gy α/β bladder = 15 Gy
31 Biological Effective Dose (BED) Scaling kwadraty wyższe α/β dla narządów krytycznych trójkąty niższe α/β dla narządów krytycznych
32 Biological Effective Dose (BED) Scaling Ograniczenia skalowania prostego równania BED: - Dawki frakcyjne > 7 Gy. - Brachyterapia LDR. - Zależność czasowa. - Niepewność oznaczenia wielkości ilorazu α/β. 1. Barendsen GW. Dose fractionation, dose rate, and isoeffect relationships for normal tissue responses. Int J Radiat Oncol Biol Phys 1982;8: Fowler, J. F. 21 years of Biologically Effective Dose. The British Journal of Radiology, 2010; Song CW, et al. Radiobiology of Stereotactic Body Radiation Therapy/Stereotactic Radiosurgery and the Linear-Quadratic Model. Int. J. Radiation Oncology Biol. Phys Park, CP, et al. Universal Survival Curve and Single Fraction Equivalent Dose: Useful Tools in Understanding Potency of Ablative Radiotherapy. Int. J. Radiation Oncology Biol. Phys. 2008; 70(3): AAPM Recommendations on Dose Prescription and Reporting Methods for Permanent Interstitial Brachytherapy for Prostate Cancer. Report of AAPM Task Group Velocity User Manual, PD0001_USM, rev /24/2016
33 Wykorzystanie potencjalne - Dose Summation Sumowanie dwu objętości dawek w jeden (Composite Dose Volume). Jest obojętne, czy jest to pojedyncze badanie CT z dwoma niezależnymi rozkładami dawki, czy też są to dwa niezależne badania CT, każdy ze swoim rozkładem dawki. Rozkład ten tworzy się na najnowszym (mającym być użytym donajnowszego planowania) badaniu CT. (CT z planu + struktury + dawka) + (nowe CT + nowa dawka) / nowa dawka ze starego CT W pierwszym przypadku jest to zwykłe sumowanie, nawet bez transformacji. W drugim jest transformacja deformacyjna między bryłami, po czym starszy rozkład dawki jest deformowany na nowszą bryłę. Na wyjściu jest transformacja między dwoma CT i rozkład dawki na nowsze CT (jeśli jest to ten przypadek) oraz suma dawek. Z izodoz można utworzyć struktury. Velocity User Manual, PD0001_USM, rev /24/2016
34 Wykorzystanie potencjalne - Structure Guided Deformation Velocity User Manual, PD0001_USM, rev /24/2016
35 Wykorzystanie potencjalne - Structure Guided Deformation Jest to hybrydowa technika łącząca informacje uzyskane od użytkownika ze standardowym algorytmem deformacyjnym. Posiada dwie cechy: - Structure guiding dopasowywane struktury są używane jako podstawy do deformacji. - Structure masking struktury mogą otrzymać inne wartości wokseli, nadane przez użytkownika (burn-in). Velocity User Manual, PD0001_USM, rev /24/2016
36 Wykorzystanie potencjalne - Create Reshaped W czasie rejestracji CBCT i CT do planowania można wykorzystać tę opcję do transformacji pierwotnej bryły CT tworząc syntetyczne CT (Synthetic CT). Tworzy się wtedy nowa bryła, której granice są takie same jak dla CT do planowania. W obszarze wspólnym dla tego CT i CBCT operacja zdeformuje pierwotne CT, a poza tym obszarem woksele zostaną na swoich miejscach. Wynikowa bryła ma identyczne wartości wokseli bryły pierwotnej, ale w regionie nakładania się jest dopasowana do CBCT za pomocą transformacji deformacyjnej. Jest to operacja tworzenia syntetycznego CT do planowania (synthetic planning CT). Velocity User Manual, PD0001_USM, rev /24/2016
37 Wykorzystanie potencjalne - Adaptive Monitoring Używane do śledzenia zmian deformacyjnych struktur między CT z planowania, a CBCT lub kvct. Dla każdego kolejnego CBCT/kVCT jest robiona transformacja deformacyjna do oryginalnego CT. Zaznaczone struktury są deformowane z CT do CBCT/kVCT za pomocą odwrotnej transformacji (inverse). Następnie struktury są kopiowane z powrotem do oryginalnego CT za pomocą sztywnej części transformacji. W dokumentacji są: przesunięcia struktur, zmiany ich objętości oraz DVH do porównania z oryginalnym DVH. Velocity User Manual, PD0001_USM, rev /24/2016
38 Wykorzystanie potencjalne Atlas Atlas jest predefiniowaną bryłą zawierającą zestaw predefiniowanych struktur. Atlasy są dedykowane do danego regionu anatomicznego. Segmentacja jest typu atlas-based. Wybiera się zestaw atlasów, a Velocity wybiera najlepszy z nich. Jest 5 zestawów: H&N (11), thorax (4), abdomen (6) oraz male pelvic (1, model-based). Można tworzyć swoje atlasy. Structure Deformation Transformuje struktury z jednego CT do drugiego na przykład przeplanowanie pacjenta na nowe CT. Potrzeba dwu CT i jednego RTStruct. Korzysta z transformacji deformacyjnej. Velocity User Manual, PD0001_USM, rev /24/2016
39 Podsumowanie + wymienione powyżej ;-) - brak korekcji artefaktów - problem z usunięciem bolusa przy deformacji dawki
40 Dziękuję za uwagę! Podziękowania: Aleksandra Grządziel Barbara Bekman Joanna Kopczyńska Tomasz Latusek
Nowe techniki radioterapii w doniesieniach z ASTRO 57
 Nowe techniki radioterapii w doniesieniach z ASTRO 57 Małgorzata Skórska Zakład Fizyki Medycznej Wielkopolskie Centrum Onkologii Nowe techniki RT SBRT & SRS MRI-Guided RT Drukarki 3D Terapia hadronowa
Nowe techniki radioterapii w doniesieniach z ASTRO 57 Małgorzata Skórska Zakład Fizyki Medycznej Wielkopolskie Centrum Onkologii Nowe techniki RT SBRT & SRS MRI-Guided RT Drukarki 3D Terapia hadronowa
OD ROZPOZNANIA DO NAPROMIENIANIA. Edyta Dąbrowska
 OD ROZPOZNANIA DO NAPROMIENIANIA Edyta Dąbrowska METODY LECZENIA NOWOTWORÓW - chirurgia - chemioterapia - radioterapia CEL RADIOTERAPII dostarczenie wysokiej dawki promieniowania do objętości tarczowej
OD ROZPOZNANIA DO NAPROMIENIANIA Edyta Dąbrowska METODY LECZENIA NOWOTWORÓW - chirurgia - chemioterapia - radioterapia CEL RADIOTERAPII dostarczenie wysokiej dawki promieniowania do objętości tarczowej
Specyfikacja dawki w radiochirurgii w technikach VMAT i CyberKnife
 Technika napromieniania Irradiation techniques Biuletyn Polskiego Towarzystwa Onkologicznego NOWOTWORY 2016, tom 1, nr 2, 124 131 Polskie Towarzystwo Onkologiczne ISSN 2543 5248 www.biuletyn.nowotwory.edu.pl
Technika napromieniania Irradiation techniques Biuletyn Polskiego Towarzystwa Onkologicznego NOWOTWORY 2016, tom 1, nr 2, 124 131 Polskie Towarzystwo Onkologiczne ISSN 2543 5248 www.biuletyn.nowotwory.edu.pl
S T R E S Z C Z E N I E
 STRESZCZENIE Cel pracy: Celem pracy jest ocena wyników leczenia napromienianiem chorych z rozpoznaniem raka szyjki macicy w Świętokrzyskim Centrum Onkologii, porównanie wyników leczenia chorych napromienianych
STRESZCZENIE Cel pracy: Celem pracy jest ocena wyników leczenia napromienianiem chorych z rozpoznaniem raka szyjki macicy w Świętokrzyskim Centrum Onkologii, porównanie wyników leczenia chorych napromienianych
Rola brachyterapii w leczeniu wznowy miejscowej raka stercza
 Rola brachyterapii w leczeniu wznowy miejscowej raka stercza dr hab. med. Roman Makarewicz, prof. UMK Katedra i Klinika Onkologii i Brachyterapii Collegium Medicum UMK Centrum Onkologii w Bydgoszczy JASTRZĘBIA
Rola brachyterapii w leczeniu wznowy miejscowej raka stercza dr hab. med. Roman Makarewicz, prof. UMK Katedra i Klinika Onkologii i Brachyterapii Collegium Medicum UMK Centrum Onkologii w Bydgoszczy JASTRZĘBIA
Radiobiologia: podstawowe modele matematyczne opisujące przeżywalność komórek
 Dostępne online www.journals.wco.pl/los Zeszyty Naukowe WCO, Letters in Oncology Science 2018;15(1):59-65 Praca poglądowa/review paper Letters in Oncology Science ISSN 2543-6724 ZESZYTY NAUKOWE WIELKOPOLSKIEGO
Dostępne online www.journals.wco.pl/los Zeszyty Naukowe WCO, Letters in Oncology Science 2018;15(1):59-65 Praca poglądowa/review paper Letters in Oncology Science ISSN 2543-6724 ZESZYTY NAUKOWE WIELKOPOLSKIEGO
Indywidualizacja leczenia promieniowaniem jonizującym. Paweł Kukołowicz Zakład Fizyki Medycznej
 Indywidualizacja leczenia promieniowaniem jonizującym Paweł Kukołowicz Zakład Fizyki Medycznej Plan wykładu Jak rozumieć indywidualizację w radioterapii? Kilka słów o historii. Indywidualizacja zagadnienia
Indywidualizacja leczenia promieniowaniem jonizującym Paweł Kukołowicz Zakład Fizyki Medycznej Plan wykładu Jak rozumieć indywidualizację w radioterapii? Kilka słów o historii. Indywidualizacja zagadnienia
Janusz Skowronek. Zakład Brachyterapii Wielkopolskie Centrum Onkologii, Poznań
 Modele radiobiologiczne w brachyterapii Janusz Skowronek Zakład Brachyterapii Wielkopolskie Centrum Onkologii, Poznań Metody frakcjonowania Ze względu na aktywność źródła (moc dawki) brachyterapię dzieli
Modele radiobiologiczne w brachyterapii Janusz Skowronek Zakład Brachyterapii Wielkopolskie Centrum Onkologii, Poznań Metody frakcjonowania Ze względu na aktywność źródła (moc dawki) brachyterapię dzieli
FIZYCZNE PODSTAWY RADIOTERAPII ZASADY RADIOTERAPII ŹRÓDŁA PROMIENIOWANIA TERAPEUTYCZNEGO ENERGIA PROMIENIOWANIA RODZAJE PROMIENIOWANIA
 FIZYCZNE PODSTAWY RADIOTERAPII ZASADY RADIOTERAPII WILHELM CONRAD ROENTGEN PROMIENIE X 1895 ROK PROMIENIOWANIE JEST ENERGIĄ OBEJMUJE WYSYŁANIE, PRZENOSZENIE I ABSORPCJĘ ENERGII POPRZEZ ŚRODOWISKO MATERIALNE
FIZYCZNE PODSTAWY RADIOTERAPII ZASADY RADIOTERAPII WILHELM CONRAD ROENTGEN PROMIENIE X 1895 ROK PROMIENIOWANIE JEST ENERGIĄ OBEJMUJE WYSYŁANIE, PRZENOSZENIE I ABSORPCJĘ ENERGII POPRZEZ ŚRODOWISKO MATERIALNE
Czas podjąć właściwą decyzję. stare wino w nowej butelce czy ślepa uliczka?
 Czas podjąć właściwą decyzję. stare wino w nowej butelce czy ślepa uliczka? Grzegorz Zwierzchowski Katedra i Zakład Elektroradiologii, Wydział Nauk o Zdrowiu Uniwersytet Medyczny im. Karola Marcinkowskiego
Czas podjąć właściwą decyzję. stare wino w nowej butelce czy ślepa uliczka? Grzegorz Zwierzchowski Katedra i Zakład Elektroradiologii, Wydział Nauk o Zdrowiu Uniwersytet Medyczny im. Karola Marcinkowskiego
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Analiza rozkładu dawki dla aplikacji dojamowo-śródtkankowych w brachyterapii raka szyjki macicy.
 Analiza rozkładu dawki dla aplikacji dojamowo-śródtkankowych w brachyterapii raka szyjki macicy. Judyta Wiercińska Renata Kabacińska Tomasz Skawiński Roman Makarewicz Brachyterapia szyjki macicy Klasyczne
Analiza rozkładu dawki dla aplikacji dojamowo-śródtkankowych w brachyterapii raka szyjki macicy. Judyta Wiercińska Renata Kabacińska Tomasz Skawiński Roman Makarewicz Brachyterapia szyjki macicy Klasyczne
Biologiczne podstawy radioterapii Wykład 4 podstawy radioterapii
 Biologiczne podstawy radioterapii Wykład 4 podstawy radioterapii czyli dlaczego komórki nowotworowe są bardziej wrażliwe na działanie promieniowania jonizującego od komórek prawidłowych? A tumor is a conglomerate
Biologiczne podstawy radioterapii Wykład 4 podstawy radioterapii czyli dlaczego komórki nowotworowe są bardziej wrażliwe na działanie promieniowania jonizującego od komórek prawidłowych? A tumor is a conglomerate
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Artykuły oryginalne Original articles
 NOWOTWORY Journal of Oncology 2008 volume 58 Number 6 499 504 Artykuły oryginalne Original articles Obrazowa brachyterapia ginekologiczna: technika zintegrowana David Bernshaw, Sylvia Van Dyk, Kailash
NOWOTWORY Journal of Oncology 2008 volume 58 Number 6 499 504 Artykuły oryginalne Original articles Obrazowa brachyterapia ginekologiczna: technika zintegrowana David Bernshaw, Sylvia Van Dyk, Kailash
Możliwości zastosowania dozymetrii promieniowania mieszanego n+γ. mgr inż. Iwona Pacyniak
 Możliwości zastosowania dozymetrii promieniowania mieszanego n+γ mgr inż. Iwona Pacyniak Dr Maria Kowalska, Dr inż. Krzysztof W. Fornalski i.pacyniak@clor.waw.pl Centralne Laboratorium Ochrony Radiologicznej
Możliwości zastosowania dozymetrii promieniowania mieszanego n+γ mgr inż. Iwona Pacyniak Dr Maria Kowalska, Dr inż. Krzysztof W. Fornalski i.pacyniak@clor.waw.pl Centralne Laboratorium Ochrony Radiologicznej
Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych
 Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki Politechnika Śląska, Gliwice Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych Algorytm SWMEB. Część
Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki Politechnika Śląska, Gliwice Szybka wielobiegunowa metoda elementów brzegowych w analizie układów liniowosprężystych Algorytm SWMEB. Część
Grzegorz Bielęda Zakład Fizyki Medycznej Wielkopolskie Centrum Onkologii
 Grzegorz Bielęda Zakład Fizyki Medycznej Wielkopolskie Centrum Onkologii Historia implanty stałe 1911 Pasteau -pierwsze doniesienie na temat brachyterapii w leczeniu raka prostaty. Leczenie polegało na
Grzegorz Bielęda Zakład Fizyki Medycznej Wielkopolskie Centrum Onkologii Historia implanty stałe 1911 Pasteau -pierwsze doniesienie na temat brachyterapii w leczeniu raka prostaty. Leczenie polegało na
The role of the fractionated stereotactic radiotherapy
 The role of the fractionated stereotactic radiotherapy Presentation of experiences of implementation and new treatment techniques Adam Maciejczyk Zakład Teleradioterapii Dolnośląskiego Centrum Onkologii
The role of the fractionated stereotactic radiotherapy Presentation of experiences of implementation and new treatment techniques Adam Maciejczyk Zakład Teleradioterapii Dolnośląskiego Centrum Onkologii
MODELOWANIE RADIOBIOLOGICZNE RADIOTERAPII HADRONOWEJ
 Seminarium Instytutu Fizyki Jądrowej PAN,19.01.2006 MODELOWANIE RADIOBIOLOGICZNE RADIOTERAPII HADRONOWEJ Michał Waligórski Centrum Onkologii Oddział w Krakowie i Instytut Fizyki Jądrowej J PAN w Krakowie
Seminarium Instytutu Fizyki Jądrowej PAN,19.01.2006 MODELOWANIE RADIOBIOLOGICZNE RADIOTERAPII HADRONOWEJ Michał Waligórski Centrum Onkologii Oddział w Krakowie i Instytut Fizyki Jądrowej J PAN w Krakowie
RADIOTERAPIA NOWOTWORÓW UKŁADU MOCZOWO PŁCIOWEGO U MĘŻCZYZN DOSTĘPNOŚĆ W POLSCE
 RADIOTERAPIA NOWOTWORÓW UKŁADU MOCZOWO PŁCIOWEGO U MĘŻCZYZN DOSTĘPNOŚĆ W POLSCE Marcin Hetnał Centrum Onkologii Instytut im. MSC; Kraków Ośrodek Radioterapii Amethyst RTCP w Krakowie Radioterapia Radioterapia
RADIOTERAPIA NOWOTWORÓW UKŁADU MOCZOWO PŁCIOWEGO U MĘŻCZYZN DOSTĘPNOŚĆ W POLSCE Marcin Hetnał Centrum Onkologii Instytut im. MSC; Kraków Ośrodek Radioterapii Amethyst RTCP w Krakowie Radioterapia Radioterapia
wymagania programowe z matematyki kl. III gimnazjum
 wymagania programowe z matematyki kl. III gimnazjum 1. Liczby i wyrażenia algebraiczne Zna pojęcie notacji wykładniczej. Umie zapisać liczbę w notacji wykładniczej. Umie porównywać liczy zapisane w różny
wymagania programowe z matematyki kl. III gimnazjum 1. Liczby i wyrażenia algebraiczne Zna pojęcie notacji wykładniczej. Umie zapisać liczbę w notacji wykładniczej. Umie porównywać liczy zapisane w różny
LUBELSKA PRÓBA PRZED MATURĄ 2018 poziom podstawowy
 LUELSK PRÓ PRZED MTURĄ 08 poziom podstawowy Schemat oceniania Zadania zamknięte (Podajemy kartotekę zadań, która ułatwi Państwu przeprowadzenie jakościowej analizy wyników). Zadanie. (0 ). Liczby rzeczywiste.
LUELSK PRÓ PRZED MTURĄ 08 poziom podstawowy Schemat oceniania Zadania zamknięte (Podajemy kartotekę zadań, która ułatwi Państwu przeprowadzenie jakościowej analizy wyników). Zadanie. (0 ). Liczby rzeczywiste.
PILNA KOREKTA URZĄDZENIA MEDYCZNEGO PILNE ZAWIADOMIENIE DOTYCZĄCE BEZPIECZEŃSTWA
 Temat: Brak automatycznego unieważnienia dawki w przypadku zmian dotyczących kolimatora wielolistkowego (MLC) Produkt, którego dotyczy zawiadomienie: System Eclipse w wersjach od 6.5 do 10 (kompilacja
Temat: Brak automatycznego unieważnienia dawki w przypadku zmian dotyczących kolimatora wielolistkowego (MLC) Produkt, którego dotyczy zawiadomienie: System Eclipse w wersjach od 6.5 do 10 (kompilacja
LUBELSKA PRÓBA PRZED MATUR pola do tego przeznaczone. Błędne
 1 MATEMATYKA - poziom podstawowy klasa 2 CZERWIEC 2015 Instrukcja dla zdaj cego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to
1 MATEMATYKA - poziom podstawowy klasa 2 CZERWIEC 2015 Instrukcja dla zdaj cego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to
ĆWICZENIE 3. Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi
 ĆWICZENIE 3 Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi Celem ćwiczenia jest wyznaczenie podstawowych parametrów charakteryzujących kinetykę
ĆWICZENIE 3 Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi Celem ćwiczenia jest wyznaczenie podstawowych parametrów charakteryzujących kinetykę
Stereotaktyczna hypofrakcjonowana radioterapia chorych na raka gruczołu krokowego doniesienie wstępne
 Artykuł oryginalny Original articles NOWOTWORY Journal of Oncology 2014, volume 64, number 1, 16 23 DOI: 10.5603/NJO.2014.0003 Polskie Towarzystwo Onkologiczne ISSN 0029-540X www.nowotwory.viamedica.pl
Artykuł oryginalny Original articles NOWOTWORY Journal of Oncology 2014, volume 64, number 1, 16 23 DOI: 10.5603/NJO.2014.0003 Polskie Towarzystwo Onkologiczne ISSN 0029-540X www.nowotwory.viamedica.pl
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM 1. 2. 3. 4. 5. 6. czytać dane przedstawione na diagramach i w tabelach przekształcać równania liniowe na równania równoważne ekształcać układy równań
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM 1. 2. 3. 4. 5. 6. czytać dane przedstawione na diagramach i w tabelach przekształcać równania liniowe na równania równoważne ekształcać układy równań
Niskie dawki poza obszarem napromieniania: symulacje Monte Carlo, pomiar i odpowiedź radiobiologiczna in vitro komórek
 Niskie dawki poza obszarem napromieniania: symulacje Monte Carlo, pomiar i odpowiedź radiobiologiczna in vitro komórek M. Kruszyna-Mochalska 1,2, A. Skrobala 1,2, W. Suchorska 1,3, K. Zaleska 3, A. Konefal
Niskie dawki poza obszarem napromieniania: symulacje Monte Carlo, pomiar i odpowiedź radiobiologiczna in vitro komórek M. Kruszyna-Mochalska 1,2, A. Skrobala 1,2, W. Suchorska 1,3, K. Zaleska 3, A. Konefal
Zastosowanie Rapid Arc w Radioterapii Raka Płuca. Marzena Janiszewska
 Zastosowanie Rapid Arc w Radioterapii Raka Płuca Marzena Janiszewska Rola radioterapii w leczeniu raka płuca Tylko ok. 25% chorych może być poddanych leczeniu chirurgicznemu Wg badań epidemiologicznych
Zastosowanie Rapid Arc w Radioterapii Raka Płuca Marzena Janiszewska Rola radioterapii w leczeniu raka płuca Tylko ok. 25% chorych może być poddanych leczeniu chirurgicznemu Wg badań epidemiologicznych
Typ histopatologiczny
 Typ histopatologiczny Wiek Stopieo zróżnicowania nowotworu Typ I (hormonozależny) Adenocarcinoma Adenoacanthoma Naciekanie przestrzeni naczyniowych Wielkośd guza Typ II (hormononiezależny) Serous papillary
Typ histopatologiczny Wiek Stopieo zróżnicowania nowotworu Typ I (hormonozależny) Adenocarcinoma Adenoacanthoma Naciekanie przestrzeni naczyniowych Wielkośd guza Typ II (hormononiezależny) Serous papillary
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
System imed24 Instrukcja Moduł Analizy i raporty
 System imed24 Instrukcja Moduł Analizy i raporty Instrukcja obowiązująca do wersji 1.8.0 Spis treści 1. Moduł Analizy i Raporty... 3 1.1. Okno główne modułu Analizy i raporty... 3 1.1.1. Lista szablonów
System imed24 Instrukcja Moduł Analizy i raporty Instrukcja obowiązująca do wersji 1.8.0 Spis treści 1. Moduł Analizy i Raporty... 3 1.1. Okno główne modułu Analizy i raporty... 3 1.1.1. Lista szablonów
Clinical radiation therapy measurements with a new commercial synthetic single crystal diamond detector
 Clinical radiation therapy measurements with a new commercial synthetic single crystal diamond detector Wolfram U. Laub,a Richard Crilly Department of Radiation Medicine, Oregon Health & Science University,
Clinical radiation therapy measurements with a new commercial synthetic single crystal diamond detector Wolfram U. Laub,a Richard Crilly Department of Radiation Medicine, Oregon Health & Science University,
LUBELSKA PRÓBA PRZED MATURĄ 2015
 1 MATEMATYKA - poziom podstawowy klasa 2 CZERWIEC 2015 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to
1 MATEMATYKA - poziom podstawowy klasa 2 CZERWIEC 2015 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to
Artykuł na zaproszenie Redakcji Invited article
 NOWOTWORY Journal of Oncology 2008 volume 58 Number 6 493 498 Artykuł na zaproszenie Redakcji Invited article Jak podnieść precyzję radioterapii: obrazowanie skojarzone i czterowymiarowe (4D) Marc Kessler
NOWOTWORY Journal of Oncology 2008 volume 58 Number 6 493 498 Artykuł na zaproszenie Redakcji Invited article Jak podnieść precyzję radioterapii: obrazowanie skojarzone i czterowymiarowe (4D) Marc Kessler
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. są podane 4 odpowiedzi:
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. są podane 4 odpowiedzi:
Brak nawrotu choroby u pacjentów z rakiem prostaty leczonych terapią protonową w czeskim Centrum Terapii Protonowej w Pradze, Republice Czeskiej
 Brak nawrotu choroby u pacjentów z rakiem prostaty leczonych terapią protonową w czeskim Centrum Terapii Protonowej w Pradze, Republice Czeskiej PhD. MD. Jiří Kubeš Dyrektor Medyczny Centrum Terapii Protonowej
Brak nawrotu choroby u pacjentów z rakiem prostaty leczonych terapią protonową w czeskim Centrum Terapii Protonowej w Pradze, Republice Czeskiej PhD. MD. Jiří Kubeš Dyrektor Medyczny Centrum Terapii Protonowej
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY PRZED MATURĄ MAJ 04. Sprawdź, czy arkusz egzaminacyjny zawiera 8 stron (zadania 33). Ewentualny brak zgłoś przewodniczącemu
WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY PRZED MATURĄ MAJ 04. Sprawdź, czy arkusz egzaminacyjny zawiera 8 stron (zadania 33). Ewentualny brak zgłoś przewodniczącemu
KOMUNIKAT DOTYCZĄCY BEZPIECZEŃSTWA STOSOWANIA PRODUKTU / POWIADOMIENIE DOTYCZĄCE PRODUKTU
 KOMUNIKAT DOTYCZĄCY BEZPIECZEŃSTWA STOSOWANIA PRODUKTU / POWIADOMIENIE DOTYCZĄCE PRODUKTU Temat: Ograniczenia dokładności oprogramowania w przypadku bardzo małych rozmiarów pola kolimatora wielolistkowego
KOMUNIKAT DOTYCZĄCY BEZPIECZEŃSTWA STOSOWANIA PRODUKTU / POWIADOMIENIE DOTYCZĄCE PRODUKTU Temat: Ograniczenia dokładności oprogramowania w przypadku bardzo małych rozmiarów pola kolimatora wielolistkowego
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 7 MAJA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Frakcjonowana radioterapia stereotaktyczna CyberKnife TM chorych na raka gruczołu krokowego prezentacja metody
 Technika napromieniania Irradiation technique NOWOTWORY Journal of Oncology 2012, volume 62, number 4, 274 282 Polskie Towarzystwo Onkologiczne ISSN 0029-540X www.nowotwory.edu.pl Frakcjonowana radioterapia
Technika napromieniania Irradiation technique NOWOTWORY Journal of Oncology 2012, volume 62, number 4, 274 282 Polskie Towarzystwo Onkologiczne ISSN 0029-540X www.nowotwory.edu.pl Frakcjonowana radioterapia
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2018 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 018 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 7 maja 018 r.
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 018 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 7 maja 018 r.
Weryfikacja modelu dozymetrycznego głowicy akceleratora biomedycznego
 Kwartalnik Opolski 2017, 4 Barbara KUŚMIERSKA, Aleksandra GRZĄDZIEL, Jacek WENDYKIER, Barbara BEKMAN, Krzysztof ŚLOSAREK Weryfikacja modelu dozymetrycznego głowicy akceleratora biomedycznego Wprowadzenie
Kwartalnik Opolski 2017, 4 Barbara KUŚMIERSKA, Aleksandra GRZĄDZIEL, Jacek WENDYKIER, Barbara BEKMAN, Krzysztof ŚLOSAREK Weryfikacja modelu dozymetrycznego głowicy akceleratora biomedycznego Wprowadzenie
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wymagania na poszczególne oceny szkolne z. matematyki. dla uczniów klasy IIIa i IIIb. Gimnazjum im. Jana Pawła II w Mętowie. w roku szkolnym 2015/2016
 Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Technika planowania boostu EBRT w leczeniu miejscowo zaawansowanego nowotworu szyjki macicy
 Technika planowania boostu EBRT w leczeniu miejscowo zaawansowanego nowotworu szyjki macicy Dominika Oborska-Kumaszyńska, Tervinder Matharu Wolverhampton Royal Hospitals, New Cross Hospital, MPCE Department,
Technika planowania boostu EBRT w leczeniu miejscowo zaawansowanego nowotworu szyjki macicy Dominika Oborska-Kumaszyńska, Tervinder Matharu Wolverhampton Royal Hospitals, New Cross Hospital, MPCE Department,
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY+ 19 MARCA 2011 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Wskaż nierówność, która
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY+ 19 MARCA 2011 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Wskaż nierówność, która
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP. V. Obliczenia procentowe. Uczeń: 1) przedstawia część wielkości jako procent tej wielkości;
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP Liczby. TEMAT Rozwinięcia dziesiętne liczb wymiernych. Zaokrąglanie liczb. Szacowanie wyników. Dodawanie i odejmowanie liczb dodatnich. Mnożenie i dzielenie
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY 7SP Liczby. TEMAT Rozwinięcia dziesiętne liczb wymiernych. Zaokrąglanie liczb. Szacowanie wyników. Dodawanie i odejmowanie liczb dodatnich. Mnożenie i dzielenie
Radioterapia w leczeniu raka pęcherza moczowego - zalecenia
 Radioterapia w leczeniu raka pęcherza moczowego - zalecenia Radioterapia w leczeniu raka pęcherza moczowego może być stosowana łącznie z leczeniem operacyjnym chemioterapią. Na podstawie literatury anglojęzycznej
Radioterapia w leczeniu raka pęcherza moczowego - zalecenia Radioterapia w leczeniu raka pęcherza moczowego może być stosowana łącznie z leczeniem operacyjnym chemioterapią. Na podstawie literatury anglojęzycznej
Lista zadań nr 2 z Matematyki II
 Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 2 czerwca 2017
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 2 czerwca 2017
Fizyczne podstawy radioterapii
 Fizyczne podstawy radioterapii odkrycie promieniu X, promieniotwórczości i swobodnego elektronu stworzyły podstawy nowych działów medycyny: diagnostyki rentgenowskiej i radioterapii pierwsze próby zastosowania
Fizyczne podstawy radioterapii odkrycie promieniu X, promieniotwórczości i swobodnego elektronu stworzyły podstawy nowych działów medycyny: diagnostyki rentgenowskiej i radioterapii pierwsze próby zastosowania
DOZYMETRIA BIOLOGICZNA DO REKONSTRUKCJI DAWEK POCHŁONIĘTYCH W WYPADKACH RADIACYJNYCH W RADIOTERAPII
 DOZYMETRIA BIOLOGICZNA DO REKONSTRUKCJI DAWEK POCHŁONIĘTYCH W WYPADKACH RADIACYJNYCH W RADIOTERAPII Andrzej Wójcik, Guenther Stephan, Sylwester Sommer Witold Urbanik 47, Paweł Kukolowicz v, Tomasz Kuszewski
DOZYMETRIA BIOLOGICZNA DO REKONSTRUKCJI DAWEK POCHŁONIĘTYCH W WYPADKACH RADIACYJNYCH W RADIOTERAPII Andrzej Wójcik, Guenther Stephan, Sylwester Sommer Witold Urbanik 47, Paweł Kukolowicz v, Tomasz Kuszewski
Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum
 Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego uczeń potrafi: czytać teksty w stylu matematycznym wykorzystywać słownictwo
Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego uczeń potrafi: czytać teksty w stylu matematycznym wykorzystywać słownictwo
Zagadnienia obrazowania w radioterapii ze szczególnym uwzględnieniem brachyterapii
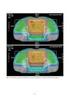 NOWOTWORY Journal of Oncology 2007 volume 57 Number 4 376 382 Artykuły oryginalne Original papers Zagadnienia obrazowania w radioterapii ze szczególnym uwzględnieniem brachyterapii Jürgen Schultze 1, Markus
NOWOTWORY Journal of Oncology 2007 volume 57 Number 4 376 382 Artykuły oryginalne Original papers Zagadnienia obrazowania w radioterapii ze szczególnym uwzględnieniem brachyterapii Jürgen Schultze 1, Markus
MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ. programowej dla klas IV-VI. programowej dla klas IV-VI.
 MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ TEMAT LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ UWAGI. LICZBY I DZIAŁANIA 6 h Liczby. Rozwinięcia
MATEMATYKA Z PLUSEM DLA KLASY VII W KONTEKŚCIE WYMAGAŃ PODSTAWY PROGRAMOWEJ TEMAT LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ UWAGI. LICZBY I DZIAŁANIA 6 h Liczby. Rozwinięcia
WPŁYW NOWOCZESNYCH TECHNIK NAPROMIENIENIA NA BEZPIECZEŃSTWO RADIOLOGICZNE W RADIOTERAPII
 PRACE NAUKOWE Akademii im. Jana Długosza w Częstochowie Technika, Informatyka, Inżynieria Bezpieczeństwa 2014, t. II, s. 165 174 http://dx.doi.org/10.16926/tiib.2014.02.14 Radosław Mandecki 1, Sylwia Mandecka
PRACE NAUKOWE Akademii im. Jana Długosza w Częstochowie Technika, Informatyka, Inżynieria Bezpieczeństwa 2014, t. II, s. 165 174 http://dx.doi.org/10.16926/tiib.2014.02.14 Radosław Mandecki 1, Sylwia Mandecka
Poniżej przedstawiono przykład ich zastosowania dla najprostszego obiektu 3D kostki.
 EDYCJA OBIEKTÓW 3D 14 Fazowanie i zaokrąglanie Fazowanie i zaokrąglanie to dwie funkcje które zostały zaprezentowane w ramach kursu dla edycji obiektów płaskich 2D. Funkcje te działają również dla obiektów
EDYCJA OBIEKTÓW 3D 14 Fazowanie i zaokrąglanie Fazowanie i zaokrąglanie to dwie funkcje które zostały zaprezentowane w ramach kursu dla edycji obiektów płaskich 2D. Funkcje te działają również dla obiektów
Brachyterapia raka szyjki macicy: czas na zmiany?
 Współczesna Onkologia (2006) vol. 10; 9 (423 428) Radioterapia, stosowana obecnie na ogół w skojarzeniu z cisplatyną, pozostaje obok postępowania chirurgicznego podstawową metodą leczenia większości inwazyjnych
Współczesna Onkologia (2006) vol. 10; 9 (423 428) Radioterapia, stosowana obecnie na ogół w skojarzeniu z cisplatyną, pozostaje obok postępowania chirurgicznego podstawową metodą leczenia większości inwazyjnych
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 2017/2018.
 Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
LUBELSKA PRÓBA PRZED MATURĄ 2013
 LUBELSKA PRÓBA PRZED MATURĄ 03 MATEMATYKA - poziom podstawowy STYCZEŃ 03 Instrukcja dla zdającego Czas pracy: 70 minut. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu
LUBELSKA PRÓBA PRZED MATURĄ 03 MATEMATYKA - poziom podstawowy STYCZEŃ 03 Instrukcja dla zdającego Czas pracy: 70 minut. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu
PRÓBNY EGZAMIN MATURALNY MATEMATYKA. MaturoBranie
 Uzupełnia zdający PESEL PRÓBNY EGZAMIN MATURALNY MATEMATYKA POZIOM PODSTAWOWY DATA: 25 stycznia 2017 r. GODZINA ROZPOCZĘCIA: 9:00 CZAS PRACY: 170 minut MaturoBranie LICZBA PUNKTÓW DO UZYSKANIA: 50 Instrukcja
Uzupełnia zdający PESEL PRÓBNY EGZAMIN MATURALNY MATEMATYKA POZIOM PODSTAWOWY DATA: 25 stycznia 2017 r. GODZINA ROZPOCZĘCIA: 9:00 CZAS PRACY: 170 minut MaturoBranie LICZBA PUNKTÓW DO UZYSKANIA: 50 Instrukcja
Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum
 Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego uczeń potrafi: Umiejętności podstawowe KONIECZNE PODSTAWOWE ROZSZERZAJĄCE
Plan wynikowy do programu MATEMATYKA 2001 klasa 3 gimnazjum Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego uczeń potrafi: Umiejętności podstawowe KONIECZNE PODSTAWOWE ROZSZERZAJĄCE
Interpolacja i modelowanie krzywych 2D i 3D
 Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
Brachyterapia w ginekologii. Grażyna Ibron Katarzyna Pawłów-Pyrka Michał Górzyński SP ZOZ MSW z WMCO OLSZTYN
 Brachyterapia w ginekologii Grażyna Ibron Katarzyna Pawłów-Pyrka Michał Górzyński SP ZOZ MSW z WMCO OLSZTYN Na początku trochęhistorii: 1896 Henri Becquerel odkrywa promieniotwórczość uranu 1898 Maria
Brachyterapia w ginekologii Grażyna Ibron Katarzyna Pawłów-Pyrka Michał Górzyński SP ZOZ MSW z WMCO OLSZTYN Na początku trochęhistorii: 1896 Henri Becquerel odkrywa promieniotwórczość uranu 1898 Maria
Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka
 Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka 1. Kompilacja aplikacji konsolowych w środowisku programistycznym Microsoft Visual Basic. Odszukaj w menu startowym systemu
Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka 1. Kompilacja aplikacji konsolowych w środowisku programistycznym Microsoft Visual Basic. Odszukaj w menu startowym systemu
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
PLAN WYNIKOWY Z MATEMATYKI DLA III KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem. PODSTAWOWE Uczeń zna: LICZBY I WYRAŻENIA ALGEBRAICZNE
 Ewa Koralewska PLAN WYNIKOWY Z MATEMATYKI DLA III KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem LP.. 2. 3. 5. OGÓLNA PODST- AWA PROGRA- MOWA a a TEMATYKA LEKCJI LICZBA GODZIN Lekcja organizacyjna.
Ewa Koralewska PLAN WYNIKOWY Z MATEMATYKI DLA III KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem LP.. 2. 3. 5. OGÓLNA PODST- AWA PROGRA- MOWA a a TEMATYKA LEKCJI LICZBA GODZIN Lekcja organizacyjna.
LUBELSKA PRÓBA PRZED MATURĄ poziom podstawowy 1 MATEMATYKA LUTY Instrukcja dla zdającego. Czas pracy: 170 minut
 LUBELSKA PRÓBA PRZED MATURĄ poziom podstawowy MATEMATYKA LUTY 0 Instrukcja dla zdającego. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3.
LUBELSKA PRÓBA PRZED MATURĄ poziom podstawowy MATEMATYKA LUTY 0 Instrukcja dla zdającego. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3.
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych
 Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
LUBELSKA PRÓBA PRZED MATURĄ 2018 poziom podstawowy M A T E M A T Y K A 14 MARCA Instrukcja dla zdającego Czas pracy: 170 minut
 Kod ucznia Nazwisko i imię M A T E M A T Y K A 14 MARCA 2018 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron (zadania 1-34). Ewentualny brak zgłoś przewodniczącemu
Kod ucznia Nazwisko i imię M A T E M A T Y K A 14 MARCA 2018 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron (zadania 1-34). Ewentualny brak zgłoś przewodniczącemu
Stowarzyszenie Nauczycieli Matematyki
 WPISUJE ZDAJĄCY KOD PESEL Miejsce na naklejkę z kodem (podczas egzaminu w maju) PRÓBNY ARKUSZ MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 1. Sprawdź czy arkusz zawiera 13 stron (zadania 1-32). STYCZEŃ 2015
WPISUJE ZDAJĄCY KOD PESEL Miejsce na naklejkę z kodem (podczas egzaminu w maju) PRÓBNY ARKUSZ MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 1. Sprawdź czy arkusz zawiera 13 stron (zadania 1-32). STYCZEŃ 2015
LUBELSKA PRÓBA PRZED MATUR 2016
 1 MATEMATYKA - poziom rozszerzony LO MARZEC 016 Instrukcja dla zdaj cego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron (zadania 1 17). Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
1 MATEMATYKA - poziom rozszerzony LO MARZEC 016 Instrukcja dla zdaj cego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron (zadania 1 17). Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
J E Z I E R S K A K A R O L I N A
 Warunki bezpiecznego stosowania promieniowania jonizującego dla wszystkich rodzajów ekspozycji medycznej: Zapobieganie i postępowanie w sytuacjach awaryjnych. J E Z I E R S K A K A R O L I N A Wypadek
Warunki bezpiecznego stosowania promieniowania jonizującego dla wszystkich rodzajów ekspozycji medycznej: Zapobieganie i postępowanie w sytuacjach awaryjnych. J E Z I E R S K A K A R O L I N A Wypadek
EGZAMIN MATURALNY Z MATEMATYKI
 UZUPEŁNIA ZDAJĄCY KOD PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY CZAS PRACY: 170 minut LICZBA PUNKTÓW DO UZYSKANIA: 50 Instrukcja dla zdającego 1. Sprawdź, czy
UZUPEŁNIA ZDAJĄCY KOD PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY CZAS PRACY: 170 minut LICZBA PUNKTÓW DO UZYSKANIA: 50 Instrukcja dla zdającego 1. Sprawdź, czy
Operacje na Wielu Arkuszach
 Operacje na Wielu Arkuszach 1. Operacje na wielu arkuszach na raz. 2. Przenoszenie i kopiowanie arkuszy pomiędzy plikami. 3. Ukrywanie arkuszy. Przykład 1. Operacje na wielu arkuszach na raz. Często pracując
Operacje na Wielu Arkuszach 1. Operacje na wielu arkuszach na raz. 2. Przenoszenie i kopiowanie arkuszy pomiędzy plikami. 3. Ukrywanie arkuszy. Przykład 1. Operacje na wielu arkuszach na raz. Często pracując
Program MC. Obliczyć radialną funkcję korelacji. Zrobić jej wykres. Odczytać z wykresu wartość radialnej funkcji korelacji w punkcie r=
 Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
I semestr WYMAGANIA EDUKACYJNE Z MATEMATYKI KLASA VI. Wymagania na ocenę dopuszczającą. Dział programu: Liczby naturalne
 WYMAGANIA EDUKACYJNE Z MATEMATYKI KLASA VI Wymagania na ocenę dopuszczającą I semestr Dział programu: Liczby naturalne Oblicza różnice czasu proste Wymienia jednostki opisujące prędkość, drogę, czas. Rozwiązuje
WYMAGANIA EDUKACYJNE Z MATEMATYKI KLASA VI Wymagania na ocenę dopuszczającą I semestr Dział programu: Liczby naturalne Oblicza różnice czasu proste Wymienia jednostki opisujące prędkość, drogę, czas. Rozwiązuje
TERAPIA PROTONOWA. Proseminarium magisterskie 18 X 2005 1/36. Marta Giżyńska
 TERAPIA PROTONOWA Proseminarium magisterskie 18 X 2005 1/36 W skrócie... Cele terapii Słownictwo Własności wiązki protonowej Cele strategiczne Technika wielopolowa Technika rozpraszania Porównanie z techniką
TERAPIA PROTONOWA Proseminarium magisterskie 18 X 2005 1/36 W skrócie... Cele terapii Słownictwo Własności wiązki protonowej Cele strategiczne Technika wielopolowa Technika rozpraszania Porównanie z techniką
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejkę Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU
Miejsce na naklejkę Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU
poniżej przykład modyfikacji UTM34N (oczywiście bez tego co w nawiasach) (elipsoida zostaje taka sama, jak zresztą we wszystkich podobnych UTMach),
 Konspekt dotyczący przygotowania danych z Urban Atlas i SRTM do analizy rastrowej, w programach rastrowych dla zaawansowanych użytkowników ( w IDRISI i ILWISIE) Warunek konieczny wykonania analiz: rastry
Konspekt dotyczący przygotowania danych z Urban Atlas i SRTM do analizy rastrowej, w programach rastrowych dla zaawansowanych użytkowników ( w IDRISI i ILWISIE) Warunek konieczny wykonania analiz: rastry
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Miejsce na naklejkę ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU
Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Miejsce na naklejkę ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU
Cele, zadania i metody radioterapii
 Cele, zadania i metody radioterapii na przykładzie Centrum Onkologii Instytutu Marii Skłodowskiej Curie w Warszawie przy ul. Wawelskiej 15 Anna Buszko Spis treści 1 Cele, zadania i metody radioterapii...2
Cele, zadania i metody radioterapii na przykładzie Centrum Onkologii Instytutu Marii Skłodowskiej Curie w Warszawie przy ul. Wawelskiej 15 Anna Buszko Spis treści 1 Cele, zadania i metody radioterapii...2
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA Instrukcja dla zdającego POZIOM PODSTAWOWY Czas pracy: 170 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1 stron (zadania
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA Instrukcja dla zdającego POZIOM PODSTAWOWY Czas pracy: 170 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1 stron (zadania
Informator na temat systemu Cyberknife. Leczenie raka prostaty
 Informator na temat systemu Cyberknife Leczenie raka prostaty Informator na temat systemu CYBERKNIFE LECZENIE RAKA PROSTATY Ponieważniedawno rozpoznano u Pana zlokalizowanego raka prostaty, ważne jest,
Informator na temat systemu Cyberknife Leczenie raka prostaty Informator na temat systemu CYBERKNIFE LECZENIE RAKA PROSTATY Ponieważniedawno rozpoznano u Pana zlokalizowanego raka prostaty, ważne jest,
Instrukcja do ćwiczeń laboratoryjnych
 UNIWERSYTET GDAŃSKI WYDZIAŁ CHEMII Pracownia studencka Katedra Analizy Środowiska Instrukcja do ćwiczeń laboratoryjnych Ćwiczenie nr 4 i 5 OCENA EKOTOKSYCZNOŚCI TEORIA Chemia zanieczyszczeń środowiska
UNIWERSYTET GDAŃSKI WYDZIAŁ CHEMII Pracownia studencka Katedra Analizy Środowiska Instrukcja do ćwiczeń laboratoryjnych Ćwiczenie nr 4 i 5 OCENA EKOTOKSYCZNOŚCI TEORIA Chemia zanieczyszczeń środowiska
LUBELSKA PRÓBA PRZED MATURĄ MATEMATYKA - poziom podstawowy
 1 MATEMATYKA - poziom podstawowy LUTY 2015 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.
1 MATEMATYKA - poziom podstawowy LUTY 2015 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.
Wyrównanie ciągu poligonowego dwustronnie nawiązanego metodą przybliżoną.
 Wyrównanie ciągu poligonowego dwustronnie nawiązanego metodą przybliżoną. Uwagi wstępne należy przeczytać przed przystąpieniem do obliczeń W pierwszej kolejności należy wpisać do dostarczonego formularza
Wyrównanie ciągu poligonowego dwustronnie nawiązanego metodą przybliżoną. Uwagi wstępne należy przeczytać przed przystąpieniem do obliczeń W pierwszej kolejności należy wpisać do dostarczonego formularza
Modelowanie matematyczne w zastosowaniach biomedycznych
 Modelowanie matematyczne w zastosowaniach biomedycznych Wykład 6: Model liniowo-kwadratowy w radioterapii nowotworów Dr Jan Poleszczuk 5/04/2017 IBIB PAN Znamiona raka ( Hallmarks of Cancer ) Hanahan &
Modelowanie matematyczne w zastosowaniach biomedycznych Wykład 6: Model liniowo-kwadratowy w radioterapii nowotworów Dr Jan Poleszczuk 5/04/2017 IBIB PAN Znamiona raka ( Hallmarks of Cancer ) Hanahan &
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 4 CZERWCA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
EGZAMIN MATURALNY Z MATEMATYKI 5 MAJA 2016 POZIOM PODSTAWOWY. Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL dyskalkulia miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL dyskalkulia miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI
RADIO TERA PIA. informacje dla lekarzy. Opracowanie: dr hab. n. med. Iwona Gisterek prof. nadzw.
 RADIO TERA PIA RT informacje dla lekarzy Opracowanie: dr hab. n. med. Iwona Gisterek prof. nadzw. Spis treści 4 Radioterapia zasada działania 5 Rodzaje radioterapii 6 Wskazania do radioterapii 7 Przygotowanie
RADIO TERA PIA RT informacje dla lekarzy Opracowanie: dr hab. n. med. Iwona Gisterek prof. nadzw. Spis treści 4 Radioterapia zasada działania 5 Rodzaje radioterapii 6 Wskazania do radioterapii 7 Przygotowanie
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2019 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
Ustalanie dostępu do plików - Windows XP Home/Professional
 Ustalanie dostępu do plików - Windows XP Home/Professional Aby edytować atrybuty dostępu do plikow/ katalogow w systemie plików NTFS wpierw sprawdź czy jest Wyłączone proste udostępnianie czyli przejdź
Ustalanie dostępu do plików - Windows XP Home/Professional Aby edytować atrybuty dostępu do plikow/ katalogow w systemie plików NTFS wpierw sprawdź czy jest Wyłączone proste udostępnianie czyli przejdź
