GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych
|
|
|
- Urszula Borowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok
2 Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki na podstawie jej opisu Komputerowa synteza grafiki to procesy algorytmiczne prowadzące do uzyskania cyfrowego obrazu na podstawie opisu jego zawartości Synteza grafiki 3D bazuje na opisie przestrzennego świata, znajdujących się w nim obiektów, ich cech, środowiska, itp. Opis wycinka świata na potrzeby syntezy grafiki 3D nazywamy sceną Celem syntezy grafiki 3D jest uzyskanie obrazu 2D będącego wizualizacją sceny przy zadanych kryteriach 2
3 Synteza grafiki 3D Scena Algorytm graficzny Geometryczny opis rozmieszczenia obiektów, oświetlenia, kamery,... Proces często nazywa się renderowaniem Obraz 2D Wizualizacja, "zdjęcie" sceny 3D widzianej w zadany sposób 3
4 Renderowanie Grafika realistyczna Renderowanie off-line Grafika czasu rzeczywistego Nieograniczony czas na przygotowanie każdej klatki animacji Celem jest uzyskanie jak najlepszego obrazu Zastosowania: Film Wizualizacja produktów Sztucznie generowane obrazy Sztuka Renderowanie on-line Konieczność szybkiego wyświetlania kolejnych klatek animacji Celem jest uzyskanie satysfakcjonującego obrazu przy zachowaniu płynności animacji Stosowane są liczne uproszczenia Zastosowania: Gry komputerowe Interaktywne symulacje Wirtualna rzeczywistość 4
5 Grafika realistyczna Nieograniczony czas na renderowanie Aby uzyskać najlepszy efekt, można poświęcić od kilku sekund do nawet kilku dni na wyrenderowanie jednej klatki animacji Algorytmy mające za zadanie naśladować rzeczywiste zjawiska optyczne Ogromna ilość obliczeń, algorytmy takie jak np.: Raytracing Photon mapping Źródło obrazu: 5
6 Grafika czasu rzeczywistego Konieczność uzyskania płynności animacji Często mniej, niż 1/60 sekundy aby wyrenderować klatkę Generowanie grafiki poprzez uproszczenia Redukcja szczegółowości Uproszczony model oświetlenia Ograniczona symulacja zjawisk wizualnych Źródło obrazu: Crysis 3, Crytek 6
7 Scena 3D Elementy sceny: Obiekty geometryczne Cechy obiektów (tzw. materiałów z których są zbudowane) Położenie, rodzaj, kolor, intensywność,... Cechy środowiska Położenie, kierunek widzenia, kąt widzenia,... Źródła światła Cechy powierzchni, kolor, tekstura,... Kamera Bryła, położenie, kierunek obrotu, skala,... Mgła, dym, dodatkowe efekty wizualne,... 7
8 Modele 3D Obiekty wirtualnego świata reprezentowane są na scenie najczęściej przez tzw. modele Modele to geometryczna reprezentacja brył obiektów Model nie jest grafiką, dopóki nie zostanie wyrenderowany on tylko opisuje obiekt Analogia do grafiki wektorowej Źródła obrazów: 8
9 Modele 3D Modele składają się z wierzchołków Wierzchołki tworzą wielokąty (ang. Polygons) które składają się na powierzchnię modelu 9
10 Modele 3D W grafice czasu rzeczywistego często stosuje się tzw. modele low-poly, czyli o małej liczbie wielokątów W ten sposób uzyskuje się znacznie większą wydajność kosztem utraty jakości (szczegółowości) High-poly Low-poly (15488 trójkątów) (968 trójkątów) 10
11 Modele 3D Modele tworzy się w wyspecjalizowanym oprogramowaniu do tworzenia grafiki 3D, np.: Blender (darmowy) 3ds Max Maya Google SketchUp (darmowy) 11
12 Modele 3D Przykładowy format, w którym zapisuje się modele: Wavefront OBJ Plik tekstowy Kolejne linijki odpowiadają m.in. pozycjom wierzchołków, wektorom normalnym, współrzędnym tekstur, ścianom 12
13 Kamera Jest to wirtualny koncept opisujący sposób oglądania sceny przez obserwatora, dla którego renderujemy obraz Istnieją dwa podstawowe rodzaje kamer: Rzut perspektywiczny Rzut prostokątny (ang. orthographic) 13
14 Kamera perspektywiczna Kamera musi być opisana w sposób matematyczny, aby możliwe było uwzględnienie jej cech w procesie renderowania Przede wszystkim musi posiadać zdefiniowane: Pozycję (punkt zaczepienia): p Kierunek widzenia: d d p 14
15 Kamera perspektywiczna Położenie w przestrzeni 3D jest po prostu 3-elementowym wektorem Zmiana położenia powoduje przemieszczenie naszego wirtualnego "aparatu fotograficznego" 15
16 Kamera perspektywiczna Kierunek w przestrzeni 3D również jest 3-elementowym wektorem Kierunek można rozumieć jako wektor leżący na półprostej łączącej punkt zaczepienia z miejscem, na które kamera ma być skierowana Kierunek zwyczajowo przechowuje się jako wektor jednostkowy ( d = 1 ) 16
17 Kamera perspektywiczna To jednak nie wystarczy, aby jednoznacznie określić sposób obserwacji sceny Oba poniższe przykłady zostały wyrenderowane z tego samego miejsca, w tym samym kierunku: 17
18 Kamera perspektywiczna Konieczne jest wprowadzenie dodatkowo wektora pionu (ang. up vector): u Najczęściej jest to (0, 1, 0) jeśli za drugą współrzędną przyjmiemy tę skierowaną ku górze świata u d p 18
19 Kamera perspektywiczna Dodatkowo kamerę określają: Kąt widzenia (najczęściej w stopniach) fov Jego zmiana odpowiada zmianie ogniskowej obiektywu (popularnie zwanej "zoomem" w aparacie fotograficznym) Nie jest tożsamy z przybliżeniem/oddaleniem kamery! Szeroki kąt Wąski kąt (krótka ogniskowa) (długa ogniskowa) 19
20 Kamera perspektywiczna Dodatkowo kamerę określają: Odległość płaszczyzn przycinania: bliskiej n i dalekiej f (ang. near/far clipping plane) Określają, od jakiej do jakiej odległości będzie renderowana scena Ma to związek z precyzją bufora głębokości Im większy zakres odległości jest renderowany, tym większa szansa powstania problemów typu z-fighting wartości powinny zostać dobrane odpowiednio do charakterystyki danej sceny f n 20
21 Kamera perspektywiczna Dodatkowo kamerę określają: Proporcje boków podstawy ściętego ostrosłupa (ang. frustum) Stosunek szerokości do wysokości 4:3, 16:9, 16:10,... 21
22 Kamera perspektywiczna Podsumowując, do jednoznacznego opisania kamery potrzebne są wartości następujących atrybutów: Cechy widoku: Położenie Kierunek Wektor pionu Cechy projekcji: Kąt widzenia Odległości płaszczyzn przycinania Proporcje 22
23 Przekształcenia geometryczne Przekształcenia geometryczne w przestrzeni 3D opisane są macierzami 4x4 Aby poddać współrzędne (x, y, z) danemu przekształceniu T, macierz T mnożona jest przez wektor (rozszerzony o dodatkową współrzędną w = 1), a cały wynik jest dzielony przez ostatnią współrzędną w' 23
24 Przekształcenia geometryczne Podstawowe transformacje geometryczne to: Translacja Rotacja Skalowanie Macierze, które je opisują: 24
25 Przekształcenia geometryczne Macierz modelu jest złożeniem odpowiednich translacji, rotacji i skalowań Czyli iloczynem macierzy odpowiadających takim transformacjom Ważna jest kolejność mnożenia! Służy do umieszczenia naszego modelu, opisanego lokalnymi współrzędnymi, w pożądanym miejscu wirtualnego świata Dzięki takiemu podejściu możliwe jest wielokrotne używanie dokładnie tego samego modelu, opisanego tymi samymi współrzędnymi wierzchołków 25
26 Przekształcenia geometryczne Macierz widoku, a więc macierz związana z transformacją kamery, jest złożeniem odpowiednich translacji i rotacji Czyli iloczynem macierzy odpowiadających takim transformacjom Macierz projekcji perspektywicznej wygląda następująco: Gdzie: f = 1 / tan(fov / 2) aspect = proporcje znear = odległość bliskiej płaszczyzny przycinania zfar = odległość dalekiej płaszczyzny przycinania 26
27 Przekształcenia geometryczne Podczas procesu renderowania sceny dokonywane są przejścia pomiędzy różnymi układami współrzędnych Współrzędne modelu Macierz modelu Współrzędne świata Macierz widoku Współrzędne kamery Macierz projekcji Współrzędne projekcji Kanoniczna bryła widzenia Normalizacja, przycinanie itp. Mapowanie na ekran Współrzędne ekranu 27
28 Renderowanie geometrii Geometria jest opisana przede wszystkim pozycjami wierzchołków Podczas procesu renderowania obiekty rysowane są za pomocą tzw. prymitywów Prymitywy to figury geometryczne odpowiadające za to, jak informacja o kolejnych pozycjach zostanie wykorzystana podczas rysowania Mogą to być np. punkty, linie, łamane, trójkąty, pasy trójkątów, czworokąty, wielokąty, itp. 28
29 Renderowanie geometrii Prymitywy dostarczane przez OpenGL: Źródło obrazu: 29
30 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Myślimy o punktach w przestrzeni 3D, nie na płaszczyźnie 30
31 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Użycie prymitywu punkty (ang. points) 31
32 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Użycie prymitywu linie (ang. lines) 32
33 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Użycie prymitywu łamana (ang. line strip) 33
34 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Użycie prymitywu łamana zamknięta (ang. line loop) 34
35 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v1 v2 v0 v3 v4 v5 Użycie prymitywu łamana zamknięta (ang. line loop) 35
36 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v2 v1 v0 v3 v4 v5 Użycie prymitywu wachlarz (ang. triangle fan) 36
37 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v2 v1 v0 v3 v4 v5 Użycie prymitywu pas trójkątów (ang. triangle strip) 37
38 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v2 v1 v0 v3 v4 v5 Dwa ostatnie wierzchołki nie są wykorzystane - aby powstał kolejny quad, potrzebne byłyby dwa następne! Użycie prymitywu czworokąty (ang. quads) 38
39 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v2 v1 v0 v3 v4 v5 Ten czworokąt jest niepoprawny ( zdegenerowany ) nie jest wypukły! Użycie prymitywu pas czworokątów (ang. quad strip) 39
40 Renderowanie geometrii Przykład: Mamy dane 6 wierzchołków o następujących położeniach: v2 v1 v3 v0 v4 v5 Ten wielokąt jest niepoprawny ( zdegenerowany ) nie jest wypukły! Użycie prymitywu wielokąt (ang. polygon) 40
41 GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i omówienie potoku renderowania Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok
42 Literatura Grafika komputerowa Peter Shirley, Stephen Robert Marschner. "Fundamentals of Computer Graphics". AK Peters, Grafika czasu rzeczywistego Tomas Akenine-Moller, Eric Haines, Naty Hoffman. "Real-Time Rendering, Third Edition". AK Peters, Mike McShaffry, David Graham. "Game Coding Complete, Fourth Edition". Course Technology, "OpenGL Blue Book", czyli dokumentacja OpenGL. "OpenGL Red Book", czyli wprowadzenie do OpenGL.
Bartosz Bazyluk SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok
 SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
 Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Grafika Komputerowa i Wizualizacja, Informatyka S1, II Rok O MNIE mgr inż. Pokój 322/WI2 lub 316/WI2 bbazyluk@wi.zut.edu.pl
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Grafika Komputerowa i Wizualizacja, Informatyka S1, II Rok O MNIE mgr inż. Pokój 322/WI2 lub 316/WI2 bbazyluk@wi.zut.edu.pl
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
 Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
 Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Grafika Komputerowa, Informatyka, I Rok
 SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Wstęp do programowania grafiki 3D z użyciem OpenGL. Transformacje geometryczne. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Wstęp do programowania grafiki 3D z użyciem OpenGL. Transformacje geometryczne. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D
Grafika Komputerowa, Informatyka, I Rok
 KAMERA W SCENIE 3D Pojęcie kamery. Implementacja interaktywnej kamery FPP. Test i bufor głębokości. Grafika Komputerowa, Informatyka, I Rok Kamera Jest to wirtualny koncept opisujący sposób oglądania sceny
KAMERA W SCENIE 3D Pojęcie kamery. Implementacja interaktywnej kamery FPP. Test i bufor głębokości. Grafika Komputerowa, Informatyka, I Rok Kamera Jest to wirtualny koncept opisujący sposób oglądania sceny
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
 Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka S1, II Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka S1, II Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Gry Komputerowe - laboratorium 0
 Gry Komputerowe - laboratorium 0 Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w ie Wydział Informatyki 28 Luty 2018 Michał Chwesiuk Laboratorium 0 28 Luty 2018 1/ 18 O mnie mgr inż. Michał
Gry Komputerowe - laboratorium 0 Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w ie Wydział Informatyki 28 Luty 2018 Michał Chwesiuk Laboratorium 0 28 Luty 2018 1/ 18 O mnie mgr inż. Michał
1. Prymitywy graficzne
 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
Plan wykładu. Akcelerator 3D Potok graficzny
 Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Bartosz Bazyluk OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery)
 OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery) Programowanie Gier Komputerowych, Informatyka S, III Rok PLAN WYKŁADU Transformacje geometryczne Pożegnanie
OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery) Programowanie Gier Komputerowych, Informatyka S, III Rok PLAN WYKŁADU Transformacje geometryczne Pożegnanie
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
 Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Grafika komputerowa i wizualizacja
 Grafika komputerowa i wizualizacja Radosław Mantiuk ( rmantiuk@wi.zut.edu.pl, p. 315 WI2) http://rmantiuk.zut.edu.pl Katedra Systemów Multimedialnych Wydział Informatyki, Zachodniopomorski Uniwersytet
Grafika komputerowa i wizualizacja Radosław Mantiuk ( rmantiuk@wi.zut.edu.pl, p. 315 WI2) http://rmantiuk.zut.edu.pl Katedra Systemów Multimedialnych Wydział Informatyki, Zachodniopomorski Uniwersytet
Architektura Procesorów Graficznych
 Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Obraz realistyczny Pojęcie obrazu realistycznego jest rozumiane w różny sposób Nie zawsze obraz realistyczny
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Obraz realistyczny Pojęcie obrazu realistycznego jest rozumiane w różny sposób Nie zawsze obraz realistyczny
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Zaawansowana Grafika Komputerowa
 Zaawansowana Komputerowa Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 28 Luty 2017 Michał Chwesiuk Zaawansowana Komputerowa 28 Luty 2017 1/11 O mnie inż.
Zaawansowana Komputerowa Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 28 Luty 2017 Michał Chwesiuk Zaawansowana Komputerowa 28 Luty 2017 1/11 O mnie inż.
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Grafika komputerowa i wizualizacja. dr Wojciech Pałubicki
 Grafika komputerowa i wizualizacja dr Wojciech Pałubicki Grafika komputerowa Obrazy wygenerowane za pomocy komputera Na tych zajęciach skupiamy się na obrazach wygenerowanych ze scen 3D do interaktywnych
Grafika komputerowa i wizualizacja dr Wojciech Pałubicki Grafika komputerowa Obrazy wygenerowane za pomocy komputera Na tych zajęciach skupiamy się na obrazach wygenerowanych ze scen 3D do interaktywnych
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL
 GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok OpenGL Open Graphics Library Jest to API pozwalające na renderowanie grafiki w czasie rzeczywistym,
GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok OpenGL Open Graphics Library Jest to API pozwalające na renderowanie grafiki w czasie rzeczywistym,
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Bartosz Bazyluk GAME LOOP Podstawowy element silnika gry komputerowej. Programowanie Gier Komputerowych, Informatyka S1, III Rok
 Bartosz Bazyluk GAME LOOP Podstawowy element silnika gry komputerowej Programowanie Gier Komputerowych, Informatyka S1, III Rok INFORMACJE ORGANIZACYJNE: Prezentacje z wykładów, materiały, informacje można
Bartosz Bazyluk GAME LOOP Podstawowy element silnika gry komputerowej Programowanie Gier Komputerowych, Informatyka S1, III Rok INFORMACJE ORGANIZACYJNE: Prezentacje z wykładów, materiały, informacje można
OpenGL i wprowadzenie do programowania gier
 OpenGL i wprowadzenie do programowania gier Wojciech Sterna Bartosz Chodorowski OpenGL i wprowadzenie do programowania gier Autorstwo rozdziałów: 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 Wojciech Sterna
OpenGL i wprowadzenie do programowania gier Wojciech Sterna Bartosz Chodorowski OpenGL i wprowadzenie do programowania gier Autorstwo rozdziałów: 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 Wojciech Sterna
System graficzny. Potok graficzny 3D. Scena 3D Zbiór trójwymiarowych danych wejściowych wykorzystywanych do wygenerowania obrazu wyjściowego 2D.
 System graficzny scena 3D algorytm graficzny obraz 2D Potok graficzny 3D Radosław Mantiuk Dane wejściowe Algorytm tworzący obraz wyjściowy na podstawie sceny 3D Dane wyjściowe Wydział Informatyki Zachodniopomorski
System graficzny scena 3D algorytm graficzny obraz 2D Potok graficzny 3D Radosław Mantiuk Dane wejściowe Algorytm tworzący obraz wyjściowy na podstawie sceny 3D Dane wyjściowe Wydział Informatyki Zachodniopomorski
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
1 LEKCJA. Definicja grafiki. Główne działy grafiki komputerowej. Programy graficzne: Grafika rastrowa. Grafika wektorowa. Grafika trójwymiarowa
 1 LEKCJA Definicja grafiki Dział informatyki zajmujący się wykorzystaniem komputerów do generowania i przetwarzania obrazów (statycznych i dynamicznych) oraz wizualizacją danych. Główne działy grafiki
1 LEKCJA Definicja grafiki Dział informatyki zajmujący się wykorzystaniem komputerów do generowania i przetwarzania obrazów (statycznych i dynamicznych) oraz wizualizacją danych. Główne działy grafiki
Trójwymiarowa grafika komputerowa rzutowanie
 Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
 RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
Wyświetlanie obrazu Techniki wyświetlania obrazu i ich zastosowanie w grach.
 Wyświetlanie obrazu Techniki wyświetlania obrazu i ich zastosowanie w grach. http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok, 2018 r. WYŚWIETLANIE OBRAZU Współczesne wyświetlacze
Wyświetlanie obrazu Techniki wyświetlania obrazu i ich zastosowanie w grach. http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok, 2018 r. WYŚWIETLANIE OBRAZU Współczesne wyświetlacze
GRAFIKA KOMPUTEROWA. Plan wykładu. 1. Początki grafiki komputerowej. 2. Grafika komputerowa a dziedziny pokrewne. 3. Omówienie programu przedmiotu
 GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
Wykład 4. Rendering (1) Informacje podstawowe
 Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
KARTA KURSU (realizowanego w module specjalności) Modelowanie 3D
 KARTA KURSU (realizowanego w module ) Multimedia i Technologie Internetowe (nazwa ) Nazwa Nazwa w j. ang. Modelowanie 3D 3D Modelling Kod Punktacja ECTS* 3 Koordynator Mgr inż. Alicja Pituła Zespół dydaktyczny:
KARTA KURSU (realizowanego w module ) Multimedia i Technologie Internetowe (nazwa ) Nazwa Nazwa w j. ang. Modelowanie 3D 3D Modelling Kod Punktacja ECTS* 3 Koordynator Mgr inż. Alicja Pituła Zespół dydaktyczny:
Grafika komputerowa Wykład 4 Geometria przestrzenna
 Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Techniki animacji komputerowej
 Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Technologie Informacyjne
 Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
KARTA KURSU (realizowanego w module specjalności) Modelowanie 3D
 KARTA KURSU (realizowanego w module ) Multimedia i Technologie Internetowe (nazwa ) Nazwa Nazwa w j. ang. Modelowanie 3D 3D Modelling Kod Punktacja ECTS* 3 Koordynator mgr inż. Alicja Pituła Zespół dydaktyczny:
KARTA KURSU (realizowanego w module ) Multimedia i Technologie Internetowe (nazwa ) Nazwa Nazwa w j. ang. Modelowanie 3D 3D Modelling Kod Punktacja ECTS* 3 Koordynator mgr inż. Alicja Pituła Zespół dydaktyczny:
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
 TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
GLKit. Wykład 10. Programowanie aplikacji mobilnych na urządzenia Apple (IOS i ObjectiveC) #import "Fraction.h" #import <stdio.h>
 #import "Fraction.h" #import @implementation Fraction -(Fraction*) initwithnumerator: (int) n denominator: (int) d { self = [super init]; } if ( self ) { [self setnumerator: n anddenominator:
#import "Fraction.h" #import @implementation Fraction -(Fraction*) initwithnumerator: (int) n denominator: (int) d { self = [super init]; } if ( self ) { [self setnumerator: n anddenominator:
GRK 2. dr Wojciech Palubicki
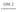 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
Rozdział VII. Przekształcenia geometryczne na płaszczyźnie Przekształcenia geometryczne Symetria osiowa Symetria środkowa 328
 Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Programowanie Procesorów Graficznych
 Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Załącznik KARTA PRZEDMIOTU. KARTA PRZEDMIOTU Wydział Automatyki, Elektroniki i Informatyki, Rok akademicki: 2009/2010 KOMPUTEROWA
 1/1 Wydział Automatyki, Elektroniki i Informatyki, Rok akademicki: 2009/2010 Nazwa przedmiotu: Kierunek: Specjalność: Tryb studiów: GRAFIKA KOMPUTEROWA INFORMATYKA Kod/nr GK PRZEDMIOT OBOWIĄZKOWY DLA WSZYSTKICH
1/1 Wydział Automatyki, Elektroniki i Informatyki, Rok akademicki: 2009/2010 Nazwa przedmiotu: Kierunek: Specjalność: Tryb studiów: GRAFIKA KOMPUTEROWA INFORMATYKA Kod/nr GK PRZEDMIOT OBOWIĄZKOWY DLA WSZYSTKICH
Systemy wirtualnej rzeczywistości. Podstawy grafiki 3D
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Podstawy grafiki 3D Wstęp: W drugiej części przedstawione zostaną podstawowe mechanizmy
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Podstawy grafiki 3D Wstęp: W drugiej części przedstawione zostaną podstawowe mechanizmy
Podstawy grafiki komputerowej
 Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
 RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Mapowanie nierówności wprowadzenie Poziomy szczegółowości Cieniowanie w układzie stycznym Generacja wektorów normalnych i stycznych Mapy
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Mapowanie nierówności wprowadzenie Poziomy szczegółowości Cieniowanie w układzie stycznym Generacja wektorów normalnych i stycznych Mapy
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2013/2014
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 013/014 Kierunek studiów: Informatyka Stosowana Forma
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 013/014 Kierunek studiów: Informatyka Stosowana Forma
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Scena 3D. Cieniowanie (ang. Shading) Scena 3D - Materia" Obliczenie koloru powierzchni (ang. Lighting)
 Zbiór trójwymiarowych danych wej$ciowych wykorzystywanych do wygenerowania obrazu wyj$ciowego 2D. Cieniowanie (ang. Shading) Rados"aw Mantiuk Wydzia" Informatyki Zachodniopomorski Uniwersytet Technologiczny
Zbiór trójwymiarowych danych wej$ciowych wykorzystywanych do wygenerowania obrazu wyj$ciowego 2D. Cieniowanie (ang. Shading) Rados"aw Mantiuk Wydzia" Informatyki Zachodniopomorski Uniwersytet Technologiczny
Grafika komputerowa. Obraz w informatyce
 Grafika komputerowa Obraz w informatyce Grafika komputerowa dziedzina informatyki (dyscyplina?)zajmująca się wykorzystaniem technik komputerowych do wizualizacji realnych lub wyimaginowanych procesów.
Grafika komputerowa Obraz w informatyce Grafika komputerowa dziedzina informatyki (dyscyplina?)zajmująca się wykorzystaniem technik komputerowych do wizualizacji realnych lub wyimaginowanych procesów.
Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu
 Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu IGK 2012 Michał Jarząbek W skrócie Funkcje niejawne opisują powierzchnie niejawne Powierzchnie niejawne metoda reprezentacji "obiektów"
Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu IGK 2012 Michał Jarząbek W skrócie Funkcje niejawne opisują powierzchnie niejawne Powierzchnie niejawne metoda reprezentacji "obiektów"
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA Computer Graphics Forma studiów: studia
Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA Computer Graphics Forma studiów: studia
Nawi zanie do gimnazjum Planimetria Trójk Rysujemy Rysujemy Rysujemy Zapisujemy t zewn trzny trójk ta, Trójk ty ze wzgl du na miary k tów Trójk
 PLANIMETRIA Lekcja 102-103. Miary kątów w trójkącie str. 222-224 Nawiązanie do gimnazjum Planimetria to., czy planimetria zajmuje się. (Dział geometrii, który zajmuje się badaniem płaskich figur geometrycznych)
PLANIMETRIA Lekcja 102-103. Miary kątów w trójkącie str. 222-224 Nawiązanie do gimnazjum Planimetria to., czy planimetria zajmuje się. (Dział geometrii, który zajmuje się badaniem płaskich figur geometrycznych)
Rok akademicki: 2017/2018 Kod: JFM s Punkty ECTS: 7. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Zatem standardowe rysowanie prymitywów wygląda następująco:
 Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
WPROWADZENIE DO GRAFIKI KOMPUTEROWEJ
 WPROWADZENIE DO GRAFIKI KOMPUTEROWEJ Dr inż.. Jacek Jarnicki Doc. PWr. Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl 1. Układ przedmiotu
WPROWADZENIE DO GRAFIKI KOMPUTEROWEJ Dr inż.. Jacek Jarnicki Doc. PWr. Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl 1. Układ przedmiotu
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Karty graficzne możemy podzielić na:
 KARTY GRAFICZNE Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
KARTY GRAFICZNE Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
Architektura Komputerów
 Studia Podyplomowe INFORMATYKA Techniki Architektura Komputerów multimedialne Wykład nr. 9 dr Artur Bartoszewski Rendering a Ray Tracing Ray tracing (dosłownie śledzenie promieni) to technika renderowania
Studia Podyplomowe INFORMATYKA Techniki Architektura Komputerów multimedialne Wykład nr. 9 dr Artur Bartoszewski Rendering a Ray Tracing Ray tracing (dosłownie śledzenie promieni) to technika renderowania
Model oświetlenia. Radosław Mantiuk. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie
 Model oświetlenia Radosław Mantiuk Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Obliczenie koloru powierzchni (ang. Lighting) Światło biegnie od źródła światła, odbija
Model oświetlenia Radosław Mantiuk Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Obliczenie koloru powierzchni (ang. Lighting) Światło biegnie od źródła światła, odbija
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
GRK 4. dr Wojciech Palubicki
 GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
 Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
KARTA KURSU. Grafika komputerowa
 KARTA KURSU Nazwa Nazwa w j. ang. Grafika komputerowa Computer graphics Kod Punktacja ECTS* 3 Koordynator dr inż. Krzysztof Wójcik Zespół dydaktyczny: dr inż. Krzysztof Wójcik dr inż. Mateusz Muchacki
KARTA KURSU Nazwa Nazwa w j. ang. Grafika komputerowa Computer graphics Kod Punktacja ECTS* 3 Koordynator dr inż. Krzysztof Wójcik Zespół dydaktyczny: dr inż. Krzysztof Wójcik dr inż. Mateusz Muchacki
Śledzenie promieni w grafice komputerowej
 Dariusz Sawicki Śledzenie promieni w grafice komputerowej Warszawa 2011 Spis treści Rozdział 1. Wprowadzenie....... 6 1.1. Śledzenie promieni a grafika realistyczna... 6 1.2. Krótka historia śledzenia
Dariusz Sawicki Śledzenie promieni w grafice komputerowej Warszawa 2011 Spis treści Rozdział 1. Wprowadzenie....... 6 1.1. Śledzenie promieni a grafika realistyczna... 6 1.2. Krótka historia śledzenia
Obraz jako funkcja Przekształcenia geometryczne
 Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
Krzyżówka oraz hasła do krzyżówki. Kalina R., Przewodnik po matematyce dla klas VII-VIII, część IV, SENS, Poznań 1997, s.20-22.
 Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
Synteza i obróbka obrazu. Modelowanie obiektów 3D
 Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA
 INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA LITERATURA: R. Reinhardt, S. Dowd, Adobe Flash Professional. Biblia. D. Hirmes, JD Hooge, K. Jokol, FLASH. AKADEMIA MATEMATYCZNYCH SZTUCZEK ZASTOSOWANIA ANIMACJI
INTERAKTYWNA KOMUNIKACJA WIZUALNA ANIMACJA LITERATURA: R. Reinhardt, S. Dowd, Adobe Flash Professional. Biblia. D. Hirmes, JD Hooge, K. Jokol, FLASH. AKADEMIA MATEMATYCZNYCH SZTUCZEK ZASTOSOWANIA ANIMACJI
Symetria w fizyce materii
 Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
dr hab. inż. Lidia Jackowska-Strumiłło, prof. PŁ Instytut Informatyki Stosowanej, PŁ
 Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki Politechnika Łódzka Środowisko pracy grafików dr hab. inż. Lidia Jackowska-Strumiłło, prof. PŁ Instytut Informatyki Stosowanej, PŁ Formaty
Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki Politechnika Łódzka Środowisko pracy grafików dr hab. inż. Lidia Jackowska-Strumiłło, prof. PŁ Instytut Informatyki Stosowanej, PŁ Formaty
Photoshop. Podstawy budowy obrazu komputerowego
 Photoshop Podstawy budowy obrazu komputerowego Wykład 1 Autor: Elżbieta Fedko O czym dzisiaj będziemy mówić? Co to jest grafika komputerowa? Budowa obrazu w grafice wektorowej i rastrowej. Zastosowanie
Photoshop Podstawy budowy obrazu komputerowego Wykład 1 Autor: Elżbieta Fedko O czym dzisiaj będziemy mówić? Co to jest grafika komputerowa? Budowa obrazu w grafice wektorowej i rastrowej. Zastosowanie
CYFROWA SYNTEZA FOTOREALISTYCZNYCH OBRAZÓW W ŚRODOWISKU 3D
 CYFROWA SYNTEZA FOTOREALISTYCZNYCH OBRAZÓW W ŚRODOWISKU 3D Daniel Jaroszewski Warszawska Wyższa Szkoła Informatyki djaroszewski@poczta.wwsi.edu.pl www.grafika3d.wwsi.edu.pl WPROWADZENIE Przykładowa wizualizacja
CYFROWA SYNTEZA FOTOREALISTYCZNYCH OBRAZÓW W ŚRODOWISKU 3D Daniel Jaroszewski Warszawska Wyższa Szkoła Informatyki djaroszewski@poczta.wwsi.edu.pl www.grafika3d.wwsi.edu.pl WPROWADZENIE Przykładowa wizualizacja
Rysunek 1: Okno timeline wykorzystywane do tworzenia animacji.
 Ćwiczenie 5 - Tworzenie animacji Podczas tworzenia prostej animacji wykorzystywać będziemy okno Timeline domyślnie ustawione na dole okna Blendera (Rys. 1). Proces tworzenia animacji polega na stworzeniu
Ćwiczenie 5 - Tworzenie animacji Podczas tworzenia prostej animacji wykorzystywać będziemy okno Timeline domyślnie ustawione na dole okna Blendera (Rys. 1). Proces tworzenia animacji polega na stworzeniu
gdzie (4.20) (4.21) 4.3. Rzut równoległy
 4.3. Rzut równoległy 75 gdzie (4.20) Punkt zbiegu, określony wzorami (4.19) (4.20), leży na prostej przechodzącej przez środek rzutowania i równoległej do wektora u. Zauważmy, że gdy wektor u jest równoległy
4.3. Rzut równoległy 75 gdzie (4.20) Punkt zbiegu, określony wzorami (4.19) (4.20), leży na prostej przechodzącej przez środek rzutowania i równoległej do wektora u. Zauważmy, że gdy wektor u jest równoległy
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: moduł specjalności obowiązkowy: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU GRAFICZNE MODELOWANIE
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: moduł specjalności obowiązkowy: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU GRAFICZNE MODELOWANIE
SYNTEZA OBRAZU. Wprowadzenie. Synteza obrazu
 SYNTEZA OBRAZU Wprowadzenie Synteza obrazu Synteza obrazu Zagadnienie wchodzące w skład ogólnie pojętej grafiki komputerowej. Synteza obrazu - tworzenie obrazu na podstawie pewnego opisu. Komputerowa (cyfrowa)
SYNTEZA OBRAZU Wprowadzenie Synteza obrazu Synteza obrazu Zagadnienie wchodzące w skład ogólnie pojętej grafiki komputerowej. Synteza obrazu - tworzenie obrazu na podstawie pewnego opisu. Komputerowa (cyfrowa)
Pracownia Technik Reklamy Semestr Jesienno-Zimowy 2012/2013
 Pracownia Technik Reklamy Semestr Jesienno-Zimowy 2012/2013 ZAJĘCIA I POWTÓRZENIE WIADOMOŚCI O RZUTOWANIU I PERSPEKTYWIE Rysunek techniczny Strona na którą chętnie zaglądamy: http://czajek3.republika.pl/
Pracownia Technik Reklamy Semestr Jesienno-Zimowy 2012/2013 ZAJĘCIA I POWTÓRZENIE WIADOMOŚCI O RZUTOWANIU I PERSPEKTYWIE Rysunek techniczny Strona na którą chętnie zaglądamy: http://czajek3.republika.pl/
PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3
 PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3 I. FUNKCJE grupuje elementy w zbiory ze względu na wspólne cechy wymienia elementy zbioru rozpoznaje funkcje wśród przyporządkowań
PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3 I. FUNKCJE grupuje elementy w zbiory ze względu na wspólne cechy wymienia elementy zbioru rozpoznaje funkcje wśród przyporządkowań
Grafika Komputerowa. Wykład 8. Przygotowanie do egzaminu. mgr inż. Michał Chwesiuk 1/32
 Grafika Komputerowa Wykład 8 Przygotowanie do egzaminu mgr inż. 1/32 Obraz Grafika Rastrowa Grafika Wektorowa Obraz przechowywany w pamięci w postaci próbki opisane za pomocą macierzy pikseli Każdy piksel
Grafika Komputerowa Wykład 8 Przygotowanie do egzaminu mgr inż. 1/32 Obraz Grafika Rastrowa Grafika Wektorowa Obraz przechowywany w pamięci w postaci próbki opisane za pomocą macierzy pikseli Każdy piksel
Wprowadzenie do grafiki komputerowej. W. Alda
 Wprowadzenie do grafiki komputerowej W. Alda Grafika komputerowa w pigułce Zacznijmy od tego co widać na ekranie Grafika rastrowa 2D Spektrum fal elektromagnetycznych Promieniowanie gamma ~ 10-12 m Fale
Wprowadzenie do grafiki komputerowej W. Alda Grafika komputerowa w pigułce Zacznijmy od tego co widać na ekranie Grafika rastrowa 2D Spektrum fal elektromagnetycznych Promieniowanie gamma ~ 10-12 m Fale
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
Temat: Transformacje 3D
 Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Przygotowanie grafiki 3D do gier komputerowych
 Grafika Komputerowa i Wizualizacja Przygotowanie grafiki 3D do gier komputerowych Rafał Piórkowski Plan wykładu 1. Ogólne wiadomości 2. Modelowanie high poly 3. Rzeźbienie 4. Modelowanie low poly 5. Model
Grafika Komputerowa i Wizualizacja Przygotowanie grafiki 3D do gier komputerowych Rafał Piórkowski Plan wykładu 1. Ogólne wiadomości 2. Modelowanie high poly 3. Rzeźbienie 4. Modelowanie low poly 5. Model
Obraz realistyczny. Realizm w grafice komputerowej. Realizm modelu: z!o#one siatki wielok$tów. Realizm modelu geometrycznego. Realizm modelu: spline'y
 Obraz realistyczny Zbli!ony jako"ci# do obrazów / animacji obserwowanych przez cz$owieka. Realizm w grafice komputerowej Rados!aw Mantiuk Zachodniopomorski Uniwersytet Technologiczny Obraz realistyczny
Obraz realistyczny Zbli!ony jako"ci# do obrazów / animacji obserwowanych przez cz$owieka. Realizm w grafice komputerowej Rados!aw Mantiuk Zachodniopomorski Uniwersytet Technologiczny Obraz realistyczny
OpenGL : Oświetlenie. mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski. Szczecin, r 1/23
 OpenGL : mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski 1/23 Folder z plikami zewnętrznymi (resources) Po odpaleniu przykładowego projektu, nie uruchomi się on poprawnie. Powodem
OpenGL : mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski 1/23 Folder z plikami zewnętrznymi (resources) Po odpaleniu przykładowego projektu, nie uruchomi się on poprawnie. Powodem
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Opis efektów kształcenia dla modułu zajęć
 Nazwa modułu: Grafika komputerowa Rok akademicki: 2015/2016 Kod: ITE-1-514-s Punkty ECTS: 5 Wydział: Informatyki, Elektroniki i Telekomunikacji Kierunek: Teleinformatyka Specjalność: - Poziom studiów:
Nazwa modułu: Grafika komputerowa Rok akademicki: 2015/2016 Kod: ITE-1-514-s Punkty ECTS: 5 Wydział: Informatyki, Elektroniki i Telekomunikacji Kierunek: Teleinformatyka Specjalność: - Poziom studiów:
GRAFIKA KOMPUTEROWA podstawy matematyczne. dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel.
 GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
Trójwymiarowa wizualizacja danych przestrzennych
 Trójwymiarowa wizualizacja danych przestrzennych Wykład Kolokwium pod koniec listopada: 30 pkt. (egzamin?) Próg zaliczenia: 15 pkt Wymagana obecność* Laboratorium Siedem ćwiczeń po 5 pkt., Wymagane zdobycie
Trójwymiarowa wizualizacja danych przestrzennych Wykład Kolokwium pod koniec listopada: 30 pkt. (egzamin?) Próg zaliczenia: 15 pkt Wymagana obecność* Laboratorium Siedem ćwiczeń po 5 pkt., Wymagane zdobycie
Transformacje. dr Radosław Matusik. radmat
 www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja m.in. przestrzeni modelu, świata, kamery oraz projekcji, a także omówienie sposobów oświetlania i cieniowania obiektów. Pierwsze
www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja m.in. przestrzeni modelu, świata, kamery oraz projekcji, a także omówienie sposobów oświetlania i cieniowania obiektów. Pierwsze
OpenGL przezroczystość
 OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
rgbf<składowa_r,składowa_g,składowa_b,filter>. Dla parametru filter przyjmij kolejno wartości: 0.60, 0.70, 0.80, 0.90, 1.00, np.:
 Temat 2: Przezroczystość. Prostopadłościan, walec i stożek. Przesuwanie i skalowanie obiektów. Omówimy teraz przezroczystość obiektów związaną z ich kolorem (lub teksturą). Za przezroczystość odpowiadają
Temat 2: Przezroczystość. Prostopadłościan, walec i stożek. Przesuwanie i skalowanie obiektów. Omówimy teraz przezroczystość obiektów związaną z ich kolorem (lub teksturą). Za przezroczystość odpowiadają
Stereometria bryły. Wielościany. Wielościany foremne
 Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
1 Wstęp teoretyczny. Temat: Manipulowanie przestrzenią. Grafika komputerowa 3D. Instrukcja laboratoryjna Układ współrzędnych
 Instrukcja laboratoryjna 9 Grafika komputerowa 3D Temat: Manipulowanie przestrzenią Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny 1.1 Układ
Instrukcja laboratoryjna 9 Grafika komputerowa 3D Temat: Manipulowanie przestrzenią Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny 1.1 Układ
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 12 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
