Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
|
|
|
- Kamil Piotr Sikora
- 8 lat temu
- Przeglądów:
Transkrypt
1 Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów. 2. Zapoznać się z zestawem komend OpenGL umożliwiającym zdefiniowanie źródeł światła i właściwości materiałów. Przebieg ćwiczenia: 1. Założenia: a. Celem prac na zajęciach laboratoryjnych jest zdefiniowanie parametrów oświetlenia i oświetlenie modelu manipulatora Puma (rysunek 1.1). b. Wynikiem prac na dzisiejszych zajęciach ma być program zbliżony w działaniu do programu puma_swiatlo.exe dostarczonego do materiałów laboratoryjnych. c. Realizacja ćwiczenia polega na uzupełnieniu kodu programu gl_template modyfikowanego na ostatnich zajęciach. d. W realizacji prac wzorować się należy na rozwiązaniach przyjętych w programie shinyjet również dołączonym do materiałów laboratoryjnych. Rys 1.1 Oświetlony model manipulatora Puma 2. Uwagi do sposobu realizacji celu dzisiejszych zajęć laboratoryjnych: a. W pierwszej kolejności należy zdefiniować parametry źródła światła. Charakterystyki źródła światła dokonuje się zwykle jednokrotnie przed wyświetlaniem sceny (w przykładowych programach definicja oświetlenia znajduje się w funkcji SetupRC() ). Szczegóły można znaleźć w materiałach wprowadzających do ćwiczenia. Poniżej zawarto przykładowy ciąg poleceń OpenGL ustalający oświetlenie na scenie: // wartości składowych oświetlenia i koordynaty źródła światła: GLfloat ambientlight[] = 0.3f, 0.3f, 0.3f, 1.0f ; GLfloat diffuselight[] = 0.7f, 0.7f, 0.7f, 1.0f ; GLfloat specular[] = 1.0f, 1.0f, 1.0f, 1.0f; GLfloat lightpos[] = 0.0f, 150.0f, 150.0f, 1.0f ;
2 GLfloat specref[] = 1.0f, 1.0f, 1.0f, 1.0f ; glenable(gl_depth_test); // usuwanie niewidocznych powierzchni glfrontface(gl_ccw); // ustalenie zewnętrznych ścian glenable(gl_cull_face); // wyłączenie obliczania wewnętrznych ścian // Uaktywnienie oświetlenia glenable(gl_lighting); // Ustawienie parametrów źródła światła 0 gllightfv(gl_light0,gl_ambient,ambientlight); gllightfv(gl_light0,gl_diffuse,diffuselight); gllightfv(gl_light0,gl_specular,specular); gllightfv(gl_light0,gl_position,lightpos); glenable(gl_light0); // Uaktywnienie śledzenia kolorów glenable(gl_color_material); // Materiały mają śledzić kolory ustalone poleceniem glcolor glcolormaterial(gl_front, GL_AMBIENT_AND_DIFFUSE); // Od tej chwili wszystkie materiały będą miały pełną odblaskowość // z dużą jasnością glmaterialfv(gl_front, GL_SPECULAR,specref); glmateriali(gl_front,gl_shininess,128); // Normalne zostaną automatycznie normalizowane glenable(gl_normalize); b. Kolejnym etapem tworzenia efektu oświetlenia jest zdefiniowanie wektorów normalnych do ścian, które chcemy widzieć jako oświetlone. Normalną można zdefiniować dla każdego wierzchołka wielokąta. Ponieważ zakładamy, że pojedynczy wielokąt wyznacza płaszczyznę, wystarczy dla wszystkich wierzchołków wielokąta wyznaczyć jedną normalną. Wyjątek w naszym programie stanowić będą tworzące walców. Dla osiągnięcia efektu wygładzenia powierzchni bocznych walca wygodniej jest definiować normalne prostopadłe do krawędzi ciągu czworokątów przybliżających tworzącą walca. c. Przykładowy fragment programu definiujący normalne dla walca zawarto poniżej: void walec(double h, double r) double angle,x,y; glbegin(gl_triangle_fan); glnormal3d(0.0,0.0,-1.0); glvertex3d(0.0f, 0.0f, 0.0f); for(angle = 0.0f; angle <= (2.0f*GL_PI); angle += (GL_PI/8.0f)) x = r*sin(angle);
3 y = r*cos(angle); glvertex2d(x, y); glbegin(gl_triangle_fan); glnormal3d(0.0,0.0,1.0); glvertex3d(0.0, 0.0, h); for(angle = 0.0f; angle >= -(2.0f*GL_PI); angle -= (GL_PI/8.0f)) x = r*sin(angle); y = r*cos(angle); glvertex3d(x, y, h); glbegin(gl_quad_strip); for(angle = 0.0f; angle >= -(2.0f*GL_PI); angle -= (GL_PI/8.0f)) x = r*sin(angle); y = r*cos(angle); glnormal3d(sin(angle),cos(angle),0.0); glvertex3d(x, y, h); glvertex3d(x, y, 0); d. Dla dowolnego wielokąta, usytuowanego dowolnie w przestrzeni trudno jest poprawnie zdefiniować wektor prostopadły o długości 1. W tym celu uzupełniono zestaw funkcji programu gltemplate o funkcję calcnormal(float v[3][3], float out[3]). Dokładny opis działania funkcji zawarto w materiałach wprowadzających do ćwiczenia. Funkcja umożliwia zdefiniowanie normalnej do wielokąta na podstawie współrzędnych trzech wierzchołków danego wielokąta. Przykład wykorzystania funkcji umieszczono poniżej: glbegin(gl_quads); float v[3][3]= 0.0f, -15.0f, 10.0f, -60.0f,-10.0f,10.0f, -60.0f,-10.0f,0.0f ; float norm[3]; calcnormal(v,norm); glnormal3d(norm[0],norm[1],norm[2]); glvertex3d(0.0, -15.0, 10.0); glvertex3d(-60.0,-10.0,10.0); glvertex3d(-60.0,-10.0,0.0); glvertex3d(0.0, -15.0, 0.0);
4 3. Przebieg ćwiczenia: a. W funkcji SetupRC() od-komentować wszystkie wywołania instrukcji i funkcji w języku C. Spowoduje to zdefiniowanie i uaktywnianie pojedynczego źródła światła. Dodatkowo nastąpi wyłączenie rysowania wszystkich tylnych ścian wielokątów (glenable(gl_cull_face);). W programie zastosowano model oświetlenia ze śledzeniem kolorów. Zdefiniowano również światło kierunkowe, które będzie modelowało białe odbłyski od wszystkich wielokątów. b. Ustalić następujący tryb rysowania wielokątów: przednie ściany wypełnione, tylne ściany rysowane jako siatka (należy w funkcji RenderScene() uaktywnić wywołanie funkcji glpolygonmode(gl_back,gl_line);) c. Dla opracowanych modeli brył: sześcian, walec, ramię robota ustalić jednolite kolory wszystkich ścian. d. Zdefiniować normalne dla modelu sześcianu. Rysunek 1 pokazuje wartości normalnych dla poszczególnych ścian. y [0,1,0] [-1,0,0] [0,0,-1] [1,0,0] [0,0,1] z [0,-1,0] x Rys. 1. Współrzędne normalnych do ścian sześcianu. Poniższy fragment kodu pokazuje zasadę wprowadzania normalnych w skrypcie OpenGL rysującym sześcian: void szescian(void) glcolor3d(0.8,0.7,0.3); glbegin(gl_quads); glnormal3d(0,0,1); glvertex3d(25,25,25); glvertex3d(-25,25,25); glvertex3d(-25,-25,25); glvertex3d(25,-25,25); glnormal3d(1,0,0); glvertex3d(25,25,25); glvertex3d(25,-25,25);
5 glvertex3d(25,-25,-25); glvertex3d(25,25,-25); // glend() e. Zdefiniować normalne dla walca. Rysunek 2 pokazuje wartości odpowiednich normalnych. Łatwo zauważyć, że normalne do podstaw walca mają odpowiednio wartości [0,0,1] oraz [0,0,-1]. Zasadę wyliczenia normalnych dla tworzącej walca pokazano na rysunku 3. y [sin(α), cos(α),0] r [0,0,-1] x [0,0,1] z h Rys. 2. Wartości normalnych dla modelu walca. Y ay α ax a α X Rys. 3. Wyznaczanie normalnej do powierzchni bocznej walca Zależności matematyczne: [ ] W punkcie 2c pokazano, jak pokazane wyżej zależności zaimplementować w skrypcie rysującym model walca.
6 f. Zdefiniować normalne dla modelu ramienia. W fragmentach modelu będących połowami siatek walca zastosować rozwiązanie zaproponowane w punktach 2c i 3e. Dwa czworokąty leżące w tych samych płaszczyznach, co podstawy połówek walca mają takie same normalne jak te połówki. Dla pozostałych dwu czworokątów należy zastosować funkcję calcnormal(), por. punkt 2d. Do funkcji przekazuje się współrzędne 3 wierzchołków wielokąta, do którego chcemy wyznaczyć normalną. Funkcja na podstawie tych 3 wierzchołków wyznacza współrzędne dwu wektorów zaczepionych w jednym z wierzchołów i mające końce w dwu pozostałych wierzchołkach. Mając współrzędne wektorów funkcja oblicza iloczyn wektorowy tych wektorów, a następnie dokonuje normalizacji tego iloczynu z zastosowaniem funkcji ReduceToUnit(). Wynikiem działania funkcji jest wektor normalny do płaszczyzny wyznaczonej przez 3 wierzchołki wielokąta. Należy zwrócić uwagę, żeby do funkcji calcnormal() przekazać tablice wierzchołków opisane wartościami typu float. g. Zadanie dodatkowe: Stosując rozwiązania zawarte w przykładowym programie spot należy zdefiniować reflektor w scenie z robotem.
OpenGL model oświetlenia
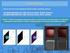 Składowe światła OpenGL Światło otaczające (ambient) OpenGL model oświetlenia Nie pochodzi z żadnego określonego kierunku. Powoduje równomierne oświetlenie obiektów na wszystkich powierzchniach i wszystkich
Składowe światła OpenGL Światło otaczające (ambient) OpenGL model oświetlenia Nie pochodzi z żadnego określonego kierunku. Powoduje równomierne oświetlenie obiektów na wszystkich powierzchniach i wszystkich
Laboratorium Grafiki Komputerowej i Animacji. Ćwiczenie V. Biblioteka OpenGL - oświetlenie sceny
 Laboratorium Grafiki Komputerowej i Animacji Ćwiczenie V Biblioteka OpenGL - oświetlenie sceny Sławomir Samolej Rzeszów, 1999 1. Wstęp Większość tworzonych animacji w grafice komputerowej ma za zadanie
Laboratorium Grafiki Komputerowej i Animacji Ćwiczenie V Biblioteka OpenGL - oświetlenie sceny Sławomir Samolej Rzeszów, 1999 1. Wstęp Większość tworzonych animacji w grafice komputerowej ma za zadanie
Oświetlenie w OpenGL. Oprogramowanie i wykorzystanie stacji roboczych. Wykład 8. Światło otaczajace. Światło rozproszone.
 Oświetlenie w OpenGL Oprogramowanie i wykorzystanie stacji roboczych Wykład 8 Dr inż. Tomasz Olas olas@icis.pcz.pl W OpenGL źródło światła w scenie składa się z trzech składowych oświetlenia: otoczenia,
Oświetlenie w OpenGL Oprogramowanie i wykorzystanie stacji roboczych Wykład 8 Dr inż. Tomasz Olas olas@icis.pcz.pl W OpenGL źródło światła w scenie składa się z trzech składowych oświetlenia: otoczenia,
Laboratorium grafiki komputerowej i animacji. Ćwiczenie III - Biblioteka OpenGL - wprowadzenie, obiekty trójwymiarowe: punkty, linie, wielokąty
 Laboratorium grafiki komputerowej i animacji Ćwicenie III - Biblioteka OpenGL - wprowadenie, obiekty trójwymiarowe: punkty, linie, wielokąty Prygotowanie do ćwicenia: 1. Zaponać się ogólną charakterystyką
Laboratorium grafiki komputerowej i animacji Ćwicenie III - Biblioteka OpenGL - wprowadenie, obiekty trójwymiarowe: punkty, linie, wielokąty Prygotowanie do ćwicenia: 1. Zaponać się ogólną charakterystyką
Materiały. Dorota Smorawa
 Materiały Dorota Smorawa Materiały Materiały, podobnie jak światła, opisywane są za pomocą trzech składowych. Opisują zdolności refleksyjno-emisyjne danej powierzchni. Do tworzenia materiału służy funkcja:
Materiały Dorota Smorawa Materiały Materiały, podobnie jak światła, opisywane są za pomocą trzech składowych. Opisują zdolności refleksyjno-emisyjne danej powierzchni. Do tworzenia materiału służy funkcja:
6 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 6 1/7 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Materiały i oświetlenie 6 Przygotował: mgr inż. Maciej Lasota 1) Wprowadzenie Specyfikacja biblioteki OpenGL rozróżnia trzy
Laboratorium nr 6 1/7 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Materiały i oświetlenie 6 Przygotował: mgr inż. Maciej Lasota 1) Wprowadzenie Specyfikacja biblioteki OpenGL rozróżnia trzy
3 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Światło. W OpenGL można rozróżnić 3 rodzaje światła
 Wizualizacja 3D Światło W OpenGL można rozróżnić 3 rodzaje światła Światło otaczające (ambient light) równomiernie oświetla wszystkie elementy sceny, nie pochodzi z żadnego konkretnego kierunku Światło
Wizualizacja 3D Światło W OpenGL można rozróżnić 3 rodzaje światła Światło otaczające (ambient light) równomiernie oświetla wszystkie elementy sceny, nie pochodzi z żadnego konkretnego kierunku Światło
Elementarne obiekty geometryczne, bufory. Dorota Smorawa
 Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
1. Prymitywy graficzne
 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie
 GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
Światła i rodzaje świateł. Dorota Smorawa
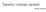 Światła i rodzaje świateł Dorota Smorawa Rodzaje świateł Biblioteka OpenGL posiada trzy podstawowe rodzaje świateł: światło otoczenia, światło rozproszone oraz światło odbite. Dodając oświetlenie na scenie
Światła i rodzaje świateł Dorota Smorawa Rodzaje świateł Biblioteka OpenGL posiada trzy podstawowe rodzaje świateł: światło otoczenia, światło rozproszone oraz światło odbite. Dodając oświetlenie na scenie
Temat: Transformacje 3D
 Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
OpenGL przezroczystość
 OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
Oświetlenie obiektów 3D
 Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Zatem standardowe rysowanie prymitywów wygląda następująco:
 Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Ćwiczenie nr 2 - Rysowanie precyzyjne
 Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
(1,10) (1,7) (5,5) (5,4) (2,1) (0,0) Grafika 3D program POV-Ray - 73 -
 Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Grafika 3D OpenGL część II
 #include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
#include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył
 Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Plan wynikowy, klasa 3 ZSZ
 Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY
 pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
2. Permutacje definicja permutacji definicja liczba permutacji zbioru n-elementowego
 Wymagania dla kl. 3 Zakres podstawowy Temat lekcji Zakres treści Osiągnięcia ucznia 1. RACHUNEK PRAWDOPODOBIEŃSTWA 1. Reguła mnożenia reguła mnożenia ilustracja zbioru wyników doświadczenia za pomocą drzewa
Wymagania dla kl. 3 Zakres podstawowy Temat lekcji Zakres treści Osiągnięcia ucznia 1. RACHUNEK PRAWDOPODOBIEŃSTWA 1. Reguła mnożenia reguła mnożenia ilustracja zbioru wyników doświadczenia za pomocą drzewa
SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD
 Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA.
 Zadanie PUMA Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA. Cały projekt składa się z następujących elementów: 1. Animacja ramion
Zadanie PUMA Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA. Cały projekt składa się z następujących elementów: 1. Animacja ramion
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Laboratorium grafiki komputerowej i animacji. Ćwiczenie IV - Biblioteka OpenGL - transformacje przestrzenne obiektów
 Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
OpenGL oświetlenie. Bogdan Kreczmer. Katedra Cybernetyki i Robotyki Wydziału Elektroniki Politechnika Wrocławska
 OpenGL oświetlenie Bogdan Kreczmer bogdan.kreczmer@pwr.wroc.pl Katedra Cybernetyki i Robotyki Wydziału Elektroniki Politechnika Wrocławska Kurs: Copyright c 2017 Bogdan Kreczmer Niniejszy dokument zawiera
OpenGL oświetlenie Bogdan Kreczmer bogdan.kreczmer@pwr.wroc.pl Katedra Cybernetyki i Robotyki Wydziału Elektroniki Politechnika Wrocławska Kurs: Copyright c 2017 Bogdan Kreczmer Niniejszy dokument zawiera
Janusz Ganczarski. OpenGL Pierwszy program
 Janusz Ganczarski OpenGL Pierwszy program Spis treści Spis treści..................................... 1 1. Pierwszy program.............................. 1 1.1. Rysowanie sceny 3D...........................
Janusz Ganczarski OpenGL Pierwszy program Spis treści Spis treści..................................... 1 1. Pierwszy program.............................. 1 1.1. Rysowanie sceny 3D...........................
Projektowanie systemów zrobotyzowanych
 ZAKŁAD PROJEKTOWANIA TECHNOLOGII Laboratorium Projektowanie systemów zrobotyzowanych Instrukcja 4 Temat: Programowanie trajektorii ruchu Opracował: mgr inż. Arkadiusz Pietrowiak mgr inż. Marcin Wiśniewski
ZAKŁAD PROJEKTOWANIA TECHNOLOGII Laboratorium Projektowanie systemów zrobotyzowanych Instrukcja 4 Temat: Programowanie trajektorii ruchu Opracował: mgr inż. Arkadiusz Pietrowiak mgr inż. Marcin Wiśniewski
Podstawowe zasady modelowania śrub i spoin oraz zestawienie najważniejszych poleceń AutoCAD 3D,
 Podstawowe zasady modelowania śrub i spoin oraz zestawienie najważniejszych poleceń AutoCAD 3D, które są niezbędne przy tworzeniu nieregularnych geometrycznie obiektów Modelowanie 3D śrub i spoin oraz
Podstawowe zasady modelowania śrub i spoin oraz zestawienie najważniejszych poleceń AutoCAD 3D, które są niezbędne przy tworzeniu nieregularnych geometrycznie obiektów Modelowanie 3D śrub i spoin oraz
Plan wykładu. Akcelerator 3D Potok graficzny
 Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
1.2. Ostrosłupy. W tym temacie dowiesz się: jak obliczać długości odcinków zawartych w ostrosłupach, jakie są charakterystyczne kąty w ostrosłupach.
 12 Ostrosłupy W tym temacie dowiesz się: jak obliczać długości odcinków zawartych w ostrosłupach, jakie są charakterystyczne kąty w ostrosłupach Ostrosłup prosty to ostrosłup, który ma wszystkie krawędzie
12 Ostrosłupy W tym temacie dowiesz się: jak obliczać długości odcinków zawartych w ostrosłupach, jakie są charakterystyczne kąty w ostrosłupach Ostrosłup prosty to ostrosłup, który ma wszystkie krawędzie
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
1 Tworzenie brył obrotowych
 1 Tworzenie brył obrotowych Do tworzenia brył obrotowych w programie Blender służą dwa narzędzia: Spin i SpinDup. Idea tworzenia brył obrotowych jest prosta i polega na narysowania połowy przekroju poprzecznego
1 Tworzenie brył obrotowych Do tworzenia brył obrotowych w programie Blender służą dwa narzędzia: Spin i SpinDup. Idea tworzenia brył obrotowych jest prosta i polega na narysowania połowy przekroju poprzecznego
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA Computer Graphics Forma studiów: studia
Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA Computer Graphics Forma studiów: studia
Wymagania kl. 3. Zakres podstawowy i rozszerzony
 Wymagania kl. 3 Zakres podstawowy i rozszerzony Temat lekcji Zakres treści Osiągnięcia ucznia 1. RACHUNEK PRAWDOPODOBIEŃSTWA 1. Reguła mnożenia reguła mnożenia ilustracja zbioru wyników doświadczenia za
Wymagania kl. 3 Zakres podstawowy i rozszerzony Temat lekcji Zakres treści Osiągnięcia ucznia 1. RACHUNEK PRAWDOPODOBIEŃSTWA 1. Reguła mnożenia reguła mnożenia ilustracja zbioru wyników doświadczenia za
Ćwiczenia nr 7. TEMATYKA: Krzywe Bézier a
 TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
Wymagania edukacyjne z matematyki dla klasy III a,b liceum (poziom podstawowy) rok szkolny 2018/2019
 Wymagania edukacyjne z matematyki dla klasy III a,b liceum (poziom podstawowy) rok szkolny 2018/2019 Oznaczenia: wymagania konieczne, P wymagania podstawowe, R wymagania rozszerzające, D wymagania dopełniające,
Wymagania edukacyjne z matematyki dla klasy III a,b liceum (poziom podstawowy) rok szkolny 2018/2019 Oznaczenia: wymagania konieczne, P wymagania podstawowe, R wymagania rozszerzające, D wymagania dopełniające,
Rys. 1. Brama przesuwna do wykonania na zajęciach
 Programowanie robotów off-line 2 Kuka.Sim Pro Import komponentów do środowiska Kuka.Sim Pro i modelowanie chwytaka. Cel ćwiczenia: Wypracowanie umiejętności dodawania własnych komponentów do programu oraz
Programowanie robotów off-line 2 Kuka.Sim Pro Import komponentów do środowiska Kuka.Sim Pro i modelowanie chwytaka. Cel ćwiczenia: Wypracowanie umiejętności dodawania własnych komponentów do programu oraz
Laboratorium nr 10. Temat: Funkcje cz.2.
 Zakres laboratorium: Laboratorium nr 10 Temat: Funkcje cz.2. przeciążanie nazw funkcji argumenty domyślne funkcji przekazywanie danych do funkcji przez wartość, wskaźnik i referencję przekazywanie tablic
Zakres laboratorium: Laboratorium nr 10 Temat: Funkcje cz.2. przeciążanie nazw funkcji argumenty domyślne funkcji przekazywanie danych do funkcji przez wartość, wskaźnik i referencję przekazywanie tablic
Graniastosłupy mają dwie podstawy, a ich ściany boczne mają kształt prostokątów.
 GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
11.3 Definiowanie granic obszaru przeznaczonego do kreskowania
 Auto CAD 14 11-1 11. Kreskowanie. 11.1 Wstęp Aby wywołać polecenie BHATCH, wybierz HATCH z paska narzędzi Draw. Po wywołaniu polecenia wyświetlane jest okno narzędziowe Boundary Hatch. Żeby narysować obiekt
Auto CAD 14 11-1 11. Kreskowanie. 11.1 Wstęp Aby wywołać polecenie BHATCH, wybierz HATCH z paska narzędzi Draw. Po wywołaniu polecenia wyświetlane jest okno narzędziowe Boundary Hatch. Żeby narysować obiekt
Wymagania na poszczególne oceny szkolne z. matematyki. dla uczniów klasy IIIa i IIIb. Gimnazjum im. Jana Pawła II w Mętowie. w roku szkolnym 2015/2016
 Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
SPRAWDZIAN NR 1. Suma długości krawędzi prostopadłościanu o wymiarach 4 cm x 6 cm x 10 cm jest równa. A. 20 cm B. 40 cm C. 60 cm D.
 SPRAWDZIAN NR 1 ARTUR ANTAS IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Zaznacz poprawną odpowiedź. Który wielokąt jest podstawą ostrosłupa o 6 wierzchołkach? A. Trójkąt. B. Czworokąt. C. Pięciokąt. D. Sześciokąt.
SPRAWDZIAN NR 1 ARTUR ANTAS IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Zaznacz poprawną odpowiedź. Który wielokąt jest podstawą ostrosłupa o 6 wierzchołkach? A. Trójkąt. B. Czworokąt. C. Pięciokąt. D. Sześciokąt.
Kryteria oceniania z matematyki Klasa III poziom podstawowy
 Kryteria oceniania z matematyki Klasa III poziom podstawowy Potęgi Zakres Dopuszczający Dostateczny Dobry Bardzo dobry oblicza potęgi o wykładnikach wymiernych; zna prawa działań na potęgach i potrafi
Kryteria oceniania z matematyki Klasa III poziom podstawowy Potęgi Zakres Dopuszczający Dostateczny Dobry Bardzo dobry oblicza potęgi o wykładnikach wymiernych; zna prawa działań na potęgach i potrafi
Systemy wirtualnej rzeczywistości. Komponenty i serwisy
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Plan wynikowy klasa 3. Zakres podstawowy
 Plan wynikowy klasa 3 Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające. RACHUNE PRAWDOPODOBIEŃSTWA
Plan wynikowy klasa 3 Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające. RACHUNE PRAWDOPODOBIEŃSTWA
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2013/2014
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 013/014 Kierunek studiów: Informatyka Stosowana Forma
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 013/014 Kierunek studiów: Informatyka Stosowana Forma
Ćwiczenie nr 5 Zautomatyzowane tworzenie dokumentacji
 Ćwiczenie nr 5 Zautomatyzowane tworzenie dokumentacji technicznej Od wersji 2013 programu AutoCAD istnieje możliwość wykonywania pełnej dokumentacji technicznej dla obiektów 3D tj. wykonywanie rzutu bazowego
Ćwiczenie nr 5 Zautomatyzowane tworzenie dokumentacji technicznej Od wersji 2013 programu AutoCAD istnieje możliwość wykonywania pełnej dokumentacji technicznej dla obiektów 3D tj. wykonywanie rzutu bazowego
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Pochylenia, Lustro. Modelowanie ramienia. Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części)
 Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
Ćwiczenie nr 6 Temat: BADANIE ŚWIATEŁ DO JAZDY DZIENNEJ
 60-965 Poznań Grupa: Elektrotechnika, sem 3., Podstawy Techniki Świetlnej Laboratorium wersja z dn. 03.11.2015 Ćwiczenie nr 6 Temat: BADANIE ŚWIATEŁ DO JAZDY DZIENNEJ Opracowanie wykonano na podstawie
60-965 Poznań Grupa: Elektrotechnika, sem 3., Podstawy Techniki Świetlnej Laboratorium wersja z dn. 03.11.2015 Ćwiczenie nr 6 Temat: BADANIE ŚWIATEŁ DO JAZDY DZIENNEJ Opracowanie wykonano na podstawie
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Zadania z podstaw programowania obiektowego
 Zadania z podstaw programowania obiektowego 1. Napisać klasę Lista, której zadaniem będzie przechowywanie listy liczb całkowitych. Klasa ta ma mieć następujące pola prywatne: int* liczby; tablica, w której
Zadania z podstaw programowania obiektowego 1. Napisać klasę Lista, której zadaniem będzie przechowywanie listy liczb całkowitych. Klasa ta ma mieć następujące pola prywatne: int* liczby; tablica, w której
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA I WIZUALIZACJA Computer
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium GRAFIKA KOMPUTEROWA I WIZUALIZACJA Computer
I. Potęgi. Logarytmy. Funkcja wykładnicza.
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ LICEUM OGÓLNOKSZTAŁCĄCEGO ZAKRES PODSTAWOWY I. Potęgi. Logarytmy. Funkcja wykładnicza. dobrą, bardzo - oblicza potęgi o wykładnikach wymiernych; - zna
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ LICEUM OGÓLNOKSZTAŁCĄCEGO ZAKRES PODSTAWOWY I. Potęgi. Logarytmy. Funkcja wykładnicza. dobrą, bardzo - oblicza potęgi o wykładnikach wymiernych; - zna
Agnieszka Kamińska, Dorota Ponczek. MATeMAtyka 3. Szczegółowe wymagania edukacyjne z matematyki w klasie trzeciej.
 Agnieszka amińska, Dorota Ponczek MATeMAtyka 3 Szczegółowe wymagania edukacyjne z matematyki w klasie trzeciej Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające;
Agnieszka amińska, Dorota Ponczek MATeMAtyka 3 Szczegółowe wymagania edukacyjne z matematyki w klasie trzeciej Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające;
R o z w i ą z a n i e Przy zastosowaniu sposobu analitycznego należy wyznaczyć składowe wypadkowej P x i P y
 Przykład 1 Dane są trzy siły: P 1 = 3i + 4j, P 2 = 2i 5j, P 3 = 7i + 3j (składowe sił wyrażone są w niutonach), przecinające się w punkcie A (1, 2). Wyznaczyć wektor wypadkowej i jej wartość oraz kąt α
Przykład 1 Dane są trzy siły: P 1 = 3i + 4j, P 2 = 2i 5j, P 3 = 7i + 3j (składowe sił wyrażone są w niutonach), przecinające się w punkcie A (1, 2). Wyznaczyć wektor wypadkowej i jej wartość oraz kąt α
Skrypt 18. Bryły. 2. Inne graniastosłupy proste rozpoznawanie, opis, rysowanie siatek, brył
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 18 Bryły 1. Prostopadłościan i sześcian rozpoznawanie,
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 18 Bryły 1. Prostopadłościan i sześcian rozpoznawanie,
Projektowanie graficzne. Wykład 2. Open Office Draw
 Projektowanie graficzne Wykład 2 Open Office Draw Opis programu OpenOffice Draw OpenOffice Draw umożliwia tworzenie prostych oraz złożonych rysunków. Posiada możliwość eksportowania rysunków do wielu różnych
Projektowanie graficzne Wykład 2 Open Office Draw Opis programu OpenOffice Draw OpenOffice Draw umożliwia tworzenie prostych oraz złożonych rysunków. Posiada możliwość eksportowania rysunków do wielu różnych
Agnieszka Kamińska, Dorota Ponczek. MATeMAtyka 3. Plan wynikowy. Zakres podstawowy
 Agnieszka amińska, Dorota Ponczek MATeMAtyka 3 Plan wynikowy Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania
Agnieszka amińska, Dorota Ponczek MATeMAtyka 3 Plan wynikowy Zakres podstawowy Oznaczenia: wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania
Temat: WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
 STUDIA NIESTACJONARNE I STOPNIA, wersja z dn. 15.10.018 KIERUNEK ELEKTROTECHNIKA, SEM.5 Podstawy Techniki Świetlnej Laboratorium Ćwiczenie nr 4 Temat: WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
STUDIA NIESTACJONARNE I STOPNIA, wersja z dn. 15.10.018 KIERUNEK ELEKTROTECHNIKA, SEM.5 Podstawy Techniki Świetlnej Laboratorium Ćwiczenie nr 4 Temat: WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
OpenGL Światło (cieniowanie)
 OpenGL Światło (cieniowanie) 1. Oświetlenie włączanie/wyłączanie glenable(gl_lighting); - włączenie mechanizmu oświetlenia gldisable(gl_lighting); - wyłączenie mechanizmu oświetlenia glenable(gl_light0);
OpenGL Światło (cieniowanie) 1. Oświetlenie włączanie/wyłączanie glenable(gl_lighting); - włączenie mechanizmu oświetlenia gldisable(gl_lighting); - wyłączenie mechanizmu oświetlenia glenable(gl_light0);
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library. OpenGL składa się z
 Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library OpenGL składa się z teoretycznego modelu grafiki 3D, zestawu typów i funkcji obsługujących różne cechy tego modelu. Funkcje OpenGL
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library OpenGL składa się z teoretycznego modelu grafiki 3D, zestawu typów i funkcji obsługujących różne cechy tego modelu. Funkcje OpenGL
Ćwiczenie nr 3 Edycja modeli bryłowych
 Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
8 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 8 1/6 Grafika Komputerowa Instrukcja laboratoryjna Temat: Listy wyświetlania i tablice wierzchołków 8 Przygotował: mgr inż. Maciej Lasota 1) Listy wyświetlania Listy wyświetlania (ang.
Laboratorium nr 8 1/6 Grafika Komputerowa Instrukcja laboratoryjna Temat: Listy wyświetlania i tablice wierzchołków 8 Przygotował: mgr inż. Maciej Lasota 1) Listy wyświetlania Listy wyświetlania (ang.
SPRAWDZIAN NR Oceń prawdziwość zdania. 2. Zaznacz poprawną odpowiedź. 3. Na rysunkach przedstawiono dwie bryły. Nazwij każdą z nich.
 SPRAWDZIAN NR 1 WIESŁAWA MALINOWSKA IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Oceń prawdziwość zdania. Zaznacz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe. A. Rysunek nie przedstawia siatki ostrosłupa
SPRAWDZIAN NR 1 WIESŁAWA MALINOWSKA IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Oceń prawdziwość zdania. Zaznacz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe. A. Rysunek nie przedstawia siatki ostrosłupa
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Katalog wymagań programowych na poszczególne stopnie szkolne Matematyka. Poznać, zrozumieć Kształcenie w zakresie rozszerzonym. Klasa 4 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego
Katalog wymagań programowych na poszczególne stopnie szkolne Matematyka. Poznać, zrozumieć Kształcenie w zakresie rozszerzonym. Klasa 4 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego
KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM
 KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM POTĘGI I PIERWIASTKI - pojęcie potęgi o wykładniku naturalnym; - wzór na mnożenie i dzielenie potęg o tych samych podstawach; - wzór na potęgowanie
KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM POTĘGI I PIERWIASTKI - pojęcie potęgi o wykładniku naturalnym; - wzór na mnożenie i dzielenie potęg o tych samych podstawach; - wzór na potęgowanie
Krzyżówka oraz hasła do krzyżówki. Kalina R., Przewodnik po matematyce dla klas VII-VIII, część IV, SENS, Poznań 1997, s.20-22.
 Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
1. Potęgi. Logarytmy. Funkcja wykładnicza
 1. Potęgi. Logarytmy. Funkcja wykładnicza Tematyka zajęć: WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM PODSTAWOWY Potęga o wykładniku rzeczywistym powtórzenie Funkcja wykładnicza i jej własności
1. Potęgi. Logarytmy. Funkcja wykładnicza Tematyka zajęć: WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM PODSTAWOWY Potęga o wykładniku rzeczywistym powtórzenie Funkcja wykładnicza i jej własności
Dziedziczenie. Zadanie 1
 Dziedziczenie Zadanie 1 Napisz klasę KolorowyPunkt, która dziedziczy po klasie Punkt a dodatkowo przechowuje informacje o kolorze. Uzupełnij ją o metody umożliwiające pobieranie i ustawianie koloru. Pamiętaj
Dziedziczenie Zadanie 1 Napisz klasę KolorowyPunkt, która dziedziczy po klasie Punkt a dodatkowo przechowuje informacje o kolorze. Uzupełnij ją o metody umożliwiające pobieranie i ustawianie koloru. Pamiętaj
Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy)
 Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy) klasa 3. PAZDRO Plan jest wykazem wiadomości i umiejętności, jakie powinien mieć uczeń ubiegający się o określone oceny na poszczególnych etapach edukacji
Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy) klasa 3. PAZDRO Plan jest wykazem wiadomości i umiejętności, jakie powinien mieć uczeń ubiegający się o określone oceny na poszczególnych etapach edukacji
OpenGL Światło (cieniowanie)
 OpenGL Światło (cieniowanie) 1. Oświetlenie włączanie/wyłączanie glenable(gl_lighting); - włączenie mechanizmu oświetlenia gldisable(gl_lighting); - wyłączenie mechanizmu oświetlenia glenable(gl_light0);
OpenGL Światło (cieniowanie) 1. Oświetlenie włączanie/wyłączanie glenable(gl_lighting); - włączenie mechanizmu oświetlenia gldisable(gl_lighting); - wyłączenie mechanizmu oświetlenia glenable(gl_light0);
DesignCAD 3D Max 24.0 PL
 DesignCAD 3D Max 24.0 PL Październik 2014 DesignCAD 3D Max 24.0 PL zawiera następujące ulepszenia i poprawki: Nowe funkcje: Tryb RedSDK jest teraz dostępny w widoku 3D i jest w pełni obsługiwany przez
DesignCAD 3D Max 24.0 PL Październik 2014 DesignCAD 3D Max 24.0 PL zawiera następujące ulepszenia i poprawki: Nowe funkcje: Tryb RedSDK jest teraz dostępny w widoku 3D i jest w pełni obsługiwany przez
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: moduł specjalności obowiązkowy: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU GRAFICZNE MODELOWANIE
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: moduł specjalności obowiązkowy: Inżynieria oprogramowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU GRAFICZNE MODELOWANIE
Rok akademicki: 2017/2018 Kod: JFM s Punkty ECTS: 7. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Grafika komputerowa 1 Rok akademicki: 2017/2018 Kod: JFM-1-507-s Punkty ECTS: 7 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
rgbf<składowa_r,składowa_g,składowa_b,filter>. Dla parametru filter przyjmij kolejno wartości: 0.60, 0.70, 0.80, 0.90, 1.00, np.:
 Temat 2: Przezroczystość. Prostopadłościan, walec i stożek. Przesuwanie i skalowanie obiektów. Omówimy teraz przezroczystość obiektów związaną z ich kolorem (lub teksturą). Za przezroczystość odpowiadają
Temat 2: Przezroczystość. Prostopadłościan, walec i stożek. Przesuwanie i skalowanie obiektów. Omówimy teraz przezroczystość obiektów związaną z ich kolorem (lub teksturą). Za przezroczystość odpowiadają
ZAKRES PODSTAWOWY CZĘŚĆ II. Wyrażenia wymierne
 CZĘŚĆ II ZAKRES PODSTAWOWY Wyrażenia wymierne Temat: Wielomiany-przypomnienie i poszerzenie wiadomości. (2 godz.) znać i rozumieć pojęcie jednomianu (2) znać i rozumieć pojęcie wielomianu stopnia n (2)
CZĘŚĆ II ZAKRES PODSTAWOWY Wyrażenia wymierne Temat: Wielomiany-przypomnienie i poszerzenie wiadomości. (2 godz.) znać i rozumieć pojęcie jednomianu (2) znać i rozumieć pojęcie wielomianu stopnia n (2)
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
OpenGL teksturowanie
 OpenGL teksturowanie Teksturowanie polega na pokrywaniu wielokątów obrazami (plikami graficznymi) Umożliwia znaczące zwiększenie realizmu sceny przy niewielkim zwiększeniu nakładu obliczeniowego Rozwój
OpenGL teksturowanie Teksturowanie polega na pokrywaniu wielokątów obrazami (plikami graficznymi) Umożliwia znaczące zwiększenie realizmu sceny przy niewielkim zwiększeniu nakładu obliczeniowego Rozwój
Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA
 Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA Polecenie 3DWYRÓWNAJ umożliwia precyzyjne przemieszczanie bryły 3D w przestrzeni projektowej Przykład poniżej pokazuje jak z pomocą poleceń - 3DWYRÓWNAJ
Przykład zastosowania poleceń 3DWYRÓWNAJ i RÓŻNICA Polecenie 3DWYRÓWNAJ umożliwia precyzyjne przemieszczanie bryły 3D w przestrzeni projektowej Przykład poniżej pokazuje jak z pomocą poleceń - 3DWYRÓWNAJ
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI ROK SZKOLNY 2018/2019 POZIOM PODSTAWOWY I ROZSZERZONY KLASA 3 UWAGI: 1. Zakłada się,
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI ROK SZKOLNY 2018/2019 POZIOM PODSTAWOWY I ROZSZERZONY KLASA 3 UWAGI: 1. Zakłada się,
WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc
 WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc 1, Ciągi zna definicję ciągu (ciągu liczbowego); potrafi wyznaczyć dowolny wyraz ciągu liczbowego określonego wzorem ogólnym;
WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc 1, Ciągi zna definicję ciągu (ciągu liczbowego); potrafi wyznaczyć dowolny wyraz ciągu liczbowego określonego wzorem ogólnym;
Zad. 6: Sterowanie robotem mobilnym
 Zad. 6: Sterowanie robotem mobilnym 1 Cel ćwiczenia Utrwalenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie dziedziczenia
Zad. 6: Sterowanie robotem mobilnym 1 Cel ćwiczenia Utrwalenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie dziedziczenia
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
9. Podstawowe narzędzia matematyczne analiz przestrzennych
 Waldemar Izdebski - Wykłady z przedmiotu SIT 75 9. odstawowe narzędzia matematyczne analiz przestrzennych Niniejszy rozdział służy ogólnemu przedstawieniu metod matematycznych wykorzystywanych w zagadnieniu
Waldemar Izdebski - Wykłady z przedmiotu SIT 75 9. odstawowe narzędzia matematyczne analiz przestrzennych Niniejszy rozdział służy ogólnemu przedstawieniu metod matematycznych wykorzystywanych w zagadnieniu
Informatyka I stopień (I stopień / II stopień) Ogólnoakademicki (ogólno akademicki / praktyczny)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod Nazwa Nazwa w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Programy grafiki rastrowej,
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod Nazwa Nazwa w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Programy grafiki rastrowej,
Stereometria bryły. Wielościany. Wielościany foremne
 Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
ANDROID. OpenGL ES 1.0. Tomasz Dzieniak
 ANDROID OpenGL ES 1.0 Tomasz Dzieniak Wymagania JRE & JDK 5.0 + IDE (Eclipse 3.3.1 + / Netbeans 7.0.0 +) Android SDK Starter Package Android SDK Components Pierwszy program Project name: OpenGL Build Target:
ANDROID OpenGL ES 1.0 Tomasz Dzieniak Wymagania JRE & JDK 5.0 + IDE (Eclipse 3.3.1 + / Netbeans 7.0.0 +) Android SDK Starter Package Android SDK Components Pierwszy program Project name: OpenGL Build Target:
KGGiBM GRAFIKA INŻYNIERSKA Rok III, sem. VI, sem IV SN WILiŚ Rok akademicki 2011/2012
 Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Wyobraźnia w budowie Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego
 Harmonogram szkolenia "AutoCAD projektowanie" - II poziom - grupa ACP II - 8 Czas trwania szkolenia - 13.01.2013 1.02.2013 AutoCAD projektowanie (80 godzin) - dr inż. Paweł Węgierek Data Godziny temat
Harmonogram szkolenia "AutoCAD projektowanie" - II poziom - grupa ACP II - 8 Czas trwania szkolenia - 13.01.2013 1.02.2013 AutoCAD projektowanie (80 godzin) - dr inż. Paweł Węgierek Data Godziny temat
Gry komputerowe, Informatyka N1, III Rok
 Oświetlenie Potok renderowania. Techniki oświetlenia i cieniowania. http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok POTOK RENDEROWANIA W grafice realistycznej stosuje się zwykle podejścia
Oświetlenie Potok renderowania. Techniki oświetlenia i cieniowania. http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok POTOK RENDEROWANIA W grafice realistycznej stosuje się zwykle podejścia
GEOPLAN Z SIATKĄ TRÓJKĄTNĄ
 TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
Bartosz Bazyluk POTOK RENDEROWANIA Etapy renderowania w grafice czasu rzeczywistego. Grafika Komputerowa, Informatyka, I Rok
 POTOK RENDEROWANIA Etapy renderowania w grafice czasu rzeczywistego. http://bazyluk.net/zpsb Grafika Komputerowa, Informatyka, I Rok POTOK RENDEROWANIA W grafice realistycznej stosuje się zwykle podejścia
POTOK RENDEROWANIA Etapy renderowania w grafice czasu rzeczywistego. http://bazyluk.net/zpsb Grafika Komputerowa, Informatyka, I Rok POTOK RENDEROWANIA W grafice realistycznej stosuje się zwykle podejścia
