Zajęcia: VBA TEMAT: VBA PROCEDURY NUMERYCZNE Metoda bisekcji i metoda trapezów
|
|
|
- Wiktor Skowroński
- 9 lat temu
- Przeglądów:
Transkrypt
1 Zajęcia: VBA TEMAT: VBA PROCEDURY NUMERYCZNE Metoda bisekcji i metoda trapezów W ramach zajęć oprogramujemy jedną, wybraną metodę numeryczną: metodę bisekcji numerycznego rozwiązywania równania nieliniowego lub metodę trapezów numerycznego obliczania całki oznaczonej. Najpierw rozwiążemy wybrane zagadnienie w środowisku Visual Basic, a następnie napisaną procedurę przeniesiemy do Excela wykorzystując możliwość powiązania kodu programu z komórkami arkusza w celu wprowadzania danych i prezentacji wyników obliczeń. Zadania do wykonania (jedno do wyboru / w zależności od grupy): 1. Napisać w Visual Basic program, w którym będzie można numerycznie rozwiązać wybrane równanie nieliniowe, czyli znaleźć przybliżoną wartość pierwiastka równania: f(x)=0. Do rozwiązania zastosować metodę bisekcji (podziału). Następnie przenieść napisaną procedurę do Excela i dokonać takich zmian w kodzie, aby umożliwić wprowadzanie danych i wyprowadzanie wyników w arkuszu Excela. 2. Napisać w Visual Basic program, w którym będzie można numerycznie obliczyć całkę oznaczoną z wybranej funkcji w zadanych granicach. Do rozwiązania zastosować metodę trapezów. Następnie przenieść napisaną procedurę do Excela i dokonać takich zmian w kodzie, aby umożliwić wprowadzanie danych i wyprowadzanie wyników w arkuszu Excela. Poznawane elementy języka: Wykonanie zadań pozwala na wykorzystanie następujących elementów języka Visual Basic: Zastosowanie pętli Zastosowanie instrukcji warunkowych Wykorzystanie odwołań do obiektów arkusza Excel Zad.J1. Numeryczne rozwiązywanie równania nieliniowego metodą bisekcji (połowienia). Metoda bisekcji (połowienia) jest jedną z najprostszych metod numerycznego rozwiązywania algebraicznych równań nieliniowych, czyli znajdowania przybliżonej wartości pierwiastka równania: f(x)=0 O funkcji f(x) zakłada się, że jest ciągła na przedziale domkniętym <x A ; x B >, wewnątrz którego znajduje się dokładnie jeden, wyizolowany pierwiastek i, na którego końcach wartości funkcji f(x) mają przeciwne znaki (czyli f(x A )f(x B )<0 ). W metodzie bisekcji, aby znaleźć ten pierwiastek, dzielimy przedział <x A ; x B > na połowy punktem 1
2 x C = (x A + x B )/2 Jeżeli f(x C ) = 0, to x C jest szukanym pierwiastkiem, jeśli zaś f(x C ) <> 0, to z otrzymanych dwóch przedziałów <x A ; x C > oraz <x C ; x B >, wybieramy do dalszej analizy ten, na końcach którego funkcja f(x) ma przeciwne znaki. To znaczy, jeśli f(x A )f(x C )<0 to wybieramy przedział <x A ; x C >, zatem wartość x C podstawiamy w miejsce x B, w przeciwnym przypadku wartość x C podstawiamy w miejsce x A. Z kolei ten nowo wybrany przedział dzielimy na połowy wyznaczając nowy punkt x C, ponownie badamy wartość funkcji f(x) w punkcie x C i znaki funkcji f(x) na końcach przedziałów itd. W wyniku takiego postępowania po pewnej liczbie kroków albo otrzymany pierwiastek dokładny, tzn. dla pewnego n otrzymamy f(xc)=0, albo ciąg przedziałów takich że : f(x i A)f(x i B)<0. Punkty x i A oraz x i B są odpowiednio początkiem i końcem przedziału w i-tej iteracji, a jego długość wynosi x i A - x i B =(x B - x A )/2 i. Ponieważ lewe końce ciągu przedziałów tworzą ciąg niemalejący i ograniczony z góry, a prawe końce ciąg nierosnący i ograniczony z dołu więc z powyższego równania wynika, że istnieje ich wspólna granica i jest nią pierwiastek rozwiązywanego równania. Ostatnia obliczona wartość x C może stanowić jego przybliżenie. Jako kryterium zakończenia obliczeń można przyjąć wykonanie maksymalnej dopuszczalnej liczby iteracji, MaxIter, lub otrzymanie przedziału < x i A ; x i B > o długości mniejszej od zadanej dokładności epsilon, tzn. x i A - x i B < eps. 2
3 Pomocą przy wykonaniu tego zadania może być następujący projekt formularza: 3
4 oraz schemat blokowy: 4
5 Zad.J2. Przeniesienie procedury "bisekcja" z Visual Basic do Visual Basic for Applications w MS Excel. Zadanie polega na przeniesieniu procedury numerycznej obliczającej pierwiastek równania nieliniowego metodą bisekcji napisanej w Visual Basic do środowiska MS Excel i wykorzystaniu jej posługując się danymi pochodzącymi z odwołań bezpośrednio do komórek arkusza. Zadanie zostanie wykonane w trzech etapach, w każdym z nich wprowadzone będą uogólnienia etapu poprzedniego. Etap 1. Przeniesienie procedury numerycznej i wykorzystanie jej tylko dla jednej, ustalonej funkcji np. Sin(x). Etap 2. Umożliwienie wprowadzania różnych funkcji jako napisów w wybranej komórce arkusza. Etap 3. Wykorzystanie obiektu ComboBox na arkuszu do wprowadzenia nazwy funkcji. Uwaga: Aby zrobić to zadanie trzeba wiedzieć jak odwoływać się w kodzie programu napisanego w Visual Basic for Applications do obiektów arkusza kalkulacyjnego Excel (patrz zajęcia 10 i 11). Dla naszych potrzeb wystarczy wiedzieć, że w Visual Basic for Applications w MS Excel do obiektów Excela takich jak skoroszyt, arkusz, komórka czy zakres można się odwoływać podając odpowiedni indeks (numer) tego elementu z kolekcji, np. Worksheets(1) odnosi się do pierwszego arkusza roboczego w skoroszycie. Innym sposobem jest odwołanie się do jego nazwy, np. Worksheets( Arkusz1 )odnosi się do arkusza roboczego o nazwie Arkusz1. Podobnie dla obiektów typu Range, które pozwalają odwołać się do poszczególnych komórek, można stosować odwołania po adresie, np. Worksheets(1).Range( A9 ) wskazujące odwołanie do komórki o adresie A9 z pierwszego arkusza roboczego, albo po nazwach zakresów zdefiniowanych uprzednio w arkuszu. Np. jeśli w arkuszu zdefiniowano nazwę lewy odnoszącą się do komórki o adresie $A$9 to odwołanie z poprzedniego przykładu może wyglądać następująco: Worksheets(1).Range( lewy ). 5
6 Etap 1. Przeniesienie procedury numerycznej i wykorzystanie jej tylko dla jednej, ustalonej funkcji np. Sin(x). W tym etapie, dla uproszczenia zakłada się, że procedura numerycznego wyznaczania pierwiastka będzie działała tylko dla jednej wybranej funkcji Sin(x). Otwórz Excel i przygotuj arkusz, w którym podawać będziesz dane potrzebne do procedury numerycznej oraz zarezerwujesz miejsce, gdzie wyświetlany będzie wynik. Przykład takiego arkusza może wyglądać tak: Otwórz edytor Visual Basic w Excelu (z menu Narzędzia wybrać Makro a następnie Edytor Visual Basic lub bezpośrednio wcisnąć Alt+F11). Będąc już w edytorze wstaw moduł (z menu Wstaw wybrać Moduł). Skopiuj teraz procedurę Oblicz() oraz funkcję funk(x) z projektu, który wykonałeś w Visual Basicu w zadaniu poprzednim (J1) do wstawionego modułu. Dokonaj zmian w kodzie programu w taki sposób, aby odwołania dotyczyły komórek arkusza, a nie obiektów na formularzu. Ogranicz rozpatrywane funkcje w funk(x) tylko do funkcji Sin(x). Umieść na arkuszu Przycisk Polecenia, za pomocą którego będziesz wywoływać napisaną procedurę (makro). 6
7 Etap 2. Umożliwienie wykonania obliczeń dla różnych funkcji wprowadzanych jako napisy w wybranej komórce arkusza. W tym etapie rozszerzymy nasz program o możliwość wykonania obliczeń dla różnych funkcji, których nazwy będziemy podawać w odpowiedniej komórce arkusza. Dokonaj zmian w kodzie funkcji funk(x) tak, aby uwzględniała napisy znajdujące się w arkuszu w komórce zawierającej nazwę obliczanej funkcji. Etap 3. Wykorzystanie obiektu Pole kombi (ComboBox) do wybierania nazwy funkcji. W tym etapie ułatwimy wybieranie nazwy funkcji, dla której wykonamy obliczenia, wykorzystując do tego celu kontrolkę ComboBox. Excel pozwala na umieszczanie na arkuszu różnych kontrolek (formantów), które znamy już z tworzenia formularzy w Visual Basic. Kontrolowanie tych obiektów jest co prawda bardziej ograniczone, niż ma to miejsce w Visual Basic, nie mniej jednak kontrolki te w pewnych przypadkach usprawniają użytkowanie Excela. W naszym ćwiczeniu wykorzystaliśmy już kontrolkę Przycisk Polecenia do uruchamiania procedury Oblicz. Teraz wykorzystamy kontrolkę Pole kombi czyli ComboBox. Zad.J3. Numeryczne obliczanie całki oznaczonej metodą trapezów. Numeryczne obliczanie całek oznaczonych polega na przybliżeniu wartości całki za pomocą ważonej sumy wartości funkcji f(x) w wybranych węzłach, x i, pomnożonych przez odpowiednie wagi, w i,: Zarówno dobór węzłów, jak i wag zależy od konkretnej metody. Metoda trapezów, numerycznego obliczania wartości całki oznaczonej danej funkcji ograniczonej na przedziale (a; b), polega na podzieleniu pola podcałkowego na n trapezów, gdzie podstawy są równoległe do osi OY, natomiast wysokości trapezów są równoległe do osi OX (patrz rysunek), a następnie na zsumowaniu pól tych trapezów. 7
8 Przedział całkowania dzielimy na dowolna liczbę równych podprzedziałów. Przybliżeniem wartości całki będzie suma pól trapezów powstałych po podzieleniu przedziału całkowania. Pola trapezów można policzyć z wzoru S i =(y i-1 +y i )*h/2 gdzie y i-1 i y i to wartości funkcji na końcach przedziału (x i-1 ; x i ), natomiast h = x i x i-1. Przy założeniu, że przedział całkowania dzielimy na n równych podprzedziałów wartość h można obliczyć ze wzoru: h=(b-a)/n gdzie a i b to końce przedziału całkowania. Im liczba podziałów n jest większa tym wynik jest dokładniejszy. Aby uprościć sumowanie, można zauważyć, że Wynik = S 1 +S S n = = (y 0 +y 1 )*h/2 +(y 1 +y 2 )*h/ (y n-1 +y n )*h/2 = = (y 0 /2 + y 1 + y y n-1 +y n /2)*h = = ((y 0 + y n )/2 + y 1 + y y n-1 )*h 8
9 Pomocą przy wykonaniu tego zadania może być następujący projekt formularza: 9
10 oraz schemat blokowy: 10
11 Zad.J4. Przeniesienie procedury "trapezy" z Visual Basic do Visual Basic for Applications w MS Excel. Zadanie polega na przeniesieniu procedury numerycznej obliczającej całkę oznaczoną metodą trapezów napisanej w Visual Basic do środowiska MS Excel i wykorzystaniu jej posługując się danymi pochodzącymi z odwołań bezpośrednio do komórek arkusza. Zadanie zostanie wykonane w trzech etapach, w każdym z nich wprowadzone będą uogólnienia etapu poprzedniego. Etap 1. Przeniesienie procedury numerycznej i wykorzystanie jej tylko dla jednej, ustalonej funkcji np. Sin(x). Etap 2. Umożliwienie wprowadzania różnych funkcji jako napisów w wybranej komórce arkusza. Etap 3. Wykorzystanie obiektu ComboBox na arkuszu do wprowadzenia nazwy funkcji. Uwaga: Aby zrobić to zadanie trzeba wiedzieć jak odwoływać się w kodzie programu napisanego w Visual Basic for Applications do obiektów arkusza kalkulacyjnego Excel (patrz zajęcia 10 i 11). Dla naszych potrzeb wystarczy wiedzieć, że w Visual Basic for Applications w MS Excel do obiektów Excela takich jak skoroszyt, arkusz, komórka czy zakres można się odwoływać podając odpowiedni indeks (numer) tego elementu z kolekcji, np. Worksheets(1) odnosi się do pierwszego arkusza roboczego w skoroszycie. Innym sposobem jest odwołanie się do jego nazwy, np. Worksheets( Arkusz1 )odnosi się do arkusza roboczego o nazwie Arkusz1. Podobnie dla obiektów typu Range, które pozwalają odwołać się do poszczególnych komórek, można stosować odwołania po adresie, np. Worksheets(1).Range( A9 ) wskazujące odwołanie do komórki o adresie A9 z pierwszego arkusza roboczego, albo po nazwach zakresów zdefiniowanych uprzednio w arkuszu. Np. jeśli w arkuszu zdefiniowano nazwę lewy odnoszącą się do komórki o adresie $A$9 to odwołanie z poprzedniego przykładu może wyglądać następująco: Worksheets(1).Range( lewy ). Etap 1. Przeniesienie procedury numerycznej i wykorzystanie jej tylko dla jednej, ustalonej funkcji np. Sin(x). W tym etapie, dla uproszczenia zakłada się, że procedura całkowania numerycznego będzie działała tylko dla jednej wybranej funkcji Sin(x). Otwórz Excel i przygotuj arkusz, w którym podawać będziesz dane potrzebne do procedury numerycznej oraz zarezerwujesz miejsce, gdzie wyświetlany będzie wynik. Przykład takiego arkusza może wyglądać tak: 11
12 Otwórz edytor Visual Basic w Excelu (z menu Narzędzia wybrać Makro a następnie Edytor Visual Basic lub bezpośrednio wcisnąć Alt+F11). Będąc już w edytorze wstaw moduł (z menu Wstaw wybrać Moduł). Skopiuj teraz procedurę Oblicz() oraz funkcję funk(x) z projektu, który wykonałeś w Visual Basicu w zadaniu poprzednim (J1) do wstawionego modułu. Dokonaj zmian w kodzie programu w taki sposób, aby odwołania dotyczyły komórek arkusza, a nie obiektów na formularzu. Ogranicz rozpatrywane funkcje w funk(x) tylko do funkcji Sin(x). Umieść na arkuszu Przycisk Polecenia, za pomocą którego będziesz wywoływać napisaną procedurę (makro). Etap 2. Umożliwienie wykonania obliczeń dla różnych funkcji wprowadzanych jako napisy w wybranej komórce arkusza. W tym etapie rozszerzymy nasz program o możliwość wykonania obliczeń dla różnych funkcji, których nazwy będziemy podawać w odpowiedniej komórce arkusza. Dokonaj zmian w kodzie funkcji funk(x) tak, aby uwzględniała napisy znajdujące się w arkuszu w komórce zawierającej nazwę obliczanej funkcji. Etap 3. Wykorzystanie obiektu Pole kombi (ComboBox) do wybierania nazwy funkcji. W tym etapie ułatwimy wybieranie nazwy funkcji, dla której wykonamy obliczenia, wykorzystując do tego celu kontrolkę ComboBox. Excel pozwala na umieszczanie na arkuszu różnych kontrolek (formantów), które znamy już z tworzenia formularzy w Visual Basic. Kontrolowanie tych obiektów jest co prawda bardziej ograniczone, niż ma to miejsce w Visual Basic, nie mniej jednak kontrolki te w pewnych przypadkach usprawniają użytkowanie Excela. W naszym ćwiczeniu wykorzystaliśmy już kontrolkę Przycisk Polecenia do uruchamiania procedury Oblicz. Teraz wykorzystamy kontrolkę Pole kombi czyli ComboBox. 12
Metody numeryczne w przykładach
 Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Visual Basic for Applications Wprowadzenie, makra
 Visual Basic for Applications Wprowadzenie, makra 1. Zarejestruj Makro o nazwie: WpiszNazwisko, które wpisuje w bieżącym arkuszu w komórce C2 Twoje Imię i Nazwisko a następnie zmienia kolor czcionki na
Visual Basic for Applications Wprowadzenie, makra 1. Zarejestruj Makro o nazwie: WpiszNazwisko, które wpisuje w bieżącym arkuszu w komórce C2 Twoje Imię i Nazwisko a następnie zmienia kolor czcionki na
Całkowanie numeryczne
 Całkowanie numeryczne Nie zawsze możliwe jest wyznaczenie analitycznego wzoru będącego wynikiem całkowania danej funkcji f(x). Praktycznie zawsze możne jednak wyznaczyć całkę oznaczoną funkcji przy podanych
Całkowanie numeryczne Nie zawsze możliwe jest wyznaczenie analitycznego wzoru będącego wynikiem całkowania danej funkcji f(x). Praktycznie zawsze możne jednak wyznaczyć całkę oznaczoną funkcji przy podanych
II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski
 II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski 1 1 Różniczkowanie numeryczne Rozważmy funkcję f(x) określoną na sieci równoodległyc węzłów. Funkcja f(x) może być dana za pomocą wzoru analitycznego
II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski 1 1 Różniczkowanie numeryczne Rozważmy funkcję f(x) określoną na sieci równoodległyc węzłów. Funkcja f(x) może być dana za pomocą wzoru analitycznego
Aplikacje w środowisku VBA. Visual Basic for Aplications
 Aplikacje w środowisku VBA Visual Basic for Aplications Podstawowe informacje o VBA Visual Basic for Aplications, w skrócie VBA, to język programowania rozwijany przez Microsoft, którego zastosowanie pozwala
Aplikacje w środowisku VBA Visual Basic for Aplications Podstawowe informacje o VBA Visual Basic for Aplications, w skrócie VBA, to język programowania rozwijany przez Microsoft, którego zastosowanie pozwala
Kubatury Gaussa (całka podwójna po trójkącie)
 Kubatury Gaussa (całka podwójna po trójkącie) Całka podwójna po trójkącie Dana jest funkcja dwóch zmiennych f (x, y) ciągła i ograniczona w obszarze trójkątnym D. Wierzchołki trójkąta wyznaczają punkty
Kubatury Gaussa (całka podwójna po trójkącie) Całka podwójna po trójkącie Dana jest funkcja dwóch zmiennych f (x, y) ciągła i ograniczona w obszarze trójkątnym D. Wierzchołki trójkąta wyznaczają punkty
AUTOMATYZACJA PRACY Z UŻYCIEM MAKR. Tom XII NPV WSP.KORELACJI ROZKŁ.EXP JEŻELI COS KOMÓRKA VBA DNI.ROBOCZE ILOCZYN LOG SUMA CZY.
 z a a w a n s o w a n y AUTOMATYZACJA PRACY Z UŻYCIEM MAKR VBA NPV WSP.KORELACJI ROZKŁ.EXP KOMÓRKA CZY.LICZBA JEŻELI COS DNI.ROBOCZE ILOCZYN LOG SUMA Tom XII Autorzy: Piotr Dynia, Jakub Kudliński Kierownik
z a a w a n s o w a n y AUTOMATYZACJA PRACY Z UŻYCIEM MAKR VBA NPV WSP.KORELACJI ROZKŁ.EXP KOMÓRKA CZY.LICZBA JEŻELI COS DNI.ROBOCZE ILOCZYN LOG SUMA Tom XII Autorzy: Piotr Dynia, Jakub Kudliński Kierownik
Czym jest całka? Całkowanie numeryczne
 Całkowanie numeryczne jest to zagadnienie z metod elementów skończonych (MES). Korzystając z całkowania numerycznego możemy obliczyć wartość dowolnej całki jednowymiarowej oznaczonej. Wynik jest zawsze
Całkowanie numeryczne jest to zagadnienie z metod elementów skończonych (MES). Korzystając z całkowania numerycznego możemy obliczyć wartość dowolnej całki jednowymiarowej oznaczonej. Wynik jest zawsze
Informatyka w Zarządzaniu
 F O R M U L A R Z E I F O R M A N T Y M S E X C E L Formanty formularza są prostsze w użyciu, gdyż nie wymagają pisania kodu w języku Visual Basic for Applications (VBA). Aby skorzystać z efektów działania
F O R M U L A R Z E I F O R M A N T Y M S E X C E L Formanty formularza są prostsze w użyciu, gdyż nie wymagają pisania kodu w języku Visual Basic for Applications (VBA). Aby skorzystać z efektów działania
Trik 1 Edycja wykresu bezpośrednio w dokumencie Worda
 :: Trik 1. Edycja wykresu bezpośrednio w dokumencie Worda :: Trik 2. Automatyczne usuwanie nadanych nazw zakresów :: Trik 3. Warunki przy określaniu jednostek miary :: Trik 4. Najszybszy sposób podświetlenia
:: Trik 1. Edycja wykresu bezpośrednio w dokumencie Worda :: Trik 2. Automatyczne usuwanie nadanych nazw zakresów :: Trik 3. Warunki przy określaniu jednostek miary :: Trik 4. Najszybszy sposób podświetlenia
Przez F(C) oznaczamy figurę narysowaną w kartezjańskim układzie współrzędnych, która ograniczona jest przez:
 Obliczanie pola figury ograniczonej krzywymi było jednym z zadań na maturze z informatyki w 2006 roku. Według mnie jest to najtrudniejsze zadania jakie zostało umieszczone w arkuszach egzaminacyjnych z
Obliczanie pola figury ograniczonej krzywymi było jednym z zadań na maturze z informatyki w 2006 roku. Według mnie jest to najtrudniejsze zadania jakie zostało umieszczone w arkuszach egzaminacyjnych z
Arkusz kalkulacyjny EXCEL
 ARKUSZ KALKULACYJNY EXCEL 1 Arkusz kalkulacyjny EXCEL Aby obrysować tabelę krawędziami należy: 1. Zaznaczyć komórki, które chcemy obrysować. 2. Kursor myszy ustawić na menu FORMAT i raz kliknąć lewym klawiszem
ARKUSZ KALKULACYJNY EXCEL 1 Arkusz kalkulacyjny EXCEL Aby obrysować tabelę krawędziami należy: 1. Zaznaczyć komórki, które chcemy obrysować. 2. Kursor myszy ustawić na menu FORMAT i raz kliknąć lewym klawiszem
Makropolecenia w Excelu
 Makropolecenia w Excelu Trochę teorii Makropolecenie w skrócie nazywane makro ma za zadanie automatyczne wykonanie powtarzających się po sobie określonych czynności. Na przykładzie arkusza kalkulacyjnego
Makropolecenia w Excelu Trochę teorii Makropolecenie w skrócie nazywane makro ma za zadanie automatyczne wykonanie powtarzających się po sobie określonych czynności. Na przykładzie arkusza kalkulacyjnego
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Program szkolenia PODSTAWY VBA (VISUAL BASIC FOR APPLICATIONS) I FORMULARZE.
 Program szkolenia PODSTAWY VBA (VISUAL BASIC FOR APPLICATIONS) I FORMULARZE SZKOLENIE JEST DLA OSÓB, KTÓRE: znają program Microsoft Excel na poziomie średniozaawansowanym, chcą poznać ogólne zasady tworzenia
Program szkolenia PODSTAWY VBA (VISUAL BASIC FOR APPLICATIONS) I FORMULARZE SZKOLENIE JEST DLA OSÓB, KTÓRE: znają program Microsoft Excel na poziomie średniozaawansowanym, chcą poznać ogólne zasady tworzenia
METODY NUMERYCZNE. Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą. prof. dr hab.inż. Katarzyna Zakrzewska
 METODY NUMERYCZNE Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą prof. dr hab.inż. Katarzyna Zakrzewska Met.Numer. Wykład 4 1 Rozwiązywanie równań nieliniowych z jedną niewiadomą
METODY NUMERYCZNE Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą prof. dr hab.inż. Katarzyna Zakrzewska Met.Numer. Wykład 4 1 Rozwiązywanie równań nieliniowych z jedną niewiadomą
Wprowadzenie (17) Część I. Makra w Excelu - podstawy (23)
 Wprowadzenie (17) Omówione zagadnienia (18) Co trzeba wiedzieć? (18) Co trzeba mieć? (18) Układ książki (18) o Część I. Makra w Excelu - podstawy (19) o Część II. Praca ze skoroszytami (19) o Część III.
Wprowadzenie (17) Omówione zagadnienia (18) Co trzeba wiedzieć? (18) Co trzeba mieć? (18) Układ książki (18) o Część I. Makra w Excelu - podstawy (19) o Część II. Praca ze skoroszytami (19) o Część III.
Excel. Tworzenie zaawansowanych aplikacji.
 Excel. Tworzenie zaawansowanych aplikacji. Autor: Sergiusz Flanczewski Zmierz się z Excelem! Narzędzia automatyzacji prac w Excelu, czyli czego można pozbyć się od ręki Przekazywanie danych pomiędzy procedurami,
Excel. Tworzenie zaawansowanych aplikacji. Autor: Sergiusz Flanczewski Zmierz się z Excelem! Narzędzia automatyzacji prac w Excelu, czyli czego można pozbyć się od ręki Przekazywanie danych pomiędzy procedurami,
Zastanawiałeś się może, dlaczego Twój współpracownik,
 Kurs Makra dla początkujących Wiadomości wstępne VBI/01 Piotr Dynia, specjalista ds. MS Office Czas, który poświęcisz na naukę tego zagadnienia, to 15 20 minut. Zastanawiałeś się może, dlaczego Twój współpracownik,
Kurs Makra dla początkujących Wiadomości wstępne VBI/01 Piotr Dynia, specjalista ds. MS Office Czas, który poświęcisz na naukę tego zagadnienia, to 15 20 minut. Zastanawiałeś się może, dlaczego Twój współpracownik,
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Elektroenergetyki Technologie informatyczne
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Elektroenergetyki Technologie informatyczne Microsoft Excel Ćw. 5 1. Wstęp 1.1. Wprowadzenie do języka VBA Zaimplementowany w MS Excel
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Elektroenergetyki Technologie informatyczne Microsoft Excel Ćw. 5 1. Wstęp 1.1. Wprowadzenie do języka VBA Zaimplementowany w MS Excel
Metody rozwiązywania równań nieliniowych
 Metody rozwiązywania równań nieliniowych Rozwiązywanie równań nieliniowych Ogólnie równanie o jednej niewiadomej x można przedstawić w postaci f ( x)=0, x R, (1) gdzie f jest wystarczająco regularną funkcją.
Metody rozwiązywania równań nieliniowych Rozwiązywanie równań nieliniowych Ogólnie równanie o jednej niewiadomej x można przedstawić w postaci f ( x)=0, x R, (1) gdzie f jest wystarczająco regularną funkcją.
Visual Basic w programie Excel
 Visual Basic w programie Excel Ćwiczenie nr 3 Obiekty, właściwości, metody. Obiekty standardowe, kolekcje standardowe. Dostęp do komórek arkusza. Operacje na standardowych bibliotekach. CEL ĆWICZENIA.
Visual Basic w programie Excel Ćwiczenie nr 3 Obiekty, właściwości, metody. Obiekty standardowe, kolekcje standardowe. Dostęp do komórek arkusza. Operacje na standardowych bibliotekach. CEL ĆWICZENIA.
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL. sin x2 (1)
 ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
Przygotowanie własnej procedury... 3 Instrukcja msgbox wyświetlanie informacji w oknie... 6 Sposoby uruchamiania makra... 8
 Przygotowanie własnej procedury... 3 Instrukcja msgbox wyświetlanie informacji w oknie... 6 Sposoby uruchamiania makra... 8 Podstawy programowania makr w Excelu 1 Aby rozpocząć pracę z makrami, należy
Przygotowanie własnej procedury... 3 Instrukcja msgbox wyświetlanie informacji w oknie... 6 Sposoby uruchamiania makra... 8 Podstawy programowania makr w Excelu 1 Aby rozpocząć pracę z makrami, należy
Rachunek całkowy - całka oznaczona
 SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
Katarzyna Bereźnicka Zastosowanie arkusza kalkulacyjnego w zadaniach matematycznych. Opiekun stypendystki: mgr Jerzy Mil
 Katarzyna Bereźnicka Zastosowanie arkusza kalkulacyjnego w zadaniach matematycznych Opiekun stypendystki: mgr Jerzy Mil 1 Działania na ułamkach Wyłączanie całości z dodatnich ułamków niewłaściwych Formuła
Katarzyna Bereźnicka Zastosowanie arkusza kalkulacyjnego w zadaniach matematycznych Opiekun stypendystki: mgr Jerzy Mil 1 Działania na ułamkach Wyłączanie całości z dodatnich ułamków niewłaściwych Formuła
METODY NUMERYCZNE. Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą. Rozwiązywanie równań nieliniowych z jedną niewiadomą
 METODY NUMERYCZNE Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą dr hab.inż. Katarzyna Zakrzewska, prof.agh Met.Numer. Wykład 4 1 Rozwiązywanie równań nieliniowych z jedną niewiadomą
METODY NUMERYCZNE Wykład 4. Numeryczne rozwiązywanie równań nieliniowych z jedną niewiadomą dr hab.inż. Katarzyna Zakrzewska, prof.agh Met.Numer. Wykład 4 1 Rozwiązywanie równań nieliniowych z jedną niewiadomą
Przewodnik dla każdego po: Dla każdego coś miłego Microsoft Excel 2010
 Przewodnik dla każdego po: Dla każdego coś miłego Microsoft Excel 2010 Czym jest Excel 2010 Excel jest programem umożliwiającym tworzenie tabel, a także obliczanie i analizowanie danych. Należy do typu
Przewodnik dla każdego po: Dla każdego coś miłego Microsoft Excel 2010 Czym jest Excel 2010 Excel jest programem umożliwiającym tworzenie tabel, a także obliczanie i analizowanie danych. Należy do typu
2. Kliknij Insert->Userform. Jeżeli Toolbox nie pojawi się automatycznie, kliknij View -> Toolbox. Otrzymany widok powinien być jak poniżej.
 Formularze VBA Przykład1 INTERAKTYWNY FORMULARZ Program tworzący interaktywny formularz. Objaśnienie: w dowolnym momencie można wprowadzić wartość w polu tekstowym ID, Excel VBA wczytuje odpowiedni rekord.
Formularze VBA Przykład1 INTERAKTYWNY FORMULARZ Program tworzący interaktywny formularz. Objaśnienie: w dowolnym momencie można wprowadzić wartość w polu tekstowym ID, Excel VBA wczytuje odpowiedni rekord.
Część I: Przypisanie makr do obiektu (przycisku).
 Przedmiot: Informatyka w inżynierii produkcji Forma: Laboratorium Temat: Zadanie 2. Przypisanie makr do przycisku. Procedury i funkcje. Celem ćwiczenia jest przedstawienie możliwości uruchamiania makr
Przedmiot: Informatyka w inżynierii produkcji Forma: Laboratorium Temat: Zadanie 2. Przypisanie makr do przycisku. Procedury i funkcje. Celem ćwiczenia jest przedstawienie możliwości uruchamiania makr
Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PODSTAWOWY.
 Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PODSTAWOWY SZKOLENIE JEST DLA OSÓB, KTÓRE: nigdy wcześniej nie programowały lub nie miały styczności z programowaniem od dłuższego czasu,
Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PODSTAWOWY SZKOLENIE JEST DLA OSÓB, KTÓRE: nigdy wcześniej nie programowały lub nie miały styczności z programowaniem od dłuższego czasu,
Wstęp do programowania
 Wstęp do programowania Wykład 5 Podstawowe techniki programownia w przykładach Janusz Szwabiński Plan wykładu: Metoda babilońska wyliczania pierwiastka Liczby pierwsze i sito Eratostenesa Metoda bisekcji
Wstęp do programowania Wykład 5 Podstawowe techniki programownia w przykładach Janusz Szwabiński Plan wykładu: Metoda babilońska wyliczania pierwiastka Liczby pierwsze i sito Eratostenesa Metoda bisekcji
FORMULARZE I FORMANTY MS EXCEL 1. TEORIA
 FORMULARZE I FORMANTY MS EXCEL 1. TEORIA Formanty formularza są prostsze w użyciu, gdyż nie wymagają pisania kodu w języku Visual Basic for Applications (VBA). Aby skorzystać z efektów działania konkretnego
FORMULARZE I FORMANTY MS EXCEL 1. TEORIA Formanty formularza są prostsze w użyciu, gdyż nie wymagają pisania kodu w języku Visual Basic for Applications (VBA). Aby skorzystać z efektów działania konkretnego
Matematyka grupa Uruchom arkusz kalkulacyjny. 2. Wprowadź do arkusza kalkulacyjnego wartości znajdujące się w kolumnach A i B.
 Zadanie nr 1 Matematyka grupa 2 Wykonaj poniższe czynności po kolei. 1. Uruchom arkusz kalkulacyjny. 2. Wprowadź do arkusza kalkulacyjnego wartości znajdujące się w kolumnach A i B. A B 32 12 58 45 47
Zadanie nr 1 Matematyka grupa 2 Wykonaj poniższe czynności po kolei. 1. Uruchom arkusz kalkulacyjny. 2. Wprowadź do arkusza kalkulacyjnego wartości znajdujące się w kolumnach A i B. A B 32 12 58 45 47
Wybrane metody przybliżonego. wyznaczania rozwiązań (pierwiastków) równań nieliniowych
 Wykład trzeci 1 Wybrane metody przybliżonego wyznaczania rozwiązań pierwiastków równań nieliniowych 2 Metody rozwiązywania równań nieliniowych = 0 jest unkcją rzeczywistą zmiennej rzeczywistej Rozwiązanie
Wykład trzeci 1 Wybrane metody przybliżonego wyznaczania rozwiązań pierwiastków równań nieliniowych 2 Metody rozwiązywania równań nieliniowych = 0 jest unkcją rzeczywistą zmiennej rzeczywistej Rozwiązanie
Laboratorium 5 Przybliżone metody rozwiązywania równań nieliniowych
 Uniwersytet Zielonogórski Wydział Informatyki, Elektrotechniki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych Elektrotechnika niestacjonarne-zaoczne pierwszego stopnia z tyt. inżyniera
Uniwersytet Zielonogórski Wydział Informatyki, Elektrotechniki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych Elektrotechnika niestacjonarne-zaoczne pierwszego stopnia z tyt. inżyniera
Excel 2016 PL w biurze i nie tylko / Sergiusz Flanczewski. Gliwice, cop Spis treści
 Excel 2016 PL w biurze i nie tylko / Sergiusz Flanczewski. Gliwice, cop. 2016 Spis treści Rozdział 1. Podstawowe informacje o obsłudze arkusza kalkulacyjnego 9 Uruchamianie i zamykanie programu 9 Wstążka
Excel 2016 PL w biurze i nie tylko / Sergiusz Flanczewski. Gliwice, cop. 2016 Spis treści Rozdział 1. Podstawowe informacje o obsłudze arkusza kalkulacyjnego 9 Uruchamianie i zamykanie programu 9 Wstążka
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych)
 Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Trik 1 Podsumowanie kwot występujących w co drugim wierszu
 :: Trik 1. Podsumowanie kwot występujących w co drugim wierszu :: Trik 2. Rozmiar kolumny arkusza w milimetrach :: Trik 3. Blokada obszaru roboczego arkusza :: Trik 4. Dostęp do róŝnych skoroszytów za
:: Trik 1. Podsumowanie kwot występujących w co drugim wierszu :: Trik 2. Rozmiar kolumny arkusza w milimetrach :: Trik 3. Blokada obszaru roboczego arkusza :: Trik 4. Dostęp do róŝnych skoroszytów za
FUNKCJE. Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 5 Teoria funkcje cz.1. Definicja funkcji i wiadomości podstawowe
 1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
Geomatyka02 Wczytanie danych, obliczenie długości, azymutu i kąta ze współrzędnych. Przygotowanie do pracy
 Przygotowanie do pracy 1. Utwórz nowy dokument Excela. 2. Plik zapisz pod nazwą N-C1-Geom02-NazwiskoImię.xls (zmieniając N na S w przypadku studiów stacjonarnych, C1 na odpowiedni numer grupy, NazwiskoImię
Przygotowanie do pracy 1. Utwórz nowy dokument Excela. 2. Plik zapisz pod nazwą N-C1-Geom02-NazwiskoImię.xls (zmieniając N na S w przypadku studiów stacjonarnych, C1 na odpowiedni numer grupy, NazwiskoImię
Visual Basic for Applications. Wstęp
 Visual Basic for Applications Materiały źródłowe: http://www.vbamania.estrefa.pl 2008-01-14 Wstęp Visual Basic for Applications to język programowania, dołączony do wielu aplikacji. Wspierają go między
Visual Basic for Applications Materiały źródłowe: http://www.vbamania.estrefa.pl 2008-01-14 Wstęp Visual Basic for Applications to język programowania, dołączony do wielu aplikacji. Wspierają go między
Excel w obliczeniach naukowych i inżynierskich. Wydanie II.
 Excel w obliczeniach naukowych i inżynierskich. Wydanie II. Autor: Maciej Gonet Sprawdź, jak Excel może pomóc Ci w skomplikowanych obliczeniach! Jak za pomocą arkusza rozwiązywać zaawansowane zadania matematyczne?
Excel w obliczeniach naukowych i inżynierskich. Wydanie II. Autor: Maciej Gonet Sprawdź, jak Excel może pomóc Ci w skomplikowanych obliczeniach! Jak za pomocą arkusza rozwiązywać zaawansowane zadania matematyczne?
Zakres tematyczny dotyczący podstaw programowania Microsoft Office Excel za pomocą VBA
 Zakres tematyczny dotyczący podstaw programowania Microsoft Office Excel za pomocą VBA 1 Rozdział 1 Praca z makropoleceniami Opis: W tym rozdziale kursanci przechodzą przez wprowadzenie do programowania
Zakres tematyczny dotyczący podstaw programowania Microsoft Office Excel za pomocą VBA 1 Rozdział 1 Praca z makropoleceniami Opis: W tym rozdziale kursanci przechodzą przez wprowadzenie do programowania
Metody numeryczne Wykład 7
 Metody numeryczne Wykład 7 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Plan wykładu Rozwiązywanie równań algebraicznych
Metody numeryczne Wykład 7 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Plan wykładu Rozwiązywanie równań algebraicznych
Przedmiot: Informatyka w inżynierii produkcji Forma: Laboratorium Temat: Zadanie 4. Instrukcja warunkowa.
 Przedmiot: Informatyka w inżynierii produkcji Forma: Laboratorium Temat: Zadanie 4. Instrukcja warunkowa. Celem ćwiczenia jest nabycie umiejętności wykorzystania w praktyce instrukcji warunkowych programowania
Przedmiot: Informatyka w inżynierii produkcji Forma: Laboratorium Temat: Zadanie 4. Instrukcja warunkowa. Celem ćwiczenia jest nabycie umiejętności wykorzystania w praktyce instrukcji warunkowych programowania
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 6 Rozwiązywanie równań nieliniowych Rozwiązaniem lub pierwiastkiem równania f(x) = 0 lub g(x) = h(x)
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 6 Rozwiązywanie równań nieliniowych Rozwiązaniem lub pierwiastkiem równania f(x) = 0 lub g(x) = h(x)
SCENARIUSZ LEKCJI. Dzielenie wielomianów z wykorzystaniem schematu Hornera
 Autorzy scenariusza: SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH
Autorzy scenariusza: SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH
Nagrywanie Makr. Na karcie Dostosowywanie Wstążki zaznaczamy kartę Deweloper.
 Nagrywanie Makr Wiele rozwiązań z wykorzystaniem makr można używać nawet bez znajomości poleceń i struktury języka programowania Visual Basic for Applications. Pozwala na to opcja nagrywania makr, którą
Nagrywanie Makr Wiele rozwiązań z wykorzystaniem makr można używać nawet bez znajomości poleceń i struktury języka programowania Visual Basic for Applications. Pozwala na to opcja nagrywania makr, którą
Podstawy programowania w języku Visual Basic dla Aplikacji (VBA)
 Podstawy programowania w języku Visual Basic dla Aplikacji (VBA) Instrukcje Język Basic został stworzony w 1964 roku przez J.G. Kemeny ego i T.F. Kurtza z Uniwersytetu w Darthmouth (USA). Nazwa Basic jest
Podstawy programowania w języku Visual Basic dla Aplikacji (VBA) Instrukcje Język Basic został stworzony w 1964 roku przez J.G. Kemeny ego i T.F. Kurtza z Uniwersytetu w Darthmouth (USA). Nazwa Basic jest
Wprowadzenie do MS Excel
 Wprowadzenie do MS Excel Czym jest Excel? Excel jest programem umożliwiającym tworzenie tabel, a także obliczanie i analizowanie danych. Należy do typu programów nazywanych arkuszami kalkulacyjnymi. W
Wprowadzenie do MS Excel Czym jest Excel? Excel jest programem umożliwiającym tworzenie tabel, a także obliczanie i analizowanie danych. Należy do typu programów nazywanych arkuszami kalkulacyjnymi. W
Metody numeryczne. materiały do wykładu dla studentów
 Metody numeryczne materiały do wykładu dla studentów 5. Przybliżone metody rozwiązywania równań 5.1 Lokalizacja pierwiastków 5.2 Metoda bisekcji 5.3 Metoda iteracji 5.4 Metoda stycznych (Newtona) 5.5 Metoda
Metody numeryczne materiały do wykładu dla studentów 5. Przybliżone metody rozwiązywania równań 5.1 Lokalizacja pierwiastków 5.2 Metoda bisekcji 5.3 Metoda iteracji 5.4 Metoda stycznych (Newtona) 5.5 Metoda
UKŁADY RÓWNAŃ LINIOWYCH
 Projekt dofinansowała Fundacja mbanku UKŁADY RÓWNAŃ LINIOWYCH CZĘŚĆ I Układ równań to przynajmniej dwa równania spięte z lewej strony klamrą, np.: x + 0 Każde z równań musi zawierać przynajmniej jedną
Projekt dofinansowała Fundacja mbanku UKŁADY RÓWNAŃ LINIOWYCH CZĘŚĆ I Układ równań to przynajmniej dwa równania spięte z lewej strony klamrą, np.: x + 0 Każde z równań musi zawierać przynajmniej jedną
1 Algorytmy. Algorytmy i VBA. 1. Zapoznaj się z symboliką schematów blokowych.
 1 Algorytmy 1. Zapoznaj się z symboliką schematów blokowych. 2. Przeanalizuj podany algorytm wyznaczający minimalną liczbę spośród danych: a, b, c. dr Piotr Borkowski 1/10 3. Przeanalizuj podany algorytm
1 Algorytmy 1. Zapoznaj się z symboliką schematów blokowych. 2. Przeanalizuj podany algorytm wyznaczający minimalną liczbę spośród danych: a, b, c. dr Piotr Borkowski 1/10 3. Przeanalizuj podany algorytm
Metody numeryczne. materiały do wykładu dla studentów. 7. Całkowanie numeryczne
 Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
Microsoft EXCEL SOLVER
 Microsoft EXCEL SOLVER 1. Programowanie liniowe z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Microsoft EXCEL SOLVER 1. Programowanie liniowe z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH
 METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH Jednym z zastosowań metod numerycznych jest wyznaczenie pierwiastka lub pierwiastków równania nieliniowego. W tym celu stosuje się szereg metod obliczeniowych np:
METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH Jednym z zastosowań metod numerycznych jest wyznaczenie pierwiastka lub pierwiastków równania nieliniowego. W tym celu stosuje się szereg metod obliczeniowych np:
ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
 Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
1 Równania nieliniowe
 1 Równania nieliniowe 1.1 Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym jest numeryczne poszukiwanie rozwiązań równań nieliniowych, np. algebraicznych (wielomiany),
1 Równania nieliniowe 1.1 Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym jest numeryczne poszukiwanie rozwiązań równań nieliniowych, np. algebraicznych (wielomiany),
7.9. Ochrona danych Ochrona i zabezpieczenie arkusza. Pole wyboru
 Pole wyboru Pole wyboru może zostać wykorzystane wtedy, gdy istnieją dwie alternatywne opcje. Umożliwia wybranie jednej z wzajemnie wykluczających się opcji przez zaznaczenie lub usunięcie zaznaczenia
Pole wyboru Pole wyboru może zostać wykorzystane wtedy, gdy istnieją dwie alternatywne opcje. Umożliwia wybranie jednej z wzajemnie wykluczających się opcji przez zaznaczenie lub usunięcie zaznaczenia
Dokąd on zmierza? Przemieszczenie i prędkość jako wektory
 A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Dokąd on zmierza? Przemieszczenie i prędkość jako wektory Łódź żegluje po morzu... Płynie z szybkością 10 węzłów (węzeł to 1 mila morska na godzinę czyli
A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Dokąd on zmierza? Przemieszczenie i prędkość jako wektory Łódź żegluje po morzu... Płynie z szybkością 10 węzłów (węzeł to 1 mila morska na godzinę czyli
Excel z elementami VBA w firmie.
 Excel z elementami VBA w firmie. Autor: Sergiusz Flanczewski Wykorzystaj potencjał Excela, by Twoja firma odniosła sukces! Jak zaprząc dodatki Excela do tworzenia dokumentacji firmowej? Jak importować
Excel z elementami VBA w firmie. Autor: Sergiusz Flanczewski Wykorzystaj potencjał Excela, by Twoja firma odniosła sukces! Jak zaprząc dodatki Excela do tworzenia dokumentacji firmowej? Jak importować
Zagadnienia - równania nieliniowe
 Zagadnienia - równania nieliniowe Sformułowanie zadania poszukiwania pierwiastków. Przedział izolacji. Twierdzenia o istnieniu pierwiastków. Warunki zatrzymywania algorytmów. Metoda połowienia: założenia,
Zagadnienia - równania nieliniowe Sformułowanie zadania poszukiwania pierwiastków. Przedział izolacji. Twierdzenia o istnieniu pierwiastków. Warunki zatrzymywania algorytmów. Metoda połowienia: założenia,
Trik 1 Autorejestrowanie zmian dokonanych w obliczeniach
 :: Trik 1. Autorejestrowanie zmian dokonanych w obliczeniach :: Trik 2. Czytelne formatowanie walutowe :: Trik 3. Optymalny układ wykresu punktowego :: Trik 4. Szybkie oznaczenie wszystkich komórek z formułami
:: Trik 1. Autorejestrowanie zmian dokonanych w obliczeniach :: Trik 2. Czytelne formatowanie walutowe :: Trik 3. Optymalny układ wykresu punktowego :: Trik 4. Szybkie oznaczenie wszystkich komórek z formułami
Pracownia Informatyczna Instytut Technologii Mechanicznej Wydział Inżynierii Mechanicznej i Mechatroniki. Podstawy Informatyki i algorytmizacji
 Pracownia Informatyczna Instytut Technologii Mechanicznej Wydział Inżynierii Mechanicznej i Mechatroniki Podstawy Informatyki i algorytmizacji wykład 1 dr inż. Maria Lachowicz Wprowadzenie Dlaczego arkusz
Pracownia Informatyczna Instytut Technologii Mechanicznej Wydział Inżynierii Mechanicznej i Mechatroniki Podstawy Informatyki i algorytmizacji wykład 1 dr inż. Maria Lachowicz Wprowadzenie Dlaczego arkusz
Algorytmy i schematy blokowe
 Algorytmy i schematy blokowe Algorytm dokładny przepis podający sposób rozwiązania określonego zadania w skończonej liczbie kroków; zbiór poleceń odnoszących się do pewnych obiektów, ze wskazaniem porządku,
Algorytmy i schematy blokowe Algorytm dokładny przepis podający sposób rozwiązania określonego zadania w skończonej liczbie kroków; zbiór poleceń odnoszących się do pewnych obiektów, ze wskazaniem porządku,
Utworzenie interfejsu graficznego za pomocą formularza użytkownika w VBA
 Utworzenie interfejsu graficznego za pomocą formularza użytkownika w VBA Po co? Potrzebne jest nam makro, które będzie wykonywać pewne czynności w osobnym oknie w Excelu. Do tego celu wykorzystamy element
Utworzenie interfejsu graficznego za pomocą formularza użytkownika w VBA Po co? Potrzebne jest nam makro, które będzie wykonywać pewne czynności w osobnym oknie w Excelu. Do tego celu wykorzystamy element
LABORATORIUM 6: ARKUSZ MS EXCEL JAKO BAZA DANYCH
 UNIWERSYTET ZIELONOGÓRSKI INSTYTUT INFORMATYKI I ELEKTROTECHNIKI ZAKŁAD INŻYNIERII KOMPUTEROWEJ Przygotował: dr inż. Janusz Jabłoński LABORATORIUM 6: ARKUSZ MS EXCEL JAKO BAZA DANYCH Jeżeli nie jest potrzebna
UNIWERSYTET ZIELONOGÓRSKI INSTYTUT INFORMATYKI I ELEKTROTECHNIKI ZAKŁAD INŻYNIERII KOMPUTEROWEJ Przygotował: dr inż. Janusz Jabłoński LABORATORIUM 6: ARKUSZ MS EXCEL JAKO BAZA DANYCH Jeżeli nie jest potrzebna
FUNKCJA KWADRATOWA. Zad 1 Przedstaw funkcję kwadratową w postaci ogólnej. Postać ogólna funkcji kwadratowej to: y = ax + bx + c;(
 Zad Przedstaw funkcję kwadratową w postaci ogólnej Przykład y = ( x ) + 5 (postać kanoniczna) FUNKCJA KWADRATOWA Postać ogólna funkcji kwadratowej to: y = ax + bx + c;( a 0) Aby ją uzyskać pozbywamy się
Zad Przedstaw funkcję kwadratową w postaci ogólnej Przykład y = ( x ) + 5 (postać kanoniczna) FUNKCJA KWADRATOWA Postać ogólna funkcji kwadratowej to: y = ax + bx + c;( a 0) Aby ją uzyskać pozbywamy się
Jak korzystać z Excela?
 1 Jak korzystać z Excela? 1. Dane liczbowe, wprowadzone (zaimportowane) do arkusza kalkulacyjnego w Excelu mogą przyjmować różne kategorie, np. ogólne, liczbowe, walutowe, księgowe, naukowe, itd. Jeśli
1 Jak korzystać z Excela? 1. Dane liczbowe, wprowadzone (zaimportowane) do arkusza kalkulacyjnego w Excelu mogą przyjmować różne kategorie, np. ogólne, liczbowe, walutowe, księgowe, naukowe, itd. Jeśli
INFORMATYKA ELEMENTY METOD NUMERYCZNYCH.
 INFORMATYKA ELEMENTY METOD NUMERYCZNYCH http://www.infoceram.agh.edu.pl METODY NUMERYCZNE Metody numeryczne zbiór metod rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
INFORMATYKA ELEMENTY METOD NUMERYCZNYCH http://www.infoceram.agh.edu.pl METODY NUMERYCZNE Metody numeryczne zbiór metod rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PRZEKROJOWY.
 Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PRZEKROJOWY SZKOLENIE JEST DLA OSÓB, KTÓRE: chcą podnieść swoje umiejętności pracy w języku VBA do poziomu średniozaawansowanego, nigdy wcześniej
Program szkolenia VBA (VISUAL BASIC FOR APPLICATIONS) W EXCELU PRZEKROJOWY SZKOLENIE JEST DLA OSÓB, KTÓRE: chcą podnieść swoje umiejętności pracy w języku VBA do poziomu średniozaawansowanego, nigdy wcześniej
Plik->Opcje->Zakladka Główne->Dostosuj Wstążkę Zaznaczamy kwadracik Developer na liscie po prawej stronie. Klikamy OK.
 Aktywacja zakładki Developer. Plik->Opcje->Zakladka Główne->Dostosuj Wstążkę Zaznaczamy kwadracik Developer na liscie po prawej stronie. Klikamy OK. Rejestracja makr. Klikamy Zakladke Developer. Klikamy
Aktywacja zakładki Developer. Plik->Opcje->Zakladka Główne->Dostosuj Wstążkę Zaznaczamy kwadracik Developer na liscie po prawej stronie. Klikamy OK. Rejestracja makr. Klikamy Zakladke Developer. Klikamy
Dane w poniższej tabeli przedstawiają sprzedaż w dolarach i sztukach oraz marżę wyrażoną w dolarach dla:
 Przykład 1. Dane w poniższej tabeli przedstawiają sprzedaż w dolarach i sztukach oraz marżę wyrażoną w dolarach dla: 24 miesięcy, 8 krajów, 5 kategorii produktów, 19 segmentów i 30 brandów. Tabela ta ma
Przykład 1. Dane w poniższej tabeli przedstawiają sprzedaż w dolarach i sztukach oraz marżę wyrażoną w dolarach dla: 24 miesięcy, 8 krajów, 5 kategorii produktów, 19 segmentów i 30 brandów. Tabela ta ma
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Metody numeryczne. dr Artur Woike. Ćwiczenia nr 2. Rozwiązywanie równań nieliniowych metody połowienia, regula falsi i siecznych.
 Ćwiczenia nr 2 metody połowienia, regula falsi i siecznych. Sformułowanie zagadnienia Niech będzie dane równanie postaci f (x) = 0, gdzie f jest pewną funkcją nieliniową (jeżeli f jest liniowa to zagadnienie
Ćwiczenia nr 2 metody połowienia, regula falsi i siecznych. Sformułowanie zagadnienia Niech będzie dane równanie postaci f (x) = 0, gdzie f jest pewną funkcją nieliniową (jeżeli f jest liniowa to zagadnienie
Rzut oka na współczesną matematykę spotkanie 3: jak liczy kalkulator i o źródłach chaosu
 Rzut oka na współczesną matematykę spotkanie 3: jak liczy kalkulator i o źródłach chaosu P. Strzelecki pawelst@mimuw.edu.pl Instytut Matematyki, Uniwersytet Warszawski MISH UW, semestr zimowy 2011-12 P.
Rzut oka na współczesną matematykę spotkanie 3: jak liczy kalkulator i o źródłach chaosu P. Strzelecki pawelst@mimuw.edu.pl Instytut Matematyki, Uniwersytet Warszawski MISH UW, semestr zimowy 2011-12 P.
MS Access formularze
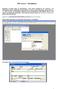 MS Access formularze Formularze to obiekty służące do wprowadzania i edycji danych znajdujących się w tabelach. O ile wprowadzanie danych bezpośrednio do tabel odbywa się zawsze w takiej samej formie (arkusz
MS Access formularze Formularze to obiekty służące do wprowadzania i edycji danych znajdujących się w tabelach. O ile wprowadzanie danych bezpośrednio do tabel odbywa się zawsze w takiej samej formie (arkusz
x y
 Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka
 Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka 1. Kompilacja aplikacji konsolowych w środowisku programistycznym Microsoft Visual Basic. Odszukaj w menu startowym systemu
Wprowadzenie do programowania w języku Visual Basic. Podstawowe instrukcje języka 1. Kompilacja aplikacji konsolowych w środowisku programistycznym Microsoft Visual Basic. Odszukaj w menu startowym systemu
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
Rys. 1. DuŜa liczba nazw zakresów. Rys. 2. Procedura usuwająca wszystkie nazwy w skoroszycie
 :: Trik 1. Hurtowe usuwanie niepotrzebnych nazw zakresów :: Trik 2. WyróŜnianie powtórzonych wartości w kolumnie :: Trik 3. Oznaczenie wierszy kolejnymi literami alfabetu :: Trik 4. Obliczanie dziennych
:: Trik 1. Hurtowe usuwanie niepotrzebnych nazw zakresów :: Trik 2. WyróŜnianie powtórzonych wartości w kolumnie :: Trik 3. Oznaczenie wierszy kolejnymi literami alfabetu :: Trik 4. Obliczanie dziennych
Metody numeryczne I Równania nieliniowe
 Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
EGZAMIN MATURALNY Z INFORMATYKI MAJ 2014 POZIOM ROZSZERZONY CZĘŚĆ I WYBRANE: Czas pracy: 90 minut. Liczba punktów do uzyskania: 20 WPISUJE ZDAJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 201 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 201 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, , tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Rozwiązanie:
 Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
3. Wprowadź opis: kolumna A J. angielski, kolumna B J. polski. Obejrzyj animację pt. Wprowadzanie danych, aby dowiedzieć się, jak to zrobić.
 Język angielski grupa 3 Zadanie nr 1 Wykonaj poniższe czynności po kolei. 1. Uruchom arkusz kalkulacyjny. 2. Wprowadź do arkusza kalkulacyjnego wyrazy znajdujące się w kolumnach A i B tabeli: A dog cat
Język angielski grupa 3 Zadanie nr 1 Wykonaj poniższe czynności po kolei. 1. Uruchom arkusz kalkulacyjny. 2. Wprowadź do arkusza kalkulacyjnego wyrazy znajdujące się w kolumnach A i B tabeli: A dog cat
Laboratorium 6. 1 Makropolecenia wprowadzenie. 2 Formatowanie komórek. 2.1 Rejestrowanie makra. Legenda: tekst do wpisania
 Laboratorium 6 1 Makropolecenia wprowadzenie Często powtarzane zadania można zautomatyzować za pomocą makropoleceń (inaczej: makr). Makro to seria poleceń wykonywanych w module języka MS Visual Basic for
Laboratorium 6 1 Makropolecenia wprowadzenie Często powtarzane zadania można zautomatyzować za pomocą makropoleceń (inaczej: makr). Makro to seria poleceń wykonywanych w module języka MS Visual Basic for
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Rozwiązywanie równań nieliniowych i ich układów. Wyznaczanie zer wielomianów.
 Rozwiązywanie równań nieliniowych i ich układów. Wyznaczanie zer wielomianów. Plan wykładu: 1. Wyznaczanie pojedynczych pierwiastków rzeczywistych równań nieliniowych metodami a) połowienia (bisekcji)
Rozwiązywanie równań nieliniowych i ich układów. Wyznaczanie zer wielomianów. Plan wykładu: 1. Wyznaczanie pojedynczych pierwiastków rzeczywistych równań nieliniowych metodami a) połowienia (bisekcji)
TEMAT: SPOSOBY ADRESOWANIA W
 CENTRUM EDUKACJI AKADEMIA SUKCESU Praca Semestralna TEMAT: SPOSOBY ADRESOWANIA W ARKUSZU KALKULACYJNYM EXCEL. Kierunek: Technik Informatyk Semestr: II Wykładowca: Jan Nosal Słuchacz: Łukasz Stocki CO TO
CENTRUM EDUKACJI AKADEMIA SUKCESU Praca Semestralna TEMAT: SPOSOBY ADRESOWANIA W ARKUSZU KALKULACYJNYM EXCEL. Kierunek: Technik Informatyk Semestr: II Wykładowca: Jan Nosal Słuchacz: Łukasz Stocki CO TO
Przykład wykorzystania dodatku SOLVER 1 w arkuszu Excel do rozwiązywania zadań programowania matematycznego
 Przykład wykorzystania dodatku SOLVER 1 w arkuszu Ecel do rozwiązywania zadań programowania matematycznego Firma produkująca samochody zaciągnęła kredyt inwestycyjny w wysokości mln zł na zainstalowanie
Przykład wykorzystania dodatku SOLVER 1 w arkuszu Ecel do rozwiązywania zadań programowania matematycznego Firma produkująca samochody zaciągnęła kredyt inwestycyjny w wysokości mln zł na zainstalowanie
Całkowanie numeryczne przy użyciu kwadratur
 Całkowanie numeryczne przy użyciu kwadratur Plan wykładu: 1. Kwadratury Newtona-Cotesa a) wzory: trapezów, parabol etc. b) kwadratury złożone 2. Ekstrapolacja a) ekstrapolacja Richardsona b) metoda Romberga
Całkowanie numeryczne przy użyciu kwadratur Plan wykładu: 1. Kwadratury Newtona-Cotesa a) wzory: trapezów, parabol etc. b) kwadratury złożone 2. Ekstrapolacja a) ekstrapolacja Richardsona b) metoda Romberga
Wprowadzenie Metoda bisekcji Metoda regula falsi Metoda siecznych Metoda stycznych RÓWNANIA NIELINIOWE
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Zazwyczaj nie można znaleźć
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Zazwyczaj nie można znaleźć
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Biotechnologia w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era inżyniera
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Biotechnologia w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era inżyniera
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
Rys. 1. Aktywne linki będą wstawiane za pomocą rozwijanej listy
 :: Trik 1. Lista rozwijana z aktywnymi hiperłączami :: Trik 2. Łączenie tabel o róŝnym układzie kolumn :: Trik 3. Automatyczne zapisywanie zmian przy zamykaniu skoroszytu :: Trik 4. Linie siatki arkusza
:: Trik 1. Lista rozwijana z aktywnymi hiperłączami :: Trik 2. Łączenie tabel o róŝnym układzie kolumn :: Trik 3. Automatyczne zapisywanie zmian przy zamykaniu skoroszytu :: Trik 4. Linie siatki arkusza
Badania operacyjne Instrukcja do c wiczen laboratoryjnych Rozwiązywanie problemów programowania liniowego z użyciem MS Excel + Solver
 Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Techniki Morskiej i Transportu Katedra Konstrukcji, Mechaniki i Technologii Okręto w Badania operacyjne Instrukcja do c wiczen laboratoryjnych
Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Techniki Morskiej i Transportu Katedra Konstrukcji, Mechaniki i Technologii Okręto w Badania operacyjne Instrukcja do c wiczen laboratoryjnych
