Grupowanie stron WWW. Funkcje oceniające.
|
|
|
- Tomasz Cieślik
- 9 lat temu
- Przeglądów:
Transkrypt
1 Eksploracja zasobów internetowych Wykład 6 Grupowanie stron WWW. Funkcje oceniające. mgr inż. Maciej Kopczyński Białystok 2015
2 Wstęp Rolą algorytmów grupujących jest pogrupowanie dokumentów na bazie ich podobieństwa lub stworzenie modelu opisującego grupę na podstawie reprezentacji obiektów składających się na grupę. Dzięki temu odzwierciedlona jest tematyka grupy dokumentów. Następnie można wykorzystać funkcje oceny do określenia jakości grup stworzonych przez poszczególne algorytmy. Jednak do wykonania oceny niezbędne jest posiadanie zbioru do- kumentów, który został stworzony (opisany) przez eksperta. 2
3 Wstęp Funkcje oceniające wraz ze zbiorami wzorcowymi (stworzonymi przez eksperta) mogą zostać wykorzystane w dwóch aspektach w przypad- ku grupowania danych: określenia miar błędów popełnianych przez algorytmy grupujące, rozszerzenia zbiorów stworzonych przez eksperta o nowe ele- menty, które są podobne pod względem cech do tych, które zosta- ły sklasyfikowane przez eksperta. 3
4 Funkcje oceniające Jedną z najbardziej popularnych funkcji oceniających jest funkcja najmniejszych kwadratów. Jej istota polega na obliczaniu różnic pomiędzy środkami klastrów (centroidami) a poszczególnymi obiek- tami należącymi do klastrów. Funkcja najmniejszych kwadratów opisana jest zależnością: k J = e i=1 gdzie m i x m i x D i jest centroidem klastra D : i m i = 1 D i x d i x 4
5 Funkcje oceniające Jaki rodzaj miary wykorzystywany jest w klasycznej metodzie naj- mniejszych kwadratów? W klasycznej metodzie najmniejszych kwadratów wykorzystywana jest miara euklidesowa. Jaką najbardziej pożądaną wartość powinna osiągać funkcja ocenia- jąca w klasycznej metodzie najmniejszych kwadratów? Funkcja oceniająca w klasycznej metodzie najmniejszych kwadratów powinna dążyć do wartości równej 0. 5
6 Funkcje oceniające W przypadku grupowania dokumentów najczęściej wykorzystywana jest miara cosinusowa. Funkcja oceniająca dla metody najmniejszych kwadratów dla miary cosinusowej zdefiniowana jest jako: k J s = i=1 sim c i,d j d j D i gdzie sim(c i, d ) j określa podobieństwo pomiędzy centroidem c oraz i dokumentem d j : sim c i,d j = c i d j c i d j 6
7 Funkcje oceniające Centroid c i określający środkowy dokument w ramach zadanego klas- tra zdefiniowany jest jako: c i = 1 D i d j d j D i Jaka jest najbardziej pożądana wartość funkcji oceniającej wykorzys- tującej miarę cosinusową? Najbardziej pożądaną wartością funkcji oceniającej wykorzystującej miarę cosinusową jest wartość jak największa. 7
8 Funkcje oceniające Grupowanie, które maksymalizuje wartość funkcji oceniającej jest określane mianem grupowania o minimalnej wariancji. Funkcje oceniające należące do tej rodziny są określane jako fun- kcje oceniające o minimalnej wariancji. Funkcje oceniające mogą również przyjmować dwie formy zależnie od rodzaju grupowania: funkcje bazujące na centroidzie, funkcje bazujące na odległościach pomiędzy parami obiektów. 8
9 Porównanie klastrów Istotną kwestią jest możliwość porównania między sobą grupowań dokumentów o różnych licznościach klastrów lub różnych strukturach hierarchicznych. W przypadku grupowania płaskiego, wartość funkcji oceniającej rośnie wraz ze zwiększaniem ilości klastrów. W przypadku grupowania hierarchicznego wartość funkcji oceniającej rośnie wraz z przemieszczaniem się w dół dendrogramu. 9
10 Porównanie klastrów przykład Na kolejnym slajdzie pokazane będzie uruchomienie algorytmu grupowania hierarchicznego (agglomerative hierarchical clustering) oraz trzy uruchomienia algorytmu k-średnich z parametrami k = 2, 3 oraz 4. Wartość funkcji oceniającej na bazie centroidów zapisana jest w nawiasie kwadratowym obok stworzonego klastra. Dany klaster składa się z dokumentów leżących poniżej w hierarchii tworzącej grupę. 10
11 11
12 Porównanie klastrów przykład W algorytmie grupowania hierarchicznego, węzeł nr 3 reprezentuje klaster składający się z następujących dokumentów: Chemistry, Computer Science, Political Science, Geography, Anthropology, Criminal Justice oraz Theatre.. Funkcja oceniająca bazująca na centroidach zwróciła wynik 5, Suma wartości w węzłach pochodnych jest różna od wartości 5, Dzieje się tak dlatego, że funkcja ocenia pojedyncze klastry bez uwzględniania zależności w drzewie. 12
13 Porównanie klastrów przykład Dzięki temu można porównać ze sobą dwa klastry znajdujące się na różnych poziomach drzewa w przypadku algorytmu hierarchicznego lub dwa klastry o różnych licznościach w przypadku algorytmu gru- powania płaskiego. Za pomocą funkcji oceniających można przeanalizować problem łą- czenia ze sobą poszczególnych klastrów. Przy analizie algorytmu hierarchicznego, najpierw należy zidentyfikować klastry,, które na najniższym poziomie pokrywają cały zbiór dokumentów. Są to klas- try: 4, 8, 10, 12, 15 oraz 17. Teraz, korzystając z kombinacji łączeń tych klastrów, można wybrać ten sposób połączenia klastrów, który da największą wartość funkcji oceniającej. 13
14 Łączenie klastrów Dla klastrów o węzłach podanych na poprzednim slajdzie, można wy- generować następujące kombinacje łączeń: Z tabeli kombinacji wynika, że im więcej klastrów powstaje w wyniku grupowania, tym większa wartość funkcji oceniającej. 14
15 Łączenie klastrów Intuicja podpowiada jednak, że chcemy tworzyć jak największe klas- try. Jednak przy łączeniu klastrów ze sobą spada wartość funkcji oce- niającej. Tak więc istotny jest kompromis pomiędzy wartością funkcji oceniają- cej, a wielkością klastrów. Można to osiągnąć poprzez: znajomość tematyki związanej z danymi klastrami (np. łączenie 4, 8, 9 oraz 14), przy braku znajomości tematyki warto łączyć klastry na tych samych poziomach (np. 3, 9 oraz 14). 15
16 Łączenie klastrów W przypadku algorytmu k-średnich można zastosować inną technikę wyszukiwania optymalnej ilości klastrów. Najpierw wykonane zostały trzy kolejne uruchomienia algorytmu k-średnich dla parametru k = 5, 6, 7 oraz 20 (ilość dokumentów w zbiorze). Dla każdego uruchomienia obliczona została wartość funkcji oceniającej bazującej na centroidach. Na kolejnym slajdzie pokazany jest wykres wartości funkcji oceniają- cej w zależności od parametru k (ilości klastrów). 16
17 17 Łączenie klastrów
18 Łączenie klastrów 18 Dla pierwszych wartości parametru k wykres jest stromy, zaś powy- żej tej wartości wykres staje się płaski. Głównym celem algorytmu k-średnich jest maksymalizacja wartości funkcji oceniającej. Czym będzie skutkowała nadmierna maksymalizacja wartości funk- cji oceniającej? Nadmierna maksymalizacja wartości funkcji będzie skutkowała zbyt dużą ilością klastrów wynikowych.
19 Łączenie klastrów Który w takim razie punkt na wykresie jest najbardziej optymalny pod względem ilości klastrów i wartości funkcji oceniającej? Najbardziej optymalnym punktem na wykresie pod względem ilości klastrów i wartości funkcji oceniającej jest miejsce, w którym wykres przechodzi z szybkiego wzrostu do części płaskiej. W przypadku danych przykładowych, taki punkt występuje dla k = 5. Rozwiązanie to jest poprawne w przypadku, gdy nie mamy żadnych informacji na temat zbioru. W przypadku naszego zbioru danych najbardziej pożądana jest war- parametru k = 2. 19
20 Wyszukiwanie wzorców Do tej pory grupowanie omawiane było jako metoda tworzenia klas- trów składających się z dokumentów o podobnych cechach. Grupowanie wraz z funkcjami oceniającymi może być również wyko- rzystane jako mechanizm do odnajdowania wzorców. Jeśli dany klas- ter składa się z względnie dużej ilości obiektów oraz wartość jego funkcji oceniającej również jest wysoka, może to świadczyć o odnale- zieniu klastra reprezentującego jakiś wzorzec. Na podstawie klastra można stworzyć reguły opisujące wzorzec. 20
21 Wyszukiwanie wzorców Wzorzec będzie opisany przez zbiór reguł, w których warunki są zdefi- niowane przez atrybuty posiadające takie same wartości dla wszyst- kich dokumentów należących do danego klastra. Zbiór przykładowych reguł może wyglądać następująco: R 1 : IF (science = 0) AND (research = 1) THEN class = A R 2 : IF (science = 1) AND (research = 0) THEN class = A R 3 : IF (science = 1) AND (research = 1) THEN class = A R 4 : IF (science = 0) AND (research = 0) THEN class = B 21
22 Wyszukiwanie wzorców Reguły mogą być później wykorzystane do klasyfikacji (grupowania) innych zbiorów danych. Przy wykorzystaniu reguły dropping conditions można uogólniać wzo- rzec poprzez usuwanie elementów części warunkowej reguł. Tworzenie nadmiernie dokładnych reguł, a także zbytnio ogólnych re- guł jest niepożądane ze względu na generowanie dwóch skrajnych ro- dzajów grup. Przy zbyt ogólnych regułach, wszystkie elementy trafią do jednego klas- tra. Przy nadmiernie szczegółowych regułach obiekty stworzą jednoele- mentowe klastry. 22
23 Miary oceny Załóżmy, że dla każdego z dokumentów na bazie jego zawartości zos- tała przyporządkowana jedna z dwóch klas: A lub B. Następnie dokumenty zostały pogrupowane ze względu na występo- wanie danego termu w ich treści. Tego typu grupowanie pozwala na pomiar błędów jakości grupowania oraz błędów doboru odpowiednich atrybutów. Kolejny slajd przedstawia grupowanie ze względu na kilka wybranych termów. Dla każdej z grup podane są wartości błędów. 23
24
25 Miary oceny Miara ilości popełnianych błędów w stosunku do wszystkich dokumen- tów jest czasami niewystarczająca. W wielu przypadkach warto jest znać rodzaj popełnianych błędów. Biorąc jako przykład system filtracji antyspamowej wiadomości , jaki rodzaj błędów popełnianych podczas klasyfikacji jest bardziej istotny? W systemie antyspamowym można obliczyć ilość wszystkich popełnia- nych przez system pomyłek, jednak dużo bardziej istotna jest błędna klasyfikacja dobrego a jako spam, niż spamu jako dobry . 25
26 Miary oceny Ze względu na to, że większość problemów grupowania i klasyfikacji operuje na problemie dwóch klas, wprowadzone zostały odpowiednie miary w zależności od typu klasyfikacji dokumentu: True positive (TP)) dokument prawdziwy sklasyfikowany jako praw- dziwy, False positive (FP)) dokument nieprawdziwy sklasyfikowany jako prawdziwy, True negative (TN)) dokument nieprawdziwy sklasyfikowany jako nieprawdziwy, False negative (FN)) dokument prawdziwy sklasyfikowany jako nie- prawdziwy. 26
27 Miary oceny Najprościej jest przedstawić wprowadzone błędy jako strukturę macie- rzową związaną z rodzajem klasyfikacji dokumentu: Jaki jest najlepszy przypadek ułożenia danych w tej macierzy? W najlepszym przypadku wartości niezerowe będą umieszczone tylko na przekątnej macierzy. 27
28 Miary oceny Przykład rozłożenia wyników dla klas A i B oraz termów research oraz hall: Term research posiada lepiej rozłożone współczynniki niż term hall. 28
29 Miary oceny Błąd ogólny z wykorzystaniem zdefiniowanych współczynników jest zdefiniowany jako: error= FP FN TP FP TN FN Ogólna dokładność klasyfikacji jest zdefiniowana jako: accuracy= TP TN TP FP TN FN 29
30 Miary oceny Podobnie jak w przypadku techniki IR, tak dla grupowania można zde- finiować współczynniki precision oraz recall. Współczynnik precision jest zdefiniowany jako: precision= TP TP FP Wartości współczynnika precision zawierają się w zakresie od 0 do 1. Współczynnik opisuje stosunek obiektów należących do klasy A do obiektów należących do klasy A w rzeczywistości oraz wg algorytmu. 30
31 Miary oceny Współczynnik recall jest zdefiniowany jako: recall= TP TP FN Wartości współczynnika recall zawierają się w zakresie od 0 do 1. Współczynnik opisuje stosunek obiektów należących do klasy A do obiektów należących do klasy A w rzeczywistości oraz należących do klasy B wg algorytmu. 31
32 Miary oceny 32 Współczynnik recall może być sprowadzony do wartości równej 1 dla przypadku, gdy wszystkie dokumenty zostaną sklasyfikowane jako obiekty należące do klasy A. Współczynnik precision może być sprowadzony do wartości równej 1 dla przypadku, gdy klasyfikacja dotyczyła będzie tylko jednego dokumentu oraz ten dokument zostanie sklasyfikowany jako dokument należący do klasy A. W idealnym przypadku współczynniki powinny być jednocześnie równe 1.
33 Miary oceny Dla termu research współczynnik precision jest równy 1,0, zaś re- call ma wartość 0,73. Dla termu hall współczynnik precision jest równy 0,6, zaś recall ma wartość 0,82. Zależnie od rozpatrywanego problemu, jeden ze współczynników można uznać za priorytetowy. W przypadku systemu antyspamowe- go, gdzie klasa positive będzie oznaczała istotną wiadomość , to drugi rodzaj klasyfikacji jest lepszy, gdyż przepuszcza więcej wia- domości istotnych (82%), pomimo tego, że współczynnik precision dla pierwszego rodzaju klasyfikacji przyjmuje wartość 100%. 33
34 Podsumowanie Funkcje oceniające są nieodłącznym elementem grupowania danych, a w szczególności dokumentów sieci WWW. Pozwalają oceniać ja- kość grupowania oraz mogą być wykorzystane do optymalizacji wartości parametrów określających ilości grup tworzone przez algo- rytmy. Funkcje oceniające mogą przyjmować różne postacie: bazujące na centroidach, bazujące na podobieństwie par obiektów czy też korzys- tające z przyporządkowania obiektów do klas. 34
35 Dziękuję za uwagę!
Wyszukiwanie dokumentów WWW bazujące na słowach kluczowych
 Eksploracja zasobów internetowych Wykład 3 Wyszukiwanie dokumentów WWW bazujące na słowach kluczowych mgr inż. Maciej Kopczyński Białystok 2014 Wstęp Wyszukiwanie dokumentów za pomocą słów kluczowych bazujące
Eksploracja zasobów internetowych Wykład 3 Wyszukiwanie dokumentów WWW bazujące na słowach kluczowych mgr inż. Maciej Kopczyński Białystok 2014 Wstęp Wyszukiwanie dokumentów za pomocą słów kluczowych bazujące
Wstęp do grupowania danych
 Eksploracja zasobów internetowych Wykład 5 Wstęp do grupowania danych mgr inż. Maciej Kopczyński Białystok 2014 Wstęp Istnieją dwie podstawowe metody klasyfikowania obiektów: metoda z nauczycielem, metoda
Eksploracja zasobów internetowych Wykład 5 Wstęp do grupowania danych mgr inż. Maciej Kopczyński Białystok 2014 Wstęp Istnieją dwie podstawowe metody klasyfikowania obiektów: metoda z nauczycielem, metoda
4.3 Grupowanie według podobieństwa
 4.3 Grupowanie według podobieństwa Przykłady obiektów to coś więcej niż wektory wartości atrybutów. Reprezentują one poszczególne rasy psów. Ważnym pytaniem, jakie można sobie zadać, jest to jak dobrymi
4.3 Grupowanie według podobieństwa Przykłady obiektów to coś więcej niż wektory wartości atrybutów. Reprezentują one poszczególne rasy psów. Ważnym pytaniem, jakie można sobie zadać, jest to jak dobrymi
Data Mining Wykład 9. Analiza skupień (grupowanie) Grupowanie hierarchiczne O-Cluster. Plan wykładu. Sformułowanie problemu
 Data Mining Wykład 9 Analiza skupień (grupowanie) Grupowanie hierarchiczne O-Cluster Plan wykładu Wprowadzanie Definicja problemu Klasyfikacja metod grupowania Grupowanie hierarchiczne Sformułowanie problemu
Data Mining Wykład 9 Analiza skupień (grupowanie) Grupowanie hierarchiczne O-Cluster Plan wykładu Wprowadzanie Definicja problemu Klasyfikacja metod grupowania Grupowanie hierarchiczne Sformułowanie problemu
Sztuczna Inteligencja w medycynie projekt (instrukcja) Bożena Kostek
 Sztuczna Inteligencja w medycynie projekt (instrukcja) Bożena Kostek Cel projektu Celem projektu jest przygotowanie systemu wnioskowania, wykorzystującego wybrane algorytmy sztucznej inteligencji; Nabycie
Sztuczna Inteligencja w medycynie projekt (instrukcja) Bożena Kostek Cel projektu Celem projektu jest przygotowanie systemu wnioskowania, wykorzystującego wybrane algorytmy sztucznej inteligencji; Nabycie
Data Mining Wykład 4. Plan wykładu
 Data Mining Wykład 4 Klasyfikacja danych Klasyfikacja poprzez indukcje drzew decyzyjnych Plan wykładu Sformułowanie problemu Kryteria oceny metod klasyfikacji Metody klasyfikacji Klasyfikacja poprzez indukcje
Data Mining Wykład 4 Klasyfikacja danych Klasyfikacja poprzez indukcje drzew decyzyjnych Plan wykładu Sformułowanie problemu Kryteria oceny metod klasyfikacji Metody klasyfikacji Klasyfikacja poprzez indukcje
9. Praktyczna ocena jakości klasyfikacji
 Algorytmy rozpoznawania obrazów 9. Praktyczna ocena jakości klasyfikacji dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Zbiór uczacy i zbiór testowy 1. Zbiór uczacy służy do konstrukcji (treningu)
Algorytmy rozpoznawania obrazów 9. Praktyczna ocena jakości klasyfikacji dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Zbiór uczacy i zbiór testowy 1. Zbiór uczacy służy do konstrukcji (treningu)
Algorytm grupowania danych typu kwantyzacji wektorów
 Algorytm grupowania danych typu kwantyzacji wektorów Wstęp Definicja problemu: Typowe, rozważane dotychczas problemy koncentrowały się na nauczeniu na podstawie zbioru treningowego i zbioru etykiet klasyfikacji
Algorytm grupowania danych typu kwantyzacji wektorów Wstęp Definicja problemu: Typowe, rozważane dotychczas problemy koncentrowały się na nauczeniu na podstawie zbioru treningowego i zbioru etykiet klasyfikacji
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych
 Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Indukowane Reguły Decyzyjne I. Wykład 8
 Indukowane Reguły Decyzyjne I Wykład 8 IRD Wykład 8 Plan Powtórka Krzywa ROC = Receiver Operating Characteristic Wybór modelu Statystyka AUC ROC = pole pod krzywą ROC Wybór punktu odcięcia Reguły decyzyjne
Indukowane Reguły Decyzyjne I Wykład 8 IRD Wykład 8 Plan Powtórka Krzywa ROC = Receiver Operating Characteristic Wybór modelu Statystyka AUC ROC = pole pod krzywą ROC Wybór punktu odcięcia Reguły decyzyjne
Adrian Horzyk
 Metody Inteligencji Obliczeniowej Metoda K Najbliższych Sąsiadów (KNN) Adrian Horzyk horzyk@agh.edu.pl AGH Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
Metody Inteligencji Obliczeniowej Metoda K Najbliższych Sąsiadów (KNN) Adrian Horzyk horzyk@agh.edu.pl AGH Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
Hierarchiczna analiza skupień
 Hierarchiczna analiza skupień Cel analizy Analiza skupień ma na celu wykrycie w zbiorze obserwacji klastrów, czyli rozłącznych podzbiorów obserwacji, wewnątrz których obserwacje są sobie w jakimś określonym
Hierarchiczna analiza skupień Cel analizy Analiza skupień ma na celu wykrycie w zbiorze obserwacji klastrów, czyli rozłącznych podzbiorów obserwacji, wewnątrz których obserwacje są sobie w jakimś określonym
Techniki grupowania danych w środowisku Matlab
 Techniki grupowania danych w środowisku Matlab 1. Normalizacja danych. Jedne z metod normalizacji: = = ma ( y =, rσ ( = ( ma ( = min = (1 + e, min ( = σ wartość średnia, r współczynnik, σ odchylenie standardowe
Techniki grupowania danych w środowisku Matlab 1. Normalizacja danych. Jedne z metod normalizacji: = = ma ( y =, rσ ( = ( ma ( = min = (1 + e, min ( = σ wartość średnia, r współczynnik, σ odchylenie standardowe
Systemy uczące się wykład 2
 Systemy uczące się wykład 2 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 19 X 2018 Podstawowe definicje Fakt; Przesłanka; Konkluzja; Reguła; Wnioskowanie. Typy wnioskowania
Systemy uczące się wykład 2 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 19 X 2018 Podstawowe definicje Fakt; Przesłanka; Konkluzja; Reguła; Wnioskowanie. Typy wnioskowania
Eksploracja danych. Grupowanie. Wprowadzanie Definicja problemu Klasyfikacja metod grupowania Grupowanie hierarchiczne. Grupowanie wykład 1
 Grupowanie Wprowadzanie Definicja problemu Klasyfikacja metod grupowania Grupowanie hierarchiczne Grupowanie wykład 1 Sformułowanie problemu Dany jest zbiór obiektów (rekordów). Znajdź naturalne pogrupowanie
Grupowanie Wprowadzanie Definicja problemu Klasyfikacja metod grupowania Grupowanie hierarchiczne Grupowanie wykład 1 Sformułowanie problemu Dany jest zbiór obiektów (rekordów). Znajdź naturalne pogrupowanie
Wprowadzenie do uczenia maszynowego
 Wprowadzenie do uczenia maszynowego Agnieszka Ławrynowicz 12 stycznia 2017 Co to jest uczenie maszynowe? dziedzina nauki, która zajmuje się sprawianiem aby komputery mogły uczyć się bez ich zaprogramowania
Wprowadzenie do uczenia maszynowego Agnieszka Ławrynowicz 12 stycznia 2017 Co to jest uczenie maszynowe? dziedzina nauki, która zajmuje się sprawianiem aby komputery mogły uczyć się bez ich zaprogramowania
WYKŁAD 7. Testowanie jakości modeli klasyfikacyjnych metodyka i kryteria
 Wrocław University of Technology WYKŁAD 7 Testowanie jakości modeli klasyfikacyjnych metodyka i kryteria autor: Maciej Zięba Politechnika Wrocławska Testowanie modeli klasyfikacyjnych Dobór odpowiedniego
Wrocław University of Technology WYKŁAD 7 Testowanie jakości modeli klasyfikacyjnych metodyka i kryteria autor: Maciej Zięba Politechnika Wrocławska Testowanie modeli klasyfikacyjnych Dobór odpowiedniego
Agnieszka Nowak Brzezińska Wykład III
 Agnieszka Nowak Brzezińska Wykład III Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną niezależność zmiennych niezależnych (tu naiwność) Bardziej opisowe
Agnieszka Nowak Brzezińska Wykład III Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną niezależność zmiennych niezależnych (tu naiwność) Bardziej opisowe
CLUSTERING. Metody grupowania danych
 CLUSTERING Metody grupowania danych Plan wykładu Wprowadzenie Dziedziny zastosowania Co to jest problem klastrowania? Problem wyszukiwania optymalnych klastrów Metody generowania: k centroidów (k - means
CLUSTERING Metody grupowania danych Plan wykładu Wprowadzenie Dziedziny zastosowania Co to jest problem klastrowania? Problem wyszukiwania optymalnych klastrów Metody generowania: k centroidów (k - means
Systemy pomiarowo-diagnostyczne. Metody uczenia maszynowego wykład III 2016/2017
 Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład III bogumil.konopka@pwr.edu.pl 2016/2017 Wykład III - plan Regresja logistyczna Ocena skuteczności klasyfikacji Macierze pomyłek Krzywe
Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład III bogumil.konopka@pwr.edu.pl 2016/2017 Wykład III - plan Regresja logistyczna Ocena skuteczności klasyfikacji Macierze pomyłek Krzywe
Grupowanie Witold Andrzejewski, Politechnika Poznańska, Wydział Informatyki 201/633
 Grupowanie Grupowanie 7 6 5 4 y 3 2 1 0-3 -2-1 0 1 2 3 4 5-1 -2-3 -4 x Witold Andrzejewski, Politechnika Poznańska, Wydział Informatyki 201/633 Wprowadzenie Celem procesu grupowania jest podział zbioru
Grupowanie Grupowanie 7 6 5 4 y 3 2 1 0-3 -2-1 0 1 2 3 4 5-1 -2-3 -4 x Witold Andrzejewski, Politechnika Poznańska, Wydział Informatyki 201/633 Wprowadzenie Celem procesu grupowania jest podział zbioru
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
Data Mining Wykład 5. Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny. Indeks Gini. Indeks Gini - Przykład
 Data Mining Wykład 5 Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny Indeks Gini Popularnym kryterium podziału, stosowanym w wielu produktach komercyjnych, jest indeks Gini Algorytm SPRINT
Data Mining Wykład 5 Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny Indeks Gini Popularnym kryterium podziału, stosowanym w wielu produktach komercyjnych, jest indeks Gini Algorytm SPRINT
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Co to są drzewa decyzji
 Drzewa decyzji Co to są drzewa decyzji Drzewa decyzji to skierowane grafy acykliczne Pozwalają na zapis reguł w postaci strukturalnej Przyspieszają działanie systemów regułowych poprzez zawężanie przestrzeni
Drzewa decyzji Co to są drzewa decyzji Drzewa decyzji to skierowane grafy acykliczne Pozwalają na zapis reguł w postaci strukturalnej Przyspieszają działanie systemów regułowych poprzez zawężanie przestrzeni
Ocena dokładności diagnozy
 Ocena dokładności diagnozy Diagnoza medyczna, w wielu przypadkach może być interpretowana jako działanie polegające na podjęciu jednej z dwóch decyzji odnośnie stanu zdrowotnego pacjenta: 0 pacjent zdrowy
Ocena dokładności diagnozy Diagnoza medyczna, w wielu przypadkach może być interpretowana jako działanie polegające na podjęciu jednej z dwóch decyzji odnośnie stanu zdrowotnego pacjenta: 0 pacjent zdrowy
Metody eksploracji danych w odkrywaniu wiedzy (MED) projekt, dokumentacja końcowa
 Metody eksploracji danych w odkrywaniu wiedzy (MED) projekt, dokumentacja końcowa Konrad Miziński 14 stycznia 2015 1 Temat projektu Grupowanie hierarchiczne na podstawie algorytmu k-średnich. 2 Dokumenty
Metody eksploracji danych w odkrywaniu wiedzy (MED) projekt, dokumentacja końcowa Konrad Miziński 14 stycznia 2015 1 Temat projektu Grupowanie hierarchiczne na podstawie algorytmu k-średnich. 2 Dokumenty
Analiza skupień. Analiza Skupień W sztucznej inteligencji istotną rolę ogrywają algorytmy grupowania
 Analiza skupień W sztucznej inteligencji istotną rolę ogrywają algorytmy grupowania Analiza Skupień Elementy składowe procesu grupowania obiekt Ekstrakcja cech Sprzężenie zwrotne Grupowanie klastry Reprezentacja
Analiza skupień W sztucznej inteligencji istotną rolę ogrywają algorytmy grupowania Analiza Skupień Elementy składowe procesu grupowania obiekt Ekstrakcja cech Sprzężenie zwrotne Grupowanie klastry Reprezentacja
Zastosowanie stereowizji do śledzenia trajektorii obiektów w przestrzeni 3D
 Zastosowanie stereowizji do śledzenia trajektorii obiektów w przestrzeni 3D autorzy: Michał Dajda, Łojek Grzegorz opiekun naukowy: dr inż. Paweł Rotter I. O projekcie. 1. Celem projektu było stworzenie
Zastosowanie stereowizji do śledzenia trajektorii obiektów w przestrzeni 3D autorzy: Michał Dajda, Łojek Grzegorz opiekun naukowy: dr inż. Paweł Rotter I. O projekcie. 1. Celem projektu było stworzenie
IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ
 IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ Celem ćwiczenia jest zapoznanie się ze sposobem działania sieci neuronowych typu MLP (multi-layer perceptron) uczonych nadzorowaną (z nauczycielem,
IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ Celem ćwiczenia jest zapoznanie się ze sposobem działania sieci neuronowych typu MLP (multi-layer perceptron) uczonych nadzorowaną (z nauczycielem,
Charakterystyki oraz wyszukiwanie obrazów cyfrowych
 Algorytmy Graficzne Charakterystyki oraz wyszukiwanie obrazów cyfrowych Autor: Mateusz Nostitz-Jackowski 1 / 7 Działanie programu: Do poprawnego działania projektu potrzeba programu Mathematica 5.2 (możliwe
Algorytmy Graficzne Charakterystyki oraz wyszukiwanie obrazów cyfrowych Autor: Mateusz Nostitz-Jackowski 1 / 7 Działanie programu: Do poprawnego działania projektu potrzeba programu Mathematica 5.2 (możliwe
Agnieszka Nowak Brzezińska Wykład III
 Agnieszka Nowak Brzezińska Wykład III Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną niezależność zmiennych niezależnych (tu naiwność) Bardziej opisowe
Agnieszka Nowak Brzezińska Wykład III Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną niezależność zmiennych niezależnych (tu naiwność) Bardziej opisowe
ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH
 1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Eksploracja danych Co to znaczy eksploracja danych Klastrowanie (grupowanie) hierarchiczne Klastrowanie
1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Eksploracja danych Co to znaczy eksploracja danych Klastrowanie (grupowanie) hierarchiczne Klastrowanie
Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl
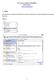 Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Aby skorzystać z możliwości RapidMinera w zakresie analizy tekstu, należy zainstalować Text Mining Extension. Wybierz: 1 Po
Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Aby skorzystać z możliwości RapidMinera w zakresie analizy tekstu, należy zainstalować Text Mining Extension. Wybierz: 1 Po
Elementy modelowania matematycznego
 Elementy modelowania matematycznego Modelowanie algorytmów klasyfikujących. Podejście probabilistyczne. Naiwny klasyfikator bayesowski. Modelowanie danych metodą najbliższych sąsiadów. Jakub Wróblewski
Elementy modelowania matematycznego Modelowanie algorytmów klasyfikujących. Podejście probabilistyczne. Naiwny klasyfikator bayesowski. Modelowanie danych metodą najbliższych sąsiadów. Jakub Wróblewski
Naiwny klasyfikator Bayesa brał pod uwagę jedynie najbliższe otoczenie. Lecz czym jest otoczenie? Jak je zdefiniować?
 Algorytm k-nn Naiwny klasyfikator Bayesa brał pod uwagę jedynie najbliższe otoczenie. Lecz czym jest otoczenie? Jak je zdefiniować? Jak daleko są położone obiekty od siebie? knn k nearest neighbours jest
Algorytm k-nn Naiwny klasyfikator Bayesa brał pod uwagę jedynie najbliższe otoczenie. Lecz czym jest otoczenie? Jak je zdefiniować? Jak daleko są położone obiekty od siebie? knn k nearest neighbours jest
Systemy pomiarowo-diagnostyczne. Metody uczenia maszynowego wykład II 2017/2018
 Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład II bogumil.konopka@pwr.edu.pl 2017/2018 Określenie rzeczywistej dokładności modelu Zbiór treningowym vs zbiór testowy Zbiór treningowy
Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład II bogumil.konopka@pwr.edu.pl 2017/2018 Określenie rzeczywistej dokładności modelu Zbiór treningowym vs zbiór testowy Zbiór treningowy
SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization
 Wrocław University of Technology SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization Jakub M. Tomczak Studenckie Koło Naukowe Estymator jakub.tomczak@pwr.wroc.pl 4.1.213 Klasteryzacja Zmienne
Wrocław University of Technology SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization Jakub M. Tomczak Studenckie Koło Naukowe Estymator jakub.tomczak@pwr.wroc.pl 4.1.213 Klasteryzacja Zmienne
Wprowadzenie do klasyfikacji
 Wprowadzenie do klasyfikacji ZeroR Odpowiada zawsze tak samo Decyzja to klasa większościowa ze zbioru uczącego A B X 1 5 T 1 7 T 1 5 T 1 5 F 2 7 F Tutaj jest więcej obiektów klasy T, więc klasyfikator
Wprowadzenie do klasyfikacji ZeroR Odpowiada zawsze tak samo Decyzja to klasa większościowa ze zbioru uczącego A B X 1 5 T 1 7 T 1 5 T 1 5 F 2 7 F Tutaj jest więcej obiektów klasy T, więc klasyfikator
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
B jest globalnym pokryciem zbioru {d} wtedy i tylko wtedy, gdy {d} zależy od B i nie istnieje B T takie, że {d} zależy od B ;
 Algorytm LEM1 Oznaczenia i definicje: U - uniwersum, tj. zbiór obiektów; A - zbiór atrybutów warunkowych; d - atrybut decyzyjny; IND(B) = {(x, y) U U : a B a(x) = a(y)} - relacja nierozróżnialności, tj.
Algorytm LEM1 Oznaczenia i definicje: U - uniwersum, tj. zbiór obiektów; A - zbiór atrybutów warunkowych; d - atrybut decyzyjny; IND(B) = {(x, y) U U : a B a(x) = a(y)} - relacja nierozróżnialności, tj.
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO
 SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
METODY INŻYNIERII WIEDZY
 METODY INŻYNIERII WIEDZY Metoda K Najbliższych Sąsiadów K-Nearest Neighbours (KNN) ĆWICZENIA Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
METODY INŻYNIERII WIEDZY Metoda K Najbliższych Sąsiadów K-Nearest Neighbours (KNN) ĆWICZENIA Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
Sztuczna Inteligencja Projekt
 Sztuczna Inteligencja Projekt Temat: Algorytm F-LEM1 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm F LEM 1. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu F LEM1
Sztuczna Inteligencja Projekt Temat: Algorytm F-LEM1 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm F LEM 1. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu F LEM1
Agnieszka Nowak Brzezińska
 Agnieszka Nowak Brzezińska jeden z algorytmów regresji nieparametrycznej używanych w statystyce do prognozowania wartości pewnej zmiennej losowej. Może również byd używany do klasyfikacji. - Założenia
Agnieszka Nowak Brzezińska jeden z algorytmów regresji nieparametrycznej używanych w statystyce do prognozowania wartości pewnej zmiennej losowej. Może również byd używany do klasyfikacji. - Założenia
Konkurs z przedmiotu eksploracja i analiza danych: problem regresji i klasyfikacji
 Konkurs z przedmiotu eksploracja i analiza danych: problem regresji i klasyfikacji Michał Witczak Data Mining 20 maja 2012 r. 1. Wstęp Dostarczone zostały nam 4 pliki, z których dwa stanowiły zbiory uczące
Konkurs z przedmiotu eksploracja i analiza danych: problem regresji i klasyfikacji Michał Witczak Data Mining 20 maja 2012 r. 1. Wstęp Dostarczone zostały nam 4 pliki, z których dwa stanowiły zbiory uczące
ALGORYTMY SZTUCZNEJ INTELIGENCJI
 ALGORYTMY SZTUCZNEJ INTELIGENCJI Sieci neuronowe 06.12.2014 Krzysztof Salamon 1 Wstęp Sprawozdanie to dotyczy ćwiczeń z zakresu sieci neuronowych realizowanym na przedmiocie: Algorytmy Sztucznej Inteligencji.
ALGORYTMY SZTUCZNEJ INTELIGENCJI Sieci neuronowe 06.12.2014 Krzysztof Salamon 1 Wstęp Sprawozdanie to dotyczy ćwiczeń z zakresu sieci neuronowych realizowanym na przedmiocie: Algorytmy Sztucznej Inteligencji.
Algorytm genetyczny (genetic algorithm)-
 Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA
 METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
6. Zagadnienie parkowania ciężarówki.
 6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Wykład 4: Statystyki opisowe (część 1)
 Wykład 4: Statystyki opisowe (część 1) Wprowadzenie W przypadku danych mających charakter liczbowy do ich charakterystyki można wykorzystać tak zwane STATYSTYKI OPISOWE. Za pomocą statystyk opisowych można
Wykład 4: Statystyki opisowe (część 1) Wprowadzenie W przypadku danych mających charakter liczbowy do ich charakterystyki można wykorzystać tak zwane STATYSTYKI OPISOWE. Za pomocą statystyk opisowych można
Laboratorium 4. Naiwny klasyfikator Bayesa.
 Laboratorium 4 Naiwny klasyfikator Bayesa. 1. Uruchom narzędzie Oracle Data Miner i połącz się z serwerem bazy danych. 2. Z menu głównego wybierz Activity Build. Na ekranie powitalnym kliknij przycisk
Laboratorium 4 Naiwny klasyfikator Bayesa. 1. Uruchom narzędzie Oracle Data Miner i połącz się z serwerem bazy danych. 2. Z menu głównego wybierz Activity Build. Na ekranie powitalnym kliknij przycisk
Klasyfikatory: k-nn oraz naiwny Bayesa. Agnieszka Nowak Brzezińska Wykład IV
 Klasyfikatory: k-nn oraz naiwny Bayesa Agnieszka Nowak Brzezińska Wykład IV Naiwny klasyfikator Bayesa Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną
Klasyfikatory: k-nn oraz naiwny Bayesa Agnieszka Nowak Brzezińska Wykład IV Naiwny klasyfikator Bayesa Naiwny klasyfikator bayesowski jest prostym probabilistycznym klasyfikatorem. Zakłada się wzajemną
Alicja Marszałek Różne rodzaje baz danych
 Alicja Marszałek Różne rodzaje baz danych Rodzaje baz danych Bazy danych można podzielić wg struktur organizacji danych, których używają. Można podzielić je na: Bazy proste Bazy złożone Bazy proste Bazy
Alicja Marszałek Różne rodzaje baz danych Rodzaje baz danych Bazy danych można podzielić wg struktur organizacji danych, których używają. Można podzielić je na: Bazy proste Bazy złożone Bazy proste Bazy
Informacje i materiały dotyczące wykładu będą publikowane na stronie internetowej wykładowcy, m.in. prezentacje z wykładów
 Eksploracja danych Piotr Lipiński Informacje ogólne Informacje i materiały dotyczące wykładu będą publikowane na stronie internetowej wykładowcy, m.in. prezentacje z wykładów UWAGA: prezentacja to nie
Eksploracja danych Piotr Lipiński Informacje ogólne Informacje i materiały dotyczące wykładu będą publikowane na stronie internetowej wykładowcy, m.in. prezentacje z wykładów UWAGA: prezentacja to nie
Barycentryczny układ współrzędnych
 SkaiWD Laboratorium 2 Barycentryczny układ współrzędnych Iwo Błądek 21 marca 2019 1 Barycentryczny układ współrzędnych Podstawowa wiedza została przekazana na wykładzie. W tej sekcji znajdują się proste
SkaiWD Laboratorium 2 Barycentryczny układ współrzędnych Iwo Błądek 21 marca 2019 1 Barycentryczny układ współrzędnych Podstawowa wiedza została przekazana na wykładzie. W tej sekcji znajdują się proste
WYKŁAD 9 METODY ZMIENNEJ METRYKI
 WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
Metody klasyfikacji danych - część 1 p.1/24
 Metody klasyfikacji danych - część 1 Inteligentne Usługi Informacyjne Jerzy Dembski Metody klasyfikacji danych - część 1 p.1/24 Plan wykładu - Zadanie klasyfikacji danych - Przeglad problemów klasyfikacji
Metody klasyfikacji danych - część 1 Inteligentne Usługi Informacyjne Jerzy Dembski Metody klasyfikacji danych - część 1 p.1/24 Plan wykładu - Zadanie klasyfikacji danych - Przeglad problemów klasyfikacji
Eksploracja Danych. wykład 4. Sebastian Zając. 10 maja 2017 WMP.SNŚ UKSW. Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja / 18
 Eksploracja Danych wykład 4 Sebastian Zając WMP.SNŚ UKSW 10 maja 2017 Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja 2017 1 / 18 Klasyfikacja danych Klasyfikacja Najczęściej stosowana (najstarsza)
Eksploracja Danych wykład 4 Sebastian Zając WMP.SNŚ UKSW 10 maja 2017 Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja 2017 1 / 18 Klasyfikacja danych Klasyfikacja Najczęściej stosowana (najstarsza)
Inspiracje kognitywne w procesie analizy pozycji szachowej
 Inspiracje kognitywne w procesie analizy pozycji szachowej C. Dendek J. Mańdziuk Warsaw University of Technology, Faculty of Mathematics and Information Science Abstrakt Główny cel Poprawa efektywności
Inspiracje kognitywne w procesie analizy pozycji szachowej C. Dendek J. Mańdziuk Warsaw University of Technology, Faculty of Mathematics and Information Science Abstrakt Główny cel Poprawa efektywności
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
SYSTEMY UCZĄCE SIĘ WYKŁAD 3. DRZEWA DECYZYJNE. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 3. DRZEWA DECYZYJNE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska BUDOWA DRZEW DECYZYJNYCH Drzewa decyzyjne są metodą indukcyjnego
SYSTEMY UCZĄCE SIĘ WYKŁAD 3. DRZEWA DECYZYJNE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska BUDOWA DRZEW DECYZYJNYCH Drzewa decyzyjne są metodą indukcyjnego
Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change
 Raport 4/2015 Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change autor: Michał Osmoła INIME Instytut nauk informatycznych i matematycznych
Raport 4/2015 Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change autor: Michał Osmoła INIME Instytut nauk informatycznych i matematycznych
Algorytm grupowania danych typu kwantyzacji wektorów
 Algorytm grupowania danych typu kwantyzacji wektorów Wstęp Definicja problemu: Typowe, problemem często spotykanym w zagadnieniach eksploracji danych (ang. data mining) jest zagadnienie grupowania danych
Algorytm grupowania danych typu kwantyzacji wektorów Wstęp Definicja problemu: Typowe, problemem często spotykanym w zagadnieniach eksploracji danych (ang. data mining) jest zagadnienie grupowania danych
4. Funkcje. Przykłady
 4. Funkcje Przykłady 4.1. Napisz funkcję kwadrat, która przyjmuje jeden argument: długość boku kwadratu i zwraca pole jego powierzchni. Używając tej funkcji napisz program, który obliczy pole powierzchni
4. Funkcje Przykłady 4.1. Napisz funkcję kwadrat, która przyjmuje jeden argument: długość boku kwadratu i zwraca pole jego powierzchni. Używając tej funkcji napisz program, który obliczy pole powierzchni
METODY INŻYNIERII WIEDZY
 METODY INŻYNIERII WIEDZY Metoda K Najbliższych Sąsiadów K-Nearest Neighbours (KNN) ĆWICZENIA Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
METODY INŻYNIERII WIEDZY Metoda K Najbliższych Sąsiadów K-Nearest Neighbours (KNN) ĆWICZENIA Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
Elementy statystyki wielowymiarowej
 Wnioskowanie_Statystyczne_-_wykład Spis treści 1 Elementy statystyki wielowymiarowej 1.1 Kowariancja i współczynnik korelacji 1.2 Macierz kowariancji 1.3 Dwumianowy rozkład normalny 1.4 Analiza składowych
Wnioskowanie_Statystyczne_-_wykład Spis treści 1 Elementy statystyki wielowymiarowej 1.1 Kowariancja i współczynnik korelacji 1.2 Macierz kowariancji 1.3 Dwumianowy rozkład normalny 1.4 Analiza składowych
Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI
 1 Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI 1. Obliczenia w arkuszu kalkulacyjnym Rozwiązywanie problemów z wykorzystaniem aplikacji komputerowych obliczenia w arkuszu kalkulacyjnym wykonuje
1 Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI 1. Obliczenia w arkuszu kalkulacyjnym Rozwiązywanie problemów z wykorzystaniem aplikacji komputerowych obliczenia w arkuszu kalkulacyjnym wykonuje
ALGORYTM RANDOM FOREST
 SKRYPT PRZYGOTOWANY NA ZAJĘCIA INDUKOWANYCH REGUŁ DECYZYJNYCH PROWADZONYCH PRZEZ PANA PAWŁA WOJTKIEWICZA ALGORYTM RANDOM FOREST Katarzyna Graboś 56397 Aleksandra Mańko 56699 2015-01-26, Warszawa ALGORYTM
SKRYPT PRZYGOTOWANY NA ZAJĘCIA INDUKOWANYCH REGUŁ DECYZYJNYCH PROWADZONYCH PRZEZ PANA PAWŁA WOJTKIEWICZA ALGORYTM RANDOM FOREST Katarzyna Graboś 56397 Aleksandra Mańko 56699 2015-01-26, Warszawa ALGORYTM
Algorytmy klasteryzacji jako metoda dyskretyzacji w algorytmach eksploracji danych. Łukasz Przybyłek, Jakub Niwa Studenckie Koło Naukowe BRAINS
 Algorytmy klasteryzacji jako metoda dyskretyzacji w algorytmach eksploracji danych Łukasz Przybyłek, Jakub Niwa Studenckie Koło Naukowe BRAINS Dyskretyzacja - definicja Dyskretyzacja - zamiana atrybutów
Algorytmy klasteryzacji jako metoda dyskretyzacji w algorytmach eksploracji danych Łukasz Przybyłek, Jakub Niwa Studenckie Koło Naukowe BRAINS Dyskretyzacja - definicja Dyskretyzacja - zamiana atrybutów
Inteligencja obliczeniowa
 Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY PRZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH
 WSOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY RZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH 1. Definicje Zbiory, które nie są zbiorami definiowalnymi, są nazywane zbiorami przybliżonymi. Zbiory definiowalne
WSOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY RZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH 1. Definicje Zbiory, które nie są zbiorami definiowalnymi, są nazywane zbiorami przybliżonymi. Zbiory definiowalne
Słowem wstępu. Część rodziny języków XSL. Standard: W3C XSLT razem XPath 1.0 XSLT Trwają prace nad XSLT 3.0
 Słowem wstępu Część rodziny języków XSL Standard: W3C XSLT 1.0-1999 razem XPath 1.0 XSLT 2.0-2007 Trwają prace nad XSLT 3.0 Problem Zakładane przez XML usunięcie danych dotyczących prezentacji pociąga
Słowem wstępu Część rodziny języków XSL Standard: W3C XSLT 1.0-1999 razem XPath 1.0 XSLT 2.0-2007 Trwają prace nad XSLT 3.0 Problem Zakładane przez XML usunięcie danych dotyczących prezentacji pociąga
Klasyfikacja publikacji biomedycznych w konkursie JRS 2012 Data Mining Competition - Szkic koncepcji
 Kierunek: Informatyka Zastosowania Informatyki w Medycynie Klasyfikacja publikacji biomedycznych w konkursie JRS 2012 Data Mining Competition - Szkic koncepcji 1. WSTĘP AUTORZY Joanna Binczewska gr. I3.1
Kierunek: Informatyka Zastosowania Informatyki w Medycynie Klasyfikacja publikacji biomedycznych w konkursie JRS 2012 Data Mining Competition - Szkic koncepcji 1. WSTĘP AUTORZY Joanna Binczewska gr. I3.1
Idea. Algorytm zachłanny Algorytmy hierarchiczne Metoda K-średnich Metoda hierarchiczna, a niehierarchiczna. Analiza skupień
 Idea jest narzędziem analizy danych służącym do grupowania n obiektów, opisanych za pomocą wektora p-cech, w K niepustych, rozłącznych i możliwie jednorodnych grup skupień. Obiekty należące do danego skupienia
Idea jest narzędziem analizy danych służącym do grupowania n obiektów, opisanych za pomocą wektora p-cech, w K niepustych, rozłącznych i możliwie jednorodnych grup skupień. Obiekty należące do danego skupienia
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
4.1. Wprowadzenie...70 4.2. Podstawowe definicje...71 4.3. Algorytm określania wartości parametrów w regresji logistycznej...74
 3 Wykaz najważniejszych skrótów...8 Przedmowa... 10 1. Podstawowe pojęcia data mining...11 1.1. Wprowadzenie...12 1.2. Podstawowe zadania eksploracji danych...13 1.3. Główne etapy eksploracji danych...15
3 Wykaz najważniejszych skrótów...8 Przedmowa... 10 1. Podstawowe pojęcia data mining...11 1.1. Wprowadzenie...12 1.2. Podstawowe zadania eksploracji danych...13 1.3. Główne etapy eksploracji danych...15
KLUCZ PUNKTOWANIA ODPOWIEDZI
 Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartości funkcji dla danych argumentów i jej miejsca zerowego. Zdający
Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartości funkcji dla danych argumentów i jej miejsca zerowego. Zdający
Statystyka. Wykład 7. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Statystyka 16 kwietnia / 35
 Statystyka Wykład 7 Magdalena Alama-Bućko 16 kwietnia 2017 Magdalena Alama-Bućko Statystyka 16 kwietnia 2017 1 / 35 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 7 Magdalena Alama-Bućko 16 kwietnia 2017 Magdalena Alama-Bućko Statystyka 16 kwietnia 2017 1 / 35 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Stan dotychczasowy. OCENA KLASYFIKACJI w diagnostyce. Metody 6/10/2013. Weryfikacja. Testowanie skuteczności metody uczenia Weryfikacja prosta
 Stan dotychczasowy OCENA KLASYFIKACJI w diagnostyce Wybraliśmy metodę uczenia maszynowego (np. sieć neuronowa lub drzewo decyzyjne), która będzie klasyfikować nieznane przypadki Na podzbiorze dostępnych
Stan dotychczasowy OCENA KLASYFIKACJI w diagnostyce Wybraliśmy metodę uczenia maszynowego (np. sieć neuronowa lub drzewo decyzyjne), która będzie klasyfikować nieznane przypadki Na podzbiorze dostępnych
Społeczna odpowiedzialność biznesu podejście strategiczne i operacyjne. Maciej Bieńkiewicz
 2012 Społeczna odpowiedzialność biznesu podejście strategiczne i operacyjne Maciej Bieńkiewicz Społeczna Odpowiedzialność Biznesu - istota koncepcji - Nowa definicja CSR: CSR - Odpowiedzialność przedsiębiorstw
2012 Społeczna odpowiedzialność biznesu podejście strategiczne i operacyjne Maciej Bieńkiewicz Społeczna Odpowiedzialność Biznesu - istota koncepcji - Nowa definicja CSR: CSR - Odpowiedzialność przedsiębiorstw
Egzamin z Metod Numerycznych ZSI, Grupa: A
 Egzamin z Metod Numerycznych ZSI, 06.2005. Grupa: A Nazwisko: Imię: Numer indeksu: Ćwiczenia z: Data: Część 1. Test wyboru, max 36 pkt Zaznacz prawidziwe odpowiedzi literą T, a fałszywe N. Każda prawidłowa
Egzamin z Metod Numerycznych ZSI, 06.2005. Grupa: A Nazwisko: Imię: Numer indeksu: Ćwiczenia z: Data: Część 1. Test wyboru, max 36 pkt Zaznacz prawidziwe odpowiedzi literą T, a fałszywe N. Każda prawidłowa
Indukowane Reguły Decyzyjne I. Wykład 3
 Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Maciej Piotr Jankowski
 Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Temat: Model SUGENO. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Model SUGENO Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Temat: Model SUGENO Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Kwerenda. parametryczna, z polem wyliczeniowym, krzyżowa
 Kwerenda parametryczna, z polem wyliczeniowym, krzyżowa Operatory stosowane w wyrażeniach pól wyliczeniowych Przykład: wyliczanie wartości w kwerendach W tabeli Pracownicy zapisano wartości stawki godzinowej
Kwerenda parametryczna, z polem wyliczeniowym, krzyżowa Operatory stosowane w wyrażeniach pól wyliczeniowych Przykład: wyliczanie wartości w kwerendach W tabeli Pracownicy zapisano wartości stawki godzinowej
Liczby zmiennoprzecinkowe i błędy
 i błędy Elementy metod numerycznych i błędy Kontakt pokój B3-10 tel.: 829 53 62 http://golinski.faculty.wmi.amu.edu.pl/ golinski@amu.edu.pl i błędy Plan wykładu 1 i błędy Plan wykładu 1 2 i błędy Plan
i błędy Elementy metod numerycznych i błędy Kontakt pokój B3-10 tel.: 829 53 62 http://golinski.faculty.wmi.amu.edu.pl/ golinski@amu.edu.pl i błędy Plan wykładu 1 i błędy Plan wykładu 1 2 i błędy Plan
7. Zagadnienie parkowania ciężarówki.
 7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu
 Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu - ogólnie Obecnie obowiązuje statystyczna metoda reprezentacyjnego pomiaru miąższości w obrębie leśnym. Metoda reprezentacyjna oznacza, iż
Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu - ogólnie Obecnie obowiązuje statystyczna metoda reprezentacyjnego pomiaru miąższości w obrębie leśnym. Metoda reprezentacyjna oznacza, iż
Konstruktory. Streszczenie Celem wykładu jest zaprezentowanie konstruktorów w Javie, syntaktyki oraz zalet ich stosowania. Czas wykładu 45 minut.
 Konstruktory Streszczenie Celem wykładu jest zaprezentowanie konstruktorów w Javie, syntaktyki oraz zalet ich stosowania. Czas wykładu 45 minut. Rozpatrzmy przykład przedstawiający klasę Prostokat: class
Konstruktory Streszczenie Celem wykładu jest zaprezentowanie konstruktorów w Javie, syntaktyki oraz zalet ich stosowania. Czas wykładu 45 minut. Rozpatrzmy przykład przedstawiający klasę Prostokat: class
Analiza danych. http://zajecia.jakubw.pl/ TEMATYKA PRZEDMIOTU
 Analiza danych Wstęp Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ TEMATYKA PRZEDMIOTU Różne aspekty analizy danych Reprezentacja graficzna danych Metody statystyczne: estymacja parametrów
Analiza danych Wstęp Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ TEMATYKA PRZEDMIOTU Różne aspekty analizy danych Reprezentacja graficzna danych Metody statystyczne: estymacja parametrów
Tworzenie prezentacji w MS PowerPoint
 Tworzenie prezentacji w MS PowerPoint Program PowerPoint dostarczany jest w pakiecie Office i daje nam możliwość stworzenia prezentacji oraz uatrakcyjnienia materiału, który chcemy przedstawić. Prezentacje
Tworzenie prezentacji w MS PowerPoint Program PowerPoint dostarczany jest w pakiecie Office i daje nam możliwość stworzenia prezentacji oraz uatrakcyjnienia materiału, który chcemy przedstawić. Prezentacje
Algorytmy rozpoznawania obrazów. 11. Analiza skupień. dr inż. Urszula Libal. Politechnika Wrocławska
 Algorytmy rozpoznawania obrazów 11. Analiza skupień dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Analiza skupień Określenia: analiza skupień (cluster analysis), klasteryzacja (clustering), klasyfikacja
Algorytmy rozpoznawania obrazów 11. Analiza skupień dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Analiza skupień Określenia: analiza skupień (cluster analysis), klasteryzacja (clustering), klasyfikacja
Jeśli X jest przestrzenią o nieskończonej liczbie elementów:
 Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH
 RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
WYKŁAD 6. Reguły decyzyjne
 Wrocław University of Technology WYKŁAD 6 Reguły decyzyjne autor: Maciej Zięba Politechnika Wrocławska Reprezentacje wiedzy Wiedza w postaci reguł decyzyjnych Wiedza reprezentowania jest w postaci reguł
Wrocław University of Technology WYKŁAD 6 Reguły decyzyjne autor: Maciej Zięba Politechnika Wrocławska Reprezentacje wiedzy Wiedza w postaci reguł decyzyjnych Wiedza reprezentowania jest w postaci reguł
Krzywe ROC i inne techniki oceny jakości klasyfikatorów
 Krzywe ROC i inne techniki oceny jakości klasyfikatorów Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego 20 maja 2009 1 2 Przykład krzywej ROC 3 4 Pakiet ROCR Dostępne metryki Krzywe
Krzywe ROC i inne techniki oceny jakości klasyfikatorów Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego 20 maja 2009 1 2 Przykład krzywej ROC 3 4 Pakiet ROCR Dostępne metryki Krzywe
