Współrzędne nawigacyjne

Położenie satelity na podstawie wiadomości nawigacyjnej w formacie RINEX. dr hab. inż. Paweł Zalewski, prof. AM

Położenie satelity na podstawie wiadomości nawigacyjnej w formacie RINEX dr hab. inż. Paweł Zalewsi, prof. AM 1. RINEX Położenie satelity - Zalewsi RINEX The Receiver Independent Exchange Format Version

Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF

GŁÓWNY URZĄD GEODEZJI I KARTOGRAFII Departament Geodezji, Kartografii i Systemów Informacji Geograficznej Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF Marcin Ryczywolski

4π 2 M = E e sin E G neu = sin z. i cos A i sin z i sin A i cos z i 1

1 Z jaką prędkością porusza się satelita na orbicie geostacjonarnej? 2 Wiedząc, że doba gwiazdowa na planecie X (stała grawitacyjna µ = 500 000 km 3 /s 2 ) trwa 24 godziny, oblicz promień orbity satelity

Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF

GŁÓWNY URZĄD GEODEZJI I KARTOGRAFII Departament Geodezji, Kartografii i Systemów Informacji Geograficznej Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF Szymon Wajda główny

SATELITARNE TECHNIKI POMIAROWE WYKŁAD 4

SATELITARNE TECHNIKI POMIAROWE WYKŁAD 4 1 K. Czarnecki, Geodezja współczesna w zarysie, Wiedza i Życie/Gall, Warszawa 2000/Katowice 2010. 2 Można skorzystać z niepełnej analogii do pomiarów naziemnymi

Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF

Pomiary statyczne GNSS i serwisy postprocessingu: POZGEO, POZGEO D i POZGEO DF Marcin Ryczywolski marcin.ryczywolski@gugik.gov.pl Główny Urząd Geodezji i Kartografii Olsztyn, 10-11 października 2013 r.

Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż

Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż

Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń

Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć

z{ } ! #$%&'()&!(*' +,-('--.'/* 0& 1!,$' 2&'3 $*4!&,'3$ -/!(*' >;H :; j k j k j k

0123 55678 23122 22 1ˆ 2!#$%&'()&!(*'+,-('--.'/*0&1!,$' 2&'3$*4!&,'3$-/!(*'567728 :;=>?@AB>;C@>;DEFG:;:HI@;H>JC@>;K@LMAAMAL NDEFGN>AB@ABMAL NDE O PQ:H:RRRSTUVSWYZ[U\]]^_:;MAaH;b=HM:Aa>ABHI@?>H@aHMA:;c>HM:AO

Wyznaczanie współrzędnych geocentrycznych odbiornika z rozwiązania nawigacyjnego GPS

Wyznaczanie współrzędnych geocentrycznych odbiornika z rozwiązania nawigacyjnego GS Wstęp Celem ćwiczenia, jest zaznajomienie z procedurą wyznaczania pozycji odbiornika GS z obserwacji kodowych Niezbędnym

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 07 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U s ł u g i s p r z» t a n i a o b i e k t Gó w d y s k i e g o C e n

Dokładność pozycji. dr inż. Stefan Jankowski

Dokładność pozycji dr inż. Stefan Jankowski s.jankowski@am.szczecin.pl Nawigacja Nawigacja jest gałęzią nauki zajmującą się prowadzeniem statku bezpieczną i optymalną drogą. Znajomość nawigacji umożliwia

Laboratorium z Miernictwa Górniczego

Laboratorium z Miernictwa Górniczego Materiały pomocnicze I Planowanie warunków obserwacji satelitów GPS/GLONASS Opracował dr inż. Jan Blachowski jan.blachowski@pwr.wroc.pl, pok. 505, bud. K-1, tel. 320

Helena Boguta, klasa 8W, rok szkolny 2018/2019

Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na

DODATKOWE ĆWICZENIA EGZAMINACYJNE

I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What

!" #$%! &" #$%'%#% '', 9;,) $!+$ #,) $!+$ # GHIJ9-KL1-MNO,.F$G ( * -2 1( &.#!! M & ' a ; ^? c 1 ' S 1 & MW / & & 1 M 1 1 c( />? / & _ _ ; P / 3

!" #$%! &" #$%'%#% '', 9;,) $!+$ #,)$!+$ # GHIJ9-KL1-MNO,.F$G (* -2 1( &.#!!M & ' a ; ^? c 1 ' S1 & MW/ & 5661&1M11c( />?/ &_ _ ; P/3'W1 1'a- 1A6 E V7 X- Z(618-3,1`JK1 ()/ &.#!!M *+,-.$/01 /. B*1*J S;

Funkcje wielu zmiennych

Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem

ᐗ升 G ឧ卷n z ) P W E L E : Graphis f udi f. l:+ 6 4 66 x:+ 6 4 6 c @g ://www c ᆗ吇g PÓŹ E ᐗ升Eᐗ升 ᐗ升 G ( H / H E 8 WE E I cj ż w ᆗ吇 ᆗ吇ᆗ吇ᆗ吇 ᆗ吇 ᆗ吇 c ᆗ吇ᆗ吇ᆗ吇 / ᆗ吇 c ᆗ吇ᆗ吇ᆗ吇 ᆗ吇ᆗ吇 ᆗ吇 ᆗ吇 w j ᆗ吇ឧ喇 j z c c ł w c l g

!"#$%&' % ( )* +,-!./0 1 % : ; < A+ 89 BCD.! )*E F GHIJ EK7LMNO PQRSTUVW89 56./0: Z[0 Z\]Y ^_`!abcn 7 E YQ "!EK GH < 8 0 0A`! 5

!"#$%&' % ( )* +,-!./0 1 % +234 56789 : ; < =>?@ A+ 89 BCD.! )*E F GHIJ EK7LMNO PQRSTUVW89 0XY+ @ 56./0: Z[0 Z\]Y ^_`!abcn 7 E YQ "!EK GH < 8 0 0A`! 5!! 5 E N ANO 5 " 2 1 ` Z\Y!! E 5!"F #$ (%&' ( ) ( #"

r = ψ x ( 5 ) = x ψ ( 6 ) dn = q(x)dx ( 7 ) dt = μdn = μq(x)dx ( 8 ) M = M ( 1 )

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X O K R E L E N I E O S I O B R O T U M A Y C H R O B O T W G Ą S I E N I C O W Y C H D L A P O T R Z E B O P I S U M O D E L

)& J, + 2? - (4 2 =1 )& 216 6)6!"#$%& '!"#$%& ' & '!"#$%&' '%% # ()*(+,-' %./01,#23 % ( :./0 :; 78 F G2H

)& 6 6 6 J, + 2? (5@2 - (4 2(@ 2 +7?%@ =1 )& 216 6)6!"#$%& '!"#$%& ' & '!"#$%&' '%% # ()*(+,-' %./01,#23 % ( 45 16789:./0 :; 78 ?@=A,BCDE F ) @ G2HIJKL MNO # 78 P # MBQ R8 PS 78TU G2 HVWXNO Y "1 78

Analiza Matematyczna MAEW101 MAP1067

Analiza Matematyczna MAEW MAP67 Wydział Elektroniki Przykłady do Listy Zadań nr 4 Funkcje wielu zmiennych. Pochodne cząstkowe Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania 4.: Wyznaczyć

!"#$ # % &'# #% # # ( )*+,-.-% /.0! 1!"#$%&' ()*+,-./% "67 8&9:;! )* DE FGHIJ/KLKMNO KM * K 9 PQR4STUVKNWX4N%&Y N )* Z[ \]B^_`ab

!"#$ # % &'# #% # # ( )*+,-.-% /.0! 1=>?@ 1!"#$%&' ()*+,-./%01 2345 "67 8&9:;! )* ?@ABC DE FGHIJ/KLKMNO KM * K 9 PQR4STUVKNWX4N%&Y N )* Z[ \]B^_`abNc LGH M QR4S!"#$%!&' "!ABC$%&' DE C /0 1 FGHIJ CKLM

Instrukcja obsługi ramek cyfrowych AD Display seria PF

Instrukcja obsługi ramek cyfrowych AD Display seria PF - 1 - Spis treści Rozdział 1 Przegląd... 1 1.1 Wprowadzenie... 1 1.2 Zawartość pudełka... 1 1.3 Informacje o używaniu nośników CF, SD i USB w AD Display

Laboratorium 10 Temat: Zaawansowane jednostki testowe. Operacje na plikach. Funkcje.

Laboratorium 10 Temat: Zaawansowane jednostki testowe. Operacje na plikach. Funkcje. 1. W języku VHDL zdefiniowano mechanizm odczytywania i zapisywania danych z i do plików. Pliki te mogą być wykorzystywane

( ( (=6) *6() )! "#$%&'! "#$ % &'"#!! "#$ $ "#! (()!"#$%& (() (()! " # $ (() % &' #! " # $ (()! " # $ (() ( ( ( ( ( *! "#$%&$#' () * + +,-. /

(((6(*=@ ( ( (=6) *6()! "#$%&'! "#$ % &'"#!! "#$ $ "#! (()!"#$%& (() (()! " # $ (() % &' #! " # $ (()! " # $ (() ( ( ( ( ( *! "#$%&$#' () * + +,-. / ( 0!1.(, () '(,,., # $ & & % "2, +,-. /, 01 +/, - -0

Suodattimet PUSSISUODATIN ALTECH GX EPM10 60PROS. 287X592X525/3 PUSSISUODATIN ALTECH GX EPM10 60PROS. 592X287X360/6

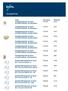Suodattimet Tuote LVI-numero Pikakoodi 7754400 OK08 GX EPM10 60PROS. 287X592X360/3 GX EPM10 60PROS. 287X592X525/3 GX EPM10 60PROS. 592X287X360/6 GX EPM10 60PROS. 592X287X525/6 GX EPM10 60PROS. 592X592X360/6

! "#$ %&'! '$! ( )!! "#$%&' ()*+,*"-./01 $%1! 2#34 567! $%1 8/9:;% + &BCD:;E 9 $%1 F$%GHI# JKLMNO & # PQRST"JKUV9 A# $%WXE%Y $%"#%(1 7! ; Z

! "#$ %&'! '$! ( )!! "#$%&' ()*+,*"-./01 $%1! 2#34 567! $%1 8/9:;% + ?@+A#$% &BCD:;E 9 $%1 F$%GHI# JKLMNO & # PQRST"JKUV9 A# $%WXE%Y $%"#%(1 7! ; Z # M[ $%1 \ # %]^!X 34 M[; ^ _` abc Z ; #E%bc;W% W%

ñ 1 9! Ù DEF+>/ P Q V { Ó bbó 1 YZ"p¼~ Þ Üb á \ V ~ Y Z#'! Ù DEF+>/P Q V g E o 9 &5

! ( *+,-./1 < =,>?@A 7 BCDE : F G,-. 2 3 H IJ B C K < L M 8, O :,-. 234567 6, :8 P,-. 2 3 8 Q R S T U V XYJ#,-. 2345 8 ( X :8,-. 2 3 Z [\], ^_ `ab'; c 8,-. 23[\ b!,-. 234567 8 [ \ U ` a, U #; c < 4567

APOLLO KISO II - PC INSTRUKCJA UŻYTKOWNIKA INSTRUKCJA OBSŁUGI PROGRAMU DO KOMUNIKACJI KASA KOMPUTER. (ver. 1.0 czerwiec 2005)

APOLLO KISO II - PC INSTRUKCJA OBSŁUGI PROGRAMU DO KOMUNIKACJI KASA KOMPUTER DLA KASY APPOLLO KIISSO IIII INSTRUKCJA UŻYTKOWNIKA (ver. 1.0 czerwiec 2005) 1 1. UWAGI OGÓLNE... 3 2. KABEL KOMUNIKACYJNY...

T00o historyczne: Rozwój uk00adu okresowego pierwiastków 1 Storytelling Teaching Model: wiki.science-stories.org , Research Group

13T 00 o h i s t o r y c z n Re o: z w ó j u k 00 a d u o k r e s o w e g o p i e r w i a s t k ó w W p r o w a d z e n i e I s t n i e j e w i e l e s u b s t a n c j i i m o g o n e r e a g o w a z e

9 6 6 0, 4 m 2 ), S t r o n a 1 z 1 1

O p i s p r z e d m i o t u z a m ó w i e n i a - z a k r e s c z y n n o c i f U s ł u g i s p r z» t a n i a o b i e k t ó w G d y s k i e g o O r o d k a S p o r t u i R e ks r e a c j i I S t a d i

Zadanie 1. Rozważ funkcję f(x, y) = (x + y)(x + 6)( y 3) określoną na zbiorze R 2.

Zadanie 1. Rozważ funkcję f(x, y) = (x + y)(x + 6)( y 3) określoną (ii) (3pt) Zbadaj, czy w punktach A = ( 3, 0), B = (1, 2), C = ( 6, 3) funkcja f ma maksimum lokalne. (iii) (2pt) Zbadaj, czy w punktach

METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ

METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza

G d y n i a W y k o n a n i e p r a c p i e l g n a c y j- n o r e n o w a c y j n y c h n a o b i e k t a c h s p o r t o w y c h G C S o r a z d o s t a w a n a s i o n t r a w, n a w o z u i w i r u

: ; : # $!" # $%& $ ' #!#!"#$%&' ( )*+,-./ :; ABCDE FGHIJ KL :; MN O1 > P>OQ< R ST U VW XY ; < 23ZY[\]^ _`ab+c U ' #!# " $N

: ; : # $!"# $%& $ '#!#!"#$%&' ()*+,-./01234567897:;?@ ABCDEFGHIJKL34567897:;MNO1 >P>OQ< RSTUVWXY;< 23ZY[\]^ _`ab+cu'#!# "$N;M 3Z5;1NMEU>XQU U1 EMU5L.M ()*$ $ (23Z +,-.$' /01$ /.$0! '$(! # /2$!"#"$%#&

Ą Ą Ą Ą Ą Ą Ą Ą Ł Ó Ę Ń Ą Ą Ę Ł Ę Ś Ś Ś Ś Ł Ą Ż Ś Ź Ł Ó Ł Ą Ł Ę Ł Ą Ą Ą Ą Ą Ą Ą ĄĄ Ą Ś Ć Ą Ę Ę Ć Ł Ł Ś Ź Ź Ó ĆŚ Ż Ł Ś Ś Ź Ź Ó Ę Ę Ę Ó Ś Ź Ą Ę Ą Ś Ę Ł Ś Ł Ś Ś Ń Ś Ę Ę Ż Ż Ó Ś Ą Ć Ą Ź Ń Ś Ś Ś Ć Ł Ś

www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part

6. K o ł a 7. M i s a

S U P 6 0 9 v. 2 0 16 G R I L L R U C H O M Y, P R O S T O K Ą T N Y, Z D O L N Ą I B O C Z N Ą P Ó Ł K Ą S U P 6 0 9 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S

ż ź ż Ś Ź Ś Ś ń ń Ś ń Ś Ś ż Ś Ś ż ćś ż ż ż Ł ć ć ć Ść ń Ś ż ż Ś ż ń Ź Ś ż ż ć Ś Ś Ś Ś Ś Ś Ś ź ż ń Ę ż ć Ś Ś ć ż Ś Ś ż ż ć Ś Ś ć Ś Ś ćś Ś Ś ń ż ń Ś ż ć ć Ć Ś ń Ź ń ć ć ć Ść ń ń Ś Ś ż ĘĄ Ś ż ć ć Ś ć ń ć

XT001_ INTRODUCTION TO EXIT INTERVIEW PYTANIE NIE JEST ZADAWANE W POLSCE W 2006 ROKU. WCIŚNIJ Ctrl+R BY PRZEJŚĆ DALEJ. 1.

Share w2 Exit Questionnaire version 2.7 2006-09-29 XT001_ INTRODUCTION TO EXIT INTERVIEW 1. Kontynuuj XT006_ PROXY RESPONDENT'S SEX 1. Mężczyzna 2. Kobieta XT002_ RELATIONSHIP TO THE DECEASED IF XT002_

Global Positioning System (GPS)

Global Positioning System (GPS) Ograniczenia dokładności odbiorników systemu GPS Satellite GPS Antenna Hard Surface 1 Błędy pozycji Niezależne od zasady działania systemu Metodyczne wynikające z zasady

SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA

Z n a k s p r a w y G C S D Z P I 2 7 1 0 1 12 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A D o s t a w a ( u d o s t p n i e n i e ) a g r e g a t u p r» d o t w

rstuv xvxyz{ z}~x}x { uƒ v x û v x}š ŒŠxy sžu x } sžu vx

rstuvxvxyz{ z}~x}x { uƒ vx û vx}š ŒŠxysŽux }sžu vx 0134561035783935870830363 3451345170830300108 598351700801!" # $%&'"'"(&%)**+)!*((% # #,(' # # - #.*%"-/ # 001.213456,1.- # 76441888 # 8%'%(- # 98893019:9013,('(!%!!"$%&'"'"(&%)**+)!*((%(&)";&

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa

W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l

v = v i e i v 1 ] T v = = v 1 v n v n [ ] U [x y z] T (X,Y,Z)

v U = e i,..., e n ) v = n v i e i i= e i i U = {X i } i=,n v T v = = v v n v n U x y z T X,Y,Z) v v v = 2 T A, ) b = 3 4 T B, ) c = + b b d = b c c d d 2 + 3b e b c = 5 3 T b d = 5 T c c = 34 d = 26 d

CMYK ()*+,-./01 "!"#$%&' "!"#$%&' ()*+,-./ :; ABCD4E B6 7% F ; E GH I JK45LBMNO PQ RS >TUV JK; WPB X Y >7 RZ [ TUV \]A^_` a 8Wb

()*+,-./01 "!"#$%&' "!"#$%&' ()*+,-./01 23456 789:; ?@ ABCD4E B6 7% F ; E GH I JK45LBMNO PQ RS >TUV JK; WPB X Y >7 RZ [ TUV \]A^_` a 8Wb c. @ ` W < J 4 () +G W a B L 7% F 4 a H 7%B 4 `B "#$' a ' > `B

Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej

Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej Denicja 1. Niech X = R n b dzie przestrzeni unormowan oraz d(x, y) = x y.

Techniki wizualizacji. Ćwiczenie 10. System POV-ray tworzenie animacji

Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Techniki wizualizacji Ćwiczenie 10 System POV-ray tworzenie animacji Celem ćwiczenia

Warszawa, dnia 26 lutego 2015 r. Poz. 273 OBWIESZCZENIE MINISTRA OBRONY NARODOWEJ. z dnia 4 lutego 2015 r.

DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 26 lutego 2015 r. Poz. 273 OBWIESZCZENIE MINISTRA OBRONY NARODOWEJ z dnia 4 lutego 2015 r. w sprawie ogłoszenia jednolitego tekstu rozporządzenia

Nierówności symetryczne

Nierówności symetryczne Andrzej Nowicki Uniwersytet Mikołaja Kopernika, Wydział Matematyki i Informatyki, ul Chopina 1 18, 87 100 Toruń (e-mail: anow@matunitorunpl) Sierpień 1995 Wstęp Jeśli x, y, z, t

Wprowadzenie do psql i SQL. Język komend psql. Podstawy instrukcji SELECT

Wprowadzenie do psql i SQL 1 Bazy Danych Wykład p.t. Wprowadzenie do psql i SQL. Język komend psql. Podstawy instrukcji SELECT Antoni Ligęza ligeza@agh.edu.pl http://galaxy.uci.agh.edu.pl/~ligeza Wykorzystano

RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych. Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych

RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych wyliczamy według wzoru (x, x 2,..., x n ) f(x, x 2,..., x n )

!"#$%&'"%()*+"(,-($'".%* /0%(-($(,*"12'$%33"*4*(%,$3 5,4*%,('$%33"*4*(%,$3*,%% #,+3#(%#, 6,4*%,('".%* -(% *,/ %,% 1",+'$%3 3"*4*(%, $3

!"#$%&'"%()*+"(,-($'".%* /0%(-($(,*"12'$%33"*4*(%,$3 5,4*%,('$%33"*4*(%,$3*,%% #,+3#(%#, 6,4*%,('".%* -(% *,/ %,% 1",+'$%3 3"*4*(%, $3 *,%% #,'".%*#,7*,8.3$(1%,- 9( *%('"* '"*4*(%,3'".%* : (, -*8$,12 #%,",%.3

f x f x(x, y) (1.1) f(x, y, z) = xyz (1.5)

1 Pochodne cząstkowo Pochodną cząstkową funkcji dwóch zmiennych z = f(x, y) względem zmiennej x oznaczamy i definiujemy jako granicę f(x + h, y) f(x, y) lim h 0 h natomiast pochodną cząstkową względem

Homogeneous hypersurfaces

Differential Geometry Seminar, ANU p. 1/14 Homogeneous hypersurfaces Michael Eastwood [based on joint work with Vladimir Ezhov] Australian National University Differential Geometry Seminar, ANU p. 2/14

BI< ¾BIèéåê A, I BI< ¾ BI V W ¼ AWE. ¾BI ë 1 ' A+ KI< ¾BI ' 1 ÙÏf ÚÛ Ü õi ¹ Ý /. â I. +I%ñª" «òóh>?n /5 c ô5 3E3. y fg " }~ IªúA*!

!"#$%& 以第 % 届 会议为视角 ' ( )*+,&''&D ( 7% & ' F # $ 1 G J K L % M&''& 1NO N 1PQR STUV WX-!-./Y 7 Z [\] ^_M`abc? P 1 (#?S ( # N - 01 ( F 2 7 $ 7 6 7 6 7 6 7 6 7? F( N 2 7 7 7! 7 $ - Y$# 1 ^ ( - 2 89 &''& 678

PAKIETY STATYSTYCZNE 5. SAS wprowadzenie - środowisko Windows

PAKIETY STATYSTYCZNE 1. Wykład wstępny 2. Statistica wprowadzenie 3. Statistica elementy analizy danych 4. Statistica wykresy 5. SAS wprowadzenie - środowisko Windows 6. SAS wprowadzenie - środowisko Linux

I V. N a d z ó r... 6

C h o r ą g i e w D o l n o l ą s k a Z H P Z a ł ą c z n i k 1 d o U c h w a ł y n r 2 2. / I X / 2 0 1 5 K o m e n d y C h o r ą g w i D o l n o 6 l ą s k i e j Z H P z d n i a 0 8. 0 62. 0 1 5 r. P

Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?

Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy

Zanim zapytasz prawnika

2 Zanim zapytasz prawnika 1 Zanim zapytasz prawnika Poradnik dla Klientów Biur Porad Prawnych i Informacji Obywatelskiej Pod redakcją Grzegorza Ilnickiego Fundacja Familijny Poznań Poznań 2012 3 N i n

Instrukcje sekwencyjne

nstrukcje sekwencyjne nstrukcje sekwencyjne są stosowane w specyfikacji behawioralnej (behavioral description) rzede wszystkim w tzw. procesach (process) roces nstrukcja F nstrukcja CASE Z 1 rocesy Konstrukcja

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 02 02 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f Z a b e z p i e c z e n i e m a s o w e j i m p r e z y s p o r t

Podstawy elektromagnetyzmu. Wykład 1. Rachunek wektorowy

Podstawy elektromagnetyzmu Wykład 1 Rachunek wektorowy Co to jest,,pole? Matematyka: odwzorowanie Rn Rm które przypisuje każdemu punktowi wartość (skalarną lub wektorową). Fizyka: Własność przestrzeni

I. DANE TECHNICZNE Opis elementów sterujących i kontrolnych Budowa Dane znamionowe... 3 II. INSTRUKCJA UśYTKOWANIA...

Sterownik CU-220 I. DANE TECHNICZNE... 2 1 Opis elemów sterujących i kontrolnych... 2 2 Budowa... 3 3 Dane znamionowe... 3 II. INSTRUKCJA UśYTKOWANIA... 4 1 Opis działania... 4 1.1 Oznaczenie parametrów...

MEBLE BIUROWE Cennik dla systemów ALFATECH, QR, TEXAR, TOGAR, SIGNAT

MEBLE BIUROWE Cennik dla systemów ALFATECH, QR, TEXAR, TOGAR, SIGNAT ALFATECH meble biurowe na stelażach QR meble biurowe płytowe ELEMENTY WSPÓLNE dla ALFATECH, QR, TEXAR, TOGAR, SIGNAT Bts1 Bts2 Bts3

OpenPoland.net API Documentation

OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets

!"#$%&'!"#$%&' ($!(#)*+,-$!./)0 1 $!.) $!23) 45$!"#6!"#789% & 8:; ); );<= );>? BCDE F GHIJK LMN O. ) )PQRS6 T U!"# V WX Y V 789 G7 WZ[ Y \E]^_ 7

!"#$%&'!"#$%&'($!(#)*+,-$!./)0 1 $!.) $!23) 45$!"#6!"#789% & 8:; ); );? );@A BCDE F GHIJK LMN O. ) )PQRS6 T U!"# V WX Y V 789 G7 WZ[ Y \E]^_ 7 `$ Wa b Y c _ U W Y B W 7 W #6!(# 8 %& WX! " #!"#$%&'()*

!"# $%&' () *+,-. /01 23# :; # + B CDE01+,- # E FG+,-HIJK# L0 1M NOM M M <PQM RSTUVWXY PQ+,- B +,- < Z+[\M 78]^9:_`a <bc B +,- &' M < M

!"# $%&' () *+,-. /01 23# 456789:; # + ?%@A B CDE01+,- # E FG+,-HIJK# L0 1M NOM M M

Nawigacja: ocena dokładności pozycji. dr hab. inż. Paweł Zalewski, prof. AMS Akademia Morska w Szczecinie

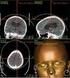Nawigacja: ocena dokładności pozycji dr hab. inż. Paweł Zalewski, prof. AMS Akademia Morska w Szczecinie Literatura Ocena dokładności pozycji w nawigacji morskiej 1) Górski S., Jackowski K., Urbański J.:

Ćwiczenia nr 4. TEMATYKA: Rzutowanie

TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej

Programowanie w CLIPS

Programowanie w CLIPS Wiedza początkowa Reguły oraz fakty początkowe dodane na początku programu za pomocą deffacts. (deffacts people "Znajomi" (person (name "Adam Kowalski") (age 24) (eye-color blue)

- :!" # $%&' &() : & *+, &( -. % /0 ( 1 $+ #2 ( #2 ) !( # ;<= &( ) >- % ( &( $+ #&( #2 A &? -4

- :!" # $%&' &() : 1. 8 -& *+, &( -. % /0 ( 1 $+ #2 ( #2 ) 3 45 167-1.!( # ;- % ( &(- 17 #(?!@- 167 1 $+ &( #&( #2 A &? -2.!"7 # ;- % #&( #2 A &? -3.!( # ;

Egzamin poprawkowy z Analizy II 11 września 2013

Egzamn poprawkowy z nalzy II 11 wrześna 13 Uwag organzacyjne: każde zadane rozwązujemy na osobnej kartce Każde zadane należy podpsać menem nazwskem własnym oraz prowadzącego ćwczena Na wszelk wypadek prosmy

ANALIZA DANYCH W STATA 8.0

ANALIZA DANYCH W STATA 8.0 ZAJĘCIA 3 1. Rozpoczęcie 1. Stwozyć w katalogu C:/temp katalog stata_3 2. Ściągnąć z intenetu ze stony http://akson.sgh.waw.pl/~mpoch plik zajecia3.zip (kyje się on pod tekstem

PRZENOŚNY ANALIZATOR SIECI AR5-L

PRZENOŚNY ANALIZATOR SIECI AR5-L INSTRUKCJA OBSŁUGI (Kod M80111 ) CIRCUTOR S.A. CONVERT sp. z o.o. rok 2007 Instrukcja użytkownika Przenośny analizator sieci AR5-L Strona 2 SPIS TREŚCI 1.- INFORMACJE PODSTAWOWE

Układy elektroniki cyfrowej - elementarz Tomasz Słupiński, Zakład Fizyki Ciała Stałego FUW

Układy elektroniki cyfrowej - elementarz Tomasz Słupiński, Zakład Fizyki Ciała Stałego FUW Elektronika cyfrowa vs analogowa - oscyloskop, generator funkcyjny - bity, układy liczenia dwójkowy, oktalny,

w ww cic oz F o r p U0 a A Zr24 H r wa w wa wa w o UazQ v7 ; V7 v7 ; V7 ; v7 rj. co.. zz fa. A o, 7 F za za za 4 is,, A ) D. 4 FU.

1 68. E E E E 69 69 69 E ) E E E E be 69 69 E n c v u S i hl. ' K cic p. D 2 v7. >- 7 v7 ; V7 v7 ; V7 ; v7 J.. ~" unli. = c.. c.. n q V. ) E- mr + >. ct >. ( j V, f., 7 n = if) is,, ) - ) D. lc. 7 Dn.

MEBLE BIUROWE Cennik dla systemów ALFATECH, QR, TEXAR, TOGAR, SIGNAT

MEBLE BIUROWE Cennik dla systemów ALFATECH, QR, TEXAR, TOGAR, SIGNAT ALFATECH meble biurowe na stelażach QR meble biurowe płytowe ELEMENTY WSPÓLNE dla ALFATECH, QR, TEXAR, TOGAR, SIGNAT Bts1 Bts2 Bts3

3 Współrzędne satelity w płaszczyźnie orbity

1 Wprowadzenie W geodezji satelitarnej funkcjonują dwa układy współrzędnych związane z ruchem obrotowym Ziemi Earth Centered Earth Fixed (ECEF), oraz układ ekwinokcjalny. Ze względu na prostą formę matematyczną

E - 0 Z W 7 - a l a I P P A B X E - 2 E N T R A L A I P P A B X O X Y T Z l 4 W a s 4 R i s S s j S X i f S W k 0 j 4 W a l W 4 ś 0 i a - i a W 7 k 4 - z ś 0 i R 4 - ó W a W i Z 4 f Z - 7 O W a s O X Y

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa

Z a ł» c z n i k n r 5 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k Zó aw m ó w i e n i a Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 1 2 0 14 W Z Ó R U M O W Y z a w a r t a w Gd y n

Programowanie deklaratywne

Programowanie deklaratywne Artur Michalski Informatyka II rok Plan wykładu Wprowadzenie do języka Prolog Budowa składniowa i interpretacja programów prologowych Listy, operatory i operacje arytmetyczne

W przypadku spostrzeżenia błędu proszę o przesłanie informacji na adres

PROJEKTOWANIE LICZNIKÓW (skrót wiadomości) Autor: Rafał Walkowiak W przypadku spostrzeżenia błędu proszę o przesłanie informacji na adres rafal.walkowiak@cs.put.poznan.pl 1. Synchroniczne łączenie liczników

Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź

5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W

5 9; STU ()* +,-. /0#1 cp 2 3 3 4567 8 + 9:Y ; :PQ ; $< + =>? : @ AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P 2 )* +. Z[\,- X ]^_` :,- a ^ bc, #,

$%& #&( )#*&+(#,- ". 0*.1& "- +(.2*%* /"0012#,#&( #2 3#(452 65,1+& 7&(&+*& $4528# 9+"*#2 &

!!"#$! "#$% &% " $ ( ) "##!!"##$%& ()!(%* &+*#,$-$*.+/!"#!$%& ()*+,-./!"" FGH,-IJKLM NO! #&##$" 0! 1! PQRIJASTU VW 9?/236 XYZ[\! # F3>GA14 [\! ] F0?4414;73=4=2 ^_ [\ "H 93=@1. abz[\ # $ ] -@?/?@1 abz[\

Angielski bezpłatne ćwiczenia - gramatyka i słownictwo.

Angielski bezpłatne ćwiczenia - gramatyka i słownictwo. Ćwiczenie 9 Przetłumacz na język angielski.klucz znajdziesz w drugiej części ćwiczenia. 1. to take a shower brać prysznic Zawsze rano biorę prysznic.

Relacje i relacje równoważności. Materiały pomocnicze do wykładu. przedmiot: Matematyka Dyskretna 1 wykładowca: dr Magdalena Kacprzak

Relacje i relacje równoważności Materiały pomocnicze do wykładu uczelnia: PJWSTK przedmiot: Matematyka Dyskretna 1 wykładowca: dr Magdalena Kacprzak Zbiór i iloczyn kartezjański Pojęcie zbioru Zbiór jest

δ δ δ 1 ε δ δ δ 1 ε ε δ δ δ ε ε = T T a b c 1 = T = T = T

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 8 9 6-7 7 X M O D E L O W A N I E P A S Z C Z Y Z N B A Z O W Y C H K O R P U S W N A P O D S T A W I E P O M W S P R Z D N O C I O W Y C H

Zestawienie porownawcze najpopularniejszych i darmowych programow GPS. dostepnych na smartfony i tablety

Zesee pre pplres r prr prr r ere, prr pree prr s sep sr ble ; > s r J Ž ˆ š š š š Ÿ š š rr e pr r p Ws ble e p ere ps rps Trs r sr l Dse r r r r r r r r ere ers prr..2 6.2..7 2. 2. 7. 8....2.2 2. 7...2

FUNKCJE WIELU ZMIENNYCH

FUNKCJE WIELU ZMIENNYCH 1. Wyznaczyć i narysować dziedziny naturalne podanych funkcji: 4 x 2 y 2 ; (b) g(x, y) = e y x 2 1 ; (c) u(x, y) = arc sin xy; (d) v(x, y) = sin(x 2 + y 2 ); (e) w(x, y) = x sin