Grafy w MATLABie. LABORKA Piotr Ciskowski
|
|
|
- Bogusław Urbaniak
- 7 lat temu
- Przeglądów:
Transkrypt
1 Grafy w MATLABie LABORKA Piotr Ciskowski
2 przykład 1 SIMBIOLOGY MODEL OF A REPRESSILATOR OSCILLATORY NETWORK
3 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne załaduj graf: >> load oscillatorgraph podejrzyj zmienne: >> whos g names >> g >> names
4 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne zamień macierz rzadką g na macierz zwykłą: >> gfull = full ( g ) ; i obejrzyj w MATLABie - albo lepiej - w Excelu
5 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne utwórz obiekt biograph (Bioinformatcs Toolbox): >> graphobject = biograph ( g, names ) Biograph object with 65 nodes and 123 edges. obejrzyj graf: >> graphfigure = view ( graphobject ) ;
6 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne znajdź wierzchołki pa, pb i pc: >> panode = find ( strcmp ('pa',names) ) ; >> pbnode = find ( strcmp ('pb',names) ) ; >> pcnode = find ( strcmp ('pc',names) ) ; więc chodź, pomaluj je na: czerwono, zielono i na niebieeeskoo >> set ( graphfigure.nodes(panode), 'Color', [ ], 'size' [ ] ) ; >> set ( graphfigure.nodes(pbnode), 'Color', [ ], 'size' [ ] ) ; >> set ( graphfigure.nodes(pcnode), 'Color', [ ], 'size' [ ] ) ; >> dolayout ( graphfigure ) ;
7 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne znajdź najkrótszą ścieżkę między węzłami pa i pc: (wszystkie krawędzie mają długość 1) >> [ dist, path, pred ] = shortestpath ( graphobject, panode, pcnode ) pokoloruj ją: >> set ( graphfigure.nodes(path), 'Color', [ ] ) >> edges = getedgesbynodeid ( graphfigure,... get ( graphfigure.nodes(path), 'ID' ) ) % get edges by node id >> set ( edges, 'LineColor', [ ] ) >> set ( edges, 'LineWidth', 1.5 )
8 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne strawersuj graf, począwszy od węzła pa: >> traverseorder = traverse ( graphobject, panode ) % domyślnie: 'Method', 'DFS' = Depth-first search znajdź alternatywną drogę z węzła pa do węzła pc: >> altpathac = traverseorder ( 1 : find ( traverseorder == pcnode ) ) ; >> set ( graphfigure.nodes(altpathac), 'Color', [ ] ) >> edges = getedgesbynodeid ( graphfigure,... get(graphfigure.nodes(altpathac),'id') ) % get edges by node id >> set ( edges, 'LineColor', [ ] ) >> set ( edges, 'LineWidth', 1.5 )
9 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne strawersuj graf, począwszy od węzła pa inną metodą: >> traverseorder = traverse ( graphobject, panode ) % poprzednio - domyślnie: 'Method', 'DFS' = Depth-first search traverseorder = >> traverseorder2 = traverse ( graphobject, panode, 'Method 'BFS' ) % teraz - umyślnie: 'Method', 'BFS' = Breadth-first search traverseorder2 =
10 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne znajdź drugą alternatywną drogę z węzła pa do węzła pc wypisz nazwy węzłów: >> nuberofnodes = length(altpathacdc) ; % 57 >> altpathacdcnames{1,1} = 'pa'; >> altpathacdcnames{numberofnodes,1} = 'pc'; >> for i = 1:numberOfNodes, end altpathacdcnames{i,1} = names { altpathacdc(i), 1 } ;
11 Repressilator oscillatory network (cokolwiek to znaczy ;-) żródło: + własne poprzednia droga niebieska nazwy węzłów: >> nuberofnodes = length(altpathac) ; % 17 >> altpathacnames{1,1} = 'pa'; >> altpathacnames{numberofnodes,1} = 'pc'; >> for i = 1:numberOfNodes, end altpathacnames{i,1} = names { altpathac(i), 1 } ;
12 przykład 2 MINIMALNE DRZEWO ROZPINAJĄCE
13 Minimalne drzewo rozpinające żródło: + własne
14 Minimalne drzewo rozpinające żródło: + własne funkcja graphminspantree: [Tree, pred] = graphminspantree(g) [Tree, pred] = graphminspantree(g, R) [Tree, pred] = graphminspantree(..., 'Method', MethodValue,...) [Tree, pred] = graphminspantree(..., 'Weights', WeightsValue,...) wybór metody: [Tree, pred] = graphminspantree(...,'method',methodvalue,...) 'Kruskal' Grows the minimal spanning tree (MST) one edge at a time by finding an edge that connects two trees in a spreading forest of growing MSTs Time complexity is O(E+X*log(N)) 'Prim' Default algorithm. Grows the minimal spanning tree (MST) one edge at a time by adding a minimal edge that connects a node in the growing MST with any other node Time complexity is O(E*log(N))
15 Minimalne drzewo rozpinające żródło: + własne zrób porządek: >> clear all >> close all >> clc
16 Minimalne drzewo rozpinające żródło: + własne utwórz graf z 6 węzłami i 11 krawędziami: >> W = [ ] ; % wagi krawędzi np. odległości między węzłami >> DG = sparse ( [ ],... [ ], W ) ; % wagi krawędzi % - elementy macierzy % krawędzie od % do indeksy elementów macierzy % % DG directed graph % - graf skierowany obejrzyj macierz wag: >> DGfull = full ( DG )
17 Minimalne drzewo rozpinające żródło: + własne w grafie nieskierowanym macierz wag musi być symetryczna: >> DGsumka = DG + DG' obejrzyj ją: >> DGsumkaFull = full ( DGsumka ) wyciągnij z niej macierz trójkątną dolną: >> UG = tril ( DGsumka ) ; % UG undirected graph % - graf nieskierowany obejrzyj ją: >> UGfull = full ( UG ) obejrzyj graf: >> view ( biograph ( UG, [], 'ShowArrows', 'off',... 'ShowWeights', 'on' ) )
18 Minimalne drzewo rozpinające żródło: + własne rozepnij drzewo: >> [ ST, pred ] = graphminspantree ( UG ) % graph min span tree obejrzyj drzewo jako macierz: >> STfull = full ( ST ) obejrzyj drzewo jako drzewo: >> view ( biograph ( ST, [], 'ShowArrows', 'off',... 'ShowWeights', 'on' ) )
19 Minimalne drzewo rozpinające żródło: + własne rozepnij drzewo: >> [ ST, pred ] = graphminspantree ( UG ) % graph min span tree obejrzyj drzewo jako macierz: >> STfull = full ( ST ) obejrzyj drzewo jako drzewo: >> view ( biograph ( ST, [], 'ShowArrows', 'off',... 'ShowWeights', 'on ) )
20 przykład 3 NAJKRÓTSZA ŚCIEŻKA GRAF SKIEROWANY
21 Najkrótsza ścieżka żródło: + własne
22 Najkrótsza ścieżka graf skierowany żródło: + własne funkcja graphshortestpath: [dist, path, pred] = graphshortestpath(g, S) [dist, path, pred] = graphshortestpath(g, S, T) [...] = graphshortestpath(..., 'Directed', DirectedValue,...) [...] = graphshortestpath(..., 'Method', MethodValue,...) [...] = graphshortestpath(..., 'Weights', WeightsValue,...) wybór metody: [Tree,pred] = graphshortestpath(...,'method',methodvalue,...) 'Bellman-Ford' Assumes weights of the edges to be nonzero entries in sparse matrix G Time complexity is O(N*E) 'BFS' Breadth-first search Assumes all weights to be equal, nonzero entries in sparse matrix G to represent edges Time complexity is O(N+E) 'Acyclic' Assumes G to be a directed acyclic graph and that weights of the edges are nonzero entries in sparse matrix G Time complexity is O(N+E) 'Dijkstra' Default algorithm. Assumes weights of the edges to be positive values in sparse matrix G Time complexity is O(log(N)*E)
23 Najkrótsza ścieżka graf skierowany żródło: + własne zrób porządek: >> clear all >> close all >> clc
24 Najkrótsza ścieżka graf skierowany żródło: + własne utwórz graf z 6 węzłami i 11 krawędziami: >> W = [ ] ; >> DG = sparse ( [ ],... [ ], W ) obejrzyj go: >> h = view ( biograph ( DG, [], 'ShowWeights', 'on' ) ) Biograph object with 6 nodes and 11 edges.
25 Najkrótsza ścieżka graf skierowany żródło: + własne znajdź najkrótszą ścieżkę z węzła 1 do węzła 6: >> [ dist, path, pred ] = graphshortestpath ( DG, 1, 6 ) % graph shortest path znajdź najkrótszą ścieżkę z węzła 1 do węzła 6 na grafie: >> set ( h.nodes(path), 'Color', [ ] ) >> edges = getedgesbynodeid ( h, get ( h.nodes(path), 'ID' ) ) ; % get edges by node id >> set ( edges, 'LineColor', [ ] ) >> set ( edges, 'LineWidth', 1.5 )
26 przykład 4 NAJKRÓTSZA ŚCIEŻKA GRAF NIESKIEROWANY
27 Najkrótsza ścieżka graf nieskierowany żródło: + własne utwórz graf nieskierowany z poprzedniego (skierowanego): >> UG = tril ( DG + DG' ) obejrzyj go: >> h = view ( biograph ( UG, [], 'ShowArrows', 'off',... 'ShowWeights', 'on ) )
28 Najkrótsza ścieżka graf nieskierowany żródło: + własne znajdź najkrótszą ścieżkę z węzła 1 do węzła 6: >> [ dist, path, pred ] = graphshortestpath ( UG, 1, 6,... 'directed', false ) % graph shortest path dist = path = pred = pokoloruj ją: >> set ( h.nodes(path), 'Color', [ ] ) >> fowedges = getedgesbynodeid ( h, get ( h.nodes(path),'id')); >> revedges = getedgesbynodeid ( h, get ( h.nodes(fliplr(path)),'id')); % get edges by node id >> edges = [ fowedges ; revedges ] ; >> set ( edges, 'LineColor', [ ] ) >> set ( edges, 'LineWidth', 1.5 )
29 przykład 5 WSZYSTKIE NAJKRÓTSZE ŚCIEŻKI GRAF SKIEROWANY
30 Wszystkie najkrótsze ścieżki żródło: + własne
31 Wszystkie najkrótsze ścieżki graf skierowany żródło: + własne nie rób porządku, wykorzystaj grafy z poprzedniego przykładu: >> clear all >> close all >> clc dla nadgorliwych - utwórz graf z 6 węzłami i 11 krawędziami: >> W = [ ] ; >> DG = sparse ( [ ],... [ ], W ) dla wszystkich obejrzyj graf: >> view ( biograph ( DG, [], 'ShowWeights', 'on' ) )
32 Wszystkie najkrótsze ścieżki graf skierowany żródło: + własne znajdź najkrótsze odległości między wszystkimi parami węzłów: >> distdg = graphallshortestpaths ( DG ) % graph all shortest paths
33 Wszystkie najkrótsze ścieżki graf skierowany żródło: + własne znajdź najkrótsze odległości między wszystkimi parami węzłów: >> distdg = graphallshortestpaths ( DG ) % graph all shortest paths distdg =
34 przykład 6 WSZYSTKIE NAJKRÓTSZE ŚCIEŻKI GRAF NIESKIEROWANY
35 Wszystkie najkrótsze ścieżki graf nieskierowany żródło: + własne nic nie rób wykorzystamy graf nieskierowany (UG) z poprzedniego przykładu >> UG dla nadgorliwych utwórz jeszcze raz graf nieskierowany o 6 węzłach i 11 krawędziach: >> UG = tril ( DG + DG' ) dla wszystkich obejrzyj graf nieskierowany: >> view ( biograph ( UG, [], 'ShowArrows', 'off',... 'ShowWeights', 'on' ) )
36 Wszystkie najkrótsze ścieżki graf nieskierowany żródło: + własne znajdź długości najkrótszych połączeń między wszystkimi parami węzłów grafu nieskierowanego: >> distug = graphallshortestpaths ( UG, 'directed', false ) % graph all shortest paths porównaj wynik z macierzą odległości dla grafu skierowanego
37 przykład 7 TRAWERS
38 Trawers żródło: + własne
39 Trawers żródło: + własne funkcja graphtraverse: [disc, pred, closed] = graphtraverse(g, S) [...] = graphtraverse(g, S,...'Depth', DepthValue,...) [...] = graphtraverse(g, S,...'Directed', DirectedValue,...) [...] = graphtraverse(g, S,...'Method', MethodValue,...) wybór metody: [...] = graphtraverse(g, S,...'Method', MethodValue,...) 'BFS' Breadth-first search Time complexity is O(N+E) 'DFS' Default algorithm. Depth-first search Time complexity is O(N+E)
40 Trawers żródło: + własne zrób porządek: >> clear all >> close all >> clc
41 Trawers żródło: + własne utwórz graf z 10 węzłami i 12 krawędziami: >> DG = sparse ( [ ],... [ ], true, 10, 10 ) obejrzyj graf jako macierz pełną: >> DGfull = full ( DG ) obejrzyj graf na rysunku: >> h = view ( biograph ( DG ) )
42 Trawers żródło: + własne strawersuj graf - zaczynając od węzła 4 - przy użyciu metody DFS przeszukiwania w głąb >> orderdfs4 = graphtraverse ( DG, 4 )
43 Trawers żródło: + własne ponumeruj węzły w kolejności ich przechodzenia >> for i = 1:10 hdfs.nodes( orderdfs4(i) ).Label =... sprintf ( '%s:%d', hdfs.nodes( orderdfs4(i) ).ID, i ) ; end hdfs.showtextinnodes = 'label' dolayout ( hdfs )
44 Trawers żródło: + własne strawersuj graf - zaczynając od węzła 4 - przy użyciu metody BFS przeszukiwania wszerz >> orderbfs4 = graphtraverse ( DG, 4, 'Method', 'BFS' )
45 Trawers żródło: + własne narysuj graf w nowym okienku >> hbfs = view ( biograph ( DG ) ) ponumeruj węzły w kolejności ich przechodzenia >> for i = 1:10 hbfs.nodes( orderdfs4(i) ).Label =... sprintf ( '%s:%d', hbfs.nodes( orderbfs4(i) ).ID, i ) ; end hbfs.showtextinnodes = 'label' dolayout ( hbfs )
46 Trawers żródło: + własne
47 Trawers żródło: + własne znajdź węzły w odległości 2 od węzła 4: >> node_idxs = graphtraverse ( DG, 4, 'depth', 2 ) node_idxs = zaznacz je na rysunku: >> set ( hdfs.nodes(node_idxs), 'Color', [ ] )
48 zadanie MIASTA WOJEWÓDZKIE
49 Miasta wojewódzkie żródło: własne Na podstawie jakiejś dobrej mapy i/lub strony, stwórz w MATLABie graf z bezpośrednimi połączeniami drogowymi między miastami wojewódzkimi
50 Miasta wojewódzkie żródło: własne Na podstawie jakiejś dobrej mapy i/lub strony, stwórz w MATLABie graf z bezpośrednimi połączeniami drogowymi między miastami wojewódzkimi: macierz krawędzi - macierz rzadka - 0 gdy nie ma połączenia - waga () gdy jest połączenie macierz nazw węzłów nazwy miast - macierz komórkowa z napisami macierz nazw krawędzi nazwy dróg (np. A4, S8, E65) - macierz komórkowa z napisami Narysuj graf do standardowego rysunku dodaj nazwy dróg w etykietach krawędzi Znajdź najkrótsze trasy między poszczególnymi miastami Uruchom Automapę i sprawdź, jakie trasy zaproponuje Hołek ;-) ewentualnie jakąkolwiek inną nawigację Dodaj MATLABowy interfejs do wyboru miasta początkowego i końcowego Do obecnych 16 miast wojewódzkich dodaj dawne miasta wojewódzkie (49) Sprawdź wydajność MATLABa przy obu wielkościach grafu Jeśli będzie za dobrze, dodaj do grafu wszystkie miasta o liczbie mieszkańców większej od liczby studentów PWr ;-)
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Algorytmy grafowe. Wykład 2 Przeszukiwanie grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Programowanie obiektowe
 Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2015 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2015 1 / 21 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2015 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2015 1 / 21 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Złożoność obliczeniowa klasycznych problemów grafowych
 Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Konspekt. 15 października Wykład III (16 października 2014 r.): optymalizacja kombinatoryczna na grafach (metody sieciowe)
 Konspekt 15 października 2014 1 Wykład III (16 października 2014 r.): optymalizacja kombinatoryczna na grafach (metody sieciowe) 1.1 Przykładowe problemy optymalizacji kombinatorycznej na grafach 1. Optymalizacja
Konspekt 15 października 2014 1 Wykład III (16 października 2014 r.): optymalizacja kombinatoryczna na grafach (metody sieciowe) 1.1 Przykładowe problemy optymalizacji kombinatorycznej na grafach 1. Optymalizacja
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 8 2 Modele danych: grafy Podstawowe pojęcia Grafy wywołań Grafy skierowane i nieskierowane Grafy planarne,
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 8 2 Modele danych: grafy Podstawowe pojęcia Grafy wywołań Grafy skierowane i nieskierowane Grafy planarne,
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, Grafy dzielimy na grafy skierowane i nieskierowane:
 Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Programowanie obiektowe
 Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2014 1 / 24 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2014 1 / 24 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Klasyfikacja Support Vector Machines
 Klasyfikacja Support Vector Machines LABORKA Piotr Ciskowski przykład 1 KLASYFIKACJA KWIATKÓW IRYSA przykład 1. klasyfikacja kwiatków irysa (versicolor-virginica) żródło: pomoc MATLABa: http://www.mathworks.com/help/stats/svmclassify.html
Klasyfikacja Support Vector Machines LABORKA Piotr Ciskowski przykład 1 KLASYFIKACJA KWIATKÓW IRYSA przykład 1. klasyfikacja kwiatków irysa (versicolor-virginica) żródło: pomoc MATLABa: http://www.mathworks.com/help/stats/svmclassify.html
Minimalne drzewa rozpinające
 KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
Informatyka w szkole - algorytm Dijkstry dla każdego. Krzysztof Diks Instytut Informatyki, Uniwersytet Warszawski
 Informatyka w szkole - algorytm Dijkstry dla każdego Krzysztof Diks Instytut Informatyki, Uniwersytet Warszawski Problem 1: Labirynt Źródło: www.dla-dzieci.ugu.pl Problem : Wilk, owca i kapusta Źródło:
Informatyka w szkole - algorytm Dijkstry dla każdego Krzysztof Diks Instytut Informatyki, Uniwersytet Warszawski Problem 1: Labirynt Źródło: www.dla-dzieci.ugu.pl Problem : Wilk, owca i kapusta Źródło:
Grafowy model danych
 Teoretyczne podstawy informatyki Wykład 7: Grafowy model danych Prof. dr hab. Elżbieta Richter-Wąs 1 Relacje Chociaż założyliśmy, że w ogólności elementy należące do zbiorów są niepodzielne, w praktyce
Teoretyczne podstawy informatyki Wykład 7: Grafowy model danych Prof. dr hab. Elżbieta Richter-Wąs 1 Relacje Chociaż założyliśmy, że w ogólności elementy należące do zbiorów są niepodzielne, w praktyce
Wykład 8. Drzewo rozpinające (minimum spanning tree)
 Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów
 Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
MODELE SIECIOWE 1. Drzewo rozpinające 2. Najkrótsza droga 3. Zagadnienie maksymalnego przepływu źródłem ujściem
 MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
Spis treści. Przykład. Przykład 1 Przykład 2. Twórcy Informacje wstępne Pseudokod Przykład. 1 Grafy skierowane z wagami - przypomnienie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,11,1 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,11,1 B. Woźna-Szcześniak (UJD) Algorytmy
WSTĘP DO INFORMATYKI. Grafy i struktury grafowe
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WTĘP DO INFORMATYKI Adrian Horzyk Grafy i struktury grafowe www.agh.edu.pl DEFINICJA GRAFU Graf to
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WTĘP DO INFORMATYKI Adrian Horzyk Grafy i struktury grafowe www.agh.edu.pl DEFINICJA GRAFU Graf to
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe.
 Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 20
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 20
AISDE ćwiczenie 5. Algorytmy grafowe
 AISDE ćwiczenie 5 Algorytmy grafowe Wstęp Ćwiczenie ma na celu zapoznanie się z przykładowymi implementacjami wybranych algorytmów grafowych. Analizowane będą dwa rodzaje algorytmów: znajdujące najkrótszą
AISDE ćwiczenie 5 Algorytmy grafowe Wstęp Ćwiczenie ma na celu zapoznanie się z przykładowymi implementacjami wybranych algorytmów grafowych. Analizowane będą dwa rodzaje algorytmów: znajdujące najkrótszą
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 39 Plan wykładu
Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 39 Plan wykładu
Algorytm wyznaczania najkrótszej ścieżki w grafie skierowanym w zbiorze liczb rozmytych
 NEUMNN Tomasz 1 lgorytm wyznaczania najkrótszej ścieżki w grafie skierowanym w zbiorze liczb rozmytych WSTĘP W systemach zarządzania transportem jedną z najbardziej istotnych kwestii jest zapewnienie najkrótszej
NEUMNN Tomasz 1 lgorytm wyznaczania najkrótszej ścieżki w grafie skierowanym w zbiorze liczb rozmytych WSTĘP W systemach zarządzania transportem jedną z najbardziej istotnych kwestii jest zapewnienie najkrótszej
Sprawozdanie do zadania numer 2
 Sprawozdanie do zadania numer 2 Michał Pawlik 29836 Temat: Badanie efektywności algorytmów grafowych w zależności od rozmiaru instancji oraz sposobu reprezentacji grafu w pamięci komputera 1 WSTĘP W ramach
Sprawozdanie do zadania numer 2 Michał Pawlik 29836 Temat: Badanie efektywności algorytmów grafowych w zależności od rozmiaru instancji oraz sposobu reprezentacji grafu w pamięci komputera 1 WSTĘP W ramach
Wstęp do programowania. Drzewa. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
G. Wybrane elementy teorii grafów
 Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Algorytmizacja procesu wyznaczania długości ścieżek w sieci rozbudowanej podstawą optymalizacji zagadnień transportowych
 Ignaciuk Szymon 1, Wawrzosek Jacek 2, Kubera Elżbieta 3, Baryła-Paśnik Małgorzata 4, Piekarski Wiesław 5 Uniwersytet Przyrodniczy w Lublinie Algorytmizacja procesu wyznaczania długości ścieżek w sieci
Ignaciuk Szymon 1, Wawrzosek Jacek 2, Kubera Elżbieta 3, Baryła-Paśnik Małgorzata 4, Piekarski Wiesław 5 Uniwersytet Przyrodniczy w Lublinie Algorytmizacja procesu wyznaczania długości ścieżek w sieci
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
IMPLEMENTACJA I PORÓWNANIE WYDAJNOŚCI WYBRANYCH ALGORYTMÓW GRAFOWYCH W WARUNKACH OBLICZEŃ RÓWNOLEGŁYCH
 IMPLEMENTACJA I PORÓWNANIE WYDAJNOŚCI WYBRANYCH ALGORYTMÓW GRAFOWYCH W WARUNKACH OBLICZEŃ RÓWNOLEGŁYCH Michał Podstawski Praca dyplomowa napisana pod kierunkiem Prof. WSTI dr hab. inż. Jarosława Śmiei
IMPLEMENTACJA I PORÓWNANIE WYDAJNOŚCI WYBRANYCH ALGORYTMÓW GRAFOWYCH W WARUNKACH OBLICZEŃ RÓWNOLEGŁYCH Michał Podstawski Praca dyplomowa napisana pod kierunkiem Prof. WSTI dr hab. inż. Jarosława Śmiei
Wykład 7. Algorytmy grafowe
 Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 7: Grafowy model danych http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Graf Graf to jest relacja binarna. Dla
Teoretyczne podstawy informatyki Wykład 7: Grafowy model danych http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Graf Graf to jest relacja binarna. Dla
Algorytmy Grafowe. dr hab. Bożena Woźna-Szcześniak, prof. UJD. Wykład 1,2,3. Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,2,3 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,2,3 B. Woźna-Szcześniak (UJD) Algorytmy
Grafy i Zastosowania. 5: Drzewa Rozpinające. c Marcin Sydow. Drzewa rozpinające. Cykle i rozcięcia fundamentalne. Zastosowania
 Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Matematyka dyskretna
 Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 9: Grafowy model danych Graf to jest relacja binarna. Dla grafów mamy ogromne możliwości wizualizacji jako zbiór punktów (zwanych wierzchołkami) połączonych liniami
Teoretyczne podstawy informatyki Wykład 9: Grafowy model danych Graf to jest relacja binarna. Dla grafów mamy ogromne możliwości wizualizacji jako zbiór punktów (zwanych wierzchołkami) połączonych liniami
ALGORYTMY OPTYMALIZACJI TRAS PRZEJAZDU POJAZDÓW
 STUDIA INFORMATICA 2011 Volume 32 Number 4A (100) Jacek WIDUCH Politechnika Śląska, Instytut Informatyki ALGORYTMY OPTYMALIZACJI TRAS PRZEJAZDU POJAZDÓW Streszczenie. Wyznaczanie tras przejazdu jest jednym
STUDIA INFORMATICA 2011 Volume 32 Number 4A (100) Jacek WIDUCH Politechnika Śląska, Instytut Informatyki ALGORYTMY OPTYMALIZACJI TRAS PRZEJAZDU POJAZDÓW Streszczenie. Wyznaczanie tras przejazdu jest jednym
DWA ZDANIA O TEORII GRAFÓW. przepływ informacji tylko w kierunku
 DWA ZDANIA O TEORII GRAFÓW Krawędź skierowana Grafy a routing Każdą sieć przedstawić składającego przedstawiają E, inaczej węzłami). komunikacyjną można w postaci grafu G się z węzłów V (które węzły sieci)
DWA ZDANIA O TEORII GRAFÓW Krawędź skierowana Grafy a routing Każdą sieć przedstawić składającego przedstawiają E, inaczej węzłami). komunikacyjną można w postaci grafu G się z węzłów V (które węzły sieci)
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,, S, GD], gdzie: N jest zbiorem wierzchołków
Digraf o V wierzchołkach posiada V 2 krawędzi, zatem liczba różnych digrafów o V wierzchołkach wynosi 2 VxV
 Graf skierowany (digraf) zbiór wierzchołków i zbiór krawędzi skierowanych łączących (co najwyżej jeden raz) uporządkowane pary wierzchołków. Mówimy wtedy, że krawędź łączy pierwszy wierzchołek z drugim
Graf skierowany (digraf) zbiór wierzchołków i zbiór krawędzi skierowanych łączących (co najwyżej jeden raz) uporządkowane pary wierzchołków. Mówimy wtedy, że krawędź łączy pierwszy wierzchołek z drugim
MATEMATYKA DYSKRETNA - KOLOKWIUM 2
 1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
Wykład 10 Grafy, algorytmy grafowe
 . Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
. Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
Egzaminy i inne zadania. Semestr II.
 Egzaminy i inne zadania. Semestr II. Poniższe zadania są wyborem zadań ze Wstępu do Informatyki z egzaminów jakie przeprowadziłem w ciągu ostatnich lat. Ponadto dołączyłem szereg zadań, które pojawiały
Egzaminy i inne zadania. Semestr II. Poniższe zadania są wyborem zadań ze Wstępu do Informatyki z egzaminów jakie przeprowadziłem w ciągu ostatnich lat. Ponadto dołączyłem szereg zadań, które pojawiały
Algorytmy grafowe. Wykład 1 Podstawy teorii grafów Reprezentacje grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
0.1. Diagram klas i pakietów
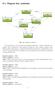 0.1. Diagram klas i pakietów Rys. 0.1. Diagram pakietów Na rysunku Rys. 0.1 przedstawiono diagram pakietów i relacje zachodzące pomiędzy nimi. Wyróżniono sześć głównych pakietów, które zostaną opisane
0.1. Diagram klas i pakietów Rys. 0.1. Diagram pakietów Na rysunku Rys. 0.1 przedstawiono diagram pakietów i relacje zachodzące pomiędzy nimi. Wyróżniono sześć głównych pakietów, które zostaną opisane
. Podstawy Programowania 2. Grafy i ich reprezentacje. Arkadiusz Chrobot. 9 czerwca 2016
 Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Podstawy Programowania 2 Grafy i ich reprezentacje. Plan. Wstęp. Teoria grafów Graf skierowany. Notatki. Notatki. Notatki. Notatki.
 Podstawy Programowania Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 7 maja 09 / 4 Plan Wstęp Zastosowania grafów / 4 Wstęp Grafy są w informatyce strukturami danych stosowanymi w wielu
Podstawy Programowania Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 7 maja 09 / 4 Plan Wstęp Zastosowania grafów / 4 Wstęp Grafy są w informatyce strukturami danych stosowanymi w wielu
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Indukowane Reguły Decyzyjne I. Wykład 3
 Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Grafy
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Grafy
Teoria grafów II. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
Algorytmy Grafowe. dr hab. Bożena Woźna-Szcześniak, prof. UJD. Wykład 5 i 6. Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 5 i 6 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 5 i 6 B. Woźna-Szcześniak (UJD) Algorytmy
. Podstawy Programowania 2. Algorytmy dfs i bfs. Arkadiusz Chrobot. 2 czerwca 2019
 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Grafy i Zastosowania. 9: Digrafy (grafy skierowane) c Marcin Sydow
 9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
prowadzący dr ADRIAN HORZYK /~horzyk e-mail: horzyk@agh tel.: 012-617 Konsultacje paw. D-13/325
 PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Animacja. Algorytm DFS Animacja. Notatki. Notatki.
 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Studia Inżynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków w odpowiadających
Wprowadzenie do Sztucznej Inteligencji Wykład Studia Inżynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków w odpowiadających
7. Teoria drzew - spinanie i przeszukiwanie
 7. Teoria drzew - spinanie i przeszukiwanie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny 7. wteoria Krakowie) drzew - spinanie i przeszukiwanie
7. Teoria drzew - spinanie i przeszukiwanie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny 7. wteoria Krakowie) drzew - spinanie i przeszukiwanie
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
Wstęp do Sztucznej Inteligencji
 Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Wstęp do programowania. Zastosowania stosów i kolejek. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1
 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona jednak ściśle związana z algebrą i
Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona jednak ściśle związana z algebrą i
Graf. Definicja marca / 1
 Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Badanie grafów Hamiltona z językiem Python
 Uniwersytet Jagielloński w Krakowie Wydział Fizyki, Astronomii i Informatyki Stosowanej Piotr Szestało Nr albumu: 1064484 Badanie grafów Hamiltona z językiem Python Praca magisterska na kierunku Informatyka
Uniwersytet Jagielloński w Krakowie Wydział Fizyki, Astronomii i Informatyki Stosowanej Piotr Szestało Nr albumu: 1064484 Badanie grafów Hamiltona z językiem Python Praca magisterska na kierunku Informatyka
Algorytmy i struktury danych
 Algorytmy i struktury danych Wykład 11 - Grafy i podstawowe algorytmy grafowe (ciąg dalszy) Janusz Szwabiński Plan wykładu: Przeszukiwanie w głąb Studium przypadku - zagadnienie skoczka szachowego (ang.
Algorytmy i struktury danych Wykład 11 - Grafy i podstawowe algorytmy grafowe (ciąg dalszy) Janusz Szwabiński Plan wykładu: Przeszukiwanie w głąb Studium przypadku - zagadnienie skoczka szachowego (ang.
Algorytmika Problemów Trudnych
 Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Teoria grafów dla małolatów. Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska
 Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
ALGORYTM POSZUKIWANIA Z ZABRONIENIAMI DLA PROBLEMU CENTRALNEGO DRZEWA ROZPINAJĄCEGO
 ALGORYM POSZUKIWANIA Z ZABRONIENIAMI DLA PROBLEMU CENRALNEGO DRZEWA ROZPINAJĄCEGO Mariusz MAKUCHOWSKI Politechnika Wrocławska, Instytut Informatyki Automatyki i Robotyki Streszczenie: W pracy analizuje
ALGORYM POSZUKIWANIA Z ZABRONIENIAMI DLA PROBLEMU CENRALNEGO DRZEWA ROZPINAJĄCEGO Mariusz MAKUCHOWSKI Politechnika Wrocławska, Instytut Informatyki Automatyki i Robotyki Streszczenie: W pracy analizuje
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
KURS MATEMATYKA DYSKRETNA
 KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
SZTUCZNA INTELIGENCJA
 Instytut Automatyki, Robotyki i Informatyki Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis Literatura SZTUCZNA INTELIGENCJA Modelowanie problemów za
Instytut Automatyki, Robotyki i Informatyki Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis Literatura SZTUCZNA INTELIGENCJA Modelowanie problemów za
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
Podejście zachłanne, a programowanie dynamiczne
 Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Algorytmy dynamiczne. Piotr Sankowski. - p. 1/14
 Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
Kilka zagadnień dotyczących Sztucznej inteligencji.
 Kilka zagadnień dotyczących Sztucznej inteligencji. Artykuł pobrano ze strony eioba.pl Jest tu kilka zagadnień dotyczących SI. Autor przygotowania: Magister inżynier Ireneusz Łukasz Dzitkowski Wałcz, dnia:
Kilka zagadnień dotyczących Sztucznej inteligencji. Artykuł pobrano ze strony eioba.pl Jest tu kilka zagadnień dotyczących SI. Autor przygotowania: Magister inżynier Ireneusz Łukasz Dzitkowski Wałcz, dnia:
Teoria obliczeń i złożoność obliczeniowa
 Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
ZASTOSOWANIE GRAFU WIDOCZNOŚCI W PLANOWANIU TRASY PRZEJŚCIA STATKU APPLICATION OF A VISIBILITY GRAPH IN SHIP S PATH PLANNING
 Zeszyty Naukowe Akademii Morskiej w Gdyni Scientific Journal of Gdynia Maritime University Nr /, ISSN - e-issn - ZASTOSOWANIE GRAFU WIDOCZNOŚCI W PLANOWANIU TRASY PRZEJŚCIA STATKU APPLICATION OF A VISIBILITY
Zeszyty Naukowe Akademii Morskiej w Gdyni Scientific Journal of Gdynia Maritime University Nr /, ISSN - e-issn - ZASTOSOWANIE GRAFU WIDOCZNOŚCI W PLANOWANIU TRASY PRZEJŚCIA STATKU APPLICATION OF A VISIBILITY
< K (2) = ( Adams, John ), P (2) = adres bloku 2 > < K (1) = ( Aaron, Ed ), P (1) = adres bloku 1 >
 Typy indeksów Indeks jest zakładany na atrybucie relacji atrybucie indeksowym (ang. indexing field). Indeks zawiera wartości atrybutu indeksowego wraz ze wskaźnikami do wszystkich bloków dyskowych zawierających
Typy indeksów Indeks jest zakładany na atrybucie relacji atrybucie indeksowym (ang. indexing field). Indeks zawiera wartości atrybutu indeksowego wraz ze wskaźnikami do wszystkich bloków dyskowych zawierających
Podstawy sztucznej inteligencji
 wykład II Problem solving 03 październik 2012 Jakie problemy możemy rozwiązywać? Cel: Zbudować inteligentnego agenta planującego, rozwiązującego problem. Szachy Kostka rubika Krzyżówka Labirynt Wybór trasy
wykład II Problem solving 03 październik 2012 Jakie problemy możemy rozwiązywać? Cel: Zbudować inteligentnego agenta planującego, rozwiązującego problem. Szachy Kostka rubika Krzyżówka Labirynt Wybór trasy
Matematyka dyskretna - 7.Drzewa
 Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Sieć (graf skierowany)
 Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Algorytmy z powracaniem
 Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy i struktury danych
 Algorytmy i struktury danych Wykład 10 - Grafy i podstawowe algorytmy grafowe Janusz Szwabiński Plan wykładu: Zagadnienie mostów królewieckich Podstawowe pojęcia Zastosowania grafów Graf jako abstrakcyjny
Algorytmy i struktury danych Wykład 10 - Grafy i podstawowe algorytmy grafowe Janusz Szwabiński Plan wykładu: Zagadnienie mostów królewieckich Podstawowe pojęcia Zastosowania grafów Graf jako abstrakcyjny
