Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń)
|
|
|
- Bronisława Kozłowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Carl Adam Petri ( ) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych za pomocą notacji graficznej metoda modelowania pozwalającą na przedstawianie i analizowanie procesów przebiegających równolegle Elementy sieci Petriego Zbiór wierzchołków grafu opisujących możliwe stany badanego systemu (sytuacje, warunki logiczne) Oznaczane graficznie elipsą (okręgiem) Zbiór wierzchołków grafu opisujących zdarzenia, które modyfikują stany badanego systemu Oznaczane graficznie prostokątami 1
2 Elementy grafu opisujące relacje pomiędzy stanami badanego systemu a zdarzeniami: wskazują stany, w których zdarzenie może zajść (warunki konieczne) wskazują stany, w których zdarzenie nie może zajść (blokady) wskazują zmianę stanu powodowaną przez zdarzenie Oznaczane graficznie liniami zakończonymi strzałkami (kółkami) Graf jest dwudzielny, tzn. łuki łączą wierzchołki różnych typów Łuki są skierowane Łuki mogą być wielokrotne (mogą mieć przypisane wagi) Tranzycje mogą być wykonywane natychmiast lub z pewnym opóźnieniem Łuki są trzech typów: wejściowe do tranzycji, wyjściowe z tranzycji, inhibitory tranzycji Mogą występować pętle Nierozróżnialne znaczniki występujące w miejscach, używane są do rozróżniania stanów sieci Petriego (znakowanie sieci) Dla miejsc opisujących warunki występowanie znacznika oznacza, że warunek jest spełniony (prawda), brak znacznika warunek nie jest spełniony (fałsz) Dla miejsc opisujących sytuacje liczba znaczników określa rodzaj sytuacji Pozwalają opisać dynamikę systemu Znakowanie początkowe, znakowania pośrednie i końcowe Reguły określające dynamikę sieci (reguły zmiany znakowania) Ta sama sieć z różnymi znakowaniami początkowymi opisuje różne systemy 2
3 Tranzycję t nazywamy aktywną przy oznakowaniu M gdy: wszystkie miejsca wejściowe tranzycji zawierają odpowiednią liczbę znaczników, wszystkie inhibitory tranzycji nie zawierają znaczników. Odpalenie tranzycji t, aktywnej przy oznakowaniu M, powoduje: usunięcie znaczników z każdego miejsca wejściowego, dodanie znaczników do wszystkich miejsc wyjściowych. to znaczy powoduje zmianę oznakowania na. Zależność ta jest zapisywana skrótowo. 3
4 Przykłady z różnych gałęzi transportu i tak dalej w nieskończoność 4
5 Sieć jest nazywana żywą, jeśli wszystkie jej tranzycje są żywe Tranzycja t jest żywa, jeśli dla każdego znakowania M (osiągalnego ze znakowania początkowego) istnieje takie znakowanie M, w którym tranzycja t jest aktywna Tranzycja, która nie jest żywa jest martwa Znakowanie martwe takie znakowanie, w którym żadna tranzycja nie jest aktywna Znakowanie M nazywamy osiągalnym z M, jeśli istnieje dowolny ciąg tranzycji, których odpalenie powoduje przejście ze znakowania M do znakowania M Analiza osiągalności jest kluczowa przy rozważaniu systemów transportowych pozwala np. znaleźć stany niebezpieczne, ocenić prawdopodobieństwo wypadku itp. Sieć Petriego nazywamy odwracalną, jeśli dla dowolnego znakowania M (osiągalnego ze znakowania początkowego M 0 ) istnieje sekwencja tranzycji, których odpalenie powoduje przejście do znakowania początkowego M 0. Sieć Petriego nazywamy k-ograniczoną, jeśli dla każdego osiągalnego znakowania, liczba znaczników w dowolnym miejscu sieci jest mniejsza niż k. Sieć Petriego, która jest 1-ograniczona nazywa się siecią bezpieczną Pułapka zbiór miejsc, które nigdy nie stracą znaczników. Zatrzask (blokada) zbiór miejsc, który po utracie wszystkich znaczników nie będzie nigdy znakowany ponownie pułapka zatrzask 5
6 Uogólniona sieć Petriego jest opisana piątką gdzie: P zbiór miejsc, T zbiór tranzycji, =, =,,,, I, O, H, to funkcje odpowiednio wejścia, wyjścia oraz inhibitory: Mając daną tranzycję t T, można zdefiniować: + = :,>0 zbiór wejść tranzycji t, = :,>0 zbiór wyjść tranzycji t, = :,>0 zbiór inhibitorów tranzycji t. Znakowana sieć Petriego jest opisany szóstką =,,,,, 0 gdzie =,,,, - uogólniona sieć Petriego, 0 : Z + jest znakowaniem początkowym, tzn. funkcją przypisującą każdemu z miejsc liczbę całkowitą nieujemną. Mówimy również, że znakowanie określa liczbę znaczników przypisanych każdemu z miejsc. Sieć miejsc i przejść jest to uogólniona, znakowana sieć Petriego, uzupełniona o charakterystykę miejsc interpretowaną jako ich pojemność, to znaczy maksymalną liczbę znaczników jakie może pomieścić każde z miejsc. =,,,,,!, 0 gdzie =,,,, - uogólniona sieć Petriego,!: N pojemność miejsc sieci, przy czym symbol oznacza, że miejsce ma nieograniczoną pojemność, 0 : Z + % : 0! znakowanie początkowe. Realizacja tranzycji nie jest natychmiastowa, lecz zajmuje określony czas. =,,,,, 0,( gdzie =,,,,, 0 znakowana sieć Petriego, (: R + funkcja opóźnień, określająca opóźnienie statyczne τ(t) tranzycji t. Czas związany z realizacją tranzycji: deterministyczny opisany zmienną losową o zadanym rozkładzie prawdopodobieństwa. Opóźnienie dynamiczne δ(t) - reszta czasu pozostałego do odpalenia tranzycji t. Znaczniki różnych typów. Typ znacznika nazywany jest kolorem. Każde miejsce ma przypisany zbiór kolorów, które może przechowywać. Łuki i przejścia mają przypisane wyrażenia, które pozwalają na manipulowanie różnymi typami znaczników. + = Γ,,,,,,+,-,., 0 gdzie =,,,,, 0 znakowana sieć Petriego, Г niepusty, skończony zbiór kolorów, C funkcja określająca jakiego koloru znaczniki mogą być przechowywane w danym miejscu: +: Γ, G funkcja określająca warunki, jakie muszą być spełnione, aby tranzycja mogła być odpalona; E funkcja opisująca tzw. wagi łuków, 6
Definicja sieci. Sieć Petriego jest czwórką C = ( P, T, I, O ), gdzie: P = { p 1, p 2,, p n } T = { t 1, t 2,, t m }
 Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
miejsca przejścia, łuki i żetony
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego. Sieć Petriego
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Analiza sieci Petriego
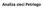 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
1. Sieci Petriego. Rys. 1-1 Przykład sieci Petriego
 1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
CZĘŚĆ PIERWSZA. Seminarium grupy RSPN. Piotr Lasek Uniwersytet Rzeszowski. Kontakt
 Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
BADANIA OPERACYJNE. dr Adam Sojda Pokój A405
 BADANIA OPERACYJNE dr Adam Sojda adam.sojda@polsl.pl http://dydaktyka.polsl.pl/roz6/asojda/default.aspx Pokój A405 Przedsięwzięcie - zorganizowanie działanie ludzkie zmierzające do osiągnięcia określonego
BADANIA OPERACYJNE dr Adam Sojda adam.sojda@polsl.pl http://dydaktyka.polsl.pl/roz6/asojda/default.aspx Pokój A405 Przedsięwzięcie - zorganizowanie działanie ludzkie zmierzające do osiągnięcia określonego
Modelowanie procesów współbieżnych
 Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego. Kolorowane sieci Petriego 1
 SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
Sterowniki Programowalne (SP) Wykład 11
 Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Wreferacie przedstawiono propozycję metody modelowania procesów transportowych
 Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Zastosowanie sieci Petriego w modelowaniu procesów biznesowych
 Zeszyty Naukowe nr 736 Akademii Ekonomicznej w Krakowie 2007 Katedra Metod Organizacji i Zarządzania Zastosowanie sieci Petriego w modelowaniu procesów biznesowych 1. Geneza i klasyczne zastosowania metody
Zeszyty Naukowe nr 736 Akademii Ekonomicznej w Krakowie 2007 Katedra Metod Organizacji i Zarządzania Zastosowanie sieci Petriego w modelowaniu procesów biznesowych 1. Geneza i klasyczne zastosowania metody
1. JĘZYK SFC WPROWADZENIE
 DODATEK: JĘZYK SFC. JĘZYK SFC PROADZENIE Język SFC jest językiem graficznym opartym na teorii sieci Petriego typu P/T (pozycja/tranzycja). Należy do grupy języków sekwencyjnych schematów funkcjonalnych
DODATEK: JĘZYK SFC. JĘZYK SFC PROADZENIE Język SFC jest językiem graficznym opartym na teorii sieci Petriego typu P/T (pozycja/tranzycja). Należy do grupy języków sekwencyjnych schematów funkcjonalnych
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Zmiany. Initial Step krok inicjujący sekwenser
 Zmiany Initial Step krok inicjujący sekwenser W ferworze walki czasem usuniemy krok inicjujący (po rozpoczęciu FB z GRAPH jest on standardowo oznaczony S1). Skutkuje to tym, że wszystko wygląda dobrze,
Zmiany Initial Step krok inicjujący sekwenser W ferworze walki czasem usuniemy krok inicjujący (po rozpoczęciu FB z GRAPH jest on standardowo oznaczony S1). Skutkuje to tym, że wszystko wygląda dobrze,
Podstawowe procedury przy tworzeniu programu do sterownika:
 Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
t i L i T i
 Planowanie oparte na budowaniu modelu struktury przedsięwzięcia za pomocą grafu nazywa sie planowaniem sieciowym. Stosuje się do planowania i kontroli realizacji założonych przedsięwzięć gospodarczych,
Planowanie oparte na budowaniu modelu struktury przedsięwzięcia za pomocą grafu nazywa sie planowaniem sieciowym. Stosuje się do planowania i kontroli realizacji założonych przedsięwzięć gospodarczych,
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Zarządzanie projektami
 Dr Adam Kucharski Spis treści Podstawowe pojęcia Metoda CPM 3 3 Przykład analizy metodą CPM 5 Podstawowe pojęcia Przedsięwzięcia złożone z wielu czynności spotykane są na każdym kroku. Jako przykład może
Dr Adam Kucharski Spis treści Podstawowe pojęcia Metoda CPM 3 3 Przykład analizy metodą CPM 5 Podstawowe pojęcia Przedsięwzięcia złożone z wielu czynności spotykane są na każdym kroku. Jako przykład może
ALGORYTMY. 1. Podstawowe definicje Schemat blokowy
 ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
PLC - język tekstu strukturalnego ST
 PLC - język tekstu strukturalnego ST Język tekstu strukturalnego ST jest odpowiednikiem języka wysokiego poziomu, zawiera podobny zestaw instrukcji jak Pascal czy C. Podstawowymi elementami języka są wyrażenia
PLC - język tekstu strukturalnego ST Język tekstu strukturalnego ST jest odpowiednikiem języka wysokiego poziomu, zawiera podobny zestaw instrukcji jak Pascal czy C. Podstawowymi elementami języka są wyrażenia
Język UML w modelowaniu systemów informatycznych
 Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 7 Przeglądowe diagramy interakcji Przeglądowe diagramy interakcji wiążą
Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 7 Przeglądowe diagramy interakcji Przeglądowe diagramy interakcji wiążą
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń.
 1.Zasada działania2 Funkcje_logiczne_wejsciowe_i_wyjsciowe_UTXvTR 16.04.09 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1.ZASADA DZIAŁANIA... 2 2. FUNKCJE WEJŚCIOWE... 4 2.1 Zasada
1.Zasada działania2 Funkcje_logiczne_wejsciowe_i_wyjsciowe_UTXvTR 16.04.09 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1.ZASADA DZIAŁANIA... 2 2. FUNKCJE WEJŚCIOWE... 4 2.1 Zasada
Modelowanie komputerowe
 Modelowanie komputerowe wykład 5- Klasyczne systemy kolejkowe i ich analiza dr Marcin Ziółkowski Instytut Matematyki i Informatyki Akademia im. Jana Długosza w Częstochowie 16,23listopada2015r. Analiza
Modelowanie komputerowe wykład 5- Klasyczne systemy kolejkowe i ich analiza dr Marcin Ziółkowski Instytut Matematyki i Informatyki Akademia im. Jana Długosza w Częstochowie 16,23listopada2015r. Analiza
LICZNIKI PODZIAŁ I PARAMETRY
 LICZNIKI PODZIAŁ I PARAMETRY Licznik jest układem służącym do zliczania impulsów zerojedynkowych oraz zapamiętywania ich liczby. Zależnie od liczby n przerzutników wchodzących w skład licznika pojemność
LICZNIKI PODZIAŁ I PARAMETRY Licznik jest układem służącym do zliczania impulsów zerojedynkowych oraz zapamiętywania ich liczby. Zależnie od liczby n przerzutników wchodzących w skład licznika pojemność
ALGORYTMY. 1. Podstawowe definicje Schemat blokowy
 ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
TECHNOLOGIE OBIEKTOWE. Wykład 3
 TECHNOLOGIE OBIEKTOWE Wykład 3 2 Diagramy stanów 3 Diagram stanu opisuje zmiany stanu obiektu, podsystemu lub systemu pod wpływem działania operacji. Jest on szczególnie przydatny, gdy zachowanie obiektu
TECHNOLOGIE OBIEKTOWE Wykład 3 2 Diagramy stanów 3 Diagram stanu opisuje zmiany stanu obiektu, podsystemu lub systemu pod wpływem działania operacji. Jest on szczególnie przydatny, gdy zachowanie obiektu
ANALIZA SIECIOWA PROJEKTÓW REALIZACJI
 WYKŁAD 5 ANALIZA SIECIOWA PROJEKTÓW REALIZACJI Podstawowe problemy rozwiązywane z wykorzystaniem programowania sieciowego: zagadnienia transportowe (rozdział zadań przewozowych, komiwojażer najkrótsza
WYKŁAD 5 ANALIZA SIECIOWA PROJEKTÓW REALIZACJI Podstawowe problemy rozwiązywane z wykorzystaniem programowania sieciowego: zagadnienia transportowe (rozdział zadań przewozowych, komiwojażer najkrótsza
procesów Współbieżność i synchronizacja procesów Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak
 Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
Information Systems Analysis
 THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci
 KNWS 2010 239 Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci Agnieszka Lasota Streszczenie: W artykule zostały opisane wytyczne, wskazujące na celowość wspomagania
KNWS 2010 239 Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci Agnieszka Lasota Streszczenie: W artykule zostały opisane wytyczne, wskazujące na celowość wspomagania
Język UML w modelowaniu systemów informatycznych
 Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Podstawy techniki cyfrowej. Układy asynchroniczne Opracował: R.Walkowiak Styczeń 2014
 Podstawy techniki cyfrowej Układy asynchroniczne Opracował: R.Walkowiak Styczeń 2014 Charakterystyka układów asynchronicznych Brak wejścia: zegarowego, synchronizującego. Natychmiastowa (niesynchronizowana)
Podstawy techniki cyfrowej Układy asynchroniczne Opracował: R.Walkowiak Styczeń 2014 Charakterystyka układów asynchronicznych Brak wejścia: zegarowego, synchronizującego. Natychmiastowa (niesynchronizowana)
SFC zawiera zestaw kroków i tranzycji (przejść), które sprzęgają się wzajemnie przez połączenia
 Norma IEC-61131-3 definiuje typy języków: graficzne: schematów drabinkowych LD, schematów blokowych FBD, tekstowe: lista instrukcji IL, tekst strukturalny ST, grafów: graf funkcji sekwencyjnych SFC, graf
Norma IEC-61131-3 definiuje typy języków: graficzne: schematów drabinkowych LD, schematów blokowych FBD, tekstowe: lista instrukcji IL, tekst strukturalny ST, grafów: graf funkcji sekwencyjnych SFC, graf
a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9] a[10] 3-2 5 8 12-4 -26 12 45-76
![a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9] a[10] 3-2 5 8 12-4 -26 12 45-76 a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9] a[10] 3-2 5 8 12-4 -26 12 45-76](/thumbs/18/918444.jpg) . p. 1 Algorytmem nazywa się poddający się interpretacji skończony zbiór instrukcji wykonania zadania mającego określony stan końcowy dla każdego zestawu danych wejściowych W algorytmach mogą występować
. p. 1 Algorytmem nazywa się poddający się interpretacji skończony zbiór instrukcji wykonania zadania mającego określony stan końcowy dla każdego zestawu danych wejściowych W algorytmach mogą występować
1. Synteza automatów Moore a i Mealy realizujących zadane przekształcenie 2. Transformacja automatu Moore a w automat Mealy i odwrotnie
 Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
W_4 Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC
 Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów wytwarzania; jest określony przez schemat funkcjonalny oraz opis słowny jego przebiegu. Do napisania programu
Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów wytwarzania; jest określony przez schemat funkcjonalny oraz opis słowny jego przebiegu. Do napisania programu
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń.
 Funkcje_logiczne_wejsciowe_i_wyjsciowe_UTXvL 15.01.10 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. Spis treści 1.ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...4 2.1.Zasada działania...4
Funkcje_logiczne_wejsciowe_i_wyjsciowe_UTXvL 15.01.10 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. Spis treści 1.ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...4 2.1.Zasada działania...4
Definicje. Algorytm to:
 Algorytmy Definicje Algorytm to: skończony ciąg operacji na obiektach, ze ściśle ustalonym porządkiem wykonania, dający możliwość realizacji zadania określonej klasy pewien ciąg czynności, który prowadzi
Algorytmy Definicje Algorytm to: skończony ciąg operacji na obiektach, ze ściśle ustalonym porządkiem wykonania, dający możliwość realizacji zadania określonej klasy pewien ciąg czynności, który prowadzi
TECHNOLOGIE OBIEKTOWE WYKŁAD 2. Anna Mroczek
 TECHNOLOGIE OBIEKTOWE WYKŁAD 2 Anna Mroczek 2 Diagram czynności Czym jest diagram czynności? 3 Diagram czynności (tak jak to definiuje język UML), stanowi graficzną reprezentację przepływu kontroli. 4
TECHNOLOGIE OBIEKTOWE WYKŁAD 2 Anna Mroczek 2 Diagram czynności Czym jest diagram czynności? 3 Diagram czynności (tak jak to definiuje język UML), stanowi graficzną reprezentację przepływu kontroli. 4
Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego
 Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
Zastosowanie kolorowej sieci Petriego do modelowania transakcji rozproszonej
 Marek IWANIAK, Włodzimierz KHADZHYNOV Wydział Elektroniki i Informatyki, Politechnika Koszalińska E mail: marek.iwaniak@tu.koszalin.pl, hadginov@ie.tu.koszalin.pl 1. Wstęp Zastosowanie kolorowej sieci
Marek IWANIAK, Włodzimierz KHADZHYNOV Wydział Elektroniki i Informatyki, Politechnika Koszalińska E mail: marek.iwaniak@tu.koszalin.pl, hadginov@ie.tu.koszalin.pl 1. Wstęp Zastosowanie kolorowej sieci
UML cz. I. UML cz. I 1/1
 UML cz. I UML cz. I 1/1 UML cz. I 2/1 UML - Unified Modeling Language ujednolicony można go współdzielić z wieloma pracownikami modelowania służy do opisu projektowanego modelu język posiada opisaną strukturę
UML cz. I UML cz. I 1/1 UML cz. I 2/1 UML - Unified Modeling Language ujednolicony można go współdzielić z wieloma pracownikami modelowania służy do opisu projektowanego modelu język posiada opisaną strukturę
Wstęp do sieci neuronowych, wykład 9 Sieci rekurencyjne. Autoasocjator Hopfielda
 Wstęp do sieci neuronowych, wykład 9. M. Czoków, J. Piersa 2010-12-07 1 Sieci skierowane 2 Modele sieci rekurencyjnej Energia sieci 3 Sieci skierowane Sieci skierowane Sieci skierowane graf połączeń synaptycznych
Wstęp do sieci neuronowych, wykład 9. M. Czoków, J. Piersa 2010-12-07 1 Sieci skierowane 2 Modele sieci rekurencyjnej Energia sieci 3 Sieci skierowane Sieci skierowane Sieci skierowane graf połączeń synaptycznych
1. SFC W PAKIECIE ISAGRAF 2. EDYCJA PROGRAMU W JĘZYKU SFC. ISaGRAF WERSJE 3.4 LUB 3.5 1
 ISaGRAF WERSJE 3.4 LUB 3.5 1 1. SFC W PAKIECIE ISAGRAF 1.1. Kroki W pakiecie ISaGRAF użytkownik nie ma możliwości definiowania własnych nazw dla kroków. Z każdym krokiem jest związany tzw. numer odniesienia
ISaGRAF WERSJE 3.4 LUB 3.5 1 1. SFC W PAKIECIE ISAGRAF 1.1. Kroki W pakiecie ISaGRAF użytkownik nie ma możliwości definiowania własnych nazw dla kroków. Z każdym krokiem jest związany tzw. numer odniesienia
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
Wstęp do Techniki Cyfrowej... Teoria automatów
 Wstęp do Techniki Cyfrowej... Teoria automatów Alfabety i litery Układ logiczny opisywany jest przez wektory, których wartości reprezentowane są przez ciągi kombinacji zerojedynkowych. Zwiększenie stopnia
Wstęp do Techniki Cyfrowej... Teoria automatów Alfabety i litery Układ logiczny opisywany jest przez wektory, których wartości reprezentowane są przez ciągi kombinacji zerojedynkowych. Zwiększenie stopnia
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri. Andrzej Blikle 29 kwietnia 2010 materiały:
 Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri Andrzej Blikle 29 kwietnia 2010 materiały: www.firmyrodzinne.pl TOC: Theory of Constraints teoria ograniczeń Goldratta STATYSTYKA PORAŻEK PROJEKTÓW
Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri Andrzej Blikle 29 kwietnia 2010 materiały: www.firmyrodzinne.pl TOC: Theory of Constraints teoria ograniczeń Goldratta STATYSTYKA PORAŻEK PROJEKTÓW
Część 3. Układy sekwencyjne. Układy sekwencyjne i układy iteracyjne - grafy stanów TCiM Wydział EAIiIB Katedra EiASPE 1
 Część 3 Układy sekwencyjne Układy sekwencyjne i układy iteracyjne - grafy stanów 18.11.2017 TCiM Wydział EAIiIB Katedra EiASPE 1 Układ cyfrowy - przypomnienie Podstawowe informacje x 1 x 2 Układ cyfrowy
Część 3 Układy sekwencyjne Układy sekwencyjne i układy iteracyjne - grafy stanów 18.11.2017 TCiM Wydział EAIiIB Katedra EiASPE 1 Układ cyfrowy - przypomnienie Podstawowe informacje x 1 x 2 Układ cyfrowy
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń.
 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1. ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...5 3. FUNKCJE WYJŚCIOWE...7 4. FUNKCJE LOGICZNE...11 Automat : ZSN 5R od: v. 1.0 Computers
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1. ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...5 3. FUNKCJE WYJŚCIOWE...7 4. FUNKCJE LOGICZNE...11 Automat : ZSN 5R od: v. 1.0 Computers
koniec punkt zatrzymania przepływów sterowania na diagramie czynności
 Diagramy czynności opisują dynamikę systemu, graficzne przedstawienie uszeregowania działań obrazuje strumień wykonywanych czynności z ich pomocą modeluje się: - scenariusze przypadków użycia, - procesy
Diagramy czynności opisują dynamikę systemu, graficzne przedstawienie uszeregowania działań obrazuje strumień wykonywanych czynności z ich pomocą modeluje się: - scenariusze przypadków użycia, - procesy
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
PROGRAMOWANIE SIECIOWE. METODA ŚCIEŻKI KRYTYCZNEJ
 PROGRAMOWANIE SIECIOWE. METODA ŚCIEŻKI KRYTYCZNEJ Maciej Patan Uniwersytet Zielonogórski WPROWADZENIE Metody programowania sieciowego wprowadzono pod koniec lat pięćdziesiatych Ze względu na strukturę
PROGRAMOWANIE SIECIOWE. METODA ŚCIEŻKI KRYTYCZNEJ Maciej Patan Uniwersytet Zielonogórski WPROWADZENIE Metody programowania sieciowego wprowadzono pod koniec lat pięćdziesiatych Ze względu na strukturę
Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC
 Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów
Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów
Schematy Piramid Logicznych
 Schematy Piramid Logicznych geometryczna interpretacja niektórych formuł Paweł Jasionowski Politechnika Śląska w Gliwicach Wydział Matematyczno-Fizyczny Streszczenie Referat zajmuje się następującym zagadnieniem:
Schematy Piramid Logicznych geometryczna interpretacja niektórych formuł Paweł Jasionowski Politechnika Śląska w Gliwicach Wydział Matematyczno-Fizyczny Streszczenie Referat zajmuje się następującym zagadnieniem:
Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające
 Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Liczniki klasyfikacja Licznik asynchroniczny:
Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Liczniki klasyfikacja Licznik asynchroniczny:
Rozkład łatwości zadań
 Klasa 3a średnia klasy: 22.52 pkt średnia szkoły: 21.93 pkt średnia ogólnopolska: 14.11 pkt Rozkład łatwości zadań 1 0.9 0.8 0.7 0.6 łatwość 0.5 0.4 0.3 0.2 0.1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Klasa 3a średnia klasy: 22.52 pkt średnia szkoły: 21.93 pkt średnia ogólnopolska: 14.11 pkt Rozkład łatwości zadań 1 0.9 0.8 0.7 0.6 łatwość 0.5 0.4 0.3 0.2 0.1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
III. ZMIENNE LOSOWE JEDNOWYMIAROWE
 III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
Języki formalne i automaty Ćwiczenia 9
 Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Matematyczna wieża Babel. 4. Ograniczone maszyny Turinga o językach kontekstowych materiały do ćwiczeń
 Matematyczna wieża Babel. 4. Ograniczone maszyny Turinga o językach kontekstowych materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 4 kwietnia 2019 1 Dodajmy kontekst! Rozważaliśmy
Matematyczna wieża Babel. 4. Ograniczone maszyny Turinga o językach kontekstowych materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 4 kwietnia 2019 1 Dodajmy kontekst! Rozważaliśmy
Przetwarzanie rozproszone
 Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA
 RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
MODELOWANIE SIECI PETRIEGO Z WYKORZYSTANIEM RELACYJNEJ BAZY DANYCH
 II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie MODELOWANIE SIECI PETRIEGO Z WYKORZYSTANIEM RELACYJNEJ BAZY DANYCH Małgorzata Kołopieńczyk Instytut
II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie MODELOWANIE SIECI PETRIEGO Z WYKORZYSTANIEM RELACYJNEJ BAZY DANYCH Małgorzata Kołopieńczyk Instytut
Diagramy czynności. Widok logiczny. Widok fizyczny
 Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Elementy logiki matematycznej
 Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri
 Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri Andrzej Blikle 13 czerwca 2011 Copyright by Andrzej Blikle. W ramach moich praw autorskich chronionych ustawą z dnia 4 lutego 1994 (z późniejszymi
Dwa paradygmaty w zarządzaniu projektami: Goldratt i Petri Andrzej Blikle 13 czerwca 2011 Copyright by Andrzej Blikle. W ramach moich praw autorskich chronionych ustawą z dnia 4 lutego 1994 (z późniejszymi
Analiza i programowanie obiektowe 2016/2017. Wykład 6: Projektowanie obiektowe: diagramy interakcji
 Analiza i programowanie obiektowe 2016/2017 Wykład 6: Projektowanie obiektowe: diagramy interakcji Jacek Marciniak Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 Plan wykładu 1. Przejście
Analiza i programowanie obiektowe 2016/2017 Wykład 6: Projektowanie obiektowe: diagramy interakcji Jacek Marciniak Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 Plan wykładu 1. Przejście
Na A (n) rozważamy rozkład P (n) , który na zbiorach postaci A 1... A n określa się jako P (n) (X n, A (n), P (n)
 MODELE STATYSTYCZNE Punktem wyjścia w rozumowaniu statystycznym jest zmienna losowa (cecha) X i jej obserwacje opisujące wyniki doświadczeń bądź pomiarów. Zbiór wartości zmiennej losowej X (zbiór wartości
MODELE STATYSTYCZNE Punktem wyjścia w rozumowaniu statystycznym jest zmienna losowa (cecha) X i jej obserwacje opisujące wyniki doświadczeń bądź pomiarów. Zbiór wartości zmiennej losowej X (zbiór wartości
Inżynieria oprogramowania. Część 8: Metoda szacowania ryzyka - PERT
 UNIWERSYTET RZESZOWSKI KATEDRA INFORMATYKI Opracował: mgr inż. Przemysław Pardel v1.01 2010 Inżynieria oprogramowania Część 8: Metoda szacowania ryzyka - PERT ZAGADNIENIA DO ZREALIZOWANIA (3H) PERT...
UNIWERSYTET RZESZOWSKI KATEDRA INFORMATYKI Opracował: mgr inż. Przemysław Pardel v1.01 2010 Inżynieria oprogramowania Część 8: Metoda szacowania ryzyka - PERT ZAGADNIENIA DO ZREALIZOWANIA (3H) PERT...
Całki podwójne. Definicja całki podwójnej. Jacek Kłopotowski. 25 maja Katedra Matematyki i Ekonomii Matematycznej
 Definicja całki podwójnej Katedra Matematyki i Ekonomii Matematycznej 25 maja 2016 Definicja całki podwójnej Załóżmy, że f : K R, gdzie K = a, b c, d R 2, jest funkcją ograniczoną. Niech x 0, x 1,...,
Definicja całki podwójnej Katedra Matematyki i Ekonomii Matematycznej 25 maja 2016 Definicja całki podwójnej Załóżmy, że f : K R, gdzie K = a, b c, d R 2, jest funkcją ograniczoną. Niech x 0, x 1,...,
Podstawy Sztucznej Inteligencji (PSZT)
 Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Uczenie maszynowe Sztuczne sieci neuronowe Plan na dziś Uczenie maszynowe Problem aproksymacji funkcji Sieci neuronowe PSZT, zima 2013, wykład 12
Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Uczenie maszynowe Sztuczne sieci neuronowe Plan na dziś Uczenie maszynowe Problem aproksymacji funkcji Sieci neuronowe PSZT, zima 2013, wykład 12
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Wykład 11: Martyngały: definicja, twierdzenia o zbieżności
 RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
Projektowanie Scalonych Systemów Wbudowanych VERILOG
 Projektowanie Scalonych Systemów Wbudowanych VERILOG OPIS BEHAWIORALNY proces Proces wątek sterowania lub przetwarzania danych, niezależny w sensie czasu wykonania, ale komunikujący się z innymi procesami.
Projektowanie Scalonych Systemów Wbudowanych VERILOG OPIS BEHAWIORALNY proces Proces wątek sterowania lub przetwarzania danych, niezależny w sensie czasu wykonania, ale komunikujący się z innymi procesami.
Algorytm. Krótka historia algorytmów
 Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Algorytm poprawny jednoznaczny szczegółowy uniwersalny skończoność efektywność (sprawność) zmiennych liniowy warunkowy iteracyjny
 Algorytm to przepis; zestawienie kolejnych kroków prowadzących do wykonania określonego zadania; to uporządkowany sposób postępowania przy rozwiązywaniu zadania, problemu, z uwzględnieniem opisu danych
Algorytm to przepis; zestawienie kolejnych kroków prowadzących do wykonania określonego zadania; to uporządkowany sposób postępowania przy rozwiązywaniu zadania, problemu, z uwzględnieniem opisu danych
Teoria układów logicznych
 Automat Moore a Automatem Moore a nazywamy uporządkowaną piątkę ( Q, X,,, ) gdzie Q jest skończonym zbiorem niepustym, nazwanym zbiorem stanów automatu, X jest skończonym zbiorem niepustym, nazwanym alfabetem
Automat Moore a Automatem Moore a nazywamy uporządkowaną piątkę ( Q, X,,, ) gdzie Q jest skończonym zbiorem niepustym, nazwanym zbiorem stanów automatu, X jest skończonym zbiorem niepustym, nazwanym alfabetem
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń.
 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1.ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE... 4 2.1 Zasada działania...4 2.2 Spis funkcji wejściowych oraz wejść...4 2.2.1 Nastawy
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1.ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE... 4 2.1 Zasada działania...4 2.2 Spis funkcji wejściowych oraz wejść...4 2.2.1 Nastawy
Analiza semantyczna. Gramatyka atrybutywna
 Analiza semantyczna Do przeprowadzenia poprawnego tłumaczenia, oprócz informacji na temat składni języka podlegającego tłumaczeniu, translator musi posiadać możliwość korzystania z wielu innych informacji
Analiza semantyczna Do przeprowadzenia poprawnego tłumaczenia, oprócz informacji na temat składni języka podlegającego tłumaczeniu, translator musi posiadać możliwość korzystania z wielu innych informacji
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki. Paweł Witas Nr albumu:178860
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Paweł Witas Nr albumu:178860 Symulator sieci Petriego ze znacznikami indywidualnymi Praca Magisterska na kierunku INFORMATYKA Praca wykonana
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Paweł Witas Nr albumu:178860 Symulator sieci Petriego ze znacznikami indywidualnymi Praca Magisterska na kierunku INFORMATYKA Praca wykonana
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014
 Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
WYMAGANIA EDUKACYJNE
 GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
1.5. Sygnały. Sygnał- jest modelem zmian w czasie pewnej wielkości fizycznej lub stanu obiektu fizycznego
 Sygnał- jest modelem zmian w czasie pewnej wielkości fizycznej lub stanu obiektu fizycznego Za pomocąsygnałów przekazywana jest informacja. Sygnałjest nośnikiem informacji. Za pomocą sygnału moŝna: badać
Sygnał- jest modelem zmian w czasie pewnej wielkości fizycznej lub stanu obiektu fizycznego Za pomocąsygnałów przekazywana jest informacja. Sygnałjest nośnikiem informacji. Za pomocą sygnału moŝna: badać
(b) Oblicz zmianę zasobu kapitału, jeżeli na początku okresu zasób kapitału wynosi kolejno: 4, 9 oraz 25.
 Zadanie 1 W pewnej gospodarce funkcja produkcji może być opisana jako Y = AK 1/2 N 1/2, przy czym A oznacza poziom produktywności, K zasób kapitału, a N liczbę zatrudnionych. Stopa oszczędności s wynosi
Zadanie 1 W pewnej gospodarce funkcja produkcji może być opisana jako Y = AK 1/2 N 1/2, przy czym A oznacza poziom produktywności, K zasób kapitału, a N liczbę zatrudnionych. Stopa oszczędności s wynosi
Automat skończony FSM Finite State Machine
 Automat skończony FSM Finite State Machine Projektowanie detektora sekwencji Laboratorium z Elektroniki Współczesnej A. Skoczeń, KOiDC, WFiIS, AGH, 2019 AGH, WFiIS, Elektronika Współczesna 1 Deterministyczny
Automat skończony FSM Finite State Machine Projektowanie detektora sekwencji Laboratorium z Elektroniki Współczesnej A. Skoczeń, KOiDC, WFiIS, AGH, 2019 AGH, WFiIS, Elektronika Współczesna 1 Deterministyczny
Przykłady zdań w matematyce. Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości a, b, c jest prostokątny (a, b, c oznaczają dane liczby dodatnie),
 Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
Modelowanie wieloskalowe. Automaty Komórkowe - podstawy
 Modelowanie wieloskalowe Automaty Komórkowe - podstawy Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p. 716 lmadej@agh.edu.pl
Modelowanie wieloskalowe Automaty Komórkowe - podstawy Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p. 716 lmadej@agh.edu.pl
Diagnozowanie sieci komputerowej metodą dialogu diagnostycznego
 Diagnozowanie sieci komputerowej metodą dialogu diagnostycznego Metoda dialogu diagnostycznego między komputerami sieci komputerowej, zalicza się do, tak zwanych, rozproszonych metod samodiagnozowania
Diagnozowanie sieci komputerowej metodą dialogu diagnostycznego Metoda dialogu diagnostycznego między komputerami sieci komputerowej, zalicza się do, tak zwanych, rozproszonych metod samodiagnozowania
Rysunek 1: Przykłady graficznej prezentacji klas.
 4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
