Fotometria CCD 4. Fotometria profilowa i aperturowa
|
|
|
- Przybysław Kowalewski
- 5 lat temu
- Przeglądów:
Transkrypt
1 Fotometria CCD 4. Fotometria profilowa i aperturowa Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010
2 Fotometria CCD Proces wyznaczania jasności gwiazd na obrazie CCD obejmuje: 1. Znajdowanie gwiazd. 2. Wyznaczanie ich położenia. 3. Szacowanie poziomu tła nieba. 4A. Wyliczenie całkowitej ilości światła pochodzącego od gwiazd w danej aperturze (fot. aperturowa), 4B. Wyliczenie PSF i dopasowanie jej do obrazów gwiazd (fot. profilowa).
3 Znajdowanie gwiazd Od programu, który będzie poszukiwał gwiazd na obrazie żądamy, aby potrafił: automatycznie znaleźć wszystkie gwiazdy, odróżnić obrazy gwiazd od: obrazów galaktyk, śladów po promieniach kosmicznych, gorących pikseli i innych defektów detektora.
4 Znajdowanie gwiazd Od programu, który będzie poszukiwał gwiazd na obrazie żądamy, aby potrafił: automatycznie znaleźć wszystkie gwiazdy, odróżnić obrazy gwiazd od: obrazów galaktyk, śladów po promieniach kosmicznych, gorących pikseli i innych defektów detektora. Przykładowa (dobra) implementacja: procedura FIND/ Daophot. Daophot: Stetson, 1987, PASP 99,191
5 Znajdowanie gwiazd Od programu, który będzie poszukiwał gwiazd na obrazie żądamy, aby potrafił: automatycznie znaleźć wszystkie gwiazdy, odróżnić obrazy gwiazd od: obrazów galaktyk, śladów po promieniach kosmicznych, gorących pikseli i innych defektów detektora. Przykładowa (dobra) implementacja: procedura FIND/ Daophot. Daophot: Stetson, 1987, PASP 99,191 Dla każdego piksela na oryginalnym obrazku D (i jego otoczenia) dopasowuje się dwuwymiarową funkcję Gaussa o zadanej szerokości. W oddzielnej tablicy zachowuje się wartości czynników skalujących H.
6 Znajdowanie gwiazd D i,j = H i0,j0 G(Δi,Δj,σ) + b
7 Znajdowanie gwiazd D i,j = H i0,j0 G(Δi,Δj,σ) + b Powyższe równanie jest liniowe, więc można podać analityczne wyrażenie na H i0,j0 :
8 Znajdowanie gwiazd D i,j = H i0,j0 G(Δi,Δj,σ) + b Powyższe równanie jest liniowe, więc można podać analityczne wyrażenie na H i0,j0 : H i0,j0 = (GD) ( G)( D)/n (G 2 ) ( G) 2 /n
9 Znajdowanie gwiazd D i,j = H i0,j0 G(Δi,Δj,σ) + b Powyższe równanie jest liniowe, więc można podać analityczne wyrażenie na H i0,j0 : H i0,j0 = (GD) ( G)( D)/n (G 2 ) ( G) 2 /n Tablicy H używa się do poszukiwania gwiazd. Zalety używania H zamiast D są następujące: poszukiwanie jest optymalne dla obiektów o kształtach (szerokościach) gwiazd, w obrazie H nie pojawia się lokalna wartość tła nieba, obrazy obiektów w H są węższe niż w D: lepsza rozdzielczość.
10 Znajdowanie gwiazd a gwiazda b gwiazda podwójna c galaktyka d ślad po pr. kosm. e wadliwy piksel
11 Znajdowanie gwiazd a gwiazda b gwiazda podwójna c galaktyka d ślad po pr. kosm. e wadliwy piksel
12 Znajdowanie gwiazd a gwiazda b gwiazda podwójna c galaktyka d ślad po pr. kosm. e wadliwy piksel Selekcja obiektów polega na przeszukiwaniu tabeli H w celu znalezienia pozycji lokalnych maksimów.
13 Znajdowanie gwiazd Dodatkowe kryteria, które pozwalają odróżnić gwiazdy od innych obiektów:
14 Znajdowanie gwiazd Dodatkowe kryteria, które pozwalają odróżnić gwiazdy od innych obiektów: Parametr 1, okrągłość (roundness): r = 2( ) h y - h x h y + h x Dla gwiazd r 0
15 Znajdowanie gwiazd Dodatkowe kryteria, które pozwalają odróżnić gwiazdy od innych obiektów: Parametr 1, okrągłość (roundness): r = 2( ) h y - h x h y + h x Dla gwiazd r 0
16 Znajdowanie gwiazd Parametr 2, ostrość (sharpness): s = D i0,j0 H i0,j0 D i,j s > 1 dla śladów po p.k. s 0 dla galaktyk 0 < s < 1 dla gwiazd
17 Znajdowanie gwiazd Parametr 2, ostrość (sharpness): s = D i0,j0 H i0,j0 D i,j s > 1 dla śladów po p.k. s 0 dla galaktyk 0 < s < 1 dla gwiazd
18 Znajdowanie centrum obrazów 1. Metoda sum częściowych W obszarze o boku a 5 FWHM, którego środek pokrywa się z centralnym pikselem gwiazdy (i 0,j 0 ), liczy się sumy brzegowe: s i = D i,j s j = D i,j, j po czym dopasowuje do nich jednowymiarowe funkcje Gaussa w celu uzyskania wartości x 0, y 0. Metoda nie pracuje dobrze dla słabych gwiazd i bliskich gwiazd podwójnych. i
19 Znajdowanie centrum obrazów 2. Metoda centrowania obrazu Znajdujemy współrzędne centralnego piksela: i 0,j 0. Liczymy sumy brzegowe s i i s j w obszarze 2a 2a, gdzie a ~ FWHM. Liczymy średnie wartości sum brzegowych: i 0 +a 1 1 X = s i Y = s 2a+1 j i = i 0 -a 2a+1 j = j 0 -a Liczymy x 0 i y 0 korzystając tylko z sum, w których sygnał jest większy niż odpowiednia średnia: x 0 = (s i X)i / (s i Y), y 0 = (s i X)i / (s i Y), Jeśli x 0,y 0 leży zbyt daleko od i 0,j 0, powtarzamy procedurę przyjmując piksel najbliższy x 0,y 0 za nowe i 0,j 0. Pracuje lepiej niż poprzednio dla bliskich gwiazd, ale zawodzi gdy separacja jest mniejsza niż 2a. j 0 +a i i j j
20 Szacowanie tła nieba Sygnał ten pochodzi od emisji nieba nocnego, słabych gwiazd, mgławic, światła rozproszonego, prądu ciemnego i in.
21 Szacowanie tła nieba Sygnał ten pochodzi od emisji nieba nocnego, słabych gwiazd, mgławic, światła rozproszonego, prądu ciemnego i in. Tło mierzy się w pierścieniu wycentrowanym na danej gwieździe. Dobór promienia wewnętrznego i zewnętrznego.
22 Szacowanie tła nieba Sygnał ten pochodzi od emisji nieba nocnego, słabych gwiazd, mgławic, światła rozproszonego, prądu ciemnego i in. Tło mierzy się w pierścieniu wycentrowanym na danej gwieździe. Dobór promienia wewnętrznego i zewnętrznego. Tło liczy się biorąc pod uwagę piksele z pierścienia jako: zwykłą średnią: S s = D i,j / N, wartość modalną: S mod = max histogramu, medianę: S med : n(d i,j < S med ) = n(d i,j > S med ), kombinację powyższych, np. S = 3 S med 2 S s.
23 Szacowanie tła nieba Sygnał ten pochodzi od emisji nieba nocnego, słabych gwiazd, mgławic, światła rozproszonego, prądu ciemnego i in. Tło mierzy się w pierścieniu wycentrowanym na danej gwieździe. Dobór promienia wewnętrznego i zewnętrznego. Tło liczy się biorąc pod uwagę piksele z pierścienia jako: zwykłą średnią: S s = D i,j / N, wartość modalną: S mod = max histogramu, medianę: S med : n(d i,j < S med ) = n(d i,j > S med ), kombinację powyższych, np. S = 3 S med 2 S s. Można też obliczać go iteracyjnie odrzucając w kolejnych iteracjach najbardziej odstające piksele.
24 Fotometria CCD
25 Fotometria CCD Fotometria aperturowa: przypomina fotometrię fotoelektryczną post factum
26 Fotometria CCD Fotometria aperturowa: przypomina fotometrię fotoelektryczną post factum
27 Fotometria aperturowa m = -2,5 log D + C, gdzie D = i,j D i,j - NS N liczba pikseli w danej aperturze, S poziom tła (ADU).
28 Fotometria profilowa/psf
29 Fotometria profilowa/psf
30 Fotometria profilowa/psf Fotometria profilowa (profile/psf photometry)
31 Fotometria profilowa/psf
32 Fotometria profilowa/psf Trzeba najpierw wyznaczyć dwuwymiarowy profil gwiazdy, (point spread function, PSF).
33 Fotometria profilowa/psf Trzeba najpierw wyznaczyć dwuwymiarowy profil gwiazdy, (point spread function, PSF). m = -2,5 log A + C, gdzie A czynnik skalujący PSF (wysokość profilu)
34 Fotometria profilowa/psf A 1 Trzeba najpierw wyznaczyć dwuwymiarowy profil gwiazdy, (point spread function, PSF). m = -2,5 log A + C, gdzie A czynnik skalujący PSF (wysokość profilu)
35 Fotometria profilowa/psf A 1 A2 Trzeba najpierw wyznaczyć dwuwymiarowy profil gwiazdy, (point spread function, PSF). m = -2,5 log A + C, gdzie A czynnik skalujący PSF (wysokość profilu)
36 Fotometria profilowa/psf A 1 A2 Trzeba najpierw wyznaczyć dwuwymiarowy profil gwiazdy, (point spread function, PSF). m = -2,5 log A + C, gdzie A czynnik skalujący PSF (wysokość profilu) Dopasowanie daje też położenie centrum gwiazdy (x 0,y 0 ) oraz poziom tła.
37 Fotometria profilowa/psf
38 Fotometria profilowa/psf
39 Fotometria profilowa: zmienna PSF Powody zmienności PSF na obrazie CCD: - wady optyczne teleskopu (ujawniają się zwłaszcza przy większym polu widzenia), - nieprostopadłość detektora do osi optycznej, - inne.
40 Fotometria profilowa: zmienna PSF Powody zmienności PSF na obrazie CCD: - wady optyczne teleskopu (ujawniają się zwłaszcza przy większym polu widzenia), - nieprostopadłość detektora do osi optycznej, - inne. Modele PSF: Analityczna PSF, np.: - 2-wymiarowa funkcja Gaussa (2 parametry), - funkcja Moffata, f(x,y) = A/(1 + z 2 ) β, gdzie z 2 = x 2 /a 2 + y 2 /b 2 + cxy, β = 1,5 lub 2,5. (3 parametry), - funkcja Penny (suma f.gaussa i Moffata) (4 lub 5 parametrów). Empiryczna PSF, określona na siatce pikseli.
41 Fotometria profilowa: zmienna PSF Analityczna: zalety: łatwość interpolacji, wady: nie oddaje dobrze rzeczywistego profilu. Empiryczna: zalety: łatwość całkowania, wady: błędy interpolacji przy wąskim profilu.
42 Fotometria profilowa: zmienna PSF Analityczna: zalety: łatwość interpolacji, wady: nie oddaje dobrze rzeczywistego profilu. Empiryczna: zalety: łatwość całkowania, wady: błędy interpolacji przy wąskim profilu. DAOPHOT: PSF jako suma funkcji analitycznej i tablicy poprawek zdefiniowanej na siatce pikseli.
43 Fotometria profilowa: zmienna PSF Stała PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ,)
44 Fotometria profilowa: zmienna PSF Stała PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ,) Liniowo zmienna PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ) + x T 1 (ν,ξ) + y T 2 (ν,ξ)
45 Fotometria profilowa: zmienna PSF Stała PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ,) Liniowo zmienna PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ) + x T 1 (ν,ξ) + y T 2 (ν,ξ) Kwadratowo zmienna PSF: PSF(x,y) = A(x,y) + T 0 (ν,ξ) + x T 1 (ν,ξ) + y T 2 (ν,ξ) + + x 2 T 3 (ν,ξ) + y 2 T 4 (ν,ξ) + xy T 5 (ν,ξ)
Fotometria CCD 5. Metoda odejmowania obrazów
 Fotometria CCD 5. Metoda odejmowania obrazów Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Gęste pole: M92 Gęste pole: M92 Gęste pole: okolice centrum Galaktyki
Fotometria CCD 5. Metoda odejmowania obrazów Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Gęste pole: M92 Gęste pole: M92 Gęste pole: okolice centrum Galaktyki
Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD
 Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 CCD CCD = Charge Coupled Device (urządzenie o sprzężeniu ładunkowym)
Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 CCD CCD = Charge Coupled Device (urządzenie o sprzężeniu ładunkowym)
Pomiary jasności nieba z użyciem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN
 Pomiary jasności nieba z użyciem aparatu cyfrowego Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum Wrocławia Pomiary
Pomiary jasności nieba z użyciem aparatu cyfrowego Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum Wrocławia Pomiary
Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky"
 Uniwersytet Warszawski Wydział Fizyki Bartłomiej Włodarczyk Nr albumu: 306849 Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky" Praca przygotowana w ramach Pracowni Fizycznej II-go stopnia pod
Uniwersytet Warszawski Wydział Fizyki Bartłomiej Włodarczyk Nr albumu: 306849 Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky" Praca przygotowana w ramach Pracowni Fizycznej II-go stopnia pod
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Złożoność obliczeniowa zadania, zestaw 2
 Złożoność obliczeniowa zadania, zestaw 2 Określanie złożoności obliczeniowej algorytmów, obliczanie pesymistycznej i oczekiwanej złożoności obliczeniowej 1. Dana jest tablica jednowymiarowa A o rozmiarze
Złożoność obliczeniowa zadania, zestaw 2 Określanie złożoności obliczeniowej algorytmów, obliczanie pesymistycznej i oczekiwanej złożoności obliczeniowej 1. Dana jest tablica jednowymiarowa A o rozmiarze
Fotometria 1. Systemy fotometryczne.
 Fotometria 1. Systemy fotometryczne. Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Fotometria Fotometria to jedna z podstawowych technik obserwacyjnych. Pozwala
Fotometria 1. Systemy fotometryczne. Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Fotometria Fotometria to jedna z podstawowych technik obserwacyjnych. Pozwala
Wstępna redukcja obrazów z kamer CCD
 Wstępna redukcja obrazów z kamer CCD Wstępna obróbka obrazów pochodzących z urządzeń takich jak kamery CCD, czy CMOS polega na usunięciu lub zminimalizowaniu niepoŝądanych efektów dawanych przez te urządzenia
Wstępna redukcja obrazów z kamer CCD Wstępna obróbka obrazów pochodzących z urządzeń takich jak kamery CCD, czy CMOS polega na usunięciu lub zminimalizowaniu niepoŝądanych efektów dawanych przez te urządzenia
Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN
 Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum
Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum
Utworzenie funkcji użytkownika w Visual Basic
 Utworzenie funkcji użytkownika w Visual Basic Po co? Potrzebna jest nam funkcja, która nie występuje w Excelu. Zadanie 1. Utwórz funkcję użytkownika kotek, która będzie funkcją dwóch zmiennych b i h i
Utworzenie funkcji użytkownika w Visual Basic Po co? Potrzebna jest nam funkcja, która nie występuje w Excelu. Zadanie 1. Utwórz funkcję użytkownika kotek, która będzie funkcją dwóch zmiennych b i h i
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
WYKŁAD 7. Obraz z wykrytymi krawędziami: gdzie 1 - wartość konturu, 0 - wartość tła.
 WYKŁAD 7 Elementy segmentacji Obraz z wykrytymi krawędziami: Detektory wzrostu (DTW); badanie pewnego otoczenia piksla Lokalizacja krawędzi metodami: - liczenie różnicy bezpośredniej, - liczenie różnicy
WYKŁAD 7 Elementy segmentacji Obraz z wykrytymi krawędziami: Detektory wzrostu (DTW); badanie pewnego otoczenia piksla Lokalizacja krawędzi metodami: - liczenie różnicy bezpośredniej, - liczenie różnicy
BIBLIOTEKA PROGRAMU R - BIOPS. Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat
 BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
PRZETWARZANIE SYGNAŁÓW
 PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VII Sygnały 2D i transformacja Fouriera 2D 2 1 2 Splot 2D d d y H F y H y F y G ), ( ), ( ), ( ), ( ), ( H(,) F(,) H(-,-) H(-,y-) G(,y) Delta Diraca 2D (,y) 0 ),
PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VII Sygnały 2D i transformacja Fouriera 2D 2 1 2 Splot 2D d d y H F y H y F y G ), ( ), ( ), ( ), ( ), ( H(,) F(,) H(-,-) H(-,y-) G(,y) Delta Diraca 2D (,y) 0 ),
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement)
 POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement) Przetwarzanie obrazów cyfrowych w celu wydobycia / uwydatnienia specyficznych cech obrazu dla określonych zastosowań. Brak
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement) Przetwarzanie obrazów cyfrowych w celu wydobycia / uwydatnienia specyficznych cech obrazu dla określonych zastosowań. Brak
Ćwiczenie 6. Transformacje skali szarości obrazów
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Sejsmologia gwiazd. Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego
 Sejsmologia gwiazd Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego XXXIV Zjazd Polskiego Towarzystwa Astronomicznego, Kraków, 16.09.2009 Asterosejsmologia: jak to działa? Z obserwacji
Sejsmologia gwiazd Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego XXXIV Zjazd Polskiego Towarzystwa Astronomicznego, Kraków, 16.09.2009 Asterosejsmologia: jak to działa? Z obserwacji
Operator rozciągania. Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości
 Operator rozciągania q = 15 ( p p1 ) ( p p ) 0 2 1 dla p < p p 1 2 dla p p, p > p 1 2 Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości q = 0 dla p p1 q2 dla p1
Operator rozciągania q = 15 ( p p1 ) ( p p ) 0 2 1 dla p < p p 1 2 dla p p, p > p 1 2 Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości q = 0 dla p p1 q2 dla p1
WYKŁAD 3 WYPEŁNIANIE OBSZARÓW. Plan wykładu: 1. Wypełnianie wieloboku
 WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
Filtracja obrazów. w dziedzinie częstotliwości. w dziedzinie przestrzennej
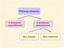 Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky
 Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky Maciej Zielenkiewicz 5 marca 2010 1 Wstęp 1.1 Projekt Pi of the Sky Celem projektu jest poszukiwanie
Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky Maciej Zielenkiewicz 5 marca 2010 1 Wstęp 1.1 Projekt Pi of the Sky Celem projektu jest poszukiwanie
1 Symulacja procesów cieplnych 1. 2 Algorytm MES 2. 3 Implementacja rozwiązania 2. 4 Całkowanie numeryczne w MES 3. k z (t) t ) k y (t) t )
 pis treści ymulacja procesów cieplnych Algorytm ME 3 Implementacja rozwiązania 4 Całkowanie numeryczne w ME 3 ymulacja procesów cieplnych Procesy cieplne opisuje równanie różniczkowe w postaci: ( k x (t)
pis treści ymulacja procesów cieplnych Algorytm ME 3 Implementacja rozwiązania 4 Całkowanie numeryczne w ME 3 ymulacja procesów cieplnych Procesy cieplne opisuje równanie różniczkowe w postaci: ( k x (t)
Soczewkowanie grawitacyjne
 Soczewkowanie grawitacyjne Obserwatorium Astronomiczne UW Plan Ugięcie światła - trochę historii Co to jest soczewkowanie Punktowa masa Soczewkowanie galaktyk... kwazarów... kosmologiczne Mikrosoczewkowanie
Soczewkowanie grawitacyjne Obserwatorium Astronomiczne UW Plan Ugięcie światła - trochę historii Co to jest soczewkowanie Punktowa masa Soczewkowanie galaktyk... kwazarów... kosmologiczne Mikrosoczewkowanie
Zbigniew Sołtys - Komputerowa Analiza Obrazu Mikroskopowego 2016 część 7
 7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
WYKŁAD 3. Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego
 WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 8 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Autodesk 3D Studio MAX Teksturowanie modeli 3D
 Autodesk 3D Studio MAX Teksturowanie modeli 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 20 Plan Wykładu
Autodesk 3D Studio MAX Teksturowanie modeli 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 20 Plan Wykładu
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Analiza Matematyczna III Mathematical Analysis III Kierunek: Rodzaj przedmiotu: obowiązkowy dla wszystkich specjalności Rodzaj zajęć: wykład, ćwiczenia Matematyka Poziom przedmiotu: I
Nazwa przedmiotu: Analiza Matematyczna III Mathematical Analysis III Kierunek: Rodzaj przedmiotu: obowiązkowy dla wszystkich specjalności Rodzaj zajęć: wykład, ćwiczenia Matematyka Poziom przedmiotu: I
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
ALA MA KOTA MEDIA - OBRAZ OBRAZ. Operacje na obrazie. Informacja ukryta w teksturach, hierarchii krawędzi. Obraz to kompozycja:
 OBRAZ Obraz to kompozycja: tła konturów tekstur PODSTAWY TECHNIK MULTIMEDIALNYCH, A.Przelaskowski MEDIA - OBRAZ f R M N k ALA MA KOTA obraz losowy bez żadnej informacji Dwuwymiarowa struktura: macierz
OBRAZ Obraz to kompozycja: tła konturów tekstur PODSTAWY TECHNIK MULTIMEDIALNYCH, A.Przelaskowski MEDIA - OBRAZ f R M N k ALA MA KOTA obraz losowy bez żadnej informacji Dwuwymiarowa struktura: macierz
Podstawy programowanie systemów wizyjnych InSight firmy Cognex. Środowisku InSight Explorer / Spreadshee
 Podstawy programowanie systemów wizyjnych InSight firmy Cognex Środowisku InSight Explorer / Spreadshee Opis zadania: Wykrycie umownych różnic pomiędzy wzorcową płytką testową i płytkami zawierającymi
Podstawy programowanie systemów wizyjnych InSight firmy Cognex Środowisku InSight Explorer / Spreadshee Opis zadania: Wykrycie umownych różnic pomiędzy wzorcową płytką testową i płytkami zawierającymi
AKWIZYCJA I PRZETWARZANIE WSTĘPNE
 WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7
 Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
PRAKTYCZNA INSTRUKCJA OBSŁUGI PAKIETU DIA
 PRAKTYCZNA INSTRUKCJA OBSŁUGI PAKIETU DIA 1 Wstęp Pakiet DIA (Difference Image Analysis) przeznaczony jest do poszukiwania i analizy obiektów zmiennych zarejestrowanych na obrazach nieba. Programy wchodzące
PRAKTYCZNA INSTRUKCJA OBSŁUGI PAKIETU DIA 1 Wstęp Pakiet DIA (Difference Image Analysis) przeznaczony jest do poszukiwania i analizy obiektów zmiennych zarejestrowanych na obrazach nieba. Programy wchodzące
Aerotriangulacja. 1. Aerotriangulacja z niezależnych wiązek. 2. Aerotriangulacja z niezależnych modeli
 Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
ASTROFOTOGRAFIA Z IRIS
 ASTROFOTOGRAFIA Z IRIS DOMINIK GRONKIEWICZ Klub Astronomiczny Almukantarat Tę pracę można rozpowszechniać wyłącznie w całości w celach edukacyjnych i dydaktycznych. TROCHĘ TEORII 2 Naświetlenie zdjęć to
ASTROFOTOGRAFIA Z IRIS DOMINIK GRONKIEWICZ Klub Astronomiczny Almukantarat Tę pracę można rozpowszechniać wyłącznie w całości w celach edukacyjnych i dydaktycznych. TROCHĘ TEORII 2 Naświetlenie zdjęć to
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 6 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
KADD Minimalizacja funkcji
 Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Podstawy OpenCL część 2
 Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
ANALIZA MATEMATYCZNA
 ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 7 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Metoda elementów brzegowych
 Metoda elementów brzegowych Tomasz Chwiej, Alina Mreńca-Kolasińska 9 listopada 8 Wstęp Rysunek : a) Geometria układu z zaznaczonymi: elementami brzegu (czerwony), węzłami (niebieski). b) Numeracja: elementów
Metoda elementów brzegowych Tomasz Chwiej, Alina Mreńca-Kolasińska 9 listopada 8 Wstęp Rysunek : a) Geometria układu z zaznaczonymi: elementami brzegu (czerwony), węzłami (niebieski). b) Numeracja: elementów
Rys. 1 Schemat układu obrazującego 2f-2f
 Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Ekspansja Wszechświata
 Ekspansja Wszechświata Odkrycie Hubble a w 1929 r. Galaktyki oddalają się od nas z prędkościami wprost proporcjonalnymi do odległości. Prędkości mierzymy za pomocą przesunięcia ku czerwieni efekt Dopplera
Ekspansja Wszechświata Odkrycie Hubble a w 1929 r. Galaktyki oddalają się od nas z prędkościami wprost proporcjonalnymi do odległości. Prędkości mierzymy za pomocą przesunięcia ku czerwieni efekt Dopplera
Operacje przetwarzania obrazów monochromatycznych
 Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładów Błędy obliczeń Błędy można podzielić na: modelu, metody, wejściowe (początkowe), obcięcia, zaokrągleń..
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładów Błędy obliczeń Błędy można podzielić na: modelu, metody, wejściowe (początkowe), obcięcia, zaokrągleń..
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 2 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Implementacja filtru Canny ego
 ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
MIKROSKOPIA OPTYCZNA 19.05.2014 AUTOFOCUS TOMASZ POŹNIAK MATEUSZ GRZONDKO
 MIKROSKOPIA OPTYCZNA 19.05.2014 AUTOFOCUS TOMASZ POŹNIAK MATEUSZ GRZONDKO AUTOFOCUS (AF) system automatycznego ustawiania ostrości w aparatach fotograficznych Aktywny - wysyła w kierunku obiektu światło
MIKROSKOPIA OPTYCZNA 19.05.2014 AUTOFOCUS TOMASZ POŹNIAK MATEUSZ GRZONDKO AUTOFOCUS (AF) system automatycznego ustawiania ostrości w aparatach fotograficznych Aktywny - wysyła w kierunku obiektu światło
Spis treści. Programowanie w ImageJ. Zadanie 1. Zadanie 2
 Spis treści 1 Programowanie w ImageJ 1.1 Zadanie 1 1.2 Zadanie 2 1.3 Zadanie 3 1.4 Zadanie 4 1.5 Zadanie 5 Programowanie w ImageJ Zadanie 1 Mamy obraz rtg płuc w formacie jpg, w 8-bitowej skali szarości.
Spis treści 1 Programowanie w ImageJ 1.1 Zadanie 1 1.2 Zadanie 2 1.3 Zadanie 3 1.4 Zadanie 4 1.5 Zadanie 5 Programowanie w ImageJ Zadanie 1 Mamy obraz rtg płuc w formacie jpg, w 8-bitowej skali szarości.
Zastosowanie filtrów w astronomii amatorskiej
 Zastosowanie filtrów w astronomii amatorskiej Wyrózniamy różne rodzaje filtrów Filtry szerokopasmowe i wąskopasmowe Filtry słoneczne, księżycowe, polaryzacyjne Filtry LP Filtry mgławicowe wizualne i astrofotograficzne
Zastosowanie filtrów w astronomii amatorskiej Wyrózniamy różne rodzaje filtrów Filtry szerokopasmowe i wąskopasmowe Filtry słoneczne, księżycowe, polaryzacyjne Filtry LP Filtry mgławicowe wizualne i astrofotograficzne
Inżynierskie metody analizy numerycznej i planowanie eksperymentu / Ireneusz Czajka, Andrzej Gołaś. Kraków, Spis treści
 Inżynierskie metody analizy numerycznej i planowanie eksperymentu / Ireneusz Czajka, Andrzej Gołaś. Kraków, 2017 Spis treści Od autorów 11 I. Klasyczne metody numeryczne Rozdział 1. Na początek 15 1.1.
Inżynierskie metody analizy numerycznej i planowanie eksperymentu / Ireneusz Czajka, Andrzej Gołaś. Kraków, 2017 Spis treści Od autorów 11 I. Klasyczne metody numeryczne Rozdział 1. Na początek 15 1.1.
Oszacowywanie możliwości wykrywania śmieci kosmicznych za pomocą teleskopów Pi of the Sky
 Mirosław Należyty Agnieszka Majczyna Roman Wawrzaszek Marcin Sokołowski Wilga, 27.05.2010. Obserwatorium Astronomiczne Uniwersytetu Warszawskiego i Instytut Problemów Jądrowych w Warszawie Oszacowywanie
Mirosław Należyty Agnieszka Majczyna Roman Wawrzaszek Marcin Sokołowski Wilga, 27.05.2010. Obserwatorium Astronomiczne Uniwersytetu Warszawskiego i Instytut Problemów Jądrowych w Warszawie Oszacowywanie
Rozkład normalny, niepewność standardowa typu A
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
DOPASOWYWANIE KRZYWYCH
 DOPASOWYWANIE KRZYWYCH Maciej Patan Uniwersytet Zielonogórski Motywacje Przykład 1. Dane o przyroście światowej populacji są aktualizowane co każde 10 lat, celem szacowania średniego przyrostu rocznego.
DOPASOWYWANIE KRZYWYCH Maciej Patan Uniwersytet Zielonogórski Motywacje Przykład 1. Dane o przyroście światowej populacji są aktualizowane co każde 10 lat, celem szacowania średniego przyrostu rocznego.
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Metody iteracyjne rozwiązywania układów równań liniowych (5.3) Normy wektorów i macierzy (5.3.1) Niech. x i. i =1
 Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Obliczenia Naukowe. Wykład 12: Zagadnienia na egzamin. Bartek Wilczyński
 Obliczenia Naukowe Wykład 12: Zagadnienia na egzamin Bartek Wilczyński 6.6.2016 Tematy do powtórki Arytmetyka komputerów Jak wygląda reprezentacja liczb w arytmetyce komputerowej w zapisie cecha+mantysa
Obliczenia Naukowe Wykład 12: Zagadnienia na egzamin Bartek Wilczyński 6.6.2016 Tematy do powtórki Arytmetyka komputerów Jak wygląda reprezentacja liczb w arytmetyce komputerowej w zapisie cecha+mantysa
ZESPÓŁ SZKÓŁ W OBRZYCKU
 Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Czy w zakresie twardego promieniowania rentgenowskiego obserwujemy kurczenie pętli magnetycznych?
 Czy w zakresie twardego promieniowania rentgenowskiego obserwujemy kurczenie pętli magnetycznych? wysokośd Seminarium z 15.12.2003 r. Obrazy CLEAN, D3-D9 W czasie fazy impulsowej ruch źródła szczytowego
Czy w zakresie twardego promieniowania rentgenowskiego obserwujemy kurczenie pętli magnetycznych? wysokośd Seminarium z 15.12.2003 r. Obrazy CLEAN, D3-D9 W czasie fazy impulsowej ruch źródła szczytowego
Automatyczne nastawianie ostrości
 Automatyczne nastawianie ostrości Systemy automatycznego nastawiania ostrości (AF) - budowa, działanie, zalety, wady, zastosowanie, algorytmy wyostrzania - przykłady Jakub Skalak http://www.fis.agh.edu.pl/~4skalak/
Automatyczne nastawianie ostrości Systemy automatycznego nastawiania ostrości (AF) - budowa, działanie, zalety, wady, zastosowanie, algorytmy wyostrzania - przykłady Jakub Skalak http://www.fis.agh.edu.pl/~4skalak/
Modelowanie zależności. Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski
 Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Metody badania kosmosu
 Metody badania kosmosu Zakres widzialny Fale radiowe i mikrofale Promieniowanie wysokoenergetyczne Detektory cząstek Pomiar sił grawitacyjnych Obserwacje prehistoryczne Obserwatorium słoneczne w Goseck
Metody badania kosmosu Zakres widzialny Fale radiowe i mikrofale Promieniowanie wysokoenergetyczne Detektory cząstek Pomiar sił grawitacyjnych Obserwacje prehistoryczne Obserwatorium słoneczne w Goseck
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 12 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 6 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
Wstęp do astrofizyki I Wykład 6 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Orientacyjnie 140 godzin lekcyjnych, tj. 35 tygodni po 4 godziny lekcyjne tygodniowo.
 6 Orientacyjnie 40 godzin lekcyjnych, tj. 35 tygodni po 4 godziny lekcyjne tygodniowo.. Śmietankowe ponad wszystko Statystyka. Powtórzenie wiadomości ze statystyki 3 Czytanka. O języku matematyki, czyli
6 Orientacyjnie 40 godzin lekcyjnych, tj. 35 tygodni po 4 godziny lekcyjne tygodniowo.. Śmietankowe ponad wszystko Statystyka. Powtórzenie wiadomości ze statystyki 3 Czytanka. O języku matematyki, czyli
Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 9. Przetwarzanie sygnałów wizyjnych. Politechnika Świętokrzyska.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
Interpolacja i modelowanie krzywych 2D i 3D
 Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
Interpolacja i modelowanie krzywych 2D i 3D Dariusz Jacek Jakóbczak Politechnika Koszalińska Wydział Elektroniki i Informatyki Zakład Podstaw Informatyki i Zarządzania e-mail: Dariusz.Jakobczak@tu.koszalin.pl
Repeta z wykładu nr 8. Detekcja światła. Przypomnienie. Efekt fotoelektryczny
 Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna
 Regresja wieloraka Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna zmienna niezależna (można zobrazować
Regresja wieloraka Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna zmienna niezależna (można zobrazować
(a 1 2 + b 1 2); : ( b a + b ab 2 + c ). : a2 2ab+b 2. Politechnika Białostocka KATEDRA MATEMATYKI. Zajęcia fakultatywne z matematyki 2008
 Zajęcia fakultatywne z matematyki 008 WYRAŻENIA ARYTMETYCZNE I ALGEBRAICZNE. Wylicz b z równania a) ba + a = + b; b) a = b ; b+a c) a b = b ; d) a +ab =. a b. Oblicz a) [ 4 (0, 5) ] + ; b) 5 5 5 5+ 5 5
Zajęcia fakultatywne z matematyki 008 WYRAŻENIA ARYTMETYCZNE I ALGEBRAICZNE. Wylicz b z równania a) ba + a = + b; b) a = b ; b+a c) a b = b ; d) a +ab =. a b. Oblicz a) [ 4 (0, 5) ] + ; b) 5 5 5 5+ 5 5
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski
 Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Ekonometria - wykªad 8
 Ekonometria - wykªad 8 3.1 Specykacja i werykacja modelu liniowego dobór zmiennych obja±niaj cych - cz ± 1 Barbara Jasiulis-Goªdyn 11.04.2014, 25.04.2014 2013/2014 Wprowadzenie Ideologia Y zmienna obja±niana
Ekonometria - wykªad 8 3.1 Specykacja i werykacja modelu liniowego dobór zmiennych obja±niaj cych - cz ± 1 Barbara Jasiulis-Goªdyn 11.04.2014, 25.04.2014 2013/2014 Wprowadzenie Ideologia Y zmienna obja±niana
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
Skalowanie wielowymiarowe idea
 Skalowanie wielowymiarowe idea Jedną z wad metody PCA jest możliwość używania jedynie zmiennych ilościowych, kolejnym konieczność posiadania pełnych danych z doświadczenia(nie da się użyć PCA jeśli mamy
Skalowanie wielowymiarowe idea Jedną z wad metody PCA jest możliwość używania jedynie zmiennych ilościowych, kolejnym konieczność posiadania pełnych danych z doświadczenia(nie da się użyć PCA jeśli mamy
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015
 Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU
 AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
Zastosowanie MES do rozwiązania problemu ustalonego przepływu ciepła w obszarze 2D
 Równanie konstytutywne opisujące sposób w jaki ciepło przepływa w materiale o danych właściwościach, prawo Fouriera Macierz konstytutywna (właściwości) materiału Wektor gradientu temperatury Wektor strumienia
Równanie konstytutywne opisujące sposób w jaki ciepło przepływa w materiale o danych właściwościach, prawo Fouriera Macierz konstytutywna (właściwości) materiału Wektor gradientu temperatury Wektor strumienia
Pomiar natężenia oświetlenia
 Pomiary natężenia oświetlenia jako jedyne w technice świetlnej nie wymagają stosowania wzorców. Pomiary natężenia oświetlenia dokonuje się za pomocą miernika zwanego luksomierzem. Powody dla których nie
Pomiary natężenia oświetlenia jako jedyne w technice świetlnej nie wymagają stosowania wzorców. Pomiary natężenia oświetlenia dokonuje się za pomocą miernika zwanego luksomierzem. Powody dla których nie
Algorytmy metaheurystyczne Wykład 11. Piotr Syga
 Algorytmy metaheurystyczne Wykład 11 Piotr Syga 22.05.2017 Drzewa decyzyjne Idea Cel Na podstawie przesłanek (typowo zbiory rozmyte) oraz zbioru wartości w danych testowych, w oparciu o wybrane miary,
Algorytmy metaheurystyczne Wykład 11 Piotr Syga 22.05.2017 Drzewa decyzyjne Idea Cel Na podstawie przesłanek (typowo zbiory rozmyte) oraz zbioru wartości w danych testowych, w oparciu o wybrane miary,
3. OPERACJE BEZKONTEKSTOWE
 3. OPERACJE BEZKONTEKSTOWE 3.1. Tablice korekcji (LUT) Przekształcenia bezkontekstowe (punktowe) to takie przekształcenia obrazu, w których zmiana poziomu szarości danego piksela zależy wyłącznie od jego
3. OPERACJE BEZKONTEKSTOWE 3.1. Tablice korekcji (LUT) Przekształcenia bezkontekstowe (punktowe) to takie przekształcenia obrazu, w których zmiana poziomu szarości danego piksela zależy wyłącznie od jego
Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET
 18 Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET Ines Moskal Studentka, Instytut Fizyki UJ Na Uniwersytecie Jagiellońskim prowadzone są badania dotyczące usprawnienia
18 Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET Ines Moskal Studentka, Instytut Fizyki UJ Na Uniwersytecie Jagiellońskim prowadzone są badania dotyczące usprawnienia
Wszechświat: spis inwentarza. Typy obiektów Rozmieszczenie w przestrzeni Symetrie
 Wszechświat: spis inwentarza Typy obiektów Rozmieszczenie w przestrzeni Symetrie Curtis i Shapley 1920 Heber D. Curtis 1872-1942 Mgławice spiralne są układami gwiazd równoważnymi Drodze Mlecznej Mgławice
Wszechświat: spis inwentarza Typy obiektów Rozmieszczenie w przestrzeni Symetrie Curtis i Shapley 1920 Heber D. Curtis 1872-1942 Mgławice spiralne są układami gwiazd równoważnymi Drodze Mlecznej Mgławice
Proste metody przetwarzania obrazu
 Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Wielkości gwiazdowe. Systematyka N.R. Pogsona, który wprowadza zasadę, że różniaca 5 wielkości gwiazdowych to stosunek natężeń równy 100
 Wielkości gwiazdowe Ptolemeusz w Almageście 6 wielkości gwiazdowych od 1 do 6 mag. 1830 r, John Herschel wiąże skalę wielkości gwiazdowych z natężeniem globlanym światła gwiazd, mówiąc, że różnicom w wielkościach
Wielkości gwiazdowe Ptolemeusz w Almageście 6 wielkości gwiazdowych od 1 do 6 mag. 1830 r, John Herschel wiąże skalę wielkości gwiazdowych z natężeniem globlanym światła gwiazd, mówiąc, że różnicom w wielkościach
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum
 Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
Obserwacje fotometryczne planetoid
 Obserwacje fotometryczne planetoid Anna Borucka 2002-01-14 Streszczenie Sprawozdanie dotyczy obserwacji planetoidy 54 Alexandra wykonanej w Borowcu 8-go października 2001. Dalej przedstawiono redukcję
Obserwacje fotometryczne planetoid Anna Borucka 2002-01-14 Streszczenie Sprawozdanie dotyczy obserwacji planetoidy 54 Alexandra wykonanej w Borowcu 8-go października 2001. Dalej przedstawiono redukcję
