Prognozowanie w hydrologii i klimatologii
|
|
|
- Aneta Górska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Prognozowanie w hydrologii i klimatologii Bartosz Czernecki Uniwersytet im. A. Mickiewicza w Poznaniu tel. (61) I nwp@amu.edu.pl I
2 Remember that all models are wrong; the practical question is how wrong do George E.P. Box (1987)
3 Czym jest model? czasami nie jest jednoznaczne! odwzorowanie sposobem model obraz, lub wzorzec Przez model systemu rzeczywistego (lub tworzonego systemu) w dogodnej dla nas postaci.
4 Podstawowe cechy modeli wykorzystania zgodnie z przeznaczeniem (na podst. opracowania A. Stacha)
5 Przeznaczenie modeli BADANIE do systemu w PROGNOZOWANIE PROJEKTOWANIE do przewidywania zachowania do optymalizacji struktury i KIEROWANIE do podejmowania decyzji w. (na podst. opracowania A. Stacha)
6 Praktyczne zastosowanie modeli atmosferycznych Macedonia (Sarigiannis D., 2008) informacji
7 Typy modeli: np. ; modele koncepcyjne atmosfery:((1) atmosfera ); (2) atmosfera izotermiczna; (3) )) Fizyczne np. model koryta rzeki w skali laboratoryjnej, lub model samolotu testowany w tunelu aerodynamicznym. Analogowe Matematyczne Komputerowe specjalnie stworzony program komputerowy.
8 atmosferycznych ze Modele globalne (GCM, AOGCM) Modele mezoskalowe / Modele LAM, RCM (Limited Area Model, Regional Climate Model) synoptyczny model prognozy pogody Model CFD (Computational Fluid Dynamics); Modele Obliczeniowej Mechaniki p Ryc. 1. Widmo pr d wiatru na maszcie meteorologicznym w Brookhaven (Nowy Jork), m n.p.t. (van der Hoven 1957), oraz odpowiada ce im typowe zakresy skal stosowania modeli atmosferycznych (mezoskalowych i LES (Large Eddy Scale)).
9 Model fizyczny (eksperyment laboratoryjny) Fale Kelvina-Helmholtza Fale Helmholtza undulatus
10 Model fizyczny (eksperyment laboratoryjny)
11 Model fizyczny (eksperyment laboratoryjny)
12 Model fizyczny (eksperyment laboratoryjny)
13 Model matematyczny model smugi gaussowski
14 Model matematyczny model smugi gaussowski
15 Model matematyczny
16 nauk o atmosferze?
17 Modelowanie numeryczne Metoda badania stanu fizycznego atmosfery poprzez utworzenie matematycznego modelu atmosfery Model atmosfery uproszczeniach
18 W modelowaniu atmosfery znaczenie prawa kinematyki i zachowania energii 2. Prawo Newtona i 1. Prawo Termodynamiki), procesy w atmosferze. Te prawa w szeregu dynamiczny modelu.
19 Drugie Prawo Newtona -. Pierwsza zasada termodynamiki pracy. = Q + W gdzie: U jako W Q
20 funkcji - zwyczajne - W W.
21 Historia... W 1904 r. V.F.K. Bjerknes i jego koledzy z tzw. norweskiej m.in. wyniki prac lorda Kelvina i polskiego fizyka L. Silbersteina w, zaproponowali w czasie. prawa hydrodynamiki i termodynamiki do opisu stworzyli podstawy nowoczesnej meteorologii dynamicznej. Niestety ten skomplikowany ruchu, termodynamiki, nie daje i
22
23 matematyk, fizyk i meteorolog Lewis Fry Richardson.... w wojsku jako sanitariusz polowy podczas w, obliczanych odcinkach,. zmiany na odcinkach znacznie
24 jednakowe, regularne kostki i na podstawie danych krok po kroku przewidywane oczku siatki.
25 prognozy pogody
26 Siatka modelu Richardsona Siatka modelu Richardsona (1922) zastosowana do ma 3 Stewart R. (2008), Numerical Weather Prediction. Weather forecasting by Computer.
27 kompletnie niezgodny z wynikami obserwacji w chwili prognozie. w Richardson nie, jakie powinny jego kostki i kroki obliczeniowe. Warunki te odkryto dopiero w latach 30. i 40. XX w. Richardson, wtedy nie : nie danych.
28 Ciekawy przypadek L. F. Richardsona Mimo niepowodzenia projektu w 1922 r. wyniki tej pracy w rozprawie pod Forecasting By Pozostaje ona, nawet negatywny wynik w wyniku rzetelnej pracy naukowej. lat na kartce papieru to, co komputery w Szukanie do mechaniki. analizy rozwoju obliczeniowej
29 w Oslo, atmosferycznych, poprawnej matematycznie i numerycznie prognozy pogody. matematykiem pochodzenia von Neumannem przeprowadzili obliczenia pod koniec roku 1952 na superkomputerze ENIAC poprawne numerycznie obliczeniowej dynamiki
30 ENIAC ENIAC = Electronic Numerical Integrator And Computer Elektroniczny, Numeryczny Integrator i Komputer Ten liczb na (
31 Edward Lorenz E.N Lorenz* dla uproszczonego - dwa wykresy coraz bardziej Wniosek: prognozy pogody nie w przypadku procesy w atmosferze Edward Lorenz article ece/alternates/w620/lorenz.jpeg prognoz Sukces poboczny: teoria chaosu, efekt motyla *Edward Lorenz AAAS w 1972 : "Predictability- Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas?"
32 Eksperyment numeryczny Lorenza (przepisany do R) gdzie: P liczba Prandtl R - B obliczeniowego Oberbecka-Boussinesqa - Schemat stabilny dla R<1 - P = 10, R = 28, B = 8/3
33 Atraktor Lorenza opublikowane w 1963 r. nauce i technice prognozy numeryczne nie ; przypadku znalezienia atmosferze w w,
34 Dalsze wnioski z pracy Lorenza modele nie Naviera Stokesa jest podstawowym dynamiki atmosfery jest nieliniowe, co oznacza, na niewielkie zmiany warunku atmosferyczne. Innymi (prognoza pogody) jest atmosfery.
35 ensembles)
36 ensembles)
37 pogody, nazywany numerycznym modelem prognostycznym ): - atmosferze ( ), - matematycznego, - kodu (programu komputerowego), pozwala na na konkretnym superkomputerze czy maszynie obliczeniowej. wyniku procedury. Przebiega ona w 2 etapach; - pierwszy polega na kontroli i weryfikacji danych z i obserwacji (odrzucenie danych obarczonych lub transmisji), - drugi do modelu prognostycznego, a.
38 modelu meteorologicznym, zakodowane w z modelu numerycznego. W pionie siatka obejmuje obszar troposfery i 40 km; przeprowadza dane uzgadnia Ten etap momencie meteorologicznych. obliczenia ewolucji siatki. Interpolowane
39 Struktra i koncepcja numerycznych modeli prognozy pogody (Numerical Weather Prediction, NWP)
40 Matematyczna koncepcja modeli numerycznych, (tj. w ). element A Gdzie: A - punkcie w przestrzeni ; t - zmiana czasu (jak daleko w ); F(A) funkcja zmiany A
41 parametru prognozy:
42 numeryczne energii i wilgoci. Problem: - / *
43 Skutki
44
45 - - ich znaczenie) w przypadku kiedy - jednak. w wiatru, pierwotnych,
46 praktyce?
47 Warunek Couranta Couranta Friedrichsa Lewy'ego - matematyczny Zwykle modelu:
48 postaci spektralnej:
49 Horizontal grid structures modelowych: MM5 i znaczna grupa modeli mezoskalowych WRF i znaczna grupa modeli mezoskalowych From Randall (1994) Randall (1994)
50 modelach: Siatka Hexagonalna Siatka Triangularna From ccrma.standford.edu/~bilbao
51 Oznaczenia: T - temperatura, p wiatru, v u w q natomiast parametry wiatru (u,v,w) dla jego postprocessingu
52 Modele hydrostatyczne i niehydrostatyczne Takie uproszczenie nie ma znaczenia w przypadku symulacji. przestrzennych (ograniczenie dla dx, dx < 10 km)
53 Modele hydrostatyczne i niehydrostatyczne, ale pozwala na jak np. p
54 symulowania tych zjawisk: Bryza morska Konieczne wykorzystanie modelu o rdzeniu niehydrostatycznym: Rolki warstwy granicznej bryzy zafalowania silnymi zafalowaniami strumienia powietrza Przemieszczanie grawitacyjnych frontu atmosferycznego Predykcja fal grawitacyjnych Oko huraganu
Numeryczna prognoza pogody
 Numeryczna prognoza pogody 1. Trochę historii. 2. Zwyczajna numeryczna prognoza pogody. 3. Uda sie czy sie nie... dynamiczna prognoza deterministyczna. 4. Edward N. Lorenz dlaczego sie nie udaje? 5. Jak
Numeryczna prognoza pogody 1. Trochę historii. 2. Zwyczajna numeryczna prognoza pogody. 3. Uda sie czy sie nie... dynamiczna prognoza deterministyczna. 4. Edward N. Lorenz dlaczego sie nie udaje? 5. Jak
Fizyka Pogody i Klimatu, zima 2017, Prognoza pogody: wykład 3. Szymon Malinowski. Historia i praktyka numerycznej prognozy pogody.
 Fizyka Pogody i Klimatu, zima 2017, Prognoza pogody: wykład 3 Szymon Malinowski Historia i praktyka numerycznej prognozy pogody. Na początku XX w. V.F.K. Bjerknes i jego koledzy z tzw. norweskiej szkoły
Fizyka Pogody i Klimatu, zima 2017, Prognoza pogody: wykład 3 Szymon Malinowski Historia i praktyka numerycznej prognozy pogody. Na początku XX w. V.F.K. Bjerknes i jego koledzy z tzw. norweskiej szkoły
Modelowanie numeryczne w fizyce atmosfery - krótka historia prognoz pogody i klimatu
 Modelowanie numeryczne w fizyce atmosfery - krótka historia prognoz pogody i klimatu Szymon Malinowski Uniwersytet Warszawski Instytut Geofizyki Zakład Fizyki Atmosfery http://www.igf.fuw.edu.pl/zfa/ Na
Modelowanie numeryczne w fizyce atmosfery - krótka historia prognoz pogody i klimatu Szymon Malinowski Uniwersytet Warszawski Instytut Geofizyki Zakład Fizyki Atmosfery http://www.igf.fuw.edu.pl/zfa/ Na
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów
 Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Dwuletnie studia II stopnia na kierunku fizyka, specjalność Geofizyka, specjalizacje: Fizyka atmosfery; Fizyka Ziemi i planet; Fizyka środowiska
 Dwuletnie studia II stopnia na kierunku fizyka, specjalność Geofizyka, specjalizacje: Fizyka atmosfery; Fizyka Ziemi i planet; Fizyka środowiska 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności Geofizyka,
Dwuletnie studia II stopnia na kierunku fizyka, specjalność Geofizyka, specjalizacje: Fizyka atmosfery; Fizyka Ziemi i planet; Fizyka środowiska 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności Geofizyka,
1. CHARAKTERYSTYKA STUDIÓW 2. SYLWETKA ABSOLWENTA
 Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Geofizyka, specjalizacje: Fizyka atmosfery; Fizyka Ziemi i planet; Fizyka środowiska 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Geofizyka, specjalizacje: Fizyka atmosfery; Fizyka Ziemi i planet; Fizyka środowiska 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności
Efekt motyla i dziwne atraktory
 O układzie Lorenza Wydział Matematyki i Informatyki Uniwersytet Mikołaja kopernika Toruń, 3 grudnia 2009 Spis treści 1 Wprowadzenie Wyjaśnienie pojęć 2 O dziwnych atraktorach 3 Wyjaśnienie pojęć Dowolny
O układzie Lorenza Wydział Matematyki i Informatyki Uniwersytet Mikołaja kopernika Toruń, 3 grudnia 2009 Spis treści 1 Wprowadzenie Wyjaśnienie pojęć 2 O dziwnych atraktorach 3 Wyjaśnienie pojęć Dowolny
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
Układ klimatyczny. kriosfera. atmosfera. biosfera. geosfera. hydrosfera
 Układ klimatyczny kriosfera atmosfera biosfera geosfera hydrosfera 1 Klimat, bilans energetyczny 30% 66% T=15oC Bez efektu cieplarnianego T=-18oC 2 Przyczyny zmian klimatycznych Przyczyny zewnętrzne: Zmiana
Układ klimatyczny kriosfera atmosfera biosfera geosfera hydrosfera 1 Klimat, bilans energetyczny 30% 66% T=15oC Bez efektu cieplarnianego T=-18oC 2 Przyczyny zmian klimatycznych Przyczyny zewnętrzne: Zmiana
Zintegrowanego Systemu
 Zintegrowany System Informacji o Zlewni - CRIS Dane meteorologiczne dla Zintegrowanego Systemu Informacji o Zlewni CRIS dr Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych w Katowicach Projekt
Zintegrowany System Informacji o Zlewni - CRIS Dane meteorologiczne dla Zintegrowanego Systemu Informacji o Zlewni CRIS dr Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych w Katowicach Projekt
Ramowy Program Specjalizacji MODELOWANIE MATEMATYCZNE i KOMPUTEROWE PROCESÓW FIZYCZNYCH Studia Specjalistyczne (III etap)
 Ramowy Program Specjalizacji MODELOWANIE MATEMATYCZNE i KOMPUTEROWE PROCESÓW FIZYCZNYCH Studia Specjalistyczne (III etap) Z uwagi na ogólno wydziałowy charakter specjalizacji i możliwość wykonywania prac
Ramowy Program Specjalizacji MODELOWANIE MATEMATYCZNE i KOMPUTEROWE PROCESÓW FIZYCZNYCH Studia Specjalistyczne (III etap) Z uwagi na ogólno wydziałowy charakter specjalizacji i możliwość wykonywania prac
Możliwości prognozowania gwałtownych burz w Polsce
 Artur Surowiecki Stowarzyszenie Skywarn Polska Możliwości prognozowania gwałtownych burz w Polsce VII Zlot Polskich Łowców Burz Wrocław 2016 Po co prognoza dotycząca siły i aktywności burz? Burze, w zależności
Artur Surowiecki Stowarzyszenie Skywarn Polska Możliwości prognozowania gwałtownych burz w Polsce VII Zlot Polskich Łowców Burz Wrocław 2016 Po co prognoza dotycząca siły i aktywności burz? Burze, w zależności
Klimat w Polsce w 21. wieku
 Klimat w Polsce w 21. wieku na podstawie numerycznych symulacji regionalnych Małgorzata Liszewska Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego UNIWERSYTET WARSZAWSKI 1/42 POGODA
Klimat w Polsce w 21. wieku na podstawie numerycznych symulacji regionalnych Małgorzata Liszewska Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego UNIWERSYTET WARSZAWSKI 1/42 POGODA
Projekt zaliczeniowy: weryfikacja krótkoterminowych prognoz pogody oraz modelowanie regresyjne
 Matematyczne modelowania procesów meteorologicznych i klimatycznych -> prognozowanie i weryfikacja modelu atmosferycznych Global Forecasting System (GFS) oraz modelowanie regresyjne Projekt zaliczeniowy:
Matematyczne modelowania procesów meteorologicznych i klimatycznych -> prognozowanie i weryfikacja modelu atmosferycznych Global Forecasting System (GFS) oraz modelowanie regresyjne Projekt zaliczeniowy:
TEORIA CHAOSU. Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska
 TEORIA CHAOSU Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska Wydział MiNI Politechnika Warszawska Rok akademicki 2015/2016 Semestr letni Krótki kurs historii matematyki DEFINICJA
TEORIA CHAOSU Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska Wydział MiNI Politechnika Warszawska Rok akademicki 2015/2016 Semestr letni Krótki kurs historii matematyki DEFINICJA
Fizyka komputerowa(ii)
 Instytut Fizyki Fizyka komputerowa(ii) Studia magisterskie Prowadzący kurs: Dr hab. inż. Włodzimierz Salejda, prof. PWr Godziny konsultacji: Poniedziałki i wtorki w godzinach 13.00 15.00 pokój 223 lub
Instytut Fizyki Fizyka komputerowa(ii) Studia magisterskie Prowadzący kurs: Dr hab. inż. Włodzimierz Salejda, prof. PWr Godziny konsultacji: Poniedziałki i wtorki w godzinach 13.00 15.00 pokój 223 lub
Globalne prognozowanie pogody.
 Globalne prognozowanie pogody. www: http://www.ksn.stawiarz.pl/ Łukasz Stawiarz email: ksn@stawiarz.pl Robert Gaździk email: valmont@fatcat.ftj.agh.edu.pl Wydział Fizyki i Informatyki Stosowanej, AGH Kraków
Globalne prognozowanie pogody. www: http://www.ksn.stawiarz.pl/ Łukasz Stawiarz email: ksn@stawiarz.pl Robert Gaździk email: valmont@fatcat.ftj.agh.edu.pl Wydział Fizyki i Informatyki Stosowanej, AGH Kraków
Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych.
 Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych. Jedną z metod symulacji dynamiki cieczy jest zastosowanie metody siatkowej Boltzmanna.
Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych. Jedną z metod symulacji dynamiki cieczy jest zastosowanie metody siatkowej Boltzmanna.
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, ćwiczenia, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Przekazanie
Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, ćwiczenia, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Przekazanie
KLIMAT POLSKI I JEGO ZMIANY. SYLABUS A. Informacje ogólne
 KLIMAT POLSKI I JEGO ZMIANY SYLABUS A. Informacje ogólne Elementy sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów Kod przedmiotu Język
KLIMAT POLSKI I JEGO ZMIANY SYLABUS A. Informacje ogólne Elementy sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów Kod przedmiotu Język
PRZEDMIOTY STUDIÓW STACJONARNYCH II STOPNIA
 PRZEDMIOTY STUDIÓW STACJONARNYCH II STOPNIA Tabela 1-1 Matematyka - Metody numeryczne 30 15 4 2a 2b Teoria sterowania (kierunek AUTOMATYKA i ROBOTYKA) Systemy mikroprocesorowe w mechatronice (kierunek
PRZEDMIOTY STUDIÓW STACJONARNYCH II STOPNIA Tabela 1-1 Matematyka - Metody numeryczne 30 15 4 2a 2b Teoria sterowania (kierunek AUTOMATYKA i ROBOTYKA) Systemy mikroprocesorowe w mechatronice (kierunek
Wstęp. Regulamin przedmiotu Efekty kształcenia Materiały na stronie www2.wt.pw.edu.pl/~akw METEOROLOGIA LOTNICZA. Wstęp.
 Wstęp METEOROLOGIA LOTNICZA Wstęp Ćwiczenie 1 Regulamin przedmiotu Efekty kształcenia Materiały na stronie www2.wt.pw.edu.pl/~akw 1 Zaliczenie Dwie kartkówki punktowane: 1. W połowie zajęć. 2. Ostatnie
Wstęp METEOROLOGIA LOTNICZA Wstęp Ćwiczenie 1 Regulamin przedmiotu Efekty kształcenia Materiały na stronie www2.wt.pw.edu.pl/~akw 1 Zaliczenie Dwie kartkówki punktowane: 1. W połowie zajęć. 2. Ostatnie
Optymalizacja inwestycji remontowych związanych z bezpieczeństwem pożarowym dzięki wykorzystaniu technik komputerowych CFD
 Optymalizacja inwestycji remontowych związanych z bezpieczeństwem pożarowym dzięki wykorzystaniu technik komputerowych CFD dr inż. Dorota Brzezińska Katedra Inżynierii Bezpieczeństwa Pracy WIPOŚ PŁ Licheń,
Optymalizacja inwestycji remontowych związanych z bezpieczeństwem pożarowym dzięki wykorzystaniu technik komputerowych CFD dr inż. Dorota Brzezińska Katedra Inżynierii Bezpieczeństwa Pracy WIPOŚ PŁ Licheń,
MECHANIKA I BUDOWA MASZYN
 Specjalność "Eksploatacja i diagnostyka pojazdów i maszyn" obowiązuje od 01.10.2017 r. zatwierdzony Decyzja RW 27.04.2017 r. 1. Technologie informacyjne w budowie maszyn I 2 1.2 0.8 0.8 ZAL OC O 51 31
Specjalność "Eksploatacja i diagnostyka pojazdów i maszyn" obowiązuje od 01.10.2017 r. zatwierdzony Decyzja RW 27.04.2017 r. 1. Technologie informacyjne w budowie maszyn I 2 1.2 0.8 0.8 ZAL OC O 51 31
Model fizykochemiczny i biologiczny
 Model fizykochemiczny i biologiczny dr Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych Projekt współfinansowany ze środków Europejskiego Funduszu Rozwoju Regionalnego w ramach Programu Operacyjnego
Model fizykochemiczny i biologiczny dr Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych Projekt współfinansowany ze środków Europejskiego Funduszu Rozwoju Regionalnego w ramach Programu Operacyjnego
Kierunek: Automatyka i Robotyka Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne. Wykład Ćwiczenia
 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Automatyka i Robotyka Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne Rocznik: 2015/2016 Język wykładowy:
Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Automatyka i Robotyka Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne Rocznik: 2015/2016 Język wykładowy:
Moduł modelowania i predykcji stanu troposfery projekt ASG+ Budowa modułów wspomagania serwisów czasu rzeczywistego systemu ASG-EUPOS
 Moduł modelowania i predykcji stanu troposfery projekt ASG+ Budowa modułów wspomagania serwisów czasu rzeczywistego systemu ASG-EUPOS Jarosław BOSY Witold ROHM Jan KAPŁON Jan SIERNY Instytut Geodezji i
Moduł modelowania i predykcji stanu troposfery projekt ASG+ Budowa modułów wspomagania serwisów czasu rzeczywistego systemu ASG-EUPOS Jarosław BOSY Witold ROHM Jan KAPŁON Jan SIERNY Instytut Geodezji i
Modele opadowe PANDa w kontekście adaptacji miast do zmian klimatu. dr hab. inż. Paweł Licznar, prof. PWr
 Modele opadowe PANDa w kontekście adaptacji miast do zmian klimatu dr hab. inż. Paweł Licznar, prof. PWr Doświadczenia projektu bydgoskiego Trudność z pozyskaniem lokalnych danych Brak metodyki opracowania
Modele opadowe PANDa w kontekście adaptacji miast do zmian klimatu dr hab. inż. Paweł Licznar, prof. PWr Doświadczenia projektu bydgoskiego Trudność z pozyskaniem lokalnych danych Brak metodyki opracowania
MECHANIKA I BUDOWA MASZYN
 Specjalność "Eksploatacja i diagnostyka pojazdów i maszyn" obowiązuje od 01.10.2017 r. zatwierdzony Decyzja RW 27.04.2017 r. 1. Technologie informacyjne w budowie maszyn I 2 0.8 1.2 0.8 ZAL OC O 51 21
Specjalność "Eksploatacja i diagnostyka pojazdów i maszyn" obowiązuje od 01.10.2017 r. zatwierdzony Decyzja RW 27.04.2017 r. 1. Technologie informacyjne w budowie maszyn I 2 0.8 1.2 0.8 ZAL OC O 51 21
Meteorologia i Klimatologia
 Meteorologia i Klimatologia Ćwiczenie I Poznań, 17.10.2008 mgr Bartosz Czernecki pok. 356 Instytut Geografii Fizycznej i Kształtowania Środowiska Przyrodniczego (Zakład Klimatologii) Wydział Nauk Geograficznych
Meteorologia i Klimatologia Ćwiczenie I Poznań, 17.10.2008 mgr Bartosz Czernecki pok. 356 Instytut Geografii Fizycznej i Kształtowania Środowiska Przyrodniczego (Zakład Klimatologii) Wydział Nauk Geograficznych
Jan A. Szantyr tel
 Katedra Energetyki i Aparatury Przemysłowej Zakład Mechaniki Płynów, Turbin Wodnych i Pomp J. Szantyr Wykład 1 Rozrywkowe wprowadzenie do Mechaniki Płynów Jan A. Szantyr jas@pg.gda.pl tel. 58-347-2507
Katedra Energetyki i Aparatury Przemysłowej Zakład Mechaniki Płynów, Turbin Wodnych i Pomp J. Szantyr Wykład 1 Rozrywkowe wprowadzenie do Mechaniki Płynów Jan A. Szantyr jas@pg.gda.pl tel. 58-347-2507
Moduł meteorologiczny w serwisie CRIS
 Zintegrowana strategia zrównoważonego zarządzania wodami w zlewni Moduł meteorologiczny w serwisie CRIS Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych Projekt finansowany ze środków funduszy
Zintegrowana strategia zrównoważonego zarządzania wodami w zlewni Moduł meteorologiczny w serwisie CRIS Czesław Kliś Instytut Ekologii Terenów Uprzemysłowionych Projekt finansowany ze środków funduszy
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
Kształcenie w Szkole Doktorskiej Politechniki Białostockiej realizowane będzie według następującego programu:
 Kształcenie w Szkole Doktorskiej Politechniki Białostockiej realizowane będzie według następującego programu: Semestr 1 2 3 4 Rodzaj Forma Forma Liczba zajęć zajęć zaliczeń godzin Szkolenie biblioteczne
Kształcenie w Szkole Doktorskiej Politechniki Białostockiej realizowane będzie według następującego programu: Semestr 1 2 3 4 Rodzaj Forma Forma Liczba zajęć zajęć zaliczeń godzin Szkolenie biblioteczne
Karta (sylabus) przedmiotu Mechanika i Budowa Maszyn Studia II stopnia. Modelowanie i symulacje eksploatacyjnych stanów śmigłowców Rodzaj przedmiotu:
 Karta (sylabus) przedmiotu Mechanika i Budowa Maszyn Studia II stopnia Przedmiot: Modelowanie i symulacje eksploatacyjnych stanów śmigłowców Rodzaj przedmiotu: Podstawowy Kod przedmiotu: MBM S 1 7-0_1
Karta (sylabus) przedmiotu Mechanika i Budowa Maszyn Studia II stopnia Przedmiot: Modelowanie i symulacje eksploatacyjnych stanów śmigłowców Rodzaj przedmiotu: Podstawowy Kod przedmiotu: MBM S 1 7-0_1
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Metody fizyki w ekonomii (ekonofizyka)
 Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Metody fizyki w ekonomii (ekonofizyka) 1. CHARAKTERYSTYKA STUDIÓW Celem kształcenia w ramach specjalności Metody fizyki w ekonomii
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Metody fizyki w ekonomii (ekonofizyka) 1. CHARAKTERYSTYKA STUDIÓW Celem kształcenia w ramach specjalności Metody fizyki w ekonomii
Proces projektowy i zaawansowane obliczenia numeryczne - projektowanie i optymalizacja zaawansowanych technicznie i złożonych produktów przemysłowych
 Proces projektowy i zaawansowane obliczenia numeryczne - projektowanie i optymalizacja zaawansowanych technicznie i złożonych produktów przemysłowych Główny Projektant Wzornictwa PESA Bydgoszcz SA dr Bartosz
Proces projektowy i zaawansowane obliczenia numeryczne - projektowanie i optymalizacja zaawansowanych technicznie i złożonych produktów przemysłowych Główny Projektant Wzornictwa PESA Bydgoszcz SA dr Bartosz
Elektrotechnika I stopień Ogólno akademicki. Przedmiot kierunkowy. Obowiązkowy Polski VI semestr zimowy
 KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
METEOROLOGIA LOTNICZA ćwiczenie 1
 METEOROLOGIA LOTNICZA ćwiczenie 1 Wstęp Regulamin przedmiotu Efekty kształcenia Materiały na stronie www2.wt.pw.edu.pl/~akw Zaliczenie Dwie kartkówki punktowane: 1. W połowie zajęć. 2. Ostatnie zajęcia.
METEOROLOGIA LOTNICZA ćwiczenie 1 Wstęp Regulamin przedmiotu Efekty kształcenia Materiały na stronie www2.wt.pw.edu.pl/~akw Zaliczenie Dwie kartkówki punktowane: 1. W połowie zajęć. 2. Ostatnie zajęcia.
Dynamika nieliniowa i chaos deterministyczny. Fizyka układów złożonych
 Dynamika nieliniowa i chaos deterministyczny Fizyka układów złożonych Wahadło matematyczne F θ = mgsinθ Druga zasada dynamiki: ma = mgsinθ a = d2 x dt 2 = gsinθ Długość łuku: x = Lθ Równanie ruchu: θ ሷ
Dynamika nieliniowa i chaos deterministyczny Fizyka układów złożonych Wahadło matematyczne F θ = mgsinθ Druga zasada dynamiki: ma = mgsinθ a = d2 x dt 2 = gsinθ Długość łuku: x = Lθ Równanie ruchu: θ ሷ
Kierownik Katedry: Prof. dr hab. inż. Tadeusz BURCZYŃSKI
 Kierownik Katedry: Prof. dr hab. inż. Tadeusz BURCZYŃSKI Zakład Inteligentnych Systemów Obliczeniowych RMT4-3 Kierownik Zakładu: Prof. dr hab. inż. Tadeusz BURCZYŃSKI Zakład Metod Numerycznych w Termomechanice
Kierownik Katedry: Prof. dr hab. inż. Tadeusz BURCZYŃSKI Zakład Inteligentnych Systemów Obliczeniowych RMT4-3 Kierownik Zakładu: Prof. dr hab. inż. Tadeusz BURCZYŃSKI Zakład Metod Numerycznych w Termomechanice
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
Przepływy Taylora-Couetta z wymianą ciepła. Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu
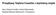 Przepływy Taylora-Couetta z wymianą ciepła Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu Typowy przepływ Taylora-Couetta to przepływ lepki pomiędzy dwoma koncentrycznymi
Przepływy Taylora-Couetta z wymianą ciepła Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu Typowy przepływ Taylora-Couetta to przepływ lepki pomiędzy dwoma koncentrycznymi
Matematyka Stosowana na Politechnice Wrocławskiej. Komitet Matematyki PAN, luty 2017 r.
 Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
PROGNOZY METEOROLOGICZNE NA POTRZEBY OSŁONY HYDROLOGICZNEJ. Teresa Zawiślak Operacyjny Szef Meteorologicznej Osłony Kraju w IMGW-PIB
 PROGNOZY METEOROLOGICZNE NA POTRZEBY OSŁONY HYDROLOGICZNEJ Teresa Zawiślak Operacyjny Szef Meteorologicznej Osłony Kraju w IMGW-PIB 11.12.2013 Prognoza pogody określenie przyszłego najbardziej prawdopodobnego
PROGNOZY METEOROLOGICZNE NA POTRZEBY OSŁONY HYDROLOGICZNEJ Teresa Zawiślak Operacyjny Szef Meteorologicznej Osłony Kraju w IMGW-PIB 11.12.2013 Prognoza pogody określenie przyszłego najbardziej prawdopodobnego
HARMONOGRAM EGZAMINÓW
 Kierunek: MECHANIKA I BUDOWA MASZYN - studia I stopnia Materiałoznawstwo Analiza matematyczna Termodynamika techniczna 2 Cały rok Mechanika II Wytrzymałość materiałów Spawalnictwo Technologia spawania
Kierunek: MECHANIKA I BUDOWA MASZYN - studia I stopnia Materiałoznawstwo Analiza matematyczna Termodynamika techniczna 2 Cały rok Mechanika II Wytrzymałość materiałów Spawalnictwo Technologia spawania
Program Obliczeń Wielkich Wyzwań Nauki i Techniki (POWIEW)
 Program Obliczeń Wielkich Wyzwań Nauki i Techniki (POWIEW) Maciej Cytowski, Maciej Filocha, Maciej E. Marchwiany, Maciej Szpindler Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego
Program Obliczeń Wielkich Wyzwań Nauki i Techniki (POWIEW) Maciej Cytowski, Maciej Filocha, Maciej E. Marchwiany, Maciej Szpindler Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego
S Y L A B U S P R Z E D M I O T U
 "Z A T W I E R D Z A M" Dziekan Wydziału Mechatroniki i Lotnictwa prof. dr hab. inż. Radosław TRĘBIŃSKI Warszawa, dnia... S Y L A B U S P R Z E D M I O T U NAZWA PRZEDMIOTU: KOMPUTEROWA ANALIZA KONSTRUKCJI
"Z A T W I E R D Z A M" Dziekan Wydziału Mechatroniki i Lotnictwa prof. dr hab. inż. Radosław TRĘBIŃSKI Warszawa, dnia... S Y L A B U S P R Z E D M I O T U NAZWA PRZEDMIOTU: KOMPUTEROWA ANALIZA KONSTRUKCJI
GODZINY ZAJĘĆ sem. zimowy FORMA ZAL. ECTS. sem. letni ćwicz. KOD. razem wyk. labor. inne. labor. inne. ćwicz. NAZWA PRZEDMIOTU. wyk.
 AS Fiz 1 - mechanika 70 30 40 E 6 Fiz 2 - elektryczność i magnetyzm 70 30 40 E 6 Fiz 3 - fizyka falowa i optyka 40 20 20 E 4 Fiz 4 - fizyka materii 40 20 20 E 4 Astronomia klasyczna 60 30 30 E 5 Astronomia
AS Fiz 1 - mechanika 70 30 40 E 6 Fiz 2 - elektryczność i magnetyzm 70 30 40 E 6 Fiz 3 - fizyka falowa i optyka 40 20 20 E 4 Fiz 4 - fizyka materii 40 20 20 E 4 Astronomia klasyczna 60 30 30 E 5 Astronomia
Rozwiązywanie równań różniczkowych zwyczajnych za pomocą komputera
 Rozwiązywanie równań różniczkowych zwyczajnych za pomocą komputera Arkadiusz Syta A. Syta (Politechnika Lubelska) 1 / 19 Wstęp Przegląd wybranych pakietów oprogramowania i funkcji Rozwiązywanie równań
Rozwiązywanie równań różniczkowych zwyczajnych za pomocą komputera Arkadiusz Syta A. Syta (Politechnika Lubelska) 1 / 19 Wstęp Przegląd wybranych pakietów oprogramowania i funkcji Rozwiązywanie równań
Spis treści. Wstęp 13. Część I. UKŁADY REDUKCJI DRGAŃ Wykaz oznaczeń 18. Literatura Wprowadzenie do części I 22
 Spis treści Wstęp 13 Literatura - 15 Część I. UKŁADY REDUKCJI DRGAŃ - 17 Wykaz oznaczeń 18 1. Wprowadzenie do części I 22 2. Teoretyczne podstawy opisu i analizy układów wibroizolacji maszyn 30 2.1. Rodzaje
Spis treści Wstęp 13 Literatura - 15 Część I. UKŁADY REDUKCJI DRGAŃ - 17 Wykaz oznaczeń 18 1. Wprowadzenie do części I 22 2. Teoretyczne podstawy opisu i analizy układów wibroizolacji maszyn 30 2.1. Rodzaje
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Matematyczne i komputerowe modelowanie procesów fizycznych
 Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Matematyczne i komputerowe modelowanie procesów fizycznych 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności Matematyczne i komputerowe
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Matematyczne i komputerowe modelowanie procesów fizycznych 1. CHARAKTERYSTYKA STUDIÓW Celem specjalności Matematyczne i komputerowe
INFORMATYKA i FINANSE KATEDRA INFORMATYKI TEORETYCZNEJ
 INFORMATYKA i FINANSE KATEDRA INFORMATYKI TEORETYCZNEJ dr hab. Czesław Bagiński, prof. PB Kierownik KIT dr hab. Wiktor Dańko, prof. PB dr hab. Piotr Grzeszczuk, prof. PB dr Ryszard Mazurek dr Jolanta Koszelew
INFORMATYKA i FINANSE KATEDRA INFORMATYKI TEORETYCZNEJ dr hab. Czesław Bagiński, prof. PB Kierownik KIT dr hab. Wiktor Dańko, prof. PB dr hab. Piotr Grzeszczuk, prof. PB dr Ryszard Mazurek dr Jolanta Koszelew
Projekt z meteorologii. Atmosfera standardowa. Anna Kaszczyszyn
 Projekt z meteorologii Atmosfera standardowa Anna Kaszczyszyn 1 1. POGODA I ATMOSFERA: Pogoda różni się w zależności od czasu i miejsca. Atmosfera standardowa jest zdefiniowana dla Ziemi, tzn. możemy powiedzieć,
Projekt z meteorologii Atmosfera standardowa Anna Kaszczyszyn 1 1. POGODA I ATMOSFERA: Pogoda różni się w zależności od czasu i miejsca. Atmosfera standardowa jest zdefiniowana dla Ziemi, tzn. możemy powiedzieć,
E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu. Dynamicznych. Elektrotechnika I stopień Ogólno akademicki. Przedmiot kierunkowy
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu Dynamicznych Nazwa modułu w języku
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu Dynamicznych Nazwa modułu w języku
PRZYKŁADY WYKORZYSTANIA NUMERYCZNEJ PROGNOZY POGODY W PROCESIE WSPOMAGANIA PODEJMOWANIA DECYZJI
 PRZYKŁADY WYKORZYSTANIA NUMERYCZNEJ PROGNOZY POGODY W PROCESIE WSPOMAGANIA PODEJMOWANIA DECYZJI Maciej WRONA, Karolina SZAFRANEK Streszczenie: Niniejszy artykuł prezentuje przykłady implementacji numerycznych
PRZYKŁADY WYKORZYSTANIA NUMERYCZNEJ PROGNOZY POGODY W PROCESIE WSPOMAGANIA PODEJMOWANIA DECYZJI Maciej WRONA, Karolina SZAFRANEK Streszczenie: Niniejszy artykuł prezentuje przykłady implementacji numerycznych
Modelowanie i Animacja
 Maciej Matyka Uniwersytet Wrocławski Maciej Matyka Plan wykładu Dlaczego animujemy używając komputera? Dlaczego animujemy używając komputera? Wyciąg z minimum programowego fizyki w liceum... Kinematyka
Maciej Matyka Uniwersytet Wrocławski Maciej Matyka Plan wykładu Dlaczego animujemy używając komputera? Dlaczego animujemy używając komputera? Wyciąg z minimum programowego fizyki w liceum... Kinematyka
Raport końcowy z symulacji CFD jakie dane powinien zawierać?
 Raport końcowy z symulacji CFD jakie dane powinien zawierać? 1. Wstęp. Raport końcowy z wykonanej symulacji CFD jest dokumentem zawierającym nie tylko wyniki końcowe oraz płynące z nich wnioski, ale również
Raport końcowy z symulacji CFD jakie dane powinien zawierać? 1. Wstęp. Raport końcowy z wykonanej symulacji CFD jest dokumentem zawierającym nie tylko wyniki końcowe oraz płynące z nich wnioski, ale również
Kierunkowe efekty kształcenia wraz z odniesieniem do efektów obszarowych. Budownictwo studia I stopnia
 Załącznik 1 do uchwały nr /d/05/2012 Wydział Inżynierii Lądowej PK Kierunkowe efekty kształcenia wraz z odniesieniem do efektów Kierunek: Budownictwo studia I stopnia Lista efektów z odniesieniem do efektów
Załącznik 1 do uchwały nr /d/05/2012 Wydział Inżynierii Lądowej PK Kierunkowe efekty kształcenia wraz z odniesieniem do efektów Kierunek: Budownictwo studia I stopnia Lista efektów z odniesieniem do efektów
Znaczenie modelowania w ocenie jakości powietrza. EKOMETRIA Sp. z o.o.
 Znaczenie modelowania w ocenie jakości powietrza EKOMETRIA Sp. z o.o. Metody oceny wstępnej i bieżą żącej Pomiary (automatyczne, manualne, wskaźnikowe) Modelowanie Obiektywne szacowanie emisji Modelowanie
Znaczenie modelowania w ocenie jakości powietrza EKOMETRIA Sp. z o.o. Metody oceny wstępnej i bieżą żącej Pomiary (automatyczne, manualne, wskaźnikowe) Modelowanie Obiektywne szacowanie emisji Modelowanie
WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/ ) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych
 WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/2018 I. Wymagania przekrojowe. Uczeń: 1) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla
WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/2018 I. Wymagania przekrojowe. Uczeń: 1) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla
MODELE I MODELOWANIE
 MODELE I MODELOWANIE Model układ materialny (np. makieta) lub układ abstrakcyjny (np..rysunki, opisy słowne, równania matematyczne). Model fizyczny (nominalny) opis procesów w obiekcie (fizycznych, również
MODELE I MODELOWANIE Model układ materialny (np. makieta) lub układ abstrakcyjny (np..rysunki, opisy słowne, równania matematyczne). Model fizyczny (nominalny) opis procesów w obiekcie (fizycznych, również
Metody Obliczeniowe w Nauce i Technice
 10. Numeryczna algebra liniowa wprowadzenie. Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
10. Numeryczna algebra liniowa wprowadzenie. Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
Wydział Nauk Technicznych
 Wydział Nauk Technicznych Plan sesji egzaminacyjnej 2018/2019 semestr LETNI Dane przesłane przez starostów Spis treści 1. Studia niestacjonarne, Mechanika i Budowa Maszyn, Rok 3, pierwszy stopień... 2
Wydział Nauk Technicznych Plan sesji egzaminacyjnej 2018/2019 semestr LETNI Dane przesłane przez starostów Spis treści 1. Studia niestacjonarne, Mechanika i Budowa Maszyn, Rok 3, pierwszy stopień... 2
EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW BUDOWNICTWO STUDIA PIERWSZEGO STOPNIA PROFIL OGÓLNOAKADEMICKI
 UCZELNIA TECHNICZNO-HANDLOWA IM. H. CHODKOWSKIEJ WYDZIAŁ IŻYNIERYJNY Warszawa, rok 2014 EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW BUDOWNICTWO STUDIA PIERWSZEGO STOPNIA PROFIL OGÓLNOAKADEMICKI Objaśnienie
UCZELNIA TECHNICZNO-HANDLOWA IM. H. CHODKOWSKIEJ WYDZIAŁ IŻYNIERYJNY Warszawa, rok 2014 EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW BUDOWNICTWO STUDIA PIERWSZEGO STOPNIA PROFIL OGÓLNOAKADEMICKI Objaśnienie
Kierunkowe efekty kształcenia wraz z odniesieniem do efektów obszarowych. Automatyka i robotyka studia I stopnia
 Załącznik 1 do uchwały nr /d/05/2012 Wydział Mechaniczny PK Kierunkowe efekty kształcenia wraz z odniesieniem do efektów Kierunek: Automatyka i robotyka studia I stopnia Lista efektów z odniesieniem do
Załącznik 1 do uchwały nr /d/05/2012 Wydział Mechaniczny PK Kierunkowe efekty kształcenia wraz z odniesieniem do efektów Kierunek: Automatyka i robotyka studia I stopnia Lista efektów z odniesieniem do
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
Dwuletnie studia II stopnia na kierunku fizyka, specjalność
 Dwuletnie studia II stopnia na kierunku fizyka, specjalność Geofizyka specjalizacje: Fizyka atmosfery (FA), Fizyka środowiska (FŚ), Fizyka Ziemi i planet (FZiP) CELE kształcenia: Modelowanie i monitorowanie
Dwuletnie studia II stopnia na kierunku fizyka, specjalność Geofizyka specjalizacje: Fizyka atmosfery (FA), Fizyka środowiska (FŚ), Fizyka Ziemi i planet (FZiP) CELE kształcenia: Modelowanie i monitorowanie
PLAN STUDIÓW STACJONARNYCH PIERWSZEGO STOPNIA
 MATEMATYKA STOSOANA PLAN STUDIÓ STACJONARNYCH PIERSZEGO STOPNIA semestr: 1. w grupach 14.4- -060 prowadzenie do psychologii 15 15 30 2 S-PP/OH 11.1- -810 stęp do logiki i teorii mnogości 30 30 60 1 8 P1
MATEMATYKA STOSOANA PLAN STUDIÓ STACJONARNYCH PIERSZEGO STOPNIA semestr: 1. w grupach 14.4- -060 prowadzenie do psychologii 15 15 30 2 S-PP/OH 11.1- -810 stęp do logiki i teorii mnogości 30 30 60 1 8 P1
Modelowanie komputerowe w zagadnieniach środowiska. Strona:
 Modelowanie komputerowe w zagadnieniach środowiska Wykład 30 godzin + Laboratorium 30 godzin Strona: http://www.icm.edu.pl/~aniat/modele/wdw1 Literatura Modelowanie Urszula Foryś, Matematyka w biologii,
Modelowanie komputerowe w zagadnieniach środowiska Wykład 30 godzin + Laboratorium 30 godzin Strona: http://www.icm.edu.pl/~aniat/modele/wdw1 Literatura Modelowanie Urszula Foryś, Matematyka w biologii,
Algorytm. Krótka historia algorytmów
 Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Definicje. Najprostszy schemat blokowy. Schemat dokładniejszy
 Definicje owanie i symulacja owanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano model, do
Definicje owanie i symulacja owanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano model, do
Co ma piekarz do matematyki?
 Instytut Matematyki i Informatyki Politechnika Wrocławska Dolnośląski Festiwal Nauki Wrzesień 2009 x x (x 1, x 2 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) (x 1, x 2, x 3, x 4 ). x
Instytut Matematyki i Informatyki Politechnika Wrocławska Dolnośląski Festiwal Nauki Wrzesień 2009 x x (x 1, x 2 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) (x 1, x 2, x 3, x 4 ). x
Metody numeryczne. dr hab inż. Tomasz Chwiej. Syllabus:
 Metody numeryczne dr hab inż. Tomasz Chwiej Syllabus: https://syllabuskrk.agh.edu.pl/pl Plan wykładu 1. Arytmetyka komputerowa, błędy numeryczne 2. Rozwiązywanie układów algebraicznych równań liniowych
Metody numeryczne dr hab inż. Tomasz Chwiej Syllabus: https://syllabuskrk.agh.edu.pl/pl Plan wykładu 1. Arytmetyka komputerowa, błędy numeryczne 2. Rozwiązywanie układów algebraicznych równań liniowych
Pracownia Komputerowa. Wyk ad I Magdalena Posiada a-zezula
 Pracownia Komputerowa Wyk ad I Magdalena Posiada a-zezula Kontakt Zak ad Cząstek i Oddzia ywań Fundamentalnych pok 4.20, Pasteura 5. http://www.fuw.edu.pl/~mposiada email: Magdalena.Posiadala@fuw.edu.pl
Pracownia Komputerowa Wyk ad I Magdalena Posiada a-zezula Kontakt Zak ad Cząstek i Oddzia ywań Fundamentalnych pok 4.20, Pasteura 5. http://www.fuw.edu.pl/~mposiada email: Magdalena.Posiadala@fuw.edu.pl
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia II stopnia (magisterskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia II stopnia (magisterskie) Temat: Analiza właściwości pilotażowych samolotu Specjalność: Pilotaż lub Awionika 1. Analiza stosowanych kryteriów
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia II stopnia (magisterskie) Temat: Analiza właściwości pilotażowych samolotu Specjalność: Pilotaż lub Awionika 1. Analiza stosowanych kryteriów
Kierunek: Energetyka Odnawialna i Zarządzanie Energią Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne.
 Wydział: Energetyki i Paliw Kierunek: Energetyka Odnawialna i Zarządzanie Energią Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne Rocznik: 2018/2019 Język wykładowy: Polski Semestr 1
Wydział: Energetyki i Paliw Kierunek: Energetyka Odnawialna i Zarządzanie Energią Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne Rocznik: 2018/2019 Język wykładowy: Polski Semestr 1
Kierunek Informatyka stosowana Studia stacjonarne Studia pierwszego stopnia
 Studia pierwszego stopnia I rok Matematyka dyskretna 30 30 Egzamin 5 Analiza matematyczna 30 30 Egzamin 5 Algebra liniowa 30 30 Egzamin 5 Statystyka i rachunek prawdopodobieństwa 30 30 Egzamin 5 Opracowywanie
Studia pierwszego stopnia I rok Matematyka dyskretna 30 30 Egzamin 5 Analiza matematyczna 30 30 Egzamin 5 Algebra liniowa 30 30 Egzamin 5 Statystyka i rachunek prawdopodobieństwa 30 30 Egzamin 5 Opracowywanie
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015
 Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Najprostszy schemat blokowy
 Definicje Modelowanie i symulacja Modelowanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego układu rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano
Definicje Modelowanie i symulacja Modelowanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego układu rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano
Uniwersytet Wirtualny VU2012
 XII Konferencja Uniwersytet Wirtualny VU2012 M o d e l N a r z ę d z i a P r a k t y k a Andrzej ŻYŁAWSKI Warszawska Wyższa Szkoła Informatyki Marcin GODZIEMBA-MALISZEWSKI Instytut Technologii Eksploatacji
XII Konferencja Uniwersytet Wirtualny VU2012 M o d e l N a r z ę d z i a P r a k t y k a Andrzej ŻYŁAWSKI Warszawska Wyższa Szkoła Informatyki Marcin GODZIEMBA-MALISZEWSKI Instytut Technologii Eksploatacji
Zintegrowane środowisko informatyczne jako narzędzie modelowania i dynamicznej wizualizacji jakości powietrza. Tomasz Kochanowski
 Zintegrowane środowisko informatyczne jako narzędzie modelowania i dynamicznej wizualizacji jakości powietrza Tomasz Kochanowski Złożoność systemu zarządzania jakością powietrza Monitoring jakości powietrza
Zintegrowane środowisko informatyczne jako narzędzie modelowania i dynamicznej wizualizacji jakości powietrza Tomasz Kochanowski Złożoność systemu zarządzania jakością powietrza Monitoring jakości powietrza
Laboratorium LAB1. Moduł małej energetyki wiatrowej
 Laboratorium LAB1 Moduł małej energetyki wiatrowej Badanie charakterystyki efektywności wiatraka - kompletnego systemu (wiatrak, generator, akumulator) prędkość wiatru - moc produkowana L1-U1 Pełne badania
Laboratorium LAB1 Moduł małej energetyki wiatrowej Badanie charakterystyki efektywności wiatraka - kompletnego systemu (wiatrak, generator, akumulator) prędkość wiatru - moc produkowana L1-U1 Pełne badania
Kierunek:Informatyka- - inż., rok I specjalność: Grafika komputerowa
 :Informatyka- - inż., rok I specjalność: Grafika komputerowa Rok akademicki 018/019 Metody uczenia się i studiowania. 1 Podstawy prawne. 1 Podstawy ekonomii. 1 Matematyka dyskretna. 1 30 Wprowadzenie do
:Informatyka- - inż., rok I specjalność: Grafika komputerowa Rok akademicki 018/019 Metody uczenia się i studiowania. 1 Podstawy prawne. 1 Podstawy ekonomii. 1 Matematyka dyskretna. 1 30 Wprowadzenie do
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Wybrane zagadnienia modelowania i obliczeń inżynierskich Chosen problems of engineer modeling and numerical analysis Dyscyplina: Budowa i Eksploatacja Maszyn Rodzaj przedmiotu: Przedmiot
Nazwa przedmiotu: Wybrane zagadnienia modelowania i obliczeń inżynierskich Chosen problems of engineer modeling and numerical analysis Dyscyplina: Budowa i Eksploatacja Maszyn Rodzaj przedmiotu: Przedmiot
Wpływ rozwoju elektromobilności w Polsce na zanieczyszczenie powietrza
 Wpływ rozwoju elektromobilności w Polsce na zanieczyszczenie powietrza Paweł Durka (1) Joanna Strużewska (1,2) Jacek W. Kamiński (1,3) Grzegorz Jeleniewicz (1) 1 IOŚ-PIB, Zakład Modelowania Atmosfery i
Wpływ rozwoju elektromobilności w Polsce na zanieczyszczenie powietrza Paweł Durka (1) Joanna Strużewska (1,2) Jacek W. Kamiński (1,3) Grzegorz Jeleniewicz (1) 1 IOŚ-PIB, Zakład Modelowania Atmosfery i
USŁUGI HIGH PERFORMANCE COMPUTING (HPC) DLA FIRM. Juliusz Pukacki,PCSS
 USŁUGI HIGH PERFORMANCE COMPUTING (HPC) DLA FIRM Juliusz Pukacki,PCSS Co to jest HPC (High Preformance Computing)? Agregowanie dużych zasobów obliczeniowych w sposób umożliwiający wykonywanie obliczeń
USŁUGI HIGH PERFORMANCE COMPUTING (HPC) DLA FIRM Juliusz Pukacki,PCSS Co to jest HPC (High Preformance Computing)? Agregowanie dużych zasobów obliczeniowych w sposób umożliwiający wykonywanie obliczeń
Plan studiów dla kierunku:
 Plan studiów dla kierunku: INFORMATYKA Specjalność: Bezpieczeństwo sieciowych systemów informatycznych, Informatyka techniczna, Technologie internetowe i techniki multimedialne Ogółem Semestr 1 Semestr
Plan studiów dla kierunku: INFORMATYKA Specjalność: Bezpieczeństwo sieciowych systemów informatycznych, Informatyka techniczna, Technologie internetowe i techniki multimedialne Ogółem Semestr 1 Semestr
KARTA KURSU. Meteorologia i klimatologia
 KARTA KURSU Geografia 1. stopnia, stacjonarne, 2017/2018, sem 2 Nazwa Nazwa w j. ang. Meteorologia i klimatologia Meteorology and climatology Koordynator Dr Joanna Jędruszkiewicz Zespół dydaktyczny Punktacja
KARTA KURSU Geografia 1. stopnia, stacjonarne, 2017/2018, sem 2 Nazwa Nazwa w j. ang. Meteorologia i klimatologia Meteorology and climatology Koordynator Dr Joanna Jędruszkiewicz Zespół dydaktyczny Punktacja
2012/2013. PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki
 PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki rok akademicki 2012/2013 Opole, styczeń 2013 r. Tekst jednolity po zmianach
PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki rok akademicki 2012/2013 Opole, styczeń 2013 r. Tekst jednolity po zmianach
mgr Anna Hulboj Treści nauczania
 mgr Anna Hulboj Realizacja treści nauczania wraz z wymaganiami szczegółowymi podstawy programowej z fizyki dla klas 7 szkoły podstawowej do serii Spotkania z fizyką w roku szkolnym 2017/2018 (na podstawie
mgr Anna Hulboj Realizacja treści nauczania wraz z wymaganiami szczegółowymi podstawy programowej z fizyki dla klas 7 szkoły podstawowej do serii Spotkania z fizyką w roku szkolnym 2017/2018 (na podstawie
Efekty kształcenia dla kierunku Budownictwo
 Efekty kształcenia dla kierunku Budownictwo 1. Umiejscowienie kierunku w obszarze kształcenia: kierunek Budownictwo naleŝy do obszaru kształcenia w zakresie nauk technicznych. Budownictwo jest powiązane
Efekty kształcenia dla kierunku Budownictwo 1. Umiejscowienie kierunku w obszarze kształcenia: kierunek Budownictwo naleŝy do obszaru kształcenia w zakresie nauk technicznych. Budownictwo jest powiązane
PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki.
 PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki rok akademicki 2014/2015 Opole, marzec 2014 r. Tekst jednolity po zmianach
PLANY STUDIÓW stacjonarnych i niestacjonarnych I-go stopnia prowadzonych na Wydziale Elektrotechniki, Automatyki i Informatyki rok akademicki 2014/2015 Opole, marzec 2014 r. Tekst jednolity po zmianach
Wsparcie projektowania badaniami modelowymi na przykładzie projektu VIDAR. Przygotował: Tomasz Płotka - StoGda
 Wsparcie projektowania badaniami modelowymi na przykładzie projektu VIDAR Przygotował: Tomasz Płotka - StoGda Patrząc na niedawno wykonywane i bieżące projekty jak również szereg zapytań ofertowych jakie
Wsparcie projektowania badaniami modelowymi na przykładzie projektu VIDAR Przygotował: Tomasz Płotka - StoGda Patrząc na niedawno wykonywane i bieżące projekty jak również szereg zapytań ofertowych jakie
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania. Studia: II stopnia (magisterskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia II stopnia (magisterskie) Temat: Układ sterowania płaszczyzną sterową o podwyższonej niezawodności 1. Analiza literatury. 2. Uruchomienie
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia II stopnia (magisterskie) Temat: Układ sterowania płaszczyzną sterową o podwyższonej niezawodności 1. Analiza literatury. 2. Uruchomienie
Podręcznik. Przykład 1: Wyborcy
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 5892 424 http://www.neuroinf.pl/members/danek/swps/ Iwo Białynicki-Birula Iwona Białynicka-Birula
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 5892 424 http://www.neuroinf.pl/members/danek/swps/ Iwo Białynicki-Birula Iwona Białynicka-Birula
Katowice GPW 2013. Zintegrowany system informatyczny do kompleksowego zarządzania siecią wodociągową. Jan Studziński
 Katowice GPW 2013 Zintegrowany system informatyczny do kompleksowego zarządzania siecią wodociągową Jan Studziński 1 1. Wstęp Cel pracy Usprawnienie zarządzania siecią wodociągową za pomocą nowoczesnych
Katowice GPW 2013 Zintegrowany system informatyczny do kompleksowego zarządzania siecią wodociągową Jan Studziński 1 1. Wstęp Cel pracy Usprawnienie zarządzania siecią wodociągową za pomocą nowoczesnych
