Metody eksploracji danych. Reguły asocjacyjne
|
|
|
- Radosław Pawłowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Metody eksploracji danych Reguły asocjacyjne
2 Analiza podobieństw i koszyka sklepowego Analiza podobieństw jest badaniem atrybutów lub cech, które są powiązane ze sobą. Metody analizy podobieństw, znane również jako analiza koszyka sklepowego, szukają nieodkrytych powiązań pomiędzy tymi atrybutami, to znaczy szukają nieodkrytych reguł do ilościowego określania relacji pomiędzy dwoma lub więcej atrybutami Reguły asocjacyjne przyjmują postać: Jeżeli poprzednik, to następnik razem z miarą wsparcia i dokładności (ufności) reguły
3 Analiza podobieństw i koszyka sklepowego - przykład W supermarkecie sporządzono raport sprzedaży, z którego m.in. wynika, że w ostatni czwartek w nocy z 1000 klientów robiących zakupy 200 kupiło chleb, a z tych 200, którzy kupili chleb, 50 kupiło masło Reguła asocjacyjna: Jeżeli kupuje chleb, to kupuje masło miarą wsparcia 5% miara dokładności 25%
4 Wsparcie i ufność reguły Niech D oznacza zbiór transakcji, gdzie każda transakcja T z D reprezentuje zbiór artykułów z I. Wsparcie (ang. support) s dla danej reguły asocjacyjnej A => B jest procentem transakcji w D, które zawierają A i B, tzn. s P A B liczba transakcji zawierajacych A i B calkowita liczba transakcji Ufność (ang. confidence) c dla danej reguły asocjacyjnej A => B jest miarą dokładności reguły, określoną jako procent transakcji zawierających A, które również zawierają B, tzn. P A B c P B A P A liczba transakcji zawierajacych A i B liczba transakcji zawierajacych A Mocna reguła reguła, dla której s i c są >= od pewnych, określonych wartości minimalnych.
5 Zbiory zdarzeń i zbiory częste Zbiór zdarzeń jest zbiorem zawartym w I (np. {fasola, kabaczki} to 2- elementowy zbiór zdarzeń, {brokuły, kukurydza, pomidory} to 3-elementowy zbiór zdarzeń). Częstość zbioru zdarzeń jest liczbą transakcji zawierającym dany zbiór zdarzeń. Zbiór częsty to zbiór zdarzeń, który występuje przynajmniej pewną minimalną liczbę razy, czyli z częstością Φ. Zbiór częstych zbiorów zdarzeń o k elementach będziemy oznaczać przez F k
6 Mówimy, że transakcja t wspiera (ang. supports) zbiór X wtedy i tylko wtedy gdy dla wszystkich elementów I k X, I k t (t zawiera co najmniej wszystkie elementy zbioru X). Wsparciem zbioru X nazywamy iloraz liczby transakcji w T, które wspierają X do liczby wszystkich transakcji w T.
7 Reguła asocjacyjna Regułą asocjacyjną nazywamy implikację postaci X Y, gdzie X i Y są dowolnymi zbiorami elementów z I i zachodzi X I, Y I i X Y=. Zbiór X nazywamy poprzednikiem reguły (ang. body, antecedent), a zbiór Y następnikiem reguły (ang. head, consequent).
8 Z każdą regułą asocjacyjną są związane dwie wartości liczbowe opisujące jej siłę i dokładność. Mówimy, że reguła X Y ma wsparcie s (ang. support), 0 s 1, jeżeli dokładnie s% transakcji w T wspiera X Y. Mówimy, że reguła X Y ma ufność c (ang. confidence), 0 c 1, jeżeli dokładnie c% transakcji w T, które wspierają X, wspiera również Y.
9
10 Ogólny algorytm generowania reguł asocjacyjnych Ogólny algorytm generowania reguł asocjacyjnych, dla zadanej bazy danych transakcji T, ma następującą postać: Krok 1: Ogólny algorytm generowania reguł Asocjacyjnych Krok 2: Generowanie reguł ze zbiorów częstych
11 Krok 1: Ogólny algorytm generowania reguł asocjacyjnych 1. Utworzyć zbiory elementów Li={Ii1, Ii2,..., Iim}, takie, że Li I, posiadające wsparcie support(li) minsup. Zbiory Li są nazywane zbiorami częstymi (ang. large, frequent itemsets). 2. Na podstawie zbiorów częstych znalezionych w kroku (1) wygenerować wszystkie reguły asocjacyjne dla elementów zbiorów częstych - zastosuj algorytm (krok 2->)
12 Krok 2: Generowanie reguł ze zbiorów częstych. 1. Dla każdego zbioru częstego Li znajdź wszystkie niepuste podzbiory subli. 2. Dla każdego podzbioru subli wygeneruj regułę postaci: subli (Li-subLi) support(li)/support(subli) minconf. jeżeli
13 Ogólny algorytm generowania reguł asocjacyjnych Algorytm (krok 1) składa się z dwóch kroków. W pierwszym kroku znajdowane są zbiory częste, które reprezentują zbiory elementów występujących wspólnie w transakcjach. Zakłada się przy tym, że interesujące są tylko te zbiory częste, których wsparcie w bazie danych jest większe, niż zadany próg wsparcia minsup. W kroku drugim, na podstawie znalezionych zbiorów częstych są generowane wszystkie reguły asocjacyjne, których ufność jest większa niż zadany próg ufności minconf.
14 przykład Załóżmy, że: minimalne wsparcie wynosi 30% (0.3), natomiast minimalna ufność 70% (0.7).
15 W pierwszym kroku są znajdowane zbiory częste 1-elementowe:
16 Funkcja apriori-gen generuje zbiory kandydujące 2-elementowe: Zbiór częsty 2-elementowy składa się z tych zbiorów częstych 2- elementowych, których wsparcie jest większe niż 0.30
17 Funkcja apriori-gen generuje zbiory kandydujące 3-elementowe
18 Na podstawie otrzymanych zbiorów częstych wygenerowano następujące reguły asocjacyjne Zauważmy, że tylko cześć otrzymanych reguł spełnia warunki na minimalne wsparcie i minimalną ufność.
19 Stąd, końcowy wynik działania algorytmu Apriori jest następujący:
20 Stąd, końcowy wynik działania algorytmu Apriori jest następujący:
21
22 Rzut ekranu z WEKA
23 Rzut ekranu z Rattle
24 Rzut ekranu z Rattle
Wprowadzenie Sformułowanie problemu Typy reguł asocjacyjnych Proces odkrywania reguł asocjacyjnych. Data Mining Wykład 2
 Data Mining Wykład 2 Odkrywanie asocjacji Plan wykładu Wprowadzenie Sformułowanie problemu Typy reguł asocjacyjnych Proces odkrywania reguł asocjacyjnych Geneza problemu Geneza problemu odkrywania reguł
Data Mining Wykład 2 Odkrywanie asocjacji Plan wykładu Wprowadzenie Sformułowanie problemu Typy reguł asocjacyjnych Proces odkrywania reguł asocjacyjnych Geneza problemu Geneza problemu odkrywania reguł
Eksploracja danych - wykład VIII
 I Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska 2 grudnia 2016 1/31 1 2 2/31 (ang. affinity analysis) polega na badaniu atrybutów lub cech, które są ze sobą powiązane. Metody
I Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska 2 grudnia 2016 1/31 1 2 2/31 (ang. affinity analysis) polega na badaniu atrybutów lub cech, które są ze sobą powiązane. Metody
Reguły asocjacyjne. Żródło: LaroseD.T., Discovering Knowledge in Data. An Introduction to Data Minig, John Wiley& Sons, Hoboken, New Jersey, 2005.
 Reguły asocjacyjne Żródło: LaroseD.T., Discovering Knowledge in Data. An Introduction to Data Minig, John Wiley& Sons, Hoboken, New Jersey, 2005. Stragan warzywny -transakcje zakupów Transakcja Produkty
Reguły asocjacyjne Żródło: LaroseD.T., Discovering Knowledge in Data. An Introduction to Data Minig, John Wiley& Sons, Hoboken, New Jersey, 2005. Stragan warzywny -transakcje zakupów Transakcja Produkty
Ćwiczenie 5. Metody eksploracji danych
 Ćwiczenie 5. Metody eksploracji danych Reguły asocjacyjne (association rules) Badaniem atrybutów lub cech, które są powiązane ze sobą, zajmuje się analiza podobieństw (ang. affinity analysis). Metody analizy
Ćwiczenie 5. Metody eksploracji danych Reguły asocjacyjne (association rules) Badaniem atrybutów lub cech, które są powiązane ze sobą, zajmuje się analiza podobieństw (ang. affinity analysis). Metody analizy
Data Mining Wykład 3. Algorytmy odkrywania binarnych reguł asocjacyjnych. Plan wykładu
 Data Mining Wykład 3 Algorytmy odkrywania binarnych reguł asocjacyjnych Plan wykładu Algorytm Apriori Funkcja apriori_gen(ck) Generacja zbiorów kandydujących Generacja reguł Efektywności działania Własności
Data Mining Wykład 3 Algorytmy odkrywania binarnych reguł asocjacyjnych Plan wykładu Algorytm Apriori Funkcja apriori_gen(ck) Generacja zbiorów kandydujących Generacja reguł Efektywności działania Własności
Odkrywanie asocjacji
 Odkrywanie asocjacji Cel odkrywania asocjacji Znalezienie interesujących zależności lub korelacji, tzw. asocjacji Analiza dużych zbiorów danych Wynik procesu: zbiór reguł asocjacyjnych Witold Andrzejewski,
Odkrywanie asocjacji Cel odkrywania asocjacji Znalezienie interesujących zależności lub korelacji, tzw. asocjacji Analiza dużych zbiorów danych Wynik procesu: zbiór reguł asocjacyjnych Witold Andrzejewski,
Odkrywanie asocjacji
 Odkrywanie asocjacji Wprowadzenie Sformułowanie problemu Typy reguł asocjacyjnych Odkrywanie asocjacji wykład 1 Wykład jest poświęcony wprowadzeniu i zaznajomieniu się z problemem odkrywania reguł asocjacyjnych.
Odkrywanie asocjacji Wprowadzenie Sformułowanie problemu Typy reguł asocjacyjnych Odkrywanie asocjacji wykład 1 Wykład jest poświęcony wprowadzeniu i zaznajomieniu się z problemem odkrywania reguł asocjacyjnych.
INDUKOWANE REGUŁY DECYZYJNE ALORYTM APRIORI JAROSŁAW FIBICH
 INDUKOWANE REGUŁY DECYZYJNE ALORYTM APRIORI JAROSŁAW FIBICH 1. Czym jest eksploracja danych Eksploracja danych definiowana jest jako zbiór technik odkrywania nietrywialnych zależności i schematów w dużych
INDUKOWANE REGUŁY DECYZYJNE ALORYTM APRIORI JAROSŁAW FIBICH 1. Czym jest eksploracja danych Eksploracja danych definiowana jest jako zbiór technik odkrywania nietrywialnych zależności i schematów w dużych
Ewelina Dziura Krzysztof Maryański
 Ewelina Dziura Krzysztof Maryański 1. Wstęp - eksploracja danych 2. Proces Eksploracji danych 3. Reguły asocjacyjne budowa, zastosowanie, pozyskiwanie 4. Algorytm Apriori i jego modyfikacje 5. Przykład
Ewelina Dziura Krzysztof Maryański 1. Wstęp - eksploracja danych 2. Proces Eksploracji danych 3. Reguły asocjacyjne budowa, zastosowanie, pozyskiwanie 4. Algorytm Apriori i jego modyfikacje 5. Przykład
Systemy Wspomagania Decyzji
 Reguły Asocjacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności March 18, 2014 1 Wprowadzenie 2 Definicja 3 Szukanie reguł asocjacyjnych 4 Przykłady użycia 5 Podsumowanie Problem Lista
Reguły Asocjacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności March 18, 2014 1 Wprowadzenie 2 Definicja 3 Szukanie reguł asocjacyjnych 4 Przykłady użycia 5 Podsumowanie Problem Lista
Inżynieria Wiedzy i Systemy Ekspertowe. Reguły asocjacyjne
 Inżynieria Wiedzy i Systemy Ekspertowe Reguły asocjacyjne Dr inż. Michał Bereta p. 144 / 10, Instytut Modelowania Komputerowego mbereta@pk.edu.pl beretam@torus.uck.pk.edu.pl www.michalbereta.pl Reguły
Inżynieria Wiedzy i Systemy Ekspertowe Reguły asocjacyjne Dr inż. Michał Bereta p. 144 / 10, Instytut Modelowania Komputerowego mbereta@pk.edu.pl beretam@torus.uck.pk.edu.pl www.michalbereta.pl Reguły
Inżynieria biomedyczna
 Inżynieria biomedyczna Projekt Przygotowanie i realizacja kierunku inżynieria biomedyczna studia międzywydziałowe współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Inżynieria biomedyczna Projekt Przygotowanie i realizacja kierunku inżynieria biomedyczna studia międzywydziałowe współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING. EKSPLORACJA DANYCH Ćwiczenia. Adrian Horzyk. Akademia Górniczo-Hutnicza
 METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Ćwiczenia Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Ćwiczenia Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej
Odkrywanie reguł asocjacyjnych. Rapid Miner
 Odkrywanie reguł asocjacyjnych Rapid Miner Zbiory częste TS ID_KLIENTA Koszyk 12:57 1123 {mleko, pieluszki, piwo} 13:12 1412 {mleko, piwo, bułki, masło, pieluszki} 13:55 1425 {piwo, wódka, wino, paracetamol}
Odkrywanie reguł asocjacyjnych Rapid Miner Zbiory częste TS ID_KLIENTA Koszyk 12:57 1123 {mleko, pieluszki, piwo} 13:12 1412 {mleko, piwo, bułki, masło, pieluszki} 13:55 1425 {piwo, wódka, wino, paracetamol}
Algorytmy odkrywania binarnych reguł asocjacyjnych
 Algorytmy odkrywania binarnych reguł asocjacyjnych A-priori FP-Growth Odkrywanie asocjacji wykład 2 Celem naszego wykładu jest zapoznanie się z dwoma podstawowymi algorytmami odkrywania binarnych reguł
Algorytmy odkrywania binarnych reguł asocjacyjnych A-priori FP-Growth Odkrywanie asocjacji wykład 2 Celem naszego wykładu jest zapoznanie się z dwoma podstawowymi algorytmami odkrywania binarnych reguł
1. Odkrywanie asocjacji
 1. 2. Odkrywanie asocjacji...1 Algorytmy...1 1. A priori...1 2. Algorytm FP-Growth...2 3. Wykorzystanie narzędzi Oracle Data Miner i Rapid Miner do odkrywania reguł asocjacyjnych...2 3.1. Odkrywanie reguł
1. 2. Odkrywanie asocjacji...1 Algorytmy...1 1. A priori...1 2. Algorytm FP-Growth...2 3. Wykorzystanie narzędzi Oracle Data Miner i Rapid Miner do odkrywania reguł asocjacyjnych...2 3.1. Odkrywanie reguł
Reguły asocjacyjne. 1. Uruchom system weka i wybierz aplikację Knowledge Flow.
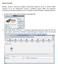 Reguły asocjacyjne Niniejsze ćwiczenie demonstruje działanie implementacji algorytmu apriori w systemie WEKA. Ćwiczenie ma na celu zaznajomienie studenta z działaniem systemu WEKA oraz znaczeniem podstawowych
Reguły asocjacyjne Niniejsze ćwiczenie demonstruje działanie implementacji algorytmu apriori w systemie WEKA. Ćwiczenie ma na celu zaznajomienie studenta z działaniem systemu WEKA oraz znaczeniem podstawowych
Zastosowanie metod eksploracji danych Data Mining w badaniach ekonomicznych SAS Enterprise Miner. rok akademicki 2014/2015
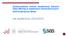 Zastosowanie metod eksploracji danych Data Mining w badaniach ekonomicznych SAS Enterprise Miner rok akademicki 2014/2015 Analiza asocjacji i sekwencji Analiza asocjacji Analiza asocjacji polega na identyfikacji
Zastosowanie metod eksploracji danych Data Mining w badaniach ekonomicznych SAS Enterprise Miner rok akademicki 2014/2015 Analiza asocjacji i sekwencji Analiza asocjacji Analiza asocjacji polega na identyfikacji
Wielopoziomowe i wielowymiarowe reguły asocjacyjne
 Wielopoziomowe i wielowymiarowe reguły asocjacyjne Wielopoziomowe reguły asocjacyjne Wielowymiarowe reguły asocjacyjne Asocjacje vs korelacja Odkrywanie asocjacji wykład 3 Kontynuując zagadnienia związane
Wielopoziomowe i wielowymiarowe reguły asocjacyjne Wielopoziomowe reguły asocjacyjne Wielowymiarowe reguły asocjacyjne Asocjacje vs korelacja Odkrywanie asocjacji wykład 3 Kontynuując zagadnienia związane
Algorytm DIC. Dynamic Itemset Counting. Magdalena Przygórzewska Karolina Stanisławska Aleksander Wieczorek
 Algorytm DIC Dynamic Itemset Counting Magdalena Przygórzewska Karolina Stanisławska Aleksander Wieczorek Spis treści 1 2 3 4 Algorytm DIC jako rozszerzenie apriori DIC Algorytm znajdowania reguł asocjacyjnych
Algorytm DIC Dynamic Itemset Counting Magdalena Przygórzewska Karolina Stanisławska Aleksander Wieczorek Spis treści 1 2 3 4 Algorytm DIC jako rozszerzenie apriori DIC Algorytm znajdowania reguł asocjacyjnych
Reguły asocjacyjne, wykł. 11
 Reguły asocjacyjne, wykł. 11 Joanna Jędrzejowicz Instytut Informatyki Przykłady reguł Analiza koszyka sklepowego (ang. market basket analysis) - jakie towary kupowane są razem, Jakie towary sprzedają się
Reguły asocjacyjne, wykł. 11 Joanna Jędrzejowicz Instytut Informatyki Przykłady reguł Analiza koszyka sklepowego (ang. market basket analysis) - jakie towary kupowane są razem, Jakie towary sprzedają się
Krzysztof Kawa. empolis arvato. e mail: krzysztof.kawa@empolis.com
 XI Konferencja PLOUG Kościelisko Październik 2005 Zastosowanie reguł asocjacyjnych, pakietu Oracle Data Mining for Java do analizy koszyka zakupów w aplikacjach e-commerce. Integracja ze środowiskiem Oracle
XI Konferencja PLOUG Kościelisko Październik 2005 Zastosowanie reguł asocjacyjnych, pakietu Oracle Data Mining for Java do analizy koszyka zakupów w aplikacjach e-commerce. Integracja ze środowiskiem Oracle
Analiza i eksploracja danych
 Krzysztof Dembczyński Instytut Informatyki Zakład Inteligentnych Systemów Wspomagania Decyzji Politechnika Poznańska Inteligentne Systemy Wspomagania Decyzji Studia magisterskie, semestr I Semestr letni
Krzysztof Dembczyński Instytut Informatyki Zakład Inteligentnych Systemów Wspomagania Decyzji Politechnika Poznańska Inteligentne Systemy Wspomagania Decyzji Studia magisterskie, semestr I Semestr letni
Odkrywanie asocjacji. Cel. Geneza problemu analiza koszyka zakupów
 Odkrywanie asocjacji Cel Celem procesu odkrywania asocjacji jest znalezienie interesujących zależności lub korelacji (nazywanych ogólnie asocjacjami) pomiędzy danymi w dużych zbiorach danych. Wynikiem
Odkrywanie asocjacji Cel Celem procesu odkrywania asocjacji jest znalezienie interesujących zależności lub korelacji (nazywanych ogólnie asocjacjami) pomiędzy danymi w dużych zbiorach danych. Wynikiem
data mining machine learning data science
 data mining machine learning data science deep learning, AI, statistics, IoT, operations research, applied mathematics KISIM, WIMiIP, AGH 1 Machine Learning / Data mining / Data science Uczenie maszynowe
data mining machine learning data science deep learning, AI, statistics, IoT, operations research, applied mathematics KISIM, WIMiIP, AGH 1 Machine Learning / Data mining / Data science Uczenie maszynowe
Odkrywanie reguł asocjacyjnych
 Odkrywanie reguł asocjacyjnych Tomasz Kubik Na podstawie dokumentu: CS583-association-rules.ppt 1 Odkrywanie reguł asocjacyjnych n Autor metody Agrawal et al in 1993. n Analiza asocjacji danych w bazach
Odkrywanie reguł asocjacyjnych Tomasz Kubik Na podstawie dokumentu: CS583-association-rules.ppt 1 Odkrywanie reguł asocjacyjnych n Autor metody Agrawal et al in 1993. n Analiza asocjacji danych w bazach
Odkrywanie wzorców sekwencji
 Odkrywanie wzorców sekwencji Sformułowanie problemu Algorytm GSP Eksploracja wzorców sekwencji wykład 1 Na wykładzie zapoznamy się z problemem odkrywania wzorców sekwencji. Rozpoczniemy od wprowadzenia
Odkrywanie wzorców sekwencji Sformułowanie problemu Algorytm GSP Eksploracja wzorców sekwencji wykład 1 Na wykładzie zapoznamy się z problemem odkrywania wzorców sekwencji. Rozpoczniemy od wprowadzenia
EKSPLORACJA DANYCH METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING. Adrian Horzyk. Akademia Górniczo-Hutnicza
 METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra
METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra
Reguły asocjacyjne w programie RapidMiner Michał Bereta
 Reguły asocjacyjne w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Reguły asocjacyjne mają na celu odkrycie związków współwystępowania pomiędzy atrybutami. Stosuje się je często do danych
Reguły asocjacyjne w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Reguły asocjacyjne mają na celu odkrycie związków współwystępowania pomiędzy atrybutami. Stosuje się je często do danych
Algorytmy optymalizacji zapytań eksploracyjnych z wykorzystaniem materializowanej perspektywy eksploracyjnej
 Algorytmy optymalizacji zapytań eksploracyjnych z wykorzystaniem materializowanej perspektywy eksploracyjnej Jerzy Brzeziński, Mikołaj Morzy, Tadeusz Morzy, Łukasz Rutkowski RB-006/02 1. Wstęp 1.1. Rozwój
Algorytmy optymalizacji zapytań eksploracyjnych z wykorzystaniem materializowanej perspektywy eksploracyjnej Jerzy Brzeziński, Mikołaj Morzy, Tadeusz Morzy, Łukasz Rutkowski RB-006/02 1. Wstęp 1.1. Rozwój
Plan wykładu. Reguły asocjacyjne. Przykłady asocjacji. Reguły asocjacyjne. Jeli warunki to efekty. warunki efekty
 Plan wykładu Reguły asocjacyjne Marcin S. Szczuka Wykład 6 Terminologia dla reguł asocjacyjnych. Ogólny algorytm znajdowania reguł. Wyszukiwanie czstych zbiorów. Konstruowanie reguł - APRIORI. Reguły asocjacyjne
Plan wykładu Reguły asocjacyjne Marcin S. Szczuka Wykład 6 Terminologia dla reguł asocjacyjnych. Ogólny algorytm znajdowania reguł. Wyszukiwanie czstych zbiorów. Konstruowanie reguł - APRIORI. Reguły asocjacyjne
Reguły decyzyjne, algorytm AQ i CN2. Reguły asocjacyjne, algorytm Apriori.
 Analiza danych Reguły decyzyjne, algorytm AQ i CN2. Reguły asocjacyjne, algorytm Apriori. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ REGUŁY DECYZYJNE Metoda reprezentacji wiedzy (modelowania
Analiza danych Reguły decyzyjne, algorytm AQ i CN2. Reguły asocjacyjne, algorytm Apriori. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ REGUŁY DECYZYJNE Metoda reprezentacji wiedzy (modelowania
ANALIZA ZACHOWAŃ UŻYTKOWNIKÓW PORTALU ONET.PL W UJĘCIU REGUŁ ASOCJACYJNYCH
 PAWEŁ WEICHBROTH POLITECHIKA GDAŃSKA, ASYSTET, ZAKŁAD ZARZĄDZAIA TECHOLOGIAMI IFORMATYCZYMI, POLITECHIKA GDAŃSKA 1 STRESZCZEIE Portale internetowe są obecnie powszechnym źródłem informacji, notując bardzo
PAWEŁ WEICHBROTH POLITECHIKA GDAŃSKA, ASYSTET, ZAKŁAD ZARZĄDZAIA TECHOLOGIAMI IFORMATYCZYMI, POLITECHIKA GDAŃSKA 1 STRESZCZEIE Portale internetowe są obecnie powszechnym źródłem informacji, notując bardzo
EKSPLORACJA DANYCH METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING. Adrian Horzyk. Akademia Górniczo-Hutnicza
 METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra
METODY INŻYNIERII WIEDZY KNOWLEDGE ENGINEERING AND DATA MINING EKSPLORACJA DANYCH Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra
A C T A UNIVERSITATIS LODZIENSIS FOLIA OECONOMICA 183,2004. Sebastian Szamański, Ryszard Budziński
 A C T A UNIVERSITATIS LODZIENSIS FOLIA OECONOMICA 183,2004 Sebastian Szamański, Ryszard Budziński METODY EKSPLORACJI REGUŁ ASOCJACYJNYCH I ICH ZASTOSOWANIE Wprowadzenie Ogromny postęp technologiczny ostatnich
A C T A UNIVERSITATIS LODZIENSIS FOLIA OECONOMICA 183,2004 Sebastian Szamański, Ryszard Budziński METODY EKSPLORACJI REGUŁ ASOCJACYJNYCH I ICH ZASTOSOWANIE Wprowadzenie Ogromny postęp technologiczny ostatnich
Analiza asocjacji i reguły asocjacyjne w badaniu wyborów zajęć dydaktycznych dokonywanych przez studentów. Zastosowanie algorytmu Apriori
 Ekonomia nr 34/2013 Analiza asocjacji i reguły asocjacyjne w badaniu wyborów zajęć dydaktycznych dokonywanych przez studentów. Zastosowanie algorytmu Apriori Mirosława Lasek *, Marek Pęczkowski * Streszczenie
Ekonomia nr 34/2013 Analiza asocjacji i reguły asocjacyjne w badaniu wyborów zajęć dydaktycznych dokonywanych przez studentów. Zastosowanie algorytmu Apriori Mirosława Lasek *, Marek Pęczkowski * Streszczenie
Sztuczna Inteligencja Projekt
 Sztuczna Inteligencja Projekt Temat: Algorytm LEM2 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm LEM 2. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu LEM 2 wygenerować
Sztuczna Inteligencja Projekt Temat: Algorytm LEM2 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm LEM 2. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu LEM 2 wygenerować
Indukcja matematyczna, zasada minimum i maksimum. 17 lutego 2017
 Indukcja matematyczna, zasada minimum i maksimum 17 lutego 2017 Liczby naturalne - Aksjomatyka Peano (bez zera) Aksjomatyka liczb naturalnych N jest nazwą zbioru liczb naturalnych, 1 jest nazwą elementu
Indukcja matematyczna, zasada minimum i maksimum 17 lutego 2017 Liczby naturalne - Aksjomatyka Peano (bez zera) Aksjomatyka liczb naturalnych N jest nazwą zbioru liczb naturalnych, 1 jest nazwą elementu
Odkrywanie wzorców sekwencyjnych z zachowaniem prywatności
 Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Instytut Informatyki Rok akademicki 2013/2013 PRACA DYPLOMOWA MAGISTERSKA Andrzej Makarewicz Odkrywanie wzorców sekwencyjnych z zachowaniem
Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Instytut Informatyki Rok akademicki 2013/2013 PRACA DYPLOMOWA MAGISTERSKA Andrzej Makarewicz Odkrywanie wzorców sekwencyjnych z zachowaniem
B jest globalnym pokryciem zbioru {d} wtedy i tylko wtedy, gdy {d} zależy od B i nie istnieje B T takie, że {d} zależy od B ;
 Algorytm LEM1 Oznaczenia i definicje: U - uniwersum, tj. zbiór obiektów; A - zbiór atrybutów warunkowych; d - atrybut decyzyjny; IND(B) = {(x, y) U U : a B a(x) = a(y)} - relacja nierozróżnialności, tj.
Algorytm LEM1 Oznaczenia i definicje: U - uniwersum, tj. zbiór obiektów; A - zbiór atrybutów warunkowych; d - atrybut decyzyjny; IND(B) = {(x, y) U U : a B a(x) = a(y)} - relacja nierozróżnialności, tj.
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Wnioskowanie z wiedzy niepełnej
 Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Instytut Informatyki Rok akademicki 2011/2012 Praca dyplomowa magisterska Jakub Siudziński Wnioskowanie z wiedzy niepełnej Opiekun pracy:
Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Instytut Informatyki Rok akademicki 2011/2012 Praca dyplomowa magisterska Jakub Siudziński Wnioskowanie z wiedzy niepełnej Opiekun pracy:
Reguły asocjacyjne, algorytm Apriori
 Reguły asocjacyjne, algorytm Apriori (przykład dla zbioru Sodowrażliwość ) Przemysław Klęsk pklesk@wi.zut.edu.pl Zakład Sztucznej Inteligencji Wydział Informatyki, ZUT Reguły asocjacyjne Zastosowania Analiza
Reguły asocjacyjne, algorytm Apriori (przykład dla zbioru Sodowrażliwość ) Przemysław Klęsk pklesk@wi.zut.edu.pl Zakład Sztucznej Inteligencji Wydział Informatyki, ZUT Reguły asocjacyjne Zastosowania Analiza
Odkrywanie wzorców sekwencji
 Odkrywanie wzorców sekwencji Prefix Span Odkrywanie wzorców sekwencji z ograniczeniami Uogólnione wzorce sekwencji Eksploracja wzorców sekwencji wykład 2 Kontynuujemy nasze rozważania dotyczące odkrywania
Odkrywanie wzorców sekwencji Prefix Span Odkrywanie wzorców sekwencji z ograniczeniami Uogólnione wzorce sekwencji Eksploracja wzorców sekwencji wykład 2 Kontynuujemy nasze rozważania dotyczące odkrywania
Reguły asocjacyjne na giełdzie
 Hurtownie danych i data mining - Grupa dra Piotra Lipińskiego II UWr 2009/2010 Adam Grycner, Mateusz Łyczek, Marta Ziobro Reguły asocjacyjne na giełdzie 1 Problem 1.1 Opis problemu - intuicyjnie Będziemy
Hurtownie danych i data mining - Grupa dra Piotra Lipińskiego II UWr 2009/2010 Adam Grycner, Mateusz Łyczek, Marta Ziobro Reguły asocjacyjne na giełdzie 1 Problem 1.1 Opis problemu - intuicyjnie Będziemy
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Logika Stosowana. Wykład 10 - Wnioskowanie indukcyjne Część 3 Indukcja reguł i ILP. Marcin Szczuka. Instytut Informatyki UW
 Logika Stosowana Wykład 10 - Wnioskowanie indukcyjne Część 3 Indukcja reguł i ILP Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana
Logika Stosowana Wykład 10 - Wnioskowanie indukcyjne Część 3 Indukcja reguł i ILP Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana
Sprawozdanie z laboratorium: Hurtownie Danych. Algorytm generowania reguł asocjacyjnych. FP-Growth. 9 czerwca 2011
 Sprawozdanie z laboratorium: Hurtownie Danych Algorytm generowania reguł asocjacyjnych 9 czerwca 2011 Prowadzący: dr inż. Izabela Szczęch dr inż. Szymon Wilk Autorzy: Łukasz Idkowiak Tomasz Kamiński Jacek
Sprawozdanie z laboratorium: Hurtownie Danych Algorytm generowania reguł asocjacyjnych 9 czerwca 2011 Prowadzący: dr inż. Izabela Szczęch dr inż. Szymon Wilk Autorzy: Łukasz Idkowiak Tomasz Kamiński Jacek
Klasyfikacja obiektów Drzewa decyzyjne (drzewa klasyfikacyjne)
 Klasyfikacja obiektów Drzewa decyzyjne (drzewa klasyfikacyjne) Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski Klasyfikacja i predykcja. Odkrywaniem reguł klasyfikacji nazywamy proces znajdowania
Klasyfikacja obiektów Drzewa decyzyjne (drzewa klasyfikacyjne) Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski Klasyfikacja i predykcja. Odkrywaniem reguł klasyfikacji nazywamy proces znajdowania
Integracja technik eksploracji danych ]V\VWHPHP]DU]G]DQLDED]GDQ\FK QDSU]\NáDG]LH2UDFOHi Data Mining
![Integracja technik eksploracji danych ]V\VWHPHP]DU]G]DQLDED]GDQ\FK QDSU]\NáDG]LH2UDFOHi Data Mining Integracja technik eksploracji danych ]V\VWHPHP]DU]G]DQLDED]GDQ\FK QDSU]\NáDG]LH2UDFOHi Data Mining](/thumbs/26/8053420.jpg) Integracja technik eksploracji danych ]V\VWHPHP]DU]G]DQLDED]GDQ\FK QDSU]\NáDG]LH2UDFOHi Data Mining 0LNRáDM0RU]\ Marek Wojciechowski Instytut Informatyki PP Eksploracja danych 2GNU\ZDQLHZ]RUFyZZGX*\FK
Integracja technik eksploracji danych ]V\VWHPHP]DU]G]DQLDED]GDQ\FK QDSU]\NáDG]LH2UDFOHi Data Mining 0LNRáDM0RU]\ Marek Wojciechowski Instytut Informatyki PP Eksploracja danych 2GNU\ZDQLHZ]RUFyZZGX*\FK
Sztuczna Inteligencja Projekt
 Sztuczna Inteligencja Projekt Temat: Algorytm F-LEM1 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm F LEM 1. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu F LEM1
Sztuczna Inteligencja Projekt Temat: Algorytm F-LEM1 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm F LEM 1. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu F LEM1
RACHUNEK ZDAŃ 7. Dla każdej tautologii w formie implikacji, której poprzednik również jest tautologią, następnik także jest tautologią.
 Semantyczne twierdzenie o podstawianiu Jeżeli dana formuła rachunku zdań jest tautologią i wszystkie wystąpienia pewnej zmiennej zdaniowej w tej tautologii zastąpimy pewną ustaloną formułą, to otrzymana
Semantyczne twierdzenie o podstawianiu Jeżeli dana formuła rachunku zdań jest tautologią i wszystkie wystąpienia pewnej zmiennej zdaniowej w tej tautologii zastąpimy pewną ustaloną formułą, to otrzymana
Laboratorium 3. Odkrywanie reguł asocjacyjnych.
 Laboratorium 3 Odkrywanie reguł asocjacyjnych. 1. Uruchom narzędzie Oracle Data Miner i połącz się z serwerem bazy danych. 2. Z menu głównego wybierz Tools SQL Worksheet. W górnym oknie wprowadź i wykonaj
Laboratorium 3 Odkrywanie reguł asocjacyjnych. 1. Uruchom narzędzie Oracle Data Miner i połącz się z serwerem bazy danych. 2. Z menu głównego wybierz Tools SQL Worksheet. W górnym oknie wprowadź i wykonaj
Matematyczne Podstawy Kognitywistyki
 Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
Machine Learning. KISIM, WIMiIP, AGH
 Machine Learning KISIM, WIMiIP, AGH 1 Machine Learning Uczenie maszynowe jest konsekwencją rozwoju idei sztucznej inteligencji i jej praktycznego wdrażania. Algorytmy pozwalają na zautomatyzowanie procesu
Machine Learning KISIM, WIMiIP, AGH 1 Machine Learning Uczenie maszynowe jest konsekwencją rozwoju idei sztucznej inteligencji i jej praktycznego wdrażania. Algorytmy pozwalają na zautomatyzowanie procesu
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Implementacja metod eksploracji danych - Oracle Data Mining
 Implementacja metod eksploracji danych - Oracle Data Mining 395 Plan rozdziału 396 Wprowadzenie do eksploracji danych Architektura Oracle Data Mining Możliwości Oracle Data Mining Etapy procesu eksploracji
Implementacja metod eksploracji danych - Oracle Data Mining 395 Plan rozdziału 396 Wprowadzenie do eksploracji danych Architektura Oracle Data Mining Możliwości Oracle Data Mining Etapy procesu eksploracji
Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl
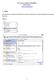 Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Aby skorzystać z możliwości RapidMinera w zakresie analizy tekstu, należy zainstalować Text Mining Extension. Wybierz: 1 Po
Text mining w programie RapidMiner Michał Bereta www.michalbereta.pl 1. Wstęp Aby skorzystać z możliwości RapidMinera w zakresie analizy tekstu, należy zainstalować Text Mining Extension. Wybierz: 1 Po
Ćwiczenia z Zaawansowanych Systemów Baz Danych
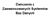 Ćwiczenia z Zaawansowanych Systemów Baz Danych Hurtownie danych Zad 1. Projekt schematu hurtowni danych W źródłach danych dostępne są następujące informacje dotyczące operacji bankowych: Klienci banku
Ćwiczenia z Zaawansowanych Systemów Baz Danych Hurtownie danych Zad 1. Projekt schematu hurtowni danych W źródłach danych dostępne są następujące informacje dotyczące operacji bankowych: Klienci banku
Wyszukiwanie reguł asocjacji i ich zastosowanie w internecie
 Bartosz BACHMAN 1, Paweł Karol FRANKOWSKI 1,2 1 Wydział Elektryczny, 2 Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie E mail: bartosz.bachman@sk.sep.szczecin.pl 1. Wprowadzenie
Bartosz BACHMAN 1, Paweł Karol FRANKOWSKI 1,2 1 Wydział Elektryczny, 2 Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie E mail: bartosz.bachman@sk.sep.szczecin.pl 1. Wprowadzenie
WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY PRZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH
 WSOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY RZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH 1. Definicje Zbiory, które nie są zbiorami definiowalnymi, są nazywane zbiorami przybliżonymi. Zbiory definiowalne
WSOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LAB IV ZBIORY RZYBLIŻONE I ODKRYWANIE REGUŁ DECYZYJNYCH 1. Definicje Zbiory, które nie są zbiorami definiowalnymi, są nazywane zbiorami przybliżonymi. Zbiory definiowalne
Technologie baz danych
 Plan wykładu Technologie baz danych Wykład 2: Relacyjny model danych - zależności funkcyjne. SQL - podstawy Definicja zależności funkcyjnych Reguły dotyczące zależności funkcyjnych Domknięcie zbioru atrybutów
Plan wykładu Technologie baz danych Wykład 2: Relacyjny model danych - zależności funkcyjne. SQL - podstawy Definicja zależności funkcyjnych Reguły dotyczące zależności funkcyjnych Domknięcie zbioru atrybutów
SAS wybrane elementy. DATA MINING Część III. Seweryn Kowalski 2006
 SAS wybrane elementy DATA MINING Część III Seweryn Kowalski 2006 Algorytmy eksploracji danych Algorytm eksploracji danych jest dobrze zdefiniowaną procedurą, która na wejściu otrzymuje dane, a na wyjściu
SAS wybrane elementy DATA MINING Część III Seweryn Kowalski 2006 Algorytmy eksploracji danych Algorytm eksploracji danych jest dobrze zdefiniowaną procedurą, która na wejściu otrzymuje dane, a na wyjściu
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
ALGEBRA Z GEOMETRIĄ BAZY PRZESTRZENI WEKTOROWYCH
 ALGEBRA Z GEOMETRIĄ 1/10 BAZY PRZESTRZENI WEKTOROWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 11, 18.12.2013 Typeset by Jakub Szczepanik. Istnienie bazy Tak jak wśród wszystkich pierścieni wyróżniamy
ALGEBRA Z GEOMETRIĄ 1/10 BAZY PRZESTRZENI WEKTOROWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 11, 18.12.2013 Typeset by Jakub Szczepanik. Istnienie bazy Tak jak wśród wszystkich pierścieni wyróżniamy
Logika. Michał Lipnicki. 15 stycznia Zakład Logiki Stosowanej UAM. Michał Lipnicki () Logika 15 stycznia / 37
 Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 15 stycznia 2011 Michał Lipnicki () Logika 15 stycznia 2011 1 / 37 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 15 stycznia 2011 Michał Lipnicki () Logika 15 stycznia 2011 1 / 37 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
1 Podstawowe oznaczenia
 Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
 Plan prezentacji 0 Wprowadzenie 0 Zastosowania 0 Przykładowe metody 0 Zagadnienia poboczne 0 Przyszłość 0 Podsumowanie 7 Jak powstaje wiedza? Dane Informacje Wiedza Zrozumienie 8 Przykład Teleskop Hubble
Plan prezentacji 0 Wprowadzenie 0 Zastosowania 0 Przykładowe metody 0 Zagadnienia poboczne 0 Przyszłość 0 Podsumowanie 7 Jak powstaje wiedza? Dane Informacje Wiedza Zrozumienie 8 Przykład Teleskop Hubble
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Pozyskiwanie wiedzy z dużych zbiorów danych z zastosowaniem adaptacyjnych procedur generowania zapytań
 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Rozprawa doktorska Pozyskiwanie wiedzy z dużych zbiorów danych z zastosowaniem adaptacyjnych
Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Rozprawa doktorska Pozyskiwanie wiedzy z dużych zbiorów danych z zastosowaniem adaptacyjnych
Zastosowanie logiki matematycznej w procesie weryfikacji wymagań oprogramowania
 Zastosowanie logiki matematycznej w procesie weryfikacji wymagań oprogramowania Testerzy oprogramowania lub osoby odpowiedzialne za zapewnienie jakości oprogramowania oprócz wykonywania testów mogą zostać
Zastosowanie logiki matematycznej w procesie weryfikacji wymagań oprogramowania Testerzy oprogramowania lub osoby odpowiedzialne za zapewnienie jakości oprogramowania oprócz wykonywania testów mogą zostać
Elementy logiki i teorii mnogości
 Elementy logiki i teorii mnogości Zdanie logiczne Zdanie logiczne jest to zdanie oznajmujące, któremu można przypisać określoną wartość logiczną. W logice klasycznej zdania dzielimy na: prawdziwe (przypisujemy
Elementy logiki i teorii mnogości Zdanie logiczne Zdanie logiczne jest to zdanie oznajmujące, któremu można przypisać określoną wartość logiczną. W logice klasycznej zdania dzielimy na: prawdziwe (przypisujemy
Wprowadzenie do technologii informacyjnej.
 Wprowadzenie do technologii informacyjnej. Data mining i jego biznesowe zastosowania dr Tomasz Jach Definicje Eksploracja danych polega na torturowaniu danych tak długo, aż zaczną zeznawać. Eksploracja
Wprowadzenie do technologii informacyjnej. Data mining i jego biznesowe zastosowania dr Tomasz Jach Definicje Eksploracja danych polega na torturowaniu danych tak długo, aż zaczną zeznawać. Eksploracja
Metody Inżynierii Wiedzy
 Metody Inżynierii Wiedzy Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and Technology Mateusz Burcon Kraków, czerwiec 2017 Wykorzystane technologie Python 3.4
Metody Inżynierii Wiedzy Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and Technology Mateusz Burcon Kraków, czerwiec 2017 Wykorzystane technologie Python 3.4
MECHANIZM PERSPEKTYW MATERIALIZOWANYCH W EKSPLORACJI DANYCH
 MECHANIZM PERSPEKTYW MATERIALIZOWANYCH W EKSPLORACJI DANYCH Mikołaj MORZY, Marek WOJCIECHOWSKI Streszczenie: Eksploracja danych to proces interaktywny i iteracyjny. Użytkownik definiuje zbiór interesujących
MECHANIZM PERSPEKTYW MATERIALIZOWANYCH W EKSPLORACJI DANYCH Mikołaj MORZY, Marek WOJCIECHOWSKI Streszczenie: Eksploracja danych to proces interaktywny i iteracyjny. Użytkownik definiuje zbiór interesujących
NEGATYWNE REGUŁY ASOCJACYJNE WYZNACZANIE, MIARY I OBSZARY ZASTOSOWANIA
 STUDIA INFORMATICA 2012 Volume 33 Number 2B (106) Anna KOTULLA Politechnika Śląska, Instytut Informatyki NEGATYWNE REGUŁY ASOCJACYJNE WYZNACZANIE, MIARY I OBSZARY ZASTOSOWANIA Streszczenie. Artykuł opisuje
STUDIA INFORMATICA 2012 Volume 33 Number 2B (106) Anna KOTULLA Politechnika Śląska, Instytut Informatyki NEGATYWNE REGUŁY ASOCJACYJNE WYZNACZANIE, MIARY I OBSZARY ZASTOSOWANIA Streszczenie. Artykuł opisuje
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
Modelowanie wzorców zachowań klientów Delikatesów Alma przy wykorzystaniu reguł asocjacyjnych
 UNIWERSYTET EKONOMICZNY WE WROCŁAWIU WYDZIAŁ ZARZĄDZANIA, INFORMATYKI I FINANSÓW Piotr Skrzypczak Modelowanie wzorców zachowań klientów Delikatesów Alma przy wykorzystaniu reguł asocjacyjnych Praca magisterska
UNIWERSYTET EKONOMICZNY WE WROCŁAWIU WYDZIAŁ ZARZĄDZANIA, INFORMATYKI I FINANSÓW Piotr Skrzypczak Modelowanie wzorców zachowań klientów Delikatesów Alma przy wykorzystaniu reguł asocjacyjnych Praca magisterska
Wielkie wolumeny danych są trudne w analizowaniu. system satelitarnej obserwacji EOS zbudowany przez NASA generuje
 Eksploracja danych - Odkrywanie wiedzy w danych Marek Wojciechowski Instytut Informatyki Politechnika Poznańska Zależności w bazach danych Przykład 1 wiek lat prawo kolor poj. moc razem kierowcy jazdy
Eksploracja danych - Odkrywanie wiedzy w danych Marek Wojciechowski Instytut Informatyki Politechnika Poznańska Zależności w bazach danych Przykład 1 wiek lat prawo kolor poj. moc razem kierowcy jazdy
Odkrywanie wiedzy w danych
 Inżynieria Wiedzy i Systemy Ekspertowe Odkrywanie wiedzy w danych dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Data Mining W pewnym teleturnieju
Inżynieria Wiedzy i Systemy Ekspertowe Odkrywanie wiedzy w danych dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Data Mining W pewnym teleturnieju
Algorytmy klasyfikacji
 Algorytmy klasyfikacji Konrad Miziński Instytut Informatyki Politechnika Warszawska 6 maja 2015 1 Wnioskowanie 2 Klasyfikacja Zastosowania 3 Drzewa decyzyjne Budowa Ocena jakości Przycinanie 4 Lasy losowe
Algorytmy klasyfikacji Konrad Miziński Instytut Informatyki Politechnika Warszawska 6 maja 2015 1 Wnioskowanie 2 Klasyfikacja Zastosowania 3 Drzewa decyzyjne Budowa Ocena jakości Przycinanie 4 Lasy losowe
Matematyka dyskretna - wykład - część Podstawowe algorytmy kombinatoryczne
 A. Permutacja losowa Matematyka dyskretna - wykład - część 2 9. Podstawowe algorytmy kombinatoryczne Załóżmy, że mamy tablice p złożoną z n liczb (ponumerowanych od 0 do n 1). Aby wygenerować losową permutację
A. Permutacja losowa Matematyka dyskretna - wykład - część 2 9. Podstawowe algorytmy kombinatoryczne Załóżmy, że mamy tablice p złożoną z n liczb (ponumerowanych od 0 do n 1). Aby wygenerować losową permutację
WYKŁAD 6. Reguły decyzyjne
 Wrocław University of Technology WYKŁAD 6 Reguły decyzyjne autor: Maciej Zięba Politechnika Wrocławska Reprezentacje wiedzy Wiedza w postaci reguł decyzyjnych Wiedza reprezentowania jest w postaci reguł
Wrocław University of Technology WYKŁAD 6 Reguły decyzyjne autor: Maciej Zięba Politechnika Wrocławska Reprezentacje wiedzy Wiedza w postaci reguł decyzyjnych Wiedza reprezentowania jest w postaci reguł
Programowanie liniowe
 Programowanie liniowe Maciej Drwal maciej.drwal@pwr.wroc.pl 1 Problem programowania liniowego min x c T x (1) Ax b, (2) x 0. (3) gdzie A R m n, c R n, b R m. Oznaczmy przez x rozwiązanie optymalne, tzn.
Programowanie liniowe Maciej Drwal maciej.drwal@pwr.wroc.pl 1 Problem programowania liniowego min x c T x (1) Ax b, (2) x 0. (3) gdzie A R m n, c R n, b R m. Oznaczmy przez x rozwiązanie optymalne, tzn.
Eksploracja danych. Plan prezentacji. Problemy eksploracji danych. Wielkie bazy danych SCHEMATY. zakresie baz danych, uczenia maszynowego i statystyki
 Problemy eksploracji danych dr inż. Maciej Zakrzewicz Instytut Informatyki Politechnika Poznańska Wielkie bazy danych Wielkie bazy danych (Very Large atabases) i hurtownie danych (ata Warehouses) Rozmiary
Problemy eksploracji danych dr inż. Maciej Zakrzewicz Instytut Informatyki Politechnika Poznańska Wielkie bazy danych Wielkie bazy danych (Very Large atabases) i hurtownie danych (ata Warehouses) Rozmiary
BAZY DANYCH model związków encji. Opracował: dr inż. Piotr Suchomski
 BAZY DANYCH model związków encji Opracował: dr inż. Piotr Suchomski Świat rzeczywisty a baza danych Świat rzeczywisty Diagram związków encji Model świata rzeczywistego Założenia, Uproszczenia, ograniczenia
BAZY DANYCH model związków encji Opracował: dr inż. Piotr Suchomski Świat rzeczywisty a baza danych Świat rzeczywisty Diagram związków encji Model świata rzeczywistego Założenia, Uproszczenia, ograniczenia
Indukcja. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Data Mining Wykład 5. Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny. Indeks Gini. Indeks Gini - Przykład
 Data Mining Wykład 5 Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny Indeks Gini Popularnym kryterium podziału, stosowanym w wielu produktach komercyjnych, jest indeks Gini Algorytm SPRINT
Data Mining Wykład 5 Indukcja drzew decyzyjnych - Indeks Gini & Zysk informacyjny Indeks Gini Popularnym kryterium podziału, stosowanym w wielu produktach komercyjnych, jest indeks Gini Algorytm SPRINT
REGU LY ASOCJACYJNE. Nguyen Hung Son. 25 lutego i 04 marca Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski.
 REGU LY ASOCJACYJNE Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski 25 lutego i 04 marca 2005 Outline 1 2 3 regu l asocjacyjnych 4 5 Motywacje Lista autorów (items) A Jane Austen C
REGU LY ASOCJACYJNE Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski 25 lutego i 04 marca 2005 Outline 1 2 3 regu l asocjacyjnych 4 5 Motywacje Lista autorów (items) A Jane Austen C
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
REGU LY ASOCJACYJNE. Nguyen Hung Son. Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski. 28.II i 6.III, 2008
 REGU LY ASOCJACYJNE Nguyen Hung Son Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski 28.II i 6.III, 2008 Nguyen Hung Son (MIMUW) W2 28.II i 6.III, 2008 1 / 38 Outline 1 Dane transakcyjne
REGU LY ASOCJACYJNE Nguyen Hung Son Wydzia l Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski 28.II i 6.III, 2008 Nguyen Hung Son (MIMUW) W2 28.II i 6.III, 2008 1 / 38 Outline 1 Dane transakcyjne
Grzegorz Harańczyk, StatSoft Polska Sp. z o.o.
 CO Z CZYM I PO CZYM, CZYLI ANALIZA ASOCJACJI I SEKWENCJI W PROGRAMIE STATISTICA Grzegorz Harańczyk, StatSoft Polska Sp. z o.o. Jednym z zagadnień analizy danych jest wyszukiwanie w zbiorach danych wzorców,
CO Z CZYM I PO CZYM, CZYLI ANALIZA ASOCJACJI I SEKWENCJI W PROGRAMIE STATISTICA Grzegorz Harańczyk, StatSoft Polska Sp. z o.o. Jednym z zagadnień analizy danych jest wyszukiwanie w zbiorach danych wzorców,
A i. i=1. i=1. i=1. i=1. W dalszej części skryptu będziemy mieli najczęściej do czynienia z miarami określonymi na rodzinach, które są σ - algebrami.
 M. Beśka, Wstęp do teorii miary, rozdz. 3 25 3 Miara 3.1 Definicja miary i jej podstawowe własności Niech X będzie niepustym zbiorem, a A 2 X niepustą rodziną podzbiorów. Wtedy dowolne odwzorowanie : A
M. Beśka, Wstęp do teorii miary, rozdz. 3 25 3 Miara 3.1 Definicja miary i jej podstawowe własności Niech X będzie niepustym zbiorem, a A 2 X niepustą rodziną podzbiorów. Wtedy dowolne odwzorowanie : A
Cel normalizacji. Tadeusz Pankowski
 Plan Normalizacja Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski 1. Cel normalizacji. 2. Klucze schematów relacyjnych atrybuty kluczowe i niekluczowe. 3. 2PN druga postać normalna. 4. 3PN trzecia
Plan Normalizacja Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski 1. Cel normalizacji. 2. Klucze schematów relacyjnych atrybuty kluczowe i niekluczowe. 3. 2PN druga postać normalna. 4. 3PN trzecia
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Algorytmy genetyczne. Paweł Cieśla. 8 stycznia 2009
 Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Mikołaj Morzy, Marek Wojciechowski: "Integracja technik eksploracji danych z systemem zarządzania bazą danych na przykładzie Oracle9i Data Mining"
 Mikołaj Morzy, Marek Wojciechowski: "Integracja technik eksploracji danych z systemem zarządzania bazą danych na przykładzie Oracle9i Data Mining" Streszczenie Eksploracja danych znajduje coraz szersze
Mikołaj Morzy, Marek Wojciechowski: "Integracja technik eksploracji danych z systemem zarządzania bazą danych na przykładzie Oracle9i Data Mining" Streszczenie Eksploracja danych znajduje coraz szersze
STATYSTYKA MATEMATYCZNA WYKŁAD 4. WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X.
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
