Zadanie było trudne, ale w dawnych czasach uczono w szkole powszechnej algorytmu rozwiązywana tego
|
|
|
- Mateusz Wojciechowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Konkurs fizyczny Autor: Zmieniony I SZKOLNY KONKURS INTERDYSCYPLINARNY "ZAGADKI" {mospagebreak heading=tytuł&title=regulamin} I. Nazwa konkursu: I Szkolny Konkurs Interdyscyplinarny "ZAGADKI". II. Organizatorzy: Organizatorem konkursu jest XXIII Liceum Ogólnokształcące im. ks. prof. Józefa Tischnera w Łodzi III. Cele konkursu: a. popularyzacja wiedzy popularnonaukowej i umiejętności logicznego myślenia wśród uczniów szkoły, b. mobilizowanie i motywowanie młodzieży do rozwiązywania problemów z dziedziny matematyki, logiki i nauk przyrodniczych, c. kształtowanie u uczniów zamiłowania do rozrywek umysłowych, d. wprowadzenie uczestników konkursów w atmosferę zdrowej rywalizacji, e. stymulowanie uczniów do samodzielnej pracy, IV. Uczestnicy Uczestnikami konkursu mogą być uczniowie XXIII Liceum Ogólnokształcącego, którzy w ciągu trwania konkursu będą systematycznie rozwiązywali zadania konkursowe. V. Etapy konkursu. Konkurs przebiega w jednym etapie, możliwa jest dogrywka, aby wyłonić zwycięzcę. VI. Organizacja Szkolnego Konkursu Interdyscyplinarnego "ZAGADKI". a. Funkcję Przewodniczącego Szkolnego Konkursu Interdyscyplinarnego "ZAGADKI" pełni Dyrektor XXIII LO - pani mgr inż. Jolanta Swiryd. b. Funkcję Sekretarza Szkolnego Konkursu Interdyscyplinarnego "ZAGADKI" pełni nauczyciel fizyki - pani mgr Barbara Makowska. c. Zadania konkursowe umieszczane są w każdy poniedziałek przed godziną 8.15 na tablicy ogłoszeń na półpiętrze oraz na stronie internetowej XXIII LO. d. Uczniowie oddają rozwiązania ma podpisanych kartkach do piątku danego tygodnia, przed godziną Sekretarzowi Konkursu. e. Każde poprawnie rozwiązane zadanie konkursowe - to jeden punkt w konkursie. f. Konkurs trwa do ostatniego tygodnia maja. g. W razie uzyskania takiej samej ilości punktów przez kilku uczniów - zorganizowana zostanie dogrywka aby wyłonić zwycięzcę. h. Nagrodą w Konkursie jest WIELKI ILUSTROWANY SŁOWNIK JĘZYKA POLSKIEGO i... satysfakcja oraz uznanie Społeczności Szkolnej. i. Pięciu uczestników, którzy uzyskają największą ilość punktów otrzyma Dyplomy :-) {mospagebreak heading=tytuł&title=tydzień 1} TYDZIEŃ PIERWSZY (pochodzi z XVII wieku) Za każdą wwożoną na targ do Paryża beczkę wina trzeba było zapłacić 13 franków cła. Wartość beczki wina wynosiła 127 franków. Celnik mógł przyjąć w naturze nie więcej niż 15 beczek z winem. Kupiec wjeżdżając do miasta dał celnikowi 5 franków a resztę należnego cła dopłacił beczkami z winem. Ile beczek wina przywiózł do Paryża kupiec i ile beczek wystawił na targu? Zadanie było trudne, ale w dawnych czasach uczono w szkole powszechnej algorytmu rozwiązywana tego
2 rodzaju problemów, współcześnie uczy się też tego we francuskich gimnazjach (zadanie pochodzi z francuskiego zbioru zadań do matematyki dla gimnazjum). Należy rozwiązać równanie z dwoma niewiadomymi - np. takie: 13(x-y) = y, gdzie: x - ilość beczek zabranych przez winiarza z domu y - ilość beczek zabranych przez celnika na poczet cła (x-y) - ilość beczek wwiezionych na targ Takie równania nazywa się diofantycznymi, na cześć greckiego matematyka z III w. n.e - Diofantosa. Algorytm do pobrania ode mnie (pracownia fizyczna) - bo długi. Odpowiedź - rano winiarz zapakował na wóz 65 beczek z winem, celnik w ramach podatku wziął 6 beczek, czyli na targ wwiezionych zostało 59 beczek. Można sprawdzić, czy się zgadza. (O rycerzach i łotrach) 1 punkt Każdy mieszkaniec pewnej wyspy jest albo rycerzem albo łotrem. Rycerze zawsze mówią prawdę a łotrzy zawsze kłamią. W ogrodzie byli trzej mieszkańcy wyspy - A, B i C. Przechodzący obok nich człowiek spytał A: - "Czy jesteś rycerzem czy łotrem?". A coś odburknął, więc przechodzień spytał B: - "Co powiedział A?". Na to B: - "A powiedział, że jest łotrem". Wtedy odezwał się trzeci człowiek, C: - "Nie wierz B, bo on kłamie". Kim byli B i C? Ani rycerz ani łotr nie może powiedzieć o sobie: "Jestem łotrem", - rycerz wtedy by skłamał a łotr powiedziałby prawdę. Czyli A nie mógł powiedzieć, "Jestem łotrem", zatem B kłamał, twierdząc, że A tak powiedział. Wniosek: B jest łotrem, a C mówiąc, że B kłamie mówił prawdę, czyli był rycerzem. Kim był A - nie wiadomo. {mospagebreak heading=tytuł&title=tydzień 2}TYDZIEŃ DRUGI Pewien bystry więzień dostał od króla szansę na ułaskawienie. Więzień miał szansę na ocalenie życia i narzeczoną lub marny koniec w paszczy zwierza, gdyż król podstępnie w dwóch komnatach nakazał umieścić damy i tygrysy (dwie damy albo dwa tygrysy albo damę i tygrysa). Król na drzwiach pokoi kazał umieścić tabliczki z informacjami, przy czym wyjaśnił, że jeden napis na drzwiach jest prawdziwy a drugi fałszywy. Napisy na drzwiach wyglądały tak: I W tym pokoju jest dama, a w tamtym pokoju jest tygrys II W jednym z tych pokojów jest dama i w jednym z tych pokojów jest tygrys
3 Które drzwi powinien wybrać więzień, żeby nie stracić życia? Gdyby napis na drzwiach nr 1 był prawdziwy, to w pokoju nr 1 jest dama a w pokoju nr 2 - tygrys, więc również napis na drzwiach nr 2 jest prawdziwy - ale przecież król powiedział, że jeden napis jest fałszywy! Wniosek: napis pierwszy jest fałszywy a drugi prawdziwy a więc należy wybrać drzwi nr 2, gdyż tygrys jest w pokoju nr 1. To też nie było trudne, prawda? 1 punkt Dwóch królewskich synów przed wyprawą wojenną udało się do zbrojowni, gdzie leżała zaczarowana broń, której szkodzi światło: cztery sztylety, trzy miecze i dwa topory. Potrzebowali tylko jednej sztuki broni każdy i zażądali od zbrojmistrza broni tego samego rodzaju. Ile sztuk broni musi wyciągnąć z ciemnej zbrojowni zbrojmistrz, aby spełnić życzenie książąt? Zbrojmistrz nie widzi, jaką broń wyciąga. Mając pecha może więc wyjąć najpierw broń pierwszego rodzaju, potem drugiego i trzeciego i czwartego. Ale czwarta sztuka MUSI być już drugą z któregoś rodzaju (podobnie jak w zadaniu ze skarpetkami w dwóch kolorach, które leżą skłębione w szufladzie; możemy wyciągnąć jako pierwszą skarpetkę koloru 1, potem koloru 2, ale trzecia skarpetka na pewno będzie od którejś pary!). {mospagebreak heading=tytuł&title=tydzień 3} TYDZIEŃ TRZECI Pewien król postanowił wydać za mąż swą córkę, ale ona miała ambicję poślubić mądrego chłopca. Obiecała wyjść za tego księcia, który odgadnie w której z trzech szkatułek księżniczka schowała swój portret. Na szkatułkach księżniczka umieściła napisy, i poinformowała, że najwyżej jeden z nich jest prawdziwy. Którą szkatułkę - złotą, srebrną czy ołowianą powinien wybrać książę?złota SREBRNA OŁOWIANA Portret jest w tej szkatułce Portretu nie ma w tej szkatułce Portretu nie ma w złotej szkatułce Napisy na szkatułkach złotej i ołowianej mówią coś przeciwnego - więc jeden z nich jest prawdziwy. Tylko jedno zdanie może być prawdziwe, więc na srebrnej musi być fałszywe. Czyli portret jest w srebrnej szkatułce.
4 1 punkt Są trzy kubki i 10 monet. Ulokuj WSZYSTKIE monety w kubkach tak, aby w każdym kubku było po tyle samo monet. :) Kubki można powkładać jeden w drugi... ;- ) {mospagebreak heading=tytuł&title=tydzień 4} TYDZIEŃ CZWARTY Kolejny bystry więzień dostał od króla szansę na ułaskawienie. Król znów nakazał umieścić w dwóch komnatach damy i tygrysy (dwie damy albo dwa tygrysy albo damę i tygrysa). Więzień miał szansę na ocalenie życia i narzeczoną lub marny koniec w paszczy zwierza. Król na drzwiach pokoi kazał umieścić tabliczki z informacjami, przy czym wyjaśnił, że oba napisy są prawdziwe bądź oba są fałszywe. Napisy na drzwiach wyglądały tak: I W co najmniej jednym z tych pokojów jest dama II Tygrys jest w tamtym pokoju Które drzwi powinien wybrać więzień, żeby nie stracić życia? Jeśli II napis jest fałszywy, to w pierwszym pokoju jest dama. To znaczy, że prawdziwy jest napis I. Ale muszą być albo oba prawdziwe albo oba fałszywe. Czyli II napis jest prawdziwy i dama jest w tym właśnie pokoju. 1 punkt Królewskie dzieci - Abel, Beniamin i Cecylia udały się pod opieką Szambelana - Sir Kaya do lasu, aby podczas polowania wprawiać się w łucznictwie. Każde dostało tyle samo strzał, a po zakończeniu polowania okazało się, że: - Sir Kay powalił więcej zwierzyny niż księżniczka, - Beniamin upolował więcej zwierzyny niż Sir Kay, - Księżniczka strzela celniej niż Abel. Które książątko strzela z łuku najcelniej?
5 Abel upolował mniej od Cecylii, ona z kolei mniej niż sir Kay a Beniamin więcej niż sir Kay, czyli najwięcej ze wszystkich. {mospagebreak heading=tytuł&title=tydzień 5} TYDZIEŃ PIĄTY Na wyspie zawsze prawdomównych rycerzy i zawsze kłamiących łotrów przybysz spotyka trzech tubylców i pyta tubylca A: - Ilu jest pośród was rycerzy? A coś wymamrotał, więc przybysz spytał tubylca B: - Co powiedział A? Na to B odpowiedział: - A powiedział, że jest wśród nas jeden rycerz. Wtedy odezwał się tubylec C: - Przybyszu, nie wierz B, on kłamie! Kim byli tubylcy B i C? B i C muszą być różni, skoro sobie przeczą, więc jeden jest rycerzem a drugi łotrem. Na wyspie jest więc albo jeden rycerz albo dwóch. Gdyby A był rycerzem, to nie może powiedzieć: Jest jeden rycerz na wyspie, bo to byłoby kłamstwo. Gdyby A był łotrem, to nie może powiedzieć: Jest jeden rycerz na wyspie, bo musi skłamać, a to byłoby zdanie prawdziwe. Czyli A w ogóle nie może powiedzieć Na wyspie jest jeden rycerz. B mówiąc, że A tak powiedział kłamał. Czyli był łotrem. Natomiast C był rycerzem. 1 punkt Wielkolud złapał królewskie dzieci Abla, Beniamina i Paulę oraz ich opiekuna - Sir Kaya. Uwięził ich w sąsiadujących ze sobą celach. Cela księcia Abla sąsiadowała z celą jego brata, ale nie z celą siostry, która z kolei nie sąsiadowała z celą Sir Kaya. Kto był uwięziony w celi obok Sir Kaya? KayAbelBenPaula I już.
6 {mospagebreak heading=tytuł&title=tydzień 6} TYDZIEŃ SZÓSTY Jeszcze jeden bystry więzień starał się o ułaskawienie. Tym razem król wyjaśnił, że oba napisy są jednocześnie prawdziwe lub fałszywe. Kto jest w pierwszym pokoju a kto w drugim? I Tygrys jest w tym pokoju lub w tamtym pokoju jest dama II Dama jest w pierwszym pokoju Tym razem dowcipny król w obu pokojach umieścił damy. Jeżeli napis II jest fałszywy, to w pokoju I jest tygrys, czyli napis I jest prawdziwy. Ale przecież oba napisy muszą być prawdziwe albo oba fałszywe! Jeżeli napis II jest prawdziwy, to oba muszą być prawdziwe, czyli w pierwszym pokoju też jest dama. (Alternatywa jest prawdziwa, gdy przynajmniej jedno z tworzących ją zdań jest prawdziwe). 1 punkt Kupiec zgubił odważniki do swojej wagi. Poradził sobie tnąc kawał ołowiu ważący 15 uncji na cztery części. Jak sprytny kupiec podzielił ten kawał ołowiu skoro mógł odważać nimi ciężary od 1 do 15 uncji? Rozwiązań jest co najmniej dwa - na przykład takie: podział na odważniki o masie 1, 2, 4 i 8 uncji - można nimi zważyć ciężary od 1 do 15 uncji, zresztą sprawdźcie sami. {mospagebreak heading=tytuł&title=tydzień 7} TYDZIEŃ SIÓDMY Pewien król postanowił wydać za mąż swą córkę, ale ona miała ambicję poślubić mądrego chłopca. Obiecała wyjść za tego księcia, który odgadnie w której z trzech szkatułek księżniczka schowała swój
7 portret. Na szkatułkach księżniczka umieściła napisy, i poinformowała, że co najmniej jeden z napisów jest prawdziwy i co najmniej jeden jest fałszywy. Którą szkatułkę - złotą, srebrną czy ołowianą powinien wybrać książę? ZŁOTA SREBRNA OŁOWIANA Portretu nie ma w srebrnej szkatułce Portretu nie ma w tej szkatułceportret jest w tej szkatułce Gdyby portret był w szkatułce ołowianej, to wszystkie trzy zdania byłyby prawdziwe, co jest sprzeczne z warunkami zadania. Gdyby portret był w srebrnej - to wszystkie zadania byłyby fałszywe, co też jest sprzeczne z warunkami zadania. Portret zatem musi być w złotej szkatułce (jedno zdanie fałszywe a dwa prawdziwe). 1 punkt Kolejny kupiec zgubił odważniki do swojej wagi. Kupił więc kawał ołowiu o wadze 40 funtów i podzielił go na 4 części tak sprytnie, że mógł ważyć ciężary o wadze od 1 do 40 funtów. Jak podzielił kawał ołowiu? Kupiec mógł podzielić kawał ołowiu na części o wagach: 1, 3, 9 i 27 funtów. Np. aby odważyć 2 funty - kładł na jedną szalę odważnik 3 funtowy a na drugą - ważony przedmiot i odważnik 1 funtowy. I tak dalej ;-) {mospagebreak heading=tytuł&title=tydzień 8} TYDZIEŃ ÓSMY W pewnym kraju w obrocie są jedynie monety 3 dolcowe i banknoty 5-dolcowe. Za szalik trzeba zapłacić w sklepie 23 dolce. Kłopot w tym, że kupujący ma tylko monety a kasjer tylko banknoty. Czy da się uregulować rachunek za szalik? Kupujący powinien dać kupcowi 11 monet 3 dolcowych i otrzymać reszty 2 banknoty 5 dolcowe.
8 Alicja weszła do Lasu Zapomnienia, gdzie mieszkali: Lew, który kłamie w poniedziałki, wtorki i środy natomiast w pozostałe dni mówi prawdę oraz Jednorożec, który kłamie w czwartki, piątki i soboty a w pozostałe dni mówi prawdę. Lew powiedział do Alicji: - Wczoraj był jeden z dni, w które kłamię. Jednorożec powiedział do Alicji: - Wczoraj był jeden z dni, w które kłamię. Z tych dwóch zdań Alicja, która była bardzo bystrą dziewczynką wydedukowała, jaki był wczoraj dzień tygodnia. Czy ty też to wykombinujesz? Lew może powiedzieć "kłamałem wczoraj" tylko w poniedziałek i w czwartek. Jednorożec może powiedzieć, że kłamał wczoraj tylko w czwartek i w niedzielę. Zatem jedyny dzień, kiedy mogą to powiedzieć i Lew i Jednorożec jest czwartek. {mospagebreak heading=tytuł&title=tydzień 9} TYDZIEŃ DZIEWIĄTY Zadanie podobne do tego z ubiegłego tygodnia: W pewnym kraju w obrocie są jedynie monety 3 dolcowe i banknoty 5-dolcowe. Za szalik trzeba zapłacić w sklepie 23 dolce. Kłopot w tym, że kupujący ma tylko banknoty a kasjer tylko 10 monet. Czy da się uregulować rachunek za szalik? Kupujący powinien dać kupcowi 7 banknotów 5 dolcowych i otrzymać reszty 4 monety 3 dolcowe. W tym zadaniu są tylko dwie osoby: A i B, z których każda jest albo rycerzem albo łotrem. A mówi: "Co najmniej jeden z nas jest łotrem" Kim jest A i kim jest B?
9 Jeśli założymy, że A jest łotrem, to zdanie, które wygłosił byłoby fałszywe, czyli obaj byliby rycerzami, a to jest niemożliwe. Zatem A jest rycerzem. A skoro tak, to B jest łotrem. {mospagebreak heading=tytuł&title=tydzień 10} TYDZIEŃ DZIESIĄTY Tym razem krótko, A mówi: -Jestem łotrem lub B jest rycerzem. Kim są A i B? Jeżeli założymy, że A jest łotrem, to zdanie, które wygłosił musi być fałszywe. Czyli ani nie jest prawdą, że A jest łotrem ani że B jest rycerzem. Czyli z założenia, żew A jest łotrem wynika, że A nie jest łotrem. Zatem A musi być rycerzem. W związku z tym jego zdanie jest prawdziwe. A więc B też musi być rycerzem. Znów o Alicji i Lwie kłamiącym w poniedziałki, wtorki i środy. Lew powiedział tak: - Wczoraj kłamałem. - Będę znów kłamał w dwa dni po jutrze. Jaki był dzień tygodnia, w którym Alicja rozmawiała z Lwem? Z pierwszego zdania lwa wynika, że jest poniedziałek lub czwartek. Z drugiego, że nie jest to czwartek. A zatem jest poniedziałek. {mospagebreak heading=tytuł&title=tydzień 11} TYDZIEŃ JEDENASTY
10 Po kradzieży złodzieje wywieźli łup samochodem. Na przesłuchanie przywieziono trzech znanych kryminalistów A,B i C. Ustalono następujące fakty: - Nikt poza A, B i C nie brał udziału w rabunku. - C nigdy nie idzie na robotę nie posłużywszy się przynajmniej A jako współsprawcą. - B nie umie prowadzić auta. Czy A jest winny czy też niewinny? Jeżeli B jest niewinny, to oczywiście A i (lub) C jest winny. Jeśli B jest winny, to musi mieć współwinnego, więc A i (lub) C też jest winny. Stąd wynika, że jeśli C jest niewinny, to A musibyć winny, a jeśli C jest winny, to A też jest winny. Jakby nie patrzeć - A zawsze jest winny. W kolejnym dochodzeniu również na przesłuchanie doprowadzono A, B i C. Ustalono następujące fakty: - Nikt poza A, B i C nie brał udziału w rabunku. - A nigdy nie pracuje bez przynajmniej jednego współsprawcy. - C jest niewinny. Czy B jest winny czy też niewinny? Jeśli A niewinny, i C niewinny, to oczywiście B winny. Jeśli A winny, to ma współwinnego, którym musi być B. Jakby nie patrzeć - B zawsze jest winny. {mospagebreak heading=tytuł&title=tydzień 12} TYDZIEŃ DWUNASTY W kolejnym dochodzeniu na przesłuchanie doprowadzono A, B i C. Ustalono, że nikt inny nie brał udziału w rabunku oraz następujące fakty: - Jeśli A jest winny i B jest niewinny, to C jest winny. - C nigdy nie pracuje sam. - A nigdy nie pracuje z C. - Co najmniej jeden z podejrzanych jest winny. Który z przestępców jest bezsprzecznie winny?
11 Załóżmy, że B jest niewinny. Wtedy A może być winny a więc i C też. Ale to oznacza, że A pracował z C a tak być nie może. Jeżeli z kolei A jest niewinny, to wtedy jedynym winny jest C a tak też być nie może. Czyli B musi być winny. Po rabunku sklepu doprowadzono na presłuchanie A, B i C. Ustalono następujące fakty - Każdy z podejrzanych był tego dnia w sklepie i nikogo innego tam nie było. - Jeśli winny jest A, to ma on dokładnie jedego współwinnego. - Jeśli B jest niewinny, to C też jest niewinny. - Jeśli jest dwóch winnych, to jednym z nich jest A. - Jeśli C jest niewinny, to B też jest niewinny. Kogo oskarżył o rabunek inspektor Craig? Doniesienie o rabunku było fałszywe! Gdyby A był winny, to miałby jednego współwinnego, czyli albo B albo C byłby winny. Ale to przeczy warunkowi, że oni są albo obaj winni albo obaj niewinni. Czyli A musi być niewinny. Stąd wynika, że B i C muszą być obaj winni (skoro ustaliliśmy, że A nie może być winny). Skoro tak, to A też powinien być winny (jako jeden z dwóch współwinnych). A to jest sprzeczność. A więc B i C też są niewinni. Skoro nikogo innego nie było tego dnia w sklepie, to nikt nie mógł go obrabować. A więc nie ma winnego - nie było więc i rabunku. {mospagebreak heading=tytuł&title=tydzień 13} TYDZIEŃ TRZYNASTY W tym tygodniu wracamy do Alicji z krainy Czarów. W Zaczarowanym Lesie spotkała ona dwóch identycznych braci, których nie potrafiła odróżnić. Tweedledum - kłamał w poniedziałki, wtorki i środy a w pozostałe dni mówił prawdę, a Tweedledee - kłamał w czwartki, piątki i soboty a w pozostałe dni mówił prawdę. Pewnego dnia Alicja spotkała braci w Lesie. Pierwszy brat powiedział: "Jestem Tweedledum". Drugi brat powiedział: "Jestem Tweedledee".
12 Który brat był który? Jaki był dzień tygodnia? Jeśli pierwsze zdanie jest prawdziwe to pierwszy jest Tweeledum a drugi Tweedledee i drugie zdanie też jest prawdziwe. Jeśli pierwsze zdanie jest fałszywe, to pierwszy jest Tweedledee a drugi Tweedledum, czyli drugie zdanie jest fałszywe. Zatem oba zdania są albo jednocześnie prawdziwe albo fałszywe. Ponieważ bracia nie mogą kłamać tego samego dnia, to spotkanie musiało nastąpić w niedzielę, kiedy obaj mówią prawdę. Innego dnia w tym samym tygodniu bracia wygłosili następujące zdania: Pierwszy: "Jestem Tweedledum". Drugi: "Jeśli to prawda, to ja jestem Tweedledee". Który brat był który? Czy można określić jaki był dzień tygodnia? Tym razem jest to ten sam tydzień (inny dzień niż niedziela). Oba zdania nie mogą więc być jednocześnie prawdziwe (jednocześnie fałszywe też nie), czyli jedno musi być prawdziwe a drugie fałszywe. Jeśli pierwsze jest więc prawdą to drugie jest fałszem a zatem pierwszy to Tweedledee a drugi Tweedledum. {mospagebreak heading=tytuł&title=tydzień 14} TYDZIEŃ CZTERNASTY W tym tygodniu zostajemy z Alicją z Krainy Czarów. W Zaczarowanym Lesie spotkała ona dwóch identycznych braci, których nie potrafiła odróżnić. Tweedledum - kłamał w poniedziałki, wtorki i środy a w pozostałe dni mówił prawdę, a Tweedledee - kłamał w czwartki, piątki i soboty a w pozostałe dni mówił prawdę. Pewnego dnia Alicja spotkała braci w Lesie i spytała jednego z nich: - "Czy kłamiesz w niedziele?" Ten odpowiedział twierdząco. Z kolei to samo pytanie zadała drugiemu z braci. Jak odpowiedział drugi brat?
13 Pierwsza odpowiedź to kłamstwo, toteż zdarzenie musiało nastąpić w zwykłym dniu tygodnia. Zatem rugi BRT musiał zgonie z prawdą odpowiedzieć "nie". Innego dnia bracia wygłosili następujące zdania: Pierwszy: (1) "Kłamię w soboty" (2) "Kłamię w niedziele". Drugi: "Będę kłamał jutro". Jaki był dzień tygodnia? Drugie zdanie pierwszego brata jest fałszywe, wiec pierwsze zdanie też jest fałszywe. Zatem pierwszy brat nie kłamie w soboty. Stąd wynika, że w soboty kłamie ten drugi brat. Skoro tak, to danego dnia drugi brat mówi prawdę. Jest to więc poniedziałek, wtorek lub środa. Jedyny dzień, kiedy zgodnie z prawdą może on powiedzieć, że będzie kłamał jutro jest środa. {mospagebreak heading=tytuł&title=tydzień 15} TYDZIEŃ PIĘTNASTY Wracamy do gry! Wracamy do szkatułek Porcji upartej dziewczyny, która testowała przyszłych mężów zagadkami. Tym razem zajmiemy się pomysłami wnuczki pierwszej Porcji, też imieniem Porcja. Na szkatułkach kazała umieszczać po jednym zdaniu, a wykonanie pudełeczek zlecała dwóm rzemieślnikom: Celliniemu i Belliniemu. Na szkatułkach Cellini zawsze umieszczał napis fałszywy, a Bellini Prawdziwy. W pierwszym teście Porcja nakazała w jednej z trzech szkatułek umieścić sztylet. Zalotnik musiał znaleźć szkatułkę, w której NIE MA sztyletu. Jeśli zgadł, mógł przystąpić do kolejnego testu. Oto napisy na szkatułkach: Złota: Sztylet jest w tej szkatułce. Srebrna: Ta szkatułka jest pusta. Ołowiana: Co najwyżej jedna z tych trzech szkatułek została zrobiona przez Belliniego. Którą szkatułkę powinien wybrać zalotnik? Jeszcze nie ma odpowiedzi. Będzie wkrótce.
14 Bystry chłopak, który rozwiązał poprzednie zadanie mógł przystąpić do kolejnego testu. Tym razem Porcja kazała wykonać dwie szkatułki i w jednej z nich ukryła swój portret. Zalotnik miał za zadanie znaleźć ten portret. Szkatułki mogły być zrobione przez Celliniego lub Belliniego. Oto napisy: Złota: Tutaj nie ma portretu. Srebrna: Dokładnie jedna z tych dwóch szkatułek została sporządzona przez Belliniego. Którą szkatułkę powinien wybrać zalotnik? Jeszcze nie ma odpowiedzi. Będzie wkrótce.
Zagadki II - reaktywacja
 Zagadki II - reaktywacja Autor: 29.11.2010. Zmieniony 15.03.2011. II SZKOLNY KONKURS INTERDYSCYPLINARNY "ZAGADKI - REAKTYWACJA" Witam wszystkich chętnych do łamania głowy Uczniów i Nauczycieli (dla których
Zagadki II - reaktywacja Autor: 29.11.2010. Zmieniony 15.03.2011. II SZKOLNY KONKURS INTERDYSCYPLINARNY "ZAGADKI - REAKTYWACJA" Witam wszystkich chętnych do łamania głowy Uczniów i Nauczycieli (dla których
Niezwykły świat pana Smullyana
 Jest to zapis odczytu wygłoszonego na Seminarium Popularyzacji Matematyki działającym na Wydziale Matematyki, nformatyki i Mechaniki Uniwersytetu Warszawskiego, październik 2003. Niezwykły świat pana Smullyana
Jest to zapis odczytu wygłoszonego na Seminarium Popularyzacji Matematyki działającym na Wydziale Matematyki, nformatyki i Mechaniki Uniwersytetu Warszawskiego, październik 2003. Niezwykły świat pana Smullyana
Logika Matematyczna Spójniki logiczne Tautologie Dowodzenie Kwantyfikatory Zagadki. Logika Matematyczna. Marcelina Borcz.
 5 marca 2009 Spis treści 1 2 3 4 5 6 Logika (z gr. logos - rozum) zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Logika matematyczna,
5 marca 2009 Spis treści 1 2 3 4 5 6 Logika (z gr. logos - rozum) zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Logika matematyczna,
Zadania z konkursów matematycznych
 przeprowadzanych w Pałacu Młodzieży w Katowicach Pałac Młodzieży w Katowicach dorota.kolany@gmail.com Konkursy matematyczne w Pałacu Młodzieży Bajkowe zadania Nudna Matematyka Przygoda z matematyką Rozkosze
przeprowadzanych w Pałacu Młodzieży w Katowicach Pałac Młodzieży w Katowicach dorota.kolany@gmail.com Konkursy matematyczne w Pałacu Młodzieży Bajkowe zadania Nudna Matematyka Przygoda z matematyką Rozkosze
Lista 1 (elementy logiki)
 Podstawy nauczania matematyki 1. Zdanie Lista 1 (elementy logiki) EE I rok W logice zdaniem logicznym nazywamy wyrażenie oznajmujące o którym można powiedzieć że jest prawdziwe lub fałszywe. Zdania z reguły
Podstawy nauczania matematyki 1. Zdanie Lista 1 (elementy logiki) EE I rok W logice zdaniem logicznym nazywamy wyrażenie oznajmujące o którym można powiedzieć że jest prawdziwe lub fałszywe. Zdania z reguły
8 + 66 =.. 48 + 20 =... 35 + 46 =... 53 7 =... 89 50 =... 72 58 =...
 Matematyka test dla uczniów klas trzecich szkół podstawowych w roku szkolnym 2011/2012 Etap szkolny (60 minut) Ryzyko dysleksji [suma punktów].... Imię i nazwisko Klasa 1. Oblicz. 8 + 66 =.. 48 + 20 =...
Matematyka test dla uczniów klas trzecich szkół podstawowych w roku szkolnym 2011/2012 Etap szkolny (60 minut) Ryzyko dysleksji [suma punktów].... Imię i nazwisko Klasa 1. Oblicz. 8 + 66 =.. 48 + 20 =...
KONSPEKT LEKCJI MATEMATYKI W KLASIE II GIMNAZJUM
 KONSPEKT LEKCJI MATEMATYKI W KLASIE II GIMNAZJUM TEMAT: Układanie równań do zadań z treścią. CZAS TRWANIA ZAJĘĆ: 45 minut CELE ZAJĘĆ: Matematyzowanie sytuacji opisanych słowami redagowanie treści z użyciem
KONSPEKT LEKCJI MATEMATYKI W KLASIE II GIMNAZJUM TEMAT: Układanie równań do zadań z treścią. CZAS TRWANIA ZAJĘĆ: 45 minut CELE ZAJĘĆ: Matematyzowanie sytuacji opisanych słowami redagowanie treści z użyciem
Tekst łatwy do czytania. foto: Anna Olszak. Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier w komunikowaniu się
 Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier w komunikowaniu się Bariery w komunikowaniu się to wszystko to, co utrudnia ci porozumiewanie
Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier w komunikowaniu się Bariery w komunikowaniu się to wszystko to, co utrudnia ci porozumiewanie
SP Klasa V, Temat 17
 Narrator: Po wielu latach od czasu sprzedania Józefa do Egiptu, w kraju Kanaan zapanował wielki głód. Ojciec Józefa Jakub wysłał do Egiptu swoich synów, by zakupili zboże. Tylko najmłodszy Beniamin pozostał
Narrator: Po wielu latach od czasu sprzedania Józefa do Egiptu, w kraju Kanaan zapanował wielki głód. Ojciec Józefa Jakub wysłał do Egiptu swoich synów, by zakupili zboże. Tylko najmłodszy Beniamin pozostał
Z reguł wnioskowania na oddzielne traktowanie zasługują reguły Claviusa:
 WYKŁAD 9 Z reguł wnioskowania na oddzielne traktowanie zasługują reguły Claviusa: ( p p) p, (p p) p Mówią one, że jeżeli z zaprzeczenia jakiegoś zdania wyprowadzimy to właśnie zdanie, to musi być ono prawdziwe.
WYKŁAD 9 Z reguł wnioskowania na oddzielne traktowanie zasługują reguły Claviusa: ( p p) p, (p p) p Mówią one, że jeżeli z zaprzeczenia jakiegoś zdania wyprowadzimy to właśnie zdanie, to musi być ono prawdziwe.
KONKURS MATEMATYCZNY KANGUREK DLA KLASY I
 KONKURS MATEMATYCZNY KANGUREK DLA KLASY I OPRACOWAŁA NAUCZYCIELKA NAUCZANIA ZINTEGROWANEGO ZE SZKOŁY PODSTAWOWEJ NR 34 W ŁODZI MGR BEATA MIĘTUS Nauczanie początkowe matematyki jest pierwszym etapem nauczania
KONKURS MATEMATYCZNY KANGUREK DLA KLASY I OPRACOWAŁA NAUCZYCIELKA NAUCZANIA ZINTEGROWANEGO ZE SZKOŁY PODSTAWOWEJ NR 34 W ŁODZI MGR BEATA MIĘTUS Nauczanie początkowe matematyki jest pierwszym etapem nauczania
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa II PŁOCK 2014
 MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa II PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 SUMA PUNKTÓW Max
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa II PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 SUMA PUNKTÓW Max
Harmonogram cyklu konkursów dla uczniów klas szóstych z terenu Gminy Jedlicze: Rachmistrz Gminy Jedlicze
 Jedlicze, 15.01.2016r. Szanowni Państwo Dyrektorzy i Nauczyciele szkół podstawowych Gimnazjum w Jedliczu serdecznie zaprasza uczniów Państwa szkoły do wzięcia udziału w konkursach organizowanych pod patronatem
Jedlicze, 15.01.2016r. Szanowni Państwo Dyrektorzy i Nauczyciele szkół podstawowych Gimnazjum w Jedliczu serdecznie zaprasza uczniów Państwa szkoły do wzięcia udziału w konkursach organizowanych pod patronatem
Karta pracy 8. Przed imprezą
 Karta pracy 8 Przed imprezą Mini rozmowy 1 D: - W weekend jest impreza u Agi. Mogę iść? R: - Impreza? Z jakiej okazji? D:- Są jej urodziny. R: -Kiedy dokładnie? D: - W piątek, zaczyna się o siódmej. Mogę
Karta pracy 8 Przed imprezą Mini rozmowy 1 D: - W weekend jest impreza u Agi. Mogę iść? R: - Impreza? Z jakiej okazji? D:- Są jej urodziny. R: -Kiedy dokładnie? D: - W piątek, zaczyna się o siódmej. Mogę
Boisko piłkarskie: stycznia
 Boisko piłkarskie: 11 17 stycznia 11.01 poniedziałek 12.01 wtorek 13.01 środa 14.01 czwartek 15.01 piątek 16.01 sobota 17.01 niedziela Organizator: rugby Boisko wielofunkcyjne: 11 17 stycznia 11.01 poniedziałek
Boisko piłkarskie: 11 17 stycznia 11.01 poniedziałek 12.01 wtorek 13.01 środa 14.01 czwartek 15.01 piątek 16.01 sobota 17.01 niedziela Organizator: rugby Boisko wielofunkcyjne: 11 17 stycznia 11.01 poniedziałek
Małe Olimpiady Przedmiotowe. Test z matematyki
 Małe Olimpiady Przedmiotowe Test z matematyki Organizatorzy: Wydział Edukacji Urzędu Miasta Centrum Edukacji Nauczycieli Szkoła Podstawowa nr 17 Szkoła Podstawowa nr 18 Drogi Uczniu, Test składa się z
Małe Olimpiady Przedmiotowe Test z matematyki Organizatorzy: Wydział Edukacji Urzędu Miasta Centrum Edukacji Nauczycieli Szkoła Podstawowa nr 17 Szkoła Podstawowa nr 18 Drogi Uczniu, Test składa się z
Czyli Wprowadzenie do logiki
 Czyli Wprowadzenie do logiki DZISIAJ Dowiemy się, czym zajmuje się logika formalna Na kilku przykładach zastanowimy się, po co warto się jej uczyć Dowiemy się, co trzeba zrobić, by zaliczyć ten przedmiot
Czyli Wprowadzenie do logiki DZISIAJ Dowiemy się, czym zajmuje się logika formalna Na kilku przykładach zastanowimy się, po co warto się jej uczyć Dowiemy się, co trzeba zrobić, by zaliczyć ten przedmiot
Matematyka Dyskretna Zestaw 2
 Materiały dydaktyczne Matematyka Dyskretna (Zestaw ) Matematyka Dyskretna Zestaw 1. Wykazać, że nie istnieje liczba naturalna, która przy dzieleniu przez 18 daje resztę 13, a przy dzieleniu przez 1 daje
Materiały dydaktyczne Matematyka Dyskretna (Zestaw ) Matematyka Dyskretna Zestaw 1. Wykazać, że nie istnieje liczba naturalna, która przy dzieleniu przez 18 daje resztę 13, a przy dzieleniu przez 1 daje
Dni tygodnia. uczymy się bawimy się rozmawiamy odkrywamy ruszamy się
 Dni tygodnia TEMATYKA ZAGADNIENIA Kalendarz, pomiar czasu. OBSZAR EDUKACJI I KLASA uczymy się bawimy się rozmawiamy odkrywamy ruszamy się CELE CELE W JĘZYKU UCZNIA poznawanie kolejności dni tygodnia; stosowanie
Dni tygodnia TEMATYKA ZAGADNIENIA Kalendarz, pomiar czasu. OBSZAR EDUKACJI I KLASA uczymy się bawimy się rozmawiamy odkrywamy ruszamy się CELE CELE W JĘZYKU UCZNIA poznawanie kolejności dni tygodnia; stosowanie
Pseudaria. Autor: Laura Robińska
 Pseudaria Autor: Laura Robińska Co to Pseudaria? Euklides, wielki grecki matematyk, jest autorem znanego dzieła Elementy. Oprócz tego napisał także inne dzieło, Pseudaria. Składało się ono z różnych błędnych
Pseudaria Autor: Laura Robińska Co to Pseudaria? Euklides, wielki grecki matematyk, jest autorem znanego dzieła Elementy. Oprócz tego napisał także inne dzieło, Pseudaria. Składało się ono z różnych błędnych
od 16 marca do 20 marca
 od 16 marca do 20 marca PONIEDZIAŁEK (16 marca) Rozpoczęcie Tygodnia Matematycznego przez Pitagorasa, Talesa, Archimedesa i Euklidesa Sześciany czwartoklasistów i piątoklasistów wspólne wykonanie na lekcji
od 16 marca do 20 marca PONIEDZIAŁEK (16 marca) Rozpoczęcie Tygodnia Matematycznego przez Pitagorasa, Talesa, Archimedesa i Euklidesa Sześciany czwartoklasistów i piątoklasistów wspólne wykonanie na lekcji
IX Regionalny Konkurs Zadań Interdyscyplinarnych w Języku Angielskim im. Marii Goeppert Mayer I Ty możesz zostać noblistą Regulamin dla gimnazjalistów
 IX Regionalny Konkurs Zadań Interdyscyplinarnych w Języku Angielskim im. Marii Goeppert Mayer I Ty możesz zostać noblistą Regulamin dla gimnazjalistów Organizator: I Liceum Ogólnokształcące im. Mikołaja
IX Regionalny Konkurs Zadań Interdyscyplinarnych w Języku Angielskim im. Marii Goeppert Mayer I Ty możesz zostać noblistą Regulamin dla gimnazjalistów Organizator: I Liceum Ogólnokształcące im. Mikołaja
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 2014
 MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
GAZETKA W ZESPOLE SZKÓŁ NR 91 W WARSZAWIE Rok szkolny 2014/15 Luty www: zssnr91.waw.pl
 GAZETKA W ZESPOLE SZKÓŁ NR 91 W WARSZAWIE Rok szkolny 2014/15 Luty www: zssnr91.waw.pl Wywiad z Panią Olą Pajączkowską, kierownikiem szkolnej akcji Zima w mieście 3 Dziennik Sylwii 4 Największe atrakcje
GAZETKA W ZESPOLE SZKÓŁ NR 91 W WARSZAWIE Rok szkolny 2014/15 Luty www: zssnr91.waw.pl Wywiad z Panią Olą Pajączkowską, kierownikiem szkolnej akcji Zima w mieście 3 Dziennik Sylwii 4 Największe atrakcje
Ewangelia wg św. Jana. Rozdział 1
 Ewangelia wg św. Jana Rozdział 1 Na początku było Słowo, a Słowo było u Boga, a Bogiem było Słowo. 2 Ono było na początku u Boga. 3 Wszystko przez Nie się stało, a bez Niego nic się nie stało, co się stało.
Ewangelia wg św. Jana Rozdział 1 Na początku było Słowo, a Słowo było u Boga, a Bogiem było Słowo. 2 Ono było na początku u Boga. 3 Wszystko przez Nie się stało, a bez Niego nic się nie stało, co się stało.
Harmonogram cyklu konkursów dla uczniów klas szóstych z terenu Gminy Jedlicze: r. poniedziałek min. troje z każdej szkoły
 Jedlicze, 30.01.2017 r. Szanowni Państwo Dyrektorzy i Nauczyciele szkół podstawowych Gimnazjum w Jedliczu serdecznie zaprasza uczniów Państwa szkoły do wzięcia udziału w konkursach organizowanych pod patronatem
Jedlicze, 30.01.2017 r. Szanowni Państwo Dyrektorzy i Nauczyciele szkół podstawowych Gimnazjum w Jedliczu serdecznie zaprasza uczniów Państwa szkoły do wzięcia udziału w konkursach organizowanych pod patronatem
Przygotowanie do SPRAWDZIANU w szóstej klasie ZESTAWY ZADAŃ
 Przygotowanie do SPRAWDZIANU w szóstej klasie ZESTAWY ZADAŃ Metoda 1 Najbardziej uniwersalna metoda polega na rozwiązaniu zadania tak, jakby było zadaniem otwartym (czyli bez podanych odpowiedzi do wyboru),
Przygotowanie do SPRAWDZIANU w szóstej klasie ZESTAWY ZADAŃ Metoda 1 Najbardziej uniwersalna metoda polega na rozwiązaniu zadania tak, jakby było zadaniem otwartym (czyli bez podanych odpowiedzi do wyboru),
Zeszyt odchudzania: Moja droga do sukcesu. czyli osiągnięcie wymarzonej figury
 Zeszyt odchudzania: Moja droga do sukcesu czyli osiągnięcie wymarzonej figury Pomysł i wykonanie: Barbara Łukowiak Jest to tylko fragment Zeszytu odchudzania Całość możesz pobrać po zapisaniu się na kurs
Zeszyt odchudzania: Moja droga do sukcesu czyli osiągnięcie wymarzonej figury Pomysł i wykonanie: Barbara Łukowiak Jest to tylko fragment Zeszytu odchudzania Całość możesz pobrać po zapisaniu się na kurs
Spis barier technicznych znajdziesz w Internecie. Wejdź na stronę www.mopr.poznan.pl
 1 Bariery techniczne to wszystko, co przeszkadza ci sprawnie funkcjonować w twoim środowisku i wśród ludzi. Bariery techniczne to również to, co przeszkadza, by inni mogli sprawnie się tobą opiekować.
1 Bariery techniczne to wszystko, co przeszkadza ci sprawnie funkcjonować w twoim środowisku i wśród ludzi. Bariery techniczne to również to, co przeszkadza, by inni mogli sprawnie się tobą opiekować.
Ćwiczenia do pobrania z Internetu
 Ćwiczenia do pobrania z Internetu wrzesień 2012 1 Prawo do edukacji Kalendarz na wrzesień Pokoloruj na czerwono wszystkie wrześniowe niedziele, a na zielono wszystkie środy. Wybranym kolorem zaznacz dzień,
Ćwiczenia do pobrania z Internetu wrzesień 2012 1 Prawo do edukacji Kalendarz na wrzesień Pokoloruj na czerwono wszystkie wrześniowe niedziele, a na zielono wszystkie środy. Wybranym kolorem zaznacz dzień,
Karta pracy 6. Jak było w szkole?
 Karta pracy 6 Jak było w szkole? Mini rozmowy 1 D:- Mam strasznie dużo lekcji na jutro a jestem bardzo zmęczony. R:- A co masz na jutro? D:- Musze przygotować się do testu z biologii z trzech działów i
Karta pracy 6 Jak było w szkole? Mini rozmowy 1 D:- Mam strasznie dużo lekcji na jutro a jestem bardzo zmęczony. R:- A co masz na jutro? D:- Musze przygotować się do testu z biologii z trzech działów i
Tekst łatwy do czytania. foto: Anna Olszak. Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier technicznych
 Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier technicznych Bariery techniczne to wszystko, co przeszkadza ci sprawnie funkcjonować
Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu sprzętu lub wykonania usług z zakresu likwidacji barier technicznych Bariery techniczne to wszystko, co przeszkadza ci sprawnie funkcjonować
PANGEA KONKURS MATEMATYCZNY
 ~ 1 ~ SP-4 PANGEA KONKURS MATEMATYCZNY Piątek, 28 marca 2014 Czas pracy: 90 minut Maksymalna liczba punktów do uzyskania: 120 W czasie testu nie wolno używać kalkulatorów ani innych pomocy naukowych. 1.
~ 1 ~ SP-4 PANGEA KONKURS MATEMATYCZNY Piątek, 28 marca 2014 Czas pracy: 90 minut Maksymalna liczba punktów do uzyskania: 120 W czasie testu nie wolno używać kalkulatorów ani innych pomocy naukowych. 1.
MATURA Przygotowanie do matury z matematyki
 MATURA 01 Przygotowanie do matury z matematyki Część III: Równania i nierówności ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej.
MATURA 01 Przygotowanie do matury z matematyki Część III: Równania i nierówności ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej.
Formularz zgłoszeniowy Przykłady dobrych praktyk w edukacji Dzielimy się doświadczeniami
 Formularz zgłoszeniowy Przykłady dobrych praktyk w edukacji Dzielimy się doświadczeniami Tytuł/nazwa projektu/przedsięwzięcia Nazwa szkoły/placówki Adres szkoły/placówki 1. miasto, gmina, powiat, ulica,
Formularz zgłoszeniowy Przykłady dobrych praktyk w edukacji Dzielimy się doświadczeniami Tytuł/nazwa projektu/przedsięwzięcia Nazwa szkoły/placówki Adres szkoły/placówki 1. miasto, gmina, powiat, ulica,
AKADEMIA KOMPETENCJI KLUCZOWYCH PROGRAM ROZWOJU UCZNIÓW SZKÓŁ PONADGIMNAZJALNYCH POLSKI WSCHODNIEJ PROJEKT REALIZOWANY PRZEZ:
 AKADEMIA KOMPETENCJI KLUCZOWYCH PROGRAM ROZWOJU UCZNIÓW SZKÓŁ PONADGIMNAZJALNYCH POLSKI WSCHODNIEJ PROJEKT REALIZOWANY PRZEZ: Bezpłatne zajęcia dodatkowe w Twojej szkole dowiedz się więcej!!!! Projekt
AKADEMIA KOMPETENCJI KLUCZOWYCH PROGRAM ROZWOJU UCZNIÓW SZKÓŁ PONADGIMNAZJALNYCH POLSKI WSCHODNIEJ PROJEKT REALIZOWANY PRZEZ: Bezpłatne zajęcia dodatkowe w Twojej szkole dowiedz się więcej!!!! Projekt
Wprowadzenie do logiki
 Czyli Wprowadzenie do logiki DZISIAJ Dowiemy się, czym zajmuje się logika formalna Na kilku przykładach zastanowimy się, po co warto się jej uczyć Dowiemy się, co trzeba zrobić, by zaliczyć ten przedmiot
Czyli Wprowadzenie do logiki DZISIAJ Dowiemy się, czym zajmuje się logika formalna Na kilku przykładach zastanowimy się, po co warto się jej uczyć Dowiemy się, co trzeba zrobić, by zaliczyć ten przedmiot
KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych 24 marca 2017 r. zawody III stopnia (wojewódzkie)
 Kod ucznia Liczba zdobytych punktów KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych 24 marca 2017 r. zawody III stopnia (wojewódzkie) Drogi Uczniu, przed Tobą test składający się z 24
Kod ucznia Liczba zdobytych punktów KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych 24 marca 2017 r. zawody III stopnia (wojewódzkie) Drogi Uczniu, przed Tobą test składający się z 24
Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum
 1 Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum Zagadnienia, które uczeń powinien znać przy rozwiązywaniu opisanych zadań: zastosowanie równań w zadaniach tekstowych, funkcje i ich monotoniczność,
1 Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum Zagadnienia, które uczeń powinien znać przy rozwiązywaniu opisanych zadań: zastosowanie równań w zadaniach tekstowych, funkcje i ich monotoniczność,
PONIEDZIAŁEK 16.02.2015 WTOREK 17.02.2015
 PONIEDZIAŁEK 16.02.2015 WTOREK 17.02.2015 ŚRODA 18.02.2015 CZWARTEK 19.02.2015 14.00-16.00 AQUAPARK: ZABAWY KOSMICZNE Z DZIEĆMI Z MUZYKĄ PIĄTEK 20.02.2015 SOBOTA 21.02.2015 NIEDZIELA 22.02.2015 PONIEDZIAŁEK
PONIEDZIAŁEK 16.02.2015 WTOREK 17.02.2015 ŚRODA 18.02.2015 CZWARTEK 19.02.2015 14.00-16.00 AQUAPARK: ZABAWY KOSMICZNE Z DZIEĆMI Z MUZYKĄ PIĄTEK 20.02.2015 SOBOTA 21.02.2015 NIEDZIELA 22.02.2015 PONIEDZIAŁEK
x 2 = a RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych 2. Proste równania kwadratowe Równanie kwadratowe typu:
 RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
Roger Bacon. Cele Konkursu:
 Liceum Ogólnokształcące im. mjra Henryka Sucharskiego w Sierpcu ogłasza IX edycję Międzygimnazjalnego Konkursu Matematycznego dla uczniów klas drugich i trzecich gimnazjów pod hasłem: Matematyka jest drzwiami
Liceum Ogólnokształcące im. mjra Henryka Sucharskiego w Sierpcu ogłasza IX edycję Międzygimnazjalnego Konkursu Matematycznego dla uczniów klas drugich i trzecich gimnazjów pod hasłem: Matematyka jest drzwiami
Sprawdzian kompetencji trzecioklasisty 2014
 Imię i nazwisko Klasa III Sprawdzian kompetencji trzecioklasisty 2014 Instrukcja dla ucznia Zestaw matematyczny Fotografia 1. Wpisz swoje imię i nazwisko oraz klasę. 2. Bardzo uważnie czytaj zadania i
Imię i nazwisko Klasa III Sprawdzian kompetencji trzecioklasisty 2014 Instrukcja dla ucznia Zestaw matematyczny Fotografia 1. Wpisz swoje imię i nazwisko oraz klasę. 2. Bardzo uważnie czytaj zadania i
Matematica Applicata
 PUBLICZNA SZKOŁA PODSTAWOWA nr 15 im. Jana Kochanowskiego 58 309 Wałbrzych, ul. Hirszfelda 1 tel. 074 841 51 89 sekretariat@psp15.edu.pl Widziałem dalej dzięki temu, że stałem na barkach gigantów. Izaak
PUBLICZNA SZKOŁA PODSTAWOWA nr 15 im. Jana Kochanowskiego 58 309 Wałbrzych, ul. Hirszfelda 1 tel. 074 841 51 89 sekretariat@psp15.edu.pl Widziałem dalej dzięki temu, że stałem na barkach gigantów. Izaak
Jak Arabowie rozwiązywali równania?
 Jak Arabowie rozwiązywali równania? Agnieszka Niemczynowicz Katedra Fizyki Relatywistycznej Uniwersytet Warmińsko-Mazurski w Olsztynie Niezwykła Matematyka 2016 Co to jest równanie? Kilka dygresji z logiki.
Jak Arabowie rozwiązywali równania? Agnieszka Niemczynowicz Katedra Fizyki Relatywistycznej Uniwersytet Warmińsko-Mazurski w Olsztynie Niezwykła Matematyka 2016 Co to jest równanie? Kilka dygresji z logiki.
KWESTIONARIUSZ DO POMIARU UMIĘTNOŚCI ROZWIĄZYWANIA PROBLEMÓW. Nazwa szkoły:. Imię i Nazwisko:.
 KWESTIONARIUSZ DO POMIARU UMIĘTNOŚCI ROZWIĄZYWANIA PROBLEMÓW Nazwa szkoły:. Imię i Nazwisko:. 1. Proszę wskazać tezę (wniosek) poniższego tekstu: Hrabia pan! zmienni w gustach są ludzie majętni! Hrabia
KWESTIONARIUSZ DO POMIARU UMIĘTNOŚCI ROZWIĄZYWANIA PROBLEMÓW Nazwa szkoły:. Imię i Nazwisko:. 1. Proszę wskazać tezę (wniosek) poniższego tekstu: Hrabia pan! zmienni w gustach są ludzie majętni! Hrabia
Najtrudniejsza Zagadka Świata
 Najtrudniejsza Zagadka Świata Sebastian Czerwiński muzg 1 grudnia 2005 Twórcy Raymond Smullyan John McCarthy Twórcy Raymond Smullyan John McCarthy The Harvard Review of Philosophy Raymond Smullyan Jaki
Najtrudniejsza Zagadka Świata Sebastian Czerwiński muzg 1 grudnia 2005 Twórcy Raymond Smullyan John McCarthy Twórcy Raymond Smullyan John McCarthy The Harvard Review of Philosophy Raymond Smullyan Jaki
KONSPEKT DO LEKCJI. Cele lekcji: ogólne:
 KONSPEKT DO LEKCJI Przedmiot: matematyka Temat: Rozwiązywanie zadań tekstowych z zastosowaniem równań. Klasa: III gimnazjum Prowadząca: mgr Julita Otok Obserwator: nauczyciele zespołu matematyczno - przyrodniczego
KONSPEKT DO LEKCJI Przedmiot: matematyka Temat: Rozwiązywanie zadań tekstowych z zastosowaniem równań. Klasa: III gimnazjum Prowadząca: mgr Julita Otok Obserwator: nauczyciele zespołu matematyczno - przyrodniczego
W ten dzień prowadziłem lekcję w dwóch klasach pierwszych.
 1.Przygotowanie Wybierając temat lekcji LDL kierowałem się moimi zainteresowaniami. Wybór nie mógł być inny niż sport. Znalazłem w Internecie nazwy różnych popularnych dyscyplin sportowych po polsku i
1.Przygotowanie Wybierając temat lekcji LDL kierowałem się moimi zainteresowaniami. Wybór nie mógł być inny niż sport. Znalazłem w Internecie nazwy różnych popularnych dyscyplin sportowych po polsku i
XVI MIĘDZYSZKOLONA LIGA PRZEDMIOTOWA PŁOCK 2010
 XVI MIĘDZYSZKOLONA LIGA PRZEDMIOTOWA PŁOCK 2010 ZADANIA KONKURSOWE Z EDUKACJI MATEMATYCZNEJ dla klas III szkoły podstawowej Opracowanie: mgr Władysława Paczesna 1 Zapraszamy Cię do wzięcia udziału w Międzyszkolnej
XVI MIĘDZYSZKOLONA LIGA PRZEDMIOTOWA PŁOCK 2010 ZADANIA KONKURSOWE Z EDUKACJI MATEMATYCZNEJ dla klas III szkoły podstawowej Opracowanie: mgr Władysława Paczesna 1 Zapraszamy Cię do wzięcia udziału w Międzyszkolnej
Szkolna Liga Matematyczna zestaw nr 3 dla klasy 3
 zestaw nr 3 dla klasy 3 W magazynie stoją dwa worki z ryżem. W pierwszym worku jest trzykrotnie więcej ryżu niż w drugim, a w drugim o 24 kg mniej niż w pierwszym. Ile ryżu znajduje się łącznie w obydwu
zestaw nr 3 dla klasy 3 W magazynie stoją dwa worki z ryżem. W pierwszym worku jest trzykrotnie więcej ryżu niż w drugim, a w drugim o 24 kg mniej niż w pierwszym. Ile ryżu znajduje się łącznie w obydwu
Oskar i pani Róża Karta pracy
 Oskar i pani Róża Karta pracy... / 49 Imię i nazwisko klasa data l-ba punktów ocena data sprawdzenia 1. Wypisz uczucia towarzyszące Ci podczas czytania listów Oskara. Podziel je na pozytywne i negatywne.
Oskar i pani Róża Karta pracy... / 49 Imię i nazwisko klasa data l-ba punktów ocena data sprawdzenia 1. Wypisz uczucia towarzyszące Ci podczas czytania listów Oskara. Podziel je na pozytywne i negatywne.
sprzętu rehabilitacyjnego Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu
 sprzętu rehabilitacyjnego Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu Sprzęt rehabilitacyjny to urządzenia, które pomogą ci wykonywać ćwiczenia konieczne do poprawy twojej sprawności
sprzętu rehabilitacyjnego Tekst łatwy do czytania foto: Anna Olszak Dofinansowanie zakupu Sprzęt rehabilitacyjny to urządzenia, które pomogą ci wykonywać ćwiczenia konieczne do poprawy twojej sprawności
XXI Konferencja SNM UKŁADY RÓWNAŃ. Kilka słów o układach równań.
 1 XXI Konferencja SNM UKŁADY RÓWNAŃ Piotr Drozdowski (Józefów), piotr.trufla@wp.pl Krzysztof Mostowski (Siedlce), kmostows@o.pl Kilka słów o układach równań. Streszczenie. 100 układów równań w 5 min, jak
1 XXI Konferencja SNM UKŁADY RÓWNAŃ Piotr Drozdowski (Józefów), piotr.trufla@wp.pl Krzysztof Mostowski (Siedlce), kmostows@o.pl Kilka słów o układach równań. Streszczenie. 100 układów równań w 5 min, jak
STARY TESTAMENT. GŁÓD W KANAAN 13. GŁÓD W KANAAN
 GŁÓD W KANAAN 63 W Kanaanie panował głód tak samo jak w Egipcie. Wtedy Jakub powiedział do swoich synów: - Idźcie do Egiptu i kupcie nam trochę jedzenia. Wyruszyli więc wszyscy synowie Jakuba do Egiptu
GŁÓD W KANAAN 63 W Kanaanie panował głód tak samo jak w Egipcie. Wtedy Jakub powiedział do swoich synów: - Idźcie do Egiptu i kupcie nam trochę jedzenia. Wyruszyli więc wszyscy synowie Jakuba do Egiptu
Akademia Zaruskiego III edycja r.szk.2016/2017 ODZNAKA MATEMATYK KLASY II-III
 Akademia Zaruskiego III edycja r.szk.2016/2017 ODZNAKA MATEMATYK KLASY II-III Uczeń starający się o odznakę matematyk powinien systematycznie wywiązywać się z prac i zadań matematycznych w ramach lekcji
Akademia Zaruskiego III edycja r.szk.2016/2017 ODZNAKA MATEMATYK KLASY II-III Uczeń starający się o odznakę matematyk powinien systematycznie wywiązywać się z prac i zadań matematycznych w ramach lekcji
Szkoła Specjalna nr 105 im. Juliana Tuwima w Poznaniu
 Gazetka szkolna - nr 4 ABeCaDło Rozwiąż rebus: Szkoła Specjalna nr 105 im. Juliana Tuwima w Poznaniu Powyższe słowa oznaczają, że rozpoczął się kolejny rok szkolny. Przed wami nowe wyzwania, trudne i radosne
Gazetka szkolna - nr 4 ABeCaDło Rozwiąż rebus: Szkoła Specjalna nr 105 im. Juliana Tuwima w Poznaniu Powyższe słowa oznaczają, że rozpoczął się kolejny rok szkolny. Przed wami nowe wyzwania, trudne i radosne
WPISUJE UCZEŃ. dzień miesiąc rok PRZYKŁADOWY ARKUSZ EGZAMINACYJNY W TRZECIEJ KLASIE GIMNAZJUM Z ZAKRESU MATEMATYKI. rrr KOTY1
 Przykładowy test Koty" WPISUJE UCZEŃ KOD UCZNIA DATA URODZENIA UCZNIA dzień miesiąc rok PRZYKŁADOWY ARKUSZ EGZAMINACYJNY W TRZECIEJ KLASIE GIMNAZJUM Z ZAKRESU MATEMATYKI rrr KOTY1 Instrukcja dia ucznia
Przykładowy test Koty" WPISUJE UCZEŃ KOD UCZNIA DATA URODZENIA UCZNIA dzień miesiąc rok PRZYKŁADOWY ARKUSZ EGZAMINACYJNY W TRZECIEJ KLASIE GIMNAZJUM Z ZAKRESU MATEMATYKI rrr KOTY1 Instrukcja dia ucznia
Matematyczna wieża Babel. 6. Nieskończoność i myślaki materiały do ćwiczeń
 Matematyczna wieża Babel. 6. Nieskończoność i myślaki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 23 maja 2019 1 Nieskończoność Zbiory A i B są równoliczne (co oznaczane
Matematyczna wieża Babel. 6. Nieskończoność i myślaki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 23 maja 2019 1 Nieskończoność Zbiory A i B są równoliczne (co oznaczane
Matura próbna klas III - harmonogram
 Matura próbna klas III - harmonogram DATA GODZINA PRZEDMIOT POZIOM UWAGI do organizacji pracy szkoły 13.02.2017r. (pon.) 14.02.2017r. (wt.) 11.20 (PP) 11.30 (PR) 8.15 10.45(PR) 11.00 13.00 (PP) język polski
Matura próbna klas III - harmonogram DATA GODZINA PRZEDMIOT POZIOM UWAGI do organizacji pracy szkoły 13.02.2017r. (pon.) 14.02.2017r. (wt.) 11.20 (PP) 11.30 (PR) 8.15 10.45(PR) 11.00 13.00 (PP) język polski
Zadanie 3.
 ł ą ł ę łę ó ź ą śń ÓŻ Ś Ó ę Ó Ó Śń Ó ą ą Ł Ó Ć Ć Ć Ć Ó Zadanie 3 http://www.sheppardsoftware.com/mathgames/numbertwins/numbertwins_add_14.htm Zadanie pochodzi z konkursu Matematyka bez granic Kółka na
ł ą ł ę łę ó ź ą śń ÓŻ Ś Ó ę Ó Ó Śń Ó ą ą Ł Ó Ć Ć Ć Ć Ó Zadanie 3 http://www.sheppardsoftware.com/mathgames/numbertwins/numbertwins_add_14.htm Zadanie pochodzi z konkursu Matematyka bez granic Kółka na
Konspekt do lekcji matematyki dn w klasie IIIa Gimnazjum nr 7 w Rzeszowie.
 Monika Łokaj III Matematyka (licencjat) Konspekt do lekcji matematyki dn. 6.01.2006 w klasie IIIa Gimnazjum nr 7 w Rzeszowie. Nauczyciel: Prowadzący: Monika Łokaj Temat lekcji: Rozwiązywanie zadań tekstowych
Monika Łokaj III Matematyka (licencjat) Konspekt do lekcji matematyki dn. 6.01.2006 w klasie IIIa Gimnazjum nr 7 w Rzeszowie. Nauczyciel: Prowadzący: Monika Łokaj Temat lekcji: Rozwiązywanie zadań tekstowych
I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 28 kwietnia 2003
 I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 8 kwietnia 003 W tym konkursie nie ma przegranych. To, że tu jesteś, jest już Twoim sukcesem. Więc Jeśli zadanie wydaje
I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 8 kwietnia 003 W tym konkursie nie ma przegranych. To, że tu jesteś, jest już Twoim sukcesem. Więc Jeśli zadanie wydaje
Oto przykład konspektu lekcji jaką przeprowadziłam w klasie pierwszej gimnazjum.
 Metody aktywizujące na lekcjach matematyki. Przygotowując lekcje matematyki staram się tak dobrać metody pracy, żebybyłyone atrakcyjne dla ucznia oraz zachęcały do intensywnej nauki. Podczas lekcji utrwalających
Metody aktywizujące na lekcjach matematyki. Przygotowując lekcje matematyki staram się tak dobrać metody pracy, żebybyłyone atrakcyjne dla ucznia oraz zachęcały do intensywnej nauki. Podczas lekcji utrwalających
Matematyka test dla uczniów klas drugich
 Matematyka test dla uczniów klas drugich gimnazjów w roku szkolnym 2011/20 Etap szkolny (60 minut) Dysleksja [suma punktów] Imię i nazwisko kl... Zadanie 1. Liczba 5 1, 75 jest równa liczbie 6 7 1 A. 2
Matematyka test dla uczniów klas drugich gimnazjów w roku szkolnym 2011/20 Etap szkolny (60 minut) Dysleksja [suma punktów] Imię i nazwisko kl... Zadanie 1. Liczba 5 1, 75 jest równa liczbie 6 7 1 A. 2
Zajęcia nr. 6: Równania i układy równań liniowych
 Zajęcia nr. 6: Równania i układy równań liniowych 13 maja 2005 1 Podstawowe pojęcia. Definicja 1.1 (równanie liniowe). Równaniem liniowym będziemy nazwyać równanie postaci: ax = b, gdzie x oznacza niewiadomą,
Zajęcia nr. 6: Równania i układy równań liniowych 13 maja 2005 1 Podstawowe pojęcia. Definicja 1.1 (równanie liniowe). Równaniem liniowym będziemy nazwyać równanie postaci: ax = b, gdzie x oznacza niewiadomą,
REGULAMIN POWIATOWEGO KONKURSU INTERDYSCYPLINARNEGO DLA UCZNIÓW GIMNAZJÓW POWIATU LUBACZOWSKIEGO NA ROK SZKOLNY 2011/2012
 REGULAMIN POWIATOWEGO KONKURSU INTERDYSCYPLINARNEGO DLA UCZNIÓW GIMNAZJÓW POWIATU LUBACZOWSKIEGO NA ROK SZKOLNY 2011/2012 (wersja elektroniczna do pobrania ze strony internetowej Zespołu Szkół w Lubaczowie)
REGULAMIN POWIATOWEGO KONKURSU INTERDYSCYPLINARNEGO DLA UCZNIÓW GIMNAZJÓW POWIATU LUBACZOWSKIEGO NA ROK SZKOLNY 2011/2012 (wersja elektroniczna do pobrania ze strony internetowej Zespołu Szkół w Lubaczowie)
Uzupełnij zdania. Wybierz liczbę spośród oznaczonych literami A i B oraz liczbę spośród oznaczonych literami C i D.
 Zadanie 14. (0 1) Dokończ zdanie wybierz odpowiedź spośród podanych. Iloczyn liczb 25,4 i 33,4 jest równy iloczynowi liczb A. 2,54 i 33,4 B. 25,4 i 334 C. 2,54 i 3,34 D. 254 i 3,34 Zadanie 15. (0 1) Na
Zadanie 14. (0 1) Dokończ zdanie wybierz odpowiedź spośród podanych. Iloczyn liczb 25,4 i 33,4 jest równy iloczynowi liczb A. 2,54 i 33,4 B. 25,4 i 334 C. 2,54 i 3,34 D. 254 i 3,34 Zadanie 15. (0 1) Na
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 3 Definicja prawdopodobieństwa Kołmogorowa. Prawdopodobieństwa warunkowe i niezależne. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko
KURS PRAWDOPODOBIEŃSTWO Lekcja 3 Definicja prawdopodobieństwa Kołmogorowa. Prawdopodobieństwa warunkowe i niezależne. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko
Gdyńscy uczniowie walczyli na słowa i argumenty
 Gdyńscy uczniowie walczyli na słowa i argumenty Najpierw 60 uczniów z 6 gdyńskich szkół przez miesiąc uczyło się, jak dobrze się prezentować i wypowiadać. Potem dyskutowali ze sobą na zadane tematy i rozmawiali
Gdyńscy uczniowie walczyli na słowa i argumenty Najpierw 60 uczniów z 6 gdyńskich szkół przez miesiąc uczyło się, jak dobrze się prezentować i wypowiadać. Potem dyskutowali ze sobą na zadane tematy i rozmawiali
Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego
 Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA Publikacja
Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA Publikacja
PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa VI marzec 2015
 PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa VI marzec 205 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa VI marzec 205 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
Instrukcja dla ucznia
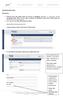 Instrukcja dla ucznia Rejestracja 1. Pierwszą rzecz jaką należy zrobić po wejściu na platformę Mermidon, to utworzenie swojego prywatnego konta. Proces ten nie różni się zbytnio od zakładania konta poczty
Instrukcja dla ucznia Rejestracja 1. Pierwszą rzecz jaką należy zrobić po wejściu na platformę Mermidon, to utworzenie swojego prywatnego konta. Proces ten nie różni się zbytnio od zakładania konta poczty
KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych województwa lubuskiego 23 lutego 2013 r. zawody III stopnia (wojewódzkie)
 Kod ucznia Ilość zdobytych punktów KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych województwa lubuskiego 23 lutego 2013 r. zawody III stopnia (wojewódzkie) Drogi Uczniu, przed Tobą test
Kod ucznia Ilość zdobytych punktów KONKURS PRZEDMIOTOWY Z MATEMATYKI dla uczniów szkół podstawowych województwa lubuskiego 23 lutego 2013 r. zawody III stopnia (wojewódzkie) Drogi Uczniu, przed Tobą test
I Łukowski Turniej Szkół Gimnazjalnych "SUDOKU 2011"
 "Suuji wa dokushin ni kagiru - liczby muszą pozostać samotne" I Łukowski Turniej Szkół Gimnazjalnych "SUDOKU 2011" Spis treści: 1. Organizator Turnieju 2. Patronat i sponsorzy Turnieju 3. Cele Turnieju
"Suuji wa dokushin ni kagiru - liczby muszą pozostać samotne" I Łukowski Turniej Szkół Gimnazjalnych "SUDOKU 2011" Spis treści: 1. Organizator Turnieju 2. Patronat i sponsorzy Turnieju 3. Cele Turnieju
POTRENUJ PRZED KONKURSEM
 POTRENUJ PRZED KONKURSEM POTYCZKI MATEMATYCZNE Konkurs matematyczny przeznaczony dla klas VI VII Szkoły Podstawowej Zadania logiczne 1. Zasady rozgrywania turnieju piłkarskiego, w którym uczestniczą cztery
POTRENUJ PRZED KONKURSEM POTYCZKI MATEMATYCZNE Konkurs matematyczny przeznaczony dla klas VI VII Szkoły Podstawowej Zadania logiczne 1. Zasady rozgrywania turnieju piłkarskiego, w którym uczestniczą cztery
Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym
 Edward Stachowski Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym W podstawie programowej obowiązującej na egzaminie maturalnym od 05r pojawiły się nowe treści programowe Wśród
Edward Stachowski Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym W podstawie programowej obowiązującej na egzaminie maturalnym od 05r pojawiły się nowe treści programowe Wśród
Lekcja 9 Charakter, osobowość
 Lekcja 9 Charakter, osobowość 2 Wysłuchaj słówek i zwrotów wraz z ich polskim tłumaczeniem, powtarzaj je za lektorem. Następnie wysłuchaj zdań ilustrujących ich prawidłowe użycie. niezależny (-a) W wieku
Lekcja 9 Charakter, osobowość 2 Wysłuchaj słówek i zwrotów wraz z ich polskim tłumaczeniem, powtarzaj je za lektorem. Następnie wysłuchaj zdań ilustrujących ich prawidłowe użycie. niezależny (-a) W wieku
SPRAWDZIAN W SZÓSTEJ KLASIE SZKOŁY PODSTAWOWEJ
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia sprawdzianu! UZUPEŁNIA ZESPÓŁ NADZORUJĄCY KOD UCZNIA DATA URODZENIA UCZNIA dzień miesiąc rok miejsce na naklejkę z kodem SPRAWDZIAN W
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia sprawdzianu! UZUPEŁNIA ZESPÓŁ NADZORUJĄCY KOD UCZNIA DATA URODZENIA UCZNIA dzień miesiąc rok miejsce na naklejkę z kodem SPRAWDZIAN W
Regulamin II Turniej Wiedzy "Matematycznie kreatywni"
 Regulamin II Turniej Wiedzy "Matematycznie kreatywni" Organizator Organizatorem turnieju jest Liceum Ogólnokształcące im. Komisji Edukacji Narodowej w Dynowie. Cele konkursu: popularyzacja wiedzy i umiejętności
Regulamin II Turniej Wiedzy "Matematycznie kreatywni" Organizator Organizatorem turnieju jest Liceum Ogólnokształcące im. Komisji Edukacji Narodowej w Dynowie. Cele konkursu: popularyzacja wiedzy i umiejętności
REGULAMIN SZKOLNEGO KONKURSU MATEMATYCZNEGO DLA KLASY TRZECIEJ
 REGULAMIN SZKOLNEGO KONKURSU MATEMATYCZNEGO DLA KLASY TRZECIEJ Szkolny konkurs matematyczny zostaje ogłoszony wcześniej na apelu szkolnym. Organizator wywiesza również informację na tablicy ogłoszeń o
REGULAMIN SZKOLNEGO KONKURSU MATEMATYCZNEGO DLA KLASY TRZECIEJ Szkolny konkurs matematyczny zostaje ogłoszony wcześniej na apelu szkolnym. Organizator wywiesza również informację na tablicy ogłoszeń o
Wstęp do logiki. Pytania i odpowiedzi
 Wstęp do logiki Pytania i odpowiedzi 1 Pojęcie pytania i odpowiedzi DEF. 1. Pytanie to wyrażenie, które wskazuje na pewien brak w wiedzy subiektywnej lub obiektywnej i wskazuje na dążenie do uzupełnienia
Wstęp do logiki Pytania i odpowiedzi 1 Pojęcie pytania i odpowiedzi DEF. 1. Pytanie to wyrażenie, które wskazuje na pewien brak w wiedzy subiektywnej lub obiektywnej i wskazuje na dążenie do uzupełnienia
JEZYKOZNAWSTWO. I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca Imię i Nazwisko:... I
 JEZYKOZNAWSTWO I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca 2013 Imię i Nazwisko:.................................................................................. I Wybierz
JEZYKOZNAWSTWO I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca 2013 Imię i Nazwisko:.................................................................................. I Wybierz
5. OKREŚLANIE WARTOŚCI LOGICZNEJ ZDAŃ ZŁOŻONYCH
 5. OKREŚLANIE WARTOŚCI LOGICZNEJ ZDAŃ ZŁOŻONYCH Temat, którym mamy się tu zająć, jest nudny i żmudny będziemy się uczyć techniki obliczania wartości logicznej zdań dowolnie złożonych. Po co? możecie zapytać.
5. OKREŚLANIE WARTOŚCI LOGICZNEJ ZDAŃ ZŁOŻONYCH Temat, którym mamy się tu zająć, jest nudny i żmudny będziemy się uczyć techniki obliczania wartości logicznej zdań dowolnie złożonych. Po co? możecie zapytać.
Regulamin. Międzyszkolnego Konkursu Języków Obcych MISTRZ GRAMATYKI EDYCJA V
 Regulamin Międzyszkolnego Konkursu Języków Obcych MISTRZ GRAMATYKI EDYCJA V 1. Organizatorem Międzyszkolnego Konkursu Języków Obcych Mistrz Gramatyki jest Zespół Szkół Ponadgimnazjalnych Centrum Kształcenia
Regulamin Międzyszkolnego Konkursu Języków Obcych MISTRZ GRAMATYKI EDYCJA V 1. Organizatorem Międzyszkolnego Konkursu Języków Obcych Mistrz Gramatyki jest Zespół Szkół Ponadgimnazjalnych Centrum Kształcenia
24 proste kroki. aby pokonac. Obrazki. logiczne. Rozwiazania. i wskazowki dla nauczyciela. Copyright Logi Urszula Marciniak 2015
 proste kroki / aby pokonac Obrazki logiczne Rozwiazania / i wskazowki dla nauczyciela Copyright Logi Urszula Marciniak 0 Szanowni Państwo Niniejsza książeczka przeznaczona jest dla osób, które nigdy nie
proste kroki / aby pokonac Obrazki logiczne Rozwiazania / i wskazowki dla nauczyciela Copyright Logi Urszula Marciniak 0 Szanowni Państwo Niniejsza książeczka przeznaczona jest dla osób, które nigdy nie
Zadania z 12 stacji zadaniowych w projekcie Matematyczne Śledztwo
 Zadania z stacji zadaniowych w projekcie Matematyczne Śledztwo Zadanie Poniżej jest przedstawiona kartka z kalendarza. Odpowiedzcie na wszystkie pytania. Niedziela Poniedziałek Wtorek Środa Czwartek Piątek
Zadania z stacji zadaniowych w projekcie Matematyczne Śledztwo Zadanie Poniżej jest przedstawiona kartka z kalendarza. Odpowiedzcie na wszystkie pytania. Niedziela Poniedziałek Wtorek Środa Czwartek Piątek
Założenia Jurajskiej Ligi Wiedzy
 Założenia Jurajskiej Ligi Wiedzy 1. Celem Jurajskiej Ligi Wiedzy jest budzenie i rozwijanie zainteresowań z zakresu przedmiotów matematyczno przyrodniczych humanistycznych uczniów klas IV VI szkoły podstawowej.
Założenia Jurajskiej Ligi Wiedzy 1. Celem Jurajskiej Ligi Wiedzy jest budzenie i rozwijanie zainteresowań z zakresu przedmiotów matematyczno przyrodniczych humanistycznych uczniów klas IV VI szkoły podstawowej.
Wymaganie nr 2 - Procesy edukacyjne są zorganizowane w sposób sprzyjający uczeniu się
 EWALUACJA POZIOMU SPEŁNIANIA WYMAGANIA 2 Procesy edukacyjne są zorganizowane w sposób sprzyjający uczeniu się Gimnazjum nr 8 im. Królowej Jadwigi w ZSO nr 3 w Katowicach maj 2017 Wymaganie nr 2 - Procesy
EWALUACJA POZIOMU SPEŁNIANIA WYMAGANIA 2 Procesy edukacyjne są zorganizowane w sposób sprzyjający uczeniu się Gimnazjum nr 8 im. Królowej Jadwigi w ZSO nr 3 w Katowicach maj 2017 Wymaganie nr 2 - Procesy
Zadania QR na Dzień Matematyki 2017
 Zadania QR na Dzień Matematyki 2017 Zadanie 1. Kuba miał 21zł. Postanowił wrzucić je do trzech skarbonek, tak aby w drugiej było dwa razy więcej pieniędzy niż w pierwszej, a w trzeciej dwa razy więcej
Zadania QR na Dzień Matematyki 2017 Zadanie 1. Kuba miał 21zł. Postanowił wrzucić je do trzech skarbonek, tak aby w drugiej było dwa razy więcej pieniędzy niż w pierwszej, a w trzeciej dwa razy więcej
Gazetka klasy I a. Numer 1 Jesień Collegium Gostomianum
 Gazetka klasy I a Numer 1 Jesień 018 Collegium Gostomianum Rok 018 wyznacza rocznicę szczególną jest to bowiem już setna rocznica odzyskania przez Polskę niepodległości. Odbudowa państwowości, po 13 latach
Gazetka klasy I a Numer 1 Jesień 018 Collegium Gostomianum Rok 018 wyznacza rocznicę szczególną jest to bowiem już setna rocznica odzyskania przez Polskę niepodległości. Odbudowa państwowości, po 13 latach
WYBUCHAJĄCE KROPKI ROZDZIAŁ 1 MASZYNY
 WYBUCHAJĄCE KROPKI ROZDZIAŁ 1 MASZYNY Witaj w podróży. Jest to podróż matematyczna oparta na historii mojej, Jamesa, która jednak nie wydarzyła się naprawdę. Kiedy byłem dzieckiem, wynalazłem maszynę -
WYBUCHAJĄCE KROPKI ROZDZIAŁ 1 MASZYNY Witaj w podróży. Jest to podróż matematyczna oparta na historii mojej, Jamesa, która jednak nie wydarzyła się naprawdę. Kiedy byłem dzieckiem, wynalazłem maszynę -
22+d+e marca, gdy d+e 9. d+e-9 kwietnia, gdy d+e>9
 KIEDY WIELKANOC Jak podają Ewangelie - Jezus zmartwychwstał w niedzielę rano podczas żydowskiego święta Paschy, obchodzonego zawsze po pierwszej wiosennej pełni księżyca. Chrześcijanie postanowili zachować
KIEDY WIELKANOC Jak podają Ewangelie - Jezus zmartwychwstał w niedzielę rano podczas żydowskiego święta Paschy, obchodzonego zawsze po pierwszej wiosennej pełni księżyca. Chrześcijanie postanowili zachować
Ziemia obraca się wokół Księżyca, bo posiadając odpowiednią wiedzę można stwierdzić, czy są prawdziwe, czy fałszywe. Zdaniami nie są wypowiedzi:
 1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
Kalendarz roku szkolnego 2015/2016. w Zespole Szkół w Choroszczy
 Kalendarz roku szkolnego 2015/2016 w Zespole Szkół w Choroszczy Szkoła Podstawowa im. Henryka Sienkiewicza Publiczne Gimnazjum im. Ks. Kard. Stefana Wyszyńskiego Publiczne Liceum Ogólnokształcące Wrzesień
Kalendarz roku szkolnego 2015/2016 w Zespole Szkół w Choroszczy Szkoła Podstawowa im. Henryka Sienkiewicza Publiczne Gimnazjum im. Ks. Kard. Stefana Wyszyńskiego Publiczne Liceum Ogólnokształcące Wrzesień
Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki
 0 1 Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki 2. W następujących dwóch prawach wyróżnić wyrażenia specyficznie matematyczne i wyrażenia z zakresu logiki (do
0 1 Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki 2. W następujących dwóch prawach wyróżnić wyrażenia specyficznie matematyczne i wyrażenia z zakresu logiki (do
dla najmłodszych. 8. polska wersja: naukapoprzezzabawe.wordpress.com
 dla najmłodszych 8 polska wersja: naukapoprzezzabawewordpresscom Prawdomównosc `` Mówienie prawdy to bardzo dobry zwyczaj Jeśli zawsze mówimy prawdę, chronimy się przed wieloma kłopotami Oto opowieść o
dla najmłodszych 8 polska wersja: naukapoprzezzabawewordpresscom Prawdomównosc `` Mówienie prawdy to bardzo dobry zwyczaj Jeśli zawsze mówimy prawdę, chronimy się przed wieloma kłopotami Oto opowieść o
dla najmłodszych. 8. polska wersja: naukapoprzezzabawe.wordpress.com
 dla najmłodszych 8 polska wersja: naukapoprzezzabawewordpresscom Prawdomównosc Mówienie prawdy to bardzo dobry zwyczaj Jeśli zawsze mówimy prawdę, chronimy się przed wieloma kłopotami Oto opowieść o kimś,
dla najmłodszych 8 polska wersja: naukapoprzezzabawewordpresscom Prawdomównosc Mówienie prawdy to bardzo dobry zwyczaj Jeśli zawsze mówimy prawdę, chronimy się przed wieloma kłopotami Oto opowieść o kimś,
V MEGAOLIMPIADA WIEDZY pod patronatem Pomorskiego Kuratorium Oświaty oraz Gazety Wyborczej
 Gdańskie Gimnazjum LINGWISTA 80-107 Gdańsk, ul. Malczewskiego 51, tel. (58) 303 30 30 e-mail: gimnazjum@oswiatalingwista.eu www.gimnazjum-lingwista.eu ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Gdańskie Gimnazjum LINGWISTA 80-107 Gdańsk, ul. Malczewskiego 51, tel. (58) 303 30 30 e-mail: gimnazjum@oswiatalingwista.eu www.gimnazjum-lingwista.eu ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Matematyka test dla uczniów klas piątych
 Matematyka test dla uczniów klas piątych szkół podstawowych w roku szkolnym 2010/2011 Etap międzyszkolny (60 minut) [suma punktów]..... Imię i nazwisko Nazwa (numer) szkoły, miejscowość W sklepie sportowym
Matematyka test dla uczniów klas piątych szkół podstawowych w roku szkolnym 2010/2011 Etap międzyszkolny (60 minut) [suma punktów]..... Imię i nazwisko Nazwa (numer) szkoły, miejscowość W sklepie sportowym
