ODWZOROWANIA MIĘDZYONTOLOGICZNE W ALGEBRZE KONGLOMERATÓW 1
|
|
|
- Emilia Olszewska
- 6 lat temu
- Przeglądów:
Transkrypt
1 STUDIA INFORMATICA 2012 Volume 33 Number 2A (105) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki ODWZOROWANIA MIĘDZYONTOLOGICZNE W ALGEBRZE KONGLOMERATÓW 1 Streszczenie. Modularyzacja i integracja ontologii to dziedziny, które w ostatnim okresie są obiektem intensywnego rozwoju. Rozwój nowych idei spowodował konieczność wprowadzenia ich systematyzacji i klasyfikacji. W niniejszym artykule przeanalizowano możliwość wyrażenia odwzorowań i złączeń za pomocą algebry konglomeratów oraz przedyskutowano możliwość wykorzystania roli algebry jako ujednoliconego medium opisu metod integracji i modularyzacji. Słowa kluczowe: ontologie, bazy wiedzy, modularyzacja, integracja, logika opisowa INTER-ONTOLOGICAL MAPPINGS IN THE ALGEBRA OF CONGLOMERATES Summary. Modularization and integration of ontologies are domains that are recently of great interest among researchers in the domain of Semantic Web. In the paper we analyze the possibility of expressing two main branches of methods: mappings and links by means of s-module algebra and discuss possibility of using the algebra as a uniform medium of description of such methods. Keywords: ontologies, knowledge bases, description logics, modularization, integration 1 Praca częściowo finansowana z funduszy NCBiR, grant nr SP/I/1/77065/10, projekt SYNAT.
2 330 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka 1. Wprowadzenie Możliwość ponownego użycia ontologii jest jednym z postulatów, który stanowi podstawę Semantycznego Internetu oraz daje nadzieję na coraz szersze zastosowanie metod opartych na wiedzy w codziennej praktyce inżyniera informatyka. Niestety okazuje się, że w wielu przypadkach wykorzystanie wprost istniejącej ontologii nie spełnia oczekiwań. Konieczne staje się stosowanie bardziej zaawansowanych sposobów sięgania do wiedzy raz opisanej przez innych. Dostrzeżenie tego zjawiska zaowocowało utworzeniem wielu technik. Wciąż dość powszechne jest podejście oparte na importowaniu istniejących ontologii. W najprostszym wariancie, wykorzystanym np. w podstawowej wersji języka OWL [1], import polega na traktowaniu wszystkich zdań i terminów ontologii importowanej tak, jakby były częścią ontologii importującej. W bardziej zaawansowanych wariantach (jak np. w propozycji wypracowanej w trakcie projektu NeOn [2] oraz w systemie P-DL [3]) ontologie importowane są przy użyciu tzw. interfejsów, które specyfikują publiczne (tj. możliwe do zaimportowania i wykorzystania) i prywatne części ontologii. Niezależnie od metod importu wypracowano również alternatywne rozwiązania, pozwalające na zachowanie większej kontroli nad pozyskiwaną zawartością. Jedną z najbardziej znanych metod jest odwzorowanie przez wykorzystanie reguł DDL ([4]; ang. Distributed Description Logics). Pozyskiwanie istniejącej wiedzy polega na sformułowaniu zestawu tzw. reguł pomostowych, opisujących zależności pomiędzy terminami 2 w ontologii źródłowej a terminami w ontologii docelowej (tworzonej przez użytkownika). Inną bardzo znaną metodą jest wykorzystanie złączeń proponowanych w ramach podejścia -Connections [5]. Tutaj do typowych części ontologii zapisanej w logice opisowej dodawany jest tzw. LBox, określający role, które łączą ze sobą osobniki z dwu ontologii. Przyjmowane jest przy tym założenie, że łączone ontologie opisują parami rozłączne dziedziny problemowe. Ogranicza to zakres stosowania metody, ale sprawia, że można przeprowadzić ścisłe rozgraniczenie pomiędzy tradycyjnymi rolami a rolami łączącymi. Przedstawione rozróżnienie pomiędzy importem, odwzorowaniem i złączeniem pochodzi z pracy [6]. Wskazano tam na znaczące różnice pomiędzy wymienionymi podejściami i konieczność podjęcia bardziej systematycznych studiów porównawczych. W niniejszym artykule podjęto temat wskazany w [6] przez próbę opisu odwzorowań (DDL) i złączeń ( -Connections) za pomocą algebry konglomeratów. Algebra ta, prezentowana we wcześniejszych pracach, stanowi narzędzie pozwalające na jednoznaczny i stosunkowo jednolity sposób zależności semantycznych pomiędzy modułami. Przeprowadzone 2 Dokładniej: zakresami terminów.
3 Odwzorowania międzyontologiczne w algebrze konglomeratów 331 studium pozwala na wskazanie ciekawych związków pomiędzy porównywanymi metodami, a także na sformułowanie wniosków dotyczących przyszłego rozwoju algebry. Pozostała część artykułu zorganizowana jest w następujący sposób. W rozdziale 2 przytoczono podstawy algebry konglomeratów, kładąc nacisk na operacje wykorzystane w dalszej części artykułu. W rozdziale 3 podjęto problem opisu DDL za pomocą działań algebry konglomeratów. W rozdziale 4 dokonano analizy możliwości wyrażenia złączeń za pomocą tej algebry, a rozdział 5 zawiera wnioski i podsumowanie oraz wskazuje kierunki dalszych prac. 2. Algebra konglomeratów Podejście konglomeratowe zostało zdefiniowane i opisane w [7]. W niniejszym rozdziale przytoczone zostaną tylko najważniejsze definicje i pojęcia. W logice opisowej przyjmuje się, że mamy do czynienia z trzema rodzajami nazw: osobniki nazywają elementy dziedziny, a koncepty i role to predykaty unarne i binarne. Każda sygnatura (słownik) S jest więc zbiorem nazw osobników, konceptów i ról i stanowi podzbiór sygnatury pełnej, zawierającej wszystkie dopuszczalne nazwy tych trzech rodzajów. Nazwy mogą być interpretowane, a każda interpretacja (bazowa) jest parą (, ) składającą się z dziedziny i funkcji interpretacyjnej przypisującej osobnikom, konceptom i rolom odpowiednio elementy, podzbiory i zbiory par elementów. Dla uproszczenia formalizmu warto przyjąć, że każda interpretacja bazowa interpretuje wszystkie terminy z. Na interpretacjach można wykonać dwa ważne działania: projekcję i przycięcie. Projekcja S polega na ograniczeniu interpretacji tylko do zadanego słownika S, przy czym ograniczenie to jest rozumiane dość specyficznie: wynikiem działania jest tu zbiór interpretacji, które przypisują terminom spoza S dowolne możliwe zakresy, a zakresy terminów z S pozostawiają niezmienione: S = { : = X S: X = X }. Z kolei przycięcie interpretacji polega na ograniczeniu jej dziedziny do pewnego podzbioru ; podobną operację przeprowadza się na zakresach terminów: S =, = S, X : X = X S. Konglomerat jest pojęciem oznaczającym moduł ontologiczny, ale rozumiany ściśle semantycznie, wyłącznie przez pryzmaty słownika i interpretacji. Definicja 1 (konglomerat): Konglomeratem K nazywamy parę (S, W), gdzie S jest sygnaturą, a W zbiorem interpretacji bazowych, takich że W S = W. Każdą interpretację z W nazywamy modelem K. W dalszej części artykułu zapisy S(M) i W(M) oznaczają odpowiednio sygnaturę i zbiór modeli danego konglomeratu M.
4 332 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka Dla każdej ontologii, rozumianej jako zbiór zdań w logice opisowej, można zbudować konglomerat M( ) taki, że S(M( )) obejmuje wszystkie terminy z, a W(M( )) = { : }. Chociaż M( ) pamięta semantykę ontologii, zapomina dokładną postać zdań, np. M({A B}) = M({A A B}). Na konglomeratach można wykonywać wiele operacji (M i L to dowolne konglomeraty, S oznacza dowolną sygnaturę, funkcję ( ) ( ), a C dowolny koncept z S(M)): M L=(S(M) S(L), W(M) W(L)) M L=(S(M) S(L), W(M) W(L)) M L=(S(M) S(L), W(M) W(L)) (M) =( (S(M)), { = (, ): W(M): S(M)=(S, W(M) S) = X : (X) = X }) L C M=(S(L) S(M), { W(M): C W(L)}) C(M)=(S(M), { C : W(M)}) Operacje przecięcia ( ), projekcji ( ) i przemianowania ( ) pozwalają na dokonanie importu wiedzy pomiędzy modułami. Przecięcie reprezentuje najprostszy sposób importu, jako że M( 1 ) M( 2 ) = M( 1 2 ). Import tylko części terminów możliwy jest dzięki projekcji, która ogranicza słownik konglomeratu, w przypadku konfliktu nazw można zaś posłużyć się operacją przemianowania. Przykład 1: Załóżmy, że do ontologii 1 = {Samochód ObiektUbezpieczenia} chcemy zaimportować elementy ontologii 2 = {Osobowy Pojazd, Sedan Osobowy, Hatchback Osobowy}. Jednak termin Pojazd chcemy odrzucić jako zbyt ogólny, koncept Osobowy zaś utożsamić z konceptem Samochód. Odpowiedni konglomerat spełniający te wymagania można skonstruować jako: M = M( 1 ) S - Pojazd( Osobowy Samochód (M( 2 ))). W przedstawionym przykładzie wykorzystano kilka skrótów notacyjnych, które będą wykorzystywane w dalszej części artykułu: przez A B rozumiemy dla funkcji, która zamienia jedynie termin A na B, pozostawiając pozostałe terminy niezmienione (czasami używana jest też notacja z wzorcami nazw, np. * 1:*), natomiast przez S - X(M) rozumiemy S(M) - {X}(M). Operacje unii ( ) i różnicy ( ) dopełniają zbiór działań do algebry Boole a. Z kolei operacja wchłonięcia ( C ) pozwala na zastosowanie zależności pomiędzy terminami ze źródłowego konglomeratu L, ale tylko w podzbiorze dziedziny docelowego konglomeratu M. Wraz z komplementarną operacją ograniczenia ( C ) wchłonięcie wprowadza do algebry środki operowania na dziedzinie (co będzie bardzo ważne w kolejnych rozdziałach). Dodatkowo w [7] wprowadzono także operację selekcji. Tutaj zostanie ona potraktowana jako pewien skrót notacyjny, jako że według przyjętych założeń (M) = M M( ).
5 Odwzorowania międzyontologiczne w algebrze konglomeratów Wyrażanie odwzorowań za pomocą algebry konglomeratów W niniejszym rozdziale opisano zagadnienie wyrażenia odwzorowań ontologicznych za pomocą algebry konglomeratów. Jako metodę odwzorowań przyjęto tutaj DDL, który opisany został w podrozdziale 3.1. Kolejne podrozdziały prezentują metody tłumaczenia coraz bardziej ekspresywnych wariantów DDL na wyrażenia algebry. Końcowy podrozdział 3.4 zawiera podsumowanie rozważań Wprowadzenie do DDL DDL (ang. Distributed Description Logics) to jedna z najszerzej znanych metod łączenia modułów ontologicznych. Zaproponowana w 2003 roku przez Borgidę i Serafiniego [4], była później rozszerzona i adaptowana w wielu pracach (m.in. [8]). Niniejszy podrozdział prezentuje metodę w uaktualnionej, współczesnej wersji (głównie na podstawie [9]), w której mówi się raczej o rodzinie logik DDL. Logiki DDL koncentrują się na odwzorowywaniu zakresów terminów z jednego modułu ontologicznego na odpowiednie zakresy w drugim. Przyjmuje się przy tym, że istnieje pewien zbiór modułów (czy też ontologii) {O i } i I, indeksowany przez zbiór I. Każdy moduł w zasadzie jest ontologią (czyli traktowany jest jako zbiór zdań). Dla każdej pary modułów O i (moduł źródłowy) i O j (moduł docelowy; i, j I, i j) określony jest (choć może być pusty) zbiór reguł pomostowych ij. Istnieją trzy rodzaje reguł pomostowych (przyjmujemy, że C i D to koncepty, a i b zaś to osobniki odpowiednio z modułów O i i O j ): i: C j: D (tzw. reguła into) i: C j: D (tzw. reguła onto) i: a j: b (tzw. odpowiedniość osobników) Rozproszoną bazą wiedzy (RBW) = ({O i } i I, { ij } i, j I, i j ) nazywamy zbiór modułów wraz ze zbiorami reguł pomostowych. Gdy dla pewnych i, j I zbiór ij jest niepusty, mówimy, że moduł O j korzysta z O i. Rozproszoną interpretacją nazywamy parę ({ i } i I, {r ij } i, j I, i j ), gdzie { i } to zbiór interpretacji (nazywanych interpretacjami lokalnymi), {r ij } zaś to relacje dziedzinowe pomiędzy dziedzinami i i j. W odróżnieniu od założeń tradycyjnej logiki opisowej DL każda interpretacja lokalna może być też tzw. dziurą, czyli specjalną interpretacją o pustej dziedzinie.
6 334 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka Rozproszona interpretacja jest modelem bazy wtedy i tylko wtedy, gdy dla każdego i I zachodzi i O i, a ponadto dla każdej pary i, j I, i j zachodzi ij, który to zapis oznacza spełnianie przez każdej reguły z ij, przy czym: i: C j: D r ij (C i ) D j i: C j: D r ij (C i ) D j i: a j: b r ij (a i ) d j W oryginalnie zaproponowanej wersji DDL relacje r ij mogły przyjmować dowolną postać. Obecnie rozważa się również ograniczone warianty DDL, które oznaczane są dodatkowymi literami umieszczonymi w nawiasach. Przykładowo, użycie litery F oznacza, że dopuszczalne są tylko funkcyjne relacje r ij, natomiast użycie litery I, że jedynie różnowartościowe. Wariant DDL(F, I) oznacza zatem zgodę jedynie na relacje r ij, które są funkcjami różnowartościowymi. DDL, w odróżnieniu od algebry konglomeratów, nie zawiera osobnych działań na słownikach modułów. W sytuacji, kiedy użytkownik chciałby zasymulować prosty import modułu, wystąpi zatem konieczność wprowadzenia wszystkich importowanych terminów do modułu docelowego, a następnie sformułowania odpowiednich reguł pomostowych. W rzeczywistych zastosowaniach, z uwagi na potencjalną liczbę takich terminów, proces ten najprawdopodobniej musiałby być zautomatyzowany. DDL wykazuje jednak swoją użyteczność także w znacznie bardziej skomplikowanych sytuacjach. DDL skonstruowany jest w taki sposób, aby spełniać wiele postulatów (ang. desiderata), a wśród nich m.in. postulat lokalnej niespójności, oznaczający, że niespójność modułu źródłowego nie może pociągać za sobą niespójności modułu docelowego i całej bazy wiedzy. Zabezpiecza to przed propagacją ewentualnych błędów na całą kolekcję modułów. Postulat ten jest spełniany przez możliwość zastosowania dziur. Inną, godną odnotowania cechą logiki DDL jest możliwość odwzorowania kilku osobników z modułu źródłowego w jednego osobnika z modułu docelowego. Dalej zilustrowano to znanym przykładem o pingwinach, pochodzącym z [5]. Przykład 2: Rozważmy dwa moduły: 1 = {Nielot Latający, Ptak Latający} oraz 2 = {Pingwin }. Definiujemy następujące odwzorowanie 12 : 1: Nielot 2: Pingwin 1: Ptak 2: Pingwin Choć mogłoby się wydawać, że Pingwin dziedziczy tu od dwóch rozłącznych konceptów (Nielot i Latający), wciąż można uzyskać niepustą interpretację lokalną modułu 2, pod warunkiem że relacja r 12 odwzorowuje przynajmniej dwa osobniki (jeden będący wystąpieniem konceptu Nielot, a drugi będący wystąpieniem konceptu Latający) w jedno wystąpienie konceptu Pingwin.
7 Odwzorowania międzyontologiczne w algebrze konglomeratów 335 Ciekawostką jest to, że przykład ten w zamierzeniu miał pokazywać nieintuicyjne zachowanie DDL w typowych zastosowaniach. W rzeczywistości doskonale ilustruje jego wyróżniającą się zdolność do łączenia wiedzy o kilku osobnikach z ontologii źródłowej. Natomiast w sytuacjach, gdy takie wnioskowanie jest niepożądane, można wykorzystać mniej ekspresywne warianty DDL, np. DDL(F, I) DDL(F, I) w algebrze konglomeratów Przystępując do rozważań na temat możliwości wyrażenia rozproszonych baz DDL w algebrze konglomeratów, skupimy się najpierw na mniej ekspresywnym wariancie tej logiki DDL(F, I). W wariancie tym relacje r ij muszą być różnowartościowymi funkcjami, stąd każdemu osobnikowi w i może odpowiadać najwyżej jeden osobnik z j i odwrotnie. To założenie znacznie upraszcza proces wyrażania bazy DDL za pomocą konglomeratów. Jako przykładowy scenariusz przyjęto tutaj rozproszoną bazę, zawierającą dwa moduły: DDL 1 = {C, D } oraz 2 = {E F} i zbiór reguł pomostowych 21 = {2:F 1:C, 2:E 1:D}. Reguły te wymuszają, że w każdym modelu bazy zachodzi 1 D C (co można też zapisać jako 1: D C). Pomimo widocznej prostoty przykładu podczas analizy przestrzeni modeli trzeba wziąć pod uwagę kilka możliwości. Otóż relacja r 21 może odwzorowywać całą dziedzinę 2 w jedynie fragment dziedziny 2 we fragment 1 lub też r 21 może być pusta, co skutkuje niespełnialnością konceptu D. Druga z wymienionych sytuacji przedstawiona jest na rys. 1a przy użyciu diagramów Venna. a) 1 2 1, C D F E b) M O 1 O 2 C D E F Rys. 1. Efekt wyrażenia bazy DDL(F, I) za pomocą konglomeratów Fig. 1. Effect of expressing DDL(F, I) knowledge base with conglomerates Aby odzwierciedlić te możliwości w świecie konglomeratów należy, w specjalny sposób skonstruować wynikowe moduły. Konstrukcja modułu M 1, reprezentującego lokalne modele 1 w, przebiega szkicowo jak następuje. Najpierw tworzymy dwa specjalne koncepty O 1 i O 2. Następnie wchłaniamy do tych konceptów odpowiednio moduły M(O 1 ) i M(O 2 ), przy
8 336 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka czym jeśli zawierają takie same nazwy, trzeba je poprzedzić prefiksem. W kolejnym kroku, za pomocą odpowiedniej selekcji, odrzucamy interpretacje niespełniające reguł pomostowych. Na koniec ograniczamy dziedzinę do konceptu O 1 i dokonujemy projekcji słownika wyłącznie do nazw występujących w O 1. Wynik przeprowadzenia pierwszych trzech kroków uwidoczniono na rys. 1b. Rezultat jest podobny jak w przypadku odpowiedniej sytuacji dla DDL. Przecięcie konceptów O 1 O 2 reprezentuje w istocie obszar r 21 ( 2 ) z rys. 1a. Ponieważ wynikowy moduł zawiera wszystkie dopuszczalne interpretacje, wymienione dla DDL sytuacje są dobrze odzwierciedlone, przykładowo pusta relacja r 21 odpowiada interpretacji, w której O 1 O 2 jest puste. Mówiąc bardziej formalnie, proces translacji RBW = ({O i } i I, { ij } i, j I, i j ) do zbioru konglomeratów {c(o i )} i I dla wariantu DDL(F, I), przy założeniu braku cyklicznych zależności wzajemnego wykorzystywania modułów, można przeprowadzić za pomocą następujących kroków: 1. Dla modułów O i, niewykorzystujących innych modułów (liści grafu relacji wykorzystywania), wyznaczamy c( i ) = M( i ). 2. Dla każdej reguły pomostowej b z niepustego zbioru ij wyznaczamy konglomerat pomostowy b, przy czym: 2.1. dla b = i: C j: D kładziemy b = M({ * i:* (C) * j:* (D)}) 2.2. dla b = i: C j: D kładziemy b = M({ * j:* (D) * i:* (C)}) 2.3. dla b = i: a j: b kładziemy b = M({i: a j: b}). 3. Dla każdego niepustego ij wyznaczamy konglomerat odwzorowujący ij = b ij b. 4. Poczynając od modułów j, wykorzystujących wyłącznie moduły i, dla których wyznaczono c( i ): 4.1. Dla każdej pary j, i, ij wyznaczamy konglomerat integrujący i i j : M ij = ij * j:*(m( j )) j M({O j }) * i:*(c( i )) i M({O i }) Wyznaczamy zintegrowany konglomerat dla j : M j = i {i: ij } M ij Wyznaczamy c(o j ) jako j:* *( S Oj ( j(m j ))). 5. Powtarzamy krok 4 aż do przetłumaczenia wszystkich modułów. Można udowodnić (dowód pomijamy ze względu na rozmiary artykułu), że dla tak skonstruowanego zbioru konglomeratów każdemu modelowi konglomeratu M j odpowiada model bazy, zachodzi też zależność odwrotna DDL(F, N n ) w algebrze konglomeratów W niniejszym podrozdziale przedstawione zostanie rozszerzenie metody pozwalające na wykorzystanie relacji dziedzinowych, które niekoniecznie są różnowartościowe. Podobnie jak
9 Odwzorowania międzyontologiczne w algebrze konglomeratów 337 poprzednio, na początek posłużymy się przykładem. Przykład ten stanowi zaadaptowaną wersję ontologii z pingwinem (patrz przykład 2), choć, dla jasności prezentacji, zastosowano w nim skrócone nazwy konceptów. Nasza RBW składa się z dwóch modułów: 1 = {Pg } oraz 2 = {NL L, Pt NL} (Pg, Pt, L i NL oznaczają odpowiednio Pingwiny, Ptaki, Latające i Nieloty). Jedyny niepusty zbiór reguł to 21 = {2:NL 1:Pg, 2:Pt 1:Pg}. Jak już wcześniej wspomniano, koncept Pg jest spełnialny, ale jedynie przy założeniu, że relacja r 21 odwzoruje dwa osobniki z 2 w jednego osobnika z 1. Taką sytuację przedstawiono schematycznie na rys. 2a. Strategia zaproponowana w poprzednim podrozdziale jest niewystarczająca, aby zamodelować tę sytuację za pomocą konglomeratów. Choć można na siebie nałożyć dziedziny dwóch modułów, samo nakładanie nie jest w stanie zasymulować możliwości odwzorowania dwóch osobników z jednego modułu w jednego osobnika z drugiego. Proponowane rozwiązanie tego problemu przedstawiono schematycznie na rys. 2b. Jak widać, polega ono na zastosowaniu takiego samego koncepcyjnego podziału (określonego przez zawartość modułu 2 ) fragmentu dziedziny (reprezentowanego zakresem konceptu O 2 ) dwukrotnie. Taką operację można wykonać przy użyciu prefiksów (dla czytelności pominiętych na rys. 1b i reprezentowanych różnymi odcieniami szarości). Odpowiednie działanie algebry konglomeratów można zapisać następująco: M 2.2 = * 2.2.1:*(M(O 2 )) * 2.2.2:*(M(O 2 )). Po wykonaniu takiej operacji dziedzina modułu M 2.2 reprezentuje de facto pary elementów dziedziny modułu M(O 2 ). a) 1 2 NL L Pg Pt p e f b) M O 1 NL L Pt Pg NL L Pt O 2 Rys. 2. Baza DDL wg przykładu z pingwinem i jej konglomeratowy odpowiednik Fig. 2. DDL Penguin example and its counterpart with conglomerates Jednakże z takim podejściem związane są dwa zasadnicze problemy. Po pierwsze, tak skonstruowany moduł reprezentuje pary osobników. Choć ten sam sposób postępowania można zastosować, by uzyskać odpowiedniki trójek, czwórek itp., trzeba znać górne ograniczenie na krotność. Proponowane podejście nie zadziała dla każdej sytuacji w DDL(F), zatem postulujemy tu wprowadzenie nowego wariantu DDL, DDL(N n ), n N, w którym każda relacja dziedzinowa r ij może odwzorowywać co najwyżej n osobników z i w jednego osobni-
10 338 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka ka z j. Stąd też tytuł niniejszego podrozdziału i ograniczenie rozważań do wariantu DDL(F, N n ). Drugi problem polega na tym, że niektóre elementy dziedziny M 2.2 reprezentują pary, których nie należy uwzględniać, np. pary (e, e). Problem ten można przezwyciężyć za pomocą pewnych chwytów matematycznych (konkretnie, można tu wykorzystać właściwość spełnialności rozłącznej unii, zdefiniowaną przez Serafiniego w [10]), niemniej jednak w sferze koncepcyjnej należy zdawać sobie sprawę z różnicy pomiędzy podwójnym nakładaniem dziedzin a wykorzystaniem par osobników. W sposób bardziej formalny proces translacji RBW = ({O i } i I, { ij } i, j I, i j ) do zbioru konglomeratów {c(o i )} i I dla wariantu DDL(F, N n ), przy założeniu braku cyklicznych zależności wzajemnego wykorzystywania modułów, można wyrazić następująco: 1. Dla modułów O i niewykorzystujących innych modułów (liści grafu relacji wykorzystywania) wyznaczamy c( i ) = M( i ). 2. Dla każdej reguły pomostowej b z niepustego zbioru ij wyznaczamy konglomerat n-pomostowy b, przy czym: 2.1. dla b = i: C j: D kładziemy b = M({ k [1..n] l [1..k] * i.k.l:*(c) * j:* (D)}), 2.2. dla b = i: C j: D kładziemy b = M({ * j:* (D) k [1..n] l [1..k] * i.k.l:*(c)}), 2.3. dla b = i: a j: b kładziemy b = k 1..n M(i.k.1: a j: b). 3. Dla każdego niepustego ij wyznaczamy konglomerat n-odwzorowujący ij = b ij b. 4. Poczynając od modułów j, wykorzystujących wyłącznie moduły i, dla których wyznaczono c( i ): 4.1. dla każdej pary j, i, ij wyznaczamy konglomeraty n-integrujące i i j : M ij = ij * i:*(c( j )) j M({O j }) k, l [1..n], k l( * i.k.l:*(c( i )) i.k.l M({O i.k O i.l : k, l [1..n], k l})), 4.2. wyznaczamy zintegrowany konglomerat dla j : M j = i {i: ij } M ij, 4.3. wyznaczamy c(o j ) jako j:* *( S Oj ( j(m j ))). 5. Powtarzamy krok 4 aż do przetłumaczenia wszystkich modułów. Tak jak poprzednio, można udowodnić, że dla takiej konstrukcji każdemu modelowi konglomeratu M ij odpowiada model bazy, zachodzi też zależność odwrotna Podsumowanie Podsumowując przedstawione w niniejszym podrozdziale przekształcenia, trzeba zauważyć, że pomimo istnienia możliwości dokonania częściowej translacji algebra konglomeratów w swoich założeniach różni się od idei leżącej u podstaw odwzorowań ontologicznych. Problemy w oddaniu specyfiki relacji dziedzinowych wydają się być trudne do przezwyciężenia
11 Odwzorowania międzyontologiczne w algebrze konglomeratów 339 nawet przez wprowadzenie do algebry nowych działań. Pewnym sposobem rozszerzenia zaprezentowanych metod do pełnego wariantu logiki DDL mogłoby być tutaj wykorzystanie mechanizmu podobnego do granic w matematyce, jednak wymagałoby to dalszej analizy. Jednakże w ramach bardziej ograniczonych wariantów DDL zaproponowane metody sprawdzają się i mogą posłużyć jako materiał do analizy porównawczej. 4. Wyrażanie złączeń za pomocą algebry konglomeratów W tym rozdziale podjęto problem wyrażenia za pomocą algebry konglomeratów kolejnej metody pozyskiwania wiedzy z innych modułów: złączeń ontologicznych. Rozważania te prowadzone są dla metody -Connections, której podstawy przypomniano w podrozdziale 4.1. W podrozdziale 4.2 zaprezentowano metodę tłumaczenia bazy -Connections na konglomeraty, w podrozdziale 4.3 zaś zawarto wnioski dotyczące opisanej konwersji Wprowadzenie do -Connections Oryginalnie metoda złączeń -Connections została zaproponowana w [11] i rozbudowana nieco później ([12]) jako środek pozwalający łączyć ze sobą systemy posługujące się zasadniczo różnymi logicznymi reprezentacjami wiedzy (oprócz różnych wariantów logiki opisowej powoływano się tu na przykłady logiki temporalnej, modalnej, logiki przestrzeni metrycznych itp.). Adaptacji -Connections jako metody modularyzacji złożonych ontologii zapisanych wyłącznie w logice opisowej, dokonano w 2004 roku w [5]. Tu opiszemy metodę właśnie w takiej (choć dostosowanej do specyfiki niniejszego artykułu) wersji. Generalnie -Connections dla logiki opisowej występuje w kilku wariantach różniących się ekspresywnością. Wspólna cechą wszystkich odmian jest jednak przyjęcie pewnych założeń. Najważniejsze z nich (charakterystyczne również dla ogólnej wersji -Connections) mówi o rozłączności dziedzin opisywanych modułów. Przyjmuje się, że dziedziny zainteresowań, opisywane przez poszczególne moduły ontologiczne, są parami ściśle rozłączne. Wszelkie powiązania pomiędzy wprowadzanymi do modułów terminami muszą być wyrażone za pomocą specyficznej odmiany ról, tzw. ról łączących (ang. linking relations), które są podobne do zwykłych ról logiki opisowej, ale łączą osobniki z różnych modułów (czyli różnych dziedzin). Każda rola łącząca p ma ściśle określone moduły źródłowy i docelowy. Ponieważ przyjmujemy, że baza wiedzy w -Connections składa się ze zbioru modułów {O i } i I, zbiór relacji łączących podzielony jest na rozłączne zbiory ij (i, j I, i j, przy czym jeśli p ij, to łączy osobniki z modułu O i z osobnikami z modułu O j ). Dodatkowym elementem bazy
12 340 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka wiedzy są tzw. komponenty LBox: ij, zawierające aksjomaty podrzędności ról łączących postaci p q (p, q ij ). Ponadto przyjmuje się, że każdy z modułów O i, i I oprócz zwykłych zdań zapisanych w logice opisowej, wykorzystujących terminy właściwe dla danego modułu może zawierać zdania wykorzystujące specjalne koncepty łączące: p.z, p.z, gdzie p ij dla pewnego ustalonego j I, Z zaś jest konceptem w O j. Interpretacja bazy wiedzy = ({O i } i I, { ij } i, j I, i j, { ij } i, j I, i j ) składa się ze zbioru rozszerzonych interpretacji lokalnych { i } i I oraz rodziny interpretacyjnych funkcji łączących { } i, j I, i j. Każda interpretacja lokalna i w standardowy sposób przypisuje każdemu osobnikowi element dziedziny, każdemu konceptowi podzbiór dziedziny każdej roli zaś zbiór par elementów. Natomiast interpretacja konceptów łączących jest uzależniona od interpretacyjnych funkcji łączących, które każdej roli łączącej p ij, i, j I, i j przypisują podzbiór zdania z ij, tj. jeśli p q. Każda funkcja musi przy tym spełniać wszystkie ij to p q. Z kolei koncepty łączące muszą być interpretowane następująco, analogicznie do odpowiednich konceptów w logice opisowej: ( p.z) = {e : f : f Z (e, f) p } ( p.z) = {e : f : f Z (e, f) p } Jak pokazuje przykład 3, odpowiednio zdefiniowana baza wiedzy pozwala na przenoszenie wniosków pomiędzy modułami. Przykład 3: Rozważmy moduły: 1 = {Turysta odwiedza.kurort, Plażowicz wypoczywa.kurortplażowy} i 2 = {KurortPlażowy Kurort}. Role wypoczywa i odwiedza są łączące i należą do = {wypoczywa odwiedza}. Z bazy tej możemy wyprowadzić wniosek, że każdy Plażowicz jest Turystą. Opisany wariant -Connections charakteryzuje się najmniejszą ekspresywnością spośród zaproponowanych w [5]. Bardziej ekspresywne warianty zezwalają na wykorzystanie ograniczeń liczebnościowych oraz odwrotnych ról łączących w konceptach łączących, a także wprowadzają uogólniony aksjomat przechodniości (patrz [5]). Jednak warianty te nie wprowadzają w zasadzie dodatkowych utrudnień związanych z przełożeniem bazy -Connections na konglomeraty., 4.2. Odwzorowanie złączeń w algebrze konglomeratów Proces przełożenia bazy -Connections na konglomeraty okazuje się być nieco prostszy niż w przypadku DDL. Charakterystyczna, upraszczająca cecha to możliwość budowy jednego konglomeratu reprezentującego połączone, rozłączne dziedziny odpowiednich modułów.
13 Odwzorowania międzyontologiczne w algebrze konglomeratów 341 Proces ten zostanie pokazany, tak jak poprzednio, na przykładzie. Posłużymy się tu bazą wiedzy z przykładu 3, w której skrócono nazwy konceptów i ról, tak że 1 = {T o.k, P w.kp} oraz 2 = {KP K}, w i o są rolami łączącymi z 12, a 12 = {w o}. Trudności, jakie można napotkać przy przekładaniu bazy na konglomeraty, mają charakter głównie techniczny. Przede wszystkim przy utrzymaniu założenia, że można posługiwać się wyłącznie konglomeratami bazowymi należącymi do M( ), gdzie to pewien dialekt logiki opisowej, nie da się dokonać bezpośredniego przekładu modułu 1 na konglomerat M( 1 ). Wynika to z tego, że 1 zawiera koncepty łączące niemieszczące się w koncepcji podstawowej logiki opisowej. Trudność tę można jednak rozwiązać, zamieniając każdy koncept łączący E z modułu i, i I (zbiór takich konceptów oznaczamy LC i ) na pewien koncept atomowy o unikatowej nazwie s i (E). Zamiany tej można dokonać w rekurencyjny sposób dla drzewa składniowego każdego ze zdań. Rezultat takiej zamiany oznaczmy przez s i ( i ). Przy takim założeniu proces translacji można naszkicować następująco. Na początku dokonujemy opisanej zamiany konceptów łączących. Następnie dla każdego modułu budujemy konglomerat M(s i ( i )). Kolejnym krokiem jest utworzenie zintegrowanego konglomeratu M, inicjalnie zawierającego zbiór parami rozłącznych konceptów O i, i I, do których wchłaniamy odpowiednio konglomeraty M(s i ( i )). Następnie uwzględniamy zawartość komponentów LBox, dokonując selekcji połączonego konglomeratu względem aksjomatów podrzędności ról łączących. W tym punkcie można już też przywrócić właściwą interpretację konceptów łączących przez selekcję względem następujących zdań {E s i (E)} dla wszystkich konceptów łączących E ze wszystkich modułów i. Po tej operacji, aby wnioskować (w szczególności o spójności) z poszczególnych modułów, wystarczy dokonać projekcji do zbioru terminów s i ( i ) (dla wybranego i I) oraz ograniczyć dziedzinę do odpowiedniego konceptu O i. Dla przykładowej ontologii efekt przekształcenia przed uwzględnieniem działania konceptów łączących pokazano na rys. 3a, końcową zaś postać połączonego konglomeratu naszkicowano na rys. 3b. Formalnie kolejne kroki translacji bazy = ({O i } i I, { ij } i, j I, i j, { ij } i, j I, i j ) do zbioru konglomeratów {c( i )} i I można wyrazić następująco: 1. Wyznaczamy wstępną postać zintegrowanego konglomeratu: a) M = i I * i:* (s i ( i )) i M({O i })). 2. Uwzględniamy zawartość komponentów LBox i specyfikę konceptów łączących: b) M = M i I, j I M ij i I {E s i (E)} E LCi. 3. Wyznaczamy c(o i ) jako i:* *( S Oi ( i(m))). Tak jak w przypadku DDL zachodzi tu odpowiedniość pomiędzy modelami konglomeratów a modelami bazy.
14 342 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka a) M O 1 T P KP K O 2 b) M O 1 P T KP K O 2 Rys. 3. Odpowiednik bazy -Connections na kolejnych etapach translacji Fig. 3. Subsequent states of conversion of an -Connections knowledge base 4.3. Podsumowanie Proces przekształcania bazy -Connections na konglomeraty jest znacznie bardziej bezpośredni niż w przypadku DDL. Decyduje o tym rozłączność dziedzin poszczególnych modułów, dzięki której utworzenie pojedynczej zintegrowanej dziedziny nie nastręcza trudności. Algebra konglomeratów w naturalny sposób radzi też sobie z możliwymi różnicami dialektów logiki opisowej, stosowanymi w różnych modułach. Pomimo tych podobieństw trzeba jednak stwierdzić, że do poprawnego odwzorowania konieczna jest ingerencja w postać przetwarzanych zdań. Ingerencja ta jest jednak stosunkowo naturalna i polega na odroczeniu interpretacji konceptów łączących do momentu skonstruowania połączonej dziedziny. 5. Wnioski Przeprowadzona analiza pozwala na wyciągnięcie wstępnych wniosków dotyczących porównania analizowanych metod odwzorowywania i złączania modułów ontologicznych oraz przydatności algebry konglomeratów do opisu tego typu zależności wraz z wyznaczeniem ewentualnych perspektyw jej rozwoju. Z punktu widzenia przeprowadzanych translacji można stwierdzić, że główną różnicą pomiędzy analizowanymi metodami jest sposób transferu wniosków między modułami. W DDL zależności między terminami w dziedzinie modułu docelowego zmieniają się dzięki temu, że odwzorowujemy dziedzinę źródłową na docelową. Po przeprowadzeniu takiego odwzorowania zależności pomiędzy terminami w module źródłowym mogą już wpływać bezpośrednio (tzn. tak jak w podstawowej logice opisowej, jeśli tylko potraktujemy reguły po-
15 Odwzorowania międzyontologiczne w algebrze konglomeratów 343 mostowe jako specyficzny sposób zapisu tradycyjnych aksjomatów) na zakresy terminów w modelu docelowym. W -Connections dziedziny są ściśle rozłączne i nie zachodzi między nimi odwzorowanie. Transfer wniosków jest możliwy dzięki istnieniu ról i konceptów łączących, czyli dodatkowych terminów, które wiążą elementy dwóch dziedzin. Pomimo tej różnicy procesy translacji dla obu metod są bardzo podobne. W obydwu zaproponowanych metodach tworzony jest zintegrowany konglomerat, na który następnie nakładane są (za pomocą specyficznego rodzaju selekcji) dodatkowe ograniczenia, wynikające z zastosowania w obu metodach specyficznych rozszerzeń DDL (tj. reguł pomostowych w DDL i ról oraz konceptów łączących w -Connections). Sposób tworzenia zintegrowanego konglomeratu także jest dość zbliżony: w obu przypadkach stosujemy wchłonięcie pod specjalnie zdefiniowane koncepty, choć w przypadku DDL, ze względu na to, że odwzorowanie między dziedzinami może być dość złożone, konieczne może okazać się kilkukrotne przeprowadzenie operacji wchłonięcia. W obu translacjach wykorzystywano też bardzo podobne operacje algebry: przecięcie, wchłonięcie, selekcję, a następnie projekcję z ograniczeniem. Zastosowanie tak podobnych sekwencji kroków zdaje się wskazywać na stosukowo duży potencjał algebry konglomeratów, jeśli chodzi o zapis semantyki różnych metod pozyskiwania wiedzy z modułów ontologicznych. Jednak przy oddawaniu pełnej semantyki DDL trzeba pamiętać o ograniczeniach algebry. Możliwość symulowania stosunkowo dużej klasy odwzorowań między dziedzinami przez kilkukrotne wchłonięcie wydaje się ciekawa, ale nie odzwierciedla do końca specyfiki relacji łączących. Być może odpowiedzią na tę kwestię mogłoby być opracowanie rozszerzenia algebry konglomeratów. Istnieją dwa kierunki działań, które mogłyby doprowadzić do rozwiązania problemu. Pierwszy polega na rozszerzeniu zbioru działań algebry w kierunku bardziej zaawansowanych operacji na dziedzinie (np. przekształcania par osobników w pojedyncze osobniki). Drugi polega na wprowadzeniu granic (odpowiednik limes), dzięki czemu za pomocą jednej operacji byłoby możliwe wprowadzanie dowolnej liczby nakładających się na siebie konglomeratów. BIBLIOGRAFIA 1. Motik B., Patel-Schneider P. F., Grau B. C.: OWL 2 Web Ontology Language Direct Semantics. Rekomendacja W3C, 2009, 2. Haase P.: Networked Ontology Model. Projekt NeOn, 2006, web-content/index.php?itemid=73&id=17.
16 344 K. Goczyła, A. Waloszek, W. Waloszek, T. Zawadzka 3. Bao J., Voutsadakis G., Slutzki G., Honavar V.: Package-Based Description Logics, [in:] Stuckenschmidt H., Parent C., Spaccapietra S. (red.): Modular Ontologies, LNCS, Vol. 5445, Springer, Berlin 2009, s Borgida A., Serafini L.: Distributed Description Logics: Assimilating Information from Peer Sources. Journal of Data Semantics, No. 1, 2003, s Grau B. C., Parsia B., Sirin E.: Working with Multiple Ontologies on the Semantic Web. The Semantic Web ISWC 2004, LNCS, Vol. 3298, Springer, Berlin 2004, s Homola M., Serafini L.: Towards Formal Comparison of Ontology Linking, Mapping and Importing. Proc. of 23rd Int. Workshop on Description Logics, CEUR-WS(573), Goczyła K., Waloszek A., Waloszek W.: Algebra konglomeratów jako narzędzie opisu problemów przetwarzania ontologii. Studia Informatica, Vol. 30, No. 2A(83), Wydawnictwo Politechniki Śląskiej, Gliwice 2009, s Ghidini Ch., Serafini L., Tessaris S.: On relating heterogeneous elements from different ontologies. Proc. of 20rd Int. Workshop on Description Logics, CEUR-WS(250), Homola M., Luciano Serafini L.: Augmenting Subsumption Propagation in Distributed Description Logics. Applied Artificial Intelligence, No. 24(1-2), 2010, s Serafini L., Borgida A., Tamilin A.: Aspects of Distributed and Modular Ontology Reasoning. Proc. of IJCAI 2005, s Kutz O., Wolter F., Zakharyaschev M.: Connecting abstract description systems. Proc. of KR 2002, Morgan Kaufmann, 2002, s Kutz O., Lutz C., Wolter F., Zakharyaschev M.: E-connections of abstract description systems. Artificial Intelligence, No. 156(1), 2004, s Wpłynęło do Redakcji 14 stycznia 2012 r. Abstract The article discusses the possibility of expressing semantics of state-of-the-art knowledge modularization methods with use of s-module algebra. The goals of this process are twofold. First, we hope to assess the s-module algebra as a uniform language for expressing various approaches to integrating knowledge from ontological modules. Second, we aim at evaluating differences and similarities of the analyzed methods from a new point of view.
17 Odwzorowania międzyontologiczne w algebrze konglomeratów 345 In the article we show that translation of DDL knowledge base to a set of s-modules is possible, if some constraining assumptions are made. We present a formal procedure for translation of acyclic distributed knowledge bases expressed with DDL(F, I). We show that the procedure may be extended towards a newly proposed variant of DDL, DDL(F, N n ) in which mapping relations are functions which map at most n individuals from the source domain to a single individual in the target domain. We also define a similar translation process for -Connections knowledge base. In the process one integrated domain is created in which linking roles and concepts may be treated as regular ones. Our preliminary conclusions suggest that the analyzed methods are close to each other in the way that they allow for transferring knowledge between modules. The main steps performed in each translation are very similar. However relating knowledge from several modules is done quite differently in DDL and -Connections: in the former case it requires to overlap the domains, while in the latter it is done by a special kind of selection based on linking relations and concepts. Adresy Krzysztof GOCZYŁA: Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki, ul. Narutowicza 11/12, Gdańsk, Polska, kris@eti.pg.gda.pl. Aleksander WALOSZEK: Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki, ul. Narutowicza 11/12, Gdańsk, Polska, alwal@eti.pg.gda.pl Wojciech WALOSZEK: Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki, ul. Narutowicza 11/12, Gdańsk, Polska, wowal@eti.pg.gda.pl. Teresa ZAWADZKA: Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki, ul. Narutowicza 11/12, Gdańsk, Polska, tegra@eti.pg.gda.pl.
Internet Semantyczny i Logika II
 Internet Semantyczny i Logika II Ontologie Definicja Grubera: Ontologia to formalna specyfikacja konceptualizacji pewnego obszaru wiedzy czy opisu elementów rzeczywistości. W Internecie Semantycznym językiem
Internet Semantyczny i Logika II Ontologie Definicja Grubera: Ontologia to formalna specyfikacja konceptualizacji pewnego obszaru wiedzy czy opisu elementów rzeczywistości. W Internecie Semantycznym językiem
Internet Semantyczny. Logika opisowa
 Internet Semantyczny Logika opisowa Ontologie Definicja Grubera: Ontologia to formalna specyfikacja konceptualizacji pewnego obszaru wiedzy czy opisu elementów rzeczywistości. W Internecie Semantycznym
Internet Semantyczny Logika opisowa Ontologie Definicja Grubera: Ontologia to formalna specyfikacja konceptualizacji pewnego obszaru wiedzy czy opisu elementów rzeczywistości. W Internecie Semantycznym
Logika Stosowana. Wykład 1 - Logika zdaniowa. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu.
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu. 1 Logika Klasyczna obejmuje dwie teorie:
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu. 1 Logika Klasyczna obejmuje dwie teorie:
S-PELLET JAKO IMPLEMENTACJA ZDANIOWEJ REPREZENTACJI MODUŁÓW ALGEBRY KONGLOMERATÓW 1
 STUDIA INFORMATICA 2012 Volume 33 Number 2A (105) Wojciech WALOSZEK Politechnika Gdańska, Katedra Inżynierii Oprogramowania S-PELLET JAKO IMPLEMENTACJA ZDANIOWEJ REPREZENTACJI MODUŁÓW ALGEBRY KONGLOMERATÓW
STUDIA INFORMATICA 2012 Volume 33 Number 2A (105) Wojciech WALOSZEK Politechnika Gdańska, Katedra Inżynierii Oprogramowania S-PELLET JAKO IMPLEMENTACJA ZDANIOWEJ REPREZENTACJI MODUŁÓW ALGEBRY KONGLOMERATÓW
Elementy logiki matematycznej
 Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
ALGEBRA KONGLOMERATÓW JAKO NARZĘDZIE OPISU PROBLEMÓW PRZETWARZANIA ONTOLOGII 1
 STUDIA INFORMATICA 2009 Volume 30 Number 2A (83) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki ALGEBRA KONGLOMERATÓW
STUDIA INFORMATICA 2009 Volume 30 Number 2A (83) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki ALGEBRA KONGLOMERATÓW
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
WEWNĘTRZNA REPREZENTACJA KONGLOMERATOWEJ BAZY WIEDZY W SYSTEMIE RKASEA
 STUDIA INFORMATIA 2010 Volume 31 Number 2A (89) Krzysztof GOZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki WEWNĘTRZNA
STUDIA INFORMATIA 2010 Volume 31 Number 2A (89) Krzysztof GOZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki WEWNĘTRZNA
domykanie relacji, relacja równoważności, rozkłady zbiorów
 1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
Andrzej Wiśniewski Logika II. Materiały do wykładu dla studentów kognitywistyki. Wykład 15. Trójwartościowa logika zdań Łukasiewicza
 Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 15. Trójwartościowa logika zdań Łukasiewicza 1 Wprowadzenie W logice trójwartościowej, obok tradycyjnych wartości logicznych,
Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 15. Trójwartościowa logika zdań Łukasiewicza 1 Wprowadzenie W logice trójwartościowej, obok tradycyjnych wartości logicznych,
Transformacja wiedzy w budowie i eksploatacji maszyn
 Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
(4) x (y z) = (x y) (x z), x (y z) = (x y) (x z), (3) x (x y) = x, x (x y) = x, (2) x 0 = x, x 1 = x
 2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
Algebrę L = (L, Neg, Alt, Kon, Imp) nazywamy algebrą języka logiki zdań. Jest to algebra o typie
 3. Wykłady 5 i 6: Semantyka klasycznego rachunku zdań. Dotychczas rozwinęliśmy klasyczny rachunek na gruncie czysto syntaktycznym, a więc badaliśmy metodę sprawdzania, czy dana formuła B jest dowodliwa
3. Wykłady 5 i 6: Semantyka klasycznego rachunku zdań. Dotychczas rozwinęliśmy klasyczny rachunek na gruncie czysto syntaktycznym, a więc badaliśmy metodę sprawdzania, czy dana formuła B jest dowodliwa
Model relacyjny. Wykład II
 Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
2
 1 2 3 4 5 Dużo pisze się i słyszy o projektach wdrożeń systemów zarządzania wiedzą, które nie przyniosły oczekiwanych rezultatów, bo mało kto korzystał z tych systemów. Technologia nie jest bowiem lekarstwem
1 2 3 4 5 Dużo pisze się i słyszy o projektach wdrożeń systemów zarządzania wiedzą, które nie przyniosły oczekiwanych rezultatów, bo mało kto korzystał z tych systemów. Technologia nie jest bowiem lekarstwem
Komputerowe Systemy Przemysłowe: Modelowanie - UML. Arkadiusz Banasik arkadiusz.banasik@polsl.pl
 Komputerowe Systemy Przemysłowe: Modelowanie - UML Arkadiusz Banasik arkadiusz.banasik@polsl.pl Plan prezentacji Wprowadzenie UML Diagram przypadków użycia Diagram klas Podsumowanie Wprowadzenie Języki
Komputerowe Systemy Przemysłowe: Modelowanie - UML Arkadiusz Banasik arkadiusz.banasik@polsl.pl Plan prezentacji Wprowadzenie UML Diagram przypadków użycia Diagram klas Podsumowanie Wprowadzenie Języki
Andrzej Wiśniewski Logika II. Wykłady 10b i 11. Semantyka relacyjna dla normalnych modalnych rachunków zdań
 Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykłady 10b i 11. Semantyka relacyjna dla normalnych modalnych rachunków zdań 1 Struktury modelowe Przedstawimy teraz pewien
Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykłady 10b i 11. Semantyka relacyjna dla normalnych modalnych rachunków zdań 1 Struktury modelowe Przedstawimy teraz pewien
1 Wstęp do modelu relacyjnego
 Plan wykładu Model relacyjny Obiekty relacyjne Integralność danych relacyjnych Algebra relacyjna 1 Wstęp do modelu relacyjnego Od tego się zaczęło... E. F. Codd, A Relational Model of Data for Large Shared
Plan wykładu Model relacyjny Obiekty relacyjne Integralność danych relacyjnych Algebra relacyjna 1 Wstęp do modelu relacyjnego Od tego się zaczęło... E. F. Codd, A Relational Model of Data for Large Shared
Reprezentacja wiedzy ontologie, logiki deskrypcyjne
 Reprezentacja wiedzy ontologie, logiki deskrypcyjne Agnieszka Ławrynowicz 24 listopada 2016 Plan wykładu 1 Powtórka: sieci semantyczne, RDF 2 Definicja ontologii 3 Logiki deskrypcyjne Semantyczny Internet
Reprezentacja wiedzy ontologie, logiki deskrypcyjne Agnieszka Ławrynowicz 24 listopada 2016 Plan wykładu 1 Powtórka: sieci semantyczne, RDF 2 Definicja ontologii 3 Logiki deskrypcyjne Semantyczny Internet
Języki programowania zasady ich tworzenia
 Strona 1 z 18 Języki programowania zasady ich tworzenia Definicja 5 Językami formalnymi nazywamy każdy system, w którym stosując dobrze określone reguły należące do ustalonego zbioru, możemy uzyskać wszystkie
Strona 1 z 18 Języki programowania zasady ich tworzenia Definicja 5 Językami formalnymi nazywamy każdy system, w którym stosując dobrze określone reguły należące do ustalonego zbioru, możemy uzyskać wszystkie
Internet Semantyczny. Wstęp do OWL 2
 Internet Semantyczny Wstęp do OWL 2 RDFS Podstawowymi elementami które określamy w RDFS są klasy (ang. class) zasobów i właściwości (ang. property) zasobów charakterystyczne dla interesującego nas fragmentu
Internet Semantyczny Wstęp do OWL 2 RDFS Podstawowymi elementami które określamy w RDFS są klasy (ang. class) zasobów i właściwości (ang. property) zasobów charakterystyczne dla interesującego nas fragmentu
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 8b: Algebra relacyjna http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2009/tpi-2009 Prof. dr hab. Elżbieta Richter-Wąs 1 Algebra relacyjna Algebra relacyjna (ang.
Teoretyczne podstawy informatyki Wykład 8b: Algebra relacyjna http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2009/tpi-2009 Prof. dr hab. Elżbieta Richter-Wąs 1 Algebra relacyjna Algebra relacyjna (ang.
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Programowanie komputerów
 Programowanie komputerów Wykład 1-2. Podstawowe pojęcia Plan wykładu Omówienie programu wykładów, laboratoriów oraz egzaminu Etapy rozwiązywania problemów dr Helena Dudycz Katedra Technologii Informacyjnych
Programowanie komputerów Wykład 1-2. Podstawowe pojęcia Plan wykładu Omówienie programu wykładów, laboratoriów oraz egzaminu Etapy rozwiązywania problemów dr Helena Dudycz Katedra Technologii Informacyjnych
Internet Semantyczny. Schematy RDF i wnioskowanie
 Internet Semantyczny Schematy RDF i wnioskowanie Ewolucja Internetu Internet dzisiaj Internet Semantyczny Jorge Cardoso, The Syntactic and the Semantic Web, in Semantic Web Services: Theory, Tools, and
Internet Semantyczny Schematy RDF i wnioskowanie Ewolucja Internetu Internet dzisiaj Internet Semantyczny Jorge Cardoso, The Syntactic and the Semantic Web, in Semantic Web Services: Theory, Tools, and
IDEOLOGICZNY I PRAKTYCZNY MODEL METAONTOLOGII
 STUDIA INFORMATICA 2009 Volume 30 Number (82) Krzysztof GOCZYŁA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki Aleksander WALOSZEK Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji
STUDIA INFORMATICA 2009 Volume 30 Number (82) Krzysztof GOCZYŁA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki Aleksander WALOSZEK Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji
Eksploracja danych. KLASYFIKACJA I REGRESJA cz. 2. Wojciech Waloszek. Teresa Zawadzka.
 Eksploracja danych KLASYFIKACJA I REGRESJA cz. 2 Wojciech Waloszek wowal@eti.pg.gda.pl Teresa Zawadzka tegra@eti.pg.gda.pl Katedra Inżynierii Oprogramowania Wydział Elektroniki, Telekomunikacji i Informatyki
Eksploracja danych KLASYFIKACJA I REGRESJA cz. 2 Wojciech Waloszek wowal@eti.pg.gda.pl Teresa Zawadzka tegra@eti.pg.gda.pl Katedra Inżynierii Oprogramowania Wydział Elektroniki, Telekomunikacji i Informatyki
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki. Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Zagadnienia (1/3) Data-flow diagramy przepływów danych ERD diagramy związków encji Diagramy obiektowe w UML (ang. Unified Modeling Language)
 Zagadnienia (1/3) Rola modelu systemu w procesie analizy wymagań (inżynierii wymagań) Prezentacja różnego rodzaju informacji o systemie w zależności od rodzaju modelu. Budowanie pełnego obrazu systemu
Zagadnienia (1/3) Rola modelu systemu w procesie analizy wymagań (inżynierii wymagań) Prezentacja różnego rodzaju informacji o systemie w zależności od rodzaju modelu. Budowanie pełnego obrazu systemu
Logika rozmyta typu 2
 Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Projektowanie relacyjnych baz danych
 Mam nadzieję, że do tej pory przyzwyczaiłeś się do tabelarycznego układu danych i poznałeś sposoby odczytywania i modyfikowania tak zapisanych danych. W tym odcinku poznasz nieco teorii relacyjnych baz
Mam nadzieję, że do tej pory przyzwyczaiłeś się do tabelarycznego układu danych i poznałeś sposoby odczytywania i modyfikowania tak zapisanych danych. W tym odcinku poznasz nieco teorii relacyjnych baz
Projekt 4: Programowanie w logice
 Języki Programowania Projekt 4: Programowanie w logice Środowisko ECL i PS e W projekcie wykorzystane będzie środowisko ECL i PS e. Dostępne jest ono pod adresem http://eclipseclp.org/. Po zainstalowaniu
Języki Programowania Projekt 4: Programowanie w logice Środowisko ECL i PS e W projekcie wykorzystane będzie środowisko ECL i PS e. Dostępne jest ono pod adresem http://eclipseclp.org/. Po zainstalowaniu
Semantic Web Internet Semantyczny
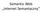 Semantic Web Internet Semantyczny Semantyczny Internet - Wizja (1/2) Pomysłodawca sieci WWW - Tim Berners-Lee, fizyk pracujący w CERN Jego wizja sieci o wiele bardziej ambitna niż istniejąca obecnie (syntaktyczna)
Semantic Web Internet Semantyczny Semantyczny Internet - Wizja (1/2) Pomysłodawca sieci WWW - Tim Berners-Lee, fizyk pracujący w CERN Jego wizja sieci o wiele bardziej ambitna niż istniejąca obecnie (syntaktyczna)
Tab. 1 Tab. 2 t t+1 Q 2 Q 1 Q 0 Q 2 Q 1 Q 0
 Synteza liczników synchronicznych Załóżmy, że chcemy zaprojektować licznik synchroniczny o następującej sekwencji: 0 1 2 3 6 5 4 [0 sekwencja jest powtarzana] Ponieważ licznik ma 7 stanów, więc do ich
Synteza liczników synchronicznych Załóżmy, że chcemy zaprojektować licznik synchroniczny o następującej sekwencji: 0 1 2 3 6 5 4 [0 sekwencja jest powtarzana] Ponieważ licznik ma 7 stanów, więc do ich
Model referencyjny doboru narzędzi Open Source dla zarządzania wymaganiami
 Politechnika Gdańska Wydział Zarządzania i Ekonomii Katedra Zastosowań Informatyki w Zarządzaniu Zakład Zarządzania Technologiami Informatycznymi Model referencyjny Open Source dla dr hab. inż. Cezary
Politechnika Gdańska Wydział Zarządzania i Ekonomii Katedra Zastosowań Informatyki w Zarządzaniu Zakład Zarządzania Technologiami Informatycznymi Model referencyjny Open Source dla dr hab. inż. Cezary
Interaktywne wyszukiwanie informacji w repozytoriach danych tekstowych
 Interaktywne wyszukiwanie informacji w repozytoriach danych tekstowych Marcin Deptuła Julian Szymański, Henryk Krawczyk Politechnika Gdańska Wydział Elektroniki, Telekomunikacji i Informatyki Katedra Architektury
Interaktywne wyszukiwanie informacji w repozytoriach danych tekstowych Marcin Deptuła Julian Szymański, Henryk Krawczyk Politechnika Gdańska Wydział Elektroniki, Telekomunikacji i Informatyki Katedra Architektury
Projektowanie systemów informatycznych. Roman Simiński siminskionline.pl. Modelowanie danych Diagramy ERD
 Projektowanie systemów informatycznych Roman Simiński roman.siminski@us.edu.pl siminskionline.pl Modelowanie danych Diagramy ERD Modelowanie danych dlaczego? Od biznesowego gadania do magazynu na biznesowe
Projektowanie systemów informatycznych Roman Simiński roman.siminski@us.edu.pl siminskionline.pl Modelowanie danych Diagramy ERD Modelowanie danych dlaczego? Od biznesowego gadania do magazynu na biznesowe
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Logika Stosowana. Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta. Marcin Szczuka. Instytut Informatyki UW
 Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Rysunek 1: Przykłady graficznej prezentacji klas.
 4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
Semantyka rachunku predykatów
 Relacje Interpretacja Wartość Spełnialność Logika obliczeniowa Instytut Informatyki Relacje Interpretacja Wartość Plan Plan Relacje O co chodzi? Znaczenie w logice Relacje 3 Interpretacja i wartościowanie
Relacje Interpretacja Wartość Spełnialność Logika obliczeniowa Instytut Informatyki Relacje Interpretacja Wartość Plan Plan Relacje O co chodzi? Znaczenie w logice Relacje 3 Interpretacja i wartościowanie
IDEOLOGICZNY I PRAKTYCZNY MODEL METAONTOLOGII
 STUDIA INFORMATICA 200 Volume 3 Number 2A (89) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki IDEOLOGICZNY
STUDIA INFORMATICA 200 Volume 3 Number 2A (89) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki IDEOLOGICZNY
Optimizing Programs with Intended Semantics
 Interaktywna optymalizacja programów 26 kwietnia 2010 Spis treści Spis treści Wstęp Omówienie zaproponowanego algorytmu na przykładzie Wewnętrzna reprezentacja reguł dotyczących optymalizacji Wybrane szczegóły
Interaktywna optymalizacja programów 26 kwietnia 2010 Spis treści Spis treści Wstęp Omówienie zaproponowanego algorytmu na przykładzie Wewnętrzna reprezentacja reguł dotyczących optymalizacji Wybrane szczegóły
Logika binarna. Prawo łączności mówimy, że operator binarny * na zbiorze S jest łączny gdy (x * y) * z = x * (y * z) dla każdego x, y, z S.
 Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
O-MaSE Organization-based Multiagent System Engineering. MiASI2, TWO2,
 O-MaSE Organization-based Multiagent System Engineering MiASI2, TWO2, 2017-2018 Materiały Strona poświęcona metodzie O-MaSE http://macr.cis.ksu.edu/projects/omase.html (Multiagent & Cooperative Reasoning
O-MaSE Organization-based Multiagent System Engineering MiASI2, TWO2, 2017-2018 Materiały Strona poświęcona metodzie O-MaSE http://macr.cis.ksu.edu/projects/omase.html (Multiagent & Cooperative Reasoning
składa się z m + 1 uporządkowanych niemalejąco liczb nieujemnych. Pomiędzy p, n i m zachodzi następująca zależność:
 TEMATYKA: Krzywe typu Splajn (Krzywe B sklejane) Ćwiczenia nr 8 Krzywe Bezier a mają istotne ograniczenie. Aby uzyskać kształt zawierający wiele punktów przegięcia niezbędna jest krzywa wysokiego stopnia.
TEMATYKA: Krzywe typu Splajn (Krzywe B sklejane) Ćwiczenia nr 8 Krzywe Bezier a mają istotne ograniczenie. Aby uzyskać kształt zawierający wiele punktów przegięcia niezbędna jest krzywa wysokiego stopnia.
Logika Stosowana. Wykład 2 - Logika modalna Część 2. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Techniki informacyjne dla wnioskowania oraz generowania, reprezentacji i zarządzania wiedzą
 Zakład Zaawansowanych Technik Informacyjnych (Z-6) Techniki informacyjne dla wnioskowania oraz generowania, reprezentacji i zarządzania wiedzą Zadanie nr 2 Relacyjne systemy dedukcyjne: teoria i zastosowania
Zakład Zaawansowanych Technik Informacyjnych (Z-6) Techniki informacyjne dla wnioskowania oraz generowania, reprezentacji i zarządzania wiedzą Zadanie nr 2 Relacyjne systemy dedukcyjne: teoria i zastosowania
INTEGRACJA METOD I DANYCH W OTWARTYM SYSTEMIE WIELOASPEKTOWEJ ANALIZY PORÓWNAWCZEJ
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XI/2, 2010, str. 120 129 INTEGRACJA METOD I DANYCH W OTWARTYM SYSTEMIE WIELOASPEKTOWEJ ANALIZY PORÓWNAWCZEJ Tomasz Dudek Zakład Logistyki i Informatyki AM
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XI/2, 2010, str. 120 129 INTEGRACJA METOD I DANYCH W OTWARTYM SYSTEMIE WIELOASPEKTOWEJ ANALIZY PORÓWNAWCZEJ Tomasz Dudek Zakład Logistyki i Informatyki AM
1. WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 KARTA PRZEDMIOTU przedmiotu Stopień studiów i forma Rodzaj przedmiotu Grupa kursów Zaawansowane techniki analizy systemowej oparte na modelowaniu warsztaty Studia podyplomowe Obowiązkowy NIE Wykład Ćwiczenia
KARTA PRZEDMIOTU przedmiotu Stopień studiów i forma Rodzaj przedmiotu Grupa kursów Zaawansowane techniki analizy systemowej oparte na modelowaniu warsztaty Studia podyplomowe Obowiązkowy NIE Wykład Ćwiczenia
Bazy danych. Andrzej Łachwa, UJ, /15
 Bazy danych Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl www.uj.edu.pl/web/zpgk/materialy 10/15 Semantyka schematu relacyjnej bazy danych Schemat bazy danych składa się ze schematów relacji i więzów
Bazy danych Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl www.uj.edu.pl/web/zpgk/materialy 10/15 Semantyka schematu relacyjnej bazy danych Schemat bazy danych składa się ze schematów relacji i więzów
Wykorzystanie standardów serii ISO 19100 oraz OGC dla potrzeb budowy infrastruktury danych przestrzennych
 Wykorzystanie standardów serii ISO 19100 oraz OGC dla potrzeb budowy infrastruktury danych przestrzennych dr inż. Adam Iwaniak Infrastruktura Danych Przestrzennych w Polsce i Europie Seminarium, AR Wrocław
Wykorzystanie standardów serii ISO 19100 oraz OGC dla potrzeb budowy infrastruktury danych przestrzennych dr inż. Adam Iwaniak Infrastruktura Danych Przestrzennych w Polsce i Europie Seminarium, AR Wrocław
Internet Semantyczny i Logika I
 Internet Semantyczny i Logika I Warstwy Internetu Semantycznego Dowód Zaufanie Logika OWL, Ontologie Podpis cyfrowy RDF, schematy RDF XML, schematy XML przestrzenie nazw URI Po co nam logika? Potrzebujemy
Internet Semantyczny i Logika I Warstwy Internetu Semantycznego Dowód Zaufanie Logika OWL, Ontologie Podpis cyfrowy RDF, schematy RDF XML, schematy XML przestrzenie nazw URI Po co nam logika? Potrzebujemy
STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI
 1-2011 PROBLEMY EKSPLOATACJI 89 Franciszek GRABSKI Akademia Marynarki Wojennej, Gdynia STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI Słowa kluczowe Bezpieczeństwo, procesy semimarkowskie,
1-2011 PROBLEMY EKSPLOATACJI 89 Franciszek GRABSKI Akademia Marynarki Wojennej, Gdynia STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI Słowa kluczowe Bezpieczeństwo, procesy semimarkowskie,
XQTav - reprezentacja diagramów przepływu prac w formacie SCUFL przy pomocy XQuery
 http://xqtav.sourceforge.net XQTav - reprezentacja diagramów przepływu prac w formacie SCUFL przy pomocy XQuery dr hab. Jerzy Tyszkiewicz dr Andrzej Kierzek mgr Jacek Sroka Grzegorz Kaczor praca mgr pod
http://xqtav.sourceforge.net XQTav - reprezentacja diagramów przepływu prac w formacie SCUFL przy pomocy XQuery dr hab. Jerzy Tyszkiewicz dr Andrzej Kierzek mgr Jacek Sroka Grzegorz Kaczor praca mgr pod
Wykład I. Wprowadzenie do baz danych
 Wykład I Wprowadzenie do baz danych Trochę historii Pierwsze znane użycie terminu baza danych miało miejsce w listopadzie w 1963 roku. W latach sześcdziesątych XX wieku został opracowany przez Charles
Wykład I Wprowadzenie do baz danych Trochę historii Pierwsze znane użycie terminu baza danych miało miejsce w listopadzie w 1963 roku. W latach sześcdziesątych XX wieku został opracowany przez Charles
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011).
 Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011). Poprzedniczka tej notatki zawierała błędy! Ta pewnie zresztą też ; ). Ćwiczenie 3 zostało zmienione, bo żądałem, byście dowodzili czegoś,
Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011). Poprzedniczka tej notatki zawierała błędy! Ta pewnie zresztą też ; ). Ćwiczenie 3 zostało zmienione, bo żądałem, byście dowodzili czegoś,
SCHEMAT KONGLOMERATOWEJ BAZY WIEDZY 1
 STUDIA INFORMATICA 2012 Volume 33 Number 2A (105) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki SCHEMAT
STUDIA INFORMATICA 2012 Volume 33 Number 2A (105) Krzysztof GOCZYŁA, Aleksander WALOSZEK, Wojciech WALOSZEK, Teresa ZAWADZKA Politechnika Gdańska, Wydział Elektroniki, Telekomunikacji i Informatyki SCHEMAT
Logika Matematyczna (1)
 Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 4 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (1) 4 X 2007 1 / 18 Plan konwersatorium Dzisiaj:
Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 4 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (1) 4 X 2007 1 / 18 Plan konwersatorium Dzisiaj:
SCENARIUSZ LEKCJI. Streszczenie. Czas realizacji. Podstawa programowa
 Autorzy scenariusza: SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH
Autorzy scenariusza: SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH
Automatyzacja procesu tworzenia i zarządzania Wirtualnymi Organizacjami w oparciu o wiedzę w zastosowaniu do architektur zorientowanych na usługi
 IT-SOA Automatyzacja procesu tworzenia i zarządzania Wirtualnymi Organizacjami w oparciu o wiedzę w zastosowaniu do architektur zorientowanych na usługi Dariusz Król, W. Funika, B. Kryza, R. Słota, J.
IT-SOA Automatyzacja procesu tworzenia i zarządzania Wirtualnymi Organizacjami w oparciu o wiedzę w zastosowaniu do architektur zorientowanych na usługi Dariusz Król, W. Funika, B. Kryza, R. Słota, J.
Zasada indukcji matematycznej
 Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
1. Problem badawczy i jego znaczenie. Gdańsk,
 prof. dr hab. inż. Krzysztof Goczyła, prof. zw. PG Politechnika Gdańska Wydział Elektroniki, Telekomunikacji i Informatyki kris@eti.pg.edu.pl Gdańsk, 31.01.2018 Recenzja rozprawy doktorskiej mgr. inż.
prof. dr hab. inż. Krzysztof Goczyła, prof. zw. PG Politechnika Gdańska Wydział Elektroniki, Telekomunikacji i Informatyki kris@eti.pg.edu.pl Gdańsk, 31.01.2018 Recenzja rozprawy doktorskiej mgr. inż.
Wstęp do Techniki Cyfrowej... Algebra Boole a
 Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Adam Meissner.
 Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Podstawy logiki pierwszego rzędu
Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Podstawy logiki pierwszego rzędu
Kraków, 14 marca 2013 r.
 Scenariusze i trendy rozwojowe wybranych technologii społeczeństwa informacyjnego do roku 2025 Antoni Ligęza Perspektywy rozwoju systemów eksperckich do roku 2025 Kraków, 14 marca 2013 r. Dane informacja
Scenariusze i trendy rozwojowe wybranych technologii społeczeństwa informacyjnego do roku 2025 Antoni Ligęza Perspektywy rozwoju systemów eksperckich do roku 2025 Kraków, 14 marca 2013 r. Dane informacja
Algorytm. Krótka historia algorytmów
 Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Algorytm znaczenie cybernetyczne Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów. znaczenie matematyczne
Zasady Nazewnictwa. Dokumentów XML 2007-11-08. Strona 1 z 9
 Zasady Nazewnictwa Dokumentów 2007-11-08 Strona 1 z 9 Spis treści I. Wstęp... 3 II. Znaczenie spójnych zasady nazewnictwa... 3 III. Zasady nazewnictwa wybrane zagadnienia... 3 1. Język oraz forma nazewnictwa...
Zasady Nazewnictwa Dokumentów 2007-11-08 Strona 1 z 9 Spis treści I. Wstęp... 3 II. Znaczenie spójnych zasady nazewnictwa... 3 III. Zasady nazewnictwa wybrane zagadnienia... 3 1. Język oraz forma nazewnictwa...
1. Synteza automatów Moore a i Mealy realizujących zadane przekształcenie 2. Transformacja automatu Moore a w automat Mealy i odwrotnie
 Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
Spis treści. Analiza i modelowanie_nowicki, Chomiak_Księga1.indb :03:08
 Spis treści Wstęp.............................................................. 7 Część I Podstawy analizy i modelowania systemów 1. Charakterystyka systemów informacyjnych....................... 13 1.1.
Spis treści Wstęp.............................................................. 7 Część I Podstawy analizy i modelowania systemów 1. Charakterystyka systemów informacyjnych....................... 13 1.1.
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
Zad. 3: Układ równań liniowych
 1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
Model relacyjny. Wykład II
 Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
Karta opisu przedmiotu Zaawansowane techniki analizy systemowej oparte o modelowanie warsztaty
 Karta opisu przedmiotu Zaawansowane techniki analizy systemowej oparte o modelowanie warsztaty przedmiotu Stopień studiów i forma: Rodzaj przedmiotu Kod przedmiotu Grupa kursów Zaawansowane techniki analizy
Karta opisu przedmiotu Zaawansowane techniki analizy systemowej oparte o modelowanie warsztaty przedmiotu Stopień studiów i forma: Rodzaj przedmiotu Kod przedmiotu Grupa kursów Zaawansowane techniki analizy
6. Zagadnienie parkowania ciężarówki.
 6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
020 Liczby rzeczywiste
 020 Liczby rzeczywiste N = {1,2,3,...} Z = { 0,1, 1,2, 2,...} m Q = { : m, n Z, n 0} n Operacje liczbowe Zbiór Dodawanie Odejmowanie Mnożenie Dzielenie N Z Q Pytanie Dlaczego zbiór liczb wymiernych nie
020 Liczby rzeczywiste N = {1,2,3,...} Z = { 0,1, 1,2, 2,...} m Q = { : m, n Z, n 0} n Operacje liczbowe Zbiór Dodawanie Odejmowanie Mnożenie Dzielenie N Z Q Pytanie Dlaczego zbiór liczb wymiernych nie
Dane porównywalne w śródrocznym sprawozdaniu finansowym. Wpisany przez Krzysztof Maksymiuk
 Zarówno Ustawa o rachunkowości, jak i MSR 34 nie określają, które jednostki powinny sporządzać i publikować śródroczne sprawozdania finansowe, ani jak często powinny to czynić. Sprawozdania finansowe sporządzane
Zarówno Ustawa o rachunkowości, jak i MSR 34 nie określają, które jednostki powinny sporządzać i publikować śródroczne sprawozdania finansowe, ani jak często powinny to czynić. Sprawozdania finansowe sporządzane
Programowanie deklaratywne
 Programowanie deklaratywne Artur Michalski Informatyka II rok Plan wykładu Wprowadzenie do języka Prolog Budowa składniowa i interpretacja programów prologowych Listy, operatory i operacje arytmetyczne
Programowanie deklaratywne Artur Michalski Informatyka II rok Plan wykładu Wprowadzenie do języka Prolog Budowa składniowa i interpretacja programów prologowych Listy, operatory i operacje arytmetyczne
2010-10-21 PLAN WYKŁADU BAZY DANYCH MODEL DANYCH. Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna HISTORIA
 PLAN WYKŁADU Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna BAZY DANYCH Wykład 2 dr inż. Agnieszka Bołtuć MODEL DANYCH Model danych jest zbiorem ogólnych zasad posługiwania
PLAN WYKŁADU Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna BAZY DANYCH Wykład 2 dr inż. Agnieszka Bołtuć MODEL DANYCH Model danych jest zbiorem ogólnych zasad posługiwania
INFORMATYKA, TECHNOLOGIA INFORMACYJNA ORAZ INFORMATYKA W LOGISTYCE
 Studia podyplomowe dla nauczycieli INFORMATYKA, TECHNOLOGIA INFORMACYJNA ORAZ INFORMATYKA W LOGISTYCE Przedmiot JĘZYKI PROGRAMOWANIA DEFINICJE I PODSTAWOWE POJĘCIA Autor mgr Sławomir Ciernicki 1/7 Aby
Studia podyplomowe dla nauczycieli INFORMATYKA, TECHNOLOGIA INFORMACYJNA ORAZ INFORMATYKA W LOGISTYCE Przedmiot JĘZYKI PROGRAMOWANIA DEFINICJE I PODSTAWOWE POJĘCIA Autor mgr Sławomir Ciernicki 1/7 Aby
Słowem wstępu. Część rodziny języków XSL. Standard: W3C XSLT razem XPath 1.0 XSLT Trwają prace nad XSLT 3.0
 Słowem wstępu Część rodziny języków XSL Standard: W3C XSLT 1.0-1999 razem XPath 1.0 XSLT 2.0-2007 Trwają prace nad XSLT 3.0 Problem Zakładane przez XML usunięcie danych dotyczących prezentacji pociąga
Słowem wstępu Część rodziny języków XSL Standard: W3C XSLT 1.0-1999 razem XPath 1.0 XSLT 2.0-2007 Trwają prace nad XSLT 3.0 Problem Zakładane przez XML usunięcie danych dotyczących prezentacji pociąga
Metody Kompilacji Wykład 3
 Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Modelowanie hierarchicznych struktur w relacyjnych bazach danych
 Modelowanie hierarchicznych struktur w relacyjnych bazach danych Wiktor Warmus (wiktorwarmus@gmail.com) Kamil Witecki (kamil@witecki.net.pl) 5 maja 2010 Motywacje Teoria relacyjnych baz danych Do czego
Modelowanie hierarchicznych struktur w relacyjnych bazach danych Wiktor Warmus (wiktorwarmus@gmail.com) Kamil Witecki (kamil@witecki.net.pl) 5 maja 2010 Motywacje Teoria relacyjnych baz danych Do czego
Elementy logiki. Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń
 Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Przygotowanie materiału uczącego dla OCR w oparciu o aplikację Wycinanki.
 Przygotowanie materiału uczącego dla OCR w oparciu o aplikację Wycinanki. Zespół bibliotek cyfrowych PCSS 6 maja 2011 1 Cel aplikacji Aplikacja wspomaga przygotowanie poprawnego materiału uczącego dla
Przygotowanie materiału uczącego dla OCR w oparciu o aplikację Wycinanki. Zespół bibliotek cyfrowych PCSS 6 maja 2011 1 Cel aplikacji Aplikacja wspomaga przygotowanie poprawnego materiału uczącego dla
3 grudnia Sieć Semantyczna
 Akademia Górniczo-Hutnicza http://www.agh.edu.pl/ 1/19 3 grudnia 2005 Sieć Semantyczna Michał Budzowski budzow@grad.org 2/19 Plan prezentacji Krótka historia Problemy z WWW Koncepcja Sieci Semantycznej
Akademia Górniczo-Hutnicza http://www.agh.edu.pl/ 1/19 3 grudnia 2005 Sieć Semantyczna Michał Budzowski budzow@grad.org 2/19 Plan prezentacji Krótka historia Problemy z WWW Koncepcja Sieci Semantycznej
Definicja: alfabetem. słowem długością słowa
 Definicja: Niech X będzie zbiorem niepustym. Zbiór ten będziemy nazywać alfabetem. Skończony ciąg elementów alfabetu X będziemy nazywać słowem a liczbę elementów tego ciągu nazywamy długością słowa. Na
Definicja: Niech X będzie zbiorem niepustym. Zbiór ten będziemy nazywać alfabetem. Skończony ciąg elementów alfabetu X będziemy nazywać słowem a liczbę elementów tego ciągu nazywamy długością słowa. Na
Instytut Technik Innowacyjnych Semantyczna integracja danych - metody, technologie, przykłady, wyzwania
 Instytut Technik Innowacyjnych Semantyczna integracja danych - metody, technologie, przykłady, wyzwania Michał Socha, Wojciech Górka Integracja danych Prosty export/import Integracja 1:1 łączenie baz danych
Instytut Technik Innowacyjnych Semantyczna integracja danych - metody, technologie, przykłady, wyzwania Michał Socha, Wojciech Górka Integracja danych Prosty export/import Integracja 1:1 łączenie baz danych
SCENARIUSZ LEKCJI. TEMAT LEKCJI: Zastosowanie średnich w statystyce i matematyce. Podstawowe pojęcia statystyczne. Streszczenie.
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
Diagramy ERD. Model struktury danych jest najczęściej tworzony z wykorzystaniem diagramów pojęciowych (konceptualnych). Najpopularniejszym
 Diagramy ERD. Model struktury danych jest najczęściej tworzony z wykorzystaniem diagramów pojęciowych (konceptualnych). Najpopularniejszym konceptualnym modelem danych jest tzw. model związków encji (ERM
Diagramy ERD. Model struktury danych jest najczęściej tworzony z wykorzystaniem diagramów pojęciowych (konceptualnych). Najpopularniejszym konceptualnym modelem danych jest tzw. model związków encji (ERM
Technologie baz danych
 Plan wykładu Technologie baz danych Wykład 2: Relacyjny model danych - zależności funkcyjne. SQL - podstawy Definicja zależności funkcyjnych Reguły dotyczące zależności funkcyjnych Domknięcie zbioru atrybutów
Plan wykładu Technologie baz danych Wykład 2: Relacyjny model danych - zależności funkcyjne. SQL - podstawy Definicja zależności funkcyjnych Reguły dotyczące zależności funkcyjnych Domknięcie zbioru atrybutów
MINISTERSTWO SPRAW WEWNĘTRZNYCH I ADMINISTRACJI DEPARTAMENT INFORMATYZACJI
 MINISTERSTWO SPRAW WEWNĘTRZNYCH I ADMINISTRACJI DEPARTAMENT INFORMATYZACJI ul. Wspólna 1/3 00-529 Warszawa ZASADY NAZEWNICTWA DOKUMENTÓW XML Projekt współfinansowany Przez Unię Europejską Europejski Fundusz
MINISTERSTWO SPRAW WEWNĘTRZNYCH I ADMINISTRACJI DEPARTAMENT INFORMATYZACJI ul. Wspólna 1/3 00-529 Warszawa ZASADY NAZEWNICTWA DOKUMENTÓW XML Projekt współfinansowany Przez Unię Europejską Europejski Fundusz
Technologie informacyjne - wykład 12 -
 Zakład Fizyki Budowli i Komputerowych Metod Projektowania Instytut Budownictwa Wydział Budownictwa Lądowego i Wodnego Politechnika Wrocławska Technologie informacyjne - wykład 12 - Prowadzący: Dmochowski
Zakład Fizyki Budowli i Komputerowych Metod Projektowania Instytut Budownictwa Wydział Budownictwa Lądowego i Wodnego Politechnika Wrocławska Technologie informacyjne - wykład 12 - Prowadzący: Dmochowski
METODA ELPAR ŁĄCZENIA ONTOLOGII OPARTA NA ICH KARTOGRAFICZNEJ REPREZENTACJI
 METODA ELPAR ŁĄCZENIA ONTOLOGII OPARTA NA ICH KARTOGRAFICZNEJ REPREZENTACJI Krzysztof GOCZYŁA*, Teresa GRABOWSKA** Streszczenie. Jednym z głównych problemów związanych z integracją wiedzy z róŝnych źródeł
METODA ELPAR ŁĄCZENIA ONTOLOGII OPARTA NA ICH KARTOGRAFICZNEJ REPREZENTACJI Krzysztof GOCZYŁA*, Teresa GRABOWSKA** Streszczenie. Jednym z głównych problemów związanych z integracją wiedzy z róŝnych źródeł
