Uniwersytet Mikołaja Kopernika. Wydział Matematyki i Informatyki. Jarosław Piersa piersaj(at)mat.uni.torun.pl
|
|
|
- Ryszard Chrzanowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Uniwersytet Mikołaja Kopernika Wydział Matematyki i Informatyki Jarosław Piersa piersaj(at)mat.uni.torun.pl Abstrakt Poniższy referat dotyczy zagadnień uczenia w sieciach neuronowych i bayesowskich(sieciach przekonań). Jest opracowaniem rozdziału 19-go książki Artificial Intelligence, A modern Approach Russela i Norviga[1]. Przygotowany został w ramach laboratorium Wstęp do Metod Sztucznej Inteligencji w roku akademickim 2008/ SieciNeuronowe 1.1 Komórkineuronowe Z biologicznego punktu widzenia neuron jest komórką(rys 1). Składa się z ciała komórki (soma), odchodzących drzewiastych dendrytów oraz zazwyczaj jednego długiego połączenia aksonu. Dendryty i akson są zakończone połączeniami synaptycznymi które umożliwaiają komunikacje między neuronami. Ilość połączeń wynosi od kilkudziesięciu do kilkuset tysięcy. Dendryty zazwyczaj przewodzą impulsy do komórki. Akson jest długim mierzącym nawet do metra połączeniem przewodzącym impulsy od ciała komórki. Impulsy elektryczne wysyłane przez neurony bazują na prądzie jonowym(a nie elektronowym). Potencjał elektryczny gromadzny na błonie komórkowej kumuluje się wraz z odbieraniem impulsów od innych neuronów i gdy przekroczy próg wysyłana jest odpowiedź impulsową wzdłóż aksonu. Po wysłaniu impulsu neuron przez pewien okrez czasu staje się niezdolny do odbierania i wysłania kolejnych impulsów, po czym powraca do normalnego stanu. Połączone ze sobą neurony tworzą ośrodki nerwowe zarówno u ludzi, jak i u ssaków, kręgowców, a także zwierząt bezstrunowych(owady, pajęczaki). Istniejące w potocznym języku szare komórki nie są niczym innym jak siecią neuronową, składającą się na zewnętrzną warstwę mózgu. Co prawda pełne zrozumienie funkcjonowania ludzkiego umysłu nadal pozostaje wyzwaniem, ale znajomość samej ogólnej budowy i dynamiki komórek nerwowych pozwala do pewnego stopnia je symulować. Sztuczne sieci neuronowe jako przedmiot badań wyrosły właśnie z nauki o prawdziwych komórkach neuronowych i do dziś są jednym z filarów sztucznej inteligencji. Modele są oczywiście znacznie uproszczone ale sprowadzają się do podebnej idei wiele prostych i podobnych do siebie jednostek współpracuje w celu osiągnięcia pewnego celu. Mimo postępu w rozwoju techniki nadal nie udało się zbudować komputera o mocy obliczeniowej choćby porównywalnej z ludzkim mózgiem. Zasadniczą zaporą zdaje się być całkowita współbieżność komórek nerwowych, podczas gdy symulacje dzielą czas kilku do kilkunastu procesorów pomiędzy wiele milionów czy miliardów jednostek w sztucznej sieci (patrz tabela 2). 1.2 Perceptron Perceptron jest najprostszym modelem komórki nerwowej. Jednostka składa się z określonej (N)liczbywejść x i, i = 1..N,wag w i, i = 1..N(jednawagaskojarzonazkażdymwejściem) oraz pewnej funkcji aktywacji f : R R. Jednostka działa synchronicznie. W danym kroku 1
2 Rysunek 1: Komórka nerwowa komputer mózg Jednostkiobliczeniowe 1CPU neuronów Pojemność 10 9 bram, dyski neuronów, synaps Czas1cyklu 10 8 s 10 3 s Przepustowość 10 9 b/s b/s Operacjinaneuronach1/s Rysunek 2: Porównanie możliwości obliczeniowych kompurerów(ok 1995) i ludzkiego mózgu. na wszystkich wejściach pojawiają się wartości(całkowite lub rzeczywiste). Jednostka liczy sumę ważoną wszystkich wejść: N in = x i w i a następnie zwraca wartość funkcji aktywacji na wyliczonej wartości(patrz rys 3) f(in) W zależności od rodzaju zagadnienia rozważa się różne postacie funkcji f: Identyczność f(s) = s takajednostkaliczypoprostusumęważonąwejść, i=1 Rysunek 3: Schemat działania perceptronu 2
3 Funkcja progowa(bipolarna) f(s) = { 0 s < p 1 s p Wartość p może być dodatkowym parametrem opisującym perceptron. Ten typ funkcji modeluje wysyłanie impulsu po przekroczeniu pewnego progu, które to zachowanie charakteryzuje komórki neuronowe. funkcja znakowa(bipolarna) f(s) = { 1 s < p +1 s p Funkcja podobna do poprzedniej z tą różnicą, że wartość 1 nie jest elementem neutralnym dodawania i odpowiedź negatywna może mieć pewien wpływ. Sigmoida f(s) = σ(s) = exp( s) Funkcja sigmoidalna może tu dziwić. Wymaga dzielenia i potęgowania, czyli więcej obliczeń, co nie powinno być wskazane przy wielokrotnym wykonywaniu. Jednakże jest ciągła i różniczkowalna co ma zasadnicze znaczenie przy algorytmach uczenia i przybliża funkcją bipolarną. Ponadto zachodzi 1.3 Uczenieperceptronu σ (s) = σ(s) (1 σ + (s)) Termin perceptron poza pojedynczą jednostką może czasem oznaczać sieć składającą się z kilku niezależnych od siebie jednostek, która zwraca nie jedną, a kilka liczb. W takim przypadkuwynikinterpretowanyjestjakojedenelement R M,gdzie Mjestilościąperceptronów. Problemuczeniasiecsprowadzasiędoznalezieniawartościwag w i iewentualnieprogu pdla wszystkich jednostek w sieci(często dla jednej). Czasami przyjmuje się, że zamiast progu neuron ma dodatkowe wejście na które zawsze przychodzi wartość 1 a jego waga wynosi w 0 = p. Danyniechbędziezestawprzykładów E = { E (1)...E (k)},gdzie E (i) = (e (i) 1,..., e(i) N ) R N iodpowiadająceimpoprawnewyniki T (1)...T (k). DanyteżmamyperceptronoN wejściach i jednym wyjściu. Weźmyprzykład E j iodpowiadającąmupoprawnąodpowiedź T j,niechsiećzbieżącym zestawem wag zwróci wartość O. Rozważmy błąd: ERR = T j O Jeżelijestdodatnitomusimyzwiększyć O,jeżeliwejście e j i > 0tozwiększeniewagi w i zwiększy O,jeżeli e j i < 0tozmniejszenie w izwiększy O. Jeżeli błąd ERR jest ujemny to musimy zmniejszyć O. Podobnie rozumując musimy zmniejszyćwagi w i jeśliwejście e j i > 0izwiększyć w iwprzeciwnymwypadkutj. e j i < 0. Podsumowując te rozważania otrzymujemy algorytm: Wylosujwagi w i małe,blisko 0. Wybierzprzykład E j iodpowiadającąmupoprawnąodpowiedź T j, Oblicz O wynikdziałaniasiecina E j Oblicz ERR = T j O 3
4 Rysunek 4: Problem liniowo separowalny(po lewej), i nieseparowalny(po prawej) Uaktualnij wszystkie wagi zgodnie ze wzorem η > 0jeststałąuczenia. w i = w i + η ERR e j i Jeżeli sieć klasyfikuje poprawnie wszystkie(większość) przykłady to zakończ, wpw wróćdo2. Warunek końcowy powinien traktowany ze szczególną uwagą. Nie musi być prawdą, że dla każdego zestawu uczącego istnieje zestaw wag, który daje poprawną klasyfikację na wszystkich przykładach. Obliczenia wykonywane przez perceptron dają równanie pewnej hiperprzestrzeni N 1 wymiarowej. Nałożenie na to funkcji progowej pozwala stwierdzić czy dany punkt leży po właściwej stronie tej hiperprzestrzeni, ale niewiele więcej. To ograniczenie nazywa się liniową separowalnością problemu i już w latach 60-tych XX wieku pokazano, że pojedynczy perceptron(a także jednowarstwowa sieć perceptronów) nie może rozwiązać problemu, który nie jest liniowo separowalny(patrz rys. 4). 1.4 Siecineuronowe Podobnie jak w mózgu, sztuczne sieci neuronowe są zestawem prostych jednostek połączonych między sobą w bardziej skomplikowane struktury. Jak się okazuje przejście z jednej jednostki do wielu współpracujących ze sobą pozwala znacznie zwiększyć możliwości obliczeniowe. W zależności od architektury wyróżniane są następujące klasy sieci: Sieci skierowane(ang. feed-forward) z jednoznacznie zdefiniowanym kierunkiem przepływu impulsów, nie dopuszczają skierowanych cykli. Sieci rekurencyjne, bardziej ogólne, dopuszczające cykle(podobnie jak sieci nerwowe) ale trudniejsze w uczeniu. Nawet najlepiej opisane z nich charakterysują się regularną strukturą, np: sieci Hopfielda, maszyny Boltzmanna. Studiowanie właściwości sieci rekurencyjnych wykracza poza materiał tego referatu. 1.5 Sieciwarstwowe Sieci warstwowe są przykładem sieci feed-forward. Perceptrony pogrupowane są w warstwy, dane wejściowe wchodzą do wszystkich jednostek w najniższej warstwie Wyniki policzone w warstwie niższej są traktowane jako wejścia w warstwie bezpośrednio wyżej. Wyniki z warstwy najwyższej są zwracane jako wyniki całej sieci na danych wejściowych(rys. 5). Warstwy, które nie są wyjściowymi nazywane są ukrytymi. Sieci neuronowe zjedną warstwą ukrytą mogą przybliżać każdą funkcję ciągłą. Sieci z dwiema i więcej warstwami nieciągłymi mogą przybliżać funkcje nieciągłe, o ile ilość jednostek w sieci jest wystarczająca. 4
5 Rysunek 5: Warstwowa sieć neuronowa O ile znane są algorytmy uczenia dla sieci warstwowych to problem optymalizacji samej architektury sieci dla zadanych danych jest trudny. Zbyt mała ilość neuronów nie zagwarantuje wystarczającej ilości pamięci by się funkcji nauczyć. Zbyt wielka da z kolei pamięć słownikową, sieć zapamięta wyniki wraz z odpowiedziami, ale straci zdolność do generalizacjitj.ocenydanych,któresą podobne dotegoczegosięuczyła(ipowinnymiećrównież podobne wyniki). Stosowane są algorytmu genetyczne lub w konkretnych wprzypadkach algorytmy konstrukcji sieci wraz z doborem wag, ale w ogólnej sytuacji problem zależy od danych, jakimi sieć ma być uczona. Najpopularniejszym algorytmem uczenia sieci neuronowych jest propagacja wsteczna czasem zwana również wsteczna propagacja błędu(ang. back-propagation, back-errorpropagation). Idea algorytmu polega na obliczeniu błędu między zwracaną odpowiedzią, a poprawnym wynikiem i następnie podzieleniu odpowiedzialności za ten błąd pomiędzy wagi. Następnie korygowane są wagi w głębszych warstwach sieci w zależności od ich wpływu na błąd. Propagacja wsteczna jest przypadkiem algorytmu spadku gradientowego. Daną mamy funkcję(błąd), którą minimalizujemy na przestrzeni wartości wag. Ponieważ w obliczeniach potrzebujemy pochodnej, w sieci powinna być stosowana sigmoidalna funkcja aktywacji. Dane Śieć neuronowa, zestaw danych wejściowych E i poprawnych odpowiedzi T. Wynik Wartościwag w i, j Algorytm Wybierz przykład E z listy przykładów i odpowiadający mu poprawny wynik T Oblicz wynik działania sieci na E, zapamiataj go, zapamietaj również wyniki w warstwachpośrednich o j,sumyważone in j (wynikiprzedzaaplikowaniemfunkcjiaktywującej)iwejsciadoneuronowwdanejwarstwie I k,j (wejsciemdowarstwypierwszej jest przykład, dla warstw wyższych j są nimi wyniki z warstwy poprzedniej k) Dla wszystkich jednostek i w zewnętrznej warstwie sieci: Obliczbłąd err i = T i o i Oblicz i = err i f (in i ) 5
6 Uaktualnij wagi w jednostce i w j,i = w j,i + η o j err i f (in i ) Dla wszystkich jednostek j w kolejnych warstwach sieci: Oblicz błąd j = f (in j ) l w j,l l Uaktualnij wagi do jednostki j Wróćdo1. w k,j = w k,j + η I k,j j Zakończ po wykonaniu określonej liczby kroków lub osiągnięciu zadowalającego poziomu błędu Gdzie: I k,j k-tewejściedojednostki j η > 0stałauczenia 1.6 Podsumowanie Sieci neuronowe znalazły zastosowanie przede wszystkim tam, gdzie metody analityczne zawodzą ze względu na poziom skomplikowania czy wymiar przestrzeni. Między innymi: rozpoznawanie obrazów, rozpoznawanie tekstu pisanego, wymawianie tekstu pisanego, kierowanie pojazdami itp. Same sieci charakteryzują się: Odpornością na szum ze względy na obliczenia na średnich ważonych i progowe funkcje. Efektywność obliczeniowa mając dane wejście, wynik może zostać obliczony w czasie liniowym względem ilości jednostek w sieci. Obliczenia to w większości mnożenia i dodawania. Generalizacja jeżeli sieć nie zostanie przeuczona, nauka na przykładach daje również porządane zachowanie na danych które nie znalazły się w zestawie uczącym. Zdolności opisu dane wejściowe mają często interpretację w świecie podobnie jak wynik. Ale już wartościom w jednostkach ukrytych trudno przypisać jakiekolwiek znaczenie. Sieci neuronowe mogą działać zarówno dla danych dyskretnych(całkowitoliczbowych) jak i ciągłych. Z drugiej strony odporność na szum, czyni je niemal niezdatnymi do obliczeń logicznych, które zależą od wartości pojedynczych zmiennych. W takich sytuacjach potrzebna jest wykładnicza wzgledem ilości zmiennych liczba jednostek ukrytych. Nieprzeźroczystość sieć neuronowa jest czarną skrzynką raz nauczona może działać stale. Przyjmuje pewne dane i zwraca wyniki, ale absolutnie nie wiadomo jak są one obliczane, ani jakie są wyniki pośrednie. Jeżeli z jakichś powodów sieć przestanie działać(uszkodzenie procesora), trudno stwierdzić dlaczego i naprawić problem. Najprostszym(często jedynym) rozwiązaniem jest wówczas ponowne uczenie sieci, czego użytkownik sam wykonać nie może. Korzystanie z wiedzy choć znane są algorytmu uczenia bez nauczyciela, w większości przypadków wiedza jest konieczna do uczenia sieci. 6
7 2 Siecibayesowskie 2.1 Co to jest sieć bayesowsja Rysunek 6: Sieć bayesowska Podobniejak sieć neuronowa, sieć bayesowska jest układem połączonych ze sobą niekomplikowanych jednostek. Graf sieci jest skierowany i acykliczny, dopuszczamy wyłącznie cykle nieskierowane np. dwie różne drogi między tą samą parą węzłów. Jednostki opisują pewne rozkłady prawdopodobieństw warunkowych zależnych od wartości ich rodziców, po jednym rozkładnie na każdą możliwą kombinację wartości. Jednostki, które nie posiadają rodziców opisują tylko jeden rozkład. W działaniu mając daną wiedzę(to jest wartości zmiennych w jednym lub więcej węźle), można za pomocą sieci bayesowskiej obliczyć prawdopodobieństwa przyjęcia konkretnych wartości przez pozostałe jednostki. Jeżeli wiedza dotyczy węzłów na początku sieci mówimy o wnioskowaniu predyktywnym, czyli co może nastąpić w wyniku aktualnej sytuacji. Jeżeli wiedza dotyczy liści sieci, wówczas wnioskowanie nazywane jest diagnostycznym co spowodowało aktualny stan. Połączenie obu tych sytuacji nazywane jest wnioskowaniem mieszanym lub hybrydowym. 2.2 Uczenie sieci bayesowskiej Zasadniczym problemem podczas uczenia(i wnioskowania) jest obliczenie wielu łańcuchów prawdopodobienstw warunkowych by z wiedzy dojść do interesującego nas węzła, którego prawdopodobieństwo próbujemy oszacować. Mając daną wiedzę D, interesujący nas węzeł Xipośredniehipotezy H 1, H 2...mamy P(X D) = i P(X H i, D)P(H i D) Jako, że hipotez pośrednich może być wiele wynik można przybliżać poprzez: P(X D) P(X H MAP )P(H MAP D) 7
8 gdzie H MAP jesthipotezą,któramaksymalizujeteniloczyn(maximumaposteriori).podstawiając dodatkowo P(H i D) = P(D H i)p(h i ) P(D) zagadnienie redukuje się do maksymalizowania licznika. Przy dodatkowym założeniu, żę hipotezy H i sąjednakowoprawdopodobne,pozostajejużtylkoznaleźć H i,któremaksymalizuje P(D H i ),oznaczaneczasemjako H ML (maximumlikehood).zauważmy,żepoczynione tu uproszczenia z jednej strony upraszczają problem i czynią go mniej podatnym na szum, ale z drugiej mogą ignorować część danych uczących i skutkować gorszymi rezultatami. Uczenie sieci bayesowskiej można rozpatrywać w kilku przypadkach: Znana jest struktura sieci, brak jednostek ukrytych. W tym przypadku uczenie ogranicza się do znalezenia tabel rozkładów warunkowych, zazwyczaj za pomocą metod statystycznych. Czasami działające już sieci, podczas pracy zbierają informacje wejściowe by uaktualniać wartości w tabelach. Nieznana struktura sieci, brak jednostek ukrytych. Poza tabelami, należy znaleźć architekturę sieci, tj połączenia między węzłami. Mogą być wykorzystywane algorytmy przeszukiwania do znalezienia optymalnego grafu i przybliżanie wartości prawdopodobieństwpoprzezhipotezy H MAP i H ML. Znana struktura sieci, obecne jednostki ukryte. Sytuacja podobna do uczenia sieci neuronowych z warstwami ukrytymi. Nieznana struktura sieci, jednostki ukryte. Problem najogólniejszy i najtrudniejszy. Na chwilę obecną nie są znane efektywne algorytmy dla tego przypadku. 2.3 Uczenie sieci ze znaną architekturą Jeżeli sieć nie ma ogromnej ilości węzłów, strukturę można dość łatwo przyporządkować zgodnie ze zdrowym rozsądkiem. Każdy węzeł(widoczny) w sieci reprezentuje pewne zdarzenie i człowiek jest w stanie jasno sprecyzować związki przyczynowo-skutkowe między nimi. Jednostki ukryte mają istotny wpływ na rozkłady w tabelach prawdopodobieństw, ale już określenie praktycznego znaczenia jednostki ukrytej może być problemem. Rozpatrywane są z kilku powodów Po pierwsze sieci z jednostkami ukrytymi mogą być znacznie mniejsze pod kątem ilości połączeń między węzłami(rys. 7). Ma to zasadnicze znaczenie gdyż, ilość danych podczas uczenia zależy wykładniczo od stopnia wejściowego jednostek. Węzeł mający Nwejśćbinarnychposiadatabelęprawdopodobieństwz2 N rozkładamiwarunkowymi. Ponadto nie jest prawdą że dla danej architektury sieci i zestawy danych da się znależć tablice, które wiernie odtwarzają te dane. Dodanie jednostek ukrytych może rozwiązać ten problem. Rozważającproblemuczeniawterminachhipotez,chcemyznaleźć H i,któremaksymalizuje P(D H i ). Metodajestpodobnadoalgorytmuspadkugradientowego,używanegow uczeniusiecineuronowych. Ponieważmaksymalizujemywartość P(D H i )tamodyfikacja będzieraczej wspinaczką gradientową.zakładając,żewagi w i odpowiadająwartościom prawdopodobieństwa w tabnlicach pozostaje znaleźć pochodną szukanego prawdopodobieństwa po danej wadze. Niech D = {D 1...D m }będziezestawemdanych.zpowodudużejilościmnożeńrozsądnym będzie liczyć pochodną po logarytmie iloczynu(przejdzie na sumę logarytmów). ln P(D) w i = ln j P(D j) = w i j ln P(D j ) w i = j 1 P(D j ) P(D j ) w i 8
9 Rysunek 7: Sieć bayesowska ze wszystkimi jednostkami widzialnymi(po lewej), równoważna sieć z dodatkową jednostką ukrytą(po prawej). P(D j )/ w i P(D j ) = w i ( x,u P(D j x, u)p(x, u)) P(D j ) Jako,żewaga w i odpowiadazadokładniejedenwpiswtabeliprawdopodobieństwwarunkowych w i = P(X = x i U = u i ) = P(x i u i ) mamy w tej sumie tylko jeden niezerowy składniek w i ( x,u P(D j x, u)p(x u)p(u)) = P(D j x i, u i )P(u i ) = P(x i, u i D j ) = P(x i, u i D j ) P(D j ) P(D j ) P(x i u i ) w i W większości przypadków tę wartość można albo uzyskać bezpośrednio albo kosztem niewielkiej ilości operacji. 2.4 Porównanie sieci neuronowych i bayesowskich Sieci neuronoew i bayesowski, w kontekście rozważań o sztucznej inteligencji, są zazwyczaj wymieniane obok siebie. Jedne i drugie pracują na danych posiadających pewne znaczenie (atrybutach). Wejścia mogą być jedno lub wielowymiarowe, dyskretne i ciągłe, choć sieci bayesowskie dla danych ciągłych są mniej rozwijane. Jednakże w sieciach bayesowskich prawie wszystkie węzły mają pewne semantyczne znaczenie, w sieciach neuronowych znaczenie (semantyczne czyli interpretację w świecie) mają tylko wejścia i jednostki wyjściowe. Sieć neuronowa ma ustaloną ilość wyjść i wejść. Wejścim do sieci bayesowskij może być dowolny (niepełny) podzbiór wierzchołków. Zeleżności między jednostkami w sieciach bayesowskich są proste do opisania i zrozumienia, w sieciach neuronowych niemal niemożliwe. Raz nauczona sieć neuronowa może działać stale i szybko, w liniowym czasie. Sieć bayesowska również nie musi wymagać dodatkowego uczenia, ale wnioskowanie w ogólnych przypadkach jest problemem NP-trudnym, zazwyczaj jednak da się je efektywnie wykonać. Patrząc z drugiej strony sień neuronowa może mieć wykładniczo wiele węzłów ukrytych. Algorytmy konstrukcji architektury sieci są słabo rozwijane w obu przypadkach. Warości w sieciach bayesowskich mają dwa poziomy same wartości zmiennych losowych i prawdopodobieństwa z jakimi są przyjmowane. Sieci neuronowe potrzebują jawnego rozróżnienia między nimi. Literatura [1] Stuart J. Russell, Peter Norvig, Artificial Intelligence, A modern Approach, Prentice Hall, Englewood Cliffs, New Jersey
Uczenie sieci neuronowych i bayesowskich
 Wstęp do metod sztucznej inteligencji www.mat.uni.torun.pl/~piersaj 2009-01-22 Co to jest neuron? Komputer, a mózg komputer mózg Jednostki obliczeniowe 1-4 CPU 10 11 neuronów Pojemność 10 9 b RAM, 10 10
Wstęp do metod sztucznej inteligencji www.mat.uni.torun.pl/~piersaj 2009-01-22 Co to jest neuron? Komputer, a mózg komputer mózg Jednostki obliczeniowe 1-4 CPU 10 11 neuronów Pojemność 10 9 b RAM, 10 10
Podstawy Sztucznej Inteligencji (PSZT)
 Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Uczenie maszynowe Sztuczne sieci neuronowe Plan na dziś Uczenie maszynowe Problem aproksymacji funkcji Sieci neuronowe PSZT, zima 2013, wykład 12
Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Uczenie maszynowe Sztuczne sieci neuronowe Plan na dziś Uczenie maszynowe Problem aproksymacji funkcji Sieci neuronowe PSZT, zima 2013, wykład 12
Wstęp do sieci neuronowych, wykład 04. Skierowane sieci neuronowe. Algorytmy konstrukcyjne dla sieci skierowanych
 Wstęp do sieci neuronowych, wykład 04. Skierowane sieci neuronowe. dla sieci skierowanych Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-25 1 Motywacja
Wstęp do sieci neuronowych, wykład 04. Skierowane sieci neuronowe. dla sieci skierowanych Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-25 1 Motywacja
Sztuczne sieci neuronowe
 www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja różnych rodzajów sztucznych sieci neuronowych. Biologiczny model neuronu Mózg człowieka składa się z około 10 11 komórek nerwowych,
www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja różnych rodzajów sztucznych sieci neuronowych. Biologiczny model neuronu Mózg człowieka składa się z około 10 11 komórek nerwowych,
Wstęp do sztucznych sieci neuronowych
 Wstęp do sztucznych sieci neuronowych Michał Garbowski Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 15 grudnia 2011 Plan wykładu I 1 Wprowadzenie Inspiracja biologiczna
Wstęp do sztucznych sieci neuronowych Michał Garbowski Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 15 grudnia 2011 Plan wykładu I 1 Wprowadzenie Inspiracja biologiczna
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa.
 Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
Sztuczna Inteligencja Tematy projektów Sieci Neuronowe
 PB, 2009 2010 Sztuczna Inteligencja Tematy projektów Sieci Neuronowe Projekt 1 Stwórz projekt implementujący jednokierunkową sztuczną neuronową złożoną z neuronów typu sigmoidalnego z algorytmem uczenia
PB, 2009 2010 Sztuczna Inteligencja Tematy projektów Sieci Neuronowe Projekt 1 Stwórz projekt implementujący jednokierunkową sztuczną neuronową złożoną z neuronów typu sigmoidalnego z algorytmem uczenia
Wprowadzenie do Sieci Neuronowych lista zadań 1
 Wprowadzenie do Sieci Neuronowych lista zadań 1 Maja Czoków, Jarosław Piersa 2010-10-04 1 Zasadyzaliczania 1.1 Oceny Zaliczenie laboratoriów na podstawie implementowania omawianych algorytmów. Każde zadanie
Wprowadzenie do Sieci Neuronowych lista zadań 1 Maja Czoków, Jarosław Piersa 2010-10-04 1 Zasadyzaliczania 1.1 Oceny Zaliczenie laboratoriów na podstawie implementowania omawianych algorytmów. Każde zadanie
Wstęp do sieci neuronowych laboratorium 01 Organizacja zajęć. Perceptron prosty
 Wstęp do sieci neuronowych laboratorium 01 Organizacja zajęć. Perceptron prosty Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-10-03 Projekt pn. Wzmocnienie potencjału
Wstęp do sieci neuronowych laboratorium 01 Organizacja zajęć. Perceptron prosty Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-10-03 Projekt pn. Wzmocnienie potencjału
8. Neuron z ciągłą funkcją aktywacji.
 8. Neuron z ciągłą funkcją aktywacji. W tym ćwiczeniu zapoznamy się z modelem sztucznego neuronu oraz przykładem jego wykorzystania do rozwiązywanie prostego zadania klasyfikacji. Neuron biologiczny i
8. Neuron z ciągłą funkcją aktywacji. W tym ćwiczeniu zapoznamy się z modelem sztucznego neuronu oraz przykładem jego wykorzystania do rozwiązywanie prostego zadania klasyfikacji. Neuron biologiczny i
Wprowadzenie do Sieci Neuronowych Laboratorium 05 Algorytm wstecznej propagacji błędu
 Wprowadzenie do Sieci Neuronowych Laboratorium Algorytm wstecznej propagacji błędu Maja Czoków, Jarosław Piersa --7. Powtórzenie Perceptron sigmoidalny Funkcja sigmoidalna: σ(x) = + exp( c (x p)) () Parametr
Wprowadzenie do Sieci Neuronowych Laboratorium Algorytm wstecznej propagacji błędu Maja Czoków, Jarosław Piersa --7. Powtórzenie Perceptron sigmoidalny Funkcja sigmoidalna: σ(x) = + exp( c (x p)) () Parametr
synaptycznych wszystko to waży 1.5 kg i zajmuje objętość około 1.5 litra. A zużywa mniej energii niż lampka nocna.
 Sieci neuronowe model konekcjonistyczny Plan wykładu Mózg ludzki a komputer Modele konekcjonistycze Perceptron Sieć neuronowa Uczenie sieci Sieci Hopfielda Mózg ludzki a komputer Twój mózg to 00 000 000
Sieci neuronowe model konekcjonistyczny Plan wykładu Mózg ludzki a komputer Modele konekcjonistycze Perceptron Sieć neuronowa Uczenie sieci Sieci Hopfielda Mózg ludzki a komputer Twój mózg to 00 000 000
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa.
 Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-11 1 Modelowanie funkcji logicznych
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-11 1 Modelowanie funkcji logicznych
1. Historia 2. Podstawy neurobiologii 3. Definicje i inne kłamstwa 4. Sztuczny neuron i zasady działania SSN. Agenda
 Sieci neuropodobne 1. Historia 2. Podstawy neurobiologii 3. Definicje i inne kłamstwa 4. Sztuczny neuron i zasady działania SSN Agenda Trochę neurobiologii System nerwowy w organizmach żywych tworzą trzy
Sieci neuropodobne 1. Historia 2. Podstawy neurobiologii 3. Definicje i inne kłamstwa 4. Sztuczny neuron i zasady działania SSN Agenda Trochę neurobiologii System nerwowy w organizmach żywych tworzą trzy
IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ
 IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ Celem ćwiczenia jest zapoznanie się ze sposobem działania sieci neuronowych typu MLP (multi-layer perceptron) uczonych nadzorowaną (z nauczycielem,
IMPLEMENTACJA SIECI NEURONOWYCH MLP Z WALIDACJĄ KRZYŻOWĄ Celem ćwiczenia jest zapoznanie się ze sposobem działania sieci neuronowych typu MLP (multi-layer perceptron) uczonych nadzorowaną (z nauczycielem,
Temat: Sieci neuronowe oraz technologia CUDA
 Elbląg, 27.03.2010 Temat: Sieci neuronowe oraz technologia CUDA Przygotował: Mateusz Górny VIII semestr ASiSK Wstęp Sieci neuronowe są to specyficzne struktury danych odzwierciedlające sieć neuronów w
Elbląg, 27.03.2010 Temat: Sieci neuronowe oraz technologia CUDA Przygotował: Mateusz Górny VIII semestr ASiSK Wstęp Sieci neuronowe są to specyficzne struktury danych odzwierciedlające sieć neuronów w
Zastosowania sieci neuronowych
 Zastosowania sieci neuronowych aproksymacja LABORKA Piotr Ciskowski zadanie 1. aproksymacja funkcji odległość punktów źródło: Żurada i in. Sztuczne sieci neuronowe, przykład 4.4, str. 137 Naucz sieć taką
Zastosowania sieci neuronowych aproksymacja LABORKA Piotr Ciskowski zadanie 1. aproksymacja funkcji odległość punktów źródło: Żurada i in. Sztuczne sieci neuronowe, przykład 4.4, str. 137 Naucz sieć taką
Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe.
 Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe. zajecia.jakubw.pl/nai Literatura: S. Osowski, Sieci neuronowe w ujęciu algorytmicznym. WNT, Warszawa 997. PODSTAWOWE ZAGADNIENIA TECHNICZNE AI
Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe. zajecia.jakubw.pl/nai Literatura: S. Osowski, Sieci neuronowe w ujęciu algorytmicznym. WNT, Warszawa 997. PODSTAWOWE ZAGADNIENIA TECHNICZNE AI
Elementy inteligencji obliczeniowej
 Elementy inteligencji obliczeniowej Paweł Liskowski Institute of Computing Science, Poznań University of Technology 9 October 2018 1 / 19 Perceptron Perceptron (Rosenblatt, 1957) to najprostsza forma sztucznego
Elementy inteligencji obliczeniowej Paweł Liskowski Institute of Computing Science, Poznań University of Technology 9 October 2018 1 / 19 Perceptron Perceptron (Rosenblatt, 1957) to najprostsza forma sztucznego
Wstęp do sieci neuronowych, wykład 03 Warstwy RBF, jednostka Adaline.
 Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Wstęp do teorii sztucznej inteligencji Wykład II. Uczenie sztucznych neuronów.
 Wstęp do teorii sztucznej inteligencji Wykład II Uczenie sztucznych neuronów. 1 - powtórzyć o klasyfikacji: Sieci liniowe I nieliniowe Sieci rekurencyjne Uczenie z nauczycielem lub bez Jednowarstwowe I
Wstęp do teorii sztucznej inteligencji Wykład II Uczenie sztucznych neuronów. 1 - powtórzyć o klasyfikacji: Sieci liniowe I nieliniowe Sieci rekurencyjne Uczenie z nauczycielem lub bez Jednowarstwowe I
Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta
 Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta www.michalbereta.pl Sieci radialne zawsze posiadają jedną warstwę ukrytą, która składa się z neuronów radialnych. Warstwa wyjściowa składa
Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta www.michalbereta.pl Sieci radialne zawsze posiadają jedną warstwę ukrytą, która składa się z neuronów radialnych. Warstwa wyjściowa składa
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa.
 Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-10-10 Projekt pn. Wzmocnienie
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-10-10 Projekt pn. Wzmocnienie
Temat: Sztuczne Sieci Neuronowe. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Sztuczne Sieci Neuronowe Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sztuczne sieci neuronowe
Temat: Sztuczne Sieci Neuronowe Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sztuczne sieci neuronowe
Metody Sztucznej Inteligencji II
 17 marca 2013 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką, która jest w stanie odbierać i przekazywać sygnały elektryczne. Neuron działanie Jeżeli wartość sygnału
17 marca 2013 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką, która jest w stanie odbierać i przekazywać sygnały elektryczne. Neuron działanie Jeżeli wartość sygnału
Wstęp do teorii sztucznej inteligencji Wykład III. Modele sieci neuronowych.
 Wstęp do teorii sztucznej inteligencji Wykład III Modele sieci neuronowych. 1 Perceptron model najprostzszy przypomnienie Schemat neuronu opracowany przez McCullocha i Pittsa w 1943 roku. Przykład funkcji
Wstęp do teorii sztucznej inteligencji Wykład III Modele sieci neuronowych. 1 Perceptron model najprostzszy przypomnienie Schemat neuronu opracowany przez McCullocha i Pittsa w 1943 roku. Przykład funkcji
Wykład 1: Wprowadzenie do sieci neuronowych
 Wykład 1: Wprowadzenie do sieci neuronowych Historia badań nad sieciami neuronowymi. - początki: badanie komórek ośrodkowego układu nerwowego zwierząt i człowieka, czyli neuronów; próby wyjaśnienia i matematycznego
Wykład 1: Wprowadzenie do sieci neuronowych Historia badań nad sieciami neuronowymi. - początki: badanie komórek ośrodkowego układu nerwowego zwierząt i człowieka, czyli neuronów; próby wyjaśnienia i matematycznego
Najprostsze modele sieci z rekurencją. sieci Hopfielda; sieci uczone regułą Hebba; sieć Hamminga;
 Sieci Hopfielda Najprostsze modele sieci z rekurencją sieci Hopfielda; sieci uczone regułą Hebba; sieć Hamminga; Modele bardziej złoŝone: RTRN (Real Time Recurrent Network), przetwarzająca sygnały w czasie
Sieci Hopfielda Najprostsze modele sieci z rekurencją sieci Hopfielda; sieci uczone regułą Hebba; sieć Hamminga; Modele bardziej złoŝone: RTRN (Real Time Recurrent Network), przetwarzająca sygnały w czasie
Uczenie sieci typu MLP
 Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
Sieci neuronowe i ich ciekawe zastosowania. Autor: Wojciech Jamrozy III rok SMP / Informatyka
 Sieci neuronowe i ich ciekawe zastosowania Autor: Wojciech Jamrozy III rok SMP / Informatyka Klasyczna algorytmika Sortowanie ciągu liczb Czy i ile razy dane słowo wystąpiło w tekście Najkrótsza droga
Sieci neuronowe i ich ciekawe zastosowania Autor: Wojciech Jamrozy III rok SMP / Informatyka Klasyczna algorytmika Sortowanie ciągu liczb Czy i ile razy dane słowo wystąpiło w tekście Najkrótsza droga
Eksploracja Danych. wykład 4. Sebastian Zając. 10 maja 2017 WMP.SNŚ UKSW. Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja / 18
 Eksploracja Danych wykład 4 Sebastian Zając WMP.SNŚ UKSW 10 maja 2017 Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja 2017 1 / 18 Klasyfikacja danych Klasyfikacja Najczęściej stosowana (najstarsza)
Eksploracja Danych wykład 4 Sebastian Zając WMP.SNŚ UKSW 10 maja 2017 Sebastian Zając (WMP.SNŚ UKSW) Eksploracja Danych 10 maja 2017 1 / 18 Klasyfikacja danych Klasyfikacja Najczęściej stosowana (najstarsza)
Projekt Sieci neuronowe
 Projekt Sieci neuronowe Chmielecka Katarzyna Gr. 9 IiE 1. Problem i dane Sieć neuronowa miała za zadanie nauczyć się klasyfikować wnioski kredytowe. W projekcie wykorzystano dane pochodzące z 110 wniosków
Projekt Sieci neuronowe Chmielecka Katarzyna Gr. 9 IiE 1. Problem i dane Sieć neuronowa miała za zadanie nauczyć się klasyfikować wnioski kredytowe. W projekcie wykorzystano dane pochodzące z 110 wniosków
Literatura. Sztuczne sieci neuronowe. Przepływ informacji w systemie nerwowym. Budowa i działanie mózgu
 Literatura Wykład : Wprowadzenie do sztucznych sieci neuronowych Małgorzata Krętowska Wydział Informatyki Politechnika Białostocka Tadeusiewicz R: Sieci neuronowe, Akademicka Oficyna Wydawnicza RM, Warszawa
Literatura Wykład : Wprowadzenie do sztucznych sieci neuronowych Małgorzata Krętowska Wydział Informatyki Politechnika Białostocka Tadeusiewicz R: Sieci neuronowe, Akademicka Oficyna Wydawnicza RM, Warszawa
Wstęp do sieci neuronowych, wykład 9 Sieci rekurencyjne. Autoasocjator Hopfielda
 Wstęp do sieci neuronowych, wykład 9. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-12-10 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu
Wstęp do sieci neuronowych, wykład 9. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-12-10 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Optymalizacja optymalizacji
 7 maja 2008 Wstęp Optymalizacja lokalna Optymalizacja globalna Algorytmy genetyczne Badane czasteczki Wykorzystane oprogramowanie (Algorytm genetyczny) 2 Sieć neuronowa Pochodne met-enkefaliny Optymalizacja
7 maja 2008 Wstęp Optymalizacja lokalna Optymalizacja globalna Algorytmy genetyczne Badane czasteczki Wykorzystane oprogramowanie (Algorytm genetyczny) 2 Sieć neuronowa Pochodne met-enkefaliny Optymalizacja
Sztuczne sieci neuronowe (SNN)
 Sztuczne sieci neuronowe (SNN) Pozyskanie informacji (danych) Wstępne przetwarzanie danych przygotowanie ich do dalszej analizy Selekcja informacji Ostateczny model decyzyjny SSN - podstawy Sieci neuronowe
Sztuczne sieci neuronowe (SNN) Pozyskanie informacji (danych) Wstępne przetwarzanie danych przygotowanie ich do dalszej analizy Selekcja informacji Ostateczny model decyzyjny SSN - podstawy Sieci neuronowe
Wstęp do sieci neuronowych, wykład 10 Sieci rekurencyjne. Autoasocjator Hopfielda
 Wstęp do sieci neuronowych, wykład 10. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 Modele sieci rekurencyjnej Energia sieci 2 3 Modele sieci
Wstęp do sieci neuronowych, wykład 10. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 Modele sieci rekurencyjnej Energia sieci 2 3 Modele sieci
Sieć Hopfielda. Sieci rekurencyjne. Ewa Adamus. ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych.
 Sieci rekurencyjne Ewa Adamus ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych 7 maja 2012 Jednowarstwowa sieć Hopfielda, z n neuronami Bipolarna funkcja przejścia W wariancie
Sieci rekurencyjne Ewa Adamus ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych 7 maja 2012 Jednowarstwowa sieć Hopfielda, z n neuronami Bipolarna funkcja przejścia W wariancie
Wstęp do sieci neuronowych, wykład 12 Wykorzystanie sieci rekurencyjnych w optymalizacji grafowej
 Wstęp do sieci neuronowych, wykład 12 Wykorzystanie sieci rekurencyjnych w optymalizacji grafowej Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2013-01-09
Wstęp do sieci neuronowych, wykład 12 Wykorzystanie sieci rekurencyjnych w optymalizacji grafowej Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2013-01-09
Wstęp do sieci neuronowych, wykład 9 Sieci rekurencyjne. Autoasocjator Hopfielda
 Wstęp do sieci neuronowych, wykład 9. M. Czoków, J. Piersa 2010-12-07 1 Sieci skierowane 2 Modele sieci rekurencyjnej Energia sieci 3 Sieci skierowane Sieci skierowane Sieci skierowane graf połączeń synaptycznych
Wstęp do sieci neuronowych, wykład 9. M. Czoków, J. Piersa 2010-12-07 1 Sieci skierowane 2 Modele sieci rekurencyjnej Energia sieci 3 Sieci skierowane Sieci skierowane Sieci skierowane graf połączeń synaptycznych
Wstęp do sieci neuronowych, wykład 10 Sieci rekurencyjne. Autoasocjator Hopfielda
 Wstęp do sieci neuronowych, wykład 10. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-12-19 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu
Wstęp do sieci neuronowych, wykład 10. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2012-12-19 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu
ALGORYTMY SZTUCZNEJ INTELIGENCJI
 ALGORYTMY SZTUCZNEJ INTELIGENCJI Sieci neuronowe 06.12.2014 Krzysztof Salamon 1 Wstęp Sprawozdanie to dotyczy ćwiczeń z zakresu sieci neuronowych realizowanym na przedmiocie: Algorytmy Sztucznej Inteligencji.
ALGORYTMY SZTUCZNEJ INTELIGENCJI Sieci neuronowe 06.12.2014 Krzysztof Salamon 1 Wstęp Sprawozdanie to dotyczy ćwiczeń z zakresu sieci neuronowych realizowanym na przedmiocie: Algorytmy Sztucznej Inteligencji.
Elementy kognitywistyki II: Sztuczna inteligencja. WYKŁAD X: Sztuczny neuron
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD X: Sztuczny neuron Koneksjonizm: wprowadzenie 1943: Warren McCulloch, Walter Pitts: ogólna teoria przetwarzania informacji oparta na sieciach binarnych
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD X: Sztuczny neuron Koneksjonizm: wprowadzenie 1943: Warren McCulloch, Walter Pitts: ogólna teoria przetwarzania informacji oparta na sieciach binarnych
Sztuczne siei neuronowe - wprowadzenie
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 2 Sztuczne siei neuronowe - wprowadzenie Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika Poznańska Poznań, 2 Wstęp
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 2 Sztuczne siei neuronowe - wprowadzenie Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika Poznańska Poznań, 2 Wstęp
Wstęp do sieci neuronowych, wykład 07 Uczenie nienadzorowane cd.
 Wstęp do sieci neuronowych, wykład 07 Uczenie nienadzorowane cd. M. Czoków, J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika w Toruniu 2013-11-26 Projekt pn. Wzmocnienie potencjału
Wstęp do sieci neuronowych, wykład 07 Uczenie nienadzorowane cd. M. Czoków, J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika w Toruniu 2013-11-26 Projekt pn. Wzmocnienie potencjału
Inteligentne systemy informacyjne
 Inteligentne systemy informacyjne Moduł 10 Mieczysław Muraszkiewicz www.icie.com.pl/lect_pw.htm M. Muraszkiewicz strona 1 Sieci neuronowe szkic Moduł 10 M. Muraszkiewicz strona 2 Dwa nurty M. Muraszkiewicz
Inteligentne systemy informacyjne Moduł 10 Mieczysław Muraszkiewicz www.icie.com.pl/lect_pw.htm M. Muraszkiewicz strona 1 Sieci neuronowe szkic Moduł 10 M. Muraszkiewicz strona 2 Dwa nurty M. Muraszkiewicz
ID1SII4. Informatyka I stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny) stacjonarne (stacjonarne / niestacjonarne)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu ID1SII4 Nazwa modułu Systemy inteligentne 1 Nazwa modułu w języku angielskim Intelligent
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu ID1SII4 Nazwa modułu Systemy inteligentne 1 Nazwa modułu w języku angielskim Intelligent
Zastosowania sieci neuronowych
 Zastosowania sieci neuronowych klasyfikacja LABORKA Piotr Ciskowski zadanie 1. klasyfikacja zwierząt sieć jednowarstwowa żródło: Tadeusiewicz. Odkrywanie własności sieci neuronowych, str. 159 Przykład
Zastosowania sieci neuronowych klasyfikacja LABORKA Piotr Ciskowski zadanie 1. klasyfikacja zwierząt sieć jednowarstwowa żródło: Tadeusiewicz. Odkrywanie własności sieci neuronowych, str. 159 Przykład
Sieć przesyłająca żetony CP (counter propagation)
 Sieci neuropodobne IX, specyficzne architektury 1 Sieć przesyłająca żetony CP (counter propagation) warstwa Kohonena: wektory wejściowe są unormowane jednostki mają unormowane wektory wag jednostki są
Sieci neuropodobne IX, specyficzne architektury 1 Sieć przesyłająca żetony CP (counter propagation) warstwa Kohonena: wektory wejściowe są unormowane jednostki mają unormowane wektory wag jednostki są
Uczenie się pojedynczego neuronu. Jeśli zastosowana zostanie funkcja bipolarna s y: y=-1 gdy z<0 y=1 gdy z>=0. Wówczas: W 1 x 1 + w 2 x 2 + = 0
 Uczenie się pojedynczego neuronu W0 X0=1 W1 x1 W2 s f y x2 Wp xp p x i w i=x w+wo i=0 Jeśli zastosowana zostanie funkcja bipolarna s y: y=-1 gdy z=0 Wówczas: W 1 x 1 + w 2 x 2 + = 0 Algorytm
Uczenie się pojedynczego neuronu W0 X0=1 W1 x1 W2 s f y x2 Wp xp p x i w i=x w+wo i=0 Jeśli zastosowana zostanie funkcja bipolarna s y: y=-1 gdy z=0 Wówczas: W 1 x 1 + w 2 x 2 + = 0 Algorytm
1. Logika, funkcje logiczne, preceptron.
 Sieci neuronowe 1. Logika, funkcje logiczne, preceptron. 1. (Logika) Udowodnij prawa de Morgana, prawo pochłaniania p (p q), prawo wyłączonego środka p p oraz prawo sprzeczności (p p). 2. Wyraź funkcję
Sieci neuronowe 1. Logika, funkcje logiczne, preceptron. 1. (Logika) Udowodnij prawa de Morgana, prawo pochłaniania p (p q), prawo wyłączonego środka p p oraz prawo sprzeczności (p p). 2. Wyraź funkcję
Wstęp do sieci neuronowych, wykład 03 Warstwy RBF, jednostka ADALINE.
 Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka ADALINE. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 218-1-15/22 Projekt pn.
Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka ADALINE. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 218-1-15/22 Projekt pn.
Algorytmy stochastyczne, wykład 08 Sieci bayesowskie
 Algorytmy stochastyczne, wykład 08 Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-04-10 Prawdopodobieństwo Prawdopodobieństwo Prawdopodobieństwo warunkowe Zmienne
Algorytmy stochastyczne, wykład 08 Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-04-10 Prawdopodobieństwo Prawdopodobieństwo Prawdopodobieństwo warunkowe Zmienne
WYKORZYSTANIE SIECI NEURONOWEJ DO BADANIA WPŁYWU WYDOBYCIA NA SEJSMICZNOŚĆ W KOPALNIACH WĘGLA KAMIENNEGO. Stanisław Kowalik (Poland, Gliwice)
 WYKORZYSTANIE SIECI NEURONOWEJ DO BADANIA WPŁYWU WYDOBYCIA NA SEJSMICZNOŚĆ W KOPALNIACH WĘGLA KAMIENNEGO Stanisław Kowalik (Poland, Gliwice) 1. Wprowadzenie Wstrząsy podziemne i tąpania występujące w kopalniach
WYKORZYSTANIE SIECI NEURONOWEJ DO BADANIA WPŁYWU WYDOBYCIA NA SEJSMICZNOŚĆ W KOPALNIACH WĘGLA KAMIENNEGO Stanisław Kowalik (Poland, Gliwice) 1. Wprowadzenie Wstrząsy podziemne i tąpania występujące w kopalniach
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Sieci neuronowe jako sposób na optymalizacje podejmowanych decyzji. Tomasz Karczyoski Wydział W-08 IZ
 optymalizacje podejmowanych decyzji Tomasz Karczyoski Wydział W-08 IZ Czym są sieci neuronowe Struktura matematycznych oraz programowy lub sprzętowy model, realizujących obliczenia lub przetwarzanie sygnałów
optymalizacje podejmowanych decyzji Tomasz Karczyoski Wydział W-08 IZ Czym są sieci neuronowe Struktura matematycznych oraz programowy lub sprzętowy model, realizujących obliczenia lub przetwarzanie sygnałów
Wstęp do sieci neuronowych, wykład 01 Neuron biologiczny. Model perceptronu prostego.
 Wstęp do sieci neuronowych, wykład 01. Model perceptronu prostego. M. Czoków, J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-04 In memoriam prof. dr hab. Tomasz Schreiber
Wstęp do sieci neuronowych, wykład 01. Model perceptronu prostego. M. Czoków, J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-10-04 In memoriam prof. dr hab. Tomasz Schreiber
Temat: ANFIS + TS w zadaniach. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: ANFIS + TS w zadaniach Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1. Systemy neuronowo - rozmyte Systemy
Temat: ANFIS + TS w zadaniach Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1. Systemy neuronowo - rozmyte Systemy
Sieci M. I. Jordana. Sieci rekurencyjne z parametrycznym biasem. Leszek Rybicki. 30 listopada Leszek Rybicki Sieci M. I.
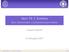 Sieci M. I. Jordana Sieci rekurencyjne z parametrycznym biasem Leszek Rybicki 30 listopada 2007 Leszek Rybicki Sieci M. I. Jordana 1/21 Plan O czym będzie 1 Wstęp do sieci neuronowych Neurony i perceptrony
Sieci M. I. Jordana Sieci rekurencyjne z parametrycznym biasem Leszek Rybicki 30 listopada 2007 Leszek Rybicki Sieci M. I. Jordana 1/21 Plan O czym będzie 1 Wstęp do sieci neuronowych Neurony i perceptrony
PROGNOZOWANIE OSIADAŃ POWIERZCHNI TERENU PRZY UŻYCIU SIECI NEURONOWYCH**
 Górnictwo i Geoinżynieria Rok 31 Zeszyt 3 2007 Dorota Pawluś* PROGNOZOWANIE OSIADAŃ POWIERZCHNI TERENU PRZY UŻYCIU SIECI NEURONOWYCH** 1. Wstęp Eksploatacja górnicza złóż ma niekorzystny wpływ na powierzchnię
Górnictwo i Geoinżynieria Rok 31 Zeszyt 3 2007 Dorota Pawluś* PROGNOZOWANIE OSIADAŃ POWIERZCHNI TERENU PRZY UŻYCIU SIECI NEURONOWYCH** 1. Wstęp Eksploatacja górnicza złóż ma niekorzystny wpływ na powierzchnię
Sieci neuronowe w Statistica. Agnieszka Nowak - Brzezioska
 Sieci neuronowe w Statistica Agnieszka Nowak - Brzezioska Podstawowym elementem składowym sztucznej sieci neuronowej jest element przetwarzający neuron. Schemat działania neuronu: x1 x2 w1 w2 Dendrites
Sieci neuronowe w Statistica Agnieszka Nowak - Brzezioska Podstawowym elementem składowym sztucznej sieci neuronowej jest element przetwarzający neuron. Schemat działania neuronu: x1 x2 w1 w2 Dendrites
Inteligentne systemy decyzyjne: Uczenie maszynowe sztuczne sieci neuronowe
 Inteligentne systemy decyzyjne: Uczenie maszynowe sztuczne sieci neuronowe Trening jednokierunkowych sieci neuronowych wykład 2. dr inż. PawełŻwan Katedra Systemów Multimedialnych Politechnika Gdańska
Inteligentne systemy decyzyjne: Uczenie maszynowe sztuczne sieci neuronowe Trening jednokierunkowych sieci neuronowych wykład 2. dr inż. PawełŻwan Katedra Systemów Multimedialnych Politechnika Gdańska
Rozpoznawanie obrazów
 Rozpoznawanie obrazów Ćwiczenia lista zadań nr 7 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Rozpoznawanie obrazów Ćwiczenia lista zadań nr 7 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Elementy kognitywistyki III: Modele i architektury poznawcze
 Elementy kognitywistyki III: Modele i architektury poznawcze Wykład VII: Modelowanie uczenia się w sieciach neuronowych Uczenie się sieci i trening nienaruszona struktura sieci (z pewnym ale ) nienaruszone
Elementy kognitywistyki III: Modele i architektury poznawcze Wykład VII: Modelowanie uczenia się w sieciach neuronowych Uczenie się sieci i trening nienaruszona struktura sieci (z pewnym ale ) nienaruszone
wiedzy Sieci neuronowe
 Metody detekcji uszkodzeń oparte na wiedzy Sieci neuronowe Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 7 Wprowadzenie Okres kształtowania się teorii sztucznych sieci
Metody detekcji uszkodzeń oparte na wiedzy Sieci neuronowe Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 7 Wprowadzenie Okres kształtowania się teorii sztucznych sieci
Oprogramowanie Systemów Obrazowania SIECI NEURONOWE
 SIECI NEURONOWE Przedmiotem laboratorium jest stworzenie algorytmu rozpoznawania zwierząt z zastosowaniem sieci neuronowych w oparciu o 5 kryteriów: ile zwierzę ma nóg, czy żyje w wodzie, czy umie latać,
SIECI NEURONOWE Przedmiotem laboratorium jest stworzenie algorytmu rozpoznawania zwierząt z zastosowaniem sieci neuronowych w oparciu o 5 kryteriów: ile zwierzę ma nóg, czy żyje w wodzie, czy umie latać,
ELEMENTY SZTUCZNEJ INTELIGENCJI. Sztuczne sieci neuronowe
 ELEMENTY SZTUCZNEJ INTELIGENCJI Sztuczne sieci neuronowe Plan 2 Wzorce biologiczne. Idea SSN - model sztucznego neuronu. Perceptron prosty i jego uczenie regułą delta Perceptron wielowarstwowy i jego uczenie
ELEMENTY SZTUCZNEJ INTELIGENCJI Sztuczne sieci neuronowe Plan 2 Wzorce biologiczne. Idea SSN - model sztucznego neuronu. Perceptron prosty i jego uczenie regułą delta Perceptron wielowarstwowy i jego uczenie
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova
 Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Sieci neuronowe w Statistica
 http://usnet.us.edu.pl/uslugi-sieciowe/oprogramowanie-w-usk-usnet/oprogramowaniestatystyczne/ Sieci neuronowe w Statistica Agnieszka Nowak - Brzezińska Podstawowym elementem składowym sztucznej sieci neuronowej
http://usnet.us.edu.pl/uslugi-sieciowe/oprogramowanie-w-usk-usnet/oprogramowaniestatystyczne/ Sieci neuronowe w Statistica Agnieszka Nowak - Brzezińska Podstawowym elementem składowym sztucznej sieci neuronowej
Uczenie Wielowarstwowych Sieci Neuronów o
 Plan uczenie neuronu o ci gªej funkcji aktywacji uczenie jednowarstwowej sieci neuronów o ci gªej funkcji aktywacji uczenie sieci wielowarstwowej - metoda propagacji wstecznej neuronu o ci gªej funkcji
Plan uczenie neuronu o ci gªej funkcji aktywacji uczenie jednowarstwowej sieci neuronów o ci gªej funkcji aktywacji uczenie sieci wielowarstwowej - metoda propagacji wstecznej neuronu o ci gªej funkcji
Podstawy sztucznej inteligencji
 wykład 5 Sztuczne sieci neuronowe (SSN) 8 grudnia 2011 Plan wykładu 1 Biologiczne wzorce sztucznej sieci neuronowej 2 3 4 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką,
wykład 5 Sztuczne sieci neuronowe (SSN) 8 grudnia 2011 Plan wykładu 1 Biologiczne wzorce sztucznej sieci neuronowej 2 3 4 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką,
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Modelowanie niezawodności prostych struktur sprzętowych
 Modelowanie niezawodności prostych struktur sprzętowych W ćwiczeniu tym przedstawione zostaną proste struktury sprzętowe oraz sposób obliczania ich niezawodności przy założeniu, że funkcja niezawodności
Modelowanie niezawodności prostych struktur sprzętowych W ćwiczeniu tym przedstawione zostaną proste struktury sprzętowe oraz sposób obliczania ich niezawodności przy założeniu, że funkcja niezawodności
Zastosowanie sztucznych sieci neuronowych w prognozowaniu szeregów czasowych (prezentacja 2)
 Zastosowanie sztucznych sieci neuronowych w prognozowaniu szeregów czasowych (prezentacja 2) Ewa Wołoszko Praca pisana pod kierunkiem Pani dr hab. Małgorzaty Doman Plan tego wystąpienia Teoria Narzędzia
Zastosowanie sztucznych sieci neuronowych w prognozowaniu szeregów czasowych (prezentacja 2) Ewa Wołoszko Praca pisana pod kierunkiem Pani dr hab. Małgorzaty Doman Plan tego wystąpienia Teoria Narzędzia
Sztuczne sieci neuronowe Ćwiczenia. Piotr Fulmański, Marta Grzanek
 Sztuczne sieci neuronowe Ćwiczenia Piotr Fulmański, Marta Grzanek Piotr Fulmański 1 Wydział Matematyki i Informatyki, Marta Grzanek 2 Uniwersytet Łódzki Banacha 22, 90-232, Łódź Polska e-mail 1: fulmanp@math.uni.lodz.pl,
Sztuczne sieci neuronowe Ćwiczenia Piotr Fulmański, Marta Grzanek Piotr Fulmański 1 Wydział Matematyki i Informatyki, Marta Grzanek 2 Uniwersytet Łódzki Banacha 22, 90-232, Łódź Polska e-mail 1: fulmanp@math.uni.lodz.pl,
Sieci neuronowe do przetwarzania informacji / Stanisław Osowski. wyd. 3. Warszawa, Spis treści
 Sieci neuronowe do przetwarzania informacji / Stanisław Osowski. wyd. 3. Warszawa, 2013 Spis treści Przedmowa 7 1. Wstęp 9 1.1. Podstawy biologiczne działania neuronu 9 1.2. Pierwsze modele sieci neuronowej
Sieci neuronowe do przetwarzania informacji / Stanisław Osowski. wyd. 3. Warszawa, 2013 Spis treści Przedmowa 7 1. Wstęp 9 1.1. Podstawy biologiczne działania neuronu 9 1.2. Pierwsze modele sieci neuronowej
I EKSPLORACJA DANYCH
 I EKSPLORACJA DANYCH Zadania eksploracji danych: przewidywanie Przewidywanie jest podobne do klasyfikacji i szacowania, z wyjątkiem faktu, że w przewidywaniu wynik dotyczy przyszłości. Typowe zadania przewidywania
I EKSPLORACJA DANYCH Zadania eksploracji danych: przewidywanie Przewidywanie jest podobne do klasyfikacji i szacowania, z wyjątkiem faktu, że w przewidywaniu wynik dotyczy przyszłości. Typowe zadania przewidywania
SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe
 SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe JOANNA GRABSKA-CHRZĄSTOWSKA Wykłady w dużej mierze przygotowane w oparciu o materiały i pomysły PROF. RYSZARDA TADEUSIEWICZA BUDOWA RZECZYWISTEGO NEURONU
SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe JOANNA GRABSKA-CHRZĄSTOWSKA Wykłady w dużej mierze przygotowane w oparciu o materiały i pomysły PROF. RYSZARDA TADEUSIEWICZA BUDOWA RZECZYWISTEGO NEURONU
Wstęp do sieci neuronowych, wykład 6 Wsteczna propagacja błędu - cz. 3
 Wstęp do sieci neuronowych, wykład 6 Wsteczna propagacja błędu - cz. 3 Andrzej Rutkowski, Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-11-05 Projekt
Wstęp do sieci neuronowych, wykład 6 Wsteczna propagacja błędu - cz. 3 Andrzej Rutkowski, Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-11-05 Projekt
Inteligentne systemy przeciw atakom sieciowym
 Inteligentne systemy przeciw atakom sieciowym wykład Sztuczne sieci neuronowe (SSN) Joanna Kołodziejczyk 2016 Joanna Kołodziejczyk Inteligentne systemy przeciw atakom sieciowym 2016 1 / 36 Biologiczne
Inteligentne systemy przeciw atakom sieciowym wykład Sztuczne sieci neuronowe (SSN) Joanna Kołodziejczyk 2016 Joanna Kołodziejczyk Inteligentne systemy przeciw atakom sieciowym 2016 1 / 36 Biologiczne
Budowa sztucznych sieci neuronowych do prognozowania. Przykład jednostek uczestnictwa otwartego funduszu inwestycyjnego
 Budowa sztucznych sieci neuronowych do prognozowania. Przykład jednostek uczestnictwa otwartego funduszu inwestycyjnego Dorota Witkowska Szkoła Główna Gospodarstwa Wiejskiego w Warszawie Wprowadzenie Sztuczne
Budowa sztucznych sieci neuronowych do prognozowania. Przykład jednostek uczestnictwa otwartego funduszu inwestycyjnego Dorota Witkowska Szkoła Główna Gospodarstwa Wiejskiego w Warszawie Wprowadzenie Sztuczne
SIEĆ NEURONOWA JAKO NARZĘDZIE APROKSYMACJI I KLASYFIKACJI DANYCH. Jakub Karbowski Gimnazjum nr 17 w Krakowie
 SIEĆ NEURONOWA JAKO NARZĘDZIE APROKSYMACJI I KLASYFIKACJI DANYCH Jakub Karbowski Gimnazjum nr 17 w Krakowie KRAKÓW 2017 1. Spis treści 2. WSTĘP 2 3. SIECI NEURONOWE 2 3.1. Co to są sieci neuronowe... 2
SIEĆ NEURONOWA JAKO NARZĘDZIE APROKSYMACJI I KLASYFIKACJI DANYCH Jakub Karbowski Gimnazjum nr 17 w Krakowie KRAKÓW 2017 1. Spis treści 2. WSTĘP 2 3. SIECI NEURONOWE 2 3.1. Co to są sieci neuronowe... 2
Automatyczna predykcja. Materiały/konsultacje. Co to jest uczenie maszynowe? Przykład 6/10/2013. Google Prediction API, maj 2010
 Materiały/konsultacje Automatyczna predykcja http://www.ibp.pwr.wroc.pl/kotulskalab Konsultacje wtorek, piątek 9-11 (uprzedzić) D1-115 malgorzata.kotulska@pwr.wroc.pl Co to jest uczenie maszynowe? Uczenie
Materiały/konsultacje Automatyczna predykcja http://www.ibp.pwr.wroc.pl/kotulskalab Konsultacje wtorek, piątek 9-11 (uprzedzić) D1-115 malgorzata.kotulska@pwr.wroc.pl Co to jest uczenie maszynowe? Uczenie
Klasyfikacja metodą Bayesa
 Klasyfikacja metodą Bayesa Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski warunkowe i bezwarunkowe 1. Klasyfikacja Bayesowska jest klasyfikacją statystyczną. Pozwala przewidzieć prawdopodobieństwo
Klasyfikacja metodą Bayesa Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski warunkowe i bezwarunkowe 1. Klasyfikacja Bayesowska jest klasyfikacją statystyczną. Pozwala przewidzieć prawdopodobieństwo
Zajęcia nr. 3 notatki
 Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 4 Modelowanie niezawodności prostych struktur sprzętowych Prowadzący: mgr inż. Marcel Luzar Cel
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 4 Modelowanie niezawodności prostych struktur sprzętowych Prowadzący: mgr inż. Marcel Luzar Cel
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Systemy pomiarowo-diagnostyczne. Metody uczenia maszynowego wykład III 2016/2017
 Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład III bogumil.konopka@pwr.edu.pl 2016/2017 Wykład III - plan Regresja logistyczna Ocena skuteczności klasyfikacji Macierze pomyłek Krzywe
Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład III bogumil.konopka@pwr.edu.pl 2016/2017 Wykład III - plan Regresja logistyczna Ocena skuteczności klasyfikacji Macierze pomyłek Krzywe
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
Sztuczne sieci neuronowe
 Wydział Zarządzania AGH Katedra Informatyki Stosowanej Sztuczne sieci neuronowe Sztuczne sieci neuronowe Wprowadzenie Trochę historii Podstawy działania Funkcja aktywacji Typy sieci 2 Wprowadzenie Zainteresowanie
Wydział Zarządzania AGH Katedra Informatyki Stosowanej Sztuczne sieci neuronowe Sztuczne sieci neuronowe Wprowadzenie Trochę historii Podstawy działania Funkcja aktywacji Typy sieci 2 Wprowadzenie Zainteresowanie
Testowanie modeli predykcyjnych
 Testowanie modeli predykcyjnych Wstęp Podczas budowy modelu, którego celem jest przewidywanie pewnych wartości na podstawie zbioru danych uczących poważnym problemem jest ocena jakości uczenia i zdolności
Testowanie modeli predykcyjnych Wstęp Podczas budowy modelu, którego celem jest przewidywanie pewnych wartości na podstawie zbioru danych uczących poważnym problemem jest ocena jakości uczenia i zdolności
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy oólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy oólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK
Wnioskowanie bayesowskie
 Wnioskowanie bayesowskie W podejściu klasycznym wnioskowanie statystyczne oparte jest wyłącznie na podstawie pobranej próby losowej. Możemy np. estymować punktowo lub przedziałowo nieznane parametry rozkładów,
Wnioskowanie bayesowskie W podejściu klasycznym wnioskowanie statystyczne oparte jest wyłącznie na podstawie pobranej próby losowej. Możemy np. estymować punktowo lub przedziałowo nieznane parametry rozkładów,
Rozdział 1 Sztuczne sieci neuronowe. Materiały do zajęć dydaktycznych - na podstawie dokumentacji programu Matlab opracował Dariusz Grzesiak
 2 Rozdział 1 Sztuczne sieci neuronowe. 3 Sztuczna sieć neuronowa jest zbiorem prostych elementów pracujących równolegle, których zasada działania inspirowana jest biologicznym systemem nerwowym. Sztuczną
2 Rozdział 1 Sztuczne sieci neuronowe. 3 Sztuczna sieć neuronowa jest zbiorem prostych elementów pracujących równolegle, których zasada działania inspirowana jest biologicznym systemem nerwowym. Sztuczną
Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
 IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
Zmienne zależne i niezależne
 Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Modele DSGE. Jerzy Mycielski. Maj Jerzy Mycielski () Modele DSGE Maj / 11
 Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
