Filtration of Mixtures Forming Compressible Sediments
|
|
|
- Ksawery Janik
- 8 lat temu
- Przeglądów:
Transkrypt
1 MIDDLE POMERANIAN SCIENTIFIC SOCIETY OF THE ENVIRONMENT PROTECTION ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Annual Set The Environment Protection Rocznik Ochrona Środowiska Volume/Tom 15. Year/Rok 201 ISSN X 9 58 Filtration of Mixtures Forming Compressible Sediments Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska Koszalin University of Technology 1. Introduction Standard theoretical analysis of the generally approached filtration process is based on Darcy s equation describing the flow of fluid through a porous medium [4 9, 11 14, 16, 50 57]. Naturally, the flow of fluid through porous media, which is the flow of a single-phase fluid, is not yet filtration [29 2]. Filtration is a process in which a mixture of a solid phase and a liquid phase flow through a porous barrier, with this process involving the retention of the solid phase in the barrier or on the barrier, or both. At the same time, the liquid phase that passes through the porous barrier is the product of filtration which is most often referred to in literature on the subject as filtrate or eluate. The other product obtained through the filtration process is the solid phase (granulate forming a mixture with the liquid) retained inside the pores of the filtration medium, or on the filtration medium, and this product is referred to in literature on the subject as the sediment. In practice, however, in the case of so-called deposit filtration, most often gravity filtration, where the porous barrier is formed by a layer of sand or gravel, the solid phase component flowing in the mixture through such a barrier is often retained inside the barrier, in the pores of the medium layer (colmatage) and the remaining part of the solid phase forms a sediment on the porous medium [2, 24, 7, 4 49]. The short analysis of different variants of the filtration process presented above already shows that it is a complex, multi-variant process and that it should be analyzed separately depending on the filtration type
2 40 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska also from the cause and effect perspective of the dependency mechanism identified. 2. Filtration with sediment storage on the filtration mesh In the present work, we will analyze the process of filtration of a mixture of a solid and a liquid flowing through a filtration mesh from the theoretical point of view. This type of filtration process is characteristic for filtration devices, such as: vacuum filters, filtering presses, and pressure filters, as well as, to a lesser extent, centrifuge filters [10, 17 22, 25 27]. Darcy s general equation describing the flow of fluid through a porous medium has the following form: V = P R -1 (1) An analogous equation adapter by Piecuch [25 28, 1, 2] to the filtration process, in which the general filtration medium resistance is the denominator, has the formula presented below: P V = μ t' A + μ F b P s V O N β N (2) O A 2 F (1 ε O )ρ S where the denominator which describes the filtration medium resistance is the sum of two components that constitute the denominator. The first component is the resistance of the filtration mesh, R 1, formulated as follows: μ R 1 =t' () A F The second component is the sediment resistance, R 2, that accumulates on the filtration mesh: R 2 =t' μ P s V O N β N b O A 2 (4) F (1 ε O )ρ S In the relevant equation (4), the formula introduced earlier to Darcy s equation and expressing the permeability K is used in the form of an empirical equation as follows:
3 Filtration of Mixtures Forming Compressible Sediments 41 K= b O P s O (5) Permeability K is used in standard analysis of the process of fluid flow through a porous medium and, thus, also in the analysis of filtration processes, as a parameter in the general equation describing the resistance R of the porous medium formulated as follows: R=α L = μ L (6) A F K A F Of course general resistance R in the equation (6) formulated above was used after transforming the equation describing filtration sediment resistance R 2. It is characteristic here that in the formulation of the empirical equation (5) describing the permeability K, the pressure P in the denominator expresses the so-called squeezing pressure [4], that is the filtration pressure drop in the sediment. The assumption stated above constitutes a firm basis for the current standard filtration theory based on Darcy s equation by his disciples Kozeny and Carman, and then repeated by many other scientists, including [5 11, 50 57], as well as in Polish literature on the subject by, for example, Ciborowski [4]. The authors of the present work modified the formulation of the empirical equation (5) in their consideration in such a way that the pressure in the denominator is assumed to be the general filtration pressure which means the pressure that constitutes a specific moving force of the process acting on the filtration surface constituted here by the surface of the filtration mesh. Of course, this means that the value of the filtration constant b 0 in the numerator of the equation (5) will be slightly different than the value obtained from the formula of the equation (5) in which the pressure in the denominator expresses the socalled squeezing pressure [4]. In relation to the assumption presented above, the Authors of the present work also used it in another work regarding filtration through a filtration mesh with the formulation of compressible sediments [40] to which we would like to refer the reader. According to the Authors, such a formulation of the pressure in the equation (5), assuming that it is the so-called initial moving pressure in the process, makes it possible to
4 42 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska calculate the efficiency of the filtration process through obtaining the general differential equation of filtration and then to integrate the equation for different values of the compressibility factor, that is generally for different compressible sediments. Applying the assumption regarding the pressure present in the empirical formulation (5) directly, the Authors demonstrated in the work [40] how the general equation of filtration can be solved directly after such a formulation is introduced, according to the following formula: P V = μ t' A + μ F b P s V O N β N (7) O A 2 F (1 ε O )ρ S Formulating the equation (7) as a differential equation for two particular variants of filtration, that is: when the flow rate is a variable and the pressure is constant and when the pressure fluctuates and the flow rate is constant for different values of the compressibility factor of the filtration sediment accumulated on the filtration mesh. According to the standard filtration theory, as demonstrated in Polish literature on the subject by, for example, Ciborowski [4], the problem is solved in a different way, which is first, by calculating the general resistance of the filtration sediment, in accordance with the formula (6), then by introducing its function form from the empirical equation (5) in the place of the permeability factor K in the equation. Thus, after the transformation, we obtain the equation of resistance R (in this case, the sediment resistance R 2 ) with the general form of: R 2 = μ b O P s O L A F (8) where pressure means the co-called sediment squeezing pressure [4]. The equation (8) is then formulated as a differential equation as the differential of the pressure fluctuation in relation to the thickness of the sediment layer L. The total sediment resistance, in accordance with the equation R 2, is obtained on this basis after integrating this equation with the limit of L=0 and p= p 0 on the sediment surface (from the side of the filtration mesh) to the sediment surface from the fluid side, that is in the integration limit of L=L and p=0, as in the formula below:
5 Filtration of Mixtures Forming Compressible Sediments 4 R 2 = μ b O (1 s O ) P s O L A F (9) The relevant detailed derivation of the equation (9) on the basis of the differential formulation of the pressure in relation to the thickness of the sediment layer in the equation (8) can be found in the study [44]. While considering and analyzing the filtration process from the point of view of standard filtration theory, it is this form of the equation (9) that is derived only from the general filtration equation to obtain the formula: p V = μ t' A + μ F b (1 s O ) P s L (10) O O A F where the pressure in the denominator means the so-called squeezing pressure [4] and it is not the same pressure value as the one used in the numerator in equation (10). However, if the assumption of the Authors (the same one made, among others, in the work [40]) is accepted, and it is therefore assumed that the denomination of the equation (5) contains the moving pressure of the process and not the squeezing pressure, then the filtration equation obtained (10) after general transformations like the ones presented above will contain the same parameter of the moving pressure of the filtration process P both in the denominator and in the numerator. Of course, the value of the constant b 0 determined on empirical basis will be different in such a case than when as proposed by the Authors the assumption that the pressure value in the denominator of the equation (10) stands for the squeezing pressure, and not the moving pressure of the process, is accepted.. It should be underlined that if the equation (5) constituting the basis for the argument is an empirical equation, defining the pressure parameter is one of the basic assumptions of the Authors of the analysis, and then the consequence of this reference applies in the interpretation of particular equation transformations describing the process. If, then, the equation (9) is an independent equation of filtration sediment resistance introduced into another filtration equation in the formula (10), such an equation describing the volume efficiency (the flow) of the filtration process can be presented as a differential formula independently, both for the filtration process in which the pressure
6 44 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska value is constant and for the filtration process in which the flow value is constant, which means that the pressure fluctuates (that is in the form of a formula relating the pressure differential to the time differential dp/dt). Let us then try to present such possible solutions of the equation (10) as a differential equation when the pressure changes in relation to the duration of the process for filtration sediments with different values of the compressibility factor s O.. Particular solutions of the differential filtration equation for compressible sediments The basis for the consideration is, thus, the general formula in accordance with the equation (10) presented for the filtration process with the accumulation of compressible sediment on the filtration mesh, with the simplified assumption that the whole volume of the suspension (V N ) available in the filtration process, for example, vacuum filtration or pressure filtration [1, 2, 24, 9], will be retained on the filtration mesh (V N β N ), which means that filtrate density will be equal to 0. Thus, the equation (10) will take the following form: P V = μ t' A + μ F b (1 s O ) P s V O N β N (11) O A 2 F (1 ε O )ρ S In order to simplify the mathematical operations, some new constant values, from the equation presented above, will be denoted as the constant A of the following form: μ A=t' (12) A F Then, the constant B will have the following form (1): B=s O (1) and the constant C will have the following form: C= μ V N β N b O A 2 (14) F (1 ε O )ρ S
7 Filtration of Mixtures Forming Compressible Sediments 45 Applying the simplifications presented above, the solution of the general differential equation (11) of the filtration process with fluctuating pressure can be presented in the form of the following integral: dx I= A+C(1 B)x B, 0<B 1 (15) where A, C certain constants. Let us analyze particular solutions of the integral expressed by means of the equation (15)..1. For B=1, the integral will have the form: I= dx A = 1 A dx = 1 A x+d=f(x) (16) where D is the constant of integration..2. For B=0,5; xb= x0,5= x, the integral (15) will have the form: I= 2dx 2A+C x (17) Substituting x=t, we obtain x=t 2, and, thus dx=2tdt, and in this way the integral (17) of an irrational function is transferred into an integral of a rational function: I=4 t 2A+Ct dt (18) The integrand f(t), which is an improper rational function, has the following formula: t f(t)= 2A+Ct = 1 C 2A 1 (19) C 2A+Ct And, thus, after integrating both sides of the equation, we obtain the following formula: t 2A+Ct dt = 1 2A t C C 2 ln 2A+Ct (20) Finally, including the result (20) in the integral (18), and using the original variable x, we obtain the integral of the following formula:
8 46 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska I= 2dx 2A+C x = 4 8 A x C C 2 ln 2A+C x +D (21) where D is the constant of integration which can be determined on the basis of the original condition. In particular, if the limit interior of integration is established and equal to a=0, and the limit superior of integration is a variable, then we obtain the solution of the filtration equation which has the following form: F(x)= 0 x 2du = 4 8 A 8A x 2A+C u C 2 ln 2A+C x + C C 2 ln(2a) (22).. For B=2/; x B =x 2/ = x 2 the integral (15) takes the following form: I= dx (2) A+C x 2 Through substituting x=t, we obtain x=t, dx=t 2 dt, and the integral of the irrational function (2) is transformed into an integral of a rational function: I=9 t2 A+Ct 2 dt (24) An integral of this type is calculated by expressing the integrand f(t), which is an improper rational function, as follows: f(t)= A+Ct 2 = 1 C A 1 (25) C A+Ct 2 Including the distribution (25) in the integral (24) and using the formula: we obtain: t 2 dt k 2 +t = 1 2 k arctg (t k ) dla k>0 (26) t2 A+Ct 2 dt = 1 A C t arctg ( C C C A t) +D (27)
9 t= x Filtration of Mixtures Forming Compressible Sediments 47 After including the result in the equation (24) and substituting we obtain the final integral (2) of the following formula: I= dx = 9 A+C x 2 C x 9 A C arctg ( C C A x ) +D (28) where D is the constant of integration, and the constants A, C are positive numbers. In particular, if the limit interior of integration is established and equal to a=0, and the limit superior of integration is a variable, then we obtain the general solution of the filtration equation which has the following form: F(x)= 0 x du A+C u 2.4. For B=1/; x B =x 1/ = x = 9 C x 9 A C C C arctg ( A x ) (29) the integral (15) takes the form: I= dx A+2C x (0) By substituting x=t, we obtain x=t, and dx=t 2 dt and the integral (0) is transformed into an integral of a rational function with the following form: I= dx =9 t2 dt (1) A+2C x A+2Ct The integrand f(t) is an improper rational function, and thus, by dividing the numerator by the denominator, we can denote it in the following form: t 2 f(t)= A+2Ct = 1 A t 2C 4C 2 + 9A 2 1 (2) 4C 2 A+2Ct After including the distribution (2) in the integral (1) and integrating both sides of the equation, we can obtain the following form of the integral on the right side of the equation:
10 48 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska I= 9 4C t2 27A 2 4C 2 t+81a 8C ln A+2Ct +D () Next, by using the original variable, ergo by substituting t= x, we obtain the general integral of the following form: I= dx = 9 A+2C x 4C x 2 27A 4C 2 x + 81A2 8C ln A+2C x +D (4) where D is the constant of integration. In particular, if the limit interior of integration is established and equal to a=0 and the limit superior of integration is a variable, then the integral (0) for B=2/ is expressed by means of the following function: 4. Conclusion x du F(x)= = 9 0 A+2C u 4C x 2 27A 4C 2 x + 81A 2 8C ln A+2C x 81A2 8C ln(a) (5) Summing up the multi-variant solution of the general differential equation of the filtration process presented above for fluctuating filtration pressure and different compressibility values of the filtration sediment accumulating on the filtration mesh (bearing in mind the previous assumption that the physical compressibility factor s O, denoted mathematically as B, that is the assumption that if 0 B 1, which means that compressibility takes the form of a numerical value greater than zero and lower than one, then B=m/n, where m n, and, thus, x B =x m/n n = x m ), then the integral (15) takes the following form: ndx I= n (6) na+(n m)c x m The integral (6) of the irrational function is calculated through n the substitution: x=t, that is x=t n, and thus dx=n t n 1 dt, and then transformed into the integral of a rational function:
11 Filtration of Mixtures Forming Compressible Sediments 49 I= ndx n na+(n m)c x m t n 1 =n 2 m dt (7) na+(n m)ct Thus, in the general case, the integrand takes the form: t n 1 f(t)= na+(n m)ct m (8) It is an improper rational function, as n 1 m, which means that if we divide the numerator by the denominator, we can denote it as a polynomial and as a proper rational function, and then we integrate it in accordance with the common rules of integrating rational functions (that is simple fractions of the first kind or simple fractions of the second kind). The result of the integral on the right side of the equation (7) is always a function which takes the form of a sum of a polynomial, a natural logarithm or an arc tangent (e.g. the results denoted with the formulas (20), n (27), ()). Applying the substitution t= x, we obtain the solution of the integral (6). However, for many sediment compressibility values s O, denoted mathematically as B, that fulfill the condition of 0 B 1, the general equation (15), which is the general solution of the filtration equation, and thus the equivalent of the physical formula (11), cannot be expressed by means of known functions, which means that we are not able to provide the primitive integral F(x) for the integrand function of the following form: 1 f(x)= A+C(1 B)x (9) B There are, however, many numerical procedures that make it possible to calculate the approximate value of the integral of the generic type in accordance with the formula (15) (e.g. the trapezoidal rule, Simpson s rule, etc.). Many computer programs, e.g. Mathematica, Mathcad, Maple or Matlab, are able to calculate numerical values of integrals. CAS programs are able to perform symbolic integrations, which means that they provide analytical expressions in the results. It is therefore recommended to use those programs as they make it possible to focus on the essence of the problem instead of arduous calculations, saving many hours of laborious algebraic calculations as well as avoiding mistakes which are, unfortunately, frequently made [41 49].
12 50 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska Certain general conclusions for the analysts of the filtration process in this case, the process of filtration through a filtration mesh with the formulation of compressible sediment on the mesh in the course of the process can be derived from the theoretical analyses performed. These are as follows: 1. It is not possible to establish a single formula of the general filtration equation in which the sediment compressibility parameter will be present in the general physical notation (here B=s O ), in which it will be possible to directly substitute any values of the compressibility factor s O, within the range from zero to one, and determine the flow of the medium through such a porous barrier in the present case, a filtration mesh. 2. In the case of the filtration process with the formulation of compressible sediments on the filtration mesh, in order to use the general formula of the differential filtration equation, one must first solve the equation every time through its integration after substituting a specific value of the compressibility factor (s O =B) into the equation. The final physical formulas of those solutions for selected values of compressibility s O are presented in table 1.. Before possible application of the general differential equation of filtration as the original equation on the basis of which we want to calculate the flow (volumetric delivery), the value of the constant b 0 must first be established from the empirical formula (5) in order to determine the value of the permeability parameter K; which is the permeability parameter whose value must be known. 4. Determining the values of constant factors present in the formula of the general filtration equation (11) (that is t, b 0 ) will be the subject of the analysis performed by the Authors of the present work for particular, typical mixtures which are used in the current engineering practice and it will constitute the subject of their subsequent publications as the continuation of their basic research on the filtration process. 5. The theoretical analysis of the process of filtration of compressible sediments, performed above, clearly demonstrates that using the general differential equation of the filtration process in practice through solving it, namely through integrating it with the assumed (that is, practically known value of the compressibility factor s O =B), is
13 Filtration of Mixtures Forming Compressible Sediments 51 nevertheless very difficult, and it therefore does not offer promising prospects of its actual application by the designers of this equation. Table 1. Physical formulas of the equation of the filtration process with the formulation of compressible sediments on the filtration mesh for selected values of the compressibility factor s O Tabela 1. Fizykalne zapisy równań procesu filtracji z tworzeniem osadów ściśliwych na siatce filtracyjnej w zależności od wartości wybranych współczynników ściśliwości s O Compressibility factor s O 1/2 Equation V =4 (1 ε O )ρ S P A -2 F b 1 8 t'a F (1 ε O ) 2 2 ρ S Ō μv N β N b 2 Ō μv 2 2 N β N Ln 2 t'μ + μv Nβ N P A F b O A 2 F (1 ε O )ρ S 2/ V =9 (1 ε O )ρ S P A -2 F b 1 Ō μv N β N 9 t'μa F -1 ( b Ō 1 μv N β N A F 2 (1 ε O )ρ S ) arctg ( A F -1 b 1 Ō V N β N P) t'(1 ε O )ρ S 1/ V = (1 ε O )ρ S P 2 A -2 F b 1 27 t'(1 ε O ) 2 ρ 2 S P Ō μv N β 4 N A - F b 2 Ō μv N β N t' 2 (1 ε O ) ρ S A F -4 b Ō μv N β N t'μ Ln + 2μV Nβ N P A F b O A 2 F (1 ε O )ρ S
14 52 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska Meaning of symbols R total resistance of the porous medium [N s/m 5 ] ΔP pressure drop [N/m 2 ] t' average resistance of the filtration mesh [m -1 ] μ dynamic viscosity factor of the suspension [N s/m 2 ] A F deposit area [m 2 ] b O sediment constant [N] s O sediment compressibility factor [-] V N feed volume [m ] β N inflow density of the solid phase [kg/m ] ε O sediment porosity [-] ρ S retained solid phase density [kg/m ] L sediment thickness [m] α proper resistance of the sediment [N s/m 4 ] K permeability factor [m 2 ] V volumetric delivery [m /s] Literatura 1. Anielak A. M, Piecuch. T.: Analityczno-empiryczne kryterium filtracji ciśnieniowej i odśrodkowej zawiesiny poflotacyjnych odpadów cynku i ołowiu. Archiwum Górnictwa PAN. Tom 29. Nr (1984). 2. Anielak A. M, Piecuch. T.: Vergleich der Entwässerung bei Druck Und Zentrifugalfiltration mit Statistischen Modellen. Chemische Technik. Nr, (1987).. Anielak A. M, Piecuch. T.: Vielstufige Druck Filtration. 17 Diskusionstagung Mechanische Flussigkeitabtronaug. Drezden, 1980, 4. Ciborowski. J.: Inżynieria chemiczna. Państwowe Wydawnictwo Naukowe, Warszawa, Dahlstrom D. A., Nickolaus N.: Theory and practice of continuous pressure filtration. Chemical Engineering Progress, Nr (1956). 6. Grace H. P.: Resistance of compressibility of filter cakes. Chemical Engineering Progress, Part I, II, No. 6, 7 (195). 7. Hertjess P. M.: Industrial filtration. Department Of Chemical Engineering. Technical University Delf (1948) 8. Hertjess P. M., Haas H.: Studies in filtration Recueil Trav. Chim. Pays- Bas. Nr 6 (1946). 9. Ives K. J.: New concepts in filtration. Water and Water Engineering. Nr 8 (1961).
15 Filtration of Mixtures Forming Compressible Sediments Kocurek J., Palica M.: Rozdzielanie zawiesin ciał stałych w cieczach na drodze filtracji z kompresją tworzonego osadu. Teoretyczny opis filtracji z równoczesną kompresją osadu. Part 1, Annual Set The Environment Protection (Rocznik Ochrona Środowiska), 4, (2002), part 2, Annual Set The Environment Protection (Rocznik Ochrona Środowiska), 5 (200). 11. Koppiz K.: Untersuchungen über die Anwendbarkeit der Filterteorie auf die Steinkohle-Filterarbeit. Teil 1. Aufbereitungs-Technik. nr 9 (1970). 12. Koppiz K.: Untersuchungen überdies Anwendbarkeit der Filterteorie auf die Steinkohle-Filterarbeit. Teil 2. Aufbereitungs-Technik. nr 12 (1970). 1. Le Lec P.: Variatons de permeabilite des gateax de filtration. Genie Chimique Nr (1962). 14. Luckert K.: Bewertung einer Apparatkombination. Doktorat Dissertation Technische Hochschule. Magdeburg (197). 15. Malatyńska G.: Przekształcenia całkowe i rachunek operatorowy. Wydawnictwo Politechniki Koszalińskiej, Orlicek A. F.: Les principes physiques dela filtration. Genie Chimique. Nr 6 (1956). 17. Palica M., Grotek A.: Opis odwadniania zawiesiny zrzutowej po wirówce filtracyjno-sedymentacyjnej BIRDa modelem SORENSENA. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 9 (2007). 18. Palica M., Pęczek K., Kurowski Ł., Niemirowski J.: Periodyczna filtracja wirowa zawiesiny zrzutowej po wirówkach BIRDa zawierającej dodatek flokulantu MAGNAFLOC 6. Annual Set The Environment Protection (Rocznik Ochrona Środowiska), 10 (2010). 19. Palica M., Gierczycki A., Lemanowicz M.: Własności filtracyjne zawiesiny po wirówkach DECANTER po dodaniu flokulantu MAGNAFLOC 919. Annual Set The Environment Protection (Rocznik Ochrona Środowiska), 11 (2009). 20. Palica M., Wątor K., Thullie J., Kurowski Ł.: Odwadnianie szlamu węglowego na drodze periodycznej filtracji wirowej. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 12 (2010). 21. Palica M., Spyrka W., Adamczyk M.: Testy filtracji ciśnieniowej zawiesiny odpadowej z odmulnika DORRa. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 1 (2011). 22. Palica M., Kocurek J.: Wybrane zagadnienia teorii filtracji i kompresji osadów. Wydawnictwo Politechniki Śląskiej. Gliwice, Piecuch T.: Badania efektywności procesu filtracji mułów węgli surowych w świetle doświadczeń. Praca doktorska. Politechnika Śląska. Gliwice, Piecuch T.: Analityczno-empiryczny model procesu filtracji próżniowej zawiesin mułów węglowych. Monografia habilitacyjna. Zeszyty Naukowe Politechniki Śląskiej. Seria Górnictwo. Nr 65 (1975).
16 54 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska 25. Piecuch T.: Analiza teoretyczna przepływu medium przez modelowe wirówki sitowe. Monografia. Wydawnictwo Polskiego Towarzystwa Nauk o Ziemi, Piecuch T.: Studium teoretyczne procesu filtracji grawitacyjnej. Monografia. Wydawnictwo Polskiego Towarzystwa Nauk o Ziemi, Piecuch T.: Równanie czasu przepływu rotacyjnego ścieku przez wirówkę filtracyjną. Archiwum Ochrony Środowiska PAN, Nr 4 (1985). 28. Piecuch T.: Równanie Darcy jako podstawa analizy teoretycznej szczególnych przypadków procesu filtracji. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 11 (2009). 29. Piecuch T.: Technika wodno-mułowa. Urządzenia i procesy. Wydawnictwo Politechniki Koszalińskiej, Piecuch T.: Technika hydroszlamowa. Wydawnictwo Politechniki Koszalińskiej, Piecuch T.: Technika wodno-mułowa. Urządzenia i procesy. Państwowe Wydawnictwo Naukowo-Techniczne. Warszawa, Piecuch T., Anielak A. M.: Technika i technologia ścieków przemysłowych. Wydawnictwo Politechniki Częstochowskiej, Piecuch T., Opiełka A.: Technologiczne badania pracy prasy filtracyjnej typu ROW. Zeszyty Naukowe AGH. Nr 574, Seria Górnictwo, Piecuch T., Piekarski J.: Badania procesu filtracji ciśnieniowej zawiesiny poprodukcyjnej z Zakładu Przetwórstwa Drewna Polspan-Kronospan. Monografie Komitetu Inżynierii środowiska PAN, Vol. 11 (200). 5. Piecuch T., Sówka J.: Stan badań teoretycznych i praktycznych nad procesem filtracji zawiesin. Zeszyty Naukowe Politechniki Śląskiej. Nr 40. Seria Górnictwo, Gliwice, Piecuch T.: Badania procesu filtracji ciśnieniowej poflotacyjnych koncentratów miedzi. Rudy i Metale Nieżelazne. Nr 10 (1978). 7. Piecuch T.: Badania procesu filtracji ciśnieniowej poflotacyjnych odpadów rud miedzi. Rudy i Metale Nieżelazne. Nr 12 (1978). 8. Piecuch T.: Hipoteza możliwości wspólnego zapisu procesu filtracji i sedymentacji jako równania pędu. Zeszyty Naukowe Politechniki Koszalińskiej. Seria Inżynieria Środowiska, Nr 12 (1988). 9. Piecuch T.: Podstawy sedymentacyjnej teorii procesu filtracji. Zeszyty Naukowe Politechniki Częstochowskiej. Seria Nauki Podstawowe. Nr 21 (1980). 40. Piecuch T., Piekarski J., Malatyńska G.: The Equation Describing The Filtration Process With Compressible Sediment Accumulation On A Filter Mesh. Archives of Environmental Protection, No (201). 41. Piekarski J.: Wybrane przykłady obliczeń komputerowych zastosowanych w inżynierii środowiska. Podręcznik. Wydawnictwo Politechniki Koszalińskiej, 200.
17 Filtration of Mixtures Forming Compressible Sediments Piekarski J, Malej J.: Wykorzystanie techniki komputerowej do projektowania i eksploatacji wysoko sprawnych oczyszczalni ścieków. Podręcznik. Wydawnictwo Politechniki Koszalińskiej, Piekarski J.: Metody numeryczne w modelowaniu przebiegu procesu sorpcji. Monografia. Wydawnictwo Komisji Ekosfery PAN. Oddział Gdańsk, Piekarski J.: Numeryczne modelowanie procesu filtracji i sorpcji. Monografia habilitacyjna. Wydawnictwo Politechniki Koszalińskiej, Piekarski J.: Analiza wybranych parametrów kolmatacji w procesie filtracji grawitacyjnej. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 11, (2009). 46. Piekarski J., Dąbrowski T.: Numerical method for assessment of sorption process of contaminants from wastewater. Mineral Resources Management, 25 (2009) 47. Piekarski J., Dąbrowski T.: Investigations on colmatation during filtration process on the porous deposit. Polish Journal of Environmental Studies, Piekarski J.: Colmatation blockage during gravitational filtration process of coal suspension on sand bed. Mineral Resources Management. Vol. 25, (2009). 49. Piekarski J.: Zastosowanie metod numerycznych do modelowania procesu filtracji grawitacyjnej. Rocznik Ochrona Środowiska (Annual Set The Environment Protection), 12 (2011). 50. Sidełko R., Chmielińska-Bernacka A.: Application of compact reactor for methane fermentation of municipal waste. Rocznik Ochrona Środowiska (Annual Set The Environment Protection). 15 (201). 51. Suttle H.K.: Filtration. Chemical Process Engineering. Nr 8 (1962). 52. Suttle H.K.: Filtration. Advances in filtration in the theoretical and practical fields. Chemical Process Engineering. Nr 2 (1960). 5. Suttle H.K., Tiller F.M.: Filtration theory today. Chemical Engineering Progress. Nr 6 (1966). 54. Tiller F.M.: Numerical methods for constant pressure filtration based on Kozeny a low. Lamar State College of Technology Beaumont Texas Chemical Engineering Progress. Nr 9 (195). 55. Tiller F.M.: The role of porosity in filtration. Analytic Equations for Constant Rate Filtration. Chemical Engineering Progress. Nr 6 (1955). 56. Zużikow W.A.: Zakonomiernosti filtrowania pri rozdielenij rassłaiwajuszczichsja suspienzji na filtrie. Chemiczieskaja Promyszlennost. Nr 4. (1960). 57. Zużikow W.A.: Filtracja. Teoria i praktyka rozdzielania zawiesin. Tłumaczenie z j. rosyjskiego WNT. Warszawa, 1985.
18 56 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska Streszczenie Filtracja mieszanin tworzących osady ściśliwe W niniejszej publikacji, rozpatrzono od strony teoretycznej proces filtracji mieszaniny cieczy i ciała stałego napływającej na siatkę filtracyjną. Ten rodzaj procesu filtracji jest charakterystyczny dla urządzeń filtracyjnych takich jak: filtry próżniowe, prasy filtracyjne oraz filtry ciśnieniowe w mniejszym stopniu wirówki filtracyjne [10, 17 22, 25 27]. Bazą rozważań jest więc ogólny zapis według równania (10) przedstawiony dla procesu filtracji z tworzeniem osadu ściśliwego na siatce filtracyjnej przy uproszczonym założeniu, że cała objętość zawiesiny (V N ) nadana do procesu filtracji, przykładowo próżniowej lub ciśnieniowej [1, 2, 24, 9] zostanie zatrzymana na siatce filtracyjnej (V N β N ), a więc zagęszczenie filtratu będzie równe zero. Zatem równanie (10) przyjmie postać (11). W równaniu tym, jak wyżej, przyjmijmy dla uproszczenia wywodu matematycznego pewne nowe stałe, a mianowicie, zapiszmy stałą A w postaci (12). Następnie stałą B określmy według zapisu (1) (1), oraz stałą C ujmijmy według zapisu (14). Biorąc pod uwagę powyższe uproszczenia można przedstawić rozwiązanie ogólne równania różniczkowego (11) procesu filtracji ze zmiennym ciśnieniem w postaci całki (15). Rozpatrzmy poszczególne przypadki rozwiązania całki zapisanej równaniem (15). Dla B=1 całka przyjmie postać (16). Dla B=0,5; x B = x 0,5 = x, całka (15) ma postać (17) Podstawiając x=t, mamy x=t 2, a stąd dx=2tdt, i tym sposobem całkę (17) z funkcji niewymiernej sprowadzamy do całki z funkcji wymiernej j (18) Funkcję podcałkową f(t), która jest funkcją wymierną niewłaściwą przedstawiamy w postaci (19) i całkując obustronnie otrzymujemy (20). Ostatecznie uwzględniając wynik (20) w całce (18) i wracając do wyjściowej zmiennej x otrzymamy, że całka wyraża się wzorem (21). W szczególności, jeśli dolna granica całkowania jest ustalona i wynosi a=0, natomiast górna granica całkowania jest zmienna, to otrzymamy rozwiązanie równania filtracji w postaci (22). Dla B=2/; x B =x 2/ = x 2 całka (15) ma postać (2). Poprzez podstawienie x=t, mamy x=t, dx=t 2 dt, i całkę z funkcji niewymiernej (2) sprowadzamy do całki z funkcji wymiernej (24). Całkę tego typu oblicza się przedstawiając funkcję podcałkową f(t), która jest funkcją wymierną niewłaściwą, w postaci (25).
19 Filtration of Mixtures Forming Compressible Sediments 57 Uwzględniając rozkład (25) w całce (24) i korzystając ze wzoru (26), otrzymamy (27). Uwzględniając ten wynik we wzorze (24) oraz wracając do podstawienia t= x otrzymamy ostatecznie, że całka (2) wyraża się wzorem (28). W szczególności, jeżeli dolna granica całkowania jest ustalona i wynosi a=0, natomiast górna granica całkowania jest zmienna, to otrzymamy ogólne rozwiązanie równania filtracji wg zapisu (29). Dla B=1/; x B =x 1/ = x całka (15) ma postać (0). Poprzez podstawienie x=t, mamy x=t, oraz dx=t 2 dt i całkę (0) sprowadzamy do całki funkcji wymiernej postaci (1). Funkcja podcałkowa f(t) jest funkcją wymierną niewłaściwą, a więc dzieląc licznik przez mianownik przedstawiamy ją w postaci (2). Uwzględniając rozkład (2) w całce (1) i całkując obustronnie otrzymamy, że całka stojąca po prawej stronie ma postać (). Następnie wracając do wyjściowej zmiennej tj. do podstawienia t= x otrzymamy, całkę ogólną postaci (4). W szczególności, jeżeli dolna granica całkowania jest ustalona i wynosi a=0, natomiast górna granica całkowania jest zmienna, to dla B=2/ całkę (0), wyrażamy za pomocą funkcji (5). Z przeprowadzonej analizy teoretycznej wynikają pewne ogólne wnioski dla badaczy procesu filtracji w tym przypadku procesu filtracji przez siatkę filtracyjną z tworzeniem osadu ściśliwego w trakcie trwania procesu na tej siatce. Otóż: nie można ustalić jednakowej formuły ogólnego równania filtracji takiego, w którym wystąpi parametr ściśliwości osadu w ogólnym zapisie fizykalnym (tutaj B=s O ), do którego to równania będzie można podstawiać wprost dowolne wartości współczynnika ściśliwości s O, w granicach pomiędzy wartością zero oraz jeden i określać przepływ medium przez taką przegrodę porowatą tu siatkę filtracyjną, w przypadku procesu filtracji z tworzeniem osadów ściśliwych na siatce filtracyjnej chcąc korzystać z ogólnego zapisu równania różniczkowego filtracji, należy je każdorazowo najpierw rozwiązać poprzez całkowanie podstawiając najpierw do tego równania, konkretną wartość współczynnika ściśliwości (s O =B). Końcowe fizykalne zapisy tych rozwiązań, dla wybranych współczynników ściśliwości s O przedstawiono w tablicy 1, przed ewentualnym wykorzystaniem ogólnego równania różniczkowego filtracji, jako równania wyjściowego, na podstawie którego chcemy wyliczyć przepływ (wydatek objętościowy) należy najpierw ustalić wartość stałej b 0 z zapisu empirycznego (5) dla określenia wartości parametru przepuszczalności K; a więc parametru przepuszczalności, który musi być znany,
20 58 Tadeusz Piecuch, Jacek Piekarski, Grażyna Malatyńska wyznaczenie wartości współczynników stałych, które występują w zapisie ogólnego równania filtracji (11) (a więc t, b 0 ) będzie przedmiotem badań Autorów publikacji dla konkretnych, typowych mieszanin, które można spotkać w bieżącej praktyce inżynierskiej i będzie przedmiotem kolejnych publikacji Autorów jako dalszy ciąg badań podstawowych nad procesem filtracji, przeprowadzona powyżej analiza teoretyczna procesu filtracji osadów ściśliwych wskazuje jednoznacznie, że wykorzystywanie w praktyce ogólnego równania różniczkowego procesu filtracji poprzez jego rozwiązanie, tj. całkowanie, przy założonej (a więc w praktyce znanej wartości współczynnika ściśliwości s O =B) jest jednak bardzo trudne i skomplikowane, a tym samym nie rokuje pozytywnych perspektyw bieżącego wykorzystywania przez projektantów tego równania.
ARCHIVES OF ENVIRONMENTAL PROTECTION
 ARCHIVES OF ENVIRONMENTAL PROTECTION vol. 39 no. 1 pp. 93-104 2013 PL ISSN 2083-4772 DOI: 10.2478/aep-2013-0009 Copyright by Polish Academy of Sciences and Institute of Environmental Engineering of the
ARCHIVES OF ENVIRONMENTAL PROTECTION vol. 39 no. 1 pp. 93-104 2013 PL ISSN 2083-4772 DOI: 10.2478/aep-2013-0009 Copyright by Polish Academy of Sciences and Institute of Environmental Engineering of the
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Wyznaczenie stałych współczynników w ogólnym równaniu filtracji grawitacyjnej dla zawiesin węglowych
 gospodarka surowcami mineralnymi mineral resources management 2015 Volume 31 Issue 3 Pages 157 174 DOI 10.1515/gospo-2015-0029 Tadeusz Piecuch*, Paweł Czapiewski**, Jacek Piekarski*** Wyznaczenie stałych
gospodarka surowcami mineralnymi mineral resources management 2015 Volume 31 Issue 3 Pages 157 174 DOI 10.1515/gospo-2015-0029 Tadeusz Piecuch*, Paweł Czapiewski**, Jacek Piekarski*** Wyznaczenie stałych
POLITECHNIKA WARSZAWSKA. Wydział Zarządzania ROZPRAWA DOKTORSKA. mgr Marcin Chrząścik
 POLITECHNIKA WARSZAWSKA Wydział Zarządzania ROZPRAWA DOKTORSKA mgr Marcin Chrząścik Model strategii promocji w zarządzaniu wizerunkiem regionu Warmii i Mazur Promotor dr hab. Jarosław S. Kardas, prof.
POLITECHNIKA WARSZAWSKA Wydział Zarządzania ROZPRAWA DOKTORSKA mgr Marcin Chrząścik Model strategii promocji w zarządzaniu wizerunkiem regionu Warmii i Mazur Promotor dr hab. Jarosław S. Kardas, prof.
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
73 Testy filtracji ciśnieniowej zawiesiny odpadowej z odmulnika DORRa
 ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 13. Rok 2011 ISSN 1506-218X 1185-1200 73 Testy filtracji ciśnieniowej zawiesiny odpadowej z odmulnika DORRa Michał
ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 13. Rok 2011 ISSN 1506-218X 1185-1200 73 Testy filtracji ciśnieniowej zawiesiny odpadowej z odmulnika DORRa Michał
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Selection of controller parameters Strojenie regulatorów
 Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
 aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
19 Zastosowanie metod numerycznych do modelowania procesu filtracji grawitacyjnej
 ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 13. Rok 2011 ISSN 1506-218X 315-332 19 Zastosowanie metod numerycznych do modelowania procesu filtracji grawitacyjnej
ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 13. Rok 2011 ISSN 1506-218X 315-332 19 Zastosowanie metod numerycznych do modelowania procesu filtracji grawitacyjnej
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y
 Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Akademia Morska w Szczecinie. Wydział Mechaniczny
 Akademia Morska w Szczecinie Wydział Mechaniczny ROZPRAWA DOKTORSKA mgr inż. Marcin Kołodziejski Analiza metody obsługiwania zarządzanego niezawodnością pędników azymutalnych platformy pływającej Promotor:
Akademia Morska w Szczecinie Wydział Mechaniczny ROZPRAWA DOKTORSKA mgr inż. Marcin Kołodziejski Analiza metody obsługiwania zarządzanego niezawodnością pędników azymutalnych platformy pływającej Promotor:
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Krytyczne czynniki sukcesu w zarządzaniu projektami
 Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
RESONANCE OF TORSIONAL VIBRATION OF SHAFTS COUPLED BY MECHANISMS
 SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI
 Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH
 POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
Matematyczny opis technologii podczyszczania ścieków zawierających kleje organiczne
 9 Matematyczny opis technologii podczyszczania ścieków zawierających kleje organiczne Barbara Juraszka, Tadeusz Piecuch Politechnika Koszalińska 1. Wstęp Woda występująca w przyrodzie ma ogromne znaczenie
9 Matematyczny opis technologii podczyszczania ścieków zawierających kleje organiczne Barbara Juraszka, Tadeusz Piecuch Politechnika Koszalińska 1. Wstęp Woda występująca w przyrodzie ma ogromne znaczenie
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS.
 ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
TYRE PYROLYSIS. REDUXCO GENERAL DISTRIBUTOR :: ::
 TYRE PYROLYSIS Installation for rubber waste pyrolysis designed for processing of used tyres and plastic waste (polyethylene, polypropylene, polystyrene), where the final product could be electricity,
TYRE PYROLYSIS Installation for rubber waste pyrolysis designed for processing of used tyres and plastic waste (polyethylene, polypropylene, polystyrene), where the final product could be electricity,
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Wpływ dodatku flokulantu Magnafloc 919 na przebieg filtracji wirowej podekantacyjnej zawiesiny odpadowej
 Wpływ dodatku flokulantu Magnafloc 919 na przebieg filtracji wirowej podekantacyjnej zawiesiny odpadowej 78 Michał Palica, Agata Dolina, Andrzej Gierczycki, Stanisław Kolorz Politechnika Śląska, Gliwice
Wpływ dodatku flokulantu Magnafloc 919 na przebieg filtracji wirowej podekantacyjnej zawiesiny odpadowej 78 Michał Palica, Agata Dolina, Andrzej Gierczycki, Stanisław Kolorz Politechnika Śląska, Gliwice
Liczbę 29 możemy zaprezentować na siedem różnych sposobów:
 Numeryczna analiza rozkładu liczb naturalnych na określoną sumę liczb pierwszych Świerczewski Ł. Od blisko 200 lat matematycy poszukują odpowiedzi na pytanie zadane przez Christiana Goldbacha, który w
Numeryczna analiza rozkładu liczb naturalnych na określoną sumę liczb pierwszych Świerczewski Ł. Od blisko 200 lat matematycy poszukują odpowiedzi na pytanie zadane przez Christiana Goldbacha, który w
LEARNING AGREEMENT FOR STUDIES
 LEARNING AGREEMENT FOR STUDIES The Student First and last name(s) Nationality E-mail Academic year 2014/2015 Study period 1 st semester 2 nd semester Study cycle Bachelor Master Doctoral Subject area,
LEARNING AGREEMENT FOR STUDIES The Student First and last name(s) Nationality E-mail Academic year 2014/2015 Study period 1 st semester 2 nd semester Study cycle Bachelor Master Doctoral Subject area,
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
QUANTITATIVE AND QUALITATIVE CHARACTERISTICS OF FINGERPRINT BIOMETRIC TEMPLATES
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Opis odwadniania zawiesiny zrzutowej po wirówce filtracyjno-sedymentacyjnej BIRDa modelem SØRENSENA
 10 Opis odwadniania zawiesiny zrzutowej po wirówce filtracyjno-sedymentacyjnej BIRDa modelem SØRENSENA Michał Palica, Aneta Grotek, Magdalena Gruca, Jan Niemirowski Politechnika Śląska, Gliwice 1. Wstęp
10 Opis odwadniania zawiesiny zrzutowej po wirówce filtracyjno-sedymentacyjnej BIRDa modelem SØRENSENA Michał Palica, Aneta Grotek, Magdalena Gruca, Jan Niemirowski Politechnika Śląska, Gliwice 1. Wstęp
SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD I PSPICE
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Outline of a method for fatigue life determination for selected aircraft s elements
 Outline TRIBOLOGY of a method for fatigue life determination for selected aircraft s elements 71 SCIENTIFIC PROBLEMS OF MACHINES OPERATION AND MAINTENANCE 4 (164) 2010 HENRYK TOMASZEK *, MICHAŁ JASZTAL
Outline TRIBOLOGY of a method for fatigue life determination for selected aircraft s elements 71 SCIENTIFIC PROBLEMS OF MACHINES OPERATION AND MAINTENANCE 4 (164) 2010 HENRYK TOMASZEK *, MICHAŁ JASZTAL
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Typ MFPCR FOR THE MOST DEMANDING REQUIREMENTS ON THE PURITY OF INDOOR AIR, WORKSTATIONS, AND DEVICES
 Typ MFPCR FOR THE MOST DEMANDING REQUIREMENTS ON THE PURITY OF INDOOR AIR, WORKSTATIONS, AND DEVICES HEPA and ULPA filters as high-efficiency particulate filters for the separation of suspended particles
Typ MFPCR FOR THE MOST DEMANDING REQUIREMENTS ON THE PURITY OF INDOOR AIR, WORKSTATIONS, AND DEVICES HEPA and ULPA filters as high-efficiency particulate filters for the separation of suspended particles
ROZPRAWA DOKTORSKA. Model obliczeniowy ogrzewań mikroprzewodowych
 POLITECHNIKA WARSZAWSKA Wydział Inżynierii Środowiska Instytut Ogrzewnictwa i Wentylacji ROZPRAWA DOKTORSKA mgr inż. Michał Strzeszewski Model obliczeniowy ogrzewań mikroprzewodowych (streszczenie) Promotor
POLITECHNIKA WARSZAWSKA Wydział Inżynierii Środowiska Instytut Ogrzewnictwa i Wentylacji ROZPRAWA DOKTORSKA mgr inż. Michał Strzeszewski Model obliczeniowy ogrzewań mikroprzewodowych (streszczenie) Promotor
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
Medical electronics part 10 Physiological transducers
 Medical electronics part 10 Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany
Medical electronics part 10 Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany
28 Odwadnianie szlamu węglowego na drodze periodycznej filtracji wirowej
 ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 12. Rok 2010 489-502 28 Odwadnianie szlamu węglowego na drodze periodycznej filtracji wirowej Michał Palica, Karolina
ŚRODKOWO-POMORSKIE TOWARZYSTWO NAUKOWE OCHRONY ŚRODOWISKA Rocznik Ochrona Środowiska Tom 12. Rok 2010 489-502 28 Odwadnianie szlamu węglowego na drodze periodycznej filtracji wirowej Michał Palica, Karolina
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
BIOPHYSICS. Politechnika Łódzka, ul. Żeromskiego 116, Łódź, tel. (042)
 BIOPHYSICS Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki
BIOPHYSICS Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
H γ0 - the standard enthalpy of g phase. H β γ - the transition enthalpy of b to g
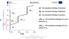 H α0 - the standard enthalpy of a phase H β0 - the standard enthalpy of b phase H γ0 - the standard enthalpy of g phase H α β - the transition enthalpy of a to b phase at T t1 H β γ - the transition enthalpy
H α0 - the standard enthalpy of a phase H β0 - the standard enthalpy of b phase H γ0 - the standard enthalpy of g phase H α β - the transition enthalpy of a to b phase at T t1 H β γ - the transition enthalpy
Streszczenie rozprawy doktorskiej
 Doskonalenie pomiaru zawartości wody w produktach spożywczych z wykorzystaniem metody wagosuszarkowej bazującej na promieniowaniu IR mgr Sławomir Janas Streszczenie rozprawy doktorskiej Promotor pracy:
Doskonalenie pomiaru zawartości wody w produktach spożywczych z wykorzystaniem metody wagosuszarkowej bazującej na promieniowaniu IR mgr Sławomir Janas Streszczenie rozprawy doktorskiej Promotor pracy:
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM
 1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
1-2011 PROBLEMY EKSPLOATACJI 205 Zbigniew ZDZIENNICKI, Andrzej MACIEJCZYK Politechnika Łódzka, Łódź ZASTOSOWANIE SPLOTU FUNKCJI DO OPISU WŁASNOŚCI NIEZAWODNOŚCIOWYCH UKŁADÓW Z REZERWOWANIEM Słowa kluczowe
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip)
 Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Extraclass. Football Men. Season 2009/10 - Autumn round
 Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
DOI: / /32/37
 . 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
. 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2014/2015
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Inżynierii Środowiska obowiązuje studentów rozpoczynających studia w roku akademickim 014/015 Kierunek studiów: Inżynieria Środowiska
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Inżynierii Środowiska obowiązuje studentów rozpoczynających studia w roku akademickim 014/015 Kierunek studiów: Inżynieria Środowiska
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
WYDZIAŁ NAUK EKONOMICZNYCH. Studia II stopnia niestacjonarne Kierunek Międzynarodowe Stosunki Gospodarcze Specjalność INERNATIONAL LOGISTICS
 Studia II stopnia niestacjonarne Kierunek Międzynarodowe Stosunki Gospodarcze Specjalność INERNATIONAL LOGISTICS Description Master Studies in International Logistics is the four-semesters studies, dedicate
Studia II stopnia niestacjonarne Kierunek Międzynarodowe Stosunki Gospodarcze Specjalność INERNATIONAL LOGISTICS Description Master Studies in International Logistics is the four-semesters studies, dedicate
Matematyka 3. Suma szeregu. Promień zbieżności szeregu. Przykład 1: Przykład 2: GenerateConditions
 Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2017/2018
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Inżynierii Lądowej obowiązuje studentów rozpoczynających studia w roku akademickim 017/018 Kierunek studiów: Budownictwo Forma sudiów:
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Inżynierii Lądowej obowiązuje studentów rozpoczynających studia w roku akademickim 017/018 Kierunek studiów: Budownictwo Forma sudiów:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Z-ZIP Równania Różniczkowe. Differential Equations
 MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Analiza porównawcza zmian w rozbiorach wody z uwzględnieniem sposobu jej dostarczania do odbiorców
 55 Analiza porównawcza zmian w rozbiorach wody z uwzględnieniem sposobu jej dostarczania do odbiorców Politechnika Koszalińska 1. Wstęp W związku z zaobserwowanym systematycznym zmniejszaniem się zużycia
55 Analiza porównawcza zmian w rozbiorach wody z uwzględnieniem sposobu jej dostarczania do odbiorców Politechnika Koszalińska 1. Wstęp W związku z zaobserwowanym systematycznym zmniejszaniem się zużycia
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
SG-MICRO... SPRĘŻYNY GAZOWE P.103
 SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA
 Politechnika Poznańska Wydział Maszyn Roboczych i Transportu Inż. NATALIA LEMTIS OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA Promotor: DR INŻ. MARCIN KICIŃSKI Poznań, 2016
Politechnika Poznańska Wydział Maszyn Roboczych i Transportu Inż. NATALIA LEMTIS OPTYMALIZACJA PUBLICZNEGO TRANSPORTU ZBIOROWEGO W GMINIE ŚRODA WIELKOPOLSKA Promotor: DR INŻ. MARCIN KICIŃSKI Poznań, 2016
The Lorenz System and Chaos in Nonlinear DEs
 The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
Relaxation of the Cosmological Constant
 Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Auditorium classes. Lectures
 Faculty of: Mechanical and Robotics Field of study: Mechatronic with English as instruction language Study level: First-cycle studies Form and type of study: Full-time studies Annual: 2016/2017 Lecture
Faculty of: Mechanical and Robotics Field of study: Mechatronic with English as instruction language Study level: First-cycle studies Form and type of study: Full-time studies Annual: 2016/2017 Lecture
THE RAIL RATES valid from 1st October 2015
 RAIL TARIFF This Rail Tariff is an integral part of intermodal transport arrangement service provided by PCC Intermodal S.A. and therefore it cannot be used as a standalone offer, only in combination with
RAIL TARIFF This Rail Tariff is an integral part of intermodal transport arrangement service provided by PCC Intermodal S.A. and therefore it cannot be used as a standalone offer, only in combination with
DM-ML, DM-FL. Auxiliary Equipment and Accessories. Damper Drives. Dimensions. Descritpion
 DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards
 INSPIRE Conference 2010 INSPIRE as a Framework for Cooperation Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards Elżbieta Bielecka Agnieszka Zwirowicz
INSPIRE Conference 2010 INSPIRE as a Framework for Cooperation Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards Elżbieta Bielecka Agnieszka Zwirowicz
ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
CEE 111/211 Agenda Feb 17
 CEE 111/211 Agenda Feb 17 Tuesday: SW for project work: Jetstream, MSP, Revit, Riuska, POP, SV On R: drive; takes time to install Acoustics today: \\cife server\files\classes\cee111\presentations Thursday:
CEE 111/211 Agenda Feb 17 Tuesday: SW for project work: Jetstream, MSP, Revit, Riuska, POP, SV On R: drive; takes time to install Acoustics today: \\cife server\files\classes\cee111\presentations Thursday:
5. REEMISJA ZWIĄZKÓW RTĘCI W CZASIE UNIESZKODLIWIANIA OSADÓW ŚCIEKOWYCH
 1. Prognozowanie procesów migracji zanieczyszczeń zawartych w odciekach wyeksploatowanych składowisk odpadów komunalnych : Kompleksowe zarządzanie gospodarką odpadami Kazimierz Szymański, Robert Sidełko,
1. Prognozowanie procesów migracji zanieczyszczeń zawartych w odciekach wyeksploatowanych składowisk odpadów komunalnych : Kompleksowe zarządzanie gospodarką odpadami Kazimierz Szymański, Robert Sidełko,
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów
 Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
PRACA DYPLOMOWA Magisterska
 POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
PRZEPISY RULES PUBLIKACJA NR 83/P PUBLICATION NO. 83/P
 PRZEPISY RULES PUBLIKACJA NR 83/P PUBLICATION NO. 83/P ZALECENIA DO METODYKI OCENY UKŁADÓW PRZELEWOWYCH BALASTU RECOMMENDATION ON A STANDARD METHOD FOR EVALUATING CROSS-FLOODING ARRANGEMENTS 0 Publikacje
PRZEPISY RULES PUBLIKACJA NR 83/P PUBLICATION NO. 83/P ZALECENIA DO METODYKI OCENY UKŁADÓW PRZELEWOWYCH BALASTU RECOMMENDATION ON A STANDARD METHOD FOR EVALUATING CROSS-FLOODING ARRANGEMENTS 0 Publikacje
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI
 Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent
 Piotr Olczak 1, Agata Jarosz Politechnika Krakowska 2 Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent Wprowadzenie Autorzy niniejszej pracy dokonali porównania
Piotr Olczak 1, Agata Jarosz Politechnika Krakowska 2 Modelowanie zagadnień cieplnych: analiza porównawcza wyników programów ZSoil i AnsysFluent Wprowadzenie Autorzy niniejszej pracy dokonali porównania
WYŁĄCZNIK CZASOWY OUTDOOR TIMER
 003-582 PL WYŁĄCZNIK CZASOWY Instrukcja obsługi (Tłumaczenie oryginalnej instrukcji) Ważny! Przed użyciem uważnie przeczytaj instrukcję obsługi! Zachowaj ją na przyszłość. EN OUTDOOR TIMER Operating instructions
003-582 PL WYŁĄCZNIK CZASOWY Instrukcja obsługi (Tłumaczenie oryginalnej instrukcji) Ważny! Przed użyciem uważnie przeczytaj instrukcję obsługi! Zachowaj ją na przyszłość. EN OUTDOOR TIMER Operating instructions
