OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU
|
|
|
- Paweł Ciesielski
- 9 lat temu
- Przeglądów:
Transkrypt
1 ZESZYTY NAUKOWE Zenon GNIAZDOWSKI 1 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Streszczenie W artykule zwrócono uwagę na znaczenie krzemu i technologii krzemowej zarówno w rozwoju mikroelektroniki a co za tym idzie także informatyki, a także w rozwoju mikrosystemów (ang.: MEMS Micro-Electromechanical System), gdzie łączy się elektronikę z mikromechaniką, oraz w rozwoju zminiaturyzowanych systemów do całkowitych analiz chemicznych (ang.: µtas Micro Total Analysis System). In this paper, the role of silicon for development of computer technology is emphasized. It is noticed that Micro-System Technology (MST) as well as Technology of Micro Total Analysis System (µtas) are also derived from silicon technology. Hence, the importance of silicon in many modern human activities is concluded. 1. WPROWADZENIE Głównym składnikiem piasku jest krzem, który pod względem ilości jest drugim po tlenie pierwiastkiem występującym w skorupie ziemskiej. Bez krzemu nie byłby możliwy tak szeroki rozwój informatyki: jest to podstawowy materiał wykorzystywany w technologii cyfrowych układów scalonych, czyli w technologii wszystkich najistotniejszych składników komputera takich jak procesor, pamięć itp. W ostatnich dziesięcioleciach dwudziestego wieku odkryto także inne możliwości zastosowania krzemu. Stwierdzono, że ma znakomite własności mechaniczne w pewnych aspektach lepsze niż stal. W związku z tym, powstały nowe dziedziny techniki, takie jak np. technologia mikrosystemów, gdzie krzem jest wykorzystywany do realizacji struktur mechanicznych oraz elektronicznych układów sterujących. Niniejszy artykuł jest popularyzatorską próbą pokazania znaczenia krzemu w mikroelektronice (a więc również w informatyce), a także w mikrosystemach mikro- -elektromechanicznych oraz w mikrosystemach do analityki chemicznej. Należy 1 Dr inż. Zenon Gniazdowski jest wykładowcą w Warszawskiej Wyższej Szkole Informatyki i adiunktem w Instytucie Technologii Elektronowej. 125
2 Zenon GNIAZDOWSKI przy tym wyjaśnić, że wobec popularyzatorskiego charakteru i szerokiego zakresu poruszanych zagadnień, artykuł z konieczności zawiera wiele uproszczeń. 2. LOGIKA, A KOMPUTERY Obserwując komputer, można wyodrębnić dwie platformy. Jedna z nich to platforma sprzętowa, druga programowa. Najważniejszym elementem platformy programowej jest system operacyjny, który zarządza pracą komputera. Poza tym, elementami tej platformy są wszystkie aplikacje współpracujące z systemem operacyjnym. Platforma sprzętowa to procesor, pamięć, wszelkie urządzenia wejściowe i wyjściowe. Truizmem jest stwierdzenie, że obydwie platformy nie mogą bez siebie funkcjonować. W świadomości powszechnej praca informatyka jest raczej związana z platformą programową bez względu na to czy jest to jej instalowanie, czy też posługiwanie się nią albo jej tworzenie. U jej podstaw leży wykorzystanie logiki. Z pewnością, żadna sensowna aplikacja nie może działać wbrew prawom logiki lub obok nich. Platforma sprzętowa jest jakby zadana z góry. Przez to jest ona mniej znana. W sensie potocznym, ta platforma jest na pewno zrealizowana zgodnie z prawami logiki podobnie jak każde dzieło inżynierskie. Z drugiej strony wcale nie jest oczywiste, że elementy składowe komputera realizują operacje logiczne w ściśle matematycznym tego słowa znaczeniu. Dlatego warto prześledzić, jaki jest związek klasycznej logiki z architekturą komputera Logika Historia logiki sięga starożytnej Grecji, gdzie Arystoteles ( p.n.e.) zbudował pierwszy system logiki formalnej, będący logiką tez zbudowanych ze stałych logicznych i zmiennych zdań oraz logiką nazw [1]. System ten służył dowodzeniu twierdzeń filozoficznych. Arystotelesowi znane było prawo wyłączonego środka oraz prawo sprzeczności [2], a więc znane mu było pojęcie prawdy i fałszu. Pierwszy system dwuwartościowej logiki zdań opracowali stoicy również w Grecji w III wieku p.n.e. Według nich każde zdanie jest prawdziwe, bądź fałszywe. W logice stoików występują m.in. spójniki międzyzdaniowe i, jeżeli..., to... oraz albo, a także negacja nie [1] Algebra Boole a W XIX w. George Boole jako pierwszy dostrzegł podobieństwo pomiędzy logiką zdań, a prawami arytmetyki. Na ich podstawie podjął on próbę zbudowania logiki formalnej, posługując się językiem arytmetyki. W ten sposób zaczęła powstawać algebra logiki, nazwana algebrą Boole a [1]. 126
3 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Tab. 1. Analogie pomiędzy logiką, a algebrą Boole a Logika W języku logiki mówi się o zdaniach. Zdanie jest fałszywe albo prawdziwe. Zdanie można zaprzeczyć: zaprzeczone zdanie prawdziwe stanie się zdaniem fałszywym i odwrotnie zaprzeczone zdanie fałszywe stanie się zdaniem prawdziwym. Dwa zdania połączone spójnikiem i nazywane są koniunkcją zdań. Koniunkcja jest prawdziwa tylko wtedy, gdy obydwa zdania składowe są jednocześnie prawdziwe. Dwa zdania połączone spójnikiem lub nazywane są alternatywą zdań. Alternatywa jest prawdziwa wtedy, gdy co najmniej jedno ze zdań składowych jest prawdziwe. Algebra Boole a Język algebry Boola posługuje się pojęciem zmiennej Zmienna może przyjąć jedną z dwóch wartości: zero albo jeden Zmienną można zanegować: zanegowana zmienna równa 1 przyjmie wartość 0 zanegowana zmienna równa 0 przyjmie wartość 1. Odpowiednikiem koniunkcji dwóch zdań w algebrze Boola jest ich iloczyn, który jest równy 1 tylko wtedy, gdy obydwie zmienne są jednocześnie równe 1. Algebraicznym odpowiednikiem alternatywy dwóch zdań jest ich suma, która jest równa 1 tylko wtedy, gdy co najmniej jeden ze składników sumy jest równy 1. Tab. 1. Przedstawia analogie pomiędzy logiką a algebrą Boole a. Na ich podstawie można powiedzieć, że algebra Boole a jest matematycznym modelem logiki zdań Technika cyfrowa Kolejnym krokiem jest budowa modeli operacji boolowskich w postaci układów elektronicznych zwanych bramkami logicznymi. Zajmuje się tym technika cyfrowa. Najprościej mówiąc, w technice cyfrowej zmienne boolowskie równe zero lub jeden reprezentowane są odpowiednio przez najniższe lub najwyższe wartości napięć występujących w układzie elektronicznym. Operacje iloczynu lub sumy dwóch zmiennych oraz negacja pojedynczej zmiennej (w logice koniunkcja lub alternatywa oraz zaprzeczenie) realizowane są przez bramki logiczne odpowiednio AND, OR oraz NOT. Przy ich pomocy można zrealizować dowolną funkcję boolowską. Oznacza to, że te trzy podstawowe bramki są konieczne i wystarczające do realizacji dowolnego układu cyfrowego. Ich symbole przedstawia Rys.1 Rys.1. Symbole podstawowych bramek logicznych AND, OR i NOT. 127
4 Zenon GNIAZDOWSKI W szczególności np. wśród rozkazów mikroprocesora jest sumowanie dwóch liczb dwójkowych. Operacja ta musi być zrealizowana sprzętowo. Sumowanie dwóch liczb binarnych można zrealizować przy pomocy bramek logicznych tworzących urządzenie zwane sumatorem. Podobnie, z bramek można zrealizować dowolne inne urządzenia cyfrowe, np. dekoder demultiplekser, który m.in. może być wykorzystany do wyboru adresu odpowiedniego urządzenia występującego w systemie komputerowym, albo podstawowe komórki pamiętające, zwane rejestrami. Rozumując podobnie, można stworzyć całą logiczną strukturę mikroprocesora. Konsekwencją przedstawionego wyżej rozumowania jest stwierdzenie, że co prawda komputer jest urządzeniem wynalezionym i zrealizowanym współcześnie, to z całą pewnością jego korzenie są umocowane w logice, a przez to sięgają starożytności. 3. MIKROELEKTRONIKA Pomijając pewne szczegóły historyczne, można powiedzieć, że w chwili obecnej do realizacji bramek logicznych potrzebne są tranzystory polowe z bramką izolowaną, zwane tranzystorami MOS 2. Układy cyfrowe realizuje się jako układy CMOS (ang. Complementary MOS). Ich charakterystyczną cechą jest to, że każde wejście bramki logicznej steruje bramkami dwóch komplementarnych tranzystorów MOS: n-kanałowego i p-kanałowego 3. Na Rys. 2 (a) pokazano schemat inwertera 4 CMOS. Na Rys. 2 (b) i (c) pokazano zasadę jego działania. Zasada ta wynika z faktu, że tranzystor MOS przy napięciu na bramce niskim (zero logiczne) lub wysokim (jedynka logiczna) działa jak klucz, który może pozwolić na przepływ prądu, lub może ten przepływ uniemożliwić. Przy podanej na bramkę tranzystora n-kanałowego jedynce logicznej, pomiędzy drenem (D) i źródłem (S) tranzystora może płynąć prąd. Przy zerze logicznym ten prąd nie płynie. W tranzystorze p-kanałowym sytuacja jest odwrotna 5 przepływ prądu może mieć miejsce przy zerze logicznym na bramce tranzystora. Stąd wynika fakt, że w stanie ustalonym (zera lub jedynki logicznej na wejściu) przez inwerter nie płynie prąd, gdyż jeden z tranzystorów jest zawsze zatkany. Oznacza to, że inwerter nie pobiera mocy. Jednocześnie, cechą wszystkich bramek CMOS jest to, że w stanie statycznym nie pobierają mocy. Pobór mocy ma miejsce tylko w trakcie przełączania bramki, a więc rośnie z częstością dokonywanych przełączeń. 2 MOS jest skrótem od angielskich słów Metal Oxide Semiconductor. W strukturze tranzystora MOS przewodząca bramka (np. aluminiowa stąd słowo Metal ) jest oddzielona od półprzewodnikowego podłoża (Semiconductor półprzewodnik) warstwą izolacyjną SiO 2 (Oxide tlenek). 3 W tranzystorze n-kanałowym nośnikami prądu są elektrony, zaś w tranzystorze p-kanałowym dziury. 4 Bramka NOT bywa nazywana inwerterem. 5 Fakt ten zaznaczono kółkiem od strony bramki tranzystora p-kanałowego. 128
5 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Rys. 2. Inwerter CMOS: (a) schemat elektryczny; (b) stan inwertera przy jedynce logicznej na wejściu; (c) stan inwertera przy zerze logicznym na wejściu; Dodając do inwertera kolejne komplementarne pary tranzystorów można otrzymać bramki NAND (NOT AND zaprzeczony iloczyn) lub NOR (NOT OR zaprzeczona suma). Inwerter oraz bramki NAND i NOR są bramkami podstawowymi dla techniki CMOS. Jednocześnie można dowieść, że bramki NAND albo NOR są bramkami uniwersalnymi w tym sensie, że z samych bramek NAND albo samych bramek NOR można zbudować bramki AND, OR i NOT. Oznacza to, że bramki NAND albo NOR są wystarczające do realizacji dowolnej funkcji boolowskiej [3]. Na Rys. 3 przedstawiono symbole dwuwejściowych bramek uniwersalnych NAND i NOR. Rys. 3. Symbole bramek uniwersalnych NAND i NOR 3.1. Technologia krzemowa Układy cyfrowe wykorzystywane w technice komputerowej realizowane są w postaci monolitycznych krzemowych planarnych układów scalonych realizowanych 129
6 Zenon GNIAZDOWSKI w technologii CMOS 6. Na Rys. 4 pokazano uproszczoną strukturę przykładowego inwertera CMOS. Na przedstawionym przykładzie tranzystor n-kanałowy jest umieszczony bezpośrednio na podłożu typu p, zaś tranzystor p-kanałowy zrealizowany jest w obszarze wyspy typu n. Rys. 4. Uproszczony przekrój inwertera CMOS z bramką polikrzemową. Przez We i Wy oznaczono odpowiednio wejście i wyjście inwertera. Symbolami VDD i VSS oznaczono odpowiednio wysoki i niski potencjał zasilania. Podstawową przyczyną dominacji technologii CMOS na rynku układów cyfrowych jest to, że układy CMOS w stanie statycznym nie pobierają mocy 7. Z drugiej strony w mikroelektronice istnieje możliwość skalowania przyrządów, polegająca z jednej strony na zmniejszaniu ich wymiarów geometrycznych, a także na idącymi za tym korzystnymi zmianami ich parametrów. W efekcie daje to mniejsze przyrządy, a więc możliwość ich większego upakowania, a w dalszej kolejności większe możliwości układu cyfrowego, oraz poprawę jego parametrów funkcjonalnych 8. Tab. 2. Rozwój technologii układów cyfrowych [4] Rok Procesor Reguły projektowania [µm] Liczba tranzystorów na strukturze Częstotliwość pracy [Hz] E E E E+06 6 Na początku lat siedemdziesiątych dwudziestego wieku firma Intel realizowała procesory 4004 i 8008 w technologii z tranzystorami p-kanałowymi (PMOS). Procesor 8080 zrealizowano w roku 1974 w technologii NMOS z tranzystorami n-kanałowymi. W drugiej połowie lat osiemdziesiątych zaczęto stosować technologię CMOS, uzyskując dzięki temu istotny spadek zużywanej mocy. 7 Należy zauważyć, że ze wzrostem częstotliwości pobór mocy rośnie. 8 Np. wzrost częstotliwości pracy układu, zmniejszenie gęstości wydzielanej mocy. 130
7 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Rok Procesor Reguły projektowania [µm] Liczba tranzystorów na strukturze Częstotliwość pracy [Hz] E E DX E DX E E DX E E Pentium E E Pentium MMX E E Pentium III E E Celeron E E Pentium M E E Itanium E E Pentium 4E E E W Tab. 2 przedstawiono zestawienie zawierające daty wprowadzenia na rynek kolejnych typów procesorów wraz z towarzyszącymi im zmianami w technologii i ich parametrach [4]. Szczególnie istotnym parametrem opisującym technologię jest tzw. wymiar charakterystyczny określający reguły projektowania. Wymiar ten określa minimalny projektowany wymiar boczny (długość, szerokość) elementu w układzie scalonym 9. Na początku lat siedemdziesiątych ten wymiar wynosił 10 µm, w roku 2005 tylko 0.09 µm, a w latach ten wymiar ma być na poziomie µm. Oznacza to, że powierzchnia przyrządów (tranzystorów) w ciągu trzydziestu kilku lat zmalała ponad dziesięć tysięcy razy. Na Rys. 5 przedstawiono wykres zmian reguł projektowania w ciągu tych lat. Rys. 5. Zmiana reguł projektowania w funkcji czasu 9 Ponieważ przyrządy (tranzystory) są definiowane przez wzajemne relacje określonych obszarów na strukturze układu, to wymiar charakterystyczny określa minimalne rozmiary obszarów, minimalne miedzy nimi odstępy w płaszczyźnie poziomej oraz minimalne zakładki obszarów leżących jeden nad drugim. 131
8 Zenon GNIAZDOWSKI Z maleniem powierzchni tranzystorów rosła ich liczba na strukturze układu scalonego. Dzięki temu rosły możliwości funkcjonalne budowanych procesorów. Najpierw były to procesory 4-bitowe, potem 8, 16, 32, a w chwili obecnej już 64-bitowe. Procesor 4004 w swojej strukturze zawierał 2300 tranzystorów. Obecnie ich liczba zbliża się do miliarda. Oznacza to, że w ciągu trzydziestu lat liczba tranzystorów w strukturze procesora wzrosła kilkadziesiąt tysięcy razy. Na Rys. 6 przedstawiono wykres zmian liczby tranzystorów w strukturze procesora w funkcji czasu. Rys. 6. Zmiana liczby tranzystorów w funkcji czasu Jak wcześniej wspomniano, wraz z maleniem tranzystorów oraz ze wzrostem ich liczby w strukturze procesora poprawiały się parametry funkcjonalne procesorów, w tym wzrosła także ich częstotliwość pracy. Pierwsze procesory pracowały z częstotliwością kilkudziesięciu khz. Obecnie ich częstotliwość przekracza 1 GHz. W ciągu trzydziestu lat nastąpił ponad tysiąckrotny jej wzrost. Na Rys. 7 pokazano zmiany częstotliwości pracy procesorów wyszczególnionych w Tab. 2 w funkcji czasu. Rys. 7. Zmiana częstotliwości pracy procesorów w funkcji czasu 132
9 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU 3.2. Prawo Moore a Wzrost upakowania liczby tranzystorów na strukturze procesora (ogólniej układu scalonego) da się opisać przy pomocy prawa sformułowanego w roku 1965 przez Gordona Moore a, współzałożyciela firm Fairchild oraz Intel. Moore zauważył, że liczba elementów na strukturze podwaja się corocznie. Na tej podstawie oszacował, że w roku 1975 na strukturze powinno być 65 tysięcy elementów. W tymże 1975 prawo Moore a zostało zrewidowane. Stwierdzono, że liczba elementów podwaja się co półtora roku [5]. Przez całe następne lata prawo Moore a wykorzystywano do prognozowania rozwoju mikroelektroniki. Rozwój ten, postępujący zgodnie z tym prawem, spowodował dramatyczne zmiany, najpierw w rozmiarze pojedynczych elementów, a w konsekwencji także w ich cenie 10. Dzięki temu nastąpił m.in. rewolucyjny rozwój informatyki. Szczególnie ostro to widać, porównując chociażby komputery używane na początku lat osiemdziesiątych dwudziestego wieku (ich wielkość, moc obliczeniową, dostępność oraz możliwe aplikacje) z tymi, które w chwili obecnej są wykorzystywane. Gdyby prawo Moore a obowiązywało w innych dziedzinach niż mikroelektronika, to jego skutki widoczne by były zarówno kosztach jak i możliwościach oferowanych przez te dziedziny. Np. koszt oraz czas przelotu samolotem z Europy do Ameryki Północnej byłby niewyobrażalnie niski. Niestety, poza mikroelektroniką prawo Moore a nie obowiązuje [5]. 4. MIKROSYSTEMY Jak wcześniej pokazano, krzemowa technologia mikroelektroniczna służąca produkcji układów scalonych (w szczególności układów cyfrowych) rozwinęła się w ciągu ostatnich trzydziestu kilku lat w sposób niezwykle dynamiczny. Jednocześnie stwierdzono, że krzem ma bardzo interesujące własności. Przede wszystkim jego własności mechaniczne są porównywalne, a nawet lepsze niż własności stali. Z drugiej strony już na początku lat pięćdziesiątych XX w. odkryto zjawisko piezorezystancyjne w krzemie, polegające na tym, że krzem ma własności umożliwiające konwersję sygnałów mechanicznych, poprzez pojawiające się w jego strukturze naprężenia, na zmiany własności rezystancyjnych warstw domieszkowanych. Do tego trzeba dodać, że technologia mikroelektroniczna wzbogacona o techniki trawienia anizotropowego pozwala rzeźbić stosowne kształty w krzemie. To wszystko dało początek systemom mikroelektromechanicznym albo mikrosystemom 11, pośród któ- 10 Rozmiar tranzystora jest obecnie taki, że na główce szpilki można by umieścić około 200 milionów tranzystorów, zaś cena jednego tranzystora jest taka sama jak cena wydrukowanej litery w gazecie [5]. 11 W literaturze anglojęzycznej na ich określenie używa się różnych skrótów: MEMS micro-electromechanical system, MST microsystem technology, albo micromachines [7]. 133
10 Zenon GNIAZDOWSKI rych wyróżnia się dwie grupy urządzeń. Są to czujniki i aktywatory, czyli elementy wykonawcze powodujące powstawanie ruchu (ang.: sensors and actuators). Technologia mikrosystemów umożliwiła przede wszystkim miniaturyzację bardzo wielu przyrządów mechanicznych, które dotychczas miniaturowymi nie były. Jednymi z pierwszych takich przyrządów były czujniki piezorezystywne. W czujnikach tych wykorzystuje obszar aktywny w postaci krzemowej membrany lub belki, na którym znajdują się odpowiednio rozmieszczone piezorezystory 12, które powinny być odpowiednio zorientowane zarówno względem krystalicznej struktury krzemu jak i względem składowych naprężenia. Przykładem takiego czujnika może być czujnik siły w postaci belki krzemowej z odpowiednio ulokowanymi piezorezystorami. Jest on przeznaczony dla mikrorobota pracującego w komorze elektronowego mikroskopu skaningowego 13 [6]. Na etapie jego projektowania przyjęto, że powinien on mierzyć siły o wartościach od pojedynczych mn do dziesiątek mn 14. Rozmiary struktury (w zależności od wariantu konstrukcyjnego) przyjmowano następujące: grubość belki około kilkadziesiąt µm 15, długość rzędu kilku tysięcy µm (kilku mm), szerokość ponad 300 µm (0.3 mm). Struktura czujnika była wykonywana na płytkach krzemowych o grubości ok. 400 µm (0.4 mm). Cztery piezorezystory umieszczono u nasady belki. Dwa z nich umieszczono wzdłuż belki w tych dominują naprężenia wzdłużne rozciągające. Pozostałe dwa piezorezystory umieszczono w poprzek tu dominują naprężenia poprzeczne rozciągające. Elektryczne połączenia pomiędzy rezystorami tworzą mostek Wheatstona. Podanie obciążenia mechanicznego na strukturę czujnika powoduje powstanie naprężeń w jego obszarze aktywnym, które z kolei powodują zmianę rezystancji piezorezystorów, wyprowadzając mostek pomiarowy z równowagi elektrycznej. Na Rys. 8 pokazano przykład wyników modelowania ugięcia czujnika pod wpływem siły. Modelowanie wykonano na etapie projektowania struktury czujnika. Rys. 8. Ugięcie belki o długości 2500µm, szerokości 350µm i grubości 20µm pod wpływem siły 1mN przyłożonej na końcu belki i skierowanej w kierunku osi Y ugięcie belki na końcu wynosi ponad 130 µm. 12 Piezorezystor jest elementem o rezystancji zależnej od naprężenia. 13 Czujnik zrealizowano w Instytucie Technologii Elektronowej w Warszawie w ramach europejskiego projektu badawczego ROBOSEM. 14 Siła 1 mn (milinewton) jest równoważna ok. 0,1G. 15 Odległość 1µm jest równa 0.001mm. 134
11 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Poza przyrządami mikromechanicznymi, buduje się także miniaturowe urządzenia do analiz chemicznych zarówno gazowych jak i cieczowych. Zastępują one dotychczasowe reaktory znane z laboratoriów chemicznych. Przyrządy te określa się mianem mikrotasy, od angielskiego skrótu microtas micro Total Analysis System. Przykładem takiego urządzenia może być zintegrowany analizator składu gazów kopalnianych, będący w praktyce przenośnym, zminiaturyzowanym chromatografem gazowym, współpracującym z komputerem. Innym przykładem może być miniaturowe urządzenie do badania próbek DNA, dla potrzeb diagnostyki medycznej. Obydwa te urządzenia charakteryzują się znacznie zmniejszonymi rozmiarami, istotnie krótszymi czasami analiz oraz tym, że są zautomatyzowane. Wszystkie te cechy wyróżniają je w porównaniu z ich klasycznymi pierwowzorami. Wspomniane wyżej mikrosystemy mechaniczne, czy też chemiczne nie zawsze są wytworzone z krzemu. Jednakże krzem i technologia krzemowa mają ogromne znaczenie w ich wytwarzaniu. Najpierw dlatego, że w bardzo wielu przypadkach krzem stanowi podłoże na którym przyrządy te są wytwarzane. Z kolei także dlatego, że do ich wykonania wykorzystuje się związki krzemu. Głównie jednak dlatego, że do realizacji mikrosystemów wykorzystuje się wiele elementów mikroelektronicznej technologii krzemowej. Bez elementów tej technologii niemożliwa byłaby miniaturyzacja. 5. ZNACZENIE KRZEMU Krzem jest pierwiastkiem z czwartej grupy układu okresowego. Jest to półprzewodnik, który przede wszystkim wykorzystywany jest w postaci monokrystalicznej. Monokryształ krzemu jest otrzymywany metodą Czochralskiego 16, a następnie cięty na płytki i stosownie obrabiany w zależności od potrzeb. Technologia krzemowa oraz krzem jako materiał mają podstawowe znaczenie zarówno w mikroelektronice jak i w mikrosystemach. W pracy [8] zwrócono uwagę, że krzem jest nośnikiem informacji obecnej epoki. Dzięki niemu dokonała się rewolucja, podobnie, jak miało to miejsce 500 lat temu, wraz z odkryciem druku przez Gutenberga. Tab. 3 zawiera analogie pomiędzy obydwoma nośnikami informacji. 16 Jan Czochralski w okresie międzywojennym był profesorem w Politechnice Warszawskiej. Był on odkrywcą metody wzrostu kryształów, która jest powszechnie wykorzystywana do wytwarzania krzemu monokrystalicznego. 135
12 Zenon GNIAZDOWSKI Tab. 3. Rewolucje w dziedzinie nośników informacji [8] Johan Gutenberg Drewno Kartka papieru Ryza papieru Drukarnia Korekta Tekst, język Wydawnictwa artystyczne, niskonakładowe edycje Gazety, tanie książki wielkonakładowe William Shockley Piasek Płytka krzemowa Monokryształ krzemu Fabryka układów scalonych Testowanie Układy logiczne Układy specjalizowane Układy standardowe Rewolucja związana z krzemem nie zatrzymała się w obrębie mikroelektroniki, lecz rozprzestrzeniła się poza tę dziedzinę, powodując również rewolucyjne zmiany, prowadzące do mikromechaniki i mikrosystemów, a także zmiany o podobnej skali w dziedzinie przyrządów do analityki chemicznej. 6. ZAKOŃCZENIE W artykule starano się przedstawić rolę i znaczenie krzemu i technologii krzemowej oraz ich wpływ na rozwój informatyki oraz innych dziedzin. Stwierdzono, że rozwój ten miał charakter rewolucji technologicznej. Można się zastanawiać, czy postęp w rozwoju mikroelektroniki krzemowej zgodny z prawem Moore a będzie miał swój rychły koniec. Mówi się, że może to nastąpić już w ciągu kilku najbliższych lat. Zapewne, dynamika zmian może w sposób istotny ulec zmniejszeniu krzywa Moore a może się spłaszczać [9], co dowodziłoby nasycania się rozwoju technologii opartych o krzem. Bez względu na to, czy to nastąpi szybko, czy też nie, znaczenia krzemu dla rozwoju technologicznego i ekonomicznego przełomu wieków dwudziestego i dwudziestego pierwszego nie da się przecenić. W balladzie Pani Twardowska A. Mickiewicza, jej bohater żąda, aby Mefisto niezwłocznie ukręcił mu bicz z piasku, mając nadzieję, że nawet diabeł nie potrafi sprostać jego wyzwaniu bicz z piasku jest synonimem rzeczy niemożliwej do zrealizowania. Tymczasem zadanie zostaje wykonane. Ale czy potrzeba aż czartowskiej mocy, aby ukręcić bicz z piasku? Opisane wyżej możliwości technologii krzemowej dowodzą tego, że współczesny człowiek potrafi zrobić znacznie więcej niż tylko bicz z piasku. 136
13 OD MIKROELEKTRONIKI DO MIKROSYSTEMÓW, CZYLI O ROLI I ZNACZENIU KRZEMU Literatura 1. Mała encyklopedia logiki. Red. W. Marciszewski. Zakład Narodowy im. Ossolińskich Wydawnictwo. Wrocław Wprowadzenie do filozofii. Praca zbiorowa. Wydawnictwo KUL. Lublin B. Wilkinson. Układy cyfrowe. WKŁ. Warszawa i pokrewne linki na tej stronie 6. Z. Gniazdowski: Krzemowe piezorezystywne czujniki wielkości mechanicznych. Teoretyczne i praktyczne aspekty modelowania i konstrukcji. 7. J. W. Judy: Microelectromechanical systems (MEMS): fabrication, design and. Applications. Smart Mater. Struct. 10 (2001) A. Jakubowski, L. Łukasiak: O telekomunikacyjnych pożytkach z elektroniki wynikających. Przegląd Telekomunikacyjny. Rocznik LXXVI. Nr 1/2003, str T. Dietl: O przyszłości miniaturyzacji. Delta. Nr 10(305) (1999) str
14 138
Ćw. 8 Bramki logiczne
 Ćw. 8 Bramki logiczne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi, poznanie ich rodzajów oraz najwaŝniejszych parametrów opisujących ich własności elektryczne.
Ćw. 8 Bramki logiczne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi, poznanie ich rodzajów oraz najwaŝniejszych parametrów opisujących ich własności elektryczne.
Bramki logiczne. 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132.
 Bramki logiczne 1. Czas trwania: 3h 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132. 3. Wymagana znajomość pojęć stany logiczne Hi, Lo, stan
Bramki logiczne 1. Czas trwania: 3h 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132. 3. Wymagana znajomość pojęć stany logiczne Hi, Lo, stan
Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych Laboratorium Przyrządów Półprzewodnikowych. Ćwiczenie 4
 Ćwiczenie 4 Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk statycznych układów scalonych CMOS oraz ich własności dynamicznych podczas procesu przełączania. Wiadomości podstawowe. Budowa i działanie
Ćwiczenie 4 Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk statycznych układów scalonych CMOS oraz ich własności dynamicznych podczas procesu przełączania. Wiadomości podstawowe. Budowa i działanie
WSTĘP. Budowa bramki NAND TTL, ch-ka przełączania, schemat wewnętrzny, działanie 2
 WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
Od Arystotelesa do Moora
 Od Arystotelesa do Moora Zenon Gniazdowski * * Autor pracuje w Instytucie Technologii Elektronowej w Warszawie oraz w Warszawskiej Wyższej Szkole Informatyki Od Arystotelesa do Moora Motywacja Logika Algebra
Od Arystotelesa do Moora Zenon Gniazdowski * * Autor pracuje w Instytucie Technologii Elektronowej w Warszawie oraz w Warszawskiej Wyższej Szkole Informatyki Od Arystotelesa do Moora Motywacja Logika Algebra
Przerzutnik ma pewną liczbę wejść i z reguły dwa wyjścia.
 Kilka informacji o przerzutnikach Jaki układ elektroniczny nazywa się przerzutnikiem? Przerzutnikiem bistabilnym jest nazywany układ elektroniczny, charakteryzujący się istnieniem dwóch stanów wyróżnionych
Kilka informacji o przerzutnikach Jaki układ elektroniczny nazywa się przerzutnikiem? Przerzutnikiem bistabilnym jest nazywany układ elektroniczny, charakteryzujący się istnieniem dwóch stanów wyróżnionych
Układy kombinacyjne Y X 4 X 5. Rys. 1 Kombinacyjna funkcja logiczna.
 Układy kombinacyjne. Czas trwania: 6h. Cele ćwiczenia Przypomnienie podstawowych praw Algebry Boole a. Zaprojektowanie, montaż i sprawdzenie działania zadanych układów kombinacyjnych.. Wymagana znajomość
Układy kombinacyjne. Czas trwania: 6h. Cele ćwiczenia Przypomnienie podstawowych praw Algebry Boole a. Zaprojektowanie, montaż i sprawdzenie działania zadanych układów kombinacyjnych.. Wymagana znajomość
Zwykle układ scalony jest zamknięty w hermetycznej obudowie metalowej, ceramicznej lub wykonanej z tworzywa sztucznego.
 Techniki wykonania cyfrowych układów scalonych Cyfrowe układy scalone dzielimy ze względu na liczbę bramek elementarnych tworzących dany układ na: małej skali integracji SSI do 10 bramek, średniej skali
Techniki wykonania cyfrowych układów scalonych Cyfrowe układy scalone dzielimy ze względu na liczbę bramek elementarnych tworzących dany układ na: małej skali integracji SSI do 10 bramek, średniej skali
Tranzystor JFET i MOSFET zas. działania
 Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
Państwowa Wyższa Szkoła Zawodowa
 Państwowa Wyższa Szkoła Zawodowa w Legnicy Laboratorium Podstaw Elektroniki i Miernictwa Ćwiczenie nr 4 BADANIE BRAMEK LOGICZNYCH A. Cel ćwiczenia. - Poznanie zasad logiki binarnej. Prawa algebry Boole
Państwowa Wyższa Szkoła Zawodowa w Legnicy Laboratorium Podstaw Elektroniki i Miernictwa Ćwiczenie nr 4 BADANIE BRAMEK LOGICZNYCH A. Cel ćwiczenia. - Poznanie zasad logiki binarnej. Prawa algebry Boole
Elektronika cyfrowa i mikroprocesory. Dr inż. Aleksander Cianciara
 Elektronika cyfrowa i mikroprocesory Dr inż. Aleksander Cianciara Sprawy organizacyjne Warunki zaliczenia Lista obecności Kolokwium końcowe Ocena końcowa Konsultacje Poniedziałek 6:-7: Kontakt Budynek
Elektronika cyfrowa i mikroprocesory Dr inż. Aleksander Cianciara Sprawy organizacyjne Warunki zaliczenia Lista obecności Kolokwium końcowe Ocena końcowa Konsultacje Poniedziałek 6:-7: Kontakt Budynek
Podstawy Automatyki. Wykład 13 - Układy bramkowe. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych
 1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
Budowa. Metoda wytwarzania
 Budowa Tranzystor JFET (zwany też PNFET) zbudowany jest z płytki z jednego typu półprzewodnika (p lub n), która stanowi tzw. kanał. Na jego końcach znajdują się styki źródła (ang. source - S) i drenu (ang.
Budowa Tranzystor JFET (zwany też PNFET) zbudowany jest z płytki z jednego typu półprzewodnika (p lub n), która stanowi tzw. kanał. Na jego końcach znajdują się styki źródła (ang. source - S) i drenu (ang.
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Architektura komputerów Wykład 2
 Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Logika binarna. Prawo łączności mówimy, że operator binarny * na zbiorze S jest łączny gdy (x * y) * z = x * (y * z) dla każdego x, y, z S.
 Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Bramki logiczne Podstawowe składniki wszystkich układów logicznych
 Układy logiczne Bramki logiczne A B A B AND NAND A B A B OR NOR A NOT A B A B XOR NXOR A NOT A B AND NAND A B OR NOR A B XOR NXOR Podstawowe składniki wszystkich układów logicznych 2 Podstawowe tożsamości
Układy logiczne Bramki logiczne A B A B AND NAND A B A B OR NOR A NOT A B A B XOR NXOR A NOT A B AND NAND A B OR NOR A B XOR NXOR Podstawowe składniki wszystkich układów logicznych 2 Podstawowe tożsamości
Automatyzacja i robotyzacja procesów produkcyjnych
 Automatyzacja i robotyzacja procesów produkcyjnych Instrukcja laboratoryjna Technika cyfrowa Opracował: mgr inż. Krzysztof Bodzek Cel ćwiczenia. Celem ćwiczenia jest zapoznanie studenta z zapisem liczb
Automatyzacja i robotyzacja procesów produkcyjnych Instrukcja laboratoryjna Technika cyfrowa Opracował: mgr inż. Krzysztof Bodzek Cel ćwiczenia. Celem ćwiczenia jest zapoznanie studenta z zapisem liczb
Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014
 Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014 Temat 1. Algebra Boole a i bramki 1). Podać przykład dowolnego prawa lub tożsamości, które jest spełnione w algebrze Boole
Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014 Temat 1. Algebra Boole a i bramki 1). Podać przykład dowolnego prawa lub tożsamości, które jest spełnione w algebrze Boole
Ćwiczenie 25 Temat: Interfejs między bramkami logicznymi i kombinacyjne układy logiczne. Układ z bramkami NOR. Cel ćwiczenia
 Ćwiczenie 25 Temat: Interfejs między bramkami logicznymi i kombinacyjne układy logiczne. Układ z bramkami NOR. Cel ćwiczenia Zapoznanie się z techniką połączenia za pośrednictwem interfejsu. Zbudowanie
Ćwiczenie 25 Temat: Interfejs między bramkami logicznymi i kombinacyjne układy logiczne. Układ z bramkami NOR. Cel ćwiczenia Zapoznanie się z techniką połączenia za pośrednictwem interfejsu. Zbudowanie
Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia
 Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia Poznanie własności i zasad działania różnych bramek logicznych. Zmierzenie napięcia wejściowego i wyjściowego bramek
Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia Poznanie własności i zasad działania różnych bramek logicznych. Zmierzenie napięcia wejściowego i wyjściowego bramek
LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI
 Wydział EAIiE LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI Temat projektu OŚMIOWEJŚCIOWA KOMÓRKA UKŁADU PAL Z ZASTOSOWANIEM NA PRZYKŁADZIE MULTIPLEKSERA Autorzy Tomasz Radziszewski Zdzisław Rapacz Rok akademicki
Wydział EAIiE LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI Temat projektu OŚMIOWEJŚCIOWA KOMÓRKA UKŁADU PAL Z ZASTOSOWANIEM NA PRZYKŁADZIE MULTIPLEKSERA Autorzy Tomasz Radziszewski Zdzisław Rapacz Rok akademicki
AKADEMIA MORSKA KATEDRA NAWIGACJI TECHNICZEJ
 KDEMI MORSK KTEDR NWIGCJI TECHNICZEJ ELEMETY ELEKTRONIKI LORTORIUM Kierunek NWIGCJ Specjalność Transport morski Semestr II Ćw. 4 Podstawy techniki cyfrowej Wersja opracowania Marzec 5 Opracowanie: mgr
KDEMI MORSK KTEDR NWIGCJI TECHNICZEJ ELEMETY ELEKTRONIKI LORTORIUM Kierunek NWIGCJ Specjalność Transport morski Semestr II Ćw. 4 Podstawy techniki cyfrowej Wersja opracowania Marzec 5 Opracowanie: mgr
Podstawy Elektroniki dla Tele-Informatyki. Tranzystory unipolarne MOS
 AGH Katedra Elektroniki Podstawy Elektroniki dla Tele-Informatyki Tranzystory unipolarne MOS Ćwiczenie 4 2014 r. 1. Wstęp. Celem ćwiczenia jest zapoznanie się z działaniem i zastosowaniami tranzystora
AGH Katedra Elektroniki Podstawy Elektroniki dla Tele-Informatyki Tranzystory unipolarne MOS Ćwiczenie 4 2014 r. 1. Wstęp. Celem ćwiczenia jest zapoznanie się z działaniem i zastosowaniami tranzystora
SWB - Wprowadzenie, funkcje boolowskie i bramki logiczne - wykład 1 asz 1. Plan wykładu
 SWB - Wprowadzenie, funkcje boolowskie i bramki logiczne - wykład 1 asz 1 Plan wykładu 1. Wprowadzenie, funkcje boolowskie i bramki logiczne, 2. Minimalizacja funkcji boolowskich, 3. Kombinacyjne bloki
SWB - Wprowadzenie, funkcje boolowskie i bramki logiczne - wykład 1 asz 1 Plan wykładu 1. Wprowadzenie, funkcje boolowskie i bramki logiczne, 2. Minimalizacja funkcji boolowskich, 3. Kombinacyjne bloki
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Rys. 2. Symbole dodatkowych bramek logicznych i ich tablice stanów.
 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z funktorami realizującymi podstawowe funkcje logiczne poprzez zaprojektowanie, wykonanie i przetestowanie kombinacyjnego układu logicznego realizującego
Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z funktorami realizującymi podstawowe funkcje logiczne poprzez zaprojektowanie, wykonanie i przetestowanie kombinacyjnego układu logicznego realizującego
Wykład nr 1 Techniki Mikroprocesorowe. dr inż. Artur Cichowski
 Wykład nr 1 Techniki Mikroprocesorowe dr inż. Artur Cichowski ix jy i j {0,1} {0,1} Dla układów kombinacyjnych stan dowolnego wyjścia y i w danej chwili czasu zależy wyłącznie od aktualnej kombinacji stanów
Wykład nr 1 Techniki Mikroprocesorowe dr inż. Artur Cichowski ix jy i j {0,1} {0,1} Dla układów kombinacyjnych stan dowolnego wyjścia y i w danej chwili czasu zależy wyłącznie od aktualnej kombinacji stanów
(12) OPIS PATENTOWY (19) PL (11) (13) B1
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 170013 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 297079 (22) Data zgłoszenia: 17.12.1992 (51) IntCl6: H01L 29/792 (
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 170013 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 297079 (22) Data zgłoszenia: 17.12.1992 (51) IntCl6: H01L 29/792 (
Skalowanie układów scalonych Click to edit Master title style
 Skalowanie układów scalonych Charakterystyczne parametry Technologia mikroelektroniczna najmniejszy realizowalny rozmiar (ang. feature size), liczba bramek (układów) na jednej płytce, wydzielana moc, maksymalna
Skalowanie układów scalonych Charakterystyczne parametry Technologia mikroelektroniczna najmniejszy realizowalny rozmiar (ang. feature size), liczba bramek (układów) na jednej płytce, wydzielana moc, maksymalna
Automatyka Lab 1 Teoria mnogości i algebra logiki. Akademia Morska w Szczecinie - Wydział Inżynieryjno-Ekonomiczny Transportu
 Automatyka Lab 1 Teoria mnogości i algebra logiki Harmonogram zajęć Układy przełączające: 1. Algebra logiki - Wprowadzenie 2. Funkcje logiczne - minimalizacja funkcji 3. Bramki logiczne - rysowanie układów
Automatyka Lab 1 Teoria mnogości i algebra logiki Harmonogram zajęć Układy przełączające: 1. Algebra logiki - Wprowadzenie 2. Funkcje logiczne - minimalizacja funkcji 3. Bramki logiczne - rysowanie układów
Układy cyfrowe. Najczęściej układy cyfrowe służą do przetwarzania sygnałów o dwóch poziomach napięć:
 Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów, którym przyporządkowywane są wartości liczbowe. Najczęściej układy cyfrowe służą do przetwarzania
Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów, którym przyporządkowywane są wartości liczbowe. Najczęściej układy cyfrowe służą do przetwarzania
Podstawy Elektroniki dla Informatyki. Tranzystory unipolarne MOS
 AGH Katedra Elektroniki Podstawy Elektroniki dla Informatyki Tranzystory unipolarne MOS Ćwiczenie 3 2014 r. 1 1. Wstęp. Celem ćwiczenia jest zapoznanie się z działaniem i zastosowaniami tranzystora unipolarnego
AGH Katedra Elektroniki Podstawy Elektroniki dla Informatyki Tranzystory unipolarne MOS Ćwiczenie 3 2014 r. 1 1. Wstęp. Celem ćwiczenia jest zapoznanie się z działaniem i zastosowaniami tranzystora unipolarnego
Ćwiczenie 23. Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia
 Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia Ćwiczenie 23 Poznanie symboli własności. Zmierzenie parametrów podstawowych bramek logicznych TTL i CMOS. Czytanie schematów elektronicznych,
Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia Ćwiczenie 23 Poznanie symboli własności. Zmierzenie parametrów podstawowych bramek logicznych TTL i CMOS. Czytanie schematów elektronicznych,
11.Zasady projektowania komórek standardowych
 LABORATORIUM PODSTAW MIKROELEKTRONIKI 39 11.Zasady projektowania komórek standardowych 11.1.Projektowanie komórek standardowych Formę komórki standardowej powinny mieć wszystkie projekty od inwertera do
LABORATORIUM PODSTAW MIKROELEKTRONIKI 39 11.Zasady projektowania komórek standardowych 11.1.Projektowanie komórek standardowych Formę komórki standardowej powinny mieć wszystkie projekty od inwertera do
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Elementy cyfrowe i układy logiczne
 Elementy cyfrowe i układy logiczne Wykład 5 Legenda Procedura projektowania Podział układów VLSI 2 1 Procedura projektowania Specyfikacja Napisz, jeśli jeszcze nie istnieje, specyfikację układu. Opracowanie
Elementy cyfrowe i układy logiczne Wykład 5 Legenda Procedura projektowania Podział układów VLSI 2 1 Procedura projektowania Specyfikacja Napisz, jeśli jeszcze nie istnieje, specyfikację układu. Opracowanie
Wprowadzenie do techniki Cyfrowej i Mikroelektroniki
 Wprowadzenie do techniki Cyfrowej i Mikroelektroniki Małgorzata Napieralska Katedra Mikroelektroniki i Technik Informatycznych tel. 26-55 mnapier@dmcs.p.lodz.pl Literatura W. Marciniak Przyrządy półprzewodnikowe
Wprowadzenie do techniki Cyfrowej i Mikroelektroniki Małgorzata Napieralska Katedra Mikroelektroniki i Technik Informatycznych tel. 26-55 mnapier@dmcs.p.lodz.pl Literatura W. Marciniak Przyrządy półprzewodnikowe
Algebra Boole a i jej zastosowania
 lgebra oole a i jej zastosowania Wprowadzenie Niech dany będzie zbiór dwuelementowy, którego elementy oznaczymy symbolami 0 oraz 1, tj. {0, 1}. W zbiorze tym określamy działania sumy :, iloczynu : _ oraz
lgebra oole a i jej zastosowania Wprowadzenie Niech dany będzie zbiór dwuelementowy, którego elementy oznaczymy symbolami 0 oraz 1, tj. {0, 1}. W zbiorze tym określamy działania sumy :, iloczynu : _ oraz
LEKCJA. TEMAT: Funktory logiczne.
 TEMAT: Funktory logiczne. LEKCJA 1. Bramką logiczną (funktorem) nazywa się układ elektroniczny realizujący funkcje logiczne jednej lub wielu zmiennych. Sygnały wejściowe i wyjściowe bramki przyjmują wartość
TEMAT: Funktory logiczne. LEKCJA 1. Bramką logiczną (funktorem) nazywa się układ elektroniczny realizujący funkcje logiczne jednej lub wielu zmiennych. Sygnały wejściowe i wyjściowe bramki przyjmują wartość
Układy sekwencyjne. Podstawowe informacje o układach cyfrowych i przerzutnikach (rodzaje, sposoby wyzwalania).
 Ćw. 10 Układy sekwencyjne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z sekwencyjnymi, cyfrowymi blokami funkcjonalnymi. W ćwiczeniu w oparciu o poznane przerzutniki zbudowane zostaną układy rejestrów
Ćw. 10 Układy sekwencyjne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z sekwencyjnymi, cyfrowymi blokami funkcjonalnymi. W ćwiczeniu w oparciu o poznane przerzutniki zbudowane zostaną układy rejestrów
Ćwiczenie 26. Temat: Układ z bramkami NAND i bramki AOI..
 Temat: Układ z bramkami NAND i bramki AOI.. Ćwiczenie 26 Cel ćwiczenia Zapoznanie się ze sposobami konstruowania z bramek NAND różnych bramek logicznych. Konstruowanie bramek NOT, AND i OR z bramek NAND.
Temat: Układ z bramkami NAND i bramki AOI.. Ćwiczenie 26 Cel ćwiczenia Zapoznanie się ze sposobami konstruowania z bramek NAND różnych bramek logicznych. Konstruowanie bramek NOT, AND i OR z bramek NAND.
Ćwiczenie 4. Parametry statyczne tranzystorów polowych JFET i MOSFET
 Ćwiczenie 4 Parametry statyczne tranzystorów polowych JFET i MOSFET Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie charakterystyk statycznych tranzystorów polowych złączowych oraz z izolowaną
Ćwiczenie 4 Parametry statyczne tranzystorów polowych JFET i MOSFET Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie charakterystyk statycznych tranzystorów polowych złączowych oraz z izolowaną
Podstawowe układy cyfrowe
 ELEKTRONIKA CYFROWA SPRAWOZDANIE NR 4 Podstawowe układy cyfrowe Grupa 6 Prowadzący: Roman Płaneta Aleksandra Gierut CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi,
ELEKTRONIKA CYFROWA SPRAWOZDANIE NR 4 Podstawowe układy cyfrowe Grupa 6 Prowadzący: Roman Płaneta Aleksandra Gierut CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi,
Tranzystory polowe FET(JFET), MOSFET
 Tranzystory polowe FET(JFET), MOSFET Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana
Tranzystory polowe FET(JFET), MOSFET Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana
Inwerter logiczny. Ilustracja 1: Układ do symulacji inwertera (Inverter.sch)
 DSCH2 to program do edycji i symulacji układów logicznych. DSCH2 jest wykorzystywany do sprawdzenia architektury układu logicznego przed rozpoczęciem projektowania fizycznego. DSCH2 zapewnia ergonomiczne
DSCH2 to program do edycji i symulacji układów logicznych. DSCH2 jest wykorzystywany do sprawdzenia architektury układu logicznego przed rozpoczęciem projektowania fizycznego. DSCH2 zapewnia ergonomiczne
Podstawy Automatyki. Wykład 13 - Układy bramkowe. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Wstęp do Techniki Cyfrowej... Algebra Boole a
 Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki
 Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki Temat ćwiczenia: Przetwornica impulsowa DC-DC typu buck
Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki Temat ćwiczenia: Przetwornica impulsowa DC-DC typu buck
ELEMENTY ELEKTRONICZNE. Układy polaryzacji i stabilizacji punktu pracy tranzystora
 Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: ELEMENTY ELEKTRONICZNE TS1C300 018 Układy polaryzacji i stabilizacji punktu
Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: ELEMENTY ELEKTRONICZNE TS1C300 018 Układy polaryzacji i stabilizacji punktu
Skalowanie układów scalonych
 Skalowanie układów scalonych Technologia mikroelektroniczna Charakterystyczne parametry najmniejszy realizowalny rozmiar (ang. feature size), liczba bramek (układów) na jednej płytce, wydzielana moc, maksymalna
Skalowanie układów scalonych Technologia mikroelektroniczna Charakterystyczne parametry najmniejszy realizowalny rozmiar (ang. feature size), liczba bramek (układów) na jednej płytce, wydzielana moc, maksymalna
I. Podstawowe zagadnienia z teorii układów cyfrowych
 I. Podstawowe zagadnienia z teorii układów cyfrowych. Wstęp Muzyka na płytach fonograficznych jest zapisana w formie kanaliku o zmiennym urzeźbieniu. Ruch igły prowadzonej przez kanalik odbywa się w sposób
I. Podstawowe zagadnienia z teorii układów cyfrowych. Wstęp Muzyka na płytach fonograficznych jest zapisana w formie kanaliku o zmiennym urzeźbieniu. Ruch igły prowadzonej przez kanalik odbywa się w sposób
Statyczne badanie przerzutników - ćwiczenie 3
 Statyczne badanie przerzutników - ćwiczenie 3. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami przerzutników w wersji TTL realizowanymi przy wykorzystaniu bramek logicznych NAND oraz NO. 2. Wykaz
Statyczne badanie przerzutników - ćwiczenie 3. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami przerzutników w wersji TTL realizowanymi przy wykorzystaniu bramek logicznych NAND oraz NO. 2. Wykaz
LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 POLITECHNIKA ŁÓDZKA KATEDRA PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH I OPTOELEKTRONICZNYCH
 LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 Parametry statyczne tranzystorów polowych złączowych Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów polowych złączowych
LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 Parametry statyczne tranzystorów polowych złączowych Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów polowych złączowych
BADANIE UKŁADÓW CYFROWYCH. CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA
 BADANIE UKŁADÓW CYFROWYCH CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA 1. OGLĘDZINY Dokonać oględzin badanego układu cyfrowego określając jego:
BADANIE UKŁADÓW CYFROWYCH CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA 1. OGLĘDZINY Dokonać oględzin badanego układu cyfrowego określając jego:
Badanie charakterystyk elementów półprzewodnikowych
 Badanie charakterystyk elementów półprzewodnikowych W ramach ćwiczenia student poznaje praktyczne właściwości elementów półprzewodnikowych stosowanych w elektronice przez badanie charakterystyk diody oraz
Badanie charakterystyk elementów półprzewodnikowych W ramach ćwiczenia student poznaje praktyczne właściwości elementów półprzewodnikowych stosowanych w elektronice przez badanie charakterystyk diody oraz
Wykład 2. Informatyka Stosowana. 8 października 2018, M. A-B. Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41
 Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) (13) B1
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 174002 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 300055 (22) Data zgłoszenia: 12.08.1993 (5 1) IntCl6: H01L21/76 (54)
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 174002 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 300055 (22) Data zgłoszenia: 12.08.1993 (5 1) IntCl6: H01L21/76 (54)
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
LABORATORIUM TECHNIKA CYFROWA BRAMKI. Rev.1.0
 LABORATORIUM TECHNIKA CYFROWA BRAMKI Rev..0 LABORATORIUM TECHNIKI CYFROWEJ: Bramki. CEL ĆWICZENIA - praktyczna weryfikacja wiedzy teoretycznej z zakresu działania bramek, - pomiary parametrów bramek..
LABORATORIUM TECHNIKA CYFROWA BRAMKI Rev..0 LABORATORIUM TECHNIKI CYFROWEJ: Bramki. CEL ĆWICZENIA - praktyczna weryfikacja wiedzy teoretycznej z zakresu działania bramek, - pomiary parametrów bramek..
Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR
 Laboratorium Podstaw Techniki Cyfrowej dr Marek Siłuszyk mgr Arkadiusz Wysokiński Ćwiczenie 01 PTC Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR opr. tech. Mirosław Maś Uniwersytet
Laboratorium Podstaw Techniki Cyfrowej dr Marek Siłuszyk mgr Arkadiusz Wysokiński Ćwiczenie 01 PTC Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR opr. tech. Mirosław Maś Uniwersytet
dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia i ich zastosowań w przemyśle" POKL
 Technika cyfrowa w architekturze komputerów materiał do wykładu 2/3 dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Technika cyfrowa w architekturze komputerów materiał do wykładu 2/3 dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania.
 adanie funktorów logicznych RTL - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania..
adanie funktorów logicznych RTL - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania..
Bramki logiczne V MAX V MIN
 Bramki logiczne W układach fizycznych napięcie elektryczne może reprezentować stany logiczne. Bramką nazywamy prosty obwód elektroniczny realizujący funkcję logiczną. Pewien zakres napięcia odpowiada stanowi
Bramki logiczne W układach fizycznych napięcie elektryczne może reprezentować stany logiczne. Bramką nazywamy prosty obwód elektroniczny realizujący funkcję logiczną. Pewien zakres napięcia odpowiada stanowi
CHARAKTERYSTYKI BRAMEK CYFROWYCH TTL
 CHARAKTERYSTYKI BRAMEK CYFROWYCH TTL. CEL ĆWICZENIA Celem ćwiczenia jest poznanie zasad działania, budowy i właściwości podstawowych funktorów logicznych wykonywanych w jednej z najbardziej rozpowszechnionych
CHARAKTERYSTYKI BRAMEK CYFROWYCH TTL. CEL ĆWICZENIA Celem ćwiczenia jest poznanie zasad działania, budowy i właściwości podstawowych funktorów logicznych wykonywanych w jednej z najbardziej rozpowszechnionych
BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO
 Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
Podstawy elektroniki cz. 2 Wykład 2
 Podstawy elektroniki cz. 2 Wykład 2 Elementarne prawa Trzy elementarne prawa 2 Prawo Ohma Stosunek natężenia prądu płynącego przez przewodnik do napięcia pomiędzy jego końcami jest stały R U I 3 Prawo
Podstawy elektroniki cz. 2 Wykład 2 Elementarne prawa Trzy elementarne prawa 2 Prawo Ohma Stosunek natężenia prądu płynącego przez przewodnik do napięcia pomiędzy jego końcami jest stały R U I 3 Prawo
płytka montażowa z tranzystorami i rezystorami, pokazana na rysunku 1. płytka montażowa do badania przerzutnika astabilnego U CC T 2 masa
 Tranzystor jako klucz elektroniczny - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi układami pracy tranzystora bipolarnego jako klucza elektronicznego. Bramki logiczne realizowane w technice RTL
Tranzystor jako klucz elektroniczny - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi układami pracy tranzystora bipolarnego jako klucza elektronicznego. Bramki logiczne realizowane w technice RTL
Cyfrowe układy scalone c.d. funkcje
 Cyfrowe układy scalone c.d. funkcje Ryszard J. Barczyński, 206 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Kombinacyjne układy cyfrowe
Cyfrowe układy scalone c.d. funkcje Ryszard J. Barczyński, 206 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Kombinacyjne układy cyfrowe
Układy TTL i CMOS. Trochę logiki
 Układy TTL i CMOS O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą
Układy TTL i CMOS O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą
Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki
 Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki Temat ćwiczenia: Przetwornica impulsowa DC-DC typu boost
Politechnika Poznańska, Instytut Elektrotechniki i Elektroniki Przemysłowej, Zakład Energoelektroniki i Sterowania Laboratorium energoelektroniki Temat ćwiczenia: Przetwornica impulsowa DC-DC typu boost
Architektura komputerów ćwiczenia Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna.
 Architektura komputerów ćwiczenia Zbiór zadań IV Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna. Wprowadzenie 1 1 fragmenty książki "Organizacja i architektura systemu
Architektura komputerów ćwiczenia Zbiór zadań IV Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna. Wprowadzenie 1 1 fragmenty książki "Organizacja i architektura systemu
1.2 Funktory z otwartym kolektorem (O.C)
 Wydział EAIiIB Laboratorium Katedra Metrologii i Elektroniki Podstaw Elektroniki Cyfrowej Wykonał zespół w składzie (nazwiska i imiona): Ćw. 4. Funktory TTL cz.2 Data wykonania: Grupa (godz.): Dzień tygodnia:
Wydział EAIiIB Laboratorium Katedra Metrologii i Elektroniki Podstaw Elektroniki Cyfrowej Wykonał zespół w składzie (nazwiska i imiona): Ćw. 4. Funktory TTL cz.2 Data wykonania: Grupa (godz.): Dzień tygodnia:
Komputerowa symulacja bramek w technice TTL i CMOS
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
Układy cyfrowe w technologii CMOS
 Projektowanie układów VLSI Układy cyfrowe w technologii MOS ramki bramki podstawowe bramki złożone rysowanie topografii bramka transmisyjna Przerzutniki z bramkami transmisyjnymi z bramkami zwykłymi dr
Projektowanie układów VLSI Układy cyfrowe w technologii MOS ramki bramki podstawowe bramki złożone rysowanie topografii bramka transmisyjna Przerzutniki z bramkami transmisyjnymi z bramkami zwykłymi dr
TEMAT: PROJEKTOWANIE I BADANIE PRZERZUTNIKÓW BISTABILNYCH
 Praca laboratoryjna 2 TEMAT: PROJEKTOWANIE I BADANIE PRZERZUTNIKÓW BISTABILNYCH Cel pracy poznanie zasad funkcjonowania przerzutników różnych typów w oparciu o różne rozwiązania układowe. Poznanie sposobów
Praca laboratoryjna 2 TEMAT: PROJEKTOWANIE I BADANIE PRZERZUTNIKÓW BISTABILNYCH Cel pracy poznanie zasad funkcjonowania przerzutników różnych typów w oparciu o różne rozwiązania układowe. Poznanie sposobów
Funkcje logiczne X = A B AND. K.M.Gawrylczyk /55
 Układy cyfrowe Funkcje logiczne AND A B X = A B... 2/55 Funkcje logiczne OR A B X = A + B NOT A A... 3/55 Twierdzenia algebry Boole a A + B = B + A A B = B A A + B + C = A + (B+C( B+C) ) = (A+B( A+B) )
Układy cyfrowe Funkcje logiczne AND A B X = A B... 2/55 Funkcje logiczne OR A B X = A + B NOT A A... 3/55 Twierdzenia algebry Boole a A + B = B + A A B = B A A + B + C = A + (B+C( B+C) ) = (A+B( A+B) )
LABORATORIUM. Technika Cyfrowa. Badanie Bramek Logicznych
 WYDZIAŁ ELEKTRYCZNY Katedra Inżynierii Systemów, Sygnałów i Elektroniki LABORATORIUM Technika Cyfrowa Badanie Bramek Logicznych Opracował: mgr inż. Andrzej Biedka 1 BADANIE FUNKCJI LOGICZNYCH 1.1 Korzystając
WYDZIAŁ ELEKTRYCZNY Katedra Inżynierii Systemów, Sygnałów i Elektroniki LABORATORIUM Technika Cyfrowa Badanie Bramek Logicznych Opracował: mgr inż. Andrzej Biedka 1 BADANIE FUNKCJI LOGICZNYCH 1.1 Korzystając
Tranzystor bipolarny wzmacniacz OE
 Tranzystor bipolarny wzmacniacz OE projektowanie poradnikowe u 1 (t) C 1 U B0 I 1 R 1 R 2 I 2 T I B0 R E I E0 I C0 V CC R C C 2 U C0 U E0 C E u 2 (t) Zadania elementów: T tranzystor- sterowane źródło prądu
Tranzystor bipolarny wzmacniacz OE projektowanie poradnikowe u 1 (t) C 1 U B0 I 1 R 1 R 2 I 2 T I B0 R E I E0 I C0 V CC R C C 2 U C0 U E0 C E u 2 (t) Zadania elementów: T tranzystor- sterowane źródło prądu
Stan/zdarzenie Nexo. Zmienne wirtualne. Zdarzenia wirtualne
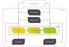 WARUNKI WARUNKI I I ZDARZENIA ZDARZENIA Określają czy pewna zależność logiczna związana ze stanem systemu jest w danej chwili spełniona lub czy zaszło w systemie określone zdarzenie. STAN SYSTEMU: stan
WARUNKI WARUNKI I I ZDARZENIA ZDARZENIA Określają czy pewna zależność logiczna związana ze stanem systemu jest w danej chwili spełniona lub czy zaszło w systemie określone zdarzenie. STAN SYSTEMU: stan
Technika Cyfrowa. dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 219, pok. 111, tel ,
 Technika Cyfrowa dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 29, pok., tel. 42 633667, e-mail: izdebski@p.lodz.pl Strona internetowa (materiały do wykładu i lab.): fizyka.p.lodz.pl/pl/dla-studentow/tc/
Technika Cyfrowa dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 29, pok., tel. 42 633667, e-mail: izdebski@p.lodz.pl Strona internetowa (materiały do wykładu i lab.): fizyka.p.lodz.pl/pl/dla-studentow/tc/
IV. TRANZYSTOR POLOWY
 1 IV. TRANZYSTOR POLOWY Cel ćwiczenia: Wyznaczenie charakterystyk statycznych tranzystora polowego złączowego. Zagadnienia: zasada działania tranzystora FET 1. Wprowadzenie Nazwa tranzystor pochodzi z
1 IV. TRANZYSTOR POLOWY Cel ćwiczenia: Wyznaczenie charakterystyk statycznych tranzystora polowego złączowego. Zagadnienia: zasada działania tranzystora FET 1. Wprowadzenie Nazwa tranzystor pochodzi z
Podstawy Automatyki. Wykład 12 - synteza i minimalizacja funkcji logicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 12 - synteza i minimalizacja funkcji logicznych Instytut Automatyki i Robotyki Warszawa, 2017 Synteza funkcji logicznych Terminy - na bazie funkcji trójargumenowej y = (x 1, x 2, x 3 ) (1) Elementarny
Wykład 12 - synteza i minimalizacja funkcji logicznych Instytut Automatyki i Robotyki Warszawa, 2017 Synteza funkcji logicznych Terminy - na bazie funkcji trójargumenowej y = (x 1, x 2, x 3 ) (1) Elementarny
Komputerowa symulacja bramek w technice TTL i CMOS
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
Podstawy Automatyki. Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
Ćwiczenie ZINTEGROWANE SYSTEMY CYFROWE. Pakiet edukacyjny DefSim Personal. Analiza prądowa IDDQ
 Ćwiczenie 2 ZINTEGROWANE SYSTEMY CYFROWE Pakiet edukacyjny DefSim Personal Analiza prądowa IDDQ K A T E D R A M I K R O E L E K T R O N I K I I T E C H N I K I N F O R M A T Y C Z N Y C H Politechnika
Ćwiczenie 2 ZINTEGROWANE SYSTEMY CYFROWE Pakiet edukacyjny DefSim Personal Analiza prądowa IDDQ K A T E D R A M I K R O E L E K T R O N I K I I T E C H N I K I N F O R M A T Y C Z N Y C H Politechnika
Technika cyfrowa Inżynieria dyskretna cz. 2
 Sławomir Kulesza Technika cyfrowa Inżynieria dyskretna cz. 2 Wykład dla studentów III roku Informatyki Wersja 5.0, 10/10/2015 Generacje układów scalonych Stopień scalenia Liczba elementów aktywnych Zastosowania
Sławomir Kulesza Technika cyfrowa Inżynieria dyskretna cz. 2 Wykład dla studentów III roku Informatyki Wersja 5.0, 10/10/2015 Generacje układów scalonych Stopień scalenia Liczba elementów aktywnych Zastosowania
PROJEKTOWANIE UKŁADÓW VLSI
 prof. dr hab. inż. Andrzej Kos Tel. 34.35, email: kos@uci.agh.edu.pl Pawilon C3, pokój 505 PROJEKTOWANIE UKŁADÓW VLSI Forma zaliczenia: egzamin Układy VLSI wczoraj i dzisiaj Pierwszy układ scalony -
prof. dr hab. inż. Andrzej Kos Tel. 34.35, email: kos@uci.agh.edu.pl Pawilon C3, pokój 505 PROJEKTOWANIE UKŁADÓW VLSI Forma zaliczenia: egzamin Układy VLSI wczoraj i dzisiaj Pierwszy układ scalony -
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Logiczne układy bistabilne przerzutniki.
 Przerzutniki spełniają rolę elementów pamięciowych: -przy pewnej kombinacji stanów na pewnych wejściach, niezależnie od stanów innych wejść, stany wyjściowe oraz nie ulegają zmianie; -przy innej określonej
Przerzutniki spełniają rolę elementów pamięciowych: -przy pewnej kombinacji stanów na pewnych wejściach, niezależnie od stanów innych wejść, stany wyjściowe oraz nie ulegają zmianie; -przy innej określonej
Dr inż. Jan Chudzikiewicz Pokój 117/65 Tel Materiały:
 Dr inż Jan Chudzikiewicz Pokój 7/65 Tel 683-77-67 E-mail: jchudzikiewicz@watedupl Materiały: http://wwwitawatedupl/~jchudzikiewicz/ Warunki zaliczenie: Otrzymanie pozytywnej oceny z kolokwium zaliczeniowego
Dr inż Jan Chudzikiewicz Pokój 7/65 Tel 683-77-67 E-mail: jchudzikiewicz@watedupl Materiały: http://wwwitawatedupl/~jchudzikiewicz/ Warunki zaliczenie: Otrzymanie pozytywnej oceny z kolokwium zaliczeniowego
Wzmacniacze operacyjne
 Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
III. TRANZYSTOR BIPOLARNY
 1. TRANZYSTOR BPOLARNY el ćwiczenia: Wyznaczenie charakterystyk statycznych tranzystora bipolarnego Zagadnienia: zasada działania tranzystora bipolarnego. 1. Wprowadzenie Nazwa tranzystor pochodzi z języka
1. TRANZYSTOR BPOLARNY el ćwiczenia: Wyznaczenie charakterystyk statycznych tranzystora bipolarnego Zagadnienia: zasada działania tranzystora bipolarnego. 1. Wprowadzenie Nazwa tranzystor pochodzi z języka
Piezorezystancyjny czujnik ciśnienia: modelowanie membrany krzemowej podstawowego elementu piezorezystancyjnego czujnika ciśnienia
 MIKROSYSTEMY - laboratorium Ćwiczenie 1 Piezorezystancyjny czujnik ciśnienia: modelowanie membrany krzemowej podstawowego elementu piezorezystancyjnego czujnika ciśnienia Zadania i cel ćwiczenia. Celem
MIKROSYSTEMY - laboratorium Ćwiczenie 1 Piezorezystancyjny czujnik ciśnienia: modelowanie membrany krzemowej podstawowego elementu piezorezystancyjnego czujnika ciśnienia Zadania i cel ćwiczenia. Celem
Spis treúci. Księgarnia PWN: Krzysztof Wojtuszkiewicz - Urządzenia techniki komputerowej. Cz. 1. Przedmowa... 9. Wstęp... 11
 Księgarnia PWN: Krzysztof Wojtuszkiewicz - Urządzenia techniki komputerowej. Cz. 1 Spis treúci Przedmowa... 9 Wstęp... 11 1. Komputer PC od zewnątrz... 13 1.1. Elementy zestawu komputerowego... 13 1.2.
Księgarnia PWN: Krzysztof Wojtuszkiewicz - Urządzenia techniki komputerowej. Cz. 1 Spis treúci Przedmowa... 9 Wstęp... 11 1. Komputer PC od zewnątrz... 13 1.1. Elementy zestawu komputerowego... 13 1.2.
WPROWADZENIE Mikrosterownik mikrokontrolery
 WPROWADZENIE Mikrosterownik (cyfrowy) jest to moduł elektroniczny zawierający wszystkie środki niezbędne do realizacji wymaganych procedur sterowania przy pomocy metod komputerowych. Platformy budowy mikrosterowników:
WPROWADZENIE Mikrosterownik (cyfrowy) jest to moduł elektroniczny zawierający wszystkie środki niezbędne do realizacji wymaganych procedur sterowania przy pomocy metod komputerowych. Platformy budowy mikrosterowników:
Układy logiczne układy cyfrowe
 Układy logiczne układy cyfrowe Jak projektować układy cyfrowe (systemy cyfrowe) Układy arytmetyki rozproszonej filtrów cyfrowych Układy kryptograficzne X Selektor ROM ROM AND Specjalizowane układy cyfrowe
Układy logiczne układy cyfrowe Jak projektować układy cyfrowe (systemy cyfrowe) Układy arytmetyki rozproszonej filtrów cyfrowych Układy kryptograficzne X Selektor ROM ROM AND Specjalizowane układy cyfrowe
Modelowanie mikrosystemów - laboratorium. Ćwiczenie 1. Modelowanie ugięcia membrany krzemowej modelowanie pracy mikromechanicznego czujnika ciśnienia
 Modelowanie mikrosystemów - laboratorium Ćwiczenie 1 Modelowanie ugięcia membrany krzemowej modelowanie pracy mikromechanicznego czujnika ciśnienia Zadania i cel ćwiczenia. Celem ćwiczenia jest dobranie
Modelowanie mikrosystemów - laboratorium Ćwiczenie 1 Modelowanie ugięcia membrany krzemowej modelowanie pracy mikromechanicznego czujnika ciśnienia Zadania i cel ćwiczenia. Celem ćwiczenia jest dobranie
Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk
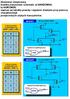 Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk przejściowych użytych tranzystorów. NOR CMOS Skale integracji
Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk przejściowych użytych tranzystorów. NOR CMOS Skale integracji
