Analiza sieci społecznych. Veslava Osińska
|
|
|
- Szymon Adamczyk
- 7 lat temu
- Przeglądów:
Transkrypt
1 Analiza sieci społecznych Veslava Osińska
2 UMK
3 Graf - przypomnienie Graf - > zbiór wierczchołków i krawędzi
4 Grafy Węzły (osoby) i kawędzie (relacje) Na wagi mogą wpływają: częstotliwość interakcji subiektywna ocena koszt komunikacji metody hybrydowe Problemy: siła wiązania węzeł centralny miary podobieństwa, spójności
5 Układy graficzne Podstawowy algorytm siły ukierunkowanej 3 czynniki rozmiar węzła siła wiązania grawitacja do środka
6 Analiza sieci społecznych (SNA) Popularna metoda analizy relacji pomiędzy jednostkami służąca do badania makrostruktur społeczeństw Węzły -> Gracze (aktorzy) Osoby Grupy (zespoły, partie, drużyny sportowe) Narody Kraje Strony internetowe Autorzy publikacji Krawędzie - > relacje społeczne interakcję podobieństwo 6/20
7 W wywiadzie
8 8/20 W zarządzaniu
9 W polityce
10 W nauce
11 Podstawowe miary Stopień liczba linków (wchodzących/wychodzących) w węźle. Centralność wg stopni wierzchołków określa, które węzły są kluczowe z punktu widzenia rozprzestrzeniania informacji. Ścieżka między dwoma węzłami Pośrednictwem (ang. betweeness) węzła v nazywamy stosunek liczby najkrótszych ścieżek między dowolnymi dwoma węzłami przechodzących przez węzeł v do łącznej liczby wszystkich najkrótszych ścieżek. Wskazuje najważniejsze węzły pod względem komunikacji. Bliskość (ang. Closeness) - średnią długość najkrótszych ścieżek między węzłem v i wszystkimi pozostałymi węzłami. Jest miarą miarą czasu, jaki jest potrzebny, aby z danego węzła dotrzeć do innych węzłów. Przydatna w sytuacji gdy podstawowym kryterium jest prędkość rozchodzenia się informacji. Średnica sieci -długość najdłuższej spośród najkrótszych ścieżek łączących dowolne dwa węzły w sieci. Istotna dla propadgacji informacji w sieci. 11/20
12 Dane zawsze najważniejsze Facebook
13 Facebook API
14 FB
15 FB API/Netviz -.GDF
16 16/20
17
18 Ponizej prosze w paru zdaniach wygenerowana mape swoich ko spolecznych, w odniesieniu do odkrylam/em nowe relacje pom znajomych, czy jestem zaskoczo wzorem?". Na szaro oznaczone są osoby n do żadnej z klas, jednak pozosta relacjach ze sporym gronem - s szkoły, lub znajomi znajomych, pojawiali się na wydarzeniach o przez nasze liceum. Poniżej ciemno niebieskim kolo zaznaczone są osoby związane Dźwięki Północy organizowanym Nadbałtyckie Centrum Kultury w Również tam, widoczne są drob ze znajomymi ze szkoły, jednak grupa zamknięta. W obrębie fe Na grafie można zauważyć kilka najsilniejszy podział pomiędzy p stroną, powstał ze względu na s znajomych pochodzących z Tor Gdańska. po lewej stronie: kolorem różowym oznaczona je gimnazjum kolorem pomarańczoym oznacz biologiczno-chemiczna z liceum kolorem zielonym oznaczona je matematyczno-fizyczno-inform liceum. Na grafie widoczne są silne zwi klasą gimnazjalną a oboma klas klasy gimnazjalnej 4 osoby nale późniejszego mat-fizu a tylko je biolchemu, jednak ilość powiąz jest porównywalna.
19
20
21
22 Ponizej prosze w paru zdaniach skomentowac wygenerowana mape swoich kontaktow spolecznych, w odniesieniu do pytania: "czy odkrylam/em nowe relacje pomiedzy grupami znajomych, czy jestem zaskoczony powstalym wzorem?". Podsumowując graf przedstawia dwie główne grupy, które pokazują dwa etapy a jednocześnie przełom w moim życiu jakim była wyprowadzka do Torunia i podjęcie studiów, znajomi z tych dwóch grup praktycznie się nie znają. Jedynymi osobami jakie łączą te dwa światy jest mój przyjaciel i narzeczona. O ile grupa z rodzinnego miasta jest dość zwarta, moi znajomi z Torunia dzielą się na 4 wyraźne grupy, które niemal nie są ze sobą powiązane. Moją szczególną Graf wykonany według moodle'a okazał się mało czytelny- zbyt zwarty, dlatego pozwoliłem sobie na pewne odstępstwa. Zmieniłem layout na "label adjust". Żeby cokolwiek zobaczyć musiałem również wyłączyć etykiety, dopiero wtedy pojawiły się kolory, które wcześniej zaduszone były przez podpisy. Zgaszone światło "uwypukla" kontrast kolorów. Przede wszystkim na grafie możemy wyróżnić dwie grupy,po lewej na doleznajomi z rodzinnego miasta,po prawej na górze znajomi, których poznałem od czasu kiedy zacząłem studia w Toruniu. Żółtym kolorem są oznaczeni znajomi z mojego osiedla, dość widocznie przeplatają się z moimi innymi znajomymi z miasta(kolor seledynowy).pomiędzy tymi grupami kreuje się również mała "fioletowa grupa" są to ludzie związani z lokalną drużyną piłkarską, "fioletowi" nieco bardzie oddaleni od zwartej grupy, ku środkowi to członkowie mojej rodziny. Czerwona grupa obok zwartej żółtej, to moi znajomi z liceum, natomiast "czerwona grupa" po "stronie Torunia" to znajomi których poznałem zamieszkując w akademiku, przeplata się ona z "grupą niebieską"-znajomi z pierwszego kierunku studiów. W centrum grafu wyraźnie wysuwają się dwa punkty. Liderem czerwonych jest mój przyjaciel z liceum, który później był moim współlokaterem w akademiku, przez co mamy wielu wspólnych znajomych. Liderem niebieskich jest moja narzeczona, która zna dobrze "środowisko toruńskie" i członków mojej rodziny,nieco poniżej niej jest mała grupa członków jej najbliższej rodziny, których poznałem. Fioletowa grupa, która nie jest zbyt duża to osoby, które poznałem podejmując pracę w Toruniu, natomiast zielonym kolorem są oznaczeni znajomi z kierunku ZIiB. Najbardziej wysuniętą w lewo zieloną kropką jest koleżanka, która pochodzi z mojego rodzinnego miasta, mamy jadnak niewielu wspólnych znajomych w Inowrocławiu.
23 Znalezione jedno z rozwiązań w 2016 Linkurio
24 Narzędzia do modulowania grafów Formaty plików
25 Aplikacje
26 Gephi (gephi.org)
27 Cytoscape (cytoscape.org) 1
28 Cytoscape (cytoscape.org) 2
29 Efekt - animacja
30 Formaty plików sieciowych
31 Formaty Węzły Ilość i atrybuty Krawędzie Waga Dwa pliki tekstowe (CSV) w Gephi 1. Id;Label;Atrybut1;atrybut2;Atrybut3. 2. Source;Target;Type;Weight (un)directed
32 *Vertices 20 1 Ania 2 Beata 3 Nikola 4 Ewa 5 Edward 6 Grzegorz *arcs Format NET (uniwersalny)
33 Konkluzja Problem nie jak a co Zadanie zbierania danych: uczy pracy w zespole czujności na zmiany w otoczeniu (analizowanie) dzielenia się danymi (nowa jakość)
34 Dziękuję za uwagę
Wprowadzenie do analizy sieci społecznych
 Wprowadzenie do analizy sieci społecznych Mikołaj Morzy Agnieszka Ławrynowicz Instytut Informatyki Poznań, rok akademicki 2010/2011 (c) Mikołaj Morzy, Agnieszka Ławrynowicz, Instytut Informatyki Politechniki
Wprowadzenie do analizy sieci społecznych Mikołaj Morzy Agnieszka Ławrynowicz Instytut Informatyki Poznań, rok akademicki 2010/2011 (c) Mikołaj Morzy, Agnieszka Ławrynowicz, Instytut Informatyki Politechniki
Suma dwóch grafów. Zespolenie dwóch grafów
 Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Gephi nowoczesne narzędzie do wizualizacji danych bibliometrycznych
 Veslava Osińska Uniwersytet Mikołaja Kopernika wieo@umk.pl Gephi nowoczesne narzędzie do wizualizacji danych bibliometrycznych Streszczenie: Po warsztatach, które odbyły się podczas konferencji Wizualizacja
Veslava Osińska Uniwersytet Mikołaja Kopernika wieo@umk.pl Gephi nowoczesne narzędzie do wizualizacji danych bibliometrycznych Streszczenie: Po warsztatach, które odbyły się podczas konferencji Wizualizacja
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Elementy teorii grafów Elementy teorii grafów
 Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Teoria grafów dla małolatów. Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska
 Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
Zastosowanie CP-grafów do generacji siatek
 Zastosowanie CP-grafów do generacji siatek 1 Cel zajęć Celem zajęć jest praktyczne zaznajomienie się z pojęciem CP-grafu i gramatyk grafowych, przy pomocy których można je tworzyć i nimi manipulować. Jako
Zastosowanie CP-grafów do generacji siatek 1 Cel zajęć Celem zajęć jest praktyczne zaznajomienie się z pojęciem CP-grafu i gramatyk grafowych, przy pomocy których można je tworzyć i nimi manipulować. Jako
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów
 Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp. autor: Łukasz Chlebda
 Segmentacja obrazów cyfrowych Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp autor: Łukasz Chlebda 1 Segmentacja obrazów cyfrowych - temat pracy Temat pracy: Aplikacja do segmentacji
Segmentacja obrazów cyfrowych Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp autor: Łukasz Chlebda 1 Segmentacja obrazów cyfrowych - temat pracy Temat pracy: Aplikacja do segmentacji
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
SPÓJNOŚĆ. ,...v k. }, E={v 1. v k. i v k. ,...,v k-1. }. Wierzchołki v 1. v 2. to końce ścieżki.
 SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
dr inż. Jarosław Forenc
 Technologie informacyjne Politechnika Białostocka - Wydział Elektryczny semestr I, studia stacjonarne I stopnia Rok akademicki 2016/2017 Pracownia nr 10 (05.12.2016) Rok akademicki 2016/2017, Pracownia
Technologie informacyjne Politechnika Białostocka - Wydział Elektryczny semestr I, studia stacjonarne I stopnia Rok akademicki 2016/2017 Pracownia nr 10 (05.12.2016) Rok akademicki 2016/2017, Pracownia
0.1. Diagram klas i pakietów
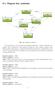 0.1. Diagram klas i pakietów Rys. 0.1. Diagram pakietów Na rysunku Rys. 0.1 przedstawiono diagram pakietów i relacje zachodzące pomiędzy nimi. Wyróżniono sześć głównych pakietów, które zostaną opisane
0.1. Diagram klas i pakietów Rys. 0.1. Diagram pakietów Na rysunku Rys. 0.1 przedstawiono diagram pakietów i relacje zachodzące pomiędzy nimi. Wyróżniono sześć głównych pakietów, które zostaną opisane
7. Teoria drzew - spinanie i przeszukiwanie
 7. Teoria drzew - spinanie i przeszukiwanie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny 7. wteoria Krakowie) drzew - spinanie i przeszukiwanie
7. Teoria drzew - spinanie i przeszukiwanie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny 7. wteoria Krakowie) drzew - spinanie i przeszukiwanie
Działanie algorytmu oparte jest na minimalizacji funkcji celu jako suma funkcji kosztu ( ) oraz funkcji heurystycznej ( ).
 Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytmy wyznaczania centralności w sieci Szymon Szylko
 Algorytmy wyznaczania centralności w sieci Szymon Szylko Zakład systemów Informacyjnych Wrocław 10.01.2008 Agenda prezentacji Cechy sieci Algorytmy grafowe Badanie centralności Algorytmy wyznaczania centralności
Algorytmy wyznaczania centralności w sieci Szymon Szylko Zakład systemów Informacyjnych Wrocław 10.01.2008 Agenda prezentacji Cechy sieci Algorytmy grafowe Badanie centralności Algorytmy wyznaczania centralności
Klasyfikacja przypadków w ND280
 Klasyfikacja przypadków w ND280 Arkadiusz Trawiński Warszawa, 20 maja 2008 pod opieką: prof Danuta Kiełczewska prof Ewa Rondio 1 Abstrakt Celem analizy symulacji jest bliższe zapoznanie się z możliwymi
Klasyfikacja przypadków w ND280 Arkadiusz Trawiński Warszawa, 20 maja 2008 pod opieką: prof Danuta Kiełczewska prof Ewa Rondio 1 Abstrakt Celem analizy symulacji jest bliższe zapoznanie się z możliwymi
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Essity Engagement Survey 2018
 Essity Engagement Survey 2018 Jak czytać raport zespołu? EUCUSA Consulting GmbH Mariahilfer Straße 187/39 A-1150 Wien Tel: +43-1-817 40 20-0 Fax: DW 20 FN 174750 k Handelsgericht Wien www.eucusa.com e-mail:
Essity Engagement Survey 2018 Jak czytać raport zespołu? EUCUSA Consulting GmbH Mariahilfer Straße 187/39 A-1150 Wien Tel: +43-1-817 40 20-0 Fax: DW 20 FN 174750 k Handelsgericht Wien www.eucusa.com e-mail:
PRACA DYPLOMOWA MAGISTERSKA
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania PRACA DYPLOMOWA MAGISTERSKA Konstrukcja autonomicznego robota mobilnego Małgorzata Bartoszewicz Promotor: prof. dr hab. inż. A. Milecki Zakres
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania PRACA DYPLOMOWA MAGISTERSKA Konstrukcja autonomicznego robota mobilnego Małgorzata Bartoszewicz Promotor: prof. dr hab. inż. A. Milecki Zakres
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wszystkie zdjęcia użyte w niniejszym dokumencie służą wyłącznie do celów szkoleniowych.
 Nadruk CMYK na kubkach reklamowych to narzędzie o ogromnych możliwościach. Nie oznacza to jednak, że technologia ta może być wykorzystywana w każdym przypadku. Nadruki te posiadają bowiem szereg ograniczeń,
Nadruk CMYK na kubkach reklamowych to narzędzie o ogromnych możliwościach. Nie oznacza to jednak, że technologia ta może być wykorzystywana w każdym przypadku. Nadruki te posiadają bowiem szereg ograniczeń,
Grafy dla każdego. dr Krzysztof Bryś. Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska.
 Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
Metaliczny button z deseniem.
 Metaliczny button z deseniem. Tutorial w programie GIMP Niniejszy tutorial jest wyłączną własnością Doroty Ciesielskiej Zapraszam na moją stronę http://www.direktorek03.wm studio.pl oraz http://www.porady.wm
Metaliczny button z deseniem. Tutorial w programie GIMP Niniejszy tutorial jest wyłączną własnością Doroty Ciesielskiej Zapraszam na moją stronę http://www.direktorek03.wm studio.pl oraz http://www.porady.wm
Jak rozpocząć pracę? Mapa
 Jak rozpocząć pracę? SWDE Manager jest aplikacją służącą do przeglądania graficznych i opisowych danych ewidencji gruntów i budynków zapisanych w formacie SWDE (.swd,.swg,.swde). Pracując w SWDE Managerze,
Jak rozpocząć pracę? SWDE Manager jest aplikacją służącą do przeglądania graficznych i opisowych danych ewidencji gruntów i budynków zapisanych w formacie SWDE (.swd,.swg,.swde). Pracując w SWDE Managerze,
MODELE SIECIOWE 1. Drzewo rozpinające 2. Najkrótsza droga 3. Zagadnienie maksymalnego przepływu źródłem ujściem
 MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
Algorytmy dynamiczne. Piotr Sankowski. - p. 1/14
 Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
Wykorzystanie metody edukacyjnej wartości dodanej do oceny efektywności pracy szkół
 Wykorzystanie metody edukacyjnej wartości dodanej do oceny efektywności pracy szkół Ewa Stożek Okręgowa Komisja Egzaminacyjna w Łodzi, Instytut Badań Edukacyjnych - Pracownia EWD e.stozek@ewd.edu.pl Informacja
Wykorzystanie metody edukacyjnej wartości dodanej do oceny efektywności pracy szkół Ewa Stożek Okręgowa Komisja Egzaminacyjna w Łodzi, Instytut Badań Edukacyjnych - Pracownia EWD e.stozek@ewd.edu.pl Informacja
Algorytmy mrówkowe. H. Bednarz. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne
 Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Teoria grafów podstawy. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
6. Wstępne pojęcia teorii grafów
 6. Wstępne pojęcia teorii grafów Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Wstępne pojęcia teorii grafów zima 2016/2017
6. Wstępne pojęcia teorii grafów Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Wstępne pojęcia teorii grafów zima 2016/2017
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Ćwiczenie 3 ANALIZA SIECI SPOŁECZNYCH (SNA) W SIECI
 Geografia Internetu Prowadzący: Krzysztof Janc Ćwiczenie 3 ANALIZA SIECI SPOŁECZNYCH (SNA) W SIECI N ZAKŁAD ZAGOSPODAROWANIA PRZESTRZENNEGO I STYTUT GEOGRAFII I ROZWOJU REGIONALNEGO U. WR. Zakład Zagospodarowania
Geografia Internetu Prowadzący: Krzysztof Janc Ćwiczenie 3 ANALIZA SIECI SPOŁECZNYCH (SNA) W SIECI N ZAKŁAD ZAGOSPODAROWANIA PRZESTRZENNEGO I STYTUT GEOGRAFII I ROZWOJU REGIONALNEGO U. WR. Zakład Zagospodarowania
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Wstęp do JUNG. Omówione elementy wykorzystane w Edge Color Project
 JUNG Java Universal Network/Graph Framework JUNG jest to biblioteka służąca do modelowania, analizy i wizualizacji danych reprezentowanych w postaci grafów lub sieci. Architektura JUNGa wspiera różnorodność
JUNG Java Universal Network/Graph Framework JUNG jest to biblioteka służąca do modelowania, analizy i wizualizacji danych reprezentowanych w postaci grafów lub sieci. Architektura JUNGa wspiera różnorodność
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Miejski System Zarządzania - Katowicka Infrastruktura Informacji Przestrzennej
 Miejski System Zarządzania - Katowicka Infrastruktura Informacji Przestrzennej Sport, promocja i turystyka Instrukcja użytkownika Historia zmian Wersja Data Kto Opis zmian 1.0 2013-12-13 MGGP S.A. Utworzenie
Miejski System Zarządzania - Katowicka Infrastruktura Informacji Przestrzennej Sport, promocja i turystyka Instrukcja użytkownika Historia zmian Wersja Data Kto Opis zmian 1.0 2013-12-13 MGGP S.A. Utworzenie
Graf. Definicja marca / 1
 Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
AiSD zadanie trzecie
 AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne
 E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
Co dalej, gimnazjalisto? Autor: Fundacja Młodzieżowej Przedsiębiorczości
 Co dalej, gimnazjalisto? Autor: Fundacja Młodzieżowej Przedsiębiorczości Treść nauczania Możliwości nauki w szkołach ponadgimnazjalnych, oferta szkół ponadgimnazjalnych profile, fakultety. Po zakończonych
Co dalej, gimnazjalisto? Autor: Fundacja Młodzieżowej Przedsiębiorczości Treść nauczania Możliwości nauki w szkołach ponadgimnazjalnych, oferta szkół ponadgimnazjalnych profile, fakultety. Po zakończonych
5c. Sieci i przepływy
 5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
Algorytmika Problemów Trudnych
 Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Grafika komputerowa. Zajęcia IX
 Grafika komputerowa Zajęcia IX Ćwiczenie 1 Usuwanie efektu czerwonych oczu Celem ćwiczenia jest usunięcie efektu czerwonych oczu u osób występujących na zdjęciu tak, aby plik wynikowy wyglądał jak wzor_1.jpg
Grafika komputerowa Zajęcia IX Ćwiczenie 1 Usuwanie efektu czerwonych oczu Celem ćwiczenia jest usunięcie efektu czerwonych oczu u osób występujących na zdjęciu tak, aby plik wynikowy wyglądał jak wzor_1.jpg
Drzewa. Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew
 Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
AUDYT DOSTĘPNOŚCI STRONY INTERNETOWEJ
 Poznań, 2012-10-04 AUDYT DOSTĘPNOŚCI STRONY INTERNETOWEJ NAZWA ADRES STRONY ILOŚĆ BŁĘDÓW WCAG 33 ILOŚĆ OSTRZEŻEŃ WCAG 3 TYP DOKUMENTU UŻYTY FORMAT (X)HTML JĘZYK OWANIE STRONY Urząd Marszałkowski Województwa
Poznań, 2012-10-04 AUDYT DOSTĘPNOŚCI STRONY INTERNETOWEJ NAZWA ADRES STRONY ILOŚĆ BŁĘDÓW WCAG 33 ILOŚĆ OSTRZEŻEŃ WCAG 3 TYP DOKUMENTU UŻYTY FORMAT (X)HTML JĘZYK OWANIE STRONY Urząd Marszałkowski Województwa
Matematyka dyskretna - 7.Drzewa
 Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Tworzenie szablonów użytkownika
 Poradnik Inżyniera Nr 40 Aktualizacja: 12/2018 Tworzenie szablonów użytkownika Program: Plik powiązany: Stratygrafia 3D - karty otworów Demo_manual_40.gsg Głównym celem niniejszego Przewodnika Inżyniera
Poradnik Inżyniera Nr 40 Aktualizacja: 12/2018 Tworzenie szablonów użytkownika Program: Plik powiązany: Stratygrafia 3D - karty otworów Demo_manual_40.gsg Głównym celem niniejszego Przewodnika Inżyniera
Spis treści 1. Wstęp Logowanie Główny interfejs aplikacji Ogólny opis interfejsu Poruszanie się po mapie...
 Spis treści 1. Wstęp... 2 2. Logowanie... 2 3. Główny interfejs aplikacji... 2 3.1. Ogólny opis interfejsu... 2 3.2. Poruszanie się po mapie... 3 3.3. Przełączanie widocznych warstw... 3 4. Urządzenia...
Spis treści 1. Wstęp... 2 2. Logowanie... 2 3. Główny interfejs aplikacji... 2 3.1. Ogólny opis interfejsu... 2 3.2. Poruszanie się po mapie... 3 3.3. Przełączanie widocznych warstw... 3 4. Urządzenia...
Wyniki sprawdzianu i egzaminu gimnazjalnego w 2015r. uczniów szkół w gminie Masłów
 Wyniki sprawdzianu i egzaminu gimnazjalnego w 2015r. uczniów szkół w gminie Masłów SPRAWDZIAN - 2015 Liczba uczniów przystępująca do sprawdzianu w 2015r. Lp Szkoła Liczba uczniów 1 Szkoła Podstawowa w
Wyniki sprawdzianu i egzaminu gimnazjalnego w 2015r. uczniów szkół w gminie Masłów SPRAWDZIAN - 2015 Liczba uczniów przystępująca do sprawdzianu w 2015r. Lp Szkoła Liczba uczniów 1 Szkoła Podstawowa w
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Kurs Adobe Photoshop Elements 11
 Kurs Adobe Photoshop Elements 11 Gladiatorx1 Narzędzie rekompozycja 2015-01- 04 Spis treści Narzędzie rekompozycja... 2 Opcje narzędzia... 2 Przykłady zastosowania narzędzia... 3 Wykonał gladiatorx1 Strona
Kurs Adobe Photoshop Elements 11 Gladiatorx1 Narzędzie rekompozycja 2015-01- 04 Spis treści Narzędzie rekompozycja... 2 Opcje narzędzia... 2 Przykłady zastosowania narzędzia... 3 Wykonał gladiatorx1 Strona
Bukiet INSTRUKCJA. autor: Wouter van Strien projekt gra czny: Przemysław Fornal
 Bukiet INSTRUKCJA autor: Wouter van Strien projekt gra czny: Przemysław Fornal ELEMENTY GRY 2 notesy Każdy notes posiada 50 dwustronnych kartek. Na każdej kartce znajduje się 6 pól gracze hodują na nich
Bukiet INSTRUKCJA autor: Wouter van Strien projekt gra czny: Przemysław Fornal ELEMENTY GRY 2 notesy Każdy notes posiada 50 dwustronnych kartek. Na każdej kartce znajduje się 6 pól gracze hodują na nich
SPIS TREŚCI. Sposób pierwszy... 3 Sposób drugi Ikony banków Ikony dostawców Strona1
 INSTRUKCJA UŻYTKOWANIA SZABLONU ALLEGRO ZAKUPIONEGO W PAKIECIE STANDARD, MAXI LUB VIP. SPIS TREŚCI 1. OTRZYMANE PLIKI.... 2 2. DODANIE SZABLONU DO SERWISU ALLEGRO ORAZ JEGO UŻYTKOWANIE.... 3 Sposób pierwszy....
INSTRUKCJA UŻYTKOWANIA SZABLONU ALLEGRO ZAKUPIONEGO W PAKIECIE STANDARD, MAXI LUB VIP. SPIS TREŚCI 1. OTRZYMANE PLIKI.... 2 2. DODANIE SZABLONU DO SERWISU ALLEGRO ORAZ JEGO UŻYTKOWANIE.... 3 Sposób pierwszy....
OSA OTWARTY SYSTEM ANTYPLAGIATOWY
 OSA OTWARTY SYSTEM ANTYPLAGIATOWY Kontrola antyplagiatowa pisemnych prac na Uniwersytecie Mikołaja Kopernika w Toruniu Mariusz Czerniak Plan prezentacji Informacje o systemie OSA Kontrola wstępnych wersji
OSA OTWARTY SYSTEM ANTYPLAGIATOWY Kontrola antyplagiatowa pisemnych prac na Uniwersytecie Mikołaja Kopernika w Toruniu Mariusz Czerniak Plan prezentacji Informacje o systemie OSA Kontrola wstępnych wersji
ELEMENTY GRY. 72 karty pokoi (6 rodzajów po 12 kart) 4 karty startowe. 4 karty zmiany punktacji 4 dodatkowe karty zmiany punktacji.
 Autor: Scott Almes Ilustracje: Adam P. McIver, Tomek Larek 72 karty pokoi (6 rodzajów po 12 kart) ELEMENTY GRY 4 karty startowe czerwone żółte zielone niebieskie fioletowe brązowe 4 karty zmiany punktacji
Autor: Scott Almes Ilustracje: Adam P. McIver, Tomek Larek 72 karty pokoi (6 rodzajów po 12 kart) ELEMENTY GRY 4 karty startowe czerwone żółte zielone niebieskie fioletowe brązowe 4 karty zmiany punktacji
NAUKOMETRY CZNY. WARSZTAT Pozapublikacyjna aktywność pracowników naukowych. Studium przypadku. Wiesława Osińska. Katowice 20 maja 2016
 Katowice 20 maja 2016 WARSZTAT Pozapublikacyjna aktywność pracowników naukowych Studium przypadku NAUKOMETRY Wiesława Osińska Uniwersytet Mikołaja Kopernika w Toruniu CZNY 1 Plan wystąpienia Trendy w naukometrii
Katowice 20 maja 2016 WARSZTAT Pozapublikacyjna aktywność pracowników naukowych Studium przypadku NAUKOMETRY Wiesława Osińska Uniwersytet Mikołaja Kopernika w Toruniu CZNY 1 Plan wystąpienia Trendy w naukometrii
WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH 12
 Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
Otwarty System Antyplagiatowy Instrukcja dla promotorów/nauczycieli. I. Logowanie do Otwartego Systemu Antyplagiatowego
 Otwarty System Antyplagiatowy Instrukcja dla promotorów/nauczycieli Opracował: Remigiusz Ciemiński, CI UAM I. Logowanie do Otwartego Systemu Antyplagiatowego Otwarty System Antyplagiatowy znajduje się
Otwarty System Antyplagiatowy Instrukcja dla promotorów/nauczycieli Opracował: Remigiusz Ciemiński, CI UAM I. Logowanie do Otwartego Systemu Antyplagiatowego Otwarty System Antyplagiatowy znajduje się
Zaznaczenie prostokątne. Zaznaczenie eliptyczne. Tekst. Okno warstw. Wypełnienie kubełkiem. Gradient. Kolor pierwszo i drugoplanowy
 Narzędzia, które wykorzystasz przy tworzeniu swojego obrazu Zaznaczenie prostokątne Zaznaczenie eliptyczne Tekst Wypełnienie kubełkiem Okno warstw Gradient Kolor pierwszo i drugoplanowy Okno obszar roboczy
Narzędzia, które wykorzystasz przy tworzeniu swojego obrazu Zaznaczenie prostokątne Zaznaczenie eliptyczne Tekst Wypełnienie kubełkiem Okno warstw Gradient Kolor pierwszo i drugoplanowy Okno obszar roboczy
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Przewodnik... Tworzenie Landing Page
 Przewodnik... Tworzenie Landing Page Spis treści Kreator strony landing page Stwórz stronę Zarządzaj stronami 2 Kreator strony landing page Kreator pozwala stworzyć własną stronę internetową z unikalnym
Przewodnik... Tworzenie Landing Page Spis treści Kreator strony landing page Stwórz stronę Zarządzaj stronami 2 Kreator strony landing page Kreator pozwala stworzyć własną stronę internetową z unikalnym
Od czego wszystko się zaczęło
 Od czego wszystko się zaczęło Przeszukując Internet w poszukiwaniu nowych pomysłów na realizację procesu dydaktycznego trafiłem na propozycję testowania nowego narzędzia do tworzenia prezentacji multimedialnych
Od czego wszystko się zaczęło Przeszukując Internet w poszukiwaniu nowych pomysłów na realizację procesu dydaktycznego trafiłem na propozycję testowania nowego narzędzia do tworzenia prezentacji multimedialnych
Lingwistyczny system definicyjny wykorzystujący korpusy tekstów oraz zasoby internetowe.
 Lingwistyczny system definicyjny wykorzystujący korpusy tekstów oraz zasoby internetowe. Autor: Mariusz Sasko Promotor: dr Adrian Horzyk Plan prezentacji 1. Wstęp 2. Cele pracy 3. Rozwiązanie 3.1. Robot
Lingwistyczny system definicyjny wykorzystujący korpusy tekstów oraz zasoby internetowe. Autor: Mariusz Sasko Promotor: dr Adrian Horzyk Plan prezentacji 1. Wstęp 2. Cele pracy 3. Rozwiązanie 3.1. Robot
Kraków, ver
 Kraków, ver. 2016.001 Spis treści I. Tworzenie nowego slajdu... 3 1. Dodanie Widgetu... 5 2. Dodanie daty i godziny... 5 3. Dodanie mediów... 5 4. Dodawania pola tekstowego... 5 5. Układy graficzne...
Kraków, ver. 2016.001 Spis treści I. Tworzenie nowego slajdu... 3 1. Dodanie Widgetu... 5 2. Dodanie daty i godziny... 5 3. Dodanie mediów... 5 4. Dodawania pola tekstowego... 5 5. Układy graficzne...
Dokumentacja administratora
 Dokumentacja administratora w ramach projektu Beneficjent: Urząd Miasta Krakowa Wersja: 1.00 Data wersji: 2015-02-24 Autor (rzy): Zespół Pentacomp Nazwa pliku: MJUP_Dokumentacja administratora_v100_20150224.docx
Dokumentacja administratora w ramach projektu Beneficjent: Urząd Miasta Krakowa Wersja: 1.00 Data wersji: 2015-02-24 Autor (rzy): Zespół Pentacomp Nazwa pliku: MJUP_Dokumentacja administratora_v100_20150224.docx
dwanaście dwadzieścia osiem trzynaście
 Imię i nazwisko, numer z dziennika Imię i nazwisko, numer z dziennika WRZESIEŃ Grupa A 1. Spośród podanych liczb podkreśl a) czarnym kolorem największą liczbę, b) zielonym kolorem najmniejszą liczbę. dwanaście
Imię i nazwisko, numer z dziennika Imię i nazwisko, numer z dziennika WRZESIEŃ Grupa A 1. Spośród podanych liczb podkreśl a) czarnym kolorem największą liczbę, b) zielonym kolorem najmniejszą liczbę. dwanaście
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Teoria grafów II. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
Teoria grafów II Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Graf planarny Graf planarny Graf, który może być narysowany tak, by uniknąć przecinania się krawędzi, nazywamy grafem
MS Office Picture Manager
 MS Office Picture Manager Edycja obrazów cyfrowych Poradnik powstał w ramach projektu Informacja dla obywateli cybernawigatorzy w bibliotekach, zainicjowanego przez polskich uczestników programu wymiany
MS Office Picture Manager Edycja obrazów cyfrowych Poradnik powstał w ramach projektu Informacja dla obywateli cybernawigatorzy w bibliotekach, zainicjowanego przez polskich uczestników programu wymiany
Tworzenie infografik za pomocą narzędzia Canva
 Tworzenie infografik za pomocą narzędzia Canva Spis treści Wstęp... 1 Układy... 3 Zmiana tekstu... 4 Obrazki... 5 Elementy... 6 Zdjęcia - Gratis... 6 Siatki... 8 Ramki... 10 Kształty... 12 Linie... 12
Tworzenie infografik za pomocą narzędzia Canva Spis treści Wstęp... 1 Układy... 3 Zmiana tekstu... 4 Obrazki... 5 Elementy... 6 Zdjęcia - Gratis... 6 Siatki... 8 Ramki... 10 Kształty... 12 Linie... 12
Opcje raportów. łatwe i czytelne raportowanie
 Rejestracja czasu pracy bez odpowiedniego i łatwego w obsłudze procesu raportowania zapisanych godzin jest niepraktyczna. Naszym celem było stworzenie kompleksowego i funkcjonalnego systemu, dzięki któremu
Rejestracja czasu pracy bez odpowiedniego i łatwego w obsłudze procesu raportowania zapisanych godzin jest niepraktyczna. Naszym celem było stworzenie kompleksowego i funkcjonalnego systemu, dzięki któremu
Kolorowanie wierzchołków Kolorowanie krawędzi Kolorowanie regionów i map. Wykład 8. Kolorowanie
 Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows 7
 5.0 5.3.3.5 Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows 7 Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium, będziesz korzystać z narzędzi administracyjnych
5.0 5.3.3.5 Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows 7 Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium, będziesz korzystać z narzędzi administracyjnych
Grafy (3): drzewa. Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków. UTP Bydgoszcz
 Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Najważniejsze sygnały używane na PKP
 Artykuł pobrano ze strony eioba.pl Najważniejsze sygnały używane na PKP Sygnały świetlne w ruchu kolejowym informują o tym, czy droga jest wolna, czy też należy zatrzymać pojazd, czy też z jaką prędkością
Artykuł pobrano ze strony eioba.pl Najważniejsze sygnały używane na PKP Sygnały świetlne w ruchu kolejowym informują o tym, czy droga jest wolna, czy też należy zatrzymać pojazd, czy też z jaką prędkością
ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
znajdujący się w prawym dolnym rogu wyświetli informacje oraz dane dotyczące Unii
 Wstęp Unia Europejska to multimedialny program edukacyjny przeznaczony dla dzieci w wieku już od 6 lat. Program podzielony jest na dwie części. Część edukacyjna zawiera podstawowe dane statystyczne o państwach
Wstęp Unia Europejska to multimedialny program edukacyjny przeznaczony dla dzieci w wieku już od 6 lat. Program podzielony jest na dwie części. Część edukacyjna zawiera podstawowe dane statystyczne o państwach
Cel ćwiczenia: Celem ćwiczenia jest nabranie wprawy w rysowaniu kół i okręgów o zadanych rozmiarach.
 Cel ćwiczenia: Celem ćwiczenia jest nabranie wprawy w rysowaniu kół i okręgów o zadanych rozmiarach. Dodatkowo w zadaniu tym, ćwiczone są umiejętności w nadawaniu kolorów wypełnienia i obrysu oraz w używaniu
Cel ćwiczenia: Celem ćwiczenia jest nabranie wprawy w rysowaniu kół i okręgów o zadanych rozmiarach. Dodatkowo w zadaniu tym, ćwiczone są umiejętności w nadawaniu kolorów wypełnienia i obrysu oraz w używaniu
Wejście na stronę. Na stronie gis.mikolow.eu klikamy w niebieskie okno z napisem GEOPORTAL. i przechodzimy do modułu drogi gminne
 Spis treści Wejście na stronę...2 Ogólny opis... 4 Serwisy mapowe...4 Warstwy... 5 Moduł drogi gminne...6 Obwody wyborcze...7 Nawierzchnie dróg...8 Obszary drogowe...9 Droga grupowa...10 Droga pojedyncza...11
Spis treści Wejście na stronę...2 Ogólny opis... 4 Serwisy mapowe...4 Warstwy... 5 Moduł drogi gminne...6 Obwody wyborcze...7 Nawierzchnie dróg...8 Obszary drogowe...9 Droga grupowa...10 Droga pojedyncza...11
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE
 WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Microsoft Small Basic
 Microsoft Small Basic Okno grafiki Szacowany czas trwania lekcji: 1 godzina Okno grafiki Podczas tej lekcji uzyskasz informacje na temat: Instrukcji używających obiektu GraphicsWindow. Właściwości obiektu
Microsoft Small Basic Okno grafiki Szacowany czas trwania lekcji: 1 godzina Okno grafiki Podczas tej lekcji uzyskasz informacje na temat: Instrukcji używających obiektu GraphicsWindow. Właściwości obiektu
Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows Vista
 5.0 5.3.3.6 Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows Vista Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium, będziesz korzystać z narzędzi administracyjnych
5.0 5.3.3.6 Laboratorium - Monitorowanie i zarządzanie zasobami systemu Windows Vista Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium, będziesz korzystać z narzędzi administracyjnych
SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA
 Załącznik nr 1 SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA CZĘŚĆ PIERWSZA: 1. Drukarka 3D 1 szt. Szczegółowy opis przedmiotu: Typ Drukarka 3D W ofercie wymagane jest podanie modelu, symbolu oraz Technologia
Załącznik nr 1 SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA CZĘŚĆ PIERWSZA: 1. Drukarka 3D 1 szt. Szczegółowy opis przedmiotu: Typ Drukarka 3D W ofercie wymagane jest podanie modelu, symbolu oraz Technologia
Wyniki sprawdzianu i egzaminu gimnazjalnego w 2016r. uczniów szkół w gminie Masłów
 Wyniki sprawdzianu i egzaminu gimnazjalnego w 2016r. uczniów szkół w gminie Masłów SPRAWDZIAN - 2016 Liczba uczniów przystępująca do sprawdzianu w 2016r. Lp Szkoła Liczba uczniów 1 Szkoła Podstawowa w
Wyniki sprawdzianu i egzaminu gimnazjalnego w 2016r. uczniów szkół w gminie Masłów SPRAWDZIAN - 2016 Liczba uczniów przystępująca do sprawdzianu w 2016r. Lp Szkoła Liczba uczniów 1 Szkoła Podstawowa w
Programowanie sieciowe. Tadeusz Trzaskalik
 Programowanie Tadeusz Trzaskalik 8.1. Wprowadzenie Słowa kluczowe Drzewo rozpinające Minimalne drzewo rozpinające Najkrótsza droga w sieci Wierzchołek początkowy Maksymalny przepływ w sieci Źródło Ujście
Programowanie Tadeusz Trzaskalik 8.1. Wprowadzenie Słowa kluczowe Drzewo rozpinające Minimalne drzewo rozpinające Najkrótsza droga w sieci Wierzchołek początkowy Maksymalny przepływ w sieci Źródło Ujście
Opracowanie prof. J. Domsta 1
 Opracowanie prof. J. Domsta 1 Algorytm FLEURY'ego: Twierdzenie 6.5 G-graf eulerowski. Wtedy cykl Eulera otrzymujemy nastepująco: a) Start w dowolnym wierzchołku b) Krawędzie w dowolnej kolejności po przebyciu
Opracowanie prof. J. Domsta 1 Algorytm FLEURY'ego: Twierdzenie 6.5 G-graf eulerowski. Wtedy cykl Eulera otrzymujemy nastepująco: a) Start w dowolnym wierzchołku b) Krawędzie w dowolnej kolejności po przebyciu
SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA
 Załącznik nr 1 SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA CZĘŚĆ PIERWSZA: 1. Drukarka 3D 1 szt. Szczegółowy opis przedmiotu: Drukarka 3D W ofercie wymagane jest podanie modelu, symbolu oraz producenta. Technologia
Załącznik nr 1 SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA CZĘŚĆ PIERWSZA: 1. Drukarka 3D 1 szt. Szczegółowy opis przedmiotu: Drukarka 3D W ofercie wymagane jest podanie modelu, symbolu oraz producenta. Technologia
Wirtualny Dziennik - INSTRUKCJA DLA RODZICÓW
 Wirtualny Dziennik - INSTRUKCJA DLA RODZICÓW Wstęp Moduł dla rodziców to grupa opcji umożliwiająca podgląd większości elementów związanych z uczęszczaniem dziecka do szkoły. W szczególności dostępne są
Wirtualny Dziennik - INSTRUKCJA DLA RODZICÓW Wstęp Moduł dla rodziców to grupa opcji umożliwiająca podgląd większości elementów związanych z uczęszczaniem dziecka do szkoły. W szczególności dostępne są
*Grafomania z. Neo4j. Praktyczne wprowadzenie do grafowej bazy danych.
 *Grafomania z Neo4j Praktyczne wprowadzenie do grafowej bazy danych. Jak zamodelować relacyjną bazę danych reprezentującą następujący fragment rzeczywistości: Serwis WWW opisuje pracowników różnych firm
*Grafomania z Neo4j Praktyczne wprowadzenie do grafowej bazy danych. Jak zamodelować relacyjną bazę danych reprezentującą następujący fragment rzeczywistości: Serwis WWW opisuje pracowników różnych firm
TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła
 TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła 1. Cel ćwiczenia Celem ćwiczenia jest nabycie umiejętności tworzenia tła poprzez wykorzystanie funkcji dostępnych w programie GIMP. 2. Wiadomości
TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła 1. Cel ćwiczenia Celem ćwiczenia jest nabycie umiejętności tworzenia tła poprzez wykorzystanie funkcji dostępnych w programie GIMP. 2. Wiadomości
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Kolorowanie
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Kolorowanie
Kamila Muraszkowska Znaczenie wąskich gardeł w sieciach białkowych. źródło: (3)
 Kamila Muraszkowska Znaczenie wąskich gardeł w sieciach białkowych źródło: (3) Interakcje białko-białko Ze względu na zadanie: strukturalne lub funkcjonalne. Ze względu na właściwości fizyczne: stałe lub
Kamila Muraszkowska Znaczenie wąskich gardeł w sieciach białkowych źródło: (3) Interakcje białko-białko Ze względu na zadanie: strukturalne lub funkcjonalne. Ze względu na właściwości fizyczne: stałe lub
