Sequential Monte Carlo: Selected topics
|
|
|
- Filip Klimek
- 4 lat temu
- Przeglądów:
Transkrypt
1 Uniwersye Warszawski Wydział Maemayki, Informayki i Mechaniki Agnieszka Borowska Nr albumu: Sequenial Mone Carlo: Seleced opics Praca licencjacka na kierunku MATEMATYKA Praca wykonana pod kierunkiem dra Pawła Wolffa Zakład Teorii Prawdopodobieńswa Wrzesień 2015
2 Oświadczenie kierującego pracą Powierdzam, że niniejsza praca zosała przygoowana pod moim kierunkiem i kwalifikuje się do przedsawienia jej w posępowaniu o nadanie yułu zawodowego. Daa Podpis kierującego pracą Oświadczenie auorki pracy Świadoma odpowiedzialności prawnej oświadczam, że niniejsza praca dyplomowa zosała napisana przeze mnie samodzielnie i nie zawiera reści uzyskanych w spośob niezgodny z obowiązujacymi przepisami. Oświadczam również, że przedsawiona praca nie byla wcześniej przedmioem procedur związanych z uzyskaniem yułu zawodowego w wyższej uczelni. Oświadczam ponado, że niniejsza wersja pracy jes idenyczna z załączoną wersją elekroniczną. Daa Podpis auorki pracy
3 Sreszczenie W pracy rozważany jes problem wnioskowania saysycznego o ukryym sygnale rządzącym dynamiką danego sysemu na podsawie obserwacji podlegających szumowi. Sysem reprezenowany jes poprzez model zmiennych sanu z uwagi na szerokie spekrum problemów możliwych do analizy przy jego pomocy. Ponieważ dla badanego problemu w ogólności nie isnieje analiyczne rozwiązanie, rozważamy klasę meod do przybliżania rozkładów a poseriori dla zmiennych sanów, zw. Sekwencyjne Mone Carlo. Opierają się one na miarach Diraca konsruowanych na podsawie próbek losowych (cząseczek) z rozkładów pochodzących z poprzednich ieracji. Szczególna uwaga poświęcona jes problemowi filracji, polegającemu na esymacji bieżącego sanu sysemu na podsawie bieżących pomiarów. Wyprowadzane są formuły charakeryzujące filry cząseczkowe, kóre służą do konsrukcji algorymów przydanych w analizie numerycznej. Omówiony jes problem degeneracji, immanenny dla sekwencyjnego losowania isonego, jak również wybrane meody do radzenia sobie z nim. Zaprezenowane są podsawowe wyniki doyczące zbieżności filrów cząseczkowych. Pracę zamyka cześć ilusrująca rzy zasosowania filrów cząseczkowych. Absrac We analyse he problem of inference abou a laen signal governing he dynamics of a sysem given only he observed noisy daa. We adop he discree-ime sae space approach due o he wide range of problems i can capure. Because in general no closed-form soluion are available in his framework, we discuss he class of mehods used for approximaing of he poserior sae disribuions, called Sequenial Mone Carlo. These mehods are based on he Dirac-measures which sem from he draws (paricles) from he disribuion consruced in he previous ieraion. A special aenion is devoed o he filering problem, where one is ineresed in he esimaion of he curren sae of he sysem given he curren sysem measuremens. We derive heoreical forms of he paricle filers, which we hen use o consruc algorihms suiable for numerical analysis. We discuss he degeneracy problem, inheren o he sequenial imporance sampling and seleced mehods o ackle i. The basic convergence resuls in he conex of paricle filers are presens. Finally, we consider hree numerical applicaion.
4 Słowa kluczowe Sekwencyjne Mone Carlo; Filry cząseczkowe; Filracja Bayesowska; Zbieżność miar; Modele przesrzeni sanów. Keywords Sequenial Mone Carlo; Paricle filers; Bayesian filering; Convergence of measures; Sae space models. Dziedzina pracy (kody wg programu Socraes-Erasmus) 11.1 Maemayka Klasyfikacja emayczna 60. Probabiliy heory and sochasic processes 60G. Sochasic processes 60G35. Signal deecion and filering 62. Saisics 62F. Parameric inference 62F15. Bayesian inference 62M. Inference from sochasic processes Tyuł pracy w języku polskim Sekwencyjne Meody Mone Carlo: Wybrane Zagadnienia 2
5 Conens 1 Inroducion 5 2 Model specificaion and he filering problem General sae space model The signal process The observaion process Addiive example Problem formulaion Bayesian recursion The filering problem Linear Gaussian example Paricle filering Mone Carlo inegraion Imporance sampling Sequenial imporance sampling Recursion for he imporance densiy Recursion for he imporance weighs SIS algorihm Degeneracy and resampling Effecive sample size SIR algorihm Selecion of he imporance funcion Opimal imporance funcion Local linearisaion The boosrap filer
6 4 Convergence The filering problem revisied Basic noaion Projecive produc Paricle filers Convergence of measure-valued random variables Convergence heorems Convergence in expecaion Almos sure convergence Boosrap example Paricle filer Resampling Convergence Discussion Applicaions Basic linear Gaussian problem Nonlinear Gaussian problem Sochasic volailiy model Opimal imporance funcion approximaion Resuls Conclusions 65 Bibliography 67 Appendix A Noaion 69 Appendix B Properies of IS esimaor 71 B.1 Dela mehod B.2 Asympoic properies of IS esimaor B.3 Efficiency of IS esimaor Appendix C Code lisings 77 C.1 Basic linear Gaussian problem C.2 Nonlinear Gaussian problem C.3 Sochasic volailiy model
7 Chaper 1 Inroducion The problem of inference abou a laen signal governing he dynamics of he sysem under sudy, given only he observed noisy daa, is ubiquious in science. In many real-life applicaions, considered e.g. in applied saisics, engineering, physics or economics, his quesion is approached using he so called sae space models (cf. Durbin and Koopman, 2012, for a deailed exposiion in he conex of ime series analysis). This class of models provides a versaile ool o analyse ime series due o is explici focus on he sae vecor. This flexibiliy, however, comes in general a he price of he lack of a closed-form soluion for hese models. Hence, one needs o resor o simulaion-based echniques. The noion of Sequenial Mone Carlo (SMC) refers o a class of simulaion-based mehods relying on he poin mass (or paricle) represenaion of probabiliy disribuions, which are used for (Bayesian) saisical inference for dynamic sysems (cf. Douce e al., 2001, for a comprehensive sudy). The key problem approached using SMC is he opimal filering problem, consising in he esimaion of he curren (unobserved) sae of he sysem, based on he observaions. Boh, he sae and he observaion processes are sochasic, as in he Hidden Markov Models (HMM) framework (cf. Cappé e al., 2006). The aim is o deermine he poserior disribuion of he saes, i.e. condiional on he observaions. This is obained by applying he Bayes Theorem, which allows for combining he prior beliefs abou he sae of he sysem, wih he informaion coming from he daa. The former may come from he compuaions in he previous ieraions, while he laer is quanified using he likelihood funcion. Imporanly, in he SMC echniques he compuaions can be performed sequenially, considerably reducing he problem s dimensionaliy. This consiues he crucial difference of he framework under consideraion as compared o he sandard, non-sequenial Markov Chain Mone Carlo (MCMC) mehods. To obain draws from a disribuion of ineres, which in general is non-sandard and difficul o sample from, one uses imporance sampling, where he draws from a candidae disribuion are assigned he so called imporance weighs o correc for heir fi o he arge. Unforunaely, he basic sequenial seing suffers from wo inrinsic problems relaed o he fac ha ofen afer jus a few ieraions only a very small par of he paricles has non-negligible weighs. This heoreically grounded phenomenon of he weigh degeneracy (cf. Kong e al., 1994) has been devoed a noiceable aenion in he lieraure (cf. Li e al., 2014, for a survey of recen approaches). The mos sraighforward soluion i o perform resampling every ieraion, so ha he weighs of he paricles are rese. In ou hesis, he main emphasis in pu on paricle filers, wih he aim o cover he mos imporan aspecs relaed o his subjec. We derive heir heoreical forms, which we hen use o consruc algorihms suiable for numerical analysis. A special aenion is paid o he above-menioned weigh degeneracy problem: we provide a heoreical moivaion for he occurrence of his phenomenon and we discuss some mehods o ackle i. Nex, we presen he basic convergence resuls in he conex of paricle filers, as 5
8 hey are essenially approximaions o he nonlinear filering equaions. Since paricle filers are based on ineracing, hence saisically dependen, samples, one canno show heir convergence by referring o he sandard Mone Carlo heorems. Finally, we consider hree numerical applicaion, which aim o demonsrae he heoreical resuls of previous secions. Throughou he hesis we adop he sae-space approach, where we resric ourselves o he discree-ime seup. The srucure of his hesis is as follows. Chaper 2 specifies he modelling framework based on he sae space models and inroduces he problem of he opimal filering. The main conceps of paricle filering and he relaed algorihms are presened in Chaper 3. In Chaper 4 we define he convergence conceps for measure-valued random variables and discusses he basic convergence resuls for paricle filers. Chaper 5 presens hree applicaions of paricle filers o differen ypes of models, saring wih he mos basic one, he local level model, o finally move o he nonlinear non-gaussian sochasic volailiy model. Chaper 6 concludes and presens he opics for furher research. The noaion used wihin he hesis is shown in Appendix A. 6
9 Chaper 2 Model specificaion and he filering problem In his Chaper we esablish he general framework for his hesis and formulae he basic filering problem. Below, we consider a general dynamic model, which is a mahemaical represenaion of imevarying phenomena in differen fields of science and engineering. The fundamenal componens of such a dynamic model are he dynamics model and he measuremen model. The former describes he evoluion of a sae process, which iself is laen bu affecs he measuremen process in an observed way, characerised by he measuremen model. These ypes of models are ubiquious in signal processing and relaed fields. Moreover, very ofen one resrics aenion o he class of he so called sae space models, where he sae is assumed o follow he firs order Markov process and he whole sysem can be described for insance by a se of firs-order differenial or difference equaions (raher han by a se of n-h-order ones). Therefore, we firs formally characerise he general sae space model. As i has been already poined ou in he Inroducion, we aim o perform inference on he unknown sae process wihin a Bayesian approach, i.e. o combine he prior knowledge of he sysem wih he informaion delivered by he daa (measuremen). In he mos general seing one is ineresed in he whole poserior disribuion of he sae process, given he daa. However, a very common pracise is limiing of aenion o he filering problem, which consiss in he recursive esimaion of he mos recen laen sae (or a measurable funcion hereof). This problem is also know as Bayesian or opimal filering problem and i will be he subjec his hesis mainly focuses on. Two framework convenions will be used in his and in he subsequen chapers, depending on he curren purposes, which is a common pracice in he lieraure (cf. Cappé e al. (2006), Douce e al. (2001), Crisan and Douce (2002), Durbin and Koopman (2012)). When inroducing he general sae space model and is componens in Secion 2.1, as well as when analysing he convergence of paricle filers in Chaper 4, we will adop a probabilisic represenaion, more appropriae for a heoreical analysis, wih he noaion based mainly on Crisan and Douce (2002) and Crisan (2001). To formulae he Bayesian filering problem in Secions and and o discuss he paricle filers in Chaper 3, we will follow a signal processing convenion, more suiable for he applicaion purposes, following e.g. Douce and Johansen (2009) and Kong e al. (1994). 2.1 General sae space model We consider he laen sae (or signal) process X = {X } N and he measuremen (or observaion) process Y = {Y } N (a more deailed exposiion of hese processes is given in he nex wo Subsecions). 7
10 The sae process ogeher wih he observaion process consiue he following general sae space model (SSM) X = F (X 1, V ), (2.1.1) Y = G (X, W ), (2.1.2) X 0 p(dx 0 ). (2.1.3) In he above specificaion F and G are known, possibly nonlinear, measurable funcions of he sae and of he whie noise processes W = {W } N and V = {V } N, and p(dx 0 ) is he iniial disribuion of he signal process. The disurbance processes are assumed o be muually independen and independen of X 0. In general, one does no make any addiional disribuional assumpions on boh noise processes, hence he inroduced framework is ofen referred o as nonlinear, non-gaussian SSM. Moreover, we assume ha all he sochasic processes are defined on (Ω, F, P), which is a fixed probabiliy space. Since below we describe he signal and measuremen processes in more deail, here le us jus briefly commen on he above specificaion. The ransiion equaion (2.1.1) defines he firs-order Markov process X wih he equivalen probabilisic descripion of he signal evoluion being p(dx +1 x ), i.e. he ransiion disribuion. The observaion equaion (2.1.2) characerises he likelihood of he observaions Y, given he sae X, so i relaes he recorded measuremen o he laen sae vecor. An equivalen probabilisic model for Y is p(dy x ), i.e. he observaion disribuion. Figure graphically presens he dependencies beween saes and observaions in he general SMM. y 1 y y +1 G 1 G G +1 F 1 x 1 x x +1 F F +1 F +2 Figure 2.1.1: A graphical represenaion of he general SSM. The SMM is a class which includes many models of ineres and provides a very flexible ool o model many real-life problems. I is because nonlinear dynamic sysems frequenly arise in science, engineering, economics and a number of oher fields, while non-gaussian disribuions are eiher naural or pracical in applicaions. Finally, i is worh noing ha in many fields he generic SSM is also known as he hidden Markov model (HMM, cf. Cappé e al. (2006)) The signal process As i has already been poined ou, he ransiion equaion (2.1.1) defines he firs-order Markov signal process X = {X } N which is a sochasic process on (Ω, F, P) wih values in R nx. The σ-algebra generaed by X is denoed by F X, F X = σ (X s, s {0, 1,..., }). Then, he Markovianiy assumpion on X means ha P ( X A F X 1) = P(X A X 1 ) a.s., A B(R nx ). 8
11 The ransiion kernel K (, ) of he Markov chain X is a funcion on R nx B(R nx ) saisfying K (x, A) = P(X A X 1 = x), N, x R nx. (2.1.4) For a fixed x R nx and N, K (x, ) is a probabiliy measure on R d ; for a fixed A B(R nx ) and N, K (, A) is a bounded, B(R nx )-measurable funcion. In he furher par of he work, we will resric ourselves o Feller ransiion kernels, i.e. ransiion kernels saisfying he Feller propery: where we define he funcion K f as follows f C b (R d ) K f C b (R d ), K f(x) := f(y)k (x, dy). R nx The ransiion kernel ogeher wih he iniial disribuion p(dx 0 ) of a Markov process X uniquely deermine is disribuion. Nex, for a fixed, consider he disribuion of a random variable X, denoed by p (dx ) and given by p (A) := P(X A), A B(R nx ). This disribuion is ofen referred o as he prior disribuion for X, because i depends only on X 1. Making use of he ransiion kernel formula (2.1.4), one can recursively express p as 1 p = p 1 K 1 = p 0 K i, where for a R nx -valued disribuion q on (Ω, F, P) we define he measure q 1 K 1 as i=0 (q 1 K )(A) := K (x, A)q 1 (dx). R nx For simpliciy, we assume ha K (x 1, dx ) and p(dx 0 ) admi densiies wih respec o he corresponding Lebesgue measures, i.e. K (x 1, dx ) = P(X dx X 1 = x 1 ) = p(x x 1 )dx, p(dx 0 ) = P(X 0 dx 0 ) = p(x 0 )dx The observaion process The observaion process Y = {Y } N, characerised by (2.1.2), is a sochasic process on (Ω, F, P) wih values in R ny, and i is assumed o be condiionally independen of he signal X (cf. Figure 2.1.1). Definiion (Condiional independence of sochasic processes). Le Z = {Z } N and U = {U } N be sochasic processes on (Ω, F, P), wih values in R nz and R nu, respecively. Nex, le { } F { } Z N, F U N be he filraions generaed by Z and U, respecively, wih F Z = σ (Z s : s [0, ]) and F U = σ (U s : s [0, ]). We say ha Z is condiionally independen of U if P(Z B σ(f Z s, F U )) = P(Z B U ), s <,, s N, B B(R nz ). 1 For his reason i can be seen as he marginal disribuion of he join disribuion of he process X up o, as i will be formally specified in Subsecions and
12 This means ha for a given he disribuion of Y depends on X only, so ha is marginal disribuion can be expressed as P(Y B X = x ) = B p(dy x ), B B(R dy ). Noice, ha in he parlance of he general SSM, he condiional independence of Y given X amouns o he noise processes V and W in (2.1.1) and (2.1.2) being serially and muually independen 2. Similarly as for he signal process, we assume for simpliciy ha p(dy x ) admis a densiy wih respec o he corresponding Lebesgue measure, i.e. p(dy x ) = p(y x )dy and ha his densiy is bounded and coninuous. Finally, we pu Y 0 = Addiive example To illusrae he link beween he probabilisic and signal processing approaches, following Crisan and Douce (2002), consider a scalar dynamic model X = f(x 1 ) + V, Y = g(x ) + W, where V = {V } N and W = {W } N\{0} are boh independen and idenically disribued (i.i.d.) sequences, also muually independen. This is a special case of he general SSM (2.1.1)-(2.1.3), where he noises addiively affec he signal and observaions. We ake which yields P(V C) = P(W D) = C D p V (dv) = p V dv, C p W (dw) = p W dw, K(x 1, x ) = p V (x f(x 1 )), D p(y x ) = p W (y g(x )). C B(R), D B(R), 2.2 Problem formulaion The key feaure of he SSM represenaion is is recursive srucure, which makes his class of dynamic models perfecly suied for he sequenial (on-line) analysis. Given he curren knowledge abou he sysem, one may be ineresed in updaing his knowledge when new informaion (observaions) become available. This is a naural framework for he Bayesian analysis, where he prior disribuion of he unknown variables is combined wih he likelihood funcion, describing he probabiliy of he daa given he hidden variables, o yield he poserior disribuion for he laen variables. Below, in Subsecion we derive he recursive formula for he poserior disribuion, which is addiionally spli ino wo seps: predicion and updaing. 2 An alernaive, ye similar definiion of condiional independence is provided by Cappé e al. (2006) wihin he HMM framework. Firs, hey define he HMM as a bivariae discree ime process {X, Y } N where {X } N is a Markov chain, and, condiional on {X } N, {Y } N is a sequence of independen variables such ha he condiional disribuion of Y depends only on X. 10
13 2.2.1 Bayesian recursion Denoe by X 0: = {X 0,..., X } and by Y 0: = {Y 0,..., Y } he pah up o ime of he signal and of he observaion process, respecively, wih he corresponding realisaion up o ime denoed by x 0: = {x 0,..., x } and by y 0: = {y 0,..., y }. We wish o deermine he poserior probabiliy disribuion p(dx 0: y 0: ) := P(X 0: dx 0: Y 0: = y 0: ), which describes he probabiliy of all he ransiions over ime given all he observaions, up o ime. Since we have assumed ha he required disribuions admi densiies, from now on we will wrie Then, he Bayes heorem yields p(x 0: y 0: ) = p(dx 0: y 0: ) = p(x 0: y 0: )dx 0:. (2.2.1) p(y 0: x 0: )p(x 0: ) (R nx )+1 p(y 0: x 0: )p(x 0: )dx 0:. (2.2.2) The aim is o derive a recursive formula for (2.2.2), i.e. o express p(x 0: y 0: ) in he following way p(x 0: y 0: ) = f (p(x 0: 1 y 0: 1 ), y ),, where f is a funcion o be deermined, possibly ime-dependen. In oher words, we wan o propagae over ime he join and he marginal disribuions p(x 0: y 0: ) and p(x y 0: ). We have p(x 0: y 0: ) = p(y 0: x 0: )p(x 0: ) p(y 0: ) = p(y, y 0: 1 x 0: )p(x 0: ) p(y, y 0: 1 ) ( ) = p(y y 0: 1, x 0: )p(y 0: 1 x 0: )p(x 0: ) p(y y 0: 1 )p(y 0: 1 ) B = p(y y 0: 1, x 0: )p(x 0: y 0: 1 )p(y 0: 1 )p(x 0: ) p(y y 0: 1 )p(y 0: 1 )p(x 0: ) = p(y y 0: 1, x 0: )p(x 0: y 0: 1 ) p(y y 0: 1 ) OI = p(y x )p(x, x 0: y 0: 1 ) p(y y 0: 1 ) ( ) = p(y x )p(x x 0: 1, y 0: 1 )p(x 0: 1 y 0: 1 ) p(y y 0: 1 ) MC p(y x )p(x x 1 )p(x 0: 1 y 0: 1 ) =, p(y y 0: 1 ) where B denoes applicaion of Bayes law, OI refers o observaions independence and MC o he Markov naure of he sae process. Wih ( ) we denoed he following sraighforward ideniy Hence, finally, we arrive a he recursive formula for he poserior p(x, y z) = p(x y, z)p(y z). (*) p(x 0: y 0: ) = p(x 0: 1 y 0: 1 ) p(y x )p(x x 1 ). (2.2.3) p(y y 0: 1 ) The compuaion of (2.2.3) can be spli ino wo subsequen seps: predicion and updaing, which is of 11
14 a significan pracical imporance. The former consiss in deriving p(x 0: y 0: 1 ), i.e. esimaion of he poserior disribuion of X up o ime given only pas observaions y 0: 1, i.e. wihou he mos recen realisaion of Y. The laer refers o re-evaluaion of our beliefs regarding he disribuion of X 0: afer having observed y, he recen realisaion of Y. The recursion seps are as follows p(x 0: y 0: 1 ) = p(x 0: 1 y 0: 1 )p(x x 1 ), (2.2.4) p(x 0: y 0: ) = C 1 p(y x )p(x 0: y 0: 1 ), (2.2.5) where C is a normalising consan, o ensure ha (2.2.5) is a proper densiy funcion, equal o C = p(y x )p(x 0: y 0: 1 )dx 0: (R nx )+1 = p(y y 0: 1 ). One can see ha he recursive sysem (2.2.4) and (2.2.5) has a sraighforward Bayesian inerpreaion. The predicive disribuion becomes he prior disribuion in he updaing equaion, which combined wih he likelihood of he new observaion delivers he poserior disribuion The filering problem One is ofen ineresed no exacly in p(x 0: y 0: ) iself, bu raher in is marginal disribuion p(x y 0: ), referred o as filering disribuion and given by p(x y 0: ) = p(x 0: y 0: )dx 0: 1. (R nx ) (2.2.6) The filering disribuion describes he curren sae of he sysem given all he observaions up o now. In oher words, he filering problem consiss of compuing he condiional disribuion of he signal given he σ-algebra generaed by he observaion process from ime 0 o he curren ime. Then, he filering counerpars of he Bayesian recursion (2.2.4) and (2.2.5) are given by p(x y 0: 1 ) = p(x 1 y 0: 1 )p(x x 1 ), (2.2.7) p(x y 0: ) = C 1 p(y x )p(x y 0: 1 ), (2.2.8) wih he normalising consan C = p(y x )p(x y 0: 1 )dx R nx = p(y y 0: 1 ). The simpliciy of he above formulae is misleading, as hese densiies are usually unavailable in closed form. A noiceable excepion is he linear Gaussian case, which admis he analyical soluion in he form of he celebraed Kalman filer (cf. e.g. Durbin and Koopman (2012)). For compleeness, we recall i briefly in he nex subsecion. 12
15 2.2.3 Linear Gaussian example Consider he linear Gaussian SSM, given by X +1 = T X + R V, Y = Z X + W, X 1 N ( X 1 0, P 1 0 ), V i.i.d N (0, H ), W i.i.d N (0, Q ), where V, W s are independen for all, s, and independen from X 1 (cf. Durbin and Koopman, 2012). The sysem marices T, Z, R, Q, H are deerminisic and have known forms. Then he unobserved sae X can be recursively esimaed from he observaions wih he Kalman filer as follows ν = Y Z X, F = Z P Z T + H, K = T P Z T F 1, X +1 = T X + K ν, P +1 = T P T T + R Q R T K F K T, for = 1,..., n, and saring wih given values for X 1 and P 1. The derivaion of he Kalman filer is based on he lemma for mulivariae normal regression heory. The proof can be found in numerous sources, e.g. Durbin and Koopman (2012), and will be omied as no direcly relaed o he main subjec of his hesis. In he above sysem X +1 and P +1 characerise he opimal sae predicions, i.e. he condiional expecaion and variance, respecively, of he random variable X +1, given he observaions up o, i.e. The filered esimaes, which are defined as are hen given by X +1 = E[X +1 Y ], P +1 = Var[X +1 Y ]. X = E[X Y ], P = Var[X Y ], X = X 1 + M ν, P = P 1 M F M T, where M = P 1 Z T F 1. Noice, ha because he model under consideraion is linear Gaussian, he disribuion of he laen sae is fully specified by is firs wo momens. Therefore, X and P describe wha one is ruly ineresed in, i.e. he filering disribuion of X p(x y 0: ) = φ(x ; X, P ). 13
16
17 Chaper 3 Paricle filering Paricle filers are sequenial Mone Carlo inegraion echniques based on paricle, i.e. poin mass, represenaion of probabiliy densiies. They are used for on-line, or sequenial, inference problems and can be applied o general sae-space model, as hey are no based on any assumpions regarding he funcional form of he model (e.g. linear) nor require disurbances o follow any paricular disribuion (e.g. Gaussian). 3.1 Mone Carlo inegraion For furher reference le us firs shorly recall he basic crude Mone Carlo inegraion mehod before describing in more deail he imporance sampling and sequenial imporance sampling echniques. Suppose we are ineresed in esimaion of he (condiional) mean of an arbirary measurable funcion f : X +1 R, given by f = E [f (X 0: ) Y 0: ] = f (x 0: )p(x 0: y 0: )dx 0:, (3.1.1) where he condiional disribuion p(x 0: y 0: ) is given by (2.2.2). To esimae (3.1.1), we can generae independenly N random sequences X (1) 0:,..., X(N) iid 0: p(x 0: y 0: ) and consider he sample average ˆf MC = 1 N N f(x (i) 0: ). (3.1.2) Indeed, by he Srong Law of Large Numbers, (3.1.2) is srongly consisen, i.e. ˆf MC a.s. N f. Moreover, by he Cenral Limi Theorem, he MC esimaor is asympoically normal since N ( ˆf MC f ) = 1 N provided ha he variance Var p f(x) exiss. N ( f (X (i) 0:n ) f ) n N (0, Varp f(x)), 15
18 3.2 Imporance sampling Since he basic building-block of paricle filering echniques is imporance sampling, we firs recall his algorihm, before discussing is recursive version, he sequenial imporance sampling. Imporance Sampling is an effecive Mone Carlo inegraion algorihm, used o esimae (3.1.1) in pracice, since i is difficul o sample from p(x 0: y 0: ). Therefore, one usually resors o drawing from he so called imporance densiy q(x 0: y 0: ), wih he suppor including he one of he sae poserior. I is assumed he sampling from q(x 0: y 0: ) is relaively easy and inexpensive. To sar wih, noice ha we can hen express (3.1.1) using q(x 0: y 0: ) in he following way f = f (x 0: ) p(x 0: y 0: ) q(x 0: y 0: ) q(x 0: y 0: )dx 0: [ = E q f (X 0: ) p(x ] 0: Y 0: ) q(x 0: Y 0: ) [ = E q f (X 0: ) W ], (3.2.1) where E q sands for expecaion wih respec o densiy q and W (x 0: ) = p(x 0: y 0: ) q(x 0: y 0: ) (3.2.2) is known as he imporance weigh funcion. Noice, ha since he imporance weigh funcion is defined as he likelihood raio, i is he Radon-Nikodým derivaive of he rue disribuion p( ) wih respec o he imporance disribuion q( ). Generally, i depends on x 0: and y 0:, however, in he remaining par of he work we skip he argumens for noaional convenience. Hence, wih some abuse of noaion, we will use he same symbols o denoe he weigh funcions as funcions of sochasic processes and of real vecors. Since he join densiy facorises as follows one can express (3.2.2) as wih p(x 0:, y 0: ) = p(x 0: y 0: )p(y 0: ), W = 1 p(x 0:, y 0: ) p(y 0: ) q(x 0: y 0: ) = 1 p(y 0: ) w, (3.2.3) w = p(x 0:, y 0: ) q(x 0: y 0: ) (3.2.4) so ha W is w correced for he (uncondiional) observaion densiy. Then, (3.2.1) becomes Noice, ha by aking f 1 one can obain from (3.2.5) ha f = 1 p(y 0: ) E q [f (X 0: ) w ]. (3.2.5) E q [ w ] = p(y 0: ), (3.2.6) 16
19 which implies ha (3.2.5) can be rewrien as follows f = E q [f (X 0: ) w ]. (3.2.7) E q [ w ] Nex, we can esimae (3.2.7) using a random sample x (1) 0:,..., x(n) 0: drawn from he imporance disribuion q(x 0: y 0: ). The required esimae has he form where w (i) ˆf = N 1 N f (x (i) 0: ) w(i) N 1 N w(i) = N (3.2.8) f (x (i) 0: )w(i), (3.2.9) = p(x(i) 0:, y 0:) q(x (i) 0: y 0:), w(i) = w (i) N w(i) so ha w (i) are he normalised imporance weighs. Noice ha he normalisaion jusifies focusing on he correced imporance weighs w (i) insead of he original ones, W (i), defined in (3.2.3). Since he former are obained from he laer by correcing by he erm 1/p(y 0: ), which is he same among all he paricles, one would obain ha W (i) = w (i), i, wih W (i) =, (i) W / N j=1 W (j). Hence, we obained a normalised Mone Carlo esimae ˆf, which, as a raio of wo esimaes, is biased. Indeed, in Appendix B we show ha E q ˆf = f 1 N Cov q [ W, f(x 0: ) W ] + f [ ] N Var q W. (3.2.10) which means he bias of he IS esimaor is of order 1/N. Neverheless, i is srongly consisen, as by he Srong Law of Large Numbers in (3.2.8) he nominaor converges o f, while he denominaor converges o 1, boh almos surely. One can inerpre he esimae ˆf as an inegral wih respec o he empirical measure ˆP (dx 0: y 0: ) = N w (i) δ (i) x (dx 0: ) (3.2.11) 0: of he funcion of ineres f, given by ˆf = f (x 0: ) ˆP (x 0: y 0: ). Then, he empirical measure resuling from he above inegraion mehod can be used o approximae he poserior disribuion p(x 0: y 0: ). This is indeed he key idea behind paricle filering, which amouns o represening he poserior disribuion by a weighed average of randomly chosen paricles (samples). Noice, however, ha o compue he esimae (3.2.9), one requires o draw new samples of x (i) 0: from q(x 0: y 0, ) a each poin in ime, so each ime new daa y becomes available. This means ha for long ime series he compuaional complexiy of his endeavour becomes exremely high. Therefore, for on-line inference more appropriae mehods have been designed, which we will discuss in he nex secion. 17
20 3.3 Sequenial imporance sampling To make he imporance sampling algorihm suiable for on-line inference problems one needs o be able o modify his mehod in such a way ha i becomes possible o compue he esimae of he poserior disribuion wihou modifying he pas simulaed rajecories. Then, each ime new informaion y becomes available, one needs only o simulae one se of curren paricles x (i), i = 1,..., N, and no a se of he whole sequences of hem, x (i) 0:. Hence, a each ime, he exising samples are simply augmened wih he new samples yielding he updaed samples Recursion for he imporance densiy To allow for his, puing of some resricions on he imporance densiy are required. We suppose ha a each, he imporance densiy q(x 0: y 0: ) facorises in he following way q(x 0: y 0: ) = q(x 0: 1 y 0: 1 )q(x x 0: 1, y 0: ) (3.3.1) = q(x 0 ) q(x k x 0:k 1, y 0:k ). k=1 Hence, he poserior is compued by updaing using he las erm in (3.3.1) of he previously compued densiy q(x 0: 1 y 0: 1 ), which plays a role of a prior densiy. As poined ou in Durbin and Koopman (2012), he above assumpion is no as demanding as i may seem a firs glance. Noice ha one can wrie wihou any addiional assumpions q(x 0: y 0: ) = q(x 0:, y 1: ) q(y 0: ) Then, o obain (3.3.1) one only needs o allow for = q(x x 0: 1, y 0: )q(x 0: 1, y 0: ) q(y 0: ) = q(x x 0: 1, y 0: )q(x 0: 1 y 0: )q(y 0: ) q(y 0: ) = q(x 0: 1 y 0: )q(x x 0: 1, y 0: ). q(x 0: 1 y 0: 1 ) q(x 0: 1 y 0: ), which means ha augmening of he se of condiional variables (i.e. y 0: 1 ) in he (already compued) imporance densiy q(x 0: 1 y 0: 1 ) by y shall no play a role. Taking ino accoun ha x 0: 1 has already been generaed based on he pas observaions y 0: 1, and ha he new value of y is independen of everyhing bu he curren sae x (so is independen of simulaed sequence x 0: 1 ), he above assumpion does no seem paricularly resricive. From (3.3.1) follows ha for he i-h paricle, i = 1,..., N, he imporance densiy updaing equaion akes he form q(x (i) 0: y 0:) = q(x (i) which is he fundamenal paricle filering recursion. 0: 1 y 0: 1)q(x (i) x (i) 0: 1, y 0:), 18
21 3.3.2 Recursion for he imporance weighs Plugging (3.3.1) ino (3.2.4), one obaines ha he imporance weighs become w = p(x 0:, y 0: ) q(x 0: y 0: ) = p(x, y x 0: 1, y 0: 1 )p(x 0: 1, y 0: 1 ) q(x x 0: 1, y 0: )q(x 0: 1 y 0: 1 ) = p(x, y x 0: 1, y 0: 1 ) p(x 0: 1, y 0: 1 ) q(x x 0: 1, y 0: ) q(x 0: 1 y 0: 1 ) = p(x, y x 0: 1, y 0: 1 ) w 1 q(x x 0: 1, y 0: ) MC = CI p(x x 1 )p(y x ) q(x x 0: 1, y 0: ) w 1, where by MC and CI we mean ha by he Markov propery of he sae process and condiional independence of he observaion process one can wrie p(x, y x 0: 1, y 0: 1 ) = p(y x )p(x x 1 ). For he i-h paricle, i = 1,..., N, he imporance weigh updaing equaion akes he form w (i) wih is normalised counerpar given by In (3.3.2), he erm = p(x(i) x (i) 1 )p(y x (i) ) q(x (i) x (i) 0: 1, y 0:) w (i) w (i) = N j=1 w(j) p(x (i) x (i) 1 )p(y x (i) ) q(x (i) x (i) 0: 1, y 0:) w (i) 1 (3.3.2) is called he incremenal weigh and i indicaes how well a cerain augmened paricle predics he nex observaion. For furher reference, noice ha since for he normalised weighs we have we ge he following recursion SIS algorihm W (i) = 1 p(y y 0: 1 ) W (i) = 1 p(y 0: ) w(i), p(x (i) x (i) 1 )p(y x (i) ) q(x (i) x (i) 0: 1, y 0:) W (i) 1. (3.3.3) A formal specificaion of he SIS procedure is given by Algorihm 1. The compuaional complexiy o generae N paricles approximaing p(x 0:T, y 0:T ) is O(N(T + 1)), where, for noaional convenience, i is assumed ha one is ineresed in performing of he compuaions up o a fixed ime T. 19
22 Algorihm 1 SIS algorihm Sep 1: iniialisaion for i := 1,..., N do Sample x (i) 0 q(x 0 ). end for Sep 2: imporance sampling for := 1,..., T do for i := 1,..., N do Sample x (i) q(x x (i) ( 1 ), y 1:). Se x (i) 0: := x (i) 0: 1, x(i). Compue he corresponding imporance weighs w (i) end for Normalise he imporance weighs Approximae he filering densiy = p(x(i) x (i) 1 )p(y x (i) ) q(x (i) w (i) w (i) = N j=1 w(j) ˆp(x y 0: ) = N x (i) 0: 1, y 0:) w (i) δ (i) x (x ). w (i) 1. Compue he required esimae end for ˆf = N f(x (i) )w (i). 3.4 Degeneracy and resampling The clever SIS weigh recursion formula (3.3.2) unforunaely leads o he degeneracy problem, i.e. he problem of he disribuion of he weighs becoming highly skewed when increases. Wih ime here remain only few paricles wih non-negligible weighs, so ha mos of he probabiliy mass is concenraed on hem, while he oher paricles are of almos zero weigh. In consequence, he SIS algorihm fails o represen adequaely he poserior disribuions of ineres. In fac, his problem is ineviable as he uncondiional variance of he imporance weighs is non-decreasing over ime, as originally shown by Kong e al. (1994). Before presening heir key heorem, le us recall some basic properies of maringale sequences. Lemma (Non-decreasing variance of a maringale sequence). Le (Ω, F, P) be a probabiliy space, le {M n } n 1 be a maringale sequence on his space wih respec o he filraion {F n } of F and le { n } be he maringale difference sequence for {M n }, i.e. n = M n M n 1. 20
23 Then for n 0 EM n = EM 0. Moreover, if EMn 2 < for some n 1, hen for j n he random variables j are uncorrelaed and square-inegrable implying n EMn 2 = EM0 2 + E 2 j. Proof. The firs par follows immediaely from he maringale naure of M n and he Law of Ieraed Expecaion, as we have For he second par, noice ha for n 1 j=1 E [M n F 0 ] = EM 0, E [E [M n F 0 ]] = E [EM 0 ], EM n = EM 0. E n = E [M n M n 1 ] = EM n EM n 1 = 0. Nex, wihou loss of generaliy, suppose ha M 0 = 0. Since we assumed ha he random variable M n is square-inegrable, hen for k n also EMk 2 <, by he Jensen inequaliy for condiional expecaion and X k = E [M n F k ]. Thus, for k n also E 2 k <, as i is a difference of wo square-inegrable random variables, which, by he Cauchy-Schwarz inequaliy, yields ha for k m n also E k m <. Since k is hen F k -measurable, we have E k m+1 = E [E k m+1 F k ] = E k [E m+1 F k ] = E k 0 = 0. Because we can decompose M n as M n = n j=1 j, i.e. ino a sum of uncorrelaed random variables, we can calculae he variance of M n as if i was a sum of mean-zero dependen random variables. Then, we 21
24 obain Var [M n ] = EMn 2 n = E j=1 j j=1 k=1 2 n n = E j k n n = E j k = = = j=1 k=1 n n n E 2 j + 2 E j k j=1 n E 2 j + 0 j=1 n E 2 j, j=1 j=1 k>j which complees he proof. The above lemma allows us o argue ha he variance of he imporance weighs is non-decreasing in ime by simply showing ha hey form a maringale sequence. This was indeed he key idea behind he heorem shown in Kong e al. (1994), which we below exend o he analysed case of he imporance densiy given by (3.3.1). Theorem (Kong-Liu-Wong). The imporance weigh w (i) is a maringale sequence in wih boh, he sample x i 0: and he observaions y 0: reaed as random. This implies ha is variance is an increasing funcion of. Proof. Consider he i-paricle x (i) 0: 1 and le { } F 1 i = σ x (i) 0: 1, y 0: 1, be a σ-algebra generaed by all he observaions and his paricle, up o ime 1. Recall ha he recursion formula (3.3.3) for he correced weighs (3.2.3) reads W (i) = 1 p(y y 0: 1 ) p(x (i) x (i) 1 )p(y x (i) ) q(x (i) x (i) 0: 1, y 0:) W (i) 1, which is due o he assumed form of he imporance funcion, which facorises according o (3.3.1) q(x (i) 0: y 0:) = q(x (i) 0: 1 y 0: 1)q(x (i) x (i) 0: 1, y 0:). Moreover, recall ha he formula for he poserior has he following form p(x (i) 0: y 0:) = p(x (i) 0: 1 y 0: 1) p(x(i) x (i) 1 )p(y x (i) p(y y 0: 1 ) Now, le us rea boh, y and x (i), as realizaions of random variables, wih x (i) ). q(x x (i) 0: 1, y 0:). 22
25 Then, he join condiional densiy is given by p(x (i), y x (i) 0: 1, y 0: 1) = q(x x (i) 0: 1, y 0:)p(y x (i) 0:k 1, y 0:k 1). (3.4.1) Noice ha he elemens x (i) 0, x(i) 1,..., x(i) 1 of x(i) 0: 1 were generaed based on y 0: 1, so one can rea y as condiionally independen of x (i) 0: 1. This allows us o rewrie (3.4.1) as p(x (i), y x (i) 0: 1, y 0: 1) = q(x x (i) 0: 1, y 0:)p(y y 0:k 1 ). (3.4.2) Nex, consider he condiional expecaion of W (i), given x (i) 0: 1, y 0: 1, wih x (i) random. By he weigh recursion formula we have [ E W (i) F i 1 ] = W (i) = W (i) 1 = W (i) 1 = W (i) 1, p(x (i), y x (i) 1 p(y y 0: 1 ) p(x (i) x (i) 0: 1, y 0: 1)dx (i) dy p(x (i) x (i) 1 )p(y x (i) 1 )p(y x (i) ) q(x (i) x (i) 0: 1, y 0:) )dx (i) dy showing ha indeed, he correced, unnormalised imporance weigh W (i) i.e. he uncondiional variance of W (i) [ ] [ [ ]] [ Var W (i) 1 = E Var W (i) F 1 Var and y reaed as q(x x (i) 0: 1, y 0:)p(y y 0:k 1 )dx (i) dy W (i) ], is a maringale in. Hence, is non-decreasing in ime. This complees he proof. For compleeness, noice ha by he variance decomposiion formula, we have for he maringale W (i) [ Var W (i) ] [ [ ]] [ [ ]] = E Var W (i) y + Var E W (i) y,, Finally, since we obain [ Var [ ] E W (i) y = 1, y, W (i) ] [ [ ]] = E Var W (i) y Effecive sample size As poined ou by Kong e al. (1994), since he SIS is a form of IS, i.e. of an MC algorihm, one can measure he efficiency of he sequenial approach by comparing i wih a direc sampling from a heoreical disribuion of ineres. As in Subsecion 3.2, consider an arbirary measurable funcion f : X R, for which we are ineresed in esimaion of he mean f = E p (f(x )). Moreover, le X (1),..., X (N) iid q(x x 0: 1, y 0: ) and Y (1),..., Y (N) iid p(x x 0: 1, y 0: ) be wo independen sequences of i.i.d. random variables, boh of lengh N. The esimaors for f delivered by boh echniques are respecively given by ˆf IS = N 1 N ˆf MC = N 1 w(i) N 1 N N (X (j) )f(x (j) w(i) f(y (j) ). (X (j) ) ), 23
26 The efficiency of he SIS esimaor (relaively o he MC one) is given by he raio [ ] Var ˆf MC [ ], (3.4.3) Var ˆf IS which, following Kong e al. (1994) and Liu (1996), can be used o define he effecive sample size as N ESS = N [ ] Var ˆf MC [ ] N. (3.4.4) Var ˆf IS I can be inerpreed as follows: an inference based on N weighed samples and he SIS esimaor is approximaely equivalen o an inference based on N ESS i.i.d. samples from he disribuion of ineres and he crude MC esimaor. In oher words, under he MC seup, one requires N ESS N samples o obain an esimaor wih he same precision as using N samples and he SIS esimaor. There are wo obsacles relaed o he way N ESS in (3.4.4) is defined. Firs, i depends on he funcion of ineres f; second generally, i canno be compued exacly, as usually he arge disribuion is known only up o normalizaion. In Appendix B we presen he derivaion of he following approximaion o (3.4.4), which is independen of f, originally inroduced by Kong e al. (1994). [ ] Var q ˆf MC [ ] Var p ˆf IC Var q [ W ], (3.4.5) Sill, i is usually difficul, or even impossible, o exacly compue (3.4.5). Thus, o measure he efficiency of SIS echnique one resors o approximaing (3.4.5) by ˆN ESS = N i 1 ( ) w i 2, (3.4.6) where w i is he normalized imporance weigh, for a SIS sample x (1),..., x (N). I can be obained as follows N N ESS = [ ] 1 + Var q W (X ) ( ) = = ( ) = = N E q [ W (X ) N N 1 N N ] 2 N 1 C 2 N ( W i ) 2 NC 1 N 1 C N 1 N ( W i ) 2 1 N ( w i ) 2. ( ) W i 2 C ( W i ) 2 24
27 where in ( ) we use he fac ha E q [ W ] = 1, in ( ) we pu C := N W i and he las sep is due o he normalised w i being equivalen o he normalized W i. Noice, ha by consrucion ˆN ESS is beween 1 and N. The laer case corresponds o a siuaion when he imporance weighs are evenly disribued, he former o an insance of severe degeneracy, wih only one acive paricle. Hence, he above approximaion o he effecive sample size consiues a suiable measure of degeneracy of he SIS algorihm. If ˆNESS N, hen he efficiency of he SIS echnique is high, since hen he SIS sample size is almos equal o N i.i.d. MC samples SIR algorihm I follows from he Kong-Liu-Wong heorem ha he degeneracy of he SIS algorihm is unavoidable. In consequence, a large compuaional effor is needed o updae paricles wih almos zero conribuion o he approximaion (3.2.9). Inuiively, i mus be waseful o keep in he recursion insignificanly conribuing paricles. Hence, o (parially) solve his problem he idea of resampling was inroduced by Gordon e al. (1993). The SIS wih resampling (SIR) amouns o including an addiional sep in he algorihms, a which rajecories wih low normalised imporance weighs are eliminaed, so ha one can concenrae on rajecories wih considerable weighs. { The heoreical foundaion for SIR is as follows. Le x (i) } N, w (i) be a weighed sample obained a. As i has he -h ieraion of he Sep 2 of Algorihm 1, wih he corresponding normalised weighs w (i) already been saed, he resuling empirical measure (3.2.11) is given by ˆP (dx 0: y 0: ) = ˆp (x 0: y 0: ) = N w (i) δ (i) x (x 0: ). 0: By he law of large numbers, an inegral of an arbirary measurable funcion f wih respec o ˆp ( ) converges o is inegral wih respec o he disribuion of ineres p ( ), i.e. ˆf = f (x 0: )ˆp (x 0: y 0: )dx 0: = N f (x (i) 0: )w(i) N f (x 0: )ˆp (x 0: y 0: )dx 0: = f. (3.4.7) Now, consider a sample of size Ñ drawn from ˆp (x 0: y 0: ) wih replacemen, i.e. P( x (j) 0: = x(i) 0: ) = w(i), j = 1,..., Ñ, where he new paricles have equal weighs, w(j) = 1. Once again, by he law of large Ñ numbers, 1 Ñ Ñ j=1 f ( x (j) 0: ) Ñ N f (x (i) 0: )w(i), so ha he inegral of f wih respec o he new, resampled empirical measure consiues a good approximaion o he original empirical measure ˆp ( ), provided we resample sufficienly many paricles. This basic resampling scheme is known as mulinomial sampling. Resampling helps o increase he number of acive paricles, however, i also generaes wo imporan problems. The firs is he sample impoverishmen, consising in decreasing diversiy wihin he paricles se. Because of replacemen and he fac ha resampling is applied o he whole paricle rajecory x (i) O:, and no only he mos recen value x (i), paricles wih high imporance weighs are likely o be seleced several ime. On he oher hand, paricles wih negligible weighs mos likely will no be chosen a all, which means he ha heir hisory will be eliminaed. Hence, he curren sample becomes less versaile and consequenly less and less able o correcly represen he arge disribuion. In he exreme case, one may ry o esimae i wih a se of paricles wih a single common ancesor, which obviously gives a poor qualiy approximaion. 25
28 The second rouble is inroducion of dependence beween paricle rajecories, which brings in unnecessary Mone Carlo variaion ino he esimae ˆf in (3.4.7) a he curren ime sep. As shown in Chopin (2004), he esimaor compued before resampling has a lower variance han he one compued afer ha sep, hence is a preferred o perform he esimaion based on he original sample. I is worh noing ha o decrease he Mone Carlo variance, oher resampling schemes were designed, for insance sraified sampling (Kiagawa, 1996) or residual resampling (Liu and Chen, 1998). Finally, because of his addiional variaion, resampling a each ime sep is derimenal, which means i should be performed only when necessary. To deec a presence of such a necessiy, he effecive sample size esimae (3.4.6) can be used. Then, he resampling sep is performed only when he effecive sample size ˆN ESS falls below a cerain hreshold N res, which usually is se o N 2 (cf. Douce and Johansen, 2009). The formal descripion of he sandard SIR algorihm is presened in Algorihm 2. 26
29 Algorihm 2 SIR algorihm Sep 1: iniialisaion for i := 1 o N do Sample x (i) 0 q(x 0 ). end for for := 1 o T do Sep 2: imporance sampling for i := 1 o N do Sample x (i) q(x x (i) ( 1 ), y 1:). Se x (i) 0: := x (i) 0: 1, x(i). Compue he corresponding imporance weighs end for Normalise he imporance weighs Compue he effecive sample size Approximae he filering densiy Compue he required esimae Sep 3: selecion if ˆNESS < N hres hen w (i) = p( x(i) x (i) 1 )p(y x (i) ) w (i) = ˆN ESS = ˆp(x y 0: ) = ˆf = q( x (i) w (i) N j=1 w(j) ( N N N { } N, from x (i) wih corresponding prob- { Resample wih replacemen N paricles, { } N abiliies w (i). ( ) Se x (i) 0: := x (i) 0: 1, x(i). Se w (i) := 1 N. end if end for x (i) 0: 1, y 0:) w (i)2 w (i). ) 1. (i)(x δ x ). f( x (i) )w (i). x (i) } N w (i) 1. 27
30 3.5 Selecion of he imporance funcion The choice of he imporance densiy q(x x 0: 1, y 0: ) is of crucial imporance for he performance of he SIS algorihm. As poined ou by Douce e al. (2000), an appropriae choice of he imporance funcion may help o limi he degeneracy problem. This appropriaeness shall be primarily seen in erms of weighs variance minimisaion, given he simulaed rajecory and he observaions, as hen such an imporance densiy gives roughly he same weigh o all paricles. Moreover, he imporance funcion should in general have relaively heavy ails o be robus for ouliers Opimal imporance funcion The following proposiion, due o Douce e al. (2000), characerises he opimal imporance funcion. Proposiion The imporance funcion which minimises he variance of he imporance weigh W (i), condiional upon x (i) 0: 1 and y 0:, is given by i.e. is equal o he arge disribuion. q(x x 0: 1, y 0: ) = p(x x (i) 1, y ), (3.5.1) Proof. Using he noaion inroduced before, we obain ha he variance of he imporance weigh under q(x x 0: 1, y 0: ) given by (3.5.1) is equal o Var q(x x 0: 1,y 0:) [ W (i) which complees he proof. ] = (W (i) 1 )2 ( ) 2 p(y x )p(x x (i) 1 ) dx p 2 (y x (i) q(x x 0: 1, y 0: ) 1 ) ( ) 2 = (W (i) p(y x )p(x x (i) 1 ) 1 )2 p(x x (i) 1, y dx p 2 (y x (i) 1 ) ) ( ) 2 = (W (i) p(y x )p(x x (i) 1 )2 p(y x (i) 1 ) 1 ) p(y x, x (i) 1 )p(x x (i) 1 )dx p 2 (y x (i) 1 ) [ CI p = (W (i) 1 )2 p(y x (i) 2 1 ) (y x )p 2 (x x (i) 1 ) ] p(y x )p(x x (i) 1 ) dx p 2 (y x (i) 1 ) [ ] = (W (i) 1 )2 p(y x (i) 1 ) p(y x )p(x x (i) 1 )dx p 2 (y x (i) 1 ) = (W (i) 1 )2 [ p 2 (y x (i) 1 ) p2 (y x (i) 1 ) ] = 0, Noice, ha wih he imporance disribuion defined as in (3.5.1), he SIS imporance weigh updaing 28
31 equaion (3.3.2) becomes w (i) = p(x(i) x (i) 1 )p(y x (i) ) p(x x (i) 1, y w (i) 1 ) = p(y x (i) 1 ) CI = p(y x (i) 1 ) w(i) 1. p(x (i) x (i) 1 )p(y x (i) ) p(x (i) x (i) 1 )p(y x (i), x (i) 1 ) w(i) The las formula looks simple, here are, however, wo serious limiaions regarding using of he opimal imporance funcion. Firs, i depends on he abiliy of drawing direcly from p(x x (i) 1, y ), he lack of which was he main reason for resoring o he imporance sampling in he firs place. Second, i requires evaluaing of he following inegral p(y x (i) 1 ) = 1, p(y x )p(x x (i) 1 )dx, (3.5.2) which in general has no analyic form. For his reason, one ofen resors o approximaive echniques, as we will discuss in he nex Subsecion. Gaussian model wih nonlinear ransiion equaion However, as poined ou in Douce e al. (2000), for an imporan class of he Gaussian sae space models wih nonlinear ransiion equaion and linear observaion equaion, analyic evaluaion of (3.5.2) is possible. Consider he following model X = f(x 1 ) + V, Y = CX + W, V i.i.d. N (0, Σ V ), W i.i.d. N (0, Σ W ), (3.5.3) where f : R nx R nx is a nonlinear funcion, C R ny R nx is an observaion marix and V, W are muually independen. Define Σ 1 = Σ 1 V + CT Σ 1 W C, (3.5.4) µ = Σ ( Σ 1 V f(x 1) + C T Σ 1 W Y ). (3.5.5) Proposiion The opimal imporance disribuion for he model (3.5.3) is given by so ha he opimal weigh updae (3.5.2) becomes q(x x 1, y ) = N (µ, Σ), p(y x (i) 1 ( ) exp 1 2 (y Cf(x 1 )) T ( ) CΣ V C T ) 1 + Σ W (y Cf(x 1 )), where Σ and µ are given by (3.5.4) and (3.5.5), respecively. Proof. Firs, model (3.5.3) implies ha he condiional disribuion of Y given X 1 can be simply derived as follows Y = CX + W = Cf(X 1 ) + CV + W, Y X 1 N (Cf(X 1 ), CΣ V C T + Σ W ), 29
32 which delivers he weigh updae formula. Second, noice ha model (3.5.3) is Gaussian, so he join disribuion of X and Y is Gaussian. In paricular, condiional on X 1, we have ([ ] [ f(x 1 ) Σ V X, Y X 1 N, Cf(X 1 ) CΣ V Σ V C T CΣ V C T + Σ W Then, by applying he sandard formula for he condiional disribuion of mulivariae normal random variable, we obain wih X Y, X 1 N ( µ, Σ), µ = f(x 1 ) + Σ V C T (CΣ V C T + Σ W ) 1 (Y Cf(X 1 )), (3.5.6) Σ = Σ V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V. (3.5.7) ]). Finally, we need o show ha (3.5.6) and (3.5.7) correspond o (3.5.5) and (3.5.4), respecively. esablish he equivalence of he variances, we will check wheher ΣΣ 1 = I. We have To ΣΣ 1 = [ Σ V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V ] [ Σ 1 V =Σ V Σ 1 V + CT Σ 1 W C] + Σ V C T Σ 1 W C Σ V C T (CΣ V C T + Σ W ) 1 CΣ V Σ 1 V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V C T Σ 1 W C =I + Σ V C T ( Σ 1 W ( =I + Σ V C T (CΣ V C T + Σ W ) 1 (CΣ V C T + Σ W )Σ 1 W ) (CΣ V C T + Σ W ) 1 CΣ V C T Σ 1 W C ( =I + Σ V C T (CΣ V C T + Σ W ) 1 (CΣ V C T + Σ W )Σ 1 =I + Σ V C T (CΣ V C T + Σ W ) 1 =I, (CΣ V C T + Σ W ) 1 (CΣ V C T + Σ W ) 1 CΣ V C T Σ 1 W W ) C (CΣ V C T + Σ W ) 1 Σ 1 W Σ W ) Σ 1 W Σ W CΣ V C T Σ 1 W ( CΣ V C T Σ 1 W + Σ W Σ 1 W Σ 1 W Σ W CΣ V C T Σ 1 W which shows ha (3.5.4) and (3.5.7) characerise he same variance marix. As far as he means are concerned, noice ha from (3.5.5) and (3.5.4) we have µ = Σ ( Σ 1 V f(x 1) + C T Σ 1 W Y ), = ΣΣ 1 V f(x 1) + ΣC T Σ 1 W Y, µ = f(x 1 ) + Σ V C T (CΣ V C T + Σ W ) 1 (Y Cf(X 1 )) ( ) = I CΣ V (CΣ V C T + Σ W ) 1 C f(x 1 ) + Σ V C T (CΣ V C T + Σ W ) 1 Y. Hence, we need o show ha C ) C ΣΣ 1 V = I CΣ V (CΣ V C T + Σ W ) 1 C, (3.5.8) ΣC T Σ 1 W = Σ V C T (CΣ V C T + Σ W ) 1. (3.5.9) 30
33 Since Σ 1 = Σ 1 V + CT Σ 1 W C, Σ = Σ V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V, Σ = Σ, we have ΣΣ 1 V = ( Σ V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V ) Σ 1 V = I Σ V C T (CΣ V C T + Σ W ) 1 C, which shows (3.5.8). For (3.5.9) we can proceed similarly and wrie compleing he proof. ( ) ΣC T Σ 1 W = Σ V Σ V C T (CΣ V C T + Σ W ) 1 CΣ V C T Σ 1 W = Σ V C T Σ 1 W Σ V C T (CΣ V C T + Σ W ) 1 CΣ V C T Σ 1 W = Σ V C T (CΣ V C T + Σ W ) 1( (CΣ V C T + Σ W ) CΣ V C T ) Σ 1 W = Σ V C T (CΣ V C T + Σ W ) 1 Σ W Σ 1 W = Σ V C T (CΣ V C T + Σ W ) 1, Local linearisaion Following Douce e al. (2000), one can selec as he imporance funcion q(x x 0: 1, y 0: ) a parameric disribuion q(x θ(x 0: 1, y 0: )), where θ is a finie-dimensional parameer, θ Θ R n θ deermined by x 1 and y via a deerminisic mapping θ : R nx R ny Θ. The cied auhors proposed wo sraegies consising in approximaion of he opimal imporance funcion using a local linearisaion, which resuls in a Gaussian imporance funcion wih parameers dependen on he simulaed rajecory. Below, we inroduce boh echniques, as we will rely on hem laer on, in he applicaion par (Chaper 4). Local linearisaion of he sae space model When he model under consideraion is nonlinear ye Gaussian, one can locally linearise he model iself, i.e. eiher he observaion equaion or he ransiion equaion. This approach is hus concepually relaed he Exended Kalman Filer, which is based on linearisaion of he ransiion and observaion equaions along he rajecories. However, compared o he laer, he curren mehod has he advanage of yielding of he imporance disribuion which is asympoically convergen o he opimal one (under he sandard assumpions on he imporance funcions). Consider he following model X = f(x 1 ) + V, Y = g(x ) + W, V i.i.d. N (0, Σ V ), W i.i.d. N (0, Σ W ), where f : R nx R nx, g : R nx R ny are differeniable and V, W are muually independen. Performing of he firs order approximaion of he observaion equaion, i.e. he linearisaion of g(x) in f(x 1 ) yields Y = g(x ) + W g(f(x 1 )) + g(x) x x=f(x 1) (X f(x 1 )) + W. (3.5.10) 31
34 Thus, X = f(x 1 ) + V, Ỹ = g(x) x x=f(x 1) X + W, Ỹ = Y g(f(x 1 )) g(x) x f(x 1 ) x=f(x 1) V i.i.d. N (0, Σ V ), W i.i.d. N (0, Σ W ), defines a sysem driven by he same ransiion equaion as he one in he model under consideraion, ye where he observaion equaion is linear Gaussian, as in he special class of models discussed in he previous subsecion. Thus, Proposiion applies if one akes as he ransiion marix C he ransiion marix of he linearised model, given by he Jacobian of g(x) evaluaed a x = f(x 1 ), i.e. g(x) x x=f(x 1) funcion is where Σ = Σ 1 V + µ = Σ [ and as he observaion Y, he ransformed observaion Ỹ. The resuling imporance g(x) x Σ 1 V f(x 1) + x=f(x 1) [ g(x) x ] T Σ 1 W q(x x 1, y ) = N (µ, Σ ), g(x) x, x=f(x 1) ] T [ Σ 1 W Y g(f(x 1 )) g(x) x x=f(x 1) )] f(x 1. x=f(x 1) Local linearisaion of he opimal imporance funcion Assume ha l(x ) log p(x x 1, y ) is wice differeniable wih respec o x on R nx and define l (x) l(x ) x l (x) 2 l(x ) x x T Performing of he second order Taylor expansion around an arbirary, hough deerminisically deermined by x 1 and y, poin x resuls in x=x, x=x. l(x ) l(x) + (l (x)) T (x x) (x x ) T l (x)(x x), Nex, suppose l (x) is negaive definie (which is he case when l(x ) is concave) and pu Σ(x) (l (x)) 1, µ(x) Σ(x)l (x). This yields (l (x)) T (x x) (x x ) T l (x)(x x) = C 1 2 (x x µ(x)) T Σ 1 (x)(x x µ(x)), where C is a consan, which suggess approximaing of he opimal imporance funcion wih he following Gaussian disribuion q(x x 1, y ) = N (µ(x) + x, Σ(x)). In case of he arge p(x x 1, y ) being unimodal, his procedure boils down o aking as he expansion 32
35 poin x he mode of p(x x 1, y ), which leads o µ(x) = The boosrap filer An imporan class of SIR algorihms arises when he imporance densiy akes he form of he prior disribuion q(x x 1, y ) = p(x x 1 ), so ha he informaion provided by y is negleced. Then, he imporance weighs simplify o w (i) = p(y x (i) ) w (i) 1. Moreover, in his class of algorihms resampling is usually performed a each sep, i.e. N hres = N. Hence,also he weighs are rese o 1/N in each ieraion, which leads o an even simpler weigh specificaion w (i) = p(y x (i) ). (3.5.11) This paricular case of SIR is called he boosrap filer and for fuure reference is given in Algorihm 3. In fac he firs paricle filer inroduced in Gordon e al. (1993) was he boosrap filer. The advanage of his mehod is clearly is simpliciy, ye i suffers from sensiiviy o ouliers. Moreover, simulaions using he prior imporance funcion are inefficien, as he informaion on he sae space brough by he observaions is discarded. 33
36 Algorihm 3 Boosrap filer Sep 1: iniialisaion for i := 1 o N do Sample x (i) 0 q(x 0 ). end for for := 1 o T do Sep 2: imporance sampling for i := 1 o N do Sample x (i) p(x x (i) ( 1 ) ). Se x (i) 0: := x (i) 0: 1, x(i). Compue he corresponding imporance weighs end for Normalise he imporance weighs Compue he effecive sample size Approximae he filering densiy Compue he required esimae w (i) = ˆN ESS = ˆp(x y 0: ) = ˆf = w (i) = p(y x (i) ). w (i) N j=1 w(j) ( N N { } N, from x (i) wih corresponding proba- Sep 3: resampling { Resample wih replacemen N paricles, { } N biliies w (i). ( ) Se x (i) 0: := x (i) 0: 1, x(i). Se w (i) := 1 N. end for N w (i)2 w (i). ) 1. (i)(x δ x ). f( x (i) )w i). ( x (i) } N 34
37 Chaper 4 Convergence In Secion 3.4 we have shown he necessiy of resampling due o he unavoidable weigh degeneracy problem. Thus, any paricle filer consiss of wo complimenary seps: he imporance sampling sep, and he resampling sep. However, repeaed resampling leads o noiceable complicaions in he reamen of he heoreical properies of paricle filers. Indeed, as poined ou in Crisan and Douce (2002), he key difference beween paricle filering mehods and classical MC mehods is he sample naure. The laer are based on he assumpion ha he samples are i.i.d., while in he former approach, he samples, i.e. he paricles, inerac, which means hey are no independen. Thus, he classical limi heorems based on independen samples are no applicable. This gives rise o posing numerous quesions, mosly relaed o he limiing properies of paricle filers. Foremos, one is ineresed wheher paricle filers converge asympoically, wih N, and if so, in wha sense. Furhermore, i is worh invesigaing wheher sandard MC convergence raes apply and wheher he error accumulaes over ime. Answering all hese quesions is sill a opic of he vas ongoing research and definiely is beyond he scope of his hesis. Therefore, we will focus only on he mos crucial problem, i.e. asympoic convergence of paricle filers. Because he oupu of any SMC algorihm is an approximaion o he poserior disribuion given by a discree random measure (linear combinaion of Dirac measures), i is necessary o define in wha way random measures may converge o anoher measure. This is wha we deal wih in Secion 4.2. Before ha, however, we resae he opimal filering problem in a probabilisic parlance, more suiable for heoreical analysis (as i has already been indicaed a he beginning of Chaper 2). Finally, we presen wo resuls on convergence, which are mainly aken form Crisan (2001) and Crisan (2014). 4.1 The filering problem revisied In his secion we rephrase he filering problem from Subsecion 2.2.2, and he recursion formulae presened here and Subsecion 3.3 in a more compac and precise way, more suiable for convergence analysis Basic noaion Recall ha in we have specified he filering problem as compuing of he condiional disribuion of he signal process X given he σ-algebra generaed by he observaion process Y 1, from ime 0 o he 1 Which, by definiion is equivalen o he his condiional disribuion given Y 0:, cf. Billingsley (1995). 35
38 curren ime. Equivalenly, one can sae i as compuing he random probabiliy measure p such ha p (A) = P(X A σ(y 0: )), A B(R nx ), p f = E[f(X ) σ(y 0: )], f B(R nx ). I is worh specifying he difference beween random and deerminisic probabiliy measures arising in he curren seup. Since he soluion o he filering problem is a condiional disribuion of he sae process, given he σ-algebra generaed by he observaion process, up o ime, i is clearly a random variable. More precisely, i is a random measure. However, if one reas he observaions as given, i.e. considers an arbirary bu fixed realisaion y 0:T of he observaion process Y 0:T, where T < is a large ime horizon, hen he filering problem boils down o finding of he condiional probabiliy given by p y0: (A) = P(X A Y 0: = y 0: ), A B(R nx ), p y0: f = E[f(X ) Y 0: = y 0: ], f B(R nx ). which is a deerminisic probabiliy measure. Noice, ha p y0: is he counerpar of he filering disribuion p(dx y 0: ) discussed in Subsecion and characerised by means of densiies firs in (2.2.6) and hen by he Bayesian recursion: predicion (2.2.7) and updaing (2.2.8). Hence, i seems naural o formulae he curren framework in a similar, Bayesian spiri, for which we need o define he predicive measures, i.e. condiional probabiliy measures given he pas observaions. These, in a random and deerminisic versions, are respecively given by p 1 (A) = P(X A Y 0: 1 ), p y0: 1 1 (A) = P(X A Y 0: 1 = y 0: 1 ), wih he corresponding inegrals defined similarly as above. Finally, we define he likelihood funcion B B(R ny ), and we assume p y expressed as p 1 dp dp 1 = p Y (B) = P(Y B X ), p y (B) = P(Y B X = x ), C b (R nx ). Then, he Bayesian recursion (2.2.7) and (2.2.8) can be = p 1 1 K 1, p Y p Y p 1(dx) p y0: 1 1 dp y 0: dp y 0: 1 1 = p y0: K 1 = p y y p p 1(dx), (4.1.1) where K is he ransiion kernel of he Markovian signal process, as characerised in The proof of boh above recursion can be found in Crisan (2001) Projecive produc Noice, ha he recurrence formulae for p and p y0: in (4.1.1) are based on wo operaions beween probabiliy measure on R nx, involving an inermediae approximaion for p 1 and p y0: 1 1, respecively. The firs one, he predicion, is jus a simple ransformaion via he ransiion kernel K 1. I akes place before he arrival of he new informaion, so ha he σ-field on which one condiions does no include Y or Y = y. The second one, he updaing, in a non-linear ransformaion requiring compuaion of he normalizing consan in boh denominaors. No only i poses considerable compuaional difficulies, bu also, in he curren form, is noaionally inconvenien. Hence, for sake of readabiliy, we inroduce 36
39 below he concep of he projecive produc, which describes a ransformaion of a probabiliy measure o anoher probabiliy measure using a given funcion. Definiion (Projecive produc). Le µ P(R n ) be a finie measure and le φ B(R n ) be a non-negaive funcion such ha µ(φ) := φdµ > 0. The projecive produc φ µ is he (se) funcion φ µ : B(R n ) R defined as φ µ(a) = A φ(x)µ(dx), A B(R n ). µ(φ) Inuiively, he projecive produc normalises any finie measure ino a probabiliy measure. This is formally saed in he following proposiion. Proposiion The projecive produc φ µ is a probabiliy measure on B(R n ). Proof. By definiion, we have φ µ( ) = 0 and φ µ(r n ) = 1. Wha remains o be verified is hus he counable addiiviy propery. For any A B(R n ) consider is pariion {A i }, i.e. A 1, A 2, B(R n ), such ha A j A k =, j k, and A = A i. Then, we have by he properies of he inegral A φdµ = I A φdµ ( ) = = I Ai φdµ I Ai φdµ A i φdµ, where in ( ) he order of inegraion can be changed by he Monoone Convergence Theorem, as he funcion I Ai φ are nonnegaive random variables. To complee he proof, noice ha we have defined he projecive produc as he above expression divided by µ(φ), so division by µ(φ) of each summand above yield he counable addiiviy propery. Noice ha he projecive produc φ µ is absoluely coninuous wih respec o µ and is Radon-Nikodým derivaive wih respec o µ is proporional o φ, i.e. so ha 1 µ(φ) d(φ µ) dµ = φ µ(φ), can be undersood as he normalising consan. In (4.1.1) he role of he funcion φ from he above definiion was played by he likelihood funcions p Y and p y, while he one of he iniial measure µ he inermediae predicive disribuions p 1 1 and p yy 1 1 way.. Hence, he concep of he projecive produc allows us o express (4.1.1) in a more compac p 1 p = p 1 1 K 1, = p Y p 1 p y0: 1 1 p y0: = p y0: K 1. (4.1.2) = p y p 1 37
40 As i has already been poined ou, he nonlinear characer of he projecive produc makes he whole recursion compuaionally challenging and in pracice requires resoring o approximaive soluions. This is indeed he idea behind he paricle filers Paricle filers In Chaper 3 we explained paricle filers from he algorihmic poin of view and showed how hey aim a approximaing he condiional filering disribuions p and p y using empirical disribuions consising of paricles clouds. Below, we provide a more absrac perspecive, where paricle filers are regarded as approximaive sequences of he probabiliy measure ransformaion. { } { } We consider he approximaive sequences p n 1 and p n, which are supposed o approximae n=1 n=1 he p 1 or p y 1 1, and p or p y, respecively. We assume ha hese approximaing sequences saisfy he following condiions 1. p n and pn 1 are random measures (no necessarily probabiliy measures); 2. p n 0 and pn 1 0; 3. p n 1 py > 0, n, = 0,..., T. Finally, we define wo random probabiliy measures p n = py p n 1, (4.1.3) p n,y = p y p n 1, (4.1.4) which by he properies of he projecive produc are absoluely coninuous wih respec o p n 1. We have ) p n f = pn 1 (fpy p n,y p n 1 py ) f = pn 1 (fpy p n 1 py Laer on, a he discussion of he boosrap filer in Secion 4.4, i will urn ou ha he measures (4.1.3) and (4.1.4) can be seen as he weighed (wih he normalised weighs) measures. They are obained by weighing of he iniial measures, which one samples from, wih he weighs of he draws, which depend on he corresponding likelihood evaluaions. The quesion is, wheher and under wha condiions p n 1 and pn converge o p 1 or p y 1 1, and p or p y, respecively. The idea of he proofs given in Secion 4.3 is presened in Figure 4.1.1, which is based on Crisan (2014). I also illusraes how he ransformaion of probabiliy measures by paricle filers corresponds o is heoreical counerpar. For simpliciy, we omi he superscrips y for he fixed observaion case, as well as we use he common noaion p y for boh p yy and p Y. Before proceeding o he heorems, however, one needs o define in wha sense paricle filers can converge. This is he aim of he nex Secion.,. 38
41 p n p n 1 p y p n p n 0 p n 1 1 p n 1 1 K 1 K 1 p 0 p 1 1 p 1 p K 1 p y Figure 4.1.1: Graphical represenaion of he recursive formula for he arge process (blue) and approximaing sequences (black). 4.2 Convergence of measure-valued random variables Recall ha a paricle filer is an approximaive random measure. To evaluae is qualiy, one needs hus o define in wha way a sequence of random measures can approximae anoher random measure. Below we analyse wo modes of convergence, convergence in expecaion and almos sure convergence. Consider a probabiliy space (Ω, F, P) and le {µ n } n=1 be a sequence of random measures, µ n : Ω M(R d ) and µ M(R d ) be a deerminisic finie measure. Definiion (Convergence in expecaion). A sequence of random measures {µ n } n=1 converge o a random measure µ in expecaion if is said o which we denoe by e lim n µ n = µ. lim E [ µ nf µf ] = 0, f C b (R d ), n Definiion (Almos sure convergence). A sequence of random measures {µ n } n=1 is said o converge o a random measure µ P almos surely if which we denoe by µ n P µ. ( ) P lim µ n = µ = 1, n Noice, ha by he Dominaed Convergence Theorem, if here exiss an inegrable random variable ω : Ω R saisfying µ n 1 ω, n, hen µ n P µ e lim n µ n = µ. This auomaically holds for probabiliy measures, as one can simply ake ω 1. For almos sure convergence analysis, i is convenien o define a disance d M on P(R nx ), in order o obain a meric space (P(R nx ), d P ). To his end, firs we consider, as in Crisan and Douce (2002), R nx endowed wih he opology of weak convergence, in which µ n converges weakly o µ if lim µ nϕ = µϕ, ϕ C b (R nx ), n which we denoe by lim n µ n = µ. Since R nx is locally compac separable meric space, here exiss a 39
42 counable se A = {ϕ i }, dense in C b(r nx ), which compleely deermines convergence, i.e. lim µ n = µ n lim µ nϕ i = µϕ i, ϕ i A. (4.2.1) n This convergence deermining se allows us o define he required disance on P(R nx ) as follows d P (µ, ν) = µϕ i νϕ i 2 i, (4.2.2) ϕ i where sands for he supremum norm. This se generaes he weak opology on A(R nx ), i.e. lim µ n = µ n lim d M(µ n, µ) = 0. n Noice, ha alhough he disance d P independen of his choice. depends on he choice of he se P, he induced opology is 4.3 Convergence heorems Below we presen and prove wo heorems, which provide necessary and sufficien condiions for convergence of he paricle filer o he poserior disribuion. Due o he limied characer of his hesis we resric ourselves o fixed observaion case, which is more naural from he pracical poin of view. To simplify he noaion we omi he superscrips y 1 and y, alhough he resuls below are derived for a given realisaion y 0:T of he process Y 0:T. Boh heorems urn ou o be raher naural: an approximaion o he arge disribuion can be obained if and only if we sar nearby he required disribuion and hen appropriaely closely follow he paricle filer recursions. Hence, he key assumpions here are he Feller propery of he ransiion kernel ogeher wih he coninuiy and boundedness of he likelihood funcion. The former requiremen ensures ha he signal process moves coninuously and ha is rajecories are sable, in a sense ha wo realisaions of X which sar from nearby saes will say close o each oher hroughou he whole horizon. The laer assumpion guaranees ha a small change in he prior disribuion of he signal does no lead o a subsanial variaion in is poserior disribuion Convergence in expecaion The following heorem gives necessary and sufficien condiions for he convergence of p n o p (filering disribuion) and p n 1 o p 1 (predicive disribuion) in expecaion. Theorem The sequences p n and pn 1 converge in expecaion o p and p 1, respecively, i.e. [ ] p n a0. lim n E f p f = 0, [ ] p n b0. lim n E 1 f p 1f = 0, if and only if [ ] p n a1. lim n E 0 0 f p 0 0f = 0, [ ] p n b1. lim n E 1 f pn 1 1 K f = 0, 40
43 [ ] p n c1. lim n E f p f = 0, f C b (R nx ), [0, T ]. Proof. ( ) We will proceed by inducion. The iniial case for a0. follows from a1. We need o show ha a0. also holds for > 0, i.e. ha if e lim n p n 1 1 = p 1 1 and e lim n p n 1 = p 1, hen also e lim n p n = p. Consider b0.. C b (R nx ), From (4.1.2) we have p 1 = p 1 1 K, hence by he riangle inequaliy, n, f p n 1 f p 1f p n 1 f pn 1 1 K f + p n 1 1 K f p 1 1 K f. (4.3.1) Then, by b1., he firs erm on he righ hand side in he above formula converges in expecaion o 0. Due o he Feller propery of he kernel, K f C b (R nx ), f C b (R nx ), so by he inducion hypohesis he second erm on he righ hand side in (4.3.1) also converges in expecaion o 0. Thus, we obain [ ] p lim E n n 1 f p 1 f = 0, (4.3.2) which is b0.. To show a0. we wan o use c1.. Thus, recall ha for p n we have p n f = pn 1 fpy p n 1 py and consider p n f p p n 1 f = fpy p n p 1fp y 1 py p 1 p y p n 1 fpy p n pn 1 fpy 1 py p 1 p y + p n 1 fpy p 1 p y p 1fp y p 1 p y f p 1 p y p n 1 py p 1 p y 1 + p 1 p y p n 1 fpy p 1 fp y, (4.3.3) where f denoes he supremum norm of f. Hence, [ ] E p n f p f f [ ] p p 1 p y n E 1 p y p 1 p y 1 [ ] p + p 1 p y n E 1 fp y p 1 fp y. Since p y C b (R nx ) 2, by (4.3.2) boh erms on he righ hand side of he above formula converge o 0, implying ha Finally, by he riangle inequaliy, we have, [ ] lim p E n n f p f = 0. (4.3.4) p n f p f p n f pn f + p n f p f. (4.3.5) Boh erms on he righ hand side of (4.3.5) converge in expecaion o 0: he firs one by c1., while he second one by (4.3.4). Thus [ ] p lim E n n f p f = 0, 2 Recall ha in Secion we have assumed ha p y = p(y x), he observaion densiy is bounded and coninuous. 41
44 which is a0.. ( ) Assume a0. and b0. boh hold. Then a1. is saisfied as a special case of a0. Nex, using again he riangle inequaliy, we obain [ ] p n E f p n f [ ] p n E f p f [ ] p + E f p n f. By (4.3.4), he second erm in he above expression converges o 0, while he firs one goes o 0 by assumpion a0, so esablishing c1.. To complee he proof, noice ha due o p 1 = p 1 1 K we have [ ] p lim E n n f p n f = 0, (4.3.6) [ ] [ ] [ ] p n E 1 f p n 1 1 K p n p 1 1 f E f p f + E K f p n 1 1 K 1f. The firs erm in his formula converges o 0 by (4.3.6). For he second erm [ ] p 1 1 E K f p n 1 1 K f so i goes o 0 by assumpion b0. Hence yielding b1.. [ ] p 1 = E f p n 1 f, [ ] p lim E n n 1 f p n 1 1 K f = 0, Almos sure convergence The following heorem is a counerpar of Theorem and characerises necessary and sufficien condiions for he almos sure convergence of p n and pn 1 o p and p 1, respecively. I makes use of he fac ha he almos sure convergence from Definiion is equivalen o ( ) P lim d P(µ n, µ) = 0 = 1, n where d P is he disance in he space of probabiliy measures over R nx, as defined in (4.2.2). Theorem The sequences p n and pn 1 converge almos surely o p and p 1, respecively, i.e. ) a0. lim n d P (p n, p = 0, P-a.s., ) b0. lim n d P (p n 1, p 1 = 0, P-a.s. if and only if a1. lim n p n 0 0 = p 0 0,, P-a.s., ) b1. lim n d P (p n 1, pn 1 1 K = 0, P-a.s., ) c1. lim n d P (p n, p = 0, P-a.s.. 42
45 Proof. ( ) Since for he probabiliy measures, he almos sure convergence implies he convergence in expecaion, if we assume ha condiions a1.-c1. hold, hen he corresponding condiions from Theorem are also saisfied. Hence, we have ha f C b (R nx ) inequaliies (4.3.1), (4.3.3) and (4.3.5) hold. Hence, in paricular hey hold for f A as defined in Secion 4.2. Then, by inducion, we obain a0. and b0.. ( ) Suppose ha p n P p and p n P 1 p 1,. Since p 1 = p 1 1 K, we have ha p n 1 1 K Therefore, almos surely, ( ) lim d P p n n 1, p 1 ( ) lim d P p n n, p = 0, lim n d P lim n d P Then, by he riangle inequaliy we obain P p 1 1 K. Then, by (4.3.3), also p P p. = 0, ) (p n 1 1 K, p 1 = 0, ( ) p n, p = 0. ) ( ) ) d P (p n 1, pn 1 1 K d P p n 1, p 1 + d P (p n 1 1 K, p 1, ) ( ) ( ) d P (p n, p d P p n, pn + d P p n, p. Taking he limis on boh sides in each of he above formulae gives ha almos surely which yields b1. and c1.. ( ) lim d P p n n 1, pn 1 1 K = 0, ( ) lim d P p n n, p = 0, 4.4 Boosrap example Below, following Crisan (2001), we presen an example of a paricle filer which saisfies he assumpion of he above heorems. I is a version of he boosrap filer described in Algorihm 3. This is a very simplisic case, discussed for purely illusraive purposes. Theoreical analysis of more complex filers is beyond he scope of his hesis Paricle filer Consider a collecion of n paricles which evolve according o a given Markov ransiion kernel K. Each period we perform mulinomial resampling wih replacemen, where he sampling probabiliies are se equal o he paricles imporance weighs. The exac seps of he procedure are specified as follows. Iniializaion. Draw a random sample of size n from he iniial disribuion p 0, where he iniial weigh of each paricle is equal 1/n. This resuls in he iniial empirical disribuion p n 0 = 1 n n δ {x (i) 0 }, 43
46 where x (i) 0 denoes he posiion of he i-h draw. Since he paricles are randomly drawn from p 0, he empirical measure p n 0 is a random measure for which we have Ieraion. Given he approximaion lim n E [p n 0 ] = p 0, lim p n 0 = p 0, P a.s.. n p n 1 1 = 1 n δ {x (i) 1 }, i.e. he empirical measure corresponding o he paricles collecion from he previous sep, recursively consruc p n as follows. Move each paricle according o he signal ransiion kernel x (i) K 1 (x (i) 1, ). Noice, ha he paricles move independenly of each oher. We obain a new empirical measure, p n given by p n = 1 δ (i) n { x }. For each paricle compue he (normalised) imporance weigh w (i) p(y x (i) ) = n j=1 p(y x (j) ) where y is he fixed realisaion of he observaion process, as assumed above. Obain ye anoher empirical measure, corresponding o (4.1.4), given by p n = Perform mulinomial resampling from { x (i) } n he obained paricles x (i) Resampling n w (i) δ (i) { x }. wih he probabiliies equal o he weighs {w(i) } n, call, i = 1,..., n. Finally, we obain he required approximaion, which is given by p n = 1 n n δ {x (i) }. Noice ha he resampling sep can be seen as replacing each paricle by a number of offspring paricles, call hem ξ (i), where each paricle has on average w (i) offspring. For simpliciy and consisency wih Algorihm 3 we impose he consrain of he consan number of paricles, i.e. n ( ) i ξ(i) = n. In general, n one needs o assume ha he resuling offspring vecor ξ = has a finie variance, i.e. c R ξ (i) v T Var[ξ ]v nc, v R n, v = ( v i) n, vi < 1, i = 1,..., n, (4.4.1) where [ ] Var[ξ ]E (ξ w ) T (ξ w ) denoes he covariance marix of ξ, where w = (w (i) ) n. 44
47 ( Wih mulinomial resampling his is indeed he case. Since ξ Mulinomial, w (1) ),..., w (n), we have [ ( E ξ (i) [ ( E ξ (i) ) T ( w (i) ξ (j) w (i) E[ξ (i) ] = w (i) ) ] 2, = nw (i) (1 w (i) ), ) ] w (j) = nww i j, i j. Then, for all v as characerised above one obains so ha we can ake c = 1. v T Var[ξ ]v = n = n n = n, n i,j=1,i j n n w i (1 w i )(v (i) ) 2 2n w (i) (v (i) ) 2 n w (i) ( n n ww i j v (i) v (j) w (i) v (i) ) Convergence As above, we fix he observaions o a given pah y 0:T. We show ha he random measures p n and pn 1 delivered by he boosrap filer described in Subsecions and converge o p y and py 1 1, respecively. To his end we define he following wo σ-algebras F = σ { x i s, x i s, s, i = 1,..., n }, { } F = σ x i s, x i s, s <, x (i), i = 1,..., n. Obviously F F. Furher, noice ha he random measure p n is F -measurable, while he random measures p n 1 and pn are F -measurable. Independen resampling in each ieraion means ha he randomly drawn paricle posiions x (i) are muually independen condiional upon F 1. Firs, we give and prove he heorem regarding he convergence in he expecaion of he boosrap filer characerised above. Then for compleeness, we sae is almos sure convergence counerpar. As before, he resuls are aken from Crisan (2001). Theorem Le {p n 1 } n=1 and {p n } n=1 be sequences of random measures obained via performing he algorihm described in Subsecions and Then, lim n E[pn 1 ] = py0: 1 1, lim n E[pn ] = py0:. Proof. We wan o use Theorem Le f C b (R nx ). Since condiion a1. holds naurally, we only need o show ha he wo remaining condiions are saisfied. Regarding b1. we have [ E f( x (i) ) ] F 1 = K 1 f(x (i) 1 ), i = 1,..., n. 45
48 Moreover, ] E [p n 1 f F 1 [ 1 = E = E ] n f( x(i) ) F 1 [ ] 1 n K 1f(x (i) 1 ) F 1 = p n 1 1 K 1f. Then, as he paricles move independenly of each oher, [ ( ) ] 2 E p n 1 f pn 1 1 K 1f F 1 = E ( 1 n n [ f( x (i) ind = 1 n [ ( n 2 E f( x (i) ) ) K 1 f(x (i) )] ) 2 ) 2 F 1 ] 1 n 2 n = 1 n pn 1 1 ( K 1 f 2 (K 1 f) 2). F 1 ( [ ]) E K 1 f(x (i) 2 )) F 1 Hence, [ ( ) ] 2 E p n 1 f pn 1 1 K 1f f 2 n, which shows b1.. Regarding c1., noe ha hus p n = 1 n δ {x (i) ] E [p n f F } = n = p n f, ξ (i) δ (i) { x }, [ ( ) ] 2 E p n f pn f F = 1 n 2 (vn ) T n Var [ξ ]v n, where v n = (f( x (i) )) n. Then, by (4.4.1) we have [ ( ) ] 2 E p n f pn f F = c f 2, n so ha implying ha also c1. holds. This complees he proof. E [(p n f p n f) 2] = c f 2, (4.4.2) n Inequaliy (4.4.2) implies ha he addiional randomness inroduced o he algorihm by he resampling sep, measured by he second momen of p n f p n f, ends o zero a he consan rae 1/n. The following heorem gives he almos sure counerpar of he previous resul. The proof, which we omi here, can be found in Crisan (2001) or Crisan and Douce (2002). In a nushell, i consiss in applying Theorem and using he funcions from A, he convergence deermining se (in he opology of weak convergence on he space of probabiliy measures) o bound he fourh momen of inegrals wih respec o boh sequences, {p n 1 } n=1 and {p n } n=1, so ha he almos sure convergence follows from he Borel-Canelli argumen. 46
49 Theorem Le {p n 1 } n=1 and {p n } n=1 be sequences of random measures obained via performing he algorihm described in Subsecions and Then, lim n pn 1 = py0: 1 1, P a.s., lim n pn = py0:, P a.s Discussion The hisorically iniial convergence resuls for paricle filers discussed in his secion are cerainly useful, in a sense ha hey provide a posiive answer o he quesion wheher he paricle filer converge o he opimal filer. Moreover, hey characerise necessary and sufficien condiions under which he approximaive soluion obained from he paricle filer well characerises he rue soluion. However, as poined ou in Hu e al. (2008), i is always imporan o address he issue under wha condiion a cerain resuls are valid. The problem wih he heorems from Secion 4.3 is ha hey hold only for bounded funcion. This excludes from he analysis e.g. he ideniy funcion, used o obain he sae esimae, and his esimae is usually he one which we are primarily ineresed in. The more general resuls, for a more general class of unbounded funcion, is provided in he cied paper Hu e al. (2008). However, such a heoreically involved analysis is beyond he scope of his hesis. 47
50
51 Chaper 5 Applicaions To presen he performance of he paricle filers, we consider hree differen models wih various specificaions of he algorihm. Firs, we analyse he basic linear Gaussian model, he so called local level model, o illusrae he degeneracy problem and he necessiy of resampling. Second, we apply paricle filer o a canonical, severely nonlinear ye Gaussian model. We compare performance of he algorihm based on wo imporance funcions: he prior (i.e. he boosrap filer) and he locally opimal one, based on he local linearisaion of he observaion equaion. The hird and he las applicaion concerns he sochasic volailiy model, which is a sandard example of he nonlinear non-gaussian sae space model. Also in his example we employ wo imporance funcions, he prior and he normal approximaion o he opimal imporance funcion (based on he local linearisaion of he laer). All he compuaions were performed in MATLAB R2014b (he code lisings are presened in Appendix C). 5.1 Basic linear Gaussian problem As he firs illusraion of he paricle filering mehod, le us use an example from Durbin and Koopman (2012) and apply he simple boosrap filer o he classical Nile daa. This is he daa se of observaions from he river Nile expressed as annual flow volume a Aswan from 1871 o We can model his ime series as a local level model given by X = X 1 + V, Y = X + W, X 1 N (x 0, σ 2 0) V i.i.d N (0, σ 2 V ), W i.i.d N (0, σ 2 W ), (5.1.1) for = 1,..., T. We assume ha V, W are muually independen, and independen of X 1. The aim of his example is firs, o show ha he paricle filering mehod can yield accurae resuls even in a simple form of he boosrap filer. The second objecive is o illusrae he imporance of resampling. Hence, we firs implemen he SIS Algorihm 1 wih he prior aken as he imporance densiy, o subsequenly exend i o he SIR Algorihm 2, wih he resampling sep being added. For he considered paricular case, he laer echnique is described in Algorihm 4. Following Durbin and Koopman (2012), we consider N = 10, 000 paricles and se he model parameers as follows: σv 2 = , σw 2 = 15, 099, x 0 = 0, σ0 2 = Finally, for he algorihm wih resampling, we performed resampling in each ieraion, so N hres = N. 49
52 Algorihm 4 Nile boosrap filer algorihm for := 1 o T do for i := 1 o N do if = 1 hen Sample x (i) N ( x 0, S 0 ). else Sample x (i) N ( x (i 1), ση). 2 end if ( Se x (i) 0: := x (i) 0: 1, x(i) ). Compue he corresponding imporance weighs w (i) = w (i) 1 exp ( 1 2 (log 2π + log σ 2ε + (y x 2 ) 2 σ 2 η )). end for Normalise he imporance weighs Compue he effecive sample size w (i) = w (i) N j=1 w(j). Compue he filered sae esimae ˆN ESS = ˆx = Compue he filered sae variance esimae Ŝ = { Resample wih replacemen N paricles, { } N w (i). ( ) Se x (i) 0: := x (i) 0: 1, x(i). end for N x (i) ( N N w (i)2 x (i) w (i). ) 1. x (i)2 w (i) ˆx 2. } N { } N, from x (i) wih correspoding probabiliies The oupu of he algorihm wihou resampling is presened in Figure 5.1.1, while he one wih resampling in Figure I can be inferred from boh figures ha resampling is indeed necessary o obain accurae filering resuls and o keep he number of acive paricles a non-negligible level in he long run. Moreover, wih resampling he filered sae variance quickly sabilises a a consan level, which is in line wih he heory, as he local level model should converge o a seady sae. This is, however, no he case wihou resampling. 50
53 Figure 5.1.1: Boosrap filer wihou resampling 51
54 Figure 5.1.2: Boosrap filer wih resampling 52
55 5.2 Nonlinear Gaussian problem In heir seminal paper Gordon e al. (1993) inroduced SMC approach for filering based on he boosrap proposal. They considered he following, highly nonlinear model X = X X 1 i.i.d 1 + X cos(1.2( 1)) + V, V N (0, σv 2 ), Y = X W, W i.i.d N (0, σ 2 W ), X 1 N (x 0, σ 2 0), (5.2.1) where V and W are muually independen,and independen from X 1. As in he original paper we se σ 2 V = 10, σ2 W = 1, x 0 = 0, σ 2 0 = 2. Figure presens he generaed ime series, wih he lengh se o T = 50. Figure 5.2.1: Sae and observaion generaed from (5.2.1). From he previous example i is clear ha resampling is crucial o reduce he degeneracy problem, prevalen in paricle filers, and in consequence, o obain a saisfacory performance of an algorihm. Hence, he aim of he curren example is o compare he performance of wo algorihms based on differen 53
56 imporance funcions. Firsly, following he cied auhors, we consider he boosrap filer wih resampling employed a every ime sep. This approach was also used in Arulampalam e al. (2002). Then, following Douce e al. (2000), we use he imporance funcion obained by local linearisaion of he sae space model, as discussed in Subsecion All he paricle filers have N = 1000 paricles and employ resampling a every ime sep, i.e. N hres = N. To sar wih, noice ha he ransiion densiy and he likelihood densiy are given by ( p(x x 1 ) = φ x ; x 1 2 ( p(y x ) = φ y ; x2 20, σ2 W + 25 x x cos(1.2( 1)), σv 2 1 ), respecively. Since p(y x 1 ) canno be evaluaed analyically, and sampling from p(x x 1, y ) is infeasible one can resor o obaining he imporance funcion via local linearisaion of he observaion equaion. Using he noaion inroduced in 3.5.2, we ge y g(f(x 1 )) + g(x ) x = f 2 (x 1 ) 20 = f 2 (x 1 ) 20 which yields he following imporance funcion q(x x 1, y ) = φ(x ; µ, σ 2 ), σ 2 x=f(x 1) + f(x 1) (x f(x 1 )) + w 10 + f(x 1) x + w, 10 = σ 2 V + f 2 (x 1 ) [ 100 f(x 1 )σ 2 V µ = σ 2 σ 2 W, + f(x 1) σ 2 W 10 (x f(x 1 )) + w ), ( y + f 2 )] (x 1 )
57 (a) SMC using prior (boosrap filer). (b) SMC using locally opimal proposal. Figure 5.2.2: Comparison of he filering resuls using differen imporance funcions. 55
58 (a) SMC using prior (boosrap filer). (b) SMC using locally opimal proposal. Figure 5.2.3: Esimaed filering disribuion using differen imporance funcions. 56
59 5.3 Sochasic volailiy model As he las example, we consider a sandard sochasic volailiy (SV) model wih he sae-space form given by X = φx 1 + σv, ( ) X Y = β exp W, 2 ( σ 2 ) X 1 N 0, 1 φ 2. V i.i.d. N (0, 1), W i.i.d. N (0, 1), (5.3.1) SV models are commonly used o analyse ime series of financial reurns. Observaions in hese models are usually daily reurns of a cerain securiy, which are defined as he naural logarihm of he raio of consecuive daily closing levels. Hence, he log-reurns are realisaions of he sochasic process Y. The key feaure of SV models is ha he variance of his process is iself randomly disribued, i.e. he reurn Y depends on he log-volailiy X, which follows a saionary auoregressive process. This volailiy, however, is no observed, and he aim is o rerieve i from he daa. A direc modelling of a dynamic process for he variance allows o capure he fundamenal propery of he observed financial reurns, i.e. volailiy clusering. To simulae he ime series of he laen log-volailiy x and observed log-reurns y, We se φ = 0.91, σ = 0.03 and β = 0.6, which corresponds o ypical values in empirical sudies for daily sock reurns (cf. Durbin and Koopman, 2012). The generaed rajecories are of lengh T = 500 and are presened in Figure Similarly as in he previous applicaion, o filer ou he hidden saes we employ paricle filers using wo imporance funcions: he prior densiy (i.e. he boosrap filer) and he one based on he opimal imporance densiy (using he local linearisaion echnique). The derivaion of he laer is given below. Boh filers use N = 500 paricles and carry ou resampling a each poin in ime, N hres = N. Figure 5.3.1: Sae and observaion generaed from (5.3.1) 57
60 5.3.1 Opimal imporance funcion approximaion I follows from (5.3.1) ha he ransiion densiy and he likelihood densiy are respecively given by p(x x 1 ) = N ( σ 2 ) x φx 1, 1 φ 2, (5.3.2) p(y x ) = N ( y 0, β 2 exp(x ) ). (5.3.3) Hence, he opimal proposal densiy, minimising he weighs variance, saisfies q(x x 0: 1, y 0: ) p(x x 1 )p(y x ) = exp 1 2π σ2 1 φ 2 ( 1 2 ( 1 2πβ2 exp (x ) exp 1 1 φ 2 2 σ 2 (x φx 1 ) 2 (x + 1 φ2 σ 2 ) ( exp 1 2 y 2 ) β 2 exp ( x ) )) (x φx 1 ) 2 + y2 β 2 exp ( x ). (5.3.4) Expression (5.3.4) may look similarly o he formula for he Gaussian densiy, however, he las erm in he exponen makes i non-sandard. Therefore, in pracice i needs o be approximaed by, e.g. he normal densiy, as discussed in Subsecion Using he noaion inroduced here, we can wrie l(x) = log(2πβ) 1 2 log ( σ 2 l (x) = φ2 σ 2 l (x) = 1 φ2 σ 2 1 φ 2 ) 1 (x + 1 ) φ2 2 σ 2 (x φx 1 ) 2 + y2 exp ( x), β2 (x φx 1 ) + y2 exp ( x), 2β2 y2 exp ( x). 2β2 Noice, ha he opimal imporance funcion is concave, which implies ha is has a unique maximiser and ha l (x) < 0, as required in he assumpions from he Subsecion Puing ˆx = arg max x R p(x x 1)p(y x), = arg max x R l(x), we can approximae q(x x 1, y ), for each, wih Σ(ˆx) = l (ˆx) 1 ( ) 1 φ 2 1 = σ 2 + y2 exp ( ˆx), 2β2 q(x x 1, y ) = N (ˆx, Σ(ˆx))). Then, he imporance weigh funcion, a ime, of he paricle i, is given by w (i) = w (i) 1 p( x (i) x (i) 1 )p(y x (i) q( x (i) x (i) 1, y ) ) Resuls To sar wih, we performed he boosrap filering using he ransiion densiy (5.3.2) as he imporance funcion. The overview of resuls is depiced in Figure Then, we carried ou filering using he locally opimal imporance funcion, as derived above. Figure shows he corresponding resuls. 58
61 One can see ha boh mehods deliver reasonable oucomes, i.e. hey are able o capure he laen sae process fairly accuraely. Wha is remarkable, he laer echnique is characerised by much higher filered sae variance and more volaile effecive sample size. To ease he comparison of he performance of he crude boosrap filer wih he one of he filer based on he locally opimal proposal, we gahered he esimaes delivered by boh filers ogeher (Figure 5.3.4). The upper plo 5.3.5a presens he oupu of he prior-based algorihm, while he lower one 5.3.4b of he algorihm employing he locally opimal proposal. As expeced, he laer one generaes much more accurae resuls, i.e. he filered ou hidden sae is more in line wih he rue one. However, he oucomes of he approximaion-based algorihm are highly uncerain, as indicaed by he wide confidence inervals. This observaion can be confirmed by considering he esimaed filering disribuions (Figure 5.3.5), which a any poin in ime are much broader han he ones from he prior-based seup. This shall come as no surprise, however, as he by consrucion, he variance in he former approach is consan, while in he laer i is ime varian. 59
62 Figure 5.3.2: SMC using prior (boosrap filer). 60
63 Figure 5.3.3: SMC using locally opimal proposal. 61
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Nonlinear data assimilation for ocean applications
 Nonlinear data assimilation for ocean applications Peter Jan van Leeuwen, Manuel Pulido, Jacob Skauvold, Javier Amezcua, Polly Smith, Met Ades, Mengbin Zhu Comparing observations and models Ensure they
Nonlinear data assimilation for ocean applications Peter Jan van Leeuwen, Manuel Pulido, Jacob Skauvold, Javier Amezcua, Polly Smith, Met Ades, Mengbin Zhu Comparing observations and models Ensure they
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Patients price acceptance SELECTED FINDINGS
 Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěsování maemaiky a fysiky Hugo Seinhaus Różne formy prawa wielkich liczb Časopis pro pěsování maemaiky a fysiky, Vol. 74 (1949), No. 2, 114--117 Persisen URL: hp://dml.cz/dmlcz/123056 Terms
Časopis pro pěsování maemaiky a fysiky Hugo Seinhaus Różne formy prawa wielkich liczb Časopis pro pěsování maemaiky a fysiky, Vol. 74 (1949), No. 2, 114--117 Persisen URL: hp://dml.cz/dmlcz/123056 Terms
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
Previously on CSCI 4622
 More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Stability of Tikhonov Regularization Class 07, March 2003 Alex Rakhlin
 Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów
 Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Cracow University of Economics Poland. Overview. Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005
 Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Multi-Criteria Decision Support using ELECTRE methods
 Muli-Crieria Decision Suppor using ELECTRE mehods Roman Słowiński Poznań Universiy of Technology, Poland Weak poins of preference modelling using uiliy (value) funcion Uiliy funcion disinguishes only 2
Muli-Crieria Decision Suppor using ELECTRE mehods Roman Słowiński Poznań Universiy of Technology, Poland Weak poins of preference modelling using uiliy (value) funcion Uiliy funcion disinguishes only 2
Inverse problems - Introduction - Probabilistic approach
 Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Sargent Opens Sonairte Farmers' Market
 Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Rachunek lambda, zima
 Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards
 INSPIRE Conference 2010 INSPIRE as a Framework for Cooperation Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards Elżbieta Bielecka Agnieszka Zwirowicz
INSPIRE Conference 2010 INSPIRE as a Framework for Cooperation Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards Elżbieta Bielecka Agnieszka Zwirowicz
STUDIES OF THE UNIVERSITY OF ŽILINA. Volume 20 Number 1 December Editorial Board
 STUDIES OF THE UNIVERSITY OF ŽILINA Volume 20 Number 1 December 2006 Special Issue: Proceedings of Conference on Differenial and Difference Equaions and Applicaions (CDDEA), Rajecké Teplice, Slovakia June
STUDIES OF THE UNIVERSITY OF ŽILINA Volume 20 Number 1 December 2006 Special Issue: Proceedings of Conference on Differenial and Difference Equaions and Applicaions (CDDEA), Rajecké Teplice, Slovakia June
Wprowadzenie do programu RapidMiner, część 5 Michał Bereta
 Wprowadzenie do programu RapidMiner, część 5 Michał Bereta www.michalbereta.pl 1. Przekształcenia atrybutów (ang. attribute reduction / transformation, feature extraction). Zamiast wybierad częśd atrybutów
Wprowadzenie do programu RapidMiner, część 5 Michał Bereta www.michalbereta.pl 1. Przekształcenia atrybutów (ang. attribute reduction / transformation, feature extraction). Zamiast wybierad częśd atrybutów
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku
 Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
INSTYTUT PODSTAWOWYCH PROBLEMÓW TECHNIKI STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI. V O L. XVI WARSZAWA, 1964 No. 4
 P O L S K A A K A D E M I A N A U K INSTYTUT PODSTAWOWYCH PROLEMÓW TECHNIKI A R C H I W U M M E C H A N I K I STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI V O L XVI WARSZAWA, 1964 No 4 P A Ń S T W
P O L S K A A K A D E M I A N A U K INSTYTUT PODSTAWOWYCH PROLEMÓW TECHNIKI A R C H I W U M M E C H A N I K I STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI V O L XVI WARSZAWA, 1964 No 4 P A Ń S T W
Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016
 Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016 Paweł Lula Cracow University of Economics, Poland pawel.lula@uek.krakow.pl Latent Dirichlet Allocation (LDA) Documents Latent
Latent Dirichlet Allocation Models and their Evaluation IT for Practice 2016 Paweł Lula Cracow University of Economics, Poland pawel.lula@uek.krakow.pl Latent Dirichlet Allocation (LDA) Documents Latent
Wybrzeze Baltyku, mapa turystyczna 1: (Polish Edition)
 Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
PROGRAMOWY GENERATOR PROCESÓW STOCHASTYCZNYCH LEVY EGO
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 69 Elecrical Engineering 0 Janusz WALCZAK* Seweryn MAZURKIEWICZ* PROGRAMOWY GENERATOR PROCESÓW STOCHASTYCZNYCH LEVY EGO W arykule opisano meodę generacji
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 69 Elecrical Engineering 0 Janusz WALCZAK* Seweryn MAZURKIEWICZ* PROGRAMOWY GENERATOR PROCESÓW STOCHASTYCZNYCH LEVY EGO W arykule opisano meodę generacji
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Department of Electrical- and Information Technology. Dealing with stochastic processes
 Dealing with stochastic processes The stochastic process (SP) Definition (in the following material): A stochastic process is random process that happens over time, i.e. the process is dynamic and changes
Dealing with stochastic processes The stochastic process (SP) Definition (in the following material): A stochastic process is random process that happens over time, i.e. the process is dynamic and changes
(LMP-Liniowy model prawdopodobieństwa)
 OGÓLNY MODEL REGRESJI BINARNEJ (LMP-Liniowy model prawdopodobieństwa) Dla k3 y α α α α + x + x + x 2 2 3 3 + α x x α x x + α x x + α x x + ε + x 4 2 5 3 6 2 3 7 2 3 Zał.: Wszystkie zmienne interakcyjne
OGÓLNY MODEL REGRESJI BINARNEJ (LMP-Liniowy model prawdopodobieństwa) Dla k3 y α α α α + x + x + x 2 2 3 3 + α x x α x x + α x x + α x x + ε + x 4 2 5 3 6 2 3 7 2 3 Zał.: Wszystkie zmienne interakcyjne
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH
 POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
Gradient Coding using the Stochastic Block Model
 Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Jak zasada Pareto może pomóc Ci w nauce języków obcych?
 Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Compressing the information contained in the different indexes is crucial for performance when implementing an IR system
 4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
Zestawienie czasów angielskich
 Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS.
 ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
European Crime Prevention Award (ECPA) Annex I - new version 2014
 European Crime Prevention Award (ECPA) Annex I - new version 2014 Załącznik nr 1 General information (Informacje ogólne) 1. Please specify your country. (Kraj pochodzenia:) 2. Is this your country s ECPA
European Crime Prevention Award (ECPA) Annex I - new version 2014 Załącznik nr 1 General information (Informacje ogólne) 1. Please specify your country. (Kraj pochodzenia:) 2. Is this your country s ECPA
Machine Learning for Data Science (CS4786) Lecture 24. Differential Privacy and Re-useable Holdout
 Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
 aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition)
 Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
2014-3-30. Urbanek J., Jabłoński A., Barszcz T ssswedfsdfurbanek J., Jabłoński A., Barszcz T., Wykonanie pomiarów
 Wykonanie pomiarów sygnałów wibroakustycznych przy stałych oraz zmiennych warunkach eksploatacyjnych na stanowisku testowym. Część II: Analiza poprawności pomiarów. Autorzy: Urbanek J., Jabłoński A., Barszcz
Wykonanie pomiarów sygnałów wibroakustycznych przy stałych oraz zmiennych warunkach eksploatacyjnych na stanowisku testowym. Część II: Analiza poprawności pomiarów. Autorzy: Urbanek J., Jabłoński A., Barszcz
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2)
 Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
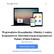 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Test sprawdzający znajomość języka angielskiego
 Test sprawdzający znajomość języka angielskiego Imię i Nazwisko Kandydata/Kandydatki Proszę wstawić X w pole zgodnie z prawdą: Brak znajomości języka angielskiego Znam j. angielski (Proszę wypełnić poniższy
Test sprawdzający znajomość języka angielskiego Imię i Nazwisko Kandydata/Kandydatki Proszę wstawić X w pole zgodnie z prawdą: Brak znajomości języka angielskiego Znam j. angielski (Proszę wypełnić poniższy
Maximum A Posteriori Chris Piech CS109, Stanford University
 Maximum A Posteriori Chris Piech CS109, Stanford University Previously in CS109 Game of Estimators Estimators Maximum Likelihood Non spoiler alert: this didn t happen in game of thrones aaab7nicbva9swnbej2lxzf+rs1tfomqm3anghywarvlcoydkjpsbfasjxt7x+6cei78cbslrwz9pxb+gzfjfzr4yodx3gwz84jecoou++0u1ty3nrek26wd3b39g/lhucveqwa8ywiz605adzdc8sykllytae6jqpj2ml6d+e0nro2i1qnoeu5hdkhekbhfk7u7j1lvne/75ypbc+cgq8tlsqvynprlr94gzmneftjjjel6boj+rjukjvm01esntygb0yhvwqpoxi2fzc+dkjordegya1skyvz9pzhryjhjfnjoiolilhsz8t+vm2j47wdcjslyxralwlqsjmnsdziqmjoue0so08lestiiasrqjlsyixjll6+s1kxnc2ve/wwlfpphuyqtoiuqehafdbidbjsbwrie4rxenmr5cd6dj0vrwclnjuepnm8fuskpig==
Maximum A Posteriori Chris Piech CS109, Stanford University Previously in CS109 Game of Estimators Estimators Maximum Likelihood Non spoiler alert: this didn t happen in game of thrones aaab7nicbva9swnbej2lxzf+rs1tfomqm3anghywarvlcoydkjpsbfasjxt7x+6cei78cbslrwz9pxb+gzfjfzr4yodx3gwz84jecoou++0u1ty3nrek26wd3b39g/lhucveqwa8ywiz605adzdc8sykllytae6jqpj2ml6d+e0nro2i1qnoeu5hdkhekbhfk7u7j1lvne/75ypbc+cgq8tlsqvynprlr94gzmneftjjjel6boj+rjukjvm01esntygb0yhvwqpoxi2fzc+dkjordegya1skyvz9pzhryjhjfnjoiolilhsz8t+vm2j47wdcjslyxralwlqsjmnsdziqmjoue0so08lestiiasrqjlsyixjll6+s1kxnc2ve/wwlfpphuyqtoiuqehafdbidbjsbwrie4rxenmr5cd6dj0vrwclnjuepnm8fuskpig==
18. Przydatne zwroty podczas egzaminu ustnego. 19. Mo liwe pytania egzaminatora i przyk³adowe odpowiedzi egzaminowanego
 18. Przydatne zwroty podczas egzaminu ustnego I m sorry, could you repeat that, please? - Przepraszam, czy mo na prosiæ o powtórzenie? I m sorry, I don t understand. - Przepraszam, nie rozumiem. Did you
18. Przydatne zwroty podczas egzaminu ustnego I m sorry, could you repeat that, please? - Przepraszam, czy mo na prosiæ o powtórzenie? I m sorry, I don t understand. - Przepraszam, nie rozumiem. Did you
WAE Jarosław Arabas Ewolucja różnicowa Rój cząstek EDA
 WAE Jarosław Arabas Ewolucja różnicowa Rój cząsek EDA Ewolucja różnicowa algorym differenial evoluion inicjuj P0 {P 01, P02... Pμ0 } H P0 0 while! sop for (i 1 :μ) P j selec (P ) P k, Pl sample (P ) M
WAE Jarosław Arabas Ewolucja różnicowa Rój cząsek EDA Ewolucja różnicowa algorym differenial evoluion inicjuj P0 {P 01, P02... Pμ0 } H P0 0 while! sop for (i 1 :μ) P j selec (P ) P k, Pl sample (P ) M
 !850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
!850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
POLITYKA PRYWATNOŚCI / PRIVACY POLICY
 POLITYKA PRYWATNOŚCI / PRIVACY POLICY TeleTrade DJ International Consulting Ltd Sierpień 2013 2011-2014 TeleTrade-DJ International Consulting Ltd. 1 Polityka Prywatności Privacy Policy Niniejsza Polityka
POLITYKA PRYWATNOŚCI / PRIVACY POLICY TeleTrade DJ International Consulting Ltd Sierpień 2013 2011-2014 TeleTrade-DJ International Consulting Ltd. 1 Polityka Prywatności Privacy Policy Niniejsza Polityka
Egzamin maturalny z języka angielskiego na poziomie dwujęzycznym Rozmowa wstępna (wyłącznie dla egzaminującego)
 112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
GRY EDUKACYJNE I ICH MOŻLIWOŚCI DZIĘKI INTERNETOWI DZIŚ I JUTRO. Internet Rzeczy w wyobraźni gracza komputerowego
 GRY EDUKACYJNE I ICH MOŻLIWOŚCI DZIĘKI INTERNETOWI DZIŚ I JUTRO Internet Rzeczy w wyobraźni gracza komputerowego NAUKA PRZEZ ZABAWĘ Strategia nauczania: Planowe, Zorganizowane Lub zainicjowane przez nauczyciela
GRY EDUKACYJNE I ICH MOŻLIWOŚCI DZIĘKI INTERNETOWI DZIŚ I JUTRO Internet Rzeczy w wyobraźni gracza komputerowego NAUKA PRZEZ ZABAWĘ Strategia nauczania: Planowe, Zorganizowane Lub zainicjowane przez nauczyciela
SubVersion. Piotr Mikulski. SubVersion. P. Mikulski. Co to jest subversion? Zalety SubVersion. Wady SubVersion. Inne różnice SubVersion i CVS
 Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
WYDZIAŁ BIOLOGII I OCHRONY ŚRODOWISKA
 WYDZIAŁ BIOLOGII I OCHRONY ŚRODOWISKA v Biologia v Biotechnologia v Ochrona środowiska studia pierwszego stopnia Dla kandydatów z NOWĄ MATURĄ Kwalifikacja obejmuje konkurs świadectw dojrzałości brane są
WYDZIAŁ BIOLOGII I OCHRONY ŚRODOWISKA v Biologia v Biotechnologia v Ochrona środowiska studia pierwszego stopnia Dla kandydatów z NOWĄ MATURĄ Kwalifikacja obejmuje konkurs świadectw dojrzałości brane są
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y
 Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Cracow University of Economics Poland
 Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
Cracow University of Economics Poland Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Keynote Speech - Presented by: Dr. David Clowes The Growth Research Unit,
PRACA DYPLOMOWA Magisterska
 POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych. mgr inż. Paweł Koszut
 Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych mgr inż. Paweł Koszut Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych Zamiast wstępu : Inspiracja GSM w Grecji
Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych mgr inż. Paweł Koszut Ukryte funkcjonalności w oprogramowaniu i urządzeniach elektronicznych Zamiast wstępu : Inspiracja GSM w Grecji
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Anonymous Authentication Using Electronic Identity Documents
 Department of Computer Science Faculty of Fundamental Problems of Technology Wroclaw University of Technology Anonymous Authentication Using Electronic Identity Documents by Kamil Kluczniak A thesis submitted
Department of Computer Science Faculty of Fundamental Problems of Technology Wroclaw University of Technology Anonymous Authentication Using Electronic Identity Documents by Kamil Kluczniak A thesis submitted
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to students
 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Poland) Wydawnictwo "Gea" (Warsaw. Click here if your download doesn"t start automatically
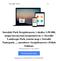 Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
EPS. Erasmus Policy Statement
 Wyższa Szkoła Biznesu i Przedsiębiorczości Ostrowiec Świętokrzyski College of Business and Entrepreneurship EPS Erasmus Policy Statement Deklaracja Polityki Erasmusa 2014-2020 EN The institution is located
Wyższa Szkoła Biznesu i Przedsiębiorczości Ostrowiec Świętokrzyski College of Business and Entrepreneurship EPS Erasmus Policy Statement Deklaracja Polityki Erasmusa 2014-2020 EN The institution is located
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition)
 Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
w łącznej analizie zmiennych licznikowych
 F O L I A O E C O N O M I C A C R A C O V I E N S I A Vol. LIII (2012) PL ISSN 0071-674X Dwuwymiarowy model TYPU ZIP-CP w łącznej analizie zmiennych licznikowych Jerzy Marzec Kaedra Ekonomerii i Badań
F O L I A O E C O N O M I C A C R A C O V I E N S I A Vol. LIII (2012) PL ISSN 0071-674X Dwuwymiarowy model TYPU ZIP-CP w łącznej analizie zmiennych licznikowych Jerzy Marzec Kaedra Ekonomerii i Badań
DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY DYNAMICZNE ASPEKTY WSPÓŁPRACY PANTOGRAFU Z SIECIĄ TRAKCYJNĄ
 TECHNICAL TRANSACTIONS ELECTRICAL ENGINEERING CZASOPISMO TECHNICZNE ELEKTROTECHNIKA DOI: 0.4467/353737XCT.6.46.6045 -E/06 MAREK DUDZIK, ADAM S. JAGIEŁŁO * DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY
TECHNICAL TRANSACTIONS ELECTRICAL ENGINEERING CZASOPISMO TECHNICZNE ELEKTROTECHNIKA DOI: 0.4467/353737XCT.6.46.6045 -E/06 MAREK DUDZIK, ADAM S. JAGIEŁŁO * DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI
 Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Rodzaj obliczeń. Data Nazwa klienta Ref. Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/ :53:55 PM
 Rodzaj obliczeń Data Nazwa klienta Ref Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/2007 10:53:55 PM Rodzaj obciążenia, parametry pracy Calculation Units SI Units (N, mm, kw...)
Rodzaj obliczeń Data Nazwa klienta Ref Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/2007 10:53:55 PM Rodzaj obciążenia, parametry pracy Calculation Units SI Units (N, mm, kw...)
