UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH W GÓRACH WYSOKICH NA PRZYKŁADZIE TATR. Jan Niedźwiecki, Natalia Kolecka
|
|
|
- Kacper Cichoń
- 8 lat temu
- Przeglądów:
Transkrypt
1 PRACE GEOGRAFICZNE, zeszyt 128 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2012, doi: / PG UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH W GÓRACH WYSOKICH NA PRZYKŁADZIE TATR Jan Niedźwiecki, Natalia Kolecka Relief and values of landscape metrics a case study from the Tatra Mts Abstract: The aim of the authors was to compare values of 2D and 3D landscape metrics in high mountains. The first part of the work takes into consideration the spatial structure of vegetation (the rank of landscape facias/ecotopes) of Kocioł Goryczkowy Świński, which was investigated in 1999 by Anna Kozłowska and Anna Jakomulska. The calculation of landscape metrics is resumed using the true surface geometries and compared with the result of traditional measurements on a reference plane. In the second part of the paper, a set of commonly used landscape metrics is calculated for the geocomplexes (rank of uroczysko unit) in the Morskie Oko catchment using both true surface and plain geometries. Finally average surface roughness is computed for the both study areas and some remarks for landscape metrics computed for geometric fields are given. The comparison shows that appropriate 2D and 3D metrics may differ significantly. Moreover, there is a strong correlation between the size of the discrepancy and the surface slope. For that reason, it is very important to distinguish between 2D and 3D metrics and to use them consciously, according to the particular problem. Keywords: landscape metrics, high mountain landscape, Tatra Mountains, 3D approach Zarys treści: W niniejszej pracy zaprezentowano wyniki porównania wartości wybranych metryk krajobrazowych otrzymanych na podstawie obliczeń wykonanych dwiema metodami: metodą tradycyjną, w której pomiarów dokonuje się po zrzutowaniu mozaiki jednostek przestrzennych na powierzchnię planimetryczną, oraz metodą uwzględniającą trzeci wymiar krajobrazu opartą na analizie numerycznego modelu terenu. Badania wykazały, że zastosowane metody mogą mieć wpływ na uzyskany obraz struktury krajobrazu wysokogórskiego. Ponadto w pracy zawarto uwagi dotyczące obliczania średniej szorstkości powierzchni oraz analiz wykonywanych przy wykorzystaniu pól geometrycznych w danym typie krajobrazu. Słowa kluczowe: metryki krajobrazowe, krajobraz wysokogórski, Tatry, podejście 3D
2 78 PRACE GEOGRAFICZNE, ZESZYT 128 Wprowadzenie Istotną cechą krajobrazu jest to, że zajmuje on wycinek przestrzeni (Zonneveld 1989; Richling, Solon 2002). Posiada granice zarówno poziome, jak i pionowe (Armand 1980), a więc jest fragmentem przestrzeni trójwymiarowej (pomijając czas). Fakt ten jest rzadko podkreślany w definicjach krajobrazu, który przez różnych autorów jest rozumiany w nieco odmienny sposób. Trójwymiarowość krajobrazu potwierdzają m.in. badania z dziedziny ekologii krajobrazu prowadzone od kilkudziesięciu lat. Można mówić o dwóch aspektach trzeciego wymiaru krajobrazu w tych badaniach: o jego pionowej strukturze (np. miąższość krajobrazu, koncepcje ekotopu, geosfer itd.) oraz jego strukturze poziomej i funkcjonowaniu na obszarach o zróżnicowanej rzeźbie terenu (np. katena geoekologiczna, sekwencja morfologiczna czy piętrowość krajobrazu). Mimo to dotychczasowe metody prezentacji struktury krajobrazu oraz pomiaru kompozycji i konfiguracji jednostek przestrzennych opierały się na założeniu, że krajobraz jest rzutem powierzchni terenu na powierzchnię planimetryczną, co jest uproszczeniem. Na obszarach nizinnych rozciągłość pozioma krajobrazu i poszczególnych jednostek przestrzennych jest na tyle duża w stosunku do ich miąższości i deniwelacji, że stosowanie tego uproszczenia nie ma zasadniczego wpływu na wyniki badań. Płaska mozaika płatów nie zawsze jest jednak reprezentatywnym modelem krajobrazu górskiego, a szczególnie wysokogórskiego, w którym nachylenie stoków dochodzi do 90 o. W tym wypadku powodem uproszczenia był brak technicznych możliwości badania krajobrazu jako trójwymiarowego przy jednoczesnej potrzebie jego kartograficznej prezentacji (często też bezpośrednie przeniesienie metod stosowanych na obszarach nizinnych). Współczesny rozwój technik GIS umożliwił konstruowanie numerycznych modeli terenu i ożywił dyskusję na temat trójwymiarowości krajobrazu i potrzeby wypracowania nowych metod jego badania. Zaczęto zwracać uwagę m.in. na fakt, że jednostki przestrzenne są bryłami (Pietrzak 2008), rozwinięto badania struktury pionowej roślinności (Blaschke i in. 2004; Drăguţ i in. 2010) i zaczęto poszukiwać możliwości precyzyjniejszego określenia cech kompozycji i konfiguracji składających się na krajobraz elementów jednostek przestrzennych na obszarach o zróżnicowanej rzeźbie terenu (Dorner i in. 2002; Hoechstetter i in. 2006, 2008; Hoechstetter 2009). Niniejsza praca dotyczy ostatniego z wymienionych tematów. Autorzy pragną zwrócić uwagę na fakt, że cechy struktury krajobrazu wysokogórskiego, który charakteryzuje się bardzo urozmaiconą rzeźbą terenu, mogą nie być precyzyjnie odzwierciedlone przy zastosowaniu tradycyjnych metod. Nowe możliwości techniczne i dostosowana do nich metodyka pozwalają uwzględnić rzeczywistą powierzchnię terenu przy obliczaniu metryk krajobrazowych. Badania trójwymiarowych metryk krajobrazowych opierano dotychczas na analizie: modeli neutralnych (Hoechstetter i in. 2008), płatów odzwierciedlających użytkowanie ziemi (Hoechstetter i in. 2006) lub modelu płatów i korytarzy (Hoechstetter, 2009). Metoda badań jest dopiero w fazie testowania i postuluje się (Hoechstetter i in. 2008) podejmowanie analiz w typach krajobrazu o różnej specyfice topograficznej. Potrzebę uwzględniania rzeczywistej rzeźby terenu przy
3 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Ryc. 1. Lokalizacja obszarów badań Fig. 1. Location of research areas określaniu różnorodności krajobrazu wysokogórskiego sygnalizowali także autorzy tego artykułu (Niedźwiecki 2005, 2009). Niniejsza praca ma na celu wykazanie znacznych różnic w wartościach metryk krajobrazowych 2D i 3D w krajobrazie wysokogórskim na przykładzie polskich Tatr, z zastosowaniem modelu geokompleksów. Badania prowadzono na dwóch obszarach: w Kotle Goryczkowym Świńskim, gdzie analizowano wydzielenia w randze facji krajobrazowych, a także w zlewni Morskiego Oka, w której badano uroczyska (ryc. 1). Opis wyników przeprowadzonych analiz podzielono na cztery części pierwsze dwie dotyczą badań porównawczych tych samych metryk krajobrazowych w 2D i 3D na poszczególnych obszarach badawczych, trzecia część dotyczy obliczania średniej szorstkości powierzchni (przykład metryki krajobrazowej obliczanej tylko w 3D), w czwartej zawarto uwagi do analiz wykonywanych przy wykorzystaniu pól geometrycznych. Metoda badań Podstawą wykonywanych analiz jest numeryczny model terenu (NMT) w postaci siatki trójkątów (TIN), których wierzchołki mogą być nieregularnie rozmieszczone na powierzchni terenu. Dzięki temu TIN może mieć wyższą rozdzielczość na obszarach
4 80 PRACE GEOGRAFICZNE, ZESZYT 128 o bardziej zróżnicowanej rzeźbie terenu lub w przypadku, gdy potrzebna jest bardziej szczegółowa informacja, a mniejszą na obszarach o mniej urozmaiconej powierzchni. Dane służące do budowy TIN mają najczęściej postać punktów i linii. Nie są one modyfikowane podczas tworzenia modelu, co pozwala na zachowanie precyzji danych wejściowych (Li i in. 2005). Modele TIN są zazwyczaj używane do analizy niewielkich obszarów, gdy wymagana jest wysoka precyzja. Proponowane przez innych autorów (Jenness 2004; Hoechstetter i in. 2008) użycie modeli grid w postaci siatki kwadratów (ryc. 2) zostało uznane za mniej dokładne. Zaprezentowano też (ryc. 3) model terenu w postaci nieregularnej siatki trójkątów i siatki kwadratów. Podstawowymi parametrami wykorzystywanymi do obliczania metryk krajobrazowych są powierzchnie i obwody poszczególnych jednostek przestrzennych w 2D i 3D. Każdy analizowany płat ma postać przestrzennego poligonu wektorowego, którego wierzchołki posiadają interpolowaną z NMT wysokość n.p.m. (ryc. 4). Granice każdego poligonu są rzutowane na model powierzchni, co pozwala zidentyfikować obszar wspólny dla obu obiektów. Wszystkie trójkąty i ich części, które mieszczą się w granicach poligonu, służą do obliczenia jego powierzchni w przestrzeni trójwymiarowej. Z wykorzystaniem oprogramowania GIS są obliczane następujące parametry: obwód 2D, obwód 3D, powierzchnia 2D i powierzchnia 3D, które są dodawane do tabeli atrybutów. Informacje te są danymi wejściowymi do obliczenia wielu metryk krajobrazowych w arkuszu kalkulacyjnym. Część metryk krajobrazowych wymaga jednak wykorzystania modelu grid, ponieważ wzory bazują na regularnym polu podstawowym (pikselu). W tym celu model TIN był konwertowany do postaci rastrowej o rozdzielczości ustalonej na podstawie analizy badanego obszaru i nominalnej dokładności NMT. Konwersję przeprowadzono za pomocą algorytmu liniowej interpolacji wysokości. Tą metodą obliczono średnią szorstkość powierzchni. Obliczane w pracy metryki krajobrazowe bazują na metrykach 2D zmodyfikowanych i podanych przez Hoechstettera (2009), a także na metrykach 2D podanych przez A. Kozłowską i A. Jakomulską (1999), zmodyfikowanych przez autorów. Badania w Kotle Goryczkowym Świńskim Badania w Kotle Goryczkowym Świńskim dotyczyły jednostek przestrzennych w randze facji krajobrazowych. Wykorzystano przy tym mapę roślinności opracowaną przez A. Kozłowską (1999) oraz założenie, że wyznaczenie granic fitocenoz jest wystarczające do wyznaczenia granic ekosystemów, ekosystemy zaś mogą być traktowane jako jednostki odniesienia w badaniach krajobrazu i jego zróżnicowania przestrzennego (Solon 2002). Kocioł Goryczkowy Świński jest górnym piętrem Doliny Goryczkowej o dnie położonym na wysokości m n.p.m. Jego zbocza są dojrzałe, w większości pokryte zwietrzeliną i w miarę jednolicie nachylone º. Jest to obszar o relatywnie słabo rozczłonkowanej rzeźbie terenu. Kulminacjami grzbietu głównego Tatr są: Goryczkowa Czuba (1913 m n.p.m.) i Pośredni Goryczkowy Wierch (1873 m n.p.m.). Największe powierzchnie zajmuje zespół muraw alpejskich Oreochloo distichae Juncetum trifidi, obok którego duże znaczenie mają borówczyska (Vaccinietum myrtilli). Charakte-
5 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Ryc. 3. Siatka trójkątów modelu TIN i siatka o rozdzielczości 50 m w rzucie ortogonalnym Fig. 3. The network of triangles in the TIN model and the network of squares in 50 m resolution Ryc. 2. Metoda określania powierzchni kwadratów i obwodu płata wg Jennessa (2004) Fig. 2. A method to determine area and perimeter of patch according to Jenness (2004) Ryc. 4. Trójwymiarowe poligony w zlewni Morskiego Oka widok perspektywiczny Fig. 4. Three-dimensional polygons in the Morskie Oko catchment perspective view
6 82 PRACE GEOGRAFICZNE, ZESZYT 128 rystyczne dla strefy przejściowej między piętrami roślinnymi są powypasowe postacie muraw alpejskich (ryc. 5 na wklejce). Badania na tym obszarze przeprowadziły ponad 10 lat temu A. Kozłowska i A. Jakomulska (1999). Autorki obliczyły kilka metryk krajobrazowych charakteryzujących strukturę przestrzenną roślinności kotła. W niniejszym opracowaniu powtórzono niektóre z tych obliczeń, wykorzystując trójwymiarową geometrię, która nie była dostępna autorkom wspomnianego opracowania. Policzono następujące parametry: całkowitą powierzchnię kotła, średnią powierzchnię wydzielenia, średnią powierzchnię wydzielenia danego typu, współczynnik zmienności powierzchni i średni wskaźnik rozczłonkowania konturu. Wskaźnik rozczłonkowania (F) jest wyrażony wzorem (Pietrzak 1989): gdzie: A powierzchnia wydzielenia, P obwód wydzielenia. Współczynnik zmienności powierzchni (V) policzono według wzoru (Bočarov, 1976): gdzie: s odchylenie standardowe danego parametru lub wskaźnika, x średnia wartość danego parametru lub wskaźnika. Obliczenia powierzchni całkowitej badanego obszaru przy uwzględnieniu rzeczywistej rzeźby terenu dały wynik o ponad m 2 (117,5%) większy, czyli m 2 zamiast m 2. W podobnym stosunku różnicuje się wartość średniej powierzchni płata odpowiednio 679 i 797 m 2. Różnice te wydają się znaczące. Nie są one stałe dla poszczególnych typów roślinności (ryc. 6). Największa rozbieżność cechuje wartości 2D i 3D powierzchni stoku skalnego pod szczytem Goryczkowej Czuby (13 Oreochloo distichae-juncetum trifidi w kompleksie z Rhizocarpetalia; odpowiednio 1851 i 2713 m 2 147%) i stromych muraw pod szczytem Pośredniego Goryczkowego Wierchu (19 Oreochloo distichae-juncetum trifidi typicum; odpowiednio 3393 i 4095 m 2 121%). Różnice w wartościach współczynnika zmienności powierzchni nie są znaczne (tab. 1). Trochę bardziej różnicują się natomiast wartości średniego wskaźnika rozczłonkowania konturu (ryc. 7). Wynika to z faktu, że dość jednostajnie nachylone stoki badanego kotła są średnio strome. Można za to zaobserwować, że płaty o kształcie wydłużonym zgodnie z linią spadku stoku mają w 3D wyższą wartość wskaźnika (np. 7 Luzuletum spadiceae zwarte), natomiast płaty wydłużone w kierunku przeciwnym do spadku stoku niższą (np. 15 Oreochloo distichae-juncetum trifidi sphagnetosum). Wartość wskaźnika nie zmienia się w przypadku zbiorowisk występujących na płaskim dnie kotła (np. 40 Calamagrostietum villosae tatricum) oraz tych, których płaty są kształtem zbliżone do koła (np. 47 Pinetum mughi carpaticum).
7 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Ryc. 6. Średnia powierzchnia płatów poszczególnych typów roślinności Objaśnienia zobacz ryc. 5 Fig. 6. Avarage area of patches of particular vegetation types Explanations see fig. 5 Ryc. 7. Średni wskaźnik rozczłonkowania konturu wg typów roślinności Objaśnienia zobacz ryc. 5 Fig. 7. Mean index of fragmentation of unit according to vegetation types Explanations see fig. 5
8 84 PRACE GEOGRAFICZNE, ZESZYT 128 Tab. 1. Metryki krajobrazowe liczone dla poszczególnych typów roślinności Table 1. Landscape metrics computed for vegetation types
9 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH... 85
10 86 PRACE GEOGRAFICZNE, ZESZYT 128 Badania w zlewni Morskiego Oka W drugiej części pracy policzono zestaw popularnych metryk krajobrazowych dla poligonu badawczego w zlewni Morskiego Oka, o bardziej urozmaiconej rzeźbie terenu niż Kocioł Goryczkowy Świński. Leży w obrębie granitoidowego trzonu krystalicznego Tatr Wysokich. Najniższym punktem jest Morskie Oko (1393 m n.p.m.), a najwyższym Rysy (2499 m n.p.m.). Występują tu cztery piętra krajobrazowe od górnoreglowego po turniowe. Na tym obszarze badano uroczyska. W przeciwieństwie do obszaru w Kotle Goryczkowym Świńskim typy geokompleksów wydzielono tu przede wszystkim na podstawie kryterium geomorfologicznego (ryc. 8). Mapę uroczysk przygotowano na podstawie opracowania J. Balona (1992). Dokonano digitalizacji oryginalnej mapy, która nie była wykonana cyfrowo, zweryfikowano jej aktualność podczas badań terenowych i na podstawie ortofotomapy (w rezultacie dodano kilka geokompleksów typu świeżych form grawitacyjnych, nieliczne geokompleksy zaliczono do innych typów, zmieniono ich zasięg, np. w związku ze zmianą granicy roślinności, podzielono itp.) oraz na podstawie wspomnianej ortofotomapy skorygowano granice wszystkich uroczysk (oryginalna mapa była wykonana na podkładzie mapy topograficznej w skali 1:10 000). W celu zwiększenia czytelności wyników zgrupowano wydzielenia w 18 typach (ryc. 3). W wersji dwuwymiarowej i trójwymiarowej policzono następujące metryki: całkowitą powierzchnię obszaru; powierzchnię (AREA): średnią płata, średnią płata danego typu, całkowitą płatów danego typu; obwód (PERIM): średni płata i średni płatów danego typu; ogólną długość granic (TE); gęstość granic (ED); gęstość płatów (PD); wskaźnik największego płata (LPI); wskaźnik kształtu (SHAPE); wymiar fraktalny (FRAC); stosunek obwodu do powierzchni (PARA). Obliczenia wykazały dużą różnicę powierzchni całkowitej badanego obszaru. W rzucie na powierzchnię planimetryczną ma on m 2, natomiast przy obliczaniu z uwzględnieniem rzeczywistej rzeźby terenu m 2 (151%). Ma to znaczny wpływ na inne metryki krajobrazowe dotyczące całego obszaru. Gęstość płatów, gęstość granic i wskaźnik największego płata obliczone jako metryki 3D przybierają wartości odpowiednio mniejsze, całkowita długość granic jest zaś większa (tab. 2). Średnia powierzchnia uroczyska przy uwzględnieniu ukształtowania terenu jest większa w tym samym stosunku co powierzchnia całkowita (151%). W mniejszym stopniu różnicuje się średni obwód (125%), co sprawia, że średni stosunek obwodu do powierzchni również się zmienia z 0,097 w 2D na 0,081 w 3D (tab. 3). Podobne są wartości metryk charakteryzujących kształt geokompleksów średni wskaźnik kształtu w 3D osiąga wartość o 0,025 wyższą, średni wymiar fraktalny ma zaś w obu przypadkach identyczną wartość. Z obliczeń metryk krajobrazowych wykonanych obiema metodami można wysnuć sprzeczne wnioski na temat niektórych cech struktury krajobrazu badanego obszaru. Jak widać na wykresie (ryc. 9) w strukturze krajobrazu odzwierciedlonego jako rzut na powierzchnię planimetryczną dominują stoki strome zwietrzelinowe, następnie stoki skalne oraz stożki i hałdy usypiskowe. Obliczenia wykonane z uwzględnieniem rzeczywistej rzeźby terenu wykazują, że największe powierzchnie zajmują ściany skalne, następnie stoki skalne i stoki strome zwietrzelinowe. Warto przy tym odnotować, że powierzchnia
11 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Tab. 2. Metryki krajobrazowe dotyczące całego obszaru badań Table 2. Landscape metrics concerning the whole study area Tab. 3. Średnie wartości metryk krajobrazowych liczonych dla poszczególnych uroczysk Table 3. Average values of landscape metrics for particular landscape units ścian skalnych obliczona metodą 3D jest większa prawie dwa i pół raza (230%). Sytuacja wygląda podobnie, jeśli chodzi o średnie powierzchnie uroczysk danego typu (ryc. 10). Na mapie dominują stożki i hałdy usypiskowe oraz łagodne stoki zwietrzelinowe (pomijając jeziora, których dla lepszej czytelności nie umieszczono na wykresie ich powierzchnia nie różnicuje się). Porównywalne średnie powierzchnie mają następnie: stoki strome zwietrzelinowe, ściany skalne oraz dna kotłów glacjalnych z wałami morenowymi. Jeżeli weźmiemy pod uwagę rzeczywistą powierzchnię terenu, sytuacja zmienia się diametralnie: ściany skalne są płatami wyraźnie dominującymi powierzchniowo, duże są także geokompleksy stoków skalnych zwietrzelinowych, a dopiero w następnej kolejności plasują się stożki i hałdy usypiskowe oraz pozostałe dwa typy stoków.
12 88 PRACE GEOGRAFICZNE, ZESZYT 128 Rys. 5. Roślinność Kotła Goryczkowego Świńskiego wg A. Kozłowskiej (1999) Objaśnienia: 1 Rhizocarpetalia, 3 inicjalne stadia wkraczania roślin zarodnikowych na nieustabilizowanym podłożu, 6 pionierskie zbiorowiska mszaków ze związku Salicion herbaceae, 7 Luzuletum spadiceae słabo zwarte, 8 Luzuletum spadiceae, 12 Luzuletum spadiceae w kompleksie ze zbior. z Deschampsia flexuosa, 13 Oreochloo distichae-juncetum trifidi w kompleksie z Rhizocarpetalia, 15 Oreochloo distichae-juncetum trifidi sphagnetosum, 16 Oreochloo distichae-juncetum trifidi typicum postać mszysta, 19 Oreochloo distichae-juncetum trifidi typicum, 20 Oreochloo distichae-juncetum trifidi cetrarietosum, 21 Oreochloo distichae-juncetum trifidi postać z Juncus trifidus, 23 Oreochloo distichae-juncetum trifidi wilgotna postać pionierska z Juncus trifidus, 25 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis, 26 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis postać wilgotna, 28 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis w kompleksie z Calamagrostietum villosae tatricum, 31 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis słabo zwarte, 32. Oreochloo distichae-juncetum trifidi powypasowa postać subalpejska, 33 Oreochloo distichae-juncetum trifidi subalpejska postać powypasowa, wilgotna, 34 Oreochloo distichae-juncetum trifidi powypasowa postać subalpejska słabo zwarta, z borówkami, 36 Oreochloo distichae-juncetum trifidi powypasowa postać subalpejska, z borówkami, w kompleksie z Calamagrostietum villosae tatricum, 37 Zbiorowisko z Festuca picta, 38 Zbiorowisko z Deschampsia flexuosa, 39 Zbiorowisko z Deschampsia flexuosa w kompleksie z Luzuletum spadiceae, 40 Calamagrostietum villosae tatricum, 41 Vaccinietum myrtilli, 42 Vaccinietum myrtilli słabo zwarte, 44 Vaccinietum myrtilli w kompleksie ze zbiorowiskiem z Deschampsia flexuosa, 45 Vaccinietum myrtilli zatorfione, 46 Empetro-Vaccinietum, 47 Pinetum mughi carpaticum Fig. 5. Vegetation of Kocioł Goryczkowy Świński according to A. Kozłowska (1999) Explanations: 1 Rhizocarpetalia, 3 cryptogamic plant communities on serce, initial phase, 6 pionieer moss-communities of the alliance Salicion herbaceae, 7 Luzuletum spadiceae sparse, 8 Luzuletum spadiceae, 12 Luzuletum spadiceae in a complex with the community of Deschampsia flexuosa, 13 Oreochloo distichae-juncetum trifidi in a complex with Rhizocarpetalia, 15 Oreochloo distichae-juncetum trifidi sphagnetosum, 16 Oreochloo distichae-juncetum trifidi typicum mossy form, 19 Oreochloo distichae-juncetum trifidi typicum, 20 Oreochloo distichae-juncetum trifii cetrarietosum, 21 Oreochloo distichae-juncetum trifidi form with Juncus trifidus, 23 Oreochloo distichae-juncetum trifidi wet pioneer form with Juncus trifidus, 25 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis, 26 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis wet form, 28 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis in a complex with Calamagrostietum villosae tatricum, 31 Oreochloo distichae-juncetum trifidi caricetosum sempervirentis sparse, 32 Oreochloo distichae-juncetum trifidi post-grazing subalpine form, 33 Oreochloo distichae-juncetum trifidi post-grazing subalpine wet form, 34 Oreochloo distichae-juncetum trifidi post-grazing subalpine sparse form with Vaccinium myrtillus, 36 Oreochloo distichae-juncetum trifidi post-grazing subalpine form with Vaccinium myrtillus in a complex with Calamagrostietum villosae tatricum, 37 Festuca picta community, 38 Deschampsia flexuosa community, 39 Deschampsia flexuosa community in a complex with Luzuletum spadiceae, 40 Calamagrostietum villosae tatricum, 41 Vaccinietum myrtilli, 42 Vaccinietum myrtilli sparse, 44 Vaccinietum myrtilli in a complex with the community of Deschampsia flexuosa, 45 Vaccinietum myrtilli Sphagnum-form, 46 Empetro-Vaccinietum, 47 Pinetum mughi carpaticum
13 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Ryc. 9. Powierzchnia całkowita typów uroczysk Objaśnienia zobacz ryc. 8 Fig. 9. Area of stow types Explanations see fig. 8 Ryc. 10. Średnia powierzchnia uroczyska wg typów Objaśnienia zobacz ryc. 8 Fig. 10. Avarage stow area Explanations see fig. 8
14 90 PRACE GEOGRAFICZNE, ZESZYT 128 Średnia szorstkość powierzchni Wykorzystanie NMT umożliwiło obliczanie tradycyjnych metryk krajobrazowych z uwzględnieniem rzeczywistej rzeźby terenu. Jego zastosowanie było również podstawą opracowania kilku nowych metryk charakteryzujących ukształtowanie powierzchni (Hoechstetter i in. 2006, 2008). Najbardziej podstawową z nich jest średnia szorstkość powierzchni (average surface roughness Ra): gdzie: N liczba pikseli w obrębie danego obszaru, h n odchyłka między wysokością n-tego piksela a średnią wysokością obszaru. Średnią szorstkość powierzchni obliczono według typów jednostek przestrzennych na obu obszarach badawczych (ryc. 11 i 12). Wskaźnik ten ukazuje średnią z odchyleń wysokości poszczególnych pikseli w poligonie od średniej wysokości tego poligonu. Otrzymane wartości są skorelowane ze średnią deniwelacją płatów poszczególnych typów. Zatem testowana metryka nie odzwierciedla oczekiwanej cechy krajobrazu jego szorstkości w analizowanym typie krajobrazu. Miarę tę zaproponowano (Hoechstetter i in. 2006) na podstawie badania wielkopowierzchniowych jednostek przestrzennych odzwierciedlających klasy użytkowania terenu w dolinie Łaby. Założeniem było występowanie w obrębie jednej jednostki przestrzennej niewielkich powierzchniowo wzniesień i obniżeń terenu. Na obszarach wysokogórskich taka sytuacja występuje niezwykle rzadko. Masywy górskie zajmują relatywnie duże powierzchnie, jednostki przestrzenne (niezależnie od przyjętego modelu) są zaś w większości częściami stoku żeby oddać szorstkość ich powierzchni, płaszczyzna odniesienia nie powinna być pozioma, a nachylona. Pola geometryczne W badaniach krajobrazu zamiast przyrodniczych jednostek przestrzennych stosuje się czasem pola geometryczne (np. Krzymowska-Kostrowicka 1988; Balon 2007). Do zalet tej metody zalicza się względny obiektywizm wynikający z przypadkowości (ich wyznaczanie jest bowiem mechaniczne) oraz równość powierzchni wydzieleń. Jeżeli jednak badania dotyczą obszaru o skomplikowanej rzeźbie terenu i uwzględniona zostanie rzeczywista jego powierzchnia, drugie z tych założeń jest błędne. Na rycinie 13 zaprezentowano 34 kwadraty (najczęściej stosowane pola geometryczne) o wymiarach m, ułożone na linii przecinającej poligon badawczy w zlewni Morskiego Oka. Powierzchnie wszystkich kwadratów są równe po zrzutowaniu na powierzchnię planimetryczną. Ich powierzchnia obliczona w 3D jest jednak bardzo zróżnicowana i może osiągać wartości ponad dwukrotnie wyższe od oczekiwanych (w obrębie ścian skalnych). Obliczenia wykonane dla całego obszaru wykazały, że powierzchnia poszczególnych kwadratów może przekraczać nawet m 2. Ma to wpływ na obliczenia statystyczne, w których natężenie zjawiska odnosi się do powierzchni pól geometrycznych.
15 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Ryc. 11. Średnia szorstkość powierzchni wg typów roślinności w Kotle Goryczkowym Świńskim Objaśnienia zobacz ryc. 5 Fig. 11. Average surface roughness according to vegetation types in Kocioł Goryczkowy Świński Explanations see fig. 5 Ryc. 12. Średnia szorstkość powierzchni wg typów uroczysk w zlewni Morskiego Oka Objaśnienia zobacz ryc. 8 Fig. 12. Average surface roughness according to stow types in the Morskie Oko catchment Explanations see fig. 8 Przykładem metryki krajobrazowej, która może być obliczana przy wykorzystaniu pól geometrycznych, jest gęstość granic (ED). Na rycinie 14 zaprezentowano wyniki obliczeń wykonanych dla zlewni Morskiego Oka. Aby ukazać zróżnicowanie wyników, zignorowano fakt, że obliczenia 3D są metodycznie niepoprawne, ponieważ zmienną (długość granic) odnosi się do zmiennej (powierzchnia), zamiast odnosić ją do stałej. Obliczenia, w których uwzględniono rzeczywistą rzeźbę terenu, są podstawą oczywistego wniosku, że gęstość granic na wielu obszarach poligonu badawczego jest mniejsza, niż by to wynikało z obliczeń 2D.
16 92 PRACE GEOGRAFICZNE, ZESZYT 128 Ryc. 13. Powierzchnia pól geometrycznych m w przekroju zlewni Morskiego Oka Fig. 13. Area of geometric fields m in the transect of the Morskie Oko catchment Ryc. 14. Porównanie gęstości granic 2D i 3D w zlewni Morskiego Oka Fig. 14. Comparison of 2D and 3D edge density in the Morskie Oko catchment
17 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Podsumowanie i wnioski Obliczanie metryk krajobrazowych to istotny aspekt badań we współczesnej ekologii krajobrazu. Pozwalają one określić cechy struktury i funkcjonowania krajobrazu, co jest jednym z podstawowych celów, jakie stawia przed sobą ta dziedzina wiedzy. Są one wykorzystywane bardzo powszechnie, a więc zaprezentowany w niniejszej pracy problem sposobu ich pomiaru (w tym wypadku na obszarach wysokogórskich) jest bardzo ważny. Nie jest to problem łatwy i autorzy zdają sobie sprawę z tego, że zasadność stosowania metryk krajobrazowych 3D może zależeć od przynajmniej trzech czynników. Po pierwsze od celu dla danego obszaru różnice między wartościami metryk krajobrazowych 2D i 3D mogą być ocenione jako nieistotne w kontekście konkretnego wykorzystania danych badań. Konstruowanie numerycznego modelu terenu jest natomiast pracochłonne. Po drugie, metodyka jest dopiero w fazie opracowań i nie wszystkie metryki 2D (dużą ich liczbę podają K. McGarigal i B.J. Marks, 1995) są opracowane dla trójwymiarowej geometrii; wiele wymaga testowania w różnych typach krajobrazu. Ostatnim z czynników jest skala. W małej skali powierzchnię górotworu na mapie kontynentu będziemy skłonni określać na podstawie pomiaru na powierzchni planimetrycznej, niezależnie od wysokości szczytów w tym wypadku bardziej istotne jest, jaki wycinek Ziemi geoidy on zajmuje. W dużych skalach, które zaprezentowano w niniejszej pracy, powinno się zdaniem autorów stosować geometrię trójwymiarową. Oczywiście również stosowany w takich badaniach NMT jest tylko modelem przybliżającym rzeźbę terenu, a nie rzeczywistym terenem, a w zależności od zastosowanego rodzaju tego modelu można otrzymać różniące się wartości metryk krajobrazowych. Jak wykazują badania (Stupariu i in., 2010), są to jednak rozbieżności nieistotne, wykazane zaś w niniejszej pracy różnice między wartościami metryk 2D i 3D są znaczne. Do głównych wniosków płynących z przeprowadzonych badań, a odnoszących się do metryk krajobrazowych w krajobrazie wysokogórskim, należy zaliczyć poniższe. 1. Krajobraz stanowi wycinek przestrzeni trójwymiarowej (pomijając czas) i należy dążyć do wypracowania takiej metodyki jego opisu, prezentacji i badania, która pozwalałaby tę cechę w pełni uwzględnić. 2. Większość wartości przeanalizowanych metryk krajobrazowych różni się w zależności od zastosowanej metody 2D lub 3D. 3. Gęstość płatów, gęstość granic i wskaźnik największego płata obliczone jako metryki 3D przybierają w stosunku do obliczeń tradycyjną metodą 2D wartości odpowiednio mniejsze, powierzchnia i całkowita długość granic są zaś większe. 4. Z obliczeń metryk krajobrazowych wykonanych dla poszczególnych typów geokompleksów w 2D i 3D można wysnuć sprzeczne wnioski na temat niektórych cech struktury krajobrazu. Dotyczy to w szczególności powierzchni zajmowanej przez poszczególne typy jednostek przestrzennych, a w mniejszym stopniu ich kształtu. 5. W strukturze krajobrazu zlewni Morskiego Oka odzwierciedlonego jako rzut na powierzchnię planimetryczną dominują stoki strome zwietrzelinowe, natomiast obliczenia wykonane z uwzględnieniem rzeczywistej rzeźby terenu wykazują, że największe powierzchnie zajmują ściany skalne. Analogicznie największymi
18 94 PRACE GEOGRAFICZNE, ZESZYT 128 powierzchniowo płatami w tym obszarze są w 2D stożki i hałdy usypiskowe, w 3D zaś ściany skalne. 6. Płaty o kształcie wydłużonym zgodnie z linią spadku stoku mają w 3D wyższą wartość wskaźnika rozczłonkowania konturu, a płaty wydłużone w kierunku przeciwnym do spadku stoku niższą. Wartość wskaźnika nie zmienia się dla płatów o kształcie zbliżym do koła. 7. Istnieją metryki krajobrazowe, których wartości 2D i 3D na badanych obszarach są porównywalne współczynnik zmienności powierzchni w Kotle Goryczkowym Świńskim, wskaźnik kształtu i wymiar fraktalny w zlewni Morskiego Oka. 8. Średnia szorstkość krajobrazu jest metryką, która, według autorów, nie znajdzie zastosowania w krajobrazie wysokogórskim, gdyż nie jest dostosowana do jego specyfiki. 9. Obliczenia wykonywane z wykorzystaniem pól geometrycznych i odnoszące się do ich powierzchni lub obwodów są w badanym typie krajobrazu (przy uwzględnieniu rzeczywistej rzeźby terenu) obarczone błędem. Literatura Armand D.L., 1980, Nauka o krajobrazie, PWN, Warszawa. Balon J Struktura i funkcjonowanie polskiej części zlewni Białki w Tatrach, rozprawa doktorska, IG UJ, Kraków. Balon J. 2007, Stabilność środowiska przyrodniczego Karpat Zachodnich powyżej górnej granicy lasu, IGiGP UJ, Kraków. Blaschke T., Tiede D., Heurich M., 2004, 3D landscape metrics to modeling forest structure and diversity based on laser scanning data, International Archives of Photogrametry, Remote Sensing and Spatial Information Sciences, 36, 8/W2, Bočarov M.K., 1976, Metody statystyki matematycznej w geografii, PWN, Warszawa. Dorner B., Lertzman K., Fall J., Landscape pattern in topographically complex landscapes: issues and techniques for analysis, Landscape Ecology 17, Drăguţ L., Walz U., Blaschke Th., 2010, The Third and Fourth Dimensions of Landscape: towards Conceptual Models of Topographically Complex Landscapes, Landscape Online, 22, Hoechstetter S., 2009, Enhanced methods for analysing landscape structure. Landscape metrics for characterising three-dimensional patterns and ecological gradients, Rhombos-Verlag, Berlin. Hoechstetter S., Thinh N.X., Walz U., 2006, 3D-indices for the analysis of spatial patterns of landscape structure [w:] H. Kremers, V. Tikunov (red.), Proceedings InterCarto-InterGIS 12, International Conference on Geoinformation for Sustainable Development, Berlin, Hoechstetter S., Walz U., Dang L.H., Thinh N.X., 2008, Effects of topography and surface roughness in analyses of landscape structure A proposal to modify the existing set of landscape metrics, Landscape Online, 3, Jenness J.S., Calculating landscape surface area from digital elevation models, Wildlife Society Bulletin 32, McGarigal K., Marks B.J., 1995, FRAGSTATS: spatial pattern analysis program for quantifying landscape structure, Portland.
19 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH Kozłowska A., 1999, Problemy kartowania roślinności wysokogórskiej w skali szczegółowej (na przykładzie map roślinności Kotła Gąsienicowego i Goryczkowego Świńskiego [w:] A. Kotarba, A. Kozłowska (red.), Badania geoekologiczne w otoczeniu Kasprowego Wierchu, Prace Geograficzne, IGiPZ PAN, 174, Kozłowska A., Jakomulska A., 1999, Struktura przestrzenna roślinności kotłów Gąsienicowego i Goryczkowego Świńskiego [w:] A. Kotarba, A. Kozłowska (red.), Badania geoekologiczne w otoczeniu Kasprowego Wierchu, Prace Geograficzne, IGiPZ PAN, 174, Krzymowska-Kostrowicka A., 1988, Zagospodarowanie i ruch turystyczny, Prace Geograficzne IGiPZ PAN, 147. Li Z., Zhu Q., Gold Ch., 2005, Digital Terrain Modeling: Principles and Methodology, USA, Boca Raton, CRC Press. Niedźwiecki J., 2005, Mozaikowość krajobrazu wysokogórskiego na wybranych przykładach w Tatrach, praca magisterska, WGiSR UW, Warszawa. Niedźwiecki J., 2009, Badanie mozaikowości krajobrazu wysokogórskiego Tatr z wykorzystaniem transektów geoekologicznych, Problemy Ekologii Krajobrazu, XXIII, Pietrzak M., 1989, Problemy i metody badania struktury geokompleksu (na przykładzie powierzchni modelowej Biskupice), UAM, Poznań. Pietrzak M., 2008, Jednostki krajobrazowe figury czy bryły?, Problemy Ekologii Krajobrazu, XX, Warszawa, Richling A., Solon J., 2002, Ekologia Krajobrazu, Wydawnictwo Naukowe PWN, Warszawa. Solon J., 2002, Ocena różnorodności krajobrazu na podstawie analizy struktury przestrzennej roślinności, Prace Geograficzne IGiPZ PAN, 185. Stupariu M.-S., Pătru-Stupariu I., Cuculici R., 2010, Geometric approaches to computing 3D-landscape metrics, Landscape Online, 24, Zonneveld I.S., 1989, The land unit A fundamental concept in landscape ecology, and its applications, Landscape Ecology, 3, 2, Jan Niedźwiecki Uniwersytet Jagielloński Instytut Geografii i Gospodarki Przestrzennej ul. Gronostajowa 7, Kraków jniedzwiecki@geo.uj.edu.pl Natalia Kolecka Uniwersytet Jagielloński Instytut Geografii i Gospodarki Przestrzennej ul. Gronostajowa 7, Kraków nkolecka@gis.geo.uj.edu.pl
20
21 wkładka nr 3 str 1 (Jan Niedźwiecki, Natalia Kolecka)
22 wkładka nr 3 str 2 (Jan Niedźwiecki, Natalia Kolecka) Rys. 8. Typy uroczysk w zlewni Morskiego Oka. Opracowano na podstawie mapy J. Balona (1992) Objaśnienia: 1 grzbiety, 2 ściany skalne, 3 stoki skalne, 4 stoki strome zwietrzelinowe, 5 stoki łagodne zwietrzelinowe, 6 żleby skalne, 7 żleby piarżyste, 8 świeże formy grawitacyjne, 9 wciosy, 10 stożki i hałdy usypiskowe, 11 powierzchnie moreny dennej, wały morenowe, 12 dna kotłów glacjalnych i niwalnych, 13 zagłębienia i równiny morenowe z misami jezior, 14 skalne koryta potoków, 15 ściany skalne pod wodospadami, 16 aluwialne koryta potoków, 17 stożki napływowe, 18 jeziora Fig. 8. Stow types in Morskie Oko catchment. Elaborated on the basis of the map of J. Balon (1992) Explanations:1 surfaces of mountain culminations, 2 rockwalls, 3 rocky slopes, 4 steep waste-covered slopes, 5 gentle waste-covered slopes, 6 rock-cut gullies, 7 gullies with debris, 8 fresh gravitational forms, 9 V-shaped valleys, 10 talus cones and heaps, 11 valley floors filled with morainic mantle, morainic ridges, 12 beds of glacial and nival cirques, 13 morainic plains and depressions with lakes, 14 rocky stream beds, 15 waterfalls (rockwalls), 16 alluvial stream beds, 17 alluvial cones, 18 lakes
UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH W GÓRACH WYSOKICH NA PRZYKŁADZIE TATR. Jan Niedźwiecki, Natalia Kolecka
 PRACE GEOGRAFICZNE, zeszyt 128 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2012, 77 95 doi: 10.4467/20833113PG.12.007.0356 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH
PRACE GEOGRAFICZNE, zeszyt 128 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2012, 77 95 doi: 10.4467/20833113PG.12.007.0356 UKSZTAŁTOWANIE POWIERZCHNI TERENU A WARTOŚCI METRYK KRAJOBRAZOWYCH
Badanie mozaikowości krajobrazu wysokogórskiego Tatr z wykorzystaniem transektów geoekologicznych
 Niedźwiecki J., 2009, Badanie mozaikowości krajobrazu wysokogórskiego Tatr z wykorzystaniem transektów geoekologicznych. Problemy ekologii krajobrazu, T. XXIII, 137 147. Niedźwiecki J., 2009, The research
Niedźwiecki J., 2009, Badanie mozaikowości krajobrazu wysokogórskiego Tatr z wykorzystaniem transektów geoekologicznych. Problemy ekologii krajobrazu, T. XXIII, 137 147. Niedźwiecki J., 2009, The research
Zakład Hydrologii i Geoinformacji, Instytut Geografii UJK. Modelowanie przestrzeni geograficznej. Konwersatorium: 11 i 12
 Modelowanie przestrzeni geograficznej Konwersatorium: 11 i 12 Temat: Analiza wybranych parametrów geomorfologicznych modelowanego terenu. Spadek wartość tego parametru w oznacza kąt nachylenia stoku w
Modelowanie przestrzeni geograficznej Konwersatorium: 11 i 12 Temat: Analiza wybranych parametrów geomorfologicznych modelowanego terenu. Spadek wartość tego parametru w oznacza kąt nachylenia stoku w
Metody obliczania obszarowych
 Metody obliczania opadów średnich obszarowych W badaniach hydrologicznych najczęściej stosowaną charakterystyką liczbową opadów atmosferycznych jest średnia wysokość warstwy opadu, jaka spadła w pewnym
Metody obliczania opadów średnich obszarowych W badaniach hydrologicznych najczęściej stosowaną charakterystyką liczbową opadów atmosferycznych jest średnia wysokość warstwy opadu, jaka spadła w pewnym
Metody obliczania obszarowych
 Metody obliczania opadów średnich obszarowych W badaniach hydrologicznych najczęściej stosowaną charakterystyką liczbową opadów atmosferycznych jest średnia wysokość warstwy opadu, jaka spadła w pewnym
Metody obliczania opadów średnich obszarowych W badaniach hydrologicznych najczęściej stosowaną charakterystyką liczbową opadów atmosferycznych jest średnia wysokość warstwy opadu, jaka spadła w pewnym
Analiza wykonalności dla wskaźnika: dostępność obszarów pod zabudowę
 Analiza wykonalności dla wskaźnika: dostępność obszarów pod zabudowę Analizę wykonalności dla wskaźnika dostępności obszarów pod zabudowę wykonamy zgodnie z przedstawionym schematem postępowania rozpoczynając
Analiza wykonalności dla wskaźnika: dostępność obszarów pod zabudowę Analizę wykonalności dla wskaźnika dostępności obszarów pod zabudowę wykonamy zgodnie z przedstawionym schematem postępowania rozpoczynając
MODELOWANIE UDZIAŁU TYPÓW SIEDLISKOWYCH LASU NA PODSTAWIE MAP POKRYCIA CORINE LAND COVER I NUMERYCZNYCH MODELI TERENU
 SEMINARIUM ZAGROŻENIA LASÓW ZALEŻNE OD STANU ATMOSFERY Instytut Badawczy Leśnictwa Sękocin Stary 10 stycznia 2013 MODELOWANIE UDZIAŁU TYPÓW SIEDLISKOWYCH LASU NA PODSTAWIE MAP POKRYCIA CORINE LAND COVER
SEMINARIUM ZAGROŻENIA LASÓW ZALEŻNE OD STANU ATMOSFERY Instytut Badawczy Leśnictwa Sękocin Stary 10 stycznia 2013 MODELOWANIE UDZIAŁU TYPÓW SIEDLISKOWYCH LASU NA PODSTAWIE MAP POKRYCIA CORINE LAND COVER
Analiza wykonalności dla wskaźnika: zmiany obszarów użytkowanych rolniczo
 Analiza wykonalności dla wskaźnika: zmiany obszarów użytkowanych rolniczo Analizę wykonalności dla kolejnego wskaźnika: zmiany obszarów użytkowanych rolniczo rozpoczniemy, podobnie do wskaźnika dostępności
Analiza wykonalności dla wskaźnika: zmiany obszarów użytkowanych rolniczo Analizę wykonalności dla kolejnego wskaźnika: zmiany obszarów użytkowanych rolniczo rozpoczniemy, podobnie do wskaźnika dostępności
ZRÓŻNICOWANIE TYPÓW GEOKOMPLEKSÓW CZĘŚCIOWYCH (MORFOTOPÓW) W POŁUDNIOWEJ CZĘŚCI DOLINY KOŚCIELISKIEJ W TATRACH ZACHODNICH. Justyna Kmiecik-Wróbel
 PRACE GEOGRAFICZNE, zeszyt 128 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2012, 55 60 doi: 10.4467/20833113PG.12.005.0354 ZRÓŻNICOWANIE TYPÓW GEOKOMPLEKSÓW CZĘŚCIOWYCH (MORFOTOPÓW) W POŁUDNIOWEJ
PRACE GEOGRAFICZNE, zeszyt 128 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2012, 55 60 doi: 10.4467/20833113PG.12.005.0354 ZRÓŻNICOWANIE TYPÓW GEOKOMPLEKSÓW CZĘŚCIOWYCH (MORFOTOPÓW) W POŁUDNIOWEJ
PROPOZYCJA ZASTOSOWANIA WYMIARU PUDEŁKOWEGO DO OCENY ODKSZTAŁCEŃ PRZEBIEGÓW ELEKTROENERGETYCZNYCH
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 56 Politechniki Wrocławskiej Nr 56 Studia i Materiały Nr 24 2004 Krzysztof PODLEJSKI *, Sławomir KUPRAS wymiar fraktalny, jakość energii
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 56 Politechniki Wrocławskiej Nr 56 Studia i Materiały Nr 24 2004 Krzysztof PODLEJSKI *, Sławomir KUPRAS wymiar fraktalny, jakość energii
METODY PREZENTACJI KARTOGRAFICZNEJ. HALINA KLIMCZAK INSTYTUT GEODEZJI I GEOINFORMATYKI WE WROCŁAWIU
 METODY PREZENTACJI KARTOGRAFICZNEJ HALINA KLIMCZAK INSTYTUT GEODEZJI I GEOINFORMATYKI WE WROCŁAWIU halina.klimczak@up.wroc.pl METODY PREZENTACJI KARTOGRAFICZNEJ Wynikiem końcowym modelowania kartograficznego
METODY PREZENTACJI KARTOGRAFICZNEJ HALINA KLIMCZAK INSTYTUT GEODEZJI I GEOINFORMATYKI WE WROCŁAWIU halina.klimczak@up.wroc.pl METODY PREZENTACJI KARTOGRAFICZNEJ Wynikiem końcowym modelowania kartograficznego
Z METODYKI WYZNACZANIA GEOKOMPLEKSÓW. From the methodology of geocomplexes delimitation
 Prace i Studia Geograficzne 2011, T. 46, ss. 143 153 Katarzyna Kaim Uniwersytet Warszawski Wydział Geografii i Studiów Regionalnych Zakład Geoekologii Z METODYKI WYZNACZANIA GEOKOMPLEKSÓW From the methodology
Prace i Studia Geograficzne 2011, T. 46, ss. 143 153 Katarzyna Kaim Uniwersytet Warszawski Wydział Geografii i Studiów Regionalnych Zakład Geoekologii Z METODYKI WYZNACZANIA GEOKOMPLEKSÓW From the methodology
Grzegorz Wałek Zakład Hydrologii i Geoinformacji Instytut Geografii UJK
 Budowa hydrologicznie poprawnego cyfrowego modelu wysokościowego - studium przypadku na przykładzie zlewni Grajcarka (pogranicze Pienin i Beskidu Sądeckiego) Grzegorz Wałek Zakład Hydrologii i Geoinformacji
Budowa hydrologicznie poprawnego cyfrowego modelu wysokościowego - studium przypadku na przykładzie zlewni Grajcarka (pogranicze Pienin i Beskidu Sądeckiego) Grzegorz Wałek Zakład Hydrologii i Geoinformacji
ZAGADNIENIE METODY OCENY DOKŁADNOŚCI CYFROWYCH MODELI TERENU W ASPEKCIE IMPLEMENTACJI EUROPEJSKIEJ DYREKTYWY INSPIRE
 JERZY WYSOCKI ZAGADNIENIE METODY OCENY DOKŁADNOŚCI CYFROWYCH MODELI TERENU W ASPEKCIE IMPLEMENTACJI EUROPEJSKIEJ DYREKTYWY INSPIRE PROBLEM OF METHOD OF ESTIMATION OF ACCURACY OF THE DIGITAL TERRAIN MODELS
JERZY WYSOCKI ZAGADNIENIE METODY OCENY DOKŁADNOŚCI CYFROWYCH MODELI TERENU W ASPEKCIE IMPLEMENTACJI EUROPEJSKIEJ DYREKTYWY INSPIRE PROBLEM OF METHOD OF ESTIMATION OF ACCURACY OF THE DIGITAL TERRAIN MODELS
ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2012
 ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2012 OPRACOWAŁY: ANNA ANWAJLER MARZENA KACZOR DOROTA LIS 1 WSTĘP W analizie wykorzystywany będzie model szacowania EWD.
ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2012 OPRACOWAŁY: ANNA ANWAJLER MARZENA KACZOR DOROTA LIS 1 WSTĘP W analizie wykorzystywany będzie model szacowania EWD.
Jarosław Balon PoDaTnoŚĆ GEosYsTEMÓw GÓrsKICH na ZMIanY antropogeniczne na PrZYKłaDZIE DolInY BIałKI w TaTraCH Wprowadzenie Obszar badań
 Jarosław Balon PODATNOŚĆ GEOSYSTEMÓW GÓRSKICH NA ZMIANY ANTROPOGENICZNE NA PRZYKŁADZIE DOLINY BIAŁKI W TATRACH Wprowadzenie Zachodzące współcześnie przemiany środowiska przyrodniczego w obrębie geosystemów
Jarosław Balon PODATNOŚĆ GEOSYSTEMÓW GÓRSKICH NA ZMIANY ANTROPOGENICZNE NA PRZYKŁADZIE DOLINY BIAŁKI W TATRACH Wprowadzenie Zachodzące współcześnie przemiany środowiska przyrodniczego w obrębie geosystemów
MAPY FITOSOCJOLOGICZNE Mapy roślinności, jej zróżnicowania na zbiorowiska i kompleksy przestrzenne zbiorowisk.
 W10 PLANOWANIE PRZESTRZENNE 14.12.10 ELEMENTY KARTOGRAFII GEOBOTANICZNEJ Mapy florystyczne Ważniejsze podstawowe iż zagadnieniowe mapy fitosocjologiczne Mapy antropocentrycznych przemian szaty roślinnej
W10 PLANOWANIE PRZESTRZENNE 14.12.10 ELEMENTY KARTOGRAFII GEOBOTANICZNEJ Mapy florystyczne Ważniejsze podstawowe iż zagadnieniowe mapy fitosocjologiczne Mapy antropocentrycznych przemian szaty roślinnej
W OPARCIU JEDNOWIĄZKOWY SONDAŻ HYDROAKUSTYCZNY
 TWORZENIE MODELU DNA ZBIORNIKA WODNEGO W OPARCIU O JEDNOWIĄZKOWY SONDAŻ HYDROAKUSTYCZNY Tomasz Templin, Dariusz Popielarczyk Katedra Geodezji Satelitarnej i Nawigacji Uniwersytet Warmińsko Mazurski w Olsztynie
TWORZENIE MODELU DNA ZBIORNIKA WODNEGO W OPARCIU O JEDNOWIĄZKOWY SONDAŻ HYDROAKUSTYCZNY Tomasz Templin, Dariusz Popielarczyk Katedra Geodezji Satelitarnej i Nawigacji Uniwersytet Warmińsko Mazurski w Olsztynie
WYKORZYSTANIE GEOINFORMATYKI DO OPRACOWYWANIA
 WYKORZYSTANIE GEOINFORMATYKI DO OPRACOWYWANIA PRZEGLĄDOWYCH MAP GEOMORFOLOGICZNYCH, NA PRZYKŁADZIE WOJEWÓDZTWA POMORSKIEGO Adriana Marcinkowska Adrian Ochtyra prof. dr hab. Jan R. Olędzki dr Elżbieta Wołk-Musiał
WYKORZYSTANIE GEOINFORMATYKI DO OPRACOWYWANIA PRZEGLĄDOWYCH MAP GEOMORFOLOGICZNYCH, NA PRZYKŁADZIE WOJEWÓDZTWA POMORSKIEGO Adriana Marcinkowska Adrian Ochtyra prof. dr hab. Jan R. Olędzki dr Elżbieta Wołk-Musiał
3a. Mapa jako obraz Ziemi
 3a. Mapa jako obraz Ziemi MAPA: obraz powierzchni Ziemi (ciała niebieskiego) lub jej części przedstawiony na płaszczyźnie, w ściśle określonym zmniejszeniu (skali), w odwzorowaniu kartograficznym (matematycznym
3a. Mapa jako obraz Ziemi MAPA: obraz powierzchni Ziemi (ciała niebieskiego) lub jej części przedstawiony na płaszczyźnie, w ściśle określonym zmniejszeniu (skali), w odwzorowaniu kartograficznym (matematycznym
Hydrologia i oceanografia Ćw. nr 11. Temat: Metody obliczania obszarowej wysokości opadów.
 Hydrologia i oceanografia Ćw. nr 11. Temat: Metody obliczania obszarowej wysokości opadów. Pomiary opadu atmosferycznego są wykonywane punktowo na posterunkach opadowych za pomocą deszczomierzy (pluwiografów).
Hydrologia i oceanografia Ćw. nr 11. Temat: Metody obliczania obszarowej wysokości opadów. Pomiary opadu atmosferycznego są wykonywane punktowo na posterunkach opadowych za pomocą deszczomierzy (pluwiografów).
BUDOWA NUMERYCZNEGO MODELU TERENU DLA CELÓW ZWIĄZANYCH Z OBLICZENIEM OBJĘTOŚCI MAKING DIGITAL TERRAIN MODEL FOR PURPOSES OF CALCULATING VOLUMES
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2004 Seria: GÓRNICTWO z. 261 Nr kol. 1650 Piotr KUJAWSKI Wyższy Urząd Górniczy, Katowice Marian PONIEWIERA Politechnika Śląska, Gliwice BUDOWA NUMERYCZNEGO MODELU
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2004 Seria: GÓRNICTWO z. 261 Nr kol. 1650 Piotr KUJAWSKI Wyższy Urząd Górniczy, Katowice Marian PONIEWIERA Politechnika Śląska, Gliwice BUDOWA NUMERYCZNEGO MODELU
ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2013
 ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2013 OPRACOWAŁY: ANNA ANWAJLER MARZENA KACZOR DOROTA LIS 1 WSTĘP W analizie wykorzystywany będzie model szacowania EWD.
ANALIZA WYNIKÓW NAUCZANIA W GIMNAZJUM NR 3 Z ZASTOSOWANIEM KALKULATORA EWD 100 ROK 2013 OPRACOWAŁY: ANNA ANWAJLER MARZENA KACZOR DOROTA LIS 1 WSTĘP W analizie wykorzystywany będzie model szacowania EWD.
PRACA LICENCJACKA SPECJALNOŚĆ: GEOINFORMACJA PROPONOWANA PROBLEMATYKA W ROKU AKADEMICKIM 2016/2017
 PRACA LICENCJACKA SPECJALNOŚĆ: GEOINFORMACJA PROPONOWANA PROBLEMATYKA W ROKU AKADEMICKIM 2016/2017 Dr Jolanta Czerniawska (jolczer@amu.edu.pl) 1. Analizy morfometryczne i wizualizacja rzeźby wybranego
PRACA LICENCJACKA SPECJALNOŚĆ: GEOINFORMACJA PROPONOWANA PROBLEMATYKA W ROKU AKADEMICKIM 2016/2017 Dr Jolanta Czerniawska (jolczer@amu.edu.pl) 1. Analizy morfometryczne i wizualizacja rzeźby wybranego
Identyfikacja siedlisk Natura 2000 metodami teledetekcyjnymi na przykładzie torfowisk zasadowych w dolinie Biebrzy
 Identyfikacja siedlisk Natura 2000 metodami teledetekcyjnymi Dominik Kopeć 1, Łukasz Sławik 2, Marcin Borowisk 2, Dorota Michalska-Hejduk 1 1 Uniwersytet Łódzki, Katedra Geobotaniki i Ekologii Roślin,
Identyfikacja siedlisk Natura 2000 metodami teledetekcyjnymi Dominik Kopeć 1, Łukasz Sławik 2, Marcin Borowisk 2, Dorota Michalska-Hejduk 1 1 Uniwersytet Łódzki, Katedra Geobotaniki i Ekologii Roślin,
ANALIZA SYSTEMU POMIAROWEGO (MSA)
 StatSoft Polska, tel. 1 484300, 601 414151, info@statsoft.pl, www.statsoft.pl ANALIZA SYSTEMU POMIAROWEGO (MSA) dr inż. Tomasz Greber, Politechnika Wrocławska, Instytut Organizacji i Zarządzania Wprowadzenie
StatSoft Polska, tel. 1 484300, 601 414151, info@statsoft.pl, www.statsoft.pl ANALIZA SYSTEMU POMIAROWEGO (MSA) dr inż. Tomasz Greber, Politechnika Wrocławska, Instytut Organizacji i Zarządzania Wprowadzenie
Wstęp. Jerzy WYSOCKI, Paweł ORŁOWSKI
 Przegląd Naukowy Inżynieria i Kształtowanie Środowiska nr 56, 2012: 58 64 (Prz. Nauk. Inż. Kszt. Środ. 56, 2012) Scientific Review Engineering and Environmental Sciences No 56, 2012: 58 64 (Sci. Rev. Eng.
Przegląd Naukowy Inżynieria i Kształtowanie Środowiska nr 56, 2012: 58 64 (Prz. Nauk. Inż. Kszt. Środ. 56, 2012) Scientific Review Engineering and Environmental Sciences No 56, 2012: 58 64 (Sci. Rev. Eng.
Analiza składowych głównych. Wprowadzenie
 Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
O TRUDNOŚCIACH ZASTOSOWANIA KONCEPCJI PŁATÓW I KORYTARZY W OBSZARZE WYSOKOGÓRSKIM Application of patches and corridors concept, high mountain studies
 Balon Jarosław O trudnościach w zastosowaniu... 168 Jarosław Balon A. Cieszewska (red.) Płaty i korytarze jako elementy struktury krajobrazu możliwości i ograniczenia koncepcji, 2004, Problemy Ekologii
Balon Jarosław O trudnościach w zastosowaniu... 168 Jarosław Balon A. Cieszewska (red.) Płaty i korytarze jako elementy struktury krajobrazu możliwości i ograniczenia koncepcji, 2004, Problemy Ekologii
Dlaczego należy uwzględniać zarówno wynik maturalny jak i wskaźnik EWD?
 EWD co to jest? Metoda EWD to zestaw technik statystycznych pozwalających oszacować wkład szkoły w końcowe wyniki egzaminacyjne. Wkład ten nazywamy właśnie edukacyjną wartością dodaną. EWD jest egzaminacyjnym
EWD co to jest? Metoda EWD to zestaw technik statystycznych pozwalających oszacować wkład szkoły w końcowe wyniki egzaminacyjne. Wkład ten nazywamy właśnie edukacyjną wartością dodaną. EWD jest egzaminacyjnym
w zależności od powierzchni, jaka została użyta do odwzorowania siatki kartograficznej, wyróżniać będziemy 3 typy odwzorowań:
 Elementy mapy mapa jest płaskim obrazem powierzchni Ziemi lub jej części przedstawionym na płaszczyźnie w odpowiednim zmniejszeniu; siatka kartograficzna będzie się zawsze różniła od siatki geograficznej;
Elementy mapy mapa jest płaskim obrazem powierzchni Ziemi lub jej części przedstawionym na płaszczyźnie w odpowiednim zmniejszeniu; siatka kartograficzna będzie się zawsze różniła od siatki geograficznej;
WYBÓR PUNKTÓW POMIAROWYCH
 Scientific Bulletin of Che lm Section of Technical Sciences No. 1/2008 WYBÓR PUNKTÓW POMIAROWYCH WE WSPÓŁRZĘDNOŚCIOWEJ TECHNICE POMIAROWEJ MAREK MAGDZIAK Katedra Technik Wytwarzania i Automatyzacji, Politechnika
Scientific Bulletin of Che lm Section of Technical Sciences No. 1/2008 WYBÓR PUNKTÓW POMIAROWYCH WE WSPÓŁRZĘDNOŚCIOWEJ TECHNICE POMIAROWEJ MAREK MAGDZIAK Katedra Technik Wytwarzania i Automatyzacji, Politechnika
ROZKŁAD PRZESTRZENNY NASŁONECZNIENIA W LUBLINIE
 PRACE GEOGRAFICZNE, zeszyt 122 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2009 Mateusz Dobek, Leszek Gawrysiak ROZKŁAD PRZESTRZENNY NASŁONECZNIENIA W LUBLINIE Zarys treści: Rozkład przestrzenny
PRACE GEOGRAFICZNE, zeszyt 122 Instytut Geografii i Gospodarki Przestrzennej UJ Kraków 2009 Mateusz Dobek, Leszek Gawrysiak ROZKŁAD PRZESTRZENNY NASŁONECZNIENIA W LUBLINIE Zarys treści: Rozkład przestrzenny
Założenia, problemy interpretacyjne
 Projekt cyfryzacji dokumentów planistycznych Metropolii Poznań Założenia, problemy interpretacyjne Lech Kaczmarek Uniwersytet im. A. Mickiewicza w Poznaniu, Stacja Ekologiczna w Jeziorach Projekt częściowo
Projekt cyfryzacji dokumentów planistycznych Metropolii Poznań Założenia, problemy interpretacyjne Lech Kaczmarek Uniwersytet im. A. Mickiewicza w Poznaniu, Stacja Ekologiczna w Jeziorach Projekt częściowo
Walidacja metod analitycznych Raport z walidacji
 Walidacja metod analitycznych Raport z walidacji Małgorzata Jakubowska Katedra Chemii Analitycznej WIMiC AGH Walidacja metod analitycznych (według ISO) to proces ustalania parametrów charakteryzujących
Walidacja metod analitycznych Raport z walidacji Małgorzata Jakubowska Katedra Chemii Analitycznej WIMiC AGH Walidacja metod analitycznych (według ISO) to proces ustalania parametrów charakteryzujących
Zastosowanie metody interpolacji warstwic do tworzenia NMT. dr inż. Ireneusz Wyczałek Zakład Geodezji POLITECHNIKA POZNAŃSKA
 Zastosowanie metody interpolacji warstwic do tworzenia NMT dr inż. Ireneusz Wyczałek Zakład Geodezji POLITECHNIKA POZNAŃSKA Zastosowanie metody interpolacji warstwic do tworzenia Numerycznego Modelu Terenu
Zastosowanie metody interpolacji warstwic do tworzenia NMT dr inż. Ireneusz Wyczałek Zakład Geodezji POLITECHNIKA POZNAŃSKA Zastosowanie metody interpolacji warstwic do tworzenia Numerycznego Modelu Terenu
Dane wejściowe do opracowania map zagrożenia powodziowego i map ryzyka powodziowego
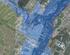 Dane wejściowe do opracowania map zagrożenia powodziowego i map ryzyka powodziowego MATEUSZ KOPEĆ Centrum Modelowania Powodzi i Suszy w Poznaniu Instytut Meteorologii i Gospodarki Wodnej Państwowy Instytut
Dane wejściowe do opracowania map zagrożenia powodziowego i map ryzyka powodziowego MATEUSZ KOPEĆ Centrum Modelowania Powodzi i Suszy w Poznaniu Instytut Meteorologii i Gospodarki Wodnej Państwowy Instytut
Skrypt 17. Podobieństwo figur. 1. Figury podobne skala podobieństwa. Obliczanie wymiarów wielokątów powiększonych bądź pomniejszonych.
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 17 Podobieństwo figur 1. Figury podobne skala
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 17 Podobieństwo figur 1. Figury podobne skala
WYKŁAD 3 - KARTODIAGRAMY HALINA KLIMCZAK
 WYKŁAD 3 - KARTODIAGRAMY HALINA KLIMCZAK METODY PREZENTACJI Dane bezpośrednie (cechy mierzalne) Dane relatywne (wskaźniki natężenia) metoda kartodiagramu metoda kropkowa metoda izolinii (dla danych występujących
WYKŁAD 3 - KARTODIAGRAMY HALINA KLIMCZAK METODY PREZENTACJI Dane bezpośrednie (cechy mierzalne) Dane relatywne (wskaźniki natężenia) metoda kartodiagramu metoda kropkowa metoda izolinii (dla danych występujących
Wynagrodzenia w sektorze publicznym w 2011 roku
 Wynagrodzenia w sektorze publicznym w 2011 roku Już po raz dziewiąty mamy przyjemność przedstawić Państwu podsumowanie Ogólnopolskiego Badania Wynagrodzeń (OBW). W 2011 roku uczestniczyło w nim ponad sto
Wynagrodzenia w sektorze publicznym w 2011 roku Już po raz dziewiąty mamy przyjemność przedstawić Państwu podsumowanie Ogólnopolskiego Badania Wynagrodzeń (OBW). W 2011 roku uczestniczyło w nim ponad sto
10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu.
 Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
STRESZCZENIE. rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne.
 STRESZCZENIE rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne. Zasadniczym czynnikiem stanowiącym motywację dla podjętych w pracy rozważań
STRESZCZENIE rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne. Zasadniczym czynnikiem stanowiącym motywację dla podjętych w pracy rozważań
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część
 Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
Instrukcja użytkowania modułu Rzeźba terenu
 Instrukcja użytkowania modułu Rzeźba terenu Kolejnym modułem, który chcemy Państwu przybliżyć jest moduł Rzeźba terenu. W module tym zostały przedstawione dane prezentujące ukształtowania powierzchni województwa
Instrukcja użytkowania modułu Rzeźba terenu Kolejnym modułem, który chcemy Państwu przybliżyć jest moduł Rzeźba terenu. W module tym zostały przedstawione dane prezentujące ukształtowania powierzchni województwa
CZYTANIE MAPY TOPOGRAFICZNEJ
 CZYTANIE MAPY TOPOGRAFICZNEJ WYSOKOŚĆ WZGLĘDNA BEZWZGLĘDNA Wysokość względna to wysokość liczona od podstawy formy terenu podawana w metrach. Wysokość bezwzględna jest wysokością liczoną od poziomu morza
CZYTANIE MAPY TOPOGRAFICZNEJ WYSOKOŚĆ WZGLĘDNA BEZWZGLĘDNA Wysokość względna to wysokość liczona od podstawy formy terenu podawana w metrach. Wysokość bezwzględna jest wysokością liczoną od poziomu morza
Analizy morfometryczne i wizualizacja rzeźby
 PRACA LICENCJACKA GEOINFORMACJA Proponowana problematyka w roku akademickim 2015/2016 Dr Jolanta Czerniawska Analizy morfometryczne i wizualizacja rzeźby na przykładzie di Pomorza lub bkujaw. Prace oparte
PRACA LICENCJACKA GEOINFORMACJA Proponowana problematyka w roku akademickim 2015/2016 Dr Jolanta Czerniawska Analizy morfometryczne i wizualizacja rzeźby na przykładzie di Pomorza lub bkujaw. Prace oparte
Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości
 Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości a) metoda rachunkowa Po wykreśleniu przekroju poprzecznego z zaznaczeniem pionów hydrometrycznych, w których dokonano punktowego
Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości a) metoda rachunkowa Po wykreśleniu przekroju poprzecznego z zaznaczeniem pionów hydrometrycznych, w których dokonano punktowego
PROJEKT Z HYDROLOGII CHARAKTERYSTYKA ZLEWNI RZEKI
 PROJEKT Z HYDROLOGII CHRKTERYSTYK ZLEWNI RZEKI Wykonał: imię nazwisko, grupa Data I. Wyznaczenie granic dorzecza Na dowolnie wybranym fragmencie mapy topograficznej (w skali od 1:10 000 do 1: 50 000) wyznaczyć
PROJEKT Z HYDROLOGII CHRKTERYSTYK ZLEWNI RZEKI Wykonał: imię nazwisko, grupa Data I. Wyznaczenie granic dorzecza Na dowolnie wybranym fragmencie mapy topograficznej (w skali od 1:10 000 do 1: 50 000) wyznaczyć
W kolejnym kroku należy ustalić liczbę przedziałów k. W tym celu należy wykorzystać jeden ze wzorów:
 Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
Wybrane zagadnienia w pracy z danymi rastrowymi w ArcGIS Marcin Paź Esri Polska
 Wybrane zagadnienia w pracy z danymi rastrowymi w ArcGIS 10.1 Marcin Paź Esri Polska Zagadnienia Koncepcja rastra Typy danych rastrowych Właściwości rastrów Modele danych rastrowych w ArcGIS Przetwarzanie
Wybrane zagadnienia w pracy z danymi rastrowymi w ArcGIS 10.1 Marcin Paź Esri Polska Zagadnienia Koncepcja rastra Typy danych rastrowych Właściwości rastrów Modele danych rastrowych w ArcGIS Przetwarzanie
QGIS w badaniach przyrodniczych. Zakład Geoekologii Wydział Geografii i Studiów Regionalnych Uniwersytet Warszawski
 QGIS w badaniach przyrodniczych Zakład Geoekologii Wydział Geografii i Studiów Regionalnych Uniwersytet Warszawski Fot. Ramdan Authentic / Unsplash Jak dotrzeć do punktu? Garmin Custom Map podkłady rastrowe
QGIS w badaniach przyrodniczych Zakład Geoekologii Wydział Geografii i Studiów Regionalnych Uniwersytet Warszawski Fot. Ramdan Authentic / Unsplash Jak dotrzeć do punktu? Garmin Custom Map podkłady rastrowe
NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 85 Electrical Engineering 016 Krzysztof KRÓL* NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU W artykule zaprezentowano
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 85 Electrical Engineering 016 Krzysztof KRÓL* NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU W artykule zaprezentowano
Zadanie Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym
 Zadanie 1 1. Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym Pierwszym etapem wykonania zadania było przycięcie danego obrazu tak aby pozostał tylko obszar grida. Obrobiony
Zadanie 1 1. Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym Pierwszym etapem wykonania zadania było przycięcie danego obrazu tak aby pozostał tylko obszar grida. Obrobiony
Wymagania edukacyjne z matematyki w klasie III gimnazjum
 Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
Główne założenia metodyk dotyczących opracowania map zagrożenia powodziowego
 Główne założenia metodyk dotyczących opracowania map zagrożenia powodziowego Robert Kęsy, Agata Włodarczyk Dyrektywa 2007/60/WE z dnia 23 października 2007 r. ws. oceny ryzyka powodziowego i zarządzania
Główne założenia metodyk dotyczących opracowania map zagrożenia powodziowego Robert Kęsy, Agata Włodarczyk Dyrektywa 2007/60/WE z dnia 23 października 2007 r. ws. oceny ryzyka powodziowego i zarządzania
EDUKACYJNA WARTOŚĆ DODANA
 ŚLĄSKIE TECHNICZNE ZAKŁADY NAUKOWE EDUKACYJNA WARTOŚĆ DODANA ANALIZA 1. INFORMACJE OGÓLNE. Wskaźnik EWD i wyniki egzaminacyjne rozpatrywane są wspólnie. W ten sposób dają nam one pełniejszy obraz pracy
ŚLĄSKIE TECHNICZNE ZAKŁADY NAUKOWE EDUKACYJNA WARTOŚĆ DODANA ANALIZA 1. INFORMACJE OGÓLNE. Wskaźnik EWD i wyniki egzaminacyjne rozpatrywane są wspólnie. W ten sposób dają nam one pełniejszy obraz pracy
SINGLE-IMAGE HIGH-RESOLUTION SATELLITE DATA FOR 3D INFORMATIONEXTRACTION
 SINGLE-IMAGE HIGH-RESOLUTION SATELLITE DATA FOR 3D INFORMATIONEXTRACTION MOŻLIWOŚCI WYDOBYCIA INFORMACJI 3D Z POJEDYNCZYCH WYSOKOROZDZIELCZYCH OBRAZÓW SATELITARNYCH J. Willneff, J. Poon, C. Fraser Przygotował:
SINGLE-IMAGE HIGH-RESOLUTION SATELLITE DATA FOR 3D INFORMATIONEXTRACTION MOŻLIWOŚCI WYDOBYCIA INFORMACJI 3D Z POJEDYNCZYCH WYSOKOROZDZIELCZYCH OBRAZÓW SATELITARNYCH J. Willneff, J. Poon, C. Fraser Przygotował:
Analiza korespondencji
 Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
ZASTOSOWANIE METOD OPTYMALIZACJI W DOBORZE CECH GEOMETRYCZNYCH KARBU ODCIĄŻAJĄCEGO
 MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 43-48, Gliwice 2010 ZASTOSOWANIE METOD OPTYMALIZACJI W DOBORZE CECH GEOMETRYCZNYCH KARBU ODCIĄŻAJĄCEGO TOMASZ CZAPLA, MARIUSZ PAWLAK Katedra Mechaniki Stosowanej,
MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 43-48, Gliwice 2010 ZASTOSOWANIE METOD OPTYMALIZACJI W DOBORZE CECH GEOMETRYCZNYCH KARBU ODCIĄŻAJĄCEGO TOMASZ CZAPLA, MARIUSZ PAWLAK Katedra Mechaniki Stosowanej,
Metryki i metadane ortofotomapa, numeryczny model terenu
 Obiekt NAZWA OBIEKTU układ 1992 Opis Obiektu Obiekt Nr_arkusza Data rr-mm-dd Skala 1:5000 Rozmiar piksela 0.5 m Ocena zbiorcza Obiektu Zał. nr 6 1/5 Ortofotomapa Identyfikator modułu:n-34-121-a-a-1-1 Identyfikator
Obiekt NAZWA OBIEKTU układ 1992 Opis Obiektu Obiekt Nr_arkusza Data rr-mm-dd Skala 1:5000 Rozmiar piksela 0.5 m Ocena zbiorcza Obiektu Zał. nr 6 1/5 Ortofotomapa Identyfikator modułu:n-34-121-a-a-1-1 Identyfikator
Rodzaje erozji lodowcowej. Rzeźbotwórcza działalność lodowców górskich i kontynentalnych. Wygłady i rysy lodowcowe. Wygłady i rysy lodowcowe
 Rodzaje erozji lodowcowej Rzeźbotwórcza działalność lodowców górskich i kontynentalnych DETRAKCJA wyrywanie z podłoża dużych okruchów i bloków skalnych EGZARACJA żłobienie podłoża w wyniku zdzieranie materiału
Rodzaje erozji lodowcowej Rzeźbotwórcza działalność lodowców górskich i kontynentalnych DETRAKCJA wyrywanie z podłoża dużych okruchów i bloków skalnych EGZARACJA żłobienie podłoża w wyniku zdzieranie materiału
Wysokościowy numeryczny model terenu (NMT) w badaniu osuwisk
 Wysokościowy numeryczny model terenu (NMT) w badaniu osuwisk Tomasz Wojciechowski Wydział Nauk o Ziemi Uniwersytet Śląski Liczba osuwisk w polskiej częś ęści Karpat - co najmniej 23 000 (Rączkowski( czkowski,,
Wysokościowy numeryczny model terenu (NMT) w badaniu osuwisk Tomasz Wojciechowski Wydział Nauk o Ziemi Uniwersytet Śląski Liczba osuwisk w polskiej częś ęści Karpat - co najmniej 23 000 (Rączkowski( czkowski,,
FOTOMAPA I ORTOFOTOMAPA NUMERYCZNY MODEL TERENU
 FTMAPA I RTFTMAPA Zdjęcie lotnicze a mapa Zniekształcenia zdjęć lotniczych wpływ nachylenia zdjęcia wpływ rzeźby terenu Modele rzutu środkowego Przetwarzanie rzutowe rtorektyfikacja Terminologia Aspekty
FTMAPA I RTFTMAPA Zdjęcie lotnicze a mapa Zniekształcenia zdjęć lotniczych wpływ nachylenia zdjęcia wpływ rzeźby terenu Modele rzutu środkowego Przetwarzanie rzutowe rtorektyfikacja Terminologia Aspekty
INSTYTUT GEOGRAFII UNIWERSYTETU PEDAGOGICZNEGO im. KOMISJI EDUKACJI NARODOWEJ w KRAKOWIE SEMINARIA MAGISTERSKIE GEOGRAFIA 2.
 INSTYTUT GEOGRAFII UNIWERSYTETU PEDAGOGICZNEGO im. KOMISJI EDUKACJI NARODOWEJ w KRAKOWIE SEMINARIA MAGISTERSKIE GEOGRAFIA 2. STOPNIA 2016/2017 Dr hab. prof. UP Krzysztof Bąk Organizacja seminarium 2. semestr:
INSTYTUT GEOGRAFII UNIWERSYTETU PEDAGOGICZNEGO im. KOMISJI EDUKACJI NARODOWEJ w KRAKOWIE SEMINARIA MAGISTERSKIE GEOGRAFIA 2. STOPNIA 2016/2017 Dr hab. prof. UP Krzysztof Bąk Organizacja seminarium 2. semestr:
Generacja źródeł wiatrowych cz.2
 Generacja źródeł wiatrowych cz.2 Autor: Adam Klepacki, ENERGOPROJEKT -KATOWICE S.A. Średnioroczne prawdopodobieństwa wystąpienia poszczególnych obciążeń źródeł wiatrowych w Niemczech dla siedmiu lat kształtują
Generacja źródeł wiatrowych cz.2 Autor: Adam Klepacki, ENERGOPROJEKT -KATOWICE S.A. Średnioroczne prawdopodobieństwa wystąpienia poszczególnych obciążeń źródeł wiatrowych w Niemczech dla siedmiu lat kształtują
Projektowanie systemów pomiarowych. 02 Dokładność pomiarów
 Projektowanie systemów pomiarowych 02 Dokładność pomiarów 1 www.technidyneblog.com 2 Jak dokładnie wykonaliśmy pomiar? Czy duża / wysoka dokładność jest zawsze konieczna? www.sparkfun.com 3 Błąd pomiaru.
Projektowanie systemów pomiarowych 02 Dokładność pomiarów 1 www.technidyneblog.com 2 Jak dokładnie wykonaliśmy pomiar? Czy duża / wysoka dokładność jest zawsze konieczna? www.sparkfun.com 3 Błąd pomiaru.
MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ
 Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Podstawy przetwarzania obrazów teledetekcyjnych. Format rastrowy
 Podstawy przetwarzania obrazów teledetekcyjnych Format rastrowy Definicja rastrowego modelu danych - podstawowy element obrazu cyfrowego to piksel, uważany w danym momencie za wewnętrznie jednorodny -
Podstawy przetwarzania obrazów teledetekcyjnych Format rastrowy Definicja rastrowego modelu danych - podstawowy element obrazu cyfrowego to piksel, uważany w danym momencie za wewnętrznie jednorodny -
SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA
 SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA Przedmiotem zamówienia jest sporządzenie bazy danych dotyczących parków krajobrazowych i obszarów chronionego krajobrazu w województwie mazowieckim III etap w formie
SZCZEGÓŁOWY OPIS PRZEDMIOTU ZAMÓWIENIA Przedmiotem zamówienia jest sporządzenie bazy danych dotyczących parków krajobrazowych i obszarów chronionego krajobrazu w województwie mazowieckim III etap w formie
Aspekty tworzenia Numerycznego Modelu Terenu na podstawie skaningu laserowego LIDAR. prof. dr hab. inż.. Andrzej Stateczny
 Aspekty tworzenia Numerycznego Modelu Terenu na podstawie skaningu laserowego LIDAR prof. dr hab. inż.. Andrzej Stateczny mgr inż.. Krzysztof W. Łogasz Numeryczny Model Terenu podstawowe pojęcia NMT pol.
Aspekty tworzenia Numerycznego Modelu Terenu na podstawie skaningu laserowego LIDAR prof. dr hab. inż.. Andrzej Stateczny mgr inż.. Krzysztof W. Łogasz Numeryczny Model Terenu podstawowe pojęcia NMT pol.
KSZTAŁTOWANIE MIKROKLIMATU W STREFIE PRZEBYWANIA LUDZI W OBIEKTACH SAKRALNYCH
 KSZTAŁTOWANIE MIKROKLIMATU W STREFIE PRZEBYWANIA LUDZI W OBIEKTACH SAKRALNYCH WOLSKI Leszek 1 JELEC Paweł 2 1,2 Zakład Instalacji Budowlanych i Fizyki Budowli, Politechnika Warszawska ABSTRACT This script
KSZTAŁTOWANIE MIKROKLIMATU W STREFIE PRZEBYWANIA LUDZI W OBIEKTACH SAKRALNYCH WOLSKI Leszek 1 JELEC Paweł 2 1,2 Zakład Instalacji Budowlanych i Fizyki Budowli, Politechnika Warszawska ABSTRACT This script
NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ SERII NORM PN-EN ISO 3740
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
WPŁYW AKTUALIZACJI NIEKTÓRYCH WSKAŹNIKÓW EKSPLOATACYJNO-EKONOMICZNYCH NA KOSZTY EKSPLOATACJI CIĄGNIKÓW ROLNICZYCH NOWEJ GENERACJI
 Inżynieria Rolnicza 2(100)/2008 WPŁYW AKTUALIZACJI NIEKTÓRYCH WSKAŹNIKÓW EKSPLOATACYJNO-EKONOMICZNYCH NA KOSZTY EKSPLOATACJI CIĄGNIKÓW ROLNICZYCH NOWEJ GENERACJI Zenon Grześ Instytut Inżynierii Rolniczej,
Inżynieria Rolnicza 2(100)/2008 WPŁYW AKTUALIZACJI NIEKTÓRYCH WSKAŹNIKÓW EKSPLOATACYJNO-EKONOMICZNYCH NA KOSZTY EKSPLOATACJI CIĄGNIKÓW ROLNICZYCH NOWEJ GENERACJI Zenon Grześ Instytut Inżynierii Rolniczej,
Wykład 5: Statystyki opisowe (część 2)
 Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Potencjał wysokorozdzielczych zobrazowań Ikonos oraz QuickBird dla generowania ortoobrazów.
 Dr inż.. Ireneusz Ewiak Instutut Geodezji i Kartografii 02-679 Warszawa, ul. Modzelewskiego 27 rene@igik.edu.pl Potencjał wysokorozdzielczych zobrazowań Ikonos oraz QuickBird dla generowania ortoobrazów.
Dr inż.. Ireneusz Ewiak Instutut Geodezji i Kartografii 02-679 Warszawa, ul. Modzelewskiego 27 rene@igik.edu.pl Potencjał wysokorozdzielczych zobrazowań Ikonos oraz QuickBird dla generowania ortoobrazów.
ZASTOSOWANIE KOMPRESJI RLE DO REDUKCJI WIELKOŚCI ZBIORÓW TYPU GRID APPLICATION OF RLE COMPRESSION FOR SIZE REDUCTION OF GRID TYPE FILES
 DARIUSZ GOŚCIEWSKI ZASTOSOWANIE KOMPRESJI RLE DO REDUKCJI WIELKOŚCI ZBIORÓW TYPU GRID APPLICATION OF RLE COMPRESSION FOR SIZE REDUCTION OF GRID TYPE FILES Streszczenie Abstract Współczesne systemy informacji
DARIUSZ GOŚCIEWSKI ZASTOSOWANIE KOMPRESJI RLE DO REDUKCJI WIELKOŚCI ZBIORÓW TYPU GRID APPLICATION OF RLE COMPRESSION FOR SIZE REDUCTION OF GRID TYPE FILES Streszczenie Abstract Współczesne systemy informacji
Modele (graficznej reprezentacji) danych przestrzennych postać danych przestrzennych
 Modele (graficznej reprezentacji) danych przestrzennych postać danych przestrzennych Jest to sposób graficznej reprezentacji połoŝenia przestrzennego, kształtu oraz relacji przestrzennych obiektów SIP
Modele (graficznej reprezentacji) danych przestrzennych postać danych przestrzennych Jest to sposób graficznej reprezentacji połoŝenia przestrzennego, kształtu oraz relacji przestrzennych obiektów SIP
Problemy Ekologii Krajobrazu The Problems of Landscape Ecology EKOLOGIA KRAJOBRAZU PROBLEMY BADAWCZE I UTYLITARNE
 Polska Asocjacja Ekologii Krajobrazu Polish Association for Landscape Ecology Problemy Ekologii Krajobrazu The Problems of Landscape Ecology Tom XXIII Volume XXIII EKOLOGIA KRAJOBRAZU PROBLEMY BADAWCZE
Polska Asocjacja Ekologii Krajobrazu Polish Association for Landscape Ecology Problemy Ekologii Krajobrazu The Problems of Landscape Ecology Tom XXIII Volume XXIII EKOLOGIA KRAJOBRAZU PROBLEMY BADAWCZE
Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich Instrukcja do ćwiczenia nr 4 Zakład Miernictwa
Podstawy Metrologii i Technik Eksperymentu Laboratorium Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich Instrukcja do ćwiczenia nr 4 Zakład Miernictwa
PRACA DYPLOMOWA Magisterska
 POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
Beata Baziak, Wiesław Gądek, Tamara Tokarczyk, Marek Bodziony
 IIGW PK Beata Baziak Wiesław Gądek Marek Bodziony IMGW PIB Tamara Tokarczyk Las i woda - Supraśl 12-14.09-2017 Celem prezentacji jest przedstawienie wzorów empirycznych do wyznaczania wartości deskryptorów
IIGW PK Beata Baziak Wiesław Gądek Marek Bodziony IMGW PIB Tamara Tokarczyk Las i woda - Supraśl 12-14.09-2017 Celem prezentacji jest przedstawienie wzorów empirycznych do wyznaczania wartości deskryptorów
System informacji o szlakach turystycznych Mazowsza
 System informacji o szlakach turystycznych Mazowsza Mateusz Troll Instytut Geografii i Gospodarki Przestrzennej UJ Tomasz Gacek GISonLine S.C. Plan prezentacji 1. Informacje o projekcie 2. Składowe systemu
System informacji o szlakach turystycznych Mazowsza Mateusz Troll Instytut Geografii i Gospodarki Przestrzennej UJ Tomasz Gacek GISonLine S.C. Plan prezentacji 1. Informacje o projekcie 2. Składowe systemu
Budowanie macierzy danych geograficznych Procedura normalizacji Budowanie wskaźnika syntetycznego
 Metody Analiz Przestrzennych Budowanie macierzy danych geograficznych Procedura normalizacji Budowanie wskaźnika syntetycznego mgr Marcin Semczuk Zakład Przedsiębiorczości i Gospodarki Przestrzennej Instytut
Metody Analiz Przestrzennych Budowanie macierzy danych geograficznych Procedura normalizacji Budowanie wskaźnika syntetycznego mgr Marcin Semczuk Zakład Przedsiębiorczości i Gospodarki Przestrzennej Instytut
Zakład Geotechniki i Budownictwa Drogowego. WYDZIAŁ GEODEZJI, INŻYNIERII PRZESTRZENNEJ I BUDOWNICTWA Uniwersytet Warmińsko-Mazurski w Olsztynie
 Zakład Geotechniki i Budownictwa Drogowego WYDZIAŁ GEODEZJI, INŻYNIERII PRZESTRZENNEJ I BUDOWNICTWA Uniwersytet Warmińsko-Mazurski w Olsztynie Hydrologia inżynierska - laboratorium Podstawy hydrologii
Zakład Geotechniki i Budownictwa Drogowego WYDZIAŁ GEODEZJI, INŻYNIERII PRZESTRZENNEJ I BUDOWNICTWA Uniwersytet Warmińsko-Mazurski w Olsztynie Hydrologia inżynierska - laboratorium Podstawy hydrologii
ELEKTROWNIE WODNE ĆWICZENIE Z PRZEDMIOTU: Skrypt do obliczeń hydrologicznych. Kraków, Elektrownie wodne
 ĆWICZENIE Z PRZEDMIOTU: ELEKTROWNIE WODNE Skrypt do obliczeń hydrologicznych Kraków, 2016. str. 1- MarT OBLICZENIE PRZEPŁYWÓW CHARAKTERYSTYCZNYCH FORMUŁA OPADOWA [na podstawie materiałów SHP dla zlewni
ĆWICZENIE Z PRZEDMIOTU: ELEKTROWNIE WODNE Skrypt do obliczeń hydrologicznych Kraków, 2016. str. 1- MarT OBLICZENIE PRZEPŁYWÓW CHARAKTERYSTYCZNYCH FORMUŁA OPADOWA [na podstawie materiałów SHP dla zlewni
Robert Olszewski, Paweł Kowalski, Andrzej Głażewski
 Robert Olszewski, Paweł Kowalski, Andrzej Głażewski Pojęcie modelu rzeczywistości geograficznej obejmuje każdą współcześnie funkcjonującą postać opisu tej rzeczywistości, która jest zwięzła, czytelna dla
Robert Olszewski, Paweł Kowalski, Andrzej Głażewski Pojęcie modelu rzeczywistości geograficznej obejmuje każdą współcześnie funkcjonującą postać opisu tej rzeczywistości, która jest zwięzła, czytelna dla
PODZIAŁY NIERUCHOMOŚCI wg standardów
 PODZIAŁY NIERUCHOMOŚCI wg standardów SPIS TREŚCI 30. Wznowienie znaków lub wyznaczenie punktów granicznych... 1 30.4. Protokół, O Którym Mowa W Art. 39 Ust. 4 Ustawy... 1 64. Dokumentacja osnowy... 3 65.
PODZIAŁY NIERUCHOMOŚCI wg standardów SPIS TREŚCI 30. Wznowienie znaków lub wyznaczenie punktów granicznych... 1 30.4. Protokół, O Którym Mowa W Art. 39 Ust. 4 Ustawy... 1 64. Dokumentacja osnowy... 3 65.
Publiczna Szkoła Podstawowa nr 14 w Opolu. Edukacyjna Wartość Dodana
 Publiczna Szkoła Podstawowa nr 14 w Opolu Edukacyjna Wartość Dodana rok szkolny 2014/2015 Edukacyjna Wartość Dodana (EWD) jest miarą efektywności nauczania dla szkoły i uczniów, którzy do danej placówki
Publiczna Szkoła Podstawowa nr 14 w Opolu Edukacyjna Wartość Dodana rok szkolny 2014/2015 Edukacyjna Wartość Dodana (EWD) jest miarą efektywności nauczania dla szkoły i uczniów, którzy do danej placówki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
ELEKTROWNIE WODNE ĆWICZENIE Z PRZEDMIOTU: Temat: Projekt małej elektrowni wodnej. Skrypt do obliczeń hydrologicznych. Kraków, 2015.
 ĆWICZENIE Z PRZEDMIOTU: ELEKTROWNIE WODNE Temat: Skrypt do obliczeń hydrologicznych Kraków, 2015. str. 1- MarT OBLICZENIE PRZEPŁYWÓW CHARAKTERYSTYCZNYCH FORMUŁA OPADOWA Dla obliczenia przepływów o określonym
ĆWICZENIE Z PRZEDMIOTU: ELEKTROWNIE WODNE Temat: Skrypt do obliczeń hydrologicznych Kraków, 2015. str. 1- MarT OBLICZENIE PRZEPŁYWÓW CHARAKTERYSTYCZNYCH FORMUŁA OPADOWA Dla obliczenia przepływów o określonym
Szczegółowy rozkład materiału dla klasy 3b poziom rozszerzny cz. 1 - liceum
 Szczegółowy rozkład materiału dla klasy b poziom rozszerzny cz. - liceum WYDAWNICTWO PAZDRO GODZINY Lp. Tematyka zajęć Liczba godzin I. Funkcja wykładnicza i funkcja logarytmiczna. Potęga o wykładniku
Szczegółowy rozkład materiału dla klasy b poziom rozszerzny cz. - liceum WYDAWNICTWO PAZDRO GODZINY Lp. Tematyka zajęć Liczba godzin I. Funkcja wykładnicza i funkcja logarytmiczna. Potęga o wykładniku
Rys. 6.2 Wizualizacja mapy DEM za pomocą palety odcieni szarości (lewa strona) i dodatkowo z wykorzystaniem cieniowania (prawa strona).
 a b c d e f Rys. 6. Tworzenie mapy EM z danych TE 2 i MPHP: a poziomice otrzymane z TE 2 (na rysunku przedstawiono co dziesiątą poziomicę); b rzeki i jeziora z mapy MPHP; c wynik działania narzędzia TOPO
a b c d e f Rys. 6. Tworzenie mapy EM z danych TE 2 i MPHP: a poziomice otrzymane z TE 2 (na rysunku przedstawiono co dziesiątą poziomicę); b rzeki i jeziora z mapy MPHP; c wynik działania narzędzia TOPO
BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI
 14 BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI 14.1 WSTĘP Ogólne wymagania prawne dotyczące przy pracy określają m.in. przepisy
14 BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI 14.1 WSTĘP Ogólne wymagania prawne dotyczące przy pracy określają m.in. przepisy
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
KARTA KURSU. Gospodarka Przestrzenna 1. stopnia, stacjonarne, , sem. 1. Opis kursu (cele kształcenia) Warunki wstępne
 Gospodarka Przestrzenna 1. stopnia, stacjonarne, 2017-2018, sem. 1 KARTA KURSU Nazwa Geodezja i kartografia 1 Nazwa w j. ang. Geodesy and Cartography 1 Koordynator dr Joanna Fidelus-Orzechowska Zespół
Gospodarka Przestrzenna 1. stopnia, stacjonarne, 2017-2018, sem. 1 KARTA KURSU Nazwa Geodezja i kartografia 1 Nazwa w j. ang. Geodesy and Cartography 1 Koordynator dr Joanna Fidelus-Orzechowska Zespół
Statystyki: miary opisujące rozkład! np. : średnia, frakcja (procent), odchylenie standardowe, wariancja, mediana itd.
 Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
RAPORT z diagnozy Matematyka na starcie
 RAPORT z diagnozy Matematyka na starcie przeprowadzonej w klasach czwartych szkoły podstawowej Analiza statystyczna Wyjaśnienie Wartość wskaźnika Liczba uczniów Liczba uczniów, którzy przystąpili do sprawdzianu
RAPORT z diagnozy Matematyka na starcie przeprowadzonej w klasach czwartych szkoły podstawowej Analiza statystyczna Wyjaśnienie Wartość wskaźnika Liczba uczniów Liczba uczniów, którzy przystąpili do sprawdzianu
