Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Techniki Cieplnej i Ochrony Środowiska
|
|
|
- Antoni Stasiak
- 9 lat temu
- Przeglądów:
Transkrypt
1 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Techniki Cieplnej i Ochrony Środowiska Rozprawa doktorska POPRAWA SKUTECZNOŚCI ODTLENIANIA STALI NISKOWĘGLOWEJ DRUTEM ALUMINIOWYM mgr inż. Mariusz Borecki Promotor dr hab. Zofia Kalicka prof. nadzw. AGH Kraków Kraków
2 Składam serdeczne podziękowania prof. nadzw., dr hab. Zofii Kalickiej promotor rozprawy za bezcenne wskazówki, rady, sugestie i korekty oraz wielką cierpliwość i wyrozumiałość podczas licznych i długich dyskusji nad niniejszą rozprawą. 2
3 SPIS TREŚCI 1. Cel i zakres pracy Wprowadzenie Cel pracy Zakres pracy Zarys procesu odtleniania stali glinem Reakcje odtleniania stali glinem Czynniki wpływające na efektywność odtleniania w warunkach przemysłowych Dodatki stopowe w postaci drutów Roztapianie się drutów aluminiowych wprowadzanych do ciekłej stali Technologiczne znaczenie prędkości wprowadzania drutów w zależności od czasu ich roztapiania się Przebieg roztapiania drutu aluminiowego w ciekłej stali i parametry wpływające na ten proces Czas roztapiania drutu aluminiowego wprowadzanego do ciekłej stali Technologia wprowadzania do stali dodatków w postaci drutów Zalety wprowadzania dodatków stopowych w postaci drutów oraz warunki pełnego wykorzystania tej technologii Hydrodynamiczne oddziaływanie kąpieli na drut wprowadzany do ciekłej stali Realizacja techniczna wprowadzania drutów Wpływ konstrukcji maszyny i własności mechanicznych drutów na parametry podawania ich do kąpieli metalowej Modelowanie roztapiania dodatków wprowadzanych do ciekłej stali Przegląd literatury na temat czynników wpływających na asymilację dodatków w ciekłej stali Parametry wpływające na roztapianie i rozpuszczanie dodatków wprowadzanych do ciekłej stali Właściwości dodatków wpływające na ich przyswajanie Parametry kąpieli metalowej, do której wprowadzane są dodatki Mechanizm asymilacji metalicznych dodatków stopowych w ciekłej stali Dodatki stopowe I klasy Dodatki stopowe klasy II Podstawowe prawa fizyczne opisujące proces nagrzewania i roztapiania się dodatków stopowych Obliczenia czasu roztapiania dodatków w ciekłej stali Obliczenia czasu roztapiania drutów aluminiowych w ciekłej stali Wyznaczanie współczynnika przejmowania ciepła Weryfikacja modeli numerycznych Zdefiniowanie warunków zastosowania oprogramowania CalcoMOS do modelowania procesu roztapiania drutów aluminiowych wprowadzanych do ciekłej stali Opis oprogramowania CalcoMos Zdefiniowanie modelu w zakresie wymiarów i geometrii obiektu w systemie CalcoMOS Określenie układu współrzędnych Określenie wymiarów modelu i sposób jego zdefiniowania Zdefiniowanie domen odpowiadających poszczególnym elementom układu
4 Określenie granic między domenami, dla których będą definiowane odmienne warunki brzegowe Wybór rodzaju, charakterystyki i gęstości siatki oraz określenie poddomen Określenie warunków początkowych i brzegowych, danych materiałowych oraz parametrów i zakresu obliczeń Opis domen i warunków brzegowych oraz zasady określania warunków symulacji w programie CalcoMOS Właściwości termofizyczne niezbędne do symulacji roztapiania drutu aluminiowego Opracowanie plików konfigurujących dla modelu roztapiania drutu aluminiowego wprowadzanego do ciekłej stali Eksperymentalne wyznaczenie współczynnika wymiany ciepła na granicy drut zakrzepła warstwa stali Koncepcja eksperymentalnego wyznaczenie współczynnika wymiany ciepła Wyznaczenie współczynnika wymiany ciepła Wyniki numerycznej symulacji roztapiania drutu aluminiowego wprowadzanego do ciekłej stali Kryteria określania głębokości na jakiej roztopi się drut aluminiowy Warianty obliczeń roztapiania drutu aluminiowego w ciekłej stali Wyniki numerycznej symulacji roztapiania drutu aluminiowego w ciekłej stali Weryfikacja przemysłowa wyników symulacji na podstawie efektywności odtleniania stali Przebieg prób przemysłowych Wyniki prób przemysłowych Efektywność odtleniania przy różnej prędkości wprowadzania drutów Analiza statystyczna istotności zaobserwowanych zależności Porównanie wyników prób przemysłowych i obliczeń numerycznych oraz weryfikacja modelu Bilans glinu Podsumowanie Wnioski Literatura Załączniki Załącznik nr Załącznik nr
5 1. Cel i zakres pracy 1.1. Wprowadzenie Jedną z podstawowych operacji technologicznych wytapiania stali jest wprowadzanie do niej różnych dodatków. Są to przeważnie żelazostopy i inne stopy lub pierwiastki, mogące pełnić role dodatków stopowych, odtleniaczy, modyfikatorów, a czasami także materiałów schładzających lub umożliwiających chemiczne podgrzewanie. Operacje te, w takiej lub innej formie zależnej od technologii, przeprowadza się na kilku, a czasami na wszystkich etapach produkcji stali, począwszy od pieca, poprzez spust i obróbkę pozapiecową, a na kadzi pośredniej lub wlewnicy kończąc. Różne są sposoby wprowadzania dodatków, od wrzucania w postaci kawałkowej na powierzchnię kąpieli metalowej, poprzez wprowadzanie w postaci drutów (litych lub rdzeniowych) po wdmuchiwanie lancą w postaci proszków. Wprowadzanie dodatków w postaci kawałkowej ma miejsce przy wprowadzaniu dużej ich masy we wstępnej fazie wytwarzania stali, szczególnie podczas spustu, wykorzystując naturalne mieszanie i zaciąganie dodatków do kąpieli. Na tym etapie nie jest wymagana wysoka precyzja, a niższy uzysk jest do zaakceptowania, ze względu na przeważnie niższą cenę tych dodatków. Natomiast w końcowych etapach produkcji podczas wprowadzania drogich dodatków i ostatecznego regulowania składu chemicznego i temperatury lub odtleniania czy modyfikowania wtrąceń w stali wymagana jest większa precyzja i stały (jak najwyższy ze względu na koszty) uzysk. Wymaganiom tym może sprostać metoda wprowadzania dodatków w postaci drutów lub wdmuchiwanych proszków. Ze względu na koszty instalacji i eksploatacji oraz prostotę rozwiązania, tam gdzie to tylko jest możliwe, stosuje się druty. Sam proces wprowadzania drutów czy to litych czy rdzeniowych z punktu widzenia mechanicznego jest prostą czynnością. Jednak od strony metalurgicznej proces ten jest już zagadnieniem znacznie bardziej skomplikowanym. Zastosowanie niewłaściwych parametrów wprowadzania, czyli prędkości podawania dla danej średnicy drutu, wielkość kadzi, temperatury stali i innych (szczególnie miejsca wprowadzania w kadzi w stosunku do kształtki porowatej lub lancy), może w znacznym stopniu niweczyć zalety tej technologii. Druty rdzeniowe stosuje się w wielu odmianach natomiast wprowadzanie drutów litych sprowadza się głównie do podawania drutów aluminiowych celem odtleniania stali. Zabieg odtleniania przeprowadzany jest w różny sposób, ale ma miejsce niemal podczas każdego wytopu. Ponadto z reguły odtlenianie stali jest przeprowadzane w więcej niż jedna operacji technologicznych. Podstawowym pierwiastkiem używanym do odtleniania stali jest glin. W zależności od gatunku i wymagań stosuje się także lub zamiennie krzem, mangan i rzadziej inne. W praktyce operacja odtleniania glinem, który ze względu na ciężar właściwy jest trudny we wprowadzaniu do stali, jest dzielona na dwa etapy. Pierwsze zgrubne odtlenianie przeprowadza się podczas spustu poprzez wprowadzenie do kadzi spustowej aluminium w postaci gąsek lub stożków wykorzystując naturalne mieszanie się stali podczas spustu prowadzące do zaciągania ich w głąb metalu. Drugi etap to końcowe, precyzyjne odtlenianie na stanowisku obróbki kadziowej lub w piecu kadziowym poprzez wprowadzanie do stali drutu aluminiowego. Podział operacji odtleniania na dwa etapy ma uzasadnienie tak technologiczne jak i ekonomiczne. W aspekcie technologicznym wczesne odtlenianie podczas spustu zapewnia długi okres czasu na usunięcie tlenków będących produktami odtleniania. Z takim wyprzedzeniem trudno jednak przewidzieć końcową zawartość tlenu w stali przed operacją odlewania. W przypadku przetlenionego żużla, może bowiem dojść do wtórnego natlenienia 5
6 metalu. Ponadto odtlenianie przy pomocy aluminium w gąskach nie pozwala na odpowiednią precyzję w dozowaniu aluminium. Z tych też względów to pierwsze odtlenianie przeprowadza się z pewnym niedomiarem (zawartość tlenu pozostaje wyższa niż wymagana, a glinu niższa). Ostateczne ustalenie poziomu tlenu w stali dokonuje się w końcowej fazie obróbki kadziowej poprzez wprowadzanie drutu aluminiowego, a więc metodą pozwalającą na znacznie dokładniejsze dozowanie ilości odtleniacza i zapewniającą większą powtarzalność wyników. W obu tych operacjach można szukać rezerw pozwalających na zmniejszenie kosztów produkcji. Efekt odtleniania drutem podczas obróbki pozapiecowej oprócz stanu żużla jest uzależniony w dużym stopniu od prędkości wprowadzania drutu aluminiowego. Właściwe dobranie tej prędkości, która jest uzależniona od czasu roztapianie się drutu w ciekłym metalu, dla konkretnych warunków przemysłowych może przynieść wymierny efekt ekonomiczny polegający na jednostkowym zmniejszeniu zużycia drutu aluminiowego oraz efekt technologiczny wyrażający się lepszą powtarzalnością wyników i lepszym końcowym odtlenieniem Cel pracy Celem pracy było: Zdefiniowanie, w oprogramowaniu CalcoMOS dedykowanym do symulacji procesów C.O.S., modelu procesu roztapiania aluminiowego drutu wprowadzanego do ciekłej stali Określenie wszystkich niezbędnych danych materiałowych i parametrów termofizycznych wymaganych przez oprogramowanie i koniecznych do zbudowania prawidłowo pracującego modelu numerycznego. Wykonanie wariantowych obliczeń symulacyjnych i określenie na tej podstawie wpływu ważniejszych parametrów technologicznych na czas roztapiania się drutów aluminiowych wprowadzanych do kadzi. Porównanie wyników obliczeń numerycznych opracowanego modelu z rozbieżnymi danymi zamieszczanymi w publikacjach poświęconych roztapianiu się drutów aluminiowych w stali. Zbadanie, na podstawie prób przemysłowych, jak zmiana prędkości wprowadzania drutu aluminiowego do kadzi wpływa na efektywność odtleniania stali i w związku z tym w jakim stopniu pozwala poprawić wykorzystanie wprowadzanego wraz z drutem aluminium. Weryfikacja modelu poprzez porównanie wyników prób przemysłowych z rezultatami obliczeń symulacyjnych dla takich samych warunków technologicznych. 6
7 1.3. Zakres pracy Zakres pracy obejmował przystosowanie oprogramowania CalcoMOS (szwajcarskiej firmy Calcom) z założenia przeznaczonego do symulacji ciągłego odlewania metali do zadania odwrotnego, czyli do procesu ciągłego roztapiania; za taki można bowiem uznać roztapianie się drutu aluminiowego wprowadzanego do kadzi z ciekłą stalą. Oba procesy różnią się w pewnych elementach na tyle istotnie, że dostosowanie programu dedykowanego do procesu ciągłego odlewania wymagało pewnych uproszczeń, ale nie mają one wpływu na samą istotę symulowanych procesów. Sama idea zastosowania programu do zadania odwrotnego niż pierwotnie założony była konsultowana z twórcami oprogramowania, którzy potwierdzili zasadność takiego zastosowania. Przesłanką do opracowania takiego modelu są duże rozbieżności odnośnie czasu roztapiania się drutów aluminiowych wprowadzanych do ciekłej stali spotykane w publikacjach na ten temat. Wykorzystanie do wyznaczania czasu roztapiania się drutu aluminiowego profesjonalnego programu komputerowego stworzonego z myślą o symulacji zjawisk ciągłej zmiany stanu skupienia, który charakteryzuje się dużą swobodą pod względem definiowania problemu, pozwoliło na opracowanie elastycznego i przydatnego dla celów technologicznych narzędzia do określania głębokości, na jakiej roztopi się drut aluminiowy wprowadzany do ciekłej stali w różnych warunkach produkcyjnych. Ponadto narzędzie to posłużyło również do zweryfikowanie wspomnianych rozbieżnych w doniesieniach literaturowych. Zbudowanie modelu roztapiania drutu aluminiowego oprócz formalnego zdefiniowania samego modelu wymagało określenia szeregu własności termofizycznych koniecznych do przeprowadzenia obliczeń oraz warunków brzegowych dla opracowanego modelu. Większość parametrów termofizycznych została pozyskana dzięki specjalistycznemu programowi JMatPro i uzupełniona danymi literaturowymi. Najważniejszym i najtrudniejszym do określenia parametrem opisującym warunki brzegowe jest współczynnik przejmowania ciepła. Został on określony eksperymentalnie poprzez porównanie wyników doświadczeń laboratoryjnych oraz symulacji odniesienia wykonanych na specjalnie do tego celu opracowanym modelu. Symulacyjne obliczenia czasu roztapiania się drutów aluminiowych skonfrontowano z wynikami prób przemysłowych polegających na wprowadzaniu do kadzi drutu aluminiowego z różnymi prędkościami. Próby przemysłowe mają jednak swoją specyfikę, zwłaszcza gdy są robione z zamiarem jak najmniejszej ingerencji w proces produkcyjny. Próby takie pozwalają, co prawda, pozyskać wartościowy materiał badawczy, jednak zebrane dane wymagają wstępnego przefiltrowania, przygotowania i standaryzacji. W wielu przypadkach do interesujących z badawczego punktu widzenia parametrów dochodzić trzeba w sposób pośredni na podstawie innych dostępnych danych. Wszystkie powyższe uwagi dotyczą również danych pozyskanych w ramach niniejszej pracy. W związku z tym istotnym jej elementem była odpowiednia obróbka standaryzująca danych przemysłowych i obliczenia parametrów nie mierzonych wprost. Kolejnym istotnym elementem analizy danych przemysłowych było wykluczenie wpływu czynników trzecich. Próby przemysłowe zwykle trudno jest zrealizować według z góry zaplanowanego harmonogramu. Charakteryzują się one występowaniem, zakłócających proces technologiczny zdarzeń losowych, podczas których priorytetem załogi jest ciągłość i jakość produkcji, a nie ścisła realizacja harmonogramu prób. Właściwa analiza danych przemysłowych wymaga, oprócz znajomości procesu, świadomości zagrożenia wynikającego z wystąpienia czynników przypadkowo wpływających na badaną korelację. 7
8 Z tego względu dane po standaryzacji poddano wstępnej analizie statystycznej celem stwierdzenia ich przydatności dla oceny badanych zjawisk. Przykładowo, otrzymaną w warunkach przemysłowych zależność pomiędzy prędkością wprowadzania drutu, a uzyskiem glinu można uznać za wiarygodną jeżeli wykluczy się przypadkowy wpływ czynników, które z racji swojego pośredniego skorelowania z prędkością wprowadzania drutu mogły oddziaływać na końcowy rezultat (np. duże jednorazowe porcje drutu mogły być z zasady podawane, ze względu na ograniczenia czasowe, z większą prędkością; większej ilości wprowadzanego aluminium na tonę stali towarzyszy natomiast zwykle wyższy uzysk tego pierwiastka). Celem wyeliminowania takich przypadkowych oddziaływań sporządzono macierz korelacji istotnych parametrów mogących wpływać na wynik końcowy i tam gdzie było to konieczne wyeliminowano ich przypadkowe oddziaływanie. W oparciu o tak przygotowane dane oceniono wpływ prędkości wprowadzania drutu na skuteczność odtleniania drutem aluminiowym dla konkretnych warunków technologicznych oraz zweryfikowano wyniki obliczeń modelowych, porównując je z wynikami prób przemysłowych. 2. Zarys procesu odtleniania stali glinem Tlen stanowi jedną z najbardziej szkodliwych domieszek w stali, powodując problemy w procesie wytwarzania stali oraz pogarszając jej jakość. Usuwania tlenu ze stali nazywa się odtlenianiem, a proces ten prowadzi się w różny sposób zależny od etapu produkcji, możliwości technicznych oraz wymagań stawianych wyrobom końcowym. Tlen w stali występuje w postaci rozpuszczonej oraz jako nierozpuszczalna faza tlenkowa, stanowiąca tzw. wtrącenia niemetaliczne. Rozpuszczalność tlenu w żelazie w zakresie temperatur procesów metalurgicznych, czyli 1500 C do 1800 C wynosi ok do 2070 ppm [1]. Dla stali wartości te będą się różnić w zależności od jej składu. Operacja odtleniania ma za zadanie usuniecie ze stali tlenu w obydwu postaciach. Pierwszym etapem odtleniania stali jest zwykle związanie tlenu rozpuszczonego przez pierwiastek o dużym powinowactwie do tlenu zwany odtleniaczem, a wynikiem tego procesu jest stały lub ciekły tlenek w postaci wtrącenia niemetalicznego. Następny etap odtleniania stali polega na usunięciu z niej produktów odtleniania. Opisany powyżej sposób odtleniania nazywa się odtlenianiem osadowym i jest powszechnie stosowany w produkcji stali [1]. Alternatywnym sposobem jest odtlenianie przy znacznie obniżonym ciśnieniu nad ciekłą stalą, nazywane odtlenianiem próżniowym. Odtlenianie w tych warunkach w głównej mierze kontrolowane jest przez reakcję węgiel-tlen w warunkach niskiego ciśnienia, a także dodatkowo jest wspomagane redukcją tlenkowych wtrąceń niemetalicznych [2]. Ze względu na wymagane odpowiednie wyposażenie techniczne jest stosowane rzadziej i tylko przy produkcji stali o wysokich wymaganiach. Usuwanie tlenu ze stali może również następować wskutek odtleniania nazywanego dyfuzyjnym lub (co lepiej oddaje jego charakter) ekstrakcyjnym [3]. Ten sposób odtleniania polega na usuwaniu tlenu ze stali, zgodnie z prawem podziału, za pomocą żużla redukcyjnego o bardzo małej zawartości FeO. 8
9 2.1. Reakcje odtleniania stali glinem W praktyce stalowniczej przy produkcji zwykłych gatunków stali dominującą pozycję zajmuje odtlenianie osadowe. Najczęściej stosowanym do odtleniania osadowego pierwiastkiem jest glin. Wprowadza się go w różnej postaci. Zwykle do odtleniania wstępnego stosuje się aluminium w kawałkach, natomiast końcowe precyzyjne odtlenianie prowadzi się za pomocą drutów aluminiowych. Pierwszy etap odtleniania polega na wiązaniu tlenu rozpuszczonego w stali przez wprowadzony do niej pierwiastek W wyniku tego powstaje nierozpuszczalny w metalu tlenek. Reakcja odtleniania glinem przebiega następująco: 2[Al] + 3[O] = (Al 2 O 3 ) (1) Powstały w wyniku tego tlenek glinu jest usuwany ze stali poprzez wypływanie oraz flotację w trakcie przedmuchiwania gazem obojętnym. Skuteczność tego zabiegu zależy od wielu czynników [4] i jest ważnym wskaźnikiem prawidłowości technologii obróbki kadziowej. Stała równowagi K reakcji (1) jest związana z aktywnością tlenu i glinu w następujący sposób [3]: log K = loga Al O 3logaO 2loga 2 3 Al (2) gdzie: a Al 2 O 3 jest aktywnością Al 2 O 3 równą 1 w przypadku gdy Al 2 O 3 nie zawiera rozpuszczonych w nim innych tlenków (stan odniesienia wg Raoulta) natomiast stanem odniesienia dla aktywności tlenu i glinu jest 1% roztwór składnika (stan odniesienia wg Henry ego). Wartość stałej równowagi dla reakcji (1) jest zależna od temperatury. W publikacjach wzory do wyznaczania tej stałej różnią się w pewnym zakresie. Przykładowo według [5, 6] stałą równowagi dla reakcji (1) zaleca się wyznaczyć z zależności: log K = / T + 20,57 (3) Występujące w równaniu (2) aktywności tlenu i glinu w kąpieli metalowej są zależne od składu chemicznego stali. Aktywność tlenu w stali wg Henry ego jest funkcja stężenia rozpuszczonego w niej tlenu oraz współczynnika aktywności: a = f [% ] (4) [ O] O O gdzie: [%O] % masowy rozpuszczonego tlenu f O współczynnik aktywności tlenu. 9
10 Podobnie aktywność glinu: gdzie: [%Al] % masowy rozpuszczonego glinu f Al współczynnik aktywności glinu. a[ A] = f Al [% Al] (5) Dla praktycznych celów współczynnik aktywności f określany jest zwykle z równania Wagnera-Chipmana, z wykorzystaniem zależnych od temperatury parametrów oddziaływania według zależności [7, 8]: gdzie: lg f k y = x= 2 e ( x) y [% x] x numeruje składnik stali z wyjątkiem żelaza (dla którego x=1) f y współczynnik aktywności składnika y, [%x] stężenie rozpuszczonego składnika x w % masowych ( <1%) ( ) ln a x y ey = parametr oddziaływania I rzędu składnika x na aktywność % x % Fe 100 składnika y w roztworze Fe. Przy większych stężeniach współczynnik aktywności liczy się z wykorzystaniem parametrów oddziaływania drugiego rzędu. W warunkach przemysłowych stężenie tlenu rozpuszczonego określa się zwykle poprzez pomiar aktywności tlenu. Wykorzystuje się w tym celu odpowiednie czujniki stanowiące półogniwo z elektrolitem stałym, które w ciekłym metalu tworzy ogniwo stężeniowe [9]. Znając skład kąpieli metalowej i jej temperaturę oraz wykorzystując zależności (4) i (6) można na podstawie aktywności tlenu w stali obliczyć jego stężenie. (6) 2.2. Czynniki wpływające na efektywność odtleniania w warunkach przemysłowych W procesie odtleniania można wyróżnić wiele etapów. Zasadnicze z nich to [1]: - Rozpuszczanie się w stali dodanego odtleniacza, - Reakcja łączenia się tlenu rozpuszczonego w żelazie z atomami odtleniacza, - Tworzenie się trwałego zarodka produktu odtleniania i powstanie powierzchni międzyfazowej metal-faza tlenkowa, - Transport tlenu i odtleniacza do utworzonej powierzchni, dalsza reakcja chemiczna i wzrost zarodków do wymiarów wtrąceń niemetalicznych, - Wypływanie produktów odtleniania z jednoczesną dalszą reakcją odtleniania na ich powierzchniach, - Wydzielanie się produktów odtleniania i wtrąceń niemetalicznych z ciekłego metalu. 10
11 Z punktu widzenia wiązania tlenu rozpuszczonego w stali najistotniejsze znaczenie mają dwa pierwsze etapy. Jakkolwiek odtlenianie trwa również podczas dalszych etapów, to pierwsze dwa warunkują cały proces wiązania tlenu rozpuszczonego w kąpieli. Prawidłowa technologia odtleniania powinna zapewnić odpowiedni czas na rozpuszczenie się odtleniacza zanim znajdzie się on w pobliżu żużla lub odsłoniętej - wskutek przedmuchiwania argonem - powierzchni kąpieli. Na powierzchni kropli glinu, które znajdują się po uwolnieniu z drutu w ciekłej stali, może tworzyć się warstewka tlenku utrudniająca dalsze odtlenianie [1, 10]. Zwiększenie czasu wypływania takiej kropli powinno istotnie poprawić wykorzystanie odtleniacza zanim osiągnie on powierzchnię metalu, gdyż w trakcie wypływania krople będą poddane siłom wynikającym z mieszania stali [1]. Z powyższego wynika, że najkorzystniejsze warunki efektywnego wykorzystania wprowadzanego dodatku występują, gdy zostanie on uwolniony do ciekłej stali przy dnie kadzi [11, 12, 13]. Potwierdzeniem tego jest różny uzysk glinu w zależności od metody wprowadzania. Podczas wprowadzania aluminium w postaci kawałkowej na powierzchnię kąpieli można osiągnąć uzysk tego pierwiastka w granicach od 30% do maksymalnie 70%, natomiast wprowadzanie aluminium w postaci drutu przy prawidłowym prowadzeniu operacji zapewnia uzysk na poziomie 80% - 90% [11]. Zastosowanie w Cleveland Works drutów aluminiowych w miejsce aluminium kawałkowego spowodowało, że odchylenie standardowe końcowej zawartości glinu w stali zmniejszyło się z ±0,016% do ±0,009%, uzysk wzrósł o 20%, a wytopy nietrafione - ze zbyt niską zawartością glinu - zostały wyeliminowane [14]. W związku z tym efektywność odtleniania rozumiana jako spadek stężenia tlenu na jednostkę masy wprowadzonego odtleniacza w danej masie stali może być parametrem, który pozwala ocenić prawidłowość technologii odtleniania drutem aluminiowym. W praktyce oznacza to, że na podstawie efektywności danej operacji odtleniania można wnioskować o miejscu (odległości od powierzchni metalu) uwolnienia glinu, a tym samym wykorzystać tą informacje do weryfikacji obliczeń czasu roztapiania się drutu aluminiowego. Porównywanie zużycia odtleniacza na obniżenie stężenia tlenu o określoną wartość wymaga jednak pewnych zastrzeżeń. Pierwsze związane jest z początkowym stężeniem tlenu w odtlenianej stali oraz docelową końcową zawartością tlenu rozpuszczonego. Zużycie glinu na jednostkowe obniżenie stężenia tlenu będzie miarodajne, jeżeli porównywane wyniki będą dotyczyły odtleniania stali o zbliżonym poziomie stężenia tlenu początkowego i końcowego oraz porównywalnej temperaturze. Wynika to z równowagi pomiędzy glinem i tlenem zgodnie z równaniem (2) - rys
12 Rys. 1. Krzywe równowagi Fe O Al w różnych temperaturach liczone według równania: -log K = log (a 2 [Al] a 3 [O])= /T+20,57. Im niższe początkowe stężenie tlenu tym dalsze odtlenianie wymaga większego wzrostu zawartości glinu metalicznego w kąpieli metalowej. Wyższa temperatura stali również przesuwa warunki równowagi w kierunku wyższych zawartości glinu w stali i tym samym osłabia efekt odtleniania. Porównywanie zużycia glinu na związanie określonej ilości zawartego w stali tlenu przy różnym stężeniu początkowym i końcowym tlenu oraz zmiennej temperaturze wymaga odpowiednich przeliczeń standaryzujących wyniki. Powyższą kwestię dobrze ilustruje przedstawiona na rys. 2 zależność uzysku aluminium od całkowitej jego masy wprowadzonej do stali. Jak widać przy małych dodatkach aluminium jego uzysk jest bliski zeru, gdyż cały glin jest praktycznie wiązany przez tlen. W miarę wzrostu masy wprowadzanego aluminium w coraz większym stopniu rozpuszcza się on w stali w postaci metalicznej i tylko w pewnym stopniu służy odtlenianiu. 12
13 *) Szybkość utleniania się glinu zawartego w kąpieli przez żużel, [% wagowe Al/minutę] Rys. 2. Uzysk glinu w zależności od masy wprowadzonego do stali aluminium (prędkość wprowadzania 73 kg/min, czas homogenizacji 1 min) przy różnym natlenieniu żużla wyrażonym szybkością utleniania glinu w kąpieli [15]. Ważnym czynnikiem wpływającym na ocenę efektywności odtleniania jest dobra homogenizacji składu kąpieli metalowej w kadzi. Brak ujednorodnienia składu grozi nie tylko błędnymi wynikami pomiarów, które nie są adekwatne do rzeczywistego stanu kąpieli, ale może mieć również bezpośredni wpływ na uzysk wprowadzanych dodatków, a w szczególności odtleniaczy w sytuacji gdy bogate w odtleniacz partie stali znajdą się w kontakcie z żużlem bogatym w FeO i/lub MnO [16]. Badania nad rozkładem stężenia glinu podczas odtleniania drutem aluminiowym wykazały znaczne różnice w zawartości glinu podczas wprowadzania drutu [17]. Na podstawie symulacji numerycznych i prób przemysłowych w 70 t kadzi mieszanej argonem o początkowej zawartości tlenu 40 ppm, do której wprowadzano drut z szybkością 2,2 m/s stwierdzono, że stężenie tlenu w pierwszej kolejności spada w obszarze centralnym kadzi i przy powierzchni. Jednocześnie koncentracja glinu jest bardzo wysoka w obszarze wprowadzania drutu. Sugeruje to, że wprowadzanie glinu jest szybsze niż jego transport ze strefy wprowadzania do pozostałej części kąpieli. Po zakończeniu wprowadzania drutu następuje ujednorodnienie kąpieli, które według obliczeń potwierdzonych próbami przemysłowymi wymaga ok. 2 minut mieszania gazem obojętnym od momentu zaprzestania wprowadzania drutu. Po około sekundach uzyskano wynikową zawartość tlenu w stali i dalsze mieszanie nie powodowało już zmian stężenia tlenu. Proces odtleniania (wiązania tlenu rozpuszczonego) w funkcji czasu dla różnych intensywności mieszania przedstawiono na rys
14 Rys. 3. Średnie stężenie tlenu wyrażone jako ułamek wagowy w funkcji czasu (kadź o średnicy 280 cm, wysokość kąpieli 234 cm, drut podawany z szybkością 2,2 m/s) [17]. Podawany w publikacjach czas na ujednorodnienie składu chemicznego kąpieli przyjmuje różne wartość. Wynika to z różnych objętości i kształtów kadzi oraz sposobu i intensywności mieszania. Zwykle jednak mieści się on w granicach 2 do 4 minut [17, 18, 19] lub nawet mniej [20, 21]. Równomierne rozcieńczenie glinu w kąpieli nie musi oznaczać, że związał on już tyle tlenu, ile z warunków równowagi powinien związać. To opóźnienie może wynikać np. ze wspomnianego już zjawiska powstawania na kroplach odtleniacza warstwy tlenku izolującego go od kąpieli. Z wykresu przedstawionego na rys. 3 wynika jednak, że nawet czas 1,5 minuty może być wystarczający, jeżeli zastosuje się odpowiednią intensywność mieszania. Ujednorodnienie składu chemicznego stali nie oznacza, że cała kąpiel rozumiana jako układ metal-żużel znajduje się w stanie równowagi. Tego zagadnienia dotyczy trzecie zastrzeżenie. Wyniki pomiarów będą porównywalne, jeżeli nie będzie następowało wtórne natlenianie stali przez żużel. Zjawisko to zależy od ilości żużla i jego potencjału utleniającego oraz intensywności mieszania i składu chemicznego stali [22]. W warunkach wzorowo prowadzonej produkcji zawartość tlenków FeO+MnO w żużlu powinna być na tyle niska, aby zjawisko ponownego natlenienia stali nie następowało. W praktyce, jak wynika z doświadczeń zebranych w polskich stalowniach, niejednokrotnie potencjał utleniający żużla jest tak duży, że powoduje natlenianie stali po opuszczeniu stanowiska obróbki pozapiecowej niemal do momentu odlewania. Z problemem tym stalownie radzą sobie stosując nadmiarową zawartość glinu w stali w momencie opuszczania stanowiska obróbki kadziowej. Chcąc w takich warunkach porównywać efektywność odtleniania poszczególnych wytopów należy dążyć do skrócenia czasu pomiędzy wprowadzeniem glinu a czasem pomiaru. Minimalizacja czasu jest jednak ograniczona koniecznością ujednorodnienia składu chemicznego i przereagowania glinu z tlenem rozpuszczonym w stali. 14
15 Wynika z tego, że dla celów porównawczych pomiar tlenu powinien następować po czasie wymaganym do uzyskania stanu bliskiego homogenizacji kąpieli, ale dalsze jego wydłużanie nie jest celowe, zwłaszcza w warunkach żużla utleniającego. Efektywność odtleniania w warunkach przemysłowych przy uwzględnieniu powyżej przedstawionych wymagań powinna stanowić miarodajny wskaźnik prawidłowości technologii wprowadzania drutu aluminiowego (właściwej prędkości wprowadzania drutu) i co za tym idzie pozwolić na weryfikację poprawności obliczeń modelowych. 3. Dodatki stopowe w postaci drutów Wprowadzanie dodatków stopowych i odtleniających w postaci drutów, ze względu na szereg zalet, jest obecnie powszechnie stosowane. Wprowadzane do ciekłej stali lub żeliwa podczas procesu produkcyjnego druty dzielą się na dwie zasadnicze grupy - druty lite i druty rdzeniowe. Druty lite to w praktyce produkcyjnej przede wszystkim druty aluminiowe stosowane do precyzyjnego regulowania zawartości glinu w stali i do jej odtleniania. Obecnie stosowanie drutów aluminiowych do końcowego, precyzyjnego, odtleniania stali odtlenianych glinem jest standardem. Druty rdzeniowe to odpowiednio przygotowane sproszkowane materiały stanowiące dodatek do kąpieli metalowej zamknięte w stalowej najczęściej otulinie stanowiącej stalową rurkę [23] (prowadzono również próby z drutami o przekroju prostokątnym [24]). Wytwórcy dostarczają bardzo szeroki asortyment drutów rdzeniowych o różnych wypełnieniach, średnicach i grubościach otuliny. Z ich pomocą wprowadza się odtleniacze, pierwiastki modyfikujące wtrącenia niemetaliczne i dozowane w mniejszych ilościach żelazostopy do kadzi i kadzi pośredniej [25]. Dodatki wprowadzane w postaci drutu rdzeniowego to między innymi CaSi, FeCa, Ca metaliczny, FeSi, FeB, FeTi, MgSi, SiC, CaC 2, oraz siarka i węgiel [26, 27, 28], a także inne oferowane standardowo lub w zależności od potrzeb produkowane na zamówienie. Stosuje się również druty rdzeniowe wypełnione żelazem (śrutem żelaznym) do precyzyjnej regulacji temperatury w kadzi pośredniej [29], a także wypełnione odpadowymi materiałami glinonośnymi [30]. Proces nagrzewania i roztapiania drutów rdzeniowych jest złożony, zależny od wielu czynników i może przebiegać według różnych schematów [31, 32, 33, 34], a jego wyznaczanie jest ważnym zagadnieniem technologicznym. W praktyce przemysłowej dąży się aby otulina drutów rdzeniowych i co za tym idzie uwolnienie materiału stanowiącego rdzeń nastąpiło w pobliżu dna kadzi, gdyż zapewnia to najefektywniejsze wykorzystanie wprowadzanego z drutem czynnika [35]. Ze względu na zakres niniejszej pracy roztapianie i przyswajanie drutów rdzeniowych nie będzie szerzej omawiane. Natomiast uwaga skupiona zostanie na procesach wprowadzania i roztapiania litych drutów aluminiowych. 15
16 3.1. Roztapianie się drutów aluminiowych wprowadzanych do ciekłej stali Technologiczne znaczenie prędkości wprowadzania drutów w zależności od czasu ich roztapiania się Jak już wspomniano jedynym mającym znaczenie technologiczne i powszechnie stosowanym w metalurgii stali reprezentantem drutów litych jest drut aluminiowy. Stosowane w praktyce przemysłowej druty mają najczęściej średnicę w granicach 9 15 mm. Zawierają powyżej 99% glinu (resztę stanowi żelazo i śladowe ilości innych pierwiastków w proporcjach zależnych od dostawcy) i w różnego rodzaju rozważaniach są zwykle traktowane jak czysty glin [17, 36, 37, 38]. Ponieważ dla praktyki przemysłowej miejsce uwolnienia glinu podawanego w postaci drutu ma duże znaczenie, proces roztapiania tych drutów oraz wpływ prędkości ich podawania na efektywność procesu odtleniania stali był wielokrotnie opisywany i badany w warunkach laboratoryjnych, przemysłowych i obliczeniach modelowych [np. 15, 17, 36, 37, 38, 39, 40, 41, 42, 43, 44]. Rozpatrywano przypadki czysto teoretyczne jak i możliwie dokładnie odpowiadające rzeczywistości. Do tych pierwszych można zaliczyć badania prowadzone dla przypadku bardzo wolnego - jak na warunki rzeczywiste - wprowadzania drutu aluminiowego [36]. W badaniach tych na podstawie eksperymentów, a następnie symulacji komputerowych określono zjawiska cieplne zachodzące podczas powolnego wprowadzania drutu aluminiowego do stali. Symulacje prowadzono dla drutu o średnicy 15 mm wprowadzanego do stali o przegrzaniu ponad likwidus 80 C z szybkością 30 mm/s (czyli 1,8 m/min). Rys. 4 przedstawia wzdłużny przekrój drutu po różnym czasie zanurzenia w kąpieli z zaznaczonymi izotermami solidusu aluminium oraz przewidywany kontur otaczającej warstewki zakrzepłej stali. Jak widać na rys. 4 w początkowej fazie roztapiana drutu cienka warstewka zakrzepłej stali otacza również dolną powierzchnię drut zanurzonego w ciekłym metalu. Konwekcja ciepła od kąpieli metalowej powoduje roztapianie powłoki na krawędzi końca drutu i w konsekwencji odpadnięcie jej dolnej powierzchni po czasie ok 4,8 s. Ciekłe aluminium skutkiem tego rozpuszcza się w stali, czemu towarzyszy efekt egzotermiczny 2400 kj/kg Al. Skutkiem wydzielania się tego ciepła warstewka zakrzepłej stali otaczająca ciekły rdzeń roztapia się. Po 7-8 sekundach drut jest wystarczająco chłodny do zamrożenia kolejnej warstewki stali od czoła i proces powtarza się. 16
17 Rys. 4. Kolejne etapy roztapiania drutu aluminiowego o średnicy 15 mm wprowadzanego do stali przegrzanej ponad likwidus o 80 C z prędkością 30 mm/s [36]. Ta symulacja odpowiada obserwacjom doświadczalnym. Jednak dla warunków przemysłowych, gdzie prędkość wprowadzania jest kilkadziesiąt razy wyższa, waga tych wahań jest niewielka i należy przyjąć stabilną głębokość penetracji oraz odrzucić możliwość zasklepiania się drutu od czoła [36]. W tych warunkach wpływ efektu egzotermicznego, występującego tylko przy końcu drutu, na czas jego roztapiania jest nieistotny i nie jest uwzględniany w symulacjach o znaczeniu utylitarnym. W przemysłowych operacjach prędkości wprowadzania drutu wynoszą zwykle od kilkudziesięciu do kilkuset metrów na minutę. Roztapianie się drutów litych jest w zasadzie podobne do roztapianie się dodatków wprowadzanych do ciekłej stali w postaci kawałków. W procesie tym zachodzą podobne etapy tworzenia i zaniku warstewki zakrzepłej stali oraz nagrzewania i roztapiania wnętrza. Ponieważ aluminium należy do dodatków których temperatura topnienia jest niższa niż stali (dodatki takie określa się jako dodatki I klasy, a podział na klasy szerzej opisano w rozdziale ), proces roztapiania przebiega według następującego schematu: 1. Po wprowadzeniu drutu do kąpieli tworzy się na nim warstewka zakrzepłej stali - rzeczywisty przekrój poprzeczny drutu w tej fazie pokazuje rysunek 5 [43]. 2. W miarę przebywania drutu w ciekłej stali następuje jego rozgrzewanie się, a warstewka do pewnego momentu powiększa się, po czym zaczyna się topić. W tym czasie drut wewnątrz otuliny jest już zwykle roztopiony. 17
18 Rys. 5. Przekrój drutu aluminiowego o średnicy 12 mm z warstewką zakrzepłej na nim stali po czasie 0,2 s przebywania w stali o temperaturze 1580 C [43]. Wynika z tego, że czynnikiem determinującym czas roztopienia drutu będzie w rzeczywistości trwałość zakrzepłej na drucie warstewki stali, a nie roztopienie się aluminium. Badania laboratoryjne, praktyka przemysłowa i obliczenia wskazują, że stosowane przemysłowo druty mające zazwyczaj średnice w zakresie od 9 do 15 mm, przy prędkościach wprowadzania do kilkuset m/min, mogą, w zależności od głębokości metalu, nie roztopić się całkowicie przed osiągnięciem dna kadzi. Następuje w tym przypadku odbicie się drutu od dna kadzi i często skierowanie ku jej górze, przy czym kierunek poruszania się drutu podlega przypadkowym zmianom. W takiej sytuacji uwolnienie glinu może nastąpić w różnych miejscach kadzi, nawet przy powierzchni metalu w pobliżu warstwy żużla. Efektem tego jest brak powtarzalności wyników operacji technologicznej oraz niski uzysk wprowadzanego glinu, co niweczy zalety, jakie niesie wprowadzanie dodatku w postaci drutu [31, 38, 39]. Przy odpowiednio dużej prędkości wprowadzania drut może nawet wynurzyć się ze stali, co prowadzi do odtleniania żużla zamiast metalu w przypadku kontynuowania operacji wprowadzania drutu. Skutki nadmiernej prędkości wprowadzania drutu przedstawiono na rys. 6 A. 18
19 Rys. 6. Zachowanie się drutu w kadzi w zależności od szybkości wprowadzania [31]. Drut wprowadzany ze zbyt małą prędkością również roztopi się przy powierzchni w pobliżu żużla, co spowoduje niższy uzysk oraz w przypadku intensywnego mieszania brak powtarzalności wyników. Przypadek taki przedstawiono na rys. 6 C. Możliwe jest również, że aluminium będzie roztopione w momencie osiągnięcia przez drut dna, ale otaczająca go warstwa zakrzepłej stali jeszcze do końca się nie roztopi. W takim przypadku warstewka ta może być już na tyle cienka, że jej wytrzymałość będzie niewielka i ulegnie ona mechanicznemu zniszczeniu w momencie uderzenia o dno kadzi [29], co doprowadzi do uwolnienia roztopionego glinu do kąpieli. Dotarcie do dna kadzi drutu z grubszą jeszcze warstwą zakrzepłej stali może spowodować rozpad drutu na stosunkowo długie odcinki. W takim przypadku należy liczyć się z uwalnianiem glinu w pewnym oddalenia od dna kadzi w wyniku wypływania fragmentów drutu odłamanych podczas uderzenia w dno kadzi [40]. Czas potrzebny do ich roztopienia zależy od grubości warstwy zakrzepłej stali oraz długości odłamanego odcinka. W kontekście powyższego, za optymalną prędkość wprowadzenia drutu należy uznać zakres prędkości, przy których drut roztapia się całkowicie przy dnie kadzi lub ciekłe aluminium otoczone jest cienką i słabą warstewką zakrzepłej stali rys. 6 B. Jak z tego wynika dobranie właściwej prędkości wprowadzania drutu wymaga znajomości czasu jego roztapiania w konkretnych warunkach, a mówiąc bardziej precyzyjnie, znajomości procesu narastania i zaniku warstwy stali zakrzepłej na drucie oraz czasu w którym aluminium ulegnie całkowitemu roztopieniu Przebieg roztapiania drutu aluminiowego w ciekłej stali i parametry wpływające na ten proces Czas roztapiania aluminium oraz proces tworzenia i zaniku warstewki zakrzepłej stali jest wynikiem przepływu ciepła z kąpieli do drutu. Zwykle zakłada się, że przepływ ciepła od kąpieli do wnętrza drutu następuje prostopadle do jego osi i pomija się nieistotny przepływ ciepła od czoła drutu (w tak precyzyjnym ujęciu należałoby również uwzględnić pomijany w literaturze wpływ wymiany ciepła z otoczeniem poprzez drut nie wprowadzony jeszcze do 19
20 kąpieli od strony maszyny podającej). Założenie to wynika z niewielkiej powierzchni przekroju drutu w stosunku do bocznej powierzchni kontaktu [37, 40]. Wobec tego drut rozpatruje się zwykle jako nieskończenie długi walec, w którym w wyniku różnicy temperatur następuje przepływ strumienia ciepła od zewnątrz do wnętrza walca. Na powierzchni drutu wprowadzanego do kadzi tworzy się warstwa zakrzepłej stali, a zawarte wewnątrz niej aluminium ulega podgrzaniu, a następnie roztopieniu. Przebieg tych procesów zależy w istotny sposób od kilku czynników związanych z parametrami drutu, kąpieli i samego procesu wprowadzania drutu do kąpieli. Parametry związane z drutem to głównie jego własności termofizyczne i średnica. Ponieważ jednak jako druty lite w praktyce stosuje się wyłącznie druty aluminiowe i to o dużej czystości, to zawężając obszar rozważań do glinu, pozostaje tylko jeden, zmienny i istotny parametr, czyli średnica drutu. Spośród parametrów kąpieli, omówionych szczegółowo w punkcie , największy wpływ na grubość powstającej warstewki zakrzepłej stali oraz czas jej trwania ma temperatura stali, a tym samym powiązane z nią przegrzanie kąpieli. Zarówno dla dodatków kawałkowych, jak i dla drutów parametry te decydują przede wszystkim o grubości i czasie trwania warstewki zakrzepłej stali. Na tym podobieństwa jednak się kończą. W przypadku dodatków kawałkowych proces przyswojenia ma miejsce dopiero po roztopieniu otoczki zakrzepłej stali. Natomiast w przypadku drutów możemy liczyć się z możliwością mechanicznego zniszczenia tej warstewki i uwolnienia dodatku, gdy drut uderzy o dno kadzi [40]. W warunkach bardzo szybkiego wprowadzania drutów do płytkiej kadzi może wystąpić sytuacja, że drut dotrze do dna kadzi w stanie stałym. Uszkodzenie otaczającej go warstewki zakrzepłej stali wywołane uderzeniem może prowadzić do powstania na odkrytych fragmentach drutu warstewki wtórnej. Taki przypadek ma jednak znaczenie wyłącznie z teoretycznego punktu widzenia. W praktyce przemysłowej stosowanie takich prędkości podawania drutu jest niedopuszczalne ze względu na nieefektywność takiej operacji. Z powyższego wynika, że bardzo istotnym parametrem mającym wpływ na przebieg roztapiania drutu jest prędkość jego wprowadzania. Znaczenie tego czynnika jest jednakże szersze niż tylko wynikające z mechaniczno-fizycznego aspektu wyznaczającego drogę, jaką drut przebędzie w kąpieli zanim się roztopi lub natrafi na przeszkody mechaniczne jak np. dno czy ściana kadzi. Wpływ prędkości wprowadzania drutu można porównać z wpływem, jaki ma intensywność mieszanie stali (szybkość przepływu) na roztapianie dodatków kawałkowych [45, 46], gdyż decyduje ona o szybkości poruszania się drutu w kąpieli W rzeczywistości prędkość poruszania się drutu w kąpieli jest znacznie większa niż dodatków kawałkowych w wyniku mieszania stali ze względu na stosowanie stosunkowo dużych prędkości wprowadzania drutu. Drugi powód to brak płynięcia dodatku z prądem metalu, co w przypadku dodatków kawałkowych zmniejsza ich prędkość w stosunku do kąpieli. Rzeczywisty ruch metalu wywołany mieszaniem stanowi podczas wprowadzania drutu tylko pewną składową, która może zwiększać lub zmniejszać ogólną prędkość drutu względem ciekłej stali. To czy prędkość wprowadzania i wynikająca z mieszania będą się sumować czy niwelować zależy od miejsca kadzi, w którym drut jest wprowadzany. Jeżeli drut wprowadzany jest w miejscu prądów wznoszących to prędkości te zsumują się. Natomiast wprowadzanie drutu w miejscu prądów zstępujących sprawi, że prędkość metalu względem drutu będzie różnicą tych dwóch prędkości [37]. Możliwy jest również wariant wprowadzania w martwy obszar kadzi, gdzie prędkość przepływu metalu wzdłuż osi pionowej jest niewielka. 20
21 Wartość prędkości wynikającej z mieszania kąpieli jest jednak zwykle niewielka w stosunku do prędkości wprowadzania drutu. W związku z tym niezależnie od wpływów mieszania, wzrost prędkości wprowadzania zwiększa zwykle prędkość poruszania się drutu w kąpieli metalowej, co skraca czas zaniku zakrzepłej na drucie warstewki stali wskutek przyspieszonej wymiany ciepła. Na rys. 7 przedstawiono, określony w oparciu o symulację programem komputerowym, czas zaniku warstewki zakrzepłej stali oraz jej grubość dla różnych prędkości wprowadzania drutu [40]. Na wykresach zaznaczono również moment początku i końca roztapiania aluminium. Jak wynika z wykresu, prędkość podawania drutu ma istotny wpływ na grubość i czas trwania warstewki zakrzepłej stali na drucie, natomiast moment początku i końca roztapiania aluminium pod powierzchnią warstewki praktycznie nie zmienia się. Rys. 7. Grubość warstewki stali zakrzepłej na drucie w funkcji czasu dla różnych prędkości wprowadzania [40]. Wpływ szybkości wprowadzania drutu na proces powstawanie warstwy zakrzepłej stali na drucie silniej zaznacza się w niższych zakresach prędkości [36]. Z przedstawionego na rys. 8 wykresu, który pokazuje największą (maksymalną) grubość jaką osiągnie warstwa zakrzepłej stali na drucie w procesie jego roztapiania się, wynika, że w miarę wzrostu prędkości wprowadzania drutu wpływ prędkości ulega osłabieniu. Dla drutu o średnicy 15 mm wzrost prędkości z 1 do 2 m/s (z 60 do 120 m/min) powoduje zmniejszenie największej osiąganej grubości warstwy z ok. 4 mm do ok. 3,1 mm, a więc o ok. 0,9 mm. Natomiast wzrost z 11 m/s do 12 m/s (z 660 do 720 m/min) powoduję, że największa osiągana grubość zmniejszy się z ok 1,25 mm do ok. 1,35 mm a więc tylko o 0,1 mm. W warunkach przemysłowych, na konkretnym stanowisku obróbki kadziowej, tak szerokich zakresów szybkości wprowadzania drutów z zasady nie stosuje się, a co za tym idzie zjawisko to ma mniejsze znaczenie praktyczne niż wynikałoby to z wykresów przedstawionych na rysunkach 7 i 8. 21
22 Rys. 8. Maksymalna grubość warstewki zakrzepłej na drucie w zależności od prędkości wprowadzania drutu i średnicy drutu [40]. Ważnym czynnikiem wpływającym na proces tworzenia się warstewki zakrzepłej stali i szybkość roztapiania drutu jest jego średnica. Określony na podstawie obliczeń popartych doświadczeniami laboratoryjnymi wpływ średnicy drutu na czas roztapiania (rozumiany jako roztopienie warstewki zakrzepłej stali i uwolnienie ciekłego aluminium), dla ciekłego metalu nie mieszanego gazem o temperaturze 1500 C przedstawiono na rys. 9 [37]. Zależność ta jest praktycznie liniowa w prezentowanym zakresie średnic 6 14 mm, przy czym dwukrotne zwiększenie średnicy drutu z 7 mm do 14 mm powoduje ponad dwukrotne wydłużenia czasu roztapiania z ok. 1,5 s do ok. 3,3 s. Wpływ średnicy drutu na tworzenia się i zanikanie warstewki zakrzepłej stali oraz czas roztapianie samego drutu ilustruje również wykres przedstawiony na rys. 10. Z wykresu wynika, że średnica drutu wpływa w istotny sposób na czas potrzebny na roztopienie się całego aluminium wewnątrz powłoki z zakrzepłej stali. Natomiast czas rozpoczęcia tego procesu zmienia się w bardzo niewielkim zakresie dla drutów o różnych średnicach. Z przedstawionych na rys. 10 zależności wypływa ponadto wniosek, że w przypadku drutów o większej średnicy, przedział czasu, w którym ciekłe aluminium jest otoczone warstewką zakrzepłej stali zwiększa się w stosunku do czasu trwania pozostałych etapów. Zależnie od średnicy drutu przebieg zmian temperatury będzie różny na jego przekroju. Oczywiste wydaje się, że im większa średnica drutu tym różnica temperatur pomiędzy osią drutu i jego powierzchnią w trakcie nagrzewania i roztapiania drutu będzie wyższa. 22
23 Potwierdza to, obliczony w wyniku symulacji komputerowych, rozkład temperatury wzdłuż promienia drutu zaprezentowany na rys. 11 dla drutu o średnicy 6 mm i na rys. 12 dla drutu o średnicy 14 mm [37]. Rys. 9. Zależność pomiędzy czasem roztapiania drutu aluminiowego wprowadzonego do ciekłej stali, a jego średnicą [37]. Rys 10. Grubość warstwy zakrzepłej stali w funkcji czasu dla różnych średnic wprowadzanego drutu [40]. 23
24 Rys. 11. Rozkład temperatury wzdłuż promienia drutu, dla kolejnych czasów od chwili wprowadzenia do ciekłej kąpieli metalowej drut o śr. 6 mm [37]. Rys. 12. Rozkład temperatury wzdłuż promienia drutu, dla kolejnych czasów od chwili wprowadzenia do ciekłej kąpieli metalowej drut o śr. 14 mm [37]. Z powyższych wykresów wynika, że różnica temperatur utrzymuje się zarówno gdy drut jest w stanie stałym jak i ciekłym temperatura topnienie glinu wynosi 660 C. Dopiero w pobliżu temperatury 950 C następuje wyrównanie się temperatury w całym przekroju. W przypadku drutu o średnicy 6 mm stan taki osiągany jest po 0.9 sekundy, a dla drutów o średnicy 14 mm po 1,3 sekundy. W nieco innym ujęciu ilustruje rozkład temperatury we wnętrzu drutu wykres zamieszczony na rys. 13. Przedstawiono tam zmianę temperatury w funkcji czasu dla dwóch wybranych punktów na przekroju drutu wprowadzonego do ciekłej kąpieli metalowej, a mianowicie w jego osi i na wewnętrznej powierzchni warstewki zakrzepłej stali. W momencie początkowym różnica temperatur, co oczywiste, jest największa. Temperatura wewnętrznej powierzchni warstwy zakrzepłej stali przez pierwsze ok. 0,1 sekundy obniża się wskutek izolującego działania samej warstewki i intensywnego odbierania ciepła przez zimny jeszcze drut. W tym czasie zwiększa się grubość zakrzepłej warstwy stali, a proces ten jak wynika z rys. 10 dla drutu o średnicy 12 mm trwa przez ok. 0,8 sekundy. Jednocześnie następuje bardzo szybki wzrost temperatury w osi drutu, która po ok. 0,2 sekundy osiąga temperaturę topnienia aluminium. W tym okresie następuje zmniejszenie różnicy temperatury pomiędzy omawianymi punktami. Jak widać z przebiegu krzywej nagrzewania, roztapianie aluminium kończy się już po ok. 0,8 sekundy od zanurzenia drutu w kąpieli. W okresie roztapiania, charakteryzującym się stabilizacją temperatury w osi drutu, następuje wzrost różnicy temperatur pomiędzy osią drutu, a wewnętrzną powierzchnią warstewki zakrzepłej stali. 24
25 Rys. 13. Temperatura w funkcji czasu na przekroju drutu Al o średnicy 12 mm wprowadzanego z prędkością 4 m/s do ciekłej kąpieli metalowej o przegrzaniu 50 C [40]. Po całkowitym roztopieniu się aluminium zachodzi ponowne wyrównywanie się temperatury na przekroju drutu, aż do roztopienia się warstewki stali. Większość publikacji jest zgodna, co do przedstawionego powyżej przebiegu roztapiania się drutów [15, 36, 37, 38, 40], aczkolwiek zdarzają się np. rozważania zaniedbujące fakt powstawania na powierzchni drutu warstwy zakrzepłej stali, a koncentrujące się na czasie potrzebnym do ogrzania drutu do temperatury topnienia aluminium. W efekcie takiego podejścia, nie uwzględniającego efektu działania zakrzepłej warstewki stali jako elementu prowadzącego ciekłe aluminium w głąb kąpieli, obliczono czas asymilacji aluminium na 0,048 sekundy dla drutu o średnicy 10 mm i w konsekwencji zalecono szybkość wprowadzania w zakresie 8 10 m/s dla kadzi o głębokości 3 m [41]. Takie prędkości wprowadzania skłoniły autorów do rozważania zachowania się uwolnionego aluminium w kadzi. Stosując wspomnianą prędkość wprowadzania należy uwzględnić, że aluminium będzie miało duża energię kinetyczna, która sprawi, że będzie ono po roztopieniu kontynuowało swój ruch w dół kadzi zanim zacznie wypływać (podobnie jak wrzucane do kadzi dodatki kawałkowe), a to powinno zapewnić dłuższy czas na jego asymilację. Z punktu widzenia rzeczywistych warunków przemysłowych rozważania te nie mają praktycznego zastosowania. Stosowane w obróbce kadziowej prędkości wprowadzania drutu są mniejsze, a ponieważ przede wszystkim dąży się do uwolnienia aluminium w pobliżu dna kadzi, to energia kinetyczna może, co najwyżej przyczynić się do powiększenia obszaru rozprzestrzeniania się aluminium przy dnie kadzi w pierwszej chwili po uwolnieniu Czas roztapiania drutu aluminiowego wprowadzanego do ciekłej stali Zgodność, co do samego przebiegu poszczególnych etapów podczas roztapiania drutów w większości publikacji, nie wyklucza różnic odnośnie czas trwania poszczególnych etapów jak i całego procesu roztapiania drutu. Najlepsze możliwości porównawcze stwarza parametr, któremu poświęca się największą uwagę ze względu na podstawowe znaczenie technologiczne, czyli czas roztopienia się drutu. Dane odnośnie czasu trwania poszczególnych etapów roztapiania się 25
26 drutu spotyka się rzadziej i w różnych ujęciach, utrudniających obiektywne porównanie miedzy nimi. Z tego też względu poniżej ograniczono się do porównania jedynie czasu roztopienia drutu według różnych autorów. W tablicy 1 przedstawiono prognozowane czasy roztapiania drutu aluminiowego według kilku publikacji. Różnice w czasach roztapiania drutów zamieszczone w tablicy 1 są na tyle istotne, że nie mogą być wynikiem przyjęcia odmiennych warunków, dla których określa się czas roztapiania drutu, takich jak temperatura stali, przegrzanie kąpieli metalowej, nieprzystające do siebie średnice drutów czy też różne prędkości wprowadzania drutu. Do porównania wyników z poszczególnych publikacji wytypowano często opisywane i stosowane druty o średnicy 9 10 mm i 15 mm. Tam gdzie zakres badań nie obejmował takiej średnicy wybrano zbliżoną wartość lub też w przypadku, gdy było to możliwe bez ryzyka popełnienia błędu (liniowa zależność), dokonano aproksymacji. W związku, ze stosowaniem odmiennych warunków, dla których określa się czas roztapianie drutu oraz sposobów ich definiowania (np. temperatura lub przegrzanie), a także różnych metod prezentacji rezultatów, porównanie wyników nastręcza pewne problemy. W związku z tym w przypadkach gdzie było to celowe podano obliczenia dla kilku wariantów, celem orientacji we wpływie poszczególnych parametrów na wynik końcowy nawet, jeżeli dotyczy on innych średnic niż wytypowane. Innym problemem przy porównywaniu wyników może być stosowanie w niektórych przypadkach nieprecyzyjnych określeń jak np. czas roztopienia drutu, który może być rozumiany jako czas roztopienia aluminium bądź jako czas zaniku warstewki zakrzepłej na drucie stali. Interpretacji tego terminu można domniemywać na podstawie podanego czasu trwania. W większości przypadków określenia są na tyle precyzyjne, że pozwalają na jednoznaczną identyfikację zjawiska, dla którego podaje się czas. Dla zapewnienia spójności danych zamieszczonych w tablicy 1 konieczne było przeliczenie niektórych wyników symulacji, które przedstawiono w postaci głębokości, na jakiej roztopi się drut, na czas, jaki upłynie zanim drut dotrze na tę głębokość. Część danych w poszczególnych publikacjach zastała podana wprost, część w postaci wykresów (rys. 7, 9, 10, 14). W tym drugim przypadku wyniki liczbowe otrzymano poprzez interpretację wykresów. Porównanie danych zamieszczonych w tablicy 1, zwraca uwagę na duże rozbieżności w obliczonym czasie roztapiania się drutów aluminiowych, jak i różną intensywność oddziaływania na ten czas poszczególnych czynników, takich jak średnica drutu czy prędkość wprowadzania. Pomijając dane z pozycji o numerze 7 i 19, które są wynikiem ignorowania zjawiska powstawania na drucie warstewki zakrzepłej stali (pomiędzy nimi też widoczne są istotne różnice, które jednak mogą wynikać z różnych średnic i temperatury stali), pozostałe czasy roztapiania są bardzo zróżnicowane. Przykładowo, dla drutu o średnicy 9 mm mieszczą się w zakresie od 0,18 sekundy (poz. nr 2) do 1,71 sekundy (poz. nr 11) przy prędkości wprowadzania drutu 4 m/s. W obu wymienionych przypadkach założono identyczne przegrzanie stali na poziomie 50 C (nie podano temperatury stali), a mimo to wyniki różnią się o rząd wielkości. 26
27 Tablica 1. Czasy roztapiania się drutu aluminiowego w zależności od warunków, według różnych źródeł literaturowych. Prędkość Czas po Temperatura Nr Średnica wprowadzania następuje którego określono którym Opis zdarzenia dla kąpieli przegrzania***) Źródło drutu zdarzenie*) czas **) [mm] [m/s] [s] [ C] ,19 całkowite roztopienie Al complete melting Al - 50 [15] ,18 całkowite roztopienie Al complete melting Al - 50 [15] ,18 całkowite roztopienie Al complete melting Al - 50 [15] ,50 całkowite roztopienie Al complete melting Al - 50 [15] ,49 całkowite roztopienie Al complete melting Al - 50 [15] ,46 całkowite roztopienie Al complete melting Al - 50 [15] ,048 temp. topnienia aluminium aluminum melting point [41] ,25 czas roztapiania drutu Al aluminum wire melting [37] ,00 czas roztapiania drutu Al aluminum wire melting [37] ,11 czas roztapiania drutu Al aluminum wire melting [37] ,71 roztopienie warstewki stali steel shell melting [40] ,5 roztopienie warstewki stali steel shell melting [40] ,80 roztopienie warstewki stali steel shell melting [40] ,10 roztopienie warstewki stali steel shell melting [40] ,3 0,40 roztopienie aluminium aluminum melting - 25 [36] ,7 0,23 roztopienie aluminium aluminum melting - 50 [36] ,2 0,78 roztopienie aluminium aluminum melting - 25 [36] ,3 0,47 roztopienie aluminium aluminum melting - 50 [36] ,2 ****) 0,11 temp. topnienia drutu wire melting point [17] topienie się drutu [47] 21 12,5 1 2,6 czas roztapiania - 90 [44] metlting time *) czas po którym następuje zdarzenie opisane w kolumnie nr 5. **) termin użyty w źródle dla opisania zdarzenia związanego z roztapianiem drutu aluminiowego dla którego liczony był czas podany w kolumnie 4, dla źródeł zagranicznych oprócz tłumaczenia polskiego podano oryginalną definicję zdarzenia. ***) temperatura przegrzania stali powyżej temperatury likwidusu. ****) prędkości nagrzewania nie powiązano z prędkością wprowadzania drutu (przyjęta prędkość służyła do określenia wielkości strumienia Al wprowadzanego do kadzi w jednostce czasu). 27
28 Zbliżone wyniki do rezultatów z pozycji nr 11 dla prędkości wprowadzania 4m/s otrzymano dla warunków w których nie odniesiono się do prędkości wprowadzania, gdzie przewidywany czas roztapiania drutu o średnicy 9 mm wynosi 2,0 sekundy poz. nr 8. Z kolei rezultaty z pozycji o numerach 15 i 16 są zbliżone do wyników z pozycji nr 2; i dla drutu o średnicy 10 mm wprowadzanego z prędkością 10,7 m/s określają czas roztapiania na 0,23 sekundy. Podobne rozbieżności mają miejsce w odniesieniu do drutów o średnicy 15 mm i mieszczą się dla prędkości wprowadzania 4 m/s w granicach od 0,49 (poz. nr 5) do 3,10 sekundy (poz. nr 14). Brak zgodności w poszczególnych publikacjach nie ogranicza się jednak tylko do prognozowanego czasu roztopienia się aluminiowego drutu wprowadzanego do ciekłej stali, ale zaznacza się również w ocenie wpływu poszczególnych parametrów technologicznych na prędkość roztapiania drutu. W przypadku danych zamieszczonych w pozycjach nr 1 do 6 [15] wpływ prędkość wprowadzania drutu na czas jego roztapiania jest znikomy, natomiast zauważalne jest silne oddziaływanie średnicy drutu. Wzrost tego parametru z 9 mm do 15 mm powoduje wydłużenie czasu roztapiania o ok. 270% przy prędkości wprowadzania 4 m/s. Inaczej wpływ prędkości wprowadzania na czas roztapiania przedstawia się w danych z pozycji 11 do 14 [40]. Dane w tym zakresie dostępne są jedynie dla drutu o średnicy 12 mm, (pozycje nr 12 i 13) ale jednoznacznie świadczą o zauważalnym wpływie prędkości wprowadzania na czas roztapiania drutu. Wzrost prędkości wprowadzania o 100% powoduje skrócenie czasu roztapiania o 28%. Wpływ średnicy jest również istotny, ale nie w takim stopniu jak w wynikach z pozycji nr 1 do 6. Wzrostowi średnicy z 9 mm do 15 mm towarzyszy wydłużenia czasu roztapiania o ok. 81% przy prędkości wprowadzania 4 m/s. Zbliżone rezultaty odnośnie wpływu średnicy drutu uzyskano dla warunków statycznych pozycje nr 8 do 10 [37]. Sposób prezentacji wyników w [36], przedstawiony na rys. 14, uniemożliwia bezpośrednie odczytanie wpływu średnicy drutu i prędkości jego wprowadzania na szybkość roztapiania. Wykres pozwala w zamian określić jaką zastosować prędkość wprowadzania drutu, aby roztopił się on na głębokości 2,5 m (i tym samym na tej głębokości doszło do uwolnienia aluminium do ciekłej stali) w zależności od średnicy drutu dla trzech różnych temperatur przegrzania kąpieli powyżej temperatury likwidus, a mianowicie: 25 C, 50 C i 75 C. Za wyjątkiem prac [37] i [40], których wyniki są porównywalne, nie podano szczegółów odnośnie sposobu realizacji obliczeń, co utrudnia odniesienie się do nich i skonfrontowanie między sobą. Zaprezentowane powyżej porównanie wyników pochodzących z różnych publikacji nasuwa wniosek, że problem wyznaczenie czasu roztapiania się drutu aluminiowego wprowadzanego do ciekłej stali pozostaje wciąż aktualny. Biorąc pod uwagę, że wpływ na ten proces może mieć kilka czynników, takich jak średnica drutu, prędkość wprowadzania, głębokość kadzi czy przegrzanie kąpieli, dobór i zalecenie właściwej prędkości dla konkretnych warunków przemysłowych może sprawiać znaczne problemy. 28
29 Rys. 14. Wymagana prędkość wprowadzania drutu powodująca uwolnienie aluminium na głębokości 2,5 m w stali w zależności od średnicy drutu i przegrzania stali ponad temperaturę likwidusu o 25 C, 50 C i 75 C [36] Technologia wprowadzania do stali dodatków w postaci drutów Zalety wprowadzania dodatków stopowych w postaci drutów oraz warunki pełnego wykorzystania tej technologii Metoda wprowadzania dodatku do kąpieli metalowej determinuje w znacznym stopniu proces jego roztapiania się i przyswojenia przez kąpiel. W praktyce przemysłowej oprócz trzech, wspomnianych już, podstawowych sposobów wprowadzania dodatków stopowych lub odtleniaczy, a mianowicie wrzucania do kadzi dodatków w postaci kawałkowej, podawania dodatków w postaci drutu litego bądź rdzeniowego oraz wdmuchiwania ich do ciekłej stali w postaci proszku poprzez lance zanurzoną w kadzi [48] spotyka się inne mniej powszechne metody. Jedną z takich metod wprowadzanie dodatków jest np. kontrolowane zanurzanie. Realizacja takiej operacji polega na nakładaniu ( nawlekaniu ) na ogniotrwały pręt prowadzący cylindrycznych pierścieni z materiału stanowiącego dodatek w ilości zależnej od potrzeb i następnie zanurzania takiego pręta do ciekłej stali na czas konieczny do roztopienia pierścieni [49]. Podawano w ten sposób kształtki ze sprasowanej mieszaniny proszków Ca i Fe. Metoda ta charakteryzowała się jednak niską powtarzalnością wyników i ograniczeniem, co do ilości wprowadzanego materiału. Inną metodą kontrolowanego w pewien sposób wprowadzania dodatków stopowych jest wstrzeliwanie pozwalające na zwiększenie głębokości penetracji materiałów o małej gęstości [38, 39, 50]. Stosuje się czasami rzucanie worków z pylistym dodatkiem na powierzchnie żużla w kadzi. Zwykle dotyczy to jednak dodatków mających reagować z żużlem i ewentualnie później pośrednio z metalem. 29
30 Spośród metod mających obecnie zastosowanie w praktyce przemysłowej wdmuchiwanie proszków jest metodą, w której czas roztapiania wprowadzanych materiałów nie decyduje o efektywności operacji technologicznej. Ze względu na małe rozmiary wprowadzanych cząstek, czas ich roztapiania jest bardzo krótki i nawet dodatek o małej gęstości zwykle zdąży się roztopić zanim wypłynie na powierzchnie. W przypadku dodatków o wyższej niż kąpiel temperaturze topnienia jest możliwe ich wypłynięcie [51], ale problem ten, jeżeli wystąpi, rozwiązać można raczej poprzez zmianę właściwości dodatku (ziarnistość, inny skład chemiczny) niż poprzez modyfikacje parametrów wdmuchiwania. W pozostałych metodach czas roztapiania jest ważnym czynnikiem wpływającym znacząco na wynik końcowy operacji wprowadzania dodatków do ciekłej stali. W przypadku wprowadzanych żelazostopów i odtleniaczy w postaci kawałkowej czas i przebieg ich roztapiania jest uzależniony od wielu wspomnianych już czynników jak np. charakterystyka mieszania, gęstość dodatku, prędkość początkowa dodatku, grubość warstwy żużla, czy też operacja technologiczna, podczas której są wprowadzane. Wpływ tak wielu, często zmiennych czynników, utrudnia prawidłowe zaplanowanie i kontrolowanie operacji wprowadzania dodatków. Prostota tej metody sprawia jednak, że mimo wspomnianych wad jest powszechnie stosowana zwłaszcza do wstępnej regulacji składu chemicznego lub odtleniania, po czym następuje precyzyjne dokończenie tych operacji za pomocą drutów [52]. Wprowadzanie dodatków w postaci drutów stosowane jest obecnie na szeroką skalę, a w niektórych zastosowaniach stanowi metodę dominującą. Wynika to z bardzo korzystnej relacji pomiędzy wysoką precyzją i dobrą kontrolą tego procesu, a stosunkowo małymi wymaganiami technicznymi i niskimi kosztami. Wprowadzanie dodatków w postaci drutów litych lub rdzeniowych w znacznym stopniu uniezależnia proces roztapiania od czynników odgrywających rolę w roztapianiu dodatków kawałkowych. Pozwala na precyzyjne określenie ich miejsca wprowadzania w płaszczyźnie poziomej oraz (pod warunkiem znajomości czasu roztapiania) głębokości, na jakiej roztopi się drut i zostanie uwolniony wprowadzany dodatek. Z reguły dąży się do roztopienia drutu (i każdego innego dodatku) możliwie jak najdalej od powierzchni metalu, pokrytej żużlem lub wystawionej na kontakt z powietrzem w wyniku intensywnego mieszania argonem. Prawidłowo przeprowadzona operacja wprowadzania drutu zapewnia lepszą stabilizację przebiegu obróbki pozapiecowej i co za tym idzie powtarzalność wyników oraz wyższy uzysk wprowadzanych komponentów. Wobec tego podstawowym warunkiem wykorzystania zalet technologii wprowadzania dodatków w postaci drutów jest taki dobór parametrów tej operacji, aby drut roztopił się w pobliżu dna kadzi. Proces ten można kontrolować prędkością wprowadzania drutu pod warunkiem znajomości czasu, w jakim ulegnie on roztopieniu [31]. Należy pamiętać, że proces roztapiania może być też w pewnym stopni wspomagany mechanicznie poprzez łamanie drutu lub uszkodzenie warstwy zakrzepłej na drucie stali w momencie uderzenia drutu o dno kadzi. Nie bez znaczenie w tym kontekście jest wytrzymałość mechaniczna samego drutu oraz siły hydrodynamiczne i hydrostatyczne jako źródło mechanicznego oddziaływania na drut [31, 40, 53]; zagadnienie to omówiono obszerniej w punkcie Hydrodynamiczne oddziaływanie kąpieli na drut wprowadzany do ciekłej stali Istotnym elementem różnicującym wprowadzanie dodatków kawałkowych w stosunku do drutów jest ciągłość procesu wprowadzania drutu. Powoduje to wymuszony ruch wprowadzanego dodatku względem ciekłej stali oraz powstawanie sił związanych z oporem hydrodynamicznym i wyporem hydrostatycznym. Z drugiej strony ważnym, z punktu widzenia metalurgicznego, zagadnieniem jest trajektoria drutu w kadzi podczas wprowadzania. Mechaniczne oddziaływanie na drut kąpieli 30
31 metalowej w powiązaniu ze zmieniającymi się wraz z nagrzewaniem własnościami mechanicznymi drutu musi być brane pod uwagę przy określaniu czy drut dotrze do dna kadzi zanim się roztopi. Drut wprowadzany z dużą prędkością napotyka na opór związany ze zjawiskami hydrodynamicznymi. Jak wykazała symulacja komputerowa przeprowadzona dla drutu rdzeniowego, przy odpowiedniej szybkości wprowadzania i kącie wprowadzania różnym od prostego w stosunku do powierzchni kąpieli, może dojść do sytuacji w której drut zaczyna wracać w kierunku powierzchni, zanim dotrze do dna kadzi, na skutek działania oporu hydrodynamicznego [53]. Mała gęstość drutu to dodatkowy czynnik utrudniający dotarcie drutu do dna kadzi. W tym wypadku działa na niego siła wyporu tym silniejsza im mniejsza jest gęstość drutu. Zachowanie się drutów aluminiowych w trakcie wprowadzania do ciekłej stali również było przedmiotem zainteresowania i symulacji [40]. Na rys. 15 przedstawiono trajektorie drutu aluminiowego o średnicy 12 mm wprowadzanego pod katem 10 do kadzi o głębokości ok. 3,5 m z prędkością 4 m/s. Linią A zaznaczono teoretyczny tor drutu aluminiowego przy braku oddziaływania na niego jakichkolwiek sił. W wyniku obliczeń ustalono, że w warunkach rzeczywistych, opisanych powyżej, drut będzie poruszać się po krzywej B, a więc powinien on dotrzeć do dna kadzi, a odchylenie od toru wprowadzania wyniesie przy dnie kadzi ok. 30 cm. Zaznaczyć należy, że odpowiednią sztywność zapewnia mu głównie warstwa zakrzepłej stali. Jak zastrzegają autorzy sytuacja może się zmienić jeżeli zależność granicy plastyczności od temperatury będzie silniejsza niż założono. Krzywa C odpowiada przewidywanej trajektorii drutu, jeżeli plastyczność zacznie odgrywać rolę na mniejszej głębokości niż w wariancie B i jeżeli drut znajdzie się w strefie prądów wstępujących powstałych w kadzi w wyniku mieszania. Jednak nawet w tych warunkach drut powinien dotrzeć do dna kadzi z odchyleniem ok. 50 cm od toru wprowadzania. W takiej sytuacji w wyniku uderzenia o dno i łamania się druta na kawałki może nastąpić ponadto rotacja drutu wokół osi poprawiająca rozprowadzanie glinu w objętości kadzi [38]. 31
32 Rys 15. Trajektoria drutu aluminiowego wprowadzanego do ciekłej stali [40] Realizacja techniczna wprowadzania drutów Wprowadzanie drutów rdzeniowych i litych prowadzi się przy użyciu specjalnych maszyn rys. 16. W zależności od potrzeb stosuje się maszyny wielożyłowe (podające dwa lub więcej drutów równocześnie) albo dwie lub kilka maszyn na jednym stanowisku obróbki kadziowej. Takie układy służą do równoczesnego podawania drutu tego samego rodzaju w celu skrócenia czasu operacji lub też do równoczesnego lub sekwencyjnego podawania drutów różnego rodzaju rys. 17. Podstawowe elementy systemu do wprowadzania drutu do kadzi to: mechanizm napędzający drut, stanowiący układ rolek prowadząco-napędzających poruszanych silnikiem elektrycznym, układy automatyki sterujące prędkością podawania i kontrolujące długość wprowadzonego drutu, szpula lub kręg z drutem rdzeniowym lub litym i rura prowadząca drut nad powierzchnię ciekłego metalu w kadzi. 32
33 Rys. 16. Maszyna do wprowadzania drutu z możliwością zadawania wymaganej długości i prędkości wprowadzania drutu [54]. Rys. 17. Układ dwóch maszyn do wprowadzania drutu z możliwością niezależnego zadawania wymaganej długości i prędkości wprowadzania drutu o różnej średnicy kontrolowanego przez system komputerowy [11]. 33
34 Układ mechaniczny oraz elementy elektroniki sterującej mogą być połączone w jedną zintegrowaną całość lub też stanowić oddzielne elementy, z których pierwszy znajduje się bezpośrednio przy kadzi, a drugi w kabinie operatora obróbki kadziowej. W obu wariantach obudową urządzenia jest szafa z blachy. Schematycznie poszczególne elementy przedstawiono na rys. 18, a układ rolek napędzających i prowadzących przedstawiono na rys. 19. Rys. 18. Schemat maszyny do wprowadzania drutów do ciekłej stali [41]. Rys. 19. Rolki napędzajaco-prowadzące drut w maszynie do wprowadzania drutów [27]. W przypadku pobierania przez maszynę drutu z kręgów leżących na podłożu przy stosowaniu wyższych prędkości podawania może wystąpić problem plątania się drutu podczas odwijania końcowej jego partii. Niedogodność ta nie występuje w przypadku umieszczenia drutu na szpuli. 34
35 W zależności od lokalnych wymagań, maszyny umożliwiają stosowanie prędkości w zakresie od 0 do 5 m/s lub nawet więcej z płynną regulacją. Maszyny do podawania drutu mogą pracować jako stacjonarne, na stałe związane z podłożem lub też mogą być umieszczone na odpowiednim układzie jezdnym. W tym drugim wariancie maszyna tylko na czas obróbki przemieszcza się w pobliże kadzi i ustawia w pozycji umożliwiającej wprowadzanie drutu. Rozwiązanie to pozostawia większą swobodę doraźnego wyboru miejsca kadzi, w które będzie wprowadzany drut, ale z drugiej strony wymaga więcej miejsca oraz podraża i komplikuje cały układ. Współczesne maszyny do wprowadzania drutu wyposażone są w odpowiednie układy elektroniczne pozwalające na wcześniejsze zaprogramowanie całej operacji tak pod względem ilości drutu, jaki ma być wprowadzony zanim maszyna wyłączy się samoczynnie jak i płynnego wyboru prędkości podawania drutu. Operator ma możliwość zadawania masy dodatku w kilogramach, która przez układy sterujące maszyny przeliczana jest na równoważną ilość metrów drutu. W stalowniach, w których proces produkcyjny jest nadzorowany komputerowo maszyny do wprowadzania drutu mogą być zintegrowane z systemami informatycznymi sterującymi i kontrolującymi operacje wprowadzania drutu Wpływ konstrukcji maszyny i własności mechanicznych drutów na parametry podawania ich do kąpieli metalowej Do parametrów wprowadzania drutów, oprócz już omówionych: prędkości wprowadzania i miejsca wprowadzania (punkt na powierzchni ciekłego metalu, w którym drut penetruje kąpiel) należy zaliczyć również kąt pod jakim drut trafia w powierzchnie metalu. Parametr ten może mieć istotny wpływ na przebieg i efektywność operacji obróbki drutem. Z punktu widzenia trajektorii drutu w ciekłym metalu z powodów przedstawionych w punkcie najbardziej pożądany jest kąt prosty pomiędzy powierzchnia metalu a drutem. Dzięki temu nawet przy wysokiej prędkości wprowadzania drutu może on dotrzeć w pobliże dna kadzi. Wpływ na kąt wprowadzania drutu do kąpieli metalowej może mieć zarówno konstrukcja maszyny do wprowadzania drutu jak i własności samego drutu. W maszynie o układzie jak na rys. 17 drut zwinięty w krąg pobierany jest przez maszynę i prostowany poprzez układ rolek napędzająco-prowadzących. Następnie przechodzi przez rurę prowadzącą o odpowiednim profilu wygięcia, które powoduje zmianę kierunku drutu z poziomego na pionowy. W momencie przechodzenia przez łuk rury prowadzącej, drut jest zginany, a następnie w prostym końcowym odcinku ponownie prostowany. Ponieważ średnica rury jest odpowiednio większa niż średnica drutu dla danej maszyny (tak, aby drut nie blokował się na łuku) istnieje luz powodujący nie całkowite wyprostowanie drutu. W konsekwencji tego, a także pewnej sprężystości drutu, opuszcza on rurę prowadzącą jako lekko zakrzywiony, co powoduje, że nie jest wprowadzany do metalu prostopadle do powierzchni, ale pod pewnym kątem w stosunku do tego kierunku. Wskutek krzywizny, również w samym metalu drut porusza się po łuku, a działająca na niego siła wyporu powoduje dalsze odchylanie się trajektorii drutu [55]. Sytuację taką przedstawiono na rys. 33. Drut po przebyciu w ciekłym metalu drogi o długości 4 m zanurzy się w kąpieli na głębokość tylko 2,5 m w wyniku zakrzywienia powstałego podczas podawania. Zakrzywienie to ma promień ok. 3 m. 35
36 Występowanie tego zjawiska zależy w dużym stopniu od usytuowania punktu wprowadzania w stosunku do geometrii kadzi oraz sposobu i intensywności mieszania kąpieli. Wprowadzenia drutu przy krawędzi kadzi może powodować, że drut opierając się o ścianę kadzi ześlizguje i nie tworzy łuku jak na rys 20. Rys. 20. Wpływ promienia zakrzywienia drutu na głębokość penetracji [55]. Zjawisko zakrzywienia drutu nie w każdych okolicznościach jest negatywne. W pewnych warunkach pozwala na stosowanie, w razie konieczności, wyższych prędkości wprowadzania w płytszych kadziach (np. pośrednich) pod warunkiem odpowiedniego doboru miejsca wprowadzania oraz roztopienia się drutu zanim natrafi on na ściany kadzi lub rozpocznie ruch powrotny ku powierzchni. Zwykle dąży się jednak do ograniczania powyższego efektu, a jeżeli jest on nie do zaakceptowania, rozwiązaniem może być maszyna do wprowadzania o konstrukcji przedstawionej na rys. 21. Dzięki pionowemu układowi podającemu, drut po przejściu przez rolki nie zmienia już swego kierunku, co sprawia, że jest pozbawiony krzywizny pozostałej po przejściu przez łuk rury prowadzącej i może penetrować kąpiel prostopadle do jej powierzchni. Gęstość drutu to druga obok sprężystości cecha, która ma wpływ na proces jego wprowadzania, gdyż skłonność drutu do wypływania jest uzależniona od siły wyporu działającej na drut, a ta jest funkcją jego gęstości. Cecha ta jest zróżnicowana, ale jej zmienność dotyczy głównie drutów rdzeniowych, które mogą mieć różne wypełnienia, a także różny stopień ich zagęszczenia. Natomiast druty aluminiowe z oczywistych względów nie wykazują w tym zakresie zróżnicowania. 36
37 Rys 21. Maszyna do wprowadzania drutu z podajnikiem z pionowym układem rolek napędzająco-prowadzących [56]. Mimo iż należy zdawać sobie sprawę z możliwych konsekwencji krzywizny drutu i wprowadzania go pod kątem, to w większości przypadków parametry te nie stanowią dominującego czynnika wpływającego na sposób i głębokość penetracji. Wynika to z tego, że ewentualna krzywizna drutu i jej wpływ na kąt penetracji są w rzeczywistości niewielkie. Potwierdzać to zdaje się fakt, że zagadnienie to jest stosunkowo rzadko poruszane w literaturze. W przypadku drutu aluminiowego ponadto, jak wynika z wcześniej omówionych obliczeń [40], prosty drut o średnicy 12 mm wprowadzany nawet pod kątem 10 i z prędkością 4 m/s dotrze do dna kadzi o głębokości ponad 3,5 metra z niewielkim odchyleniem. Z drugiej strony mogące wpływać na sposób penetracji zakrzywienie drutu jest w pewnej mierze spowodowane sprężystością stosowanego drutu, a ta jest w większym stopniu raczej cechą drutów rdzeniowych, posiadających stalową otulinę niż drutów aluminiowych. Stosowane przemysłowo druty rdzeniowe różnią się miedzy sobą wieloma parametrami mającymi wpływ na zachowanie się ich podczas wprowadzania. Mają one zróżnicowane grubości otuliny, kształty przekroju, stopień zagęszczenia wypełnienia i własności mechaniczne (sprężystość, granicę plastyczności itp.). Natomiast w przypadku drutów aluminiowych istotny wpływ na ich trajektorię może mieć głównie siła wyporu. W każdym przypadku przy niewłaściwie wybranym miejscu wprowadzania negatywnie oddziaływać będą prądy wznoszące występujące w kadzi związane z mieszaniem kąpieli podczas operacji wprowadzania drutu. W przypadku drutów aluminiowych zróżnicowanie teoretycznie sprowadza się do ich średnicy. Jak jednak wynika z rozeznania przeprowadzonego w polskich hutach, druty aluminiowe w zależności od dostawcy różnią się i to istotnie z punktu widzenia procesu wprowadzania właściwościami mechanicznymi. W zależności od nich może zmieniać się górna graniczna prędkość wprowadzania. Wiąże się to z oporami powstającymi podczas prowadzeniem drutu w maszynie. Drut po przejściu przez układ rolek natrafia w łuku rury prowadzącej, który stawia opór związany z tarciem o wewnętrzną powierzchnię tejże rury. W zależności od sztywności drut jest w stanie pokonać większą lub mniejszą siłę tarcia. 37
38 W praktyce przemysłowej problem ten uwidacznia się na przykład w ten sposób, że druty miękkie już przy prędkościach ok. 2,5 m/s klinują się w maszynie, tworząc pętle przed wejściem do rury prowadzącej, podczas gdy druty twardsze nie sprawiają problemów na tych samych urządzeniach przy prędkościach ponad 4 m/s. Zaklinowanie się drutu wymaga interwencji obsługi, co wydłuża czas obróbki, a to przy harmonogramie czasowym narzuconym przez COS może prowadzić do dezorganizacji produkcji. 4. Modelowanie roztapiania dodatków wprowadzanych do ciekłej stali Właściwie prowadzony proces wprowadzania dodatków stopowych powinien uwzględniać czas konieczny na ich asymilację. Określenie czasu roztapiania się żelazostopów kawałkowych oraz drutów litych i rdzeniowych można dokonywać na podstawie prób laboratoryjnych [57, 58, 59]. W wielu jednak przypadkach odtworzenie w skali laboratoryjnej rzeczywistych warunków obejmujących wszystkie możliwe czynniki i ich warianty oddziaływania jest na tyle trudne i pracochłonne, a ilość możliwych kombinacji tak duża, że zwykle nie prowadzi się takich badań w pełnym zakresie zmienności wszystkich parametrów. Optymalizacja każdego procesu technologicznego jest znacznie ułatwiona i mniej kosztowna, gdy można korzystać z komputerowej symulacji danego procesu. Zbudowanie wiarygodnego modelu procesu czy operacji technologicznej, bazującego na matematycznym opisie danego zagadnienia, wymaga wiedzy w zakresie zjawisk fizycznych z nim związanych oraz reguł nimi rządzących, a także konkretnych wartości istotnych parametrów termofizycznych Przegląd literatury na temat czynników wpływających na asymilację dodatków w ciekłej stali Parametry wpływające na roztapianie i rozpuszczanie dodatków wprowadzanych do ciekłej stali Przyswajanie wszelkiego rodzaju dodatków (stopowych, odtleniających, modyfikujących) może przebiegać w różny sposób, zależny od wielu czynników. W zależności od nich dodatki ulegają roztapianiu lub rozpuszczaniu. Proces rozpuszczania, a zwłaszcza roztapiania może zachodzić według różnych schematów o zmiennym czasie trwania. W każdym przypadku na powierzchni dodatku wprowadzonego do kąpieli metalowej tworzy się warstewka zakrzepłej stali, która z czasem zanika i umożliwia kontakt ciekłej stali z dodatkiem w stanie ciekłym lub stałym. Proces przyswajania dodatków wprowadzanych do ciekłej stali zależy od parametrów związanych z właściwościami samych dodatków, charakterystyką środowiska, do którego są wprowadzane i metodą ich wprowadzania. Parametry związane z własnościami dodatków to głównie własności termofizyczne oraz kształt i ciężar właściwy. Podstawowe cechy kąpieli, do której wprowadza się dodatki stopowe, mające wpływ na przebieg ich roztapiania to temperatura oraz zjawiska hydrodynamiczne w kadzi. Poza tym wpływ mają również własności termofizyczne kąpieli i w pewnym stopniu jej skład chemiczny. 38
39 Sposób wprowadzania dodatków jest zdeterminowany w dużym stopniu ich wielkością oraz kształtem (drut, kawałki lub proszek). Poszczególne sposoby pozwalają na różną swobodę i precyzję wyboru miejsca podawania w kadzi i to zarówno w pionie, jak i w poziomie kąpieli. W zależności od sposobu wprowadzania dodatków, niektóre parametry nabierają większego lub mniejszego znaczenia. Do tej grupy można zaliczyć np. prędkość podawania. Największe znaczenie odgrywa ona przy wprowadzaniu dodatków w postaci drutów Właściwości dodatków wpływające na ich przyswajanie Temperatura topnienia dodatków Temperatura topnienia dodatków wprowadzanych do stali odgrywa pierwszorzędną rolę w procesie ich asymilacji, decydując o tym czy dodatek będzie się roztapiał czy rozpuszczał. Znaczenie tego parametru jest tak istotne, że w szeregu rozważaniach, stanowi on podstawę podziału dodatków stopowych na klasy i tym samym oddzielnego rozpatrywania mechanizmu przyswajania dodatków w poszczególnych klasach. Generalnie podział ten opiera się na wzajemnej relacji temperatury kąpieli metalowej i temperatury topnienia dodatku. Zasadniczo dodatki dzieli się na dwie podstawowe klasy, a mianowicie: I klasa - dodatki o temperaturze topnienia niższej niż temperatura krzepnięcia stali II klasa - dodatki o temperaturze topnienia wyższej niż temperatura krzepnięcia stali W rzeczywistości podział ten nie jest tak jednoznaczny ze względu na spotykane w publikacjach odmienne kryteria podziału dodatków. Oprócz wspomnianego kryterium różnicującego dodatki w zależności od tego czy temperatura topnienia dodatku jest niższa czy wyższa od temperatury krzepnięcia stali [36, 60, 61] stosuje się podział uzależniony od tego czy temperatura topnienia dodatku jest wyższa czy niższa od rzeczywistej temperatury stali w kadzi [51, 62, 63] i bierze pod uwagę reakcje egzotermiczne. W bardziej precyzyjnym ujęciu pierwszego kryterium pod uwagę bierze się relację pomiędzy temperaturą likwidus dodatku, a temperaturą solidus kąpieli [64]. Pierwsze kryterium, bazujące na temperaturze krzepnięcia stali, jest bardziej arbitralne i pozwala jednoznacznie przypisać dodatki do poszczególnych klas, przynajmniej dla danej grupy gatunkowej stali. Drugie jest mniej jednoznaczne i powoduje, że ten sam dodatek może należeć do różnych klas w zależności od stopnia przegrzania stali ponad temperaturę krzepnięcia, ale lepiej oddaje rzeczywisty charakter przyswajania (topienie, rozpuszczanie). W praktyce różnica pomiędzy oboma podziałami ma znaczenie tylko dla grupy dodatków o temperaturze topnienia zbliżonej do temperatury topnienia stali, a dla pozostałych nie ma specjalnego znaczenia i czasami ci sami autorzy w zależności od publikacji posługują się obydwoma definicjami, a nawet zdarza się, że wykazują brak konsekwencji, używając obu definicji w jednej publikacji [65]. Stosuje się również podział na trzy klasy, który uwzględnia zachodzenie reakcji egzotermicznych. Bardziej szczegółowe omówienie podziału na klasy i różnice w sposobie przyswajania dodatków w poszczególnych klasach przedstawiono, w powiązaniu z opisem mechanizmu roztapiania i rozpuszczania dodatków stopowych, w rozdziale Należy nadmienić, że stosuje się również inne podziały dodatków. Sformułowano na przykład podział oparty na relacjach pomiędzy temperaturą topnienia dodatku, a temperaturą krzepnięcia stali 39
40 i rzeczywistą temperaturą stali. Wydzielono trzy grupy obejmujące dodatki łatwo topliwe, trudnotopliwe i bardzo trudnotopliwe [66]. Pierwsza obejmuje dodatki o temperaturze topnienia niższej niż temperatura krzepnięcia stali, do której się je wprowadza. Do grupy drugiej zaliczono dodatki, których temperatura topnienia leży pomiędzy temperaturą krzepnienia stali, a jej rzeczywistą temperaturą w kadzi, a do trzeciej grupy dodatki o temperaturze topnienia wyższej niż temperatura ciekłej stali. Jak z powyższego wynika jest to podział w którym pierwsza grupa jest zdefiniowana jednoznacznie lecz do drugiej lub trzeciej grupy mogą być przypisywane te same dodatki w zależności od przegrzania stali i tym samym też nie są jednoznacznie sklasyfikowane. Właściwości termofizyczne dodatków oraz reakcje egzotermiczne zachodzące podczas ich roztapiania i rozpuszczania Własności termofizyczne, obejmujące przewodność cieplną i ciepło właściwe oraz ciepło topnienia i przemian polimorficznych, wpływają w mniejszym lub większym stopniu na czas oraz sposób roztapiania lub rozpuszczania dodatków stopowych. Przewodność cieplna odgrywa wśród własności termofizycznych wiodącą rolę, wpływając na proces przyswajania dodatków stopowych. W zależności od tego parametru roztapianie może przebiegać w różny sposób oraz w innym czasie [36, 51, 61, 63, 67, 68]. Generalnie wyższa przewodność cieplna sprzyja szybszemu roztapianiu się dodatków [68]. Ciepło topnienia i przemian polimorficznych oraz ciepło właściwe także rzutują na proces roztapiania. Ich znajomość jest konieczna do wyznaczenia czasu roztapiania [61, 67]. Przykładowo różnica pomiędzy dodatkami krzemomanganu a żelazokrzemu w przyroście entalpii związanej z podgrzaniem ich do temperatury 1500 C powoduje, że FeMn roztapia się o ok. 30% dłużej [61]. Wpływ własności termofizycznych na proces roztapiania należy rozpatrywać łącznie, gdyż np. duże ciepło właściwe dodatku może nie utrudnić szybkiego nagrzania go, jeżeli jest powiązane z dobrą przewodnością cieplną. Oprócz własności termofizycznych znaczący wpływ na sposób i czas przyswajania wprowadzanych do ciekłej stali dodatków mogą mieć reakcje egzotermiczne. Wprowadzane do ciekłej stali dodatki stopowe mieszają się z nią tworząc z żelazem związki międzymetaliczne. W wielu przypadkach procesowi temu towarzyszy wydzielanie ciepła. Efekt egzotermiczny o różnym stopniu nasilenia towarzyszy tworzeniu związków międzymetalicznych pomiędzy żelazem i wieloma metalami wprowadzanymi do stali. Należą do nich między innymi: kobalt, nikiel, krzem, chrom, molibden, wanad, niob, tantal, tytan i wolfram [51, 62, 69]. Ogólnie reakcje tworzenia takich związków międzymetalicznych na bazie żelaza można opisać równaniem [69]: x Fe + y Me = Fe x Me y (7) Wprowadzanie żelazostopów w odróżnieniu od czystych pierwiastków powoduje z reguły mniejszy efekt cieplny. Wynika to z tego, że wprowadzany żelazostop zawiera już pewną, (zależną od składu) ilość związku międzymetalicznego. Możliwa jest również sytuacja, że wprowadzany żelazostop ma skład odpowiadający ściśle związkowi międzymetalicznemu i jego mieszaniu z żelazem nie będzie towarzyszył żaden efekt cieplny [70]. 40
41 Oprócz wprowadzania dodatków stopowych w postaci kawałkowej stosuje się również sprasowane lub wprowadzane w drucie rdzeniowym mieszaniny proszków dwóch różnych pierwiastków lub stopów. Dodatki te mogą przyjmować postać sprasowanych brykietów [71, 72, 73] lub też stanowić wypełnieniu drutu rdzeniowego [51, 63]. Stosowanie takich sproszkowanych dodatków ma na celu uzyskanie maksymalnego efektu egzotermicznego, a co za tym idzie skrócenie czasu koniecznego na roztopienie i tym samym szybsze przyswojenie wprowadzanego składnika stopowego. Innego typu reakcje egzotermiczne mogą wystąpić w specjalnie przygotowanych mieszankach stanowiących np. wypełnienie drutów rdzeniowych, w których zachodzi reakcja redukcji tlenków. W wyniku tych reakcji nie tylko wydziela się duża ilość ciepła, ale przede wszystkim powstaje materiał, który ma stanowić dodatek stopowy [74, 75]. Ze względu na podobieństwo do opisanych poprzednio reakcji mikroegzotermicznych, dodatki takie można zaliczyć do tej samej grupy, jako pewna ich odmiana. Właściwości fizyczne dodatków i ich wpływ na szybkość przyswojenia Z własności fizycznych należy wymienić wielkość, kształt i gęstość, jako te, które mają istotny wpływ na czas przyswajania dodatków wprowadzanych do ciekłej stali. Kawałki o większych rozmiarach, ale o tym samym kształcie będą wymagały dłuższego czasu na całkowite roztopienia lub rozpuszczenie niż małe [45, 46, 51, 76, 77], a ponadto wielkość wpływa również na przebieg roztapiania (np. mniejsze kawałki ulegną całkowitemu roztopieniu zanim zaniknie otaczające je warstwa zakrzepłej stali, a większe mogą ulec w tym czasie tylko częściowemu roztopieniu) [60, 61]. Kształt decyduje o stosunku powierzchni kontaktu kawałka dodatku z ciekłą stalą do masy tego kawałka. Wynika z tego, że dodatki o kształcie kuli będą się rozgrzewały i topiły wolniej niż płaskie lub o nie regularnym kształcie [64]. Także jakość powierzchni odgrywa pewna rolę w procesie roztapiania dodatków. Chropowata lub zanieczyszczona powierzchnia może utrudnić transport ciepła, pomiędzy dodatkiem i warstwą zakrzepłej stali, co sprzyja szybkiemu zanikowi tejże warstwy i tym samym przy nie zmienionych pozostałych warunkach w końcowym efekcie skraca czas roztapiania [60]. Pośredni wpływ na roztapianie dodatków stopowych ma ich gęstość, gdyż decyduje o zanurzeniu dodatku w ciekłej stali [69, 76]. Niezależnie od fizycznych własności komponentów żelazostopu, ilość masy w jednostce objętości zależy również od porowatości danego materiału. Niższe stopień zagęszczenia materiału dodatku będący wynikiem porowatości prowadzi do skrócenia czasu roztapiania (mniejsza masa do roztopienia). Z drugiej strony porowaty materiał charakteryzuje się mniejszym przewodnictwem cieplnym, co wydłuża czas roztapiania. Zachodzi tym samym wzajemne znoszenie się wpływów dwóch czynników [68]. Porównanie czasów roztapiania żelaza gąbczastego i zwartego prowadzi do wniosku, że w tym przypadku silniejsze oddziaływanie ma zmniejszenie masy, gdyż żelazo gąbczaste roztapia się szybciej rys
42 Rys. 22. Całkowity czas roztapiania kul żelaznych o różnej porowatości w funkcji początkowego promienia [68] W bardziej szczegółowych i mających znaczenie teoretyczne rozważaniach uwzględnia się także wpływ gęstości wprowadzanego dodatku po roztopieniu na rozkład (przepływ) jego fazy ciekłej wywołany grawitacją i siłami wyporu w warunkach konwekcji naturalnej [67, 58]. Brany pod uwagę jest także współczynnik rozszerzalność cieplnej [58, 60, 67] i stężeniowy współczynnik rozszerzalności [58, 67] Parametry kąpieli metalowej, do której wprowadzane są dodatki Temperatura, przegrzanie, właściwości termofizyczne i skład chemiczny Powstawanie i roztapianie warstewki zakrzepłej stali na powierzchni wprowadzanego dodatku oraz proces roztapiania dodatku po zaniku warstewki zależy w dużej mierze od parametrów kąpieli metalowej, do których zaliczyć należy temperaturę, przegrzanie, własności termofizyczne i skład chemiczny. Poniżej przedstawiono ich wpływ na przyswajanie dodatków wprowadzanych do stali. Temperatura kąpieli Temperaturę kąpieli metalowej, ze względu na jej znaczenie należy uznać za podstawowy czynnik decydujący o szybkości przyswajania żelazostopów. Stanowi ona niezbędny parametr wejściowy do określenia sposobu i czasu roztopienia się dodatku [51, 78, 79]. Różnica temperatur pomiędzy dodatkiem a otoczeniem, stymuluje kluczowy dla określenia czasu roztapiania parametr, jakim jest intensywność przepływu ciepła z kąpieli metalowej do wprowadzanego dodatku. 42
43 Ponadto temperatura kąpieli wpływa na grubość tworzącej się na powierzchni dodatku warstewki zakrzepłej stali [31]. Zależność czasu roztapiania i grubości warstwy zakrzepłej stali od temperatury ilustruje rys. 23. W przypadku dodatków o temperaturze topnienia wyższej niż temperatura kąpieli metalowej, temperatura stali decyduje o kinetyce transportu masy z dodatku do stali, a więc decyduje o szybkości rozpuszczania [80, 81]. Temperatura stali może ponadto decydować - w przypadku dodatków o temperaturze topnienia zbliżonej do temperatury topnienia stali, czy przyswajanie będzie wynikiem roztapiania czy też rozpuszczania. Rys 23. Zmiana w funkcji czasu grubości zakrzepłej na drucie warstewki stali i czas roztapiania otuliny drutu rdzeniowego ( drut CaSi o średnicy 13 mm), [27]. Przegrzanie Przegrzanie to drugi bardzo istotny parametr, ale o wtórnym, wynikowym charakterze, gdyż związany jest bezpośrednio z temperaturą kąpieli. Parametr ten rozumiany jako różnica pomiędzy temperaturą krzepnięcia a aktualną temperaturą kąpieli metalowej jest bardzo istotnym czynnikiem wpływającym na przebieg tworzenia się i zaniku warstewki ciekłej stali na powierzchni wprowadzanego dodatku. Znaczenie tego procesu wynika z faktu, że w okresie, gdy na wprowadzanych do ciekłej stali dodatkach stopowych utrzymuje się warstewka zakrzepłej stali mamy w praktyce do czynienia z roztapianiem się kawałków metalu we własnej przegrzanej kąpieli [68, 78]. W związku z tym, że przy małym przegrzaniu warstewka zakrzepłej stali ma temperaturę zbliżoną do własnej temperatury krzepnięcia należy oczekiwać w tych warunkach długiego czasu jej zaniku. Takie warunki panują np. w kadzi pośredniej. Wobec ostrych limitów czasowych wprowadzanie dodatków stopowych do kadzi pośredniej może wiązać się ze znacznymi 43
44 trudnościami z ich przyswojeniem. Szczególnie dotyczy to dodatków, których przyswajaniu nie towarzyszy reakcja egzotermiczna [51, 58, 82]. Parametr ten brany jest pod uwagę w wielu rozważaniach dotyczących procesu roztapiania dodatków stopowych [36, 51, 60, 61, 78]. Właściwości termofizyczne Znajomość właściwości termofizycznych kąpieli, do której wprowadza się dodatki jest niezbędna do obliczenia czasu przyswojenia tych dodatków. Parametry te mają istotny wpływ na przebieg roztapiania się dodatków stopowych, jednak w przypadku procesów stalowniczych ich zmienność jest stosunkowo niewielka i w związku z tym nie poświęca się wiele uwagi wpływowi zmienności właściwości termofizycznych ciekłej stali na proces roztapiania dodatku. Zwykle przyjmuje się stałe wartości stosowne - według autorów publikacji - dla określonych warunków i na tym się poprzestaje. Większą uwagę poświęca się im w przypadku istotnego zróżnicowania parametrów termofizycznych, co ma miejsce przy rozpatrywaniu zjawisk odnoszących się zarówno do stali i żeliwa [83]. Temperatura topnienia kąpieli metalowej to istotna właściwość termofizyczna, ale raczej nie poświęca się uwagi wpływowi tej wielkości na sam proces roztapiania dodatków. Wynika to z jej stosunkowo małej zmienności w konkretnych zakresach, których dotyczą poszczególne rozważania. Nie zmienia to faktu jej dużego znaczenia, chociażby dla określenia przegrzania. W bardziej dokładnych rozważaniach istotna jest znajomość zakresu solidus likwidus. Dotyczy to zwłaszcza rozważań dla stali stopowych lub żeliw [84]. W opisie procesu roztapiania i rozpuszczania dodatków stopowych uwzględnia się również takie parametry termofizyczne jak przewodność cieplną kąpieli i ciepło właściwe. Są to parametry wpływające na proces tworzenia i zaniku warstewki zakrzepłej stali na dodatku oraz determinujące przepływ przez nią ciepła. Ze względu na ich małe zróżnicowanie nie rozpatruje się zwykle wpływu zmienności tych parametrów na proces przyswajania dodatków stopowych. Wpływ ten jest widoczny przy porównywaniu roztapiania w różnych rodzajach kąpieli jak np. stal i żeliwo [83]. Podobnie jest traktowane ciepło przemian fazowych metalu, do którego wprowadza się dodatki. Skład chemiczny kąpieli metalowej W danych wejściowych - jak już wspomniano - zwykle nie odwołując się bezpośrednio do składu chemicznego, przyjmuje się, że jest on pośrednio uwzględniany przez inne parametry. Takie podejście przy utylitarnych zastosowaniach wydaje się wystarczające, ale tylko w odniesieniu do dodatków przyswajanych przez roztapianie. Natomiast w przypadku gdy wprowadzane dodatki stopowe ulegają rozpuszczaniu wymagana jest większa ostrożność. Związane jest to z tym, że np. zawartość w stali tlenu może być istotnym, dodatkowym i niezależnym parametrem regulującym ten proces [10, 83]. Dlatego też określając parametry wpływające na proces przyswajania dodatków stopowych w niektórych warunkach nie można pominąć składu chemicznego kąpieli, zakładając, że jest on już w sposób pośredni uwzględniony poprzez pozostałe czynniki. Przykładowo, tlen rozpuszczony w stali spowalnia rozpuszczanie np. żelazoniobu i żelazowanadu [10, 83]. Wpływ zawartości tlenu w stali na prędkość rozpuszczania żelazoniobu ilustruje rys
45 Rys. 24. Wpływ tlenu rozpuszczonego w stali na prędkość rozpuszczania się w niej żelazo-niobu [83]. Zjawisko to wiąże się z powstawaniem na powierzchni wolno rozpuszczającego się stopu ochronnej warstewki stałego tlenku - w tym przypadku niobu - która izoluje wprowadzony dodatek od stali i spowalnia rozpuszczanie w stosunku do prędkości dla stali odtlenionej [10]. W przypadku dodatków stopowych, które ulegają roztapianiu zjawiska to nie odgrywa znaczącej roli. Skład chemiczny kąpieli może mieć również znaczenie z punktu widzenia teoretycznego opisu mechanizmu powstawania warstwy zakrzepłej na dodatku stali. W kąpieli o wysokiej zawartości węgla (dotyczy to np. żeliw) w szybko krzepnącej na powierzchni dodatku warstewce występują tendencje do zmiany zawartości węgla zgodne z diagramem fazowym Fe-C. Ze względu jednak na dynamikę procesu oraz fakt, że transport ciepła jest ok. 40 razy szybszy niż transport masy, skład chemiczny powłoki w pierwszym okresie jej powstawania jest praktycznie tożsamy ze składem kąpieli. Później w miarę jak prędkość narastania warstewki spada, zmiany składu mogą zmieniać się w kierunku stanu równowagi [84]. Procesy te mogą mieć pewien wpływ na czas i temperaturę krzepnięcia warstwy na dodatku. W obliczeniach dla celów przemysłowych przyjmuje się jednak zwykle ogólne określenie stal (ewentualnie inne tworzywo), dla którego określa się temperaturę topnienia i ewentualnie inne własności. Wpływ mieszania i hydrodynamiki na szybkość przyswajania dodatków Mieszanie stali w kadzi ma istotniejszy wpływ na szybkość przyswajania dodatków, które ulegają rozpuszczaniu, ponieważ mieszanie przyspiesza wymianę masy, która limituje proces rozpuszczania [36, 51, 61], a ponadto (tak jak i w przypadku dodatków ulegających roztapianiu) przyspieszeniu ulega proces roztapiania się warstwy stali zakrzepłej na dodatku. 45
46 Czynniki wpływające na wielkość strumienia masy to współczynnik dyfuzji dla danego pierwiastka, temperatura topnienia dodatku oraz związane już z własnościami kąpieli, temperatura stali i intensywność jej mieszanie oraz skład chemiczny stali [60, 80]. Wobec tego, że szybkość rozpuszczania zależy od wspominanych powyżej parametrów może się ona zmieniać w szerokim zakresie w zależności od warunków lokalnych. W związku z tym szybkość rozpuszczania jest parametrem, którego wyznaczenie, czy to na drodze doświadczalnej, czy też poprzez obliczenia jest konieczne w celu prawidłowego zaprojektowania technologii. W przypadku dodatków ulegających roztapianiu, mieszanie wpływa głównie na czas roztapiania zakrzepłej na tych dodatkach warstewki stali, a samych dodatków tylko w pewnych warunkach, na przykład, gdy są podawane w dużych kawałkach, kiedy to po roztopieniu warstewki stali dochodzi do kontaktu kąpieli z nieroztopionymi jeszcze kawałkami [61, 85]. W badaniach laboratoryjnych polegających na wyznaczaniu czasu roztapiania kulistych dodatków aluminium w ciekłym aluminium rys. 25 i dodatków stalowych w ciekłej stali stwierdzono, że w objętym badaniami zakresie prędkości wynoszącej 0 40 cm/s występuje liniowa zależność pomiędzy prędkością kulistego dodatku względem ciekłego metalu a czasem jego roztapiania [86, 87]. Mieszanie wpływa ponadto pozytywnie na ujednorodnienie składu chemicznego stali po wprowadzeniu do niej dodatków stopowych i może przy prawidłowym prowadzeniu poprawiać uzysk [76, 88], co sprawia, że jest z zasady integralnym elementem operacji wprowadzania dodatków stopowych. Uwzględnianie w procesach roztapiania dodatków stopowych wpływu oddziaływania czynników związanych z hydrodynamiką metalu w kadzi wymaga znajomości pewnych wielkości fizycznych ciekłej stali jak np. ciężar właściwy czy lepkości [78]. Parametry te oczywiście w pewnym zakresie mogą zmieniać się np. wraz z temperaturą. W praktyce jednak nie rozpatruje się wpływu tych zmian na proces mieszania stali. Hydromechanika stali w kadzi stanowi przedmiot wielu prac opisujących modelowanie numeryczne, modelowanie fizyczne w oparciu o zimne modele wodne lub olejowe, ze znaczonymi pierwiastkami w ciekłym metalu oraz przemysłowe w warunkach rzeczywistych. Bada się wpływ sposobów wymuszających mieszanie na charakter przepływu i rozkład prędkości w objętości kadzi. Przedmiotem zainteresowania jest również wpływ mieszania na czystość stali, jednorodność składu, czas i przebieg roztapiania wprowadzanych do kadzi żelazostopów i odtleniaczy oraz ich uzysk. 46
47 Rys 25. Czas roztapiania aluminiowej kuli o średnicy 35 mm w zależności od szybkości jej poruszania się w kąpieli aluminiowej o temperaturach , 732 i 754 C [86]. Rozważane są zarówno raczej teoretyczne warunki występowania ruchu stali tylko w wyniku naturalnej konwekcji [89], jak i różne przypadki wywołanego operacjami technologicznymi lub wymuszonego celowo mieszania stali [20, 76,79, 90, 91, 92]. Wyniki tych badań wskazują na istotny wpływ mieszania stali wywołanego przez różne czynniki na przebieg roztapiania i rozpuszczania się wprowadzanych dodatków stopowych w warunkach przemysłowych. W przypadku podawania dodatków podczas spustu oprócz mających znaczenie takich parametrów jak: gęstość, temperatura topnienia i rozmiar dodatku istotny wpływ na uzysk wprowadzanych podczas spustu żelazostopów ma stopień napełnienia kadzi w trakcie operacji podawania dodatków [76, 93, 94]. Zachowanie się wprowadzanych do kąpieli materiałów przedstawia się odmiennie w przypadku dodatków kawałkowych i dodatków w postaci drutów. Dodatki kawałkowe z reguły zaczynają przemieszczać się wraz ze strumieniem stali ( płyną z prądem ), co zmniejsza ich prędkość względną w stosunku do otaczającej kąpieli. Dodatki o małej gęstości, które po wypłynięciu utrzymują się na powierzchni ciekłej stali, jedynie fluktuują zgodnie z turbulencjami kąpieli, a ich prędkość względna jest niewielka lub nawet zerowa [95]. W przypadku wprowadzania drutów zjawisko przemieszczania z przepływającą stalą nie występuje, a prędkość drutu w stosunku do metalu zależy przede wszystkim od prędkości wprowadzania. Ze względów technologicznych należy dążyć do wprowadzania drutu jak i dodatków kawałkowych w obszarze prądów zstępujących rys. 26. Roztopiony dodatek dłużej przebywa wówczas w ciekłej stali zanim wejdzie w kontakt z żużlem, a drut napotyka mniejszy opór hydrodynamiczny. Ponadto zastosowanie zbyt małej prędkości wprowadzania 47
48 drutu w takich warunkach jest częściowo niwelowane prądem zstępującym, oddalającym uwolniony dodatek od powierzchni kąpieli. Spełnienie tego postulatu w pewnych przypadkach komplikuje jednak duża zmienność warunków mieszania w praktyce przemysłowej, zwłaszcza przy stosowaniu kształtek porowatych, które mogą zmieniać swoja charakterystykę pracy w trakcie eksploatacji, lub tracić drożność. W przypadku stosowania kilku kształtek zmieniających w trakcie eksploatacji swą przepuszczalność w różnym stopniu, zmieniać się będzie charakterystyka przepływów metalu w kadzi. Przeważnie jednak drut wprowadzany jest do kadzi w ustalonym miejscu, ze stałą i zwykle dużą - w stosunku do ruchu wywołanego mieszaniem - prędkością. Tym samym ruch metalu w kadzi związany z mieszaniem nie ma tak istotnego wpływu na prędkość przemieszczania się drutu względem kąpieli jak w przypadku dodatków kawałkowych. A przedmuchiwanie przez kształtkę, B przedmuchiwanie lancą. Rys. 26. Wybór miejsca wprowadzania drutu w przypadku mieszania kąpieli metalowej argonem [88]. Ze względu na to, że w przypadku drutów mieszanie kąpieli nie jest głównym powodem poruszania się dodatku w kąpieli to nie stanowi czynnika mającego decydujący wpływ na czas roztapianie się drutu. Proces mieszania ma natomiast duże znaczenie odnośnie uzysku i homogenizacji składu zarówno w przypadku dodatków wprowadzanych w postaci kawałków jak i drutów [88, 91] Mechanizm asymilacji metalicznych dodatków stopowych w ciekłej stali Transport masy z fazy stałej (dodatek) do ciekłej (kąpiel metalowa) może zachodzić poprzez roztapianie lub rozpuszczanie. W pierwszym przypadku proces jest limitowany przepływem ciepła, który zachodzi w wyniku kontaktu chłodnego dodatku z ciekłą stalą o temperaturze wyższej niż temperatura topnienia wprowadzanego materiału. W tych warunkach po pewnym czasie dodatek nagrzewa 48
49 się do temperatury topnienia, a następnie przechodzi w stan ciekły i pomijając kwestie zakrzepłej na nim warstewki stali, miesza się z otaczającą kąpielą metalową, w której ulega rozcieńczeniu. Rozpuszczanie jest procesem limitowanym transportem masy pomiędzy znajdującym się w stanie stałym dodatkiem, a ciekłą stalą i zachodzi, gdy temperatura topnienia dodatku jest wyższa niż temperatura otaczającej go kąpieli metalowej. W tych warunkach przyswajanie dodatku jest wynikiem dwóch następujących po sobie procesów. Pierwszym jest reakcja powierzchniowa polegająca na przemianie fazowej ze stanu stałego do ciekłego. Drugi, to transport rozpuszczonych atomów z powierzchni do ciekłej kąpieli poprzez warstwę graniczną w wyniku dyfuzji. Każdy z tych procesów może limitować proces rozpuszczania [60]. Jak z powyższego wynika decydujące znaczenie dla sposobu przyswajania dodatków stopowych ma temperatura topnienia dodatku w stosunku do temperatury otaczającej kąpieli metalowej. Wpływ sposobu przyswajania dodatku na czas tego procesu jest bardzo duży. Rozpuszczanie może trwać wielokrotnie dłużej niż roztapianie. Niewielka zmiana składu dodatku powodująca podwyższenie jego temperatury topnienia powyżej wartości granicznej, którą stanowi temperatura kąpieli, powoduje drastyczne wydłużenia czasu asymilacji. Zilustrowano to na rys. 27, gdzie przedstawiono czas przyswajania żelazowanadu w stali o temperaturze 1600 C w zależności od zawartości w nim wanadu, czyli temperatury topnienia. temp. topnienia żelaza: 1535 C temp. topnienia wanadu: 1902 C temp. stali: 1600 C Rys. 27. Prognozowany czas roztapiania/rozpuszczania dla pręta z żelazowanadu o śr. 2,54 cm w stali o temperaturze 1600 C w zależności od zawartości wanadu [71]. Zawartość wanadu w tym dodatku poniżej 70 % sytuuje go wśród żelazostopów ulegających roztapianiu (temperaturą topnienia poniżej 1600 C), natomiast żelazowanad 80% ulega rozpuszczaniu (temperatura topnienia ok C) [59]. 49
50 Dodatkowym, ważnym elementem, który może wpływać na charakter tego procesu, a tym samym szybkość przyswajania, są w przypadku niektórych dodatków reakcje egzotermiczne. W związku z tym, w zależności od wspomnianych właściwości, dodatki stopowe wprowadzane do ciekłej stali zostały, jak już wspomniano, podzielone na klasy. W zależności od publikacji wyróżnia się dwie klasy (biorąc pod uwagę tylko temperaturę topnienia) [36, 61, 64, 65] lub trzy klasy (wyodrębniając dodatki w których zachodzą reakcje egzotermiczne) [51, 62, 63, 73]. Do klasy I zalicza się dodatki, których temperatura topnienia leży poniżej temperatury krzepnięcia kąpieli metalowej. Przyswajanie dodatków tej klasy następuje wobec tego w wyniku topienia. Do klasy II należą dodatki, których temperatura topnienia leży powyżej temperatury krzepnięcia kąpieli metalowej. Z tego powodu przyswajanie dodatków tej klasy następuje w wyniku rozpuszczania. Do klasy III zaliczone zostały dodatki stopowe określane jako mikroegzotermiczne, czyli wprowadzane do kąpieli metalowej w postaci sproszkowanej mieszanki dwóch pierwiastków lub związków w odpowiednich proporcjach, które reagując ze sobą wydzielają ciepło. Sproszkowana mieszanina może zawierać dodatki, które samodzielnie należą do I lub II klasy. Takie przygotowanie wprowadzanych komponentów jest jednak szczególnie pożądane i częściej praktykowany w odniesieniu do wolno przyswajanych dodatków klasy II. Również w przypadku kawałkowych dodatków tak I jak i II klasy dodatkowym czynnikiem mającym wpływ na proces roztapiania lub rozpuszczania mogą być reakcje egzotermiczne towarzyszące tworzeniu związków międzymetalicznych. Reakcje te w powiązaniu z różnymi właściwościami termofizycznymi i zmiennym stopniem przegrzania kąpieli powodują, że proces przyswajania dodatków stopowych w ramach jednej klasy przebiegać może według różnych wariantów [60, 61, 62, 69]. Dobrym przykładem żelazostopu, który w zależności od składu może być zaliczane do I lub II klasy jest żelazochrom. W zależności od zawartości chromu może stanowić dodatek I klasy - FeCr 55% lub II klasy FeCr - 80% [61]. Drugi taki żelazostop to omówiony już żelazowanad rys. 27. Z kolei żelazostop będący związkiem pierwiastków ziem rzadkich (33% Si, 30% pierwiastki ziem rzadkich, reszta Fe) może być sytuowany w klasie I lub II w zależności od temperatury stali, a co za tym idzie jej przegrzania [64]. Poniżej opisano mechanizmy roztapiania i rozpuszczania się dodatków stopowych w zależności od przynależności do danej klasy oraz zachodzenia bądź też nie zachodzenia reakcji egzotermicznych Dodatki stopowe I klasy Do pierwszej klasy dodatków stopowych, zgodnie z powyższym, zalicza się materiały, których temperatura topnienia powoduje, że ich przyswajanie następuje w wyniku roztapiania. Z najczęściej stosowanych dodatków stopowych w grupie tej znajdują się miedzy innymi żelazomangan, żelazokrzem, krzemomangan, magnez, żelazochrom (poniżej 55% Cr), żelazowanad (poniżej 65% V) oraz glin. 50
51 Proces roztapiania dodatków stopowych I klasy może przebiegać według czterech podstawowych scenariuszy składających się z kolejnych etapów, z których niektóre są wspólne dla wszystkich przypadków [60, 61, 62, 70]. W każdym scenariuszu w wyniku wprowadzenia zimnego dodatku do gorącej kąpieli metalowej zachodzi proces tworzenia się warstewki zakrzepłej stali na powierzchni zimnego dodatku, która z czasem ulega ponownemu roztopieniu. Jednocześnie następuje podgrzewanie dodatku i w efekcie jego wcześniejsze lub późniejsze roztopienie się. Procesy te mogą występować z różnym nasileniem i w różnym czasie, a wpływ na to mają właściwości termofizyczne dodatku oraz różnica pomiędzy temperaturą topnienia wprowadzanego materiału a temperaturą stali. Rysunki 28 do 31 [61] ilustrują cztery możliwe warianty zachowania się dodatków I klasy po wprowadzeniu do ciekłej stali. Na rysunkach tych w przekroju przedstawiono dodatek stopowy na różnych etapach roztapiania. W pierwszym wariancie przedstawionym na rys. 28, po wprowadzeniu zimnego dodatku (etap A) następuje tworzenie się na powierzchni wprowadzanego dodatku warstewki zakrzepłej stali (etap B). Warstewka ta powiększa się do pewnego momentu, osiągając maksymalną grubość, a wprowadzony dodatek zaczyna pod nią roztapiać się od zewnątrz (C). Rys 28. Proces roztapiania dodatków stopowych I klasy według wariantu 1 [61]. Bardzo często wprowadzany dodatek stopowy ulega całkowitemu roztopieniu zanim otaczająca go warstwa zakrzepłej stali ulegnie ponownemu roztopieniu (D). Warstwa to staje się coraz cieńsza, aż do całkowitego roztopienia, po czym następuje uwolnienie ciekłego stopu do kąpieli metalowej. Jeżeli warstewka stali roztopi się wcześniej niż otoczony nią dodatek wówczas w zależności od warunków roztapianie będzie przebiegało według wariantu 2 lub 3. W przypadku wysokiego przegrzania, dużych rozmiarów wprowadzanych kawałków oraz małej przewodności cieplnej wprowadzanego materiału przebieg procesu roztapiania będzie zgodny z wariantem 2 na rys
52 Rys 29. Proces roztapiania dodatków stopowych I klasy według wariantu 2 [61]. W tych warunkach dochodzi do stopienia się warstewki zakrzepłej stali dodatek ulegnie roztopieniu. Stały dodatek zostaje wystawiony na działanie ciekłego metalu (etap C). Dla dodatków o niskiej temperaturze krzepnięcia różnica temperatury wywołująca konwekcyjny przepływ ciepła radykalnie wzrasta. Wynika to z tego, że temperatura przegrzania definiowana zwykle jako różnica pomiędzy aktualną temperaturą stali, a jej temperaturą likwidus (np C) w tym przypadku będzie równoznaczna różnicy temperatury ciekłej stali i temperatury topnienia wprowadzanego dodatku (np C) [61]. Oznacza to bardzo istotny wzrost tak rozumianego przegrzania. Biorąc pod uwagę fakt, że konwekcyjna wymiana ciepła rośnie proporcjonalnie do różnicy temperatury pomiędzy kąpielą metalową, a powierzchnia stałego dodatku szybkość roztapiania się może wzrosnąć nawet 5-krotnie [61]. Bardzo wysokie przegrzanie przy pozostałych warunkach takich jak w wariancie drugim, prowadzi przeważnie do roztapiania dodatku zgodnie z wariantem nr 3 przedstawionym na rys. 30. W takim przypadku nastąpi częściowe roztopienie wprowadzanego dodatku przed roztopieniem się zakrzepłej na nim warstwy stali (etap C). Po roztopieniu warstewki na powierzchni jego nieroztopionej pozostałości, po zetknięciu się z kąpielą metalową, ponownie utworzy się cienka warstewka zakrzepłej stali (etap D). Wynika to z dużej różnicy temperatur pomiędzy powierzchnią dodatku a kąpielą metalową w warunkach bardzo wysokiego przegrzania stali. Rys 30. Proces roztapiania dodatków stopowych I klasy według wariantu 3 [61]. 52
53 Wariant 4 przedstawiony na rys. 31 dotyczy przypadku wprowadzania żelazostopu, którego rozpuszczaniu się towarzyszy silnie egzotermiczna reakcja z żelazem. Najbardziej popularnym przykładem takiej sytuacji jest wprowadzanie krzemu lub żelazokrzemu do ciekłej stali. Po wprowadzeniu zimnego dodatku (etap A), tworzy się na nim warstwa zakrzepłej stli, a na granicy styku pomiędzy nimi tworzą się związki międzymetaliczne - w przypadku krzemu FeSi, FeSi 2 i Fe 2 Si [91], co powoduje wyzwalanie się ciepła (etap B). Zjawisko to może znacznie przyspieszyć roztapianie się stopu szczególnie przy niskim przegrzaniu kąpieli. Rys 31. Proces roztapiania dodatków stopowych I klasy według wariantu 4 [61]. Wariant 4 nie ogranicza się jednak tylko do dodatków I klasy. Rozpuszczanie dodatków II klasy, któremu towarzyszą reakcje egzotermiczne omówiono poniżej Dodatki stopowe klasy II. Do dodatków klasy II zalicza się stopy, których temperatura topnienia leży powyżej temperatury topnienia stali. W grupie tej znajdują się takie żelazostopy jak żelazowolfram, żelazoniob czy żelazomolibden, żelazochrom (powyżej 80% Cr, i żelazowand (powyżej 70% V). Przebieg ich rozpuszczania według wariantu 5 zaprezentowano na rys. 32. Jest on podobny do wariantu 2, ale w etapach C i D zamiast roztapiania zachodzi rozp[uszczanie. Rys 32. Proces roztapiania dodatków stopowych II klasy według wariantu 5 [61]. 53
54 Po wprowadzeniu stopu do ciekłej stali (etap A) tworzy się na nim jak w poprzednich przypadkach warstwa zakrzepłej stali (etap B). Następnie warstwa ta ulega roztopieniu (etap C) i następuje bezpośredni kontakt rozgrzanego dodatku z ciekłą stalą. W tych warunkach dodatek zaczyna się powoli rozpuszczać. Proces ten jest kontrolowany poprzez transport masy w warstwie granicznej, a jego szybkość zależy od rozpuszczalności samego żelazostopu i współczynnika dyfuzji w fazie ciekłej. Istotny wpływ na proces rozpuszczania się ma również intensywność mieszania kąpieli metalowej. Ponieważ transport masy jest zwykle znacznie wolniejszy niż transport ciepła dla ciekłych układów metalicznych, czas trwania etapu C jest znacznie dłuższy niż czas etapu B. W przypadku wprowadzania tych dodatków do stali o temp 1600 C w postaci kul o średnicy 6 cm w raczej teoretycznych warunkach wyłącznie naturalnej konwekcji cieplnej (brak mieszania) czas rozpuszczania FeNb i FeW może przekroczyć nawet 30 minut. [36]. Czasy rozpuszczania wybranych dodatków stopowych w warunkach braku mieszania przedstawiono na rys. 33. Opisane warianty nie wyczerpują wszystkich możliwych scenariuszy przeswajania dodatków. Podobnie jak w przypadku dodatków I klasy, procesowi rozpuszczania dodatków II klasy mogą towarzyszyć reakcje egzotermiczne związane z tworzeniem się związków międzymetalicznych. Schematycznie proces ten można przypisać do wariantu nr 4 rys. 31. średnica dodatku ok. 60 mm Rys. 33. Czas rozpuszczania w stali wybranych żelazostopów w wa-runkach konwekcji naturalnej [36]. W takiej sytuacji podobnie jak w przypadku dodatków I klasy rozpuszczanie ulega znacznemu przyspieszeniu, przy czym w rzeczywistości sam proces przyswajania w zależności od własności wprowadzanego dodatku i parametrów kąpieli może być złożony i wielofazowy. Na podstawie badań fizycznych i modelowania numerycznego stwierdzono np., że proces rozpuszczania tytanu zachodzi w dwóch etapach. Pierwszy obejmuje procesy na granicy tytanu i zakrzepłej powłoki, a drugi procesy swobodnego rozpuszczania na granicy tytan ciekła stal [96]. W pierwszym etapie po utworzeniu się warstewki zakrzepłej stali i podniesieniu temperatury na granicy pomiędzy tą warstewką, a tytanem, do ok C następuje zapoczątkowanie reakcji rozpuszczania. Powstaje ciekła błonka o składzie eutektyki i zostaje zainicjowana reakcja egzotermiczna. Taki podwójny efekt cieplny (otaczająca ciekła stal i reakcja egzotermiczna) działający na zakrzepłą warstewkę stali powoduje przyspieszone jej roztapianie się. Oszacowano, że strumień cieplny wynikający z reakcji egzotermicznej wynosił 3,97 ± 0,63 W/m 2 w warunkach naturalnej konwekcji i przy przegrzaniu ok. 100 C. 54
55 W drugim etapie podczas swobodnego rozpuszczania w ciekłej stali temperatura na powierzchni ciekłego tytanu wzrasta i tym samym przyspiesza dalszy proces rozpuszczania. W pierwszym okresie temperatura powierzchni tytanu jest niższa niż temperatura jego topnienia. W dalszym okresie temperatura wzrasta, osiągając wartość umożliwiającą topienie się tytanu i rozpoczyna się proces charakterystyczny dla dodatków I klasy, czyli roztapianie. Wspomniane zjawisko daje podstawy do stwierdzenia, że podział na klasy w pewnych warunkach (głównie reakcje makroegzotermiczne) nie opisuje jednoznacznie sposobu przyswajania dodatków stopowych. Względne proporcje pomiędzy okresem rozpuszczania i roztapiania zależą od wymiarów dodatku, przegrzania stali i warunków hydrodynamicznych Podstawowe prawa fizyczne opisujące proces nagrzewania i roztapiania się dodatków stopowych Roztapianie się dodatków wprowadzanych do ciekłej stali następuje w wyniku transportu ciepła pomiędzy fazą ciekłą i stałą oraz dalszego transportu ciepła wewnątrz dodatku w stanie stałym lub ciekłym. Określenie czasu potrzebnego na roztapianie się dodatku wymaga wyznaczenie czasu koniecznego do przepływu takiej ilości ciepła, aby dodatek nagrzał się do temperatury topnienia, a następnie roztopił. Uwzględnić należy również powstawanie i roztapianie się warstwy zakrzepłej stali, która tworzy się na materiale wprowadzanym do ciekłego metalu. W wyniku zanurzenia zimnego dodatku w gorącej kąpieli metalowej następuje przepływ ciepła pomiędzy cieczą, a stałym dodatkiem (lub zazwyczaj otaczającą go warstwą zakrzepłej stali); przepływ ten przebiega w wyniku konwekcji. Ponieważ w warunkach przemysłowych występuje z reguły ruch dodatku względem otaczającej kąpieli i/lub przepływ metalu względem dodatku, wymiana ciepła zachodzi w wyniku konwekcji wymuszonej. Intensywność strumienia ciepła przypływającego w wyniku konwekcji poprzez nieskończenie małą powierzchnię może być wyrażona zgodnie z prawem Newtona następująco [97]: dq da s = h T T ) [W/m 2 ] (8) ( s gdzie: Q strumień ciepła [W], h współczynnik przejmowania ciepła [W/m 2 K], A s pole powierzchni ciała stałego [m 2 ], T temperatura płynu w dużej odległości od ciała stałego [K], T s temperatura ciała stałego [K] Pozorna prostota tego równania jest wynikiem zastosowania współczynnika przejmowania ciepła h uwzględniającego wiele czynników wpływających na konwekcyjną wymianę ciepła. 55
56 Prawidłowe oszacowanie tego współczynnika jest w rzeczywistości trudne i wyznacza się go doświadczalnie dla konkretnego typu warunków. Na jego wartość, która może zmieniać się w szerokim zakresie, wpływa prędkość i kierunek przepływu płynu względem ciała stałego, parametry płynu takie jak gęstość, lepkość i przewodność cieplna oraz kształt ciała stałego, a także charakter przepływu (laminarny, turbulentny). Współczynnik przejmowania ciepła w takim przypadku wyznacza się zwykle korzystając z liczb podobieństwa (Nusselta, Prandtla i Reynoldsa), według zależności [97, 98]: Nu kl h = [W/m 2 K] (9) l gdzie: Nu liczba Nusselta, Nu = f N, N, N ) (10) ( Re Pr Ma N Re liczba Reynoldsa = ρul, (11) µ C pµ N Pr liczba Prandtla =, (12) kl h - współczynnik przejmowania ciepła [W/m 2 K], N Ma liczba Macha, l charakterystyczny wymiar liniowy ciała stałego [m], u prędkość przepływu [m/s], µ lepkość [kg/m s], C p ciepło właściwe przy stałym ciśnieniu [J/kgK], ρ gęstość płynu [kg/m 3 ], k l przewodność cieplna płynu [W/mK], W zależności od rozpatrywanych warunków, jak np. kształt ciała opływanego przez płyn czy charakter przepływu, liczba Reynoldsa może być liczona według innych zależności uwzględniających np. promień obiektu kulistego [78, 99]. Dla niskich prędkości przepływu (w stosunku do prędkości dźwięku w danym płynie) liczbę Macha można pominąć i wówczas: Nu = f N Re, N ) (13) ( Pr Zależność pomiędzy liczbą Nusselta, a pozostałymi liczbami bardziej szczegółowo omówiono w dalszej części tego rozdziału w powiązaniu z opisem poszczególnych modeli, które przepływ ciepła od kąpieli do dodatku wyznaczają z powyższej zależności. Przepływ ciepła wewnątrz stałego dodatku jest wynikiem przewodzenia. Proces przepływu ciepła zachodzący w warunkach ustalonych dla jednego kierunku np. rzędnej y można opisać zgodnie z prawem Fouriera następującym równaniem [97]: 56
57 gdzie: q y dt = λ [W/m 2 ] (14) dy q y natężenie strumienia cieplnego przepływającego przez warstwę y [W/m 2 ], λ przewodność cieplna [W/mK], T temperatura [K], y grubość warstwy przewodzącej [m]. Generalizując problem przewodzenia dla układu trójwymiarowego podobne równania można ułożyć dla osi x oraz z i wówczas: q= q x +q y +q z [W/m 2 ] (15) Przepływ ciepła Q w kierunku rzędnej y w czasie dt przez dane pole powierzchni A można opisać równaniem: dq y dt dt = λ A (16) dy Nagrzewanie się i w konsekwencji topienie stałych dodatków wprowadzonych do kąpieli metalowej następuje w wyniku przejmowania ciepła przez ich całą zewnętrzną powierzchnię oraz akumulacji ciepła we wprowadzanym materiale (oraz ewentualnie generowania ciepła wewnątrz dodatku). Ponadto dodatki te mają z reguły kształty brył, które z mniejszym lub większym przybliżeniem można określić jako kule lub cylindry. W takiej sytuacji nagrzewanie dodatku o kształcie kulistym w wyniku przewodzenia ciepła można opisać równaniem [97]: T 2 T T = a t r r r gdzie: λ a = - przewodność temperaturowa [m 2 /s], ρc p (17) T temperatura [K], r współrzędna radialna, t czas [s], ρ gęstość [kg/m 3 ], C p ciepło właściwe [J/kgK], 57
58 Dla cylindra (np. drut) równanie przyjmuje postać: T 2 T T = a t r r r Równania (17) i (18) są podstawą większości modeli opisujących nagrzewanie i w konsekwencji roztapianie dodatków stopowych. (18) 4.3. Obliczenia czasu roztapiania dodatków w ciekłej stali Przedstawione powyżej równania przepływu ciepłą dotyczą obiektów jednorodnych pod względem właściwości. W rzeczywistości problem nagrzewania i roztapiania dodatków jest bardziej złożony. Wynika to z faktu tworzenia się na powierzchni dodatku warstewki zakrzepłej stali oraz istnienia różnych wariantów przebiegu samego roztapiania w zależności od wielkości dodatku i jego właściwości termofizycznych (rysunki 28, 29, 30 i 31). Poszczególne modele zwłaszcza o znaczeniu utylitarnym z reguły zakładają pewne uproszczenia w zależności od charakteru opisywanego procesu. Pozwala to budować prostszy model bez większych konsekwencji odnośnie przydatności otrzymanych rezultatów. Przykładowo, w zależności od przewodności cieplnej dodatku, zmienia się rola, jaką odgrywa przewodność cieplna warstewki zakrzepłej na dodatku stali. W przybliżonych obliczeniach dla pewnych warunków można założyć, że tworząca się warstewka stali jest przeźroczysta dla przepływu ciepła, czyli nie odgrywa istotnej roli w ograniczeniu przepływu ciepła do dodatku. Ma to miejsce, gdy przewodność cieplna dodatku jest mniejsza niż tworzącej się otuliny. Takie założenie przyjąć można np. odnośnie powłoki skrzepniętej stali na kawałkach żelaza gąbczastego [68, 77]. Powłoka z litej stali o większej przewodności cieplnej otacza rdzeń z żelaza gąbczastego o mniejszej przewodności cieplnej. Wówczas powierzchnia rdzenia nie jest w stanie przyjąć ciepła, jakie dostarczone może być przez powłokę do wnętrza dodatku i powłoka ta nie stanowi bariery ograniczającej jego przepływ. Model z przeźroczystą powłoką W modelu bazującym na powyższym założeniu proces nagrzewania dodatku o kształcie kulistym opisany został równaniem (17) z następująco zdefiniowanymi warunkami [77]: dla t=0 T = T T = T 0 M dla dla dla r = R 0 : T = T M gdzie: r < R 0 r = R T 0 początkowa temperatura dodatku [K], T M temperatura krzepnięcia kąpieli [K], R 0 początkowy promień dodatku [m], 0 (19) 58
59 W celu uogólnienia i uproszczenia dalszych przekształceń zastosowano bezwymiarową temperaturę Θ, czas Fo (liczba Fouriera), i bezwymiarową współrzędną radialną w r, które zostały zdefiniowane następująco [77]: T T at Θ =, Fo =, 2 T M M T 0 R 0 r w = (20) R 0 gdzie: a - przewodność temperaturowa [m 2 /s] r - współrzędna radialna [m], a równanie (17) i warunki (19) zapisano w bezwymiarowej postaci: 2 Θ Θ Θ = Fo w w w (21) dla Fo = 0 Θ = -1 dla w < 1 Θ = 0 dla w = 1 (22) dla w=1 Θ=0 Rozwiązanie tego równania przyjmuje postać: Θ = 2 n= 1 ( 1) n sin( nπw) e nπw 2 2 n π Fo (23) Gradient temperatury na powierzchni dodatku (w=1) wynosi: (24) Tworzenie się na dodatku warstewki zakrzepłej stali można opisać równaniem: (25) 59
60 z warunkiem początkowym: dla t =0, R=R 0 (26) gdzie: λ przewodność cieplna stałej stali [W/mK], ρ gęstość stałej stali [kg/m 3 ], H M st entalpia topnienia stali [J/kg], R promień dodatku (włączając w to warstewkę zakrzepłej stali) [m], h współczynnik przejmowania ciepła z kąpieli do dodatku [W/m 2 K], T M temperatura topnienia/krzepnięcia kąpieli [K]. T K temperatura kąpieli [K]. W powyższym równaniu lewa strona opisuje strumień ciepła z granicy dodatek/warstwa zakrzepłej stali do wnętrza. Pierwszy człon prawej strony opisuje tworzenie lub roztapianie się warstwy zakrzepłej stali, a drugi strumień ciepła z kąpieli do dodatku. Wprowadzono założenie upraszczające gdzie R zastąpione zostało przez R 0 i równanie (25) zapisano w postaci bezwymiarowej: Θ w dw ρ' s=1 = Ph + BiΘ M (27) dfo ρ przy następująco zdefiniowanych liczbach bezwymiarowych: gdzie: Ph = C H, ) hr0 Bi =, λ W = R R M st P ( TS T0 0 ρ gęstość żelaza gąbczastego [kg/m 3 ], Ph bezwymiarowa entalpia przemiany fazowej, Bi liczba Biota Funkcja wzrostu i zaniku warstwy zakrzepłej stali na dodatku jest rozpatrywana w zależności od wartości bezwymiarowego strumienia ciepła - BiΘ; oddzielnie dla BiΘ 1 oraz dla BiΘ > 1. rys. 34 (28) 60
61 Rys 34. Powstawanie i zanik warstewki zakrzepniętej stali dla przepadków: BiΘ <1, BiΘ =1, BiΘ > 1 W pierwszym przypadku (BiΘ 1) temperatura dodatku ulegnie wyrównaniu, czyli dodatek osiągnie temperaturę równą temperaturze topnienia zanim zaniknie otaczająca go warstewka zakrzepłej stali. W drugim przypadku warstewka ulegnie roztopieniu zanim nastąpi ujednorodnienie temperatury w dodatku. Wyrażony bezwymiarowo czas jaki jest wymagany na wyrównanie temperatury w objętości dodatku wynosi Fo =1/π. Model uwzględniający opór zakrzepłej warstwy Założenia określające warstwę zakrzepłej stali jako obiekt przeźroczysty dla przepływu ciepła są uprawnione, gdy przewodność cieplna zakrzepłej warstwy stali jest wyższa niż samego dodatku. W rzeczywistości wiele materiałów wprowadzanych do ciekłej stali w tym również aluminium posiada wyższą przewodność cieplną niż ta warstwa. Wobec tego współczynnik przewodzenia ciepła warstwy zakrzepłej na dodatku stali nie może być ignorowany i opisany model musi być skorygowany. W takim przypadku model opisujący roztapianie należy rozbudować formułując oddzielnie równania nagrzewania dodatku i zakrzepłej na nim warstwy stali. Takie ujęcie zagadnienia przedstawiono w pracy [84], gdzie proces roztapiania analizowano numerycznie za pomocą metody różnic skończonych. W modelu tym w odróżnieniu od poprzedniego odniesiono się do zagadnienia rozkładu temperatury i przenoszenia ciepła w warstwie zakrzepłej stali. 61
62 Równania zostały zapisane w postaci [84]: - dla wprowadzonego dodatku T t 2 T 2 r d d 2 = ad dla t = 0 + r T d r 0 < r < R 0 (29) T0 dla r < R0 Td = (30) TM, w dla r = R0 T dla r = 0 = 0 (31) r gdzie: T M,w temperatura topnienia warstwy zakrzepłej na dodatku [K], a przewodność temperaturowa [m 2 /s], r współrzędna radialna. indeksy: d odnosi się do dodatku, w odnosi się do warstwy zakrzepłej stali. - dla warstwy zakrzepłej stali: T t 2 T 2 r w w 2 = aw + r T w r R 0 < r < R (32) dla t=0 R=R 0 (33) dla t=0 T w = T M,w (34) dla r=r T = T M,w (35) - na granicy kąpiel/dodatek: Tw dr λ w = ρ w H M, w + h( TK TM, w ) (36) r dt r= R dla t=0 R=R 0 (37) gdzie: T K temperatura kąpieli [K], H M,w - entalpia topnienie/krzepnięcia warstwy [J/kg], λ przewodność cieplna [W/mK], - na granicy dodatek/warstwa zakrzepłej stali stosownie do ciągłości temperatury i strumienia ciepła: T d, r= R = Tw r= R (38) 0, 0 62
63 Td Tw λ d = λw (39) r r r= R r= 0 R 0 gdzie: + w równaniu oznacza zewnętrzną stronę granicy, - w równaniu oznacza wewnętrzną stronę granicy. + Z równań tych wynika, że przebieg roztapiania różnych żelazostopów jest zależny od relacji λ d / λ w oraz a a czyli C ρ /C. gdzie: Cp ciepło właściwe [J/kgK], ρ gęstość [kg/m 3 ], d / w P, w w P,d ρd Jeżeli ustalone są warunki brzegowe odnośnie własności kąpieli i jej temperatury oraz temperatury początkowej dodatku to wynik jest zależny od własności dodatku. Własności te uwzględniono w postaci następujących bezwymiarowych współczynników dla dodatku i warstwy zakrzepłej stali: Bezwymiarowy współczynnik przewodzenia ciepła r = λ λ (40) λ d / w Bezwymiarowy współczynnik przewodności temperaturowej: r = a / a (41) a d w Powyższe wielkości oraz współczynnik przejmowania ciepła (zależny od względnej prędkości dodatku w stosunku do kąpieli, który zawarty jest w bezwymiarowym strumieniu ciepła BiΘ M ) stanowiły parametry, dla których wyznaczano czas tworzenia i zaniku warstewki zakrzepłej stali. Równania omawianego modelu rozwiązano numerycznie. Poszukiwano odpowiedzi, kiedy warstewka zakrzepłej stali zaniknie i ile ciepła w tym czasie przepłynie przez nią do dodatku. Równania (29) do (39) są słuszne dla przypadku, kiedy dodatek nie roztopi się do momentu zaniku warstwy zakrzepłej na dodatku stali. W wielu przypadkach jednak dodatek ulega częściowemu lub całkowitemu roztopieniu zanim ta warstwa zaniknie. Dokładne matematyczne opisanie przypadku, gdy warstwa ciekłego dodatku oddziela warstwę zakrzepłej stali od dodatku w stanie stałym według autorów [84] nie jest możliwe. Wynika to z trudności w sformułowaniu modelu przepływu w tej warstwie. Wobec tego rozważono dwa przypadki: a) ciecz nie płynie w ogóle (zachowuje się jak ciało stałe) b) ciecz płynie tak szybko, że temperatura fazy ciekłej dodatku jest jednorodna. 63
64 W rzeczywistości jak twierdzą autorzy [84] prawda leży pośrodku i obliczenia w pierwszym przypadku będą niedoszacowane, a w drugim przeszacowane. Przed rozpatrzeniem obydwu przypadków założono, że warstwa zakrzepłej stali nie rozpuszcza się od środka w roztopionym dodatku i tym samym uznano, że granica ta jest nieruchoma. W pierwszym wariancie należy dodać warunki brzegowe dla ciekłej fazy za warstwą zakrzepłej stali. Obliczenia prowadzono numerycznie zgodnie z opisanym równaniami (29) do (39) modelem z uwzględnieniem oddzielnych obszarów dodatku w stanie ciekłym i w stanie stałym oraz poniższym warunkiem brzegowym [84]: gdzie: T T drst λ d, l r= R λd s r R d H st, = ρ + = st M, d (42) r r dt λ d,l przewodność cieplna fazy ciekłej [W/mK], λ d,s przewodność cieplna fazy stałej [W/mK], H M,d entalpia topnienie/krzepnięcia dla dodatku [J], R st promień dodatku w stanie stałym [m]. Dla drugiego przypadku zakładamy, że obszar roztopionego dodatku ma wyrównaną temperaturę, która jest równoważna temperaturze topnienia dodatku, z którego częścią w stanie stałym styka się bezpośrednio. Przemieszczanie się granicy faza stała/faza ciekła dodatku opisano w oparciu o bilans cieplny równaniem [30]: 2 T 2 T 4πR0 λw 4πRst λd = ρd H d 4πR r r r= R0 r= Rst 2 st dr dt st (43) Równania (42) i (43) podobnie jak poprzednie w omawianym modelu zostały zapisane w formie bezwymiarowej, a następnie rozwiązane numerycznie. Obliczenia prowadzono dla dodatku manganu do ciekłej stali Obliczenia czasu roztapiania drutów aluminiowych w ciekłej stali Obliczenia czasu i przebiegu roztapiania się drutów aluminiowych posiłkują się, przynajmniej w niektórych elementach, danymi bliższymi prawdy niż obliczenia dla dodatków kawałkowych. Wynika to z tego, że wprowadzany drut ma ściśle określony kształt i wymiar. W przypadku dodatków kawałkowych założenie, że są one kuliste, lub cylindryczne zwykle jest dalekie od rzeczywistości, a rozrzut wymiarów poszczególnych kawałków może być znaczny. Ponieważ druty w obliczeniach traktowane są jak cylindry, dochodzi do tego pewne ułatwienie wynikające z faktu, że przepływ ciepła w praktyce odbywa się tylko w dwóch wymiarach (przepływ ciepła wzdłuż drutu można zaniedbać) [37]. 64
65 Z powyższymi zastrzeżeniami opis samego mechanizmu roztapiania drutów litych w ciekłej stali może być analogiczny jak dla dodatków kawałkowych. Uwaga ta dotyczy wyłącznie drutów litych. Natomiast odnośnie drutów rdzeniowych obliczenia ulegają znacznemu skomplikowaniu. Trudności zaczynają się od właściwego określenia właściwości termofizycznych rdzenia drutu, a kończą na opisie zjawisk występujących w materiale wypełniającym drut, który może składać się z kilku pierwiastków lub związków chemicznych oddziałujących w wyniki podgrzania wzajemnie na siebie i/lub na otulinę [32, 33, 100]. Roztapianie drutów aluminiowych, ze względu na niską temperaturę topnienia glinu przebiega według wariantu 1 rys. 28. Rozpatrując roztapianie się dodatku o jednoznacznie określonych właściwościach oraz określonym sposobie roztapiania, można zastosować pewne uproszczenia i pominąć rozpatrywanie przypadków, co do których zachodzi pewność, że w praktyce przemysłowej nie wystąpią (np. roztapiania się dodatku po zaniku warstwy zakrzepłej stali). Poniżej przedstawiono dwa modele roztapiania drutu aluminiowego bazujące na odmiennym matematycznym opisie procesu i różnym stopniu uproszczenia. Model oparty o równania przepływu ciepła w stanie nieustalonym. W pracy [40] przedstawiono model, w którym wymiana ciepła w trzech wyróżnionych obszarach roztapianego drutu opisana została odpowiednimi równaniami przepływu ciepła w stanie nieustalonym. W drucie, określonym jako obiekt o kształcie cylindrycznym, zdefiniowano trzy obszary obejmujące aluminium w stanie stałym, aluminium w stanie ciekłym i stal w stanie stałym (warstwa zakrzepłej na drucie stali) z dwiema ruchomymi granicami pomiędzy fazami (ciekłe aluminium/stałe aluminium i ciekła stal/stała stal). Równania te zgodnie z równaniem (18) przyjmują ogólną postać: Ti t ai = λ r i Ti rλi r r (44) gdzie: indeks i odnosi się do poszczególnych obszarów i przyjmuje następujące oznaczenie dla poszczególnych obszarów: 1 - stałe Al, 2 - ciekłe Al, 3 - warstwa zakrzepłej stali. warunek początkowy: warunki brzegowe: T 1 = 0 r T 1 = T t,al jeżeli t=0 i 0 r R (45) dla r = 0 (46) T 1 T2 = T k, st = dla r = R D 2 (t) (47) 65
66 T3 T2 λ 3 = λ2 = hr T ' dla r = R (48) r r T = T k,st dla r = R + D 3 (t) (49) warunki roztapiania: ρ ALAv T2 T1 = λ 2 1 dla r = R D 2 (t) (50) r r 2 λ gdzie: T3 L v3 = λ 3 j dla r = R+D 3 (t) (51) r ρs S T t,al temperatura topnienia aluminium [K], T k,st temperatura krzepnięcia stali [K], R średnica drutu [m], T różnica temperatury: warstwa zakrzepłej stali aluminiowy drut [K] h R współczynnik przejmowania ciepła: warstwa zakrzepłej stali aluminium [W/m 2 K], L A ciepło topnienia glinu [J/kg], L S ciepło topnienia stali [J/kg], ρ A gęstość glinu [kg/m 3 ], ρ S gęstość stali [kg/m 3 ], D 2 grubość warstwy roztopionego aluminium [m], v 2 prędkość roztapiania się aluminium [m/s], D 3 grubość warstwy zakrzepłej stali [m], v 3 prędkość krzepnięcia stali [m/s], j natężenie strumienia cieplnego z ciekłej stali do warstwy zakrzepłej stali [W/m 2 ]. Wymiana ciepła pomiędzy kąpielą, a warstwą zakrzepłej stali zachodzi poprzez konwekcję. Zgodnie z zasadami wspomnianymi w punkcie 4.2 wartość natężenia strumienia ciepła j określono korzystając z liczby Nusselta według zależności: Nul ( Tst Tk, st ) j = λ l gdzie: Nu l liczba Nusselta dla charakterystycznego wymiaru l [m] λ - przewodność cieplna ciekłej stali [W/mK], T st temperatura ciekłej stali [K] (52) 66
67 Równanie (53) wyznaczające liczbę Nusselta dla turbulentnego przepływu wzdłuż płaskiej płyty jest odpowiednie dla cylindra pod warunkiem uwzględnienia charakterystycznego rozmiaru przy wyznaczaniu liczby Reynoldsa. Nu l, turb Re, Re Pr 0, 8 l = 0 11 / l 2 3 ( Pr 1) (53) W tym przypadku charakterystyczny wymiar dla stałego (niezmiennego) toru wprowadzania drutu wyniesie: gdzie: l = L (54) L całkowita długość drutu znajdującego się w kąpieli [m]. W rzeczywistych warunkach podczas wprowadzania drutu występuje również składowa pozioma ruchu drutu wynikająca z mieszania kąpieli i drgań drutu wychodzącego z maszyny. Wobec tego przybliżoną wartość l można określić z zależności: gdzie: w l d << L (55) w h d średnica drutu [m], w prędkość wprowadzania drutu [m/s], w h składowa pozioma prędkości drutu [m/s]. Z obserwacji wynika, że stosunek w/w h można oszacować w przybliżeniu jako wartość równą 10. Przepływ laminarny musi być uwzględniony w przypadku małej wartości w l. Zastosowanie do omawianego przypadku zależności dla przepływu laminarnego wzdłuż płaskiej płyty prowadzi do wzoru: Nu l,lam 0, 5 0, 5 113, Re Pr = (56) 1 / 3 ( ) 1 / +, Pr 2 Złożenie efektów przepływu laminarnego i turbulentnego zostało określone za pomocą równania: Nu = Nu + Nu (57) l 2 l,turb 2 l,lam Udział konwekcji naturalnej w przenoszeniu ciepła został zaniedbany. 67
68 Obliczenia według równań (44) do (51) zostały wykonane numerycznie, a współrzędne przestrzenne zostały przekształcone tak, że obliczenia można było prowadzić przy ustalonych granicach pomiędzy poszczególnymi obszarami. Symulacje procesu roztapiania prowadzono dla różnych średnic drutu i prędkości wprowadzania. Wybrane wyniki przedstawiono na rysunkach 7, 8, 10 i 13 oraz w odpowiednich wierszach tablicy 1 strona 27. Model opisany równaniami przepływu ciepła w stanie ustalonym. Odmienne podejście do obliczania czasu roztapiania drutu aluminiowego zaprezentowano w pracy [37]. Sformułowano model przydatny do celów praktycznych w sposób pozwalający znacznie uprościć obliczenia. Wykorzystując możliwości, jakie dają obliczenia numeryczne proces nagrzewania drutu został opisany równaniami przepływu ciepła w stanie ustalonym. Pewne wielkości wymagane do obliczeń wyznaczono za pomocą doświadczeń laboratoryjnych. Obliczenia w omawianym modelu bazują na równaniu (16) w postaci: gdzie: Q t A pole powierzchni [m 2 ] T = λ A (58) x Q ilość ciepła przepływająca w czasie t [J]. Drut został podzielony na n centrycznie ułożonych cylindrów o grubości g jak na rys. 35. Roztopienie danego cylindra jest możliwe, gdy osiągnie on temperaturę topnienia aluminium oraz dostarczone zostanie do niego ciepło wymagane do zmiany stanu skupienia. d średnica drutu aluminiowego g grubość i-tego cylindra g w grubość zakrzepłej warstewki stali Rys 35. Podział drutu aluminiowego na cylindry z zaznaczoną warstwą zakrzepłej stali [37]. 68
69 Przyrost temperatury w kolejnym cylindrze jest wynikiem różnicy pomiędzy ciepłem dostarczonym przez cylinder zewnętrzny i ciepłem odebranym przez cylinder wewnętrzny. Dla cylindra i ciepło, jakie do niego dopływa z cylindra i+1 można opisać równaniem: gdzie: Q id Ti +1 Ti = λ Ai t (59) g Q id ciepło dostarczone do cylindra i z cylindra i+1 [J], A i zewnętrzna powierzchnia cylindra i [m 2 ] Ciepło przenoszone z cylindra i do cylindra i-1 opisuje równanie: gdzie: Q io Ti Ti 1 λ Ai 1 t (60) g = Q io ciepło przykazane z cylindra i do cylindra i-1 [J], A i-1 zewnętrzna powierzchnia cylindra i-1 [m 2 ] Ilość ciepła pozostająca w cylindrze i, powodująca wzrost jego temperatury wynika z bilansu ciepła wpływającego i wypływającego z cylindra zgodnie z równaniem: Q i = Q Q (61) id gdzie: Q i ilość ciepła pozostająca w cylindrze [J]. Q id ilość ciepła doprowadzona do cylindra i [J]. io Wzrost temperatury w cylindrze i wskutek dostarczonego do niego ciepła wyznacza się z równania: Q m C i T = (62) i P,Al gdzie: m i masa aluminium w i-tym cylindrze [kg], C P, Al ciepło właściwe aluminium [J/kgK]. 69
70 Równania (59) do (62) są słuszne dla wszystkich cylindrów z wyjątkiem zewnętrznego i wewnętrznego (w osi drutu). Z ostatniego, wewnętrznego cylindra leżącego w osi drutu, ciepło nie jest odbierane, ale w całości służy do jego podgrzania. Natomiast cylinder zewnętrzny jest podgrzewany przez kąpiel metalową poprzez warstwę zakrzepłej stali. W pracy [37] w oparciu o dane literaturowe oraz doświadczenia laboratoryjne polegające na wprowadzaniu do metalu o temperaturze 1500 C drutu aluminiowego o średnicy 10 mm, a następnie wyjmowaniu po określonym czasie, określono grubość tworzącej się na drucie warstwy zakrzepłej stali. Przyjęto dla poszczególnych średnic następujące grubości warstwy zakrzepłej stali: 1,3 mm dla drutu o średnicy 6 mm, 1,6 mm dla drutu φ 8mm, 1,8 mm dla drutu φ 10 mm, 2,1 mm dla drutu φ 12 mm i 2,3 mm dla drutu φ 14 mm. Iteracyjnie prowadzone obliczenia pozwalają na określenie wzrostu temperatury w każdym z cylindrów dla przyjętego kroku czasowego. Do obliczeń numerycznych przyjęto cylindry grubości 0,1 mm, a krok czasowy wynosił 0,000 01s. Znając temperaturę cylindra porównywano ją z temperaturą topnienia aluminium i w momencie osiągnięcia tej temperatury zakładano początek procesu roztapiania. Masę roztopionego aluminium określano z równania: gdzie: m Q mc ( T T ) i P, A t i x = (63) LAl m x masa roztopionego aluminium [kg], m masa aluminium w zewnętrznym cylindrze [kg], Q i ilość ciepła pozostająca w zewnętrznym cylindrze obliczona z równania (61) [J]. L Al ciepło topnienia aluminium [J/kg], T t temperatura topnienia aluminium [K], T i temperatura aluminium w cylindrze obliczona w poprzednim kroku czasowym [K]. Grubość warstwy roztopionego aluminium jest określana na podstawie masy roztopionego aluminium. Analogicznie prowadzone były obliczenia dla warstwy zakrzepłej na drucie stali w uwzględnieniu jej własności termofizycznych i założonej grubości. Obliczenia kończono w momencie, gdy temperatura ciekłego aluminium osiągała temperaturę topnienia kąpieli i warstwa zakrzepłej na drucie stali uległa całkowitemu roztopieniu. Wybrane wyniki obliczeń [37] zamieszczono w odpowiednich wierszach tablicy 1 na str. 27 i na rysunkach 9, 11 i 12 w rozdziale Jak widać, z przedstawionych tam rezultatów, mimo przyjęcia odmiennej koncepcji liczenia czasu roztapiania się drutu niż w poprzednio opisanym modelu [40] wyniki obu modeli są bardzo zbliżone. Jeżeli przyjąć, że obliczenia właśnie tych modeli są bliskie rzeczywistości wynika z tego wniosek, że właściwie przyjęte założenia upraszczające modelowanie nie muszą ujemnie wpływać na praktyczną użyteczność rezultatów. Z punktu widzenia technologii najważniejszy jest czas roztapiania drutu, natomiast dokładny opis wszystkich zjawisk towarzyszących procesowi wprowadzania i roztapiania dodatku ma drugorzędne znaczenie 70
71 z punktu widzenia praktyki produkcyjnej. Z tego też powodu większość z publikowanych modeli o utylitarnym znaczeniu zakłada pewne uproszczenia, które nie powodując istotnego pogorszenia dokładności znacznie ułatwiają i przyspieszają obliczenia. Z drugiej strony im bardziej uniwersalny ma być model tym mniejszy pozostaje margines na wprowadzanie uproszczeń stosownych dla wszystkich możliwych przypadków poddanych obliczeniom. Profesjonalne komercyjne programy do modelowania różnych zjawisk, w tym również roztapiania i krzepnięcia, uwzględniają na ogól wiele elementów, które mogą odgrywać role w zależności od charakteru symulowanego procesu i dzięki temu zapewniają takiemu oprogramowaniu dużą uniwersalność. Opisy takich programów zawierają jednak zwykle tylko ogólnikowe informacje o praktycznej realizacji obliczeń, gdyż mają one wymierną wartość komercyjną dla ich twórców Wyznaczanie współczynnika przejmowania ciepła Określenie współczynnika wymiany ciepła pomiędzy zimnym metalowym przedmiotem wprowadzonym do kąpieli metalowej, a tworzącą się na jego powierzchni zakrzepłą warstewką jest zagadnieniem trudnym i złożonym [15, 101, 102]. Znajomość tego parametru jest jednak niezbędna w przypadku obliczeń symulacyjnych procesu krzepnięcia i roztapiania. Eksperymentalne wyznaczanie współczynnika przejmowania ciepła jest zagadnieniem złożonym. Duże znaczenie ma opracowanie właściwej metodyki pomiaru oraz określenie czynników mających wpływ na dokładność pomiaru [101]. Problem określania, dla konkretnych warunków, współczynnika wymiany ciepła pomiędzy ciałem zanurzonym w kąpieli metalowej, a tą kąpielą [15, 58, 103, 104] lub pomiędzy formą (kokilą) a krzepnącym w niej odlewem [105, 106], był przedmiotem wielu rozważań i badań opisywanych w literaturze. Zagadnienie to wspomina się także przy okazji opisywania modeli symulacyjnych lub innych problemów jako wątek poboczny lub towarzyszący głównemu problemowi [15, 68, 77, 78, 79, 102, 107]. W takich przypadkach autorzy często nie zamieszczają dokładnej wartości współczynnika zastosowanego podczas obliczeń lub też stwierdzają, że oszacowanie dokładnej wartości tego współczynnika jest trudne i podają kilka wartości, które zastosowali w obliczeniach badając przy okazji wpływ jego zmienności na rezultat obliczeń [15]. Zróżnicowane warunki (zakres temperatury, różne metale) dla których wyznacza się współczynniki wymiany ciepła znacznie zawężają grupę wartości odpowiednich do zastosowania w konkretnych okolicznościach. Ze względu na charakter wymiany ciepła wartości współczynnika wymiany ciepła zamieszczane w publikacjach należy podzielić na te, które wyznaczano dla wymiany ciepła między formą, a odlewem i te, które odnoszą się do tej wymiany między ciałem stałym (w postaci np. pręta) zanurzonym w kąpieli metalowej i tą kąpielą. Oba z powyższych wariantów modeluje się fizycznie na specjalnie konstruowanych stanowiskach badawczych umożliwiających doświadczalne wyznaczanie współczynnika przejmowania ciepła. [104, 105, 106]. Opis wymiana ciepła między formą i odlewem jest bardziej skomplikowany, gdyż uwzględnić musi zazwyczaj zjawisko powstawania szczeliny (w wyniku skurczu odlewu) między formą i odlewem - rys. 37. Stosowanie różnorodnych materiałów pomocniczych jak np. pokrycia do form (grafitowe lub ceramiczne) lub utwardzacze do mas formierskich dodatkowo wpływają na warunki wymiany ciepła na granicy odlew/forma [106, 108, 109]. 71
72 Ponadto proces wymiany ciepła komplikuje fakt, że kurczący się odlew zwykle styka się z formą jakąś częścią powierzchni zależną od jego kształtu wskutek działania siły grawitacji, co w innych obszarach powoduje z kolei, że szczelina jest większa niż wynikałoby to z samego skurczu [110]. W miejscach styku formy z odlewem ma miejsce kontakt niedoskonały ciał w stanie stałym rys. 36. Rys. 36. Teoretyczne (linia przerywana) i rzeczywiste rozkłady temperatury na granicy forma odlew w przypadku kontaktu niedoskonałego w stanie stałym i szczeliny powietrznej [106] Wszystko to sprawia, że opór dla przepływu ciepła zwykle zmienia się w czasie i to nawet w miejscach gdzie odlew pozostaje w kontakcie z formą. Wynika to, z występującej zwykle zmiany siły docisku na powierzchni styku oraz zmiany podatności na odkształcenia odlewu wraz ze zmianą jego temperatury, co ma wpływ na jakość kontaktu. Dodatkowym czynnikiem zmieniającym warunki przepływu ciepła może być utlenianie się powierzchni odlewu. Odrębne zagadnienie to przypadek ciągłego odlewania. Krystalizatory mają na ogół odpowiednią zbieżność, aby zapobiec powstawaniu szczeliny, niemniej jednak należy liczyć się z jej powstawaniem [111] i tym samym ze zmiennymi warunkami na granicy wlewek - krystalizator. Dodatkowym elementem w procesie COS jest stosowanie zasypki smarującej, która może zmieniać warunki wymiany ciepła między wlewkiem, a krystalizatorem [104]. W przypadku elementów zanurzanych w ciekłym metalu warunki są najmniej skomplikowane. Zanurzany przedmiot nagrzewa się i tym samym rozszerza, co powoduje, że między warstewką zakrzepłego metalu a ogrzewanym ciałem mamy do czynienia wyłącznie z kontaktem niedoskonałym dwóch ciał znajdujących się w stanie stałym. Jak wynika z doświadczeń wartość współczynnika przejmowania ciepła w tym przypadku jest bliska 72
73 stałej i bez popełnienia większego błędu w obliczeniach symulacyjnych można przyjąć założenie, że nie zmienia się ona w czasie [15, 105, 108, 112], Niewielkie zmiany wartości współczynnika w funkcji czasu, które mogą wystąpić wynikają, jak już wspomniano, z utleniania powierzchni kontaktu oraz ze zmiany podatności na odkształcenia (w funkcji temperatury) stykających się metali oraz możliwych zmian siły nacisku spowodowanych różną rozszerzalnością cieplną zanurzonego przedmiotu i zakrzepłej na nim warstewki [104]. Wobec powyższego wartość współczynnika przejmowania ciepła w warunkach kontaktu dwóch ciał w stanie stałym jest w dużej mierze funkcją chropowatości stykających się powierzchni [105, 106, 113], ale również wielkości i ułożenia kryształów w warstewce zakrzepłego metalu [113], a więc pośrednio może zależeć od przegrzania kąpieli ponad temperaturę likwidus i szybkości chłodzenia. Na rys. 37 przedstawiono schematycznie dwie płaskie powierzchnie znajdujące się w kontakcie w stanie stałym. W obszarach odległych od powierzchni styku przepływ ciepła jest zasadniczo jednowymiarowy. Jednakże w obszarze przylegającym do granicy podziału zachodzi w trzech kierunkach, co wynika z tego, że rozkład temperatury w tym obszarze jest zależny od przedstawionych na rys. 37 możliwych dróg przepływu ciepła. Rys 37. Rozkład temperatury na styku dwóch powierzchni dla różnych warunków przepływu ciepła w danym miejscu powierzchni oraz wartość uśredniona (linia przerywana) [105]. W praktycznych zastosowaniach, wymiary nierówności na powierzchni stykających się ciał są mniejsze od wymiaru tych ciał, między którymi zachodzi przepływ ciepła. W związku z tym oprócz mikroskopowego ujęcia problemu, w którym bierze się pod uwagę przepływy ciepła jedynie w miejscach styku obu ciał, można rozpatrywać to zagadnienie w skali makroskopowej. W tym drugim przypadku przyjmuje się uśrednioną temperaturę dla 73
74 umownej, jednolitej, powierzchni styku (kontaktu) pomiędzy obu ciałami. Na tej podstawie określa się makroskopowy współczynnika wymiany ciepła, który ma praktyczne zastosowanie i jest powszechnie wykorzystywany w różnorodnych obliczeniach. Warto zwrócić uwagę, że występujące w ujęciu mikroskopowym różnice temperatury na powierzchni obu ciał w miarę oddalania się od powierzchni wyrównują się i w pewnej odległości od powierzchni styku temperatura staje się jednorodna, a tym samym występujące na powierzchni styku zróżnicowanie zostaje w naturalny sposób uśrednione. Rozkład temperatury w układzie ciekły metal - zanurzone w nim ciało - zakrzepła na tym ciele warstewka metalu w ujęciu makroskopowym przedstawiono na rysunku 38. Rys 38. Charakterystyka rozkładu temperatury na granicach (i w ich pobliżu): zanurzone ciało/warstewka zakrzepłego metalu/ciekły metal [103]. Wyznaczenie tak zdefiniowanego współczynnika przejmowania ciepła jest możliwe poprzez zastosowania odpowiednich metod matematycznych pozwalających na wyznaczenia jego wartości na podstawie zmierzonych zmian temperatury w czasie. Pomiarów takich dokonuje się za pomocą odpowiednio rozmieszczonych (w różnej odległości od powierzchni styku) termopar mierzących zmiany temperatury wewnątrz stykających się ciał. Wykorzystując te dane możliwe jest określenie dwóch umownych temperatur T 1 i T 2 (dla powierzchni obu stykających się ciał) na podstawie ekstrapolacji temperatur wewnętrznych po obu stronach powierzchni podziału. Średni makroskopowy współczynnik przejmowania ciepła wynika z zależności [104]: q h = (64) T 2 T 1 gdzie: h - współczynnik przejmowania ciepła [W/m 2 K], q średni strumień ciepła przepływający przez granicę [W/m 2 ], T 1, T 2 temperatury obu stykających się powierzchni [K]. 74
75 W przypadku, gdy pomiędzy powierzchniami tworzy się (np. w wyniku skurczu) szczelina, temperatury T 1 i T 2 mogą być (przynajmniej teoretycznie) jednoznacznie określone jako rzeczywiste wartości dla obu powierzchni. Równanie (64) w takim przypadku pozwala wyznaczyć współczynnik przejmowania ciepła bez potrzeby uśredniania temperatury na powierzchniach po obu stronach szczeliny. Równanie (64) jest właściwe przy założeniu, że przepływ ciepła odbywa się w stanie ustalonym. W przeciwnym wypadku strumień ciepła wchodzącego i wypływającego jest różny i równanie to nie ma zastosowania. Przy założeniu, że szerokość strefy granicznej jest wystarczająco mała w analizowanym przedziale czasu możliwe jest założenie, że przepływ ciepła jest bliski stanowi ustalonemu i strumień wpływający i wypływający są prawie identyczne [105]. Ponieważ w rzeczywistości jest to bliskie prawdy takie podejście jest uprawnione, a jak wynika z omawianego w rozdziale 4.4 modelu roztapiania drutu [37], gdzie przyjęto podobne założenie, daje realistyczne rezultaty. Wyznaczanie współczynnika przejmowania ciepła w sposób doświadczalny prowadzi się w oparciu o pomiary temperatury w funkcji czasu wykonywane na specjalnie konstruowanych stanowiskach badawczych, a następnie poprzez różne metody matematyczne rozwiązując zagadnie odwrotne [ , 109, 113]. W zależności od celu pracy konstruuje się stanowiska badawcze, na których dopuszcza się do powstawania szczeliny między formą i odlewem [106, 113, 114], unika się tego zjawiska [104] lub też kontroluje ten proces [105]. Wymianę ciepła pomiędzy dwoma ciałami będącymi w kontakcie niedoskonałym lub oddzielonymi wąską szczeliną opisuje się w publikacjach współczynnikiem przejmowania ciepła wyrażonym w [W/m 2 K] (albo w innych jednostkach np. [cal/cm 2 s K]) lub opornością wyrażoną w [m 2 K/W]. Po przeliczeniu tych jednostek celem standaryzacji danych zamieszczonych w różnych źródłach zauważalny jest duży rozrzut wyznaczonych wartości dla analogicznych lub zbliżonych warunków. Wyznaczone wartości dla różnych par metali mają zwykle wielkości rzędu 10 3 W/m 2 K. Stosunkowo często w badaniach brany jest pod uwagę zestaw miedź-aluminium lub stal-miedź. Wartości odnoszących się do aluminium i stali jest mniej, ale rozrzut spotykanych tu wyników jest znaczny. Spotykane wartości w [W/m 2 K] to: 4400 [104], 4060 do [15], 4100 [112], ok. 230 [113] - wartość dla układu model/forma (aluminium odlewane do stalowej formy). Nawet pomijając wartość dla układu forma-odlew, która z zasady powinna być znacznie niższa, zauważalne jest duże zróżnicowanie spotykanych wartości współczynnika przejmowania ciepła. Wynika to zapewne z różnych przyczyn, które podzielić można na dwie grupy. Pierwsza obejmuje przyczyny związane z samą metodologią wyznaczania, czyli zastosowanym sposobem pomiaru, dokładnością pomiarów i zastosowanymi metodami matematycznymi. Zagadnienia odwrotne są czułe na jakość danych wejściowych. Niewielkie błędy czy niedokładności mogą istotnie oddziaływać na wynik obliczeń [101]. Do drugiej grupy zaliczyć można przyczyny wynikające z samej charakterystyki badanego układu, jak np. jakość i czystość powierzchni, wielkość zanurzanych elementów, a więc i sił na nie działających, temperaturę i przegrzanie kąpieli. Ponieważ wpływy czynników z obu grup mogą nakładać swoje działania w sposób w zwiększający lub zmniejszający wyznaczane wartości takie zróżnicowanie publikowanych współczynników nie powinno dziwić. 75
76 Wobec powyższego powstaje pytanie, jak istotny wpływ wywiera dokładność wyznaczenia współczynnika przejmowania ciepła na jakość wyników obliczeń symulacyjnych. Kwestia ta nie jest jednoznacznie rozstrzygnięta, szczególnie wobec tak ogólnie postawionego pytania. Jak wynika z rezultatów takich obliczeń zmiana przyjętej wartość współczynnika wymiany ciepła nawet w stosunkowo szerokich granicach nie musi powodować radykalnych zmian otrzymanych wyników. Obliczenia z zastosowaniem współczynników wymiany ciepła wynoszących 1,7 i 5,0 [cal/cm 2 sk] dały rezultat w postaci różnicy głębokości, na jakiej roztopi się drut około 20 cm przy prędkości wprowadzania 240 m/min [15]. Przyjmując niższą prędkość wprowadzania ta różnica będzie odpowiednio mniejsza (drut w danym czasie przebędzie krótszą drogę). Z drugiej strony niektórzy autorzy [105] twierdzą, że jakkolwiek w przypadku form piaskowych dokładna znajomość tego współczynnika nie odgrywa zbyt istotnej roli, to w przypadku form metalowych ma duże znaczenie. Biorąc pod uwagę duży rozrzut publikowanych wyników nawet dla bardzo podobnych warunków eksperymentu oraz wpływ wielu czynników na rzeczywistą wartość współczynnika przejmowania ciepła wydaje się wskazane, wszędzie tam, gdzie jest to możliwe, wyznaczanie wartość tego parametru eksperymentalnie - najlepiej w warunkach możliwie wiernie oddających rzeczywistość, dla której poszukiwana jest wartość współczynnika przejmowania ciepła Weryfikacja modeli numerycznych Wyniki obliczeń modelowych często poddaje się weryfikacji fizycznej. Zwykle, ze względów praktycznych, czyni się to jednak tylko w wybranym zakresie parametrów, a w przypadku pozytywnych rezultatów zakłada, że model powinien dać prawidłowe obliczenia w pozostałym zakresie. W wielu przypadkach, do których należy również roztapianie się drutów wprowadzanych do ciekłego metalu, możliwa jest jedynie weryfikacja pośrednia lub cząstkowa, gdyż nie jest możliwa bezpośrednia obserwacja symulowanego procesu. Weryfikację prowadzi się mając na uwadze dwa elementy decydujące o prawidłowości obliczeń modelowych. Pierwszy obejmuje sprawdzenie prawidłowości formalnego ujęcia problemu pod względem matematycznego opisu fizyko-chemicznych procesów, prawidłowego i kompletnego ujęcia bilansu masy i energii oraz uwzględnienia wszystkich istotnych parametrów. Drugi dotyczy właściwego oszacowania wartości współczynników zależnych od konkretnych warunków jak np. współczynniki określające konwekcyjną wymianę ciepła w zależności od intensywności mieszania i/lub kształtu dodatku lub współczynnik przejmowania ciepła na granicy dodatek warstwa zakrzepłej stali. Weryfikacja obliczeń modelowych różnorodnych procesów metalurgicznych może być prowadzono w oparciu o porównanie wyników obliczeń z innym modelami [68], doświadczenia laboratoryjne na modelach fizycznych [20, 37, 57, 58, 59, 115] lub w warunkach przemysłowych [76, 81]. Porównanie rezultatów obliczeń z wynikami innych modeli może być użyteczne, gdy rezultaty uzyskiwane przez te modele są ze sobą zgodne. Prawdopodobieństwo popełnienia pomyłek przez kilka zespołów lub osób tworzących porównywane modele jest mniejsze niż w pojedynczym przypadku. Użyteczność takiej weryfikacji poprawia się gdy któryś z modeli 76
77 porównawczych był przynajmniej częściowo weryfikowany laboratoryjnie lub przemysłowo. Metoda weryfikacji przez porównanie zawodzi, gdy wyniki porównywanych modeli różnią się znacznie. Weryfikacja w warunkach laboratoryjnych może odbywać się w oparciu o tzw. zimne modele (woda, lód, olej, roztwór soli) [20, 58, 115] pozwalające ocenić, czy obliczenia oddają przebieg danego zjawiska, lub też gorące [58, 103, 104], czyli bliskie rzeczywistości z zastosowaniem metali i temperatur właściwych dla symulowanego procesu. Doświadczenia takie służą zarówno ocenie wiarygodności obliczeń poprzez porównywanie wyników obliczeń z danymi zmierzonymi jak też szacowaniu wartości współczynników stosowanych w obliczeniach [103, 104]. Weryfikacje w warunkach przemysłowych prowadzi się poprzez wprowadzanie zmian w technologii w oparciu o rezultaty obliczeń symulacyjnych. Na podstawie pomiarów prowadzonych na obiektach przemysłowych oraz analizy wskaźników technologicznych, które są zgodne/niezgodne z przewidywaniami modelowymi wyciąga się wnioski odnośnie zgodności modelu z rzeczywistością. Weryfikacja przemysłowa ma ograniczone zastosowanie w korygowaniu modelu w przypadku wyników odbiegających od rzeczywistości. Związane jest to z możliwością występowania wielu zakłóceń, które są trudne do wyeliminowania w warunkach konieczności podporządkowania eksperymentów wymogom procesu produkcyjnego. 5. Zdefiniowanie warunków zastosowania oprogramowania CalcoMOS do modelowania procesu roztapiania drutów aluminiowych wprowadzanych do ciekłej stali 5.1. Opis oprogramowania CalcoMos Do obliczeń czasu roztapiania się drutów aluminiowych przystosowano i wykorzystano oprogramowanie CalcoMos. Jest to produkt Szwajcarskiej firmy Calcom (obecnie stanowiącej część międzynarodowej firmy ESI Group z siedzibą w Paryżu), którego podstawowym zastosowaniem jest numeryczne symulowania procesu ciągłego odlewania metali w oparciu o metodę elementów skończonych - FE (Finite Elements) oraz tzw. metody CA-FE będącej połączeniem algorytmów: automatu komórkowego (CA - Cellular Automata) i elementów skończonych (FE - Finite Elements) do obliczeń np. makrostruktury krzepnącego wlewka [116, 117]. Oprogramowanie CalcoMOS to zestaw podstawowych (wymaganych) i opcjonalnych modułów obliczeniowych (wymiana ciepła, przepływ cieczy, transport fazy stałej, krystalizacja, segregacja i inne), które mogą ponadto odwoływać się do definiowanych przez użytkownika procedur pisanych (z zachowaniem odpowiedniej struktury) w języku Fortran oraz modułów usługowych (wchodzących w skład pre- i post-processora) przeznaczonych do różnych zadań (geometryczne definiowanie modelu, generowanie siatki, statyczna i dynamiczna wizualizacja wyników itp.). Funkcje pisane w Fortranie umożliwiają np. definiowanie poszczególnych parametrów wejściowych w funkcji czasu lub temperatury (np. ruch oscylacyjny krystalizatora). Dzięki tym cechom oprogramowanie CalcoMOS ma charakter dedykowanego środowiska programistycznego. Wersja programu zastosowana w niniejszej pracy umożliwia obliczenia w dwóch wymiarach. Istnieje jednak możliwość zdefiniowania zadania w układzie osiowo- 77
78 symetrycznym, co w przypadkach roztapianie drutu umożliwia zadawalające oddanie trójwymiarowej rzeczywistości. Definiowanie zadania w zakresie wymiarów i geometrii symulowanego układu oraz generowanie siatki odbywa się w module pre-procesora oferującym interaktywną pracę podobną do programów typu CAD. Natomiast określanie wszystkich pozostałych parametrów niezbędnych do zdefiniowania modelu przeprowadza się przy pomocy plików tekstowych w formacie ASCII zawierających parametry konfigurujące proces obliczeń, warunki początkowe i brzegowe definiujące właściwości termofizyczne materiałów i ewentualne procedury w języku Fortran. Ponadto wykonywanie symulacji oprogramowaniem CalcoMOS jest możliwe wyłącznie na komputerze z zainstalowanym kompilatorem języka Fortran, który na bieżąco kompiluje poszczególne procedury do postaci bibliotek dynamicznie łączonych, co umożliwia komunikację między nimi i poszczególnymi modułami wywoływanymi przez program nadrzędny. Taka koncepcja pracy systemu z jednej strony komplikuje i wydłuża proces definiowania symulacji czyniąc go, przy większych i złożonych zadaniach, żmudnym i obarczonym ryzykiem pomyłek, ale z drugiej zapewnia elastyczność, szybkość modyfikacji wybranych parametrów i możliwość przygotowania gotowych zestawów danych dla poszczególnych symulacji. Przykładem możliwości, jakie daje taka koncepcja oprogramowania jest wykorzystanie w niniejszej pracy systemu CalcoMOS stworzonego z myślą o symulacji procesu ciągłego odlewania do symulacji procesu odwrotnego niż zakładano, czyli ciągłego roztapiania drutu aluminiowego wprowadzanego do ciekłej stali. Należy nadmienić, że w trakcie bezpośrednich rozmów przeprowadzonych w siedzibie firmy Calcom twórcy oprogramowania stwierdzili, że jakkolwiek system nie był tworzony z myślą o takim zastosowaniu i testowany pod tym kątem, to algorytmicznie jest do tego w pełni przygotowany i powinien dawać poprawne wyniki przy właściwym sformułowaniu zadania. Przemawia za tym również fakt, że w dokumentacji i materiałach szkoleniowych do programu CalcoMOS znajdują się przykłady obliczeń dla zagadnień nie związanych z ciągłym odlewaniem, jak np. procesy ogrzewania, chłodzenia, roztapiania i krzepnięcia statycznych układów zbudowanych z różnych materiałów. Symulowanie procesu roztapiania drutu aluminiowego wprowadzanego do ciekłej stali natrafia co prawda na pewne ograniczenia i wymaga zastosowania uproszczeń, jednak jak już wykazano w rozdziale 4.4, nie wpływają one na użyteczność wyników pod warunkiem, że celem jest otrzymanie wyników istotnych z technologicznego punktu widzenia, czyli do określenia czasu roztapiania drutu (w rzeczywistości interesująca jest głębokości na jakiej roztopi się drut), a nie teoretyczne rozważania wszystkich możliwych czynników i zjawisk o pomijalnym znaczeniu zwykle nieuchwytnych w warunkach przemysłowych. Symulacja w pełni oddająca rzeczywistość wymaga napisania złożonego dedykowanego oprogramowania symulującego w trzech wymiarach i pracującego w oparciu o liczne i dokładne dane wejściowe, które w warunkach przemysłowych są zwykle tylko bardzo zgrubnie szacowane, a ponadto w dużym stopniu zmienne. W związku z tym mimo oczywistych walorów poznawczych takich symulacji problematyczna staje się jej przewaga w stosunku do symulacji na modelu uproszczonym. 78
79 5.2. Zdefiniowanie modelu w zakresie wymiarów i geometrii obiektu w systemie CalcoMOS Zdefiniowanie zadania obliczeniowego w systemie CalcoMOS wymaga następujących kolejnych czynności: - określenie układu współrzędnych (kartezjański, biegunowy), - zadeklarowanie wymiarów obiektu i określenie sposobu jego zdefiniowania, - zdefiniowanie występujących w modelu domen (obszarów o wspólnych parametrach odnośnie ruchu i właściwości termofizycznych) i ewentualnych poddomen (np. wydzielonych obszarów w ramach jednej domeny dla których pożądane jest np. zastosowanie odmiennych parametrów siatki) oraz wykreślenie ich za pomocą narzędzi modułu preprocesora systemu CalcoMOS, - określenie i oznaczenie granic między domenami do których będą przypisane właściwe warunki brzegowe, - wybór rodzaju, charakterystyki i gęstości siatki dla poszczególnych domen i poddomen, - połączenie poddomen (o ile je zdefiniowano), co pozwoli traktować je pod względem fizycznym jak jedną całość, ale odmiennie pod względem programowym (różne parametry siatki i/lub różny zakres obliczeń), - określenie w plikach konfiguracyjnych warunków początkowych, warunków brzegowych pomiędzy domenami oraz na zewnętrznej granicy symulowanego układu, a także parametrów opisujących właściwości poszczególnych domen Określenie układu współrzędnych Oprogramowanie CalcoMOS zastosowane w obliczeniach roztapiania drutów pozwala na symulacje obiektów dwuwymiarowych, przy czym do wyboru są dwa układy współrzędnych: kartezjański (osie x i y) i biegunowy (dla obiektów osiowo-symetrycznych). Druga z możliwości jest naturalnym rozwiązaniem dla procesu wprowadzania okrągłego w przekroju drutu do także okrągłej w przekroju poprzecznym kadzi i pozwala na dogodne opisanie symulowanego obiektu. Z tych też względów przyjęte zostały współrzędne biegunowe. W takiej sytuacji jako celowe uznano zbudowanie połowy modelu, co pozwoliło przy tych samych parametrach siatki na przyspieszenie obliczeń i zmniejszenie wymagań odnośnie pamięci. Zastosowane rozwiązanie wymagało założenia, że drut wprowadza się w środek kadzi (wzdłuż jej osi symetrii) Określenie wymiarów modelu i sposób jego zdefiniowania W praktyce przemysłowej stosuje się kadzie o zróżnicowanych wymiarach oraz druty aluminiowe o różnej średnicy. Znacznie większą różnorodnością cechują się wymiary stosowanych kadzi, które są dostosowane do pojemności eksploatowanych przez daną hutę pieców. Z punktu widzenia poprawności symulacji nie ma potrzeby tworzenia geometrii konkretnej, stosowanej w linii produkcyjnej kadzi. Aby otrzymać uniwersalne narzędzie wystarczające jest zbudowanie modelu dla kadzi o największych stosowanych wymiarach. Wynik symulacji roztapiania drutu aluminiowego w kadzi głębszej niż rzeczywista jest w pełni użyteczny z technologicznego punktu widzenia. Znając rzeczywistą głębokość kąpieli w konkretnej kadzi można na podstawie takich obliczeń określić czy drut roztopi się w pobliżu dna, odbije od niego, czy też nastąpi to dużo wcześniej zanim znajdzie się na 79
80 maksymalnej możliwej głębokości. Natomiast w przypadku gdy głębokość symulowanej kadzi jest mniejsza niż w rzeczywistości, przy większych prędkościach wprowadzania, prawidłowe określenie czasu roztopienia drutu będzie niemożliwe, gdyż drut do dna kadzi dotrze nieroztopiony, a wówczas trudno jest określić ile jeszcze czasu pozostało do roztopienia się aluminium. Wobec powyższego zdefiniowano kadź o większej głębokości niż ta, w której wykonywano przemysłową weryfikacje obliczeń modelowych. Jest to tym bardziej wskazane, że w przypadku, gdy drut nie roztopi się przed dotarciem do miejsca odpowiadającego rzeczywistej głębności kadzi można określić ile jeszcze czasu musi upłynąć do pełnego roztopienia drutu. To z kolei pozwala oszacować, na jakim etapie ewentualnej drogi powrotnej drut powinien się roztopić. Zastosowana w symulacji głębokość kadzi to 4000 mm. Średnica kadzi w zasadzie nie odgrywa tak istotnej roli. Jednak jej wielkość określona w zadaniu symulacyjnym musi być taka, aby analogicznie do warunków rzeczywistych zminimalizować wpływ drutu na zmianę temperatury kąpieli metalowej. W symulacji, ze względu na powyższe, przyjęto w przybliżeniu średnice kadzi, w której prowadzono przemysłową weryfikację modelu, czyli 3146 mm na poziomie żużla przy nowej wymurówce. Uwzględniając fakt, że zgodnie z wcześniejszymi uwagami zbudowano połowę modelu, objęty symulacja obszar ciekłej stali miał wymiary 4000 mm wysokości i 1500 mm szerokości. Znacznie istotniejszym parametrem niż wielkość kadzi jest średnica drutu wprowadzanego do stali. Ma ona istotny wpływ na czas jego nagrzewania się i roztapiania oraz wielkość tworzącego się w początkowej fazie kontaktu drutu z kąpielą metalową naskórka zakrzepłej stali. W tym przypadku dla każdego drutu należy zbudować oddzielny model. W niniejszej pracy opracowano warianty dla drutów o najczęściej spotykanych w warunkach przemysłowych średnicach tj. 10 i 13 mm. Zasadniczym zagadnieniem, które wymagało rozwiązania na etapie definiowania modelu, było znalezienie sposobu na ujecie problemu uwzględniające ograniczenia systemu CalcoMOS. Tworzony z przeznaczeniem do ciągłego odlewania metali program nie przewiduje mieszania (rozcieńczania) się składników zawartych w odrębnych domenach. Zakłada on również bilansowanie się masy w obrębie poszczególnych domen (nie ma wymiany masy pomiędzy domenami, a jedynie z zewnętrznymi obszarami modelu) oraz wyklucza zmianę raz zadanych wymiarów domenach w trakcie symulacji. Model wprowadzania i roztapiania drutu wymagał takiego zaprojektowania, aby powyższe ograniczenia nie stanowiły bariery dla wykonania obliczeń symulacyjnych. Opracowany model bazuje na dwóch podstawowych domenach: stali (ciekłej jak również zakrzepłej na powierzchni drutu w postaci naskórka) oraz drutu aluminiowego w postaci stałej i ciekłej. Ponieważ wprowadzana do układu, z zadaną intensywnością, masa aluminium musi być też wyprowadzana z układu, nie ma możliwości przeprowadzenia symulacji zgodnej z rzeczywistością, gdzie mamy do czynienia z przyrostem masy kąpieli wynikającym z wprowadzonego drutu. W tej sytuacji jedynym sposobem, jak się wydaje, obejścia występujących ograniczeń było skonstruowanie modelu jak na rys. 39. Rozwiązanie to opiera się na założeniu, że z góry do ciekłej stali wprowadzany jest zimny drut aluminiowy, a z dołu kadzi wyprowadzany jest w zależności od zadanych parametrów, rozgrzany drut aluminiowy lub też strumień ciekłego aluminium z prędkością równą prędkości wprowadzanego drutu. Wariant, w którym dołem kadzi wyprowadzane jest aluminium w stanie stałym odpowiada zbyt dużej prędkości wprowadzania drutu, kiedy to w rzeczywistości odbija się on od dna kadzi lub łamie. Sytuacja, w której dołem wyprowadzane jest ciekłe aluminium ma miejsce przy niższych 80
81 prędkościach wprowadzania drutu, kiedy drut zdąży roztopić się zanim osiągnie dno kadzi. W rzeczywistości w tym drugim przypadku ciekłe aluminium nie dociera do dna kadzi jak to ma miejsce w modelu, ale miesza się ze stalą i odtlenia ją. Zastosowane formalne uproszczenie nie odzwierciedla co prawda dokładnie rzeczywistości jednak ze względu na fakt, że oczekiwanym rezultatem obliczeń jest jedynie określenie głębokości, na jakiej dochodzi do roztopienia i uwolnienia glinu zaproponowane rozwiązanie spełnia postawiony cel. W uzupełnieniu należy dodać, że opisane powyżej ujęcie problemu było konsultowane z twórcami oprogramowania z firmy Calcom i nie zostało zakwestionowane. Uznano również, że jest to prawdopodobnie jedyny sposób na zasymulowanie procesu wprowadzania drutu do stali w tym programie. Rys. 39. Konstrukcja modelu wprowadzania drutu (stan ustalony) z bilansem masy w ramach jednej domeny możliwa do zrealizowania w programie CalcoMOS. Należy zaznaczyć, że na powyższym rysunku, tak jak i na następnych przedstawiających schematycznie model, w celach poglądowych zmieniono proporcje pomiędzy wielkością kadzi a średnicą drutu Zdefiniowanie domen odpowiadających poszczególnym elementom układu Najistotniejszą, z punktu widzenia celu symulacji, domeną jest domena nr 1 (rys. 39) odzwierciedlająca drut aluminiowy. Przebiega ona przez całą wysokość stali zawartej w kadzi, a ponadto obejmuje odcinek długości 200 mm ponad lustrem metalu (bardziej w celach poglądowych niż z rzeczywistej potrzeby). Po przeciwnej stronie dochodzi do dna 81
82 kadzi i odprowadza poza jej granice aluminium w ilości wynikającej z bilansu masy. W zależności od przyjętych parametrów symulacji domena ta w stanie ustalonym może być na całej długości w stanie stałym, lub też od pewnego momentu przechodzić w stan ciekły. Drugą domeną, oznaczoną numerem 2 na rys. 39, jest ciekła stal wypełniająca obszar o wymiarach ograniczonych wielkością kadzi. W momencie startu symulacji jest ona w stanie ciekłym, jednak na skutek wprowadzania drutu pojawiają się w niej niewielkie obszary w stanie stałym powstałe przy powierzchni wprowadzanego drutu. W związku z tym, że zastosowano zróżnicowaną charakterystyką siatki w obrębie tej domeny (zagadnienie doboru siatki szerzej omówiono w rozdziale 5.2.5), w pierwszej fazie budowania modelu, zgodnie z wymogami oprogramowania, konieczne było zdefiniowanie dwóch poddomen o odmiennej charakterystyce siatki, które następnie zostały połączone w całość. Domena ta podobnie jak odzwierciedlająca drut ma kształt walca. Kadź stalownicza zwykle różni się od tej bryły geometrycznej, gdyż posiada pewną zbieżność (średnica u góry jest większa niż przy dnie) ale pomijając procesy mieszania kąpieli cecha ta nie ma istotnego znaczenia dla wyników obliczeń. Pozostałe parametry poszczególnych domen zostały szczegółowo omówione w dalszej części niniejszego rozdziału. Należy jeszcze wspomnieć o odwzorowaniu kadzi, w której układ drut-stal powinien się mieścić. Z punktu widzenia wyników symulacji nie ma ona znaczenia dla procesu obliczeń, a może jedynie wydłużyć czas tego procesu. Odpowiednie warunki brzegowe na krawędzi domeny ciekłej stali można zdefiniować bezpośrednio, bez żadnej warstwy pośredniczącej, zwłaszcza, że nie zakłada się spadku temperatury stali podczas trwającej z reguły kilkadziesiąt sekund (czasem kilka minut) operacji wprowadzania drutu. W związku z tym na granicy tej domeny założono warunki brzegowe odpowiadające brakowi odpływu ciepła w czasie symulacji, zabezpieczając tym samym program przed wykonaniem zbędnej pracy. Nie zamyka to drogi do takiego zdefiniowania warunków, które będą odzwierciedlały odpływ ciepła występujący w warunkach rzeczywistych. Podobnie jak w przypadku kadzi także żużel nie został graficznie odwzorowany. Tutaj również odpowiednie warunki brzegowe można zdefiniować na górnej granicy domeny reprezentującej ciekłą stal i tak też zrobiono zakładając brak odpływu ciepła, co również redukuje ilość obliczeń i tym samym skraca ich czas Określenie granic między domenami, dla których będą definiowane odmienne warunki brzegowe Po wykonaniu graficznego odwzorowania symulowanego układu program wymaga, aby wszystkim granicom pomiędzy domenami oraz zewnętrznym granicom całego modelu przypisać numery, poprzez które użytkownik może odwoływać się do poszczególnych granic w plikach konfiguracyjnych. W utworzonym modelu nadano poszczególnym granicom lub ich grupom następującą numeracje - rys. 40: nr 1 granica pomiędzy ciekłą stalą, a drutem aluminiowym, nr 2 na osi symetrii, nr 3 górna granica drutu (miejsce wprowadzania aluminium do układu), nr 4 boczna powierzchnia drutu przed wprowadzeniem, nr 5 górna granica stali (miejsce kontaktu z żużlem), 82
83 nr 6 boczna i dolna granica ciekłej stali (miejsce kontaktu z wymurówką kadzią), nr 7 dolna granica drutu (miejsce wyprowadzania aluminium z układu) Rys. 40. Numeracja granic w modelu pomiędzy domenami i na zewnątrz układu Wybór rodzaju, charakterystyki i gęstości siatki oraz określenie poddomen Wybór rodzaju i gęstości siatki ma istotny wpływ na dokładność obliczeń wykonywanych metodą elementów skończonych. Program CalcoMOS oferuje do wyboru dwa typy siatki. Są to siatka prostokątna i trójkątna. Siatki te mogą ponadto występować w odmianach o zmiennym zagęszczeniu przy powierzchni - trójkątna z efektem naskórkowym ( Skin effekt ), a prostokątna jako progresywna o zmiennym zagęszczeniu zgodnie z zadanym kierunkiem dla każdej z osi. Siatki te wraz z ekranem programu zaprezentowano na rys
84 Rys. 41. Rodzaje siatek generowanych przez program CalcoMOS (ekran roboczy programu). A - trójkątna zwykła B - trójkątna z efektem naskórkowym C - prostokątna D - prostokątna progresywna Siatka prostokątna jest zalecana dla domen w kształcie czworoboku, a zwłaszcza o kątach prostych. W przypadku domen o kształtach wieloboku, krzywoliniowych lub okrągłych konieczna jest siatka trójkątna, która zapewnia jej wpasowanie się w kształt domeny tego typu. Ponieważ w opracowanym modelu roztapiania drutów aluminiowych wszystkie domeny maja kształt prostokątów, zastosowana w nich została siatka prostokątna. W przedstawionym modelu najistotniejsze zjawiska zachodzą wewnątrz drutu i w stali w bezpośrednim otoczeniu drutu. Z tego względu są to obszary szczególnego zainteresowania. W pozostałych obszarach kadzi, w odległości np. 100 cm od wprowadzanego drutu nie zachodzą istotne dla przebiegu jego roztapiania zjawiska, które należałoby rozpatrywać z dokładnością do części milimetra. Zastosowanie siatki o dużej gęstości w całej objętości kadzi prowadziłoby do wielogodzinnych obliczeń i to pod warunkiem dysponowania odpowiednią ilością pamięci RAM. W związku z tym celowe było zastosowanie siatki o zmiennych parametrach. Zastosowania takiej siatki szczególnie celowe wydaje się właśnie w bardzo obszernej domenie odpowiadającej ciekłej stali, gdzie w pobliżu wprowadzanego drutu zachodzą zjawiska o niewielkiej liczonej w milimetrach skali. Jednak zastosowanie siatki progresywnej w tak obszernej domenie jak kadź prowadzi do zbyt dużych elementów po przeciwnej stronie domeny. 84
85 Rozwiązanie powyższego problemu możliwe jest dzięki zastosowaniu mechanizmu łączenia domen. W fazie projektowania domena ciekłej stali składała się z dwóch poddomen - A i B. Pierwsza - A stosunkowo wąska biegnie wzdłuż strefy kontaktu ciekłej stali z drutem oraz druga B wypełniająca pozostały obszar kadzi. W pierwszej zastosowano siatkę zagęszczająca się w miarę zbliżania się do powierzchni drutu, przy której osiąga rozmiary 0,3 mm, a w drugiej regularną siatkę o boku 10 cm. Rozwiązanie to pozwala to na stopniowe przejście rozmiaru siatki od niewielkich do dużych oczek. Schematycznie poddomeny przedstawiono na rys. 42, wydruk z programu CalcoMOS, przedstawiający fragment zagęszczającej się siatki w pobliżu drutu na rys. 43, a większy fragment siatki z zaznaczonym miejscem polaczenia poddomen z siatką progresywną i kwadratową na rys. 44. Natomiast rys. 45 przedstawia pełną szerokość siatki wraz z oznaczonymi kolorowymi cyframi (na rysunku nieczytelne) granicami domen. Rys.42. Domeny i poddomeny w zbudowanym modelu symulacyjnym. 85
86 Rys. 42. Powiększony fragment siatki w domenie odpowiadającej ciekłej stali w pobliżu drutu i w drucie. Rys. 43. Fragment siatki w domenie z zaznaczonym (czerwoną linią) miejscem połączenia poddomen z siatką progresywną i kwadratową. 86
87 Rys. 44. Fragment siatki modelu roztapiania drutu aluminiowego w kadzi (w osi poziomej pełny wymiar) 87
88 5.3. Określenie warunków początkowych i brzegowych, danych materiałowych oraz parametrów i zakresu obliczeń Opis domen i warunków brzegowych oraz zasady określania warunków symulacji w programie CalcoMOS Podstawowe informacje niezbędne do przeprowadzenia symulacji umieszcza się w tekstowym pliku konfiguracyjnym. Plik ten, mający ściśle określoną strukturę oraz składnię poleceń, zawiera ponadto odnośniki do kolejnych plików zawierających dalsze dane wymagane do wykonania obliczeń. Poszczególne pliki używane przez program CalcoMOS są identyfikowane za pomocą narzuconych przez twórców oprogramowania rozszerzeń i sufiksów zawartych w nazwie, a oddzielanych znakiem _ (podkreślnika). Przykładowo dla plików zawierających dane materiałowe stosuje się sufiks _phys i rozszerzenie.d. Tak wiec plik zawierający dane dla miedzi można nazwać miedz_phys.d, copper_phys.d lub w inny sposób zmieniając jednak tylko pierwszy człon nazwy (pisany kursywą). Odwoływanie się do takiego pliku z poziomu głównego pliku konfiguracyjnego odbywa się również tylko poprzez część zasadniczą, a więc odpowiednio: miedz lub copper Plik taki posiada ściśle określoną w dokumentacji oprogramowania strukturę. Dane zawarte w pliku konfiguracyjnym można podzielić na trzy grupy o różnym charakterze. W poszczególnych grupach określa się: - Parametry pracy programu i ogólne cechy modelu. - Parametry opisujące domeny - w tym warunki początkowe, - Parametry dla granic pomiędzy domenami i zewnętrznych granic modelu, czyli warunki brzegowe. Zakres informacji opisujących parametry pracy programu i ogólne cechy modelu ustala się poprzez system słów kluczowych i dyrektyw (włączników) im towarzyszących włączających lub wyłączających daną funkcjonalność (np. heat on uaktywnia obliczenia cieplne, a fluid off wyłącza moduł obliczania przepływ płynu - rozwiązanie równania Naviera-Stokes a) oraz parametrów podawanych w postaci stosownych i dopuszczalnych wartości np. number.of.steps 20 deklaruje, że obliczenia powinny obejmować wykonanie 20 iteracji. Do pozostałych parametrów z tej grupy zaliczyć można parametry wskazujące na typ współrzędnych (kartezjańskie, biegunowe), kierunek grawitacji i jej siłę, krok czasowy iteracji, częstotliwość zapisu wyników pośrednich, kryteria zakończenia obliczeń. Zakres informacji opisujących domenę wynika z jej definicji w systemie CalcoMOS [118]. Domena według tej definicji jest ciągłym obszarem charakteryzowanym poprzez własności termofizyczne materiału, z którego jest zbudowana oraz warunki początkowe, a także informacje dodatkowe związane z zakresem obliczeń dla niej. Materiał domeny definiuje się poprzez wskazanie pliku z odpowiednimi własnościami termofizycznymi niezbędnymi do przeprowadzenia obliczeń. Plik ten został szerzej omówiony w rozdziale Warunki początkowe obejmują temperaturę początkową i prędkość początkową domeny (składowa x i y ). Definiuje się również prędkość fazy stałej w domenie ciekłej, jeżeli takowa może się pojawić (również składowe x i y ). Ponadto przy definiowaniu każdej domeny należy określić dla niej zakres obliczeń z zestawu zadeklarowanego wcześniej w części ogólnej (ciepło, przepływ cieczy, transport fazy stałej 88
89 itp.). Poszczególne parametry przypisuje się do domeny poprzez odwołanie do jej numeru; każda domena musi posiadać swój własny indywidualny numer. Parametry opisujące granice pomiędzy poszczególnymi domenami i zewnętrzne granice modelu są zależne od zadeklarowanego typu warunków brzegowych. W zależności od przyjętych warunków brzegowych, parametry opisujące granicę obejmują temperaturę zewnętrzną, warunki przepływu ciepła (przewodzenie, promieniowanie, konwekcja), współczynniki dla wybranego przepływu ciepła i narzuconą prędkość na zewnętrznej granicy modelu lub granicy ciekłej domeny. Stosowne warunki brzegowe są przyporządkowane do granic domen przez odwołanie do numeru danej granicy. Tu jednak, odmienni niż w przypadku domen, użytkownik ma większą swobodę w nadawaniu poszczególnych numerów, co pozwala zastosować jeden wspólny numer dla kilku granic o takich samych warunkach. System CalcoMOS oferuje sześć różnych typów warunków brzegowych. Dla zewnętrznych granic modelu, lub zewnętrznych granic domen w stanie ciekłym: - Dirichleta, - Neumanna, - Cauchy'ego, - Radiacyjny (wymiana ciepła przez promieniowanie), Dla pozostałych granic wewnątrz modelu (pomiędzy domenami): - Heat-Link (opisane współczynnikiem wymiany ciepła ), - Kontaktu doskonałego. Poniżej opisano szerzej dwa ostatnie warunki brzegowe, gdyż ich zastosowanie w opracowanym modelu miało miejsce na jego wewnętrznych granicach i tym samym warunki te odgrywały podstawową rolę w obliczeniach symulacyjnych. Heat-Link - ten typ warunku brzegowego jest stosowany do opisu przepływu ciepła pomiędzy dwoma stykającymi się domenami reprezentującymi obiekty będące w stanie stałym. Obiekty takie, zgodnie z tym co przedstawiono w rozdziale 4.5, z zasady znajdują się w kontakcie niedoskonałym, co wynika z chropowatości ich powierzchni. Stosownie do tego wymianę ciepła opisuje się za pomocą współczynnika wymiany ciepła określającego przepływ ciepła przez granicę styku obu ciał. W dokumentacji użytkowania programu CalcoMOS [118] oraz dostarczonych z oprogramowaniem przykładowych modelach warunek ten jest standardowo stosowany na granicy wlewek-krystalizator. Dokumentacja ta definiuje go jako konwekcyjną wymianę ciepła pomiędzy dwoma domenami (na wewnętrznej granicy modelu) opisaną poprzez współczynnik wymiany ciepła i różnicę temperatury powierzchni obu domen. Wynika z tego, że strumień ciepła na takiej granicy jest równoważny iloczynowi współczynnika wymiany ciepła i różnicy temperatur obu wspomnianych powierzchni. Od użytkownika wymagane jest jedynie określenie makroskopowego współczynnik wymiany ciepła, natomiast temperatury obu powierzchni stykających się domen są obliczane na podstawie dostarczonych w plikach konfiguracyjnych danych. Z dokumentacji oprogramowania wynika, że dla potrzeb obliczeń numerycznych, które wymagają, aby przypisać odmienną temperaturę do obu stron granicy, generator siatki tworzy wirtualną podwójną granicę, przy czym obie te granice przebiegają w tym samym miejscu (zerowa odległość). 89
90 Kontakt doskonały ten warunek ma zastosowanie przy definiowaniu poddomen celem wydzielania pewnych obszarów, dla których prowadzi się odmienny czy też dodatkowy typ obliczeń lub stosuje inną ich dokładność, a które powinny stanowić pod względem formalnym integralną całość z pozostałą częścią domeny. W związku z tym z punktu widzenia wymiany ciepła granica z takim warunkiem brzegowym nie istnieje (jest przeźroczysta) i tak też jest traktowana podczas obliczeń. Jej rolą jest oddzielanie poddomen, a więc fragmentów domeny w których zastosowano odmienne parametry obliczeniowe jak np. (gęstość siatki, progresja siatki, obliczanie struktury krystalizacji dla danej poddomeny itp. W związku z tym jest to wyłącznie granica ograniczająca zakres skomplikowanych obliczeń celem zwiększenia ich szybkości lub lepszego wykorzystania pamięci operacyjnej komputera. Nie ma natomiast ta granica fizycznego odzwierciedlenia w rzeczywistości. Pozostałe warunki brzegowe, na zewnętrznych granicach modelu, zdefiniowano zgodnie z zaleceniami instrukcji do programu, ale w istocie nie miały one wpływu na wyniki obliczeń Właściwości termofizyczne niezbędne do symulacji roztapiania drutu aluminiowego Pliki definiujące własności termofizyczne materiałów stanowiących poszczególne domeny posiadają jednoznacznie określoną strukturę, która składa się z kolejnych sekcji odnoszących się do poszczególnych własności. Sekcje te zawierają informacje o przewodności cieplnej materiału, cieple właściwym, gęstości, lepkości, cieple przemiany i współczynniku rozszerzalności liniowej oraz ułamku fazy stałej w danej temperaturze. W przypadku parametru zależnego od temperatury jak np. ciepło właściwe czy przewodność cieplna można określić go w sposób stabelaryzowany dla zadanego przedziału temperatury z praktycznie dowolnym krokiem. Twórcy oprogramowania nie zalecają jednak bez wyraźnej potrzeby tworzenia zbyt dużej liczby przedziałów. Wymagane przez program parametry dla aluminium i stali takie jak ułamek objętościowy fazy stałej, ciepło właściwe, przewodność cieplna, gęstość, lepkość w zależności od temperatury oraz ciepło przemiany fazowej obliczone zostały za pomocą programu JMatPro 4.0 brytyjskich firm Thermotech Ltd. i Sente Software Ltd [119]. Dla aluminium przyjęto skład chemiczny zgodny z analizą chemiczną drutu aluminiowego stosowanego do odtleniania stali. W przypadku stali przyjęto skład chemiczny odpowiadający średnim wartościom z wytopów, podczas których prowadzono przemysłowe badania efektywności odtleniania w zależności od prędkości wprowadzania drutu. Była to stal niskowęglowa gatunków UG i F0. Składy chemiczne aluminium i stali, dla których przeprowadzono obliczenia w programie JMatPro przedstawiono w tablicy 2. Tablica 2. Składy chemiczne stali i aluminium, dla których określono programem JMatPro własności termofizyczne zastosowane w obliczeniach symulacyjnych. Materiał Skład chemiczny [%] Fe C Mn Si S P Al Stal 99,63 0,060 0,256 0,011 0,013 0,010 0,035 Aluminium 1,31 0,17 0,22 98,30 90
91 Program JMatPro generuje wyniki obliczeń w formie wykresów lub tabelarycznych zestawień z zadanym przez użytkownika krokiem. Przykładowy wykres generowanych przez program JMatPro zamieszczona na rys. 46. Do celów niniejszej pracy bardziej praktyczne w zastosowaniu były jednak tabelaryczne zestawienia parametrów, które były zgodne z formatem plików konfiguracyjnych programu CalcoMOS. Rys. 46. Wykres przedstawiający ułamek fazy stałej aluminium technicznego w zależności od temperatury wygenerowany programem JMatPro. Przykładowy plik w standardzie CalcoMOS z pełnym opisem właściwości stali wykonany na podstawie obliczeń programem JMatPro zawierający wyliczone ułamki masowe fazy stałej w zależności od temperatury dla średniego składu stali, zamieszczono w załączniku nr 1. 91
92 Z przeprowadzonych programem JMatPro obliczeń wynikało, że dla aluminium temperatura solidus wynosi 544 C, a likwidusu 655 C. W przypadku stali było to odpowiednio 1493 C i 1532 C. Pełne zestawienie pozostałych parametrów opisujących aluminium i stal dla wybranych temperatur zestawiono w tablicy 3. Tablica 3. Parametry termofizyczne stali i aluminium dla wybranych temperatur zastosowane w obliczeniach symulacyjnych. Parametr Gęstość [kg/m 3 ] Przewodność cieplna [W/mK] Ciepło właściwe [J/m 3 K] Lepkość [kg/m s] Aluminium Stal wartość w temp. [ C] wartość W temp. [ C] ,1 88, , , ,7 35, , Solidus Likwidus Opracowanie plików konfigurujących dla modelu roztapiania drutu aluminiowego wprowadzanego do ciekłej stali Model roztapiania drutu aluminiowego wprowadzanego do ciekłej stali został zdefiniowany w systemie CalcoMOS zgodnie z opisanymi powyżej zasadami za pomocą głównego pliku konfiguracyjnego oraz plików pomocniczych w uwzględnieniu narzuconej przez oprogramowanie struktury danych wejściowych. Ze względu na symulowanie różnych warunków wprowadzania drutu, takich jak temperatura stali, prędkość wprowadzania drutu jak i stosowanie różnej średnicy drutu, główny plik konfiguracyjny został utworzonych w kilku wariantach, które w połączeniu z dwoma modelami o różnej średnicy drutu dały sumarycznie 60 symulacji. Parametry dla domen zdefiniowanych w modelu. W omawianym modelu poszczególnym domenom numerowanym zgodnie ze schematem przedstawionym na rys. 43, przypisano następujące parametry: Domenie nr 1, odpowiadającej drutowi aluminiowemu, została nadana temperatura początkowa równa 20 C, a jako materiał zadeklarowano aluminium techniczne (wskazano przygotowany wcześniej i omówiony już pliku Aluminium_phys.d, który zawierał komplet danych termofizycznych wymaganych przez program). Ponadto określono prędkość początkową w osi y, różną w zależności od przyjętej w danej serii obliczeń prędkości wprowadzania drutu [m/s]. Zadeklarowano obliczenia przepływu ciepła, płynu i transportu fazy stałej. 92
93 Domenie nr 2, odzwierciedlającej ciekłą stal, przypisywano temperaturę początkową zależną od założeń przyjętych dla danej serii obliczeń. Własności termofizyczne materiału, stanowiącego domenę nr 2 zostały określone przez wskazanie pliku Stal_phys.d zawierającego podobnie jak w przypadku aluminium wszystkie konieczne dane. Ponadto określono prędkości fazy stałej w tej domenie. Ponieważ faza ta pojawi się tylko wokół wprowadzanego drutu aluminiowego, jej prędkość w osi y została określona stosownie do prędkości wprowadzania tegoż drutu. Pozostałe dyrektywy jak w domenie nr 1. Parametry dla granic zewnętrznych modelu i wewnętrznych pomiędzy domenami. W omawianym modelu poszczególnym granicom, numerowanym zgodnie ze schematem przedstawionym na rys. 43, przypisano następujące warunki brzegowe: Granica nr 1. Granica pomiędzy ciekła stalą, a drutem aluminiowym jest najważniejsza z punktu widzenia prawidłowości procesu symulacji. Dla tej granicy ustalono warunki brzegowe typu Heat-Link. Warunek ten i zakres jego stosowania omówiony już szerzej w rozdziale Z zamieszczonych tam informacji wynika, że jest on przewidziany dla wymiany ciepła poprzez przewodzenie w warunkach kontaktu niedoskonałego dwóch ciał w stanie stałym, a więc dla warunków występujących pomiędzy drutem, a zakrzepłą na nim warstewką stali. Przepływ ciepła dla granicy z przypisanymi warunkami brzegowymi typu Heat-Link jest opisany współczynnikiem wymiany ciepła. Program CalcoMOS uwzględnia samodzielnie powstanie warstwy zakrzepłej stali na powierzchni drutu i zgodnie ze zmianą temperatury określa własności termofizycznymi materiałów według danych zdefiniowanych przez użytkownika. W przypadku tego warunku bardzo ważna, z punktu widzenia wiarygodności symulacji, jest kwestia prawidłowego zadeklarowania wartości współczynnika wymiany ciepła pomiędzy drutem aluminiowym, a powstałą na nim warstewką zakrzepłej stali. Ze względu na fakt, że wartość tego współczynnika zależy od wielu parametrów mogących zmieniać ją w szerokim zakresie opieranie się na danych literaturowych uznano za bardzo ryzykowne. W związku z tym dla potrzeb niniejszej pracy współczynnik ten został wyznaczony eksperymentalnie. Istota eksperymentu i jego rezultaty zostały opisane w rozdziale 6. Granica nr 2 Granica na osi, ze względu na swój umowny charakter i swoją funkcję określenia środka symetrii układu jest z założenia granicą martwą. Nie zachodzą tam żadne procesy wymiany ciepła, a ruch powinien być swobodny i zgodny z założeniami określonymi dla domeny, którą oś symetrii przecina. Zgodnie z powyższym zadeklarowano stosowne wartości. Granica nr 3 Górna granica domeny odpowiadającej drutowi aluminiowemu, to miejsce określenia prędkości, z jaką następuje wprowadzanie drutu. Ponieważ celem modelu były symulacje wprowadzania drutu z różną prędkością to parametry przypisane do tej granicy były zależne od aktualnie symulowanego wariantu. Wymiana ciepła w przypadku tej granicy jest praktycznie nie istotna i analogicznie do odpowiednich symulacji spotykanych w literaturze została pominięta. Dla granicy tej zadeklarowano wartości stosowne dla warunku brzegowego Dirichleta i określono temperaturę zewnętrzną na 20 C (temperatura otoczenia w jakie 93
94 znajduje się drut przed wprowadzeniem do stali). Prędkość w osi x wynosi zero, a w osi y stosownie do symulowanego warianty od 1,0 do 2,5 m/s (60 do 150 m/min). Granica nr 4 Granicy pomiędzy zewnętrzną (boczną) powierzchnią drutu zanim znajdzie się on w stali, a otoczeniem nadano (podobnie jak dla granic nr 5 i 6) warunek Cauchy ego z zerową wymianą ciepła. W tym obszarze drut ma zwykle temperaturę otoczenia, w którym znajduje się przez dłuższy czas. Uprawnione jest w tej sytuacji założenie braku przepływu ciepła pomiędzy drutem i otoczeniem (w rzeczywistości powierzchnia kąpieli może oddziaływać już na drut głównie przez promieniowanie, ale z reguły jest to bardzo krótki czas, gdyż drut na tym etapie znajduje się w rurze prowadzącej. Granica nr 5 i 6 Górna (nr 5) i boczna oraz dolna (nr 6) granica domeny odwzorowującej ciekłą stal to granice styku ciekłego metalu z żużlem i wewnętrzną powierzchnią kadzi (wymurówką). W pełni realistyczna symulacja, która uwzględnia również ubytek ciepła z kadzi poprzez wymurówkę w trakcie operacji wprowadzania drutu powinna brać pod uwagę przewodnictwo cieplne żużla oraz przewodnictwo cieplne wymurówki, stalowego pancerza kadzi i temperaturę otoczenia. W przypadku symulowania procesu tak krótkiego jak wprowadzanie drutu, niewielki ubytek ciepła występujący w tym czasie (rekompensowany utlenianie aluminium) można pominąć. W doniesieniach literaturowych poruszających problem głębokości roztapiania się drutów również nie uwzględnia się tego parametru. Przyjmuje się temperaturę stali w czasie wprowadzania drutu za stałą. Ma to dodatkowo tą zaletę, że nie obciąża symulacji dodatkowymi zbędnymi obliczeniami. Na granicach 5 i 6 zadeklarowano warunki brzegowe Cauchy ego i ustalono przepływ ciepła na zero. Oddzielny numer dla górnej granicy domeny ciekłej stali i bocznej wraz z dolną został zastosowany ze względu na ich odmienny charakter i możliwość ewentualnej rozbudowy modelu w przyszłości. Granica nr 7 Dolna granica domeny odpowiadającej drutowi aluminiowemu, to miejsce określania prędkości wyprowadzania aluminium, zgodnie z przyjętą koncepcją zapewnienia bilansu masy w ramach jednej domeny. Na granicy tej nie można zadeklarować konkretnej temperatury, gdyż jest wynikiem obliczeń symulacyjnych. W związku z tym zadeklarowano granicę Neumana z zerową wymianą ciepłą, gdyż w przypadku tej granicy podobnie jak granicy nr 3 nie odgrywa ona istotnej roli (a w praktyce nie istnieje). Prędkość w osi x zadeklarowano zerową, a y analogiczną jak dla granicy nr 3. Wszystkie dane konfigurujące warunki brzegowe (podobnie jak opisujące domeny) zostały umieszczone w odpowiednim pliku konfiguracyjnym programu CalcoMOS. Ze względu na wariantowość symulacji należało utworzyć pliki o różnych wartościach temperatury stali i prędkości wprowadzania dla poszczególnych przypadków. Przykładowy plik dla wariantu: temperatura stali C, prędkość wprowadzania drutu - 90 m/min (1,5m/s) zamieszczono w załączniku nr 2. 94
95 6. Eksperymentalne wyznaczenie współczynnika wymiany ciepła na granicy drut zakrzepła warstwa stali W rozdziale 4.5 przedstawiono różne aspekty eksperymentalnego wyznaczania współczynnika wymiany ciepła między ciałami znajdującymi się w stanie kontaktu niedoskonałego w trakcie procesu krzepnięcia lub roztapiania. W związku z przedstawionymi tam faktami, a mianowicie dużym rozrzutem publikowanych danych eksperymentalnych oraz znacznym wpływem różnorodnych czynników na wartość współczynnika wymiany ciepła uznano, że wykorzystanie wartości oszacowanej dla podobnego układu tylko na podstawie ogólnej analogii głównych cech obiektu bez uwzględnienia parametrów powierzchni oraz występujących w nim sił nacisku jest ryzykowne i może być obarczone dużym błędem. W związku z tym w pracy oszacowano współczynnik wymiany ciepła w warunkach zbliżonych do rzeczywistych poprzez porównywanie wyników symulacji z danymi rzeczywistymi otrzymanymi w warunkach laboratoryjnych. Zastosowana metoda ma tą zaletę, że współczynnik określany był w bardzo podobnych warunkach jak rzeczywiste będące przedmiotem symulacji. Zastosowano dokładnie taki sam drut jaki używa się do odtleniainia stali, a kąpiel metalowa miała skład chemiczny zbliżony do rzeczywistego składu stali z wytopów podczas których wykonywano badania przemysłowe Koncepcja eksperymentalnego wyznaczenie współczynnika wymiany ciepła Eksperyment polegał na określeniu współczynnika wymiany ciepła poprzez porównanie wyników z prób laboratoryjnych z wynikami komputerowej symulowaniu tego procesu programem CalcoMOS. W pierwszym etapie badań w ramach laboratoryjnego doświadczenia fizycznego wykonano próby w piecu indukcyjnym typu VSG50-Balzers o pojemności 25 kg, w którym roztopiono żelazo armco. Do podgrzanego do temperatury 1600 C metalu był szybko wprowadzany drutu aluminiowy o średnicy 10 mm na głębokość ok cm i wyciągany po różnym okresie czasu. Jako wyznacznik opisujący proces roztapiania drutu przyjęto zmiany grubość warstewki żelaza zakrzepłego na drucie po różnym czasie zanurzenia w kąpieli. W zależności od czasu przebywania drutu w ciekłej kąpieli spodziewano się obserwować różne fazy jego roztapiania i stan ich zaawansowania. Drugim elementem eksperymentu była symulacja komputerowa roztapiania drutu. Realizowana była na specjalnie opracowanym do tego celu modelu, z zastosowaniem różnych współczynników wymiany ciepła. Założono, że zgodność wyników eksperymentu fizycznego i obliczeń numerycznych będzie podstawą do uznania, że wartość zastosowanego współczynnika wymiany ciepła jest bliska rzeczywistej. Symulacje wykonywano z zastosowaniem różnych współczynników wymiany ciepła między drutem a kąpielą metalową (lub raczej tworzącą się na nim warstewką zakrzepłej stali). Model numeryczny na potrzeby tego eksperymentu zaplanowano w odmienny sposób niż model roztapiania drutu aluminiowego wprowadzanego do ciekłej stali. W modelu tym w stanie początkowym drut jest zanurzony na pewną głębokość i w tej pozycji pozostaje do końca eksperymentu nie ma potrzeby budowania układu z ciągłym wprowadzaniem aluminium. Schematycznie model przedstawiono na rys
96 Założono, że współczynnik wymiany ciepła, przy którym wyniki symulacji będą odpowiadały rzeczywistym rezultatom osiągniętym podczas prób laboratoryjnych powinien, jako bliski rzeczywistemu, zostać zastosowany w dalszych symulacjach numerycznych procesu roztapiania drutów aluminiowych Rys. 47. Schemat modelu roztapiania drutu wprowadzanego do ciekłego żelaza wykorzystanego do porównawczego określenia współczynnika wymiany ciepła. Model posiada dwie domeny, z których domena nr 1 odzwierciedla drut o średnicy 10 mm, a domena nr 2 ciekłe żelazo znajdujące się w piecu. Pod względem granic model jest prostszy niż docelowy, gdyż posiada tylko cztery granice, z których tylko jedna oznaczona nr 1 jest istotna dla symulowanego procesu. Granica nr 2 stanowi oś symetrii, na której nie występuje wymiana ciepła. Granice 3 (zewnętrzna granica kąpieli metalowej) i 4 (zewnętrzna granica drutu) wyznaczają zewnętrzną granicę modelu, ale nie zadeklarowano na nich wymiany ciepła. Ponieważ model ten ma mniejsze rozmiary niż model przemysłowy, można było zastosować gęstą siatkę, a obliczenia mimo to były wykonywane stosunkowo szybko. Materiał drutu został zdefiniowany identycznie jak przedstawiono w rozdziale 5.3.2, natomiast do domeny nr 2 zostały przypisane, wyznaczone programem JMatPro, własności termofizyczne użytego do eksperymentu żelaza armco o składzie chemicznym jak w tablicy 4. Skład ten jest na tyle zbliżony do stali niskowęglowej, w której prowadzono przemysłowe próby odtleniania drutem aluminiowym, że uzyskane tym modelem wyniki powinny być miarodajne dla symulacji przemysłowej. Temperatura solidus została określona na 1501 C, a likwidus na 1535 C. Warunki brzegowe na granicy nr 1 (rys. 47) modelu laboratoryjnego zostały zdefiniowane podobnie jak dla granicy nr 1 w modelu przemysłowym, czyli jako Heat-link. Różnica polega na braku ruchu domeny odzwierciedlającej drut aluminiowy, ale nie ma to wpływu na warunki wymiany ciepła na granicy drutu, gdyż warstewka zakrzepła na drucie nie przemieszcza się w stosunku do niego również w modelu przemysłowym. Wobec dużego zróżnicowania spotykanych wartość współczynnika wymiany ciepła przyjęto szeroki zakres 96
97 badanych wartości. Testy rozpoczęto od wartość 1000 [m 2 K/W] i zwiększano ją o 1000 [m 2 K/W] w każdej następnej symulacji, porównując wyniki kolejnych symulacji z wynikami osiągniętymi podczas fizycznego eksperymentu laboratoryjnego. Po wstępnym wyznaczeniu wartości zbliżonej do rzeczywistej planowano obliczenia z mniejszemu krokiem celem dokładnego wyznaczenia współczynnika wymiany ciepła. Tablica. 4. Skład chemiczny żelaza armco, do którego wprowadzano drut aluminiowy podczas laboratoryjnego eksperymentu określania współczynnika wymiany ciepła. lp. Pierwiastek Zawartość [%] 1 C 0,03 2 Si 0,01 3 Mn 0,15 4 S 0,01 5 P 0,01 6 Al 0, Wyznaczenie współczynnika wymiany ciepła W fizycznej części eksperymentu wyznaczania współczynnika wymiany ciepła odpowiednio przycięte druty aluminiowe o średnicy ok. 10 mm wprowadzano do ciekłego żelaza na czas 1, 2, 3, 4 i 5 sekund. Dokumentacja fotograficzne tego eksperymentu, została przedstawiona na rysunkach 48 i 49. Należy zaznaczyć, że drut zanurzany na 1 i 2 sekundy nie wprowadzano na pełną planowaną głębokość 10 cm ze względu na krótki czas zanurzenie w kąpieli. Zastosowanie pełnej głębokości doprowadziłaby do sytuacji, w której drut jest praktycznie w ciągłym ruchu (co może zmienić warunki wymiany ciepła), a zadany czas przebywania drutu w kąpieli dotyczyłby i tak tylko jego końcowej części. Dodatkowo za takim podejściem przemawiały względy bezpieczeństwa. Natomiast, jak wykazały następne próby, lekkie wahania poziomu zanurzenia drutu były konieczne, zwłaszcza, przy dłuższych czasach zanurzenia, gdyż bez tego zabiegu drut roztapiał się powyżej powierzchni metalu i odcinek drutu z zakrzepłą powłoką odpadał pozostając w kąpieli. Należy zaznaczyć, że wyjmowanie drutów z kąpieli realizowana z jak największą szybkością (i przyspieszeniem), aby doprowadzić do jak najpełniejszego ścieknięcia resztek stali z drutu (w wyniku jej bezwładności). Na drutach zanurzanych w kąpieli metalowej na krótszy okres czasu (1 lub 2 sekundy) tworzyła się warstewka zakrzepłego żelaza pokrywająca wprowadzony druty również od spodu rys. 48 a i b. Na drutach wyciąganych po dłuższym czasie nadal widoczna była warstwa zakrzepłego żelaza, ale aluminium wyciekało z jej wnętrza podczas wyciągania drutu z kąpieli pozostawiając pustą rurkę rys. 48 c i d oraz rys. 49 a i b. Rysunek 49 dobrze ilustruje proces roztapiania się zakrzepłej warstwy żelaza po roztopieniu się aluminium. Proces ten zachodził szczególnie intensywnie w pobliżu końca drutu, co wynikało zapewne z oddziaływaniem na dużej powierzchni gorącej kąpieli mieszającej się z aluminium w tym miejscu. Drut, który przebywał najdłużej w roztopionym żelazie (5 sek.) rozgrzał się na tyle, że mimo stosowania wahań poziomu zanurzenia aluminium ponad zakrzepłą stalą uległo roztopieniu i w związku z tym zanurzona część druta pozostała w kąpieli. Górną część nadtopionego drutu aluminiowego przedstawiono na rys. 48 e. W związku z tym do wyznaczanie współczynnika wymiany ciepła możliwe było wykorzystanie danych z czterech prób. 97
98 a b c d e [s] Rys. 48. Stan drutów zanurzanych w ciekłym żelazie na różny okres czasu (od 1 do 5 sekund). Rys. 49. Końcówka drutu zanurzonego na 3 sekundy (a) i 4 sekundy (b). Wspomniane powyżej warunki wprowadzania drutów powodują, że założony czas pobytu w metalu odnosi się głównie do jego dolnej część. W związku z tym na rys. 48 widoczne jest zróżnicowanie grubości zakrzepłej na drucie warstwy żelaza. Należy przyjąć, że odcinek drutu, który w przybliżeniu przebywał w kąpieli przez okres czasu założony w harmonogramie prób to ostatnie kilka centymetrów. Sama końcówka drutu nie jest jednak reprezentatywna, ze względu na inny sposób wymiany ciepła (również od dołu) jak 98
99 też możliwość ściekania i gromadzenia się tam resztek roztopionego żelaza podczas wyjmowania drutu z kąpieli. W związku z tym pomiary wykonano w odległości 10 mm od końca drutu, przy czym jako koniec drutu uznawano miejsce w którym drut miał jeszcze pełny obwód (w przypadku widocznym na rys. 48 d nie wzięto pod uwagę resztkę zakrzepłej warstwy po prawej stronie drutu). Oględziny drutów po eksperymencie wykazały, że powstała na nich warstwa nie jest idealnie symetryczna. Występują miejsca o większej i mniejszej grubości. Jest to po części spowodowane tym, że sam drut też nie jest idealnie gładki, a po części może wynikać z nie idealnie pionowego wyciągania drutu z kąpieli. Można sądzić, że zjawisko to nie pojawia się wyłącznie w opisywanych tu eksperymentach, lecz jest często spotykane, czego dowodem jest przekroju drutu przedstawiony na rys. 5 [43] (strona 18). Z tego względu do porównania z wynikami obliczonymi przyjęto wartość średnią z 4 pomiarów przekroju z przesunięciem co 45 jak na rys. 50. Rys. 50. Sposób wykonywania czterech pomiarów średnicy drutu po wyjęciu z ciekłego żelaza, celem określenia grubości zakrzepłej na drucie warstewki stali. Do określenia grubości zakrzepłej na drucie warstewki stali konieczna była również dokładna znajomość średnicy drutu. Dokładne pomiary wykazały, że nie jest on idealnie symetryczny, a jego średnica jest nieco mniejsza niż 10 mm. Średnia z pomiarów wyniosła 9,8 mm, a zmierzone, według zasad przedstawionych na rys. 53, wartości wahały się od 9,7 do 9,9 mm. Na podstawie różnicy średnicy drutu przed wprowadzeniem do ciekłego metalu oraz średnicy drutu z zakrzepniętą na nim warstwą metalu obliczono średnią grubość powłoki zakrzepłego żelaza dla poszczególnych czasów zanurzenia. Wyniki pomiarów grubości warstwy zakrzepłej stali oraz przeprowadzonych obliczeń zamieszczono w tablicy 5. Dalsza część eksperymentu polegała na porównaniu wyników obliczeń numerycznych otrzymanych dla modelu laboratoryjnego, przy zastosowaniu różnych współczynników wymiany ciepła, z wynikami zamieszczonymi w tablicy 5. Obliczoną przez program grubość warstwy zakrzepłego żelaza na drucie dla różnych współczynników wymiany ciepła w zależności od czasu zanurzenia zamieszczono w tablicy 6. 99
100 Tablica 5. Wyniki pomiarów grubości warstewki zakrzepłego na drucie aluminiowym żelaza po różnym czasie przebywania drutu w ciekłym żelazie. Czas zanurzenia Zewnętrzna średnica warstewki zakrzepłej na drucie Pomiar nr Średnia z pomiarów Średnia grubość zakrzepłej warstwy [s] [mm] [mm] [mm] [mm] [mm] [mm] 1 10,5 10,5 10,5 10,4 10,48 0, ,8 11,4 11,9 12,0 11,78 0, ,2 13,1 13,3 13,1 13,18 1, ,6 13,8 13,6 13,5 13,63 1,91 Tablica 6. Obliczona grubość warstwy żelaza zakrzepłej na aluminiowym drucie przy różnych współczynnikach wymiany ciepła. Grubość zakrzepłej warstewki w [mm] przy Czas współczynniku: zanurzenia [s] [W/m 2 K] [W/m 2 K] [W/m 2 K] [W/m 2 K] 1 0 0,17 0,46 0, ,63 1,02 1,64 3 0,18 1,02 1,52 1,94 4 0,31 1,39 1,83 2,04 Wyniki obliczone i uzyskane w trakcie eksperymentu fizycznego zestawiono i przedstawiono graficznie w formie wykresu na rys. 51. Rys. 51. Obliczona i określona eksperymentalnie grubość zakrzepłej warstwy żelaza na drucie aluminiowym. 100
101 Jak wynika z wykresu współczynnik wymiany ciepła, który daje wyniki najbardziej zbliżone do rzeczywistości ma wartość ok W/m 2 K. Przebiegi wykresów wartości eksperymentalnych i obliczonych wzajemnie się przecinają. Taka charakterystyka sprawia, że dalsze poszukiwanie dokładniejszego dopasowania wydają się niecelowe. Przyrost grubości zakrzepłej warstwy w pierwszym okresie jest w rzeczywistości nieco szybszy niż wynika to z obliczeń, a później nieco wolniejszy, ale generalnie wartości eksperymentalne i obliczone są bardzo zbliżone. Należy też uwzględnić fakt że, druty były wprowadzane ręcznie i podane wartości sekund, na jakie druty zostały wprowadzone muszą być obarczone pewnym błędem. Szczególnie dotyczy to drutów zanurzonych na 1 sekundę, gdyż odchylenie od założonego czasu o zaledwie 0,2 sekundy stanowi błąd o wielkości 20%. Jednakże jak wynika z rys. 51 rezultat dla tego pomiaru pod względem odchylania od wartości obliczonej jest porównywalny z rezultatami dla 3 i 4 sekund zanurzenia w ciekłym metalu. W związku z tym wynik ten można uznać za wiarygodny. Celem pełniejszej oceny wiarygodności wyników symulacji porównano w miarę możliwości przebieg czasowy innych charakterystycznych zjawisk towarzyszących roztapianiu się drutu. Jak widać z rysunków 48 i 49 otwarcie od spodu zaszło w drutach przebywających w kąpieli metalowej 3 i więcej sekund. Druty przebywające krócej są zasklepione warstwą zakrzepłej stali. Na rys. 52 zamieszczono graficzne wyniki obliczeń z zastosowaniem współczynnika wymiany ciepła równego 3000 W/m 2 K obejmujące koniec drutu. a a czas zanurzenia 2 sekundy, b b czas zanurzenia 3 sekundy. Rys. 52. Graficzne wyniki obliczeń numerycznych roztapiania się drutu aluminiowego w ciekłym żelazie. Kolor niebieski faza stała, kolor biały faza ciekła. 101
102 Z rys. 52 wynika, że obliczenia symulacyjne dobrze odzwierciedlają to, co uzyskano w wyniku eksperymentu fizycznego. Po 2 sekundach (rys. 52 a) naroże końca drutu jest jeszcze pokryte warstewką zakrzepłego żelaza, co odpowiada wynikom rzeczywistymi przedstawionymi na rys. 48 b. Natomiast po 3 sekundach (rys. 52 b) naroże końca drutu jest już odsłonięte i ciekłe aluminium może wypływać pozostawiając pustą warstwę zakrzepłego żelaza jak na rys. 49. Wyniki wskazujące, że po ok. 2 sekundach grubość warstwy stali zakrzepłej na krawędzi drutu powinna być cienka jak na rys. 52a znalazło odzwierciedlenie w rzeczywistości. Jak wynika z obserwacji poczynionych podczas wstępnych prób wykonywanych celem opracowania metodyki pomiaru, po czasie ok. 2 sekund zdarzały się przypadki wypływu ciekłego aluminium na krawędzi, gdyż cienka warstwa zakrzepłego żelaza ulegała uszkodzeniu lub przetopieniu i w tym miejscu (na krawędzi) pojawiało się ciekłe aluminium rys. 53. Rys. 53. Końcówka drutu zanurzonego w kąpieli metalowej na ok. 2 sekundy (widoczny wyciek aluminium na krawędzi) Obliczenia numeryczne wykazały, że faktycznie aluminium roztapia się w drugiej sekundzie zanurzenia i po tym okresie czasu powinno być już roztopione rys. 54 (zwłaszcza przy końcu drutu, gdzie wymiana ciepła jest znacznie intensywniejsza). Należy zauważyć, że mimo roztopienia się aluminium warstewka żelaza nadal się powiększa, gdyż aluminium o temperaturze ok. 700 C ciągle oddziałuje chłodząco na otaczającą stal o temperaturze ok C. Podsumowując, z wykresu przedstawionego na rys. 51 wynika, że współczynnik wymiany ciepła ma zapewne wartość zbliżoną do 3000 W/m 2 K. Przemawia za tym również wysoka zgodność wyników eksperymentu fizycznego i numerycznego, odnośnie innych procesów towarzyszących roztapianiu się drutów aluminiowych - rys. 52, 53 i 54. Poszukiwanie bardziej dokładnej wartości, biorąc pod uwagę precyzję ręcznego regulowania czasu zanurzenia drutu, jak i zmienną jakość powierzchni drutu uznano za niecelowe. Sam przebieg wykresu na rys. 51 również nie skłania do dalszego precyzowania wartości współczynnika wymiany ciepła ze względu na to, że część punktów wyznaczonych doświadczalnie leży powyżej wartości obliczonych, a część poniżej. 102
103 a b c a czas zanurzenia 1 sek., b czas zanurzenia 2 sek., c czas zanurzenia 3 sekundy Rys 54. Przebieg narastania warstwy zakrzepłego żelaza i roztapiania się aluminium w zanurzanych drutach według obliczeń numerycznych (po lewej stronie drut, po prawej ciekłe żelazo - kolor ciemno niebieski faza stała). To czy ewentualne błędy szacowania współczynnika przejmowania ciepła będą miały istotne znaczenie dla rezultatów obliczeń modelowych określono na podstawie dodatkowych obliczeń z zastosowaniem współczynnika wymiany ciepła o wartości o 500 W/m 2 K większej oraz mniejszej od przyjętej wartości 3000 W/m 2 K. Rezultaty obliczeń, na modelu docelowym, opisanym w rozdziale 5, wykonane dla temperatury stali 1600 C i prędkości wprowadzania drutu 60, 90 i 120 m/min zamieszczone zostały w tablicy 7; głębokość (tak jak we wszystkich obliczeniach modelem docelowym) odczytywano z dokładnością do 1 cm. Z danych zamieszczonych w tablicy 7 wynika, że dla prędkości wprowadzania 60 m/min zastosowanie współczynnika większego o 500 W/m 2 K niż wyznaczona wartość 3000 W/m 2 K powoduje zmniejszenie wyliczonej głębokości na jakiej roztopi się drut o 9 cm, natomiast zmieszenie go o tę samą wartość spowoduje zwiększenie głębokości roztopienia drutu o 11 cm w stosunku do wartości wyjściowej. Są to różnice mniejsze niż wynikające ze zmiennej masy wytopu lub zużycia wymurówki. Można więc uznać, że możliwy błąd, wynikający z istoty zastosowanej metody eksperymentalnego wyznaczania współczynnika przejmowania ciepła (ręczne wprowadzanie drutów do kąpieli i ręczny pomiar czasu), nie powinien powodować istotnego zafałszowania wyników. Ponadto w miarę zwiększania prędkości wprowadzania drutu wrażliwość modelu na zmianę wartości współczynnika przejmowania ciepła spada i przy prędkości wprowadzania drutu 120 m/min błąd wyniesie nie więcej niż 5 cm jeżeli błąd współczynnika przejmowania ciepła nie przekroczy ± 500 W/m 2 K. 103
104 Tablica. 7. Wpływ zastosowanego współczynnika wymiany ciepła między drutem i zakrzepłą na nim warstwą stali na wyniki obliczeń modelowych dla drutu o średnicy 10 mm, temperatury stali 1600 C i różnej prędkości wprowadzania drutu. Prędkość wprowadzania drutu Zastosowany współczynniki przejmowania ciepła Czas roztapiania zakrzepłej na drucie warstwy stali Głębokość roztopienia drutu Różnica [m/min] W/m 2 K [s] [m] [m] ,200 2,20 0, ,090 2,09 0, ,000 2,00-0, ,900 2,85 0, ,847 2,77 0, ,807 2,71-0, ,775 3,55 0, ,750 3,50 0, ,730 3,46-0,04 W podobnych próbach szacowania wpływu współczynnika przejmowania ciepła, na wyniki obliczeń przedstawionych na rys. 55 [15] również stwierdzono że głębokość na jakiej roztopi się aluminium istotnie się różni dopiero dla szerokiego zakresu testowanych wartości, znacznie większych niż uwzględnione w tablicy 7. *) Wartości przeliczone z [cal/cm 2 s K] Rys. 55. Wpływ współczynnika przejmowania ciepła na obliczoną głębokość roztapiania drutu Al o średnicy 12 mm, przy przegrzaniu stali powyżej temperatury likwidus 50 C i prędkości wprowadzania 4 m/s [15]. 104
105 Wobec powyższego, na podstawie przeprowadzonych badań, można stwierdzić, że wartość współczynnika wymiany ciepła pomiędzy aluminiowym drutem wprowadzanym do ciekłego żelaza, a tym żelazem jest bliska 3000 W/m 2 K, a ewentualny błąd lezący w granicach ± 500 W/m 2 K nie powinien w istotny sposób wpłynąć na wyniki obliczeń. Taka też wielkość (3000 W/m 2 K) została przyjęta w dalszych numerycznych symulacyjnych roztapiania drutu aluminiowego wprowadzanego do stali niskowęglowej. Jest to wartość stosunkowo niska w kontekście przytoczonych w rozdziale 4.5. Biorąc jednak pod uwagę, że dotyczy ona współczynnika dla przemysłowego drutu z porowatą i pokrytą tlenkiem powierzchnią to wartość ta może być zbliżona do rzeczywistej wartości. W specjalnie konstruowanych, na potrzeby symulacji odwrotnej stanowiskach, powierzchnia jest zwykle znacznie lepszej jakości, a większe wymiary opomiarowanego elementu zanurzanego do kąpieli metalowej sprzyjają większym siłom związanym z rozszerzalnością cieplną i stąd podawane wartości mogą być większe. Natomiast w przypadku wymiany ciepła między krystalizatorem, a wlewkiem w procesie COS stosuje się wartości mniejsze, co też ma logiczne uzasadnienie (luźniejszy kontakt, zasypki smarujące) Pozornie model pomocniczy można by wykorzystać do określania głębokości, na jakiej roztopi się drut obliczając drogę, jaką przebędzie on przy danej prędkości wprowadzania w czasie potrzebnym do jego roztopienia się (aluminiowego rdzenia lub zakrzepłej warstwy - zależnie od przyjętego kryterium). W rzeczywistości problem jest bardziej skomplikowany gdyż według szeregu publikacji [15, 36, 40] na prędkość roztapiania istotnie wpływa prędkość wprowadzania drutu do metalu. Z tego względu wymagany jest model pełnowymiarowy. 7. Wyniki numerycznej symulacji roztapiania drutu aluminiowego wprowadzanego do ciekłej stali 7.1. Kryteria określania głębokości na jakiej roztopi się drut aluminiowy Wyznaczenie głębokości, na jakie roztopi się drut aluminiowy wymaga jednoznacznego określenia, co przez to pojecie będzie rozumiane. Jak wynika z informacji zamieszczonych we wcześniejszych rozdziałach, określenie roztapianie drutu aluminiowego w ciekłej stali to w rzeczywistości ogólny termin opisujący dwa procesy z których każdy może być uznany za wyznacznik określający zakończenie roztapiania drutu. Pierwszy proces, zwykle krótszy, to roztapianie się samego aluminium, czyli drutu właściwego, a drugi to roztopienie warstewki stali zakrzepłej na drucie, tworzącej się zaraz po wprowadzeniu go do kąpieli metalowej. Zdecydowanie się na konkretne kryterium powinno zależeć od celu, któremu ma służyć wyznaczany parametr. W przypadku operacji odtleniania stali drutem aluminiowym - biorąc pod uwagę, że roztopienie aluminium następuje wcześniej niż warstwa zakrzepłej stali - nie można jednoznacznie wskazać, na zjawisko będące jedynym parametrem wpływającym na głębokość uwolnienia aluminium do kąpieli metalowej. Gdyby w pierwszej kolejności roztapiała się zakrzepła warstwa jednoznacznym kryterium byłoby roztopienie się aluminium. W sytuacji, gdy pierwsze roztapia się aluminium, uwzględnić należy, że uwolnienie aluminium może zachodzić w wyniku roztopienia zakrzepłej warstwy lub też w wyniku fizycznego zniszczenia zakrzepłej warstwy, ale tylko w przypadku jego wcześniejszego roztopienia się i tym samym uwolnieniu roztopionego aluminium. Zniszczenie to nastąpi albo z powodu kolizji drutu z dnem kadzi, albo w wyniku działania sił 105
106 hydrodynamicznych. Sposób zniszczenia zdecyduje, czy aluminium uwolni się zaraz przy dnie, czy też połamane odcinki drutu będą na tyle długie by jakiś czas wypływać ku górze. Biorąc pod uwagę powyższe i przedstawione w rozdziałach 3 i 4 fakty należy przyjąć, że uwolnienie aluminium do kąpieli może przebiegać według różnych mechanizmów. 1. Drut, a właściwie zakrzepła na nim warstwa, roztopi się zanim osiągnie dno kadzi. W związku z tym, że aluminium roztapia się wcześniej niż zakrzepła na nim stal nastąpi uwolnienie ciekłego aluminium do kąpieli na głębokości zależnej od drogi jaką drut przebywa w czasie potrzebnym do roztopienie warstwy stali zakrzepłej na drucie. Ten przypadek zapewnia najbardziej stabilne warunki asymilacji aluminium. 2. Drut, a właściwie zakrzepła na nim warstwa, uderza w dno kadzi lub łamie się w wyniku sił hydrodynamicznych w momencie, gdy aluminiowy rdzeń uległ już roztopieniu (lub jest częściowo roztopiony), ale zakrzepła na nim warstwa stali nie uległa jeszcze roztopieniu. Wówczas w zależności od stanu zakrzepłej na drucie warstwy stali, i co za tym idzie sposobu jej zniszczenia, aluminium szybciej lub wolniej miesza się ze stalą. Jeżeli warstewka jest już cienka dojdzie do szybkiego uwolnienia aluminium przy dnie kadzi. Natomiast w sytuacji dotarcia drutu do dna, gdy warstwa ta jest jeszcze gruba może dochodzić do łamania się drutu na dłuższe odcinki, które będą samodzielnie wypływać w kierunku powierzchni, co wpłynie na znaczne zróżnicowanie miejsca uwolnienia aluminium. Może się też zdarzyć, że taki drut odbije się od dna kadzi i zacznie podążać ku górze. Taki mechanizm wydarzeń uwiarygodniają wyniki doświadczenia laboratoryjnego, które udowadnia, że warstewka po roztopieniu aluminium jest znacznej grubości i dopiero po pewnym czasie ulega osłabieniu sprzyjającemu miejscowym perforacjom lub uszkodzeniom mechanicznym. 3. Drut uderzy w dno kadzi w momencie, gdy nie roztopiło się jeszcze aluminium. Ten scenariusz może zachodzić przy wprowadzaniu drutu z dużą prędkością. W takich warunkach drut uderzy w dno kadzi i odbije się od tegoż dna wracając ku powierzchni kąpieli. Doprowadzi to do uwalniania się aluminium w drodze powrotnej drutu zgodnie ze mechanizmem pierwszym lub drugim, gdy uderzy on o ściany boczne kadzi. W tym mechanizmie scenariuszu proces uwalniania aluminium jest najmniej stabilny, a poruszanie się drutu w kadzi ma charakter stochastyczny. W związku z powyższym uznano, że celowym będzie rejestrowanie wszystkich istotnych zjawisk mogących wpływać na sposób przyswojenia aluminium. Podczas poszczególnych symulacji rejestrowano czas początku roztapiania się aluminium, końca roztapiania się aluminium i końca roztapiania się zakrzepłej na drucie warstewki stali. Skonfrontowanie wyników obliczeń z danymi przemysłowymi powinno dać odpowiedź na pytania odnośnie sposobu uwalniania aluminium. Między innymi powinny dać odpowiedź, czy zakrzepła na roztopionym drucie warstwa stali rozpada się w wyniku uderzenia w dno kadzi czy w skutek działania sił hydrodynamicznych, zwłaszcza, że wprowadzaniu drutu towarzyszy zwykle mieszanie stali argonem. 7.2 Warianty obliczeń roztapiania drutu aluminiowego w ciekłej stali Obliczenia symulacyjne wykonywano dla drutów aluminiowych o dwóch najczęściej spotykanych w krajowych stalowniach średnicach to znaczy 10 i 13 mm. Dla każdej z tych średnic obliczenia wykonano w trzech temperaturach 1570 C, 1600 C i 1630 C, co odpowiada przegrzaniu stali o ok. 40 C, 70 C i 100 C. Średnia temperatura wytopów 106
107 przemysłowych, które stanowiły materiał do weryfikacji wyników symulacji wynosiła 1596,4 C, a wartość minimalna i maksymalna wyniosły odpowiednio 1585 C i 1608 C. Tym samym w badanym zakresie mieściły się wszystkie analizowane wytopy przemysłowe, a także zdecydowana większość typowych wytopów przemysłowych poddawanych operacji odtleniania stali w kadzi drutem aluminiowym jakie są tam wykonywane. Dla każdej ze średnic i każdej temperatury wykonano obliczenia dla dziesięciu prędkości wprowadzania drutu, a mianowicie dla prędkości 60, 70, 80, 90, 100, 110, 120, 130, 140, i 150 m/min. Szczegóły znajdują się w tablicy 8. Tablica 8. Wykaz i numeracja poszczególnych wariantów obliczeń symulacyjnych. prędkość Średnica drutu [mm] wprowadzania Temperatura [ C] [m/min] Jak wynika z tablicy 8, wykonano w sumie obliczenia dla 60 wariantów operacji wprowadzania aluminiowego drutu do ciekłej stali. Po zakończeniu każdej symulacji wyniki odczytywano korzystając z interfejsu graficznego modułu postprocesora oprogramowania CalcoMOS. Wynik symulacji w formie graficznej jest prezentowany na ekranie monitora, a wyświetlana informacja zależy od wybranej opcji. Do określania czasu roztapiania się drutu stosowano opcję przedstawiającą rozkład fazy stałej i ciekłej w symulowanym obiekcie. Na ekranie można wyświetlać kolejne etapy procesu z krokiem czasowym wynikającym z zadanych wcześniej parametrów opisujących symulację. Obliczenia wykonywano z krokiem czasowym równym 0,1 sekundy. Wyniki odczytywano dopiero po osiągnięciu stanu ustalonego (gdy drutu przebył drogę równą wysokości modelu). Zwykle zajmowało to kilka sekund, ale dla zachowania marginesu bezpieczeństwa odczyt rozpoczynano po 15 sekundach obliczeń. Odczyt (np. grubości zakrzepłej warstwy lub głębokości danego miejsca) wykonywano poprzez wskazane odpowiedniego punktu na ekranie postprocesora wizualizującego wyniki symulacji kursorem myszki. W wyniku tego w lewym górnym rogu ekranu były wyświetlane współrzędne x i y danego punktu modelu w jednostkach zdefiniowanych podczas budowania modelu. Ekran postprocesora w trakcie odczytywania wyników obliczeń przedstawiono na rys. 56. Na ekranie widoczny jest drut w którym dobiegło końca roztapianie aluminium oraz pozostała warstwa zakrzepłej stali. 107
108 Rys. 56. Ekran roboczy modułu postprocesora programu CalcoMos do wizualizacji wyników obliczeń (po lewej stronie drut, po prawej ciekłe żelazo - kolor ciemno niebieski faza stała) Wyniki numerycznej symulacji roztapiania drutu aluminiowego w ciekłej stali Odczyt z ekranu postprocesora wyników obliczeń został poprzedzony ustaleniem jednoznacznych reguł interpretacji wyników. Kryterium do jednoznacznego i precyzyjnego określenia miejsca (głębokości kadzi) zachodzenia poszczególnych etapów roztapiania drutu były następujące zasady: - początek roztapiania aluminium poziom na którym dochodzi do pojawienia się w drucie pierwszego obszaru bez 100% udziału fazy stałej (rys. 57 miejsce zaznaczone czerwoną linią),, - koniec roztapiania aluminium poziom na którym dochodzi do zaniku ostatniego obszaru ze 100% udziałem fazy stałej w drucie (rys. 58 miejsce zaznaczone czerwoną linią), - koniec roztapiania warstewki zakrzepłej stali poziom na którym dochodzi do zaniku ostatniego obszaru ze 100% udziałem fazy stałej w warstewce zakrzepłej stali (rys. 59 miejsce zaznaczone czerwoną linią). 108
109 Rys. 57. Wizualizacja wyników symulacji pokazująca moment początku roztopienia się drutu aluminiowego (poziom zaznaczono czerwoną linią). Rys. 58. Wizualizacja wyników symulacji pokazująca moment całkowitego roztopienia się drutu aluminiowego (poziom zaznaczono czerwoną linią). 109
110 Rys. 59. Wizualizacja wyników symulacji pokazująca moment całkowitego roztopienia się warstewki zakrzepłej stali (poziom zaznaczono czerwoną linią). Wyniki odczytane z wizualizacji poszczególnych symulacji pozwalały określić odległość od powierzchni kąpieli metalowej (głębokość) poszczególnych zjawisk. Znając prędkość wprowadzania drutu można te wartości przeliczyć na czas po jakim dochodzi do danego zjawiska. Ponadto dysponując informacją o głębokości kąpieli w kadzi można również określić odległość od dna w jakiej dane zjawisko zaszło. Czas roztapiania się jest wartością bardziej uniwersalną, którą można wykorzystać w projektowaniu technologii w różnych stalowniach niezależnie od wielkości kadzi jaką dysponują. Jednakże docelowo powinien on być przeliczony na głębokość, gdyż to ona (a właściwie odległość od dna) jest miarodajnym parametrem oceny technologii. W związku z tym konieczne było określenie głębokości metalu w kadzi przemysłowej, która posłużyła do weryfikacji wyników obliczeń. Według rysunków technicznych kadzi ma ona całkowitą wysokość 3924 mm rys. 60. Po odliczeniu, na podstawie innych rysunków, grubości dna kadzi 560 mm, górnej strefy sfazowania wymurówki 86 mm i przyjmując wolną burtę na poziomie 100 mm można założyć, że głębokość metalu w takim przypadku wynosi 3184 mm. W rzeczywistych warunkach przemysłowych ta wielkość będzie się zmieniać ze względu na zużywanie się wymurówki kadzi oraz zmienną masę wytopów. Z obserwacji wynika, że kadź bywa napełniana tak, że wolna burta wynosi tylko mm lub też 200 mm (a nawet więcej, ale zdarza się to rzadko. To oznacza, że głębokość może się wahać od ok do ok mm. W związku z tym przyjęto, że przeciętna głębokość stali w kadzi wynosi 3200 mm. Dysponując modelem kadzi o głębokości 4000 mm można było (o ile dane zjawisko nie zaszło przed dotarciem drutu do dna kadzi) ocenić jak głęboko pod dnem kadzi zajdzie dane zjawisko; oczywiście pod warunkiem, że nie było to więcej niż wysokość modelu 4000 mm. Jest to istotna z poznawczego punktu widzenia informacja, gdyż w przypadku 110
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Zespół Szkół Samochodowych
 Zespół Szkół Samochodowych Podstawy Konstrukcji Maszyn Materiały Konstrukcyjne i Eksploatacyjne Temat: OTRZYMYWANIE STOPÓW ŻELAZA Z WĘGLEM. 2016-01-24 1 1. Stopy metali. 2. Odmiany alotropowe żelaza. 3.
Zespół Szkół Samochodowych Podstawy Konstrukcji Maszyn Materiały Konstrukcyjne i Eksploatacyjne Temat: OTRZYMYWANIE STOPÓW ŻELAZA Z WĘGLEM. 2016-01-24 1 1. Stopy metali. 2. Odmiany alotropowe żelaza. 3.
KRYSTALIZACJA METALI I STOPÓW. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 KRYSTALIZACJA METALI I STOPÓW Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Krzepnięcie przemiana fazy ciekłej w fazę stałą Krystalizacja przemiana
KRYSTALIZACJA METALI I STOPÓW Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Krzepnięcie przemiana fazy ciekłej w fazę stałą Krystalizacja przemiana
Ćwiczenie 1: Wyznaczanie warunków odporności, korozji i pasywności metali
 Ćwiczenie 1: Wyznaczanie warunków odporności, korozji i pasywności metali Wymagane wiadomości Podstawy korozji elektrochemicznej, wykresy E-pH. Wprowadzenie Główną przyczyną zniszczeń materiałów metalicznych
Ćwiczenie 1: Wyznaczanie warunków odporności, korozji i pasywności metali Wymagane wiadomości Podstawy korozji elektrochemicznej, wykresy E-pH. Wprowadzenie Główną przyczyną zniszczeń materiałów metalicznych
STATYCZNA PRÓBA ROZCIĄGANIA
 Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: STATYCZNA PRÓBA ROZCIĄGANIA oprac. dr inż. Jarosław Filipiak Cel ćwiczenia 1. Zapoznanie się ze sposobem przeprowadzania statycznej
Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: STATYCZNA PRÓBA ROZCIĄGANIA oprac. dr inż. Jarosław Filipiak Cel ćwiczenia 1. Zapoznanie się ze sposobem przeprowadzania statycznej
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej
 Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ
 WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ Instrukcja do ćwiczenia T-06 Temat: Wyznaczanie zmiany entropii ciała
WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ Instrukcja do ćwiczenia T-06 Temat: Wyznaczanie zmiany entropii ciała
Brykietowany środek do upłynniania żużli rafinacyjnych (brykietowany żużel syntetyczny)
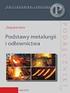 Brykietowany środek do upłynniania żużli rafinacyjnych (brykietowany żużel syntetyczny) Brykietowany środek do upłynniania żużli rafinacyjnych został wyprodukowany z mieszanki proszku korundowego, dolomitu
Brykietowany środek do upłynniania żużli rafinacyjnych (brykietowany żużel syntetyczny) Brykietowany środek do upłynniania żużli rafinacyjnych został wyprodukowany z mieszanki proszku korundowego, dolomitu
Naprężenia i odkształcenia spawalnicze
 Naprężenia i odkształcenia spawalnicze Cieplno-mechaniczne właściwości metali i stopów Parametrami, które określają stan mechaniczny metalu w różnych temperaturach, są: - moduł sprężystości podłużnej E,
Naprężenia i odkształcenia spawalnicze Cieplno-mechaniczne właściwości metali i stopów Parametrami, które określają stan mechaniczny metalu w różnych temperaturach, są: - moduł sprężystości podłużnej E,
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
(12) OPIS PATENTOWY (19) PL (11) (13) B1
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 166501 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 294586 (22) Data zgłoszenia: 14.05.1992 (51) IntCl6: B22D 27/13 B22D
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 166501 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 294586 (22) Data zgłoszenia: 14.05.1992 (51) IntCl6: B22D 27/13 B22D
OBRÓBKA CIEPLNA STOPÓW ŻELAZA. Cz. II. Przemiany austenitu przechłodzonego
 OBRÓBKA CIEPLNA STOPÓW ŻELAZA Cz. II. Przemiany austenitu przechłodzonego WPŁYW CHŁODZENIA NA PRZEMIANY AUSTENITU Ar 3, Ar cm, Ar 1 temperatury przy chłodzeniu, niższe od równowagowych A 3, A cm, A 1 A
OBRÓBKA CIEPLNA STOPÓW ŻELAZA Cz. II. Przemiany austenitu przechłodzonego WPŁYW CHŁODZENIA NA PRZEMIANY AUSTENITU Ar 3, Ar cm, Ar 1 temperatury przy chłodzeniu, niższe od równowagowych A 3, A cm, A 1 A
1. Wprowadzenie: dt q = - λ dx. q = lim F
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy i Eksploatacji Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA PRZEWODNOŚCI
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy i Eksploatacji Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA PRZEWODNOŚCI
NAGRZEWANIE WSADU STALOWEGO
 NAGRZEWANIE WSADU STALOWEGO Ważnym tematem prowadzonym w Katedrze są badania utleniania stali kierowane przez Prof. M. Kielocha. Z tego zakresu wykonano kilkanaście prac badawczych i opublikowano ponad
NAGRZEWANIE WSADU STALOWEGO Ważnym tematem prowadzonym w Katedrze są badania utleniania stali kierowane przez Prof. M. Kielocha. Z tego zakresu wykonano kilkanaście prac badawczych i opublikowano ponad
Oddziaływanie wirnika
 Oddziaływanie wirnika W każdej maszynie prądu stałego, pracującej jako prądnica lub silnik, może wystąpić taki szczególny stan pracy, że prąd wirnika jest równy zeru. Jedynym przepływem jest wówczas przepływ
Oddziaływanie wirnika W każdej maszynie prądu stałego, pracującej jako prądnica lub silnik, może wystąpić taki szczególny stan pracy, że prąd wirnika jest równy zeru. Jedynym przepływem jest wówczas przepływ
Sonochemia. Schemat 1. Strefy reakcji. Rodzaje efektów sonochemicznych. Oscylujący pęcherzyk gazu. Woda w stanie nadkrytycznym?
 Schemat 1 Strefy reakcji Rodzaje efektów sonochemicznych Oscylujący pęcherzyk gazu Woda w stanie nadkrytycznym? Roztwór Znaczne gradienty ciśnienia Duże siły hydrodynamiczne Efekty mechanochemiczne Reakcje
Schemat 1 Strefy reakcji Rodzaje efektów sonochemicznych Oscylujący pęcherzyk gazu Woda w stanie nadkrytycznym? Roztwór Znaczne gradienty ciśnienia Duże siły hydrodynamiczne Efekty mechanochemiczne Reakcje
Politechnika Białostocka INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH. Doświadczalne sprawdzenie zasady superpozycji
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Doświadczalne sprawdzenie zasady superpozycji Numer ćwiczenia: 8 Laboratorium
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Doświadczalne sprawdzenie zasady superpozycji Numer ćwiczenia: 8 Laboratorium
11. PRZEBIEG OBRÓBKI CIEPLNEJ PREFABRYKATÓW BETONOWYCH
 11. Przebieg obróbki cieplnej prefabrykatów betonowych 1 11. PRZEBIEG OBRÓBKI CIEPLNEJ PREFABRYKATÓW BETONOWYCH 11.1. Schemat obróbki cieplnej betonu i konsekwencje z niego wynikające W rozdziale 6 wskazano
11. Przebieg obróbki cieplnej prefabrykatów betonowych 1 11. PRZEBIEG OBRÓBKI CIEPLNEJ PREFABRYKATÓW BETONOWYCH 11.1. Schemat obróbki cieplnej betonu i konsekwencje z niego wynikające W rozdziale 6 wskazano
Funkcjonalność urządzeń pomiarowych w PyroSim. Jakich danych nam dostarczają?
 Funkcjonalność urządzeń pomiarowych w PyroSim. Jakich danych nam dostarczają? Wstęp Program PyroSim zawiera obszerną bazę urządzeń pomiarowych. Odczytywane z nich dane stanowią bogate źródło informacji
Funkcjonalność urządzeń pomiarowych w PyroSim. Jakich danych nam dostarczają? Wstęp Program PyroSim zawiera obszerną bazę urządzeń pomiarowych. Odczytywane z nich dane stanowią bogate źródło informacji
Odwracalność przemiany chemicznej
 Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego
 Politechnika Częstochowska Katedra Inżynierii Energii NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego dr hab. inż. Zbigniew BIS, prof P.Cz. dr inż. Robert ZARZYCKI Wstęp
Politechnika Częstochowska Katedra Inżynierii Energii NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego dr hab. inż. Zbigniew BIS, prof P.Cz. dr inż. Robert ZARZYCKI Wstęp
PRZECIWZUŻYCIOWE POWŁOKI CERAMICZNO-METALOWE NANOSZONE NA ELEMENT SILNIKÓW SPALINOWYCH
 PRZECIWZUŻYCIOWE POWŁOKI CERAMICZNO-METALOWE NANOSZONE NA ELEMENT SILNIKÓW SPALINOWYCH AUTOR: Michał Folwarski PROMOTOR PRACY: Dr inż. Marcin Kot UCZELNIA: Akademia Górniczo-Hutnicza Im. Stanisława Staszica
PRZECIWZUŻYCIOWE POWŁOKI CERAMICZNO-METALOWE NANOSZONE NA ELEMENT SILNIKÓW SPALINOWYCH AUTOR: Michał Folwarski PROMOTOR PRACY: Dr inż. Marcin Kot UCZELNIA: Akademia Górniczo-Hutnicza Im. Stanisława Staszica
LABORATORIUM PODSTAW BUDOWY URZĄDZEŃ DLA PROCESÓW MECHANICZNYCH
 LABORATORIUM PODSTAW BUDOWY URZĄDZEŃ DLA PROCESÓW MECHANICZNYCH Temat: Badanie cyklonu ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZIAŁ BMiP 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie
LABORATORIUM PODSTAW BUDOWY URZĄDZEŃ DLA PROCESÓW MECHANICZNYCH Temat: Badanie cyklonu ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZIAŁ BMiP 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA
 METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
Politechnika Białostocka INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Zwykła próba rozciągania stali Numer ćwiczenia: 1 Laboratorium z przedmiotu:
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Zwykła próba rozciągania stali Numer ćwiczenia: 1 Laboratorium z przedmiotu:
DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA
 71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
Okres realizacji projektu: r r.
 PROJEKT: Wykorzystanie modułowych systemów podawania i mieszania materiałów proszkowych na przykładzie linii technologicznej do wytwarzania katod w bateriach termicznych wraz z systemem eksperckim doboru
PROJEKT: Wykorzystanie modułowych systemów podawania i mieszania materiałów proszkowych na przykładzie linii technologicznej do wytwarzania katod w bateriach termicznych wraz z systemem eksperckim doboru
PROCEDURA DOBORU POMP DLA PRZEMYSŁU CUKROWNICZEGO
 PROCEDURA DOBORU POMP DLA PRZEMYSŁU CUKROWNICZEGO Wskazujemy podstawowe wymagania jakie muszą być spełnione dla prawidłowego doboru pompy, w tym: dobór układu konstrukcyjnego pompy, parametry pompowanego
PROCEDURA DOBORU POMP DLA PRZEMYSŁU CUKROWNICZEGO Wskazujemy podstawowe wymagania jakie muszą być spełnione dla prawidłowego doboru pompy, w tym: dobór układu konstrukcyjnego pompy, parametry pompowanego
STRUKTURA STOPÓW UKŁADY RÓWNOWAGI FAZOWEJ. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 STRUKTURA STOPÓW UKŁADY RÓWNOWAGI FAZOWEJ Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Wykresy układów równowagi faz stopowych Ilustrują skład fazowy
STRUKTURA STOPÓW UKŁADY RÓWNOWAGI FAZOWEJ Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Wykresy układów równowagi faz stopowych Ilustrują skład fazowy
Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA
 Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA PRZEDMIOT: INŻYNIERIA WARSTWY WIERZCHNIEJ Temat ćwiczenia: Badanie prędkości zużycia materiałów
Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA PRZEDMIOT: INŻYNIERIA WARSTWY WIERZCHNIEJ Temat ćwiczenia: Badanie prędkości zużycia materiałów
WPŁYW ZAKŁÓCEŃ PROCESU WZBOGACANIA WĘGLA W OSADZARCE NA ZMIANY GĘSTOŚCI ROZDZIAŁU BADANIA LABORATORYJNE
 Górnictwo i Geoinżynieria Rok 33 Zeszyt 4 2009 Stanisław Cierpisz*, Daniel Kowol* WPŁYW ZAKŁÓCEŃ PROCESU WZBOGACANIA WĘGLA W OSADZARCE NA ZMIANY GĘSTOŚCI ROZDZIAŁU BADANIA LABORATORYJNE 1. Wstęp Zasadniczym
Górnictwo i Geoinżynieria Rok 33 Zeszyt 4 2009 Stanisław Cierpisz*, Daniel Kowol* WPŁYW ZAKŁÓCEŃ PROCESU WZBOGACANIA WĘGLA W OSADZARCE NA ZMIANY GĘSTOŚCI ROZDZIAŁU BADANIA LABORATORYJNE 1. Wstęp Zasadniczym
WPŁYW DODATKÓW STOPOWYCH NA WŁASNOŚCI STOPU ALUMINIUM KRZEM O NADEUTEKTYCZNYM SKŁADZIE
 WYDZIAŁ ODLEWNICTWA AGH Oddział Krakowski STOP XXXIV KONFERENCJA NAUKOWA Kraków - 19 listopada 2010 r. Marcin PIĘKOŚ 1, Stanisław RZADKOSZ 2, Janusz KOZANA 3,Witold CIEŚLAK 4 WPŁYW DODATKÓW STOPOWYCH NA
WYDZIAŁ ODLEWNICTWA AGH Oddział Krakowski STOP XXXIV KONFERENCJA NAUKOWA Kraków - 19 listopada 2010 r. Marcin PIĘKOŚ 1, Stanisław RZADKOSZ 2, Janusz KOZANA 3,Witold CIEŚLAK 4 WPŁYW DODATKÓW STOPOWYCH NA
Optymalizacja wież stalowych
 Optymalizacja wież stalowych W przypadku wież stalowych jednym z najistotniejszych elementów jest ustalenie obciążenia wiatrem. Generalnie jest to zagadnienie skomplikowane, gdyż wiąże się z koniecznością
Optymalizacja wież stalowych W przypadku wież stalowych jednym z najistotniejszych elementów jest ustalenie obciążenia wiatrem. Generalnie jest to zagadnienie skomplikowane, gdyż wiąże się z koniecznością
Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra Urządzeń Elektrycznych i Techniki Wysokich Napięć. Dr hab.
 Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra Urządzeń Elektrycznych i Techniki Wysokich Napięć Dr hab. Paweł Żukowski Materiały magnetyczne Właściwości podstawowych materiałów magnetycznych
Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra Urządzeń Elektrycznych i Techniki Wysokich Napięć Dr hab. Paweł Żukowski Materiały magnetyczne Właściwości podstawowych materiałów magnetycznych
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów
 Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
XIXOLIMPIADA FIZYCZNA (1969/1970). Stopień W, zadanie doświadczalne D.. Znaleźć doświadczalną zależność T od P. Rys. 1
 KOOF Szczecin: www.of.szc.pl XIXOLIMPIADA FIZYCZNA (1969/197). Stopień W, zadanie doświadczalne D. Źródło: Olimpiady fizyczne XIX i XX Autor: Waldemar Gorzkowski Nazwa zadania: Drgania gumy. Działy: Drgania
KOOF Szczecin: www.of.szc.pl XIXOLIMPIADA FIZYCZNA (1969/197). Stopień W, zadanie doświadczalne D. Źródło: Olimpiady fizyczne XIX i XX Autor: Waldemar Gorzkowski Nazwa zadania: Drgania gumy. Działy: Drgania
Wskaźnik szybkości płynięcia termoplastów
 Katedra Technologii Polimerów Przedmiot: Inżynieria polimerów Ćwiczenie laboratoryjne: Wskaźnik szybkości płynięcia termoplastów Wskaźnik szybkości płynięcia Wielkością która charakteryzuje prędkości płynięcia
Katedra Technologii Polimerów Przedmiot: Inżynieria polimerów Ćwiczenie laboratoryjne: Wskaźnik szybkości płynięcia termoplastów Wskaźnik szybkości płynięcia Wielkością która charakteryzuje prędkości płynięcia
ZAMRAŻANIE PODSTAWY CZ.2
 METODY PRZECHOWYWANIA I UTRWALANIA BIOPRODUKTÓW ZAMRAŻANIE PODSTAWY CZ.2 Opracował: dr S. Wierzba Katedra Biotechnologii i Biologii Molekularnej Uniwersytetu Opolskiego Odmienność procesów zamrażania produktów
METODY PRZECHOWYWANIA I UTRWALANIA BIOPRODUKTÓW ZAMRAŻANIE PODSTAWY CZ.2 Opracował: dr S. Wierzba Katedra Biotechnologii i Biologii Molekularnej Uniwersytetu Opolskiego Odmienność procesów zamrażania produktów
Skraplanie czynnika chłodniczego R404A w obecności gazu inertnego. Autor: Tadeusz BOHDAL, Henryk CHARUN, Robert MATYSKO Środa, 06 Czerwiec :42
 Przeprowadzono badania eksperymentalne procesu skraplania czynnika chłodniczego R404A w kanale rurowym w obecności gazu inertnego powietrza. Wykazano negatywny wpływ zawartości powietrza w skraplaczu na
Przeprowadzono badania eksperymentalne procesu skraplania czynnika chłodniczego R404A w kanale rurowym w obecności gazu inertnego powietrza. Wykazano negatywny wpływ zawartości powietrza w skraplaczu na
OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI
 Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
Nowa ekologiczna metoda wykonywania odlewów z żeliwa sferoidyzowanego lub wermikularyzowanego w formie odlewniczej
 PROJEKT NR: POIG.01.03.01-12-061/08 Badania i rozwój nowoczesnej technologii tworzyw odlewniczych odpornych na zmęczenie cieplne Nowa ekologiczna metoda wykonywania odlewów z żeliwa sferoidyzowanego lub
PROJEKT NR: POIG.01.03.01-12-061/08 Badania i rozwój nowoczesnej technologii tworzyw odlewniczych odpornych na zmęczenie cieplne Nowa ekologiczna metoda wykonywania odlewów z żeliwa sferoidyzowanego lub
INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH
 INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH BADANIE ZACHOWANIA SIĘ MATERIAŁÓW PODCZAS ŚCISKANIA Instrukcja przeznaczona jest dla studentów
INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH BADANIE ZACHOWANIA SIĘ MATERIAŁÓW PODCZAS ŚCISKANIA Instrukcja przeznaczona jest dla studentów
PODSTAWY OBLICZEŃ CHEMICZNYCH.. - należy podać schemat obliczeń (skąd się biorą konkretne podstawienia do wzorów?)
 Korozja chemiczna PODSTAWY OBLICZEŃ CHEMICZNYCH.. - należy podać schemat obliczeń (skąd się biorą konkretne podstawienia do wzorów?) 1. Co to jest stężenie molowe? (co reprezentuje jednostka/ metoda obliczania/
Korozja chemiczna PODSTAWY OBLICZEŃ CHEMICZNYCH.. - należy podać schemat obliczeń (skąd się biorą konkretne podstawienia do wzorów?) 1. Co to jest stężenie molowe? (co reprezentuje jednostka/ metoda obliczania/
INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH
 INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH BADANIE ZACHOWANIA SIĘ MATERIAŁÓW PODCZAS ŚCISKANIA Instrukcja przeznaczona jest dla studentów
INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH BADANIE ZACHOWANIA SIĘ MATERIAŁÓW PODCZAS ŚCISKANIA Instrukcja przeznaczona jest dla studentów
NUMERYCZNA SYMULACJA ROZTAPIANIA DRUTÓW ALUMINIOWYCH WPROWADZANYCH DO CIEKŁEJ STALI
 Prace IMŻ 1 (12) 179 Mariusz BORECKI Instytut Metalurgii Żelaza im. St. Staszica NUMERYCZNA SYMULACJA ROZTAPIANIA DRUTÓW ALUMINIOWYCH WPROWADZANYCH DO CIEKŁEJ STALI Przedstawiono wyniki numerycznej symulacji
Prace IMŻ 1 (12) 179 Mariusz BORECKI Instytut Metalurgii Żelaza im. St. Staszica NUMERYCZNA SYMULACJA ROZTAPIANIA DRUTÓW ALUMINIOWYCH WPROWADZANYCH DO CIEKŁEJ STALI Przedstawiono wyniki numerycznej symulacji
NAGRZEWANIE ELEKTRODOWE
 INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia Nr 7 NAGRZEWANIE ELEKTRODOWE 1.WPROWADZENIE. Nagrzewanie elektrodowe jest to nagrzewanie elektryczne oparte na wydzielaniu, ciepła przy przepływie
INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia Nr 7 NAGRZEWANIE ELEKTRODOWE 1.WPROWADZENIE. Nagrzewanie elektrodowe jest to nagrzewanie elektryczne oparte na wydzielaniu, ciepła przy przepływie
WIROWYCH. Ćwiczenie: ĆWICZENIE BADANIE PRĄDÓW ZAKŁ AD ELEKTROENERGETYKI. Opracował: mgr inż. Edward SKIEPKO. Warszawa 2000
 SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ KATEDRA TECHNIKI POŻARNICZEJ ZAKŁ AD ELEKTROENERGETYKI Ćwiczenie: ĆWICZENIE BADANIE PRĄDÓW WIROWYCH Opracował: mgr inż. Edward SKIEPKO Warszawa 000 Wersja 1.0 www.labenergetyki.prv.pl
SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ KATEDRA TECHNIKI POŻARNICZEJ ZAKŁ AD ELEKTROENERGETYKI Ćwiczenie: ĆWICZENIE BADANIE PRĄDÓW WIROWYCH Opracował: mgr inż. Edward SKIEPKO Warszawa 000 Wersja 1.0 www.labenergetyki.prv.pl
Sieci obliczeniowe poprawny dobór i modelowanie
 Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
Ć w i c z e n i e K 4
 Akademia Górniczo Hutnicza Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji Nazwisko i Imię: Nazwisko i Imię: Wydział Górnictwa i Geoinżynierii Grupa
Akademia Górniczo Hutnicza Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji Nazwisko i Imię: Nazwisko i Imię: Wydział Górnictwa i Geoinżynierii Grupa
POLITECHNIKA BIAŁOSTOCKA
 POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II
 TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II Czas trwania testu 120 minut Informacje 1. Proszę sprawdzić czy arkusz zawiera 10 stron. Ewentualny brak należy zgłosić nauczycielowi. 2. Proszę rozwiązać
TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II Czas trwania testu 120 minut Informacje 1. Proszę sprawdzić czy arkusz zawiera 10 stron. Ewentualny brak należy zgłosić nauczycielowi. 2. Proszę rozwiązać
Metoda Elementów Skończonych
 Projekt Metoda Elementów Skończonych w programie COMSOL Multiphysics 3.4 Wykonali: Helak Bartłomiej Kruszewski Jacek Wydział, kierunek, specjalizacja, semestr, rok: BMiZ, MiBM, KMU, VII, 2011-2012 Prowadzący:
Projekt Metoda Elementów Skończonych w programie COMSOL Multiphysics 3.4 Wykonali: Helak Bartłomiej Kruszewski Jacek Wydział, kierunek, specjalizacja, semestr, rok: BMiZ, MiBM, KMU, VII, 2011-2012 Prowadzący:
Wykład 8. Przemiany zachodzące w stopach żelaza z węglem. Przemiany zachodzące podczas nagrzewania
 Wykład 8 Przemiany zachodzące w stopach żelaza z węglem Przemiany zachodzące podczas nagrzewania Nagrzewanie stopów żelaza powyżej temperatury 723 O C powoduje rozpoczęcie przemiany perlitu w austenit
Wykład 8 Przemiany zachodzące w stopach żelaza z węglem Przemiany zachodzące podczas nagrzewania Nagrzewanie stopów żelaza powyżej temperatury 723 O C powoduje rozpoczęcie przemiany perlitu w austenit
GRAWITACYJNE ZAGĘSZCZANIE OSADÓW
 PRZERÓBKA I UNIESZKODLIWIANIE OSADÓW ŚCIEKOWYCH Ćwiczenie nr 4 GRAWITACYJNE ZAGĘSZCZANIE OSADÓW 1. CHARAKTERYSTYKA PROCESU Proces zagęszczania osadów, który polega na rozdziale fazy stałej od ciekłej przy
PRZERÓBKA I UNIESZKODLIWIANIE OSADÓW ŚCIEKOWYCH Ćwiczenie nr 4 GRAWITACYJNE ZAGĘSZCZANIE OSADÓW 1. CHARAKTERYSTYKA PROCESU Proces zagęszczania osadów, który polega na rozdziale fazy stałej od ciekłej przy
Wyboczenie ściskanego pręta
 Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ
 Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
EGZAMIN POTWIERDZAJĄCY KWALIFIKACJE W ZAWODZIE Rok 2017 CZĘŚĆ PRAKTYCZNA
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 216 Nazwa kwalifikacji: Organizacja i prowadzenie procesów metalurgicznych oraz obróbki plastycznej metali
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 216 Nazwa kwalifikacji: Organizacja i prowadzenie procesów metalurgicznych oraz obróbki plastycznej metali
RECENZJA. Prof. dr hab. inż. Zdzisław Kudliński. Katowice, dn
 Katowice, dn. 30.08.2013 Prof. dr hab. inż. Zdzisław Kudliński Katedra Metalurgii Wydział Inżynierii Materiałowej i Metalurgii Politechniki Śląskiej ul. Krasińskiego 8 40-019 Katowice RECENZJA pracy doktorskiej
Katowice, dn. 30.08.2013 Prof. dr hab. inż. Zdzisław Kudliński Katedra Metalurgii Wydział Inżynierii Materiałowej i Metalurgii Politechniki Śląskiej ul. Krasińskiego 8 40-019 Katowice RECENZJA pracy doktorskiej
CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU.
 CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU. Projekt zrealizowany w ramach Mazowieckiego programu stypendialnego dla uczniów szczególnie uzdolnionych
CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU. Projekt zrealizowany w ramach Mazowieckiego programu stypendialnego dla uczniów szczególnie uzdolnionych
Ćwiczenie laboratoryjne Parcie wody na stopę fundamentu
 Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
Karta (sylabus) modułu/przedmiotu [Inżynieria Materiałowa] Studia I stopnia
![Karta (sylabus) modułu/przedmiotu [Inżynieria Materiałowa] Studia I stopnia Karta (sylabus) modułu/przedmiotu [Inżynieria Materiałowa] Studia I stopnia](/thumbs/55/37776790.jpg) Karta (sylabus) modułu/przedmiotu [Inżynieria Materiałowa] Studia I stopnia Przedmiot: Metalurgia i technologie odlewnicze Rodzaj przedmiotu: Obowiązkowy Kod przedmiotu: IM 1 N 0 6-0_0 Rok: I Semestr:
Karta (sylabus) modułu/przedmiotu [Inżynieria Materiałowa] Studia I stopnia Przedmiot: Metalurgia i technologie odlewnicze Rodzaj przedmiotu: Obowiązkowy Kod przedmiotu: IM 1 N 0 6-0_0 Rok: I Semestr:
Technologie wytwarzania. Opracował Dr inż. Stanisław Rymkiewicz KIM WM PG
 Technologie wytwarzania Opracował Dr inż. Stanisław Rymkiewicz KIM WM PG Technologie wytwarzania Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki
Technologie wytwarzania Opracował Dr inż. Stanisław Rymkiewicz KIM WM PG Technologie wytwarzania Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki
lim Np. lim jest wyrażeniem typu /, a
 Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Ruch drgający i falowy
 Ruch drgający i falowy 1. Ruch harmoniczny 1.1. Pojęcie ruchu harmonicznego Jednym z najbardziej rozpowszechnionych ruchów w mechanice jest ruch ciała drgającego. Przykładem takiego ruchu może być ruch
Ruch drgający i falowy 1. Ruch harmoniczny 1.1. Pojęcie ruchu harmonicznego Jednym z najbardziej rozpowszechnionych ruchów w mechanice jest ruch ciała drgającego. Przykładem takiego ruchu może być ruch
Temat: NAROST NA OSTRZU NARZĘDZIA
 AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technologii Maszyn i Automatyzacji Ćwiczenie wykonano: dnia:... Wykonał:... Wydział:... Kierunek:... Rok akadem.:... Semestr:... Ćwiczenie zaliczono:
AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technologii Maszyn i Automatyzacji Ćwiczenie wykonano: dnia:... Wykonał:... Wydział:... Kierunek:... Rok akadem.:... Semestr:... Ćwiczenie zaliczono:
1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru
 1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru Wzór związku chemicznego podaje jakościowy jego skład z jakich pierwiastków jest zbudowany oraz liczbę atomów poszczególnych pierwiastków
1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru Wzór związku chemicznego podaje jakościowy jego skład z jakich pierwiastków jest zbudowany oraz liczbę atomów poszczególnych pierwiastków
Kryteria oceniania z chemii kl VII
 Kryteria oceniania z chemii kl VII Ocena dopuszczająca -stosuje zasady BHP w pracowni -nazywa sprzęt laboratoryjny i szkło oraz określa ich przeznaczenie -opisuje właściwości substancji używanych na co
Kryteria oceniania z chemii kl VII Ocena dopuszczająca -stosuje zasady BHP w pracowni -nazywa sprzęt laboratoryjny i szkło oraz określa ich przeznaczenie -opisuje właściwości substancji używanych na co
LIV OLIMPIADA FIZYCZNA 2004/2005 Zawody II stopnia
 LIV OLIMPIADA FIZYCZNA 004/005 Zawody II stopnia Zadanie doświadczalne Masz do dyspozycji: cienki drut z niemagnetycznego metalu, silny magnes stały, ciężarek o masie m=(100,0±0,5) g, statyw, pręty stalowe,
LIV OLIMPIADA FIZYCZNA 004/005 Zawody II stopnia Zadanie doświadczalne Masz do dyspozycji: cienki drut z niemagnetycznego metalu, silny magnes stały, ciężarek o masie m=(100,0±0,5) g, statyw, pręty stalowe,
MODEL FIZYCZNY KONWERTORA TLENOWEGO Z DMUCHEM KOMBINOWANYM. Jacek Pieprzyca, Grzegorz Perzyński
 MODEL FIZYCZNY KONWERTORA TLENOWEGO Z DMUCHEM KOMBINOWANYM. Jacek Pieprzyca, Grzegorz Perzyński Katedra Metalurgii Politechniki Śląskiej, Katowice, Poland Abstrakt W pracy przedstawiono przeprowadzoną
MODEL FIZYCZNY KONWERTORA TLENOWEGO Z DMUCHEM KOMBINOWANYM. Jacek Pieprzyca, Grzegorz Perzyński Katedra Metalurgii Politechniki Śląskiej, Katowice, Poland Abstrakt W pracy przedstawiono przeprowadzoną
Konferencja. Ograniczanie strat energii w elektroenergetycznych liniach przesyłowych w wyniku zastosowania nowych nisko-stratnych przewodów
 Konferencja Elektroenergetyczne linie napowietrzne i kablowe wysokich i najwyższych napięć Wisła, 18-19 października 2017 Ograniczanie strat energii w elektroenergetycznych liniach przesyłowych w wyniku
Konferencja Elektroenergetyczne linie napowietrzne i kablowe wysokich i najwyższych napięć Wisła, 18-19 października 2017 Ograniczanie strat energii w elektroenergetycznych liniach przesyłowych w wyniku
Laboratorium. Hydrostatyczne Układy Napędowe
 Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
KONSTRUKCJE METALOWE - LABORATORIUM. Produkcja i budowa stali
 KONSTRUKCJE METALOWE - LABORATORIUM Produkcja i budowa stali Produkcja stali ŻELAZO (Fe) - pierwiastek chemiczny, w stanie czystym miękki i plastyczny metal o niezbyt dużej wytrzymałości STAL - stop żelaza
KONSTRUKCJE METALOWE - LABORATORIUM Produkcja i budowa stali Produkcja stali ŻELAZO (Fe) - pierwiastek chemiczny, w stanie czystym miękki i plastyczny metal o niezbyt dużej wytrzymałości STAL - stop żelaza
W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych:
 W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych: Zmienne losowe skokowe (dyskretne) przyjmujące co najwyżej przeliczalnie wiele wartości Zmienne losowe ciągłe
W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych: Zmienne losowe skokowe (dyskretne) przyjmujące co najwyżej przeliczalnie wiele wartości Zmienne losowe ciągłe
Nauka o Materiałach. Wykład XI. Właściwości cieplne. Jerzy Lis
 Nauka o Materiałach Wykład XI Właściwości cieplne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Stabilność termiczna materiałów 2. Pełzanie wysokotemperaturowe 3. Przewodnictwo cieplne 4. Rozszerzalność
Nauka o Materiałach Wykład XI Właściwości cieplne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Stabilność termiczna materiałów 2. Pełzanie wysokotemperaturowe 3. Przewodnictwo cieplne 4. Rozszerzalność
Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej
 Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej - - Wstęp teoretyczny Jednym ze sposobów wymiany ciepła jest przewodzenie.
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej - - Wstęp teoretyczny Jednym ze sposobów wymiany ciepła jest przewodzenie.
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE EFEKTÓW ROZDRABNIANIA POJEDYNCZYCH ZIAREN
 Akademia Górniczo Hutnicza im. Stanisława Staszica Wydział Górnictwa i Geoinżynierii Katedra Inżynierii Środowiska i Przeróbki Surowców Rozprawa doktorska ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE
Akademia Górniczo Hutnicza im. Stanisława Staszica Wydział Górnictwa i Geoinżynierii Katedra Inżynierii Środowiska i Przeróbki Surowców Rozprawa doktorska ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE
Politechnika Białostocka
 Politechnika Białostocka WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA Katedra Geotechniki i Mechaniki Konstrukcji Wytrzymałość Materiałów Instrukcja do ćwiczeń laboratoryjnych Ćwiczenie nr 6 Temat ćwiczenia:
Politechnika Białostocka WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA Katedra Geotechniki i Mechaniki Konstrukcji Wytrzymałość Materiałów Instrukcja do ćwiczeń laboratoryjnych Ćwiczenie nr 6 Temat ćwiczenia:
Nowoczesne technologie materiałowe stosowane w przemyśle lotniczym r Nałęczów
 Seminarium zadań badawczych Seminarium ZB1, ZB2, ZB5 Projektu Kluczowego Nowoczesne Zakładu technologie Automatyzacji, materiałowe Obrabiarek stosowane i Obróbki w Skrawaniem przemyśle lotniczym 03.10.2013
Seminarium zadań badawczych Seminarium ZB1, ZB2, ZB5 Projektu Kluczowego Nowoczesne Zakładu technologie Automatyzacji, materiałowe Obrabiarek stosowane i Obróbki w Skrawaniem przemyśle lotniczym 03.10.2013
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Czym jest prąd elektryczny
 Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
MIKROSKOPIA METALOGRAFICZNA
 MIKROSKOPIA METALOGRAFICZNA WYKŁAD 3 Stopy żelazo - węgiel dr inż. Michał Szociński Spis zagadnień Ogólna charakterystyka żelaza Alotropowe odmiany żelaza Układ równowagi fazowej Fe Fe 3 C Przemiany podczas
MIKROSKOPIA METALOGRAFICZNA WYKŁAD 3 Stopy żelazo - węgiel dr inż. Michał Szociński Spis zagadnień Ogólna charakterystyka żelaza Alotropowe odmiany żelaza Układ równowagi fazowej Fe Fe 3 C Przemiany podczas
Wnikanie ciepła przy konwekcji swobodnej. 1. Wstęp
 Wnikanie ciepła przy konwekcji swobodnej 1. Wstęp Współczynnik wnikania ciepła podczas konwekcji silnie zależy od prędkości czynnika. Im prędkość czynnika jest większa, tym współczynnik wnikania ciepła
Wnikanie ciepła przy konwekcji swobodnej 1. Wstęp Współczynnik wnikania ciepła podczas konwekcji silnie zależy od prędkości czynnika. Im prędkość czynnika jest większa, tym współczynnik wnikania ciepła
ODRZUCANIE WYNIKÓW POJEDYNCZYCH POMIARÓW
 ODRZUCANIE WYNIKÓW OJEDYNCZYCH OMIARÓW W praktyce pomiarowej zdarzają się sytuacje gdy jeden z pomiarów odstaje od pozostałych. Jeżeli wykorzystamy fakt, że wyniki pomiarów są zmienną losową opisywaną
ODRZUCANIE WYNIKÓW OJEDYNCZYCH OMIARÓW W praktyce pomiarowej zdarzają się sytuacje gdy jeden z pomiarów odstaje od pozostałych. Jeżeli wykorzystamy fakt, że wyniki pomiarów są zmienną losową opisywaną
Roztwory rzeczywiste (1)
 Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 rzyczyny dodatnich i ujemnych odchyleń od prawa Raoulta konsekwencja
Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 rzyczyny dodatnich i ujemnych odchyleń od prawa Raoulta konsekwencja
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Modelowanie bilansu energetycznego pomieszczeń (1)
 Wydział Inżynierii Środowiska Politechnika Wrocławska Modelowanie bilansu energetycznego pomieszczeń (1) 2 / 7 Na czym polega ćwiczenie? Ćwiczenie polega na badaniu modelu nagrzewnicy wodnej i chłodnicy
Wydział Inżynierii Środowiska Politechnika Wrocławska Modelowanie bilansu energetycznego pomieszczeń (1) 2 / 7 Na czym polega ćwiczenie? Ćwiczenie polega na badaniu modelu nagrzewnicy wodnej i chłodnicy
Badania efektywności systemu zarządzania jakością
 Opracowanie to z łagodniejszym podsumowaniem ukazało się w Problemach jakości 8/ 2007 Jacek Mazurkiewicz Izabela Banaszak Magdalena Wierzbicka Badania efektywności systemu zarządzania jakością Aby w pełni
Opracowanie to z łagodniejszym podsumowaniem ukazało się w Problemach jakości 8/ 2007 Jacek Mazurkiewicz Izabela Banaszak Magdalena Wierzbicka Badania efektywności systemu zarządzania jakością Aby w pełni
BADANIE WYMIENNIKÓW CIEPŁA
 1.Wprowadzenie DNIE WYMIENNIKÓW CIEPŁ a) PŁSZCZOWO-RUROWEGO b) WĘŻOWNICOWEGO adanie wymiennika ciepła sprowadza się do pomiaru współczynników przenikania ciepła k w szerokim zakresie zmian parametrów ruchowych,
1.Wprowadzenie DNIE WYMIENNIKÓW CIEPŁ a) PŁSZCZOWO-RUROWEGO b) WĘŻOWNICOWEGO adanie wymiennika ciepła sprowadza się do pomiaru współczynników przenikania ciepła k w szerokim zakresie zmian parametrów ruchowych,
H a. H b MAGNESOWANIE RDZENIA FERROMAGNETYCZNEGO
 MAGNESOWANIE RDZENIA FERROMAGNETYCZNEGO Jako przykład wykorzystania prawa przepływu rozważmy ferromagnetyczny rdzeń toroidalny o polu przekroju S oraz wymiarach geometrycznych podanych na Rys. 1. Załóżmy,
MAGNESOWANIE RDZENIA FERROMAGNETYCZNEGO Jako przykład wykorzystania prawa przepływu rozważmy ferromagnetyczny rdzeń toroidalny o polu przekroju S oraz wymiarach geometrycznych podanych na Rys. 1. Załóżmy,
C/Bizkargi, 6 Pol. Ind. Sarrikola E LARRABETZU Bizkaia - SPAIN
 Mosiądz Skład chemiczny Oznaczenia Skład chemiczny w % (mm) EN Symboliczne Numeryczne Cu min. Cu maks. Al maks. Fe maks. Ni maks. Pb min. Pb maks. Sn maks. Zn min. Inne, całkowita maks. CuZn10 CW501L EN
Mosiądz Skład chemiczny Oznaczenia Skład chemiczny w % (mm) EN Symboliczne Numeryczne Cu min. Cu maks. Al maks. Fe maks. Ni maks. Pb min. Pb maks. Sn maks. Zn min. Inne, całkowita maks. CuZn10 CW501L EN
KOMPENDIUM WIEDZY. Opracowanie: BuildDesk Polska CHARAKTERYSTYKA ENERGETYCZNA BUDYNKÓW I ŚWIADECTWA ENERGETYCZNE NOWE PRZEPISY.
 Sprawdzanie warunków cieplno-wilgotnościowych projektowanych przegród budowlanych (wymagania formalne oraz narzędzie: BuildDesk Energy Certificate PRO) Opracowanie: BuildDesk Polska Nowe Warunki Techniczne
Sprawdzanie warunków cieplno-wilgotnościowych projektowanych przegród budowlanych (wymagania formalne oraz narzędzie: BuildDesk Energy Certificate PRO) Opracowanie: BuildDesk Polska Nowe Warunki Techniczne
Prawa gazowe- Tomasz Żabierek
 Prawa gazowe- Tomasz Żabierek Zachowanie gazów czystych i mieszanin tlenowo azotowych w zakresie użytecznych ciśnień i temperatur można dla większości przypadków z wystarczającą dokładnością opisywać równaniem
Prawa gazowe- Tomasz Żabierek Zachowanie gazów czystych i mieszanin tlenowo azotowych w zakresie użytecznych ciśnień i temperatur można dla większości przypadków z wystarczającą dokładnością opisywać równaniem
Etapy modelowania ekonometrycznego
 Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
