Czech Technical University in Prague Faculty of Nuclear Science and Physical Engineering BACHELOR THESIS
|
|
|
- Sabina Chmielewska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Czech Technical University in Prague Faculty of Nuclear Science and Physical Engineering BACHELOR THESIS QUANTUM WAVEGUIDES WITH ROBIN BOUNDARY CONDITIONS Martin Jílek June 29, 26
2 I would like to thank my supervisor Mgr. David Krejčiřík, Ph.D. for valuable advices, explanation of notions, and careful reading a previous version of this thesis. Prohlášení Prohlašuji, že jsem svou bakalářskou práci vypracoval samostatně a použil jsem pouze podklady uvedené v přiloženém seznamu. Nemám žádný důvod proti užití tohoto školního díla ve smyslu 6 Zákona č. 121/2 Sb., o právu autorském, o právech souvisejících s právem autorským a o změně některých zákonů (autorský zákon). Declaration I declare that I wrote my bachelor thesis independently and exclusively with the use of cited bibliography. I agree with the usage of this thesis in a purport of the Act 121/2 (Copyright Act). Praha, June 29, 26 Martin Jílek
3 Název práce: Kvantové vlnovody s Robinovými okrajovými podmínkami Autor: Martin Jílek Obor: Matematické inženýrství Druh práce: Bakalářská práce Vedoucí práce: Mgr. David Krejčiřík, Ph.D. ÚJF AV ČR, Řež Abstrakt: Studujeme spektrum Laplaciánu v zakřiveném rovinném pásku podél nekonečné křivky s Robinovými okrajovými podmínkámi. Dokazujeme, že esenciální spektrum je stabilní, pokud má křivost referenční křivky kompaktní nosič a že vždy, když pásek není rovný, existují vlastní hodnoty pod prahem esenciálního spektra. Klíčová slova: kvantové vlnovody, Robinovy hraniční podmínky, vázané stavy, Robinův Laplacián.
4 Title: Quantum waveguides with Robin boundary conditions Author: Martin Jílek Abstract: We study the spectrum of the Laplacian in a curved planar strip built along an infinite curve, subject to Robin boundary conditions. We prove that the essential spectrum is stable under any compactly supported curvature of the reference curve and that there always exist eigenvalues below the bottom of the essential spectrum unless the strip is straight. Key words: quantum waveguides, Robin boundary conditions, bound states, Robin Laplacian.
5 Contents 1 Introduction 1 2 Review of some abstract results in spectral theory 3 3 The Robin Laplacian 5 4 Straight waveguide The transversal Hamiltonian The point spectrum The eigenfunctions Neumann case Dirichlet case The essential spectrum Numerical results The longitudinal Hamiltonian The Hamiltonian of a straight planar strip Curved waveguide The Geometry The Hamiltonian The stability of essential spectrum The existence of bound states Conclusion 31
6 1 Introduction Modern experimental techniques make it possible to fabricate tiny semiconductor structures which are small enough to exhibit quantum effects. These systems are sometimes called nanostructures because of their typical size in a direction and they are expected to become the building elements of the next-generation electronics. Since the used materials are very pure and of crystallic structure, the particle motion inside a nanostructure can be modeled by a free particle with an effective mass m living in a spatial planar region Ω. That is, the quantum Hamiltonian can be identified with the operator H = 2 2m (1) in the Hilbert space L 2 (Ω), where denotes the Planck constant. We refer to [11, 5] for more information on the physical background. An important category of nanostructures is represented by quantum waveguides, which are modeled by Ω being an infinitely stretched tubular region in R 2 or R 3. In principle, one can consider various conditions on the boundary of Ω in order to model the fact that the particle is confined to Ω. However, since the particle wavefunctions ψ are observed to be suppressed near the interface between two different semiconductor materials, one usually imposes Dirichlet boundary conditions, i.e. ψ = on Ω. (2) Such a model was successfully used by P. Exner and P. Šeba in 1989 to describe the binding effect in curved quantum waveguides [7]. We refer to [8, 5] for subsequent generalizations and references on the Dirichlet model. A fresh impetus to the theoretical studies of curved quantum waveguides has been given by the recent letter [4] of Dittrich and Kříž from 22 who demonstrated that an alteration of the boundary conditions changes the physical picture completely. More specifically, the authors introduced a waveguide with combined Dirichlet and Neumann boundary conditions and showed that the presence of the latter may lead to the absence of bound states which always exist in the Dirichlet waveguides. We refer to [1] for further studies of the Dirichlet-Neumann model. Summing up, both the geometry and the choice of boundary conditions are important for the physical interpretation of a quantum-waveguide model. In this thesis, we introduce and study a new model by imposing Robin boundary conditions on the boundary of 1
7 a quantum waveguide. These conditions can be considered as a generalization of the Dirichlet and Neumann boundary conditions mentioned above, however, our model is closer to the Dirichlet one since we consider a uniform coupling constant α >. More specifically, putting the physical constant in (1) equal to one, we are interested in the solutions ψ of the following stationary Schrödinger equation for a free particle in Ω having energy λ and satisfying Robin boundary conditions on Ω: ψ n ψ = λψ in Ω, (3) + α ψ = on Ω. (4) Here Ω is an unbounded curved planar strip, i.e. a neighborhood of constant width of an infinite curve in R 2, α is a given positive number and n is the outward unit normal vector to Ω. Later on, we interpret the boundary-value problem (3), (4) rigorously as the spectral problem for a self-adjoint operator in the Hilbert space L 2 (Ω). While to impose the Dirichlet boundary conditions means to require the vanishing of wavefunction on the boundary of Ω, see (2), the Robin conditions (4) correspond to the weaker requirement of vanishing of the probability current, in the sense that its normal component vanishes on the boundary, i.e. j n = on Ω, where the probability current j is defined by j := i 2m [ ψ ψ ψ ψ ]. This less restrictive requirement may in principle model different types of interface in materials. The Laplacian subject to Robin boundary conditions can be also used in the problem to find the electro-magnetic field outside the object consisting of a conducting core covered by a dielectric layer. If the thickness of the layer is too small compared to the dimension of the conductive core, the numerical methods of solving this problem fail because of instabilities that then arise. In this case, the problem can by solved by approximation of the dielectric layer by appropriate boundary conditions of the Robin type. We refer to [2, 6] for more information. The very interesting phenomenon in the curved Dirichlet (and in certain Dirichlet- Neumann) quantum waveguides is the existence of bound states, i.e., the eigenvalues under 2
8 essential spectrum, which classically do not exist. The main aim of the thesis is to show that the geometrically induced discrete spectrum exists also in the Robin waveguides, and this under exactly the same conditions as in the Dirichlet waveguides. The thesis is organised as follows. In Section 2, we present some notions and tools from spectral theory used in the thesis. Section 3 is devoted to the precise definition of the Robin Laplacian. In Section 4, we find spectrum of straight waveguides, treating separately the longitudinal and transversal motions. The main results are presented in Section 5; firstly, we show that the essential spectrum on a curved strip does not change if the strip is curved only locally; secondly, we prove the existence of discrete spectrum in a non-trivially curved strip. 2 Review of some abstract results in spectral theory In this section we will summarize some basic results of spectral theory, which we will use in the thesis. Let H be a separable complex Hilbert space with the scalar product (, ) and the norm = (, ). A linear operator H on H is, by definition, a linear mapping of a subspace D(H) H into H; D(H) is called the domain of H. H is said to be densely defined if D(H) is dense in H. H is called an extension of H (or H is a restriction of H) if we have D(H) D( H) and ψ D(H), Hψ = Hψ. An operator H on H is said to be symmetric if it is densely defined and φ, ψ D(H), (φ, Hψ) = (Hφ, ψ). If H is a densely defined operator on H then the adjoint operator H is uniquely determined by the condition that We have φ D(H ), ψ D(H), (φ, Hψ) = (H φ, ψ). D(H ) = { φ H η H, ψ D(H), (φ, Hψ) = (η, ψ) }. If H is symmetric then it is easy to see that the adjoint H is an extension of H, i.e. D(H) D(H ). We say that H is self-adjoint if H is symmetric and D(H) = D(H ). 3
9 The spectrum of a self-adjoint operator H on H, denoted by σ(h), is defined as the set of points λ C such that either H λi, where I is the identity operator, is not invertible or it is invertible but has range smaller than H. It is easy to see that σ(h) R. The set σ p (H) of all eigenvalues of H, i.e. σ p (H) := { λ R ψ D(H), ψ = 1, Hψ = λψ }, is called the point spectrum of H, which is obviously contained in σ(h). If λ is an eigenvalue of H then the dimension of the kernel of H λi is called the multiplicity of λ. The discrete spectrum of a self-adjoint operator H, denoted by σ disc (H), consists of those eigenvalues of H which are isolated points of σ(h) and have finite multiplicity. The set σ ess (H) := σ(h) \ σ disc (H) is called the essential spectrum of H and, by definition, it contains either accumulation points of σ(h) or isolated eigenvalues of infinite multiplicity. The spectral theorem provides the following characterization of the spectrum of selfadjoint operators, which we will often use for showing that some value lies in the spectrum (cf [3, Lemma 4.1.2]): Theorem 2.1 (Weyl criterion). Let H be a self-adjoint operator on H. A point λ R belongs to σ(h) if, and only if, there exists a sequence {ψ n } n N D(H) such that 1. n N, ψ n = 1, 2. Hψ n λψ n as n. We say that a self-adjoint operator H on H is semi-bounded if there exists a real number c such that ψ D(H), (ψ, Hψ) c ψ 2 ; in this case we simply write H c. We have the following variational formula for the spectral threshold (cf [3, Sec. 4.5]): Theorem 2.2 (Rayleigh-Ritz). Let H be a semi-bounded self-adjoint operator on H. Then (ψ, Hψ) inf σ(h) = inf. (5) ψ D(H)\{} ψ 2 4
10 As a consequence of Theorem 2.2, H c implies σ(h) [c, ). On the other hand, inf σ(h) (ψ, Hψ) ψ 2 for any test function ψ D(H)\{}. Theorem 2.2 is a special case of the following theorem, which is a highly useful tool for analysing the eigenvalues below the threshold of the essential spectrum (cf [3, Sec. 4.5]): Theorem 2.3 (minimax principle). Let H be a semi-bonded self-adjoint operator on H. Let {λ k } k=1 be a non-decreasing sequence of numbers defined by { (ψ, Hψ) λ k := inf sup ψ P ψ 2 }. P D(H) & dim(p) = k (6) Then one of the following cases occurs: 1. There exists λ R {+ } such that k, λ k < λ & lim k λ k = λ. Then λ = inf σ ess (H) (with the convention that the essential spectrum is empty if λ = + ), and the part of the spectrum of H in (, λ ) consists of the eigenvalues λ k each repeated a number of times equal to its multiplicity. 2. There exists λ R and N N such that k N, λ k < λ & k > N, λ k = λ. Then λ = inf σ ess (H), and the part of the spectrum of H in (, λ ) consists of the eigenvalues λ 1,..., λ N each repeated a number of times equal to its multiplicity. Remark 2.4. D(H) in (5) and (6) can be replaced by the form domain of H ( cf [3, Sec. 4.5]). 3 The Robin Laplacian In this section we introduce the Laplacian in a general domain with Robin boundary conditions, in a proper way as an operator associated with a closed symmetric form. 5
11 Let Ω be an open connected set in R N, with N 1. We assume that the boundary is nice, in particular, we require that there exists a unique continuous outward unit normal vector n : Ω R N. We are interested in the solutions ψ of the following stationary Schrödinger equation for a free particle in Ω having energy λ and satisfying Robin boundary conditions on Ω: ψ = λψ in Ω, ψ n + α ψ = on Ω, (7) where α is a given positive number. This problem can be reconsidered in a mathematically rigorous way as the spectral problem for a self-adjoint operator, denoted by Ω α and called the Robin Laplacian here, in the Hilbert space L 2 (Ω). It turns out that the correct Hamiltonian Ω α is defined by } ψ D( Ω α {ψ ) := W 2,2 (Ω) ψ + α ψ = on Ω, Ω αψ := ψ, (8) n but several remarks have to be added: 1. The Sobolev space W 2,2 (Ω) is, by definition, the space of functions (or rather equivalence classes of functions) with square-integrable weak derivatives up to the second order, hence the act of the Laplacian should be understood in the distributional sense. 2. The values of ψ and ψ on the boundary Ω should be understood in the trace sense; this requires additional hypotheses about the boundary regularity. 3. While it is easy to see that Ω α prove that it is self-adjoint. is symmetric [1, Thm. 2.19], it is quite difficult to In order to avoid the above difficulties, we use the quadratic form approach to define the Hamiltonian (cf [3, Sec. 4.4]). Let Q Ω α be the quadratic form defined in L 2 (Ω) by ψ D( Q Ω α ) := D(Ω), Q Ω α [ψ] := ψ 2 + α ψ 2, (9) where the domain Ω D(Ω) := { ψ L 2 (Ω) Ψ C (RN ), ψ = Ψ Ω } (1) 6 Ω
12 is chosen in such a way that the integrals in (9) are well defined. is clearly densely defined, non-negative and the corresponding sesquilinear form is symmetric. Let us denote by Q Ω α the closure (i.e. the smallest closed extension) of Q Ω α. By definition, D(Q Ω α ) is the completion of D(Ω) with respect to the norm α := Q Ω α[ ] + 2 and ψ D(Q Ω α ), QΩ α [ψ] := lim n Q Ω α [ψ n], where {ψ n } n=1 is any sequence of D( Q Ω α ) converging to ψ in L2 (Ω) and such that Q Ω α [ψ n ψ m ] for n, m. Proposition 3.1. One has: 1. D(Q Ω α ) is independent of α, 2. D(Q Ω α ) W 1,2 (Ω). Proof. The first property follows from the algebraic inequalities α 1 < α 2, α1 α2 α 2 α 1 α1. Given any ψ D(Q Ω α ), let {ψ n} n=1 be as above and denote by η ψ the limit of the sequence { ψ n } n=1 in L 2 (Ω). Then φ C (Ω), ( φ, ψ) = lim ( φ, ψ n) = lim (φ, ψ n ) = (φ, η ψ ), n n which tells us that ψ possesses weak derivatives (η ψ L 2 (Ω) is the distributional gradient of ψ), i.e. ψ W 1,2 (Ω). As a consequence of the second property, we can write ψ D(Q Ω α ), QΩ α [ψ] = ψ 2 + α lim ψ n Ω n Ω 2. Now, let H Ω α be the non-negative self-adjoint operator associated with QΩ α, i.e., D(H Ω α ) = { ψ D(Q Ω α ) η L2 (Ω), φ D(Q Ω α ), QΩ α (φ, ψ) = (φ, η)}, φ D(Q Ω α ), ψ D(HΩ α ), QΩ α (φ, ψ) = (φ, HΩ α ψ). Q Ω α 7
13 Using the Green theorem, it is easy to see that Hα Ω is an extension of an operator which acts as the Laplacian on sufficiently regular functions satisfying the Robin boundary conditions: Proposition 3.2. One has where L α (Ω) D(H Ω α ) and ψ L α(ω), H Ω α ψ = ψ, { L α (Ω) := ψ D(Ω) ψ n } + α ψ = on Ω. Remark 3.3. Assuming certain regularity of Ω and using advanced methods of the theory of elliptic partial differential equations, it is possible to show that H Ω α = Ω α, but this proof is out of the scope of the present thesis. Nevertheless, we shall demonstrate the ideas of the proof in the case of Ω being a bounded one-dimensional interval, cf Proposition Straight waveguide In this section, we are interested in a straight waveguide of width d, i.e., we consider the Cartesian product Ω := R (, d), where d is a given positive number. The problem can be formally simplified as follows. Assuming that the solution of (7) has a form and putting this Ansatz to (7), we get ψ(x, y) = X(x)Y (y). X (x) X(x) Y (y) Y (y) = λ in Ω. This formula has a good sense only for such (x, y) Ω that X(x) and Y (y). It follows that, necessarily, λ + Y (y) Y (y) = (x) X X(x) = C, 8
14 where C is a constant. From the boundary conditions in (7), we get the following boundary conditions for Y : Y () + αy () =, Y (d) + αy (d) =. This sort of separation leads us to the study of two independent one-dimensional spectral problems, the transversal and the longitudinal one. 4.1 The transversal Hamiltonian If Ω = (, d), with d being a positive number, then it is easy to see that D(Q (,d) α ) = W 1,2 ((, d)) because W 1,2 ((, d)) is embedded in the space of uniformly continuous functions on [, d] due to the Sobolev embedding theorem [1, Thm. 5.4, part II]. By the same argument, the boundary conditions in (8) are defined without problems because W 2,2 ((, d)) is embedded in the space of uniformly smooth functions C 1 ([, d]). The fact that (,d) α is self-adjoint can be proved directly using von Neumann s theory of deficiency indices. Here we prove it by means of the definition of the self-adjoint H α (,d) via the associated quadratic form: Proposition 4.1. H (,d) α Proof. Let ψ D( (,d) α every φ D(Q (,d) α of (,d) D(H (,d) α α. = (,d) α ). An integration by parts shows that Q (,d) α ) with η := ψ L 2 ((, d)). This proves that H (,d) α (φ, ψ) = (φ, η) for is an extension We are inspired by [9, Example VI. 2.16] to prove the converse inclusion. Let ψ ) and H α (,d) ψ =: η L 2 ((, d)). The relation (φ, η) = (φ, H α (,d) ψ) = (φ, η) for every φ D(Q (,d) α ) means d φη = d φ ψ + αφ(d)ψ(d) + αφ()ψ() (11) for every φ W 1,2 ((, d)). Let z be an indefinite integral of η (which is integrable): z = η. Then d d d φη = φz = φ z + φ(d)z(d) φ()z() (12) 9
15 for every φ W 1,2 ((, d)). Combining (11) with (12), we get the central identity d φ (ψ + z) + φ(d)[αψ(d) z(d)] + φ()[αψ() + z()] = (13) for every φ W 1,2 ((, d)). For any φ L 2 ((, d)) such that d φ =, φ(x) := x φ satisfies the conditions φ W 1,2 ((, d)) and φ() = φ(d) =, so that ψ + z is orthogonal to φ by (13). Thus ψ + z must be equal to a constant c, being orthogonal to all functions orthogonal to 1. Substituting this into (13) with arbitrary φ, we obtain φ(d)[c + αψ(d) z(d)] + φ()[ c + αψ() + z()] = (14) for every φ W 1,2 ((, d)). Since φ() and φ(d) vary over all complex numbers when φ varies over W 1,2 ((, d)), their coefficients in (14) must vanish. Noting that c = ψ (d) + z(d) = ψ () + z(), we thus obtain ψ (d) + αψ(d) = and ψ () + αψ() =. (15) From ψ + z = c it follows (cf [3, Lem ]) that ψ W 1,2 ((, d)) and ψ = z = η. (16) In this way we have proved that each ψ D(H α (,d) ) has the properties (15) and (16), proving therefore H α (,d) (,d) α. We divide the study of the spectral problem of H α (,d) into several steps. Firstly, we find its point spectrum. Secondly, we establish some properties of the corresponding eigenfunctions we shall need later. Thirdly, we mention two limit situations, the case of Dirichlet and Neumann boundary conditions, respectively. Fourthly, we prove that the essential spectrum of H α (,d) is empty. Finally, we present some numerical results to visualise the features of the Robin boundary conditions The point spectrum For finding the point spectrum of H α (,d), we search such λ R for which there exists a function χ W 2,2 ((, d)) normalised to 1 in L 2 ((, d)) satisfying χ = λχ in (, d) (17) 1
16 together with the Robin boundary conditions χ() + αχ() = χ(d) + αχ(d) =. (18) We will demonstrate that, necessarily, λ >. This can be shown by multiplying (17) by χ, integrating over (, d) and by using an integration by parts: d λ = = d χ χ = [ χ χ] d + d χ 2 χ 2 + α χ() 2 + α χ(d) 2 >. The inequality is strict, because the equality gives the trivial solution. Since d χ 2 + α χ() 2 + α χ(d) 2 is, in fact, the quadratic form corresponding to H α (,d), the inequality implies that the operator H α (,d) is positive. The general solution of (17) has the form χ(y) = A sin( λ y) + B cos( λ y), (19) where A, B C are to be determined by the boundary conditions (18) and the normalisation condition. Restricting the general solution (19) by the boundary conditions (18), we get the system ( ) A m =, (2) B where λ α m :=. (21) λ cos( λ d) + α sin( λ d) λ sin( λ d) + α cos( λ d) Because we are looking for non-trivial solutions of (2), we require that det m =. This leads to the following implicit equation for the spectral parameter λ: 2α λ cos( λ d) + (α 2 λ) sin( λ d) =. (22) 11
17 4.1.2 The eigenfunctions In order to get the corresponding eigenfunctions, we solve the system (2), where λ is determined by implicit equation (22). The system (2) is equivalent to the equation whence we can express A in terms of B: λa + αb =, A = α λ B. The solution (19) can be then written like ( α λ χ(y) = B sin( λ y) + cos( ) λ y). (23) The normalisation of χ yields the following condition on B: [( ) ) 1 = B α2 d (1 λ 2 + α2 1 λ 2 λ sin( λ d) cos( λ d) + α λ sin2 ( ] λ d) (24) We can choose B real and positive. We show some properties of eigenfunctions χ α n, which we will need later. The physical interpretation of the first two lemmas is that the Robin boundary conditions are for the particle strictly more repulsive than the Neumann ones. Lemma 4.2. If α >, then E α 1 lies in the open interval (, π2 /d 2 ). Proof. Since we have already shown that E1 α is non-negative, it is enough to prove that the equation (22) has a solution in the interval (, π 2 /d 2 ). Define The first derivative of f is f( λ) := 2α λ cos( λ d) + (α 2 λ) sin( λ d). f ( λ) = 2α cos( λ d) 2α λd sin( λ d) 2 λ sin( λ d) + (α 2 λ)d cos( λ d). One has f() = f () = 2α + α 2 > f(π/d) = 2πα/d <. This and the fact that f is a continuous function follows that the implicit equation (22) has a solution for λ (, π 2 /d 2 ). 12
18 Lemma 4.3. If α >, then χ α 1 ()2 < χ N 1 ()2 = 1/d. Proof. From (22) we can express α in terms of λ: α = λ(±1 cos( λ d)) sin(, λ d) where the sign is to be chosen in such a way that α >. In our case λ (, π 2 /d 2 ) we therefore have λ(1 cos( λ d)) α = sin(. (25) λ d) If we put (25) to (24), we get B 2 = λ(1 + cos( λ d)) ( λ d) + sin( λ d). Since λd lies in (, π) and sin x > x cos x for all x (, π), the following inequality holds: λ(1 + cos( λ d)) λ(1 + cos( λ d)) χ α 1 () 2 = B 2 = < = 1/d. λd + sin( λ d) λd + λd cos( λ d) In the following lemma we establish certain symmetry of the first eigenfunction: Lemma 4.4. y [, d], χ α 1 (y) = χα 1 (d y). Proof. Since by Lemma 4.2 the eigenvalue E1 α (, π 2 /d 2 ), the parameter α satisfies (25) and we can write α = 1 cos( λ d) λ sin(. λ d) 13
19 Then following equalities hold: χ α 1 (d y) = α sin( λ(d y)) + cos( λ(d y)) = B λ = 1 cos( λ d) sin( λ d) 1 cos( λ d) sin( λ d) sin( λ d) cos( λ y) cos( λ d) sin( λ y)+ + cos( λ d) cos( λ y) + sin( λ d) sin( λ y) = = cos( λ y) cos( λ d) cos( λ y) + cos( λ d) cos( λ y)+ + cos( λ d) + cos 2 ( λ d) + sin 2 ( λ d) sin( λ d) = α λ sin( λ y) + cos( λ y) = = χα 1 (y) B sin( λ y) = Neumann case Now, let us explicitly express the eigenvalues and corresponding eigenfunctions of the Laplacian on (, d) with Neumann boundary conditions. Let us denote H (,d) N := H (,d) and Q (,d) N := Q (,d), where H (,d) and Q (,d) can be defined in the same way as H α (,d) and Q (,d) α, respectively, with α > (cf Section 3). Notice that Proposition 4.1 holds also for α =. From (22) we get the equation for eigenvalues of H (,d) N : λ sin( λ d) =. Here λ can be equal to zero, because it does not lead to the trivial solution, but to the constant one. If follows that the eigenvalues of H (,d) N arranged in increasing order are given by En N = (n 1)2 π 2 /d 2, where n N \ {}. 14
20 From (23) we get the corresponding family of eigenfunctions normalised to 1: 1 χ N n (y) = if n = 1, d cos((n 1)πy/d) if n 2. 2 d {χ N n } n=1 forms a complete orthonormal family (cf [12, Kap. 16.2, Pozn. 13]). This and the fact that En N (,d) as n imply that the essential spectrum of H N is empty (cf [3, Thm ]). Hence Dirichlet case σ(h (,d) N ) = σ disc(h (,d) N ) = {EN n } n=1. Another limit case of Robin boundary conditions (corresponding formally to α + ) is the Dirichlet Laplacian, denoted by (,d) D and defined by (,d) D χ := χ, χ D( (,d) D ) := { χ W 2,2 ((, d)) χ() = χ(d) = }. The general solution of the equation (17) is of the form (19). The boundary conditions lead to the system of equations ( ) 1 sin( λ d) cos( λ d) ) ( A B =. (26) The requirement 1 sin( λ d) cos( λ d) = gives the equation for λ: Hence the eigenvalues are given by sin( λ d) = (27) E D n = n 2 π 2 /d 2, n N \ {}. The case λ = (which also solves (27) ) corresponds to the trivial solution, because the system (26) implies that B =. The eigenfunctions are then given by 2 χ D n (y) = sin(nπy/d), n N \ {}. d 15
21 By the same reason as in the Neumann case, the essential spectrum of (,d) D i.e. σ( (,d) D ) = σ disc( (,d) D ) = {ED n } n= The essential spectrum is empty, We demonstrate, that the essential spectrum of H (,d) α is empty. Proposition 4.5. If α, then σ ess (H (,d) α ) =. Proof. Let { λ N n } n=1 and { λ α n } n=1 be the sequence of numbers associated with Q(,d) N Q (,d) α, respectively, by the minimax principle, i.e. and λ N n λ α n := := inf P D(Q (,d) sup N ) ψ P dim(p)=n sup inf P D(Q α (,d) ) ψ P dim(p)=n d ψ 2, d ψ 2 d ψ 2 + ψ() 2 + ψ(d) 2 d. ψ 2 Let λ N and λα i.e. Since D(Q (,d) N be the threshold of essential spectrum of H (,d) N λ N := lim n λn n, λα := lim n λα n. ) = D(Q(,d) α ), the following inequality holds: and H α (,d), respectively, n N \ {}, λ N n λα n. Hence λ N λα. From this and the fact that σ ess (H (,d) ) = (cf Section 4.1.3) we get the desired claim. N Thus, the spectrum of the transversal Hamiltonian can be written like σ(h α (,d) ) = σ disc (H α (,d) ) = {En α } n=1. 16
22 4.1.6 Numerical results In this section, we show some numerical results of solving the problem of the transversal Hamiltonian. Rewriting the implicit equation (22) into the form λ cot( λ d) = λ α 2 2α, (28) we can visualise its solutions as the intersections of the graph of the function at the l.h.s. and at the r.h.s. in (28) (see Figure 1). The solution of (22) can be also drawn as a dependence of energies E α n on the parameter α, see Figure 2. Figure 3 shows how the parameter α influences the first eigenfunction. The quadrate of eigenfunctions corresponding to higher energies are presented in Figure 4. Figure 1: Graphical solution of implicit equation for various α in the case d = 1. 17
23 Figure 2: Dependence of the excited energies on α in the case d = Α Α Α Α Α Α Figure 3: First eigenfunctions of H (,d) α for various α in the case d = 1. 18
24 Figure 4: The quadrate of first four eigenfunctions of H (,d) α for α = 4, d = The longitudinal Hamiltonian If Ω = R, the boundary is empty and we have D( R ) = W 2,2 (R) (we omit the superfluous index α here). On the other hand, since D(R) = L α (R) = C (R) and is just the W 1,2 -norm, we have (by the definition of the space W 1,2 ) D(Q R ) = W 1,2 (R). 19
25 Again, we shall omit the index α in the notation for the quadratic form Q R associated operator H R. and the Proposition 4.6. One has σ(h R ) = [, ). Proof. Since the form Q R is non-negative, it follows that σ(h R ) [, ). The proof of the converse inclusion depends upon the use of Theorem 2.1. We need show that for every E [, ) there exists a sequence of functions ψ n D(H R ) with ψ n L 2 (R) = 1 such that lim n H R ψ n Eψ n L 2 (R) =. We define this sequence as follows. Let ϕ C (R) has the support in [-1,1] and let ϕ L 2 (R) = 1. We define the sequence of functions ψ n C (R) = D(R) = L(R) D(H R ) by ψ n (x) := ϕ n (x)e i Ex, where ϕ n (x) := n 1/2 ϕ(x/n). (29) Here D and L were defined in (1) and Proposition 3.2, respectively. Notice that H R acts on L(R) as the Laplacian (cf Proposition 3.2). We show that ψ n is normalised to 1: ψ n L 2 (R) = ϕ n L 2 (R) = n 1 ϕ(x/n) dx = ϕ(u)du = ϕ L 2 (R) = 1. R One has H R ψ n (x) Eψ n (x) = d [ (i ] Eϕ n (x) + ϕ n (x))e i Ex Ee i Ex ϕ n (x) dx = ( ϕ n (x) 2i E ϕ n (x))e i Ex and for the norm: Since H R ψ n Eψ n L 2 (R) = ϕ n + 2i E ϕ n L 2 (R) ϕ n L 2 (R) + 2 E ϕ n L 2 (R). R (3) ϕ n L 2 (R) = n 1 ϕ L 2 (R) and ϕ n L 2 (R) = n 2 ϕ L 2 (R), (31) it follows that H R ψ n Eψ n L 2 (R) as n. Thus, [, ) σ(h R ). 2
26 4.3 The Hamiltonian of a straight planar strip The spectrum of H Ω α is equal to the sum of the spectrum of longitudinal Hamiltonian and the transversal one: Theorem 4.7. For α, one has σ(h Ω α ) = [E1 α, ). Proof. We prove this claim in two steps. Firstly, we show by using Theorem 2.1 that [E1 α, ) σ(hω α ). Secondly, we demonstrate that H Ω α is bounded from below by Eα 1. Let λ E1 α and {ψ n } n=1 D(H Ω α ) be a sequence of functions defined by ψ n (x, y) := ϕ n (x)e i λ E α 1 x χ α 1 (y), where ϕ n are given by (29). The functions ψ n indeed lie in D(H Ω α ), because they are contained in L α (Ω ). Notice, that H Ω α acts on L α(ω ) as the Laplacian (cf Proposition 3.2). Since χ α 1 fulfils χα 1 (y) = Eα 1 χα 1 (y), one get H Ω α ψ n(x, y) λψ n (x, y) = ( ϕ n (x) + 2i λ E1 α ϕ n(x))e i λ E1 αx H Ω α ψ n (x, y) λψ n (x, y) = ϕ n + 2i λ E1 α ϕ n L 2 (R) ϕ n L 2 (R) + 2 λ E α 1 ϕ n L 2 (R) It follows that [E1 α, ) σ(hω α ) by Theorem 2.1. For proving the inverse inclusion it is enough to show that Q Ω ψ D(Ω ), a dense subspace of D(Q Ω α can write by Theorem 2.2 and Remark 2.4 for all χ D(H (,d) (,d) ).Since the spectrum of H α α ): Q (,d) α [χ] = χ 2 L 2 (,d) + α χ() 2 + α χ(d) 2 E 1 χ 2 L 2 (,d). α [ψ] E1 α ψ 2 for all starts by E1 α, we Using this inequality, together with Fubini s theorem, we get for all ψ D(Ω ) Q Ω α Ω [ψ] = x ψ 2 + y ψ 2 + α ψ 2 Ω Ω y ψ(x, y) 2 dxdy + α ψ(x, ) 2 dx + α ψ(x, d) 2 dx Ω R R [ d ] = dx y ψ(y) 2 dy + α ψ(x, ) 2 + α ψ(x, d) 2 R R dxe α 1 d ψ 2 dy = E α 1 ψ 2. We have used the fact that y ψ(x, y) with x R fixed belongs to D((, d)) D(Q (,d) α ). It follows that σ(h α ) [E α 1, ). 21
27 5 Curved waveguide 5.1 The Geometry Let Γ (Γ 1, Γ 2 ) be an infinite unit-speed plane curve, i.e. a C 2 -smooth mapping Γ : R R 2 satisfying Γ(s) = 1 for all s R. Define a unit normal vector field N := ( Γ 2, Γ 1 ) and a tangent field T := ( Γ 1, Γ 2 ). The couple (T, N) is a Frenet Frame of Γ. The curvature of Γ defined by k := det( Γ, Γ) is a continuous function of the arc-length parameter s. We define a curved strip of the width d as Ω := L(Ω ), where L : R 2 R 2 : (s, u) Γ(s) + un(s). (32) Actually, the image Ω has indeed a geometrical meaning of a non-self-intersecting strip only if we impose some additional hypotheses on d and on the global geometry of Γ. Namely, we want to find sufficient conditions ensuring that the mapping L : Ω Ω is a diffeomorphism. By means of the inverse function theorem, it is enough to assume that the restriction L Ω is injective and that the Jacobian of L is non-zero on Ω. Using the Frenet formulae ) we find ( d T (s) ds N(s) = ( k(s) k(s) 1 L = Γ + uṅ = (1 uk) Γ. ) ( T (s) N(s) ). (33) At the same time, 2 L = N and it follows that the Jacobian of L is given by det( 1 L, 2 L) = (1 uk) Γ 1 N 1 (1 uk) Γ 2 N 2 = (1 uk) Γ 2 = 1 uk. (34) The Jacobian is non-zero if we assume that k(s)u < 1 for all s R and all u (, d). This follows from the condition that d sup s R k(s) < 1. More restrictively, we will always assume that (r1) L Ω is injective, (r2) k + d < 1, where k + := max{, k}. The first condition ensures that the outward unit normal vector n : Ω R 2 is defined uniquely. 22
28 5.2 The Hamiltonian Our main strategy is to replace the simple operator Hα Ω on a complicated space L 2 (Ω, dxdy) by a more complicated operator H α on the simpler Hilbert space L 2 (Ω, (1 uk)dsdu) by using the diffeomorphism L : Ω Ω. In other terms, we express the quadratic form Q Ω α associated with Hα Ω in the curvilinear coordinates (s, u) defined by L. That is, for any given ψ L 2 (Ω) there is a unique φ L 2 (Ω, (1 uk)dsdu) defined by φ := ψ L, and vice versa, and the transformed quadratic form Q α in L 2 (Ω, (1 uk)dsdu) is defined by Q α [φ] := Q Ω α[φ L 1 ], D( Q α [φ]) = {φ L 2 (Ω, (1 uk)dsdu) φ L 1 L 2 (Ω)}. The gradient in the curvilinear coordinates is expressed in the following way: ψ 2 = x ψ 2 + y ψ 2 { 1 = (1 uk) 2 N φ (1 uk)t 2 2 φ + N 1 1 φ + (1 uk)t 1 2 φ = 1φ 2 (1 uk) 2 + 2φ 2. (35) The first part of Q Ω α has in the curvilinear coordinates the form ψ 2 1 φ dxdy = Ω Ω 2 1 uk dsdu + 2 φ 2 (1 uk)dsdu. Ω The boundary part of Q Ω α is transformed as ψ 2 = φ 2 + Ω R {} R {d} φ 2 (1 dk). Summing up, the quadratic form in curvilinear coordinates has the form 1 φ Q α [φ] = Ω 2 1 uk dsdu + 2 φ 2 (1 uk)dsdu+ Ω + α φ 2 + α φ 2 (1 dk). (36) R {} R {d} The operator H α is the unique self-adjoint operator associated with the form (36). Notice that following equality holds on L α (Ω ): 1 H α = (1 uk(s)) 2 2 s u k(s) (1 uk(s)) 3 s 2 u } k(s) 1 uk(s) u. (37)
29 5.3 The stability of essential spectrum As shown in Theorem 4.7, the essential spectrum of the Robin Laplacian on the straight strip Ω is [E1 α, ). In this section, we prove that the essential spectrum of a curved strip Ω coincides with the straight one if we assume that (k) the curvature k has a compact support. Theorem 5.1. Suppose (r1), (r2), and (k). If α >, then σ ess (H Ω α ) = [E α 1, ). The proof of this theorem is achieved in two steps. Firstly, in Lemma 5.2, we prove that all values above E1 α belongs to the essential spectrum. Secondly, in Lemma 5.3, we show that the threshold of essential spectrum does not descent below the energy E1 α. Lemma 5.2. Suppose (r1), (r2), and (k). If α >, then [E α 1, ) σ ess(h Ω α ). Proof. First of all, notice that showing that [E1 α, ) σ(hω α ), we actually prove that the set [E1 α, ) belongs to the essential spectrum of H α Ω, because intervals do not contain isolated points. Let λ [E1 α, ). Define ψ n (s, u) := ϕ n (s)χ α 1 (u)ei λ E1 αs, ϕ n (s) := 1 ϕ( s n n n), where ϕ is defined in the proof of Theorem 4.6. We show that the sequence {ψ n } satisfies the conditions of Theorem 2.1. It is easy to see that ψ n L 2 (Ω,(1 uk)dsdu) = 1 for sufficiently large n. Note that supp ϕ n [n 2 n, n 2 + n]. One has ψ n (s, u) 2 (1 uk(s))dsdu = ψ n (s, u) 2 dsdu Ω Ω d χ α 1 (u) 2 du ϕ n (s) 2 k(s)ds. R For sufficiently large n the second term at the r.h.s. is equal to zero, because ϕ n and k have a disjoint supports. It follows that ψ n L 2 (Ω,(1 uk)dsdu) = ψ n L 2 (Ω ), if n is large enough. The derivatives of the functions ψ n are 1 ψ n (s, u) = e i λ E α 1 s ( ϕ n (s)χ α 1 (u) + ϕ n (s)χ α 1 (u)), 2 1ψ n (s, u) = e i λ E α 1 s χ α 1 (u)[ ϕ n (s) + 2i λ E α 1 ϕ n (s) (λ E α 1 )ϕ n (s)], 2 ψ n (s, u) = ϕ n (s) χ α 1 (u)ei λ E α 1 s, 2 2 ψ n(s, u) = ϕ n (s) χ α 1 (u)ei λ E α 1 s. 24
30 Since the operator H α acts as (37), we get ( H α ψ n λψ n )(s, u) = 1 (1 uk(s)) 2 ( ϕ n(s) + 2i λ E α 1 ϕ n(s))χ α 1 (u)ei λ Eα 1 s u k(s) (1 uk(s)) ( ϕ n(s) + λ E α 3 1 ϕ n (s))χ α 1 (u)e i λ Eα 1 s (2 uk(s))uk(s) + E α (1 uk(s)) 2 1 ϕ n(s)χ α 1 (u)ei λ Eα 1 s + k(s) 1 uk(s) ϕ n(s) χ α 1 (u)e i λ Eα 1 s (2 uk(s))uk(s) + λϕ (1 uk(s)) 2 n (s)χ α 1 (u)ei λ Eα 1 s All terms at the r.h.s. except of the first one are zero for sufficiently large n. The equalities (31) imply that the norm H α ψ n λψ n L 2 (Ω ) = = tends to zero as n. R ( ϕ n (s) + 2i λ E α 1 ϕ n(s) 2 d χ α 1 (u) 2 1 d (1 d k + ) 4 ( ϕ n L 2 (R) + 2 λ E α 1 ϕ n L 2 (R) ) (1 uk(s)) du ds 4 ) Lemma 5.3. Suppose (r1), (r2), and (k). If α >, then inf σ ess (H Ω α ) Eα 1. Proof. For proving this theorem we will use an argument called Neumann bracketing. Let {λ α n(ω)} n=1 be a sequence of numbers associated with Q Ω α by the minimax principle, i.e. λ α n := Ω ψ 2 + α Ω Ω ψ 2. (38) ψ 2 inf P D(Q Ω α ) dim P=n sup ψ P Let λ α (Ω) be the spectral threshold of the essential spectrum of H Ω α, i.e. λ α (Ω) := lim n λα n (Ω). Since k has a compact support, there exists a number s > such that s s, k(s) =. 25
31 Let Γ + and Γ be curves defined by Γ ± := L({±s } (, d)). They divide Ω into three disjoint domains Ω, Ω c, Ω +, i.e. where Ω = Ω Γ Ω c Γ + Ω + and Ω Ω c = Ω c Ω + = Ω + Ω =, Ω := L((, s ) (, d)) Ω c := L(( s, s ) (, d)) Ω + := L((s, ) (, d)) We impose an additional Neumann boundary condition on Γ + and Γ by introducing the quadratic form Q Ω αn [ψ] := ψ 2 + α ψ, ψ D(Q Ω αn ) := T T c T +, Ω Ω where T := { ψ L 2 (Ω) ψ Ω W 1,2 (Ω ) ψ = a.e. in Ω \ Ω }, T c := { ψ L 2 (Ω) ψ Ω c W 1,2 (Ω c ) ψ = a.e. in Ω \ Ω c }, T + := { ψ L 2 (Ω) ψ Ω + W 1,2 (Ω + ) ψ = a.e. in Ω \ Ω + }. by the minimax prin- Let {λ αn n (Ω)} n=1 be the sequence of numbers associated with QΩ αn ciple, i.e. λ αn n (Ω) := inf P T Tc T + dim(p)=n sup ψ P, ψ c P c, ψ + P + sup ψ P = inf P T, Pc Tc, P + T + dim(p )+dim(p c)+dim(p + )=n Since D(Q Ω α) D(Q Ω αn ), we clearly have Ω ψ 2 + α Ω ψ 2 Ω ψ 2 Ω ψ 2 + Ω c ψ c 2 + Ω + ψ α Ω ψ 2 Ω ψ 2 + Ω c ψ c 2 + Ω + ψ + 2. n N \ {}, λ α n (Ω) λαn n (Ω). (39) 26
32 In particular, It follows from (38) that λ α (Ω) λαn (Ω) := lim n λαn n (Ω). n N \ {}, P D(Q Ω α), dim(p) = n, λ α n(ω) sup ψ P and similarly for λ α n (Ω ), λ α n (Ω c), and λ α n (Ω +). Consequently, sup ψ P, ψ c P c, ψ + P + max { λ α n (Ω ), λ α n c (Ω c ), λ α n + (Ω + ) }, Ω ψ 2 + α Ω ψ 2 Ω ψ 2, Ω ψ 2 + Ω c ψ c 2 + Ω + ψ α Ω ψ 2 Ω ψ 2 + Ω c ψ c 2 + Ω + ψ + 2 where n := dim(p ), n c := dim(p c ), and n + := dim(p + ), with the convention that λ α n (Ω ) = or λ α n c (Ω c ) = or λ α n + (Ω + ) = if n = or n c = or n + =, respectively. Hence n N \ {}, Taking the limit n, we get λ αn n (Ω) min max { λ α n n +n c+n + =n (Ω ), λ α n c (Ω c ), λ α n + (Ω + ) } λ αn (Ω) min { λ α (Ω ), λ α (Ω c), λ α (Ω +) }. In [3, Thm ], it is shown that the essential spectrum of the Neumann Hamiltonian in a bounded region with smooth boundary is empty. The condition to the boundary can be generalized to our case, i.e., to the piecewise smooth boundary, such that the angle at each vertex lies in an open interval (, 2π) (cf [3, Exercise 7.3]). The Robin boundary conditions are bounded from bellow by Neumann ones, in the sense that ψ D(Q Ωc α ), QΩc α [ψ] QΩc N [ψ]. This inequality holds also for the lower bound of the spectrum of operators associated with this forms. Therefore the operator Hα Ωc has empty essential spectrum. Since it can be established by the same way as Theorem 4.7 that inf σ ess (H Ω α ) = inf σ ess (H Ω + α ) = E1 α, we get the desired claim. 27
33 5.4 The existence of bound states In this section we show that the non-trivial curvature of the strip pushes the spectral threshold down the value E α 1. Theorem 5.4. Suppose (r1), (r2). If k and α >, then inf σ( H α ) < E α 1. Proof. By the Rayleigh-Ritz principle (Theorem 2.2), it is enough to find a function ψ α D( Q α ) such that We define S α [ψ α ] := Q α [ψ α ] E α 1 ψ α 2 L 2 (Ω,(1 uk)dsdu) <. ψ α n (s, u) := ϕ n(s)χ α 1 (u), where ϕ n (s) is defined by 1 if s [, n), ϕ n (s) := 2 s /n if s [n, 2n), if s [2n, ). Then (4) S α [ψn Ω α ] = ϕ n (s) 2 χ α dsdu 1 (u)2 1 uk(s) + + ϕ n (s) 2 χ α 1 (u) 2 (1 uk(s))dsdu+ Ω + α ϕ n (s) 2 χ α 1 ()2 ds+ R + α ϕ n (s) 2 χ α 1 (d) 2 (1 dk(s))ds R E1 α ϕ n (s) 2 χ α 1 (u)2 (1 uk(s))dsdu. (41) Ω The second term at the r.h.s. can be written by integration by parts like ϕ n (s) 2 χ α 1 (u) 2 (1 uk(s))dsdu = ϕ n (s) 2 χ α 1 (d)χ α 1 (d)(1 dk(s))ds Ω R ϕ n (s) 2 χ α 1 ()χ α 1 ()ds ϕ n (s) R Ω 2 χ α 1 (u)χ α 1 (u)(1 uk(s))dsdu+ + ϕ n (s) 2 χ α 1 (u)χ α 1 (u)k(s)dsdu (42) Ω 28
34 Since χχ = 1 2 (χ2 ), the last term in (42) is ϕ n (s) 2 χ α 1 (u)χ α 1 (u)k(s)dsdu = 1 Ω 2 (χα 1 (d) 2 χ α 1 () 2 ) ϕ n (s) 2 k(s)ds and it is equal to zero by Lemma 4.4. Substituting the equalities to (42), we get Since the function χ α 1 (u) = E 1χ α 1 (u) χ α 1 () = αχα 1 () χ α 1 (d) = αχ α 1 (d). (43) S α [ψn] α = ϕ n (s) 2 χ α 1 (u) 2 dsdu Ω 1 uk(s). d χ α 1 (u) 2 1 uk(s) du d χ α 1 (u) 2 1 uk(s) du 1, 1 d k + f(s) = d χ α 1 (u)2 1 uk(s) du is bounded. Moreover ϕ n L 2 (R) and we have the limit n S α [ψ α n ] n. Now we modify the function ψ n in a curved part of the waveguide by defining ψn,ε α (s, u) := ψα n (s, u) + ερ(s, u), where ε R and ρ(s, u) := φ(s)uχ α 1 (u). Here φ C (R) is a real, non-negative, non-zero function with compact support contained in a bounded interval, where k and does not change sign. We have S α [ψ α n,ε ] = S α[ψ α n ] + 2εS α(ρ, ψ α n ) + ε2 S α [ρ]. R 29
35 The first term at the r.h.s. tends to zero as n and the last one does not depend on n. So we need to calculate the central term: S α (ρ, ψn Ω α ) = ϕ n (s)uχ α dsdu 1 (u)2 φ(s) 1 uk(s) + + ϕ n (s) χ α 1 (u)φ(s)χα 1 (u)(1 uk(s))dsdu+ Ω + ϕ n (s)uχ α 1 (u)2 φ(s)(1 uk(s))dsdu+ Ω + α ϕ n (s)dχ α 1 (d)2 φ(s)(1 dk(s))ds R E 1 Ω ϕ n (s)uχ α 1 (u)2 φ(s)(1 uk(s))dsdu. (44) We can write the third term at the r.h.s by integration by parts like ϕ n (s)uχ α 1 (u) 2 φ(s)(1 uk(s))dsdu = Ω = ϕ n (s)dχ α 1 (d)χ α 1 (d)φ(s)(1 uk(s))ds R ϕ n (s)φ(s)u χ α 1 (u)χα 1 (u)(1 uk(s))dsdu Ω ϕ n (s)φ(s)χ α 1 (u) χ α 1 (u)(1 uk(s))dsdu+ Ω + ϕ n (s)φ(s)uχ α 1 (u)χα 1 (u)k(s)dsdu. (45) Ω Putting (43) to (44) we finally get S α (ρ, ψn Ω α ) = ϕ n (s)uχ α dsdu 1 (u)2 φ(s) 1 uk(s) + + ϕ n (s)φ(s)uχ α 1 (u)χα 1 (u)k(s)dsdu = Ω = ϕ n (s)uχ α dsdu 1 (u)2 φ(s) Ω 1 uk(s) ( dχ α 2 1 (d) 2 1 ) ϕ n (s)φ(s)k(s)ds. (46) R 3
36 Summing up, S α [ψ α n,ε ] n ε ( dχ α 1 (d)2 1 ) φ(s)k(s)ds + ε 2 Q α 1 [ρ]. (47) R Since the integral in 47 is non-zero by the construction of φ and the term in brackets is negative by Lemma 4.4 and Lemma 4.3, we can take ε sufficiently small so that the term at the r.h.s. is negative. Hence we choose n sufficiently large so that S α [ψ α n,ε] <. As a consequence of Theorem 5.4 and Theorem 5.1 we get following corollary: Corollary 5.5. Suppose (r1),(r2), and α >. If the strip is not straight but the assumption (k) holds, then H α has at least one eigenvalue of finite multiplicity below its essential spectrum [E α 1, ), i.e., σ disc ( H α ). Remark 5.6. Notice that for Neumann boundary conditions, i.e. α =, the spectrum is purely essential and there are no bound states. Indeed, in the same way as in Theorem 5.1, one can prove that σ ess ( H ) = [E 1, ) = [, ). 6 Conclusion We were interested in spectral properties of a curved planar waveguide, subject to Robin boundary conditions. We demonstrated the stability of the essential spectrum under the condition that the waveguide is curved only locally (cf Theorem 5.1). As the main result, we proved that there always exist quantum bound states bellow the bottom of the essential spectrum whenever the waveguide is not straight (cf Theorem 5.4 and Corollary 5.5). The present thesis was motivated by the theory of quantum waveguides where the bound states are known to exist in waveguides with Dirichlet (and certain Dirichlet- Neumann) boundary coditions. The principal objective of the thesis was to demonstrate that the bound states exist also for other kinds of boundary conditions. The Robin boundary conditions may in principle model different types of interface in materials or approximate very thin layer structures. There are several possible directions to which the results of the present thesis could be extended. For instance, one can consider the case where the boundary conditions are not uniform, letting the parameter α depend on the longitudinal coordinate s. It is also possible to consider the Robin Laplacian in higher-dimensional tubes. Finally, a detailed numerical study of the bound states would help to understand the interplay between the geometry and spectrum of quantum waveguides with Robin boundary conditions. 31
37 References [1] Adams, R. A., Sobolev spaces, Academic Press, New York, [2] Bendali, A. and Lemrabet, K., The effect of a thin coating on the scattering of a time-harmonic wave for the Helmholtz equation, SIAM J. Appl. Math., 56, 6 (Dec. 1996), [3] Davies, E. B., Spectral theory and differential operators, Camb. Univ. Press, Cambridge, [4] Dittrich, J. and Kříž, J., Curved planar quantum wires with Dirichlet and Neumann boundary conditions, J. Phys. A, 35 (22), L [5] Duclos, P. and Exner, P., Curvature-induced bound states in quantum waveguides in two and three dimensions, Rev. Math. Phys., 7 (1995), [6] Engquist, B. and Nedelec J. C., Effective boundary conditions for electro-magnetic scattering in thin layers, Rapport interne 278, CMAP [7] Exner, P. and Šeba, P., Bound states in curved quantum waveguides, J. Math. Phys., 3 (1989), [8] Goldstone, J. and Jaffe, R. L., Bound states in twisting tubes, Phys. Rev. B, 45 (1992), [9] Kato, T., Perturbation theory for linear operators, Springer-Verlag, Berlin, [1] Krejčiřík, D. and Kříž, J., On the spectrum of curved planar waveguides, Publ. RIMS, Kyoto Univ., 41 (25), [11] Londergan, J. T., Carini, J. P. and Murdock, D. P., Binding and scattering in twodimensional systems, Lect. Note in Phys., m6, Springer, Berlin, [12] Rektoris, K., Přehled užité matematiky, Prometheus, Prague,
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Stability of Tikhonov Regularization Class 07, March 2003 Alex Rakhlin
 Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Rachunek lambda, zima
 Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Unitary representations of SL(2, R)
 Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Roland HINNION. Introduction
 REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
O przecinkach i nie tylko
 O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Title: On the curl of singular completely continous vector fields in Banach spaces
 Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
harmonic functions and the chromatic polynomial
 harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
Steeple #3: Gödel s Silver Blaze Theorem. Selmer Bringsjord Are Humans Rational? Dec RPI Troy NY USA
 Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
 aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Faculty of Nuclear Sciences and Physical Engineering Department of Physics. Bachelor thesis
 CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of Nuclear Sciences and Physical Engineering Department of Physics Bachelor thesis Operator theoretic approach to the theory of metamaterials Filip Hložek Supervisor:
CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of Nuclear Sciences and Physical Engineering Department of Physics Bachelor thesis Operator theoretic approach to the theory of metamaterials Filip Hložek Supervisor:
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
 Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition)
 Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2)
 Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Click here if your download doesn"t start automatically Emilka szuka swojej gwiazdy / Emily Climbs (Emily, #2) Emilka szuka swojej gwiazdy / Emily
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Dupin cyclides osculating surfaces
 Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
Installation of EuroCert software for qualified electronic signature
 Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Wybrzeze Baltyku, mapa turystyczna 1: (Polish Edition)
 Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Permutability Class of a Semigroup
 Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Model standardowy i stabilność próżni
 Model standardowy i stabilność próżni Marek Lewicki Instytut Fizyki teoretycznej, Wydzia l Fizyki, Uniwersytet Warszawski Sympozjum Doktoranckie Warszawa-Fizyka-Kraków, 4 Marca 2016, Kraków Na podstawie:
Model standardowy i stabilność próżni Marek Lewicki Instytut Fizyki teoretycznej, Wydzia l Fizyki, Uniwersytet Warszawski Sympozjum Doktoranckie Warszawa-Fizyka-Kraków, 4 Marca 2016, Kraków Na podstawie:
SubVersion. Piotr Mikulski. SubVersion. P. Mikulski. Co to jest subversion? Zalety SubVersion. Wady SubVersion. Inne różnice SubVersion i CVS
 Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Vacuum decay rate in the standard model and beyond
 KEK-PH 2018 Winter, Dec 4-7 2018 Vacuum decay rate in the standard model and beyond Yutaro Shoji (KMI, Nagoya U.) Phys. Lett. B771(2017)281; M. Endo, T. Moroi, M. M. Nojiri, YS JHEP11(2017)074; M. Endo,
KEK-PH 2018 Winter, Dec 4-7 2018 Vacuum decay rate in the standard model and beyond Yutaro Shoji (KMI, Nagoya U.) Phys. Lett. B771(2017)281; M. Endo, T. Moroi, M. M. Nojiri, YS JHEP11(2017)074; M. Endo,
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Counting quadrant walks via Tutte s invariant method
 Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Lecture 20. Fraunhofer Diffraction - Transforms
 Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
RESONANCE OF TORSIONAL VIBRATION OF SHAFTS COUPLED BY MECHANISMS
 SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is
 1. Introduction Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is made of aluminum and steel mesh as one of the coolest enclosures available. It s also small
1. Introduction Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is made of aluminum and steel mesh as one of the coolest enclosures available. It s also small
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku
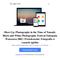 Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering
 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering Geometrically induced properties of the ground state of quantum mechanical Hamiltonians with contact interactions
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering Geometrically induced properties of the ground state of quantum mechanical Hamiltonians with contact interactions
DOI: / /32/37
 . 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
. 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip)
 Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Relaxation of the Cosmological Constant
 Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Jak zasada Pareto może pomóc Ci w nauce języków obcych?
 Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
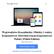 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
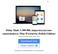 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS.
 ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI
 Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Bergman Kernel and Kobayashi Pseudodistance in Convex Domains
 Bergman Kernel and Kobayashi Pseudodistance in Convex Domains Zbigniew B locki Uniwersytet Jagielloński, Kraków, Poland http://gamma.im.uj.edu.pl/ blocki (Joint work with W lodzimierz Zwonek) NORDAN Reykjavík,
Bergman Kernel and Kobayashi Pseudodistance in Convex Domains Zbigniew B locki Uniwersytet Jagielloński, Kraków, Poland http://gamma.im.uj.edu.pl/ blocki (Joint work with W lodzimierz Zwonek) NORDAN Reykjavík,
OBWIESZCZENIE MINISTRA INFRASTRUKTURY. z dnia 18 kwietnia 2005 r.
 OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
How to translate Polygons
 How to translate Polygons Translation procedure. 1) Open polygons.img in Imagine 2) Press F4 to open Memory Window 3) Find and edit tlumacz class, edit all the procedures (listed below) 4) Invent a new
How to translate Polygons Translation procedure. 1) Open polygons.img in Imagine 2) Press F4 to open Memory Window 3) Find and edit tlumacz class, edit all the procedures (listed below) 4) Invent a new
Poland) Wydawnictwo "Gea" (Warsaw. Click here if your download doesn"t start automatically
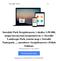 Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
DODATKOWE ĆWICZENIA EGZAMINACYJNE
 I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
Previously on CSCI 4622
 More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
Compressing the information contained in the different indexes is crucial for performance when implementing an IR system
 4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
Camspot 4.4 Camspot 4.5
 User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
EPS. Erasmus Policy Statement
 Wyższa Szkoła Biznesu i Przedsiębiorczości Ostrowiec Świętokrzyski College of Business and Entrepreneurship EPS Erasmus Policy Statement Deklaracja Polityki Erasmusa 2014-2020 EN The institution is located
Wyższa Szkoła Biznesu i Przedsiębiorczości Ostrowiec Świętokrzyski College of Business and Entrepreneurship EPS Erasmus Policy Statement Deklaracja Polityki Erasmusa 2014-2020 EN The institution is located
ZDANIA ANGIELSKIE W PARAFRAZIE
 MACIEJ MATASEK ZDANIA ANGIELSKIE W PARAFRAZIE HANDYBOOKS 1 Copyright by Wydawnictwo HANDYBOOKS Poznań 2014 Wszelkie prawa zastrzeżone. Każda reprodukcja lub adaptacja całości bądź części niniejszej publikacji,
MACIEJ MATASEK ZDANIA ANGIELSKIE W PARAFRAZIE HANDYBOOKS 1 Copyright by Wydawnictwo HANDYBOOKS Poznań 2014 Wszelkie prawa zastrzeżone. Każda reprodukcja lub adaptacja całości bądź części niniejszej publikacji,
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz
![[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz](/thumbs/101/148499235.jpg) [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
Lecture 18 Review for Exam 1
 Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION
 Glasgow Math. J.: page 1 of 12. C Glasgow Mathematical Journal Trust 2012. doi:10.1017/s0017089512000353. EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION SEAN SATHER-WAGSTAFF Mathematics Department,
Glasgow Math. J.: page 1 of 12. C Glasgow Mathematical Journal Trust 2012. doi:10.1017/s0017089512000353. EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION SEAN SATHER-WAGSTAFF Mathematics Department,
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition)
 Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Egzamin maturalny z języka angielskiego na poziomie dwujęzycznym Rozmowa wstępna (wyłącznie dla egzaminującego)
 112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
Complex Analysis Theorems
 Complex Analysis Theorems Chapter : Complex Numbers Proposition. (Basic Identities and Inequalities). Let z, z, z 2, z 3 C. Let z = x + iy = r(cos θ + i sin θ) and z k = x k + iy k = r k (cos θ k + i sin
Complex Analysis Theorems Chapter : Complex Numbers Proposition. (Basic Identities and Inequalities). Let z, z, z 2, z 3 C. Let z = x + iy = r(cos θ + i sin θ) and z k = x k + iy k = r k (cos θ k + i sin
Arrays -II. Arrays. Outline ECE Cal Poly Pomona Electrical & Computer Engineering. Introduction
 ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
