Densities of the Raney Distributions
|
|
|
- Emilia Wrona
- 6 lat temu
- Przeglądów:
Transkrypt
1 Documenta Math Densities of the Raney Distributions Wojciech M lotkowski 1, Karol A. Penson 2, Karol Życzkowski3 Received: October 7, 2012 Revised: November 2, 2013 Communicated by Friedrich Götze Abstract. We prove that if p 1 and 0 < r p then the sequence ) mp+r r m mp+r is positive definite. More precisely, it is the moment sequence of a probability measure µp, r) with compact support contained in [0, + ). This family of measures encompasses the multiplicative free powers of the Marchenko-Pastur distribution as well as the Wigner s semicircle distribution centered at x = 2. We show that if p > 1 is a rational number and 0 < r p then µp,r) is absolutely continuous and its density W p,r x) can be expressed in terms of the generalized hypergeometric functions. In some cases, including the multiplicative free square and the multiplicative free square root of the Marchenko-Pastur measure, W p,r x) turns out to be an elementary function Mathematics Subject Classification: Primary 44A60; Secondary 33C20 Keywords and Phrases: Mellin convolution, free convolution, Meijer G-function, generalized hypergeometric function. 1 W. M. is supported by the Polish National Science Center grant No. 2012/05/B/ST1/ K. A. P. acknowledges support from PAN/CNRS under Project PICS No and from Agence Nationale de la Recherche Paris, France) under Program PHYSCOMB No. ANR-08-BLAN K. Ż. is supported by the Grant DEC-2011/02/A/ST1/00119 of Polish National Centre of Science.
2 1574 W. M lotkowski, K. A. Penson, K. Życzkowski Introduction For p, r R we define the Raney numbers or two-parameter Fuss-Catalan numbers) by A m p,r) := r m 1 mp+r i), 1) m! i=1 A 0 p,r) := 1. We can also write ) mp+r r A m p,r) = m mp+r, 2) unless mp+r = 0), where the generalized binomial is defined by ) a := aa 1)...a m+1). m m! Let B p z) denote the generating function of the sequence {A m p,1)} m=0, the Fuss numbers of order p: B p z) := A m p,1)z m, 3) m=0 convergent in some neighborhood of 0. For example Lambert showed that B 2 z) = B p z) r = z. 4) A m p,r)z m, 5) m=0 see [9]. These generating functions also satisfy B p z) = 1+zB p z) p, 6) which reflects the identity A m p,p) = A m+1 p,1), and B p z) = B p r zbp z) r). 7) Using the free probability theory see [28, 18, 6]) it was shown in [16] that if p 1 and 0 r p then the sequence {A m p,r)} m=0 is positive definite, i.e. is the moment sequence of a probability measure µp, r) on R. Moreover, µp, r) has compact support and therefore is unique) contained in the positive half-line [0, ) for example µp,0) = δ 0 ). The measures µp,r) satisfy some interesting relations, for example µp 1,r) µ1+p 2,1) = µp 1 +rp 2,r) 8)
3 Densities of the Raney Distributions 1575 and µp,r) µp+s,s) = µp+s,r+s), 9) see [16], where and denotes the multiplicative free and the monotonic convolution see [17]). A relation analogous to 9) is also satisfied by the threeparameter family of distributions studied by Arizmendi and Hasebe [4]. Among the measures µp, r) perhaps the most important is the Marchenko- Pastur called also the free Poisson) distribution µ2,1) = 1 4 x dx on [0,4], 10) 2π x which plays an important role in the theory of random matrices, see [29, 10, 11, 2, 1, 5]. It was proved in [1] that the multiplicative free power µ2,1) n = µn+1,1)is the limit ofthe distribution ofsquaredsingularvaluesof the power G n of a random matrix G, when the size of the matrix G goes to infinity. The moments of µ2,1), A m 2,1) = ) 2m+1 m /2m+1), are called Catalan numbers and play an important role in combinatorics, see A in OEIS [24]. In this paper we aregoing to provepositive definiteness of{a m p,r)} m=0 using more classical methods. Namely, we show that if p > 1, 0 < r p and if p is a rational number then µp, r) is absolutely continuous and can be represented as Mellin convolution of modified beta measures. Next we provide a formula for the density W p,r x) of µp,r) in terms of the Meijer G-function and of the generalized hypergeometric functions cf. [30, 21], where p was assumed to be an integer). This allows us to draw graphs of these densities and, in some particular cases, to express W p,r x) as an elementary function. Let us mention that the measures µ2,1) p = µ1+p,1) were also studied by Banica, Belinschi, Capitaine and Collins [5] as a special case of the free Bessel laws. They showed in particular that for p > 0 this measure is absolutely continuous and its support is [0,p + 1) p+1 p p ]. Liu, Song and Wang [14] found a formula expressing the density of µ2,1) n, n natural, as integral of a certain kernel over [0,1] n. Recently Haagerup and Möller [12] studied a twoparameter family µ α,β, α,β > 0, of probability measures. The measures µ α,0 coincide with our µ1+α,1), but if β > 0 then µ α,β has noncompact support, so it does not coincide with any of µp,r). The authors found a formula for the density function of µ α,β, which in the case of W 1+p,1 reads as follows: sin p+1 ) p+1)t) W 1+p,1 sintsin p = sin2 tsin p 1 pt) pt) πsin p p+1)t), 11) for 0 < t < π/p +1). It can be used for drawing the graph of W 1+p,1 x) by computer.
4 1576 W. M lotkowski, K. A. Penson, K. Życzkowski 1 Preliminaries For probability measures µ 1, µ 2 on the positive half-line [0, ) the Mellin convolution is defined by µ 1 µ 2 )A) := A xy)dµ 1 x)dµ 2 y) 12) for every Borel set A [0, ). This is the distribution of product X 1 X 2 of two independent nonnegative random variables with X i µ i. In particular, µ δ c c > 0) is the dilation of µ: ) 1 µ δ c )A) = D c µa) := µ c A. If µ has density fx) then D c µ) has density fx/c)/c. If both the measures µ 1,µ 2 have all moments finite then so has µ 1 µ 2 and s m µ i ) := 0 x m dµ i x) s m µ 1 µ 2 ) = s m µ 1 ) s m µ 2 ) for all m. If µ 1,µ 2 are absolutely continuous, with densities f 1,f 2 respectively, then so is µ 1 µ 2 and its density is given by the Mellin convolution: f 1 f 2 )x) := 0 f 1 x/y)f 2 y) dy y. We will need the following modified beta measures: Lemma 1.1. Let u,v,l > 0. Then { Γu+n/l)Γu+v) Γu+v +n/l)γu) } is the moment sequence of the probability measure bu+v,u,l) := on [0,1], where B is the Euler beta function. Proof. Using the substitution t = x l we obtain: Γu+n/l)Γu+v) Γu+v +n/l)γu) = Bu+n/l,v) Bu, v) = l Bu, v) n=0 l Bu,v) xlu 1 1 x l) v 1 dx 13) 1 0 = 1 Bu, v) 1 x lu+n 1 1 x l) v 1 dx. 0 t u+n/l 1 1 t) v 1 dt
5 Densities of the Raney Distributions 1577 Note that if X is a positive random variable whose distribution has density fx) and if l > 0 then the distribution of X 1/l has density lx l 1 fx l ). In particular, if the distribution of a random variable X is bu+v,u,1) then the distribution of X 1/l is bu+v,u,l). For u,l > 0 we also define 2 Applying Mellin convolution bu,u,l) := δ 1. 14) From now on we assume that p > 1 is a rational number, say p = k/l, with 1 l < k, and that 0 < r p. We will show that then A m p,r) is the moment sequence of a probability measure µp, r), which can be represented as Mellin convolution of modified beta measures. In particular, µp, r) is absolutely continuous and we will denote its density by W p,r. The case when p is an integer was studied in [21, 30]. First we need to express the numbers A m p,r) in a special form. Lemma 2.1. If p = k/l, where k,l are integers, 1 l < k and 0 < r p then ) r k r p A m p,r) = l j=1 Γβ j +m/l) 2πkp 1) p 1 k j=1 Γα j +m/l) cp)m, 15) where cp) = p p p 1) 1 p, j if 1 j l, α j = l 16) r +j l if l+1 j k, k l r+j 1 β j =, 1 j k. 17) k Proof. First we write: ) mp+r r m mp+r = rγmp+r) Γm+1)Γmp m+r+1). 18) Now we apply the Gauss s multiplication formula: Γnz) = 2π) 1 n)/2 n nz 1/2 Γz)Γ z + 1 ) Γ n to get: m Γmp+r) = Γ k l + r k )) = 2π) 1 k)/2 k mk/l+r 1/2 k Γm+1) = Γ l m+1 ) l j=1 z + 2 n m Γ + l = 2π) 1 l)/2 l m+1/2 l )...Γ z + n 1 ) n j=1 ) r+j 1, k m Γ + j ) l l
6 1578 W. M lotkowski, K. A. Penson, K. Życzkowski and m Γmp m+r+1) = Γ k l) + r+1 )) l k l = 2π) 1 k+l)/2 k l) mk l)/l+r+1/2 k j=l+1 m Γ + l ) r+j l. k l It remains to use them in 18). In order to apply Lemma 1.1 we need to modify enumeration of α s. Lemma 2.2. For 1 i l+1 denote i 1)k j i := +1, l where is the floor function, so that 1 = j 1 < j 2 <... < j l < k < k +1 = j l+1. For 1 j k define α j = i l r+j i k l if j = j i, 1 i l, if j i < j < j i+1. 19) Then the sequence { α j } k j=1 is a rearrangement of {α j} k j=1. Moreover, if 0 < r p = k/l then we have β j α j for all j k. Proof. It is easy to verify the first statement. Assume that j = j i for some i l. We have to show that which is equivalent to r +j i 1 k i l, ki 1) lr+l ki. l The latter is a consequence of the fact that x x and the assumption that r p = k/l. Now assume that j i < j < j i+1. We ought to show that which is equivalent to r+j 1 k r+j i, k l lr+lj +k l ki 0.
7 Densities of the Raney Distributions 1579 Using the inequality x +1 > x we obtain lj +k l ki lj i +1)+k l ki which completes the proof, as r > 0. = lj i +k ki > ki 1)+k ki = 0, Now we are ready to prove the main theorem of this section. Theorem 2.3. Suppose that p = k/l, where k,l are integers, 1 l < k, and that r is a real number such that 0 < r p. Then there exists a unique probability measure µp,r) such that 1) is its moment sequence. Moreover µp, r) can be represented as the following Mellin convolution: where µp,r) = b α 1,β 1,l)... b α k,β k,l) δ cp), cp) := p p p 1) p 1. Consequently, µp, r) is absolutely continuous and its support is [0, cp)]. It is easy to see that the density function is positive on 0,cp)). The representation of densities in the form of Mellin convolution of modified beta measures was used in different context in [8], see its Appendix A. Example. For the Marchenko-Pastur measure we get the following decomposition: µ2,1) = b1,1/2,1) b2,1,1) δ 4, 20) where b1,1/2,1) has density 1/π x x 2 ) on [0,1], the arcsine distribution with the moment sequence 2m m) 4 m, and b2,1,1) is the Lebesgue measure on [0,1] with the moment sequence 1/m+1). Proof. In view of Lemma 2.1 and Lemma 2.2 we can write A m p,r) = D k j=1 Γβ j +m/l)γ α j ) Γ α j +m/l)γβ j ) cp)m for some constant D. Taking m = 0 we see that D = 1. Note that a part of the theorem illustrates a result of Kargin [13], who proved that if µ is a compactly supported probability measure on [0, ), with expectation 1 and variance V, and if L n denotes the supremum of the support of the multiplicative free convolution power µ n, then L n lim = ev, 21) n n where e = is the Euler s number. The Marchenko-Pastur measure µ2,1) has expectation and variance equal to 1 and µ2,1) n = µn+1,1), so
8 1580 W. M lotkowski, K. A. Penson, K. Życzkowski in this case L n = n+1) n+1 /n n this was also proved in [29] and [11]) and 21) holds. The density function for µp,r) will be denoted by W p,r x). Since A m p,p) = A m+1 p,1), we have W p,p x) = x W p,1 x), 22) for example W 2,2 x) = 1 x4 x) on [0,4], 23) 2π which is the semicircle Wigner distribution with radius 2, centered at x = 2. Now we can reprove the main result of [16]. Theorem 2.4. Suppose that p,r are real numbers satisfying p 1, 0 r p. Then there exists a unique probability measure µp, r), with compact support contained in [0,cp)], such that {A m p,r)} m=0 is its moment sequence. Proof. It follows from the fact that the class of positive definite sequence is closed under pointwise limits. Remark. In view of Theorem 2.1 in [5], for every p > 1 the measure µp,1) is absolutely continuous and its support is equal [0, cp)], see also [14, 12]. 3 Applying Meijer G-function The aim of this section is to describe the density function W p,r x) of µp,r) in terms of the Meijer G-function see [19] for example) and consequently, as a linear combination of generalized hypergeometric functions. We will see that in some particular cases W p,r can be represented as an elementary function. For p > 1, r > 0 define an analytic function φ p,r σ) = rγ σ 1)p+r ) Γσ)Γ σ 1)p 1)+r +1 ), which is well defined whenever σ 1)p+r is not a nonpositive integer. Note that φ p,1 σ +1) = φ p,p σ) and if m is a natural number then ) mp+r r φ p,r m+1) = m mp+r. Then we define W p,r as the inverse Mellin transform: W p,r x) = 1 2πi d+i d i x σ φ p,r σ)dσ, x > 0, if exists, see [25] for details. It turn out that if p > 1 is a rational number then W p,r can be expressed in terms of the Meijer G-function and its Mellin transform is φ p,r. For the theory of the Meijer G-functions we refer to [15, 23, 19].
9 Densities of the Raney Distributions 1581 Theorem 3.1. Suppose that p = k/l, where k,l are integers, 1 l < k and r > 0. Then W p,r x) is well defined and W p,r x) = rp r x l xp 1) r+1/2 2kπ Gk,0 k,k cp) l α ) 1,..., α k, 24) β 1,..., β k x 0,cp)), where cp) = p p p 1) 1 p and the parameters α j,β j are given by 16) and 17). Moreover, φ p,r is the Mellin transform of W p,r, namely for Rσ > 1 r/p. φ p,r σ) = cp) 0 x σ 1 W p,r x)dx, 25) If 0 < r p then W p,r x) > 0 for 0 < x < cp) and therefore W p,r is the density function of the probability distribution µp, r). Proof. Putting m = σ 1 in 15) we get φ p,r σ) = rp 1)p r 3/2 lp p r 2kπ k j=1 Γβ j 1/l+σ/l) k j=1 Γα j 1/l+σ/l) cp)σ. 26) Writing the right hand side as Φσ/l 1/l)cp) σ, using the substitution σ = lu + 1 and the definition of the Meijer G-function see [19] for example), we obtain W p,r x) = 1 2πi = lcp) 2πxi = d+i d i d+i d i Φσ/l 1/l)cp) σ x σ dσ rp r xp 1) r+1/2 2kπ Gk,0 k,k Φu) x l /cp) l) u du z α ) 1,..., α k, β 1,..., β k where z = x l /cp) l. Recall that for the Meijer function of type G k,0 k,k there is no restriction on the parameters and the integral converges for 0 < x < cp) see in [19]). On the other hand, substituting x = cp)t 1/l we can write cp) 0 x σ 1 W p,r x)dx rp r = p 1) r+1/2 2kπ rp r cp) σ 1 = lp 1) r+1/2 2kπ cp) x σ 2 G k,0 x l k,k cp) l α ) 1,..., α k dx. β 1,..., β k t σ 1)/l 1 G k,0 k,k t α ) 1,..., α k dt. β 1,..., β k
10 1582 W. M lotkowski, K. A. Penson, K. Życzkowski Since k j=1 β j α j ) = 3/2 < 0, so the assumptions of ) in [23], the third case, are satisfied and therefore the last integral is convergent provided r k = minβ j < R σ 1, l equivalently: Rσ > 1 r/p) and the whole expression is equal to the right hand side of 26). For the last statement we note that in view of Theorem 2.3, of the uniqueness part of the Riesz representation theorem for linear functionals on C[0, cp)] and of the Weierstrass approximation theorem, for 0 < r p the density function of µp,r) must coincide with W p,r. Now applying Slater s formula we can express W p,r as a linear combination of hypergeometric functions. Theorem 3.2. For p = k/l, with 1 l < k, r > 0, and x 0,cp)) we have k ah,k,l,r) W p,r x) = γk,l,r) ch,k,l,r) k F k 1 bh,k,l,r) )z z r+h 1)/k 1/l, where z = x l /cp) l, ch,k,l,r) = h=1 27) γk,l,r) = rp 1)p r 3/2 p p r, 28) 2kπ ) h 1 j=1 Γ j h k ) k j=h+1 Γ j h k l j=1 Γ j l r+h 1 k ) k j=l+1 Γ r+j l k l r+h 1 k and the parameter vectors of the hypergeometric functions are {r+h 1 ah,k,l,r) = j l } l { r+h 1 k l k bh,k,l,r) = {k +h j k } h 1 j=1, j=1 { k +h j, k } k j=h+1 ) r+j k k l ), 29) } k j=l+1 ), 30). 31) Proof. Putting z = x l /cp) l, and hence x = cp)z 1/l, we can rewrite 24) as W p,r x) = rp 1)p r 3/2 z 1/l p p r 2kπ Gk,0 k,k z α ) 1,..., α k, 32) β 1,..., β k x 0,cp)). Observe that for 1 i < j k the difference β j β i = j i)/k is never an integer. Therefore we can apply formula ) in [23] see also ) in [19] or formula 7) on page 145 in [15]), so that j h ch,k,l,r) = Γβ j β h ) k j=1 Γα j β h ),
11 Densities of the Raney Distributions 1583 which gives 29). For the parameter vectors we have and ah,k,l,r) j = 1+β h α j bh,k,l,r) j = 1+β h β j, j h, which leads to 30) and 31). Finally, the summand with index h is in addition multiplied by z β h 1/l. Theorem 3.1 and Theorem 3.2 are sufficient for drawing graphs of the functions W p,r with help of computer programs. In some cases however it is possible to express W p,r as an elementary function. The most tractable case is p = 2. We know already that W 2,1 x) = 1 4 x 2π x, W 2,2x) = 1 x4 x). 2π Now we can give a simple formula for W 2,r. Corollary 3.3. For p = 2, r > 0, the function W 2,r is W 2,r x) = sin r arccos ) x/4 πx 1 r/2, 33) x 0,4). If 0 < r 2 then W 2,r is the density function of the measure µ2,r). In particular for r = 1/2 and r = 3/2 we have 2 x W 2,1/2 x) =, 34) 2πx3/4 W 2,3/2 x) = x+1) 2 x. 35) 2πx 1/4 Note that if r > 2 then W 2,r x) < 0 for some values of x 0,4). Proof. We take k = 2, l = 1 so that c2) = 4, z = x/4 and γ2,1,r) = r2 r /8 π). Using the Euler s reflection formula and the identity Γ1+r/2) = Γr/2)r/2 we get Γ1/2) c1,2,1,r) = Γ1 r/2)γ1+r/2) = 2sinπr/2) r, π Γ 1/2) c2,2,1,r) = Γ 1 r)/2 ) Γ 1+r)/2 ) = 2cosπr/2). π
12 1584 W. M lotkowski, K. A. Penson, K. Życzkowski We also need formulas for two hypergeometric functions, namely r 2F 1 2, r 2 ; 1 ) 2 z = cosrarcsin z), 1+r 2F 1 2, 1 r 2 ; 3 ) 2 z = sinrarcsin z) r, z see and in [19]. Now we can write sinπr/2) cos rarcsin ) x/4 cosπr/2) sin rarcsin ) x/4 W 2,r x) = = πx 1 r/2 sin πr/2 rarcsin ) x/4 = πx 1 r/2 sin rarccos ) x/4. πx 1 r/2 For the special cases we use the identity sin 1 2 arccost)) = 1 t)/2, which is valid for 0 t 1. Remark. Note that W 2,1 x) 2 x = 1 x 4 W 2,1/2 = 4) 4 x. 36) 4πx3/4 It means that if X,Y are random variables such that X µ2,1) and Y µ2,1/2) then X 2 4Y. This can be also derived from the relation A m 2,1/2)4 m = A 2m 2,1) = ) 4n+1 2n /4n + 1), A in OEIS [24]. Hence A is the moment sequence of the density function 36), x 0,16). 4 Some particular cases In this part we will see that for k = 3 some densities still can be represented as elementary functions. We need two families of formulas cf in [19]). Lemma 4.1. For c 0, 1, 2,... we have c 2F 1 2, c 1 ) 2 ; c z = 2 c z ) 1 c, 37) c+1 2F 1 2, c 2 ) 2 ; c z = 2c 1 ) 1 c ) 1+ 1 z c 1+ 1 z. 38) c Proof. We know that 2 F 1 a,b; c z) is the unique function f which is analytic at z = 0, with f0) = 1, and satisfies the hypergeometric equation: z1 z)f z)+ [ c a+b+1)z ] f z) abfz) = 0 see [3]). Now one can check that this equation is satisfied by the right hand sides of 37) and 38) for given parameters a,b,c.
13 Now consider p = 3/2. Densities of the Raney Distributions 1585 Theorem 4.2. Assume that p = 3/2. Then for r = 1/2,1,3/2 we have W 3/2,1/2 x) = 1+ ) 2/3 1 4x 2 /27 1 ) 2/3 1 4x 2 /27 2 5/3 3 1/2 πx 2/3, 39) W 3/2,1 x) = 3 1/2 1+ ) 1/3 1 4x 2 /27 1 ) 1/3 1 4x 2 /27 2 4/3 πx 1/3 40) 1+ ) 2/3 1 4x 2 /27 1 ) 2/3 1 4x 2 / /2 x 1/3 2 5/3 π and, finally, W 3/2,3/2 x) = x W 3/2,1 x), with x 0,3 3/2). Proof. For arbitrary r we have W 3/2,r x) = 21 2r/3 sin 2πr/3 ) 3+2r 3F 3 3/2 r 2, r π 6 3, 2r 3 ; 2 3, 1 ) 3 z z r/3 1/2 24 2r)/3 rsin 1 2r)π/3 ) 5+2r 3F 3 3/2 r 2, 1+r π 6 3, 1 2r ; 4 3 3, 2 ) 3 z z r+1)/3 1/2 r1+2r)sin 1+2r)π/3 ) 7+2r 3F 2 1+2r)/3 3 3/2 r 2, 2+r π 6 3, 2 2r ; 5 3 3, 4 3 )z z r+2)/3 1/2, where z = 4x 2 /27. If r = 1/2 or r = 1 then one term vanishes and in the two others the hypergeometric functions reduce to 2 F 1. For r = 1/2 we apply 37) to obtain: W 3/2,1/2 x) = z 1/ /3 3 1/2 π 2 F 1 6, 1 3 ; 1 ) 3 z z1/ /3 3 1/2 π 2 F 1 6, 1 3 ; 5 ) 3 z = z 1/3 2 1/3 3 1/2 π 2 2/ z ) 2/3 z 1/3 2 5/3 3 1/2 π 22/ z ) 2/3 = z 1/ /2 π = z 1/ /2 π and this yields 39). For r = 1 we use 38): 1+ 1 z ) 2/3 z 1/ /2 π 1+ 1 z ) 2/3 z 1/3 W 3/2,1 x) = z 1/ /3 π 2 F 1 6, 2 3 ; 2 ) 3 z 2 3 1/2 π 1 1 z z ) 2/3 1 1 z ) 2/3 + z1/ /3 π 2 F 1 6, 1 3 ; 4 ) 3 z
14 1586 W. M lotkowski, K. A. Penson, K. Życzkowski = z 1/6 4π = z 1/6 4π Now we have ) 1/3 ) z 1/6 ) 1/3 ) 1+ 1 z 3 1 z z 3 1 z +1 4π ) 1/3 ) z 1/6 ) 1/3 ) 1+ 1 z 3 1 z z 3 1 z +1. 4π 1+ 1 z ) 1/3 3 1 z 1 ) = 1+ 1 z ) 1/ z 2 ) and similarly = 3z 1/3 1 1 z ) 2/ z ) 1/3 1 1 z ) 1/3 3 1 z+1 ) = 3z 1/ z ) 2/ z ) 1/3. Therefore W 3/2,1 x) = z 1/6 2π + 3z1/6 4π 1+ 1 z ) 1/3 1 1 z ) 1/3 ) 1+ 1 z ) 2/3 1 1 z ) 2/3 ), which entails 40). The last statement is a consequence of 22). The dilation D 2 µ3/2,1/2), with the density W 3/2,1/2 x/2)/2, is known as the Bures distribution, see 4.4) in [26]. The integer sequence ) 3m/2+1/2 4 4 m m A m 3/2,1/2)= n 3m+1, moments of the density function W 3/2,1/2 x/4)/4 on the interval 0,6 3), appears as A in [24] and counts the number of symmetric noncrossing connected graphs on 2n+1 equidistant nodes on a circle. The axis of symmetry is a diameter of a circle passing through a given node, see [7]. The measure µ3/2,1) is equal to µ2,1) 1/2, the multiplicative free square root of the Marchenko-Pastur distribution and the integer sequence ) 3m/2+1 4 m 4 m A m 3/2,1) = n 3m/2+1, moments of the density function W 3/2,1 x/4)/4 on 0,6 3), appears in [24] as A For the sake of completeness we also include the densities for the sequences A m 3,1) A in [24]) and A m 3,2) A006013), which have already appeared in [20, 21].
15 Densities of the Raney Distributions 1587 Theorem 4.3. Assume that p = 3. Then for r = 1,2,3 we have /3 1 4x/27) 2 2/3 x 1/3 W 3,1 x) = 2 4/3 3 1/2 πx 1+ ) 1/3, 41) 2/3 1 4x/ /3 1 4x/27) 2 4/3 x 2/3 W 3,2 x) = 2 5/3 3 3/2 πx 1+ ) 2/3 42) 1/3 1 4x/27 and, finally, W 3,3 x) = x W 3,1 x), with x 0,27/4). Proof. For arbitrary r we have W 3,r x) = 26 2r)/3 sin πr/3 ) 3 3 r π 24 2r)/3 rsin 1+r)π/3 ) 3 3 r π + rr 1)sin 1 r)π/3 ) 2 1+2r)/3 3 3 r π r 3F 2 3, 3 r 6, r 6 ; 2 3, 1 3 3F 2 1+r 3, 5 r 6, 2 r 3F 2 2+r 3, 7 r 6, 4 r ) z z r 3)/3 6 ; 4 3, 2 ) 3 z z r 2)/3 6 ; 5 3, 4 3 )z z r 1)/3, where z = 4x/27. For r = 1 and r = 2 we have similar reduction as in the previous proof. Here we will be using only 37). Taking r = 1 we get W 3,1 x) = 21/3 z 2/3 3 3/2 π which implies 41). Now we take r = 2: 1 2F 1 3, 1 6 ; 2 ) 3 z z 1/ /3 3 3/2 π 2 F 1 = z 2/3 ) 1/3 z 1/3 ) 1/ z 1+ 1 z 3 3/2 π 3 3/2 π ) 2/ z z 1/3 = 3 3/2 πz 2/ z ), 1/3 W 3,2 x) = z 1/3 2 1/3 3 1/2 π 2 F 1 1 6, 1 3 ; 1 ) 3 z z1/ /3 3 1/2 π 2 F 1 = z 1/3 ) 2/3 z 1/3 ) 2/ z 1+ 1 z 2 3 1/2 π 2 3 1/2 π ) 4/ z z 2/3 = 2 3 1/2 πz 1/ z ), 2/3 and this gives us 42). Finally we apply 22). 3, 1 6 ; 4 ) 3 z 6, 1 3 ; 5 ) 3 z Recall that the measure µ3,1) is equal to µ2,1) 2, the multiplicative free square of the Marchenko-Pastur distribution.
16 1588 W. M lotkowski, K. A. Penson, K. Życzkowski Figure 1: Raney distributionsw 3/2,r x) with values ofthe parameterr labeling each curve. For r > p solutions drawn with dashed lines are not positive. 5 Graphical representation of selected cases The explicit form of W p,r x) given in Theorem 3.2 permits a graphical visualization for any rational p > 0 and arbitrary r > 0. We shall represent some selected cases in Figures 1 9. These graphs which are partly negative are drawn as dashed curves. In Fig. 1 the graphs of the functions W 3/2,r x) for values of r ranging from 0.9 to 2.3 are given. For r 3/2 these functions are positive, otherwise they develop a negative part. In Fig. 2 we represent W 5/2,r x) for r ranging from 2 to 3.4. In Fig. 3 we display the densities W p,p x) for p = 6/5, 5/4, 4/3 and 3/2. All these densities are unimodal and vanish at the extremities of their supports. They can be therefore considered as generalizations of the Wigner s semicircle distribution W 2,2 x), see equation 23). In Fig. 4 we depict the functions W 4/3,r x), for values r ranging from 0.8 to 2.4. Here for r 1.4 negative contributions clearly appear. In Fig. 5 and 6 we present six densities expressible through elementary functions, namely W 3/2,r x) for r = 1/2,1,3/2, see Theorem 4.2 and W 3,r x) for r = 1,2,3, see Theorem 4.3. In Fig. 7 the set of densities W p,1 x) for five fractional values of p is presented. The appearance of maximum near x = 1 corresponds to the fact that µp,1) weakly converges to δ 1 as p 1 +. In Fig. 8 the fine details of densities W p,1 x) for p = 5/2,7/3,9/4,11/5, on a narrower range 2 x 4.5 arepresented. In Fig. 9 wedisplay the densities W p,1 x) forp = 2,5/2,3,7/2,4, near the upper edge of their respective supports, for 3 x 9.5.
17 Densities of the Raney Distributions 1589 Figure 2: As in Fig. 1 for Raney distributions W 5/2,r x). Figure 3: Diagonal Raney distributions W p,p x) with values of the parameter p labeling each curve.
18 1590 W. M lotkowski, K. A. Penson, K. Życzkowski Figure 4: The functions W 4/3,r x) for r ranging from 0.8 to 2.4. Figure 5: Raney distributionsw 3/2,r x) with values ofthe parameterr labeling each curve. The case W 3/2,1 x) represents MP 1/2, the multiplicative free square root of the Marchenko-Pastur distribution.
19 Densities of the Raney Distributions 1591 Figure 6: Raney distributions W 3,r x) with values of the parameter r labeling each curve. The case W 3,1 x) represents MP 2, the multiplicative free square of the Marchenko-Pastur distribution. Figure 7: Raney distributions W p,1 x) with values of the parameter p labeling each curve. The case W 3/2,1 x) represents the multiplicative free square root of the Marchenko Pastur distribution, MP 1/2.
20 1592 W. M lotkowski, K. A. Penson, K. Życzkowski Figure 8: Tails of the Raney distributions W p,1 x) with values of the parameter p labeling each curve. Figure 9: As in Fig. 8 for larger values of the parameter p.
21 Densities of the Raney Distributions 1593 Figure 10: Parameter plane p, r) describing the Raney numbers. The shaded set Σ corresponds to nonnegative probability measures µp, r). The vertical line p = 2 and the stars represent values of parameters for which W p,r x) is an elementary function. Here MP denotes the Marchenko Pastur distribution, MP s its s-th free mutiplicative power, B-the Bures distribution while SC denotes the semicircle law. For p > 1 the points p,p) on the upper edge of Σ represent the generalizations of the Wigner semicircle law, see Fig. 3. The Fig. 10 summarizes our results in the p > 0,r > 0 quadrant of the p,r) plane, describing the Raney numbers c.f. Fig. 5.1 in [16] and Fig. 7 in [21]). The shaded region Σ indicates the probability measures µp, r) i.e. where W p,r x) is a nonegativefunction). The vertical line p = 2 and the stars indicate the pairs p,r) for which W p,r x) is an elementary function, see Corollary 3.3, Theorem 4.2 and Theorem 4.3. The points 3/2,1) and 3,1) correspond to the multiplicative free powers MP 1/2 and MP 2 of the Marchenko-Pastur distribution MP. Symbol B at 3/2, 1/2) indicates the Bures distribution and SC at 2,2) denotes the semicircle law centered at x = 2, with radius 2. It is our pleasure to thank M. Bożejko, Z. Burda, K. Górska, I. Nechita and M. A. Nowak for fruitful interactions. References [1] N. Alexeev, F. Götze, A. Tikhomirov, Asymptotic distribution of singular values of powers of random matrices, Lith. Math. J ), [2] G. W. Anderson, A. Guionnet, O. Zeitouni, An introduction to random matrices, Cambridge Studies in Advanced Mathematics, 118. Cambridge University Press, Cambridge, 2010.
22 1594 W. M lotkowski, K. A. Penson, K. Życzkowski [3] G. E. Andrews, R. Askey, R. Roy, Special Functions, Cambridge University Press, Cambridge [4] O. Arizmendi, T. Hasebe, On a class of explicit Cauchy-Stieltjes transforms related to monotone stable and free Poisson laws, arxiv: , to appear in Bernoulli. [5] T. Banica, S. Belinschi, M. Capitaine, B. Collins, Free Bessel laws, Canad. J. Math ), [6] P. Biane, Free probability and combinatorics, Proceedings of the International Congress of Mathematics, Higher Ed. Press, Beijing 2002, Vol. II 2002), [7] P. Flajolet and M. Noy, Analytic combinatorics of non-crossing configurations, Discrete Math., ) [8] K. Górska, K. A. Penson, A. Horzela, G. H. E. Duchamp, P. Blasiak, A. I. Solomon, Quasiclassical asymptotics and coherent states for bounded discrete spectra, J. Math. Phys ), , 12 pp. [9] R. L. Graham, D. E. Knuth, O. Patashnik, Concrete Mathematics. A Foundation for Computer Science, Addison-Wesley, New York [10] U. Haagerup, F. Larsen, Brown s spectral distribution measure for R- diagonal elements in finite von Neumann algebras, J. Funct. Anal ), [11] U. Haagerup, S. Thorbjørnsen, A new application of random matrices: ExtC red F 2)) is not a group, Ann. of Math ), [12] U. Haagerup, S. Möller, The law of large numbers for the free multiplicative convolution, Operator Algebra and Dynamics, Nordforsk Network Closing Conference, Faroe Islands, May 2012, Springer Proceedings in Mathematics and Statistics, Vol. 58, Carlsen, T. M.; Eilers, S.; Restorff, G.; Silvestrov, S. Eds.), [13] V. Kargin, On asymptotic growth of the support of free multiplicative convolutions, Elec. Comm. Prob ), [14] D. Liu, C. Song, Z. Wang, On explicit probability densities associated with Fuss-Catalan numbers, Proc. Amer. Math. Soc. 139/ ) [15] Y. L. Luke, The Special Functions and Their Approximations, Vol. I. New York: Academic Press 1969). [16] W. M lotkowski, Fuss-Catalan numbers in noncommutative probability, Documenta Math )
23 Densities of the Raney Distributions 1595 [17] N. Muraki, Monotonic independence, monotonic central limit theorem and monotonic law of small numbers, Inf. Dim. Anal. Quantum Probab. Rel. Topics ) [18] A. Nica, R. Speicher, Lectures on the Combinatorics of Free Probability, Cambridge University Press, [19] F. W. J. Olver, D. W. Lozier, R. F. Boisvert, C. W. Clark, NIST Handbook of Mathematical Functions, Cambridge University Press, Cambridge [20] K. A. Penson, A. I. Solomon, Coherent states from combinatorial sequences, Quantum theory and symmetries, Kraków 2001, World Sci. Publ., River Edge, NJ, 2002, [21] K. A. Penson, K. Życzkowski, Product of Ginibre matrices: Fuss-Catalan and Raney distributions, Phys. Rev. E ) , 9 pp. [22] A. D. Polyanin, A. V. Manzhirov, Handbook of Integral Equations, CRC Press, Boca Raton, [23] A. P. Prudnikov, Yu. A. Brychkov, O. I. Marichev, Integrals and Series, Gordon and Breach, Amsterdam 1998) Vol. 3: More special functions. [24] N. J. A. Sloane, The On-line Encyclopedia of Integer Sequences, 2013), published electronically at: [25] I. N. Sneddon, The use of integral transforms, Tata Mac Graw-Hill Publishing Company, [26] H.-J. Sommers, K. Życzkowski, Statistical properties of random density matrices, J. Phys. A: Math. Gen ) [27] R. P. Stanley, Enumerative Combinatorics, vol. 2, Cambridge University Press, Cambridge [28] D. V. Voiculescu, K. J. Dykema, A. Nica, Free random variables, CRM, Montréal, [29] R. Wegmann, The asymptotic eigenvalue-distribution for a certain class of random matrices, J. Math. Anal. Appl ) [30] K. Życzkowski, K. A. Penson, I. Nechita, B. Collins, Generating random density matrices, J. Math. Phys ) , 20 pp.
24 1596 W. M lotkowski, K. A. Penson, K. Życzkowski W. M lotkowski Instytut Matematyczny, Uniwersytet Wroc lawski Plac Grunwaldzki 2/ Wroc law, Poland mlotkow@math.uni.wroc.pl K. A. Penson Laboratoire de Physique Théorique de la Matière Condensée LPTMC) Université Pierre et Marie Curie CNRS UMR 7600 Tour 13-5ième ét. Boîte Courrier place Jussieu F Paris Cedex 05 France penson@lptl.jussieu.fr K. Życzkowski Institute of Physics Jagiellonian University ul. Reymonta Kraków, Poland and Center for Theoretical Physics Polish Academy of Sciences al. Lotników 32/ Warszawa, Poland karol@tatry.if.uj.edu.pl
Fuss-Catalan numbers in noncommutative probability
 Fuss-Catalan numbers in noncommutative probability Wojciech M lotkowski (Wroc law) Bielefeld, 28.08.2018 Wojciech M lotkowski Fuss-Catalan numbers 28.08.2018 1 / 35 Abstract The generalized Fuss-Catalan
Fuss-Catalan numbers in noncommutative probability Wojciech M lotkowski (Wroc law) Bielefeld, 28.08.2018 Wojciech M lotkowski Fuss-Catalan numbers 28.08.2018 1 / 35 Abstract The generalized Fuss-Catalan
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Rachunek lambda, zima
 Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
Rachunek lambda, zima 2015-16 Wykład 2 12 października 2015 Tydzień temu: Własność Churcha-Rossera (CR) Jeśli a b i a c, to istnieje takie d, że b d i c d. Tydzień temu: Własność Churcha-Rossera (CR) Jeśli
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
O przecinkach i nie tylko
 O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Steeple #3: Gödel s Silver Blaze Theorem. Selmer Bringsjord Are Humans Rational? Dec RPI Troy NY USA
 Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Steeple #3: Gödel s Silver Blaze Theorem Selmer Bringsjord Are Humans Rational? Dec 6 2018 RPI Troy NY USA Gödels Great Theorems (OUP) by Selmer Bringsjord Introduction ( The Wager ) Brief Preliminaries
Title: On the curl of singular completely continous vector fields in Banach spaces
 Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Stability of Tikhonov Regularization Class 07, March 2003 Alex Rakhlin
 Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Unitary representations of SL(2, R)
 Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
 aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Gradient Coding using the Stochastic Block Model
 Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Gradient Coding using the Stochastic Block Model Zachary Charles (UW-Madison) Joint work with Dimitris Papailiopoulos (UW-Madison) aaacaxicbvdlssnafj3uv62vqbvbzwarxjsqikaboelgzux7gcaeywtsdp1mwsxeaepd+ctuxcji1r9w5984bbpq1gmxdufcy733bcmjutn2t1fawl5zxsuvvzy2t7z3zn29lkwyguktjywrnqbjwigntuuvi51uebqhjlsdwfxebz8qiwnc79uwjv6mepxgfcoljd88uiox0m1hvlnzwzgowymjn7tjyzertmvpareju5aqkndwzs83thawe64wq1j2httvxo6eopirccxnjekrhqae6wrkuuykl08/gmnjryqwsoqurubu/t2ro1jkyrzozhipvpz3juj/xjdt0ywxu55mina8wxrldkoetukairuekzbubgfb9a0q95fawonqkjoez/7lrdi6trzbcm7pqvwrio4yoarh4aq44bzuwq1ogcba4be8g1fwzjwzl8a78tfrlrnfzd74a+pzb2h+lzm=
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Compressing the information contained in the different indexes is crucial for performance when implementing an IR system
 4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
4.2 Compression Compressing the information contained in the different indexes is crucial for performance when implementing an IR system on current hardware it is typically much faster to read compressed
Curriculum Vitae doktorat z matematyki teoretycznej (za prace pt.,,macierzowy problem momentów ) grant IM PAN dla doktorantów.
 Curriculum Vitae Dane Osobowe Marcin J. Zygmunt adres zamieszkania: ul. Fliegera 18/26 40 060, Katowice tel: +48 693829707 e-mail: marcin.jakub.zygmunt@gmail.com data ur.: 08-02-1970 stan cywilny: kawaler
Curriculum Vitae Dane Osobowe Marcin J. Zygmunt adres zamieszkania: ul. Fliegera 18/26 40 060, Katowice tel: +48 693829707 e-mail: marcin.jakub.zygmunt@gmail.com data ur.: 08-02-1970 stan cywilny: kawaler
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
 Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
OBWIESZCZENIE MINISTRA INFRASTRUKTURY. z dnia 18 kwietnia 2005 r.
 OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
OBWIESZCZENIE MINISTRA INFRASTRUKTURY z dnia 18 kwietnia 2005 r. w sprawie wejścia w życie umowy wielostronnej M 163 zawartej na podstawie Umowy europejskiej dotyczącej międzynarodowego przewozu drogowego
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Counting quadrant walks via Tutte s invariant method
 Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Rev Źródło:
 KamPROG for AVR Rev. 20190119192125 Źródło: http://wiki.kamamilabs.com/index.php/kamprog_for_avr Spis treści Introdcution... 1 Features... 2 Standard equipment... 4 Installation... 5 Software... 6 AVR
KamPROG for AVR Rev. 20190119192125 Źródło: http://wiki.kamamilabs.com/index.php/kamprog_for_avr Spis treści Introdcution... 1 Features... 2 Standard equipment... 4 Installation... 5 Software... 6 AVR
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
SOME INTRIGUING LIMITS CONTINUATION
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2013 Seria: MATEMATYKA STOSOWANA z. 3 Nr kol. 1899 Piotr LORENC, Roman WITUŁA Institute of Mathematics Silesian University of Technology SOME INTRIGUING LIMITS CONTINUATION
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2013 Seria: MATEMATYKA STOSOWANA z. 3 Nr kol. 1899 Piotr LORENC, Roman WITUŁA Institute of Mathematics Silesian University of Technology SOME INTRIGUING LIMITS CONTINUATION
Wybrzeze Baltyku, mapa turystyczna 1: (Polish Edition)
 Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Installation of EuroCert software for qualified electronic signature
 Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
n [2, 11] 1.5 ( G. Pick 1899).
![n [2, 11] 1.5 ( G. Pick 1899). n [2, 11] 1.5 ( G. Pick 1899).](/thumbs/98/135090138.jpg) 1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
Mixed-integer Convex Representability
 Mixed-integer Convex Representability Juan Pablo Vielma Massachuse=s Ins?tute of Technology Joint work with Miles Lubin and Ilias Zadik INFORMS Annual Mee?ng, Phoenix, AZ, November, 2018. Mixed-Integer
Mixed-integer Convex Representability Juan Pablo Vielma Massachuse=s Ins?tute of Technology Joint work with Miles Lubin and Ilias Zadik INFORMS Annual Mee?ng, Phoenix, AZ, November, 2018. Mixed-Integer
Model standardowy i stabilność próżni
 Model standardowy i stabilność próżni Marek Lewicki Instytut Fizyki teoretycznej, Wydzia l Fizyki, Uniwersytet Warszawski Sympozjum Doktoranckie Warszawa-Fizyka-Kraków, 4 Marca 2016, Kraków Na podstawie:
Model standardowy i stabilność próżni Marek Lewicki Instytut Fizyki teoretycznej, Wydzia l Fizyki, Uniwersytet Warszawski Sympozjum Doktoranckie Warszawa-Fizyka-Kraków, 4 Marca 2016, Kraków Na podstawie:
Camspot 4.4 Camspot 4.5
 User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
Permutability Class of a Semigroup
 Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Journal of Algebra 226, 295 310 (2000) doi:10.1006/jabr.1999.8174, available online at http://www.idealibrary.com on Permutability Class of a Semigroup Andrzej Kisielewicz 1 Mathematical Institute, University
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Arrays -II. Arrays. Outline ECE Cal Poly Pomona Electrical & Computer Engineering. Introduction
 ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
Roland HINNION. Introduction
 REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
REPORTS ON MATHEMATICAL LOGIC 47 (2012), 115 124 DOI:10.4467/20842589RM.12.005.0686 Roland HINNION ULTRAFILTERS (WITH DENSE ELEMENTS) OVER CLOSURE SPACES A b s t r a c t. Several notions and results that
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
Lecture 20. Fraunhofer Diffraction - Transforms
 Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
POLITYKA PRYWATNOŚCI / PRIVACY POLICY
 POLITYKA PRYWATNOŚCI / PRIVACY POLICY TeleTrade DJ International Consulting Ltd Sierpień 2013 2011-2014 TeleTrade-DJ International Consulting Ltd. 1 Polityka Prywatności Privacy Policy Niniejsza Polityka
POLITYKA PRYWATNOŚCI / PRIVACY POLICY TeleTrade DJ International Consulting Ltd Sierpień 2013 2011-2014 TeleTrade-DJ International Consulting Ltd. 1 Polityka Prywatności Privacy Policy Niniejsza Polityka
DOI: / /32/37
 . 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
. 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
The Lorenz System and Chaos in Nonlinear DEs
 The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:.
 ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
CS 6170: Computational Topology, Spring 2019 Lecture 09
 CS 6170: Computtionl Topology, Spring 2019 Lecture 09 Topologicl Dt Anlysis for Dt Scientists Dr. Bei Wng School of Computing Scientific Computing nd Imging Institute (SCI) University of Uth www.sci.uth.edu/~beiwng
CS 6170: Computtionl Topology, Spring 2019 Lecture 09 Topologicl Dt Anlysis for Dt Scientists Dr. Bei Wng School of Computing Scientific Computing nd Imging Institute (SCI) University of Uth www.sci.uth.edu/~beiwng
SNP SNP Business Partner Data Checker. Prezentacja produktu
 SNP SNP Business Partner Data Checker Prezentacja produktu Istota rozwiązania SNP SNP Business Partner Data Checker Celem produktu SNP SNP Business Partner Data Checker jest umożliwienie sprawdzania nazwy
SNP SNP Business Partner Data Checker Prezentacja produktu Istota rozwiązania SNP SNP Business Partner Data Checker Celem produktu SNP SNP Business Partner Data Checker jest umożliwienie sprawdzania nazwy
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Complex Analysis Theorems
 Complex Analysis Theorems Chapter : Complex Numbers Proposition. (Basic Identities and Inequalities). Let z, z, z 2, z 3 C. Let z = x + iy = r(cos θ + i sin θ) and z k = x k + iy k = r k (cos θ k + i sin
Complex Analysis Theorems Chapter : Complex Numbers Proposition. (Basic Identities and Inequalities). Let z, z, z 2, z 3 C. Let z = x + iy = r(cos θ + i sin θ) and z k = x k + iy k = r k (cos θ k + i sin
 !850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
!850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
Zmiany techniczne wprowadzone w wersji Comarch ERP Altum
 Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
Previously on CSCI 4622
 More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip)
 Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
DODATKOWE ĆWICZENIA EGZAMINACYJNE
 I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
Hippo Boombox MM209N CD. Instrukcja obsługi User s Manual
 Hippo Boombox Instrukcja obsługi User s Manual OPIS PRZYCISKÓW: PL ON-OFF/MODE: 1. Włącz on/off: Naciśnij przycisk, aby włączyć urządzenie. Przytrzymaj dłużej, aby wyłączyć. 2. MODE: Wybierz źródło sygnału:
Hippo Boombox Instrukcja obsługi User s Manual OPIS PRZYCISKÓW: PL ON-OFF/MODE: 1. Włącz on/off: Naciśnij przycisk, aby włączyć urządzenie. Przytrzymaj dłużej, aby wyłączyć. 2. MODE: Wybierz źródło sygnału:
Zestawienie czasów angielskich
 Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Agnostic Learning and VC dimension
 Agnostic Learning and VC dimension Machine Learning Spring 2019 The slides are based on Vivek Srikumar s 1 This Lecture Agnostic Learning What if I cannot guarantee zero training error? Can we still get
Agnostic Learning and VC dimension Machine Learning Spring 2019 The slides are based on Vivek Srikumar s 1 This Lecture Agnostic Learning What if I cannot guarantee zero training error? Can we still get
Standardized Test Practice
 Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
harmonic functions and the chromatic polynomial
 harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
Probability definition
 Probability Probability definition Probability of an event P(A) denotes the frequency of it s occurrence in a long (infinite) series of repeats P( A) = A Ω Ω A 0 P It s s represented by a number in the
Probability Probability definition Probability of an event P(A) denotes the frequency of it s occurrence in a long (infinite) series of repeats P( A) = A Ω Ω A 0 P It s s represented by a number in the
Extraclass. Football Men. Season 2009/10 - Autumn round
 Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
Wydział Fizyki, Astronomii i Informatyki Stosowanej Uniwersytet Mikołaja Kopernika w Toruniu
 IONS-14 / OPTO Meeting For Young Researchers 2013 Khet Tournament On 3-6 July 2013 at the Faculty of Physics, Astronomy and Informatics of Nicolaus Copernicus University in Torun (Poland) there were two
IONS-14 / OPTO Meeting For Young Researchers 2013 Khet Tournament On 3-6 July 2013 at the Faculty of Physics, Astronomy and Informatics of Nicolaus Copernicus University in Torun (Poland) there were two
Dupin cyclides osculating surfaces
 Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
photo graphic Jan Witkowski Project for exhibition compositions typography colors : +48 506 780 943 : janwi@janwi.com
 Jan Witkowski : +48 506 780 943 : janwi@janwi.com Project for exhibition photo graphic compositions typography colors Berlin London Paris Barcelona Vienna Prague Krakow Zakopane Jan Witkowski ARTIST FROM
Jan Witkowski : +48 506 780 943 : janwi@janwi.com Project for exhibition photo graphic compositions typography colors Berlin London Paris Barcelona Vienna Prague Krakow Zakopane Jan Witkowski ARTIST FROM
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
MULTI CRITERIA EVALUATION OF WIRELESS LOCAL AREA NETWORK DESIGNS
 STUDIA INFORMATICA 2015 Volume 36 Number 2 (120) Remigiusz OLEJNIK West Pomeranian University of Technology, Szczecin, Faculty of Computer Science and Information Technology MULTI CRITERIA EVALUATION OF
STUDIA INFORMATICA 2015 Volume 36 Number 2 (120) Remigiusz OLEJNIK West Pomeranian University of Technology, Szczecin, Faculty of Computer Science and Information Technology MULTI CRITERIA EVALUATION OF
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
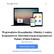 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:.
 ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
ZGŁOSZENIE WSPÓLNEGO POLSKO -. PROJEKTU NA LATA: APPLICATION FOR A JOINT POLISH -... PROJECT FOR THE YEARS:. W RAMACH POROZUMIENIA O WSPÓŁPRACY NAUKOWEJ MIĘDZY POLSKĄ AKADEMIĄ NAUK I... UNDER THE AGREEMENT
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz
![[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz](/thumbs/101/148499235.jpg) [assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition)
 Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Probabilistic Methods and Statistics. Computer Science 1 st degree (1st degree / 2nd degree) General (general / practical)
 MODULE DESCRIPTION Module code Module name Metody probabilistyczne i statystyka Module name in English Probabilistic Methods and Statistics Valid from academic year 2012/2013 MODULE PLACEMENT IN THE SYLLABUS
MODULE DESCRIPTION Module code Module name Metody probabilistyczne i statystyka Module name in English Probabilistic Methods and Statistics Valid from academic year 2012/2013 MODULE PLACEMENT IN THE SYLLABUS
