Tomasz Greczyło. The Use of Digital Techniques in an Investigation of Coupled Oscillations of a Wilberforce Pendulum
|
|
|
- Paweł Markiewicz
- 6 lat temu
- Przeglądów:
Transkrypt
1 Universiy of Wrocław Faculy of Physics and Asronomy Insiue of Experimenal Physics Tomasz Greczyło The Use of Digial Techniques in an Invesigaion of Coupled Oscillaions of a Wilberforce Pendulum The hesis wrien in Division of Physics Teaching Promoor: prof. Ewa D bowska Amserdam / Wrocław 00
2 The hesis wrien in academic year 000/00 during a sudy in frame of Socraes/Erasmus program a Amsel Insiue of Universiy of Amserdam
3 Conens I. PREFACE...4 II. ABSTRACT...4 STRESZCZENIE...4 INTRODUCTION...6 AIMS OF THE THESIS...6 III. SUBSTANCE...8 IV. CHAPTER. MECHANICS OF DEFORMABLE BODIES Mechanical Properies of Maerials Torional oscillaion Influence of a Mass of a Spring on is Saic and Dynamic Torsion and Bending of a Helical Spring Two Coupled Pendulums, Normal Modes and Beas Wilberforce Pendulum Fourier analysis...6 CHAPTER. CREATING VIDEO CLIPS, PREPARING TO MEASURE AND ANALYSING RESULTS Seing up Experimens and Recording Video Clips Ediing Digial Movies wih AdobePremiere Program Coach 5 and Daa Video MS Excel and is Fas Fourier Transform...3 CHAPTER 3. THE EXPERIMENTS AND RESULTS The Experimens Saemens of Experimenal Resuls Some Consideraion of Video Measuremen Accuracy Conclusions...47 CLOSING REMARKS...49 V. LITERATURE...50 VI. ACKNOWLEDGEMENTS...5 THANKS...5 PODZI Ę KOWANIA...5 3
4 I. Preface Absrac In his paper phases of work compleed before and during making measuremens on video clips and heir resuls are presened. I includes preparaion of experimens, recording and processing video clips, acquiring and analyzing resuls. Daa Video mode of Coach 5 was used o monior moion of Wilberforce pendulum and o measure changes of boh is coordinaes: verical displacemen of he bob and is roaional angle over ime. The experimens were carried ou wih differen combinaions of iniial condiions and recorded from wo camera perspecives. Fourier analysis of he resuls confirm he presence of wo frequencies corresponding o normal modes. The resuls of measuremens also show beas beween he normal modes and each of hem separaely and allow verifying he equaions of Wilberforce pendulum moion. Sreszczenie Niniejsza praca prezenuje zasosowanie echnik cyfrowych do badania ruchu wahadła Wilberforce'a oraz przedsawia wyniki pomiarów wideo drga podłu nych i drga skr nych (orsyjnych) ego wahadła. Auor opisuje poszczególne eapy pracy zwi zanej z ym rodzajem pomiarów j. przygoowanie eksperymenu, jego rejesracj za pomoc cyfrowej kamery wideo, obróbk filmów wideo, pomiary wideo z zasosowaniem programu Coach 5 oraz analiz FFT (szybka ransformaa Fouriera) wyników z u yciem arkusza kalkulacyjnego Excel. Eksperymeny zosały przeprowadzone dla przypadku rezonansu drga podłu nych i skr nych, dla ró nych kombinacji warunków pocz kowych: wydłu enia spr yny i skr cenia dysku wahadła. Wyniki umo liwiły znalezienie waro ci cz soliwo ci własnych układu, obserwacj dudnie zwi zanych z wys powaniem dwóch nieznacznie ró ni cych si cz soliwo ci oraz ka dego z dwóch modów oddzielnie, a ak e obliczenie sałej sprz enia. 4
5 W pierwszym rozdziale pracy prezenowane s zagadnienia eoreyczne niezb dne do analiycznego opisu ruchu wahadła Wilberforca, kóre obejmuj : podsawowe własno ci mechaniczne maeriałów, drgania orsyjne, wpływ masy spr yny na sayczne i dynamiczne charakerysyki wahadła spr ynowego, cinanie i zginanie spr yny spiralnej, wahadła sprz one, mody oraz dudnienia, wahadło Wilberforce'a, analiz Fouriera. Rozdział drugi opisuje proces worzenia cyfrowych filmów wideo, ich obróbk, przygoowanie do pomiarów oraz analiz wyników. W ej cz ci pracy szczególn uwag po wi cono programom kompuerowym u yym do: obróbki filmów cyfrowych Adobe Premierer, pomiarów wideo Coach 5, obróbki, prezenacji i analizy danych MS Excel. Rozdział rzeci zawiera opis badanego wahadła Wilberforca, przebieg do wiadcze oraz sposób obróbki danych. Orzymane wyniki s w ej cz ci przedsawione w abelach i na wykresach. Zasosowanie echniki cyfrowej obróbki obrazu oraz rejesracji danych pozwoliło na wizualizacj podłu nych i orsyjnych oscylacji wahadła Wilberforce'a; zgodnie ze sanem mojej wiedzy jes o pierwsza wizualizacja ego ypu. Zebrane wyniki zosały porównane z opublikowanymi w [] i pozwoliły zweryfikowa równania opisuj ce ruch wahadła Wilberforca oraz obliczy waro sałej sprz enia. Praca zawiera ak e sugesie jak usprawni proces orzymywania wyników podczas pomiarów wideo oraz jak zwi kszy ich dokładno, by mogły by w przyszło ci cz ciej wykorzysywane. Do pracy zał czone s dwie płyy CD zawieraj ce cyfrowe filmy wideo, na kórych auor dokonał pomiarów wideo. 5
6 II. Inroducion Aims of he Thesis Using digial echniques for invesigaions in naural phenomena is a modern mehod o develop many ineresing aspecs in physics as well as in oher disciplines. The use of digial cameras, hardware and sofware o produce a movie and powerful programs o ake measuremens from i opens new ways o explore a variey of scienific subjecs. Also developing of elecronic devices and significan improvemen of exising mehod of digial signal processing encourage us o ake heir advanages in (re)invesigaion of some imporan feaures of moion and/or many oher aspecs ha are relaed o i. A number of compuer programs such as Coach 5, VideoPoin, VideoGraph, Vidshell can be used o make measuremens of he posiion of an objec whose moion has been covered and produced as a video clip. Informaion abou x- and y-axis are usually gained from cerain frames of a scaled and made wih known frame rae digial movie. The presen hesis is aimed o inroduce video measuremen wih is useful ools ha can be used in science exploraion. As an example of such a program Video Measuremen of Coach 5 was chosen. The auhor would like o illusrae and describe in deails he use of digial echniques (video producion, video measuremen) wih a scienific example of Wilberforce pendulum moion. Therefore he preparaion of experimens, processing, measuring and analysing phases of work are described. He believes ha obained resuls allow making experimenal verificaion of his coupled pendulum moion. The paper shows ha i is possible o invesigae, wih sufficien accuracy, he ime dependence of he verical displacemen and he roaional angle of he pendulum, wih use of Coach 5 Video Measuremen. I will be, according o his knowledge, firs measuremen of he roaion angle of Wilberforce pendulum bob and he second visualisaion of is moion. Obained resuls are compared wih hose described in [] where experimenal verificaion of he imporan feaures of he moion of he Wilberforce pendulum and resuls of he experimen, during which longiudinal displacemen of is bob is measured wih a ulrasound sensor, are presened. 6
7 The auhor also presens verificaion of moion equaions of Wilberforce pendulum and calculaes he value of a coupling consan for measured device. 7
8 III. Subsance Chaper. Mechanics of Deformable Bodies.. Mechanical Properies of Maerials When exernal forces or momens of forces are applied o a solid body is shape and/or volume can be changed. If hese forces are no large he body will reurn o is original shape and volume immediaely afer he disoring forces are removed. This propery of a solid body is called elasiciy. If applied forces are sufficienly large he solid body can be permanenly sreched. This is called plasiciy. The way in which forces are applied deermines he elasic behaviour of a solid body. One can specify hree such ways, namely: longiudinal, volumeric and shearing forces. Firs he case when a parallelepiped block of uniform cross-secional area S is under compression due o equal and opposie forces applied along is z- axis will be considered. Figure.. ha was aken from [] shows such a siuaion. The problem can be Figure... A parallelepiped solid block of elasic maerial under ension described wih analogy if a ension force is applied o increase he lengh of he parallelepiped in he z-direcion. In boh cases he same effec is observed. When he compression force is increased from F n o F n + F, he iniial lengh of he parallelepiped z will change o z- z. Observing dependence of he fricional change in lengh (so called longiudinal srain defined as z/z) on he force per uni area (so called longiudinal sress defined as F/S) one can see ha as long as force is no oo large z/z is proporional o F/S. Tha is: z F z S or F S z = E z (..) where E is consan of proporionaliy wih uni [N/m ] and characerises he maerial from which he body is made. 8
9 The consan is called he Young modulus of he maerial and is defined by: z df E (..) S dz Examples of values of he Young modulus for a number of solids are given in a able.. [3]. Table... Elasic consans of some common subsances a 0 o C Subsance Young modulus Shear modulus bulk modulus N m - N m - N m - aluminium 7,0 0 0, ,6 0 0 brass,0 0 # 4,0 0 0,0 0 # copper,3 0 4,8 0 0,4 0 gold 7,8 0 0,7 0 0, 0 seel (mild), 0 8, 0 0,7 0 # denoes approximae values In a case of permanen sreching he relaionship beween sress and srain is no longer linear. The forces produce he dislocaion and process can no be compleely reversed. The poin a which he behaviour of a solid becomes non-linear and non-reversible is called he elasic limi. The second consideraion of elasic properies of solid deals wih volumeric sress. In his case forces ha produce he exension of a solid are applied o he body equally in all direcions. I causes a change in volume. Such a siuaion for a cube is shown in figure... ha was found in [3]. All forces F are applied perpendicularly o all six faces and produce a volume change V. Assuming ha he elasic limi is no exceeded one can see ha he volumeric srain V/V is proporional o he volumeric sress F/S, where S is he area of one face of a cube. I can be wrien as: Figure... A cubical solid block under a volumeric sress V V F S or F S V = K V (..3) where K is a consan of proporionaliy wih uni [N/m ] and called he bulk modulus. The consan is a characerisic of he maerial under sudy. 9
10 The bulk modulus is defined as: V df K (..4) S dv The minus sign is included so ha K is posiive because df/dv is always negaive (an increase of applied force causes a decrease in volume). Examples of he bulk modulus for a number of maerials are presened in able... As a las case he siuaion of a shearing sress will be considered. When equal and opposie forces are applied o opposie faces of a solid block i will ac showing differen elasic behaviour. Assume ha he elasic limi is no exceeded and he cuboid reurns o is original shape when he forces are removed. To invoke his effec one can consider he disorion of a solid cuboid by equal and opposie forces F s ha are applied angenially o opposie faces of a cuboid. The siuaion is shown in figure..3, which was aken from []. Figure..3. A solid parallelepiped block under a shearing sress The ne effec of such forces is ha he recangular faces of he parallelepiped in he plane of he applied forces become parallelogram. A force per uni area applied angenially is called a shearing sress. The corresponding shearing srain is defined (for a small z) as z/y or γ. Taking o accoun recen assumpion one can see ha he sress is proporional o srain: F F γ or = G γ S S (..5) where G is a consan of proporionaliy wih uni [N/m ]. The consan is characerisic of he maerial called a shear modulus and defined as: df G (..6) S dγ Examples of he shear modulus for a number of maerials are given in able... 0
11 As i is shown in figure.. he change in lengh z of a parallelepiped solid block in paricular and bodies of differen shape under a shearing sress in general is accompanying by changes of oher dimensions - x and y. For isoropic bodies he following equaion is valid: x y = x y z = ν (..6) z where ν is a consan of proporionaliy called Poisson s raio. The consan has no uni and for majoriy of maerials is enclosed beween 0, and 0,4. When during deformaion he change in volume does no ake place ν is equal o 0,5. The presened consans saisfy he equaion: E G = (..7) ( + ν ).. Torional oscillaion When rigid body is suspended from a verical lengh of wire (or a rod) ha is aached o a fixed poin and a small wis has been given o i and hen released from res one can observe orsional oscillaion. If angular displacemen is θ and resoring orque is proporional o i, T= -cθ, one can wrie an equaion: T dl d d d θ = ( I) = I = I = cθ (..) d d d d = where L is an angular momenum, indicaes angular velociy and I represens momen of ineria of he rigid body abou he axis of he wire or rod. Looking a a las par of he equaion one ges: d θ I + cθ = 0 (..) d This is an equaion of a simple harmonic oscillaor. The rigid body execues simple harmonic oscillaion abou wire s axis wih a period: I T = π (..3) c
12 A well-known example of a simple harmonic oscillaor is a spring oscillaor wih a mass m aached o a helical spring wih an elasic consan k. In his case he equaion deermining a period has a form: m T = π (..4) k.3. Influence of a Mass of a Spring on is Saic and Dynamic Usually calculaions of an elongaion or an oscillaion period of a spring pendulum are done wih an assumpion ha he spring is massless. In realiy his mass affecs pendulum moion. As in [4] and [5] firs a saic case will be discussed. To find he soluion one assumes ha l is he unloaded spring lengh, m represens is mass and k is an elasic consan of a spring. The elongaion of he uni of spring due o a force G = k l is: l G l = = (.3.) l lk Therefore porion of he lengh dz suffers an elongaion: Since: G ( dz) = dz l = dz lk (.3.) G ( dz) = k (.3.3) one can consider an elasic consan of a small porion of a spring lengh dz as: kl k = (.3.4) dz When a mass M is placed a he end of he spring he load acing o he elemen beween z and z+dz becomes equal o:
13 G`=(M+m (l-z)/l) g (.3.5) and i suffers an elongaion: G M + m( l z) / l ( dz) = = g dz (.3.6) k kl Inegraing according o z from z=0 o z=l one ges he oal elongaion of he spring: l = l 0 ( M + m / ) g dz = k (.3.7) I leads o conclusion ha in saic condiions he elongaion suffered by a non-null mass spring is equivalen o supposing he spring is massless and adding a mass equal o half he mass of he spring o he bob s mass M a is end. Elaboraing a dynamic case one sars wih assumpion ha mass M has been placed a he end of he spring, displaced from equilibrium posiion and hen released. So, oscillaions occur and he elemen of he spring dz suffers a deformaion du ha is produced by he force: besides: According o he equaion: one ges: kl u u F = k du = dz = kl dz z z (.3.8) F m df = dz dm = dz z l (.3.9) u df = dm (.3.0) hence: F m u dz = dz z l (.3.) d u kl z = m u l (.3.) 3
14 This is he equaion of a wave whose velociy is: V kl = (.3.3) m To porrai he elongaion u of he abscissa of a poin z and he force one can wrie: u(z,)=a sin(β z+ϕ) sin( +α) (.3.4) u F( z, ) = kl (.3.5) z where is an angular frequency and β = /V and α, β are phase angles. The boundary condiions a he upper and lower ends are: z = 0; u(0,) = 0 (.3.6a) u z = l; F( l, ) = M (.3.6b) which, when enered in o (.3.4) and (.3.5), wih assumpion ϕ = 0, gives: u(z,)=a sin(β z)sin( +α) (.3.7) F(z,)=klAβ cos(βz) sin( +α) (.3.8) Therefore: u( l, ) F ( l, ) = M = M Asin βl sin( + α) (.3.9) hence, =(klβ)/(m g(βl)) (.3.0) which, ogeher wih (.3.3) and definiion of β, gives an equaion : g(βl)=(m/m)βl (.3.) 4
15 This allows o conclude ha for each raio beween he mass M and spring mass m here is a se of soluions ha correspond o he differen modes of vibraion of a sysem. As he relaion M/m grows he soluions end o he value (βl) n =(n-)π, where n is he order number of a harmonics. For n= here is a fundamenal vibraion. When he mass of a spring m is exremely small in comparison o M he value of fundamenal (βl) ends o zero and equaion becomes he classical formula of a harmonic oscillaor formula (..4). In any oher case, one can wrie: =k/(m+m/d) (.3.) where m/d is a porion of whole mass of a spring m (D is an real number). When combined wih (.3.0) one obains: D = m M βl ( g( βl) βl) (.3.3) For m/m O, D = 3 and for m/m, D = π /,467. For a spring whose lengh is small compared o ¼ of he wavelengh of he characerisic vibraion wavelengh an assumpion ha he displacemens of he elemens of he spring are proporional o z can be made. In such a case, he whole sysem energy is given by: l l Az A m E = ( M A ) + dm = ( M A ) + z dz = A M + m 3 (.3.4) l l where M is a mass of a bob and A an ampliude of is displacemen from equilibrium posiion. I leads o conclusion ha in dynamic condiions one has o add a mass equal o one-hird of he mass of he spring o he bob s mass M a is end in order o obain he same energy. 5
16 .4. Torsion and Bending of a Helical Spring One can obain a helical spring by winding a few layers of a hin wire on a circular cylinder and hen removing he mandrel. Such a spring is presened in figure.4.a. ha was found in []. The wire in he diagram has been drawn wih a ribbon shape o indicae behaviour of he spring when force F or momen M are applied, bu he behaviour is independen of he acual shape. Figure.4.. Silhouee of a helical spring: a) in an equilibrium posiion, b) under orsion (force F, verical displacemen y), c) as a subjec o bending (momen M, roaional displacemen x) If one end of such a spring is aached o a fixed poin and he oher end loaded wih a puck-shaped bob one obains a sysem o be sudied. When he bob s weigh is small so ha he resuling pich of he spring is small comparing o he radius of he cylinder r s one can observe a small load acing along he axis of he spring which resuls in a slighly increased pich and a corresponding lenghening of he spring. This kind of loading is accompanied by orsion of he wire and illusraed in figure.4.b. When he bob is urned in is own plane he pich remains essenially unchanged and he spring yields o he orque by a sligh diminuion of he cylinder radius r s. In his case, as shown in figure.4.c he wire is ben. 6
17 In orsion he individual cross-secions of he wire are loaded by a orque abou he polar axis while in bending he momen acs abou on an axis in he plane of he cross-secion. The load F acing along he cylinder axis has he momen F r s abou he cenre of he crosssecion, he so called orsional momen M, since is axial vecor is normal o he cross-secion. In he case of bending he momen of force F acs upon he bob whose diameer has been assumed as r s. This momen has a characer of a bending momen M b since is axial vecor coincides wih he cylinder axis and can be ransferred parallel o iself o he cenre of he marled cross-secion. In he loading here will be shear sresses in he plane of he crosssecion which increase proporionally o he disance from he wire axis and will be denoed by τ. Therefore one has: r τ df = M (.4.) where df is he area elemen of he cross secion of a wire. In he loading normal sresses σ ac upon he cross-secion and hey are proporional o he disance y which can be expressed as: y σ df = M b (.4.) The enire orsion energy E T for he helical spring is equal o: E T P s M l F r l = = (.4.3) GJ GJ where l represens a lengh of a spring, G is a shear modulus and J p denoes a polar momen of ineria of he cross-secion which in he case of circular area is wice he equaorial momen of ineria [6]. The enire bending energy conained in he spring is: P E B M l F b rs l = = (.4.4) EI EI where I represens he equaorial momen of ineria and E is a Young modulus [6]. 7
18 The expressions (.4.3) and (.4.4) represen he energy conen of he spring in an elasic deformaion in which he spring passes hrough a sequence of saes of equilibrium. These formulas can be compare wih equaions of he mechanical work performed along he pah y and x when he load F and momen M increase gradually from 0 o heir final value, which are: W T Fy F x = WB = (.4.5) These lead o he deerminaion of displacemens x and y o be: r l y = GJ s p F rs l x = F EI (.4.6) According o he above and denoing m o represen mass of bob, L is momen of ineria and m he mass of spring iself one ges he equaions of he free orsional and bending oscillaions as: d y GJ P + y = 0 (.4.7) d ( m + m ) r l 3 s d x EI + x = 0 d ( L + m r ) r l 3 s s (.4.8) The associaed circular frequencies are: GJ P EI = T B = ( m + m ) r l ( L + m r ) (.4.9) r l 3 s 3 s s When hey are equal or almos so resonance occurs and he behaviour of a spring is very sensiive o small changes of he parameers involved. Then he presen heory is no longer sufficien and indeed one has wo coupled modes of oscillaions. Taking ino accoun F and F as inerial forces: d y d x F = m F = ( m + 3 m ) (.4.0) d d he following equaions ha describe coupled oscillaion of he spring are obained: 8
19 d y + ( y kx) = 0 T d (.4.) d x + ( x ky) = 0 B d (.4.).5. Two Coupled Pendulums, Normal Modes and Beas When observing he moion of coupled pendulums shown in a figure.5.a-c, ha was aken from [7] a several differen aspecs of is behaviour, which depend of iniial condiions of a device, can be noiced. Figure.5.. Two pendulums coupled wih a spring: a) held a res and displaced o perform oscillaions, b) oscillaions in phase, c) oscillaions in ani-phase When pendulum is held a res and pendulum le o perform a few oscillaions one observes ha he firs pendulum gradually begins o swing wih increasing ampliude while he ampliude of he second pendulum diminishes. Afer cerain amoun of ime he pendulum iniially held a res is swinging wih he ampliude of he second pendulum a he beginning of is moion. Siuaion repeas and pendulum loses is energy o pendulum. One can easily noice wo periods, he one of oscillaion of each pendulum and he second of he wandering energy from one pendulum o he oher. When boh pendulums sar heir oscillaion ogeher and in phase as i is shown in figure.5.b he exchange of energy is no observed. If i was no for fricional losses or ransfer of energy ino he surroundings he oscillaions would go undamped. The diminishing of ampliude is also no noiceable for he moion of a sysem when he pendulums are sared ogeher bu in ani-phase (siuaion in figure.5.c). This moion is 9
20 characerised by a single frequency. Every par of a sysem mainains a consan phase relaionship wih respec o every oher par. Such oscillaions are called naural (or normal) modes. The oscillaion frequency f sym of he pendulums oscillaing in phase is pracically he same as ha of free pendulum because he spring is hardly neiher conraced nor exended during moion. This mode is also called a symmeric mode. When pendulums oscillae in ani-phase he spring acs a every ime and similarly o graviy force ends o resore equilibrium. Siuaion can be hen described as moion of a pendulum wih sronger graviaional force bigger value of graviaional consan g. Therefore he frequency of he second mode, he so called ani-symmeric mode, is higher hen ha of he firs: f asym > f sym. Every free oscillaion of he sysem can be regarded as a superposiion of normal modes. Some examples are presened in figure.5.. As i has been already menioned wo modes do no proceed wih he same frequency so ime required for a full oscillaion is: T sym > T asym. In ime T asym one mode makes one full oscillaion and has T sym -T asym o cover a par of he nex oscillaion. So: π T asym = T sym x T asym π ( T x = T sym T asym asym ) = Figure.5.. Examples of superposiion of normal modes π ( f f sym asym f sym ) (.5.) Since during each oscillaion he gain is x one ges n oscillaions of he firs mode when he second has gained he amoun π in phase: f sym n = π = (.5.) x ( f f ) asym sym 0
21 When n is inegral or a half-inegral number he ransfer of energy from pendulum o pendulum will be compleed. The oal energy of a pendulum for small angular displacemen is given by: mg A E = (.5.3) l where m is he bob s mass, l he lengh of a pendulum, g represens acceleraion of graviy and A characerises ampliude of displacemen. Since mg/l is he same for all cases shown in a figure.5., one ges, for he superposiion of modes, he balance of energy: (½A) + (½A) + (½A) + (½A) =A (.5.4) Similar balance holds for he poenial energy of a spring, which is proporional o he square of is exension (or conracion). As long as superposiion principle applies (small oscillaion) he oal energy is equal o he sum of he energies of he normal modes ino which he moion can be decomposed. Coordinaes exhibiing he oal energy as a sum over normal modes are called normal coordinaes. If one assumes x as a displacemen of he pendulum and x as a displacemen of he pendulum hose coordinaes can be wrien as: ζ = ½ (x +x ) η = ½ (x -x ) (.5.5a) (.5.5b) Considering he general case when n is neiher inegral nor half-inegral one can conclude ha he moion will be sricly periodic if he frequencies f sym and f asym saisfy he condiion: p f = q sym f asym = τ (.5.6) where p and q are inegers. In such a siuaion moion will repea iself afer ime τ bu reurn of energy will in general ake a fracion of he ime τ. If f sym / f asym is no a raional number, moion of a sysem will no be sricly periodic.
22 When coupling is weak (a delicae spring) he value of n is large because n is inversely proporional o (f asym f sym ). The ime ha elapses unil he faser mode has gained a phase angle afer n oscillaions is given by: nt sym = n = (.5.7) f ( f f ) sym asym sym Thus energy will reurn o he firs pendulum afer a period ha is wice so. This period - nt sym is called bea period. Denoing his as B one has: There is N beas in one second hen: B = ntsym = (.5.8) f f asym sym N = = f asym f sym (.5.9) B.6. Wilberforce Pendulum The Wilberforce pendulum was named for is invenor, Lionel Rober Wilberforce and represens an ineresing case of coupled oscillaions. The device consiss of a helical spring of almos meers and a cylindrical bob of he same radius. The bob has four vanes proruding from i and here is a nu on each of he vanes, which can be moved o change he momen of ineria of he sysem. Such a pendulum is illusraed in figure.6.. which was found in [8]. I can be reaed as a special case of he coupled oscillaions of he longiudinal and he orsional modes for a mass hanging in a flexible helical spring. A weak coupling is due o orsional srains coming from sreching and shrinking of he spring and he axial srains during wising. When he frequencies of boh modes are almos equal he energy of he sysem is ransferred back and forh beween hese wo modes. Figure.6.. Silhouee of he Wilberforce pendulum
23 One can analyse analyically his phenomenon assuming here are wo coordinaes z - he verical displacemen of a bob and θ - he angle of is roaion and ha in he equilibrium posiion z=θ=0. If one considers a massless spring, wih is longiudinal consan k and a orsional consan δ, o which a mass m, wih a momen of ineria abou is verical axis I, has been aached and assumes a linear coupling of he form εzθ/, he Lagrangian of he sysem has a form: = mz& + m & θ kz δθ εzθ (.6.) L Thus he equaions of moion of Wilberforce pendulum are: d z m + kz + εθ = 0 (.6.a) d d θ I + δθ + εz = 0 d (.6.b) As i has been already shown in paragraph. when he coupling does no ake place one can observe simple oscillaions. In order o eliminae coordinae z from he equaions of moion, one can solve he firs of hem for θ : m d z zk θ = (.6.3) ε d mε and using he values for he longiudinal and roaional frequencies: ge fourh order derivaion equaion of a form: = k / m ; θ = δ I (.6.4) z / 4 d θ d θ ε + ( + ) + ( ) θ = 0 4 z θ z θ (.6.5) d d 4mI Assuming a soluion o be: θ ) = Ae i ( (.6.6) 3
24 one comes up wih a bi-quadraic equaion: 4 ε ( z + θ ) + ( zθ ) = 0 (.6.7) 4mI By solving his formula frequencies of wo normal modes can be calculaed: ε = { z + θ [( z θ ) )] } (.6.8a) mi ε = { z + θ + [( z θ ) )] } (.6.8b) mi For z = θ = hey can be simplified o: ε = + ( ) (.6.9a) 4mI ε = ( ) (.6.9a) 4mI Being analogous o he siuaion described in paragraph.5. he values of and are close o each oher and heir difference B = - is he bea frequency beween he wo normal modes. The general form of he roaion angle as a funcion of ime will be a combinaion of he wo normal modes: θ ( ) = Asin + B cos + C sin + D cos (.6.0) when A, B, C, D are ampliudes of sine and cosine componens of he modes. Thus: & θ ( ) = A cos B sin + C cos D sin (.6.) & θ ( ) = A sin B cos C sin D cos (.6.) 4
25 5 Using he equaion of moion one ges general equaion for z as a funcion of ime in a form: ) cos sin cos sin )( (/ ) cos sin )( / ( ) cos sin )( / ( ) ( D C B A D C I B A I z δ ε ε = (.6.3) from which ) sin cos sin cos )( (/ ) sin cos )( / ( ) sin cos )( / ( ) ( 3 3 D C B A D C I B A I z δ ε ε + + = & (.6.4) From he iniial condiions, 0 (0) (0) 0 (0) 0) ( 0 0 = = = = θ θ θ & &z z z (.6.5) where an iniial verical displacemen and iniial wis (bu no iniial velociy in eiher coordinae) are given, one can gain values for he ampliudes: A = C = 0 (.6.) ] ) ( / [ ) ( 0 0 θ ε θ = I z B (.6.3) ] ) ( / [ ) ( 0 0 θ ε θ = I z D (.6.4) Therefore he equaions for boh coordinaes as funcions of ime have he form: ] )cos ( )cos [( ) ( ) cos (cos ) )( / ( ) ( 0 0 I z θ ε θ θ θ + = (.6.5) ) cos (cos ) )( ( ) )( / ( ] ) cos ( ) cos [( ) ( ) ( 0 0 I z z ε θ θ θ θ θ = (.6.6) The vecor Xˆ describing he moion by such equaions is a linear combinaion of he wo normal modes wih ẑ describing longiudinal uni vecor andθˆ orsional uni vecor:
26 ˆ ( ) = z( ) zˆ + θ ( ) ˆ θ = A ˆ η cos + A ˆ η cos (.6.7) X where ˆη and ˆη are he normal coordinaes of he form: ˆ I ˆ η = θ + ( )( θ ) zˆ ε (.6.8a) ˆ I ˆ η = θ + ( )( θ ) zˆ ε (.6.8b) Also from equaions (.6.9) he coupling consan can be calculaed: ε = ( ) mi (.6.9).7. Fourier analysis A mahemaical echnique known as Fourier analysis can be used o represen any funcion f(x) (where x may be posiion or ime) as a series of periodic funcions ha is called Fourier series and can be wrien as: F(x) = ½ a 0 + a cosx + a cosx + + a cosnx n + b sinx + b sinx b n sinnx +... = () ½ a 0 + n= a n cosnx + n= b sin nx n The series consiss a consan erm ½a 0 and sum of sine and cosine erms of differen ampliudes a n, b n. The frequencies of he rigonomeric funcions are harmonics of he fundamenal frequency of x. To represen a cerain waveform by Fourier series values of he coefficiens have o be deermined by inegraion of f(x) over period π wih formulas: π a n = π f ( x)cos nxdx () 0 π b n = π f ( x)sin nxdx (3) 0 6
27 The firs erm can be obained by solving: π a 0 = π f ( x) dx (4) 0 Wih use of Fourier analysis fundamenal frequencies of signals can be deermined. Exac formulas for coefficiens vary for differen funcions f(x) (periodic, nonperiodic funcion, wave packe) being analyse [9]. 7
28 Chaper. Creaing Video Clips, Preparing o Measure and Analysing Resuls.. Seing up Experimens and Recording Video Clips Real experimens on moion of Wilberforce pendulum were carried ou wih he same device as described in []. The figure.. illusraes such a pendulum which conains: a spring of 7 urns of a seel wire wih radius r=7,5 0-4 m whose unloaded lengh is equal o l 0 =, m and projeced radius of he helix is R s =, m; and whose mass is m s =3, kg, a cylindrical bob wih a radius R b =3, m and mass m=4, kg ha conains wo vanes proruding from i on which idenical, free-o-move, nus are locaed. Basing on founding abou resonance of longiudinal and orsional oscillaions repored in [], experimens were done for he pendulum wih is nus placed symmerically a a disance R = 3, m from he edge of a bob which corresponds o a value of a momen of ineria I = 0, kgm - and wih differen combinaions of he iniial condiions deermined by he longiudinal displacemen z 0 and an angle of wis of a bob θ 0. These combinaions are presened in able... Figure.. Silhouee of a used pendulum Table... Combinaion of he iniial condiions experimen s iniial condiions number z 0 [m] θ 0 [rad] π/ π/ 5 0 -π/ π/ 7 0 π/ π/ Experimens were carefully se up in a way ha allows placing a video camera under he pendulum s bob as well as in fron of i. Special aenion has been given o background and lighing. 8
29 For each se of iniial condiions a number of one-minue clips of Wilberforce pendulum moion from boh camera perspecives has been recorded, using a Sony digial video camera DCR-TRV 8E. Specific informaion abou he camera and is feaures can be found in [0]. All digial movies were carefully viewed on a big screen and he bes one for every se of iniial condiions has been chosen for furher processing. Approximaely 00 capured frames for every combinaion of z 0 and θ 0 wih a program for video ediing were used... Ediing Digial Movies wih AdobePremiere AdobePremiere is an advanced program for creaing and ediing digial movies. I allows capuring and performing necessary processing (cuing, adding ransiions, iles, moion, ransparency ec.). Afer processing wih he program a final clip can be produced in various formas. More informaion abou he program and is feaures can be found []. To prepare video clips for daa video measuremen only a few simple processing acs have been performed. Afer capuring, each movie was cu o consis of 05 frames presening moion of he pendulum. Every movie was also cropped o reduce is size from pixels (PAL sandard) o a size shown in able... Because during process of covering a digial camera inerlaces movie s frames as a las an operaion of deinerlacing was proceeded. Finally all video clips were convered ino an *.avi forma. The able.. conains informaion abou boh kinds of movies made wih a differen camera perspecive. Table... General informaion abou video clips camera perspecive boom face frame widh 380 pixels 480 pixels frame heigh 380 pixels 30 pixels frame lengh 4 sec 4 sec frame coun frame rae 5 per sec 5 per sec average size 4 Mb 4 Mb video compression Cinepak Codec Cinepak Codec The figure..a presens a firs frame of a movie covered from he boom and consising of moion of he pendulum ha has been released wih iniial longiudinal displacemen z 0 = 0.04 m and iniial roaional angle θ 0 = 0. The figure b shows a firs frame of a movie done from fron perspecive and wih he same iniial condiions. 9
30 Figure... Firs frames of video clips aken: a) from he boom b) from he fron Figure... An explanaion of a movie file name All movies (*.avi files) are recorded on CDs (Wilberforce_b and Wilberforce_f) and enclosed in he hesis. Figure... explains names ha have been given o hem..3. Program Coach 5 and Daa Video Coach 5 is an inegraed sofware package developed by he CMA Foundaion of he Universiy of Amserdam. The program is an open environmen for invesigaion in science and echnology and inegraes measuring, daa analysis and processing, modelling, conrolling and video measuring. Only he las mode of he program Daa Video is essenial for he presen case and will be described in deph. Video measuremen allows collecing daa from digial video clips in form of poins ha consis of x, y coordinaes of a moniored elemen aken a cerain ime. The locaion of he iem of ineres is marked by clicking on is posiion in chosen frames of he whole movie. The 30
31 program suppors *.avi and *.mov digial video formas. Alhough Coach 5 allows ploing daa in graphs, viewing and calculaing new quaniies in ables and performing analysis, obained daa were expored from he program as a *.dif file. Furher mahemaical elaboraion was carried ou wih a Microsof Excel 97 spreadshee. To proceed wih video measuremen one has o deermine: a scaling facor he disance on he movie frame ha corresponds o acual (real life) disance, a locaion of he axis for fuure measuremens, a seing of he origin, a ime calibraion by noing he rae (x/per second) wih which he processing movie has been made. All hose requiremens have been aken ino accoun during he process of preparaion of a movie o be measured and herefore: as a scaling facor a value of a bob s diameer has been used, movies were covered wih a rae of 5 frames per second, informaion abou a locaion of he origin and measuremen procedure is described in he nex chaper. Specific informaion abou Daa Video mode of Coach 5 can be found in []. Examples of Daa Video aciviies are provided in [3]..4. MS Excel and is Fas Fourier Transform Program Microsof Excel is used o calculae, analyze and plo resuls of video measuremens. Daa is mahemaically calculaed in Excel spreadshee and resuls are ploed in separae shees. A daa analysis ool Fourier analysis ha uses fas Fourier ransform (FFT) is applied o ime domain daa z=f() or θ=f() o find heir componens. As a resul of such a ransformaion a se of complex numbers frequency domain oupu is gained. Fourier ransform is based on he principle ha any funcion can be represened as a superposiion of sinusoidal componens wih cerain ampliude. A frequency sep in Excel FFT is indicaed by he number of measured poin which has o be an even number power of and ampliude is obained from an absolue value (modulus) of a 3
32 complex number. These are displayed as a graph of ampliudes of he componens agains heir frequencies. Such a graph is called a specrum. 3
33 Chaper 3. The Experimens and Resuls 3.. The Experimens The video measuremens were carried ou wih aid of he program Coach 5. On he series of 8 clips wih a moion of Wilberforce pendulum viewed from is fron he measuremens of bob s posiion on each frame were aken. The daa, obained by marking wih Coach 5 Daa Video mode a cerain poin on he device, conained 04 riples of ime and posiion coordinaes x and y. Only he pieces of informaion on y as a funcion of ime were expored as a *.dif files and analyzed laer on. Figure 3.. shows a par of Daa Video window wih a frame of a movie wih a measured poin. Also an axis and a scaling facor are shown. On he nex 8 clips, aken from he boom of he pendulum, measuremens of a posiion of he nu on a pendulum s vanes have been aken. They also conained 04 riples of ime and posiion coordinaes x and y. According o he fac ha an origin of he coordinae sysem was marked in he cener of he pendulum, a roaion angle was mahemaically calculaed from boh x and y coordinaes. Figure 3.. presens a par of Daa Video window wih a frame of a movie wih a measured poin, an axis and scaling facor. To presen all finding and carry on calculaions a Microsof Excel 97 spreadshee was used. Figure 3... A par of a Daa Video window for a movie recorded from he fron Figure 3... A par of a Daa Video window for a movie recorded from he boom 33
34 3.. Saemens of Experimenal Resuls The able 3.. presens a par of a Microsof Excel spreadshee able in which daa has been mahemaically elaboraed. The firs column conains an index number, which is he same as a number of a frame on which he measuremen ook place. The nex column conains ime relaed o a frame a which a value of y was deermined in a cerain video clip. Because he axis was se as he same for every frame he quaniy calculaed wih use of a formula: yn y average represens verical displacemen of he pendulum bob z. An average value of y ha represens an equilibrium posiion of a bob is shown in a fourh column. The nex column of he able encloses values of displacemen z. On hose resuls a fas Fourier ransformaion has been performed. The resul of he procedure a se of complex numbers is presened in he sixh column. Informaion abou ampliude of a cerain frequency componen is indicaed by he absolue value (modulus) of hose complex numbers. Those values are presened in eighh column, which is preceded by a column ha shows values of frequencies. To normalise ampliudes, corresponding o Fourier analysis o uniy a maximum value of his quaniy has been deermined and used o creae he las column of he able according o an equaion: n An Anor =. A max Table 3.. conains daa and calculaed resuls relaed o he second coordinae, he angle of roaion θ. Similarly o he firs able hree firs columns enclosed index, ime and y. The nex one presens informaion abou x posiion componen of he locaion of a bob s nu. The origin has been placed on every frame in a cenre of a bob so is roaion angle can be calculaed from x and y wih use of rigonomery. Therefore he value of c - hypoenuse Figure 3... Coordinaes x, y and c for video clips covered from he boom in a riangle shown in a figure 3.. has been deermined and presened in a fifh column. 34
35 To calculae an angle a following if-and-saemen has been used: IF {AND (y<0,x<0), π - ACOS(y/c), IF [AND (y>0,x<0), -ACOS(y/c), ACOS(y/c)]} Such a formula was used o overcome difficulies ha appear when funcion arcangen was used for angles ouside he range [0,π]. Resuls of he calculaions are conained in a sixh column of he able 3.. and were used o obain he average value of he angle ha represens an equilibrium posiion of a bob (placed in he nex column). A formula: α n α avrage allows calculaing he second coordinae orsional displacemen of he pendulum bob θ. This informaion is presened in he eighh column. Similarly o he firs able nex columns consis of informaion abou he resuls of he fas Fourier ransformaion, ampliudes of cerain frequency componens, maximum ampliude and normalised ampliudes. Based on he calculaions a number of diagrams have been drawn. Diagrams 3.. o 3..6 wih even numbers presen verical displacemen z as a funcion of ime for differen iniial condiion while hose of odd numbers illusrae Fourier specrum for z(). The diagrams 3..7 o 3..3 wih even numbers presen roaion angle θ as a funcion of ime for differen iniial condiion while hose of odd numbers illusrae Fourier specrum for θ(). Values of frequencies of modes f =,03 [Hz] and f = 0.98 [Hz] where hen used o calculae a frequency of a produced one, a beaing rae and he coupling consan (formula (9) in paragraph.6.) which were found o be: f =/(f + f )=,007[Hz] f b = f - f =0,049[Hz] ε = 0,046 [kg m rad/ s] 35
36 36
37 37
38 38
39 39
40 40
41 4
42 4
43 43
44 44
45 45
46 3.3. Some Consideraion of Video Measuremen Accuracy Esablishing accuracy for video measuremen is problemaic because i is no a commonly used mehod. The accuracy of such a measuremen is mainly deermined by he qualiy of a movie (focus) and is size (resoluion). During a process of scaling boh kinds of movies, he number of pixels indicaing a real lengh has been measured o be: for he video clip aken from boom perspecive: 5pix = 7,0 0 - m (pix = 5,6 0-4 m), for he video clip aken from face perspecive: 55pix = 7,0 0 - m (pix = 4,5 0-4 m). I has been experimenally checked ha he movie of dimensions pixels presened in a full size on a compuer screen of 7, wih a resoluion has a lengh l =, m. The resoluion of movies and heir focus allows locaing a cerain poin wih accuracy ± pixels which on such a screen is equal o l = ±,3 0-3 m. Therefore esimaed accuracy of he video measuremen from a movie is: for he video clip aken from fron perspecive (one marked poin on every frame): y = ± 0,9 0-3 m for he video clip aken from boom perspecive (a poin and axis marked on every frame): y = x = ±, 0-3 m. According o accuracy of a posiion and a fac ha a frequency sep of fas Fourier ransformaion depends on a number of measured poins he accuracy for frequency has been esimaed as: for he video clip aken from face perspecive: f = ± 0,05 Hz, for he video clip aken from boom perspecive: f = ± 0,05 Hz. 46
47 3.4. Conclusions Video measuremens of moion of he Wilberforce pendulum allowed observing boh ypes of he coupled oscillaions, longiudinal and orsional ones. Visualizaion of he orsional oscillaions is especially ineresing, as in he previous paper [], where ulrasonic sensor was used insead of a video camera and only he longiudinal oscillaions were observed. All experimens in his paper were carried ou for he cases of resonance beween boh kinds of oscillaions. Fourier analyses of he resuls have revealed presence of one or wo normal modes in each ype of oscillaions. According o moion of coupled pendulums, shown in he figure.5. he normal modes of he Wilberforce pendulum are obained for cerain iniial condiions corresponding o releasing he coupled pendulums in he same phase (firs mode) or in ani-phase (second mode). Table 3.4. summarises locaion of he peaks of frequency in specrums. Table Frequency values for peaks in specrums Experimen s iniial condiions face perspecive boom perspecive number z 0 [m] θ 0 [rad] f [Hz] f [Hz] f [Hz] f [Hz] π/ π/ π/ π/ π/ π/ The firs mode is visible as a dominaing in he experimen 6 when he spring is pulled downwards and wound more ighly (figure 3..5, 3..6, 3..3, 3..3) and in he experimen 8 when he spring is lifed and unwound (figures 3.., 3.., 3..7, 3..8). The second mode is dominan in experimen 4 when he spring is pulled downwards and unwound (figure 3..7, 3..8, 3..9, 3..0) and in he experimen when he spring is lifed and wound (figure 3..3, 3..4, 3..3, 3..4). Because i is very difficul o se he pendulum in moion very accuraely, for almos all cases he oher mode is noiceably presen bu is ampliude is very small. For he res of he experimens (, 3, 5, 7) he beas of boh modes are observable. I is indicaed by almos he same (or close) value of he ampliudes corresponding o he wo 47
48 modes in he specrum (figure 3.., 3.., 3..5, 3..6, 3..9, 3..0, 3..3, 3..4, 3..7, 3..8, 3.., 3.., 3..5, 3..6, 3..9, 3..30). For measuremens done on video clips covered from a face perspecive (longiudinal oscillaions) all peaks of frequency in specrums are observed when f = 0,98[Hz] and f =,03[Hz]. The same resuls, wihin experimenal accuracy, are gained for orsional oscillaions. The average frequency f =,006[Hz] ( one frequency) and he beaing rae f b = 0,049[Hz] are in agreemen wih heoreical values for case of resonance (f = f =,0[Hz]) and resuls presened in []. The resuls allowed calculaing he value of coupling consan and confirm ha he assumpion abou he linear coupling used when wriing he moion equaions (.6.a-b) is valid. An increase of accuracy can be obained by enlarging a number of measured poins or/and a size of a video movie (is widh and heigh). This changes cos increase of ime for aking dae and size of a movie (in Mb). 48
49 IV. Closing Remarks The use of digial echniques seems o be useful and powerful ool for (re)invesigaion of various phenomena. Alhough i requires considerable work o prepare a movie and special processing o make measuremens, i is sill worh doing. The fac ha once produced he movie which can be copied and used by many invesigaors encourages aking advanage of such a measuremen. Especially having in mind he growing number of compuers ha are used in educaion a he secondary and universiy level i indicaes one new fuure use of ICT in schools. Use of a daa video measuremen allows sudens o go wih heir ineres ouside of school. I can also be used o explore and analyze many aspecs of moion in everyday life. The presen sudy shows ha already exising programs such as Coach 5, AdobePremiere and Excel can be used wih grea success in he field of scienific invesigaion. I also poins ou ha an increase in accuracy of daa video and decrease in ime necessary o ake measuremens would be welcome especially when he number of video poins is large. This can be obained by auomaing he daa collecion process. Therefore a procedure of auomaically recognising and marking a characerisic poin on every frame (for example one cerain colour) could be implemened ino a program. Neverheless also more complicaed examples of moion and aspecs relaed o i can be invesigaed wih use of daa video. An example of such an ineresing problem for furher consideraion can be a sudy on moion of a human body. 49
50 V. Lieraure. Ewa D bowska, Sanisław Jakubowicz, Zygmun Mazur, Compuer visualizaion of he beaing of a Wilberforce pendulum, European Journal of Physics 0, 89-95, 999. Henryk Szydłowski, Pracownia fizyczna, PWN, Warszawa Michael Mansfield, Colm O Sullivan, Undersanding Physics, Johan Wiley & Sons, Chicheser Ernesso E. Galloni, Mario Kohen, Influence of he mass of he spring on is saic and dynamic effecs, American Journal of Physics , Ronald Geballe, Saics and Dynamics of a Helical Spring, American Journal of Physics , Arnold Sommmerfeld, Mechanics of Deformable Bodies: Lecures on Theoreical Physics vol. II, New York Academic, Joseph Aharoni, Lecures on mechanics: for sudens of physics and engineering, Oxford Universiy Press, Oxford Richard E. Berg, Todd S. Marshall, Wilberforce pendulum oscillaions and normal modes, American Journal of Physics 59, 3-8, Frank S. Crawford, Jr., Berkeley Physics Course vol III, Waves, Mcgraw-hill Book Company, Berkeley Manual of Digial Video Camera Recorder, Sony Corporaion 999. Adobe Premiere 5. User Guide, Adobe Sysem Incorporaed 998. Guide o Coach 5, CMA/Amsel Insiue, Amserdam Ewa Mioduszewska, Coach Sysem Workbook, CMA/Amsel Insiue, Amserdam
51 VI. Acknowledgemens Thanks I would like o hank my promoor prof. Ewa D bowska for her valuable remarks and commens during developmen of he hesis. I also hank dr. William Wehrbein who checked he paper from a language sandpoin and gave me quie an English lesson. Special words of appreciaion are addressed o my program co-ordinaor dr. Ton L. Ellermeijer and all workers of Amsel Insiue who helped, suppored and encouraged me during my sudy a Universiy of Amserdam. This hesis could no have been wrien wihou a suppor from my Parens whom I owe all of my educaion. Las bu no leas, I hank Jola for her persisence and paience. Podzię kowania Składam wyrazy podzi kowania Pani promoor, prof. Ewie D bowskiej, za cenne uwagi oraz komenarz podczas worzenia niniejszej pracy. Dzi kuj ak e dr. Willamowi Wehrbein, kóry podj ł si koreky j zykowej pracy i udzielił mi cennych lekcji angielskiego. Szczególne słowa podzi kowania kieruj do dr. Tona L. Ellermeijera oraz pracowników Insyuu Amsel za ich pomoc, zrozumienie i wsparcie podczas mojego pobyu na Uniwersyecie w Amserdamie. Praca a nie powsałaby bez pomocy i wsparcia moich Rodziców, kórym dzi kuje za wszyskie laa sp dzone w szkole. Dzi kuj równie Jolancie za jej wyrwało i cierpliwo. 5
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Lecture 18 Review for Exam 1
 Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Lecture 20. Fraunhofer Diffraction - Transforms
 Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/2007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Katowicach
 ROZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Kaowicach WYZNAZANIE PARAMETRÓW FUNKJI PEŁZANIA DREWNA W UJĘIU LOSOWYM * Kamil PAWLIK Poliechnika
ROZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Kaowicach WYZNAZANIE PARAMETRÓW FUNKJI PEŁZANIA DREWNA W UJĘIU LOSOWYM * Kamil PAWLIK Poliechnika
ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL
 Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Read Online and Download Ebook ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA JEZYKOWA) BY DOUGLAS KENT HALL DOWNLOAD EBOOK : ARNOLD. EDUKACJA KULTURYSTY (POLSKA WERSJA Click link bellow and free register
Mathematical modelling of hen s egg shape by rotation curve
 Annals of Warsaw Universiy of Life Sciences SGGW Agriculure No 6 (Agriculural and Fores Engineering) 204: 59 64 (Ann. Warsaw Univ. Life Sci. SGGW, Agricul. 6, 204) Mahemaical modelling of hen s egg shape
Annals of Warsaw Universiy of Life Sciences SGGW Agriculure No 6 (Agriculural and Fores Engineering) 204: 59 64 (Ann. Warsaw Univ. Life Sci. SGGW, Agricul. 6, 204) Mahemaical modelling of hen s egg shape
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Wybrzeze Baltyku, mapa turystyczna 1: (Polish Edition)
 Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Click here if your download doesn"t start automatically Wybrzeze Baltyku, mapa turystyczna 1:50 000 (Polish Edition) Wybrzeze Baltyku, mapa
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY DYNAMICZNE ASPEKTY WSPÓŁPRACY PANTOGRAFU Z SIECIĄ TRAKCYJNĄ
 TECHNICAL TRANSACTIONS ELECTRICAL ENGINEERING CZASOPISMO TECHNICZNE ELEKTROTECHNIKA DOI: 0.4467/353737XCT.6.46.6045 -E/06 MAREK DUDZIK, ADAM S. JAGIEŁŁO * DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY
TECHNICAL TRANSACTIONS ELECTRICAL ENGINEERING CZASOPISMO TECHNICZNE ELEKTROTECHNIKA DOI: 0.4467/353737XCT.6.46.6045 -E/06 MAREK DUDZIK, ADAM S. JAGIEŁŁO * DYNAMIC ASPECTS OF INTERACTION: PANTOGRAPH CATENARY
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is
 1. Introduction Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is made of aluminum and steel mesh as one of the coolest enclosures available. It s also small
1. Introduction Jazz EB207S is a slim, compact and outstanding looking SATA to USB 2.0 HDD enclosure. The case is made of aluminum and steel mesh as one of the coolest enclosures available. It s also small
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Rolki i arkusze stosowane w handlu Commercial rolls and sheets. ko-box.pl
 0100 Rolki i arkusze stosowane w handlu Commercial rolls and sheets 0100 0110 10 0200 Pud a klapowe sà to pude ka z o one zasadniczo z jednej cz Êci, których brzeg jest klejony, szyty, albo które majà
0100 Rolki i arkusze stosowane w handlu Commercial rolls and sheets 0100 0110 10 0200 Pud a klapowe sà to pude ka z o one zasadniczo z jednej cz Êci, których brzeg jest klejony, szyty, albo które majà
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS.
 ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition)
 Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Patients price acceptance SELECTED FINDINGS
 Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to students
 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
The Lorenz System and Chaos in Nonlinear DEs
 The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS
 KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
KONSPEKT DO LEKCJI MATEMATYKI W KLASIE 3 POLO/ A LAYER FOR CLASS 3 POLO MATHEMATICS Temat: Funkcja logarytmiczna (i wykładnicza)/ Logarithmic (and exponential) function Typ lekcji: Lekcja ćwiczeniowa/training
OSTC GLOBAL TRADING CHALLENGE MANUAL
 OSTC GLOBAL TRADING CHALLENGE MANUAL Wrzesień 2014 www.ostc.com/game Po zarejestrowaniu się w grze OSTC Global Trading Challenge, zaakceptowaniu oraz uzyskaniu dostępu to produktów, użytkownik gry będzie
OSTC GLOBAL TRADING CHALLENGE MANUAL Wrzesień 2014 www.ostc.com/game Po zarejestrowaniu się w grze OSTC Global Trading Challenge, zaakceptowaniu oraz uzyskaniu dostępu to produktów, użytkownik gry będzie
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH
 POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
POLITECHNIKA ŚLĄSKA INSTYTUT AUTOMATYKI ZAKŁAD SYSTEMÓW POMIAROWYCH Gliwice, wrzesień 2005 Pomiar napięcia przemiennego Cel ćwiczenia Celem ćwiczenia jest zbadanie dokładności woltomierza cyfrowego dla
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
DM-ML, DM-FL. Auxiliary Equipment and Accessories. Damper Drives. Dimensions. Descritpion
 DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
DM-ML, DM-FL Descritpion DM-ML and DM-FL actuators are designed for driving round dampers and square multi-blade dampers. Example identification Product code: DM-FL-5-2 voltage Dimensions DM-ML-6 DM-ML-8
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Rodzaj obliczeń. Data Nazwa klienta Ref. Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/ :53:55 PM
 Rodzaj obliczeń Data Nazwa klienta Ref Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/2007 10:53:55 PM Rodzaj obciążenia, parametry pracy Calculation Units SI Units (N, mm, kw...)
Rodzaj obliczeń Data Nazwa klienta Ref Napędy z pasami klinowymi normalnoprofilowymi i wąskoprofilowymi 4/16/2007 10:53:55 PM Rodzaj obciążenia, parametry pracy Calculation Units SI Units (N, mm, kw...)
INSTYTUT PODSTAWOWYCH PROBLEMÓW TECHNIKI STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI. V O L. XVI WARSZAWA, 1964 No. 4
 P O L S K A A K A D E M I A N A U K INSTYTUT PODSTAWOWYCH PROLEMÓW TECHNIKI A R C H I W U M M E C H A N I K I STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI V O L XVI WARSZAWA, 1964 No 4 P A Ń S T W
P O L S K A A K A D E M I A N A U K INSTYTUT PODSTAWOWYCH PROLEMÓW TECHNIKI A R C H I W U M M E C H A N I K I STOSOWANEJ ARCHIVES DE MECANIQUE APPLIQUEE 4 XVI V O L XVI WARSZAWA, 1964 No 4 P A Ń S T W
Cracow University of Economics Poland. Overview. Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005
 Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Cracow University of Economics Sources of Real GDP per Capita Growth: Polish Regional-Macroeconomic Dimensions 2000-2005 - Key Note Speech - Presented by: Dr. David Clowes The Growth Research Unit CE Europe
Nazwa projektu: Kreatywni i innowacyjni uczniowie konkurencyjni na rynku pracy
 Nazwa projektu: Kreatywni i innowacyjni uczniowie konkurencyjni na rynku pracy DZIAŁANIE 3.2 EDUKACJA OGÓLNA PODDZIAŁANIE 3.2.1 JAKOŚĆ EDUKACJI OGÓLNEJ Projekt współfinansowany przez Unię Europejską w
Nazwa projektu: Kreatywni i innowacyjni uczniowie konkurencyjni na rynku pracy DZIAŁANIE 3.2 EDUKACJA OGÓLNA PODDZIAŁANIE 3.2.1 JAKOŚĆ EDUKACJI OGÓLNEJ Projekt współfinansowany przez Unię Europejską w
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
ROZPRAWY NR 128. Stanis³aw Mroziñski
 UNIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY IM. JANA I JÊDRZEJA ŒNIADECKICH W BYDGOSZCZY ROZPRAWY NR 128 Stanis³aw Mroziñski STABILIZACJA W ASNOŒCI CYKLICZNYCH METALI I JEJ WP YW NA TRWA OŒÆ ZMÊCZENIOW BYDGOSZCZ
UNIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY IM. JANA I JÊDRZEJA ŒNIADECKICH W BYDGOSZCZY ROZPRAWY NR 128 Stanis³aw Mroziñski STABILIZACJA W ASNOŒCI CYKLICZNYCH METALI I JEJ WP YW NA TRWA OŒÆ ZMÊCZENIOW BYDGOSZCZ
TACHOGRAPH SIMULATOR DTCOSIM
 TACHOGRAPH SIMULATOR DTCOSIM Service Manual USB-KSIM interface General description The simulator is a device that is used as a replacement for tachograph in the vehicle where the tachograph is not mandatory,
TACHOGRAPH SIMULATOR DTCOSIM Service Manual USB-KSIM interface General description The simulator is a device that is used as a replacement for tachograph in the vehicle where the tachograph is not mandatory,
Camspot 4.4 Camspot 4.5
 User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
Życie za granicą Studia
 - Uczelnia I would like to enroll at a university. Wyrażenie chęci zapisania się na uczelnię I want to apply for course. an undergraduate a postgraduate a PhD a full-time a part-time an online I would
- Uczelnia I would like to enroll at a university. Wyrażenie chęci zapisania się na uczelnię I want to apply for course. an undergraduate a postgraduate a PhD a full-time a part-time an online I would
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Krytyczne czynniki sukcesu w zarządzaniu projektami
 Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
Seweryn SPAŁEK Krytyczne czynniki sukcesu w zarządzaniu projektami MONOGRAFIA Wydawnictwo Politechniki Śląskiej Gliwice 2004 SPIS TREŚCI WPROWADZENIE 5 1. ZARZĄDZANIE PROJEKTAMI W ORGANIZACJI 13 1.1. Zarządzanie
SubVersion. Piotr Mikulski. SubVersion. P. Mikulski. Co to jest subversion? Zalety SubVersion. Wady SubVersion. Inne różnice SubVersion i CVS
 Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016
 PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016 Krzysztof Rokicki 1 GPS AND OBD DATA IN TESTING OF THE VEHICLE DYNAMICS 1. Introduction Previously to determine the speed of the vehicle during dynamic
PROCEEDINGS OF THE INSTITUTE OF VEHICLES 5(109)/2016 Krzysztof Rokicki 1 GPS AND OBD DATA IN TESTING OF THE VEHICLE DYNAMICS 1. Introduction Previously to determine the speed of the vehicle during dynamic
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Poland) Wydawnictwo "Gea" (Warsaw. Click here if your download doesn"t start automatically
 Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
Suwalski Park Krajobrazowy i okolice 1:50 000, mapa turystyczno-krajoznawcza =: Suwalki Landscape Park, tourist map = Suwalki Naturpark,... narodowe i krajobrazowe) (Polish Edition) Click here if your
Sargent Opens Sonairte Farmers' Market
 Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Multi-Criteria Decision Support using ELECTRE methods
 Muli-Crieria Decision Suppor using ELECTRE mehods Roman Słowiński Poznań Universiy of Technology, Poland Weak poins of preference modelling using uiliy (value) funcion Uiliy funcion disinguishes only 2
Muli-Crieria Decision Suppor using ELECTRE mehods Roman Słowiński Poznań Universiy of Technology, Poland Weak poins of preference modelling using uiliy (value) funcion Uiliy funcion disinguishes only 2
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Jak zasada Pareto może pomóc Ci w nauce języków obcych?
 Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
SG-MICRO... SPRĘŻYNY GAZOWE P.103
 SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
SG-MICRO... SG-MICRO 19 SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 32 SG-MICRO 32H SG-MICRO 32R SG-MICRO SG-MICRO H SG-MICRO R SG-MICRO 45 SG-MICRO SG-MICRO SG-MICRO 75 SG-MICRO 95 SG-MICRO 0 cylindra body
Remember to set your printer to omit this page when running off copies.using this document.
 Remember to set your printer to omit this page when running off copies.using this document. The booklets are all produced using MS Publisher, so that is necessary on the computer being used. This document
Remember to set your printer to omit this page when running off copies.using this document. The booklets are all produced using MS Publisher, so that is necessary on the computer being used. This document
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
 !850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
!850016! www.irs.gov/form8879eo. e-file www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C,
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
European Crime Prevention Award (ECPA) Annex I - new version 2014
 European Crime Prevention Award (ECPA) Annex I - new version 2014 Załącznik nr 1 General information (Informacje ogólne) 1. Please specify your country. (Kraj pochodzenia:) 2. Is this your country s ECPA
European Crime Prevention Award (ECPA) Annex I - new version 2014 Załącznik nr 1 General information (Informacje ogólne) 1. Please specify your country. (Kraj pochodzenia:) 2. Is this your country s ECPA
Egzamin maturalny z języka angielskiego na poziomie dwujęzycznym Rozmowa wstępna (wyłącznie dla egzaminującego)
 112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
QUANTITATIVE AND QUALITATIVE CHARACTERISTICS OF FINGERPRINT BIOMETRIC TEMPLATES
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2014 Seria: ORGANIZACJA I ZARZĄDZANIE z. 74 Nr kol. 1921 Adrian KAPCZYŃSKI Politechnika Śląska Instytut Ekonomii i Informatyki QUANTITATIVE AND QUALITATIVE CHARACTERISTICS
Test sprawdzający znajomość języka angielskiego
 Test sprawdzający znajomość języka angielskiego Imię i Nazwisko Kandydata/Kandydatki Proszę wstawić X w pole zgodnie z prawdą: Brak znajomości języka angielskiego Znam j. angielski (Proszę wypełnić poniższy
Test sprawdzający znajomość języka angielskiego Imię i Nazwisko Kandydata/Kandydatki Proszę wstawić X w pole zgodnie z prawdą: Brak znajomości języka angielskiego Znam j. angielski (Proszę wypełnić poniższy
Belt Conveyors Calculations
 Conveyors Deparmen of Mining, Dressing and Transpor Machines AGH Be Conveyors Cacuaions Pior Kuinowski, Ph. D. Eng. Pior Kasza, Ph. D. Eng. - pior.kuinowski@agh.edu.p ( 12617 30 92 B-2 ground-foor room
Conveyors Deparmen of Mining, Dressing and Transpor Machines AGH Be Conveyors Cacuaions Pior Kuinowski, Ph. D. Eng. Pior Kasza, Ph. D. Eng. - pior.kuinowski@agh.edu.p ( 12617 30 92 B-2 ground-foor room
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku
 Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Blow-Up: Photographs in the Time of Tumult; Black and White Photography Festival Zakopane Warszawa 2002 / Powiekszenie: Fotografie w czasach zgielku Juliusz and Maciej Zalewski eds. and A. D. Coleman et
Forms with combo boxes and subforms
 S t r o n a 1 Author: Jacek Kierklo Forms with combo boxes and subforms Introduction The article is intended for high school students getting to know the programs to support databases in particular Microsoft
S t r o n a 1 Author: Jacek Kierklo Forms with combo boxes and subforms Introduction The article is intended for high school students getting to know the programs to support databases in particular Microsoft
Surname. Other Names. For Examiner s Use Centre Number. Candidate Number. Candidate Signature
 A Surname _ Other Names For Examiner s Use Centre Number Candidate Number Candidate Signature Polish Unit 1 PLSH1 General Certificate of Education Advanced Subsidiary Examination June 2014 Reading and
A Surname _ Other Names For Examiner s Use Centre Number Candidate Number Candidate Signature Polish Unit 1 PLSH1 General Certificate of Education Advanced Subsidiary Examination June 2014 Reading and
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
Zarządzanie sieciami telekomunikacyjnymi
 SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
SNMP Protocol The Simple Network Management Protocol (SNMP) is an application layer protocol that facilitates the exchange of management information between network devices. It is part of the Transmission
Zestawienie czasów angielskich
 Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
Zestawienie czasów angielskich Present Continuous I am, You are, She/ He/ It is, We/ You/ They are podmiot + operator + (czasownik główny + ing) + reszta I' m driving. operator + podmiot + (czasownik główny
BIOPHYSICS. Politechnika Łódzka, ul. Żeromskiego 116, Łódź, tel. (042)
 BIOPHYSICS Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki
BIOPHYSICS Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
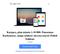 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Eksperymenty reaktorowe drugiej generacji wyznaczenie ϑ 13
 Eksperymenty reaktorowe drugiej generacji wyznaczenie ϑ 13 v Przypomnienie wyniku eksperymentu KamLAND - weryfikującego oscylacje neutrin słonecznych v Formuły na prawdopodobieństwo disappearance antyneutrin
Eksperymenty reaktorowe drugiej generacji wyznaczenie ϑ 13 v Przypomnienie wyniku eksperymentu KamLAND - weryfikującego oscylacje neutrin słonecznych v Formuły na prawdopodobieństwo disappearance antyneutrin
2014-3-30. Urbanek J., Jabłoński A., Barszcz T ssswedfsdfurbanek J., Jabłoński A., Barszcz T., Wykonanie pomiarów
 Wykonanie pomiarów sygnałów wibroakustycznych przy stałych oraz zmiennych warunkach eksploatacyjnych na stanowisku testowym. Część II: Analiza poprawności pomiarów. Autorzy: Urbanek J., Jabłoński A., Barszcz
Wykonanie pomiarów sygnałów wibroakustycznych przy stałych oraz zmiennych warunkach eksploatacyjnych na stanowisku testowym. Część II: Analiza poprawności pomiarów. Autorzy: Urbanek J., Jabłoński A., Barszcz
Extraclass. Football Men. Season 2009/10 - Autumn round
 Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
Extraclass Football Men Season 2009/10 - Autumn round Invitation Dear All, On the date of 29th July starts the new season of Polish Extraclass. There will be live coverage form all the matches on Canal+
SPIS TREŚCI / INDEX OGRÓD GARDEN WYPOSAŻENIE DOMU HOUSEHOLD PRZECHOWYWANIE WINA WINE STORAGE SKRZYNKI BOXES
 KATALOG 2016 CATALOGUE 2016 SPIS TREŚCI / INDEX WYPOSAŻENIE DOMU HOUSEHOLD OGRÓD GARDEN PRZECHOWYWANIE WINA WINE STORAGE 31-38 21-30 4-20 SKRZYNKI BOXES 39-65 3 WYPOSAŻENIE DOMU HOUSEHOLD 4 WYPOSAŻENIE
KATALOG 2016 CATALOGUE 2016 SPIS TREŚCI / INDEX WYPOSAŻENIE DOMU HOUSEHOLD OGRÓD GARDEN PRZECHOWYWANIE WINA WINE STORAGE 31-38 21-30 4-20 SKRZYNKI BOXES 39-65 3 WYPOSAŻENIE DOMU HOUSEHOLD 4 WYPOSAŻENIE
 www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
www.irs.gov/form990. If "Yes," complete Schedule A Schedule B, Schedule of Contributors If "Yes," complete Schedule C, Part I If "Yes," complete Schedule C, Part II If "Yes," complete Schedule C, Part
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to teachers
 1 z 7 2015-05-14 18:32 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to teachers Tworzenie ankiety Udostępnianie
1 z 7 2015-05-14 18:32 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to teachers Tworzenie ankiety Udostępnianie
Aktualizacja Oprogramowania Firmowego (Fleszowanie) Microprocessor Firmware Upgrade (Firmware downloading)
 Aktualizacja Oprogramowania Firmowego (Fleszowanie) Microprocessor Firmware Upgrade (Firmware downloading) ROGER sp.j. Gościszewo 59 82-416 Gościszewo Poland tel. 055 2720132 fax 055 2720133 www.roger.pl
Aktualizacja Oprogramowania Firmowego (Fleszowanie) Microprocessor Firmware Upgrade (Firmware downloading) ROGER sp.j. Gościszewo 59 82-416 Gościszewo Poland tel. 055 2720132 fax 055 2720133 www.roger.pl
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition)
 Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Arrays -II. Arrays. Outline ECE Cal Poly Pomona Electrical & Computer Engineering. Introduction
 ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
ECE 114-9 Arrays -II Dr. Z. Aliyazicioglu Electrical & Computer Engineering Electrical & Computer Engineering 1 Outline Introduction Arrays Declaring and Allocation Arrays Examples Using Arrays Passing
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Microsystems in Medical Applications Liquid Flow Sensors
 Microsystems in Medical Applications Liquid Flow Sensors Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka
Microsystems in Medical Applications Liquid Flow Sensors Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka
Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo
 POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
POPRAWKA do POLSKIEJ NORMY ICS 29.060.10 PNEN 50182:2002/AC Wprowadza EN 50182:2001/AC:2013, IDT Przewody do linii napowietrznych Przewody z drutów okrągłych skręconych współosiowo Poprawka do Normy Europejskiej
