MiiHiicTapcTBO opocbste, nayne m TexHonoiuKor pasboja Peny6miKe Cp6n e flpyujibo MAIEA/IATI/1HAPA CPBMJE
|
|
|
- Ignacy Adamczyk
- 6 lat temu
- Przeglądów:
Transkrypt
1 MiiHiicTapcTBO opocbste, nayne m TexHonoiuKor pasboja Peny6miKe Cp6n e flpyujibo MAIEA/IATI/1HAPA CPBMJE [JJKOJICKQ TAKMM4ELbE M3 MATEiViATMKE YHEHI/IKA OCHOBHMX iukojia IIS PABPEfl, 1. Ofl HajBelier TpoL(M(j)peHor 6poja o,qy3mm 36np HajBefier HenapHor 6poja Tpefie CTOTMHe v\ HajMai-ber naphor 6poja neie CTOTi/iHe. 2. Mapra je KpeHyo Ha nyt flyr 730km Kojw >Kenn fla npetje 3a Tpw flaha. ripbor flaha je npeiuao 240km, a flpyror flaha 120km Bnnie Hero npbor flaha. Kojiwko KH/iOMeiapa My je npeocra/io fla npe1)e Tpefier flaha? 3. flopefjaj no Be/iMHHHH c/ieflefie pnmcke 6pojeBe, ofl HajMarber flo HajBefier: CVIII, DCCXVI, CCXXXIV, CMXLVII, LX, XL, XIX, D, CXII, CDXV. 4. ripabe avid Ha c/ii/ipi/i cy Me1)yco6Ho HopMaaHe,aTaKoljeh npabecue. 3am/iwi/i: а) CBe oiijtpe ymobe; б) CBe Tyne yrnobe Kojn noctoje Ha oiv\u,ia. 5. 3anniun CBe HenapHe 6pojeBe ocme CTOTnHe nnji/i je 36np pw^apa jeflhak 19. Cb3kh 3aflaiaK ce 6oflyje ca no 20 6oflOBa. l/l3pafla 3aflaTaKa Tpaje 120 MnHyia. Peuuerbe CBaKor 3aflaTKa KpaTKO ia jacho o6pa3jio>ki/rra.
2 lü PÄ3PEfi Î1pM3HaBaTiw CBaKi/i Ta^an nocrynak ko m ce pa3/imkyje ofl «byna. Boflosaifee npi/uiarofli/rm KOHKpeTHOM Hani/iHy penmabah>a. 1. (MJ153-2) ( ) [10 golosa] = [5 ÖoflOBa] = 298 [5 ôoflûba], 2. (MH53-2) flpyror flaha je npeiuao 240km + 120km = 360km [5 6oflo- Ba], a 3a npba flba flaha ykynho 240km + 360km = 600km [5 öofloba], ripeocta/io iviyje fla npefje joui 730km -600km = 130km [10 öofloba], 3. (MJS53-1 ) XIX, XL, LX, CVIII, CXII, CCXXXIV, CDXV, D, DCCXVI, CMXLVII [BoflOBai-be: nomho>kmtm ca 2,qy>KMHy Hajflywer Hma öpojeßa y KojeM je pefloc/iefl TaMaH. Ha npi/nviep, ano je ynehmk HaBeo öpojeße uieflefimm peflocneflom D, XL, LX, XIX, CVIII, CXII, CCXXXIV, CDXV, DCCXVI, CMXLVII OHfla HMa HH3 ofl 7 öpojeßa y ncnpabhom nopetky, na floönja 14 öofloba.] 4. a) oiiupn: iaob, iaoc, 4-bOc, íbod, 4-cOd, 4-dOe [3a CBakh TanHo HaBefleHM yrao 2 öofla, 3a HeTanHO HaBefleHM -1 6ofl, c tmm fla ykynah öpoj öofloba y obom fle/iy 3aflaTKa He öyfle HeraTHBaH]; 6) Tynn: 4-aOe, 4-bOe [3a cbbkm TauHO HaBefleHM yrao 4 öofla, 3a HeianHo HaBefleHM -2 öofla, c tmm fla ykynah öpoj öofloba y obom fle/iy 3aflaTKa He öyfle HeraTMBaH]. 5. Bpoj 800 He 3aflOBon>aBa yc/iobe 3aflaTKa, na cbm TpaweHM ópojebm Miviajy MM())py ciotmha jeflhaky 7, a 3ÖMp npeocra/ie flße phcjjpe mm je 12. HenapHM öpojebm KojM OBe ycriobe 3aflOBO/baBajy cy 739, 757, 775 m 793 [3a CBaKM TaMHO HaBefleHM öpoj 5 öofloba; 3a cb3km HeianHo HaBefleHM öpoj -3 öofla, c tmm fla ykynah 3Önp öofloba He óyfle HeraTMBaH],
3 Mi/iHiicrapcTBO rspocbeie, nayxe mtexhonoiükor pa3boja PenyôiiMKe Cp6i/ je flpyujtbo MATEMATMHAPA CPBMJE ÜUKO/ÎCKO TAKMMHEhbE M3 M ATEM ATMKE YHEHMKA OCHOBHMX LUKOJIÄ IV PABPEfl, 1. 6paï M cectpa cy ce poroßopi/uii/i pa npi/mowe CBoje penappe y 3ajeflHMMKy Kaci/ipy, ykynho 3456 pwhapa. A ko cectpa npi/ipo>ki/i 923 pi/ihapa Mähte, a 6paT 487 pi/mapa Bi/iuue op porobopehe cyivie, koji h ko lie HOBpa 6htm y Ka ćupu? 2. ripepptaj Ha nani/ip Koji/i Hem npepati/i païy Taöni/ipy, na y npa3ha no/ba ynnmn öpojeße TaKO pa po6njeiu warn h h i/i KBappaï" (îj. pa 3ÖHpoBM y CBaKOM pepy, kopohi/i h pi/ijarohajiw ôypyjephakw) Kojii/iko TpoymoBa ce moxæ yohhth Ha c,nnpn? 4. flonmuh oprobapajyfie pn< )pe t3ko pa HejepHaKoc 6ypy TaHHe: < _ 5 06 < Kojihko wvia npwpoflhmx öpojeßa, TaKBi/ix pa je y hti/ima CBaxa pi/i(j>pa, noneb op ppyre, pboctpyko Beîia op npeixophe? Hanniiii/i Te öpojeße. CßaKM 3apaîaK ce ôopyje ca no 20 öopoßa. H3papa 3apaîaKa Tpaje 120 MWHyia. Peuiehte CBaKor 3apaTKa KpaTKO h jacho oôpa3/io>kmti/i. U ključu Društva matematičara za bodovanje prvog zadatka u IV razredu je greška. Tačan rezultat je 3020.
4 IV PA3PEfl npw3haba CB9KH TanaH nocrynak kojm ce pa3nwkyje oa KJbyMa. BoflOBatt>e npi/marofli/itm KOHKpeTHOiw Ham/iHy pemaeaita. 1. (M/153-1) [10 öofloba] = 2950 [10 ôofloba]. 2. [1 TaMHO ynucah 6poj 6 öofloba, 2-12 öofloba, 3-14 öofloba, 4-16 öofloba, 5-18 ôofloba, 6-20 öofloba.] (MJTI53-2) 12 [3a oflrobop iviahbn Ofl 7: 0 öofloba; 3a 8-10:10 öofloba; 3a 11:15 öofloba; 3a 12:20 öofloba]. 4. (MJ152-1) < < [3a jeflhy TaMHO ynncahy pn^py 5 öofloba, 3a flße: 10 öofloßa, 3a CBe Tpn: 20 öofloßa], 5. Mivia hx 7. To cy: 12, 124, 1248, 24, 248, 36, 48 [3a 1-2 HaljeHa 6poja 4 6ofla; 3a 3 6poja 6 öofloßa; 3a 4 6poja 8 öoaoba; 3a 5 öpojeßa 11 öofloba; 3a 6 öpojeßa 15 öofloba; 3a cbmx 7 öpojeßa 20 öofloba].
5 Mi/iHi/icrapcTBO npocbete, HayKC /i TexHO/ioiuKor pa3boja Penyöni/iKe Cpöwje flpyiijtbo MATEMATMHAPA CPBMJE UJ KOJI CKO TAKMI/IWEHjE MB MATEMATI/1KE YHEHMKA OCHOBHMX UJKOM V PA3PEA 1. Y jeflhom oflerbehty cbbkm y-iehmk yqn 6ap no je,qah crpahm je3mk, ehmeckm mjim c^pahpyckm. EHmecKM je3mk ynn 21 ymem/ik. (PpaHpyckm je3mk ym/i fomx 14, luto je nojiobmha 6poja ynehmka Tor OAen>eK>a. Kojimko ymem/ika yqm o6a je3mka? 2. a) Kojimko fly>km ce wiowe yommtm Ha cjimlim? 6) Kojimko TpoymoBa ce iviowe yommtm Ha cjimpm? 3. OflpeflM CBe netbopopmcjjpehe ripmpoflhe öpojeße KOjMivia cy pncjjpe jeflmhmpa MXMJbafla jeflhake 8 m kojm cy pejbmbm ca 4 m flelum(()pyj caômpat-be TPM + TPM = PEMM. Hctmm cjiobmma OflroBapajy Mere, a pa3jimmmtmm pa3jimhmte pmcjrpe. HafjM CBa peiuejba. 5. Ako fly>kmhy CBaKe MBMpe KopKe nobefiaivio 3a 1cm, rteha nobpuimha ce noßefia 3a 138cm2. OflpeflM 3anpewiMHy KopKe npe nobefiarba MBMpe. CßaKM 3aflaTaK ce öoflyje ca no 20 öofloba. l/bpapa 3aflaîaKa Tpaje 120 MMHyTa. Pewerte CBaKor 3a,qaTKa KpaTKo m jacho o6pa3jio>kmtm.
6 V PA3PEfi ripi/i3haba cea Ta^iaH nocrynak Koju ce pasnmkyje ofl K/byna. BoflOBaifce npi/marofli/m/i KOHKpeTHOM Ham/my peluaeatba. 1. (SVW52-2) = 7[20 6oflOBa]. 2. (MJ152-1 ) a) 22 fly>km [10 ôofloba]; 6) 8 TpoymoBa [10 öofloba], 3. (WIJ153-2) fla 6m TaKaB 6poj 6mo fle/bmb ca 4, pmcj)pa flecetmpa Mopa 6mtm napha, a fla 6m 6mo fle/bmb ca 9, 36mp pmcj/apa Mopa 6mtm fle/bmb ca 9. To cy öpojebm: 8208, 8028, 8928, 8748, 8568, 8388 [3a 1-2 TaMHO HaBefleHa 6poja: 5 ôofloba; 3a 3-4:10 ôofloba; 3a 5:15 öofloba; 3a cbmx 6: 20 öofloba; 3a cbbkm HeTaMHO HaBefleHM 6poj: -3 6o,qa, c tmm fla ykynah 6poj öofloba He 6yfle HeraTMBaH]. 4. JlaKO ce bmam fla je l/l = 0 m P = 1 [5 öofloba]; CBa peweiba cy: = 1420, = 1620, = 1820 (He Möwe 6mtm T = 5 hm T = 6, jep 6m ce Tafla HeKe pmcj^pe nohab/bane). [3a cb3ko TaMHo pewe/be 5 ôofloba; 3a HaBefleHO HeiaHHO -3 6ofla, c tmm fla ykynah 6poj öofloba He 6yfle HeraTMBaH.] 5. A ko ce ca x 03HaMM fly>kmha MBMpe Kopne npe nobefiaiba, OHfla ce nobefiai+em MBMpe 3a 1cm nobpiumha jeflhe CTpaHe KopKe nobetia 3a (2x + 1)cm2 [8 ôofloba] (c/imka). no yc/ioby 3aflaTKa to nobefia/be M3HOCM 138cm2 : 6 = 23cm2, na M3 2x + 1 = 23 floömjamo fla je x = 11 cm [7 öofloba], 3anpeMMHa npboômthe KopKe je (11cm)3 = 1331cm3 [5 öofloba]. 1 X X X X 1
7 ÍVI w ini/i era p CT b o npoesere, Mayice i/ TexHQíiouiKor passoja Penyö/iwKe Cp6i/ije flpyujtbo MATEMATMMAPA CP5MJE IUKOJ1CKO TAKMMMEHjE M3 M ATEM ATM KE YHEHMKA OCHOBHMX UJKO/1A VI PABPEfl, 1. Haqpïaj,qy>K AB = 5cm, na KOHcrpyi/imn Tam<y C Koja je ofl Tam<e A Ha pactojahby 3cm, a ofl Tanne B Ha pacrojatt>y 4cm. 3aTi/iM KOHcrpyniun TaMKy M Koja je Ha jeflhakhm pacrojai+nma ofl Tanana A, B u C. 2. Ano cetpopi/icjjpehi/i öpojxcaöepe ca 13,36i/ipjefleit>nBca 13.AKOce ofl 6poja X 0fly3Me 17, pa3jiwna je fle/bi/iba ca 17. A ko ce 6poj x nofle/iw ca 2, nojinnhhn je napah 6poj. Oflpefln 6pojx. 3. Peuin HejeflHaHHHy 2 x + 5 < 3 ako je x peo 6poj Befm ofl l/bpanyhaj OcaM ynehhna cy nrpann 6p3onoTe3HH inaxobcnn TypHwp Ha KOivie je CB3KM nrpan i/irpao ca CBannivi ofl npeocranhx no 4 napinje. Kojiuko je ykynho OflnrpaHO napmja Ha obom TypHnpy? CßaKn 3aflaiaK ce öoflyje ca no 20 öofloba. l/hpafla 3aflaiaKa Tpaje 120 ivinhyia. Pewei+e œanor 3aflatKa KpaTKO n jacho o6pa3/io>khtn.
8 Vi PÄ3PEfl ripn3habatn cbaki/i Ta^aw nocrynak iío w ce pa3/imkyje ofl ismyna. Bofloeaifee npwjiaroflmtm KOHKpeTHOiw HaHMHy pemabah^a. 1. (M/152-5) [3a Tpoyrao ABC: 5 ÖoflOBa (npn3hati/i v\ ako je HappTaH camo jeflah Tpoyrao); 3a Tam<y M, nofl yaiobom fla je (6ap npmö/im>kho) Ha,qy>Kn AB: 15 öofloba.] 2. (MJ152-1) H3 npßa flßa yoioßa cneflm fla je x fle/bmb ca 13 u 17 [10 öofloba], a M3 Tpelier fla je fle/bmb ca 4 [5 öofloba]. JeflMHM Tpopn^peHM 6poj ca tum ocoömhaivia je x = = 884 [5 öofloba], 3. (MJ152-5) 2 x < -2, x < -1 [10 ôofloea], na M3 x > -5 c/ieflm fla cy pewert>a -4, -3 m -2 [10 ôofloea] [20 Oofloea] = = -1 = 1 5. CßaKM ofl 8 ynechmka je y cb3kom Ko/iy Mrpao 7 naptmja, na je y 8 * 7 jeflh O M KO/iy OflMrpaHO = 28 naptmja (npom3bofl 8 7 fle/im ce ca flba, jep 6m ce MHane CBaKa naptmja 6poja/ia flßanyt) [15 öofloba], Y MeTMpM Kona je OflMrpaHO 28 4 = 112 naptmja [5 öofloba],
9 1. Mi/iHi/icrapcrBO npoœeïe, HayKe m TaxHononiKor paaboja PenyÖBMKe Cpöwje flpyiutbo MÄTEMATl/ä^ÄPÄ CP5Ê/UE LU KOJI CKO TAKMMHEhbE M3 MATEMATMKE YHiEHMKÄ OCHOBHMX U JKO M ! PÄSPEfl l/bpaqyhaj noßpwi/ihy npaboyraohuka ABCD, npi/ika3ahor Ha cnv\uy\, ako je AECF pomö Muja je nobpwi/iha 24V2cm2. cm 2. Hexa je M cpeflmuie xnnoiehy3e AB npaßoymor Tpoyma ABC. A ko cy oöi/imm Tpoymoßa ABC, AMC u BMC, peflom, jeflhakm 80cm, 50cm i/i 64cm, i/opanyhaj nobpnimhy Tpoyma ABC. 3. l/tepanyhaj BpeflHocr H3pa3a VÔJ6 \ ) (Vs) KopHCTeÜH CBaKy o fl pi/i4>apa TanHo jeflahnyt, ca daß u Hajßefm i/i HajMa^H flecetopn( )pehh 6poj Koju je fle/bi/ib ca MmiaumH je npoßeo 9 flaha Ha ni/ijapi/i npoflajyfiw JiyöeHMpe. CßaKor flaha, noheß ofl flpyror, npoflaßao je no jeflhy jiyöehi/ipy Burne Hero npeïxoflhor flaha. Y npbwx net flaha npoflao je hcto toauko nyöehhpa ko/ihko h y nocneflt-ba Meinpn flaha. Ko/ihko je ykynho Mw^auJHH npoflao /lyöehupa 3a thx 9 flaha? CßaKH 3aflaTaK ce 6o,qyje ca no 20 öofloba. M3pafla 3aflaiaKa Tpaje 120 MMHyia. Peiuehbe CBaxor 3aflaTKa KpaTKO i/i jacho o6pa3no>kmtm.
10 VfB PA3PEfl Ülpi/i3H3B3TN CB3KM TaMaH nocrynak kojm ce pa3nm<yje oß sobyna. BoflOßaite npi/maroßi/m/i KOHKpe oiw Hani/my pemabatba. 1. (MJ153-1) H3 24^2= AE-4-JÏ floönja ce fla je crpahupa AE - EC - 6cm [7 ÖQflöBa]. H3 npaßoyrnor Tpoyr/ia EBC je EB2+{4\Í2.f = 6 2, oflakíie je EB = 2cm [7 öofloea]. Cafla je AB = AE + EB = 8cm, na je nobpiunha npaßoyraohi/ika AB-BC = 32V2cm2 [6 6oßOBa], 2. (MÍ152-5) 03Ham/iMO ca a vi b fly>khhe KaieTa, a ca c fly>khhy xnnotehy3e. KaKO je MC = MA = MB = to H3 flamx noflataka c/ieflm fla je: a + b + c = 80cm, b + c= 50cm n a + c = 64cm [10 öofloba]. fla/be ce TiaKO floönja fla je a = 30cm, b = 16cm [5 öoßoba], na je nobpnii/iha Tpoyraa /IßCjeflHaKa 240cm2 [5 öoßoba]. 3. (MJ152-1) 5' V _T Š, -VÔJ6 J (VŠ)2 1-0,4 [7 öofloea] 5 ) '5 ^7 0flOBa-l = [6 öofloba]. 4. CßaKi/i flecet0i4h(j)pehn 6poj cacrab/beh ofl pa3tihhhtnx pi/i^apa je flen^nb ca 9 (jep iviy je 361/ip pi/kjjapa jeflhak 45). fla 6n 6no fle/bmb ca 10, nouieflh>a pn^pa Mopa 6hti/i 0, a fla 6n 6no fle/bhb n ca 20, npemooieflhba pn(j)pa wiopa 6htm napha. Hajßefii/i TaKaB 6poj je [10 öoflosa], a HajiviaH^n [10 SoßOBaj HaHHMO ca n 6poj npoflainx JiyóeHupa npbor flaha. Y npßnx 5 flaha je npoflato n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 5n + 10, a y nocneflhba 4 flaha (n + 5) + [n + 6) + {n + 7) + (n + 8) = 4n + 26 /lyöem/ipa [7 öofloba], npema yc/ioby 3aflaTKa, n3 5n + 10 = 4n + 26 ce floönja fla je n = 16 [7 öofloba], YKynaH 6poj npoflatnx ziyöehnpa je = 180 [6 öofioea].
11 MiiHMcrapcTBO npocsete, Hayxe vi TexHonouiKor pasisoja PenyômiKe Cpßi/ije flpyuitbo MATEMATMMAPA CPBWJE lukoucko TAKMMWEHjE 3 MATEMATIKE YHEHMKA OCHOBHMX LUKOAA !IS PA3PEfl 1. OflpeflM 3Önp CBMX npoctux npupoflhmx öpojeßa x koju 3aflOBO/baBajy HejeflHaMMHy OApeflu cxyn sajeflhumknx pewerba HejeflHaHMHa: 3x-1 3 x - 5 < 4 x M (x-2 )2< (x + 4)2, 2 3. Y npaboyomom Tpoymy ABC ynncah je npaboyraohmk ADEF, Kao ujto je npnka3aho Ha aimflm. A ko je AD = 9cm, DE - 6cm u AC - 10cm, VBpanyHaj nobpuji/ihy Tpoyma ABC. 4. MMjianiMH je npobeo 9 flaha Ha nwjau n npoflajyiim jiyöehhue. Csaxor flaha, noneb ofl flpyror, npoflaßao je no jeflhy nyöehmpy Bi/nue Hero npeïxoflhor flaha. Y npbwx net flaha npoflao je hcto to/imko nyöehhüia kojimko h y nooieflhba neti/ipi/i flaha. Kojimko je yxynho MnnaiunH npoflao jiyöehmfla 3a tux 9 flaha? 5. Y Kpyr nobpujmhe 100n cm2 ynwcah je Tpoyrao Hwje ce crpahmuie oflhoce Kao 5:12:13. OflpeflM nobpuimhy tot Tpoyrna. CßaKH 3aflaTaK ce öoflyje ca no 20 öofloba. H3pafla 3aflaiaKa Tpaje 120 MMHyra. Pewei-be CBaKor 3aflaTKa KpaTKO u jacho o6pa3jio>kmtm.
12 118 PA3PEfl npvbt-äabaiw CB3 KM tanan noctynak Koju ce pa3/iwkyje 03 irabyna. BoAOBasfoe npiinaroflhtm HaniiHy peuiabatba. 1. ( 1J153-1) flata HejeflHaMMHa je peflom ekbuba/iemha ca < ^ < - + 3, -1 <x-1 < 1 1, 0 < x < [12 Sofiosa]. ripoctm öpojebm Koju 3aflOBOJbaßajy noaieahaw ycnob cy 2,3,5,7 n 11, a HjMxob 361/ip je 28 [ a]. 2. (IMI152-1) Peujehba npße HejeflHanuHe cy oflpeljeha ca x < 11 [ a], a flpyre ca x > -1 [ a], Tpawem/i cxyn je {xer -1 <x< 1 1} [4603a]. 3. (MJÎ52-5) KaTeie npaboymor Tpoyrna FEC cy 4cm m 9cm, a jeflha xa- TeTa hbemy cni/im-ior Tpoyr/ia DBE je 6cm, na ce m 4cm : 9cm = 6cm : DB Aoöwja fla je D ß = ^ ^ c m = ^ c m [ a]. Kaieie flator Tpoyrna 45 cy 10cm M 271cm = cm, 2 y cm cm cm2 [5 SoflOBa]. 4.03HannMO ca n 6poj npoflatnx nyöehi/ma npßor flaha. Y npeux 5 flaha je npoflato n + (n + 1) + (n + 2) + [n + 3) + (n + 4) = 5n + 10, a y nocjieafoa 4 AaHa (n + 5) + (n + 6) + (n + 7) + (n + 8) = 4n + 26 nyöehupa [ a]. flpe/vsa ycnoßy 3aAaTKa, 1/13 5n + 10 = 4n + 26 ce Aoönja Aa je n = 16 [7 6oAOBa].Yi<ynaH 6poj npoaatnx nyöehupa je [6 ßofiOBa]. 5. Tpoyrao MMje ce crpahmpe OAHOce xao 5 :12 :13 je npaboymn, na ce pemap tt>erobor onncahor xpyra (m/ijn je nonynpenhmk 10cm) Hana3M y cpeanimy xnnotehy3e. flax/ie, xnnotehy3a Tpoyrna wvia AywMHy 20cm [8 öoaoba]. Ako KaTeie 03Ham/iMO ca xv\y, wviamo Aa je 5 : 13 = x : 20 m :13 = y : 20, na cy Ay>KMHe xaieia x = cm u y = ----cm [ , rji, Ba],a nobpuimhaipoyrnaje cm = cm [4603a]
lq7 'tfedjoag rnovdjoaj v\ OMDO)VdJ03J OMDUdD jo;i;nouohx3i M 3)^:vH 'sisaoocl! cai:
lq7 'tfedjoag rnovdjoaj v\ OMDO)VdJ03J OMDUdD jo;i;nouohx3i M 3)^:vH 'sisaoocl! cai: 1. floperjajte no crapoc noriyneh _TOK flynasa.anybujanha pasanfl. CDpyiuKa ropa. Kana/i flynas - Tuca -flynas ( 2 x
OniUTUHCKO TAKMMMEhbE V\3 TEOrPAOMJE 3A 7. PASPEfl
MHHUCTAPCTBO HPOCBETE, HAVKE H TEXHO/lOLUKOr PA3BOJA PEnYB/lMKE CPBMJE V\ CPnCKO TEOrPA0CKO flpvlutbo OniUTUHCKO TAKMMMEhbE V\3 TEOrPAOMJE 3A 7. PASPEfl Beorpafl, 2013. ,;«'-S;. ill OmumuHCKO makmu^ei-be
OKPV>KHOTAKMWHEHDE M3 TEOrPAOHJE 3A 7. PASPEfl
Mi/IHKCTAPCTBO flpocbete, HAVKE V\ TEXHO/lOIHKOr PA3BOJA PEHYB/IHKE CPBMJE M CPHCKO TEOrPAOCKO flpyujtbo OKPV>KHOTAKMWHEHDE M3 TEOrPAOHJE 3A 7. PASPEfl 5eorpafl,2013. a) 3eM/ba ponipa y crv-epy 3anafl-ncTOK/
5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W
![5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W](/thumbs/96/128964612.jpg "5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W")
5 9; STU ()* +,-. /0#1 cp 2 3 3 4567 8 + 9:Y ; :PQ ; $< + =>? : @ AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P 2 )* +. Z[\,- X ]^_` :,- a ^ bc, #,
ć Ó ć Ź ć ć ć ć ć ć Ś Ą ć ź Ź ć Ź Ź ć ć ć Ą Ź ĄĄ ć ź ć ć ć ć ć ć Ą ź Ó ć ć ć ć ć ć ć Ą ć ź ć ć ć Ś Ą ź ć Ó ć ć ć Ł ć ć Ą ć ć Ą Ó ć ć ć ć ź ć ć ć ć ć ć Ść ć ć Ó ć Ę ć ć ÓĄ Ś ć ć ć Ą ć ć Ź ź Ś ć Ź ć ć ć
Z Z Z ] P D U W Z \ F K Z V W D Q F \ S O )(5,(=,02:( ZZZ]PDUWZ\FKZVWDQF\SO '1,6.83,(1,$'/$0à2'=,( < Ä&20$0&=
HAnOMEHE Y3 OMHAHCMJCKE M3BELLITAJE
\ r i p u B p e f l H O A p y L U T B o " E j i e K T p o M 3 r p j a f l H 3 a B a j n H a B a i u T a " a. f l. HAnOMEHE Y3 OMHAHCMJCKE M3BELLITAJE 3 1. 1 2. 2 0 1 1. r o f l M H e v 1. OnujTe MHcfc>opMamije
T00o historyczne: Rozwój uk00adu okresowego pierwiastków 1 Storytelling Teaching Model: wiki.science-stories.org , Research Group
13T 00 o h i s t o r y c z n Re o: z w ó j u k 00 a d u o k r e s o w e g o p i e r w i a s t k ó w W p r o w a d z e n i e I s t n i e j e w i e l e s u b s t a n c j i i m o g o n e r e a g o w a z e
A4 Klub Polska Audi A4 B6 - sprężyny przód (FWD/Quattro) Numer Kolory Weight Range 1BA / 1BR 1BE / 1BV
Audi A4 B6 - sprężyny przód E0 411 105 BA żółty niebieski różowy 3 E0 411 105 BB żółty niebieski różowy różowy 4 E0 411 105 BC żółty zielony różowy 5 E0 411 105 BD żółty zielony różowy różowy 6 E0 411
! " # $%!&" '! ("") " #!* +
! " # $%!&" '! ("" " #!* + !" # $ %! # % & '" # % '( * " ++ " & " ' $ + -! "!" '. / % " ( % 0 1 %"0 2 3 4!"& 5% " +! 3# 67 "## & % +0 58 0 9:7+ 0(.!+ %8. ;. ; 7%. %!"( < %8( #=!" 0 # 0 # ( " " 3 + #- >
0 5 F: X ^ ' F ' % 6 [ + F : `a[ F C ^ $< < W F MD4 4 = 9 B Z S ` '" 4 2> $ R&^ 6 7 \ = 9Q : > L,,U [, [ B P < 3. 3 A _ < \ F 4 M? cf $ 3
0 5 F: X ^ ' F ' % 6 [ + F + 6 + : `a[ F C ^ $< < W F MD4 4 = 9 B Z S ` '" 4 2> $ R&^ 6 7 \ = 9Q : > L,,U [, [ B P < 3. 3 A _ < L= @,, \ F 4 M? cf $ 3 ' K W : 7 cf FZ 6 = $ / W & J F W bl c4 6 < - 7 8
Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa
W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l
u l. W i d o k 8 t e l. 2 2 6 9 0 6 9 6 9
T A D E U S Z R O L K E J U T R O B Ę D Z I E L E P I E J T o m o r r o w W i l l B e B e t t e r K a w i a r n i a F a f i k, K r a k ó w, 1 9 9 2 F a f i k C a f e, C r a c o w, 1 9 9 2 W ł a c i c i
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa w Gdyni Rozdział 2. Informacja o trybie i stosowaniu przepisów
Z n a k s p r a w y G C S D Z P I 2 7 1 03 7 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e r e m o n t u n a o b i e k c i e s p o r t o w y mp
2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l
Instrukcja zarządzania systemem informatycznym przetwarzającym dane osobowe w Chorągwi Dolnośląskiej ZHP Spis treści
C h o r ą g i e w D o l n o l ą s k a Z H P Z a ł ą c z n i k 5 d o U c h w a ł y n r 2 2 / I X / 2 0 1 5 K o m e n d y C h o r ą g w i D o l n o 6 l ą s k i e j Z H P z d n i a 0 8. 0 62. 0 1 5 r. I n
!" #$!%&' %' # ' ()*+(,-!"#$%&' "#$ !"#$%&' ()*+,-./01) %& ' :! #$%& -%& '; #$ < =!%& '; #$ ' DE5 1FGHI
!" #$!%&' %' #' ()*+(,-!"#$%&' "#$1 2.345...67!"#$%&'()*+,-./01) %& ' 2345 6789:! #$%& -%& '; #$
1 8 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu M E C H A N I K - O P E R A T O R P O J A Z D Ó W I M A S Z Y N R O L N I C Z Y C H K o d z k l a s y f i k a c j i
!"#$%&'!"#$%&' () *+,-./ : ; /0 7 < = FG-C, FHIJ!KLMN-O ) P =QRSTU VW 6XY Z[\ < =] F F^ _`ab a ) V 4 = < 5-[ =>
![!#$%&'!#$%&' () *+,-./ : ; /0 7 < = FG-C, FHIJ!KLMN-O ) P =QRSTU VW 6XY Z[\ < =] F F^ _`ab a ) V 4 = < 5-[ =>](/thumbs/96/127817587.jpg "!#$%&'!#$%&' () *+,-./ : ; /0 7 < = FG-C, FHIJ!KLMN-O ) P =QRSTU VW 6XY Z[\ < =] F F^ _`ab a ) V 4 = < 5-[ =>")
!"#$%&'!"#$%&' () *+,-./0123456789: ; /0 7 < = >?@AB6C,DE89 FG-C, FHIJ!KLMN-O )P =QRSTU VW 6XY Z[\ < =] F F^ _`ab a QRSc @ ^@ ) \ @a V 4 = < 5-[ => & W = -[ < = @ > @
I n f o r m a c j e n a t e m a t p o d m i o t u k t ó r e m u z a m a w i a j» c y p o w i e r z y łk p o w i e r z y l i p r o w a d z e p o s t p
A d r e s s t r o n y i n t e r n e t o w e j, n a k t ó r e j z a m i e s z c z o n a b d z i e s p e c y f i k a c j a i s t o t n y c h w a r u n k ó w z a m ó w i e n i a ( j e e ld io t y c z y )
Chorągiew Dolnośląska ZHP 1. Zarządzenia i informacje 1.1. Zarządzenia
C h o r ą g i e w D o l n o l ą s k a Z H P W r o c ł a w, 3 0 l i s t o p a d a2 0 1 4 r. Z w i ą z e k H a r c e r s t w a P o l s k i e g o K o m e n d a n t C h o r ą g w i D o l n o 6 l ą s k i e
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa w Gdyni Rozdział 2. Informacja o trybie i stosowaniu przepisów
Z n a k s p r a w y G C S D Z P I 2 7 1 0 2 8 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e ro b ó t b u d o w l a n y c h w b u d y n k u H
K S I Ą Ż Ę TŻP P R U S C Y A H O H E N Z O L L E R N O W I E PWP X VŁ X I XPW.P 2 4 1
K S I Ą Ż Ę TŻ R U S C Y A 2 4 1 Ż L B R E C H T M A 2 4 2 O j c i e c- F R Y D E R Y K S TŻ R S Z Y s. W B I O G R.ŻL B R E C H TŻ M a t k a-z O F IŻJŻ G I E L L O N KŻ s. R o d z e ń s t w o-b I O G
- :!" # $%&' &() : & *+, &( -. % /0 ( 1 $+ #2 ( #2 ) !( # ;<= &( ) >- % ( &( $+ #&( #2 A &? -4
- :!" # $%&' &() : 1. 8 -& *+, &( -. % /0 ( 1 $+ #2 ( #2 ) 3 45 167-1.!( # ;- % ( &(- 17 #(?!@- 167 1 $+ &( #&( #2 A &? -2.!"7 # ;- % #&( #2 A &? -3.!( # ;
M P A P S - 50 X 100
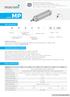ul. Hauke Bosaka 15, 25-217 Kielce; e-mail: marketing@obreiup.com.pl MP seria Jak zamawiać? M P A P S - 50 X 100 M: Marani A: Dwustronnego działania (typ podstawowy) S: Magnes na tłoku Średnica x Skok
/ +)* ; ; ) / )/ 0! 1H>!! "#$ % & ' % $ (!"#$%&' )( ()*&'+, (! " # $ %!& ' ( ' ' ( # )! * ( )! )( ' ' * +,-! -. $ ('! " # $ %!& ' ( */ +/ *//! "# $ %&
/ +)* ; ; ) / )/ 0! 1H>!! "#$ % & ' % $ (!"#$%&' )( ()*&'+, (! " # $ %!& ' ( ' ' ( # )! * ( )! )( ' ' * +,-! -. $ ('! " # $ %!& ' ( */ +/ *//! "# $ %&' &# ( ) *+, ) -. -) + / 01 + +- + & ' '!.,% -. /&
Wrocław, dnia 31 marca 2017 r. Poz UCHWAŁA NR XXXVII/843/17 RADY MIEJSKIEJ WROCŁAWIA. z dnia 23 marca 2017 r.
ZENN URZĘY EÓZTA LNŚLĄE, 31 2017.. 1547 UHAŁA NR XXXV/843/17 RAY EE RŁAA 23 2017. p ó p gó N p. 18. 2 p 15 8 1990. ą g (. U. 2016. p. 814, 1579 1948). 210. 1. 4 14 g 2016. p pą ę - ś (. U. 2017. p. 60),
KURS GEOMETRIA ANALITYCZNA
KURS GEOMETRIA ANALITYCZNA Lekcja 1 Działania na wektorach bez układu współrzędnych. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie
Technika Próżniowa. Przyszłość zależy od dobrego wyboru produktu. Wydanie Specjalne.
Technika Próżniowa Przyszłość zależy od dobrego wyboru produktu Wydanie Specjalne www.piab.com P6040 Dane techniczne Przepływ podciśnienia Opatentowana technologia COAX. Dostępna z trójstopniowym wkładem
Władcy Skandynawii opracował
W Ł~ D C Y S K~ N D Y N~ W I I K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 1 K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 2 Władcy Skandynawii G E N E~ L O G I~ K R Ó L Ó W D~ N O R
G d y n i a W y k o n a n i e p r a c p i e l g n a c y j- n o r e n o w a c y j n y c h n a o b i e k t a c h s p o r t o w y c h G C S o r a z d o s t a w a n a s i o n t r a w, n a w o z u i w i r u
Jak ni ost o a Pols y so ali i i dzy o nia ob f no nu bolsz iz u
Jak ni ost o a Pols y so ali i i dzy o nia ob f no nu bolsz iz u Piotr Ku igowski U m. A m M P p. l.1990@ m l. m P l P m M m R l j ZSRR m, j m m l h P Z m. W j m m j, 6 7.11.1917. j j l ó. C j, l - p j
Wrocław, dnia 27 marca 2015 r. Poz UCHWAŁA NR VIII/113/15 RADY MIEJSKIEJ WROCŁAWIA. z dnia 19 marca 2015 r.
ZE URZĘY JEÓZTA LŚLĄE, 27 2015 P 1376 UCHAŁA R V/113/15 RAY EJEJ RCŁAA 19 2015 b ó ó ą 4,5% ( ą ), 18 2 15 8 1990 ą g ( U 2013 594, óź 1) ) ą 12 1 26 ź 1982 źś ( U 2012 1356, óź 2) ) R, ę: 1 1 U ś bę ó
2372829797728297727 2777787 73772327 227728297827 28237 7372327227 728297727 7!7" 7 # 7 $%7 "7!7# 7 " 7 %7 &2'7# 7 7 7 23789722772277287 77277232227897 227 27!""7 #2$7!""7%7!&"7 #2$7!&"7%7'""7 #2$7'""7%7'&"7
Rozdział 1. Nazwa i adres Zamawiającego Rozdział 2. Informacja o trybie i stosowaniu przepisów Rozdział 3. Przedmiot zamówienia
Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 0 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f S p r z» t a n i e i u t r z y m a n i e c z y s t o c i g d y
!!" #! $ %&'!&!"#$ %&' ()*+,-./ / :; 9: 8 7 5B C D E F B C D G H I J) > 67 8 KL./01 8 M N O P Q R ' ( - ) * +, ST B CD;
!!" #!$ %&'!&!"#$ %&'()*+,-./0 1 2 3 4 5. / 2 6 7 8 9 :; 9: 87 ?@A34 5B C D E F B C D G H I J) > 67 8KL./018 M N O P Q R ' ( - ) * +, ST B CD;U3V 3W-X'YCZ -GHIJ)9:[\ 3 4 5]^ 67 8 _`abc ) = L) a] -U
()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8"\)* M T U P Q ] ^_
![()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8\)* M T U P Q ] ^_](/thumbs/99/141555539.jpg "()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8\)* M T U P Q ] ^_")
()*+,-. 01 ( 2 / /03456789(:58; 8)? @ A B0((1C - D E D B FGHIJK % L?BMNO
Internetowe Ko³o M a t e m a t yc z n e
Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 1 szkice rozwiązań zadań 1 W wierszu zapisano kolejno 2010 liczb Pierwsza zapisana liczba jest równa 7 oraz
Odbicie lustrzane, oś symetrii
Odbicie lustrzane, oś symetrii 1. Określ, czy poniższe figury są swoimi lustrzanymi odbiciami. Jeśli nie, odpowiedź uzasadnij. 2. Dokończ rysunki, tak aby dorysowana część była odbiciem lustrzanym. 3.
!"#$%&' ()*+,-./ :; #$/!" #$ <=1 >,-. CDE () :; AB -.F- GH IJKLM /N O, P ' CDQRS- / TU -.VWXY OZ[\ -. P ][\ ^ -._`P ]a bklm / -._`P
![!#$%&' ()*+,-./ :; #$/! #$ <=1 >,-. CDE () :; AB -.F- GH IJKLM /N O, P ' CDQRS- / TU -.VWXY OZ[\ -. P ][\ ^ -._`P ]a bklm / -._`P](/thumbs/98/135517631.jpg "!#$%&' ()*+,-./ :; #$/! #$ <=1 >,-. CDE () :; AB -.F- GH IJKLM /N O, P ' CDQRS- / TU -.VWXY OZ[\ -. P ][\ ^ -._`P ]a bklm / -._`P")
!"#$%&' ()*+,-./01 2345 6789:;#$/!" #$ ,-. %&?@ABCDE() :;AB -.F-GHIJKLM /NO,P ' CDQRS-/TU -.VWXY OZ[\-. P ][\^-._`P ]a bklm/-._`p coz-.!" #$ AB CPCD, -.ZF0P P _,-.! ()*!,1_CD1,b" "#$ "CPPCD() P1 %&'
Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.
Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 3 12 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f O b s ł u g a o p e r a t o r s k aw r a z z d o s t a w» s p r
!"#$%& ' ()*+,-./-%+01( % (2 3 % :; % 5 - +B% 5; CDE :? F-. GHIJ%KLMN%=O PQRST 1 #U% VW XY % Z VW%+[\]\^_`a\]\bc " L+ > J % a -.K V )
![!#$%& ' ()*+,-./-%+01( % (2 3 % :; % 5 - +B% 5; CDE :? F-. GHIJ%KLMN%=O PQRST 1 #U% VW XY % Z VW%+[\]\^_`a\]\bc L+ > J % a -.K V )](/thumbs/94/118819365.jpg "!#$%& ' ()*+,-./-%+01( % (2 3 % :; % 5 - +B% 5; CDE :? F-. GHIJ%KLMN%=O PQRST 1 #U% VW XY % Z VW%+[\]\^_`a\]\bc L+ > J % a -.K V )")
!"#$%& '()*+,-./-%+01( %(23 %456789 +:;% 5 - ?%@A +B% 5;CDE :?F-. GHIJ%KLMN%=OPQRST 1 #U%VW XY% Z VW%+[\]\^_`a\]\bc" L+ > J%a -.K V)*%+01( VW +:# %H % ( 1# VW+:% %K1.UJ+:%=O V^% B +[ %BH %VW67V ^
KINO IDZIE ZA OPOWIEŚCIĄ
KINO IDZIE ZA OPOWIEŚCIĄ O óh P A Uęś D P ą ą ę ąą śą ź W K N óą M N ó f J V ą ż A W K N PAU A K A K f P f ę 1945 ąh h ń h ż hh P f ę N ż f ś h fh Ł ó - T f W ś ś ż ż ć ż ą ą ó ż A K f: Mh H W Z K G- W
Opis i zakres czynności sprzątania obiektów Gdyńskiego Centrum Sportu
O p i s i z a k r e s c z y n n o c is p r z» t a n i a o b i e k t ó w G d y s k i e g o C e n t r u m S p o r t u I S t a d i o n p i ł k a r s k i w G d y n i I A S p r z» t a n i e p r z e d m e c
K R Ó L O W I E PD Ż N I IPWP.P K J S O L D U N G O W I E P 1 0
1 0 A Królowie Danii K J O L D U N G O W I E. S K J O L D U N G O W I E. E S T R Y D S E N O W I E K R Ó L O W I E D Ż N I IW. S. U N IŻ KŻ L MŻ R S KŻ. O L D E N B U R G O W I E. G L Ü C K S B U R G O
Wrocław, dnia 24 czerwca 2016 r. Poz UCHWAŁA NR XXVI/540/16 RADY MIEJSKIEJ WROCŁAWIA. z dnia 16 czerwca 2016 r.
DZE UZĘDY EÓDZA DLŚLĄE, d 24 2016 2966 UCHAŁA XXV/540/16 ADY EE CŁAA d 16 2016 ś g bdó b ó d gó d 18 2 15 d 8 1990 ąd g (D U 2016 446) 12 11 92 1 d 5 1998 ąd (D U 2015 1445 1890), ą 17 4 5 d 7 ś 1991 ś
3. Unia kalmarska IE W O EN MAŁGORZATA I 116 ERYK VII POMORSKI 119 KRZYSZTOF III BAWARSKI ESTRYDSII IE DAN W LO KRÓ 115
K R Ó L O W I E D ~ N I IW. S TE R Y D S E N O W I E 1 1 4 3. Unia kalmarska K R Ó L O W I E D ~ N I IW. S TE R Y D S E N O W I E M~ Ł G O R Z~ T~ I E R Y K V I I O M O R S K I K R Z Y S Z T O F I I I
h P. Wst 290 Ogrody Nauk i Sztuk nr 2017 (7)
doi: 10.15503/onis2017.289.299 Dzi ko z ni nos ra no i sto niu zna zny ro si duka i M Je U s W s P.U s 1, 50-137 W m.je @wp.pl A strakt Te. I j j j ó m s m s - s j s m s s b m s ó s s j. K j j j s h s
!!" #! $ %&'!&! "#! $%! &' () *+,-. /01 ' :; <=>? +7 8 A B CD B :% E : 1 4 ( C() 0 )) )+, : ) F789:;GCHI GJ1 7 89:; FK?L/ () > A M N O N
!!" #!$ %&'!&! "#! $%! &' () *+,-. /01 ' 2345 6789:;?+7 8 9 @ A B CD B :% E : 1 4 ( C() 0 )) )+, :) F789:;GCHIGJ17 89:; FK?L/() > A M N O N * K :P *QR S0KC+,MTOT QR K:S0 U PK C1 VWXY :C1.789:;?L1Z[\]+
I. STADHOUDERZY NIDERLANDÓW
68 I. STADHOUDERZY NIDERLANDÓW I. TŻS D H O U D E R Z Y N I D E R LŻ N D Ó W R o z d z i a ł I I. KRÓLOWIE HOLANDII LUDWIK I 70 LUDWIK II 79 6 9 I. TŻS D H O U D E R Z Y N I D E R LŻ N D Ó W LUDWIK I Król
! " #$ %! $ &#' & &"
!" #$ %!$&#'&&" Wykonanie opracowania INPLUS Doradztwo Inwestycyjne 10-686 Olsztyn Ul. Wilczyskiego 25E/220 biuro@inplus.pl www.inplus.pl BDK s.c. BIURO ARCHITEKTONICZNO - URBANISTYCZNE 10-686 OLSZTYN,
Y upznory Aorrfica.qocraBJbaMo peiueme o rr3mehr.r r{ AorryHr{ [osnone 3a pa[,
Peny6nura Cp1uja MI4HI4CTAPCTB O TIP OCBETE, HAYKE I4 TEXHOJIOIIIKO PA3BOJA Epoj :6 12-0 0-020651201 6-06 flaryna: 1 4.07.2016. roai4he Beorpa.q Heuamrana 22-26 Ynnnepsrarer y Huruy tipi4p OAHO -MATEMATI4TIKI4
S.A RAPORT ROCZNY Za 2013 rok
O P E R A T O R T E L E K O M U N I K A C Y J N Y R A P O R T R O C Z N Y Z A 2 0 1 3 R O K Y u r e c o S. A. z s i e d z i b t w O l e ~ n i c y O l e ~ n i c a, 6 m a j a 2 0 14 r. S p i s t r e ~ c
@ < $%& ABC DE- E, E 2 & # Q *= 5 $ &$K I B Z I? # & N G I Q )GM ()* I? Q +, -. * # 3* /01 /. &&& # L S *L U> 23 Y S 0] Q 2 3"#* 7G QUV : V "#
![@ < $%& ABC DE- E, E 2 & # Q *= 5 $ &$K I B Z I? # & N G I Q )GM ()* I? Q +, -. * # 3* /01 /. &&& # L S *L U> 23 Y S 0] Q 2 3#* 7G QUV : V #](/thumbs/101/148749767.jpg "@ < $%& ABC DE- E, E 2 & # Q *= 5 $ &$K I B Z I? # & N G I Q )GM ()* I? Q +, -. * # 3* /01 /. &&& # L S *L U> 23 Y S 0] Q 2 3#* 7G QUV : V #")
@ @JY? 23 Y S 0] Q 2 3"#* 7G QUV : V "# G 8 c% ZJ E4 M Q Gc Q + 8 # F J=$ "-UV _KZ & A I LM
!!" # " $ $ $ %&'(!! " # " $%%&'$%()* +!! ", -. /
!!" # " $ $ $ %&'(!! " +!. / #! " ", $%%&'$%()* - )*+$,* -.* %&'(.%&%&/ #"$ $$ 0* $ 1 + + 23 3 40 05 # %&'(.%&%& * *6 * * 6 7 2* $ 8 * 239. 6 39 0 *6 39 *6 6 *6 39 8 7$ 7 + *$ * + 6 6 7 * + $ * + * * #
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów
Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c
Raport roczny R Komisja Nadzoru Finansowego WYBRANE DANE FINANSOWE
NOVITA skorygowany R KOMISJA NADZORU FINANSOWEGO Raport roczny R 2013 (rok) (zgodnie z 82 ust. 1 pkt 3 Rozporządzenia Ministra Finansów z dnia 19 lutego 2009 r. Dz. U. Nr 33, poz. 259, z późn. zm.) dla
z d n i a 2 3. 0 4.2 0 1 5 r.
C h o r ą g i e w D o l n o l ą s k a Z H P I. P o s t a n o w i e n i a p o c z ą t k o w e U c h w a ł a n r 1 5 / I X / 2 0 1 5 K o m e n d y C h o r ą g w i D o l n o l ą s k i e j Z H P z d n i a
1 3. N i e u W y w a ć w o d y d o d o g a s z a n i a g r i l l a! R e k o m e n d o w a n y j e s t p i a s e k Z a w s z e u p e w n i ć s i
M G 4 2 7 v.1 2 0 1 6 G R I L L P R O S T O K Ą T N Y R U C H O M Y 5 2 x 6 0 c m z p o k r y w ą M G 4 2 7 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S z a n o w
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów
Z n a k s p r a w y G C S D Z P I 2 7 1 01 82 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A P r o m o c j a G m i n y M i a s t a G d y n i a p r z e z z e s p óp
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA
Z n a k s p r a w y GC S D Z P I 2 7 1 0 1 42 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e p r a c p i e l g n a c y j n o r e n o w a c y j n
!" #$%%$&' () &(% +,%*-)$&.%&!*),)!%&$(.(***$*% 1 $*$&.%&!% &!0*%* ()' +.,5( ; A; :: !,#$2*!%!&&!,!$*
" #"$ '" "#$ SPIS TRECI 1. IDENTYFIKACJA/INFORMACJE WSTPNE... 5 2. PRZEGLD REALIZACJI PROGRAMU OPERACYJNEGO... 6 " #%$' () (% * +,%*-)$.%*),)%$(.(***$*% /$,%*0(),0 1 $*$.%% 0*%.2*$3 %* ()4 0*%* ()' 0*%
WOJEWÓDZKI IN S P EKT OR A T OC H R ON Y ŚR ODOWIS KA W KR A KOWIE M 2 0 0 2 U RAPORT O STANIE ŚRODOWISK A W WOJ EWÓ DZ TWIE AŁ OPOL SK IM W ROK BIBLIOTEKA MON ITOR IN G U ŚR OD OW IS KA K r a k ó w 2003
Lista Cen 01/2015 Samochodów marki Fiat Professional Rok Produkcji 2015 Obowiązuje od 01.12.2014
Lista Cen 01/2015 Samochodów marki Fiat Professional Rok Produkcji 2015 Obowiązuje od 01.12.2014 Model / Wersja Kod Silnik Nadwozie Cena PLN Cena PLN bez VAT z VAT NOWA PANDA VAN (2 osobowy) Nowa Panda
K R Ó L O W I E PS Z W E C J I PWP.P O LF K U N G O W I E P 5 2 2
5 2 2 3. Folkungowie WŻ L D E MŻ R B I R G E R S S O N MŻ G N U S I LŻ D U L Å S B I R G E R MŻ G N U S S O N MŻ G N U S I I E R I K S S O N E R Y K MŻ G N U S S O N HŻŻ K O N MŻ G N U S S O N 5 2 3 W
L U D O L F I N G O W I E PWP XŁ X IPW.P L U D O L F I N G O W I E X MX IPw.A P 8 0
L U D O L F I N G O W I E X MX Iw.A 8 0 K O N RŻ D I H E N R Y K I TŻ S Z N I K O T T O I W I E L K I O T T O I I O T T O I I I H E N R Y K I I WŚ I Ę T Y 8 1 K O N RŻ D I M A 8 2 O j c i e c- K O N RŻ
Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.
Z n a k s p r a w y G O S i R D Z P I 2 7 1 0 3 62 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A Z a p e w n i e n i e z a s i l a n i ea n e r g e t y c z ne g o
Repetytorium z Matematyki Elementarnej Wersja Olimpijska
Repetytorium z Matematyi Elemetarej Wersja Olimpijsa Podae tutaj zadaia rozwiązywae były w jedej z grup ćwiczeiowych Są w więszości ieco trudiejsze od pozostałych zadań przygotowaych w ramach przedmiotu
B FB A D AEA D A A D E B E DE D A D D B A F EC AEAA D A DA E A BEA A D C D DC A B D B A D DA F EA BC B D F D B B A A E B C F DA E D D EA
AB CDEF FC FC A BC DECF B A F E C C DC B E A D CDC EC D DFA C C A C A A DD B B A A B ECD D E A D A B BC DA DC A E D D EA CEA A C EE FCB EB D C A D D E BF D B B A A C B D AE F A E A D A D D F D B A D EC
ñ 1 9! Ù DEF+>/ P Q V { Ó bbó 1 YZ"p¼~ Þ Üb á \ V ~ Y Z#'! Ù DEF+>/P Q V g E o 9 &5
! ( *+,-./1 < =,>?@A 7 BCDE : F G,-. 2 3 H IJ B C K < L M 8, O :,-. 234567 6, :8 P,-. 2 3 8 Q R S T U V XYJ#,-. 2345 8 ( X :8,-. 2 3 Z [\], ^_ `ab'; c 8,-. 23[\ b!,-. 234567 8 [ \ U ` a, U #; c < 4567
Ł Ń Ś Ó Ó Ę Ó Ó Ó Ń Ś ć ć Ó Ł ć ć ć ć ć ć ć ć ć ć ć Ę ć ć Ę ć ć ć ć ć ć Ę ć ć ć Ę ć ć ć ć ć ć ć ĄĄ ć ć ć ć Ę ć ć ć Ę ć ć ć ć ć ć Ę ć ćę ć ć ć ć Ę Ę ć ć ć ć ć Ę ć Ą ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ę ć Ę ć ć
Podstawowe działania w rachunku macierzowym
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
%!! 8 9 : ;!!!"#$%&' ()*+,-./ # " < " & U / & U!"# $%&' ()*+, -. $/ # 89 :; 23 <. A B C D E < :;. 'FGHIJKLMNO 4 PJQRSLT JE 4UVW XY 4
%!! 8 9 : ;!!!"#$%&' ()*+,-./ # " < " & U / & U!"# $%&' ()*+, -. $/ 01 23453673# 89 :; 23 ?@ A B C D E < :;. 'FGHIJKLMNO 4 PJQRSLT JE 4UVW XY 4 Z[\]^ _` abe 6=>c2 E
S: Magnes na tłoku. Amortyzacja P: pneumatyczna regulowana
Siłowniki zgodne z ISO 15552 seria MP Jak zamawiać? M P A P S 50 x 100 M: Marani P: Zgodne z ISO 15552 tuleja profilowa A: Dwustronnego działania (typ podstawowy) Amortyzacja P: pneumatyczna regulowana
: : !", #$%&' ( 200)*+% 2009,-./01, (ElinorOstrom) 234 &567%&'$ 89:; 9 <= E FG,HIJ [ (!"# ) $ %&', () *+]:,-)./01 ),23./ )89:;,
![: : !, #$%&' ( 200)*+% 2009,-./01, (ElinorOstrom) 234 &567%&'$ 89:; 9 <= E FG,HIJ [ (!# ) $ %&', () *+]:,-)./01 ),23./ )89:;,](/thumbs/94/119051921.jpg ": : !, #$%&' ( 200)*+% 2009,-./01, (ElinorOstrom) 234 &567%&'$ 89:; 9 <= E FG,HIJ [ (!# ) $ %&', () *+]:,-)./01 ),23./ )89:;,")
: :2011 5 6!", #$%&' ( 200)*+% 2009,-./01, (ElinorOstrom) 234 &567%&'$ 89:; 9 ? @ABC+D E FG,HIJ [ (!"# ) $ %&', () *+]:,-)./01 ),23./01 4567)89:;, 9:; ( ; ( 9, ?@AB) (C: DE ), FGHIJ KL (,M923 )
ZADANIE 2 Czy istnieje taki wielokat, który ma 2 razy więcej przekatnych niż boków?
PLANIMETRIA 2 ZADANIE 1 W rombie jedna z przekatnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekatnych pole rombu jest większe od 5cm 2? 1 ZADANIE 2 Czy istnieje taki wielokat, który ma 2
Regulamin turnieju TOP AMATOR CUP 2016
Międzynarodowe Mistrzostwa ŚLĄSKA I ZAOLZIA w motocrossie TOP AMATOR CUP 2016 Regulamin turnieju TOP AMATOR CUP 2016 Terminy zawodów: Czerwionka ( Polska ) I Runda 08.05.2016 r. III Runda 03.07.2016 r.
8. N i e u W y w a ć u r z ą d z e n i a, g d y j e s t w i l g o t n e l ug b d y j e s t n a r a W o n e n a b e z p o 6 r e d n i e d z i a ł a n i
M G 4 0 1 v 4 G R I L L E L E K T R Y C Z N Y M G 4 0 1 I N S T R U K C J A M O N T A V U I B E Z P I E C Z N E G O U V Y T K O W A N I A S z a n o w n i P a s t w o, d z i ę k u j e m y z a z a k u p
Gdyńskim Ośrodkiem Sportu i Rekreacji jednostką budżetową Zamawiającym Wykonawcą
W Z Ó R U M O W Y n r 1 4 k J Bk 2 0 Z a ł» c z n i k n r 5 z a w a r t a w G d y n i w d n i u 1 4 ro ku p o m i 2 0d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j ei d n o s t k» b
Lista Cen 05/2014 Samochodów marki Fiat Professional Rok Produkcji 2014 Obowiązuje od 10.09.2014
Model / Wersja Kod Silnik Nadwozie Cena PLN Cena PLN bez VAT z VAT NOWA PANDA VAN (2 osobowy) Nowa Panda Van 1.2 69KM 519.618.0 1242 ccm 5-drzwiowy 32 800 40 344 Nowa Panda Van 0.9 Twiniair 65KM S&S 519.614.0
DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ
DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 23 lipca 2015 r. Poz. 1024 ROZPORZĄDZENIE MINISTRA FINANSÓW 1) z dnia 6 lipca 2015 r. w sprawie zmiany obszaru składu wolnocłowego na terenie Portu
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów
Z n a k s p r a w y G C S D Z P I 2 7 1 07 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U s ł u g i s p r z» t a n i a o b i e k t Gó w d y s k i e g o C e n
w ww cic oz F o r p U0 a A Zr24 H r wa w wa wa w o UazQ v7 ; V7 v7 ; V7 ; v7 rj. co.. zz fa. A o, 7 F za za za 4 is,, A ) D. 4 FU.
1 68. E E E E 69 69 69 E ) E E E E be 69 69 E n c v u S i hl. ' K cic p. D 2 v7. >- 7 v7 ; V7 v7 ; V7 ; v7 J.. ~" unli. = c.. c.. n q V. ) E- mr + >. ct >. ( j V, f., 7 n = if) is,, ) - ) D. lc. 7 Dn.
O F E R T A H o t e l Z A M E K R Y N * * * * T a m, g d z i e b łł k i t j e z i o r p r z e p l a t a s ił z s o c z y s t z i e l e n i t r a w, a r a d o s n e t r e l e p t a z m i a r o w y m s z
!"#$ %&!'"()$*+$",&%-!.,*/
!" #!"#$ %&!'"($*+$",&%-!.,*/! "'* 0 $% & ' ((#* #*" % % +,-./+0 ((#* #*" % % (1" # 11 2 +,-./+0 ((#* #*" % % (1" # 3 456*/%&("& %4 7$%&!./'*!4%%,4-58*/.98 $*58!6(,.'(3333333333333333333333333333333333333333333333333:!"#$%&'("*+$,",'-."/0"
9( 9 9; ;!. $!!%'!" #$%&'!"#$ % & &$ ' " %!"#$%&' () *+,-#$%&'./ (! " # $ % #&'! '!%!! $ ' #% ( ) '!%!! $ ' * % + )!' + ' % &!!! ( )!! %,!' $ - ( ' *
9( 9 9; ;!. $!!%'!" #$%&'!"#$ % & &$ ' "%!"#$%&' () *+,-#$%&'./ (! "# $ % #&'! '!%!! $ ' #% ( ) '!%!! $ ' *% + )!' + ' % &!!! ( )!! %,!' $ - ( ' * * * )*! " "! #$%&'&!### ( # # ) ") *# # # # )# # ( # #
0 ( 1 ) Q = Q T W + Q W + Q P C + Q P R + Q K T + Q G K + Q D M =
M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X O P T Y M A L I Z A C J A K O N S T R U K C J I F O R M Y W T R Y S K O W E J P O D K Ą T E M E F E K T Y W N O C I C H O D
XV WOJEWÓDZKI KONKURS Z MATEMATYKI
XV WOJEWÓDZKI KONKURS Z MATEMATYKI DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW ORAZ KLAS DOTYCHCZASOWYCH GIMNAZJÓW PROWADZONYCH W SZKOŁACH INNEGO TYPU WOJEWÓDZTWA ŚWIĘTOKRZYSKIEGO W ROKU SZKOLNYM 2017/2018 ETAP
ś ź Ą ś Ą ś ś Ę Ą ń ń ń ś ń ńś ś ń ć ń ś ś ź ć ś ś ź ź Ę Ę ś ć ś ś ć ś ść ń Ę ć ć ć ś ń ć ć ć ś ś Ą ź ść ĘĄ ś ś ć ść ć Ś ś ś ś Ą ś ź ś ś ź ń Ą ś ź Ń ś ś ś Ń ń ź ć ś ś ś ć Ń ś ń ś ź ś ń ń ć ć ś ń ć ń ć
() () *+, )# -"#),." ) / ()0)1,+0. ),." "./+0" ("0+ 0"/ 1. * )1,+0.) "0."1",0"#! "# $% &' $ && # %!"#$%&' ' ' ()* +,-./ :; 5 <9:; = $A$
() () *+, )# -"#),." ) / ()0)1,+0. ),." "./+0" ("0+ 0"/ 1. * )1,+0.) "0."1",0"#! "# $% &'$ && # %!"#$%&' ' '()* +,-./01 23456789:; 5 ?2@ $A$BCDE FG H IJ>#KLMN=OPQRS:;TU: ; TUV -. %.#! " #! $% &'
aangażowanie lokalnego biznesu w sponsoring i mecenat kultury jest niewielkie, czego przyczyną jest brak odpowiedniego kapitału kulturowego u
g Z gż llg b g l l, g ą b g ł lg ó, ll g b, żść g l ó łg, ż l f, ż f łą g, ó. R l b ą, ż ó ó gh ą lę ę łś llh, ó ą b h ó łg. Sg l g h, ó f b g gh lh. Gl g: ęb l źl, h g l l l. Mą ą ę l, óó ąą l ęh gh l
Zadania otwarte krótkiej odpowiedzi na dowodzenie
Zadania otwarte krótkiej odpowiedzi na dowodzenie Zadanie 1. Na bokach trójkąta równobocznego ABC tak wybrano punkty E, F oraz D, że AE = BF = CD = 1 AB (rysunek obok). a) Udowodnij, że trójkąt EFD jest
Zarządzenia i informacje 1.1. Zarządzenia
C h o r ą g i e w D o l n o l ą s k a Z H P W r o c ł a w, 3 1 p a U d z i e r n i k a 2 0 1 5 r. Z w i ą z e k H a r c e r s t w a P o l s k i e g o K o m e n d a n t C h o r ą g w i D o l n o 6 l ą s
MiNI Akademia Matematyki na Politechnice Warszawskiej
MiNI Akademia Matematyki na Politechnice Warszawskiej Krzysztof Che lmiński Okr egi i styczne MiNI PW, 14.10.2017 Podstawowe twierdzenia wykorzystywane w zadaniach z ćwiczeń Twierdzenie 1 (najmocniesze
I N F O R M A TO R. są dopalacze nowe narkotyki? Co to. cze nowe narkotyki? Co to są dopalacze tyki? Co to są dopalacze nowe narkotyki?
ą l l?? C? C l C l? C? C l? C l? l? C? C l l? C I N F O R M A TO R l ó ul ggó? C l? C l? l? C? C l l? C ? ą C? C l? C ą l ą? C l? ą l C l? l ą l? C? l ą C? ą C? l? C l C? l ą C? l C l? l l? C ą? C? ą C?
Liturgia eucharystyczna. Modlitwa nad darami œ
Msza święta Liturgia eucharystyczna K. Pa - nie, nasz Bo - że, niech ta O - fia - ra, któ - rą skła - da - my...... Przez Chry - stu - sa, Pa - na na - sze - go. Modlitwa nad darami... Któ - ry ży - e
Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.
Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 5 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e p r z e g l» d ó w k o n s e r w a c y j n o -
Typ G M4 3x120. A B C D E F G H I J K L M N O Typ [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] G2S076
![Typ G M4 3x120. A B C D E F G H I J K L M N O Typ [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] G2S076](/thumbs/67/57675439.jpg "Typ G M4 3x120. A B C D E F G H I J K L M N O Typ [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] [mm] G2S076")
8.1. wentylatory promieniowe 8.1.1 WENTYLATORY PROMIENIOWE Z WEWNĘTRZNYM SILNIKIEM Wlot jednostronny Napięcie Częstotliwość Wydajność Liczba Moc Prąd Kondensator Poziom hałasu Dop.tem. pracy Masa [V] [Hz]
&' & &"& C " # ()*+ +,+ -./&'/ 01&"&!" #!"#$%&' ()* +,-./01 23 / 01 *$%&' :;- </01 => :; AB :;CDE / * F +,*$%&'456
&' & &"& C " # ()*++,+-./&'/ 01&"&!" #!"#$%&'()* +,-./01 23 / 01*$%&'456789 :;- 4678 9 :;?@ :; AB :;CDE/0 1789- :;?@,*F 1GH?@ +,*$%&'456789 :;- I < +,?@46789 :;?@ :; ABJ +,KLA789 - :;?@,MN :; AB,GH