O ROZWIĄZYWANIU ZADAŃ Z RACHUNKU
|
|
|
- Szczepan Jaworski
- 9 lat temu
- Przeglądów:
Transkrypt
1 Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego. O ROZWIĄZYWANIU ZADAŃ Z RACHUNKU PRAWDOPODOBIEŃSTWA Autor: Edward Stachowski Materiały konferencyjne Wrzesień 2010 Centralna Komisja Egzaminacyjna Zespół ds. realizacji projektów współfinansowanych z Europejskiego Funduszu Społecznego ul. Lewartowskiego 6, Warszawa tel./fax (022) tel. (022)
2 Rachunek prawdopodobieństwa Wstęp 1. Przed wprowadzeniem na lekcjach treści programowych z teorii prawdopodobieństwa niezbędne jest wcześniejsze omówienie zagadnień dotyczących elementów kombinatoryki w zakresie przewidzianym dla danego poziomu nauczania. Kombinatoryka jest to dział matematyki wykorzystywany często w teorii prawdopodobieństwa. Zapoznanie uczniów z elementami kombinatoryki w ramach teorii prawdopodobieństwa prowadzi do sytuacji, którą mamy aktualnie - większość uczniów nie rozumie kombinatoryki i nie umie rachunku prawdopodobieństwa. 2. Szkolna teoria prawdopodobieństwa jest znacznie trudniejsza od akademickiej. Akademicka teoria prawdopodobieństwa zaczyna się od podania modelu: dana jest przestrzeń probabilistyczna ( Ω, FP, ). W szkolnej teorii prawdopodobieństwa w wielu zadaniach opisane jest doświadczenie losowe i podany problem z nim związany. Dla tego doświadczenia i podanego problemu musimy zbudować model probabilistyczny i to na ogół sprawia wiele kłopotów. Koniecznie należy pamiętać o tym, że dla danego doświadczenia losowego, w wielu przypadkach, model można zbudować na kilka sposobów, czyli Ω nie jest jednoznacznie wyznaczona przez doświadczenie losowe. Np. model zbudowany za pomocą drzewa jest często różny od modelu klasycznego. Pojęciem pierwotnym teorii prawdopodobieństwa jest zdarzenie elementarne. Jak wiadomo pojęcia pierwotnego nie definiuje się, jednak przy rozwiązywaniu zadań, budując model, musimy zdecydować, co w danym doświadczeniu losowym jest zdarzeniem elementarnym. Proponujemy następujący sposób postępowania. Analizujemy doświadczenie losowe i sporządzamy listę jego możliwych wyników, tak aby lista ta spełniała następujące warunki: 1) ma być kompletna, tzn. doświadczenie nie może zakończyć się wynikiem, którego nie ma na liście, 2) elementy listy muszą być parami rozłączne, tzn. każdy wynik umieszczony na liście musi wykluczać wszystkie inne wyniki tej listy. 3) elementy listy są nierozkładalne, tzn. żadnego z elementów listy nie można przedstawić w postaci sumy dwóch wyników. Elementy tak sporządzonej listy przyjmujemy za zdarzenia elementarne. Pamiętamy o postulacie rozróżnialności: Jeżeli jest kilka monet o tym samym nominale, kilka sześciennych kostek do gry, kilka kul tego samego koloru (ogólnie kilka elementów tego samego rodzaju optycznie nierozróżnialnych ), to w naszych rozważaniach będą one zawsze rozróżnialne, to znaczy ponumerowane. umawiamy się, że jest element pierwszy, element drugi,... 1
3 Zbiór wszystkich zdarzeń elementarnych oznaczamy Ω. Zdarzeniem losowym nazywamy każdy podzbiór skończonego zbioru wszystkich zdarzeń elementarnych. Prawdopodobieństwo jest to funkcja P, określona na wszystkich zdarzeniach losowych zawartych w danym zbiorze Ω, spełniająca następujące warunki: 1. Dla każdego zdarzenia losowego A jest PA ( ) 0 2. P( Ω ) = 1 3. Dla każdej pary zdarzeń rozłącznych A, B jest PA ( B) = PA ( ) + PB ( ). Podstawowe własności prawdopodobieństwa 1. P( ) = Jeżeli A B, to PB ( \ A) = PB ( ) PA ( ). 3. Jeżeli A B, to PA ( ) PB ( ). 4. Dla każdego A, PA ( ) 1.. PA ( ) = 1 PA ( ). 6. PA ( B) = PA ( ) + PB ( ) PA ( B). Ważną konsekwencją własności 4 oraz 6 jest nierówność PA ( B) PA ( ) + PB ( ) 1. Twierdzenie. Klasyczna definicja prawdopodobieństwa Jeżeli zbiór wszystkich zdarzeń elementarnych Ω jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są równoprawdopodobne, to dla każdego zdarzenia losowego A Ω A PA= ( ). Ω Wyróżniamy następujące typowe doświadczenia losowe: 1) w doświadczeniu polegającym na losowaniu po jednym elemencie z każdego ze zbiorów A1, A2,..., A k, zdarzeniami elementarnymi są wszystkie ciągi ( x, x,..., x ) takie, że x A dla i {1, 2,..., k}, jest to model klasyczny 1 2 k i 1 2 Ω= A A... A k ; i i 2) w doświadczeniu polegającym na k-krotnym losowaniu po jednym elemencie ze zwracaniem, ze zbioru A, zdarzeniami elementarnymi są wszystkie funkcje f :{1,2,..., k} A, lub równoważnie wszystkie ciągi ( x1, x2,..., xk ) takie, że x A dla i {1,2,..., k}, lub równoważnie wszystkie k-elementowe wariacje i k z powtórzeniami zbioru A, jest to model klasyczny i jeżeli A = n, to Ω= n ; 3) w doświadczeniu polegającym na k-krotnym losowaniu po jednym elemencie bez zwracania, ze zbioru A, takiego, że A = n i k n, zdarzeniami elementarnymi są wszystkie funkcje różnowartościowe f :{1, 2,..., k} A, lub równoważnie wszystkie 2
4 ciągi różnowartościowe ( x1, x2,..., xk ) takie, że xi A dla i {1,2,..., k}, lub równoważnie wszystkie k-elementowe wariacje bez powtórzeń zbioru A, n! jest to model klasyczny i Ω = n ( n 1)... ( n k+ 1) = ; ( n k)! 4) w doświadczeniu polegającym na porządkowaniu wszystkich elementów zbioru A takiego, że A = n, zdarzeniami elementarnymi są wszystkie funkcje różnowartościowe f :{1,2,..., n} A, lub równoważnie wszystkie ciągi różnowartościowe ( x, x,..., x ) takie, 1 2 n że x A dla i {1,2,..., n}, lub równoważnie wszystkie permutacje zbioru A, i jest to model klasyczny i Ω= n!; ) w doświadczeniu polegającym na jednoczesnym losowaniu k elementów ze zbioru A lub k-krotnym losowaniu po jednym elemencie bez zwracania, ze zbioru A takiego, że A = n i k n, ale nie interesuje nas kolejność losowania a tylko to czy dany element został wylosowany czy nie, zdarzeniami elementarnymi są wszystkie k-elementowe n n! podzbiory zbioru A,jest to model klasyczny i Ω= =. k k! ( n k)! Zakres podstawowy Zadania z teorii prawdopodobieństwa, w zakresie podstawowym, dotyczą prostych doświadczeń losowych typu: a) losowanie jednego elementu z podanego zbioru, b) losowaniu po jednym elemencie z dwóch (trzech) zbiorów, c) kilkukrotnym losowaniu po jednym elemencie ze zwracaniem z danego zbioru np. rzuty kostką to losowanie po jednym elemencie ze zwracaniem ze zbioru { 1, 2,3, 4,,6 }, d) kilkukrotnym losowaniu po jednym elemencie bez zwracania z danego zbioru. Przykład 1. Dane są liczby 2 oraz 4. Ze zbioru liczb { 1, 2,3, 4,,6,7,8 } wybieramy losowo jedną liczbę i oznaczamy ją k. Oblicz prawdopodobieństwo zdarzenia: istnieje trójkąt o długościach boków 2, 4, k. Zdarzeniami elementarnymi są wszystkie elementy zbioru { 1, 2,3, 4,,6,7,8 }. Zdarzenia jednoelementowe są równoprawdopodobne, spełnione są założenia twierdzenia klasyczna definicja prawdopodobieństwa. Ω= 8. Określamy zdarzenia A: 3
5 A - liczby 2, 4 k są długościami boków trójkąta, czyli spełniają nierówności trójkąta tzn. suma długości każdych dwóch boków jest większa od długości trzeciego boku. 2+ 4> k k < k > 4 stąd k > 2 czyli 4 + k > 2 k > 2 k { 3, 4,}, stąd A = 3 i 3 PA= ( ). 8 Przykład 2. Są dwa pojemniki. W każdym z nich są cztery kule. W pierwszym pojemniku jest 1 kula biała i 3 kule czarne, w drugim są 2 kule białe i dwie kule czarne. Z każdego pojemnika losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzeń: A - otrzymamy dwie kule białe, B - otrzymamy dokładnie jedną kulę białą. I sposób rozwiązania Pamiętamy o postulacie rozróżnialności i numerujmy kule w każdym pojemniku. W pojemniku pierwszym kula biała ma numer 1, kule czarne numery 2,3,4; w pojemniku drugim kule białe mają numery 1,2, kule czarne mają numery 3,4. Zdarzeniami elementarnymi w tym doświadczeniu są wszystkie ciągi dwuelementowe ( ab, ) o wartościach w zbiorze {1,2,3,4}. Zdarzenia jednoelementowe są równoprawdopodobne, mamy model klasyczny. Korzystając z twierdzenia o mnożeniu Ω= 4 4 = 16. Zdarzeniu A sprzyjają wszystkie ciągi odpowiadające wyborowi kuli białej z każdego pojemnika, 2 A = 1 2 = 2 i PA ( ) = = 0, Zdarzenie B jest sumą dwóch zdarzeń rozłącznych B= B B, gdzie 1 2 B 1 - z pierwszego pojemnika wylosujemy kulę białą i z drugiego czarną, B 2 - z pierwszego pojemnika wylosujemy kulę czarną i z drugiego białą B1 = 1 2 = 2, B = 3 2 = 6. 2 Zdarzenia B1, B 2 są rozłączne, stąd 8 B = B1 + B2 = 8 i PB ( ) = = 0,. 16 4
6 II sposób rozwiązania (metoda tabeli) Ponumerujmy kule w każdym pojemniku. Niech w pojemniku pierwszym kula biała ma numer 1, kule czarne numery 2,3,4; w pojemniku drugim kule białe mają numery 1,2, kule czarne mają numery3,4. Zdarzeniami elementarnymi w tym doświadczeniu są wszystkie ciągi dwuelementowe ( ab, ) o wartościach w zbiorze {1,2,3,4}. Zdarzenia jednoelementowe są równoprawdopodobne, jest to model klasyczny. Zbiór wszystkich zdarzeń elementarnych Ω możemy przedstawić w postaci tabeli 4x4. Rysujemy dwie tabele. W pierwszej zaznaczamy zdarzenia elementarne sprzyjające zdarzeniu A, w drugiej zaznaczamy zdarzenia elementarne sprzyjające zdarzeniu B i obliczamy odpowiednie prawdopodobieństwo. Uwaga. Możemy narysować tabelę 2x2, ale w tak opisanym zbiorze Ω zdarzenia jednoelementowe nie są równoprawdopodobne, nie byłby to model klasyczny. III sposób rozwiązania (metoda drzewa) Rysujemy drzewo, które ma dwa poziomy. Drzewo może mieć 16 gałęzi, albo w prostszej wersji 4 gałęzie. Zapisujemy prawdopodobieństwa przy odcinkach drzewa i obliczamy prawdopodobieństwo. Przykład 3. W pewnym liceum ogólnokształcącym są dwie klasy trzecie, których skład osobowy przedstawiono w tabeli. klasa liczba wszystkich uczniów liczba dziewcząt IIIa IIIb Z każdej klasy wybieramy losowo jednego ucznia. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że zostanie wybrana dziewczynka i chłopiec. Wynik podaj w postaci ułamka zwykłego nieskracalnego. I sposób rozwiązania Na podstawie tabeli odczytujemy skład obu klas: IIIa 18 dziewczynek i 12 chłopców IIIb 16 dziewczynek i 16 chłopców. Zdarzeniami elementarnymi są wszystkie pary (a, b), gdzie a oznacza ucznia klasy IIIa b oznacza ucznia klasy IIIb. Zdarzenia jednoelementowe są równoprawdopodobne, mamy schemat klasyczny.
7 Ω= = 960 Zdarzenie A jest sumą dwóch zdarzeń: A 1 - z klasy IIIa zostanie wybrana dziewczynka i z klasy IIIb zostanie wybrany chłopiec A 2 - z klasy IIIa zostanie wybrany chłopiec i z klasy IIIb zostanie wybrana dziewczynka. A= A1 A2. A1 A2 =, stąd A = A1 + A2, A1 = = 288 A = = A = = 480 i A PA= ( ) = =. Ω II sposób rozwiązania (metoda drzewa) Rysujemy drzewo, które ma dwa poziomy. Drzewo dla zdarzenia A, na którym są tylko istotne gałęzie, ma 4 gałęzie (wyróżniamy płeć). Zapisujemy prawdopodobieństwa przy odcinkach drzewa i obliczamy prawdopodobieństwo dodając odpowiednie iloczyny PA= ( ) + = Przykład 4. Ze zbioru liczb {0,1,2,3,4,} losujemy kolejno dwa razy po jednej liczbie bez zwracania i oznaczając pierwszą wylosowaną liczbę przez a, drugą przez b, tworzymy liczbę x = 10a + b. Oblicz prawdopodobieństwo zdarzeń: A - x będzie dwucyfrową liczbą parzystą, B - x będzie dwucyfrową liczbą podzielną przez trzy. I sposób rozwiązania Zdarzeniami elementarnymi są wszystkie dwuelementowe ciągi różnowartościowe ( a, b) o wartościach w zbiorze {0,1,2,3,4,} - dwuelementowe wariacje bez powtórzeń zbioru sześcioelementowego, Zdarzenia jednoelementowe są równoprawdopodobne, jest to model klasyczny i Ω= 6 = 30. Obliczamy P ( A). Zauważmy, że A = A 1 A 2, gdzie A 1 - pierwsza liczba będzie parzysta, różna od zera i druga liczba będzie parzysta (różna od pierwszej), A 2 - pierwsza liczba będzie nieparzysta i druga liczba będzie parzysta. 6
8 A 1 = 2 2 = 4, A 2 = 3 3 = 9, A A =, stąd A = A1 + A2 = 13 i 1 2 Obliczamy P ( B). 13 PA= ( ). 30 Liczba jest podzielna przez trzy, gdy suma jej cyfr jest podzielna przez trzy, stąd {( 1,2,1,,2,1,2,4,3,0,4,2,4,,,1,,4 ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )} B =, B = 9 i PB ( ) = 0,3. II sposób rozwiązania (metoda tabeli) Zbiór wszystkich zdarzeń elementarnych Ω możemy przedstawić w postaci tabeli 6x6 z usuniętą przekątną zawierającą (0,0). W tabeli jest = 30 pól. Rysujemy dwie tabele. W pierwszej zaznaczamy zdarzenia elementarne sprzyjające zdarzeniu A, w drugiej zdarzenia elementarne sprzyjające zdarzeniu B i obliczamy odpowiednie prawdopodobieństwa. III sposób rozwiązania (metoda drzewa) Rysujemy dwa drzewa, pierwsze dla zdarzenia A, drugie dla zdarzenia B. Drzewo ma 2 poziomy. Zapisujemy prawdopodobieństwa przy odcinkach drzewa i obliczamy prawdopodobieństwo dodając odpowiednie iloczyny. Drzewo dla zdarzenia A, na którym są tylko istotne gałęzie, na ma 4 gałęzie PA= ( ) + = Drzewo dla zdarzenia B, na którym są tylko istotne gałęzie, ma 10 gałęzi PB ( ) = 4 + = = 0, Przykład. stosowanie własności prawdopodobieństwa. Zdarzenia losowe AB, są zawarte w Ω i PB ( ) = 0,6; PA ( B) = 0,; PA ( B) = 0, 2. Oblicz: a) PA ( ), b) PB ( \ A ). PB ( ) = 1 PB ( ), stąd PB ( ) = 0,3. Korzystając z wzoru PA ( B) = PA ( ) + PB ( ) PA ( B) obliczamy PA ( ). PA ( ) = PA ( B) PB ( ) + PA ( B) = 0, 0,3 + 0, 2 = 0,3. Korzystając z wzoru PB ( \ A) = PB ( ) PA ( B) obliczamy PB ( \ A ). PB ( \ A ) = 0,3 0, 2 = 0,1. 7
9 Zakres rozszerzony Przykład 1. Zdarzenia losowe AB, są zawarte w Ω. Liczby PA ( B), PA ( ), PB ( ) są w podanej kolejności pierwszym, trzecim i czwartym wyrazem ciągu arytmetycznego oraz PA ( B) = 0,6 i PB ( \ A) = 0,3. Oblicz P( A B). Niech ( a n ) będzie ciągiem arytmetycznym o pierwszym wyrazie a 1 i różnicy r. PA ( B) = a1, PA ( ) = a1+ 2 r, PB ( ) = a1+ 3 r. Korzystając z własności prawdopodobieństwa zapisujemy układ równań: PA ( B) = PA ( ) + PB ( ) PA ( B) PB ( \ A) = PB ( ) PA ( B) Podstawiając dane otrzymujemy: 0, 6 = a1+ 2r+ a1+ 3r a1 0,3 = a1+ 3r a1 0,6 = a1 + r 0,3 = 3r stąd a1 = 0,1, r = 0,1 i PA ( B) = 0,1, PA ( ) = 0,1 + 0, 2 = 0,3, PB ( ) = 0,1 + 0,3 = 0, 4. ( ) ( ) ( ) P A B = PA ( ) + PB ( ) P A B = 1 PA ( ) + PB ( ) PB+ PA ( B) = 0,8. Przykład 2. Pięć ponumerowanych kul rozmieszczamy losowo w trzech ponumerowanych komórkach. Oblicz prawdopodobieństwo zdarzeń: A - pierwsza komórka będzie pusta, B - pierwsza komórka będzie pusta lub druga komórka będzie pusta. Zdarzeniami elementarnym są wszystkie pięcioelementowe wariacje z powtórzeniami zbioru trzyelementowego (każdej kuli przyporządkujemy numer komórki, w której będzie umieszczona). Zdarzenia jednoelementowe są równoprawdopodobne, jest to model klasyczny i Ω= 3 = 243. Zdarzeniu A - pierwsza komórka będzie pusta, sprzyjają zdarzenia elementarne odpowiadające rozmieszczeniu wszystkich kul w drugiej i trzeciej komórce - pięcioelementowe wariacje z powtórzeniami zbioru dwuelementowego A = 2 i PA ( ) = =
10 Zdarzenie B jest sumą dwóch zdarzeń, B = B 1 B2, gdzie zdarzenie B i oznacza zdarzenie, że komórka o numerze i będzie pusta, i {1,2 }. P( B) = P( B1 B2 ) = P( B1 ) + P( B2 ) P( B1 B2 ). B = B = 2, B B = 1, (jest tylko jedno rozmieszczenie, w którym pierwsza i druga komórka będą puste wszystkie kule będą w trzeciej komórce) PB ( ) = =. Przykład 3. Osiem ponumerowanych kul rozmieszczamy losowo w trzech ponumerowanych pojemnikach. Oblicz prawdopodobieństwo zdarzeń: A - w pierwszym pojemniku będą cztery kule, B - w pierwszym pojemniku będą cztery kule i w drugim pojemniku będą trzy kule. Zdarzeniami elementarnymi są wszystkie ośmioelementowe wariacje z powtórzeniami zbioru trójelementowego - każdej kuli przyporządkujemy numer komórki, w której będzie umieszczona. Zdarzenia jednoelementowe są równoprawdopodobne, jest to model klasyczny 8 i Ω= 3 = 661. Zdarzeniu A sprzyjają te rozmieszczenia, w których cztery kule są w pierwszym pojemniku a pozostałe cztery kul są rozmieszczone dowolnie w pozostałych dwóch pojemnikach. Obliczamy A : 8 numery kul, które będą w pierwszym pojemniku wybieramy na sposobów, 4 4 pozostałe kule, w dwóch pozostałych pojemnikach rozmieszczamy na 2 sposobów, korzystając z reguły mnożenia, otrzymujemy 8 4 A = 2 = 1120 i PA ( ) = 0, Zdarzeniu B sprzyjają te rozmieszczenia, w których cztery kule są w pierwszym pojemniku, trzy w drugim pojemniku i jedna w trzecim pojemniku. Obliczamy B : 8 numery kul, które będą w pierwszym pojemniku wybieramy na sposoby, 4 4 numery kul, które będą w drugim pojemniku wybieramy na sposoby, 3 korzystając z reguły mnożenia, otrzymujemy 8 4 B = = 280 i PB ( ) = 0,
11 Przykład 4. Doświadczenie losowe polega na pięciokrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że otrzymamy dokładnie trzy razy ściankę z trzema oczkami i suma liczb oczek uzyskanych we wszystkich rzutach będzie parzysta. Zdarzeniami elementarnymi są wszystkie pięcioelementowe wariacje z powtórzeniami zbioru{ 1, 2,3, 4,,6 }. Jest to model klasyczny, Ω= 6. Zdarzenie A polega na tym, że dokładnie w trzech rzutach otrzymamy trzy oczka, w jednym z pozostałych dwóch rzutów otrzymamy jedno albo pięć oczek, a w drugim parzystą liczbę oczek. Obliczamy A : numery trzech rzutów dla trzech oczek wybieramy na = 10 sposobów, 3 numer rzutu, z dwóch pozostałych, dla liczby oczek ze zbioru {1,} wybieramy na 2 sposoby, liczbę oczek na 2 sposoby parzystą liczbę oczek na 3 sposoby; korzystając z reguły mnożenia, otrzymujemy A = = Stąd PA= 120 ( ) 6 = 324. Przykład. Doświadczenie losowe polega na pięciokrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że otrzymamy dokładnie trzy razy ściankę z trzema oczkami i iloczyn liczb oczek uzyskanych we wszystkich rzutach będzie parzysty. Zdarzeniami elementarnymi są wszystkie pięcioelementowe wariacje z powtórzeniami zbioru{ 1, 2,3, 4,,6 }. Jest to model klasyczny, Ω= 6. Zdarzenie A polega na tym, że w dokładnie trzech rzutach otrzymamy trzy oczka i w pozostałych dwóch rzutach otrzymamy co najmniej raz parzystą liczbę oczek. Obliczamy A : numery trzech rzutów dla trzech oczek wybieramy na = 10 sposobów, 3 co najmniej raz parzystą liczbę oczek, w pozostałych dwóch rzutach, możemy otrzymać na = 21 sposobów - możliwe są wyniki ze zbioru {1,2,4,,6} (albo = 21sposobów), 10
12 korzystając z reguły mnożenia, otrzymujemy Stąd PA= ( ) 6 = A = 21 = Przykład 6. Doświadczenie losowe polega na pięciokrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że otrzymamy dokładnie trzy razy ściankę z trzema oczkami i iloczyn liczb oczek uzyskanych we wszystkich rzutach będzie podzielny przez 4. Zdarzeniami elementarnymi są wszystkie pięcioelementowe wariacje z powtórzeniami zbioru{ 1, 2,3, 4,,6 }. Jest to model klasyczny, Ω= 6. Zdarzenie A polega na tym, że w dokładnie trzech rzutach otrzymamy trzy oczka i w pozostałych dwóch rzutach otrzymamy co najmniej raz pięć oczek. Obliczamy A : numery trzech rzutów dla trzech oczek wybieramy na = 10 sposobów, 3 co najmniej raz pięć oczek w pozostałych dwóch rzutach możemy otrzymać na sposobów możliwe są wyniki ze zbioru {1,2,4,,6} (albo = 9 sposobów), korzystając z reguły mnożenia, otrzymujemy A = 9 = Stąd PA= 90 ( ) 6 = = 9 Przykład 7. Doświadczenie losowe polega na pięciokrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że otrzymamy dokładnie trzy razy ściankę z trzema oczkami i suma liczb oczek uzyskanych we wszystkich rzutach będzie podzielna przez 3. Zdarzeniami elementarnymi są wszystkie pięcioelementowe wariacje z powtórzeniami zbioru{ 1, 2,3, 4,,6 }. Jest to model klasyczny, Ω= 6. Zdarzenie A polega na tym, że dokładnie w trzech rzutach otrzymamy trzy oczka i w pozostałych dwóch rzutach otrzymamy liczby oczek, których suma jest podzielna przez 3, 11
13 tzn. otrzymamy dwa razy 6 oczek albo w jednym z rzutów będzie liczba oczek ze zbioru {1,4}, a w drugim ze zbioru {2,}. Obliczamy A : numery trzech rzutów dla trzech oczek wybieramy na = 10 sposobów, 3 otrzymamy dwa razy 6 oczek na 1 sposób albo wybieramy numer rzutu, w którym będzie liczba oczek ze zbioru {1,4} na 2 sposoby, liczbę ze zbioru {1,4} na 2 sposoby i liczbę ze zbioru {2,} na 2 sposoby; razem = 9sposobów, korzystając z reguły mnożenia, otrzymujemy A = 9 = Stąd PA= 90 ( ) 6 = 432. Przykład 8. Ze zbioru liczb {1, 2,3, 4,,6,7,8,9} losujemy trzy razy po jednej liczbie bez zwracania. Oznaczając kolejno wylosowane liczby przez abc,, tworzymy liczbę x= 100a+ 10 b+ c. Oblicz prawdopodobieństwo zdarzenia A - liczba x będzie nieparzysta. I sposób rozwiązania - pełna informacja o wyniku doświadczenia Zdarzeniami elementarnymi są wszystkie trzyelementowe wariacje bez powtórzeń zbioru{ 1, 2,3, 4,,6,7,8,9 }, jest to model klasyczny, Ω= = 04 Zdarzeniu A sprzyjają zdarzenia elementarne, w których c jest liczbą nieparzystą. W typowym rozwiązaniu zdarzenie A jest sumą czterech parami rozłącznych zdarzeń A= A 1 A 2 A 3 A 4, gdzie A 1 - abc,, są nieparzyste, A 1 = 4 3 = 60 A 2 - ac, są nieparzyste, b jest parzysta, A 2 = 4 4 = 80 A 1 - bc, nieparzyste, a parzysta, A 3 = 4 4 = 80 A 1 - ab, są parzyste, c jest nieparzysta, A 4 = 4 3 = 60 A = 280 i PA ( ) = 9 II sposób rozwiązania Aby sprawdzić, czy liczba x jest trzycyfrowa i nieparzysta wystarczy znać liczbę c, liczby a oraz b są nieistotne. Na trzecim miejscu może wystąpić każda z dziewięciu liczb i są to sytuacje jednakowo możliwe. Zdarzeniami elementarnymi są wszystkie liczby ze zbioru {1, 2,...,9}, jest to model klasyczny, Ω= 9 i A = i PA ( ) =. 9 12
14 Uwaga 1. Fakt, że na trzecim miejscu może wystąpić każda z liczb ze zbioru {1,2,...,9} nie budzi sprzeciwu, ale to, że wszystkie mają równe prawdopodobieństwo nie jest dla wielu osób oczywisty. Nie jest też oczywiste, że najpierw możemy wybrać liczbę c, potem pozostałe w dowolnej kolejności i otrzymamy ten sam model. Uwaga 2. Jak wynika z rozwiązania, w którym stosujemy II sposób rozwiązania, przy uogólnieniu tego zadania na przypadek, gdy losujemy k liczb bez zwracania i tworzymy liczbę k 1 k x= 10 a + 10 a a k (2 k 10), wynik tego zadania nie zależy od tego ile liczb losujemy. Uwaga 3. Zadanie, którego rozwiązanie przedstawiliśmy, ma wiele innych wariantów historyjek, idea jest ta sama, można je rozwiązać w pamięci budując odpowiednik II sposób rozwiązania. Przykład - typowe zadanie z wielu zbiorów zdań Z pojemnika, w którym jest siedem kul białych i cztery kule czarne, losujemy trzy razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo otrzymania kuli czarnej w trzecim losowaniu. Większość zalecanych sposobów rozwiązania, to odpowiednik I sposobu rozwiązania z pełną informacją o wyniku doświadczenia. Uwaga 4. Pomocą w kształceniu intuicji w tym zagadnieniu może być leżąca na stole talia kart. Powinno być jasne, że zdarzenia: A - pierwsza karta jest pikiem, B - trzecia karta jest pikiem są równoprawdopodobne. Przykład 9. Ze zbioru liczb {0,1, 2,3, 4,,6,7,8,9} losujemy trzy razy po jednej liczbie bez zwracania. Oznaczając kolejno wylosowane liczby przez abc,, tworzymy liczbę x= 100a+ 10 b+ c. Oblicz prawdopodobieństwo zdarzenia A - liczba x będzie trzycyfrowa i nieparzysta. I sposób rozwiązania - pełna informacja o wyniku doświadczenia Zdarzeniami elementarnymi są wszystkie trzyelementowe wariacje bez powtórzeń zbioru{ 0,1, 2,3, 4,,6,7,8,9 }, jest to model klasyczny, Ω= = 720 Zdarzeniu A sprzyjają zdarzenia elementarne, w których a 0 oraz cjest liczbą nieparzystą. W typowym rozwiązaniu zdarzenie A jest sumą czterech parami rozłącznych zdarzeń A= A 1 A 2 A 3 A 4, gdzie A 1 - abc,, są nieparzyste, A 1 = 4 3 = 60 A 2 - ac, są nieparzyste, b jest parzysta, A 2 = 4 =
15 A 3 - bc, są nieparzyste, a jest parzysta, A 3 = 4 4 = 80 A 4 - ab, są parzyste, c jest nieparzysta, A 4 = 4 4 = 80 4 A = 320 i PA ( ) = 9 II sposób rozwiązania Aby sprawdzić, czy liczba x jest trzycyfrowa i nieparzysta wystarczy znać liczby a oraz c, liczba b jest nieistotna. Zdarzeniami elementarnymi są wszystkie dwuelementowe wariacje bez powtórzeń zbioru{ 0,1, 2,3, 4,,6,7,8,9 }, jest to model klasyczny, Ω= 10 9 Zdarzeniu A sprzyjają zdarzenia elementarne, w których a 0 oraz cjest liczbą nieparzystą. 4 A = 8 = 40, (najpierw wybieramy c, potem a), PA= ( ) 9 Uwaga Jak wynika z rozwiązania, w którym stosujemy II sposób rozwiązania, przy uogólnieniu tego zadania na przypadek, gdy losujemy k, (2 k 10), liczb bez zwracania i tworzymy k 1 k 2 liczbę x= 10 a1+ 10 a a k. Wynik tego zadania nie zależy od tego ile liczb losujemy. W przypadku losowania np. sześciu liczb rozwiązanie, w którym stosujemy I sposób rozwiązania (pełna informacja) jest bardzo uciążliwe rachunkowo. Sygnalizujemy tu bardzo ważne zagadnienie. Ucząc rozwiązywania zadań dotyczących rachunku prawdopodobieństwa należy pokazywać uczniom, że czasami model zbudowany zgodnie ze szczegółami technicznymi przebiegu doświadczenia jest rachunkowo bardzo uciążliwy, a model uwzględniający tylko problem związany z tym doświadczeniem pozwala rozwiązać zadanie w pamięci. Przykład 10. Zbiór liczb {1,2,...,7} porządkujemy w sposób losowy. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że suma każdych dwóch sąsiednich liczb będzie liczbą nieparzystą. Wynik podaj w postaci ułamka zwykłego nieskracalnego. Zdarzeniami elementarnymi są wszystkie permutacje zbioru siedmioelementowego, zdarzenia elementarne są równoprawdopodobne, jest to model klasyczny i Ω= 7!. Zdarzeniu A sprzyjają te permutacje zbioru {1,2,...,7}, w których na miejscach o numerach nieparzystych będą liczby nieparzyste, a na miejscach o numerach parzystych liczby parzyste. Stąd 4! 3! 1 A = 4! 3! i PA ( ) = =. 7! 3 14
16 Przykład 11. Liczby 1,2,3,4,,6,7 ustawiamy w szeregu w sposób losowy. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba 1 nie będzie stała obok liczby 2 oraz iloczyn każdych dwóch sąsiednich liczb będzie parzysty. Zdarzeniami elementarnymi są wszystkie permutacje zbioru{ 1, 2,3, 4,,6,7 }. Jest to model klasyczny, Ω= 7! = 040. Zdarzenie A polega na tym, że liczby nieparzyste stoją na miejscach o numerach nieparzystych, liczby parzyste stoją na miejscach o numerach parzystych i liczby 1 oraz 2 nie stoją obok siebie. Wyróżniamy dwa przypadki, liczba 1 stoi na miejscu pierwszym lub ostatnim albo liczba 1 stoi w środku. Obliczamy A : gdy liczba 1 stoi na miejscu pierwszym lub ostatnim, to liczbę 2 możemy ustawić na 2 sposoby, a gdy liczba 1 stoi w środku to liczbę 2 możemy ustawić na 1 sposób, pozostałe liczby nieparzyste ustawiamy na 3! = 6 sposobów i pozostałe liczby parzyste ustawiamy na 2! = 2 sposoby; korzystając z reguły mnożenia otrzymujemy A = ( ) 62 = 72. Stąd 72 1 PA= ( ) = Przykład 12. Liczby 1,2,3,4,,6,7,8 ustawiamy w szeregu w sposób losowy. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba 1 nie będzie stała obok liczby 2 oraz suma każdych dwóch sąsiednich liczb będzie nieparzysta. Zdarzeniami elementarnymi są wszystkie permutacje zbioru{ 1, 2,3, 4,,6,7,8 }. Jest to model klasyczny, Ω= 8! = Zdarzenie A polega na tym, że liczby nieparzyste stoją na miejscach o numerach nieparzystych, liczby parzyste stoją na miejscach o numerach parzystych albo odwrotnie i liczby 1 oraz 2 nie stoją obok siebie. Wyróżniamy dwa przypadki, liczba 1 stoi na miejscu pierwszym lub ostatnim albo liczba 1 stoi w środku. Obliczamy A : gdy liczba 1 stoi na miejscu pierwszym lub ostatnim, to liczbę 2 możemy ustawić na 3 sposoby, a gdy liczba 1 stoi w środku to liczbę 2 możemy ustawić na 2 sposoby, pozostałe liczby nieparzyste ustawiamy na 3! = 6 sposobów i pozostałe liczby parzyste ustawiamy na 3! = 6 sposobów; korzystając z reguły mnożenia otrzymujemy A = ( ) 6 6 =
17 Stąd PA= ( ) = Przykład 13. Liczby 1,2,3,4,,6,7,8 ustawiamy w szeregu w sposób losowy. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba 1 będzie stała obok liczby 2 oraz liczba 3 będzie stała obok liczby 4. Zdarzeniami elementarnymi są wszystkie permutacje zbioru{ 1, 2,3, 4,,6,7,8 }. Jest to model klasyczny, Ω= 8! = I sposób obliczenia A : Zdarzenie A polega na tym, że liczby 1 i 2 stoją obok siebie oraz liczby 3 i 4 stoją obok siebie. Jest 7 par kolejnych miejsc. Wyróżniamy dwa przypadki: 1) gdy liczby 1 i 2 stoją na miejscach 1,2 albo 7,8, to dla pary 3 i 4 mamy par kolejnych miejsc, 2) w pozostałych przypadkach (gdy liczby 1 i 2 stoją na miejscach 2,3 albo 3,4 albo 4, albo,6 albo 6,7) dla pary 3 i 4 mamy 4 pary kolejnych miejsc. Obliczamy A : gdy liczby 1 i 2 stoją na miejscach 1,2 albo 7,8-2 możliwości, to dla pary 3 i 4 mamy par kolejnych miejsc, w pozostałych przypadkach dla pary 3 i 4 mamy 4 pary kolejnych miejsc; na wybranych miejscach liczby 1,2 oraz 3,4 ustawiamy na 22 = 4 sposoby, pozostałe 4 liczby na pozostałych 4 miejscach ustawiamy na 4! = 24 sposoby; korzystając z reguły mnożenia otrzymujemy A = ( 2 + 4) = II sposób obliczenia A : Potraktujmy parę (1,2) jako jeden element oraz parę (3,4) jako jeden element. Zatem wraz z pozostałymi 4 liczbami ustawiamy w szeregu 6 elementów na 6! sposobów, w każdym z tych ustawień parę (1,2) można ustawić na 2 dwa sposoby i parę (3,4) na dwa sposoby. Korzystając z reguły mnożenia otrzymujemy A = 2 2 6! = Stąd PA= ( ) = Przykład 14. Liczby 1,2,3,4,,6,7,8 ustawiamy w szeregu w sposób losowy. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że liczba 1 będzie stała obok liczby 2 lub liczba 3 będzie stała obok liczby 4. 16
18 Zdarzeniami elementarnymi są wszystkie permutacje zbioru{ 1, 2,3, 4,,6,7,8 }. Jest to model klasyczny, Ω= 8! = Zdarzenie A jest sumą dwóch zdarzeń A= A1 A2. Zdarzenie A 1 polega na tym, że liczby 1 i 2 stoją obok siebie, zdarzenie A 2 polega na tym, że liczby 3 i 4 stoją obok siebie. A = A1 A2 = A1 + A2 A1 A2 Jest 7 par kolejnych miejsc. Zdarzenie A 1 polega na tym, że liczby 1 i 2 zajmują kolejne miejsca. Obliczamy A 1. Kolejne miejsca wybieramy na 7 sposobów, liczby 1,2 ustawiamy na tych miejscach na 2 sposoby, pozostałe 6 liczb na pozostałych 6 miejscach ustawiamy na 6! = 720 sposobów; korzystając z reguły mnożenia otrzymujemy A 1 = 7 2 6! = Analogicznie obliczamy A2 = A1 = Zdarzenie A1 A2 polega na tym, że liczby 1,2 będą obok siebie oraz liczby 3,4 będą obok siebie. I sposób obliczenia A1 A2 : Zdarzenie A1 A2 polega na tym, że liczby 1 i 2 stoją obok siebie oraz liczby 3 i 4 stoją obok siebie. Jest 7 par kolejnych miejsc. Wyróżniamy dwa przypadki: 1) gdy liczby 1 i 2 stoją na miejscach 1,2 albo 7,8, to dla pary 3 i 4 mamy par kolejnych miejsc, 2) w pozostałych przypadkach (gdy liczby 1 i 2 stoją na miejscach 2,3 albo 3,4 albo 4, albo,6 albo 6,7) dla pary 3 i 4 mamy 4 pary kolejnych miejsc. Obliczamy A1 A2 : gdy liczby 1 i 2 stoją na miejscach 1,2 albo 7,8 2 możliwości, to dla pary 3 i 4 mamy par kolejnych miejsc, w pozostałych przypadkach dla pary 3 i 4 mamy 4 pary kolejnych miejsc; na wybranych miejscach liczby 1,2 oraz 3,4 ustawiamy na 22 = 4 sposoby, pozostałe 4 liczby na pozostałych 4 miejscach ustawiamy na 4! = 24 sposoby; korzystając z reguły mnożenia otrzymujemy: A A ( ) II sposób obliczenia A1 A2 : 1 2 = = Potraktujmy parę (1,2) jako jeden element oraz parę (3,4) jako jeden element. Zatem wraz z pozostałymi 4 liczbami ustawiamy w szeregu 6 elementów na 6! sposobów, w każdym z tych ustawień parę (1,2) można ustawić na 2 dwa sposoby i parę (3,4) na dwa sposoby. Korzystając z reguły mnożenia otrzymujemy A = 2 2 6! = Stąd A = =
19 i PA= ( ) = Przykład 1. (Arkusz I. Matura Zadanie 3). Po wiadomościach z kraju i ze świata telewizja TVG ma nadać pięć reklam: trzy reklamy różnych proszków do prania oraz dwie reklamy różnych past do zębów. Kolejność nadawania reklam jest ustalana losowo. Oblicz prawdopodobieństwo, że dwie reklamy produktów tego samego rodzaju nie będą nadane bezpośrednio jedna po drugiej. Wynik podaj w postaci nieskracalnego ułamka zwykłego. Rozwiązania Dla ustalenia uwagi przyporządkujemy proszkom do prania liczby 1,2,3, a pastom do zębów liczby 4,. Przez A oznaczmy zdarzenie opisane w treści zadania. I sposób rozwiązania - pełna informacja o wyniku doświadczenia Zdarzeniami elementarnymi są wszystkie permutacje zbioru {1, 2,3, 4,}, jest to model klasyczny, Ω=! = 120 Zdarzeniu A sprzyjają permutacje, w których proszki stoją na miejscach o numerach 1,3,, a pasty na miejscach 2,4. 1 A = 3! 2! = 12, PA ( ) =. 10 II sposób rozwiązania Zauważmy, że aby odpowiedzieć na pytanie, czy dwie reklamy produktów tego samego rodzaju nie będą nadane bezpośrednio jedna po drugiej, wystarczy wiedzieć, które miejsce zajmuje pierwsza pasta i które miejsce zajmuje druga pasta (albo, które miejsca zajmują kolejne proszki). Zdarzeniami elementarnymi są wszystkie dwuelementowe wariacje bez powtórzeń zbioru pięcioelementowego, jest to model klasyczny, Ω= 4 = 20 (albo wszystkie trójelementowe trzyelementowe wariacje bez powtórzeń zbioru pięcioelementowego, jest to model klasyczny, Ω= 4 3 = 60 ) 2 1 A = 2 1 = 2, PA ( ) = = (albo A = = 6, PA ( ) = = ) III sposób rozwiązania Zauważmy, że aby odpowiedzieć na pytanie, czy dwie reklamy produktów tego samego rodzaju nie będą nadane bezpośrednio jedna po drugiej, wystarczy wiedzieć, które miejsca zajmują pasty - bez precyzowania ustawienia (albo, które miejsca zajmują proszki). 18
20 Zdarzeniami elementarnymi są wszystkie dwuelementowe podzbiory zbioru pięcioelementowego, jest to model klasyczny, Ω= = 10 2 (albo wszystkie trzyelementowe podzbiory zbioru pięcioelementowego, mamy jest to klasyczny, Ω= = 10 ) 3 Zdarzeniu A sprzyja jeden podzbiór 1 A = 1, PA ( ) =. 10 Przykład osób, wśród których są panowie X oraz Y ustawia się w sposób losowy w szeregu. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że pomiędzy panami X i Y będą stały dokładnie dwie osoby. I sposób rozwiązania - pełna informacja o wyniku doświadczenia Zdarzeniami elementarnymi są wszystkie permutacje zbioru dziesięcioelementowego, jest to model klasyczny, Ω= 10! 7 A = 2 7 8!, PA ( ) = 4 II sposób rozwiązania Aby sprawdzić, czy pomiędzy panami X i Y stoją dokładnie dwie osoby, wystarczy wiedzieć, na którym miejscu stoi pan X, a na którym pan Y. Zdarzeniami elementarnymi są wszystkie dwuelementowe wariacje bez powtórzeń zbioru dziesięcioelementowego, jest to model klasyczny, Ω= 10 9 = 90 7 A = 2 7 = 14, PA ( ) = 4 III sposób rozwiązania Aby sprawdzić, czy pomiędzy panami X i Y stoją dokładnie dwie osoby, wystarczy wiedzieć, które miejsca zajmują panowie X i Y, bez precyzowania ustawienia. Zdarzeniami elementarnymi są wszystkie podzbiory dwuelementowe zbioru 10 dziesięcioelementowego, jest to model klasyczny, Ω= = A = 7, PA ( ) =. 4 19
21 Przykład 17. Ze zbioru liczb {1, 2,3, 4,,6,7,8} wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7. Zdarzeniami elementarnymi są wszystkie podzbiory czteroelementowe zbioru 8 { 1, 2,3, 4,,6,7,8 }. Jest to model klasyczny, Ω= = Zdarzenie A jest sumą dwóch zdarzeń A= A1 A2. Zdarzenie A 1 polega na tym, że najmniejszą liczbą jest 3, zdarzenie A 2 polega na tym, że największą liczbą jest 7. A = A1 A2 = A1 + A2 A1 A2 Zdarzenie A 1 polega na tym, że wśród wylosowanych liczb jest 3 oraz trzy liczby ze zbioru{ 4,, 6, 7,8 }. Stąd A1 = = Zdarzenie A 2 polega na tym, że wśród wylosowanych liczb jest 7 oraz trzy liczby ze 6 zbioru{ 1, 2,3, 4,, 6 }. Stąd A2 = = Zdarzenie A1 A2 polega na tym, że wśród wylosowanych liczb są 3 i 7 oraz dwie liczby ze 3 zbioru{ 4,,6 }. Stąd A1 A2 = = Otrzymujemy: A = = 27 i PA= ( ). 70 Przykład 18. Ze zbioru liczb {1, 2,3, 4,,6,7,8,9,10} wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że wśród wylosowanych liczb będą dokładnie dwie liczby parzyste oraz dokładnie jedna liczba podzielna przez. Zdarzeniami elementarnymi są wszystkie podzbiory czteroelementowe zbioru 10 { 1, 2,3, 4,,6,7,8,9,10 }. Jest to model klasyczny, Ω= = Zdarzenie A polega na tym, że wśród wylosowanych liczb będą dokładnie dwie liczby parzyste oraz dokładnie jedna liczba podzielna przez. Wyróżniamy dwa przypadki: wśród wylosowanych liczb jest liczba 10 i nie ma liczby, 20
22 wśród wylosowanych liczb jest liczba i nie ma liczby 10. Obliczamy A : gdy wśród wylosowanych liczb jest liczba 10, to spośród pozostałych liczb parzystych należy wybrać jedną na 4 sposoby i spośród nieparzystych różnych od należy wybrać dwie na 4 = 6 sposobów; 2 gdy wśród wylosowanych liczb nie ma liczby 10, to musi być liczba, spośród pozostałych 4 liczb parzystych należy wybrać dwie na = 6 sposobów i spośród nieparzystych różnych 2 od należy wybrać jedną na 4 sposoby. Stąd A = = 48 i 48 8 PA= ( ) = Przykład 19. Dwunastu zawodników, wśród których są X, Y oraz Z podzielono losowo na dwie równoliczne grupy eliminacyjne, czerwoną i zieloną. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że zawodnicy X i Y będą w tej samej grupie eliminacyjnej, a zawodnik Z w innej. I sposób rozwiązania (podział na grupy) Zdarzeniami elementarnymi są wszystkie sześcioelementowe kombinacje zbioru dwunastoelementowego np. skład grupy czerwonej. 12 Jest to model klasyczny, Ω= = Oznaczmy przez A 1 zdarzenie polegające na tym, że zawodnicy X i Y będą w grupie czerwonej, a zawodnik Z w zielonej oraz przez A 2 zdarzenie polegające na tym, że zawodnicy X i Y będą w grupie zielonej, a zawodnik Z w czerwonej. Obliczamy A. 1 Do zawodników X i Y należy dobrać 4 zawodników spośród 9 pozostałych. 9 9 Możemy to zrobić na sposobów, stąd A1 = = Analogicznie obliczamy A2 = = Zatem 9 A = 2 = 22, więc A 4 3 PA ( ) = = =. Ω
23 II sposób rozwiązania (grupa z X) Zdarzeniami elementarnymi są wszystkie pięcioelementowe kombinacje zbioru jedenastoelementowego, skład grupy, w której będzie zawodnik X. 11 Jest to model klasyczny, Ω= = 462. Obliczamy A. Do zawodników X i Y należy dobrać 4 zawodników spośród 9 pozostałych. 9 Możemy to zrobić na sposobów Zatem A = A 4 3 = 126, więc PA ( ) = = =. 4 Ω III sposób rozwiązania (uporządkowanie zawodników) Ustawiamy losowo wszystkich zawodników w szeregu. Zawodnicy zajmujący miejsca od 1 do 6 to grupa czerwona, a zajmujący miejsca od 7 do 12 to grupa zielona. Zdarzeniami elementarnymi są wszystkie trójki ( xyz,, ) parami różnych liczb ze zbioru {1,2,...,12}, x to numer miejsca zawodnika X, y to numer miejsca zawodnika Y, z to numer miejsca zawodnika Z informacje o pozostałych zawodnikach są nieistotne. Jest to model klasyczny, Ω= = Dla każdej wartości x jest sprzyjających wartości y oraz 6 sprzyjających wartości z. 3 Zatem A = 12 6 = 360, więc PA= ( ). 11 Przykład 20. Ze zbioru liczb { 1,2,3,...,20 } losujemy jednocześnie 8 liczb. Oblicz prawdopodobieństwo, że wśród wylosowanych liczb będą dokładnie dwie pary liczb, których suma jest równa 21. Zdarzeniami elementarnymi są wszystkie ośmioelementowe kombinacje zbioru 20 { 1,2,3,...,20 }. Jest to model klasyczny, Ω= = Oznaczmy przez A zdarzenie polegające na tym, że wśród wylosowanych liczb będą dokładnie dwie pary liczb, których suma jest równa 21. Obliczamy A. 22
24 Jest 10 par liczb, których suma jest równa 21. Aby zaszło zdarzenie A, muszą wystąpić dwie pary, wybieramy je na 10 sposobów oraz z czterech spośród ośmiu pozostałych par, które 2 wybieramy na A = = 2 4 sposobów, ma występować po jednej liczbie na i A 1680 PA= ( ) =. Ω sposobów. Stąd 23
1. Rozwiązać układ równań { x 2 = 2y 1
 Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
KOMBINATORYKA I RACHUNEK PRAWDOPODOBIEŃSTWA
 KOMBINATORYKA I RACHUNEK PRAWDOPODOBIEŃSTWA Ile róŝnych liczb trzycyfrowych podzielnych przez moŝna zapisać za pomocą cyfr :,,,4, Na ile sposobów moŝna ustawić na półce sześć ksiąŝek tak, aby dwie wybrane
KOMBINATORYKA I RACHUNEK PRAWDOPODOBIEŃSTWA Ile róŝnych liczb trzycyfrowych podzielnych przez moŝna zapisać za pomocą cyfr :,,,4, Na ile sposobów moŝna ustawić na półce sześć ksiąŝek tak, aby dwie wybrane
Zadania. SiOD Cwiczenie 1 ;
 1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
14.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe.
 Matematyka 4/ 4.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe. I. Przypomnij sobie:. Wiadomości z poprzedniej lekcji... Że przy rozwiązywaniu zadań tekstowych wykorzystujących
Matematyka 4/ 4.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe. I. Przypomnij sobie:. Wiadomości z poprzedniej lekcji... Że przy rozwiązywaniu zadań tekstowych wykorzystujących
Czas pracy 170 minut
 ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI DLA UCZNIÓW LICEUM MARZEC ROK 015 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron..
ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI DLA UCZNIÓW LICEUM MARZEC ROK 015 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron..
Wykład 1 Tomasz Żak Instytut Matematyki i Informatyki C-11, pok. 313, www.im.pwr.wroc.pl/ zak
 Wykład 1 Tomasz Żak Instytut Matematyki i Informatyki C-11, pok. 313, www.im.pwr.wroc.pl/ zak Zasady zaliczenia Zajęcia są obowiązkowe, wolno opuścić 4 godziny. W semestrze 2 kolokwia po 50 punktów. Rozwiązywanie
Wykład 1 Tomasz Żak Instytut Matematyki i Informatyki C-11, pok. 313, www.im.pwr.wroc.pl/ zak Zasady zaliczenia Zajęcia są obowiązkowe, wolno opuścić 4 godziny. W semestrze 2 kolokwia po 50 punktów. Rozwiązywanie
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejk z kodem szko y dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-P1A1P-061 POZIOM PODSTAWOWY Czas pracy 10 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 1 stron.
Miejsce na naklejk z kodem szko y dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-P1A1P-061 POZIOM PODSTAWOWY Czas pracy 10 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 1 stron.
Prawdopodobieństwo. Zad. 1: Ze zbioru Z =
 Prawdopodobieństwo Zad. : Ze zbioru Z x x N i x + x > : losujemy kolejno bez zwracania dwie liczby log log i tworzymy z nich liczbę dwucyfrową, w której cyfrą dziesiątek jest pierwsza z wylosowanych liczb.
Prawdopodobieństwo Zad. : Ze zbioru Z x x N i x + x > : losujemy kolejno bez zwracania dwie liczby log log i tworzymy z nich liczbę dwucyfrową, w której cyfrą dziesiątek jest pierwsza z wylosowanych liczb.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 D A D A A B A B B C B D C C C D B C C B. Schemat oceniania zadań otwartych.
 Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych LICEUM Klucz odpowiedzi do zadań zamkniętych 6 7 8 9 0 6 7 8 9 0 D A D A A B A B B C B D C C C D B C C B Zadanie. (pkt) Rozwiąż
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych LICEUM Klucz odpowiedzi do zadań zamkniętych 6 7 8 9 0 6 7 8 9 0 D A D A A B A B B C B D C C C D B C C B Zadanie. (pkt) Rozwiąż
Czas pracy 170 minut
 ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
nie zdałeś naszej próbnej matury z matematyki?
 Szanowny Maturzysto, nie zdałeś naszej próbnej matury z matematyki? To prawie niemożliwe, ale jeżeli jednak tak, to Pewnie sądzisz, że przyczyna tkwi w bardzo trudnym arkuszu! Zobaczmy, jak to wygląda
Szanowny Maturzysto, nie zdałeś naszej próbnej matury z matematyki? To prawie niemożliwe, ale jeżeli jednak tak, to Pewnie sądzisz, że przyczyna tkwi w bardzo trudnym arkuszu! Zobaczmy, jak to wygląda
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+
 '()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
Regulamin szkolnego konkursu matematycznego dla uczniów klasy II i III: Mały Matematyk
 Marzena Kococik Olga Kuśmierczyk Szkoła Podstawowa im. Marii Konopnickiej w Krzemieniewicach Regulamin szkolnego konkursu matematycznego dla uczniów klasy II i III: Mały Matematyk Konkursy wyzwalają aktywność
Marzena Kococik Olga Kuśmierczyk Szkoła Podstawowa im. Marii Konopnickiej w Krzemieniewicach Regulamin szkolnego konkursu matematycznego dla uczniów klasy II i III: Mały Matematyk Konkursy wyzwalają aktywność
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
Podstawowe działania w rachunku macierzowym
 Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
pobrano z (A1) Czas GRUDZIE
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 014/015 MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA (A1) W czasie trwania egzaminu zdaj cy mo e korzysta z zestawu wzorów matematycznych, linijki i cyrkla
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 014/015 MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA (A1) W czasie trwania egzaminu zdaj cy mo e korzysta z zestawu wzorów matematycznych, linijki i cyrkla
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI
 Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 9
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 9
Kurs wyrównawczy dla kandydatów i studentów UTP
 Kurs wyrównawczy dla kandydatów i studentów UTP Część III Funkcja wymierna, potęgowa, logarytmiczna i wykładnicza Magdalena Alama-Bućko Ewa Fabińska Alfred Witkowski Grażyna Zachwieja Uniwersytet Technologiczno
Kurs wyrównawczy dla kandydatów i studentów UTP Część III Funkcja wymierna, potęgowa, logarytmiczna i wykładnicza Magdalena Alama-Bućko Ewa Fabińska Alfred Witkowski Grażyna Zachwieja Uniwersytet Technologiczno
MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI
 MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI LUTY 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera strony (zadania 1 ).. Arkusz zawiera 4 zadania zamknięte i 9
MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI LUTY 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera strony (zadania 1 ).. Arkusz zawiera 4 zadania zamknięte i 9
Matematyka z plusemdla szkoły ponadgimnazjalnej WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM. KATEGORIA B Uczeń rozumie:
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM POZIOMY WYMAGAŃ EDUKACYJNYCH: K - konieczny ocena dopuszczająca P - podstawowy ocena dostateczna (dst.) R - rozszerzający ocena dobra (db.) D
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM POZIOMY WYMAGAŃ EDUKACYJNYCH: K - konieczny ocena dopuszczająca P - podstawowy ocena dostateczna (dst.) R - rozszerzający ocena dobra (db.) D
EGZAMIN MATURALNY Z MATEMATYKI CZERWIEC 2012 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50 WPISUJE ZDAJĄCY
 Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 010 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN
Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 010 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN
Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą.
 Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą. Po pierwsze - notacja - trzymasz swoją kostkę w rękach? Widzisz ścianki, którymi można ruszać? Notacja to oznaczenie
Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą. Po pierwsze - notacja - trzymasz swoją kostkę w rękach? Widzisz ścianki, którymi można ruszać? Notacja to oznaczenie
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
KONSPEKT LEKCJI MATEMATYKI. Z WYKORZYSTANIEM METOD AKTYWIZUJĄCYCH w klasie I gimnazjum. TEMAT: Działania łączne na liczbach wymiernych
 KONSPEKT LEKCJI MATEMATYKI Z WYKORZYSTANIEM METOD AKTYWIZUJĄCYCH w klasie I gimnazjum TEMAT: Działania łączne na liczbach wymiernych Cele lekcji: Cel ogólny: - utrwalenie wiadomościiumiejętności z działu
KONSPEKT LEKCJI MATEMATYKI Z WYKORZYSTANIEM METOD AKTYWIZUJĄCYCH w klasie I gimnazjum TEMAT: Działania łączne na liczbach wymiernych Cele lekcji: Cel ogólny: - utrwalenie wiadomościiumiejętności z działu
XIII KONKURS MATEMATYCZNY
 XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
ARKUSZ PRÓBNEJ MATURY ZESTAW ĆWICZENIOWY Z MATEMATYKI
 ARKUSZ PRÓBNEJ MATURY ZESTAW ĆWICZENIOWY Z MATEMATYKI Styczeń 2013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron. 2. W zadaniach od 1. do 25. są
ARKUSZ PRÓBNEJ MATURY ZESTAW ĆWICZENIOWY Z MATEMATYKI Styczeń 2013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron. 2. W zadaniach od 1. do 25. są
Wymagania na poszczególne oceny klasa 4
 Wymagania na poszczególne oceny klasa 4 a) Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające uczniowi dalszą naukę, bez których uczeń nie jest w stanie zrozumieć
Wymagania na poszczególne oceny klasa 4 a) Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające uczniowi dalszą naukę, bez których uczeń nie jest w stanie zrozumieć
K P K P R K P R D K P R D W
 KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
NUMER IDENTYFIKATORA:
 Społeczne Liceum Ogólnokształcące z Maturą Międzynarodową im. Ingmara Bergmana IB WORLD SCHOOL 53 ul. Raszyńska, 0-06 Warszawa, tel./fax 668 54 5 www.ib.bednarska.edu.pl / e-mail: liceum.ib@rasz.edu.pl
Społeczne Liceum Ogólnokształcące z Maturą Międzynarodową im. Ingmara Bergmana IB WORLD SCHOOL 53 ul. Raszyńska, 0-06 Warszawa, tel./fax 668 54 5 www.ib.bednarska.edu.pl / e-mail: liceum.ib@rasz.edu.pl
Matematyka dyskretna. Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 8/14
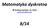 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 8/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 8/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Analiza wyników egzaminu gimnazjalnego. Test matematyczno-przyrodniczy matematyka. Test GM-M1-122,
 Analiza wyników egzaminu gimnazjalnego Test matematyczno-przyrodniczy Test GM-M1-122, Zestaw zadań z zakresu matematyki posłużył w dniu 25 kwietnia 2012 r. do sprawdzenia, u uczniów kończących trzecią
Analiza wyników egzaminu gimnazjalnego Test matematyczno-przyrodniczy Test GM-M1-122, Zestaw zadań z zakresu matematyki posłużył w dniu 25 kwietnia 2012 r. do sprawdzenia, u uczniów kończących trzecią
ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 2012 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 pobrano z www.sqlmedia.pl Centralna Komisja Egzaminacyjna ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 01 POZIOM PODSTAWOWY 1. Sprawd, czy arkusz wiczeniowy zawiera strony (zadania 1 ).. Rozwi zania zada i odpowiedzi
pobrano z www.sqlmedia.pl Centralna Komisja Egzaminacyjna ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 01 POZIOM PODSTAWOWY 1. Sprawd, czy arkusz wiczeniowy zawiera strony (zadania 1 ).. Rozwi zania zada i odpowiedzi
KLAUZULE ARBITRAŻOWE
 KLAUZULE ARBITRAŻOWE KLAUZULE arbitrażowe ICC Zalecane jest, aby strony chcące w swych kontraktach zawrzeć odniesienie do arbitrażu ICC, skorzystały ze standardowych klauzul, wskazanych poniżej. Standardowa
KLAUZULE ARBITRAŻOWE KLAUZULE arbitrażowe ICC Zalecane jest, aby strony chcące w swych kontraktach zawrzeć odniesienie do arbitrażu ICC, skorzystały ze standardowych klauzul, wskazanych poniżej. Standardowa
MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA NR 2. Miejsce na naklejk z kodem szko y CKE MARZEC ROK Czas pracy 150 minut
 Miejsce na naklejk z kodem szko y CKE MATEMATYKA POZIOM ROZSZERZONY MARZEC ROK 2008 PRZYK ADOWY ZESTAW ZADA NR 2 Czas pracy 150 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera
Miejsce na naklejk z kodem szko y CKE MATEMATYKA POZIOM ROZSZERZONY MARZEC ROK 2008 PRZYK ADOWY ZESTAW ZADA NR 2 Czas pracy 150 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera
Tytuł. Autor. Dział. Innowacyjne cele edukacyjne. Czas. Przebieg. Etap 1 - Wprowadzenie z rysem historycznym i dyskusją
 Tytuł Sztuka szybkiego liczenia Cz. I Autor Dariusz Kulma Dział Liczby wymierne Innowacyjne cele edukacyjne Techniki szybkiego liczenia w pamięci niestosowane na lekcjach matematyki Wybrane elementu systemu
Tytuł Sztuka szybkiego liczenia Cz. I Autor Dariusz Kulma Dział Liczby wymierne Innowacyjne cele edukacyjne Techniki szybkiego liczenia w pamięci niestosowane na lekcjach matematyki Wybrane elementu systemu
SPRAWDZIANY Z MATEMATYKI
 SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejk z kodem szko y dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 007 Czas pracy 180 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny
Miejsce na naklejk z kodem szko y dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 007 Czas pracy 180 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI DLA KLAS IV VI
 PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI DLA KLAS IV VI Kryteria ocen 1. Wymagania edukacyjne na poszczególne oceny: Ocenę celującą otrzymuje uczeń, który: Posiadł wiedzę i umiejętności obejmujące pełny
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI DLA KLAS IV VI Kryteria ocen 1. Wymagania edukacyjne na poszczególne oceny: Ocenę celującą otrzymuje uczeń, który: Posiadł wiedzę i umiejętności obejmujące pełny
WYMAGANIA EDUKACYJNE SPOSOBY SPRAWDZANIA POSTĘPÓW UCZNIÓW WARUNKI I TRYB UZYSKANIA WYŻSZEJ NIŻ PRZEWIDYWANA OCENY ŚRÓDROCZNEJ I ROCZNEJ
 WYMAGANIA EDUKACYJNE SPOSOBY SPRAWDZANIA POSTĘPÓW UCZNIÓW WARUNKI I TRYB UZYSKANIA WYŻSZEJ NIŻ PRZEWIDYWANA OCENY ŚRÓDROCZNEJ I ROCZNEJ Anna Gutt- Kołodziej ZASADY OCENIANIA Z MATEMATYKI Podczas pracy
WYMAGANIA EDUKACYJNE SPOSOBY SPRAWDZANIA POSTĘPÓW UCZNIÓW WARUNKI I TRYB UZYSKANIA WYŻSZEJ NIŻ PRZEWIDYWANA OCENY ŚRÓDROCZNEJ I ROCZNEJ Anna Gutt- Kołodziej ZASADY OCENIANIA Z MATEMATYKI Podczas pracy
TEORIA GIER W EKONOMII WYKŁAD 1: GRY W POSTACI EKSTENSYWNEJ I NORMALNEJ
 TEORIA GIER W EKONOMII WYKŁAD : GRY W POSTACI EKSTENSYWNEJ I NORMALNEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Schemat gry. Początek gry. 2. Ciąg kolejnych posunięć
TEORIA GIER W EKONOMII WYKŁAD : GRY W POSTACI EKSTENSYWNEJ I NORMALNEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Schemat gry. Początek gry. 2. Ciąg kolejnych posunięć
REGULAMIN TURNIEJU SPORTOWEJ GRY KARCIANEJ KANASTA W RAMACH I OGÓLNOPOLSKIEGO FESTIWALU GIER UMYSŁOWYCH 55+ GORZÓW WLKP. 2013 R.
 REGULAMIN TURNIEJU SPORTOWEJ GRY KARCIANEJ KANASTA W RAMACH I OGÓLNOPOLSKIEGO FESTIWALU GIER UMYSŁOWYCH 55+ GORZÓW WLKP. 2013 R. Termin: 13 kwietnia 2013 r. godz. 10:45 15:45 Miejsce: WiMBP im. Zbigniewa
REGULAMIN TURNIEJU SPORTOWEJ GRY KARCIANEJ KANASTA W RAMACH I OGÓLNOPOLSKIEGO FESTIWALU GIER UMYSŁOWYCH 55+ GORZÓW WLKP. 2013 R. Termin: 13 kwietnia 2013 r. godz. 10:45 15:45 Miejsce: WiMBP im. Zbigniewa
Rozdział 6. Pakowanie plecaka. 6.1 Postawienie problemu
 Rozdział 6 Pakowanie plecaka 6.1 Postawienie problemu Jak zauważyliśmy, szyfry oparte na rachunku macierzowym nie są przerażająco trudne do złamania. Zdecydowanie trudniejszy jest kryptosystem oparty na
Rozdział 6 Pakowanie plecaka 6.1 Postawienie problemu Jak zauważyliśmy, szyfry oparte na rachunku macierzowym nie są przerażająco trudne do złamania. Zdecydowanie trudniejszy jest kryptosystem oparty na
OFERTA WYKŁADÓW, WARSZTATÓW I LABORATORIÓW DLA UCZNIÓW KLAS IV- VI SZKÓŁ PODSTAWOWYCH, GIMNAZJALNYCH I ŚREDNICH
 OFERTA WYKŁADÓW, WARSZTATÓW I LABORATORIÓW DLA UCZNIÓW KLAS IV- VI SZKÓŁ PODSTAWOWYCH, GIMNAZJALNYCH I ŚREDNICH Strona 1 z 9 SPIS ZAJĘĆ WRAZ Z NAZWISKAMI WYKŁADOWCÓW dr hab. Mieczysław Kula Poznaj swój
OFERTA WYKŁADÓW, WARSZTATÓW I LABORATORIÓW DLA UCZNIÓW KLAS IV- VI SZKÓŁ PODSTAWOWYCH, GIMNAZJALNYCH I ŚREDNICH Strona 1 z 9 SPIS ZAJĘĆ WRAZ Z NAZWISKAMI WYKŁADOWCÓW dr hab. Mieczysław Kula Poznaj swój
EGZAMIN MATURALNY Z MATEMATYKI MAJ 2014 POZIOM ROZSZERZONY. Czas pracy: 180 minut. Liczba punktów do uzyskania: 50. pobrano z
 Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 2013 WPISUJE ZDAJ CY KOD PESEL Miejsce na naklejk z kodem dysleksja EGZAMIN MATURALNY Z MATEMATYKI MAJ 2014
Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 2013 WPISUJE ZDAJ CY KOD PESEL Miejsce na naklejk z kodem dysleksja EGZAMIN MATURALNY Z MATEMATYKI MAJ 2014
Arkusz maturalny treningowy nr 7. W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź.
 Czas pracy: 170 minut Liczba punktów do uzyskania: 50 Arkusz maturalny treningowy nr 7 W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie 1. (0-1) Wyrażenie (-8x 3
Czas pracy: 170 minut Liczba punktów do uzyskania: 50 Arkusz maturalny treningowy nr 7 W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie 1. (0-1) Wyrażenie (-8x 3
KLASA 3 GIMNAZJUM. 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1. 2. System dziesiątkowy 2-4. 3. System rzymski 5-6
 KLASA 3 GIMNAZJUM TEMAT LICZBA GODZIN LEKCYJNYCH 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1 2. System dziesiątkowy 2-4 WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z XII 2008 R.
KLASA 3 GIMNAZJUM TEMAT LICZBA GODZIN LEKCYJNYCH 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1 2. System dziesiątkowy 2-4 WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z XII 2008 R.
DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15
 DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15 Wykonawcy ubiegający się o udzielenie zamówienia Dotyczy: postępowania prowadzonego w trybie przetargu nieograniczonego na Usługę druku książek, nr postępowania
DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15 Wykonawcy ubiegający się o udzielenie zamówienia Dotyczy: postępowania prowadzonego w trybie przetargu nieograniczonego na Usługę druku książek, nr postępowania
KONKURSY MATEMATYCZNE. Treść zadań
 KONKURSY MATEMATYCZNE Treść zadań Wskazówka: w każdym zadaniu należy wskazać JEDNĄ dobrą odpowiedź. Zadanie 1 Wlewamy 1000 litrów wody do rurki w najwyższym punkcie systemu rurek jak na rysunku. Zakładamy,
KONKURSY MATEMATYCZNE Treść zadań Wskazówka: w każdym zadaniu należy wskazać JEDNĄ dobrą odpowiedź. Zadanie 1 Wlewamy 1000 litrów wody do rurki w najwyższym punkcie systemu rurek jak na rysunku. Zakładamy,
Zadanie 1. Liczba szkód w każdym z trzech kolejnych lat dla pewnego ubezpieczonego ma rozkład równomierny:
 Matematyka ubezpieczeń majątkowych 5.2.2008 r. Zadanie. Liczba szkód w każdym z trzech kolejnych lat dla pewnego ubezpieczonego ma rozkład równomierny: Pr ( N = k) = 0 dla k = 0,, K, 9. Liczby szkód w
Matematyka ubezpieczeń majątkowych 5.2.2008 r. Zadanie. Liczba szkód w każdym z trzech kolejnych lat dla pewnego ubezpieczonego ma rozkład równomierny: Pr ( N = k) = 0 dla k = 0,, K, 9. Liczby szkód w
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI W ZESPOLE SZKÓŁ NR 32 im. K. K. Baczyńskiego W WARSZAWIE
 PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI W ZESPOLE SZKÓŁ NR 32 im. K. K. Baczyńskiego W WARSZAWIE I. Przedmiotowy System Oceniania z matematyki jest zgodny z Wewnątrzszkolnym Systemem Oceniania (WSO)
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI W ZESPOLE SZKÓŁ NR 32 im. K. K. Baczyńskiego W WARSZAWIE I. Przedmiotowy System Oceniania z matematyki jest zgodny z Wewnątrzszkolnym Systemem Oceniania (WSO)
REGULAMIN REKRUTACJI UCZNIÓW/SŁUCHACZY DO ZESPOŁU SZKÓŁ TECHNICZNYCH I OGÓLNOKSZTAŁCĄCYCH IM. KAZIMIERZA WIELKIEGO W BUSKU-ZDROJU
 do Statutu ZSTiO REGULAMIN REKRUTACJI UCZNIÓW/SŁUCHACZY DO ZESPOŁU SZKÓŁ TECHNICZNYCH I OGÓLNOKSZTAŁCĄCYCH IM. KAZIMIERZA WIELKIEGO W BUSKU-ZDROJU 2 Wstęp Zasady rekrutacji uczniów regulują: - Rozporządzenie
do Statutu ZSTiO REGULAMIN REKRUTACJI UCZNIÓW/SŁUCHACZY DO ZESPOŁU SZKÓŁ TECHNICZNYCH I OGÓLNOKSZTAŁCĄCYCH IM. KAZIMIERZA WIELKIEGO W BUSKU-ZDROJU 2 Wstęp Zasady rekrutacji uczniów regulują: - Rozporządzenie
art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny (Dz. U. Nr 16, poz. 93 ze zm.),
 Istota umów wzajemnych Podstawa prawna: Księga trzecia. Zobowiązania. Dział III Wykonanie i skutki niewykonania zobowiązań z umów wzajemnych. art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny
Istota umów wzajemnych Podstawa prawna: Księga trzecia. Zobowiązania. Dział III Wykonanie i skutki niewykonania zobowiązań z umów wzajemnych. art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny
2.Prawo zachowania masy
 2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
Konspekt lekcji otwartej
 Konspekt lekcji otwartej Przedmiot: Temat lekcji: informatyka Modelowanie i symulacja komputerowa prawidłowości w świecie liczb losowych Klasa: 2 g Data zajęć: 21.12.2004. Nauczyciel: Roman Wyrwas Czas
Konspekt lekcji otwartej Przedmiot: Temat lekcji: informatyka Modelowanie i symulacja komputerowa prawidłowości w świecie liczb losowych Klasa: 2 g Data zajęć: 21.12.2004. Nauczyciel: Roman Wyrwas Czas
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej
 Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 8 stycznia 2014 r. 120 minut Informacje dla
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 8 stycznia 2014 r. 120 minut Informacje dla
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejk z kodem szko y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 16 stron (zadania
Miejsce na naklejk z kodem szko y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 16 stron (zadania
Przedmiotowe zasady oceniania. zgodne z Wewnątrzszkolnymi Zasadami Oceniania. obowiązującymi w XLIV Liceum Ogólnokształcącym.
 Przedmiotowe zasady oceniania zgodne z Wewnątrzszkolnymi Zasadami Oceniania obowiązującymi w XLIV Liceum Ogólnokształcącym. Przedmiot: biologia Nauczyciel przedmiotu: Anna Jasztal, Anna Woch 1. Formy sprawdzania
Przedmiotowe zasady oceniania zgodne z Wewnątrzszkolnymi Zasadami Oceniania obowiązującymi w XLIV Liceum Ogólnokształcącym. Przedmiot: biologia Nauczyciel przedmiotu: Anna Jasztal, Anna Woch 1. Formy sprawdzania
Temat: Funkcje. Własności ogólne. A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1
 Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
USTAWA. z dnia 26 czerwca 1974 r. Kodeks pracy. 1) (tekst jednolity)
 Dz.U.98.21.94 1998.09.01 zm. Dz.U.98.113.717 art. 5 1999.01.01 zm. Dz.U.98.106.668 art. 31 2000.01.01 zm. Dz.U.99.99.1152 art. 1 2000.04.06 zm. Dz.U.00.19.239 art. 2 2001.01.01 zm. Dz.U.00.43.489 art.
Dz.U.98.21.94 1998.09.01 zm. Dz.U.98.113.717 art. 5 1999.01.01 zm. Dz.U.98.106.668 art. 31 2000.01.01 zm. Dz.U.99.99.1152 art. 1 2000.04.06 zm. Dz.U.00.19.239 art. 2 2001.01.01 zm. Dz.U.00.43.489 art.
Zadania zamknięte. A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki. C) a 4 = 2 3
 Zadania zamknięte ZADANIE 1 (1 PKT) Równanie x2 3x+2 = 0 ma: x 2 4 A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki ZADANIE 2 (1 PKT) Liczba b jest 3 razy większa od liczby a. Wtedy
Zadania zamknięte ZADANIE 1 (1 PKT) Równanie x2 3x+2 = 0 ma: x 2 4 A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki ZADANIE 2 (1 PKT) Liczba b jest 3 razy większa od liczby a. Wtedy
MATEMATYKA 4 INSTYTUT MEDICUS FUNKCJA KWADRATOWA. Kurs przygotowawczy na studia medyczne. Rok szkolny 2010/2011. tel. 0501 38 39 55 www.medicus.edu.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 2009/2010 SEMESTR 3
 PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 29/2 SEMESTR 3 Rozwiązania zadań nie były w żaden sposób konsultowane z żadnym wiarygodnym źródłem informacji!!!
PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 29/2 SEMESTR 3 Rozwiązania zadań nie były w żaden sposób konsultowane z żadnym wiarygodnym źródłem informacji!!!
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. s podane 4 odpowiedzi:
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. s podane 4 odpowiedzi:
PROCEDURA AWANSU ZAWODOWEGO NA STOPIEŃ NAUCZYCIELA MIANOWANEGO W ZESPOLE SZKÓŁ INTEGRACYJNYCH NR 1 W KATOWICACH
 PROCEDURA AWANSU ZAWODOWEGO NA STOPIEŃ NAUCZYCIELA MIANOWANEGO W ZESPOLE SZKÓŁ INTEGRACYJNYCH NR 1 W KATOWICACH Opracowano na podstawie następujących aktów prawnych: - rozdział 3a Karty Nauczyciela, ustawa
PROCEDURA AWANSU ZAWODOWEGO NA STOPIEŃ NAUCZYCIELA MIANOWANEGO W ZESPOLE SZKÓŁ INTEGRACYJNYCH NR 1 W KATOWICACH Opracowano na podstawie następujących aktów prawnych: - rozdział 3a Karty Nauczyciela, ustawa
BADANIE UMIEJĘTNOŚCI UCZNIÓW W TRZECIEJ KLASIE GIMNAZJUM CZĘŚĆ MATEMATYCZNO-PRZYRODNICZA
 BADANIE UMIEJĘTNOŚCI UCZNIÓW W TRZECIEJ KLASIE GIMNAZJUM CZĘŚĆ MATEMATYCZNO-RZYRODNICZA MATEMATYKA TEST 4 Zadanie 1 Dane są punkty A = ( 1, 1) oraz B = (3, 2). Jaką długość ma odcinek AB? Wybierz odpowiedź
BADANIE UMIEJĘTNOŚCI UCZNIÓW W TRZECIEJ KLASIE GIMNAZJUM CZĘŚĆ MATEMATYCZNO-RZYRODNICZA MATEMATYKA TEST 4 Zadanie 1 Dane są punkty A = ( 1, 1) oraz B = (3, 2). Jaką długość ma odcinek AB? Wybierz odpowiedź
Umowa o pracę zawarta na czas nieokreślony
 Umowa o pracę zawarta na czas nieokreślony Uwagi ogólne Definicja umowy Umowa o pracę stanowi dokument stwierdzający zatrudnienie w ramach stosunku pracy. Według ustawowej definicji jest to zgodne oświadczenie
Umowa o pracę zawarta na czas nieokreślony Uwagi ogólne Definicja umowy Umowa o pracę stanowi dokument stwierdzający zatrudnienie w ramach stosunku pracy. Według ustawowej definicji jest to zgodne oświadczenie
Twierdzenie Bayesa. Indukowane Reguły Decyzyjne Jakub Kuliński Nr albumu: 53623
 Twierdzenie Bayesa Indukowane Reguły Decyzyjne Jakub Kuliński Nr albumu: 53623 Niniejszy skrypt ma na celu usystematyzowanie i uporządkowanie podstawowej wiedzy na temat twierdzenia Bayesa i jego zastosowaniu
Twierdzenie Bayesa Indukowane Reguły Decyzyjne Jakub Kuliński Nr albumu: 53623 Niniejszy skrypt ma na celu usystematyzowanie i uporządkowanie podstawowej wiedzy na temat twierdzenia Bayesa i jego zastosowaniu
40. Międzynarodowa Olimpiada Fizyczna Meksyk, 12-19 lipca 2009 r. ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA
 ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
29. TRZY W LINII CZYLI O POSZUKIWANIU ZWIĄZKÓW
 129 Anna Pregler 29. TRZY W LINII CZYLI O POSZUKIWANIU ZWIĄZKÓW Cele ogólne w szkole podstawowej: myślenie matematyczne umiejętność korzystania z podstawowych narzędzi matematyki w życiu codziennym oraz
129 Anna Pregler 29. TRZY W LINII CZYLI O POSZUKIWANIU ZWIĄZKÓW Cele ogólne w szkole podstawowej: myślenie matematyczne umiejętność korzystania z podstawowych narzędzi matematyki w życiu codziennym oraz
SPRAWDZIAN W KLASIE SZÓSTEJ SZKOŁY PODSTAWOWEJ OD ROKU SZKOLNEGO 2014/2015
 Centralna Komisja Egzaminacyjna ul. J. Lewartowskiego 6, 00-190 Warszawa www.cke.edu.pl sekret.cke@cke.edu.pl SPRAWDZIAN W KLASIE SZÓSTEJ SZKOŁY PODSTAWOWEJ OD ROKU SZKOLNEGO 2014/2015 Cześć! W kwietniu
Centralna Komisja Egzaminacyjna ul. J. Lewartowskiego 6, 00-190 Warszawa www.cke.edu.pl sekret.cke@cke.edu.pl SPRAWDZIAN W KLASIE SZÓSTEJ SZKOŁY PODSTAWOWEJ OD ROKU SZKOLNEGO 2014/2015 Cześć! W kwietniu
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM ROZSZERZONY. S x 3x y. 1.5 Podanie odpowiedzi: Poszukiwane liczby to : 2, 6, 5.
 Nr zadania Nr czynno ci... ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etapy rozwi zania zadania Wprowadzenie oznacze : x, x, y poszukiwane liczby i zapisanie równania: x y lub: zapisanie
Nr zadania Nr czynno ci... ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etapy rozwi zania zadania Wprowadzenie oznacze : x, x, y poszukiwane liczby i zapisanie równania: x y lub: zapisanie
W tym elemencie większość zdających nie zapisywała za pomocą równania reakcji procesu zobojętniania tlenku sodu mianowanym roztworem kwasu solnego.
 W tym elemencie większość zdających nie zapisywała za pomocą równania reakcji procesu zobojętniania tlenku sodu mianowanym roztworem kwasu solnego. Ad. IV. Wykaz prac według kolejności ich wykonania. Ten
W tym elemencie większość zdających nie zapisywała za pomocą równania reakcji procesu zobojętniania tlenku sodu mianowanym roztworem kwasu solnego. Ad. IV. Wykaz prac według kolejności ich wykonania. Ten
WZÓR SKARGI EUROPEJSKI TRYBUNAŁ PRAW CZŁOWIEKA. Rada Europy. Strasburg, Francja SKARGA. na podstawie Artykułu 34 Europejskiej Konwencji Praw Człowieka
 WZÓR SKARGI EUROPEJSKI TRYBUNAŁ PRAW CZŁOWIEKA Rada Europy Strasburg, Francja SKARGA na podstawie Artykułu 34 Europejskiej Konwencji Praw Człowieka oraz Artykułu 45-47 Regulaminu Trybunału 1 Adres pocztowy
WZÓR SKARGI EUROPEJSKI TRYBUNAŁ PRAW CZŁOWIEKA Rada Europy Strasburg, Francja SKARGA na podstawie Artykułu 34 Europejskiej Konwencji Praw Człowieka oraz Artykułu 45-47 Regulaminu Trybunału 1 Adres pocztowy
UCHWAŁA Nr XLIII/522/2014 RADY MIEJSKIEJ W BORNEM SULINOWIE z dnia 29 maja 2014 r.
 UCHWAŁA Nr XLIII/522/2014 RADY MIEJSKIEJ W BORNEM SULINOWIE z dnia 29 maja 2014 r. w sprawie zasad rozliczania tygodniowego obowiązkowego wymiaru godzin zajęć nauczycieli zatrudnionych w szkołach prowadzonych
UCHWAŁA Nr XLIII/522/2014 RADY MIEJSKIEJ W BORNEM SULINOWIE z dnia 29 maja 2014 r. w sprawie zasad rozliczania tygodniowego obowiązkowego wymiaru godzin zajęć nauczycieli zatrudnionych w szkołach prowadzonych
12. 1. REGUŁA MNOśENIA I REGUŁA DODAWANIA
 2.. REGUŁA MNOśENIA I REGUŁA DODAWANIA Zasada mnoŝenia: JeŜeli wybór polega na podjęciu kolejno k decyzji, przy czym pierwszą z nich moŝna podjąć na n sposobów, drugą na n 2 sposobów,..., n tą na n k sposobów,
2.. REGUŁA MNOśENIA I REGUŁA DODAWANIA Zasada mnoŝenia: JeŜeli wybór polega na podjęciu kolejno k decyzji, przy czym pierwszą z nich moŝna podjąć na n sposobów, drugą na n 2 sposobów,..., n tą na n k sposobów,
Wójt Gminy Bobrowniki ul. Nieszawska 10 87-617 Bobrowniki WNIOSEK O PRZYZNANIE STYPENDIUM SZKOLNEGO W ROKU SZKOLNYM 2010/2011
 Nr wniosku.../... Bobrowniki, dnia... Wójt Gminy Bobrowniki ul. Nieszawska 10 87-617 Bobrowniki WNIOSEK O PRZYZNANIE STYPENDIUM SZKOLNEGO W ROKU SZKOLNYM 2010/2011 1. Dane osobowe WNIOSKODAWCY Nazwisko
Nr wniosku.../... Bobrowniki, dnia... Wójt Gminy Bobrowniki ul. Nieszawska 10 87-617 Bobrowniki WNIOSEK O PRZYZNANIE STYPENDIUM SZKOLNEGO W ROKU SZKOLNYM 2010/2011 1. Dane osobowe WNIOSKODAWCY Nazwisko
Wyznaczanie współczynnika sprężystości sprężyn i ich układów
 Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Matematyka dla liceum/funkcja liniowa
 Matematyka dla liceum/funkcja liniowa 1 Matematyka dla liceum/funkcja liniowa Funkcja liniowa Wstęp Co zawiera dział Czytelnik pozna następujące informacje: co to jest i jakie ma własności funkcja liniowa
Matematyka dla liceum/funkcja liniowa 1 Matematyka dla liceum/funkcja liniowa Funkcja liniowa Wstęp Co zawiera dział Czytelnik pozna następujące informacje: co to jest i jakie ma własności funkcja liniowa
PRZEDMIOTOWY SYSTEM OCENIANIA Z PRZYRODY KLASA CZWARTA, PIĄTA I SZÓSTA
 PRZEDMIOTOWY SYSTEM OCENIANIA Z PRZYRODY KLASA CZWARTA, PIĄTA I SZÓSTA PROGRAM: Przyrodo, witaj! WSiP, PODRĘCZNIK, ZESZYT UCZNIA, ZESZYT ĆWICZEŃ (tylko klasa piąta) Przyrodo, witaj! E.Błaszczyk, E.Kłos
PRZEDMIOTOWY SYSTEM OCENIANIA Z PRZYRODY KLASA CZWARTA, PIĄTA I SZÓSTA PROGRAM: Przyrodo, witaj! WSiP, PODRĘCZNIK, ZESZYT UCZNIA, ZESZYT ĆWICZEŃ (tylko klasa piąta) Przyrodo, witaj! E.Błaszczyk, E.Kłos
Załącznik nr 1 do specyfikacji Umowa Nr. zawarta w dniu...2014r. pomiędzy. zwanym dalej Zamawiającym a...
 Załącznik nr 1 do specyfikacji Umowa Nr. zawarta w dniu...2014r. pomiędzy MIEJSKIM OŚRODKIEM POMOCY SPOŁECZNEJ W KATOWICACH, z siedzibą w Katowicach przy ul. Jagiellońskiej 17, reprezentowanym przez: DYREKTORA
Załącznik nr 1 do specyfikacji Umowa Nr. zawarta w dniu...2014r. pomiędzy MIEJSKIM OŚRODKIEM POMOCY SPOŁECZNEJ W KATOWICACH, z siedzibą w Katowicach przy ul. Jagiellońskiej 17, reprezentowanym przez: DYREKTORA
UCHWAŁ A SENATU RZECZYPOSPOLITEJ POLSKIEJ. z dnia 18 października 2012 r. w sprawie ustawy o zmianie ustawy o podatku dochodowym od osób fizycznych
 UCHWAŁ A SENATU RZECZYPOSPOLITEJ POLSKIEJ z dnia 18 października 2012 r. w sprawie ustawy o zmianie ustawy o podatku dochodowym od osób fizycznych Senat, po rozpatrzeniu uchwalonej przez Sejm na posiedzeniu
UCHWAŁ A SENATU RZECZYPOSPOLITEJ POLSKIEJ z dnia 18 października 2012 r. w sprawie ustawy o zmianie ustawy o podatku dochodowym od osób fizycznych Senat, po rozpatrzeniu uchwalonej przez Sejm na posiedzeniu
Scenariusz nr 30 zajęć edukacji wczesnoszkolnej. Metryczka zajęć edukacyjnych. Cele operacyjne. Środki dydaktyczne
 Scenariusz nr 30 zajęć edukacji wczesnoszkolnej Metryczka zajęć edukacyjnych Miejsce realizacji zajęć: sala szkolna Ośrodek tematyczny realizowanych zajęć: Świat wokół nas Temat zajęć: Tradycyjne potrawy
Scenariusz nr 30 zajęć edukacji wczesnoszkolnej Metryczka zajęć edukacyjnych Miejsce realizacji zajęć: sala szkolna Ośrodek tematyczny realizowanych zajęć: Świat wokół nas Temat zajęć: Tradycyjne potrawy
Harmonogramowanie projektów Zarządzanie czasem
 Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
Matematyka z plusem dla szkoły ponadgimnazjalnej
 1 ZAŁOŻENIA DO PLANU REALIZACJI MATERIAŁU NAUCZANIA MATEMATYKI W KLASIE III (zakres podstawowy) Program nauczania: Matematyka z plusem, numer dopuszczenia DKW-4015-37/01. Liczba godzin nauki w tygodniu:
1 ZAŁOŻENIA DO PLANU REALIZACJI MATERIAŁU NAUCZANIA MATEMATYKI W KLASIE III (zakres podstawowy) Program nauczania: Matematyka z plusem, numer dopuszczenia DKW-4015-37/01. Liczba godzin nauki w tygodniu:
Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu.
 pobrano z www.sqlmedia.pl Uk ad graficzny CKE 00 KOD Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. WPISUJE ZDAJ CY PESEL Miejsce na naklejk
pobrano z www.sqlmedia.pl Uk ad graficzny CKE 00 KOD Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. WPISUJE ZDAJ CY PESEL Miejsce na naklejk
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów województwa wielkopolskiego
 Kod ucznia Data urodzenia ucznia Dzień miesiąc rok Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów ETAP SZKOLNY Rok szkolny 2012/2013 Instrukcja dla ucznia 1. Sprawdź, czy test zawiera 12 stron.
Kod ucznia Data urodzenia ucznia Dzień miesiąc rok Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów ETAP SZKOLNY Rok szkolny 2012/2013 Instrukcja dla ucznia 1. Sprawdź, czy test zawiera 12 stron.
Zbudujmy z klocków prostopadłościan
 Zapewne niemal każdy z młodszych Czytelników miał okazję w dzieciństwie bawić się klockami Lego. Zbudujmy z klocków prostopadłościan Michał KIEZA, Warszawa Wprowadzenie Zazwyczaj za wielomino (ang. polymino)
Zapewne niemal każdy z młodszych Czytelników miał okazję w dzieciństwie bawić się klockami Lego. Zbudujmy z klocków prostopadłościan Michał KIEZA, Warszawa Wprowadzenie Zazwyczaj za wielomino (ang. polymino)
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
PROCEDURA OCENY RYZYKA ZAWODOWEGO. w Urzędzie Gminy Mściwojów
 I. Postanowienia ogólne 1.Cel PROCEDURA OCENY RYZYKA ZAWODOWEGO w Urzędzie Gminy Mściwojów Przeprowadzenie oceny ryzyka zawodowego ma na celu: Załącznik A Zarządzenia oceny ryzyka zawodowego monitorowanie
I. Postanowienia ogólne 1.Cel PROCEDURA OCENY RYZYKA ZAWODOWEGO w Urzędzie Gminy Mściwojów Przeprowadzenie oceny ryzyka zawodowego ma na celu: Załącznik A Zarządzenia oceny ryzyka zawodowego monitorowanie
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE
 PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE Przedmiotowy system oceniania z matematyki jest zgodny z Rozporządzeniem Ministra Edukacji Narodowej
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE Przedmiotowy system oceniania z matematyki jest zgodny z Rozporządzeniem Ministra Edukacji Narodowej
USTAWA. z dnia 26 stycznia 1982 r. Karta Nauczyciela. (tekst jednolity) Rozdział 3a. Awans zawodowy nauczycieli
 USTAWA z dnia 26 stycznia 1982 r. Karta Nauczyciela (tekst jednolity) Rozdział 3a Awans zawodowy nauczycieli Art. 9a. 1. Ustala się stopnie awansu zawodowego nauczycieli: 1) nauczyciel stażysta; 2) nauczyciel
USTAWA z dnia 26 stycznia 1982 r. Karta Nauczyciela (tekst jednolity) Rozdział 3a Awans zawodowy nauczycieli Art. 9a. 1. Ustala się stopnie awansu zawodowego nauczycieli: 1) nauczyciel stażysta; 2) nauczyciel
i danej prędkości; stosuje jednostki prędkości: km/h, m/s; umiejętności rachunkowe, a także własne poprawne metody.
 Propozycja rozkładu materiału nauczania Matematyka wokół nas Rozkład materiału nauczania z odniesieniami do wymagań z podstawy programowej. Matematyka wokół nas KLASA 5 Nr lekcji Temat lekcji Zagadnienie
Propozycja rozkładu materiału nauczania Matematyka wokół nas Rozkład materiału nauczania z odniesieniami do wymagań z podstawy programowej. Matematyka wokół nas KLASA 5 Nr lekcji Temat lekcji Zagadnienie
ZAPYTANIE OFERTOWE. Nr sprawy 15/2016r.
 Załącznik nr 1/1... nazwa i adres wykonawcy... pieczęć zamawiającego...... ZAPYTANIE OFERTOWE Nr sprawy 15/2016r. 1. Towarzystwo Budownictwa Społecznego Sp. z o. o. ogłasza zapytanie ofertowe na wynajem
Załącznik nr 1/1... nazwa i adres wykonawcy... pieczęć zamawiającego...... ZAPYTANIE OFERTOWE Nr sprawy 15/2016r. 1. Towarzystwo Budownictwa Społecznego Sp. z o. o. ogłasza zapytanie ofertowe na wynajem
