III OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy ZADANIA I ROZWIĄZANIA 13 stycznia 2011r.

Zadanie domowe.

Zdnie doowe www.izyk-kury.pl Dźwi unoi w órę iężr o ie =500k ze łą wrośią przypiezeni =,/ n wyokośd h=0. Obliz prę W jką wykon ilnik dźwiu. Odp. 55 kj www.izyk-kury.pl W prku rozrywki znjduje ię oron kruzel,

Oscylator harmoniczny tłumiony drgania wymuszone

Oscylor hroniczny łuiony rgni wyuszone x / Γ x e x Oscylor swoony łuiony Γ x Jeśli Γ

3. Równanie Bernoulliego dla przepływu płynów doskonałych

Równnie Bernoullieo l rzeływu łynów okonłyc Równnie Bernoullieo wyrż zę, że w rucu utlony nieściśliweo łynu ielneo obywjący ię w olu ił ciężkości, cłkowit eneri łynu kłjąc ię z enerii kinetycznej, enerii

Modele odpowiedzi do arkusza próbnej matury z OPERONEM. Fizyka Poziom rozszerzony

Modele odowiedzi do rkuz rónej ury z OPEONEM Fizyk Pozio rozzerzony Grudzieƒ 007 zdni Prwid ow odowiedê Licz... z zinie wzoru n n enie ol grwicyjnego k GM z zinie wrunku k v GM c v, gdzie M lney, roieƒ

ý Ą Ż í đ í ż Ż Ż ĺ Ł ĺ ź ż Ż Í Í ĺ ĺ ĺ ĺ ĺ ĺ ĺ ĺ ý ý ń ť Ż Ż ć ż ń Í í ń ż ĺ ĺ Ó Í ĺ ť Ż ĺ ĺ ý Ę Ś ń ĺ ý ý Í ý ĺ í ĺ ĺ ĺ ĺ Í Ę ĺ ĺ ĺ ĺ ĺ ĺ Ś ż ĺ ż ż ć ż ż ć ĺ ý Ż ż đ ĺ ż ż đ í ŕ Ż Ż ő ż Ę í Ż ŕ ń ż Ż

Modele odpowiedzi do arkusza próbnej matury z OPERONEM. Fizyka Poziom rozszerzony

Modele odowiedzi do rkuz róbnej mtury z OPEONEM Fizyk Poziom rozzerzony Grudzieƒ 007 zdni Prwid ow odowiedê Liczb unktów... z zinie wzoru n nt enie ol grwitcyjnego kt GM z zinie wrunku kt m v GM m c, gdzie

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA

DROGI i CYKLE HAMILTONA w grfh kierownh Dl grfu kierownego D = ( V, A ) rogą wierhołk 0 V o V nwm iąg (npremienn) wierhołków i łuków grfu: ( 0,,,,...,,, ), pełniją wrunek i = ( i, i ) l i =,..., rogę nwm

Zadanie 1. Rozwiązanie. opracował: Jacek Izdebski.

Zaanie 1 Jaką pracę należy wykonać, aby w przetrzeń mięzy okłakami konenatora płakiego wunąć ielektryk całkowicie tę przetrzeń wypełniający, jeśli napięcie na okłakach zmienia ię w trakcie tej operacji

motocykl poruszał się ruchem

Tet powtórzeniowy nr 1 W zadaniach 1 19 wtaw krzyżyk w kwadracik obok wybranej odpowiedzi Inforacja do zadań 1 5 Wykre przedtawia zależność prędkości otocykla od czau Grupa B 1 Dokończ zdanie, określając,

Identyfikacja parametrów modelu maszyny synchronicznej jawnobiegunowej

Akemi Górniczo-Hutnicz im. Stniłw Stzic w Krkowie Wyził Elektrotechniki, Automtyki, Inormtyki i Elektroniki KATEA MASZYN ELEKTYCZNYCH Stuenckie Koło Nukowe Mzyn Elektrycznych Ientyikcj prmetrów moelu mzyny

Lista 3 z rozwiązaniami. Autorzy rozwiązań Zad mgr. D.Karp Zad dr. A.Kolarz. Dynamika ruch prosto- i krzywoliniowy; siły bezwładności

Li z rozwiąznii Auorzy rozwiązń Zd. 6 75 r. D.rp Zd. 76-8 dr. A.orz Dynik ruc proo- i krzywoiniowy; iły bezwłdności Ruc prooiniowy pod dziłnie łej iły 6. Socód o ie = 9 k pod dziłnie łej iły npędowej =

KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Fizyka i astronomia Poziom podstawowy

KRYTERIA OCEIAIA ODPOWIEDZI Próbn Mtur z OPEROEM izyk i tronoi Pozio podtwowy Litopd 0 W niniejzy heie oenini zdń otwrtyh ą prezentowne przykłdowe poprwne odpowiedzi. W tego typu h nleży również uznć odpowiedzi

KONKURS FIZYCZNY DLA UCZNIÓW GIMNAZJUM

Konkury w województwie podkarpacki w roku zkolny 2005/2006... pieczątka nagłówkowa zkoły... kod pracy ucznia KONKURS FIZYCZNY DLA UCZNIÓW GIMNAZJUM ETAP SZKOLNY Drogi Uczniu, Witaj na I etapie konkuru

MECHANIKA BUDOWLI 5 UWZGLĘDNIENIE WPŁYWU TEMPERATURY, OSIADANIA PODPÓR I BŁĘDÓW MONTAŻOWYCH W RÓWNANIU PRACY WIRTUALNEJ.

WYKŁ DY Z ECHNIKI BUDOWLI WPŁYW TEPERTURY I BŁĄDÓW, SPOSÓB WERESZCZEGIN- OHR OBLICZNI CŁEK O Kopcz, m Łoowski, Wojciec Pwłowski, icł Płokowik, Krzszof Tmper Konsucje nukowe: prof. r. JERZY RKOWSKI Poznń

Dynamika punktu materialnego. Ciało o znanych właściwościach Otoczenie Warunki początkowe (prędkość) Jaki będzie ruch ciała? masa ciężar ilość materii

Dnik punku eilnego iło o nnch łściościch Oocenie Wunki pocąkoe pękość Jki ęie uch cił? s cięż ilość eii sił Sił nie jes poen o uni cił uchu le o jego in. 564-64 64-77 IZYKA - 6 W-5 hp://.if.p.lo.pl/ogn.oloski/

Zadania. ze zbioru 25 lat Olimpiad Fizycznych Waldemara Gorzkowskiego. a, skierowane równolegle do równi (w górę, ku

76 FOTON 4, Wion 04 Zdni ze zbioru 5 lt Olimpid Fizycznych Wldemr Gorzkowkiego Od Redkcji: Cytowny w tym zezycie profeor Iwo Biłynicki-Birul jet luretem I Olimpidy Fizycznej Poniżej przytczmy pouczjące

5. Zadania tekstowe.

5. Zni tekstowe. Przykł. Kolrz połowę rogi pokonł ze śrenią prękością 0 km/, rugą połowę z prękością 50 km /. Wyzncz śrenią prękość kolrz n cłej trsie. nliz : pierwsz połow rogi rug połow rogi 0 km/ prękość

Ćwiczenie 39 KLOCEK I WALEC NA RÓWNI POCHYŁEJ - STATYKA.

Ćwiczenie 39 KLOCEK WALEC A ÓW POCHYŁEJ - SAYKA. 39... Wiadoości ogólne Zjawiko tarcia jet jedny z najbardziej rozpowzechnionych w nazej codziennej rzeczywitości. W świecie w jaki żyjey tarcie jet dołownie

ZADANIA Układy nieliniowe. s 2

Przykłd Okrślić punky równowgi podngo ukłdu ZDNI Ukłdy niliniow u f(,5 y Ry. Część niliniow j okrślon z poocą funkcji: f ( Zkłdy, ż wyuzni j zrow: u. Punky równowgi odpowidją yucji, gdy pochodn części

Co można zrobić za pomocą maszyny Turinga? Wszystko! Maszyna Turinga potrafi rozwiązać każdy efektywnie rozwiązywalny problem algorytmiczny!

TEZA CHURCHA-TURINGA Mzyn Turing: m końzenie wiele tnów zpiuje po jenym ymolu n liniowej tśmie Co możn zroić z pomoą mzyny Turing? Wzytko! Mzyn Turing potrfi rozwiązć kży efektywnie rozwiązywlny prolem

ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM

ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.

SPRAWDZIAN WIADOMOŚCI I UMIEJĘTNOŚCI Z DYNAMIKI KLASA I GIMNAZJUM GRUPA I

SPRAWDZIAN WIADOMOŚCI I UMIEJĘTNOŚCI Z DYNAMIKI KLASA I GIMNAZJUM GRUPA I 1. (3p) Jaki rodzaj oddziaływań zachodzi w podanych ytuacjach? a) Spadanie jabłka z drzewa -... b) Uderzenie łotkie w gwóźdź...

Zadania do rozdziału 3. Zad.3.1. Rozważmy klocek o masie m=2 kg ciągnięty wzdłuż gładkiej poziomej płaszczyzny

Zadania do rozdziału 3. Zad.3.1. Rozważy klocek o aie kg ciągnięty wzdłuż gładkiej pozioej płazczyzny przez iłę P. Ile wynoi iła reakcji F N wywierana na klocek przez gładką powierzchnię? Oblicz iłę P,

Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych

Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc

Ó Ń Ć ź Ś Ć Ć Ą Ć Ś Ó Ł Ś ź ź Ż ź ź Ę Ę Ę Ś Ó Ś Ą Ś Ł Ł Ę Ę Ę Ę Ć Ć Ś Ś Ę Ą Ę Ł Ę ź Ż Ę Ł Ę Ś Ó Ś Ł Ł ź Ę Ą Ą Ę Ś Ę Ą ź Ą ź ź Ś Ł Ł Ć Ć Ć Ś Ę Ć Ś Ę Ć Ć Ć Ć Ś Ę Ę Ć Ł Ę Ś Ó Ó Ę Ą Ę Ę Ć Ś Ś Ę Ą Ą Ł Ę Ę Ł

Ą Ę ŁĘ Ł Ą ń Ł ć Ż ż Ł ń ż ń Ó ń Ż ć Ł ń ć ż Ż Ż ż ż ż ń ć ń ń ń Ą Ś Ż Ż Ż ż ż ć ż Ą Ś Ś Ż ż Ś ż Ś ż ż ż Ż ż ń Ł ż Ż ń ż ń Ą Ś ń ż ń ń Ł ń ż Ż ń ń ć ż Ś ń ń ń Ś ż ż ń ń ń ń Ż ń ń Ł ń ń ż ń ń ń ż Ł ń Ż

Temperatura czarnej kulki umieszczonej w ognisku soczewki i ogrzanej promieniami słonecznymi zadanie z XXIX Olimpiady fizycznej 1979/1980 1

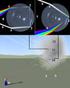6 FOTON 130, Jeień 015 Temperatura czarnej kulki umiezczonej w ogniku oczewki i ogrzanej promieniami łonecznymi zaanie z XXIX Olimpiay fizycznej 1979/1980 1 Taeuz Molena topień III, zaanie teoretyczne

Rozwiązywanie zadań z dynamicznego ruchu płaskiego część I 9

ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone

Blok 2: Zależność funkcyjna wielkości fizycznych

Blok : Zależność funkcyjna wielkości fizycznych ZESTAW ZADAŃ NA ZAJĘCIA 1. Na podtawie wykreu oblicz średnią zybkość ciała w opianym ruchu.. Na ryunku przedtawiono wykre v(t) pewnego pojazdu jadącego po

Podstawy elektrotechniki

Wyział Mechaniczno-Energetyczny Postawy elektrotechniki Prof. r hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bu. A4 Stara kotłownia, pokój 359 Tel.: 71 320

RÓWNANIA TRYGONOMETRYCZNE Z PARAMETREM

ÓWNANIA TYGONOMETYCZNE Z PAAMETEM Do grupy zgdnień eycznyc, w kóryc wysępuje pojęcie preru, nleżą równni rygonoeryczne. ozprywnie równń rygonoerycznyc z prere swrz ożliwość powórzeni i urwleni ożsości

λ = 92 cm 4. C. Z bilansu cieplnego wynika, że ciepło pobrane musi być równe oddanemu

Odpowiedzi i rozwiązania:. C. D (po włączeniu baterii w uzwojeniu pierwotny płynie prąd tały, nie zienia ię truień pola agnetycznego, nie płynie prąd indukcyjny) 3. A (w pozotałych przypadkach na trunie

Mikrosilniki synchroniczne

Mikoilniki ynchoniczne Specyfika eoii: R >0 z uwagi na ounkowo dużą waość ezyancji ojana nie wolno jej pomijać w analizie zjawik mikomazyny ynchonicznej. Zwykle wykozyywane ą óżne odzaje momeny ynchonicznego:

Dynamika punktu materialnego

Dynaia punu aerialnego dr inż. Sebaian Pauła Wydział Inżynierii Mechanicznej i Roboyi Kaedra Mechanii i Wibroauyi ail: paula@agh.edu.pl www: hoe.agh.edu.pl/~paula/ dr inż. Sebaian Pauła - Kaedra Mechanii

Układy inercjalne i nieinercjalne w zadaniach

FOTON 98 Jeień 007 53 Układy inercjalne i nieinercjalne w zadaniach Jadwia Salach Zadanie 1 Urzędnik pracujący w biurowcu wiadł do windy która ruzył dół i przez 1 ekundę jechała z przypiezenie o wartości

Zagadnienie brachistochrony jako przyk lad zastosowania rachunku wariacyjnego

Zgnienie brchistochrony jko przyk l zstosowni rchunku wricyjnego 1. Przestwienie problemu. Równni Euler-Lgrenge 3. Tożsmość Beltrmiego 4. Równnie cykloiy 5. Zs Fermt 1 Przestwienie problemu Brchistochron

ODPOWIEDZI, KRYTERIA OCENIANIA I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY. ZADANIE punktów. r r r

Okęoa Koija zainacyjna Poznaniu Maeiał ćiczenioy z fizyki i aonoii 011. Pozio ozzezony Kyeia oceniania i chea punkoania 1 ODPOWIDZI, KYTIA OCNIANIA I SCHMAT PUNKTOWANIA POZIOM OZSZZONY ZADANI 1. 10 punkó

1. Wykres momentów zginających M(x) oraz sił poprzecznych Q(x) Rys2.

Zadanie. Zginanie prote belek. Dla belki zginanej obciążonej jak na Ry. wyznaczyć:. Wykre oentów zginających M(x) oraz ił poprzecznych Q(x).. Położenie oi obojętnej.. Wartość akyalnego naprężenia noralnego

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Fizyka i astronomia Poziom podstawowy

Modele odpowiedzi do arkuza Próbnej Matury z OPERONEM Fizyka i atronoia Pozio podtawowy Litopad 00 W klu czu ą pre zen to wa ne przy kła do we pra wi dło we od po wie dzi. Na le ży rów nież uznać od po

PRZYGOTOWANIE DO EGZAMINU GIMNAZJALNEGO Z FIZYKI DZIAŁ III. SIŁA WPŁYWA NA RUCH

DZIAŁ III. SIŁA WPŁYWA NA RUCH Wielkość fizyczna nazwa ybol Przypiezenie (II zaada dynaiki) a Jednotka wielkości fizycznej Wzór nazwa ybol F N w a niuton na kilogra kg Ciężar Q Q g niuton N Przypiezenie

Drobiną tą jest: A) proton B) neutron C) atom wodoru D) elektron

ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Koiji Wojewódzkiego Konkuru Przediotowego z Fizyki Iię i nazwiko ucznia... Szkoła... Punkty

1. Samochód jadący z szybkością 10 m/s na prostoliniowym odcinku trasy zwolnił i osiągnął szybkość 5 m/s.

Iię i nazwiko Daa Klaa Werja A Sprawdzian 1 opi ruchu poępowego 1. Saochód jadący z zybkością 1 / na prooliniowy odcinku ray zwolnił i oiągnął zybkość 5 /. 1 a. Przyro prędkości a warość 5 / i zwro zgodny

2. Obliczyć natężenie pola grawitacyjnego w punkcie A, jeżeli jest ono wytwarzane przez bryłę o masie M, która powstała przez wydrążenie kuli o

Grwitcj. Obliczyć, jką siłą jest przyciągn s, jeżeli znn jest s plnety orz gęstość i proień drugiej plnety tkże odległości, jk n rysunku. (,, / F ) 5 F G.5.5 7 Sił t jest położon do poziou pod kąte β tki,

Ą Ą ż ż ś ż ż ż ć ś ż ść ś ś ż ć ść ż ż ć ś ś ż ż ć ś ś ś ż ś ć ć Ę ś Ł ś ś Ń Ń ż ż Ń ść ż ść ż Ą ź ż ść Ń ś ż ś Ł ść ż ść ś ż ś ż Ó Ś ż ż ż ż ć ść ś ż ż ć ść ś ś ż ść ż ż ść ś ż ż ź ś ść ż ś ś ś ć Ł Ą

Ń ź ź Ń Ó ŁĄ Ó Ę Ł Ł Ó Ł Ę Ę Ł Ę ź Ó ź Ę Ę Ę Ę Ę Ą Ą Ł Ź Ę Ę Ę Ę Ę Ę ź Ł Ś Ś Ę Ł Ę Ę Ę ŚĆ Ą Ś Ś Ó Ę Ń Ę Ę Ł Ę Ł Ć Ż Ę Ć ź Ó Ę Ę Ę Ę Ó Ę Ś Ń Ą Ę Ą Ę Ł Ę Ó Ń Ą Ł Ć Ę Ę Ł Ę Ó Ą Ó Ę Ó Ę Ę Ę Ę Ą Ó Ź ź Ć Ó ź

ź ŁĄ ó ś ó ś ó ó ó ś ó ó ó ó ó ś ó ó ó ó ó ó ó ó ó ó ś ó ó ó ó Ż Ż ó ó ó ó ó ó ó ó ó ó ó ń ó ó ó ć ó ó ó ś ó ó ó ó ó ó ó ó ó ś ó ś Ł ś ó ó ó ó ó Ż Ż ć ó ó ś ó ó ó ó ó ó ś ó ó ó ó Ę Ż ó ś ó ó ó ó ó ś ś

ź ź ź Ę Ę ź ź ź ź Ź ć ć ć ć ć ć Ź Ł ć ć Ż ć Ż ć Ę Ł Ż Ń ć ć ć Ż ć ć ć ć ć ć Ę ć Ę Ł ć ć ć ć ć ć ć ć ć Ż ć ć ć ć ć Ż Ń ź ć Ł ć ć ć ć ć ź ź ć ć ć Ł ć ć ć Ż ć ć Ż ź ć ć ć Ż ć ć ć ć Ń ć Ę ć Ż Ł ć Ń ć ć ć Ź

ą Ą Ę Ś Ł ź ź ą ń ń ą ć ą Ę ą ą ą ą ć ą ć ą ą Ź ć Ż Ł Łą ń ń ą ą ą ą Ę ą ą ń Ź Ń ą ą ć ąć ć ć ą ą ń ą ź ą ą ą ą ą ą ą ć ą ą ą ą ć Ź ą ń ą ą Ź ą ą ą ą ą ą ć ą ą ą ą ć ą ą ą ą ć ą ć ć ą ą ń ą ń ń ń ć ą ą

Ą ć ć ć ŁĄ ć Ę Ł ć ć ć ć ź ć ć Ą ć ć Ą ć ć ć ć Ę ć ć Ę ć ć ć ć ć ź ć ć ć ć ć ć ć ć ć Ł Ś ć ć ź ć ć ć ć ć ć ź ć ź ć ź ć ź ć ć Ą ć ć Ę ź Ą ć ć ć ć ć ć ć ć ź Ę ć ć Ą ć ć ć Ł ć ć Ą ć ć ć ć ć Ę ź ć ć ć ć ć

Ę Ę Ś ć Ł ć ż ż ż ż ż Ł Ł Ą Ń ż ć ź ż ć ć ż Ł Ę Ś ż ż ż Ł Ś ż ż ż Ś ż ż ż Ł Ł ż ż ż ć Ś Ę Ę Ś Ś Ę ć Ś Ł Ł ć ć ć ć ć ć ć Ł ć Ł Ę ć Ę ć Ę Ś Ł Ł ć ć ć ż ć ć ź ż Ł Ą Ą Ą Ę Ą Ś Ę Ś Ł Ś ć ŁĄ Ź Ę Ł Ś Ń Ę ć

ń Ż ń ź ć ć ń ć ć ć ć ź ć ń ń ć ń ć ć ć ć ź ć ń Ż ć Ż ć ć ć ć ń ć ń ć ń ć ń ć ć ń ń ć ń ć ń ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ż Ż Ż ć ć ć ć ń ć ć ć ć ć ć ć Ż ć ć ć ź ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć

ŚĆ ŁĄ Ś Ć Ć Ś ŁĄ Ł Ż Ł Ś Ż Ł Ę Ł Ż Ł Ł Ś Ś Ś Ł Ś Ł Ś Ś Ć Ś Ś ć Ś Ś Ś Ś ć Ś Ż ć Ć Ć Ś Ś Ż Ś Ż Ś Ś ć Ś Ś Ć Ś Ć Ż Ś ż Ś ż Ż Ś Ż Ś Ż Ł Ś Ś Ł Ś Ą Ę Ą Ż ż ć ć ć Ą ż ć Ś Ś Ś Ś Ż ż ć ć ć Ę Ś ż ć Ś ć Ś Ś ć Ś Ś

ó Ż ó Ę ń ó ó ń ń ę ć Ś ż Ż Ż Ż ą ą ę ń Ś ń ą ń ń ż ń ó ó ó Ś ń ć ż ń ń ń Ś Ż ż ń ó ń ą ę ń ż ą ć Ś Łą ę ą ż ą Ż ó ó Ó Ą ó ń ń Ż ę Ś ć ę ż ę ń ż ą Ż ą ą ń Ż ź ń ń ń ń ń ż ó ó ż ń Łą ę ą ż ą ó ó ó ó

KATEDRA ENERGOELEKTRONIKI I ELEKTROENERGETYKI LABORATORIUM ELEKTROENERGETYKI. Rys. 7.7.1. Pomiar impedancji pętli zwarcia dla obwodu L2

6.7. ntrukcj zczegółow Grup:... 4.. 6.7. Cel ćwiczeni Celem ćwiczeni jet zpoznnie ię z metodmi pomirowymi i przepimi dotyczącymi ochrony przeciwporżeniowej w zczególności ochrony przed dotykiem pośrednim.

KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów. Schemat punktowania zadań

1 KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów 10 marca 2017 r. zawody III topnia (finałowe) Schemat punktowania zadań Makymalna liczba punktów 60. 90% 5pkt. Uwaga! 1. Za poprawne rozwiązanie zadania

SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA

Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I

ź Ś ś ś Ś Ś ś ś ś ś ś ś ź ś ś Ś Ś Ś źś Ń Ś ś Ą Ź ś ś ś ś Ś ś ś Ą Ś Ą Ą ś ś Ś Ś ść ś Ś ś ś Ś ś ś ś ź ś Ś Ś Ś Ś ś Ś Ź ś ś ś ś ś Ś ś Ś ć ć Ś Ś Ą ć ć Ś Ś Ś ś Ś ś Ę Ś Ę ś Ś Ś Ś Ś ś ś ś Ś Ś Ś Ś ś ś ć Ć Ę Ś Ś

Zad. 4 Oblicz czas obiegu satelity poruszającego się na wysokości h=500 km nad powierzchnią Ziemi.

Grawitacja Zad. 1 Ile muiałby wynoić okre obrotu kuli ziemkiej wokół włanej oi, aby iła odśrodkowa bezwładności zrównoważyła na równiku iłę grawitacyjną? Dane ą promień Ziemi i przypiezenie grawitacyjne.

Zadania do sprawdzianu

Zadanie 1. (1 pkt) Na podtawie wykreu możemy twierdzić, że: Zadania do prawdzianu A) ciało I zaczęło poruzać ię o 4 później niż ciało II; B) ruch ciała II od momentu tartu do chwili potkania trwał 5 ;

WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 2009/2010 Czas trwania: 120 minut

KOD UCZESTNIKA KONKURSU WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 009/010 Cza trwania: 10 inut Tet kłada ię z dwóch części. W części pierwzej az do rozwiązania 15 zadań zakniętych, za które

Analiza instrumentów pochodnych

Analiza inrumenów pochonych Dr Wiolea owak Wykła 7 Wycena opcji na akcję bez ywieny moel Blacka-cholea z prawami o ywieny moel Merona Założenia moelu Blacka-cholea. Ceny akcji zachowują logarymiczno-normalnym.

Roztwory rzeczywiste (1) Roztwory rzeczywiste (2) Funkcje nadmiarowe. Również w temp. 298,15K, ale dla CCl 4 (A) i CH 3 OH (B).

Roztwory rzezywiste (1) Również w tep. 98,15K, le dl CCl 4 () i CH 3 OH (). 15 Τ S 5 H,,4,6,8 1-5 - -15 G - Che. Fiz. TCH II/1 1 Roztwory rzezywiste () Ty rze dl (CH 3 ) CO () i CHCl 3 (). 15 5 Τ S -5,,4

Ś Ń ź Ś ź Ś Ś Ś Ś Ś Ś Ś Ą Ś Ż ż ż Ż ć ć ź ź ÓĆ ć Ż Ą ć Ż ż ć Ą Ł Ś Ń ć Ś Ą Ą ż Ż Ą ź Ą ź Ą ż Ś Ń Ł Ś Ś Ó Ą ż ż Ś Ń Ł Ś ż ź ź Ą ć ż ż ć ć ż ć ż Ą ż Ł ż ć ż ż Ż ż ż ż ć Ąć ż ż ż Ż Ż ż ż ć ż ć ż ż ż Ż ż ż

, , , , 0

S T E R O W N I K G R E E N M I L L A Q U A S Y S T E M 2 4 V 4 S E K C J I G B 6 9 6 4 C, 8 S E K C J I G B 6 9 6 8 C I n s t r u k c j a i n s t a l a c j i i o b s ł u g i P r z e d r o z p o c z ę

1Coulomb 1Volt. Rys. 1. Schemat kondensatora płaskiego. Jednostką pojemności w układzie SI, jest Farad (F):

POJEMNOŚĆ ELEKTRYZNA Konenstor służy o mgzynowni energii potencjlnej w polu elektrycznym. Typowy konenstor płski, skł się z wóch równoległych, przewozących okłek o polu przekroju S umieszczonych w oległości

I 3 + d l a : B E, C H, C Y, C Z, ES, F R, G B, G R, I E, I T, L T, L U V, P T, S K, S I

M G 6 6 5 v 1. 2 0 1 5 G R I L L G A Z O W Y T R Ó J P A L N I K O W Y M G 6 6 5 I N S T R U K C J A U 7 Y T K O W A N I A I B E Z P I E C Z E Ń S T W A S z a n o w n i P a s t w o, D z i ę k u j e m y

Modele odpowiedzi do arkusza próbnej matury z OPERONEM. Fizyka i astronomia Poziom rozszerzony

Modee odpowiedzi do arkuza próbnej aury z OPRONM Fizyka i aronoia Pozio rozzerzony iopad 009 kuczu à prezenowane przyk adowe prawid owe odpowiedzi. Nae y równie uznaç odpowiedzi ucznia, jeêi à inaczej

Doświadczenie Atwood a

Doświadczenie Atwood a Dwa kocki o maach m 1 i m 2 = m 1 wiza na inie przewiezonej przez boczek. Oś boczka podwiezona jet do ufitu. Trzeci kocek o maie m 3 zota po ożony na pierwzym kocku tak że oba poruzaja

A. Kasperski, M. Kulej, BO -Wyk lad 5, Optymalizacja sieciowa 1

A. Kaperki, M. Kulej, BO -Wyk lad, Opymalizacja ieciowa 1 Zagadnienie makymalnego przep lywu (MP). Przyk lad. W pewnym mieście inieje fragmen wodoci agów zadany w poaci naȩpuj acej ieci: 1 Luki oznaczaj

Modele odpowiedzi do arkusza próbnej matury z OPERONEM. Fizyka Poziom rozszerzony

Modele odowiedzi do arkuza róbnej matury z OPEONEM Fizyka Poziom rozzerzony Grudzieƒ 007... za zaianie wzoru na nat enie ola grawitacyjnego kt GM za zaianie warunku kt m v GM m c, gdzie M maa lanety, romieƒ

Blok 4: Dynamika ruchu postępowego. Równia, wielokrążki, układy ciał

Blok 4: Dynaika ruchu potępowego Równia, wielokrążki, układy ciał I Dynaiczne równania ruchu potępowego Chcąc rozwiązać zagadnienie ruchu jakiegoś ciała lub układu ciał bardzo częto zaczynay od dynaicznych

1 10BKPANC 6,5 0:21:10 03:15 [min/km] 0:21:10. 3 TRZEBIEL 6,5 0:22:35 03:28 [min/km] 0:22:34

I 10NC U C I E J O Ł J 2 3 9 9 I E O Ó, O I I U E I E C O I I I C E U O Ó N O C Š C E C E I O C Y Ł O I E J 1 0 a n c E U J 4 O 8, I Ł O Y O 5 U U I U Y E I I, I E O E J E U Ł Ó N J E C I N O Ł Y U I N

Zadania do rozdziału 2.

Zadania do rozdziału. Zad..1. Saochód na auoradzie poruza ię ruche jednoajny prooliniowy z prędkością υ100 k/odz. W jaki czaie przebędzie on droę 50 k? Rozwiązanie: Zad... υ 50 k / odz 0.5 odz. υ 100 k

MECHANIKA. Podstawy kinematyki Zasady dynamiki. Zasada zachowania pędu Zasada zachowania energii Ruch harmoniczny i falowy

MECHANIKA Podswy kineyki Zsdy dyniki Siły Równnie ruchu Ukłdy inercjlne i nieinercjlne Zsd zchowni pędu Zsd zchowni energii Ruch hroniczny i flowy ruch rejesrowne w czsie w sposób ciągły ziny położeni

Wymagania na poszczególne oceny przy realizacji programu i podręcznika Świat fizyki klasa II

LINKI WAŻNE DLA KLAS III hp://fizyka.zamkor.pl/image/maerialy/men_om_5_11110.pdf hp://fizyka.zamkor.pl/arykul/63/1188-obowiazkowe-dowiadczenia-fizyczne/ Wymagania na pozczególne oceny przy realizacji i

Regionalne Koło Matematyczne

Regionlne Koło Mtemtyzne Uniwersytet Mikołj Kopernik w Toruniu Wyził Mtemtyki i Informtyki http://www.mt.umk.pl/rkm/ List rozwiązń zń nr 8, grup zwnsown (3.03.200) O izometrih (..) Wektorem uporząkownej