MECHANIKA PŁYNÓW - LABORATORIUM
|
|
|
- Patrycja Milewska
- 8 lat temu
- Przeglądów:
Transkrypt
1 MECHANIKA PŁYNÓW - LABORATORIUM Ćwiczenie nr 1 Wypływ cieczy przez przystawki Celem ćwiczenia jest eksperymentalne wyznaczenie współczynnika wydatku przystawki przy wypływie ustalonym, nieustalonym oraz wyznaczenie współczynnika prędkości. 1. Wprowadzenie Wypływ przez otwór swobodny. Otworem swobodnym nazywamy otwór, przez który ciecz wypływa w powietrze lub inny ośrodek gazowy. W zjawiskach wypływu cieczy rzeczywistych wskutek istnienia oporów ruchu prędkość wypływu jest mniejsza od teoretycznej prędkości wypływu, obliczonej przez Torricelliego (v teor = gh ). Uwzględniamy to za pomocą współczynnika doświadczalnego, zwanego współczynnikiem prędkości. Jego wartość liczbowa zależy głównie od lepkości wypływającej cieczy, a ponadto od wielkości i kształtu otworu oraz od wysokości napełnienia zbiornika. Prędkość rzeczywista v rz w przekroju wypływowym otworu wynosi zatem: v rz = gh [1.1] Warto tu nadmienić, że współczynnik dla wody i innych cieczy o tej samej lepkości wynosi = 0,97 0,98. W zagadnieniach technicznych bardziej istotne od prędkości wypływu jest natężenie wypływu Q, tj. objętość cieczy wypływającej przez otwór w jednostce czasu. Gdyby wypływający strumień cieczy miał ten sam przekrój co otwór, wówczas natężenie wypływu Q = F o v rz [1.] W rzeczywistości - strumień wypływający przez otwór o ostrym brzegu (rysunek 1.) zwęża się, tak iż jego przekrój F str jest mniejszy od przekroju otworu F o. Rys. 1. Rozmieszczenie linii prądu przy wypływie cieczy przez ostro brzeżny otwór 1
2 Zjawisko to wywołane jest niemożliwością nagłej zmiany kierunku przepływu cząstek, poruszających się wzdłuż ścian zbiornika i wypływających przez otwór na zewnątrz, a także dławieniem strumienia wzdłuż krawędzi otworu. Stosunek przekroju strugi w miejscu przewężenia do przekroju otworu nazywamy współczynnikiem zwężenia (kontrakcji) ϰ: Fstr ϰ = [1.3] F Wartość liczbowa współczynnika zwężenia dla otworów o ostrych brzegach o dowolnym konturze zawarta jest w granicach: ϰ = 0,61 0,64. Rzeczywiste natężenie wypływu określa zależność: o Iloczyn: Q = ϰ F o gh = F o gh [1.4] ϰ = [1.5] nazywa się współczynnikiem wypływu. Wartość współczynnika dla otworów o ostrych brzegach wynosi: = 0,59 0, Określenie i podział przystawek. Przystawkami nazywamy króćce rurowe, umieszczone w dnie lub ścianach bocznych zbiornika, bądź też u wylotu rury. Przystawki dzielimy na: poziome (o osi poziomej), pionowe (o osi pionowej) i ukośne. Mogą być one umieszczone na zewnątrz zbiornika (przystawki zewnętrzne) lub wpuszczone do jego wnętrza (przystawki wewnętrzne). Przekrój przepływowy przystawki może być różny: kołowy, kwadratowy, prostokątny itp. Pole przekroju może być niezmienne (np. przystawki cylindryczne) lub zmieniać się w kierunku osi w dowolny, ale ciągły sposób (np. przystawki stożkowe zbieżne lub rozbieżne, przystawki dyszowe itp.). Przystawki umieszcza się w celu nadania odpowiedniego kierunku strumieniowi wypływającej cieczy i zwiększenia natężenia przepływu wywołanego wytworzeniem podciśnienia w przewężeniu strumienia (patrz punkt 1.3.). Cylindryczne przystawki pionowe o ściętym wylocie umieszcza się w dnach zbiorników mierniczych w celu osiągnięcia normalnego stanu wykroplenia przy całkowitym jego opróżnieniu Wypływ cieczy przez zewnętrzną przystawkę o osi poziomej. Przy wypływie cieczy przez zewnętrzną poziomą przystawkę cylindryczną o ostrej krawędzi wlotowej następuje dławienie strumienia, polegające na zmniejszeniu jego przekroju poprzecznego na ogół przy równoczesnym zmniejszeniu ciśnienia bez wykonania pracy użytecznej. Jeżeli przystawka jest dostatecznie długa (l/d ), wówczas strumień rozszerza się, a jego zewnętrzne cząsteczki omywają wnętrze przystawki. Gdybyśmy w przekroju przewężenia (na rysunku 1.. w punkcie A) umieścili piezometr P zanurzony swym dolnym końcem w naczyniu N napełnionym jakąkolwiek cieczą manometryczną, zaobserwowalibyśmy podniesienie się cieczy w piezometrze na wysokość z odpowiadającą panującemu w przystawce podciśnieniu. Spadek ciśnienia poniżej ciśnienia atmosferycznego powoduje ssanie cieczy ze zbiornika, wskutek czego natężenie wypływu przez przystawkę jest większe niż przez otwór o tym samym przekroju. Efekt ten maleje w miarę zwiększania się długości przystawki; wtedy wysokość podciśnienia z zużywa się częściowo lub całkowicie na pokonanie oporów hydraulicznych w przewodzie (tu: przystawce).
3 Rys.. Wypływ cieczy przez poziomą przystawkę cylindryczną Aby wyznaczyć wartość liczbową współczynnika wypływu, napiszmy równanie D.Bernoulliego dla cząstki cieczy znajdującej się w poziomie zwierciadła i u wylotu przystawki: gdzie: v 0 g pa + + H = v g pa Δh str [1.6] v o - prędkość opadania zwierciadła w [m/s], v - prędkość u wylotu przystawki w [m/s], p a - ciśnienie atmosferyczne w [Pa], γ - ciężar właściwy cieczy w [N/m 3 ], H - wysokość napełnienia nad osią otworu (położenia, wzniesienia) w [m], Δh str - wysokość strat energetycznych (hydraulicznych) w [m]. Straty energetyczne spowodowane zwiększeniem się przekroju strugi z F str = ϰ F p do F p (przekrój przystawki), a zatem zmniejszeniem średniej prędkości przepływu z v c (w największym przewężeniu strugi) do v, określa wzór J.C.Bordy: 3
4 Δh str = ( v c v) g [1.7] Wstawiając tę wartość w równanie [1.6] oraz dokonując uproszczeń (m.in. przy ruchu ustalonym i znacznie większym przekroju poziomym zbiornika w stosunku do przekroju przystawki możemy przyjąć v o = 0 - patrz punkt 1.4.) i przekształceń - otrzymamy: Prędkość w przewężeniu strumienia : v + (v c v) = gh [1.8] v c = Fp v = v ϰ -1 [1.9] F str przy czym współczynnik zwężenia dla przystawki o ostrej krawędzi wlotowej ϰ = 0,65. Po wstawieniu tej wartości w równanie [1.8] otrzymamy: v [1 + (ϰ -1 1) ] = gh [1.10] skąd po uwzględnieniu oporów tarcia, określonych współczynnikiem prędkości = 0.97 otrzymamy: v = gh 1 1 ( 1) = 0,83 gh [1.11] Natężenie wypływu: Q = 0,83 F p gh [1.1] Gdyby wypływ odbywał się przez okrągły otwór o ostrym brzegu, wówczas przy założeniu ϰ = 0,65 i = 0.97 natężenie wypływu wynosiłoby: Q otw = 0,606 F p gh [1.13] Widzimy zatem, że zwiększenie natężenia przepływu spowodowane zastosowaniem przystawki wyraża się stosunkiem: Q 0,83 = = 1,37 0, 606 Q otw Wartości współczynników wypływu dla poziomych przystawek cylindrycznych zależą od stosunku l/d. Rezultaty prowadzonych przez siebie doświadczeń J.Weisbach ujął w poniższej tabeli: l/d ,6 0,8 0,77 0,73 0,68 0,63 0,60 4
5 Z powyższej tabelki wynika, że zwiększenie natężenia wypływu wywołane umieszczeniem przystawki zanika, gdy jej długość l 50d. 1.4 Wypływ ustalony. Wypływem ustalonym nazywamy taki wypływ, którego parametry są niezmienne w czasie, przy czym głównie chodzi tu o niezmienną wysokość napełnienia H. Na podstawie wzoru [1.4] (Q = F p gh ) wyliczać możemy dowolny parametr, jeżeli wielkości pozostałe są znane lub zostały określone metodą pomiaru. Wzór ten dotyczy przypadku gdy prędkość dopływającej cieczy do zbiornika prędkość opadania zwierciadła v o może być pominięta oraz gdy ciśnienia zewnętrzne po obu stronach otworu (bądź przystawki) są sobie równe. W warunkach doświadczenia pierwsze zastrzeżenie można uznać za spełnione, gdy v o < 0, [m/s]. Jeżeli v o 0, [m/s] wówczas wysokość napełnienia H należy zwiększyć o wysokość prędkości v o /g. Z kolei drugie zastrzeżenie w warunkach prowadzonego przez nas doświadczenia jest spełnione zawsze Wypływ nieustalony. Wypływem nieustalonym nazywamy taki wypływ, którego parametry są zmienne w czasie. Przy obliczaniu tegoż wypływu najczęściej poszukiwanym parametrem jest czas opróżnienia zbiornika. Stosujemy wówczas wzór: gdzie: t = 1 H 1 F p g H F zb z -0,5 dz [1.14] t - czas częściowego lub całkowitego opróżnienia zbiornika w [s], F zb - pole przekroju poziomego zbiornika na wysokości z nad osią przystawki w [m ], z - chwilowe wzniesienie zwierciadła wody nad osią przystawki (otworu) w [m], H 1 - początkowy poziom wody w zbiorniku w [m], H - końcowy poziom wody w zbiorniku w [m]. Wzór [1.14] (podobnie jak i przy wypływie ustalonym) dotyczy przypadku, gdy nie uwzględniamy ani prędkości opadania zwierciadła v o, ani różnicy ciśnień nad zwierciadłem cieczy w zbiorniku i w płaszczyźnie otworu co jest spełnione przy wykonywaniu niniejszego ćwiczenia. Dla zbiornika o stałym przekroju poziomym (F zb = const) wzór [1.14] po scałkowaniu przybiera postać: t = F F p zb g ( H - 1 H ) [1.15]. Opis stanowiska badawczego. Stanowisko badawcze stanowi zbiornik z tubusem bocznym i z podziałką pionową, której punkt 0 pokrywa się z osią tubusa. Na wyposażeniu są komplety przystawek cylindrycznych każda osadzona centralnie w korku pasującym do tubusa zbiornika. W każdym komplecie przystawki mają tę samą średnicę wewnętrzną, parami mają tę samą długość (par może być lub 3), a w każdej parze przystawki różnią się charakterem wlotu jedna posiada ostrą krawędź wlotową, a druga posiada stożkowy wlot. Kolejnymi elementami wyposażenia są: układ współrzędnych x-y (o osi y skierowanej w dół) zaopatrzony w dużą poziomicę, malutka poziomica do ustawienia przystawek w poziomie, stoper oraz kilka cylindrów miarowych o różnych objętościach. 5
6 3. Część doświadczalna Wyznaczanie współczynnika wydatku przystawek przy wypływie nieustalonym. Czynności do wykonania: 1. Należy pomierzyć długość i średnicę wewnętrzną przystawek i zapisać je w tabeli najlepiej w określonej kolejności co ułatwia potem porównywanie obliczonych wielkości.. Zmierzyć parametry potrzebne do wyliczenia przekroju zwierciadła swobodnego cieczy F zb. 3. Osadzoną w korku przystawkę umieścić w tubusie bocznym zbiornika, korzystając przy tym z małej poziomicy. Wlot przystawki winien pokrywać się ze ścianą zbiornika. 4. Przy zatkanym wylocie przystawki napełniamy zbiornik powyżej (zadanej przez prowadzącego ćwiczenia) początkowej wartości napełnienia H Odcinamy dopływ wody, otwieramy wylot przystawki i włączamy stoper w momencie gdy opadające zwierciadło osiągnie zadaną wysokość H 1, a wyłączamy przy zadanej wartości końcowej H. W ten sam sposób postępujemy z kolejnymi przystawkami. 6. Współczynnik wydatku przystawki liczymy ze wzoru: = t F F p zb g ( H - 1 H ) [1.16] który jest prostym przekształceniem wzoru [1.15]. 7. Wyniki doświadczeń i obliczeń należy zebrać w poniższej tabeli: Przystawka charakter wlotu, długość... d F p H 1 H t Uwagi [m] [m ] [m] [m] [s] [-] 8. W dyskusji wyników uwzględnić wpływ charakteru wlotu oraz długości na wartość współczynnika. 3.. Wyznaczanie współczynnika wydatku przystawek przy wypływie ustalonym. Czynności do wykonania: 1. Należy pomierzyć długość i średnicę wewnętrzną przystawek i zapisać je w tabeli najlepiej w określonej kolejności co ułatwia potem porównywanie obliczonych wielkości. 6
7 . Osadzoną w korku przystawkę umieścić w tubusie bocznym zbiornika, korzystając przy tym z małej poziomicy. Wlot przystawki winien pokrywać się ze ścianą zbiornika. 3. Przy zatkanym początkowo wylocie przystawki napełniamy zbiornik do górnych stanów napełnienia, po czym otwieramy wylot przystawki i tak regulujemy dopływem wody, aby uzyskać stałą (w czasie) wysokość napełnienia H. 4. Odbieramy w czasie t określoną objętość V wypływającej przez przystawkę wody, starając się tak dobrać cylindry miarowe, aby zmierzony czas wypływu mieścił się w granicach [s]. 5. Współczynnik wydatku przystawki liczymy ze wzoru: = t F V p gh [1.17] 6. Wyniki doświadczeń i obliczeń należy zebrać w poniższej tabeli: Przystawka charakter wlotu, długość... d F p l H V t Uwagi d [m] [m ] [-] [m] [m 3 ] [s] [-] 7. W dyskusji wyników uwzględnić wpływ charakteru wlotu oraz długości na wartość współczynnika. 8. Dla przystawek o ostrej krawędzi wlotowej uzupełnić poniższą tabelę (wg rosnącego l/d) - korzystając z danych zawartych w tabeli w punkcie 6, a następnie porównać otrzymane wyniki z tabelą Weisbacha patrz punkt 1.3. l/d 9. Analogiczną tabelę jak wyżej (punkt 8) utworzyć dla przystawek o stożkowym wlocie. 10. Dla przystawek o największej średnicy obliczyć prędkość opadania zwierciadła v o = Q/F zb a następnie obliczyć podstawiając we wzorze [1.17] zamiast H sumę (H + v o /g). Wyniki zebrać w poniższej tabeli: 7
8 Przystawka charakter wlotu, długość d F p H V t v o Uwagi [m] [m ] [m] [m 3 ] [s] [m/s] [-] 3.3. Wyznaczanie współczynnika prędkości. Współczynnik prędkości (dla przystawek) wyznaczamy ze wzoru, który otrzymujemy rozwiązując poniższe zadanie (patrz rysunek 1.3.) Cząstka cieczy wypływająca ze zbiornika w kierunku poziomym przez otwór (lub przystawkę), którego oś znajduje się na głębokości H pod zwierciadłem, z prędkością v rz zajmie po upływie czasu t położenie P, określone współrzędnymi x i y. Pomijając opór powietrza możemy zapisać: x = v rz t oraz y = 1 gt [1.18] Eliminując czas t oraz uwzględniając wzór [1.1], dochodzimy do interesującej nas zależności: x = [1.19] yh Rys. 3. Cząstka cieczy wypływająca ze zbiornika przez otwór w kierunku poziomym 8
9 Czynności do wykonania: 1. Należy pomierzyć długość i średnicę wewnętrzną przystawek i zapisać je w tabeli najlepiej w określonej kolejności co ułatwia potem porównywanie obliczonych wielkości.. Osadzoną w korku przystawkę umieścić w tubusie bocznym zbiornika, korzystając przy tym z małej poziomicy. Wlot przystawki winien pokrywać się ze ścianą zbiornika. 3. Przy zatkanym początkowo wylocie przystawki napełniamy zbiornik do górnych stanów napełnienia, po czym otwieramy wylot przystawki i tak regulujemy dopływem wody, aby uzyskać stałą (w czasie) wysokość napełnienia H. 4. Przy wylocie przystawki ustawiamy układ współrzędnych x-y wraz z dużą poziomicą, tak aby oś y pokrywała się z wylotem przystawki, a oś x znajdowała się w osi przystawki. 5. Dla zadanych przez prowadzącego ćwiczenia wartości x odczytujemy odpowiadające im wartości y starając się trafić w środek wypływającego strumienia. 6. Uzyskane wyniki i obliczenia zebrać w poniższej tabeli: Przystawka charakter wlotu, długość... H x y śr Uwagi [m] [m] [m] [-] [-] 7. W dyskusji wyników uwzględnić wpływ charakteru wlotu oraz długości na wartość współczynnika. W końcowych wnioskach: - podać przyczynę takiego a nie innego wpływu charakteru wlotu oraz długości przystawki na wartości współczynników:, ustalone, nieustalone. - określić na ile odtworzyliśmy doświadczenie Weisbacha (zależność od ilorazu l/d) dla przystawek o ostrej krawędzi (zarówno co do uzyskanych wielkości jak i charakteru zmian). - określić, czy prędkość opadania zwierciadła w wykonanym przez nas doświadczeniu miała wpływ na wartość ustalone. 9
BADANIE WYPŁYWU CIECZY ZE ZBIORNIKA
 BADANIE WYPŁYWU CIECZY ZE ZBIORNIKA 1. Wprowadzenie Spośród zagadnień związanych z wypływem cieczy ze zbiornika do najważniejszych należą: - obliczenie natężenia wypływu cieczy przez otwór w ścianie lub
BADANIE WYPŁYWU CIECZY ZE ZBIORNIKA 1. Wprowadzenie Spośród zagadnień związanych z wypływem cieczy ze zbiornika do najważniejszych należą: - obliczenie natężenia wypływu cieczy przez otwór w ścianie lub
MECHANIKA PŁYNÓW LABORATORIUM
 MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
Zadanie 1. Zadanie 2.
 Zadanie 1. Określić nadciśnienie powietrza panujące w rurociągu R za pomocą U-rurki, w której znajduje się woda. Różnica poziomów wody w U-rurce wynosi h = 100 cm. Zadanie 2. Określić podciśnienie i ciśnienie
Zadanie 1. Określić nadciśnienie powietrza panujące w rurociągu R za pomocą U-rurki, w której znajduje się woda. Różnica poziomów wody w U-rurce wynosi h = 100 cm. Zadanie 2. Określić podciśnienie i ciśnienie
Zastosowania Równania Bernoullego - zadania
 Zadanie 1 Przez zwężkę o średnicy D = 0,2 m, d = 0,05 m przepływa woda o temperaturze t = 50 C. Obliczyć jakie ciśnienie musi panować w przekroju 1-1, aby w przekroju 2-2 nie wystąpiło zjawisko kawitacji,
Zadanie 1 Przez zwężkę o średnicy D = 0,2 m, d = 0,05 m przepływa woda o temperaturze t = 50 C. Obliczyć jakie ciśnienie musi panować w przekroju 1-1, aby w przekroju 2-2 nie wystąpiło zjawisko kawitacji,
MECHANIKA PŁYNÓW LABORATORIUM
 MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 6 Wyznaczanie współczynnika wydatku przelewu Celem ćwiczenia jest wyznaczenie wartości współczynnika wydatku dla różnyc rodzajów przelewów oraz sporządzenie ic
MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 6 Wyznaczanie współczynnika wydatku przelewu Celem ćwiczenia jest wyznaczenie wartości współczynnika wydatku dla różnyc rodzajów przelewów oraz sporządzenie ic
Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości
 LABORATORIUM MECHANIKI PŁYNÓW Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA, WYDZ. BMiP, PŁOCK
LABORATORIUM MECHANIKI PŁYNÓW Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA, WYDZ. BMiP, PŁOCK
Statyka płynów - zadania
 Zadanie 1 Wyznaczyć rozkład ciśnień w cieczy znajdującej się w stanie spoczynku w polu sił ciężkości. Ponieważ na cząsteczki cieczy działa wyłącznie siła ciężkości, więc składowe wektora jednostkowej siły
Zadanie 1 Wyznaczyć rozkład ciśnień w cieczy znajdującej się w stanie spoczynku w polu sił ciężkości. Ponieważ na cząsteczki cieczy działa wyłącznie siła ciężkości, więc składowe wektora jednostkowej siły
Ćwiczenie laboratoryjne Parcie wody na stopę fundamentu
 Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI ĆWICZENIE NR 4 OKREŚLENIE WSPÓŁCZYNNIKA STRAT LOEKALNYCH
 INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 4 OKREŚLENIE WSPÓŁCZYNNIKA STRAT LOEKALNYCH . Cel ćwiczenia Celem ćwiczenia jest doświadczalne
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 4 OKREŚLENIE WSPÓŁCZYNNIKA STRAT LOEKALNYCH . Cel ćwiczenia Celem ćwiczenia jest doświadczalne
Grupa 1 1.1). Obliczyć średnicę zastępczą przewodu o przekroju prostokątnym o długości boków A i B=2A wypełnionego wodą w 75%. Przewód ułożony jest w
 Grupa 1 1.1). Obliczyć średnicę zastępczą przewodu o przekroju prostokątnym o długości boków A i B=2A wypełnionego wodą w 75%. Przewód ułożony jest w taki sposób, że dłuższy bok przekroju znajduje się
Grupa 1 1.1). Obliczyć średnicę zastępczą przewodu o przekroju prostokątnym o długości boków A i B=2A wypełnionego wodą w 75%. Przewód ułożony jest w taki sposób, że dłuższy bok przekroju znajduje się
LABORATORIUM MECHANIKI PŁYNÓW
 Ćwiczenie numer 2 Pomiar współczynnika oporu liniowego 1. Wprowadzenie Stanowisko służy do analizy zjawiska liniowych strat energii podczas przepływu laminarnego i turbulentnego przez rurociąg mosiężny
Ćwiczenie numer 2 Pomiar współczynnika oporu liniowego 1. Wprowadzenie Stanowisko służy do analizy zjawiska liniowych strat energii podczas przepływu laminarnego i turbulentnego przez rurociąg mosiężny
LABORATORIUM MECHANIKI PŁYNÓW
 Ćwiczenie numer Pomiar współczynnika oporu liniowego 1. Wprowadzenie Stanowisko służy do analizy zjawiska liniowych strat energii podczas przepływu laminarnego i turbulentnego przez rurociąg mosiężny o
Ćwiczenie numer Pomiar współczynnika oporu liniowego 1. Wprowadzenie Stanowisko służy do analizy zjawiska liniowych strat energii podczas przepływu laminarnego i turbulentnego przez rurociąg mosiężny o
LABORATORIUM MECHANIKI PŁYNÓW
 Ćwiczenie numer 5 Wyznaczanie rozkładu prędkości przy przepływie przez kanał 1. Wprowadzenie Stanowisko umożliwia w eksperymentalny sposób zademonstrowanie prawa Bernoulliego. Układ wyposażony jest w dyszę
Ćwiczenie numer 5 Wyznaczanie rozkładu prędkości przy przepływie przez kanał 1. Wprowadzenie Stanowisko umożliwia w eksperymentalny sposób zademonstrowanie prawa Bernoulliego. Układ wyposażony jest w dyszę
MECHANIKA PŁYNÓW Płyn
 MECHANIKA PŁYNÓW Płyn - Każda substancja, która może płynąć, tj. pod wpływem znikomo małych sił dowolnie zmieniać swój kształt w zależności od naczynia, w którym się znajduje, oraz może swobodnie się przemieszczać
MECHANIKA PŁYNÓW Płyn - Każda substancja, która może płynąć, tj. pod wpływem znikomo małych sił dowolnie zmieniać swój kształt w zależności od naczynia, w którym się znajduje, oraz może swobodnie się przemieszczać
Filtracja - zadania. Notatki w Internecie Podstawy mechaniki płynów materiały do ćwiczeń
 Zadanie 1 W urządzeniu do wyznaczania wartości współczynnika filtracji o powierzchni przekroju A = 0,4 m 2 umieszczono próbkę gruntu. Różnica poziomów h wody w piezometrach odległych o L = 1 m wynosi 0,1
Zadanie 1 W urządzeniu do wyznaczania wartości współczynnika filtracji o powierzchni przekroju A = 0,4 m 2 umieszczono próbkę gruntu. Różnica poziomów h wody w piezometrach odległych o L = 1 m wynosi 0,1
WYZNACZENIE WSPÓŁCZYNNIKA OPORU LINIOWEGO PRZEPŁYWU LAMINARNEGO
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 WYZNACZENIE WSPÓŁCZYNNIKA OPORU LINIOWEGO PRZEPŁYWU LAMINARNEGO 1. Cel ćwiczenia Doświadczalne wyznaczenie zaleŝności współczynnika oporu linioweo przepływu
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 WYZNACZENIE WSPÓŁCZYNNIKA OPORU LINIOWEGO PRZEPŁYWU LAMINARNEGO 1. Cel ćwiczenia Doświadczalne wyznaczenie zaleŝności współczynnika oporu linioweo przepływu
POMIAR STRUMIENIA PŁYNU ZA POMOCĄ ZWĘŻEK.
 POMIAR STRUMIENIA PŁYNU ZA POMOCĄ ZWĘŻEK. Strumieniem płynu nazywamy ilość płynu przepływającą przez przekrój kanału w jednostce czasu. Jeżeli ilość płynu jest wyrażona w jednostkach masy, to mówimy o
POMIAR STRUMIENIA PŁYNU ZA POMOCĄ ZWĘŻEK. Strumieniem płynu nazywamy ilość płynu przepływającą przez przekrój kanału w jednostce czasu. Jeżeli ilość płynu jest wyrażona w jednostkach masy, to mówimy o
Przepływ w korytach otwartych. kanał otwarty przepływ ze swobodną powierzchnią
 Przepływ w korytach otwartych kanał otwarty przepływ ze swobodną powierzchnią Przepływ w korytach otwartych Przewody otwarte dzielimy na: Naturalne rzeki strumienie potoki Sztuczne kanały komunikacyjne
Przepływ w korytach otwartych kanał otwarty przepływ ze swobodną powierzchnią Przepływ w korytach otwartych Przewody otwarte dzielimy na: Naturalne rzeki strumienie potoki Sztuczne kanały komunikacyjne
WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH
 WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH Pomiar strumienia masy i strumienia objętości metoda objętościowa, (1) q v V metoda masowa. (2) Obiekt badań Pomiar
WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH Pomiar strumienia masy i strumienia objętości metoda objętościowa, (1) q v V metoda masowa. (2) Obiekt badań Pomiar
Badania modelowe przelewu mierniczego
 LABORATORIUM MECHANIKI PŁYNÓW Badania modelowe przelewu mierniczego dr inż. Przemysław Trzciński ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZ. BMiP, PŁOCK Płock 2007 1. Cel ćwiczenia Celem
LABORATORIUM MECHANIKI PŁYNÓW Badania modelowe przelewu mierniczego dr inż. Przemysław Trzciński ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZ. BMiP, PŁOCK Płock 2007 1. Cel ćwiczenia Celem
dn dt C= d ( pv ) = d dt dt (nrt )= kt Przepływ gazu Pompowanie przez przewód o przewodności G zbiornik przewód pompa C A , p 1 , S , p 2 , S E C B
 Pompowanie przez przewód o przewodności G zbiornik przewód pompa C A, p 2, S E C B, p 1, S C [W] wydajność pompowania C= d ( pv ) = d dt dt (nrt )= kt dn dt dn / dt - ilość cząstek przepływających w ciągu
Pompowanie przez przewód o przewodności G zbiornik przewód pompa C A, p 2, S E C B, p 1, S C [W] wydajność pompowania C= d ( pv ) = d dt dt (nrt )= kt dn dt dn / dt - ilość cząstek przepływających w ciągu
J. Szantyr Wykład nr 26 Przepływy w przewodach zamkniętych II
 J. Szantyr Wykład nr 6 Przepływy w przewodach zamkniętych II W praktyce mamy do czynienia z mniej lub bardziej złożonymi rurociągami. Jeżeli strumień płynu nie ulega rozgałęzieniu, mówimy o rurociągu prostym.
J. Szantyr Wykład nr 6 Przepływy w przewodach zamkniętych II W praktyce mamy do czynienia z mniej lub bardziej złożonymi rurociągami. Jeżeli strumień płynu nie ulega rozgałęzieniu, mówimy o rurociągu prostym.
TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA
 Doświadczenie nr 1 TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA 1. Cel ćwiczenia Instrukcja dla studenta (opracowana przez dr Danutę Piwowarską ) Celem
Doświadczenie nr 1 TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA 1. Cel ćwiczenia Instrukcja dla studenta (opracowana przez dr Danutę Piwowarską ) Celem
Wyznaczanie charakterystyk przepływu cieczy przez przelewy
 Ć w i c z e n i e 1 Wyznaczanie charakterystyk przepływu cieczy przez przelewy 1. Wprowadzenie Cele ćwiczenia jest eksperyentalne wyznaczenie charakterystyk przelewu. Przelew ierniczy, czyli przegroda
Ć w i c z e n i e 1 Wyznaczanie charakterystyk przepływu cieczy przez przelewy 1. Wprowadzenie Cele ćwiczenia jest eksperyentalne wyznaczenie charakterystyk przelewu. Przelew ierniczy, czyli przegroda
PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
Rys.1. Zwężki znormalizowane: a) kryza, b) dysza, c) dysza Venturiego [2].
![Rys.1. Zwężki znormalizowane: a) kryza, b) dysza, c) dysza Venturiego [2]. Rys.1. Zwężki znormalizowane: a) kryza, b) dysza, c) dysza Venturiego [2].](/thumbs/54/35211555.jpg) WYZNACZANIE WSPÓŁCZYNNIKA PRZEPŁYWU W ZWĘŻKACH POMIAROWYCH DLA GAZÓW 1. Wprowadzenie Najbardziej rozpowszechnioną metodą pomiaru natężenia przepływu jest użycie elementów dławiących płyn. Stanowią one
WYZNACZANIE WSPÓŁCZYNNIKA PRZEPŁYWU W ZWĘŻKACH POMIAROWYCH DLA GAZÓW 1. Wprowadzenie Najbardziej rozpowszechnioną metodą pomiaru natężenia przepływu jest użycie elementów dławiących płyn. Stanowią one
J. Szantyr Wykład nr 27 Przepływy w kanałach otwartych I
 J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
prędkości przy przepływie przez kanał
 Ćwiczenie numer 5 Wyznaczanie rozkładu prędkości przy przepływie przez kanał 1. Wprowadzenie Stanowisko umożliwia w eksperymentalny sposób zademonstrowanie prawa Bernoulliego. Układ wyposażony jest w dyszę
Ćwiczenie numer 5 Wyznaczanie rozkładu prędkości przy przepływie przez kanał 1. Wprowadzenie Stanowisko umożliwia w eksperymentalny sposób zademonstrowanie prawa Bernoulliego. Układ wyposażony jest w dyszę
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI ĆWICZENIE NR 7 BADANIE POMPY II
 INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 7 BADANIE POMPY II 2 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i działaniem
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 7 BADANIE POMPY II 2 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i działaniem
1.10 Pomiar współczynnika lepkości cieczy metodą Poiseuille a(m15)
 66 Mechanika 1.10 Pomiar współczynnika lepkości cieczy metodą Poiseuille a(m15) Celem ćwiczenia jest wyznaczenie współczynnika lepkości wody. Współczynnik ten wyznaczany jest z prawa Poiseuille a na podstawie
66 Mechanika 1.10 Pomiar współczynnika lepkości cieczy metodą Poiseuille a(m15) Celem ćwiczenia jest wyznaczenie współczynnika lepkości wody. Współczynnik ten wyznaczany jest z prawa Poiseuille a na podstawie
Laboratorium. Hydrostatyczne Układy Napędowe
 Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
POLITECHNIKA WROCŁAWSKA, INSTYTUT INŻYNIERII BIOMEDYCZNEJ I POMIAROWEJ LABORATORIUM POMIARÓW WIELKOŚCI NIEELEKTRYCZNYCH I-21
 POLITECHNIKA WROCŁAWSKA, INSTYTUT INŻYNIERII BIOMEDYCZNEJ I POMIAROWEJ LABORATORIUM POMIARÓW WIELKOŚCI NIEELEKTRYCZNYCH I-21 Ćwiczenie nr 5. POMIARY NATĘŻENIA PRZEPŁYWU GAZÓW METODĄ ZWĘŻOWĄ 1. Cel ćwiczenia
POLITECHNIKA WROCŁAWSKA, INSTYTUT INŻYNIERII BIOMEDYCZNEJ I POMIAROWEJ LABORATORIUM POMIARÓW WIELKOŚCI NIEELEKTRYCZNYCH I-21 Ćwiczenie nr 5. POMIARY NATĘŻENIA PRZEPŁYWU GAZÓW METODĄ ZWĘŻOWĄ 1. Cel ćwiczenia
Gęstość i ciśnienie. Gęstość płynu jest równa. Gęstość jest wielkością skalarną; jej jednostką w układzie SI jest [kg/m 3 ]
![Gęstość i ciśnienie. Gęstość płynu jest równa. Gęstość jest wielkością skalarną; jej jednostką w układzie SI jest [kg/m 3 ] Gęstość i ciśnienie. Gęstość płynu jest równa. Gęstość jest wielkością skalarną; jej jednostką w układzie SI jest [kg/m 3 ]](/thumbs/62/48017275.jpg) Mechanika płynów Płyn każda substancja, która może płynąć, tj. dowolnie zmieniać swój kształt w zależności od naczynia, w którym się znajduje oraz może swobodnie się przemieszczać (przepływać), np. przepompowywana
Mechanika płynów Płyn każda substancja, która może płynąć, tj. dowolnie zmieniać swój kształt w zależności od naczynia, w którym się znajduje oraz może swobodnie się przemieszczać (przepływać), np. przepompowywana
1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8
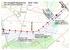 H h = 0,8H Przykładowe obliczenia odwodnienia autor: mgr inż. Marek Motylewicz strona 1 z 5 1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8 1:m1 1:m2 c Przyjęte parametry: rów o przekroju trapezowym
H h = 0,8H Przykładowe obliczenia odwodnienia autor: mgr inż. Marek Motylewicz strona 1 z 5 1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8 1:m1 1:m2 c Przyjęte parametry: rów o przekroju trapezowym
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN KATEDRA URZĄDZEŃ MECHATRONICZNYCH LABORATORIUM FIZYKI INSTRUKCJA
 POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN KATEDRA URZĄDZEŃ MECHATRONICZNYCH LABORATORIUM FIZYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 1 Temat: Wyznaczanie współczynnika
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN KATEDRA URZĄDZEŃ MECHATRONICZNYCH LABORATORIUM FIZYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 1 Temat: Wyznaczanie współczynnika
Zasada działania maszyny przepływowej.
 Zasada działania maszyny przepływowej. Przyrost ciśnienia statycznego. Rys. 1. Izotermiczny schemat wirnika maszyny przepływowej z kanałem miedzy łopatkowym. Na rys.1. pokazano schemat wirnika maszyny
Zasada działania maszyny przepływowej. Przyrost ciśnienia statycznego. Rys. 1. Izotermiczny schemat wirnika maszyny przepływowej z kanałem miedzy łopatkowym. Na rys.1. pokazano schemat wirnika maszyny
OBLICZENIA SILNIKA TURBINOWEGO ODRZUTOWEGO (rzeczywistego) PRACA W WARUNKACH STATYCZNYCH. Opracował. Dr inż. Robert Jakubowski
 OBLICZENIA SILNIKA TURBINOWEGO ODRZUTOWEGO (rzeczywistego) PRACA W WARUNKACH STATYCZNYCH DANE WEJŚCIOWE : Opracował Dr inż. Robert Jakubowski Parametry otoczenia p H, T H Spręż sprężarki, Temperatura gazów
OBLICZENIA SILNIKA TURBINOWEGO ODRZUTOWEGO (rzeczywistego) PRACA W WARUNKACH STATYCZNYCH DANE WEJŚCIOWE : Opracował Dr inż. Robert Jakubowski Parametry otoczenia p H, T H Spręż sprężarki, Temperatura gazów
Zapora ziemna analiza przepływu nieustalonego
 Przewodnik Inżyniera Nr 33 Aktualizacja: 01/2017 Zapora ziemna analiza przepływu nieustalonego Program: MES - przepływ wody Plik powiązany: Demo_manual_33.gmk Wprowadzenie Niniejszy Przewodnik przedstawia
Przewodnik Inżyniera Nr 33 Aktualizacja: 01/2017 Zapora ziemna analiza przepływu nieustalonego Program: MES - przepływ wody Plik powiązany: Demo_manual_33.gmk Wprowadzenie Niniejszy Przewodnik przedstawia
Parametry układu pompowego oraz jego bilans energetyczny
 Parametry układu pompowego oraz jego bilans energetyczny Układ pompowy Pompa może w zasadzie pracować tylko w połączeniu z przewodami i niezbędną armaturą, tworząc razem układ pompowy. W układzie tym pompa
Parametry układu pompowego oraz jego bilans energetyczny Układ pompowy Pompa może w zasadzie pracować tylko w połączeniu z przewodami i niezbędną armaturą, tworząc razem układ pompowy. W układzie tym pompa
PRZEPŁYW CIECZY W KORYCIE VENTURIEGO
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 9 PRZEPŁYW CIECZY W KORYCIE VENTURIEGO . Cel ćwiczenia Sporządzenie carakterystyki koryta Venturiego o przepływie rwącym i wyznaczenie średniej wartości współczynnika
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 9 PRZEPŁYW CIECZY W KORYCIE VENTURIEGO . Cel ćwiczenia Sporządzenie carakterystyki koryta Venturiego o przepływie rwącym i wyznaczenie średniej wartości współczynnika
WYKŁAD 11 POMPY I UKŁADY POMPOWE
 WYKŁAD 11 POMPY I UKŁADY POMPOWE Historia Czerpak do wody używany w Egipcie ok. 1500 r.p.n.e. Historia Nawadnianie pól w Chinach Historia Koło wodne używane w Rzymie Ogólna klasyfikacja pomp POMPY POMPY
WYKŁAD 11 POMPY I UKŁADY POMPOWE Historia Czerpak do wody używany w Egipcie ok. 1500 r.p.n.e. Historia Nawadnianie pól w Chinach Historia Koło wodne używane w Rzymie Ogólna klasyfikacja pomp POMPY POMPY
Ćwiczenie 2: Wyznaczanie gęstości i lepkości płynów nieniutonowskich
 Gęstość 1. Część teoretyczna Gęstość () cieczy w danej temperaturze definiowana jest jako iloraz jej masy (m) do objętości (V) jaką zajmuje: Gęstość wyrażana jest w jednostkach układu SI. Gęstość cieczy
Gęstość 1. Część teoretyczna Gęstość () cieczy w danej temperaturze definiowana jest jako iloraz jej masy (m) do objętości (V) jaką zajmuje: Gęstość wyrażana jest w jednostkach układu SI. Gęstość cieczy
SPRĘŻ WENTYLATORA stosunek ciśnienia statycznego bezwzględnego w płaszczyźnie
 DEFINICJE OGÓLNE I WIELKOŚCI CHARAKTERYSTYCZNE WENTYLATORA WENTYLATOR maszyna wirnikowa, która otrzymuje energię mechaniczną za pomocą jednego wirnika lub kilku wirników zaopatrzonych w łopatki, użytkuje
DEFINICJE OGÓLNE I WIELKOŚCI CHARAKTERYSTYCZNE WENTYLATORA WENTYLATOR maszyna wirnikowa, która otrzymuje energię mechaniczną za pomocą jednego wirnika lub kilku wirników zaopatrzonych w łopatki, użytkuje
Pomiar siły parcie na powierzchnie płaską
 Pomiar siły parcie na powierzchnie płaską Wydawać by się mogło, że pomiar wartości parcia na powierzchnie płaską jest technicznie trudne. Tak jest jeżeli wyobrazimy sobie pomiar na ściankę boczną naczynia
Pomiar siły parcie na powierzchnie płaską Wydawać by się mogło, że pomiar wartości parcia na powierzchnie płaską jest technicznie trudne. Tak jest jeżeli wyobrazimy sobie pomiar na ściankę boczną naczynia
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY
 ĆWICZENIE 10 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY Wprowadzenie W strudze przepływającej cieczy każdemu jej punktowi można przypisać prędkość będącą funkcją położenia r i r czasu V = V ( x y z t ).
ĆWICZENIE 10 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY Wprowadzenie W strudze przepływającej cieczy każdemu jej punktowi można przypisać prędkość będącą funkcją położenia r i r czasu V = V ( x y z t ).
Opory przepływu powietrza w instalacji wentylacyjnej
 Wentylacja i klimatyzacja 2 -ćwiczenia- Opory przepływu powietrza w instalacji wentylacyjnej Przepływ powietrza w przewodach wentylacyjnych Powietrze dostarczane jest do pomieszczeń oraz z nich usuwane
Wentylacja i klimatyzacja 2 -ćwiczenia- Opory przepływu powietrza w instalacji wentylacyjnej Przepływ powietrza w przewodach wentylacyjnych Powietrze dostarczane jest do pomieszczeń oraz z nich usuwane
09 - Dobór siłownika i zaworu. - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika
 - Dobór siłownika i zaworu - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika OPÓR PRZEPŁYWU W ZAWORZE Objętościowy współczynnik przepływu Qn Przepływ oblicza się jako stosunek
- Dobór siłownika i zaworu - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika OPÓR PRZEPŁYWU W ZAWORZE Objętościowy współczynnik przepływu Qn Przepływ oblicza się jako stosunek
Mechanika płynów : laboratorium / Jerzy Sawicki. Bydgoszcz, Spis treści. Wykaz waŝniejszych oznaczeń 8 Przedmowa
 Mechanika płynów : laboratorium / Jerzy Sawicki. Bydgoszcz, 2010 Spis treści Wykaz waŝniejszych oznaczeń 8 Przedmowa 1. POMIAR CIŚNIENIA ZA POMOCĄ MANOMETRÓW HYDROSTATYCZNYCH 11 1.1. Wprowadzenie 11 1.2.
Mechanika płynów : laboratorium / Jerzy Sawicki. Bydgoszcz, 2010 Spis treści Wykaz waŝniejszych oznaczeń 8 Przedmowa 1. POMIAR CIŚNIENIA ZA POMOCĄ MANOMETRÓW HYDROSTATYCZNYCH 11 1.1. Wprowadzenie 11 1.2.
1. Część teoretyczna. Przepływ jednofazowy przez złoże nieruchome i ruchome
 1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
LABORATORIUM MECHANIKI PŁYNÓW. Ćwiczenie N 2 RÓWNOWAGA WZGLĘDNA W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N RÓWNOWAGA WZGLĘDNA W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ . Cel ćwiczenia Pomiar współrzędnych powierzchni swobodnej w naczyniu cylindrycznym wirującym wokół
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N RÓWNOWAGA WZGLĘDNA W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ . Cel ćwiczenia Pomiar współrzędnych powierzchni swobodnej w naczyniu cylindrycznym wirującym wokół
Siatka spiętrzająca opis czujnika do pomiaru natężenia przepływu gazów. 1. Zasada działania. 2. Budowa siatki spiętrzającej.
 Siatka spiętrzająca opis czujnika do pomiaru natężenia przepływu gazów. 1. Zasada działania. Zasada działania siatki spiętrzającej oparta jest na teorii Bernoulliego, mówiącej że podczas przepływów płynów
Siatka spiętrzająca opis czujnika do pomiaru natężenia przepływu gazów. 1. Zasada działania. Zasada działania siatki spiętrzającej oparta jest na teorii Bernoulliego, mówiącej że podczas przepływów płynów
. Cel ćwiczenia Celem ćwiczenia jest porównanie na drodze obserwacji wizualnej przepływu laminarnego i turbulentnego, oraz wyznaczenie krytycznej licz
 ZAKŁAD MECHANIKI PŁYNÓW I AERODYNAMIKI ABORATORIUM MECHANIKI PŁYNÓW ĆWICZENIE NR DOŚWIADCZENIE REYNODSA: WYZNACZANIE KRYTYCZNEJ ICZBY REYNODSA opracował: Piotr Strzelczyk Rzeszów 997 . Cel ćwiczenia Celem
ZAKŁAD MECHANIKI PŁYNÓW I AERODYNAMIKI ABORATORIUM MECHANIKI PŁYNÓW ĆWICZENIE NR DOŚWIADCZENIE REYNODSA: WYZNACZANIE KRYTYCZNEJ ICZBY REYNODSA opracował: Piotr Strzelczyk Rzeszów 997 . Cel ćwiczenia Celem
WYDZIAŁ LABORATORIUM FIZYCZNE
 1 W S E i Z W WARSZAWIE WYDZIAŁ LABORATORIUM FIZYCZNE Ćwiczenie Nr 3 Temat: WYZNACZNIE WSPÓŁCZYNNIKA LEPKOŚCI METODĄ STOKESA Warszawa 2009 2 1. Podstawy fizyczne Zarówno przy przepływach płynów (ciecze
1 W S E i Z W WARSZAWIE WYDZIAŁ LABORATORIUM FIZYCZNE Ćwiczenie Nr 3 Temat: WYZNACZNIE WSPÓŁCZYNNIKA LEPKOŚCI METODĄ STOKESA Warszawa 2009 2 1. Podstawy fizyczne Zarówno przy przepływach płynów (ciecze
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 13: Współczynnik lepkości
 Nazwisko i imię: Zespół: Data: Ćwiczenie nr 13: Współczynnik lepkości Cel ćwiczenia: Wyznaczenie współczynnika lepkości gliceryny metodą Stokesa, zapoznanie się z własnościami cieczy lepkiej. Literatura
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 13: Współczynnik lepkości Cel ćwiczenia: Wyznaczenie współczynnika lepkości gliceryny metodą Stokesa, zapoznanie się z własnościami cieczy lepkiej. Literatura
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY NA PODSTAWIE PRAWA STOKESA
 ĆWICZENIE 8 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY NA PODSTAWIE PRAWA STOKESA Cel ćwiczenia: Badanie ruchu ciał spadających w ośrodku ciekłym, wyznaczenie współczynnika lepkości cieczy metodą Stokesa
ĆWICZENIE 8 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY NA PODSTAWIE PRAWA STOKESA Cel ćwiczenia: Badanie ruchu ciał spadających w ośrodku ciekłym, wyznaczenie współczynnika lepkości cieczy metodą Stokesa
Ćwiczenie 3: Wyznaczanie gęstości pozornej i porowatości złoża, przepływ gazu przez złoże suche, opory przepływu.
 1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ
 POLITECHNIKA BIAŁOSTOCKA Wydział Budownictwa i Inżynierii Środowiska Instrukcja do zajęć laboratoryjnych Temat ćwiczenia: POWIERZCHNIA SWOBODNA CIECZY W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ Ćwiczenie
POLITECHNIKA BIAŁOSTOCKA Wydział Budownictwa i Inżynierii Środowiska Instrukcja do zajęć laboratoryjnych Temat ćwiczenia: POWIERZCHNIA SWOBODNA CIECZY W NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ Ćwiczenie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Przygotowanie zadania sterowania do analizy i syntezy zestawienie schematu blokowego
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Przygotowanie zadania sterowania do analizy i syntezy zestawienie schematu blokowego
Laboratorium komputerowe z wybranych zagadnień mechaniki płynów
 FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
WNIKANIE CIEPŁA PRZY WRZENIU CIECZY
 WNIKANIE CIEPŁA PRZY WRZENIU CIECZY 1. Wprowadzenie Z wrzeniem cieczy jednoskładnikowej A mamy do czynienia wówczas, gdy proces przechodzenia cząstek cieczy w parę zachodzi w takiej temperaturze, w której
WNIKANIE CIEPŁA PRZY WRZENIU CIECZY 1. Wprowadzenie Z wrzeniem cieczy jednoskładnikowej A mamy do czynienia wówczas, gdy proces przechodzenia cząstek cieczy w parę zachodzi w takiej temperaturze, w której
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej
 Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
HYDROGEOLOGIA I UJĘCIA WODY. inż. Katarzyna Wartalska
 HYDROGEOLOGIA I UJĘCIA WODY -projektmgr inż. Katarzyna Wartalska rok akademicki 2016/2017 1. Wstęp 1.1. Przedmiot opracowania - należy podać co jest celem ćwiczenia projektowego: Przedmiotem opracowania
HYDROGEOLOGIA I UJĘCIA WODY -projektmgr inż. Katarzyna Wartalska rok akademicki 2016/2017 1. Wstęp 1.1. Przedmiot opracowania - należy podać co jest celem ćwiczenia projektowego: Przedmiotem opracowania
Wersja z dnia: Metoda piknometryczna jest metodą porównawczą. Wyznaczanie gęstości substancji ciekłych
 Wersja z dnia: 2008-02-25 Wyznaczanie gęstości metodą piknometryczną Gęstości ciała (ρ) jest definiowana jako masa (m) jednostkowej objętości tego ciała (V). Jeśli ciało jest jednorodne, to jego gęstość
Wersja z dnia: 2008-02-25 Wyznaczanie gęstości metodą piknometryczną Gęstości ciała (ρ) jest definiowana jako masa (m) jednostkowej objętości tego ciała (V). Jeśli ciało jest jednorodne, to jego gęstość
Ćwiczenie N 13 ROZKŁAD CIŚNIENIA WZDŁUś ZWĘśKI VENTURIEGO
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N ROZKŁAD CIŚNIENIA WZDŁUś ZWĘśKI VENTURIEGO . Cel ćwiczenia Doświadczalne wyznaczenie rozkładu ciśnienia piezometrycznego w zwęŝce Venturiego i porównanie go z
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N ROZKŁAD CIŚNIENIA WZDŁUś ZWĘśKI VENTURIEGO . Cel ćwiczenia Doświadczalne wyznaczenie rozkładu ciśnienia piezometrycznego w zwęŝce Venturiego i porównanie go z
Przewód wydatkujący po drodze
 Przewód wydatkujący po drodze Współczesne wodociągi, występujące w postaci mniej lub bardziej złożonych systemów obiektów służą do udostępniania wody o pożądanej jakości i w oczekiwanej ilości. Poszczególne
Przewód wydatkujący po drodze Współczesne wodociągi, występujące w postaci mniej lub bardziej złożonych systemów obiektów służą do udostępniania wody o pożądanej jakości i w oczekiwanej ilości. Poszczególne
STATYKA I DYNAMIKA PŁYNÓW (CIECZE I GAZY)
 STTYK I DYNMIK PŁYNÓW (CIECZE I GZY) Ciecz idealna: brak sprężystości postaci (czyli brak naprężeń ścinających) Ciecz rzeczywista małe naprężenia ścinające - lepkość F s F n Nawet najmniejsza siła F s
STTYK I DYNMIK PŁYNÓW (CIECZE I GZY) Ciecz idealna: brak sprężystości postaci (czyli brak naprężeń ścinających) Ciecz rzeczywista małe naprężenia ścinające - lepkość F s F n Nawet najmniejsza siła F s
Warszawa, dnia 9 sierpnia 2013 r. Poz. 906 ROZPORZĄDZENIE MINISTRA GOSPODARKI 1) z dnia 2 lipca 2013 r.
 DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 9 sierpnia 2013 r. Poz. 906 ROZPORZĄDZENIE MINISTRA GOSPODARKI 1) z dnia 2 lipca 2013 r. zmieniające rozporządzenie w sprawie wymagań, którym powinny
DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 9 sierpnia 2013 r. Poz. 906 ROZPORZĄDZENIE MINISTRA GOSPODARKI 1) z dnia 2 lipca 2013 r. zmieniające rozporządzenie w sprawie wymagań, którym powinny
S P I S R O Z D Z I A Ł Ó W,
 S P I S R O Z D Z I A Ł Ó W, str. 1-21 Wiadomości ogólne..... 3 HTDROSTATSKA. 2,0 22-28 Ciśnienie hydrostatyczne.. 20 29-33 Powierzchnia jednakowego ciśnienia /ekwipotencjalna/...42 34 Prawo Pascala..............
S P I S R O Z D Z I A Ł Ó W, str. 1-21 Wiadomości ogólne..... 3 HTDROSTATSKA. 2,0 22-28 Ciśnienie hydrostatyczne.. 20 29-33 Powierzchnia jednakowego ciśnienia /ekwipotencjalna/...42 34 Prawo Pascala..............
Człowiek najlepsza inwestycja FENIKS
 Człowiek najlepsza inwestycja ENIKS - długofalowy program odbudowy, popularyzacji i wspomagania fizyki w szkołach w celu rozwijania podstawowych kompetencji naukowo-technicznych, matematycznych i informatycznych
Człowiek najlepsza inwestycja ENIKS - długofalowy program odbudowy, popularyzacji i wspomagania fizyki w szkołach w celu rozwijania podstawowych kompetencji naukowo-technicznych, matematycznych i informatycznych
Wyznaczanie współczynnika sprężystości sprężyn i ich układów
 Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
III r. EiP (Technologia Chemiczna)
 AKADEMIA GÓRNICZO HUTNICZA WYDZIAŁ ENERGETYKI I PALIW III r. EiP (Technologia Chemiczna) INŻYNIERIA CHEMICZNA I PROCESOWA (przenoszenie pędu) Prof. dr hab. Leszek CZEPIRSKI Kontakt: A4, p. 424 Tel. 12
AKADEMIA GÓRNICZO HUTNICZA WYDZIAŁ ENERGETYKI I PALIW III r. EiP (Technologia Chemiczna) INŻYNIERIA CHEMICZNA I PROCESOWA (przenoszenie pędu) Prof. dr hab. Leszek CZEPIRSKI Kontakt: A4, p. 424 Tel. 12
Chłodnictwo i Kriogenika - Ćwiczenia Lista 4
 Chłodnictwo i Kriogenika - Ćwiczenia Lista 4 dr hab. inż. Bartosz Zajączkowski bartosz.zajaczkowski@pwr.edu.pl Politechnika Wrocławska Wydział Mechaniczno-Energetyczny Katedra Termodynamiki, Teorii Maszyn
Chłodnictwo i Kriogenika - Ćwiczenia Lista 4 dr hab. inż. Bartosz Zajączkowski bartosz.zajaczkowski@pwr.edu.pl Politechnika Wrocławska Wydział Mechaniczno-Energetyczny Katedra Termodynamiki, Teorii Maszyn
Pomiar natężenia przepływu płynów ściśliwych metodą zwężki pomiarowej
 Politechnika Lubelska i Napędów Lotniczych Instrukcja laboratoryjna Pomiar natężenia przepływu płynów ściśliwych metodą zwężki pomiarowej 016 /. Cel ćwiczenia Celem ćwiczenia jest poznanie zasady pomiarów
Politechnika Lubelska i Napędów Lotniczych Instrukcja laboratoryjna Pomiar natężenia przepływu płynów ściśliwych metodą zwężki pomiarowej 016 /. Cel ćwiczenia Celem ćwiczenia jest poznanie zasady pomiarów
LABORATORIUM TERMODYNAMIKI I TECHNIKI CIEPLNEJ. Badanie charakterystyki wentylatorów połączenie równoległe i szeregowe. dr inż.
 LABORATORIUM TERMODYNAMIKI I TECHNIKI CIEPLNEJ Badanie charakterystyki wentylatorów połączenie równoległe i szeregowe. dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZIAŁ
LABORATORIUM TERMODYNAMIKI I TECHNIKI CIEPLNEJ Badanie charakterystyki wentylatorów połączenie równoległe i szeregowe. dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA WYDZIAŁ
ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ
 ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ 1. Cel i zakres ćwiczenia Celem ćwiczenia jest opanowanie umiejętności dokonywania pomiarów parametrów roboczych układu pompowego. Zapoznanie z budową
ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ 1. Cel i zakres ćwiczenia Celem ćwiczenia jest opanowanie umiejętności dokonywania pomiarów parametrów roboczych układu pompowego. Zapoznanie z budową
BADANIE PRZELEWU MIERNICZEGO
 BADANIE PRZELEWU MIERNICZEGO Pytania zaliczające: 1. Pomiar przepływu za pomocą jednego z przelewów mierniczych. 2. Charakterystyka przelewu mierniczego. METODA PRZELEWOWA bezpośrednia metoda pomiaru przepływu;
BADANIE PRZELEWU MIERNICZEGO Pytania zaliczające: 1. Pomiar przepływu za pomocą jednego z przelewów mierniczych. 2. Charakterystyka przelewu mierniczego. METODA PRZELEWOWA bezpośrednia metoda pomiaru przepływu;
OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH
 ĆWICZENIE II OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą określania oporów przepływu w przewodach. 2. LITERATURA 1. Informacje z wykładów i ćwiczęń
ĆWICZENIE II OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą określania oporów przepływu w przewodach. 2. LITERATURA 1. Informacje z wykładów i ćwiczęń
Ćwiczenie 2: Wyznaczanie gęstości i lepkości płynów. Rodzaje przepływów.
 Ćwiczenie : Wyznaczanie gęstości i lepkości płynów. Rodzaje przepływów. Gęstość 1. Część teoretyczna Gęstość () cieczy w danej temperaturze definiowana jest jako iloraz jej masy (m) do objętości (V) jaką
Ćwiczenie : Wyznaczanie gęstości i lepkości płynów. Rodzaje przepływów. Gęstość 1. Część teoretyczna Gęstość () cieczy w danej temperaturze definiowana jest jako iloraz jej masy (m) do objętości (V) jaką
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia III. Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
POLITECHNIKA ŁÓDZKA INSTRUKCJA Z LABORATORIUM W ZAKŁADZIE BIOFIZYKI. Ćwiczenie 5 POMIAR WZGLĘDNEJ LEPKOŚCI CIECZY PRZY UŻYCIU
 POLITECHNIKA ŁÓDZKA INSTRUKCJA Z LABORATORIUM W ZAKŁADZIE BIOFIZYKI Ćwiczenie 5 POMIAR WZGLĘDNEJ LEPKOŚCI CIECZY PRZY UŻYCIU WISKOZYMETRU KAPILARNEGO I. WSTĘP TEORETYCZNY Ciecze pod względem struktury
POLITECHNIKA ŁÓDZKA INSTRUKCJA Z LABORATORIUM W ZAKŁADZIE BIOFIZYKI Ćwiczenie 5 POMIAR WZGLĘDNEJ LEPKOŚCI CIECZY PRZY UŻYCIU WISKOZYMETRU KAPILARNEGO I. WSTĘP TEORETYCZNY Ciecze pod względem struktury
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Praca domowa nr 2. Kinematyka. Dynamika. Nieinercjalne układy odniesienia.
 Praca domowa nr 2. Kinematyka. Dynamika. Nieinercjalne układy odniesienia. Grupa 1. Kinematyka 1. W ciągu dwóch sekund od wystrzelenia z powierzchni ziemi pocisk przemieścił się o 40 m w poziomie i o 53
Praca domowa nr 2. Kinematyka. Dynamika. Nieinercjalne układy odniesienia. Grupa 1. Kinematyka 1. W ciągu dwóch sekund od wystrzelenia z powierzchni ziemi pocisk przemieścił się o 40 m w poziomie i o 53
Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości
 Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości a) metoda rachunkowa Po wykreśleniu przekroju poprzecznego z zaznaczeniem pionów hydrometrycznych, w których dokonano punktowego
Obliczenie objętości przepływu na podstawie wyników punktowych pomiarów prędkości a) metoda rachunkowa Po wykreśleniu przekroju poprzecznego z zaznaczeniem pionów hydrometrycznych, w których dokonano punktowego
WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ
 WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ Instrukcja do ćwiczenia T-06 Temat: Wyznaczanie zmiany entropii ciała
WOJSKOWA AKADEMIA TECHNICZNA Wydział Mechaniczny Katedra Pojazdów Mechanicznych i Transportu LABORATORIUM TERMODYNAMIKI TECHNICZNEJ Instrukcja do ćwiczenia T-06 Temat: Wyznaczanie zmiany entropii ciała
Pomiar pompy wirowej
 Pomiar pompy wirowej Instrukcja do ćwiczenia nr 20 Badanie maszyn - laboratorium Opracował: dr inŝ. Andrzej Tatarek Zakład Miernictwa i Ochrony Atmosfery Wrocław, grudzień 2006 r. 1. Wstęp Pompami nazywamy
Pomiar pompy wirowej Instrukcja do ćwiczenia nr 20 Badanie maszyn - laboratorium Opracował: dr inŝ. Andrzej Tatarek Zakład Miernictwa i Ochrony Atmosfery Wrocław, grudzień 2006 r. 1. Wstęp Pompami nazywamy
MECHANIKA PŁYNÓW LABORATORIUM
 MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 7 Waga hydrostatyczna, wypór. Cele ćwiczenia jest wyznaczenie gęstości ciał stałych za poocą wagi hydrostatycznej i porównanie tej etody z etodai, w których ierzona
MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 7 Waga hydrostatyczna, wypór. Cele ćwiczenia jest wyznaczenie gęstości ciał stałych za poocą wagi hydrostatycznej i porównanie tej etody z etodai, w których ierzona
Ćw. M 12 Pomiar współczynnika lepkości cieczy metodą Stokesa i za pomocą wiskozymetru Ostwalda.
 Ćw. M 12 Pomiar współczynnika lepkości cieczy metodą Stokesa i za pomocą wiskozymetru Ostwalda. Zagadnienia: Oddziaływania międzycząsteczkowe. Ciecze idealne i rzeczywiste. Zjawisko lepkości. Równanie
Ćw. M 12 Pomiar współczynnika lepkości cieczy metodą Stokesa i za pomocą wiskozymetru Ostwalda. Zagadnienia: Oddziaływania międzycząsteczkowe. Ciecze idealne i rzeczywiste. Zjawisko lepkości. Równanie
OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH
 ĆWICZENIE II OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą określania oporów przepływu w przewodach. 2. LITERATURA 1. Informacje z wykładów i ćwiczeń
ĆWICZENIE II OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą określania oporów przepływu w przewodach. 2. LITERATURA 1. Informacje z wykładów i ćwiczeń
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
Hydrostatyczne Układy Napędowe Laboratorium
 Hydrostatyczne Układy Napędowe Laboratorium Temat: Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracował: Z. Kudźma, P. Osiński, J. Rutański, M. Stosiak CEL
Hydrostatyczne Układy Napędowe Laboratorium Temat: Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracował: Z. Kudźma, P. Osiński, J. Rutański, M. Stosiak CEL
z nastawnymi łopatkami kierującymi Typu TDV-SilentAIR Zalecane do stosowania w pomieszczeniach o wysokości od ok. 2,6 do 4,0 m
 2/7.1/PL/6 Nawiewniki wirowe z nastawnymi łopatkami kierującymi Typu TDV-SilentAIR Zalecane do stosowania w pomieszczeniach o wysokości od ok. 2,6 do 4,0 m TROX AUSTRIA GmbH (Sp. z o.o.) Oddział w Polsce
2/7.1/PL/6 Nawiewniki wirowe z nastawnymi łopatkami kierującymi Typu TDV-SilentAIR Zalecane do stosowania w pomieszczeniach o wysokości od ok. 2,6 do 4,0 m TROX AUSTRIA GmbH (Sp. z o.o.) Oddział w Polsce
BADANIA W INSTALACJACH WENTYLACYJNYCH
 ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA W INSTALACJACH WENTYLACYJNYCH 1 WSTĘP Stanowisko laboratoryjne poświęcone badaniom instalacji wentylacyjnej zlokalizowane jest w pomieszczeniu
ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA W INSTALACJACH WENTYLACYJNYCH 1 WSTĘP Stanowisko laboratoryjne poświęcone badaniom instalacji wentylacyjnej zlokalizowane jest w pomieszczeniu
RÓWNANIE MOMENTÓW PĘDU STRUMIENIA
 RÓWNANIE MOMENTÓW PĘDU STRUMIENIA Przepływ osiowo-symetryczny ustalony to przepływ, w którym parametry nie zmieniają się wzdłuż okręgów o promieniu r, czyli zależą od promienia r i długości z, a nie od
RÓWNANIE MOMENTÓW PĘDU STRUMIENIA Przepływ osiowo-symetryczny ustalony to przepływ, w którym parametry nie zmieniają się wzdłuż okręgów o promieniu r, czyli zależą od promienia r i długości z, a nie od
Ćwiczenie Nr 2. Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów
 Ćwiczenie Nr 2 Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów 1. Wprowadzenie Sterowanie prędkością tłoczyska siłownika lub wału silnika hydraulicznego
Ćwiczenie Nr 2 Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów 1. Wprowadzenie Sterowanie prędkością tłoczyska siłownika lub wału silnika hydraulicznego
PL B1. Sposób i reaktor do oczyszczania gazów, zwłaszcza spalinowych, z zanieczyszczeń gazowych, zwłaszcza kwaśnych
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204324 (13) B1 (21) Numer zgłoszenia: 376908 (51) Int.Cl. B01D 53/34 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 05.09.2005
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204324 (13) B1 (21) Numer zgłoszenia: 376908 (51) Int.Cl. B01D 53/34 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 05.09.2005
BADANIE WYMIENNIKÓW CIEPŁA
 1.Wprowadzenie DNIE WYMIENNIKÓW CIEPŁ a) PŁSZCZOWO-RUROWEGO b) WĘŻOWNICOWEGO adanie wymiennika ciepła sprowadza się do pomiaru współczynników przenikania ciepła k w szerokim zakresie zmian parametrów ruchowych,
1.Wprowadzenie DNIE WYMIENNIKÓW CIEPŁ a) PŁSZCZOWO-RUROWEGO b) WĘŻOWNICOWEGO adanie wymiennika ciepła sprowadza się do pomiaru współczynników przenikania ciepła k w szerokim zakresie zmian parametrów ruchowych,
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej
 Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej - - Wstęp teoretyczny Jednym ze sposobów wymiany ciepła jest przewodzenie.
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie współczynnika przenikania ciepła dla przegrody płaskiej - - Wstęp teoretyczny Jednym ze sposobów wymiany ciepła jest przewodzenie.
ĆWICZENIE I POMIAR STRUMIENIA OBJĘTOŚCI POWIETRZA. OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH
 ĆWICZENIE I POMIAR STRUMIENIA OBJĘTOŚCI POWIETRZA. OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą pomiaru strumienia objętości powietrza przy pomocy
ĆWICZENIE I POMIAR STRUMIENIA OBJĘTOŚCI POWIETRZA. OPORY PRZEPŁYWU PRZEWODÓW WENTYLACYJNYCH CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z metodą pomiaru strumienia objętości powietrza przy pomocy
Straty energii podczas przepływu wody przez rurociąg
 1. Wprowadzenie Ć w i c z e n i e 11 Straty energii podczas przepływu wody przez rurociąg Celem ćwiczenia jest praktyczne wyznaczenie współczynników strat liniowych i miejscowych podczas przepływu wody
1. Wprowadzenie Ć w i c z e n i e 11 Straty energii podczas przepływu wody przez rurociąg Celem ćwiczenia jest praktyczne wyznaczenie współczynników strat liniowych i miejscowych podczas przepływu wody
