Kurs komputerowy T. System składu publikacji LATEX. c Sławomir Zelek
|
|
|
- Angelika Kozłowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Kurs komputerowy T System składu publikacji LATEX c Sławomir Zelek
2 Środowisko picture \begin{picture}(szer,wys)(x,y) tekst \end{picture} \unitlengthwymiar ustala wielkość jednostki \thicklines ustala grubość linii (grubsze) \thinlines ustala grubość linii (cieńsze, domyślnie) \linethicknes{wymiar} ustala grubość linii poziomych i pionowych \put(x,y){obiekt} umieszcza w punkcie (x,y) obiekt; punktem odniesienia jest lewy dolny narożnik \multiput(x,y)(dx,dy){n}{obiekt} n razy umieszcza obiekt w punktach o wsp. (x,y), (x+dx,y+dy)... \makebox(długość,wysokość) [lrtb] {tekst} umieszcza tekst w pudełku o podanych wymiarach \framebox(długość,wysokość) [lrtb] {tekst} umieszcza tekst w ramce o podanych wymiarach \dashbox{d}(długość,wysokość)[lrtb] {tekst} umieszcza tekst w przerywanej ramce o podanych wymiarach; d jest długością kreski i przerwy \savebox{\nazwa}(długość,wysokość)[lcr] {tekst} definiuje szufladę nazwa o podanych wymiarach \shortstack[lr] {tekst} umieszcza tekst w jednokolumnowej tabeli maksymalnie jeden z lr i jeden z tb jeden z wymienionych długość, wysokość, oraz x i y są wielkościami wyrażonymi w jednostkach unitlength c Sławomir Zelek 39
3 Środowisko picture \qbezier[n](x,y )(x,y )(x 3,y 3 ) \line(x,y){długość} \vector(x,y){długość} \circle{promień} \circle*{promień} \oval(szerokość,wysokość)[lrtb] rysuje krzywą Bezier; n określa ilość punktów w całej krzywej rysuje linię o nachyleniu arc tg x/y o podanej długości (długość jest długością rzutu na oś poziomą) x oraz y są liczbami całkowitymi z zakresu 6 6 bez wspólnych dzielników; minimalna długość linii 3mm rysuje wektor o nachyleniu arc tg x/y o podanej długości (j.w.); x oraz y są liczbami całkowitymi z zakresu 4 4 bez wspólnych dzielników rysuje okrąg o podanym promieniu (max. 4 mm) rysuje koło o podanym promieniu (max. 5. mm) rysuje prostokąt o zaokrąglonych rogach l,r,t,b określa, która część owalu ma być rysowana (lewa, prawa, górna, dolna); promień zaokrągleń jest połową krótszego boku c Sławomir Zelek 4
4 Środowisko picture ograniczenia nachylenia linii największy okrąg linie standardowe nachylenia wektorów 7 największe koło linie pogrubione c Sławomir Zelek 4
5 Środowisko picture przykład B mb D RDB A m A RKA S RCB R KB RCA β D γ K RK RD ϕ m C C Rysunek : Definicja współrzędnych walencyjnych ( RCA, RCB, ϕ), Jacobiego ( RCA, RDB, γ) oraz Radau ( RKA, RKB, β) dla trójatomowej cząsteczki ACB c Sławomir Zelek 4
6 Środowisko picture źródło przykładu \begin{figure}[h] \begin{center}\begin{picture}(,5.8) \put(,4){\circle*{.}}\put(.5,4.){a} \put(5,){\circle*{.}}\put(5.,-.){c} \put(9,6){\circle*{.}}\put(9.,6.){b} \put(5,){\circle*{.}}\put(5.,.8){k} \put(3,){\circle*{.}}\put(.6,.6){d} \put(5,5){\circle*{.}}\put(4.8,5.){$d_$} \put(5,3){\circle*{.}}\put(4.6,.8){s} \put(.5,3.5){$m_a$}\put(4.4,-.3){$m_c$} \put(9.,5.5){$m_b$} \put(5,){\vector(-,){}} \put(3,){\vector(-,){}} \put(5,){\vector(,3){4}} \put(5,){\vector(,){4}} \put(3,){\vector(3,){6}} \put(5,){\vector(,){}} \put(5,){\vector(-,){4}} \put(.5,.4){\ve{r}{ca}} \put(8.,3.6){\ve{r}{cb}} \put(3.5,.5){\ve{r}{d}} \put(4.4,.){\ve{r}{k}} \put(.5,3.5){\ve{r}{ka}} \put(5.,3.){\ve{r}{kb}} \put(5.7,4.5){\ve{r}{db}} \put(4.8,.4){$\varphi$} \bezier{}(4.5,.5)(5,.8)(5.35,.55) \put(4.9,.){$\beta$}\put(3.,.9){$\gamma$} \bezier{}(4.,.4)(4.9,.7)(5.5,.5) \bezier{}(3.5,.5)(3.8,.)(3.5,.3) \end{picture}\end{center} \caption{definicja współrzędnych walencyjnych (\ve{r}{ca}, \ve{r}{cb}, $\varphi$), Jacobiego (\ve{r}{ca}, \ve{r}{db}, $\gamma$) oraz Radau (\ve{r}{ka}, \ve{r}{kb}, $\beta$) dla trójatomowej cząsteczki ACB} \end{figure} c Sławomir Zelek 43
7 Pakiet pstricks kolory szare kolorowe \black czarny \red czerwony \darkgray ciemnoszary \green zielony \gray szary \blue niebieski \lightgray jasnoszary \cyan błękitny \white biały \magenta fioletowy \yellow żółty \newgray{kolor}{n} definiuje kolor o odpowiednim stopniu jasności n \newrgbcolor{kolor}{n n n 3 } definiuje kolor w konwencji red green blue \newhsbcolor{kolor}{n n n 3 } definiuje kolor w konwencji hue saturation brightness \newcmykcolor{kolor}{n n n 3 n 4 }definiuje kolor w konwencji cyan magenta yellow black n i c Sławomir Zelek 44
8 Pakiet pstricks parametry graficzne \psset{par =wart,par =wart } ustawianie globalnych wartości poszczególnym parametrom (np. grubość linii, kolor, itp.). Niezależnie od wartości globalnych można chwilowo zmienić wartości parametrów dla poszczególnych poleceń unit=jednostka cm ustawia wielkość jednostki xunit=jednostka cm ustawia wielkość jednostki poziomej yunit=jednostka cm ustawia wielkość jednostki pionowej runit=jednostka cm ustawia wielkość pozostałych jednostek linewidth=grubość.8pt ustawia grubość linii linecolor=kolor black ustawia kolor linii fillstyle=styl none ustawia odpowiedni styl wypełnienia fillcolor=kolor white ustawia kolor wypełnienia arrows=strzałka - ustawia styl strzałki showpoints=wart. logiczna false określa rysowanie punktów na linii linearc=promień pt promień zaokrąglenia wierzchołków framearc=liczba promień zaokrąglenia wierzchołków określony jako liczba*szerokość (wysokość) ramki; liczba jest z przedziału <, > c Sławomir Zelek 45
9 Pakiet pstricks podstawowe obiekty \psline* [parametry ]{strzałka}(x,y )(x,y )... \psline(,) \psline{->}(5,)(,)(3,) \psline*[linearc=.5cm](6,)(,)(4,) \qline(x,y )(x,y ) \qline(,)(,) \pspolygon* [parametry ](x,y )(x,y )(x,y )... \pspolygon[linearc=.cm](,)(,) \pspolygon*[linearc=.cm](,)(,)(3,)(3,) \pspolygon*(3,)(3.4,)(4,)(5,)(5.5,)(6,) obowiązkowe elementy są pogrubione; pozostałe można pominąć wówczas przyjmowane są wartości domyślne strzałka sposób zakończenia linii (grot strzałki); domyślnie brak strzałki (x,y ) punkt początkowy; domyślnie punkt (,) c Sławomir Zelek 46
10 Pakiet pstricks podstawowe obiekty \psframe* [parametry ](x,y )(x,y ) \psframe[fillstyle=solid,fillcolor=lightgray] (,)(4,) \psframe*[linecolor=white,framearc=.] (,.5)(,.5) \pscircle* [parametry](x,y ){promień} \pscircle{} \pscircle*(.5,.5){.5} \qdisk(x,y ){promień} równoważne poleceniu \pscircle*(x,y){promień} c Sławomir Zelek 47
11 Pakiet pstricks podstawowe obiekty \pswedge* [parametry ](x,y ){promień}{kąt }{kąt } \pswedge[fillstyle=solid]{}{}{75} \pswedge*(,){}{3}{9} \pswedge(5,){}{8}{} \psellipse* [parametry ](x,y )(x,y ) \psellipse(,)(,) \psellipse*(3,)(,.5) \psellipse[fillstyle=solid](3,)(.5,.5) \psarc* [parametry ]{strzałka}(x,y ){promień}{kąt }{kąt }łuk rysowany przeciwnie \psarcn* [parametry ]{strzałka}(x,y ){promień}{kąt }{kąt }zgodnie z ruchem wskazówek zegara \psarc[showpoints=true]{->}(.5,.5){.5}{5}{} \psarc*(4,){}{}{35} \psarc[arcsepa=](4,){}{8}{} \psarcn[arcsepb=]{->}(5,){}{-9}{9} arcsepa=odległość arcsepb=odległość arcsep=odległość połowa grubości ramienia A połowa grubości ramienia B połowa grubości obu ramieni c Sławomir Zelek 48
12 Kurs T: Pakiet pstricks podstawowe obiekty \psbezier* [parametry ]{strzałka}(x,y )(x,y )(x,y )(x 3,y 3 ) \psbezier[showpoints=true]{->}(,)(.5,)(,)(,) \psbezier*(,)(.5,)(3.5,)(4,) \psbezier[showpoints=true](4,)(5.5,)(6,)(5,) \pscurve* [parametry ]{strzałka}(x,y )... \pscurve[showpoints=true]{<->}(,.3)(.7,.8) (3,.3)(3.8,.6)(.4,.4) \pscurve{->}(3,)(4,)(5,)(4,)(3,) \psecurve* [parametry ]{strzałka}(x,y )... \psecurve[showpoints=true]{<->}(,.3)(.7,.8) (3,.3)(3.8,.6)(.4,.4) \psecurve{->}(3,)(4,)(5,)(4,)(3,) \psccurve* [parametry ](x,y )... \psccurve[showpoints=true](,.3)(.7,.8) (3,.3)(3.8,.6)(.4,.4) \psccurve(3,)(4,)(5,)(4,)(3,) c Sławomir Zelek 49
13 Kurs T: Pakiet pstricks podstawowe obiekty \parabola* [parametry ]{strzałka}(x,y )(x,y ) \parabola{->}(,)(,) \parabola*(,)(,) \parabola(,)(,) dotstyle=styl * 3 4 styl * o przykład styl square square* pentagon pentagon* przykład triangle triangle* dotsize=wymiar n.5pt.5 określa wielkość punktu (n linewidth + wymiar) dotscale=n n skalowanie w poziomie (n ) i pionie (n ) dotangle=kąt obraca znacznik o kąt \psdots* [parametry ](x,y )... rysuje punkty dla każdej pary wsp. c Sławomir Zelek 5
14 Pakiet pstricks przykład k j K ı N I θ ϕ χ N θ J Rysunek : Definicja kątów Eulera: ( I, J, K) są wersorami układu LFS, natomiast ( ı, j, k ) wersorami układu MFS. Linia NN jest linią węzłów c Sławomir Zelek 5
15 Pakiet pstricks źródło przykładu \begin{figure}[!b] \begin{center} \begin{picture}(.,8.) \psset{linewidth=pt} \psline{->}(5.,4.)(3.,.7) \put(.8,.){\ve{i}{}} \psline{->}(5.,4.)(9.,4.) \put(9.,3.8){\ve{j}{}} \psline{->}(5.,4.)(5.,8.) \put(5.,7.5){\ve{k}{}} \psset{linestyle=dashed,dash=4pt pt} \psline{->}(5.,4.)(7.4,6.) \put(7.6,5.8){\ve{\imath}{}} \psline{->}(5.,4.)(3.7,6.5) \put(3.4,6.6){\ve{\jmath}{}} \psline{->}(5.,4.)(.5,6.5) \put(.3,6.6){\ve{k}{}} \rput{7}(5.,4.){ \psellipse[linewidth=.5pt](,)(3.5,.5)} \psset{linewidth=.5pt,linestyle=solid} \psellipse(5.,4.)(4.,.5) \psline{-}(.85,5.5)(7.5,.75) \psbezier{->}(4.,3.4)(4.6,3.)(5.6,3.3) (5.9,3.5)\put(5.,3.){$\varphi$} \psbezier{->}(8.,3.)(8.,3.4)(7.9,3.7) (7.5,3.8)\put(8.,3.4){$\theta$} \psbezier{->}(5.,4.7)(4.8,4.8)(4.5,4.7) (4.4,4.6)\put(4.7,4.8){$\theta$} \psbezier{->}(6.,3.4)(6.3,3.7)(6.3,4.4) (5.9,4.8)\put(6.3,4.){$\chi$} \put(7.3,.4){$n$}\put(.4,5.4){$n $} \end{picture} \caption{definicja kątów Eulera: (\ve{i}{}, \ve{j}{}, \ve{k}{}) są wersorami układu LFS, natomiast (\ve{\imath}{}, \ve{\jmath}{}, \ve{k}{})~---~wersorami układu MFS. Linia $NN $ jest linią węzłów} \end{center} \end{figure} c Sławomir Zelek 5
16 Kurs T: Pakiet pstricks przykład HOMO } } 3πu LUMO αo S O [ ] ɛ [E H ].5 6b 5σu 9a 5b 6σg. a 3b 4b 3πu -.5 πg 8a πu 4σu 7a b Rysunek 3: Diagram Walsha dla obojętnej cząsteczki SO c Sławomir Zelek 53
17 Pakiet pstricks wyciąg ze źródła przykładu \begin{figure}[!p] \begin{picture}(5,)(,-) \psset{unit=cm,dotscale=.5,linewidth=.pt}... \psecurve{-}(.46,-.86)(.9,.8)(3.38,.7) (3.83,.4)(4.9,.47)(4.75,.73)(5.,.96) (5.67,.97)(6.,.4)(7.5,.5)(8.88,.6) (.5,.)(.6,.8)(3.,.8)(3.,.8) \psdots[dotstyle=o](3.38,.7)(4.75,.73) (5.,.96)(5.67,.97)(6.,.4)(7.5,.5) (8.88,.6)(.5,.)(.6,.8)(3.,.8)... \psecurve{->}(.,6.)(.,6.)... (3.,.77)(4.,.7)(4.5,.67) \psdots[dotstyle=triangle](.,6.)...(3.,.77) \psecurve{-}(.,6.53)(.,6.53)(3.38,6.73) (4.75,7.3)(5.,7.4)(5.67,7.3) \psline[linestyle=dashed,dash=pt 6pt](5.,7.4) (5.67,.73) \psecurve{->}(5.67,.73)(5.67,.73)...(4.5,.44) \psdots[dotstyle=triangle*](.,6.53)(3.38,6.73)...(.6,.38)(3.,.43)... \psline{->}(3.5,4.)(4.,4.) \put(3.,4.){$\left.\begin{picture}(,.) \end{picture}\right\}$}... \psecurve[linewidth=.pt]{-}(.,8.84)(.,8.84) (.5,8.55)...(4.5,6.46) \put(3.7,6.6){homo} \psecurve[linewidth=.pt,linestyle=dashed,dash=5pt 6pt] (.,4.54)(.,4.54)...(4.,.4)(4.5,.4) \put(3.7,.7){lumo} %OSIE \psset{linewidth=.pt}\psline{->}(.,.)(5.,.) \psline{->}(.,.)(.,.) \multiput(.,)(.75,){5}{\line(,-){.}} \put(.75,-.7){3}...\put(.65,-.7){5} \put(3.,.){$\alpha_{o-s-o}\ [^{\circ}]$} \put(.4,9.8){$\epsilon$}\put(-.3,9.){[\eh]} \multiput(.,4.7)(,7.){3}{\line(-,){.}} \put(-.,4.7){\makebox(.8,)[r]{-.5}}... \put(4.,.3){$\pi_u$}\put(4.,4.){$\pi_g$} \put(4.,5.86){$3\pi_{u_\parallel}$} \end{picture} \caption{diagram Walsha dla obojętnej cząsteczki SO$_$} \end{figure} c Sławomir Zelek 54
18 Pakiet pstricks siatka \psgrid[parametry ](x,y )(x,y )(x,y ) gridwidth=grubość.8pt określa grubość linii siatki gridcolor=kolor black określa kolor linii griddots=n n = linia ciągła; n > linia kropkowana (n kropek na jednostkę) gridlabels=wielkość pt określa wielkość opisu jednostek gridlabelcolor=kolor black określa kolor opisu jednostek subgriddiv=n 5 subgridwidth=grubość.4pt grubość podrzędnych linii siatki subgridcolor=kolor gray określa kolor podrzędnych linii siatki subgriddots=n analogicznie jak griddots c Sławomir Zelek 55
19 Pakiet pstricks siatki \psgrid(,)(5,) [subgriddiv=] [griddots=, subgriddiv=] [gridwidth=.pt, subgriddiv=5] [gridlabels=6pt] [gridcolor=red, gridlabelcolor=red] [subgriddiv=5, subgriddots=3] [gridcolor=blue, subgridcolor=red]... c Sławomir Zelek 56
20 Pakiet pstricks strzałki strzałka przykład strzałka przykład - (-) <-> o-o >-< *-* <<->> oo-oo >>-<< **-** - c-c *- * cc-cc [-] C-C c Sławomir Zelek 57
21 Pakiet pstricks inne \newpsobject{nazwa}{obiekt}{par=wart,...} definiuje nowy obiekt nazwa na bazie obiektu z odpowiednimi parametrami \newpsstyle{nazwa}{par=wart,...} definiuje nowy styl nazwa jako zbiór odpowiednich wartości parametrów linestyle=styl solid określa styl linii spośród: none, solid, dashed i dotted dash=dł dł 5pt 3pt określa długość kreski i przerwy dotsep=odstęp 3pt określa odstęp między kropkami doubleline=wart. logiczna false określa rysowanie linią pojedynczą lub podwójną doublesep=odległość.5linewidth określa odstęp między liniami doublecolor=kolor white określa kolor między liniami shadow=wart. log. false określa rysowanie cienia shadowsize=odległość 3pt określa odległość cienia od obiektu shadowangle=kąt -45 określa kąt umieszczenia cienia shadowcolor=kolor darkgray określa kolor cienia c Sławomir Zelek 58
22 Pakiet pstricks inne \psline[linestyle=dotted](,.)(5,.) \psline[linestyle=dotted,dotsep=pt](,.)(5,.) \psline[linestyle=dashed](,.)(5,.) \psline[linestyle=dashed,dash=pt pt](,.) (5,.) \psline[doubleline=true](,)(,)(3,) \psline[doubleline=true,doublesep=5pt](,)(,)(3,) \psline[doubleline=true,doublesep=5pt, doublecolor=red](,)(,)(3,) \pscircle[shadow=true](,){.5} \psframe[shadow=true,shadowangle=35](,)(4,) \psframe[shadow=true,shadowsize=pt](,)(,) \psframe[shadow=true,shadowsize=7pt, shadowcolor=blue](,)(4,) c Sławomir Zelek 59
23 Pakiet pstricks wypełnienia fillstyle=styl none określa styl wypełnienia z następujących: none brak wypełnienia solid wypełnienie ciągłe vlines pionowe linie hlines poziome linie crosshatch pionowe i poziome linie vlines* hlines* crosshatch* fillcolor=kolor white określa kolor wypełnienia hatchwidth=grubość.8pt określa grubość linii hatchsep=odstęp 4pt określa odstęp między liniami hatchcolor=kolor black określa kolor linii hatchangle=kąt 45 określa kąt nachylenia linii analogicznie jak styl bez gwiazdki, lecz z możliwością wypełnienia tła c Sławomir Zelek 6
24 Pakiet pstricks wypełnienia \psframe[fillstyle=solid,fillcolor=green](,)(,) \psframe[fillstyle=vlines,hatchwidth=4pt](,)(,) \psframe[fillstyle=hlines,hatchwidth=4pt](,)(,) \psframe[fillstyle=hlines,hatchsep=pt](,)(,) \psframe[fillstyle=hlines*,fillcolor=lightgray, hatchcolor=red](,)(,) \psframe[fillstyle=hlines,hatchangle=5](,)(,) \psframe[fillstyle=crosshatch,hatchangle=5](,)(,) \psframe[fillstyle=crosshatch,hatchcolor=white, fillcolor=blue](,)(,) c Sławomir Zelek 6
25 Pakiet graphics \scalebox{liczba}{obiekt} \scalebox{}{duży tekst} \scalebox{}{normalny tekst} \scalebox{.5}{mały tekst} \usepackage{graphics} skaluje obiekt liczba razy duży tekst normalny tekst mały tekst \resizebox{szerokość}{wysokość}{obiekt} \resizebox{cm}{.3cm}{szeroki} \resizebox{cm}{3cm}{wysoki tekst} skaluje obiekt nieproporcjonalnie wysoki tekst szeroki c Sławomir Zelek 6
26 Pakiet graphics \rotatebox{kąt}{obiekt} \rotatebox{3}{wyraz} \rotatebox{9}{wyraz} \rotatebox{8}{wyraz} \reflectbox{obiekt} wyraz$ $\reflectbox{wyraz} wyraz obraca obiekt o kąt przeciwnie do ruchu wskazówek zegara wyraz wyraz ramki dodane dodatkowo lustrzane odbicie obiektu wyraz wyraz c Sławomir Zelek 63
27 Pakiet graphics \includegraphics{plik} włącza grafikę we formacie EPS \includegraphics{umklogo.eps} \rotatebox{45}{\includegraphics{umklogo.eps}} c Sławomir Zelek 64
28 Pakiet epsfig \epsfig{file=plik} włącza grafikę we formacie EPS \epsfig{file=umklogo.eps} \epsfig{file=umklogo.eps,width=3cm} c Sławomir Zelek 65
29 Pakiet epsfig \epsfig{file=umklogo.eps,angle=9} \epsfig{file=umklogo.eps,width=3cm,height=cm} c Sławomir Zelek 66
Paweł Kaźmierczak. styczeń 2009
 Wstęp Wstawianie i tworzenie grafiki w systemie składu tekstu LaTeX Instytut Matematyki i Informatyki PWSZ Płock styczeń 2009 Wstęp Kilka słów... Dzięki grafice, nasze dokumenty mają atrakcyjniejszą formę.
Wstęp Wstawianie i tworzenie grafiki w systemie składu tekstu LaTeX Instytut Matematyki i Informatyki PWSZ Płock styczeń 2009 Wstęp Kilka słów... Dzięki grafice, nasze dokumenty mają atrakcyjniejszą formę.
Grafika w LaTeXu Łukasz Daros & Jakub Jakubiec
 Grafika w LaTeXu Łukasz Daros & Jakub Jakubiec Wydział Fizyki i Informatyki Stosowanej Informatyka Stosowana rok 3 GRAFIKA Dzięki grafice, nasze dokumenty mają atrakcyjniejszą formę. Wykresy, ilustracje
Grafika w LaTeXu Łukasz Daros & Jakub Jakubiec Wydział Fizyki i Informatyki Stosowanej Informatyka Stosowana rok 3 GRAFIKA Dzięki grafice, nasze dokumenty mają atrakcyjniejszą formę. Wykresy, ilustracje
Pascal - grafika. Uruchomienie trybu graficznego. Moduł graph. Domyślny tryb graficzny
 Moduł graph Pascal - grafika Pascal zawiera standardowy moduł do tworzenia obiektów graficznych linii, punktów, figur geometrycznych itp. Chcąc go użyć należy w programie (w nagłówku) wstawić deklarację:
Moduł graph Pascal - grafika Pascal zawiera standardowy moduł do tworzenia obiektów graficznych linii, punktów, figur geometrycznych itp. Chcąc go użyć należy w programie (w nagłówku) wstawić deklarację:
Tik Z wiadomości wstępne
 Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
KGGiBM GRAFIKA INŻYNIERSKA Rok III, sem. VI, sem IV SN WILiŚ Rok akademicki 2011/2012
 Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Scilab - podstawy. Wersje instalacyjne programu Scilab mogą zostać pobrane ze strony
 Scilab - podstawy Scilab jest środowiskiem numerycznym, programistycznym i numerycznym dostępnym za darmo z INRIA (Institut Nationale de Recherche en Informatique et Automatique). Jest programem podobnym
Scilab - podstawy Scilab jest środowiskiem numerycznym, programistycznym i numerycznym dostępnym za darmo z INRIA (Institut Nationale de Recherche en Informatique et Automatique). Jest programem podobnym
Grafika 3D program POV-Ray - 1 -
 Temat 1: Ogólne informacje o programie POV-Ray. Interfejs programu. Ustawienie kamery i świateł. Podstawowe obiekty 3D, ich położenie, kolory i tekstura oraz przezroczystość. Skrót POV-Ray to rozwinięcie
Temat 1: Ogólne informacje o programie POV-Ray. Interfejs programu. Ustawienie kamery i świateł. Podstawowe obiekty 3D, ich położenie, kolory i tekstura oraz przezroczystość. Skrót POV-Ray to rozwinięcie
Wstęp Pierwsze kroki Pierwszy rysunek Podstawowe obiekty Współrzędne punktów Oglądanie rysunku...
 Wstęp... 5 Pierwsze kroki... 7 Pierwszy rysunek... 15 Podstawowe obiekty... 23 Współrzędne punktów... 49 Oglądanie rysunku... 69 Punkty charakterystyczne... 83 System pomocy... 95 Modyfikacje obiektów...
Wstęp... 5 Pierwsze kroki... 7 Pierwszy rysunek... 15 Podstawowe obiekty... 23 Współrzędne punktów... 49 Oglądanie rysunku... 69 Punkty charakterystyczne... 83 System pomocy... 95 Modyfikacje obiektów...
Wymiarowanie i teksty. Polecenie:
 11 Wymiarowanie i teksty Polecenie: a) Utwórz nowy rysunek z pięcioma warstwami, dla każdej warstwy przyjmij inny, dowolny kolor oraz grubość linii. Następnie narysuj pokazaną na rysunku łamaną warstwie
11 Wymiarowanie i teksty Polecenie: a) Utwórz nowy rysunek z pięcioma warstwami, dla każdej warstwy przyjmij inny, dowolny kolor oraz grubość linii. Następnie narysuj pokazaną na rysunku łamaną warstwie
Prostokąt. AutoCAD pozwala na szybkie rysowanie figur o czterech bokach prostokątów. Do tego celu służy funkcja Prostokąt. Funkcję tą można wywołać:
 Prostokąt 5 AutoCAD pozwala na szybkie rysowanie figur o czterech bokach prostokątów. Do tego celu służy funkcja Prostokąt. Funkcję tą można wywołać: wybierając ikonę z paska narzędziowego wpisując nazwę
Prostokąt 5 AutoCAD pozwala na szybkie rysowanie figur o czterech bokach prostokątów. Do tego celu służy funkcja Prostokąt. Funkcję tą można wywołać: wybierając ikonę z paska narzędziowego wpisując nazwę
b) Dorysuj na warstwie pierwszej (1) ramkę oraz tabelkę (bez wymiarów) na warstwie piątej (5) według podanego poniżej wzoru:
 Wymiarowanie i teksty 11 Polecenie: a) Utwórz nowy rysunek z pięcioma warstwami, dla każdej warstwy przyjmij inny, dowolny kolor oraz grubość linii. Następnie narysuj pokazaną na rysunku łamaną na warstwie
Wymiarowanie i teksty 11 Polecenie: a) Utwórz nowy rysunek z pięcioma warstwami, dla każdej warstwy przyjmij inny, dowolny kolor oraz grubość linii. Następnie narysuj pokazaną na rysunku łamaną na warstwie
CorelDRAW. wprowadzenie
 CorelDRAW wprowadzenie Źródło: Podręcznik uŝytkownika pakietu CorelDRAW Graphics Suite 12 Rysowanie linii 1. Otwórz program CorelDRAW. 2. Utwórz nowy rysunek i zapisz go w swoich dokumentach jako [nazwisko]_1.cdr
CorelDRAW wprowadzenie Źródło: Podręcznik uŝytkownika pakietu CorelDRAW Graphics Suite 12 Rysowanie linii 1. Otwórz program CorelDRAW. 2. Utwórz nowy rysunek i zapisz go w swoich dokumentach jako [nazwisko]_1.cdr
Rysowanie precyzyjne. Polecenie:
 7 Rysowanie precyzyjne W ćwiczeniu tym pokazane zostaną różne techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2010, między innymi wykorzystanie punktów charakterystycznych. Z uwagi na
7 Rysowanie precyzyjne W ćwiczeniu tym pokazane zostaną różne techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2010, między innymi wykorzystanie punktów charakterystycznych. Z uwagi na
1. OPEN OFFICE RYSUNKI
 1. 1 1. OPEN OFFICE RYSUNKI 1.1 Wiadomości podstawowe Po uruchomieniu programu Draw okno aplikacji wygląda jak na poniższym rysunku. Składa się ono z głównego okna, w którym edytuje się rysunek oraz czterech
1. 1 1. OPEN OFFICE RYSUNKI 1.1 Wiadomości podstawowe Po uruchomieniu programu Draw okno aplikacji wygląda jak na poniższym rysunku. Składa się ono z głównego okna, w którym edytuje się rysunek oraz czterech
Modelowanie krawędziowe detalu typu wałek w szkicowniku EdgeCAM 2009R1
 Modelowanie krawędziowe detalu typu wałek w szkicowniku EdgeCAM 2009R1 Rys.1 Widok rysunku wykonawczego wałka 1. Otwórz program Edgecam. 2. Zmieniamy środowisko frezowania (xy) na toczenie (zx) wybierając
Modelowanie krawędziowe detalu typu wałek w szkicowniku EdgeCAM 2009R1 Rys.1 Widok rysunku wykonawczego wałka 1. Otwórz program Edgecam. 2. Zmieniamy środowisko frezowania (xy) na toczenie (zx) wybierając
Łożysko z pochyleniami
 Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Układ scalony UL 1111
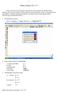 1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
4. Rysowanie krzywych
 1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
Języczek zamka typu Ostrołęka
 Języczek zamka typu Ostrołęka Zagadnienia: 1. Rysowanie a) linie: - pojedyncza - styczna do dwóch okręgów - oś symetrii b) łuki c) okręgi d) praca na warstwach 2. Edycja: a) obracanie ( z kopiowaniem)
Języczek zamka typu Ostrołęka Zagadnienia: 1. Rysowanie a) linie: - pojedyncza - styczna do dwóch okręgów - oś symetrii b) łuki c) okręgi d) praca na warstwach 2. Edycja: a) obracanie ( z kopiowaniem)
MODELE KOLORÓW. Przygotował: Robert Bednarz
 MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
Uwaga! CorelDRAW ćwiczenia kl. III Strona 1 z 6
 Uwaga! Korzystaj z POMOCY programu CorelDRAW!!! Wpisz słowo kluczowe, które szukasz w odpowiednie miejsce (Zakładka POMOC- Tematy pomocy Indeks) Po wykonaniu każdego rysunku zgrupuj jego elementy (zaznacz
Uwaga! Korzystaj z POMOCY programu CorelDRAW!!! Wpisz słowo kluczowe, które szukasz w odpowiednie miejsce (Zakładka POMOC- Tematy pomocy Indeks) Po wykonaniu każdego rysunku zgrupuj jego elementy (zaznacz
Następnie zdefiniujemy utworzony szkic jako blok, wybieramy zatem jak poniżej
 Zadanie 1 Wykorzystanie opcji Blok, Podziel oraz Zmierz Funkcja Blok umożliwia zdefiniowanie dowolnego złożonego elementu rysunkowego jako nowy blok a następnie wykorzystanie go wielokrotnie w tworzonym
Zadanie 1 Wykorzystanie opcji Blok, Podziel oraz Zmierz Funkcja Blok umożliwia zdefiniowanie dowolnego złożonego elementu rysunkowego jako nowy blok a następnie wykorzystanie go wielokrotnie w tworzonym
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
Znak wersja podstawowa
 Księga znaku Spis treści Znak wersja podstawowa...2 Układ poziomy...2 Układ pionowy...2 Konstrukcja znaku...3 Symbol...3 Napis...3 Siatka modułowa...4 Układ poziomy...4 Układ pionowy...4 Pole ochronne
Księga znaku Spis treści Znak wersja podstawowa...2 Układ poziomy...2 Układ pionowy...2 Konstrukcja znaku...3 Symbol...3 Napis...3 Siatka modułowa...4 Układ poziomy...4 Układ pionowy...4 Pole ochronne
Komputerowy skład w L A T E X
 Komputerowy skład w L A T E X dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Laboratorium 7 B. Woźna-Szcześniak (UJD)
Komputerowy skład w L A T E X dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Laboratorium 7 B. Woźna-Szcześniak (UJD)
 Przykład 1 wałek MegaCAD 2005 2D przykład 1 Jest to prosty rysunek wałka z wymiarowaniem. Założenia: 1) Rysunek z branży mechanicznej; 2) Opracowanie w odpowiednim systemie warstw i grup; Wykonanie 1)
Przykład 1 wałek MegaCAD 2005 2D przykład 1 Jest to prosty rysunek wałka z wymiarowaniem. Założenia: 1) Rysunek z branży mechanicznej; 2) Opracowanie w odpowiednim systemie warstw i grup; Wykonanie 1)
Rysowanie punktów na powierzchni graficznej
 Rysowanie punktów na powierzchni graficznej Tworzenie biblioteki rozpoczniemy od podstawowej funkcji graficznej gfxplot() - rysowania pojedynczego punktu na zadanych współrzędnych i o zadanym kolorze RGB.
Rysowanie punktów na powierzchni graficznej Tworzenie biblioteki rozpoczniemy od podstawowej funkcji graficznej gfxplot() - rysowania pojedynczego punktu na zadanych współrzędnych i o zadanym kolorze RGB.
4.6 OpenOffice Draw tworzenie ilustracji
 4-82 4.6 OpenOffice Draw tworzenie ilustracji 4.6.1 Podstawowe informacje o grafice komputerowej Istnieją dwa rodzaje grafiki komputerowej: mapy bitowe (grafika rastrowa), grafiki wektorowe. Mapy bitowe
4-82 4.6 OpenOffice Draw tworzenie ilustracji 4.6.1 Podstawowe informacje o grafice komputerowej Istnieją dwa rodzaje grafiki komputerowej: mapy bitowe (grafika rastrowa), grafiki wektorowe. Mapy bitowe
SZa 98 strona 1 Rysunek techniczny
 Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
4.2. ELIPSA. 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie:
 4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
Program Ogólny Solidarność i zarządzanie przepływami migracyjnymi SOLID
 Program Ogólny Solidarność i zarządzanie przepływami migracyjnymi SOLID Wytyczne dla partnerów projektów realizowanych w trybie bezkonkursowym według nowych zasad implementacyjnych w ramach Funduszu Granic
Program Ogólny Solidarność i zarządzanie przepływami migracyjnymi SOLID Wytyczne dla partnerów projektów realizowanych w trybie bezkonkursowym według nowych zasad implementacyjnych w ramach Funduszu Granic
Rys 3-1. Rysunek wałka
 Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
zajęcia 2 Definiowanie wektorów:
 zajęcia 2 Plan zajęć: definiowanie wektorów instrukcja warunkowa if wykresy Definiowanie wektorów: Co do definicji wektora: Koń jaki jest, każdy widzi Definiowanie wektora w Octave v1=[3,2,4] lub: v1=[3
zajęcia 2 Plan zajęć: definiowanie wektorów instrukcja warunkowa if wykresy Definiowanie wektorów: Co do definicji wektora: Koń jaki jest, każdy widzi Definiowanie wektora w Octave v1=[3,2,4] lub: v1=[3
Dodatek A. Palety. QuarkXPress 4.1. Projekty praktyczne. Podstawowe palety
 Dodatek A. Palety Podstawowe palety Paleta Tools, czyli paleta narzędziowa. Jest to typowa paleta pływająca, w której zostały umieszczone podstawowe narzędzia. Rysunek A 1. Paleta Tools Item narzędzie
Dodatek A. Palety Podstawowe palety Paleta Tools, czyli paleta narzędziowa. Jest to typowa paleta pływająca, w której zostały umieszczone podstawowe narzędzia. Rysunek A 1. Paleta Tools Item narzędzie
Księgarnia PWN: Andrzej Jaskulski - AutoCAD 2010/LT Podstawy projektowania parametrycznego i nieparametrycznego
 Księgarnia PWN: Andrzej Jaskulski - AutoCAD 2010/LT2010+. Podstawy projektowania parametrycznego i nieparametrycznego Spis treści 1. Koncepcja i zawartość podręcznika...11 1.1. Zawartość programowa...11
Księgarnia PWN: Andrzej Jaskulski - AutoCAD 2010/LT2010+. Podstawy projektowania parametrycznego i nieparametrycznego Spis treści 1. Koncepcja i zawartość podręcznika...11 1.1. Zawartość programowa...11
4.2. ELIPSA. 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie:
 4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
Zastosowania informatyki w geologii ćwiczenia 1,2 INKSCAPE 1
 INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),
INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),
TWORZENIE WYKRESÓW (1)
 TWORZENIE WYKRESÓW (1) Pewne wykresy można wygenerować za pomocą jednego polecenia, np.: graf2d, graf2d2, peaks, membrane, penny, earthmap, xfourier, xpklein, Lorenz, graf3d. Okno graficzne można wyczyścić
TWORZENIE WYKRESÓW (1) Pewne wykresy można wygenerować za pomocą jednego polecenia, np.: graf2d, graf2d2, peaks, membrane, penny, earthmap, xfourier, xpklein, Lorenz, graf3d. Okno graficzne można wyczyścić
Ćwiczenie nr 2 - Rysowanie precyzyjne
 Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
Szybkie tworzenie grafiki w GcIde
 Szybkie tworzenie grafiki w GcIde Opracował: Ryszard Olchawa Poniższy opis dotyczy aplikacji okienkowej w systemie Windows lub Linux bazującej na obiektowej bibliotece rofrm stworzonej w środowisku GcIde.
Szybkie tworzenie grafiki w GcIde Opracował: Ryszard Olchawa Poniższy opis dotyczy aplikacji okienkowej w systemie Windows lub Linux bazującej na obiektowej bibliotece rofrm stworzonej w środowisku GcIde.
Tworzenie i edycja dokumentów w aplikacji Word.
 Tworzenie i edycja dokumentów w aplikacji Word. Polskie litery, czyli ąłóęśźżń, itd. uzyskujemy naciskając prawy klawisz Alt i jednocześnie literę najbardziej zbliżoną wyglądem do szukanej. Np. ł uzyskujemy
Tworzenie i edycja dokumentów w aplikacji Word. Polskie litery, czyli ąłóęśźżń, itd. uzyskujemy naciskając prawy klawisz Alt i jednocześnie literę najbardziej zbliżoną wyglądem do szukanej. Np. ł uzyskujemy
ECDL/ICDL CAD 2D Moduł S8 Sylabus - wersja 1.5
 ECDL/ICDL CAD 2D Moduł S8 Sylabus - wersja 1.5 Przeznaczenie Sylabusa Dokument ten zawiera szczegółowy Sylabus dla modułu ECDL/ICDL CAD 2D. Sylabus opisuje zakres wiedzy i umiejętności, jakie musi opanować
ECDL/ICDL CAD 2D Moduł S8 Sylabus - wersja 1.5 Przeznaczenie Sylabusa Dokument ten zawiera szczegółowy Sylabus dla modułu ECDL/ICDL CAD 2D. Sylabus opisuje zakres wiedzy i umiejętności, jakie musi opanować
Plan wykładu. Wykład 3. Rzutowanie prostokątne, widoki, przekroje, kłady. Rzutowanie prostokątne - geneza. Rzutowanie prostokątne - geneza
 Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks.
 1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
GRAFIKA. Rodzaje grafiki i odpowiadające im edytory
 GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
O czym należy pamiętać?
 O czym należy pamiętać? Podczas pracy na płaszczyźnie możliwe jest wprowadzanie współrzędnych punktów w następujących układach: - układ współrzędnych kartezjańskich: x, y służy do rysowania odcinków o
O czym należy pamiętać? Podczas pracy na płaszczyźnie możliwe jest wprowadzanie współrzędnych punktów w następujących układach: - układ współrzędnych kartezjańskich: x, y służy do rysowania odcinków o
Projekt współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Projekt graficzny z metamorfozą (ćwiczenie dla grup I i II modułowych) Otwórz nowy rysunek. Ustal rozmiar arkusza na A4. Z przybornika wybierz rysowanie elipsy (1). Narysuj okrąg i nadaj mu średnicę 100
Projekt graficzny z metamorfozą (ćwiczenie dla grup I i II modułowych) Otwórz nowy rysunek. Ustal rozmiar arkusza na A4. Z przybornika wybierz rysowanie elipsy (1). Narysuj okrąg i nadaj mu średnicę 100
Tworzenie grafiki matematycznej
 Rozdział 5 Tworzenie grafiki matematycznej Większość ludzi używa L A TEXa do składania tekstów. Ponieważ jednak podejście strukturalno-logiczne do tworzenia dokumentów jest tak wygodne, L A TEX oferuje
Rozdział 5 Tworzenie grafiki matematycznej Większość ludzi używa L A TEXa do składania tekstów. Ponieważ jednak podejście strukturalno-logiczne do tworzenia dokumentów jest tak wygodne, L A TEX oferuje
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne.
 AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne. RYSOWANIE 2D Polecenie LINIA Polecenie LINIA tworzy linię, której punkty
AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne. RYSOWANIE 2D Polecenie LINIA Polecenie LINIA tworzy linię, której punkty
4.3 WITRAś. 1. UŜywając polecenia Linia (_Line) narysować odcinek, podając jako punkt początkowy współrzędną 90,-300 i punkt końcowy 90,55.
 4.3 WITRAś 1. UŜywając polecenia Linia (_Line) narysować odcinek, podając jako punkt początkowy współrzędną 90,-300 i punkt końcowy 90,55. 2. Narysować głowicę słupa, rozpoczynając od narysowania górnego
4.3 WITRAś 1. UŜywając polecenia Linia (_Line) narysować odcinek, podając jako punkt początkowy współrzędną 90,-300 i punkt końcowy 90,55. 2. Narysować głowicę słupa, rozpoczynając od narysowania górnego
RYSUNEK TECHNICZNY I GEOMETRIA WYKREŚLNA INSTRUKCJA Projekt instalacji c.o.
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska Zakład Informacji Przestrzennej Inżynieria Środowiska INSTRUKJA KOMPUTEROWA z Rysunku technicznego i geometrii wykreślnej RYSUNEK TEHNIZNY
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska Zakład Informacji Przestrzennej Inżynieria Środowiska INSTRUKJA KOMPUTEROWA z Rysunku technicznego i geometrii wykreślnej RYSUNEK TEHNIZNY
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Wizualizacja funkcji w programie MATLAB
 Instytut Informatyki Uniwersytetu Śląskiego 15 listopada 2008 Funckja plot Funkcja plot3 Wizualizacja funkcji jednej zmiennej Do wizualizacji funkcji jednej zmiennej w programie MATLAB wykorzystywana jest
Instytut Informatyki Uniwersytetu Śląskiego 15 listopada 2008 Funckja plot Funkcja plot3 Wizualizacja funkcji jednej zmiennej Do wizualizacji funkcji jednej zmiennej w programie MATLAB wykorzystywana jest
Elementy okna MatLab-a
 MatLab część IV 1 Elementy okna MatLab-a 2 Elementy okna MatLab-a 3 Wykresy i przydatne polecenia Wywołanie funkcji graficznej powoduje automatyczne otwarcie okna graficznego Kolejne instrukcje graficzne
MatLab część IV 1 Elementy okna MatLab-a 2 Elementy okna MatLab-a 3 Wykresy i przydatne polecenia Wywołanie funkcji graficznej powoduje automatyczne otwarcie okna graficznego Kolejne instrukcje graficzne
Ćwiczenie 4-PowerPoint
 Ćwiczenie 4-PowerPoint 1. Otworzyć plik o nazwie Pierwsza prezentacja.ppt znajdujący się na dysku D i zapisać prezentację pod nazwą Podsumowanie.ppt na dysku D. 2. W widoku normalnym ustawić powiększenie
Ćwiczenie 4-PowerPoint 1. Otworzyć plik o nazwie Pierwsza prezentacja.ppt znajdujący się na dysku D i zapisać prezentację pod nazwą Podsumowanie.ppt na dysku D. 2. W widoku normalnym ustawić powiększenie
Układy współrzędnych GUW, LUW Polecenie LUW
 Układy współrzędnych GUW, LUW Polecenie LUW 1 Układy współrzędnych w AutoCAD Rysowanie i opis (2D) współrzędnych kartezjańskich: x, y współrzędnych biegunowych: r
Układy współrzędnych GUW, LUW Polecenie LUW 1 Układy współrzędnych w AutoCAD Rysowanie i opis (2D) współrzędnych kartezjańskich: x, y współrzędnych biegunowych: r
AUTOCAD MIERZENIE I PODZIAŁ
 AUTOCAD MIERZENIE I PODZIAŁ Czasami konieczne jest rozmieszczenie na obiekcie punktów lub bloków, w równych odstępach. Na przykład, moŝe zachodzić konieczność zlokalizowania na obiekcie punktów oddalonych
AUTOCAD MIERZENIE I PODZIAŁ Czasami konieczne jest rozmieszczenie na obiekcie punktów lub bloków, w równych odstępach. Na przykład, moŝe zachodzić konieczność zlokalizowania na obiekcie punktów oddalonych
Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw.
 Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
TWORZENIE SZEŚCIANU. Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian
 TWORZENIE SZEŚCIANU Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian ZADANIE Twoim zadaniem jest zaprojektowanie a następnie wydrukowanie (za pomocą drukarki 3D)
TWORZENIE SZEŚCIANU Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian ZADANIE Twoim zadaniem jest zaprojektowanie a następnie wydrukowanie (za pomocą drukarki 3D)
MiASI Laboratorium 2 Zadanie
 MiASI Laboratorium 2 Zadanie 11.03.2014 Opracować dokument o dowolnej treści za pomocą środowiska LaTeX zawierajacy opisane poniżej elementy (w tym min. 4 grafiki, min. jedna grafika i jedna tabela "oblane"
MiASI Laboratorium 2 Zadanie 11.03.2014 Opracować dokument o dowolnej treści za pomocą środowiska LaTeX zawierajacy opisane poniżej elementy (w tym min. 4 grafiki, min. jedna grafika i jedna tabela "oblane"
Ćwiczenie pochodzi ze strony
 Ćwiczenie pochodzi ze strony http://corel.durscy.pl/ Celem ćwiczenia jest poznanie właściwości obiektu Elipsa oraz możliwości tworzenia za pomocą niego rysunków. Dodatkowo, w zadaniu tym, ćwiczone są umiejętności
Ćwiczenie pochodzi ze strony http://corel.durscy.pl/ Celem ćwiczenia jest poznanie właściwości obiektu Elipsa oraz możliwości tworzenia za pomocą niego rysunków. Dodatkowo, w zadaniu tym, ćwiczone są umiejętności
2. Korzystając z ikony Warstwy stwórz nowe warstwy według podanego schematu:
 Modyfikacja obiektów kreskowanie 8 Polecenie: Korzystając z warstw narysuj przedstawiony poniżej na rysunku (a) obiekt (dwa współśrodkowe okręgi o promieniach R 1 = 15 i R 2 = 35, pięciokąt o boku 25 jednostek
Modyfikacja obiektów kreskowanie 8 Polecenie: Korzystając z warstw narysuj przedstawiony poniżej na rysunku (a) obiekt (dwa współśrodkowe okręgi o promieniach R 1 = 15 i R 2 = 35, pięciokąt o boku 25 jednostek
INSTRUKCJA CIĘCIA PO KONTURZE Z WYKORZYSTANIEM EASYSIGN ORAZ PLOTERA TNĄCEGO ULTIMA
 INSTRUKCJA CIĘCIA PO KONTURZE Z WYKORZYSTANIEM EASYSIGN ORAZ PLOTERA TNĄCEGO ULTIMA STRONA 1/8 Drogi użytkowniku, w instrukcji tej zawarto informacje pozwalające przygotować pracę do wycięcia po konturze
INSTRUKCJA CIĘCIA PO KONTURZE Z WYKORZYSTANIEM EASYSIGN ORAZ PLOTERA TNĄCEGO ULTIMA STRONA 1/8 Drogi użytkowniku, w instrukcji tej zawarto informacje pozwalające przygotować pracę do wycięcia po konturze
Grafika inżynierska i rysunek geodezyjny
 Akademia Górniczo-Hutnicza Grafika inżynierska i rysunek geodezyjny Mgr inż. Aleksandra Szabat-Pręcikowska Normalizacja w rysunku technicznym i geodezyjnym W Polsce istnieją następujące rodzaje norm: polskie
Akademia Górniczo-Hutnicza Grafika inżynierska i rysunek geodezyjny Mgr inż. Aleksandra Szabat-Pręcikowska Normalizacja w rysunku technicznym i geodezyjnym W Polsce istnieją następujące rodzaje norm: polskie
Polecenie LUSTRO _MIRROR Lustro Pasek narzędzi: Menu: Klawiatura: UWAGA
 Polecenie LUSTRO _MIRROR Symetria osiowa obiektów względem dowolnej osi. Otrzymane obiekty są odbiciem oryginałów. Lustro Pasek narzędzi: Zmiana > Lustro; Menu: Zmiana > Lustro; Klawiatura: LUSTRO, _MIRROR
Polecenie LUSTRO _MIRROR Symetria osiowa obiektów względem dowolnej osi. Otrzymane obiekty są odbiciem oryginałów. Lustro Pasek narzędzi: Zmiana > Lustro; Menu: Zmiana > Lustro; Klawiatura: LUSTRO, _MIRROR
Dzięki arkuszom zewnętrznym uzyskujemy centralne sterowanie wyglądem serwisu. Zewnętrzny arkusz stylów to plik tekstowy z rozszerzeniem css.
 Kaskadowe arkusze stylów CSS Geneza - oddzielenie struktury dokumentu HTML od reguł prezentacji - poszerzenie samego HTML Korzyści - przejrzystość dokumentów - łatwe zarządzanie stylem (wyglądem) serwisu
Kaskadowe arkusze stylów CSS Geneza - oddzielenie struktury dokumentu HTML od reguł prezentacji - poszerzenie samego HTML Korzyści - przejrzystość dokumentów - łatwe zarządzanie stylem (wyglądem) serwisu
- biegunowy(kołowy) - kursor wykonuje skok w kierunku tymczasowych linii konstrukcyjnych;
 Ćwiczenie 2 I. Rysowanie precyzyjne Podczas tworzenia rysunków często jest potrzeba wskazania dokładnego punktu na rysunku. Program AutoCad proponuje nam wiele sposobów zwiększenia precyzji rysowania.
Ćwiczenie 2 I. Rysowanie precyzyjne Podczas tworzenia rysunków często jest potrzeba wskazania dokładnego punktu na rysunku. Program AutoCad proponuje nam wiele sposobów zwiększenia precyzji rysowania.
Programowanie: grafika w SciLab Slajd 1. Programowanie: grafika w SciLab
 Programowanie: grafika w SciLab Slajd 1 Programowanie: grafika w SciLab Programowanie: grafika w SciLab Slajd 2 Plan zajęć 1. Wprowadzenie 2. Wykresy 2-D 3. Wykresy 3-D 4. Rysowanie figur geometrycznych
Programowanie: grafika w SciLab Slajd 1 Programowanie: grafika w SciLab Programowanie: grafika w SciLab Slajd 2 Plan zajęć 1. Wprowadzenie 2. Wykresy 2-D 3. Wykresy 3-D 4. Rysowanie figur geometrycznych
Zadanie 1. Wykorzystanie opcji Szyk wzdłuż ścieżki. Załóżmy że mamy obszar o wymiarach jak poniżej
 Zadanie 1 Wykorzystanie opcji Szyk wzdłuż ścieżki Załóżmy że mamy obszar o wymiarach jak poniżej Załóżmy, że jest to krawędź obszaru, wzdłuż którego chcemy wysadzić rośliny (np. iglaki) w odległości 30
Zadanie 1 Wykorzystanie opcji Szyk wzdłuż ścieżki Załóżmy że mamy obszar o wymiarach jak poniżej Załóżmy, że jest to krawędź obszaru, wzdłuż którego chcemy wysadzić rośliny (np. iglaki) w odległości 30
Ćwiczenie nr 2 - Rysowanie precyzyjne
 Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
Ćwiczenie nr 2 - Rysowanie precyzyjne Materiały do kursu Skrypt CAD AutoCAD 2D strony: 37-46. Wprowadzenie Projektowanie wymaga budowania modelu geometrycznego zgodnie z określonymi wymiarami, a to narzuca
SCILAB. Wprowadzenie do Scilaba: http://www.scilab.org/content/download/1754/19024/file/introscilab.pdf
 SCILAB Wprowadzenie Scilab jest środowiskiem programistycznym i numerycznym dostępnym za darmo z INRIA (Institut Nationale de Recherche en Informatique et Automatique). Jest programem podobnym do MATLABa
SCILAB Wprowadzenie Scilab jest środowiskiem programistycznym i numerycznym dostępnym za darmo z INRIA (Institut Nationale de Recherche en Informatique et Automatique). Jest programem podobnym do MATLABa
Instrukcje do przedmiotu Komputerowe wspomaganie prac inżynierskich. Opracowała: Dr inż. Joanna Bartnicka
 Instrukcje do przedmiotu Komputerowe wspomaganie prac inżynierskich Opracowała: Dr inż. Joanna Bartnicka Instrukcja I Temat laboratorium: PODSTAWY KOMPUTEROWEGO ZAPISU KONSTRUKCJI Z ZASTOSOWANIEM PROGRAMU
Instrukcje do przedmiotu Komputerowe wspomaganie prac inżynierskich Opracowała: Dr inż. Joanna Bartnicka Instrukcja I Temat laboratorium: PODSTAWY KOMPUTEROWEGO ZAPISU KONSTRUKCJI Z ZASTOSOWANIEM PROGRAMU
Moduł graph w Pascalu
 Moduł graph w Pascalu Wykład: uses graph, InitGraph, Detect, SetGraphMode, kolory, wypełnienia, linie, SetFillStyle, FloodFill, SetLineStyle, SetTextStyle, OutTextXY, SetTextJustify, GetMaxX, ClearDevice,
Moduł graph w Pascalu Wykład: uses graph, InitGraph, Detect, SetGraphMode, kolory, wypełnienia, linie, SetFillStyle, FloodFill, SetLineStyle, SetTextStyle, OutTextXY, SetTextJustify, GetMaxX, ClearDevice,
INSTRUKCJA DO ĆWICZENIA NR 4. Wymiarowanie rysunków.
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska kierunek studiów: Budownictwo st. stacjonarne INSTRUKCJA DO ĆWICZENIA NR 4 Temat ćwiczenia: Wymiarowanie rysunków. Opracowała: dr inż.
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska kierunek studiów: Budownictwo st. stacjonarne INSTRUKCJA DO ĆWICZENIA NR 4 Temat ćwiczenia: Wymiarowanie rysunków. Opracowała: dr inż.
Wstawianie nowej strony
 Wstawianie nowej strony W obszernych dokumentach będziemy spotykali się z potrzebą dzielenia dokumentu na części. Czynność tę wykorzystujemy np.. do rozpoczęcia pisania nowego rozdziału na kolejnej stronie.
Wstawianie nowej strony W obszernych dokumentach będziemy spotykali się z potrzebą dzielenia dokumentu na części. Czynność tę wykorzystujemy np.. do rozpoczęcia pisania nowego rozdziału na kolejnej stronie.
2 cos α 4. 2 h) g) tgx. i) ctgx
 ZESTAW I - FUNKCJE TRYGONOMETRYCZNE - powtórzenie. Znajdź wartości pozostałych funkcji trygonometrycznych, jeśli: sin α b). Oblicz wartość wyrażenia: tg ctg 77 = b) sin 0 (cos ) = c) sin = d) [( sin 0
ZESTAW I - FUNKCJE TRYGONOMETRYCZNE - powtórzenie. Znajdź wartości pozostałych funkcji trygonometrycznych, jeśli: sin α b). Oblicz wartość wyrażenia: tg ctg 77 = b) sin 0 (cos ) = c) sin = d) [( sin 0
3.3. dwie płaszczyzny równoległe do siebie α β Dwie płaszczyzny równoległe do siebie mają ślady równoległe do siebie
 Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Techniki wstawiania tabel
 Tabele w Wordzie Tabela w Wordzie to uporządkowany układ komórek w postaci wierszy i kolumn, w które może być wpisywany tekst lub grafika. Każda komórka może być formatowana oddzielnie. Możemy wyrównywać
Tabele w Wordzie Tabela w Wordzie to uporządkowany układ komórek w postaci wierszy i kolumn, w które może być wpisywany tekst lub grafika. Każda komórka może być formatowana oddzielnie. Możemy wyrównywać
Wykład A1. AutoCAD Dr inż. Jarosław Bydłosz
 Wykład A1 AutoCAD Dr inż. Jarosław Bydłosz 1 Tematyka zajęć Rysunek techniczny Elementy geometrii wykreślnej Pakiet CAD (AutoCAD 2008) 2 Prowadzący zajęcia Wykłady: Prof. Jadwiga Maciaszek (pok. 204) Ćwiczenia
Wykład A1 AutoCAD Dr inż. Jarosław Bydłosz 1 Tematyka zajęć Rysunek techniczny Elementy geometrii wykreślnej Pakiet CAD (AutoCAD 2008) 2 Prowadzący zajęcia Wykłady: Prof. Jadwiga Maciaszek (pok. 204) Ćwiczenia
54. Układy współrzędnych
 54 54. Układy współrzędnych Współrzędne punktów i dostępne układy współrzędnych na płaszczyźnie (2D) omówiono w rozdziale 8. Współrzędne 2D. W tym rozdziale podane zostaną informacje dodatkowe konieczne
54 54. Układy współrzędnych Współrzędne punktów i dostępne układy współrzędnych na płaszczyźnie (2D) omówiono w rozdziale 8. Współrzędne 2D. W tym rozdziale podane zostaną informacje dodatkowe konieczne
PODSTAWY GRAFIKI INŻYNIERSKIEJ projektowanie SZKICOWANIE TECHNICZNE
 MATERIAŁY POMOCNICZE Zajęcia 5 Temat: Szkic techniczny. Kompozycja rysunku. Widoki SZKICOWANIE TECHNICZNE 1. Rodzaje linii i ich podstawowe zastosowanie Linia ciągła gruba widoczne krawędzie i wyraźne
MATERIAŁY POMOCNICZE Zajęcia 5 Temat: Szkic techniczny. Kompozycja rysunku. Widoki SZKICOWANIE TECHNICZNE 1. Rodzaje linii i ich podstawowe zastosowanie Linia ciągła gruba widoczne krawędzie i wyraźne
WYTYCZNE DOTYCZĄCE PROMOCJI
 Unia Europejska Europejski Fundusz Rozwoju Regionalnego Załącznik nr 12 do PRZEWODNIKA BENEFICJENTA RPO WP 2007-2013 WYTYCZNE DOTYCZĄCE PROMOCJI PROJEKTÓW UE DLA BENEFICJENTÓW REGIONALNEGO PROGRAMU OPERACYJNEGO
Unia Europejska Europejski Fundusz Rozwoju Regionalnego Załącznik nr 12 do PRZEWODNIKA BENEFICJENTA RPO WP 2007-2013 WYTYCZNE DOTYCZĄCE PROMOCJI PROJEKTÓW UE DLA BENEFICJENTÓW REGIONALNEGO PROGRAMU OPERACYJNEGO
Rys. 1. Rozpoczynamy rysunek pojedynczej części
 Inventor cw1 Otwieramy nowy rysunek typu Inventor Part (ipt) pojedyncza część. Wykonujemy to następującym algorytmem, rys. 1: 1. Na wstędze Rozpocznij klikamy nowy 2. W oknie dialogowym Nowy plik klikamy
Inventor cw1 Otwieramy nowy rysunek typu Inventor Part (ipt) pojedyncza część. Wykonujemy to następującym algorytmem, rys. 1: 1. Na wstędze Rozpocznij klikamy nowy 2. W oknie dialogowym Nowy plik klikamy
Wstawianie elementów w edytorze symboli oraz edytorze widoku aparatów
 Wstawianie elementów w edytorze symboli oraz edytorze widoku aparatów Końcówki Polecenie umożliwia wstawianie końcówek. Wstaw > Końcówkę Wskazać kursorem położenie końcówki Określić jej właściwości w dialogu
Wstawianie elementów w edytorze symboli oraz edytorze widoku aparatów Końcówki Polecenie umożliwia wstawianie końcówek. Wstaw > Końcówkę Wskazać kursorem położenie końcówki Określić jej właściwości w dialogu
Cel ćwiczenia: Kreskowanie
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZENIA NR 3 Temat ćwiczenia: Polecenie kreskuj, wypełnij, polilinia multilinia. Wymiarowanie i opisywanie rysunków
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZENIA NR 3 Temat ćwiczenia: Polecenie kreskuj, wypełnij, polilinia multilinia. Wymiarowanie i opisywanie rysunków
Kolektor. Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk. Wykonajmy model kolektora jak na rys. 1.
 Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Przetwarzanie grafiki rastrowej na wektorową
 Przetwarzanie grafiki rastrowej na wektorową Inaczej wektoryzacja, lub trasowanie, czyli zastąpienie rysunku rastrowego rysunkiem wektorowym. Wykonanie: Piotr Dróżdż Podstawowe różnice między grafiką wektorową,
Przetwarzanie grafiki rastrowej na wektorową Inaczej wektoryzacja, lub trasowanie, czyli zastąpienie rysunku rastrowego rysunkiem wektorowym. Wykonanie: Piotr Dróżdż Podstawowe różnice między grafiką wektorową,
Wektory, układ współrzędnych
 Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Inkscape. Narzędzia informatyki
 Inkscape Narzędzia informatyki Inkscape Narzędzie do tworzenia grafiki wektorowej kompatybilnej z formatem SVG Rozwijane od 2003 r. Dostępne dla Windows, Mac OS X i Linux a Dostępne na licencji GNU www.inkscape.org
Inkscape Narzędzia informatyki Inkscape Narzędzie do tworzenia grafiki wektorowej kompatybilnej z formatem SVG Rozwijane od 2003 r. Dostępne dla Windows, Mac OS X i Linux a Dostępne na licencji GNU www.inkscape.org
Ćwiczenie 4 - Tabele
 Ćwiczenie 4 - Tabele W ćwiczeniu tym zajmujemy się tabelami. Tabele moŝna wykorzystywać do róŝnych celów. W tabelach moŝna prezentować dane i je wyliczać, moŝna ustalić określony układ treści i stworzyć
Ćwiczenie 4 - Tabele W ćwiczeniu tym zajmujemy się tabelami. Tabele moŝna wykorzystywać do róŝnych celów. W tabelach moŝna prezentować dane i je wyliczać, moŝna ustalić określony układ treści i stworzyć
Logo cz pl Zasady stosowania logotypów
 Logo cz pl 2014 2020 Zasady stosowania logotypów 1 Spis treści 2 Wstęp 3 Logo cz pl Opis 4 Pole ochronne 5 Umiejscowienie 6 Formaty danych logo 7 Kolory 8 Niebieski 9 Pomarańczowy 10 Wersja monochromatyczna
Logo cz pl 2014 2020 Zasady stosowania logotypów 1 Spis treści 2 Wstęp 3 Logo cz pl Opis 4 Pole ochronne 5 Umiejscowienie 6 Formaty danych logo 7 Kolory 8 Niebieski 9 Pomarańczowy 10 Wersja monochromatyczna
Geometria i grafika komputerowa
 Geometria i grafika komputerowa Anna Franczyk Katedra Geoinformatyki i Informatyki Stosowanej Wydział Geologii, Geofizyki i Ochrony Środowiska Akademia Górniczo Hutnicza Kraków Podstawowe informacje gdzie
Geometria i grafika komputerowa Anna Franczyk Katedra Geoinformatyki i Informatyki Stosowanej Wydział Geologii, Geofizyki i Ochrony Środowiska Akademia Górniczo Hutnicza Kraków Podstawowe informacje gdzie
Inżynieria Materiałowa i Konstrukcja Urządzeń - Projekt
 Inżynieria Materiałowa i Konstrukcja Urządzeń - Projekt Przygotowanie dokumentacji mechanicznej A9CAD Cel i zadania: Celem ćwiczenia jest zapoznanie się z programem do tworzenia rysunków mechanicznych
Inżynieria Materiałowa i Konstrukcja Urządzeń - Projekt Przygotowanie dokumentacji mechanicznej A9CAD Cel i zadania: Celem ćwiczenia jest zapoznanie się z programem do tworzenia rysunków mechanicznych
Materiały pomocnicze z programu AutoCAD 2014.
 Materiały pomocnicze z programu AutoCAD 2014. Poniżej przedstawiony zostanie przykładowy rysunek wykonany w programie AutoCAD 2014. Po uruchomieniu programu należy otworzyć szablon KKM, w którym znajdują
Materiały pomocnicze z programu AutoCAD 2014. Poniżej przedstawiony zostanie przykładowy rysunek wykonany w programie AutoCAD 2014. Po uruchomieniu programu należy otworzyć szablon KKM, w którym znajdują
Płaszczyzny, żebra (pudełko)
 Płaszczyzny, żebra (pudełko) Zagadnienia. Płaszczyzny, Żebra Wykonajmy model jak na rys. 1. Wykonanie Rysunek 1. Model pudełka Prostopadłościan z pochylonymi ścianami Wykonamy zamknięty szkic na Płaszczyźnie
Płaszczyzny, żebra (pudełko) Zagadnienia. Płaszczyzny, Żebra Wykonajmy model jak na rys. 1. Wykonanie Rysunek 1. Model pudełka Prostopadłościan z pochylonymi ścianami Wykonamy zamknięty szkic na Płaszczyźnie
Symbole graficzne. 1. Rezystor Rysujemy symbol graficzny rezystora
 Symbole graficzne. Uruchamiamy i konfigurujemy program MegaCAD 16.01. 1. Rezystor Rysujemy symbol graficzny rezystora 1.1. Rysujemy prostokąt Rysujemy prostokąt o wymiarach: 6x2 mm. a) ołówek nr 1 (L1;
Symbole graficzne. Uruchamiamy i konfigurujemy program MegaCAD 16.01. 1. Rezystor Rysujemy symbol graficzny rezystora 1.1. Rysujemy prostokąt Rysujemy prostokąt o wymiarach: 6x2 mm. a) ołówek nr 1 (L1;
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki. Ćwiczenie laboratoryjne 1
 Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 1 Temat: Modelowanie krzywych 2D i 3D przy użyciu programu Autodesk Inventor 2009 Spis treści 1. Wprowadzenie...
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 1 Temat: Modelowanie krzywych 2D i 3D przy użyciu programu Autodesk Inventor 2009 Spis treści 1. Wprowadzenie...
Kurs Adobe Photoshop Elements 11
 Kurs Adobe Photoshop Elements 11 Gladiatorx1 Kształty, kształty własne 2015-01- 01 Spis treści Wstęp... 2 Kształty... 2 Opcje narzędzia... 2 Rysujemy kształty... 5 Opcje dodawania, odejmowania obszaru
Kurs Adobe Photoshop Elements 11 Gladiatorx1 Kształty, kształty własne 2015-01- 01 Spis treści Wstęp... 2 Kształty... 2 Opcje narzędzia... 2 Rysujemy kształty... 5 Opcje dodawania, odejmowania obszaru
