Janusz Ganczarski CIE XYZ
|
|
|
- Helena Baran
- 6 lat temu
- Przeglądów:
Transkrypt
1 Janusz Ganczarski CIE XYZ
2 Spis treści Spis treści CIE XYZ Współrzędne trójchromatyczne Wykres chromatyczności Transformacja CIE XYZ - CIE RGB Gamy barw Konwersja CIE XYZ - RGB FCC - RGB EBU CIE XYZ Dodatek - tabele wartości składowych widmowych i współrzędnych trójchromatycznych Plik cie xyz.h Plik ccciexyz 1931.h Plik ccciexyz 1964.h Plik ciexyz 1931.h Plik ciexyz 1964.h Literatura
3 1. CIE XYZ Trójchromatyczny model barw CIE XYZ został opracowany w 1931 roku przez Międzynarodową Komisję Oświetleniową CIE i stanowi rozwinięcie układu CIE RGB. System CIE XYZ wykorzystuje trzy fikcyjne barwy podstawowe x, y i z, otrzymane przez przekształcenie składowych widmowe x λ, ȳ λ i z λ, które są nieujemne na całym zakresie fal. Składowa y zawiera informację o strumieniu światła, a składowe x i z zawierają wyłącznie informację o barwie. Rysunek 1 przedstawia wykres zależności wartości składowych trójchromatycznych CIE XYZ (krzywe x λ, ȳ λ, z λ ) od długości fali. Rysunek 1. Składowe trójchromatyczne CIE XYZ System CIE XYZ został zdefiniowany dla normalnego obserwatora CIE 1931 (kąt obserwacji 2 ) i jest zalecany do używania przy polach widzenia nie przekraczających w świetle dziennym Współrzędne trójchromatyczne Podobnie jak w przypadku systemu CIE RGB określone zostały współrzędne trójchromatyczne w trójwymiarowej przestrzeni XYZ. Analogicznie płaszczyzna barw ma równanie x + y + z = 1. Poszczególne wartości współrzędnych trójchromatycznych x λ, y λ i z λ wyznaczane są z następujących zależności: z λ x λ = x λ + ȳ λ + z λ ȳ λ y λ = x λ + ȳ λ + z λ
4 1. CIE XYZ 2 z λ = z λ x λ + ȳ λ + z λ Oczywiście dla tak zdefiniowanych współrzędnych trójchromatycznych zachodzi równość: x λ + x λ + x λ = 1 Tabela 1 zawiera zestawienie wartości składowych trójchromatycznych widmowych, a tabela 2 współrzędnych trójchromatycznych w układzie CIE XYZ dla fal o długości co 5 nm. λ [nm] x λ ȳ λ z λ 360 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
5 1. CIE XYZ 3 λ [nm] x λ ȳ λ z λ 515 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
6 1. CIE XYZ 4 λ [nm] x λ ȳ λ z λ 720 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Tabela 1: Składowe widmowe CIE XYZ 1931 λ [nm] x λ y λ z λ 360 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,823490
7 1. CIE XYZ 5 λ [nm] x λ y λ z λ 425 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,000093
8 1. CIE XYZ 6 λ [nm] x λ y λ z λ 630 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,000000
9 1. CIE XYZ 7 λ [nm] x λ y λ z λ 830 0, , , Tabela 2: Współrzędne trójchromatyczne CIE XYZ Wykres chromatyczności Światła widzialne w przestrzeni CIE XYZ zawarte są w bryle o kształcie zbliżonym do stożka o wierzchołku w początku układu współrzędnych. Całość bryły znajduje się w pierwszym oktancie. Jednak w praktyce stosuje się tzw. wykres chromatyczności (ang. chromaticity diagram), uzyskiwany poprzez rzutowanie płaszczyzny x + y + z = 1, która przecina bryłę CIE XYZ, na płaszczyznę Z = 0. Wykres chromatyczności dla obserwatora CIE 1931 przedstawiono na rysunku 2. Na brzegu obszaru rozmieszczone są nasycone barwy widmowe określone przez dominujące długości fal. Rysunek 2. Wykres chromatyczności CIE XYZ 1931
10 1. CIE XYZ 8 Wnętrze obszaru wraz z brzegiem reprezentuje wszystkie widzialne kombinacje wartości współrzędnych x, y. Barwy o tych samych współrzędnych trójchromatycznych, lecz o różnych luminacjach reprezentowane są przez ten sam punkt na wykresie chromatyczności. Zatem wykres nie zawiera pełnej palety barw, np. barwa brązowa czyli barwa pomarańczowoczerwona o małej luminacji występuje w innym przekroju bryły CIE XYZ. Standardowe światło białe przybliżające światło słoneczne, nazywane bielą C, ma współrzędne x = 0, 310, y = 0, 316, z = 0, 374. Biel równoenergetyczna E ma w tym układzie wszystkie trzy współrzędne równe (x = y = z = 1 3 ). Wykres chromatyczności posiada cechy przydatne przy addytywnym mieszaniu barw. Addytywne zmieszanie barw reprezentowanych przez współrzędne trójchromatyczne (x 1, y 1 ) i (x 2, y 2 ) da barwę (x 3, y 3 ), która leży na odcinku łączącym punkty reprezentujące mieszane barwy. Położenie punktu (x 3, y 3 ) będzie zależało od proporcji, w jakich zostaną zmieszane barwy początkowe. Przykładowo jeżeli jako barwy początkowe zostaną wybrane barwa biała i odcień barwy nasyconej, reprezentowanej przez punkt leżący na brzegu wykresu chromatyczności, to na odcinku łączącym te barwy znajdują się wszystkie nienasycone odcienie barwy pierwotnej Transformacja CIE XYZ - CIE RGB Transformację składowych trójchromatycznych układów CIE RGB i CIE XYZ można przedstawić w postaci poniższego równania: x y z = 0, , , , , , , , , Jak łatwo sprawdzić macierz transformacji spełnia warunki zachowania równości składowych trójchromatycznych w obu układach dla światła o barwie białej E (x = y = z = 1 3 ). r g b 1.4. Gamy barw Zasadę mieszania dwóch barw można rozszerzyć na trzy barwy, których współrzędne trójchromatyczne nie leżą na jednej prostej. W takim przypadku wszystkie możliwe do uzyskania barwy leżą wewnątrz trójkąta o wierzchołkach określonych przez barwy pierwotne. W szczególności może to dotyczyć przestrzeni barw RGB. Porównamy dwa układy kolorymetryczne stosowane powszechnie w telewizji kolorowej. Pierwszy to układ RGB FCC, opracowany w 1951 roku przez FCC (ang. Federal Communication Commission) na potrzeby systemu NTSC. Drugi porównywanym układem jest RGB EBU opracowany
11 1. CIE XYZ 9 w 1970 roku przez brytyjskie stowarzyszenie EBU (ang. European Broadcasting Union) na podstawie przeciętnych barw luminoforów stosowanych w odbiornikach telewizyjnych. Zakresy barw możliwych do wyświetlenia przez powyższe urządzenia (ang. gamut) wykreślimy na diagramie chromatyczności CIE XYZ. Przedstawiają to rysunki 3 i 4. Jak widać z powyższych rysunków powierzchnia trójkąta RGB EBU jest niewiele mniejsza od powierzchni trójkąta RGB FCC. Układ RGB EBU ogranicza nieco gamę odtwarzanych zieleni, dając jednocześnie pewną poprawę w zakresie barw o krótszych dominujących długościach fali. Rysunek 3. Gama barw RGB FCC Powyższy przykład obrazuje jeden z podstawowych problemów w reprodukcji barw - niezgodność gamy barw osiągalnych przez różne urządzenia. Różnorodne techniki rozwiązania tego problemu Czytelnik pozna w następnych rozdziałach.
12 1. CIE XYZ 10 Rysunek 4. Gama barw RGB EBU 1.5. Konwersja CIE XYZ - RGB FCC - RGB EBU Konwersję pomiędzy układami CIE XYZ, RGB FCC i RGB EBU przedstawiają poniższe równania. x y z = 0, 607 0, 174 0, 2 0, 299 0, 587 0, , 066 1, 116 r F CC g F CC b F CC r F CC g F CC b F CC = 1, 910 0, 532 0, 288 0, 985 1, 999 0, 028 0, 058 0, 118 0, 898 x y z x y z = 0, 429 0, 343 0, 178 0, 222 0, 707 0, 071 0, 019 0, 132 0, 939 r EBU g EBU b EBU
13 1. CIE XYZ 11 r EBU g EBU b EBU = 3, 073 1, 403 0, 475 0, 970 1, 877 0, 042 0, 074 0, 235 1, 068 x y z 1.6. CIE XYZ 1964 W 1964 roku CIE opracowała model normalnego obserwatora CIE 10, o kącie obserwacji 10. Użycie tego obserwatora jest zalecane przy kątach obserwacji przekraczających 4. Opracowanie tego modelu związane było z krytyką, iż typowy obserwator patrzy zwykle z kątem większym niż 4. Zastosowanie tego obserwatora spowodowało konieczność przeliczenia wartości współrzędnych trójchromatycznych i składowych trójchromatycznych widmowych układu CIE XYZ. Nowy układ funkcjonuje pod nazwą CIE XYZ 1964 lub CIE X 10 Y 10 Z 10. Rysunek 5 przedstawia wykres chromatyczności CIE XYZ Rysunek 5. Wykres chromatyczności CIE XYZ 1964
14 1. CIE XYZ 12 Tabela 3 przedstawia składowe widmowe CIE XYZ 1964 (wartości co 5 nm). Tabela 4 przedstawia współrzędne trójchromatyczne CIE XYZ 1964 (wartości także co 5 nm). λ [nm] x λ ȳ λ z λ 360 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
15 1. CIE XYZ 13 λ [nm] x λ ȳ λ z λ 545 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,
16 1. CIE XYZ 14 λ [nm] x λ ȳ λ z λ 750 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Tabela 3: Składowe widmowe CIE XYZ 1964 λ [nm] x λ y λ z λ 360 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,812560
17 1. CIE XYZ 15 λ [nm] x λ y λ z λ 455 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,000000
18 1. CIE XYZ 16 λ [nm] x λ y λ z λ 660 0, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Tabela 4: Współrzędne trójchromatyczne CIE XYZ 1964
19 1. CIE XYZ Dodatek - tabele wartości składowych widmowych i współrzędnych trójchromatycznych Przedstawione poniżej pliki nagłówkowe zawierają wartości składowych widmowych i współrzędnych trójchromatycznych układów CIE XYZ 1931 i CIE XYZ 1964 (wartości co 1 nm). Dane zawarte są w tabeli ze strukturami CIE XYZ Plik cie xyz.h // ( c ) J a n u s z G a n c z a r s k i ( Power ) // h t t p : / /www. j a n u s z g. hg. p l // JanuszG@enter. n e t. p l #i f n d e f CIE XYZ #define CIE XYZ // d e f i n i c j a s t r u k t u r y do p r z e c h o w y w a n i a w a r t o ś c i w s p ó ł r z ę d n y c h // t r ó j c h r o m a t y c z n y c h i s k ł a d o w y c h widmowych modelu CIE XYZ struct CIE XYZ { int wavelength ; double x, y, z ; } ; #endif // CIE XYZ Plik ccciexyz 1931.h // ( c ) J a n u s z G a n c z a r s k i ( Power ) // h t t p : / /www. j a n u s z g. hg. p l // JanuszG@enter. n e t. p l #i f n d e f CCIEXYZ 1931 H #define CCIEXYZ 1931 H #include c i e x y z. h // współrzędne tr ój c hr oma tyc zne CIE XYZ 1931 // ( ang. c h r o m a t i c i t y c o o r d i n a t e s ) const CIE XYZ CC CIE XYZ 1931 [ ] = { { 3 6 0, , , }, { 3 6 1, , , }, { 3 6 2, , , }, { 3 6 3, , , }, { 3 6 4, , , }, { 3 6 5, , , }, { 3 6 6, , , }, { 3 6 7, , , }, { 3 6 8, , , }, { 3 6 9, , , }, { 3 7 0, , , }, { 3 7 1, , , }, { 3 7 2, , , }, { 3 7 3, , , }, { 3 7 4, , , }, { 3 7 5, , , }, { 3 7 6, , , }, { 3 7 7, , , }, { 3 7 8, , , }, { 3 7 9, , , }, { 3 8 0, , , }, { 3 8 1, , , }, { 3 8 2, , , }, { 3 8 3, , , }, { 3 8 4, , , }, { 3 8 5, , , }, { 3 8 6, , , },
20 1. CIE XYZ 18 { 3 8 7, , , }, { 3 8 8, , , }, { 3 8 9, , , }, { 3 9 0, , , }, { 3 9 1, , , }, { 3 9 2, , , }, { 3 9 3, , , }, { 3 9 4, , , }, { 3 9 5, , , }, { 3 9 6, , , }, { 3 9 7, , , }, { 3 9 8, , , }, { 3 9 9, , , }, { 4 0 0, , , }, { 4 0 1, , , }, { 4 0 2, , , }, { 4 0 3, , , }, { 4 0 4, , , }, { 4 0 5, , , }, { 4 0 6, , , }, { 4 0 7, , , }, { 4 0 8, , , }, { 4 0 9, , , }, { 4 1 0, , , }, { 4 1 1, , , }, { 4 1 2, , , }, { 4 1 3, , , }, { 4 1 4, , , }, { 4 1 5, , , }, { 4 1 6, , , }, { 4 1 7, , , }, { 4 1 8, , , }, { 4 1 9, , , }, { 4 2 0, , , }, { 4 2 1, , , }, { 4 2 2, , , }, { 4 2 3, , , }, { 4 2 4, , , }, { 4 2 5, , , }, { 4 2 6, , , }, { 4 2 7, , , }, { 4 2 8, , , }, { 4 2 9, , , }, { 4 3 0, , , }, { 4 3 1, , , }, { 4 3 2, , , }, { 4 3 3, , , }, { 4 3 4, , , }, { 4 3 5, , , }, { 4 3 6, , , }, { 4 3 7, , , }, { 4 3 8, , , }, { 4 3 9, , , }, { 4 4 0, , , }, { 4 4 1, , , }, { 4 4 2, , , }, { 4 4 3, , , }, { 4 4 4, , , }, { 4 4 5, , , }, { 4 4 6, , , }, { 4 4 7, , , }, { 4 4 8, , , }, { 4 4 9, , , }, { 4 5 0, , , }, { 4 5 1, , , }, { 4 5 2, , , }, { 4 5 3, , , }, { 4 5 4, , , }, { 4 5 5, , , }, { 4 5 6, , , }, { 4 5 7, , , }, { 4 5 8, , , }, { 4 5 9, , , }, { 4 6 0, , , }, { 4 6 1, , , }, { 4 6 2, , , }, { 4 6 3, , , }, { 4 6 4, , , }, { 4 6 5, , , }, { 4 6 6, , , },
21 1. CIE XYZ 19 { 4 6 7, , , }, { 4 6 8, , , }, { 4 6 9, , , }, { 4 7 0, , , }, { 4 7 1, , , }, { 4 7 2, , , }, { 4 7 3, , , }, { 4 7 4, , , }, { 4 7 5, , , }, { 4 7 6, , , }, { 4 7 7, , , }, { 4 7 8, , , }, { 4 7 9, , , }, { 4 8 0, , , }, { 4 8 1, , , }, { 4 8 2, , , }, { 4 8 3, , , }, { 4 8 4, , , }, { 4 8 5, , , }, { 4 8 6, , , }, { 4 8 7, , , }, { 4 8 8, , , }, { 4 8 9, , , }, { 4 9 0, , , }, { 4 9 1, , , }, { 4 9 2, , , }, { 4 9 3, , , }, { 4 9 4, , , }, { 4 9 5, , , }, { 4 9 6, , , }, { 4 9 7, , , }, { 4 9 8, , , }, { 4 9 9, , , }, { 5 0 0, , , }, { 5 0 1, , , }, { 5 0 2, , , }, { 5 0 3, , , }, { 5 0 4, , , }, { 5 0 5, , , }, { 5 0 6, , , }, { 5 0 7, , , }, { 5 0 8, , , }, { 5 0 9, , , }, { 5 1 0, , , }, { 5 1 1, , , }, { 5 1 2, , , }, { 5 1 3, , , }, { 5 1 4, , , }, { 5 1 5, , , }, { 5 1 6, , , }, { 5 1 7, , , }, { 5 1 8, , , }, { 5 1 9, , , }, { 5 2 0, , , }, { 5 2 1, , , }, { 5 2 2, , , }, { 5 2 3, , , }, { 5 2 4, , , }, { 5 2 5, , , }, { 5 2 6, , , }, { 5 2 7, , , }, { 5 2 8, , , }, { 5 2 9, , , }, { 5 3 0, , , }, { 5 3 1, , , }, { 5 3 2, , , }, { 5 3 3, , , }, { 5 3 4, , , }, { 5 3 5, , , }, { 5 3 6, , , }, { 5 3 7, , , }, { 5 3 8, , , }, { 5 3 9, , , }, { 5 4 0, , , }, { 5 4 1, , , }, { 5 4 2, , , }, { 5 4 3, , , }, { 5 4 4, , , }, { 5 4 5, , , }, { 5 4 6, , , },
22 1. CIE XYZ 20 { 5 4 7, , , }, { 5 4 8, , , }, { 5 4 9, , , }, { 5 5 0, , , }, { 5 5 1, , , }, { 5 5 2, , , }, { 5 5 3, , , }, { 5 5 4, , , }, { 5 5 5, , , }, { 5 5 6, , , }, { 5 5 7, , , }, { 5 5 8, , , }, { 5 5 9, , , }, { 5 6 0, , , }, { 5 6 1, , , }, { 5 6 2, , , }, { 5 6 3, , , }, { 5 6 4, , , }, { 5 6 5, , , }, { 5 6 6, , , }, { 5 6 7, , , }, { 5 6 8, , , }, { 5 6 9, , , }, { 5 7 0, , , }, { 5 7 1, , , }, { 5 7 2, , , }, { 5 7 3, , , }, { 5 7 4, , , }, { 5 7 5, , , }, { 5 7 6, , , }, { 5 7 7, , , }, { 5 7 8, , , }, { 5 7 9, , , }, { 5 8 0, , , }, { 5 8 1, , , }, { 5 8 2, , , }, { 5 8 3, , , }, { 5 8 4, , , }, { 5 8 5, , , }, { 5 8 6, , , }, { 5 8 7, , , }, { 5 8 8, , , }, { 5 8 9, , , }, { 5 9 0, , , }, { 5 9 1, , , }, { 5 9 2, , , }, { 5 9 3, , , }, { 5 9 4, , , }, { 5 9 5, , , }, { 5 9 6, , , }, { 5 9 7, , , }, { 5 9 8, , , }, { 5 9 9, , , }, { 6 0 0, , , }, { 6 0 1, , , }, { 6 0 2, , , }, { 6 0 3, , , }, { 6 0 4, , , }, { 6 0 5, , , }, { 6 0 6, , , }, { 6 0 7, , , }, { 6 0 8, , , }, { 6 0 9, , , }, { 6 1 0, , , }, { 6 1 1, , , }, { 6 1 2, , , }, { 6 1 3, , , }, { 6 1 4, , , }, { 6 1 5, , , }, { 6 1 6, , , }, { 6 1 7, , , }, { 6 1 8, , , }, { 6 1 9, , , }, { 6 2 0, , , }, { 6 2 1, , , }, { 6 2 2, , , }, { 6 2 3, , , }, { 6 2 4, , , }, { 6 2 5, , , }, { 6 2 6, , , },
23 1. CIE XYZ 21 { 6 2 7, , , }, { 6 2 8, , , }, { 6 2 9, , , }, { 6 3 0, , , }, { 6 3 1, , , }, { 6 3 2, , , }, { 6 3 3, , , }, { 6 3 4, , , }, { 6 3 5, , , }, { 6 3 6, , , }, { 6 3 7, , , }, { 6 3 8, , , }, { 6 3 9, , , }, { 6 4 0, , , }, { 6 4 1, , , }, { 6 4 2, , , }, { 6 4 3, , , }, { 6 4 4, , , }, { 6 4 5, , , }, { 6 4 6, , , }, { 6 4 7, , , }, { 6 4 8, , , }, { 6 4 9, , , }, { 6 5 0, , , }, { 6 5 1, , , }, { 6 5 2, , , }, { 6 5 3, , , }, { 6 5 4, , , }, { 6 5 5, , , }, { 6 5 6, , , }, { 6 5 7, , , }, { 6 5 8, , , }, { 6 5 9, , , }, { 6 6 0, , , }, { 6 6 1, , , }, { 6 6 2, , , }, { 6 6 3, , , }, { 6 6 4, , , }, { 6 6 5, , , }, { 6 6 6, , , }, { 6 6 7, , , }, { 6 6 8, , , }, { 6 6 9, , , }, { 6 7 0, , , }, { 6 7 1, , , }, { 6 7 2, , , }, { 6 7 3, , , }, { 6 7 4, , , }, { 6 7 5, , , }, { 6 7 6, , , }, { 6 7 7, , , }, { 6 7 8, , , }, { 6 7 9, , , }, { 6 8 0, , , }, { 6 8 1, , , }, { 6 8 2, , , }, { 6 8 3, , , }, { 6 8 4, , , }, { 6 8 5, , , }, { 6 8 6, , , }, { 6 8 7, , , }, { 6 8 8, , , }, { 6 8 9, , , }, { 6 9 0, , , }, { 6 9 1, , , }, { 6 9 2, , , }, { 6 9 3, , , }, { 6 9 4, , , }, { 6 9 5, , , }, { 6 9 6, , , }, { 6 9 7, , , }, { 6 9 8, , , }, { 6 9 9, , , }, { 7 0 0, , , }, { 7 0 1, , , }, { 7 0 2, , , }, { 7 0 3, , , }, { 7 0 4, , , }, { 7 0 5, , , }, { 7 0 6, , , },
24 1. CIE XYZ 22 { 7 0 7, , , }, { 7 0 8, , , }, { 7 0 9, , , }, { 7 1 0, , , }, { 7 1 1, , , }, { 7 1 2, , , }, { 7 1 3, , , }, { 7 1 4, , , }, { 7 1 5, , , }, { 7 1 6, , , }, { 7 1 7, , , }, { 7 1 8, , , }, { 7 1 9, , , }, { 7 2 0, , , }, { 7 2 1, , , }, { 7 2 2, , , }, { 7 2 3, , , }, { 7 2 4, , , }, { 7 2 5, , , }, { 7 2 6, , , }, { 7 2 7, , , }, { 7 2 8, , , }, { 7 2 9, , , }, { 7 3 0, , , }, { 7 3 1, , , }, { 7 3 2, , , }, { 7 3 3, , , }, { 7 3 4, , , }, { 7 3 5, , , }, { 7 3 6, , , }, { 7 3 7, , , }, { 7 3 8, , , }, { 7 3 9, , , }, { 7 4 0, , , }, { 7 4 1, , , }, { 7 4 2, , , }, { 7 4 3, , , }, { 7 4 4, , , }, { 7 4 5, , , }, { 7 4 6, , , }, { 7 4 7, , , }, { 7 4 8, , , }, { 7 4 9, , , }, { 7 5 0, , , }, { 7 5 1, , , }, { 7 5 2, , , }, { 7 5 3, , , }, { 7 5 4, , , }, { 7 5 5, , , }, { 7 5 6, , , }, { 7 5 7, , , }, { 7 5 8, , , }, { 7 5 9, , , }, { 7 6 0, , , }, { 7 6 1, , , }, { 7 6 2, , , }, { 7 6 3, , , }, { 7 6 4, , , }, { 7 6 5, , , }, { 7 6 6, , , }, { 7 6 7, , , }, { 7 6 8, , , }, { 7 6 9, , , }, { 7 7 0, , , }, { 7 7 1, , , }, { 7 7 2, , , }, { 7 7 3, , , }, { 7 7 4, , , }, { 7 7 5, , , }, { 7 7 6, , , }, { 7 7 7, , , }, { 7 7 8, , , }, { 7 7 9, , , }, { 7 8 0, , , }, { 7 8 1, , , }, { 7 8 2, , , }, { 7 8 3, , , }, { 7 8 4, , , }, { 7 8 5, , , }, { 7 8 6, , , },
25 1. CIE XYZ 23 { 7 8 7, , , }, { 7 8 8, , , }, { 7 8 9, , , }, { 7 9 0, , , }, { 7 9 1, , , }, { 7 9 2, , , }, { 7 9 3, , , }, { 7 9 4, , , }, { 7 9 5, , , }, { 7 9 6, , , }, { 7 9 7, , , }, { 7 9 8, , , }, { 7 9 9, , , }, { 8 0 0, , , }, { 8 0 1, , , }, { 8 0 2, , , }, { 8 0 3, , , }, { 8 0 4, , , }, { 8 0 5, , , }, { 8 0 6, , , }, { 8 0 7, , , }, { 8 0 8, , , }, { 8 0 9, , , }, { 8 1 0, , , }, { 8 1 1, , , }, { 8 1 2, , , }, { 8 1 3, , , }, { 8 1 4, , , }, { 8 1 5, , , }, { 8 1 6, , , }, { 8 1 7, , , }, { 8 1 8, , , }, { 8 1 9, , , }, { 8 2 0, , , }, { 8 2 1, , , }, { 8 2 2, , , }, { 8 2 3, , , }, { 8 2 4, , , }, { 8 2 5, , , }, { 8 2 6, , , }, { 8 2 7, , , }, { 8 2 8, , , }, { 8 2 9, , , }, { 8 3 0, , , } } ; #endif // CCIEXYZ 1931 H Plik ccciexyz 1964.h // ( c ) J a n u s z G a n c z a r s k i ( Power ) // h t t p : / /www. j a n u s z g. hg. p l // JanuszG@enter. n e t. p l #define #define CCCIEXYZ 1964 H CCCIEXYZ 1964 H #include c i e x y z. h // współrzędne tr ój c hr oma tyc zne CIE XYZ 1964 // ( ang. c h r o m a t i c i t y c o o r d i n a t e s ) const CIE XYZ CC CIE XYZ 1964 [ ] = { { 3 6 0, , , }, { 3 6 1, , , }, { 3 6 2, , , }, { 3 6 3, , , }, { 3 6 4, , , }, { 3 6 5, , , }, { 3 6 6, , , }, { 3 6 7, , , }, { 3 6 8, , , }, { 3 6 9, , , }, { 3 7 0, , , }, { 3 7 1, , , }, { 3 7 2, , , },
Fotometria i kolorymetria
 12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). http://www.if.pwr.wroc.pl/~wozniak/
Fotometria i kolorymetria
 13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
WYKŁAD 14 PODSTAWY TEORII BARW. Plan wykładu: 1. Wrażenie widzenia barwy. Wrażenie widzenia barwy Modele liczbowe barw
 WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
WYKŁAD 11. Kolor. fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony
 WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
PODSTAWY TEORII BARW
 WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
PODSTAWY BARWY, PIGMENTY CERAMICZNE
 PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
Pojęcie Barwy. Grafika Komputerowa modele kolorów. Terminologia BARWY W GRAFICE KOMPUTEROWEJ. Marek Pudełko
 Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
MODELE KOLORÓW. Przygotował: Robert Bednarz
 MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
Fotometria i kolorymetria
 11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
Luminancja jako jednostka udziału barwy składowej w mierzonej:
 Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Kolor w grafice komputerowej. Światło i barwa
 Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Spis treści Spis treści 1. Model CMYK Literatura
 Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
Kolorymetria. Akademia Sztuk Pięknych Gdańsk październik Dr inŝ. Paweł Baranowski
 Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy.
 Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Wprowadzenie do cyfrowego przetwarzania obrazów
 Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
Laboratorium Grafiki Komputerowej Przekształcenia na modelach barw
 Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw.
 Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Marcin Wilczewski Politechnika Gdańska, 2013/14
 Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Dzień dobry. Miejsce: IFE - Centrum Kształcenia Międzynarodowego PŁ, ul. Żwirki 36, sala nr 7
 Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
Kurs grafiki komputerowej Lekcja 2. Barwa i kolor
 Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Białe jest piękne. Światło białe wytwarzane przez same diody LED.
 Białe jest piękne Mechanizm generowania światła w strukturze diody LED umożliwia uzyskanie promieniowania o wąskim zakresie długości fal, niemal monochromatycznego. Tak więc pojedyncze złącze LED nie może
Białe jest piękne Mechanizm generowania światła w strukturze diody LED umożliwia uzyskanie promieniowania o wąskim zakresie długości fal, niemal monochromatycznego. Tak więc pojedyncze złącze LED nie może
ZADANIA MATURALNE - ANALIZA MATEMATYCZNA - POZIOM ROZSZERZONY Opracowała - mgr Danuta Brzezińska. 2 3x. 2. Sformułuj odpowiedź.
 ZADANIA MATURALNE - ANALIZA MATEMATYCZNA - POZIOM ROZSZERZONY Opracowała - mgr Danuta Brzezińska Zad.1. (5 pkt) Sprawdź, czy funkcja określona wzorem x( x 1)( x ) x 3x dla x 1 i x dla x 1 f ( x) 1 3 dla
ZADANIA MATURALNE - ANALIZA MATEMATYCZNA - POZIOM ROZSZERZONY Opracowała - mgr Danuta Brzezińska Zad.1. (5 pkt) Sprawdź, czy funkcja określona wzorem x( x 1)( x ) x 3x dla x 1 i x dla x 1 f ( x) 1 3 dla
Akwizycja obrazów. Zagadnienia wstępne
 Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
8. TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO.
 WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
Wprowadzenie do cyfrowego przetwarzania obrazów medycznych.
 Przetwarzanie obrazów medycznych Wprowadzenie do cyfrowego przetwarzania obrazów medycznych. dr. inż Robert Kazała Diagnostyka obrazowa Diagnostyka obrazowa (obrazowanie medyczne) grupa badań wykorzystująca
Przetwarzanie obrazów medycznych Wprowadzenie do cyfrowego przetwarzania obrazów medycznych. dr. inż Robert Kazała Diagnostyka obrazowa Diagnostyka obrazowa (obrazowanie medyczne) grupa badań wykorzystująca
Przetwarzanie obrazów Grafika komputerowa. dr inż. Marcin Wilczewski 2016/2017
 Przetwarzanie obrazów Grafika komputerowa dr inż. Marcin Wilczewski 216/217 1 Zagadnienia, wykład, laboratorium Wykład: Reprezentacja danych multimedialnych na przykładzie obrazów cyfrowych oraz wideo.
Przetwarzanie obrazów Grafika komputerowa dr inż. Marcin Wilczewski 216/217 1 Zagadnienia, wykład, laboratorium Wykład: Reprezentacja danych multimedialnych na przykładzie obrazów cyfrowych oraz wideo.
GRAFIKA RASTROWA GRAFIKA RASTROWA
 GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
Modele i przestrzenie koloru
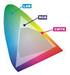 Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji wizualnej i modeli barw
 Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji i modeli barw Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 38 Wprowadzenie do
Wprowadzenie do grafiki maszynowej. Wprowadzenie do percepcji i modeli barw Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 38 Wprowadzenie do
Fotometria i kolorymetria
 13. x,y,y. Jednowymiarowe skale barw (długość fali dominującej i czystość bodźca; temperatura barwowa). Iluminanty i źródła normalne CIE. Układ CIE 1960 (u,v). Przestrzeń barw CIE 1964 (UVW). Układ CIE
13. x,y,y. Jednowymiarowe skale barw (długość fali dominującej i czystość bodźca; temperatura barwowa). Iluminanty i źródła normalne CIE. Układ CIE 1960 (u,v). Przestrzeń barw CIE 1964 (UVW). Układ CIE
Grafika Komputerowa. Percepcja wizualna i modele barw
 Grafika Komputerowa. Percepcja wizualna i modele barw Aleksander Denisiuk Polsko-Japońska Akademia Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk denisjuk@pja.edu.pl 1
Grafika Komputerowa. Percepcja wizualna i modele barw Aleksander Denisiuk Polsko-Japońska Akademia Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk denisjuk@pja.edu.pl 1
3. ZJAWISKO BARWY W SZKŁACH. Rodzaje POSTRZEGANIA
 3. ZJAWISKO BARWY W SZKŁACH Rodzaje POSTRZEGANIA Wyróżniamy trzy rodzaje POSTRZEGANIA: a) Skotopowe opiera się na czynności samych pręcików; duża czułośd na kontrast; brak widzenia barw; dostrzegane kontury
3. ZJAWISKO BARWY W SZKŁACH Rodzaje POSTRZEGANIA Wyróżniamy trzy rodzaje POSTRZEGANIA: a) Skotopowe opiera się na czynności samych pręcików; duża czułośd na kontrast; brak widzenia barw; dostrzegane kontury
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Grafika komputerowa. Dla DSI II
 Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach
 TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Kolorymetria. Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą.
 Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
Plan wykładu. Wykład 3. Rzutowanie prostokątne, widoki, przekroje, kłady. Rzutowanie prostokątne - geneza. Rzutowanie prostokątne - geneza
 Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM 1. 2. 3. 4. 5. 6. czytać dane przedstawione na diagramach i w tabelach przekształcać równania liniowe na równania równoważne ekształcać układy równań
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE III GIMNAZJUM 1. 2. 3. 4. 5. 6. czytać dane przedstawione na diagramach i w tabelach przekształcać równania liniowe na równania równoważne ekształcać układy równań
Geometria w R 3. Iloczyn skalarny wektorów
 Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
FUNKCJA LINIOWA. A) B) C) D) Wskaż, dla którego funkcja liniowa określona wzorem jest stała. A) B) C) D)
 FUNKCJA LINIOWA 1. Funkcja jest rosnąca, gdy 2. Wskaż, dla którego funkcja liniowa jest rosnąca Wskaż, dla którego funkcja liniowa określona wzorem jest stała. 3. Funkcja liniowa A) jest malejąca i jej
FUNKCJA LINIOWA 1. Funkcja jest rosnąca, gdy 2. Wskaż, dla którego funkcja liniowa jest rosnąca Wskaż, dla którego funkcja liniowa określona wzorem jest stała. 3. Funkcja liniowa A) jest malejąca i jej
Zad. 5: Układ równań liniowych liczb zespolonych
 Zad. 5: Układ równań liniowych liczb zespolonych 1 Cel ćwiczenia Wykształcenie zdolności abstrahowania operacji arytmetycznych od konkretnych typów. Unaocznienie problemów związanych z programowaniem uogólnionym
Zad. 5: Układ równań liniowych liczb zespolonych 1 Cel ćwiczenia Wykształcenie zdolności abstrahowania operacji arytmetycznych od konkretnych typów. Unaocznienie problemów związanych z programowaniem uogólnionym
Grafika komputerowa. Adam Wojciechowski
 Grafika komputerowa Adam Wojciechowski Grafika komputerowa Grafika komputerowa podstawowe pojęcia i zastosowania Grafika komputerowa - definicja Grafika komputerowa -dział informatyki zajmujący się wykorzystaniem
Grafika komputerowa Adam Wojciechowski Grafika komputerowa Grafika komputerowa podstawowe pojęcia i zastosowania Grafika komputerowa - definicja Grafika komputerowa -dział informatyki zajmujący się wykorzystaniem
Funkcje trygonometryczne w trójkącie prostokątnym
 Funkcje trygonometryczne w trójkącie prostokątnym Oznaczenia boków i kątów trójkąta prostokątnego użyte w definicjach Sinus Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
Funkcje trygonometryczne w trójkącie prostokątnym Oznaczenia boków i kątów trójkąta prostokątnego użyte w definicjach Sinus Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Rozdział VII. Przekształcenia geometryczne na płaszczyźnie Przekształcenia geometryczne Symetria osiowa Symetria środkowa 328
 Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
K O L O R Y M E T R I A
 Elektrotechnika Studia niestacjonarne K O L O R Y M E T R I A Rys. 1. Układ optyczny oka z zaznaczoną osią optyczną. Rogówka Źrenica Soczewka Jest soczewką wypukło-wklęsłą i ma kształt czaszy sferycznej.
Elektrotechnika Studia niestacjonarne K O L O R Y M E T R I A Rys. 1. Układ optyczny oka z zaznaczoną osią optyczną. Rogówka Źrenica Soczewka Jest soczewką wypukło-wklęsłą i ma kształt czaszy sferycznej.
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Przestrzenie barw. 1. Model RGB
 Przestrzenie barw Przeciętny człowiek, nie posiadający zaburzeń wzorku, potrafi dostrzec i opisać otaczające go barwy. Co prawda ilość rozpoznawanych odcieni kolorów bywa różna (wiek, płeć, indywidualne
Przestrzenie barw Przeciętny człowiek, nie posiadający zaburzeń wzorku, potrafi dostrzec i opisać otaczające go barwy. Co prawda ilość rozpoznawanych odcieni kolorów bywa różna (wiek, płeć, indywidualne
TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA SKIEROWANEGO
 TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Ś Ó Ł
 Ę Ę Ę Ę Ę Ń Ż ć ż ć Ś Ó Ł Ń Ó Ś Ó Ę ć ż Ó Ź ż Ó Ś ż Ó Ó Ś Ó Ó ż ż ć ć Ó ć ż Ż Ś Ś Ż Ó Ś ż Ó ź Ó Ś ż Ś Ś Ś Ę ż ć Ś Ś Ś ż Ż Ś ć ż Ó ć Ć ż Ó ć Ś Ś ż Ż ć ż Ś ż ż ż Ę Ę ż ż Ś ż ć Ż Ś ż Ż ż ć Ó Ę Ś Ł Ś Ś Ś
Ę Ę Ę Ę Ę Ń Ż ć ż ć Ś Ó Ł Ń Ó Ś Ó Ę ć ż Ó Ź ż Ó Ś ż Ó Ó Ś Ó Ó ż ż ć ć Ó ć ż Ż Ś Ś Ż Ó Ś ż Ó ź Ó Ś ż Ś Ś Ś Ę ż ć Ś Ś Ś ż Ż Ś ć ż Ó ć Ć ż Ó ć Ś Ś ż Ż ć ż Ś ż ż ż Ę Ę ż ż Ś ż ć Ż Ś ż Ż ż ć Ó Ę Ś Ł Ś Ś Ś
Wykład 2. Fotometria i kolorymetria
 Wykład 2 Fotometria i kolorymetria Fala elektromagnetyczna Fala elektromagnetyczna Światło widzialne Gwiazdy Temperatura barwowa Światło widzialne Pomiar światła - fotometria 1729 Pierre Bouger Essai
Wykład 2 Fotometria i kolorymetria Fala elektromagnetyczna Fala elektromagnetyczna Światło widzialne Gwiazdy Temperatura barwowa Światło widzialne Pomiar światła - fotometria 1729 Pierre Bouger Essai
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w.
 1. C e l s p o t k a n i a. C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w., ż e : B y d z b a w i o n y m
1. C e l s p o t k a n i a. C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w., ż e : B y d z b a w i o n y m
Wymagania edukacyjne z matematyki Klasa III zakres rozszerzony
 Wymagania edukacyjne z matematyki Klasa III zakres rozszerzony Program nauczania zgodnie z: Kurczab M., Kurczab E., Świda E., Program nauczania w liceach i technikach. Zakres Rozszerzony., Oficyna Edukacyjna
Wymagania edukacyjne z matematyki Klasa III zakres rozszerzony Program nauczania zgodnie z: Kurczab M., Kurczab E., Świda E., Program nauczania w liceach i technikach. Zakres Rozszerzony., Oficyna Edukacyjna
Ć ć ć Ś ć
 ź Ę Ę Ę ź ć ć ć Ć ć ć Ś ć ź ć ć ć Ć Ś ź Ś Ć ć Ż ź ć Ż Ś Ł ŚĆ ć ć ć Ć ć Ść ć Ż ć ć ć ć ć ć ć ć Ą ć ć Ś ć Ś ć Ż Ś ć Ó ć Ś ć Ś ć ć ć ć Ś ć ć Ś ć Ć Ż ć Ć ć ć ć ć Ę ć ź ć ć ć ć ć ź ć ć ć Ć ź ć Ż ć ć ć Ś ć Ć
ź Ę Ę Ę ź ć ć ć Ć ć ć Ś ć ź ć ć ć Ć Ś ź Ś Ć ć Ż ź ć Ż Ś Ł ŚĆ ć ć ć Ć ć Ść ć Ż ć ć ć ć ć ć ć ć Ą ć ć Ś ć Ś ć Ż Ś ć Ó ć Ś ć Ś ć ć ć ć Ś ć ć Ś ć Ć Ż ć Ć ć ć ć ć Ę ć ź ć ć ć ć ć ź ć ć ć Ć ź ć Ż ć ć ć Ś ć Ć
ż ć
 Ł Ł ż ć ć ż ć Ą Ł ó ó ć ż ć ć ż ć Ę ć Ę ć ć Ę ć ć ć Ę ż ć ć ć Ś ć Ę Ę ż ż ć ż Ę ć ć Ę ż ż Ę Ł ć ć Ą Ę Ł ć ć ć ż ć Ę Ł Ść Ą Ę Ł ć ć ć ć Ę Ł Ść Ą Ę Ł ć ć ć Ł ć Ę Ę ć ć ć ć Ł Ść ć ć Ę Ę Ł Ś Ą Ś Ś Ł Ą Ą ż
Ł Ł ż ć ć ż ć Ą Ł ó ó ć ż ć ć ż ć Ę ć Ę ć ć Ę ć ć ć Ę ż ć ć ć Ś ć Ę Ę ż ż ć ż Ę ć ć Ę ż ż Ę Ł ć ć Ą Ę Ł ć ć ć ż ć Ę Ł Ść Ą Ę Ł ć ć ć ć Ę Ł Ść Ą Ę Ł ć ć ć Ł ć Ę Ę ć ć ć ć Ł Ść ć ć Ę Ę Ł Ś Ą Ś Ś Ł Ą Ą ż
Przenośne urządzenia pomiarowe...59. Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64
 Barwa - wprowadzenie...55 Przenośne urządzenia pomiarowe...59 Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64 Wyposażenie do przenośnych urządzeń pomiarowych...66
Barwa - wprowadzenie...55 Przenośne urządzenia pomiarowe...59 Nowy spectro-guide...59 Color-guide do małych detali...64 Color-guide do proszków... 64 Wyposażenie do przenośnych urządzeń pomiarowych...66
ć Ś Ś Ść
 ć Ś Ś Ść Ś Ł Ź Ść ć ć ć Ść ć Ść Ś Ść ć ć Ś Ó Ś Ś ć ć Ś Ś Ó Ś Ś ć Ą ć Ś Ś Ł ć Ś Ś Ł ć Ą Ść ć Ś Ó Ź ć ć Ś Ś ć ć ć Ś Ść Ść Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ą Ś Ą Ś Ś Ź Ź ć ć Ś Ę Ź Ł ź Ę Ę Ś Ś Ś Ę Ą Ź ć Ł Ś Ś Ś Ś ć Ś
ć Ś Ś Ść Ś Ł Ź Ść ć ć ć Ść ć Ść Ś Ść ć ć Ś Ó Ś Ś ć ć Ś Ś Ó Ś Ś ć Ą ć Ś Ś Ł ć Ś Ś Ł ć Ą Ść ć Ś Ó Ź ć ć Ś Ś ć ć ć Ś Ść Ść Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ą Ś Ą Ś Ś Ź Ź ć ć Ś Ę Ź Ł ź Ę Ę Ś Ś Ś Ę Ą Ź ć Ł Ś Ś Ś Ś ć Ś
ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć
 Ł Ź Ł Ł ź ź Ż Ż ż Ż ć Ś ż ć ć Ę ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć Ł ć ć ć ć Ł Ż ć Ł ź ć Ś Ż Ż Ż ż Ż Ż ż Ż Ś Ż Ą Ł Ż ź Ż Ż Ż Ż Ż Ż Ś Ż Ż ż Ż Ż ż ż Ł Ż Ś Ż Ż Ż Ż Ż Ż Ś Ż Ę Ł Ź Ó ż Ę Ł ź Ł Ź Ż ż Ł Ż Ż ż
Ł Ź Ł Ł ź ź Ż Ż ż Ż ć Ś ż ć ć Ę ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć Ł ć ć ć ć Ł Ż ć Ł ź ć Ś Ż Ż Ż ż Ż Ż ż Ż Ś Ż Ą Ł Ż ź Ż Ż Ż Ż Ż Ż Ś Ż Ż ż Ż Ż ż ż Ł Ż Ś Ż Ż Ż Ż Ż Ż Ś Ż Ę Ł Ź Ó ż Ę Ł ź Ł Ź Ż ż Ł Ż Ż ż
Inżynieria obrazów cyfrowych. Ćwiczenie 3. Wybrane modele kolorów i ich zastosowania
 Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Inżynieria obrazów cyfrowych Ćwiczenie 3 Wybrane modele kolorów i ich zastosowania
Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Inżynieria obrazów cyfrowych Ćwiczenie 3 Wybrane modele kolorów i ich zastosowania
Ćwiczenie 42 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ. Wprowadzenie teoretyczne.
 Ćwiczenie 4 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ Wprowadzenie teoretyczne. Soczewka jest obiektem izycznym wykonanym z materiału przezroczystego o zadanym kształcie i symetrii obrotowej. Interesować
Ćwiczenie 4 WYZNACZANIE OGNISKOWEJ SOCZEWKI CIENKIEJ Wprowadzenie teoretyczne. Soczewka jest obiektem izycznym wykonanym z materiału przezroczystego o zadanym kształcie i symetrii obrotowej. Interesować
ć
 Ł Ę Ę Ą ć Ś ć ć ź ź ć ć ź ź ź ć ć ź Ś ć ć ć ć ć Ś ć Ż ć ŚĆ Ć Ż Ś Ż Ś Ż ć Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ć ć Ć ć Ć ć Ś Ś Ś ć Ć Ż Ć ć ć Ś Ż Ż Ś Ć Ż ć ć ć ć ć Ś Ś Ś ć Ż Ż ć ć Ś Ś ć Ś Ż ć Ś ć ć ć Ż Ć ć ć Ż Ś Ż Ć
Ł Ę Ę Ą ć Ś ć ć ź ź ć ć ź ź ź ć ć ź Ś ć ć ć ć ć Ś ć Ż ć ŚĆ Ć Ż Ś Ż Ś Ż ć Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ć ć Ć ć Ć ć Ś Ś Ś ć Ć Ż Ć ć ć Ś Ż Ż Ś Ć Ż ć ć ć ć ć Ś Ś Ś ć Ż Ż ć ć Ś Ś ć Ś Ż ć Ś ć ć ć Ż Ć ć ć Ż Ś Ż Ć
Ą Ź ć ć Ó Ó Ć Ć Ś
 Ł Ł ź Ę Ą Ą Ź ć ć Ó Ó Ć Ć Ś Ł Ą Ą Ó ć ć ć Ś Ś Ó Ś Ó Ó Ó Ó Ó Ó Ó ć Ść Ó Ć ć Ź Ó ć Ó Ó Ó Ś Ź Ó ć ć ć Ł Ć Ź Ó Ó Ś ć Ź ć ć Ć ć ć ć Ź Ó ć Ó Ó Ś Ź Ó Ó Ś Ó ć ć ć Ś Ś Ó Ó Ó ć Ź Ł Ó ć Ś Ś Ó Ó ć Ź ć Ź Ł Ó Ó ć Ź
Ł Ł ź Ę Ą Ą Ź ć ć Ó Ó Ć Ć Ś Ł Ą Ą Ó ć ć ć Ś Ś Ó Ś Ó Ó Ó Ó Ó Ó Ó ć Ść Ó Ć ć Ź Ó ć Ó Ó Ó Ś Ź Ó ć ć ć Ł Ć Ź Ó Ó Ś ć Ź ć ć Ć ć ć ć Ź Ó ć Ó Ó Ś Ź Ó Ó Ś Ó ć ć ć Ś Ś Ó Ó Ó ć Ź Ł Ó ć Ś Ś Ó Ó ć Ź ć Ź Ł Ó Ó ć Ź
ć ć ź ć ć ć Ść ć ź ź ź ć ź Ą ź
 ć ć ć ź ć ć ć ć ź ć Ż ź ź ć ć ź ć ć ć Ść ć ź ź ź ć ź Ą ź ć ć ć ć ć ć ź ź Ż ć ć ć ć ć Ś ć ć Ź ć Ś ź ć ź ć ź ć ź ć ź Ź ć ć Ś ź ć ć ź Ć ć ź Ó Ż ć ć ź Ś ź ź ć ć ć ź ć ć ć ć ć ć ć ź ź ć ć ć Ś Ć Ó ź ć ź ć ć
ć ć ć ź ć ć ć ć ź ć Ż ź ź ć ć ź ć ć ć Ść ć ź ź ź ć ź Ą ź ć ć ć ć ć ć ź ź Ż ć ć ć ć ć Ś ć ć Ź ć Ś ź ć ź ć ź ć ź ć ź Ź ć ć Ś ź ć ć ź Ć ć ź Ó Ż ć ć ź Ś ź ź ć ć ć ź ć ć ć ć ć ć ć ź ź ć ć ć Ś Ć Ó ź ć ź ć ć
Fotometria i kolorymetria
 10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
Obliczenie punktu przecięcia półprostej i płaszczyzny w przestrzeni 3-D wymaga rozwiązania równania liniowego.
 RÓWNANIA, PRAWA, WZORY Obliczenie punktu przecięcia półprostej i płaszczyzny w przestrzeni 3-D wymaga rozwiązania równania liniowego. Znalezienie punktu przecięcia powierzchni kwadryki i półprostej wymaga
RÓWNANIA, PRAWA, WZORY Obliczenie punktu przecięcia półprostej i płaszczyzny w przestrzeni 3-D wymaga rozwiązania równania liniowego. Znalezienie punktu przecięcia powierzchni kwadryki i półprostej wymaga
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
ć ć Ą ć Ęć Ó Ą ź ć ć ć ć ź ź Ą ć Ę ć ź ć ć ć ź ć ź ć ć ć Ś Ź ź
 ź Ó ć Ę ć Ó ć ć ć ć Ź ć ź ć ć Ź ć ć ć Ą ć Ęć Ó Ą ź ć ć ć ć ź ź Ą ć Ę ć ź ć ć ć ź ć ź ć ć ć Ś Ź ź ć Ą ć Ą ć ź ć ź ć Ę ć ć Ź ź Ę ć ć ć ć Ę Ę ź ć Ó ć ć ć ć ć ć ć ć ć Ź Ź ć ć ć ź Ę ć ć ć ć Ę Ąć ź Ź ć Ą ć ć
ź Ó ć Ę ć Ó ć ć ć ć Ź ć ź ć ć Ź ć ć ć Ą ć Ęć Ó Ą ź ć ć ć ć ź ź Ą ć Ę ć ź ć ć ć ź ć ź ć ć ć Ś Ź ź ć Ą ć Ą ć ź ć ź ć Ę ć ć Ź ź Ę ć ć ć ć Ę Ę ź ć Ó ć ć ć ć ć ć ć ć ć Ź Ź ć ć ć ź Ę ć ć ć ć Ę Ąć ź Ź ć Ą ć ć
Ś Ż Ó Ś ż Ó ć ź ż ż Ą
 Ś ż Ż Ż Ś Ż Ó ż ż ż Ą Ś Ż Ó Ś ż Ó ć ź ż ż Ą Ą Ó ż ż Ó Ś Ż Ó ż ż ż Ż Ź ź Ć Ó ż Ż ć Ż ż Ś ć Ś Ś Ż Ą Ż Ż Ó Ż Ż Ś Ż Ż Ź Ż Ż Ż Ę Ś Ż Ż Ś Ó Ż Ż ż Ą Ż Ą Ż Ś Ś ć Ź ć ć Ó ć Ś Ą Ó Ó ć Ż ż Ż Ó ż Ś Ś Ó Ś Ż Ż Ż Ż Ż
Ś ż Ż Ż Ś Ż Ó ż ż ż Ą Ś Ż Ó Ś ż Ó ć ź ż ż Ą Ą Ó ż ż Ó Ś Ż Ó ż ż ż Ż Ź ź Ć Ó ż Ż ć Ż ż Ś ć Ś Ś Ż Ą Ż Ż Ó Ż Ż Ś Ż Ż Ź Ż Ż Ż Ę Ś Ż Ż Ś Ó Ż Ż ż Ą Ż Ą Ż Ś Ś ć Ź ć ć Ó ć Ś Ą Ó Ó ć Ż ż Ż Ó ż Ś Ś Ó Ś Ż Ż Ż Ż Ż






















