Fotometria i kolorymetria
|
|
|
- Filip Król
- 6 lat temu
- Przeglądów:
Transkrypt
1 12. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK). Miejsce i termin konsultacji (zima 2013/2014): pokój 18/11 bud. A-1
2 UKŁADY BARW CIE 1931 Ustalone tam zalecenia formułowały zasady wprowadzenia tzw. normalnego obserwatora kolometrycznego, wprowadzenie źródeł normalnych A, B, C oraz ustalenia warunków oświetlenia i obserwowania powierzchni odbijających. Obserwator normalny kąt pola widzenia barw 2 stopnie.
3 UKŁAD BODŹCÓW FIZYCZNYCH [R G B] Bodźcami głównymi są bodźce nazwane: R, G, B nm [R] z tej części czerwieni, w której zanika zdolność rozróżniania odcieni; - 546,1nm [G] i 435,8nm [B] prążki łuku rtęciowego. Luminancje jednostkowych ilości tych bodźców są w stosunku: L r : Lg : Lb 1,000: 4,5907: 0,0601
4 WYKRES CHROMATYCZNOŚCI [R G B]
5 KRZYWA BARW WIDMOWYCH (spectrum locus) miejsce geometryczne stanowiące zbiór o współrzędnych trójchromatycznych promieniowania monochromatycznego: r g b r r r g b
6 SKŁADOWE TRÓJCHROMATYCZNE WIDMOWE [R G B]
7 WYKRES CHROMATYCZNOŚCI [R G B] z krzywą barw widmowych
8 UKŁAD BODŹCÓW FIKCYJNYCH (X Y Z) CIE ) Żadna część krzywej barw widmowych nie powinna być znacznie bliżej punktu promieniowania równoenergetycznego niż inne; 2) Jeden z boków nowego trójkąta barw powinien być styczny do krzywej barw widmowych w jej końcu długofalowym; 3) Drugi bok trójkąta barw powinien być możliwie zbliżony do krzywej barw widmowych; 4) Długość fali dominującej jednego z nowych bodźców powinna odpowiadać promieniowaniu, które w zwykłych warunkach widzenia jest postrzegane jako jednoznacznie niebieskie; 5) Trzecim bokiem nowego trójkąta powinno być miejsce geometryczne punktów barw fikcyjnych o luminancji równej zeru.
9 BODŹCE O LUMINANCJI ZEROWEJ Luminancja każdej barwy w układzie bodźców głównych [RGB] jest równa sumie luminancji trzech składowych. C L C r R r L r g G g L W nowym układzie ma być proporcjonalna do luminancji jednego tylko bodźca! Równanie względnej luminancji jednostek bodźców układu [RGB]: k LC 1,000 r 4,5907 g 0, 0601b Po podstawieniu b=1-(r+g) daje to: k L C g b 0,9399 r 4,5306 g B b L b 0,0601
10 BODŹCE O LUMINANCJI ZEROWEJ Zatem miejscami geometrycznymi barw o stałej luminancji w przestrzeni barw [RGB] są płaszczyzny równoległe określone równaniem: 1,000 R 4,5907G 0, 0601B const A na płaszczyźnie trójkąta barw w tym układzie proste równoległe: 0,9399 r 4,5306 g 0, 0601 const
11 BODŹCE O LUMINANCJI ZEROWEJ - ALYCHNE Na jednej z tych prostych: 0,9399 r 4,5306 g 0, leżą punkty o luminancji zerowej nazywa się ona alychne. Alychne przecina oś odciętych w punkcie r=-0,0640 a oś rzędnych w punkcie g=-0,0133.
12 UKŁAD [R G B] A UKŁAD (X Y Z) Równania trójchromatyczne jednostkowe nowych bodźców odniesienia w funkcji bodźców głównych, wiążące oba układy, są dane przez: X 1,2750 R 0,2778 G 0, 0028 Y 1,7393 R 2,7673 G Z 0,7431 R 0,1409 G 1, 6022 B B B
13 UKŁAD [R G B] A UKŁAD (X Y Z) Zależność podana w uchwale CIE ujęta została odwrotnie: R 0,73469 X 0,26531 Y 0, G 0,27368 X 0,71743 Y 0, B 0,16654 X 0,00888 Y 0, Z Z Z
14 SKŁADOWE TRÓJCHROMATYCZNE WIDMOWE W UKŁADZIE (X Y Z) CIE 1931.
15 WYKRES CHROMATYCZNOŚCI (x,y)
16 LINIE BARW NIEODRÓŻNIANE PRZEZ PROTANOPÓW
17 LINIE BARW NIEODRÓŻNIANE PRZEZ DEUTERANOPÓW
18 LINIE BARW NIEODRÓŻNIANE PRZEZ TRITANOPÓW
19 UKŁAD (X 10 Y 10 Z 10 ) CIE 1964 Obserwator kolorymetryczny normalny CIE 1931 określony jest dla wąskiego, dwustopniowego pola fotometrycznego. Tymczasem porównywanie i zrównywanie barw w procesach przemysłowych opiera się często na obserwacjach wzrokowych prowadzonych w szerokim polu widzenia. Obserwator związany z polem widzenia 10 (dodatkowy, normalny obserwator kolorymetryczny)
20 UKŁAD (X 10 Y 10 Z 10 ) CIE 1964
21 MUTACJE UKŁADU RBG CIE 1931 W monitorach telewizji kolorowej i niektórych sposobach reprodukcji obrazów stosuje się określanie barw w układzie RGB, ale ze względu na stosowane luminofory bodźce główne mają inne współrzędne trójchromatyczne. Luminofory EBU, SMPTE, NTSC
22 UKŁADY CMY, CMYK Podczas odtwarzania barw nie zawsze zachodzi proces mieszania wybranych kolorów podstawowych. Częściej barwy tworzy się przez oświetlanie obiektów kolorowych światłem białym. Filtry pochłaniają pewien kolor a do obserwatora dociera światło mające barwę dopełniająca do pochłoniętej. Gdy filtr pochłania czerwień (R) do obserwatora dochodzi cyjan (C); gdy zieleń (G) dochodzi magenta (M); gdy niebieski (B) obserwator widzi żółty (Y, yellow). W przypadkach złożonych obserwator widzi efekt mieszania się barw C,M,Y. Barwy podstawowe układu CMY są dopełniające do RGB. Dopełniająca jest też luminancja. C 1 R Wartości C=M=Y=1 odpowiada kolor czarny. M Y 1 1 G B
23 UKŁADY CMY, CMYK Co przedstawiają obrazki?; -)
24 UKŁADY CMY, CMYK Sposób powstawania barwnych obrazów, wykorzystujących to subtraktywne mieszanie barw polega na mieszaniu barwników np. w druku. Światło białe pada na powierzchnię pokrytą czterema warstwami częściowo przepuszczającego światło atramentu czwartą warstwą jest atrament czarny K, służący do korygowania baw o małej luminancji.
25 UKŁADY CMY, CMYK Inny sposób wykorzystano m.in. w komputerowych drukarkach atramentowych i niektórych technikach poligraficznych. Polega on na pokryciu powierzchni kartki mikroskopijnymi punktami atramentów C,M,Y,K oko nie widzi poszczególnych punktów, ale ich uśrednione działanie (raster!).
26 UKŁADY CMY, CMYK Przy stosowaniu techniki rastrowej, w celu uniknięcia efektu Moiry, stosuje się układ rastrów dla poszczególnych kolorów CMYK inne kąty.
27 Płaszczyzna barw PRZYPOMNIENIE: Przekształcenie przestrzeni barw Aby przekształcić jedną przestrzeń (płaszczyznę) barw na inną, należy: a) rozłożyć wektor barwy [C] na składowe wzdłuż osi nowego układu; b) rozłożyć wektor bodźca równoenergetycznego [E] na składowe wzdłuż osi nowego układu; c) obliczyć składowe trójchromatyczne bodźca (C) jako stosunek wartości składowych [C] do wartości składowych [E]; d) obliczyć współrzędne trójchromatyczne bodźca (C) jako stosunek jego składowych trójchromatycznych do ich sumy.
28 Przekształcenie płaszczyzny barw Przekształcenie płaszczyzny barw Przykład graficznego wyznaczenia współrzędnych trójchromatycznych barwy przy przejściu z układu (X Y Z) do [R G B]
29 Przekształcenie płaszczyzny barw Współrzędne trójchromatyczne barwy (C) w układzie (X Y Z): x y z 0,450 0,400 0,150
30 Przekształcenie płaszczyzny barw Udział barwy (R) w stosunku do barwy (P): PC CR 0,230 0,310 (pamiętajmy, że długości odcinków są odwrotnie proporcjonalne do udziału danej barwy w mieszaninie!) Względny udział barw (G) i (B): BP PG 0,500 0,215 BP PG 0,715
31 Przekształcenie płaszczyzny barw PC CR 0,230 0,310 BP PG 0,500 0,215 BP PG 0,715 A więc udział nowych bodźców odniesienia (R), (G) i (B) w barwie (C) (ale ciągle jeszcze wyrażony w jednostkach trójchromatycznych układu (X Y Z)!) wynosi: 0,230; 0,500 0,715 0,215 0,715 0,310 0,310 0,217; 0,093;
32 Przekształcenie płaszczyzny barw Celem jest jednak wyrażenie barwy (C) w jednostkach układu [R G B] nie są one proporcjonalne do powyższych, bo punkt E bodźca równoenergetycznego nie leży w środku trójkąta (R,G,B). Trzeba znowu wyrazić ten bodziec poprzez udział poszczególnych składowych. Mierząc analogiczne odcinki dla punktu (E): EQ 3 RQ 0,667 ES 3 GS 1,132 ET 3 BT 1,201
33 Przekształcenie płaszczyzny barw W nowej skali otrzymujemy więc: R G B 0,230 0,667 0,217 1,132 0,093 1,201 0,344 0,192 0,077 A współrzędne trójchromatyczne bodźca [C] w układzie [R G B] wyrażone są ostatecznie jako: R G B r 0,563 g 0, 312 b 0, 125 R G B R G B R G B
Fotometria i kolorymetria
 13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
13. (współrzędne i składowe trójchromatyczne promieniowania monochromatycznego; układ bodźców fizycznych RGB; krzywa barw widmowych; układ barw CIE 1931 (XYZ); alychne; układy CMY i CMYK) http://www.if.pwr.wroc.pl/~wozniak/
Luminancja jako jednostka udziału barwy składowej w mierzonej:
 Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Luminancja jako jednostka udziału barwy składowej w mierzonej: L : L : L 1,0000: 4,5907 :0,0601 L L : L 98,9%:1,1 % WNIOSEK: Trzeba wprowadzić skalę, w której luminancja trzech bodźców byłaby oceniana
Janusz Ganczarski CIE XYZ
 Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
Janusz Ganczarski CIE XYZ Spis treści Spis treści..................................... 1 1. CIE XYZ................................... 1 1.1. Współrzędne trójchromatyczne..................... 1 1.2. Wykres
Pojęcie Barwy. Grafika Komputerowa modele kolorów. Terminologia BARWY W GRAFICE KOMPUTEROWEJ. Marek Pudełko
 Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
Grafika Komputerowa modele kolorów Marek Pudełko Pojęcie Barwy Barwa to wrażenie psychiczne wywoływane w mózgu człowieka i zwierząt, gdy oko odbiera promieniowanie elektromagnetyczne z zakresu światła
WYKŁAD 11. Kolor. fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony
 WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
WYKŁAD 11 Modelowanie koloru Kolor Światło widzialne fiolet, indygo, niebieski, zielony, żółty, pomarańczowy, czerwony ~400nm ~700nm Rozróżnialność barw (przeciętna): 150 czystych barw Wrażenie koloru-trzy
PODSTAWY BARWY, PIGMENTY CERAMICZNE
 PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
PODSTAWY BARWY, PIGMENTY CERAMICZNE Barwa Barwą nazywamy rodzaj określonego ilościowo i jakościowo (długość fali, energia) promieniowania świetlnego. Głównym i podstawowym źródłem doznań barwnych jest
WYKŁAD 14 PODSTAWY TEORII BARW. Plan wykładu: 1. Wrażenie widzenia barwy. Wrażenie widzenia barwy Modele liczbowe barw
 WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
WYKŁAD 14 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? PODSTAWY TEOII AW Światło Przedmiot (materia) Organ wzrokowy człowieka Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw
PODSTAWY TEORII BARW
 WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
WYKŁAD 12 PODSTAWY TEORII BARW Plan wykładu: Wrażenie widzenia barwy Modele liczbowe barw 1. Wrażenie widzenia barwy Co jest potrzebne aby zobaczyć barwę? Światło Przedmiot (materia) Organ wzrokowy człowieka
Teoria światła i barwy
 Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
Teoria światła i barwy Powstanie wrażenia barwy Światło może docierać do oka bezpośrednio ze źródła światła lub po odbiciu od obiektu. Z oka do mózgu Na siatkówce tworzony pomniejszony i odwrócony obraz
MODELE KOLORÓW. Przygotował: Robert Bednarz
 MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
MODELE KOLORÓW O czym mowa? Modele kolorów,, zwane inaczej systemami zapisu kolorów,, są różnorodnymi sposobami definiowania kolorów oglądanych na ekranie, na monitorze lub na wydruku. Model RGB nazwa
Fotometria i kolorymetria
 11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
11. Mieszanie barw (addytywne równoczesne i następcze; subtraktywne); metameryzm; prawa rassmanna. Jednostka trójchromatyczna; równanie trójchromatyczne; przestrzeń i płaszczyzna barw; przekształcenie
Kolor w grafice komputerowej. Światło i barwa
 Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Kolor w grafice komputerowej Światło i barwa Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe składa się ze wszystkich długości
Modele i przestrzenie koloru
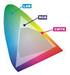 Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Modele i przestrzenie koloru Pantone - międzynarodowy standard identyfikacji kolorów do celów przemysłowych (w tym poligraficznych) opracowany i aktualizowany przez amerykańską firmę Pantone Inc. System
Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw.
 Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Modele barw Do opisu kolorów używanych w grafice cyfrowej śluzą modele barw. Każdy model barw ma własna przestrzeo kolorów, a co za tym idzie- własny zakres kolorów możliwych do uzyskania oraz własny sposób
Kolorymetria. Akademia Sztuk Pięknych Gdańsk październik Dr inŝ. Paweł Baranowski
 Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Kolorymetria Akademia Sztuk Pięknych Gdańsk październik 2004 Dr inŝ. Paweł Baranowski Eksperymenty Newtona Angielski fizyk Isaac Newton (1643-1727) odkrył w 1704 roku podczas badań, ze światło słoneczne,
Anna Barwaniec Justyna Rejek
 CMYK Anna Barwaniec Justyna Rejek Wstęp, czyli czym jest tryb koloru? Tryb koloru wyznacza metodę wyświetlania i drukowania kolorów danego obrazu pozwala zmieniać paletę barw zastosowaną do tworzenia danego
CMYK Anna Barwaniec Justyna Rejek Wstęp, czyli czym jest tryb koloru? Tryb koloru wyznacza metodę wyświetlania i drukowania kolorów danego obrazu pozwala zmieniać paletę barw zastosowaną do tworzenia danego
Dzień dobry. Miejsce: IFE - Centrum Kształcenia Międzynarodowego PŁ, ul. Żwirki 36, sala nr 7
 Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
Dzień dobry BARWA ŚWIATŁA Przemysław Tabaka e-mail: przemyslaw.tabaka@.tabaka@wp.plpl POLITECHNIKA ŁÓDZKA Instytut Elektroenergetyki Co to jest światło? Światło to promieniowanie elektromagnetyczne w zakresie
M10. Własności funkcji liniowej
 M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
K O L O R Y M E T R I A
 Elektrotechnika Studia niestacjonarne K O L O R Y M E T R I A Rys. 1. Układ optyczny oka z zaznaczoną osią optyczną. Rogówka Źrenica Soczewka Jest soczewką wypukło-wklęsłą i ma kształt czaszy sferycznej.
Elektrotechnika Studia niestacjonarne K O L O R Y M E T R I A Rys. 1. Układ optyczny oka z zaznaczoną osią optyczną. Rogówka Źrenica Soczewka Jest soczewką wypukło-wklęsłą i ma kształt czaszy sferycznej.
Fotometria i kolorymetria
 10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
10. Opis barwy; cechy psychofizyczne barwy; indukcja przestrzenna i czasowa; widmo bodźca a wrażenie barwne; wady postrzegania barw; testy Ishihary. http://www.if.pwr.wroc.pl/~wozniak/ Miejsce i termin
Kurs grafiki komputerowej Lekcja 2. Barwa i kolor
 Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Barwa i kolor Barwa to zjawisko, które zachodzi w trójkącie: źródło światła, przedmiot i obserwator. Zjawisko barwy jest wrażeniem powstałym u obserwatora, wywołanym przez odpowiednie długości fal świetlnych,
Kolorymetria. Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą.
 Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
Kolorymetria Wykład opracowany m.in. dzięki materiałom dra W.A. Woźniaka, za jego zgodą. Widmo światła białego 400-450 nm - fiolet 450-500 nm - niebieski 500-560 nm - zielony 560-590 nm - żółty 590-630
GRAFIKA RASTROWA GRAFIKA RASTROWA
 GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
GRAFIKA KOMPUTEROWA GRAFIKA RASTROWA GRAFIKA RASTROWA (raster graphic) grafika bitmapowa: prezentacja obrazu za pomocą pionowo-poziomej siatki odpowiednio kolorowanych pikseli na monitorze komputera, drukarce
Akwizycja obrazów. Zagadnienia wstępne
 Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
Akwizycja obrazów. Zagadnienia wstępne Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 A. Przelaskowski, Techniki Multimedialne,
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE
 OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
OP6 WIDZENIE BARWNE I FIZYCZNE POCHODZENIE BARW W PRZYRODZIE I. Wymagania do kolokwium: 1. Fizyczne pojęcie barwy. Widmo elektromagnetyczne. Związek między widmem światła i wrażeniem barwnym jakie ono
Tajemnice koloru, część 1
 Artykuł pobrano ze strony eioba.pl Tajemnice koloru, część 1 Jak działa pryzmat? Dlaczego kolory na monitorze są inne niż atramenty w drukarce? Możemy na to odpowiedzieć, uświadamiając sobie, że kolory
Artykuł pobrano ze strony eioba.pl Tajemnice koloru, część 1 Jak działa pryzmat? Dlaczego kolory na monitorze są inne niż atramenty w drukarce? Możemy na to odpowiedzieć, uświadamiając sobie, że kolory
Laboratorium Grafiki Komputerowej Przekształcenia na modelach barw
 Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Laboratorium rafiki Komputerowej Przekształcenia na modelach barw mgr inż. Piotr Stera Politechnika Śląska liwice 2004 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi modelami barw stosowanymi
Adam Korzeniewski p Katedra Systemów Multimedialnych
 Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych Zastosowania grafiki komputerowej Światło widzialne Fizjologia narządu wzroku Metody powstawania barw Modele barw
Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych Zastosowania grafiki komputerowej Światło widzialne Fizjologia narządu wzroku Metody powstawania barw Modele barw
Przetwarzanie obrazów wykład 1. Adam Wojciechowski
 Przetwarzanie obrazów wykład 1 Adam Wojciechowski Teoria światła i barwy Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe
Przetwarzanie obrazów wykład 1 Adam Wojciechowski Teoria światła i barwy Światło Spektrum światła białego: 400nm 700nm fiolet - niebieski - cyan - zielony - żółty - pomarańczowy - czerwony Światło białe
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 4 listopada 2013 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Grafika komputerowa. Adam Wojciechowski
 Grafika komputerowa Adam Wojciechowski Grafika komputerowa Grafika komputerowa podstawowe pojęcia i zastosowania Grafika komputerowa - definicja Grafika komputerowa -dział informatyki zajmujący się wykorzystaniem
Grafika komputerowa Adam Wojciechowski Grafika komputerowa Grafika komputerowa podstawowe pojęcia i zastosowania Grafika komputerowa - definicja Grafika komputerowa -dział informatyki zajmujący się wykorzystaniem
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach
 TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
TEORIA BARW (elementy) 1. Podstawowe wiadomości o barwach definicja barwy (fizjologiczna) wrażenie wzrokowe powstałe w mózgu na skutek działającego na oko promieniowania 1 maszyny nie posiadają tak doskonałego
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy.
 Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
Współrzędne trójchromatyczne x,y określają chromatyczność barwy, składowa Y wyznacza od razu jasność barwy. Barwa achromatyczna (biała) ma w tej skali jasność Y=100, gdy zakres promieniowania obejmuje
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 WYDZIAŁ Podstawowych Problemów Techniki Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim..fotometria i kolorymetria. Nazwa w języku angielskim.photometry and colorimetry. Kierunek studiów
WYDZIAŁ Podstawowych Problemów Techniki Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim..fotometria i kolorymetria. Nazwa w języku angielskim.photometry and colorimetry. Kierunek studiów
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli
 Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
Białość oznaczana jednostką CIE, oznacza wzrokowy odbiór białego papieru, do którego produkcji wykorzystano (lub nie) wybielacze optyczne (czyli poddano procesowi wybielania), z zachowaniem parametrów
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
Newton Isaac ( ), fizyk, matematyk, filozof i astronom angielski.
 Pierwsze wyjaśnienie bogactwa barw w świecie zawdzięczamy geniuszowi Newtona. Oto jak opisuje on jedno ze swych doświadczeń: W roku 1666 sporządziłem sobie trójkątny pryzmat szklany, aby za jego pomocą
Pierwsze wyjaśnienie bogactwa barw w świecie zawdzięczamy geniuszowi Newtona. Oto jak opisuje on jedno ze swych doświadczeń: W roku 1666 sporządziłem sobie trójkątny pryzmat szklany, aby za jego pomocą
PROBLEMATYKA DOBORU KOLORÓW
 PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
PROBLEMATYKA DOBORU KOLORÓW DO CELÓW DIAGNOZOWANIA ZABURZEŃ WIDZENIA BARW MACIEJ LASKOWSKI M.LASKOWSKI@POLLUB.PL LABORATORIUM AKWIZYCJI RUCHU I ERGONOMII INTERFEJSÓW INSTYTUT INFORMATYKI POLITECHNIKA LUBELSKA
Funkcja liniowa - podsumowanie
 Funkcja liniowa - podsumowanie 1. Funkcja - wprowadzenie Założenie wyjściowe: Rozpatrywana będzie funkcja opisana w dwuwymiarowym układzie współrzędnych X. Oś X nazywana jest osią odciętych (oś zmiennych
Funkcja liniowa - podsumowanie 1. Funkcja - wprowadzenie Założenie wyjściowe: Rozpatrywana będzie funkcja opisana w dwuwymiarowym układzie współrzędnych X. Oś X nazywana jest osią odciętych (oś zmiennych
Komunikacja Człowiek-Komputer
 Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Komunikacja Człowiek-Komputer Kolory Wojciech Jaśkowski Instytut Informatyki Politechnika Poznańska Wersja: 10 sierpnia 2016 Światło Źródło: Practical Colour management R. Griffith Postrzegany kolor zależy
Wprowadzenie do cyfrowego przetwarzania obrazów
 Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
Cyfrowe przetwarzanie obrazów I Wprowadzenie do cyfrowego przetwarzania obrazów dr. inż Robert Kazała Barwa Z fizycznego punktu widzenia światło jest promieniowaniem elektromagnetycznym, które wyróżnia
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
BARWA. Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle;
 BARWA Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle; Barwa psychofizyczna scharakteryzowanie bodźców świetlnych, wywołujących wrażenie barwy; ODRÓŻNIENIE BARW KOLORYMETR
BARWA Barwa postrzegana opisanie cech charakteryzujących wrażenie, jakie powstaje w umyśle; Barwa psychofizyczna scharakteryzowanie bodźców świetlnych, wywołujących wrażenie barwy; ODRÓŻNIENIE BARW KOLORYMETR
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
KOLORY KOMPLEMENTARNE
 BARWY W DRUKU KOŁO (BARW) KOLORÓW KOLORY KOMPLEMENTARNE PODWÓJNE DOPEŁNIENIE DOPEŁNIENIE TRÓJDZIELNE KOLORY SĄSIADUJĄCE MIESZANIE BARW Synteza addytywna - polega na nakładaniu się na siebie świateł trzech
BARWY W DRUKU KOŁO (BARW) KOLORÓW KOLORY KOMPLEMENTARNE PODWÓJNE DOPEŁNIENIE DOPEŁNIENIE TRÓJDZIELNE KOLORY SĄSIADUJĄCE MIESZANIE BARW Synteza addytywna - polega na nakładaniu się na siebie świateł trzech
Laboratorium systemów wizualizacji informacji. Pomiary charakterystyk spektralnych elementów modułu displeja. Kolorymetria.
 Laboratorium systemów wizualizacji informacji Pomiary charakterystyk spektralnych elementów modułu displeja. Kolorymetria. Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska
Laboratorium systemów wizualizacji informacji Pomiary charakterystyk spektralnych elementów modułu displeja. Kolorymetria. Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska
Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII
 Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII Temat 1. System rzymski. 2. Własności liczb naturalnych. 3. Porównywanie
Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII Temat 1. System rzymski. 2. Własności liczb naturalnych. 3. Porównywanie
Grafika komputerowa. Dla DSI II
 Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Chemia Procesu Widzenia
 Chemia Procesu Widzenia barwy H.P. Janecki Miłe spotkanie...wykład 11 Spis treści Światło Powstawanie wrażenia barwy Barwa Modele barw 1. Model barw HSV 2. Model barw RGB 3. Sprzętowa reprezentacja barwy
Chemia Procesu Widzenia barwy H.P. Janecki Miłe spotkanie...wykład 11 Spis treści Światło Powstawanie wrażenia barwy Barwa Modele barw 1. Model barw HSV 2. Model barw RGB 3. Sprzętowa reprezentacja barwy
K O L O R Y M E T R I A
 K O L O R Y M E T R I A dr inż. Krzysztof Wandachowicz, / studenci/pomoce.html pok. 807, tel. 6652585, 0602 655505, Literatura: 1. Żagan W.: Podstawy techniki świetlnej. Oficyna Wydawnicza Politechniki
K O L O R Y M E T R I A dr inż. Krzysztof Wandachowicz, / studenci/pomoce.html pok. 807, tel. 6652585, 0602 655505, Literatura: 1. Żagan W.: Podstawy techniki świetlnej. Oficyna Wydawnicza Politechniki
Fotometria i kolorymetria
 13. x,y,y. Jednowymiarowe skale barw (długość fali dominującej i czystość bodźca; temperatura barwowa). Iluminanty i źródła normalne CIE. Układ CIE 1960 (u,v). Przestrzeń barw CIE 1964 (UVW). Układ CIE
13. x,y,y. Jednowymiarowe skale barw (długość fali dominującej i czystość bodźca; temperatura barwowa). Iluminanty i źródła normalne CIE. Układ CIE 1960 (u,v). Przestrzeń barw CIE 1964 (UVW). Układ CIE
Wykład 2. Fotometria i kolorymetria
 Wykład 2 Fotometria i kolorymetria Fala elektromagnetyczna Fala elektromagnetyczna Światło widzialne Gwiazdy Temperatura barwowa Światło widzialne Pomiar światła - fotometria 1729 Pierre Bouger Essai
Wykład 2 Fotometria i kolorymetria Fala elektromagnetyczna Fala elektromagnetyczna Światło widzialne Gwiazdy Temperatura barwowa Światło widzialne Pomiar światła - fotometria 1729 Pierre Bouger Essai
Poniżej przedstawiony został podział wymagań na poszczególne oceny szkolne:
 Prosto do matury klasa d Rok szkolny 014/015 WYMAGANIA EDUKACYJNE Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające
Prosto do matury klasa d Rok szkolny 014/015 WYMAGANIA EDUKACYJNE Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające
Prosta i płaszczyzna w przestrzeni
 Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA
 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA zna znaki używane do zapisu liczb w systemie rzymskim; zna zasady zapisu liczb w systemie rzymskim; umie zapisać
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA zna znaki używane do zapisu liczb w systemie rzymskim; zna zasady zapisu liczb w systemie rzymskim; umie zapisać
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Wymagania edukacyjne z matematyki
 Wymagania edukacyjne z matematyki Klasa I - program Matematyka z plusem" Dział: LICZBY I DZIAŁANIA Poziom konieczny - ocena dopuszczająca porównywać liczby wymierne, zaznaczać liczby wymierne na osi liczbowej,
Wymagania edukacyjne z matematyki Klasa I - program Matematyka z plusem" Dział: LICZBY I DZIAŁANIA Poziom konieczny - ocena dopuszczająca porównywać liczby wymierne, zaznaczać liczby wymierne na osi liczbowej,
Grafika komputerowa Wykład 11 Barwa czy kolor?
 Grafika komputerowa Wykład 11 czy kolor? Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 2 3 Mieszanie addytywne barw
Grafika komputerowa Wykład 11 czy kolor? Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 2 3 Mieszanie addytywne barw
Podstawy grafiki komputerowej
 Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Rys. 1 Interferencja dwóch fal sferycznych w punkcie P.
 Ćwiczenie 4 Doświadczenie interferencyjne Younga Wprowadzenie teoretyczne Charakterystyczną cechą fal jest ich zdolność do interferencji. Światło jako fala elektromagnetyczna również może interferować.
Ćwiczenie 4 Doświadczenie interferencyjne Younga Wprowadzenie teoretyczne Charakterystyczną cechą fal jest ich zdolność do interferencji. Światło jako fala elektromagnetyczna również może interferować.
Rozdział VII. Przekształcenia geometryczne na płaszczyźnie Przekształcenia geometryczne Symetria osiowa Symetria środkowa 328
 Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
FUNKCJA LINIOWA - WYKRES. y = ax + b. a i b to współczynniki funkcji, które mają wartości liczbowe
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
PRZEDMIOTOWY SYSTEM OCENIANIA- MATEMATYKA KLASA 6. Rok szkolny 2012/2013. Tamara Kostencka
 PRZEDMIOTOWY SYSTEM OCENIANIA- MATEMATYKA KLASA 6 Rok szkolny 2012/2013 Tamara Kostencka 1 LICZBY NA CO DZIEŃ LICZBY NATURALNE I UŁAMKI Wymagania programowe dla klasy VI szkoły podstawowej DZIAŁ WYMAGANIA
PRZEDMIOTOWY SYSTEM OCENIANIA- MATEMATYKA KLASA 6 Rok szkolny 2012/2013 Tamara Kostencka 1 LICZBY NA CO DZIEŃ LICZBY NATURALNE I UŁAMKI Wymagania programowe dla klasy VI szkoły podstawowej DZIAŁ WYMAGANIA
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Matematyka licea ogólnokształcące, technika
 Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Fizyczne Metody Badań Materiałów 2
 Fizyczne Metody Badań Materiałów 2 Dr inż. Marek Chmielewski G.G. np.p.7-8 www.mif.pg.gda.pl/homepages/bzyk Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Fizyczne Metody Badań Materiałów 2 Dr inż. Marek Chmielewski G.G. np.p.7-8 www.mif.pg.gda.pl/homepages/bzyk Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Dostosowuje wygląd kolorów na wydruku. Uwagi:
 Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów informują o sposobach wykorzystania funkcji drukarki w celu zmiany ustawień wydruków kolorowych i dostosowania ich według potrzeby. Menu jakości
Strona 1 z 7 Jakość koloru Wskazówki dotyczące jakości kolorów informują o sposobach wykorzystania funkcji drukarki w celu zmiany ustawień wydruków kolorowych i dostosowania ich według potrzeby. Menu jakości
AUTORKA: ELŻBIETA SZUMIŃSKA NAUCZYCIELKA ZESPOŁU SZKÓŁ OGÓLNOKSZTAŁCĄCYCH SCHOLASTICUS W ŁODZI ZNANE RÓWNANIA PROSTEJ NA PŁASZCZYŹNIE I W PRZESTRZENI
 UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ
 KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
GRAFIKA. Rodzaje grafiki i odpowiadające im edytory
 GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
GRAFIKA Rodzaje grafiki i odpowiadające im edytory Obraz graficzny w komputerze Może być: utworzony automatycznie przez wybrany program (np. jako wykres w arkuszu kalkulacyjnym) lub urządzenie (np. zdjęcie
Wymagania edukacyjne z matematyki
 Wymagania edukacyjne z matematyki Klasa I - program Matematyka z plusem" LICZBY I DZIAŁANIA POZIOM KONIECZNY - ocena dopuszczająca porównywać liczby wymierne, zaznaczać liczby wymierne na osi liczbowej,
Wymagania edukacyjne z matematyki Klasa I - program Matematyka z plusem" LICZBY I DZIAŁANIA POZIOM KONIECZNY - ocena dopuszczająca porównywać liczby wymierne, zaznaczać liczby wymierne na osi liczbowej,
Reprezentacje danych multimedialnych - kolory. 1. Natura wiatła 2. Widzenie barwne 3. Diagram chromatycznoci 4. Modele koloru
 Reprezentacje danych multimedialnych - kolory 1. Natura wiatła 2. Widzenie barwne 3. Diagram chromatycznoci 4. Modele koloru Natura wiatła, spektra wiatło fala elektromagnetyczna z zakresu 400 nm 700 nm
Reprezentacje danych multimedialnych - kolory 1. Natura wiatła 2. Widzenie barwne 3. Diagram chromatycznoci 4. Modele koloru Natura wiatła, spektra wiatło fala elektromagnetyczna z zakresu 400 nm 700 nm
Spis treści Spis treści 1. Model CMYK Literatura
 Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
Spis treści Spis treści...................................... Model CMYK.................................. Sześcian CMY...............................2. Konwersje RGB, CMY i CMYK.................... 2.2..
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII Uczeń na ocenę dopuszczającą: - zna znaki używane do zapisu liczb w systemie rzymskim, - umie zapisać i odczytać liczby naturalne dodatnie w systemie rzymskim
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII Uczeń na ocenę dopuszczającą: - zna znaki używane do zapisu liczb w systemie rzymskim, - umie zapisać i odczytać liczby naturalne dodatnie w systemie rzymskim
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Teoria koloru Co to jest?
 Teoria koloru Teoria koloru Co to jest? Dział wiedzy zajmujący się powstawaniem u człowieka wrażeń barwnych oraz teoretycznymi i praktycznymi aspektami czynników zewnętrznych biorących udział w procesie
Teoria koloru Teoria koloru Co to jest? Dział wiedzy zajmujący się powstawaniem u człowieka wrażeń barwnych oraz teoretycznymi i praktycznymi aspektami czynników zewnętrznych biorących udział w procesie
FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI
 FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI DEFINICJA (funkcji elementarnych) Podstawowymi funkcjami elementarnymi nazywamy funkcje: stałe potęgowe wykładnicze logarytmiczne trygonometryczne Funkcje, które można
FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI DEFINICJA (funkcji elementarnych) Podstawowymi funkcjami elementarnymi nazywamy funkcje: stałe potęgowe wykładnicze logarytmiczne trygonometryczne Funkcje, które można
Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej
 Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło widzialne jest to promieniowanie elektromagnetyczne (zaburzenie poła elektromagnetycznego rozchodzące
Ćwiczenie 12 (44) Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło widzialne jest to promieniowanie elektromagnetyczne (zaburzenie poła elektromagnetycznego rozchodzące
Logo cz pl Zasady stosowania logotypów
 Logo cz pl 2014 2020 Zasady stosowania logotypów 1 Spis treści 2 Wstęp 3 Logo cz pl Opis 4 Pole ochronne 5 Umiejscowienie 6 Formaty danych logo 7 Kolory 8 Niebieski 9 Pomarańczowy 10 Wersja monochromatyczna
Logo cz pl 2014 2020 Zasady stosowania logotypów 1 Spis treści 2 Wstęp 3 Logo cz pl Opis 4 Pole ochronne 5 Umiejscowienie 6 Formaty danych logo 7 Kolory 8 Niebieski 9 Pomarańczowy 10 Wersja monochromatyczna
Fotometria i kolorymetria
 9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
9. (rodzaje receptorów; teoria Younga-Helmholtza i Heringa; kontrast chromatyczny i achromatyczny; dwu- i trzywariantowy system widzenia ssaków; kontrast równoczesny). http://www.if.pwr.wroc.pl/~wozniak/
Grafika komputerowa. Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Żółty
 Grafika komputerowa Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Czerwony czopek
Grafika komputerowa Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya Oko posiada pręciki (100 mln) dla detekcji składowych luminancji i 3 rodzaje czopków (9 mln) do detekcji koloru Czerwony czopek
PODKARPACKI SPRAWDZIAN PRZEDMATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
 KOD UZUPEŁNIA ZDAJĄCY PESEL PODKARPACKI SPRAWDZIAN PRZEDMATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 3 CZERWCA 2016 R. GODZINA ROZPOCZĘCIA: 9:00 CZAS PRACY: 170 MINUT LICZBA PUNKTÓW DO UZYSKANIA: 50
KOD UZUPEŁNIA ZDAJĄCY PESEL PODKARPACKI SPRAWDZIAN PRZEDMATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 3 CZERWCA 2016 R. GODZINA ROZPOCZĘCIA: 9:00 CZAS PRACY: 170 MINUT LICZBA PUNKTÓW DO UZYSKANIA: 50
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
Prawo Bragga. Różnica dróg promieni 1 i 2 wynosi: s = CB + BD: CB = BD = d sinθ
 Prawo Bragga Prawo Bragga Prawo Bragga Różnica dróg promieni 1 i 2 wynosi: s = CB + BD: CB = BD = d sinθ d - odległość najbliższych płaszczyzn, w których są ułożone atomy, równoległych do powierzchni kryształu,
Prawo Bragga Prawo Bragga Prawo Bragga Różnica dróg promieni 1 i 2 wynosi: s = CB + BD: CB = BD = d sinθ d - odległość najbliższych płaszczyzn, w których są ułożone atomy, równoległych do powierzchni kryształu,
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Geometria w R 3. Iloczyn skalarny wektorów
 Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Zajęcia nr 1 (1h) Dwumian Newtona. Indukcja. Zajęcia nr 2 i 3 (4h) Trygonometria
 Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Wykład 17: Optyka falowa cz.1.
 Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
2) R stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
 ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
Przykład Łuk ze ściągiem, obciążenie styczne. D A
 Przykład 1.4. Łuk ze ściągiem, obciążenie styczne. Rysunek przedstawia łuk trójprzegubowy, kołowy, ze ściągiem. Łuk obciążony jest obciążeniem stycznym do łuku, o stałej gęstości na jednostkę długości
Przykład 1.4. Łuk ze ściągiem, obciążenie styczne. Rysunek przedstawia łuk trójprzegubowy, kołowy, ze ściągiem. Łuk obciążony jest obciążeniem stycznym do łuku, o stałej gęstości na jednostkę długości
Funkcja liniowa i prosta podsumowanie
 Funkcja liniowa i prosta podsumowanie Definicja funkcji liniowej Funkcja liniowa określona jest wzorem postaci: y = ax + b, x R, a R, b R a, b współczynniki funkcji dowolne liczby rzeczywiste a- współczynnik
Funkcja liniowa i prosta podsumowanie Definicja funkcji liniowej Funkcja liniowa określona jest wzorem postaci: y = ax + b, x R, a R, b R a, b współczynniki funkcji dowolne liczby rzeczywiste a- współczynnik
Marcin Wilczewski Politechnika Gdańska, 2013/14
 Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
Algorytmy graficzne Marcin Wilczewski Politechnika Gdańska, 213/14 1 Zagadnienia, wykład, laboratorium Wykład: Światło i barwa. Modele barw. Charakterystyki obrazu. Reprezentacja i opis. Kwantyzacja skalarna
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ
 INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
GRAKO: ŚWIATŁO I CIENIE. Modele barw. Trochę fizyki percepcji światła. OŚWIETLENIE: elementy istotne w projektowaniu
 GRAKO: ŚWIATŁO I CIENIE Metody oświetlania Metody cieniowania Przykłady OŚWIETLENIE: elementy istotne w projektowaniu Rozumienie fizyki światła w realnym świecie Rozumienie procesu percepcji światła Opracowanie
GRAKO: ŚWIATŁO I CIENIE Metody oświetlania Metody cieniowania Przykłady OŚWIETLENIE: elementy istotne w projektowaniu Rozumienie fizyki światła w realnym świecie Rozumienie procesu percepcji światła Opracowanie
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
