POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHATRONIKI
|
|
|
- Alina Pluta
- 7 lat temu
- Przeglądów:
Transkrypt
1 POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHATRONIKI Rozprawa doktorska mgr inż. Alicja Siewnicka Modelowanie działania pulsacyjnego zespołu wspomagania pracy serca Promotor prof. dr hab. inż. Krzysztof Janiszowski WARSZAWA 217
2
3 Podziękowania Chciałabym serdecznie podziękować za udzielone wsparcie przy pisaniu niniejszej pracy: Prof. dr. hab. inż. Krzysztofowi Janiszowskiemu, Promotorowi pracy, za przyjęcie do zespołu badawczego i zaangażowanie w prowadzone prace naukowe. Dziękuję za poświęcony czas, wsparcie merytoryczne oraz cenne uwagi dotyczące przygotowanej rozprawy. Dr. inż. Maciejowi Gawlikowskiemu za przekazane informacje dotyczące urządzeń wspomagania pracy serca i udzieloną pomoc przy prowadzeniu badań. Prof. dr. hab. inż. Tadeuszowi Pałko za umożliwienie przeprowadzenia badań eksperymentalnych na hybrydowym symulatorze układu krążenia. W szczególności dziękuję moim Rodzicom, Andrzejowi i Natalii Golnik, za ogromne wsparcie oraz pomoc w łączeniu obowiązków rodzinnych i służbowych. Praca była częściowo finansowana w ramach: - programu wieloletniego Polskie Sztuczne Serce na lata , przedsięwzięcie: Opracowanie technologii metrologicznych, informatycznych i teleinformatycznych dla potrzeb protez serca, finansowanego na podstawie umowy projektowej nr 12/WK/P2/1/SPB-PSS/29 przez Narodowe Centrum Badań i Rozwoju, - projektu p.t.: Modelowanie urządzeń wspomagania pracy serca, pracujących w układzie koniuszek komory tętnica, na potrzeby opracowania algorytmów sterowania, finansowanego na podstawie umowy projektowej nr Pol- Nor/27657/71/213 w ramach Norweskiego Mechanizmu Finansowego na lata , programu Polsko-Norweska Współpraca Badawcza prowadzonego przez Narodowe Centrum Badań i Rozwoju.
4
5 Streszczenie Celem pracy było wyznaczenie opisu umożliwiającego oszacowanie wartości przepływu objętościowego krwi w sterowanym pneumatycznie, pulsacyjnym urządzeniu wspomagania pracy serca. Wartość realizowanego wydatku urządzenia jest kluczowa dla skuteczności prowadzonej terapii. W praktyce klinicznej nie ma jednak możliwości wykonania pomiaru jego wielkości czy wartości ciśnień w urządzeniu. Wartość realizowanego przepływu zależna jest od warunków sterowania, ale również od wydolności krążeniowej pacjenta, która nie jest monitorowana w sposób ciągły. Z tego względu istniała potrzeba opracowania metody estymacji wartości przepływu krwi w oparciu o standardowe pomiary z jednostki sterującej urządzenia. W tym celu przeprowadzono analizę budowy urządzenia, zidentyfikowano występujące problemy i wyznaczono kierunki niezbędnych prac eksperymentalnych. Przeprowadzono trzy eksperymenty badawcze dla różnych jednostek sterujących urządzenia i różnych warunków pracy zespołu wspomagania. Na podstawie wszystkich sygnałów pomiarowych, dostępnych w warunkach eksperymentu, przeprowadzono badania wstępne, mające na celu wskazanie najskuteczniejszej metody modelowania. Zaproponowano rozwiązanie w postaci modelu analitycznego urządzenia wykorzystującego sygnał niosący w sposób pośredni informację o wielkości realizowanego przepływu. Zaobserwowano, że może to być sygnał przepływu powietrza w drenie zasilającym lub różnica wartości ciśnienia sterującego w warunkach wspomagania i w przypadku biegu jałowego. W pierwszym przypadku wyznaczono model cechujący się wysoką dokładnością, lecz wymagający zastosowania dodatkowych elementów pomiarowych znajdujących się po stronie pneumatycznej urządzenia. W drugim podejściu zaproponowano model o strukturze dwustopniowej. Model pierwszego stopnia estymuje wartości ciśnienia zasilania dla biegu jałowego. Jego sygnał wyjściowy wykorzystywany jest w modelu drugiego stopnia, umożliwiającym estymację wartości przepływu krwi w warunkach pracy urządzenia. W ten sposób otrzymano model bazujący wyłącznie na sygnałach pomiarowych dostępnych w jednostce sterującej. Uzyskana dokładność jest porównywalna dla wszystkich przebadanych warunków sterowania i obciążenia oraz niezależna od stopnia napełnienia urządzenia. Przeprowadzono analizę użyteczności wyznaczonego modelu do celów oszacowania wartości wydatku minutowego i automatycznej detekcji skrajnych stanów napełnienia komory krwistej urządzenia. Otrzymano rezultaty potwierdzające użyteczność wyznaczonego modelu. Opracowano wnioski i przedstawiono planowane kierunki dalszych badań w zakresie klinicznego wykorzystania modelu. Słowa kluczowe: modelowanie, estymacja przepływu, wspomaganie serca, VAD.
6 Abstract The aim of this work was to derive a description that yields the blood flow rate estimation of the pneumatically controlled, pulsatile ventricular assist device. An adequate flow rate is crucial for the effectiveness of the therapy. Unfortunately, during clinical heart support, neither blood flow nor pressures can be measured from the device. In general, the flow rate depends on the device control and patient conditions. However, the patient s hemodynamic parameters are not constantly monitored. For this reason, there was a need for development of a method of blood flow evaluation which would base on the standard measurements from the device control unit. For this purpose, an analysis of the device construction was carried out, the problems were identified and the directions of the necessary experimental work were defined. Three research experiments have been conducted for the different control units and various operating conditions of the cardiac assist system. Based on all signals available under the experimental conditions, preliminary tests were conducted to identify the most effective modeling method. A solution was proposed in the form of analytical model of the device based on the signal, which can contain information about the blood flow rate. It has been observed that this may be a signal of the air flow in the supply drain or a value of difference between supply pressure during assist and idle run. In the first case, a model with a high accuracy was defined but the additional measurements on the pneumatic side of the device were required. In the second approach a two-stage model was proposed. The first-stage model estimates the value of air supply pressure for the idle run. Its output signal is used in a second-stage model to estimate the blood flow in the normal operation of the device. In this way, a model based solely on the measurement signals available in the control unit was obtained. The achieved accuracy is comparable to all tested control and load conditions and is independent from the level of the device filling. An analysis of the utility of the developed model was carried out due to the purpose of device stroke volume estimation and the automatic detection of the extreme filling conditions. The obtained results have confirmed the utility of the developed model. The final conclusions from the conducted research were formulated and possible directions of the further research on the clinical use of the model were presented. Key words: modelling, flow estimation, ventricular assist device, VAD.
7 Spis treści Streszczenie... 5 Abstract Wstęp Cel Pracy Wprowadzenie teoretyczne i przegląd literatury Środowisko pracy zespołów wspomagania pracy serca Budowa układu krążenia i sposób wszczepiania urządzeń VAD Hybrydowy symulator układu krążenia Zespół wspomagania pracy serca Konstrukcja i elementy zespołu wspomagania pracy serca POLCAS Sterowanie zespołu wspomagania pracy serca POLCAS Przegląd metod pomiarowych dotyczących wydatku minutowego Modelowanie urządzeń wspomagania pracy serca Modele obliczeniowej mechaniki płynów Modele bazujące na analogii elektrycznej Modele komory POLVAD-MEV Eksperymenty i metody Eksperyment identyfikacyjny (nr 1) Eksperyment uzupełniający i diagnostyczny (nr 2) Eksperyment identyfikacyjny dla połączenia koniuszek serca aorta (nr 3) Oprogramowanie symulacyjne PExSim IdCAD MATLAB System Identification Toolbox Modele urządzenia wspomagania pracy serca Modele bazujące na wszystkich dostępnych danych pomiarowych
8 Modele elastancyjne Model oparty na ciśnieniu zasilania Modele parametryczne Model oparty na wnioskowaniu rozmytym Model oparty na sieci neuronowej Model o parametrach skupionych Posumowanie Model przepływu krwi bazujący na danych z jednostki sterującej i części pneumatycznej urządzenia wspomagającego Model przepływu krwi bazujący na danych z jednostki sterującej Model zaworu liniowego Model przepływu krwi Podsumowanie uzyskanych wyników Algorytm wykrywania całkowitego wyrzutu i napełnienia Algorytm oszacowania wydatku minutowego Wnioski końcowe Proponowane kierunki dalszych badań Bibliografia Załączniki
9 1. Wstęp Choroby układu krążenia są aktualnie jedną z głównych przyczyn zgonów w krajach wysokorozwiniętych [1]. Jedną z częstszych przypadłości jest niewydolność komory serca, która skutkuje m.in. zmniejszeniem wartości rzutu minutowego (CO, ang. Cardiac Output). Oznacza to, że do układu naczyniowego pompowana jest zbyt mała ilość krwi pod niedostatecznym ciśnieniem. W takim przypadku możliwe jest zastosowanie urządzeń wspomagania pracy serca (VAD, ang. Ventricular Assist Device). Stosowane są one zazwyczaj jako pomost do przeszczepu, ale również mogą stanowić terapię docelową. Urządzenia te zastępują częściowo lub całkowicie działanie mięśnia sercowego poprzez bocznikowanie przepływu. Krew pobierana jest z przedsionka lub koniuszka komory serca i pompowana bezpośrednio do tętnicy zbiorczej równolegle do pracy naturalnej komory serca (Rys. 1.1). Można wyodrębnić dwa podstawowe typy urządzeń wspomagania pracy serca: pompy o przepływie pulsacyjnym oraz pompy o przepływie ciągłym [2]. Pierwszy typ urządzeń składa się w większości przypadków z komory krwistej, do której doprowadzone są dwie kaniule: wlotowa i wylotowa zaopatrzone w zastawki mechaniczne [3] [5]. Odpowiedni układ sterowania zapewnia naprzemienne zwiększanie i zmniejszanie objętości komory krwistej, co powoduje jej napełnianie krwią, a następnie opróżnienie. Urządzenia wspomagania o przepływie ciągłym generują w przybliżeniu stałą wartość przepływu. Charakteryzują się też mniejszymi problemami związanymi z wykrzepianiem krwi w urządzeniu i łatwiejszym sterowaniem. Problemem jest natomiast niszczenie składników krwi w wyniku dużych prędkości ścinania. Niektóre prace wskazują również [6], że pulsacyjny charakter przepływu krwi jest korzystniejszy ze względów medycznych. Dlatego też, pulsacyjne zespoły wspomagania pracy serca są nadal wykorzystywane klinicznie. Rys. 1.1 Urządzenie wspomagania pracy serca (VAD) [12] Pierwszym zastosowaniem urządzenia mechanicznego do celów przejęcia funkcji serca było zastosowanie płuco-serca przez Johna Gibbona w 1953 roku [7]. Wśród urządzeń wspomagających w początkowym okresie najczęściej stosowana była wewnątrz-aortalna pompa balonowa (IABP, ang. Intra-Aortic Balloon Pump). Pierwsze zastosowanie kliniczne urządzenia VAD wykonane zostało w 1963 roku [8]. W późniejszym okresie, wraz 9
10 z rozwojem techniki pojawiło się wiele pulsacyjnych urządzeń wspomagania pracy serca, jak np. HeartMate I, PVAD, HeartMate XVE, Berlin Heart Excor, Novacor [9], [1]. Na fali rosnącego zapotrzebowania na coraz nowsze i lepsze rozwiązania techniczne urządzeń, mających zastępować pracę serca, w 1991 r. założona została Fundacja Rozwoju Kardiochirurgii w Zabrzu, której jednym z celów było opracowanie polskiego sztucznego serca. W 1999 r. [11] wprowadzony został do użytku klinicznego zespół wspomagania POLCAS, składający się z pulsacyjnego urządzenia wspomagania pracy serca POLVAD- MEV wraz z dedykowaną jednostką sterującą POLPDU. W kolejnych latach uruchomiony został program Polskie Sztuczne Serce mający na celu opracowanie rodziny polskich protez serca w tym pomp całkowicie wszczepialnych. Urządzenie wspomagające POLVAD-MEV jest wyporową pompą krwi o konstrukcji typowej dla pulsacyjnych urządzeń wspomagających. Składa się z komory krwistej i powietrznej odseparowanych ruchomą membraną (Rys. 1.2). W wyniku odpowiedniego sterowania pneumatycznego następuje ruch membrany i zmiana objętości komory krwistej. Powoduje ona naprzemienne zasysanie krwi przez kaniulę wlotową i jej wyrzut przez kaniulę wylotową. Odpowiedni kierunek przepływu krwi zapewniony jest poprzez zastosowanie mechanicznych zastawek dyskowych. Generacja fali ciśnienia zasilającego komorę powietrzną urządzenia realizowana jest przez jednostkę sterującą POLPDU zgodnie z parametrami sterowania ustalonymi przez operatora. d) g) a) c) e) f) b) Rys. 1.2 Urządzenie wspomagania pracy serca POLVAD-MEV o działaniu pulsacyjnym [12]. a) komora pneumatyczna, b) komora krwista (wykonawcza), c) dren pneumatyczny, d) kaniula wlotowa, e) kaniula wylotowa, f), g) zastawki mechaniczne (dyskowe). Głównymi ograniczeniami przy stosowaniu pulsacyjnych urządzeń wspomagania pracy serca są problemy z występującymi zakażeniami, uszkodzeniami mechanicznymi sprzętu oraz z wysoką tendencją do wykrzepiania się krwi, a w rezultacie powstawaniem zatorów. 1
11 Szczególnie istotna jest ostatnia z wymienionych komplikacji. Stosowanie leków przeciwzakrzepowych nie zawsze jest wystarczająco skuteczne, a jednocześnie zwiększa ryzyko wystąpienia wylewu. Przyczyną problemów z wykrzepianiem są charakterystyczne warunki przepływowe występujące w komorze. Krew strumieniem o wysokiej prędkości pokonuje obszar zastawki tworząc następnie duży wir odpowiedzialny za obmycie komory wykonawczej urządzenia. Wysoka prędkość strumienia w trakcie napełniania skutkuje powstawaniem dużych szybkości ścinających powodujących aktywację płytek krwi. Następnie uszkodzona krew trafia do obszaru o względnie niskich naprężeniach ścinających, występujących zwłaszcza na ścianach komory, gdzie może się zbierać i tworzyć skrzepliny. Choć dokładny mechanizm niszczenia i agregacji płytek krwi w komorze nie jest znany, to wiadomo, że występuje silna zależność pomiędzy występowaniem dużych naprężeń ścinających w polu przepływu a aktywacją płytek krwi, natomiast ich agregacja jest bardziej prawdopodobna w strefach o małych szybkościach ścinania [13] [15]. Mechanizm niszczenia składników krwi i formowania się skrzeplin jest więc silnie zależny od konstrukcji komory [13], [16], ale również od sposobu jej sterowania. Wynika to z faktu, że dla takiej samej częstości pracy urządzenia VAD, komora krwista może być napełniania i opróżniania w różny sposób (Rys. 1.3). a) b) c) V/V max t/t napełnianie przestój opróżnianie V/V max Rys. 1.3 Schematyczna reprezentacja różnych wariantów napełniania komory krwistej urządzenia wspomagania pracy serca. V/Vmax stosunek objętości chwilowej komory do maksymalnej objętości, t/t stosunek aktualnej długości trwania cyklu pracy do okresu. a) sterowanie z przestojami, b) sterowanie optymalne, c) sterowanie z niepełnym wyrzutem i napełnianiem. Szybkie napełnianie komory sprzyjać będzie występowaniu dużych szybkości ścinających, a ewentualny przestój w pozycji całkowicie napełnionej, agregacji uszkodzonych składników krwi (Rys. 1.3, a). Analogiczna sytuacja ma miejsce w fazie wyrzutu krwi z komory. Z drugiej strony, zbyt wolne napełnianie komory krwistej spowoduje wystąpienie niecałkowitego napełnienia lub opróżnienia komory (Rys. 1.3, c). Niecałkowite napełnienie skutkuje niższym potencjalnym rzutem jednostkowym (VSV, ang. VAD Stroke Volume), t/t 11 napełnianie opróżnianie V/V max t/t napełnianie opróżnianie
12 a niepełny wyrzut z komory sprawia, że część uszkodzonych krwinek pozostaje w komorze na kolejny cykl pracy. Wpływa to negatywnie na sposób obmywania komory oraz skutkuje wydłużonym czasem przebywania krwi w obszarach o małych szybkościach ścinania. Duża ilość cząsteczek pozostających w komorze na kolejny cykl roboczy zwiększa ryzyko tworzenia się skrzeplin [13]. Z wymienionych powodów, istotnym zagadnieniem jest opracowanie sterowania urządzeniem VAD, które zapewni pracę z całkowitym napełnieniem i wyrzutem oraz bez okresów przestoju w pozycjach skrajnych. Będzie to skutkowało najlepszymi warunkami obmywania komory krwistej urządzenia. Drugim aspektem związanym ze sterowaniem jest zapewnienie odpowiedniej wartości wydatku minutowego, czyli odpowiedniej objętości krwi, która jest pompowana w ciągu minuty przez zespół wspomagający. Wartość tego wydatku jest kluczową informacją dla personelu medycznego, pozwalającą na dopasowanie kuracji do stanu wydolności układu krążenia wspomaganego pacjenta. W przypadku pracy optymalnej, czyli przy całkowitym napełnieniu i opróżnieniu komory krwistej, wartość rzutu jednostkowego w założeniu odpowiada maksymalnej objętości komory krwistej urządzenia. Wartość wydatku minutowego urządzenia wspomagającego w założeniu można oszacować na podstawie iloczynu rzutu jednostkowego i częstości pracy. Jednak ze względu na specyfikę budowy i stosowania pulsacyjnych urządzeń wspomagania pracy serca nie zawsze istnieje możliwość stwierdzenia, czy występuje całkowite napełnianie i opróżnianie komory krwistej. Dodatkowo, wyniki badań identyfikacyjnych urządzenia POLVAD-MEV wskazują, że ze względu na zastosowanie zastawek mechanicznych, w zależności od warunków pracy urządzenia, występują zjawiska niedomykania i odbijania dysków zastawek. Powoduje to występowanie przepływów wstecznych o różnym natężeniu i czasie trwania. Dlatego, nawet przy pracy komory z całkowitym napełnieniem i wyrzutem, obserwowano różną wartość realizowanego wydatku minutowego. Liczne prace badawcze, dotyczące opracowania dedykowanych układów pomiarowych do pomiaru przepływu krwi, czy szacowania chwilowej objętości komory krwistej, nie przyniosły jak dotąd oczekiwanych rezultatów (rozdział 3.2.3). Z tego względu zapewnienie odpowiedniego sterowania sprowadza się w praktyce do intuicyjnego doboru nastaw jednostki sterującej przez personel medyczny. Wykonywane jest to wyłącznie na podstawie wiedzy fachowej i doświadczenia personelu oraz informacji o ogólnym stanie klinicznym osoby wspomaganej. Stan taki wpływa negatywnie na komfort i bezpieczeństwo użytkowania zespołu wspomagania i zwiększa ryzyko formowania się zakrzepów. 12
13 Zaproponowanym rozwiązaniem powyższego problemu było wyznaczenie modelu zespołu wspomagania pracy serca, który na podstawie dostępnych w warunkach klinicznych informacji pomiarowych, pozwalałby na estymację wartości przepływu krwi w urządzeniu (Rys. 1.4). Stanowiłoby on podstawę dla opracowania algorytmów detekcji całkowitego wyrzutu i napełnienia komory oraz oszacowania wielkości wydatku minutowego. Dzięki temu personel medyczny uzyskałby narzędzie ułatwiające dobór parametrów sterowania, a w przyszłości możliwe byłoby opracowanie algorytmów automatycznego doboru nastaw. Zastosowanie takiego rozwiązania miałoby korzystny wpływ na bezpieczeństwo i komfort prowadzenia terapii z użyciem zespołu wspomagającego. personel medyczny lub automatyczny układ sterowania detekcja całkowitego wyrzutu i napełnienia algorytm wyznaczania wydatku minutowego warunki zasilania (parametry sterujące) wielkości pomiarowe dostępne klinicznie model przepływu krwi w VAD estymowana wartość przepływu warunki obciążenia (układ krążenia) urządzenie VAD nieznana, rzeczywista wartość przepływu Rys. 1.4 Schemat koncepcji użycia modelu przepływu krwi w urządzeniu wspomagania pracy serca. 13
14 2. Cel Pracy Celem niniejszej pracy było wyznaczenie modelu pulsacyjnego zespołu wspomagania pracy serca na przykładzie urządzenia POLVAD-MEV. Model miał na celu estymację wartości przepływu krwi w urządzeniu wyłącznie na podstawie wielkości dostępnych pomiarowo w warunkach klinicznych. Opracowany model powinien uwzględniać następujące ograniczenia i warunki eksploatacji urządzenia: wartość przepływu jest silnie zależna od stanu wydolności i warunków hemodynamicznych występujących w układzie krwionośnym wspomaganego pacjenta. W warunkach klinicznych nie ma możliwości pomiaru wielkości związanych z tym stanem; aktualna wersja urządzenia wspomagającego nie jest wyposażona w układy umożliwiające pomiar lub estymację wartości przepływów i ciśnień w urządzeniu VAD. Oznacza to, że nieznane są objętości chwilowe komór urządzenia, wartości przepływów w kaniulach dołączeniowych komory krwistej, czy przewodzie zasilania pneumatycznego. W warunkach klinicznych nie są mierzone wartości ciśnienia w żadnym punkcie urządzenia. Nieznany jest również przebieg zmienności stopnia otwarcia zastawek; podstawowymi wielkościami pomiarowymi, na których powinien bazować model przepływu krwi są sygnały pomiarowe dostępne w jednostce sterującej zespołu wspomagania; wielkościami pomiarowymi dostępnymi z urządzenia VAD, które warunkowo mogą zostać wykorzystane dla celów modelowania, są: wartość przepływu powietrza w przewodzie zasilania pneumatycznego i ciśnienie w komorze pneumatycznej; skrajne ograniczenia objętości komory krwistej stanowią nieliniowość w opisie działania urządzenia, która musi być uwzględniona w modelu; funkcjonowanie mechanicznych zastawek dyskowych wprowadza silne nieliniowości w opisie działania urządzenia; brak możliwości prowadzenia eksperymentów identyfikacyjnych urządzenia w warunkach klinicznych (na pacjentach). 14
15 Teza pracy: Możliwa jest estymacja wartości przepływu krwi w urządzeniu wyłącznie na podstawie wielkości dostępnych pomiarowo w warunkach klinicznych. Zakres pracy obejmuje: przygotowanie odpowiednich stanowisk badawczych do celów przeprowadzenia testów zespołu wspomagania pracy serca; przeprowadzenie eksperymentów identyfikacyjnych i zebranie danych pomiarowych dla różnych parametrów sterowania i warunków obciążenia urządzenia wspomagającego; analizę zebranych wyników i opracowanie metodyki umożliwiającej estymację wartości przepływu krwi w urządzeniu z wykorzystaniem wielkości dostępnych pomiarowo w warunkach klinicznych; wyznaczenie efektywnego modelu przepływu krwi bazującego wyłącznie na standardowych sygnałach pomiarowych wykonywanych w jednostce sterującej; Praca ma charakter badawczy i składa się z czterech głównych części. W pierwszej kolejności przedstawione zostały informacje dotyczące środowiska pracy zespołów wspomagania oraz sposobów jego modelowania. Opisany został zespół wspomagania POLCAS, omówiono występujące problemy związane ze sterowaniem i estymacją wartości przepływu krwi w urządzeniu. Przedstawiono dotychczasowe prace dotyczące modelowania urządzeń wspomagających. W drugiej części opisano przygotowane układy pomiarowe i przeprowadzone eksperymenty oraz przedstawiono możliwości oprogramowania wykorzystywanego do modelowania. Trzecia część zawiera opis właściwych badań nad wyznaczeniem modelu umożliwiającego estymację wartości przepływu krwi w urządzeniu wspomagającym, w tym, modelu bazującego wyłącznie na wielkościach dostępnych pomiarowo w warunkach klinicznych. W podsumowaniu zawarto opis metody wykrywania całkowitego wyrzutu i napełnienia oraz algorytmu szacowania wydatku minutowego na podstawie wyznaczonego modelu przepływu krwi przez komorę krwistą urządzenia. Sformułowano wnioski dotyczące wyników prowadzonych badań i przedstawiono kierunki dalszych prac. 15
16 3. Wprowadzenie teoretyczne i przegląd literatury 3.1. Środowisko pracy zespołów wspomagania pracy serca W niniejszym rozdziale przedstawiono podstawy budowy układu krążenia człowieka i omówiono sposób dołączania pulsacyjnych urządzeń wspomagających. Ze względów etycznych, ekonomicznych i organizacyjnych niektóre badania, zwłaszcza prototypów urządzeń nie powinny być wykonywane na zwierzętach a tym bardziej pacjentach. W takich przypadkach możliwe jest wykorzystanie do testów modelu układu krążenia. W dalszej części rozdziału przedstawiono poszczególne rozwiązania dotyczące tego zagadnienia, jak również szczegółowo omówiono rozwiązanie hybrydowego modelu układu krążenia, na którym prowadzone były badania identyfikacyjne urządzenia POLVAD przeprowadzone na potrzeby niniejszej pracy Budowa układu krążenia i sposób wszczepiania urządzeń VAD Układ krwionośny człowieka składa się z serca i dwóch głównych obiegów krwi: dużego (systemowego) i małego (płucnego). Obieg systemowy odpowiada za dostarczanie tlenu i substancji odżywczych do komórek ciała oraz odbiór zbędnych produktów przemiany materii. Obieg płucny odpowiada za dystrybucję krwi w płucach, gdzie następuje jej natlenowanie. Każdy z obiegów składa się z układu tętniczego, dostarczającego krew do naczyń włosowatych i układu żylnego, którym krew wraca do serca. Samo serce składa się z dwóch przedsionków i dwóch komór oddzielonych od siebie zastawkami. Do lewego przedsionka napływa krew z układu żylnego płuc i przez zastawkę mitralną wpływa do lewej komory. W wyniku skurczu komory, krew, poprzez zastawkę aortalną pompowana jest do tętnicy głównej układu systemowego, czyli aorty. Następnie, mniejszymi układami tętniczymi zasila poszczególne części ciała i organy, w tym sam mięsień sercowy (krążenie wieńcowe). Krew wraca układem żylnym do prawego przedsionka, skąd poprzez zastawkę trójdzielną wpływa do prawej komory. W wyniku skurczu serca zostaje przepompowana przez zastawkę pnia płucnego do układu tętniczego płucnego. Po wymianie gazowej, układem żylnym powraca do lewego przedsionka i cykl obiegu krwi się zamyka. Serce człowieka pompuje średnio 6 do 7 litrów krwi na minutę. Cykl pracy serca można podzielić na siedem faz (Rys. 3.1): skurcz przedsionków, izowolumetryczny skurcz komór, szybki wyrzut, zredukowany wyrzut, rozkurcz izowolumetryczny, szybkie wypełnienie komór oraz zredukowane wypełnienie komór. 16
17 Ciśnienie (mmhg) Objętość (ml) Zredukowany wyrzut Szybki wyrzut Skurcz izowolumetryczny Otwarcie zastawki aortalnej Zamknięcie zastawki mitralnej Rozkurcz izowolumetryczny Szybkie wypełnianie zredukowane wypełnianie Skurcz przedsionków Zamknięcie zastawki aortalnej Otwarcie zastawki mitralnej Ciśnienie aortalne Ciśnienie przedsionkowe Ciśnienie komorowe Objętość komory Elektrokardiogram Rys. 3.1 Wykres cyklu pracy serca na podstawie [17] Jednym z ważniejszych mechanizmów występujących w naturalnej komorze serca jest zależność siły skurczu mięśnia sercowego od stopnia jego rozciągnięcia. Siła ta jest tym większa, im większy jest poprzedzający ją stopień rozciągnięcia włókien mięśniowych, który zależy od poziomu napełnienia serca. Stąd, gdy stopień napełnienia komory jest większy niż zwykle, zwiększeniu ulega siła skurczu. Pierwszy raz zjawisko to zostało opisane przez dwóch fizjologów: Otto Franka i Ernesta Starlinga i obecnie nazwane jest prawem Franka- Starlinga. W przypadku wzrostu ciśnienia wypełniającego komorę serca (przedsionkowego) zwiększa się objętość końcoworozkurczowa komory a wynikowo rozciągnięcie włókien i siła skurczu. Skutkuje to wzrostem objętości wyrzutowej, umożliwiając adaptację wydatku do panujących warunków obciążenia wejściowego. Również w przypadku wzrostu ciśnienia w aorcie, serce zwiększy siłę wyrzutu. Zmniejszona objętość wyrzutowa powoduje, że na początku rozkurczu w komorze pozostaje pewna objętość szczątkowa krwi. Po napełnieniu krwią z przedsionka sumaryczna objętość komory staje się większa niż początkowa a skurcz silniejszy. Dzięki temu możliwe jest zapewnienie normalnej objętości wyrzutowej pomimo zwiększonego obciążenia wyjściowego. W przypadku niewydolności komory serca (zazwyczaj lewej) spada siła skurczu mięśnia sercowego. Oznacza to, że krew w sposób niedostateczny odbierana jest z obiegu płucnego i pompowana do aorty. Jedną z terapii przy tego typu niewydolności jest zastosowanie urządzeń wspomagania pracy serca. W ogólności, urządzenia te włączane są do układu krwionośnego równolegle względem naturalnej komory serca, pozwalając na bocznikowanie przepływu. W przypadku urządzeń pulsacyjnych, początkowo kaniula wlotowa pompy 17
18 umieszczana była w przedsionku niewydolnej komory a kaniula wylotowa, w tętnicy głównej (Rys. 3.2, A). W wyniku analizy prowadzonych terapii zauważono, że w niektórych przypadkach korzystniejsze okazuje się wszczepianie urządzeń w układzie koniuszek komory tętnica (Rys. 3.2, B). W połączeniu tym lepiej obmywana jest naturalna komora serca, co zmniejsza ryzyko formowania się zakrzepów. Dołączenie urządzenia VAD do układu krążenia wykonywane jest z wykorzystaniem kaniul medycznych, będących specjalistycznymi przewodami biozgodnymi. A) krążenie płucne żylne krążenie płucne tętnicze B) krążenie płucne żylne krążenie płucne tętnicze lewy przedsionek prawy przedsionek lewy przedsionek prawy przedsionek LVAD lewa komora prawa komora LVAD lewa komora prawa komora krążenie systemowe tętnicze krążenie systemowe żylne krążenie systemowe tętnicze krążenie systemowe żylne Rys. 3.2 Schemat układu pracy urządzenia wspomagania pracy serca na przykładzie wspomagania lewokomorowego. A) układ przedsionek aorta, B) układ koniuszek komory aorta. Pulsacyjne urządzenia VAD znajdują się zazwyczaj całkowicie poza ciałem pacjenta. Ich kroćce dolotowy i wylotowy połączone są kaniulami medycznymi z odpowiednimi punktami układu krążenia pacjenta. Powoduje to, że w ciele wspomaganej osoby znajdują się dwa wyprowadzenia o dość dużej średnicy. Takie rozwiązanie zwiększa ryzyko wystąpienia infekcji w tym obszarze i ma negatywny wpływ na komfort prowadzonej terapii. Dlatego dąży się do opracowania urządzeń częściowo wszczepialnych, gdzie urządzenie znajduje się wewnątrz ciała pacjenta, a wyprowadzony jest jedynie cienki, pneumatyczny dren zasilający. Docelowym rozwiązaniem jest zastosowanie urządzeń całkowicie wszczepialnych, gdzie zasilanie urządzenia realizowane jest bezprzewodowo Hybrydowy symulator układu krążenia Postępujący rozwój urządzeń wspomagania pracy serca wymaga przeprowadzenia dokładnych testów działania kolejnych konstrukcji. Przed wprowadzeniem do praktyki klinicznej, każde urządzenie przechodzi szereg badań prowadzonych na zwierzętach. Jednak na wcześniejszych etapach prac preferowane jest prowadzenie badań in-vitro. Z tego względu opracowywane są modele układu krążenia, umożliwiające odwzorowanie hydraulicznych warunków obciążenia urządzenia i badanie wpływu ich działania na układ krążenia pacjenta. 18
19 Na przestrzeni ostatnich dekad, dla różnych celów badawczych, edukacyjnych i projektowych powstało wiele modeli układu krążenia człowieka. W ogólności można wyszczególnić modele matematyczne, gdzie układ krążenia opisany jest w sposób numeryczny [18], [19] oraz modele fizyczne, będące układami odpowiednich elementów fizycznych [2] [22]. Modele fizyczne powstawały zazwyczaj na potrzeby konkretnych zadań badawczych. Wykonywane były zarówno różne modele samego serca i lewej komory [23], [24], jaki i całe hydrauliczne modele układu krążenia [25] [27]. Jednak wykorzystanie elementów fizycznych i dedykowanie układu pod konkretne zastosowanie powoduje, że są to modele stosunkowo kosztowne i mało elastyczne. Również dokładność modelu jest często ograniczona. Modele numeryczne są dużo dokładniejsze, tańsze i umożliwiają dużą elastyczność opisu. Niestety w wielu przypadkach, kiedy badana ma być interakcja urządzeń fizycznych i układu krążenia, ich zastosowanie nie jest możliwe. W celu połączenia zalet obu powyższych rozwiązań opracowany został hybrydowy symulator układu krążenia [28] [3]. Było to pierwsze urządzenie, które umożliwiało symulację numeryczną układu krążenia i odtwarzanie warunków fizycznych panujących w wybranych punktach modelu. Podejście to zyskało aprobatę środowiska naukowego i w kolejnych latach inne grupy badawcze opracowywały swoje rozwiązania związane z modelowaniem hybrydowym [31], [32]. Symulator hybrydowy jest urządzeniem składającym się z numerycznego modelu układu krążenia zaimplementowanego i pracującego na platformie czasu rzeczywistego oraz dedykowanej części fizycznej umożliwiającej odwzorowanie hydraulicznych warunków krążeniowych panujących w wybranym punkcie układu [3], [33], [34]. Dzięki temu możliwa jest łatwa zmiana parametrów modelu w środowisku wirtualnym, umożliwiająca w pełni powtarzalną symulację warunków hydrodynamicznych dla różnych typów pacjentów, patologii układu krążenia czy warunków krążenia. Urządzenie to posiada interfejs fizyczny, umożliwiający dołączanie urządzeń wspomagania i badanie wpływu ich pracy na warunki krążenia. Symulator wykorzystywany był między innymi dla symulacji warunków krążenia przy wspomaganiu w układzie przedsionek aorta pompami pulsacyjnymi [35], jak i urządzeniami o przepływie ciągłym [36], [37]. Wykorzystywany był również do badań związanych z rozwojem urządzeń wspomagania pracy serca przez Fundację Rozwoju Kardiochirurgii w Zabrzu. Od kilku lat znajduje się na wyposażeniu Instytutu Metrologii i Inżynierii Biomedycznej Wydziału Mechatroniki Politechniki Warszawskiej w ramach utworzonego Centrum Technologii Biomedycznych i Fizyki Medycznej (BIOFIM) będącego częścią Centrum Badań Przedklinicznych i Technologii (CePT). Pomiary identyfikacyjne 19
20 omówione w dalszej części pracy były prowadzone z wykorzystaniem takiego symulatora, początkowo dzięki uprzejmości fundacji FRK, a następnie Instytutu IMIB PW. Część numeryczna symulatora oparta jest na modelu o parametrach skupionych, który może zostać przedstawiony w formie analogii układu elektrycznego (Rys. 3.3). Model ten składa się ze źródeł ciśnienia (komór) oraz elementów takich jak pojemności, oporności i indukcyjności, reprezentujących między innymi podatność, opór i inertancję naczyń krwionośnych [38], [39]. UK_PZ UK_ST LK PK UK_PT UK_SZ Rys. 3.3 Elektryczna analogia modelu układu krążenia [4]. Poszczególne układy reprezentują: UK_ST, UK_SZ układ krążenia systemowego odpowiednio tętniczego i żylnego, UK_PT, UK_PZ układ krążenia płucnego odpowiednio tętniczego i żylnego, LK lewą komorę z przedsionkiem, PK prawą komorę z przedsionkiem. Model lewej i prawej komory serca opiera się na prawie Franka-Starlinga [41]. Podstawową zależnością jest funkcja umożliwiająca wyznaczenie wartości ciśnienia wewnątrzkomorowego [38], [42]: gdzie: P v (t) = (V v (t) V ) E v (t) E max f (V v (t), V v(t), V vmax(t)) + +A e k V v(t) + B e j V v(t) + C, (3.1) P v (t) ciśnienie w komorze serca, V v (t) objętość komory, V objętość szczątkowa komory, E v (t) funkcja elastancji znormalizowana do wartości jeden, E max wartość maksymalna funkcji elastancji (końcowo-skurczowa), f (V v (t), V v(t), V vmax(t)) funkcja korekcyjna zależna od objętości komory i tempa wyrzutu, A,B,C,j,k parametry stałe. 2
21 Wartości przepływów silnie zależą zarówno od kształtu, jak i maksymalnej wartości funkcji elastancji. Stanowi więc ona podstawową część opisu działania komory. Zmiana wartości maksymalnej funkcji elastancji pozwala na symulację zmiany stopnia wydolności komory serca. Pozostałe wielkości w modelu wyznaczane są zgodnie z podstawowymi zależnościami fizycznymi, bazując na dwóch podstawowych zależnościach: Q = P, (3.2) R P = Q, (3.3) C gdzie: Q natężenie przepływu krwi, ΔP spadek ciśnienia krwi na modelowanym odcinku układu naczyniowego, R oporność układu naczyniowego, P ciśnienie panujące w wybranym punkcie układu, ΔQ różnica przepływu wejściowego i wyjściowego krwi z układu, C podatność układu naczyniowego. Wartości natężeń przepływów obliczane są, jako iloraz wartości spadku ciśnienia i oporów przepływu. Wartości ciśnień wyznaczane są z równania (3.3), będącego ilorazem różnicy rozpływów w systemie (ΔQ) oraz sumarycznej podatności tego systemu. Podatność jest wielkością opisującą zdolność ścian naczyń krwionośnych do rozszerzania się i kurczenia pod wpływem zmian ciśnienia i jest definiowana, jako stosunek zmiany objętości naczynia do zmiany ciśnienia. W wyniku przeprowadzenia obliczeń w tak zdefiniowanym modelu układu krążenia, możliwe jest uzyskanie przebiegów zmienności ciśnień i przepływów dla charakterystycznych punktów układu krążenia Rys. 3.4 Hybrydowy symulator układu krążenia człowieka. 1 - zamknięty zbiornik roboczy, 2,3 - transformator impedancji złożony z pompy hydraulicznej (2) i silnika elektrycznego (3), 4 - zbiornik o regulowanej objętości umożliwiający zapewnienie poduszki powietrznej nad zbiornikiem roboczym, 5 - zbiornik spływowy. 21
22 Część fizyczna symulatora (Rys. 3.4) pozwala na rzeczywiste odtworzenie warunków hydrodynamicznych obliczonych w części numerycznej dla wybranych punktów układu krążenia oraz dołączanie do nich różnego typu urządzeń wspomagania pracy serca. Składa się ona z zamkniętego zbiornika roboczego, w którym odtwarzane są warunki hydrauliczne równe obliczonym w części numerycznej modelu, zbiornika spływowego otwartego do atmosfery oraz umieszczonego między nimi transformatora impedancji. Zbiornik roboczy wyposażony jest w poduszkę powietrzną o regulowanej objętości, która stanowi reprezentację fizyczną podatności naczyń występującej w danym punkcie układu krążenia oraz odpowiednie przyłącze, umożliwiające dołączenie jednej z kaniul urządzenia wspomagającego. Transformatory impedancji [43] składają się z proporcjonalnych, sterowanych elektrycznie źródeł przepływu, zbudowanych z hydraulicznej pompy zębatej napędzanej silnikiem elektrycznym prądu stałego. Ciecz robocza jest naprzemiennie dopompowywana i wypompowywana ze zbiornika roboczego, powodując w nim zmiany ciśnienia. Źródła przepływu sterowane są napięciowo, gdzie generowany przepływ jest liniowo proporcjonalny do napięcia sterującego i niezależny od spadku ciśnienia na pompie. Dzięki temu, wyliczony w części numerycznej przepływ może być odtworzony fizycznie powodując odpowiednią zmianę ciśnienia w zbiorniku roboczym. Uzyskana wartość ciśnienia stanowi podstawę do wyznaczenia w części numerycznej nowej wartości przepływu dla pompy. Dzięki temu w zbiorniku roboczym otrzymujemy zmienną wartość ciśnienia, zgodną z warunkami zamodelowanymi dla danego punktu układu krążenia. W oryginalnej wersji, odpowiednie oprogramowanie symulatora, pozwalało na fizyczne modelowanie warunków hemodynamicznych panujących w przedsionku wybranej komory serca oraz w aorcie lub tętnicy płucnej [35]. Umożliwiało to dołączanie urządzeń wspomagających pracujących w układzie przedsionek-tętnica (Rys. 3.5) poprzez transformatory impedancji (T1, T2). Sterowanie modelu odbywa się poprzez pomiar ciśnienia panującego w części fizycznej, wyliczenie na jego podstawie przepływów dolotowego i wylotowego z danego punktu w części numerycznej i wygenerowanie przepływu fizycznego będącego różnicą wyznaczonych przepływów. 22
23 Q xi LVAD Q xo Część fizyczna P T1 P T2 C la C il Q T1 T1 Transformatory impedancji Q T2 T2 R vp R li P lv R lo P as R cs P cas P la Q vp Część numeryczna Q li Q lo Lewa komora Q cor Q l Rys. 3.5 Schemat dołączenia wspomagania w układzie przedsionek - aorta Przykładowo, dla dołączenia urządzenia LVAD w układzie przedsionek aorta, dla symulacji warunków w przedsionku (T1) wykonywane są następujące obliczenia: mierzone jest ciśnienie P T1 w części fizycznej urządzenia, która reprezentuje przedsionek lewej komory (P la ). Na podstawie wartości tego ciśnienia w części numerycznej obliczany jest przepływ wlotowy (Q vp ) i wylotowy (Q li ) z przedsionka zgodnie z zależnościami: Q vp = P vp P la R vp (3.4) Q li = P la P lv R li (3.5) gdzie: Q vp przepływ w żyłach płucnych, P vp ciśnienie w żyłach płucnych, P la ciśnienie w lewym przedsionku, R vp oporność żył płucnych, Q li przepływ wlotowy do lewej komory, P lv ciśnienie lewokomorowe, R li oporność wejściowa lewej komory. Ciśnienie w lewej komorze obliczane jest zgodnie z zależnością (3.1). W kolejnym kroku modelowania, różnica pomiędzy obliczonymi przepływami podawana jest jako wartość zadana dla transformatora impedancji, który generuje odpowiedną wartość fizyczną przepływu (Q T1 ). Ciśnienie P T1 w części fizycznej zmienia się w wyniku sumy oddziaływań przepływu transformatora (Q T1 ), przepływu wlotowego do urządzenia wspomagającego (Q xi ) oraz podatności przedsionka (C la ) reprezentowanej przez fizyczny kondensator powietrzny. Ciśnienie to jest ponownie mierzone a cała procedura obliczeniowa powtarzana. 23
24 3.2. Zespół wspomagania pracy serca Na przestrzeni ostatnich 25 lat Fundacja Rozwoju Kardiochirurgii w Zabrzu im. Prof. Zbigniewa Religi zajmowała się opracowywaniem rozwiązań technologicznych różnych protez serca, które mogłyby mieć zastosowanie w praktyce klinicznej. W ramach prowadzonych prac powstał pozaustrojowy system wspomagania serca POLCAS, który został wdrożony do praktyki klinicznej u ponad 3 pacjentów [44]. W ramach wieloletniego programu rządowego Polskie Sztuczne Serce skonstruowana, wytworzona i przebadana została unowocześniona wersja systemu wspomagania - ReligaHeart EXT, która aktualnie znajduje się w fazie badań klinicznych dla uzyskania znaku CE. W ramach tego samego programu opracowany i wstępnie przebadany został prototyp pulsacyjnej implantowalnej pompy wspomagania serca ReligaHeart IMPL oraz wirowej, odśrodkowej pompy wspomagania serca ReligaHeart ROT. Aktualne działania badawcze Pracowni Sztucznego Serca koncentrują się na opracowaniu pulsacyjnego systemu wspomagania serca dla dzieci RELIGA HEART PED, opracowaniu ultradźwiękowej metody detekcji i różnicowania mikrozatorów w płynącej krwi oraz systemu pomiaru przepływu przeznaczonego dla protezy ReligaHeart EXT. Do tej pory, system POLCAS stanowi jedyne rozwiązanie Fundacji, które zostało wprowadzone do praktyki klinicznej. Niemniej jednak obserwowano pewne problemy związane z jego użytkowaniem. Najistotniejszym jest ryzyko wystąpienia powikłań zakrzepowo-zatorowych, które często związane są z niewłaściwym sterowaniem urządzenia. Dla zapewnienia prawidłowego przebiegu wspomagania wymagana jest znajomość wartości przepływu objętościowego krwi wytwarzanego przez pompę. Aktualnie nie ma jednak możliwości jego pomiaru czy estymacji. Wpływa to negatywnie na bezpieczeństwo wspomaganego pacjenta oraz ilość powikłań. W niniejszym podrozdziale omówiono szczegółowo budowę zespołu wspomagania serca POLCAS, wyniki prac badawczych mających na celu estymację wartości przepływu w komorze krwistej urządzenia oraz efekty wcześniejszych prac związanych z modelowaniem tego urządzenia Konstrukcja i elementy zespołu wspomagania pracy serca POLCAS Polskie urządzenie wspomagania pracy serca POLVAD-MEV jest pulsacyjną, pozaustrojową pompą krwi opracowaną na potrzeby zarówno terapii krótko, jak i długoterminowej. Może być wykorzystywane do wspomagania jedno- lub obukomorowego. Stosowane jest w czasie operacji kardiologicznych, w czasie rekonwalescencji 24
25 po niektórych operacjach czy jako rozwiązanie czasowe do chwili przeszczepu serca. Pulsacyjny zespół wspomagania POLCAS składa się z urządzenia wspomagania pracy serca oraz dedykowanej jednostki sterującej POLPDU. Urządzenie POLVAD-MEV pracuje w połączeniu równoległym do naturalnej komory serca. Może być stosowane zarówno w połączeniu przedsionek aorta, jak i koniuszek serca aorta. Sama pompa jest konstrukcją typową dla tego rodzaju urządzeń. Składa się z komory krwistej i powietrznej odseparowanych ruchomą membraną (Rys. 3.6, rozdział 1 Rys. 1.2). Komora powietrzna połączona jest drenem pneumatycznym z jednostką sterującą. Doprowadzenie wysokiego ciśnienia do komory powoduje ruch membrany i wyrzut cieczy z komory krwistej. Następujące po nim podanie podciśnienia powoduje powstanie siły ssącej, następuje przemieszczenie membrany w kierunku przeciwnym i napełnianie komory krwistej. Jednostka sterująca POLPDU (Rys. 3.6) jest urządzeniem zasilająco-sterującym dla urządzenia wspomagającego. Generuje ona falę ciśnienia zasilającego komorę powietrzną. A) B) Rys. 3.6 Pulsacyjny zespół wspomagania pracy serca. A) urządzenie wspomagania pracy serca POLVAD-MEV, B) jednostka sterująca POLPDU-51 VAD zawór upustowy zbiornik ciśnienia zasilania systoli (+) zawór liniowy kompresor zbiornik ciśnienia zasilania diastoli (-) zawór dopuszczający Rys. 3.7 Schemat poglądowy modułu pneumatycznego jednostki sterującej POLPDU-51 dedykowanego pneumatycznym urządzeniom wspomagania pracy serca. 25
26 Kompresor jednostki (Rys. 3.7) odpowiada za wytwarzanie ciśnienia wysokiego w zbiorniku zasilania systoli (ciśnienie sterujące w fazie opróżniania komory krwistej) i podciśnienia w zbiorniku zasilania diastoli (ciśnienie sterujące w fazie napełniania komory krwistej). Odpowiednie układy zaworów dopuszczających i upuszczających powietrze pozwalają na ustalanie w zbiornikach wartości ciśnień zbliżonych do zadanych. Przetwornik elektropneumatyczny, będący zaworem liniowym, pozwala na naprzemienne łączenie komory pneumatycznej urządzenia z odpowiednim zbiornikiem zasilającym zgodnie z zadanymi warunkami sterowania (Rys. 3.8). Parametrami sterowania jednostki, które mogą być ustawiane przez operatora, są: - SDP (ang. Systolic Driving Pressure) zadane ciśnienie zasilania systoli (8 3 mmhg), - DDP (ang. Diastolic Driving Pressure) zadane ciśnienie zasilania diastoli ( -75 mmhg), - AHR (ang. Artificial Heart Rate) ilość cykli pracy na minutę (3.6), (3 11 bpm), - %SYS (ang. Systole Percent) wypełnienie sygnału sterującego w procentach (3.7), (2 8%), - DEL czas opóźnienia początku wyrzutu względem skurczu naturalnej komory serca ( 8% czasu trwania ostatniego cyklu pracy serca). ster SYS DIAS t t s t (s) T Rys. 3.8 Schematyczna prezentacja sygnału sterującego pulsacyjnego zespołu wspomagania pracy serca. t początek fazy wyrzutu, t s koniec fazy wyrzutu i początek napełniania komory krwistej, T koniec fazy napełniania. AHR = 1 T t 6, (3.6) %SYS = t s t T t 1%, (3.7) gdzie: T czas zakończenia fazy napełniania, t czas rozpoczęcia fazy wyrzutu, t s czas zakończenia fazy wyrzutu (systoli). 26
27 Sterowanie zespołu wspomagania pracy serca POLCAS Jak opisano w poprzednim podrozdziale, sterowanie pracą pulsacyjnego urządzenia wspomagania pracy serca odbywa się poprzez doprowadzanie do komory powietrznej pompy naprzemiennie ciśnienia wysokiego i podciśnienia. Odbywa się to poprzez naprzemienne łączenie drenu zasilającego z odpowiednim zbiornikiem jednostki sterującej. W zbiornikach utrzymywana jest w przybliżeniu stała wartość ciśnienia sterującego, w założeniu równa ciśnieniu zadanemu poprzez parametry SDP i DDP. Zadanie naprzemiennego łączenia zbiorników zasilających z drenem realizuje dedykowany zawór liniowy, który jest konstrukcją własną producenta zespołu (FRK). Aktualnie, w praktyce klinicznej, personel medyczny musi zadawać wartości parametrów sterowania, takich jak: wartości ciśnienia w zbiornikach zasilających oraz wypełnienie sygnału sterującego w procentach, czyli stosunek czasu trwania fazy wyrzutu do fazy napełniania komory krwistej urządzenia. Wybierany jest również tryb wspomagania: synchrony lub asynchroniczny. W pierwszym przypadku mierzony jest sygnał EKG pacjenta i częstotliwość pracy urządzenia jest taka sama jak naturalnej komory. W tym przypadku należy nastawić wartość parametru DEL, czyli opóźnienia wyrzutu z urządzenia względem początku skurczu naturalnej komory. Czas ten powinien być dobrany w taki sposób, aby wydatek pompy był podawany do aorty pod koniec fazy skurczu izotonicznego. Taki sposób prowadzenia terapii pozwala na w przybliżeniu fizjologiczną pracę naturalnej komory. Zapobiega sytuacjom, gdy wydatek pompy powoduje znaczny wzrost ciśnienia aortalnego w chwili skurczu komory i w rezultacie przeciwdziała wyrzutowi z naturalnej komory. W takim wypadku może dochodzić do zastoju krwi, złego obmywania komory i w konsekwencji zwiększonego ryzyka tworzenia się zakrzepów. Jednocześnie w przypadku pracy synchronicznej obserwuje się przypadki (około 8%) znacznej poprawy funkcjonowania niewydolnej komory. Nieuszkodzone rejony narządu zwiększają swoją wydolność i w rezultacie może nastąpić częściowa regeneracja komory, umożliwiająca wyszczepienie urządzenia i powrót pacjenta do funkcjonowania w warunkach pozaszpitalnych. Niestety ze względu na trudności w prowadzeniu ciągłego pomiaru sygnału EKG, w większości przypadków klinicznych, stosowany jest tryb pracy asynchronicznej. W tym przypadku ustawiana jest stała ilość cykli pracy urządzenia na minutę (AHR). Niezależnie od wybranego trybu wspomagania, jedyną informacją zwrotną dla personelu, dotyczącą pracy urządzenia, jest przebieg fali ciśnienia zasilania urządzenia (ciśnienie mierzone na wylocie zaworu liniowego) oraz ogólny stan pacjenta, oceniany okresowo. Nie ma możliwości oceny wartości realizowanego rzutu minutowego komory, który jest 27
28 najistotniejszą informacją z punktu widzenia prowadzonej terapii. Przyjmuje się, że rzut ten nie powinien być mniejszy niż 2.3 l/min na metr kwadratowy powierzchni ciała pacjenta (obliczanej z zależności pomiędzy wzrostem i masą), przy czym zalecaną wartością jest 2.8 l/min na m 2. Należy podkreślić, że wartość wydatku urządzenia jest silnie zależna od obciążenia wstępnego (na wlocie) i następczego (na wylocie) pompy. Dla tych samych parametrów sterowania a różnego stanu pacjenta wartość przepływu krwi znacznie się różni (Rys. 3.9). Jak do tej pory, nie udało się opracować odpowiedniej metody wykonywania pomiaru ciśnień obciążenia urządzenia w warunkach klinicznych. Trwają prace nad opracowaniem odpowiedniego układu pomiarowego do oszacowania wydatku minutowego (rozdział 3.2.3), ale jak dotąd nie uzyskano satysfakcjonującego rozwiązania. Przepływ wylotowy (l/min) Czas (s) obciążenie 6 mmhg obciążenie 1 mmhg obciążenie 17 mmhg Rys. 3.9 Zależność wartości objętościowego przepływu wylotowego z komory krwistej urządzenia VAD od ciśnienia obciążenia na wylocie. Parametry zasilania takie same dla każdego przypadku (SDP 2, DDP -5, AHR 6, %SYS 4). Jedynym źródłem informacji dotyczącej pracy urządzenia jest więc przebieg zmian ciśnienia zasilania w drenie pneumatycznym (Rys. 3.1, a). Ciśnienie to ma przebieg o charakterze zbliżonym do prostokątnego, w przybliżeniu zgodnym czasowo z przebiegiem sygnału sterującego. W fazie wyrzutu ma wartość niższą od nastawionej wartości ciśnienia w zbiorniku zasilania systoli. Dopiero w chwili osiągnięcia pełnego wyrzutu ciśnienie to wzrasta do wartości równej wartości ciśnienia zasilania. Podobna sytuacja ma miejsce w przypadku napełniania, po osiągnięciu całkowitego napełnienia komory ciśnienie lekko spada do wartości nastawionego ciśnienia zasilania. Wizualne rozpoznanie wystąpienia całkowitego wyrzutu jest stosunkowo proste, większych problemów dostarcza rozpoznanie całkowitego napełnienia komory krwistej urządzenia. Analogicznie, automatyczne algorytmy detekcji stanów skrajnego napełnienia na podstawie analizy ciśnienia zasilania dają lepsze rezultaty dla pierwszego przypadku i są znacznie mniej skuteczne w drugim (więcej w rozdziale 6.1). 28
29 Znajomość przebiegu wartości przepływu krwi w komorze pozwoliłaby na ocenę wielkości wydatku minutowego urządzenia. Dodatkowo umożliwiłaby skuteczniejszą ocenę wystąpienia stanów skrajnego napełnienia. Znaczny spadek wielkości przepływu w końcowej fazie trwania systoli oznacza, że komora została opróżniona całkowicie (Rys. 3.1a). Analogicznie, spadek wartości przepływu wlotowego w końcowej fazie diastoli informuje o całkowitym napełnieniu urządzenia. Dlatego też możliwość oszacowania wartości chwilowej przepływu krwi w komorze stanowiłaby cenną informację dla personelu medycznego i mogłaby się przyczynić do opracowania automatycznego systemu adaptacji parametrów sterowania do aktualnych warunków wspomagania. a) b) Przepływ wylotowy (l/min) Przepływ wlotowy (l/min) Czas (s) Czas (s) Rys. 3.1 Ciśnienie zasilania na wyjściu zaworu liniowego (P z ) dla obciążenia na wylocie komory odpowiednio 6 i 17 mmhg. a) zestawienie z przebiegiem wartości przepływu wylotowego z komory i zaznaczeniem chwili wystąpienia pełnego wyrzutu, b) zestawienie z przebiegiem wartości przepływu wlotowego i zaznaczeniem chwili wystąpienia całkowitego napełnienia. Parametry zasilania takie same dla każdego przypadku (SDP 2, DDP -5, AHR 6, %SYS 4) Przegląd metod pomiarowych dotyczących wydatku minutowego Jak opisano w rozdziale 3.2.2, pulsacyjne urządzenia wspomagania pracy serca powinny być wyposażone w możliwość oszacowania wartości przepływu na wylocie z urządzenia lub inny sposób oceny wartości wydatku minutowego. Z punktu widzenia metodyki pomiarów zadanie wykonania tego typu oszacowania wydaje się być proste w realizacji. Jednak w praktyce instalacja odpowiednich sensorów okazuje się być bardzo skomplikowana a nawet 29 Pz dla Pob=6 mmhg Pz dla Pob=17 mmhg Qout dla Pob=6 mmhg Qout dla Pob=17 mmhg Pz dla Pob=6 mmhg Pz dla Pob=17 mmhg Qin dla Pob=6 mmhg Qin dla Pob=17 mmhg Ciśnienie zasilania (mmhg) Ciśnienie zasilania (mmhg)
30 niemożliwa. W większości wymaga ona dodatkowych doprowadzeń elektrycznych czy zmian w konstrukcji samego urządzenia. Może to powodować wiele komplikacji zarówno z technicznego, jak i medycznego punktu widzenia, w tym ryzyko powstawania zakrzepów czy występowania zakażeń. Ewentualne zastosowanie bezprzewodowej transmisji danych pomiarowych z czujnika może stwarzać problemy ze względu na obecność wrażliwego sprzętu medycznego. Dlatego odpowiednia metoda pomiarowa powinna być bezinwazyjna, nie powinna wymagać bezpośredniego kontaktu z krwią i być odporna na zakłócenia. Nie powinna również wymagać wprowadzania zmian w konstrukcji urządzenia, zwłaszcza od strony komory krwistej. Wymagana dokładność estymacji wielkości mierzonej wynosi około 1% [11]. Przy czym podkreślić należy, że przepływ w urządzeniu jest silnie zmienny, z całkowitym okresem zmienności wartości przepływu wynoszącym około jednej sekundy. Obecnie, w warunkach eksperymentów badawczych, do pomiaru wartości przepływu wylotowego z pompy VAD wykorzystuje się często przepływomierze ultradźwiękowe z sensorami nakładanymi na kaniule medyczne (Transonic TS41 Tubing Module). Dokładność tego pomiaru wynosi około 5%. Jego zastosowanie w warunkach klinicznych jest jednak niewskazane, ze względu na znaczące rozmiary urządzenia pomiarowego, bardzo wysoki koszt i wymóg dodatkowej obsługi układu ze strony personelu medycznego. Dodatkowo wykorzystanie tego typu układu pomiarowego jest niemożliwe do zastosowania w przypadku urządzeń częściowo i całkowicie wszczepialnych. W dalszej części rozdziału przedstawiono niektóre z podejść, których zastosowanie było badane dla urządzenia POLVAD-MEV. W ramach pracy [11] przebadana została możliwość wykorzystania znanych metod pomiarowych zaadaptowanych na potrzeby urządzenia POLVAD. Metoda impedancyjna bazowała na zjawisku objętościowej przewodności elektrycznej krwi. Zmiana objętości komory powoduje zmianę wartości impedancji elektrycznej. Zastosowanie tytanowych pierścieni zastawek umożliwiło wykorzystanie ich jako elektrod mających bezpośredni kontakt z krwią na wlocie i wylocie komory. Badając zmianę impedancji pomiędzy zastawkami możliwe było oszacowanie jej objętości. Właściwości przewodności elektrycznej krwi zostały również wykorzystane w metodzie pojemnościowej. Na zewnętrznej stronie obudowy komory krwistej utworzony został kondensator z materiału przewodnika, a po stronie komory powietrznej utworzono osłonę izolacyjną połączoną z uziemieniem. Zmiana proporcji objętości krwi (przewodnika) i powietrza (izolatora) w urządzeniu powodowała zmiany pojemności elektrycznej systemu. W metodzie ultradźwiękowej starano się dokonać 3
31 pomiaru położenia membrany wykorzystując zjawisko odbicia wiązki ultradźwiękowej od jej powierzchni. Zastosowano osobno nadajnik i odbiornik umieszczone na ścianie komory krwistej i badano czas powrotu fali odbitej. Na tej podstawie szacowana była odległość membrany od obudowy, a w rezultacie objętość komory krwistej. W metodzie akustycznej starano się wykorzystać właściwości rezonansowe komory pneumatycznej. Ruch membrany powoduje zmianę kształtu komory powietrznej, a w rezultacie wpływa na częstotliwości rezonansowe. Najlepszą dokładność pomiaru uzyskano dla metody impedancyjnej, lecz była ona podatna na zmienność oporności krwi, która jest silnie zależna od jej składu biochemicznego. Z tego względu zastosowanie metody w praktyce wymagałoby wprowadzenia adaptacyjnej metody kalibracji układu dla konkretnego przypadku. Metoda pojemnościowa okazała się mało dokładna i podatna na zakłócenia. Metody akustyczna i ultradźwiękowa okazały się korzystne ze względu na brak konieczności zmian w konstrukcji urządzenia VAD. Otrzymana dokładność pomiaru była zadowalająca, lecz dla metody ultradźwiękowej obserwowano problemy związane z maskowaniem czujników przez membranę w przypadku całkowitego wyrzutu. Emiter stosowany w metodzie akustycznej był zbyt duży dla zastosowania w warunkach docelowych. Ostatecznie oceniono, że żadna z przedstawionych metod nie umożliwia wykorzystania jej w warunkach klinicznych, biorąc jednak pod uwagę dokładność, stopień izolacji względem krwi i właściwości metrologiczne, najbardziej obiecującą była metoda akustyczna. Prace nad rozwojem metody impedancyjnej opisano w pracach [45] [47]. Wykonane zostały dedykowane układy pomiarowe i opracowane odpowiednie metody analizy sygnału. Przeprowadzono liczne testy w warunkach laboratoryjnych i na żywym organizmie. Otrzymano dobre rezultaty dotyczące możliwości oszacowania objętości komory tą metodą. Podkreślono jednak, że do jej poprawnego działania niezbędne jest wykonanie pierścieni zastawek z materiału przewodzącego, co może uniemożliwić jej zastosowanie w praktyce. Zbadania wymaga kwestia wpływu wysokoczęstotliwościowego prądu aplikacyjnego na układ krzepnięcia krwi. Konieczne jest również opracowanie sposobu kalibracji pomiarów. W pracy [48] badano możliwość wykorzystania metody analizy obrazu do oceny stanu odkształcenia membrany oddzielającej komory urządzenia VAD. Wykonane zostało stanowisko badawcze składające się z pneumatycznej komory urządzenia połączonej z membraną (usunięta została czasza komory krwistej). Na centralny punkt membrany naniesiono kolisty znacznik graficzny. Przy pomocy kamery rejestrowano obraz poruszającej się membrany. Określono, że uzyskane wyniki wskazują na możliwość oszacowania wartości 31
32 przepływu krwi w urządzeniu przy założeniu pewnej modyfikacji układu optycznego. Uznano, że konieczne byłoby użycie kamery o szerokokątnym obiektywie oraz pokrycie membrany warstwą przeciw-odbiciową. Niezbędne byłoby również zamontowanie dedykowanego oświetlenia membrany. Autorzy nie wyjaśniają, czy układ ten mógłby zostać zminiaturyzowany, umożliwiając wykorzystanie metody w warunkach klinicznych. Inne zastosowanie metody optoelektronicznej do oceny objętości komory przedstawiono w pracy [49]. System, umieszczony na czaszy komory pneumatycznej, składał się z zestawu wielu diod emitujących światło oraz zestawu fotodiod absorpcyjnych mierzących natężenie światła odbitego od membrany. Uzyskana niepewność pomiaru chwilowej objętości komory wyniosła poniżej 1%. Układ charakteryzuje się kompaktową budową jednak nadal niezbędna jest ingerencja w budowę komory oraz doprowadzenie przewodów elektrycznych do diod. Zastosowany układ wymaga również dużej mocy obliczeniowej. Jednym z podejść do rozwoju metody akustycznej dla celów oszacowania objętości komory powietrznej urządzenia, było wykorzystanie układu akustycznego rezonatora Helmholtza [5], [51]. Do komory powietrznej, za pośrednictwem wąskiej szyjki, dołączona została dodatkowa komora rezonacyjna. Badając częstotliwość rezonansową drgań masy powietrza w szyjce możliwe było wyznaczenie objętości chwilowej komory powietrznej. Na tej podstawie można oszacować objętość chwilową komory krwistej, wychodząc z założenia stałej sumy objętości obu komór dla dowolnej chwili czasowej. Uzyskano niepewność oszacowania mniejszą niż 1%. Zastosowanie tej metody wymaga jednak odpowiedniego systemu obliczeniowego oraz dołączenia do komory powietrznej dodatkowej objętości, co negatywnie wpływa na gabaryty układu. Podjęte zostały również próby wykorzystania metody ultradźwiękowej zastosowanej do pomiaru przepływu krwi w postaci dedykowanego przepływomierza dopplerowskiego [52]. Wykonany został układ pomiarowy w postaci konektora zintegrowanego z ultradźwiękowym systemem pomiarowym. Konektor włączany był w kaniulę urządzenia. Układ pozwalał na pomiar prędkości przepływu z niedokładnością rzędu 2%, która znacznie wzrasta dla okresów występowania przepływów turbulentnych. Główną zaletą metody jest możliwość wykrycia zmian w charakterze przepływu, które mogą świadczyć o tworzeniu się skrzepliny w obrębie zastawki. Jak dotąd żadna z wymienionych metod nie jest stosowana standardowo w warunkach wspomagania klinicznego. 32
33 3.3. Modelowanie urządzeń wspomagania pracy serca Ze względu na poszukiwanie innych niż pomiarowe metod estymacji wartości przepływu w komorze krwistej urządzenia VAD postanowiono opracować model, umożliwiający oszacowanie jego wartości na podstawie dostępnych danych pomiarowych. Niniejszy rozdział zawiera przegląd literaturowy prac związanych z modelowaniem urządzeń wspomagania pracy serca w celu oceny użyteczności przedstawionych w nich rozwiązań do celów estymacji wielkości natężenia przepływu objętościowego krwi w urządzeniu Modele obliczeniowej mechaniki płynów Do badań oraz projektowania konstrukcji urządzeń wspomagania pracy serca często wykorzystywana jest obliczeniowa mechanika płynów (CFD, ang. Computational Fluid Dynamics). Umożliwia ona rozwiązanie układu nieliniowych równań różniczkowych dotyczących złożonego problemu przepływu w komorze poprzez podział dziedziny obliczeń na wiele układów uproszczonych (tzw. siatkowanie). W wyniku dyskretyzacji równania różniczkowe zastępowane są układem równań algebraicznych a rozwiązania otrzymuje się w wybranych punktach przestrzeni tzw. węzłach lub wewnątrz objętości kontrolnych, przy czym dokładność rozwiązania zależy m. in. od rodzaju i gęstości siatki. Metody CFD są bardzo rozpowszechnione w analizie i projektowaniu pomp krwi (głównie o przepływie ciągłym) [53] i używane już od wczesnych lat dziewięćdziesiątych. Również wiele opracowywanych modeli pulsacyjnych pomp krwi wykonywanych jest przy wykorzystaniu tej techniki obliczeniowej. Do rozwiązania równań Naviera-Stokesa, opisujących ruch płynu, stosuje się obecnie metodę elementów skończonych (ang.: Finite Element Method) [54] lub metody objętości skończonych (ang. Finite Volume Method) [55]. Większość badań dotyczących modelowania VAD-ów jest prowadzona przy użyciu komercyjnych pakietów oprogramowania CFD (Fluent, ANSYS, CFX i STAR-CD). Tworzenie modelu opartego na metodzie obliczeniowej wymaga w pierwszym etapie określenia granic fizycznych przepływu lub geometrii części przepływowej urządzenia. W przypadku pulsacyjnych urządzeń wspomagających zazwyczaj jest ona importowana bezpośrednio z programu wspomagania projektowania (CAD). W kolejnym kroku generowana jest siatka numeryczna pokrywająca obszar obliczeniowy. Odpowiedni dobór rodzaju i gęstości siatki jest istotną częścią budowy modelu, gdyż od jej parametrów w znacznym stopniu zależą otrzymane wyniki oraz uzyskiwany błąd. Obszary o nieskomplikowanej geometrii mogą być dyskretyzowane siatkami strukturalnymi, w których wyróżnić można wiersze, kolumny i warstwy komórek [56], przy czym podział 33
34 może być nierównomierny np. zagęszczony przy brzegu [57]. Dla obszarów o wysoce skomplikowanej geometrii stosowane są siatki niestrukturalne a zagęszczenie siatki występuje w obszarach o szybko zmieniającym się gradiencie wielkości symulowanych. Po siatkowaniu niezbędne jest określenie warunków brzegowych symulacji, czyli wartości rozwiązania na brzegach obszaru obliczeniowego. Wyróżnia się: wlot z zadanym odpowiednim rozkładem zmiennych (dla VAD jest to zazwyczaj rozkład prędkości), wylot (najczęściej zadawany jest rozkład ciśnienia) oraz ściany, na których zazwyczaj przyjmowany jest warunek braku poślizgu. Na koniec niezbędne jest zdefiniowanie reologii płynu (gęstość, lepkość, właściwości newtonowskie) oraz rodzaju przepływu (turbulentny/laminarny, ściśliwy/nieściśliwy itp.). W razie potrzeby wyznacza się również model dodatkowych zjawisk fizycznych, które mają być symulowane np. model aktywacji płytek krwi lub hemolizy (przedostawanie się hemoglobiny do osocza na skutek niszczenia czerwonych krwinek). Ostatnim etapem jest porównanie uzyskanych rezultatów symulacji z wartościami oczekiwanymi. W 1999 roku C.S. König i inni [58] porównali utworzony model CFD prototypu pulsacyjnego urządzenia wspomagania pracy serca (VAD) z danymi eksperymentalnymi. Dane uzyskano przy użyciu wizualizacji przepływu, polegającej na obserwacji rozchodzenia się cząstek wprowadzonych do strugi, oraz pomiarów profilu prędkości przepływu wlotowego dopplerowskim anemometrem laserowym LDA (ang. Laser-Doppler Anemometry) [59]. Pole prędkości uzyskane z symulacji nie było w pełni zgodne z uzyskanym z eksperymentu, lecz stanowiło dobre przybliżenie. Stwierdzono, że modelowane wartości prędkości wlotowej były zaniżone względem sytuacji rzeczywistej. Wykonany model został wykorzystany w pracy [6] do analizy strumieni przepływu przez urządzenie dla dwóch cieczy newtonowskich o różnych właściwościach. W kolejnej pracy [61] wprowadzono na wlocie dodatkową wartość skalarną określając dla niej równanie transportu. W ten sposób uzyskano możliwość wizualizacji ruchu cząstek, a więc badań jakościowych zawirowań przepływu oraz możliwość oceny czasu przebywania płynu w komorze. Wyniki symulacji oceniono jako poprawne. Modelowano również przebieg zmian wartości ciśnienia w komorze krwistej uzyskując częściową zgodność z wynikami eksperymentalnymi. W 23 roku, Eiji Okamoto i inni [62] wykorzystali technikę CFD do udoskonalenia projektu pulsacyjnej, tłokowej pompy krwi w której występowały duże problemy związane z tworzeniem się zakrzepów. Wykonano model CFD oraz zaproponowano metodę wyliczania dwóch współczynników oceny jakości warunków przepływowych na podstawie danych 34
35 symulacyjnych. Pierwszym z nich był współczynnik szybkości rozpadu krwinek czerwonych obliczany w funkcji wartości naprężeń i czasu ekspozycji na nie. Drugim znormalizowany indeks hemolizy (NIH, ang. Normalized Index of Hemolysis) określający przewidywaną ilość krwinek, które ulegać będą uszkodzeniu. Na podstawie uzyskanych wyników zaproponowano taką zmianę konstrukcji obszarów wlotu i wylotu z urządzenia, która powodowała znaczną poprawę zaproponowanych współczynników oraz eliminację obszarów stagnacji, które występowały w przypadku pierwszej konstrukcji. Model zespółu Avrahamiego i innych [63] zastosowany został do symulowania przepływu w komorze wspomagania serca typu workowego [64], składającego się z elastycznego pęcherza roboczego z dwoma doprowadzeniami wyposażonymi w zastawki mechaniczne. Wyrzut i napełnienie komory realizowane było poprzez umieszczenie komory w zbiorniku z cieczą, w którym ciśnienie było cyklicznie zmieniane. Wykonane zostały dwa modele CFD: bazowy oraz rozszerzony, wykorzystujący sprzężenie płyn-struktura (FSI, ang. Fluid Structure Interaction). Celem badań było porównanie otrzymywanych rezultatów symulacji dla obu modeli z danymi eksperymentalnymi. Rozkład wektorów prędkości przepływu w przekroju podłużnym został lepiej odwzorowany przez model FSI. Stwierdzono globalną zgodność symulowanych prędkości w osiach przekroju dla obu modeli, jednak lokalnie występowały zauważalne różnice w odniesieniu do przepływu rzeczywistego. Model bazowy został wykorzystany w dalszych badaniach hemodynamiki urządzenia [13] do porównania modelu zawierającego zastawkę jednopłatkową z modelem o zastawce dwupłatkowej. Celem badań było określenie, przy której konfiguracji wystąpi mniejsze ryzyko formowania się skrzeplin. W przypadku modelu o zastawce dwupłatkowej stwierdzono lepsze wymywanie cząsteczek z komory lecz wyższą wartość naprężeń ścinających w rejonie zastawek. Na podstawie wartości naprężenia ścinającego działającego na cząsteczki oraz czasu trwania tego oddziaływania wyznaczony został współczynnik poziomu aktywacji płytek krwi. Jego wartość dla zastawki jednopłatkowej była niższa, co oznacza, że pomimo lepszego obmywania komory z zastawkami dwupłatkowymi, przewidywane ryzyko wystąpienia w niej zakrzepów określono jako wyższe, ze względu na wyższe wartości naprężeń w rejonie zastawek. Modele CFD urządzenia wspomagania pracy serca (VAD) opracowanego na Uniwersytecie Stanu Pensylwania [65] [67] wykorzystywano do analizy warunków przepływowych panujących w komorze. Medvitz i inni [65] zamodelowali pompę wyporową 5cc Penn State zawierającą zastawki dyskowe Bjork-Shiley Monostrut (BSM). 35
36 Przeanalizowany został wpływ ustawienia zastawki mitralnej na warunki przepływowe (model bez zastawek, z zastawkami w pozycji bazowej i z zastawką mitralną obróconą nieznacznie względem własnej osi). Badano również rozkład pól prędkości przepływu i prędkości ścinania. Otrzymano wysoką zgodność modelowanych wielkości z danymi eksperymentalnymi. Bardzo ciekawym rozwinięciem prowadzonych prac jest wykorzystanie opracowanego modelu do predykcji obszarów występowania mikroskrzeplin. W pracy [67] Stephen i inni porównali wyniki symulacji numerycznej z wynikami eksperymentu in vitro na zwierzęciu. Wykonano analizę mikroskopową powierzchni wewnętrznej komory, która została wyszczepiona po 3 dniach pracy. Obrazy z mikroskopu elektronowego i konfokalnego uwidaczniały rejony, w których utworzyły się mikro-skrzepliny. Porównano je z mapami prędkości ścinania na ścianach urządzenia uzyskanymi z symulacji. Zaobserwowano korelację pomiędzy obszarami formowania się skrzeplin a występowaniem niskiej wartości prędkości ścinania na ścianie urządzenia. Pozwoliło to na zaproponowanie ujęcia liczbowego prawdopodobieństwa formowania się osadów w postaci potencjału podatności na wykrzepianie (TSC, ang. Thrombus Susceptibility Potential). Pomimo przeprowadzenia badań tylko dla jednego zwierzęcia korelację pomiędzy wynikami z modelu CFD i in vitro określono jako obiecującą. Podsumowując, modele utworzone z wykorzystaniem obliczeniowej mechaniki płynów pozwalają na wyznaczenie pól prędkości i ciśnienia wewnątrz urządzenia, obliczenie wartości występujących naprężeń ścinających, oceny efektywności obmywania komory, analizy powstawania ewentualnych rejonów stagnacji przepływu czy oceny ryzyka powstawania skrzeplin. Często modelowanie stosowane było do badania wpływu zmiany konstrukcji urządzenia czy ustawienia zastawek na warunki hemodynamiczne panujące w komorze, pozwalając na opracowanie korzystniejszego rozwiązania. Równocześnie występuje jednak wiele problemów związanych z zastosowaniem metod CFD dla pulsacyjnych urządzeń wspomagających. Przykładowo, dokładna symulacja przepływu choćby przez jedną zastawkę wymaga użycia bardzo drobnej siatki, dwukierunkowego sprzężenia płyn-struktura (FSI) [68] czy wykorzystania modeli turbulencji dla niskich wartości liczby Reynoldsa uwzględniających przepływy przejściowe [69], [7]. Dlatego też, do tej pory nie została utworzona symulacja, która uwzględniałaby choćby wszystkie aspekty dynamiki przepływu występujące w obszarze zastawek. Z tego względu bardzo dużym wyzwaniem jest zamodelowanie całego urządzenia z dwoma zastawkami, których ruch wynika z warunków 36
37 hydrodynamicznych panujących w komorze i kaniulach dolotowych urządzenia. Dodatkowo ruch płynu wymuszany jest w sposób czynny poprzez elastyczne ściany urządzenia, co wprowadza ruchome granice obszaru obliczeniowego. Jednocześnie ruch membrany nie jest dokładnie znany i może być różny dla każdego cyklu pracy. Z punktu widzenia prowadzonych prac nad wyznaczeniem modelu zespołu wspomagania pracy serca dla celów oszacowania wielkości przepływu w komorze krwistej uznano technikę CFD za nieprzydatną. Nie znaleziono danych literaturowych związanych z takim zastosowaniem wspomnianej techniki. Wiąże się to z faktem, że obliczeniowa mechanika płynów pozwala na określenie warunków przepływu, ale przy znanych warunkach brzegowych symulacji (najczęściej jest to rozkład prędkości na wlocie komory krwistej oraz rozkład ciśnienia na wylocie). W warunkach klinicznych wartości te są nieznane. Dodatkowo czas wykonywania obliczeń jest bardzo długi i uniemożliwia zastosowanie modelu do obliczeń w czasie rzeczywistym Modele bazujące na analogii elektrycznej Jedną z metod wyznaczania modeli pulsacyjnych urządzeń wspomagających jest próba opisu ich działania przy pomocy analogii do układów elektrycznych. Jest to metoda często stosowana do modelowania układu krążenia człowieka z wykorzystaniem opisu matematycznego o elementach skupionych [18], [19], [33], [35], [39]. Metoda ta polega na przybliżeniu oddziaływań występujących w całych segmentach układu krążenia przy pomocy pojedynczych elementów rezystancyjnych, indukcyjnych i pojemnościowych. Dzięki temu możliwy staje się uproszczony zapis występujących zjawisk. Metodę tę w wielu pracach stosowano również w celu opisu działania urządzeń wspomagających. Dla pomp o przepływie ciągłym opis tego typu jest dość prosty i szeroko omówiony w literaturze [71] [75]. W przypadku urządzeń pulsacyjnych zagadnienie jest znacznie bardziej skomplikowane, między innymi ze względu na konieczność opisania zmiennego w czasie ciśnienia zasilania urządzenia, które w wielu przypadkach jest zależne od warunków wspomagania. Dodatkowo niezbędne jest wprowadzenie opisu zastawek, które są elementami silnie nieliniowymi. Z tego względu powstało niewiele prac związanych z tym zagadnieniem. W pracy [76] zamodelowane zostało membranowe urządzenie VAD o napędzie pneumatycznym dla celów prowadzenia badań symulacyjnych nad wpływem stosowania wspomagania na warunki hemodynamiczne panujące w układzie krążenia człowieka. Opis matematyczny urządzenia sprowadza się do jego opisu w postaci źródła ciśnienia z zastawkami reprezentowanymi przez zmienną w czasie rezystancję, zależną od wartości 37
38 ciśnienia zasilania pneumatycznego. Opis uzupełniono o inercję płynu w króćcu dolotowym i wylotowym (Rys. 3.11). Rys Schematyczny diagram (a) i model elektryczny (b) pneumatycznej membranowej pompy krwi [76] Wartość przepływu wylotowego z urządzenia została określona przy pomocy równania różniczkowego, gdzie przyrost wartości przepływu opisano jako: dq (t) dt = 1 L (P p(t) P a (t) Q (t)r v (t)) gdzie: Q (t) - przepływ wylotowy z urządzenia VAD, P p (t) - ciśnienie zmierzone w komorze pneumatycznej urządzenia, P a (t) ciśnienie obciążenia na wyjściu komory, R v (t), L estymowana wartość oporu zastawki wylotowej i bezwładności płynu. Rezystancja zastawki została opisana przy pomocy funkcji trapezowej o parametrach czasu rozpoczęcia otwarcia i zamknięcia zastawki wyznaczanych na podstawie przebiegu ciśnienia zasilania oraz stałej długości czasu trwania otwierania i domykania zastawki. Wartości graniczne rezystancji w pozycjach całkowicie otwartej i zamkniętej wyznaczone zostały jako wartości stałe. Na podstawie wartości pomiarowych przebiegu ciśnienia w komorze pneumatycznej urządzenia (P p ) oraz ciśnienia obciążenia wyjściowego (P a ) wyznaczono estymowaną wartość przepływu. Przedstawione wyniki wskazują na osiągnięcie wysokiej zgodności z danymi pomiarowymi. Należy jednak zwrócić uwagę, że model wymaga znajomości ciśnienia obciążenia następczego (na wylocie VAD). Przedstawione wyniki pomiarowe i symulacyjne dotyczą wyłącznie jednego przypadku warunków pracy urządzenia, co utrudnia ocenę poziom uniwersalności wyznaczonego opisu. W pracy [77] przedstawiony został model pompy cewnikowej. Jest to urządzenie sterowanie pneumatycznie z membraną rozdzielającą komory robocze, jednak zamiast kaniuli wlotowej i wylotowej z zastawkami wyposażone jest w jeden cewnik, który umieszczany jest w komorze serca i aorcie. W czasie napełniania komory, krew zasysana jest do urządzenia. 38
39 W fazie wyrzutu odpowiedni układ zastawek w cewniku powoduje wypływ krwi do aorty. Jest to urządzenie przeznaczone do zastosowania na krótki okres czasu, umożliwiające wspomaganie naturalnej komory bez konieczności wykonywania dużej operacji. Celem opracowania modelu było wyznaczenie minimalnej średnicy cewnika, dla której możliwe będzie zapewnienie zadanego przepływu bez wystąpienia mechanicznego uszkodzenia składników krwi. Otrzymane dane symulacyjne porównano z wynikami eksperymentalnymi. Modelowane ciśnienie zasilania w znacznym stopniu zgodne było z wartością zmierzoną, ale profile prędkości różniły się znacznie. W pracy [78] wyznaczono model pneumatycznego urządzenia wspomagania pracy serca, który łączono z numerycznym modelem układu krążenia w miejsce modelu naturalnej komory. Miało to na celu ocenę jego wrażliwości na obciążenie wstępne. Zamodelowana została zależność ciśnienia w komorze powietrznej urządzenia od ciśnień zasilania systoli i diastoli. Zamodelowano oporność i elastyczność drenu pneumatycznego w postaci szeregowego połączenia pięciu układów RC. Ze względu na modelowanie przepływu powietrza pominięto wpływ bezwładności. Na wyjściu modelu drenu wyznaczana była wartość ciśnienia i objętości komory pneumatycznej z uwzględnieniem zmian gęstości powietrza w funkcji ciśnienia. Następnie zamodelowano wartość ciśnienia w komorze krwistej, jako funkcję zależną od ciśnienia w komorze powietrznej, aktualnej objętości komory i charakterystyki membrany. W ten sposób otrzymano model urządzenia VAD w postaci źródła ciśnienia. Zmiana ciśnień w modelu układu krążenia na wejściu lub wyjściu urządzenia powoduje zmianę wartości obliczonego przepływu dolotowego i wylotowego. Zmiana ta wpływa na zmianę objętości komory krwistej, która powoduje zmianę objętości komory powietrznej a więc, na podstawie charakterystyki membrany, ciśnienia pneumatycznego. Zmiana w ciśnieniu pneumatycznym wpływa na zmianę ciśnienia w komorze krwistej i cykl obliczeń powtarza się. Model ten do poprawnego działania wymaga więc informacji o wartościach ciśnień na wlocie i wylocie urządzenia. Nie zostały przedstawione wyniki badań porównawczych modelu i danych eksperymentalnych. Podsumowując wyniki przeglądu literatury fachowej, nie udało się odnaleźć opisu modelu numerycznego, który umożliwiałby estymację wartości przepływu w komorze krwistej urządzenia VAD na podstawie wielkości pomiarowych dostępnych wyłącznie w jednostce sterującej oraz pneumatycznej części urządzenia wspomagającego. 39
40 Modele komory POLVAD-MEV W ramach realizacji programu Polskie Sztuczne Serce kilka grup badawczych zajmowało się modelowaniem urządzenia POLVAD. W 29 r. opracowany został pierwszy wieloskalowy model urządzenia wspomagającego oparty na obliczeniowej mechanice płynów [79]. Składał on się z modelu w skali makro wykonanego z wykorzystaniem oprogramowania komercyjnego oraz modelu w skali mikro, opartego na oprogramowaniu autorskim. Model w skali mikro umożliwiał modelowanie nanopowłok sosowanych w komorze krwistej i przewidywanie obszarów, w których mogło dojść do ich uszkodzenia. Dzięki temu możliwe było lepsze dobranie materiałów powłokowych czy kształtu komory. Kolejne badania [8] poświęcone były modelowaniu nanopowłoki biokompatybilnego azotku tytanu osadzanej za pomocą metody impulsowej na polimerze, będącym materiałem ściany komory. Model wykonywany był w celu analizy parametrów mających decydujący wpływ na zjawisko utraty spójności pomiędzy powłoką i podłożem. Kolejne prace umożliwiły dalsze udoskonalenie modelu również dla komory POLVAD-EXT [81], [82]. Wprowadzono również możliwość modelowania zależności własności polimeru podłoża od temperatury i przeprowadzono testy porównawcze modelu i wyników eksperymentalnych [83]. Prowadzone były również badania symulacyjne warunków przepływowych panujących w komorze krwistej urządzenia dla przepływu ciągłego i trzech różnych typów zastawek [84]. Badane były pola przepływu w rejonie samych zastawek w celu wyznaczenia wpływu kąta ich otwarcia na warunki przepływu, rozkład ciśnienia oraz występowanie obszarów stagnacji. W pracy przedstawiono również metodykę i wyniki symulacji dla warunków przepływu zmiennego wymuszonego przez ruch membrany. Modele oparte na obliczeniowej mechanice płynów służyły do celów opracowania odpowiedniego kształtu komory, dobrania odpowiedniej powłoki czy typu i orientacji zastawki. Nie przedstawiono jednak możliwości ich wykorzystania do wyznaczania wydatku minutowego urządzenia dla nieznanych warunków brzegowych. Podejściem do estymacji wartości przepływu wylotowego z komory krwistej przy wykorzystaniu metod modelowania było wyznaczenie opisu opartego na sieci neuronowej [85]. Opracowany został model, którego sygnałami wejściowymi było ciśnienie i przepływ w drenie pneumatycznym (P pn, Q pn ) natomiast wielkością modelowaną wartość przepływu wylotowego z komory krwistej (Q out ). Zauważono, że bardzo istotnym zagadnieniem dla procesu wyznaczenia i weryfikacji modelu jest odpowiednie przygotowanie zestawów danych uczących i testowych. Pierwsze próby zamodelowania działania urządzenia VAD pozwoliły na zidentyfikowanie problemu związanego z poprawnym działaniem modelu dla całego 4
41 zakresu parametrów sterowania urządzenia. Oszacowano, że parametrem, który ma znaczący wpływ na zachowanie modelu jest ciśnienie zasilania systoli (SDP). Dlatego też podzielono cały zakres tego ciśnienia na odpowiednie podzakresy i wyznaczono osobne modele VAD dla każdego z nich. Przedstawione wyniki estymacji wskazują na dobrą predykcję modelu dla danego podzakresu ciśnienia sterującego. Nie została jednak przedstawiona koncepcja modelu sprawdzającego się dla całego zakresu zmian ciśnienia lub wyniki dla punktu pracy urządzenia znacząco różniącego się od punktu, dla którego uczona była sieć. Aspekty te sprawiają, że ciężko oszacować uniwersalność wyznaczonego opisu. Podsumowując, nie odnaleziono w literaturze opisu modelu numerycznego urządzenia POLVAD-MEV, który umożliwiałby estymację wypracowanej wartości przepływu na podstawie wielkości pomiarowych dostępnych klinicznie. 41
42 4. Eksperymenty i metody W celu wyznaczenia modelu pulsacyjnego zespołu wspomagania pracy serca niezbędne było przeprowadzenie analizy jego działania i przeprowadzenie odpowiednich eksperymentów na urządzeniu wspomagania pracy serca. Warunki pracy urządzenia VAD charakteryzują się dużą zmiennością ze względu na szeroki zakres wartości parametrów sterujących oraz zmienne warunki obciążenia, zależne od stanu wydolności układu krążenia pacjenta. Z tego względu przeprowadzony został szereg eksperymentów w celu uzyskania danych niezbędnych do zamodelowania działania zespołu wspomagania dla szerokiego zakresu warunków pracy urządzenia. W celu uzyskania odpowiedniego układu obciążenia zespołu VAD, zapewniającego powtarzalne i sterowalne obciążenie hydrauliczne, prowadzone pomiary realizowane były na hybrydowym symulatorze układu krążenia człowieka (rozdział 3.1.2). W ramach pracy przeprowadzono trzy serie eksperymentów badawczych umożliwiające uzyskanie unikalnych danych dotyczących zespołu wspomagania pracy serca. Pierwszym etapem były badania identyfikacyjne urządzenia wspomagania pracy serca pracującego w połączeniu z hybrydowym symulatorem układu krążenia w konfiguracji odpowiadającej wspomaganiu w układzie przedsionek aorta. Uzyskane dane pozwoliły na opracowanie wstępnych modeli przepływu krwi w kaniulach oraz wyznaczenie metody wykrywania pełnego wyrzutu i napełnienia. Wyznaczone modele jako sygnał wejściowy wymagały informacji o obciążeniu komory, czyli ciśnieniu w przedsionku i aorcie. Na tym etapie prac nie udało się wyznaczyć modeli, które bazowały wyłącznie na danych z jednostki sterującej i części pneumatycznej urządzenia wspomagającego, tzn. ciśnienia powietrza w drenie zasilającym jednostkę POLVAD-MEV oraz ciśnień powietrza w zbiornikach jednostki sterującej POLPDU-42. W okresie wstępnych badań nad modelem, opracowana została przez producenta sprzętu nowsza wersja sterownika urządzenia wspomagającego: POLPDU-51. Z tego względu przygotowany i przeprowadzony został uzupełniający eksperyment identyfikacyjny dla nowej jednostki sterującej. Przeprowadzone zostały również badania dla celów diagnostyki stanów uszkodzeń zespołu wspomagania. Dane te pozwoliły na sformułowanie koncepcji wyznaczenia wartości przepływu krwi w komorze wyłącznie na podstawie danych pomiarowych pochodzących z jednostki sterującej oraz przeprowadzenie pierwszych prób jego wyznaczenia. 42
43 Oprócz zmian sprzętowych następowała ewolucja w zakresie miejsc wszczepiania urządzenia wspomagającego do układu krążenia pacjenta. Pierwotna konfiguracja pracy, w układzie przedsionek serca aorta, została zastąpiona układem koniuszek komory serca aorta. Jest to układ korzystniejszy z medycznego punktu widzenia, gdyż pozwala na lepsze obmywanie naturalnej komory serca. Z tego względu pozyskany został przez autorkę pracy grant badawczy ukierunkowany na badania zespołu wspomagania pracującego w nowej konfiguracji. W ramach jego realizacji opracowano metodę symulacji warunków panujących w koniuszku serca na hybrydowym układzie krążenia i ponownie przeprowadzono eksperyment identyfikacyjny. Uzyskano wyniki, które pozwoliły na opracowanie modelu przepływu krwi w komorze wyłącznie na podstawie danych mierzonych w układzie zasilającym zespołu wspomagania. Pełne zestawienie przeprowadzonych eksperymentów przedstawia Tabela 4.1. Tabela 4.1 Eksperymenty pomiarowe nr Eksperyment Jednostka sterująca Eksperyment identyfikacyjny Eksperyment uzupełniający i diagnostyczny Eksperyment identyfikacyjny dla połączenia koniuszek serca aorta POLPDU-42 POLPDU-51 POLPDU-51 Obciążenie urządzenia Hybrydowy symulator układu krążenia (pracujący głównie, jako generator obciążeń stałych) Hybrydowy symulator układu krążenia (odtwarzający warunki w przedsionku i aorcie) Zmodyfikowany hybrydowy symulator układu krążenia (odtwarzający warunki w koniuszku komory serca i aorcie) Główny cel badań Zebranie danych identyfikacyjnych zespołu wspomagania niezbędnych do wyznaczenia modelu urządzenia oraz wstępnego opracowania metody wykrywania pełnego wyrzutu i całkowitego napełnienia urządzenia wspomagającego. Zebranie danych eksperymentalnych dla nowszej wersji sterownika oraz do celów opracowania systemu diagnostyki urządzenia. Zebranie danych eksperymentalnych dla innego połączenia urządzenia nastawione na identyfikację obiektu. 43
44 4.1. Eksperyment identyfikacyjny (nr 1) Głównym celem pierwszego eksperymentu identyfikacyjnego było zebranie danych pomiarowych dla zespołu wspomagania pracy serca z pompą POLVAD-MEV. Dane miały posłużyć do wyznaczenia modelu urządzenia oraz wstępnego opracowania metody wykrywania pełnego wyrzutu i całkowitego napełnienia komory krwistej urządzenia wspomagającego. Badania identyfikacyjne zostały przeprowadzone na stanowisku badawczym w Fundacji Rozwoju Kardiochirurgii im. prof. Zbigniewa Religi w Zabrzu. Pomiary dotyczyły zespołu wspomagania pracy serca POLCAS sterowanego jednostką POLPDU-42 i wyposażonego w pulsacyjne pozaustrojowe urządzenie wspomagania pracy serca POLVAD-MEV (Rys. 4.1). Zostało ono dołączone do hybrydowego symulatora układu krążenia (rozdział 3.1.2) odtwarzającego warunki hydrauliczne dla wspomagania w układzie przedsionek serca aorta. Oznacza to, że na wlocie urządzenia odtwarzane były warunki panujące w lewym przedsionku a na wylocie warunki hemodynamiczne panujące w aorcie. Układ pracował na cieczy krwiopodobnej, będącej mieszaniną wody i gliceryny w proporcjach 6 4%. W skład układu pomiarowego (Rys. 4.1) wchodziły czujniki ciśnienia rejestrujące wartość ciśnienia hydraulicznego w kaniuli wlotowej i wylotowej urządzenia wspomagającego (P in, P out ), ciśnienie pneumatyczne w drenie zasilającym komorę powietrzną (P pin ) oraz przepływy cieczy w kaniulach urządzenia (Q in, Q out ). Pomiar wartości przepływu hydraulicznego realizowany był przy pomocy bezinwazyjnego, ultradźwiękowego przetwornika przepływu cieczy Transonic (T42, TS41 z sondami ME-PXL). Rejestrowane były również warunki obciążenia pompy, czyli wielkości uzyskiwane w fizycznej części hybrydowego symulatora układu krążenia, takie jak: ciśnienia w zbiornikach transformatorów impedancji (PT1, PT2) oraz zadane wartości przepływu dla pomp transformatorów (QT1, QT2). W trakcie pomiarów układ hybrydowy pracował w dwóch różnych trybach: w warunkach modelowania niewydolności lewej komory serca z dołączonym wspomaganiem równoległym oraz przy względnie stałym obciążeniu na wlocie i wylocie z komory krwistej. Miało to na celu uzyskanie danych identyfikacyjnych dla różnych wartości spadku ciśnienia na pompie. Odtwarzanie niewydolności lewej komory uzyskiwane było poprzez następujące ustawienie parametrów symulatora: - maksymalnej wartości funkcji elastancji lewej komory E maxl =.67 mmhg/cm 3 oraz - wielkości objętości szczątkowej lewej komory V l =15 cm 3. 44
45 SYMULATOR HYBRYDOWY PT1, PT2 QT1, QT2 Pomiary 1 4 Q in 1 Q out P in P out Pomiary P pin 5 POLPDU-42 Rys. 4.1 Widok i schemat układu pomiarowego dla eksperymentu nr 1: 1 urządzenie wspomagania pracy serca POLVAD-MEV, 2 część fizyczna hybrydowego symulatora układu krążenia, 3 sondy do pomiaru przepływu w kaniulach, 4 pomiar ciśnień na wlocie i wylocie z komory, 5 pomiar ciśnienia na wejściu komory pneumatycznej. Ustalona wartość ciśnień obciążających uzyskiwana była poprzez zmianę wartości oporów systemowych R as przy następujących ustawieniach symulatora: - maksymalna wartość funkcji elastancji lewej komory E maxl = mmhg/cm3, - maksymalna wartość funkcji elastancji prawej komory E maxr = mmhg/cm3 - wartość oporu obu zastawek obu komór R li = R lo = R ri = R ro =3 g*s/cm4 W obu przypadkach pozostałe wartości parametrów przyjęto zgodnie z [3]. Opisany etap badań prowadzony był z nastawieniem na analizę działania samego urządzenia, dlatego identyfikację wykonywano głownie przy działaniu symulatora hybrydowego jako generatora obciążeń stałych (około 75 serii pomiarowych, Tabela 4.3). Dla symulacji niewydolności wykonano 7 serii pomiarowych (Tabela 4.2). Dla badań pracy zespołu w warunkach obciążenia stałego dla każdego ciśnienia zasilania (5 wartości) prowadzone były pomiary dla 36 kombinacji pozostałych parametrów sterujących (3 wartości podciśnienia, 3 wartości wypełnienia sygnału sterującego i 4 wartości częstotliwości). Następnie dla każdego zestawu parametrów sterujących (w sumie 18 przypadków) nastawiano ciśnienie obciążenia wyjściowego kolejno na 6 różnych wartości. Ciśnienie wejściowe wynosiło zawsze około 2-5 mmhg. Docelowo powinno zostać uzyskanych 18 różnych przypadków pracy. Wykorzystywany symulator krążenia nie był jednak idealnym 45
46 narzędziem do ustalania stałych wartości obciążenia urządzenia wspomagającego i z tego względu, w niektórych przypadkach, nie było możliwości osiągnięcia wszystkich założonych wartości obciążenia. Dlatego też, sumaryczna liczba serii pomiarowych była nieznacznie niższa od zakładanej. Zestawienie wartości parametrów sterowania i obciążeń przedstawia Tabela 4.3. Dla wszystkich przypadków rejestrowanych było sześć sekund pracy z okresem próbkowania.1 s. Tabela 4.2 Serie pomiarowe dla modelowania niewydolności pracy serca Nr serii Ciśnienie zasilania Podciśnienie Wypełnienie Częstotliwość pracy SDP (mmhg) DDP (mmhg) sygnału SYS (%) AHR (bpm) Tabela 4.3 Serie pomiarowe dla pracy zestawu wspomagania pod obciążeniem stałym Ciśnienie Nr Podciśnienie Wypełnienie Częstotliwość zasilania zestawu (mmhg) sygnału (%) pracy (bpm) (mmhg) , 5, 75 25, 4, 55 3, 6, 9, , 5, 75 25, 4, 55 3, 6, 9, , 5, 75 25, 4, 55 3, 6, 9, , 5, 75 25, 4, 55 3, 6, 9, , 5, 75 25, 4, 55 3, 6, 9, 11 Obciążenie wyjściowe (mmhg) 5, 2, 6, 1, 14, 17 5, 2, 6, 1, 14, 17 5, 2, 6, 1, 14, 17 5, 2, 6, 1, 14, 17 5, 2, 6, 1, 14, 17 46
47 4.2. Eksperyment uzupełniający i diagnostyczny (nr 2) Eksperyment uzupełniający i diagnostyczny miał na celu zebranie danych eksperymentalnych dla nowszej wersji sterownika: POLPDU-51, głównie do celów opracowania systemu diagnostyki urządzenia. Uzyskane dane okazały się kluczowe dla badań nad modelem, ze względu na informacje uzyskane w trakcie badań z całkowicie niedrożnym drenem pneumatycznym. Przypadek ten odpowiadał pracy jałowej urządzenia. Zauważono, że różnica pomiędzy wartością ciśnienia sterowania dla biegu jałowego i ciśnienia w trakcie normalnej pracy urządzenia jest skorelowana z wielkością przepływu krwi w urządzeniu (więcej w rozdziale 5.3). Schemat układu pomiarowego przedstawiono na rysunku 4.2. Urządzenie wspomagania napędzane było przy pomocy pneumatycznego sterownika POLPDU-51 (Rys. 4.2, blok POLPDU 51). Obciążeniem dla protezy serca był hybrydowy model układu krążenia, skonfigurowany w trybie wspomagania lewej komory serca z napływem z przedsionka i wyrzutem do aorty (Rys. 4.2, blok MODEL HYBRYDOWY). EKG pomiary IPPT P VAD_out P VAD_in pomiary ITAM MODEL HYBRYDOWY F dop P VAD_k P VAD_p P ref_krew P ref_in P ref_out F in F out SYNC P ref_pneumo pomiary PW F pneumo EP1 EP2 P PDU_OUT P PDU- P PDU+ POLPDU 51 Rys. 4.2 Schemat układu pomiarowego dla eksperymentu nr 2 [86] Badaniom została poddana wersja prototypowa urządzenia POLVAD-MEV wyposażona w system metrologiczny, w skład którego wchodziły następujące układy pomiarowe: pomiary ITAM oraz pomiary PW. 47
48 Przy wykorzystaniu układu pomiarowego pomiary ITAM (Rys. 4.2) zbierane były sygnały z czujników ciśnienia z separatorami membranowymi opracowanymi przez Instytut Techniki i Aparatury Medycznej. Urządzenie wspomagające wyposażone było w 3 czujniki tego typu: dwa czujniki ciśnienia umieszczone w specjalnych poliuretanowych króćcach, montowanych tuż przed konektorami wlotowym i wylotowym komory krwistej (P VAD_in/out ) oraz czujnik ciśnienia umieszczony w drenie pneumatycznym w bezpośrednim sąsiedztwie konektora pneumatycznego (P VAD_p ). Planowany był również pomiar czujnikiem ciśnienia tego typu umieszczonym w ścianie komory krwistej (P VAD_k ). W trakcie prowadzenia pomiarów zauważono, że w badanym urządzeniu uszkodzeniu uległa jedna z zastawek. Z tego względu niezbędna była jego wymiana na inne, które wyposażone było jedynie w odejście pomiarowe dla standardowego czujnika ciśnienia. Dlatego ostatecznie ciśnienie w komorze krwistej mierzone było czujnikiem PELTRON (P ref_krew ), którego sygnał dołączony został do karty pomiarowej National Instruments (Rys. 4.2, blok pomiary PW). Rejestrowana była również wartość sygnału EKG pochodząca z dedykowanego generatora (EKG). Analiza tego sygnału pozwalała na detekcję załamka QRS, który służył do sterowania jednostką POLPDU w trybie synchronicznym. Sygnał z detektora użyty został również do synchronizacji pomiarów z bloku pomiary ITAM z pomiarami z bloku pomiary PW. W układzie pomiarowym pomiary PW (Rys. 4.2) prowadzony był pomiar redundantny ciśnień na wlocie i wylocie z komory krwistej urządzenia (P ref_in/out ) oraz pomiar ciśnienia pneumatycznego w drenie w okolicy jego dołączenia do komory powietrznej (P ref_pneumo ). Rejestrowany był również sygnał z czujnika ciśnienia dołączonego do komory krwistej (P ref_krew ). Pomiary wykonywano przy pomocy czujników typu PELTRON NPXG2 o klasie.2% i paśmie 1 khz. Pomiary przepływu w kaniulach wlotowej i wylotowej (F in, F out ) wykonywane były przy pomocy przetwornika ultradźwiękowego (Transonic z sondami nakładanymi na kaniule ME-PXL). W tor napływu do komory miał zostać dodatkowo włączony układ umożliwiający pomiar przepływu profilometryczną metodą dopplerowską (F dop ), który ze względów technicznych nie był jednak realizowany. Ze sterownika POLPDU- 51 rejestrowane były wartości ciśnień w zbiorniku wysokiego i niskiego ciśnienia zasilania (P PDU+/- ), fala pneumatycznego ciśnienia sterującego (P PDU_out ) oraz dwa sygnały sterujące pracą zaworów liniowych jednostki sterującej (EP1/2). Rejestrowany był również sygnał przepływu powietrza w drenie pneumatycznym uzyskiwany przy pomocy przepływomierza opracowanego w Fundacji Rozwoju Kardiochirurgii (F pneum ). W celu zapewnienia możliwości 48
49 zsynchronizowania danych rejestrowanych przez bloki pomiary ITAM i pomiary PW, rejestrowany był sygnał analogowy z detektora QRS (SYNC). Wszystkie sygnały próbkowane były z częstotliwością 25 Hz. Wykaz stosowanych czujników wraz z określeniem dokładności, pasm przenoszenia i danych kalibracyjnych znajduje się w załącznikach do pracy (Tabela.1). Na opisanym stanowisku prowadzone były badania dla różnych konfiguracji układu (załączniki, Tabela.2). W celu oszacowania wpływu oporów w kaniulach na pracę urządzenia, przeprowadzone zostały pomiary dla dwóch długości kaniul (3 i 7 cm) łączących symulator hybrydowy z urządzeniem wspomagającym. Większość pomiarów przeprowadzona została dla kaniul krótkich. W tej konfiguracji zostały przeprowadzone pomiary dla trybu asynchronicznego i synchronicznego (rozdział 3.2.2). W trybie asynchronicznym urządzenie POLVAD pracuje niezależnie od rytmu pracy serca pacjenta. Wówczas w jednostce sterującej możliwe są do nastawienia parametry zasilania takie jak: częstość pracy sztucznej komory serca (AHR), nominalna wartość podciśnienia w fazie diastoli (DDP), nominalna wartość nadciśnienia w fazie systoli (SDP), czas trwania systoli do czasu jednego cyklu wyrażona w procentach (%SYS). Tryb synchroniczny polega na pracy urządzenia w przeciw-fazie względem pracy komory serca pacjenta modelowanej w symulatorze hybrydowym. W tym celu, sygnał synchronizujący, generowany przez symulator pacjenta (układ hybrydowy IBIB), doprowadzony był do urządzenia zasilającego POLPDU-51 nastawionego na pracę synchroniczną. Wartość czasu opóźnienia początku wyrzutu z urządzenia VAD względem skurczu symulowanej komory serca pacjenta określana jest poprzez parametr sterowania TAU. Jest on, wyrażonym w procentach, ułamkiem czasu trwania ostatnio wykrytego okresu jednego skurczu komory serca. Typowe zakresy ustawiane klinicznie to 1-6%. W trybie tym nie ustala się za to wartości częstości pracy komory, ponieważ jest ona zgodna z pulsem pacjenta. Rozróżniane były trzy tryby prowadzania pomiarów: - Optymalny punkt pracy pomiary wykonywane w tym trybie polegały na znalezieniu warunków zasilania umożliwiających pracę z pełnym napełnieniem i pełnym wyrzutem lub, jeżeli nie było to możliwe, z maksymalną średnią wartością przepływu wylotowego z komory. Następnie badany był wpływ zmian parametrów na warunki pracy urządzenia. W tym celu zmieniano kolejno wartości wybranych parametrów zasilania, przy pozostawieniu pozostałych wartości parametrów zgodnych 49
50 z ich wartościami w ustalonym punkcie pracy. Sprawdzano, czy przy zadanych parametrach sterowania wystąpił pełen wyrzut lub całkowite napełnienie, - Zmieniane parametry prowadzono w nim pomiary z kolejnymi zmianami parametrów zasilania w taki sposób, aby zebrać dane dla różnych dopuszczalnych kombinacji wartości parametrów, - Punkt pracy pacjent - pomiary miały na celu badanie wpływu stanu pacjenta na efekty wspomagania. Przy stałych warunkach zasilania urządzenia wspomagania zmieniane były wybrane parametry symulatora układu krążenia modelujące stan pacjenta. Rozróżnianymi warunkami wspomagania były wartości oporów układu tętniczego symulowanego pacjenta oraz jego stan wydolności. Opory duże symulowano poprzez ustawienie w symulatorze hybrydowym wartości oporu systemu tętniczego (R as ), na wartość 1,1. Dla oporów średnich była to wartość,71 a dla niskich,51. Wydolność pacjenta zmieniana była przy pomocy parametru E maxl, czyli maksymalnej wartość funkcji elastancji dla lewej komory serca, przy czym dla pacjenta niewydolnego wartość ta była ustawiana na,1 dla obu komór, pacjent częściowo wydolny to typowa patologia lewej komory (E maxl =,67, E maxr =,5), pacjent wydolny symulowany był poprzez nastawienie wartości elastancji lewokomorowej na E maxl = 2,5. Dodatkowo, dla różnych stanów zasilania zbierane były dane pomiarowe, w trakcie których, symulowane były różnego typu stany awaryjne urządzenia wspomagającego. Były to między innymi: zagięcie drenu pneumatycznego, nieszczelność i odłączenie drenu pneumatycznego, zablokowanie zastawki wlotowej lub wylotowej symulowane poprzez zaciskanie odpowiedniej kaniuli Eksperyment identyfikacyjny dla połączenia koniuszek serca aorta (nr 3) W trakcie stosowania klinicznego zespołu wspomagania pracy serca POLCAS zaobserwowano, że z medycznego punktu widzenia korzystniejsze może być wszczepianie urządzeń wspomagania w konfiguracji koniuszek serca aorta. W takim przypadku naturalna komora serca jest lepiej obmywana, co redukuje ryzyko formowania się zakrzepów. Z tego względu powstała potrzeba uwzględnienia pracy w takim połączeniu w wyznaczanym modelu urządzenia wspomagającego. Wymagało to przeprowadzenia badań identyfikacyjnych dla urządzenia pracującego w warunkach obciążenia podobnych do panujących w czasie pracy w konfiguracji koniuszek serca aorta. W tym celu konieczne było opracowanie odpowiedniej metody modyfikacji stanowiska badawczego. 5
51 W pierwotnej konfiguracji (rozdział 3.1.2) symulator hybrydowy umożliwiał odtwarzanie fizyczne warunków hemodynamicznych panujących w biernych punktach układu: przedsionku wybranej komory serca oraz w aorcie lub tętnicy płucnej. Umożliwiało to dołączanie urządzeń wspomagających pracujących w tym układzie (Rys. 4.3). Połączenie odbywało się poprzez transformatory impedancji (T1, T2). Sterowanie modelu polegało na pomiarze ciśnienia panującego w części fizycznej, wyliczenie na jego podstawie przepływów dolotowego i wylotowego z danego punktu w części numerycznej i wygenerowanie przepływu fizycznego będącego różnicą wyznaczonych przepływów. LVAD Część fizyczna zbiornik roboczy P T1 Q xi Q xo P T2 zbiornik roboczy C la Zbiornik spływowy C il Q T1 T1 T2 QT2 Transformator impedancji aorty Transformator impedancji przedsionka P la R li P lv R lo P as R cs P cas Q vp R vp Q li E Q lo Lewa komora Q cor Q l Część numeryczna Rys. 4.3 Schemat dołączenia wspomagania w układzie przedsionek aorta. W celu dostosowania hybrydowego symulatora układu krążenia do fizycznego odtworzenia warunków panujących w koniuszku serca niezbędne było przeniesienie transformatora T1 do punktu odpowiadającego komorze serca (P lv ). W ogólności metoda obliczeń zastosowana dla sterowania układu przy symulacji układu przedsionek aorta może być wykorzystana dla innych punktów układu krążenia. Jedynym punktem, w którym nie można zastosować prostego przeniesienia opisanej metody obliczeń jest właśnie komora serca, ponieważ jest ona opisana w modelu matematycznym jako źródło ciśnienia. Z tego 51
52 względu nie ma możliwości sterowania źródłem przepływu na podstawie pomiaru ciśnienia w transformatorze, ponieważ ciśnienie to jest wyznaczane numerycznie (rozdział 3.1.2, zależność (3.1)). Dlatego też, zaproponowano modyfikację modelu numerycznego, która bazuje na podziale rezystancji wyjściowej komory na niewielką rezystancję R ax i pozostałą część R lo ' (Rys. 4.4), przy czym: R ax + R lo = R lo. (4.1) zbiornik roboczy P T1 LVAD Q xi Q xo P T2 Część fizyczna zbiornik roboczy C ax Zbiornik spływowy C il Transformator impedancji koniuszka komory Q T1 T1 Transformator impedancji aorty T2 Q T2 P la R li P lv R ax P ax R' lo P as R cs P cas C la Q vp R vp Q li E Q ax Q lo Lewa komora Q cor Q l Część numeryczna Rys. 4.4 Schemat koncepcyjny modyfikacji układu krążenia poprzez wyodrębnienie koniuszka komory. W ten sposób otrzymano punkt P ax, który może być uznany za reprezentację koniuszka komory serca. Dzięki takiemu podziałowi nie ma konieczności uwzględniania wartości przepływu przez transformator impedancji T1 w równaniu opisującym objętość komory serca. Zmiana objętości może więc być opisana jako różnica pomiędzy przepływem wlotowym Q li i wylotowym Q ax dla punktu reprezentującego koniuszek serca (4.2): dv lv = Q li Q ax. (4.2) 52
53 Na jej podstawie wyliczane jest ciśnienie komorowe P lv (rozdział 3.1.2, zależność (3.1)). Wartości przepływów w punkcie P ax mogą następnie być wyznaczone z zależności pomiędzy ciśnieniami i odpowiednimi rezystancjami: Q ax = P lv P T1 R ax (4.3) Q lo = P T1 P as R (4.4) lo Różnica obliczonych przepływów podawana jest jako wartość zadana przepływu dla transformatora T1 (Q T1 ). Relacja między wartościami fizycznymi generowanego przez transformator przepływu oraz przepływu dolotowego urządzenia wspomagającego (Q xi ) prowadzi do wyznaczenia nowej wartości ciśnienia w punkcie dołączenia (P T1 ) i procedura obliczeniowa jest powtarzana. Pozostałe wartości zmiennych hemodynamicznych dla modelu układu krążenia wyznaczane są w sposób analogiczny, co w przypadku podstawowego modelu. Dokładny opis działania symulatora po modyfikacji opisano w [87]. W eksperymencie identyfikacyjnym nr 3, do zmodyfikowanego symulatora dołączono urządzenie wspomagające pracę serca POLVAD-MEV wraz z układem pomiarowym i jednostką sterującą. Wykonano oprogramowanie umożliwiające zmianę parametrów modelu układu krążenia oraz parametrów sterujących urządzenia wspomagania. Zapewniono możliwość synchronicznej rejestracji danych sterujących i pomiarowych z hybrydowego symulatora układu krążenia, urządzenia wspomagania oraz jednostki sterującej. W ten sposób uzyskano kompleksowe stanowisko badawcze (Rys. 4.5) umożliwiające dołączenie i badanie urządzeń wspomagania pracy serca dla konfiguracji koniuszek serca aorta i rejestrację sygnałów pomiarowo-sterujących (Tabela 4.4). Układ pomiarowy urządzenia wspomagającego składał się z: - czterech czujników ciśnienia firmy Wika (S-2, product No.: ), - czujnika przepływu powietrza CKD (FSM2) umieszczonego na drenie powietrznym pomiędzy jednostką sterującą POLPDU 51 a komorą powietrzną pompy MEV, - przetwornika przepływu cieczy Transonic (T42 + 2xTS41) z dwoma sondami nakładanymi na kaniule (ME-11PXL). 53
54 QT1, QT2 SDP, DDP, %SYS, AHR, DEL PT1, PT2, Qtach1, Qtach2 Pz+, Pz-, Pz, ster Karta pomiarowa Q out Q in P out P in P b P p Q p ZMODYFIKOWANY MODEL HYBRYDOWY POLPDU-51 sygnał synchronizujący Rys. 4.5 Schemat układu pomiarowego dla eksperymentu identyfikacyjnego urządzenia wspomagania pracy serca pracującego w połączeniu koniuszek serca aorta. Wyjaśnienie oznaczeń z rysunku znajduje się w Tabeli 4.4. Na tak przygotowanym stanowisku przeprowadzono pomiary dla różnych przypadków pomiarowych (Tabela 4.5). Zarejestrowano dane dla różnych parametrów sterowania urządzenia i symulowanych stanów układu krążenia (Tabela 4.5, dane oznaczone literą a). Dla celów kontrolnych zebrano również dane dla przypadku pracy hybrydowego symulatora układu krążenia bez dołączonego urządzenia wspomagającego (Tabela 4.5, dane oznaczone literą d) oraz dla biernego przepływu przez urządzenie wspomagające (Tabela 4.5, dane oznaczone literą c). Oznacza to, że urządzenie było fizycznie dołączone do symulatora układu krążenia, ale jednostka sterująca nie była uruchomiona. Ostatnią serią badań było zebranie pomiarów dla biegu jałowego jednostki sterującej, czyli zarejestrowanie przebiegu sygnału sterującego i zmienności ciśnień zasilających w przypadku odłączonego urządzenia i zablokowanego wyjścia pneumatycznego z jednostki. W takim przypadku nie występuje przepływ powietrza sterującego (Tabela 4.5, dane oznaczone literą b). Ten cykl pomiarów był przeprowadzony w celu wykrycia różnic pomiędzy działaniem układu zasilania urządzenia wspomagającego w stanie obciążenia i dla przypadku biegu jałowego. 54
55 Tabela 4.4 Rejestrowane dane pomiarowo-sterujące dla eksperymentu identyfikacyjnego urządzenia wspomagania pracy serca pracującego w połączeniu koniuszek serca aorta. Hybrydowy symulator układu krążenia Urządzenie POLVAD-MEV Jednostka sterująca POLPDU-51 Parametry i sygnały sterujące Dane mierzone Parametry i sygnały sterujące Dane mierzone Parametry i sygnały sterujące Dane mierzone QT1 przepływ zadany transformatora impedancji koniuszka komory, QT2 przepływ zadany transformatora impedancji aorty, 8 parametrów dotyczących zadanego stanu układu krążenia. 34 sygnały z numerycznego modelu układu krążenia (ciśnienia, przepływy, objętości), PT1, PT2 ciśnienia w zbiornikach transformatorów impedancji, Qtach1, Qtach2 pomiar tachometryczny przepływu wygenerowanego przez transformatory. brak Q pn przepływ powietrza sterującego w drenie pneumatycznym, P pn ciśnienie w komorze powietrznej urządzenia wspomagającego, P b ciśnienie w komorze krwistej urządzenia wspomagającego, P in ciśnienie w kaniuli dolotowej urządzenia wspomagającego, P out ciśnienie w kaniuli wylotowej urządzenia wspomagającego, Q in przepływ w kaniuli dolotowej urządzenia wspomagającego, Q out przepływ w kaniuli wylotowej urządzenia wspomagającego. SDP zadane ciśnienie zasilania systoli, DDP zadane ciśnienie zasilania diastoli, %SYS długość fazy systoli, AHR częstotliwość pracy, DEL opóźnienie wyrzutu względem skurczu komory serca. P z+ zmierzone ciśnienie w zbiorniku ciśnienia zasilania systoli, P z- zmierzone ciśnienie w zbiorniku ciśnienia zasilania diastoli, P z zmierzone ciśnienie zasilania na wyjściu jednostki sterującej, ster sygnał sterujący zaworu liniowego jednostki sterującej. 55
56 Tabela 4.5 Serie pomiarowe dla pracy urządzenia wspomagającego w układzie koniuszek serca aorta. Ustawienie Zestaw parametrów jednostki symulatora sterującej hybrydowego Nazwa przypadku SDP DDP AHR %SYS DEL Symulowany stan układu krążenia Dołączone urządzenie wspomagania Pomiary dla biegu jałowego Odłączone urządzenie wspomagania a1 b a2 b a3 b a4 b a5 b a6 b6 patologia a7 b a8 b a9 b a a11 X a12 b niewydolność a fizjologia a fizjologia a niewydolność a16 b patologia a patologia a niewydolność a19 b fizjologia a2 patologia c1 d1 X niewydolność c2 X d2 fizjologia c3 d3 56
57 4.4. Oprogramowanie symulacyjne W celu wyznaczenia modelu urządzenia wspomagania pracy serca wykorzystywane były głownie trzy pakiety programowe: PExSim (ang. Process Explorer and Simulator) [88] [9], IdCAD [91] oraz MATLAB [92] PExSim Pakiet symulacyjny PExSim jest programem opracowanym w Instytucie Automatyki i Robotyki Politechniki Warszawskiej. W ogólności umożliwia on przetwarzanie zmiennych systemowych w postaci swobodnie konfigurowalnych torów przetwarzania. Moduł PExSim projektowany był głównie z myślą o wykonywaniu bieżących obliczeń związanych z realizacją zaawansowanych algorytmów modelowania, monitorowania oraz diagnostyki procesów przemysłowych. Z czasem rozszerzony jednak został o elementy pozwalające na budowę złożonych symulatorów. W efekcie, oprogramowanie to jest elastycznym narzędziem, umożliwiającym modelowanie rozbudowanych układów dynamicznych. W jego skład wchodzi zestaw predefiniowanych bloków funkcyjnych, zarówno statycznych, jak i dynamicznych oraz różnorodne bloki umożliwiające modelowanie podstawowych zależności matematycznych, logicznych czy obsługujących operacje wejścia/wyjścia. Otwarta architektura pozwala na implementację dodatkowych elementów m. in. poprzez dodawanie własnych bloków funkcyjnych, które mogą być grupowane w osobne biblioteki. Pakiet programowy PExSim wyposażony jest dodatkowo w moduł PExSim Optimizer. Jest to moduł wykorzystujący algorytmy optymalizacji statycznej do optymalizacji modelu wykonanego w pakiecie PExSim. Oznacza to, że pozwala on na automatyczny dobór współczynników występujących w równaniach modelu w taki sposób, aby minimalizować zadaną funkcję celu, jaką może być np. zgodność wyniku modelu z wartością uzyskaną pomiarowo IdCAD Kolejnym oprogramowaniem, które wykorzystywane było w pracach dotyczących modelowania urządzenia wspomagania pracy serca, jest pakiet IdCAD, który posiada unikalne możliwości w zakresie identyfikacji modeli parametrycznych. Liniowe modele parametryczne są podstawowym rodzajem opisu właściwości dynamicznych badanego procesu. Sygnał wyjściowy procesu y(k) jest w tym opisie (4.5) zależny liniowo od: - znanych wielkości ν i (k), i=1,,m wektora wejść do modelu ν(k) w chwili k, - nieznanej wielkości η(k) reprezentującej niemierzalne zakłócenie oraz - wartości tworzących wektor współczynników modelu θ i. 57
58 y(k) = θ 1 ν 1 (k) + θ 2 ν 2 (k) + + θ m ν m (k) = i=1 θ i ν i (k) = ν(k)θ. (4.5) Celem identyfikacji parametrycznej jest wyznaczenie nieznanych współczynników modelu (wektora θ i ). W pakiecie IdCAD zaimplementowane mogą być następujące struktury szukanego modelu: - AR (ang. Auto Regressive), którego wektor wejść ν(k) zawiera wyłącznie wyrazy pomierzonego wcześniej sygnału wyjściowego; - ARX, o strukturze AR, w której uwzględniony jest wpływ zakłóceń; - MA (FIR), gdzie wektor wejść modelu ν(k) zawiera wyłącznie wartości sygnału wejściowego procesu; - MAX, o strukturze MA, w której uwzględniony jest wpływ zakłóceń; - ARMA, będący najczęściej stosowaną strukturą, gdzie wektor wejść ν(k) zawiera zarówno wartości sygnału wejściowego jak wyrazy pomierzonego wcześniej sygnału wyjściowego; - ARMAX, o strukturze ARMA, w której uwzględniony jest wpływ zakłóceń. Do wyznaczania wartość nieznanych współczynników modelu można wybrać jedną z pięciu metod obliczeniowych (estymatorów): LS, GLS, IV, ML, LSA [93]. Wyznaczony w pakiecie IdCAD model procesu może być następnie poddany weryfikacji, co umożliwia wyznaczenie takich parametrów jak wartość średniokwadratowa błędu, znormalizowana wartość średniokwadratowa (w procentach) oraz wartość wskaźnika FPE (ang. Final Prediction Error), czyli błędu predykcji: FPE = M+m σ 2 M η (k) = (M+m) 1 (M m) M m M k=1 η (k)2, (4.6) gdzie: m liczba współczynników modelu, M liczba próbek pomiarowych, η - błąd modelu (zmienna resztowa). Omawiany pakiet obliczeniowy pozwala również na wyznaczanie modeli nieliniowych, czyli modeli, w których współczynniki modelu mogą być wyrażone przy pomocy funkcji wielomianowych (maksymalnie trzeciego rzędu). Możliwy jest wybór struktury MA, AR i ARMA oraz rzędu modelu. Innym dostępnym typem modeli są modele parametryzowane za pomocą zbiorów rozmytych o strukturze TSK (ang. Takagi-Sugeno-Kanga). W modelach tych, zakres zmienności zmiennej rozmywającej ν (wejściowej) dzielony jest na podobszary, dla których wyznaczana jest wartość funkcji przynależności, przy czym krańce podziałów ustalane są w sposób rozmyty (przykład Rys. 4.6). Wartość funkcji przynależności określa, w jakim 58
59 stopniu (od do 1) dana wartość ν należy do danego obszaru, przy czym spełniony musi być warunek: n j=1 φ j (v) = 1. (4.7) Następnie przyjmuje się, że każdemu z wyznaczonych podobszarów zmiennej rozmywającej v odpowiada model parametryczny, o takiej samej strukturze i rzędzie, z wektorem współczynników θ j. i wartości niskie wartości średnie zmienna rozmywająca wartości wysokie Rys. 4.6 Przykładowe funkcje przynależności dla zmiennej rozmywającej Wektor współczynników modelu wyznaczany jest, jako suma ważona z poszczególnych modeli obszarowych: m θ = j=1 φ j θ j, (4.8) gdzie wagami są wartości funkcji przynależności φ j. Ostatnim udostępnionym typem modelu jest model o parametrach wyznaczanych przy pomocy sieci neuronowych. Pakiet umożliwia użytkownikowi wybór struktury (AR, FIR, ARMA) i rzędu modelu oraz struktury i algorytmu uczącego sieci neuronowej MATLAB System Identification Toolbox W celu wyznaczenia modelu urządzenia wspomagania pracy serca w znacznej mierze wykorzystywane było również oprogramowanie Matlab, będące interaktywnym środowiskiem do wykonywania obliczeń, a zwłaszcza jego część pakiet Simulink. Jest to środowisko oparte na diagramach blokowych przeznaczone do symulacji i projektowania w oparciu o model. Zapewnia edytor graficzny, biblioteki standardowych bloków funkcyjnych, możliwość dołączania bloków i funkcji zdefiniowanych przez użytkownika oraz rozwiązywania równań niezbędnych do modelowania i symulacji układów dynamicznych. W części badań dotyczących identyfikacji obiektów wykorzystywane było narzędzie System Identification Toolbox pakietu obliczeniowego Matlab. Jest to aplikacja umożliwiająca wyznaczanie modeli matematycznych układów dynamicznych na podstawie 59
60 danych pomiarowych sygnałów wejściowych i wyjściowych. W założeniu umożliwia ona wyznaczanie modeli układów dynamicznych trudnych lub niemożliwych do opisania przy pomocy podstawowych zależności lub na podstawie specyfikacji. W celu wyznaczenia modelu wykorzystywane mogą być sygnały wejść i wyjść w dziedzinie czasu oraz częstotliwości. Narzędzie pozwala na reprezentację modeli przy pomocy ośmiu opisów, pięciu liniowych i trzech nieliniowych. Wśród modeli liniowych dostępne są następujące typy: Transfer function, gdzie model obiektu opisany jest wielomianową transmitancją operatorową a parametrami modelu są bieguny i zera transmitancji oraz wartość opóźnienia transportowego; Process model, gdzie model ma postać prostej funkcji transmitancji o czasie ciągłym (transmitancji zastępczej) z możliwością wpływania na jej strukturę poprzez wybór rzędu modelu (ilości biegunów), uwzględnienia opóźnienia transportowego, występowania zera licznika, biegunów zespolonych (oscylacji) czy właściwości całkujących; State-space model, gdzie modele mają postać opisu w przestrzeni stanów, czyli zestawu równań różniczkowych pierwszego rzędu opisujących stany wewnętrzne układu; Polynomial models, czyli liniowych modeli parametrycznych będących podstawowym rodzajem opisu własności dynamicznych procesu, dla których sygnał wyjściowy y(t) jest zależny liniowo od sygnałów wejściowych u(t), niemierzalnego zakłócenia e(t) oraz współczynników modelu. W programie zaimplementowane są struktury ARX (wspólny opis dynamiki dla wejść i zakłóceń), ARMAX (bardziej elastyczna możliwość opisu dynamiki dla zakłóceń, stosowane w przypadku zakłóceń na wejściu procesu), wersje ARIX i ARIMAX dla przypadków procesów z niestacjonarnymi zakłóceniami, czyli o ruchomej średniej (wprowadzone całkowanie do modelu dynamiki zakłócenia), struktura Boxa-Jenkinsa, która pozwala na niezależną parametryzację dla każdego z pobudzeń oraz strukturę Output-Error dla procesów, gdzie zakłócenie występuje na wyjściu obiektu; Grey-box model, będący narzędziem do wyznaczania wartości nieznanych parametrów przy znanej, liniowej strukturze modelu (optymalizacja parametrów). Wśród modeli nieliniowych dostępne są następujące struktury: Nonlinear ARX Models, używane do modelowania złożonych zachowań nieliniowych; 6
61 Hammerstein-Wiener Models, używane do modelowania obiektów z fizycznymi efektami nieliniowymi, jak strefy martwe i nasycenia; Nonlinear Grey-Box Models, będące narzędziem do wyznaczania wartości nieznanych parametrów przy znanej, nieliniowej strukturze modelu określonej w przestrzeni stanów (optymalizacja parametrów). W programie podawaną miarą dopasowania sygnału wyjściowego z modelu do danych pomiarowych jest stopień dopasowania (fit) obliczany procentowo jako: fit = 1 (1 gdzie: y dane pomiarowe, y dane z modelu. y y y mean(y) ), (4.9) Powyższe równanie przedstawia procentowo wartość różnicy jedności i znormalizowanej wartości średniej kwadratowej błędów (RMSE), czyli pierwiastka kwadratowego z błędu średniokwadratowego (MSE). 61
62 5. Modele urządzenia wspomagania pracy serca 5.1. Modele bazujące na wszystkich dostępnych danych pomiarowych Celem prowadzonych prac było wstępne wyznaczenie modelu przepływu krwi w urządzeniu wspomagania pracy serca na podstawie wszystkich danych pomiarowych dostępnych w trakcie badań identyfikacyjnych. Miało to pozwolić na lepsze poznanie modelowanego obiektu i możliwości stosowania wybranych metod modelowania w dalszych etapach badań. Jednocześnie założeniem prowadzonych prac było wyznaczenie modelu do celów opracowania algorytmu adaptacyjnego sterowania zespołu wspomagania. Z tego względu uznano za celowe opracowanie modelu urządzenia, który mógłby być łączony z modelem układu krążenia człowieka w celu badania wpływu jego pracy na parametry układu. Koncepcję takiego układu przedstawiono na rysunku 5.1. W ten sposób otrzymana informacja o stanie układu krążenia mogłaby posłużyć do zmiany parametrów pracy urządzenia, a w konsekwencji opracowania układu sterowania na podstawie modelu komputerowego. Model matematyczny układu krążenia człowieka lewa komora krążenie systemowe tętnicze krążenie systemowe żylne prawy przedsionek LVAD RVAD lewy przedsionek krążenie płucne żylne krążenie płucne tętnicze prawa komora Rys. 5.1 Schemat budowy modelu komputerowego układu krążenia człowieka z możliwością dołączania modeli urządzeń wspomagania pracy serca (LVAD lewej komory, RVAD prawej komory) Modele elastancyjne W pierwszym etapie badań, prowadzonych we współpracy z mgr. inż. Bartłomiejem Fajdkiem, podjęte zostały próby wyznaczenia modelu urządzenia w oparciu o opis elastancyjny zbliżony do opisu pracy naturalnej komory serca. Opis tego typu stosowany jest w modelach układu krążenia o parametrach skupionych (rozdział 3.1.2). W podejściu tym ciśnienie generowane wewnątrz komory opisane jest zależnością: P v (t) = E v (t) E max (V v (t) V ) f (V vad (t), V vad(t), V vadmax(t)) + (5.1) +A e k V v(t) + B e j V v(t) + C, 62
63 gdzie: P v (t) ciśnienie w komorze serca, V v (t) objętość komory, V objętość szczątkowa komory (przy zerowym ciśnieniu), E v (t) funkcja elastancji znormalizowana do wartości jeden, E max wartość maksymalna funkcji elastancji (końcowo-skurczowa), A,B,C,j,k stałe parametry, modyfikujące kształt i pozycję charakterystyki napełniania, f funkcja korekcyjna zależna od objętości komory i tempa wyrzutu. Natomiast wartość przepływu wlotowego i wylotowego z komory wyliczana jest, jako stosunek różnicy ciśnień na zastawkach i oporności zastawki: Q li (t) = P la(t) P lv (t) R li, (5.2) Q lo (t) = P lv (t) P as(t) R lo, (5.3) gdzie: Q li (t) natężenie przepływu wlotowego komory, Q lo (t) natężenie przepływu wylotowego z komory, P la (t) ciśnienie w przedsionku, P as (t) ciśnienie w układzie tętniczym krążenia systemowego, R li, R lo oporność zastawki wlotowej i wylotowej komory. Sama zastawka zamodelowana jest w postaci zaworu zwrotnego o nieskończenie dużym oporze w kierunku zaporowym i stałym oporem w kierunku przewodzenia. W celu wykonania pierwszego przybliżenia modelu urządzenia zastosowano powyższy opis z funkcją elastancji przesuniętą w czasie względem jej wartości dla modelu lewej i prawej komory. Przesunięcia dokonano w taki sposób, aby odtworzyć warunki pracy synchronicznej urządzenia względem układu krążenia, to znaczy, aby wyrzut z urządzenia wspomagającego następował w końcowej fazie wyrzutu ze wspomaganej komory serca. Parametry modelu dobrane zostały tak, aby dostosować jego działanie do przybliżonego odtwarzania dynamiki urządzenia wspomagającego. Bardzo istotnym parametrem jest maksymalna wartość elastancji, będąca główną wielkością wpływającą na wartość przepływu wyjściowego. Model urządzenia wspomagającego i układu krążenia człowieka zaimplementowany został w środowisku symulacyjnym PExSim (rozdział 4.4.1). Model VAD miał postać bloku funkcyjnego, którego wejściami było ciśnienie w przedsionku (P a ) i ciśnienie w aorcie (P i ) oraz przebieg funkcji elastancji E (Rys. 5.2, a). Na wyjściu modelu estymowana była wartość przepływu wlotowego i wylotowego oraz ciśnienia i objętości komory krwistej urządzenia wspomagającego. Parametrami była wartość maksymalna elastancji, parametry jej kształtu i wartości oporności zastawek. 63
64 a) b) Rys. 5.2 Widok zaimplementowanych w programie PExSim bloków modeli urządzeń wspomagania pracy serca. a) model podstawowy, b) model dwuelastancyjny. P a - ciśnienie w przedsionku, P i - ciśnienie w aorcie, E - przebieg funkcji elastancji, Q i, Q o natężenie przepływu wlotowego i wylotowego, P v, V v - ciśnienie i objętości komory krwistej urządzenia wspomagającego, El In, El out przebieg funkcji elastancji dla napełniania i opróżniania komory krwistej. Sam układ krążenia człowieka zaimplementowany został w pakiecie programowym PExSim na podstawie znanego z literatury matematycznego modelu układu krążenia człowieka o parametrach skupionych (rozdział 3.1.2). Składa się on z sześciu bloków funkcyjnych odpowiadających poszczególnym częściom układu krwionośnego (Rys. 5.3). Bloki systemowego krążenia tętniczego i płucnego krążenia żylnego zostały odpowiednio zmodyfikowane w celu umożliwienia dołączenia modelu urządzenia wspomagającego lewą komorę serca [94] [96]. Rys. 5.3 Widok modelu układu krążenia z dołączonym urządzeniem wspomagającym LVAD w programie symulacyjnym PExSim. Przeprowadzono symulacje mające na celu sprawdzenie poprawności działania modelu układu krążenia ze wspomaganiem lewokomorowym. Głównym celem stosowania wspomagania układu krążenia jest zwiększenie rzutu minutowego, zmniejszenie ciśnienia przedsionkowego (P la ) i zwiększenie ciśnienia w układzie tętniczym (P as ). Wyniki otrzymane w wyniku modelowania były zgodne z powyższymi założeniami. Wartość ciśnienia przedsionkowego zmalała (Rys. 5.4), co wiąże się z przepompowaniem krwi przez urządzenie 64
65 wspomagające. Bez jego pomocy, przy niewydolności komory, krew zbiera się w układzie żylnym powodując znaczny wzrost ciśnienia. Pojawienie się dodatkowego rzutu, wypracowanego przez urządzenie wspomagające, spowodowało oczekiwany wzrost ciśnienia w układzie tętniczym krążenia systemowego (Rys. 5.4). 8 7 Ciśnienie (mmhg) P as P as patologia P as LVAD P la P la patologia P la LVAD Rys. 5.4 Wynik symulacji ciśnienia przedsionkowego (P la ) oraz ciśnienia w układzie tętniczym systemowym (P as ) dla warunków fizjologicznych prawidłowych, patologii oraz patologii ze wspomaganiem. Niestety, tak zdefiniowany model urządzenia w sposób mierny odtwarzał wartości przepływów względem wartości odniesienia, czyli wyników pomiarów uzyskanych w trakcie badań identyfikacyjnych. W celu lepszej adaptacji modelu przebadano koncepcję wykonania modelu dwuelastancyjnego polegającą na zdefiniowaniu dwóch funkcji elastancji, osobno dla fazy napełniania i wyrzutu z urządzenia: P vad (t) = (V vad (t) V vad (t)) (E in (t) E m_in + E out (t) E m_out ) (5.4) f(v vad (t), V vad(t)) + A e k V vad(t) + B e j V vad(t) + C gdzie: P vad ciśnienie w komorze po stronie krwistej, V vad objętość komory po stronie krwistej, V ovad objętość komory po stronie krwistej przy zerowym ciśnieniu, E in funkcja elastancji przy napełnianiu komory, E out funkcja elastancji przy opróżnianiu komory, E m_in, E m_out maksymalne wartości odpowiednich elastancji. Parametry modelu zostały dobrane w sposób automatyczny (PExSim Optimizer), przy pomocy algorytmu stochastycznego PSO (ang. Particle Swarm Optimization). Przyjęto dwa wskaźniki optymalizacji: różnicę pomiędzy przepływem wejściowym modelowanym oraz rzeczywistym oraz różnicę pomiędzy przepływem wyjściowym modelowanym oraz rzeczywistym Czas (s) 65
66 a) b) 1 15 Q in pomiar przepływ (l/min) Q in model 1 5 przepływ (l/min) 5-5 Q out pomiar Q out model czas (s) czas (s) Rys. 5.5 Przebiegi czasowe zmierzonej (Q pomiar) i zamodelowanej przy użyciu modelu dwuelastancyjnego (Q model) wartości przepływu wlotowego (a) i wylotowego (b) z pulsacyjnego urządzenia wspomagania pracy serca. Jak widać na rysunku 5.5, otrzymane rezultaty modelowania cechowały się średnią jakością odtwarzania wartości mierzonej, zwłaszcza w przypadku przepływu wylotowego z urządzenia. Dodatkowo utworzony model miał charakter lokalny a każda zmiana warunków pracy urządzenia wymagała ponownego doboru parametrów modelu. Z tego względu uznano, że zmodyfikowane opisy elastancyjne nie sprawdzą się dla celów modelowania pracy urządzenia wspomagania pracy serca w szerokim zakresie zmian parametrów Model oparty na ciśnieniu zasilania W podejściu opartym na ciśnieniu zasilania próbowano wyznaczyć prosty model działania urządzenia w oparciu o dodatkową informację o wartości ciśnienia zasilania w drenie pneumatycznym (dodatkowe wejście modelu). Ciśnienie wewnątrz komory krwistej przyjęto początkowo w postaci zależności od chwilowej wartości ciśnienia zasilania w drenie pneumatycznym: P v = a P pn + b, (5.5) natomiast przepływ wylotowy wyznaczany był w następujący sposób: Q o = { P v P a R o P v P a c 66 dla P v P a gdzie a, b, c, d parametry modelu o wartościach stałych. + d dla P v < P a, (5.6) Parametry modelu, tak jak w poprzednim przypadku, zostały dobrane w sposób automatyczny z wykorzystaniem programu PExSim Optimizer. Tak utworzony model umożliwiał odtwarzanie wartości przepływu z podobną dokładnością niezależnie od parametrów sterowania i warunków obciążenia urządzenia (Rys. 5.6). Nie udało się jednak
67 otrzymać dostatecznej zbieżności wartości modelowanej i mierzonej. modyfikacji modelu nie przyniosły poprawy uzyskiwanych rezultatów. Dalsze próby a) 8 b) 6 przepływ (l/min) Q out pomiar Q out model przepływ (l/min) Q out pomiar Q out model c) 8 czas (s) d) 6 czas (s) przepływ (l/min) Q out pomiar Q out model przepływ (l/min) Q out pomiar Q out model czas (s) czas (s) Rys. 5.6 Porównanie przykładowych przebiegów modelowanych i zmierzonych natężenia przepływu wylotowego z urządzenia wspomagającego dla różnych wartości zadanego ciśnienia zasilania: a) SDP = 175 mmhg, b) SDP = 1 mmhg, oraz różnych wartości wypełnienia sygnału sterującego: c) %SYS = 4, d) %SYS = 6. Pozostałe parametry sterowania zgodnie z Tabela 4.2, odpowiednio serie: 7, 1, 6 i Modele parametryczne W ramach prowadzonych prac, poszukiwany był również model parametryczny, zarówno liniowy, jak i nieliniowy, o strukturze przedstawionej na Rys Wejściami modelu było zmierzone ciśnienie w kaniuli wlotowej i wylotowej urządzenia wspomagania serca oraz ciśnienie w drenie pneumatycznym a modelowaną wielkością przepływ wylotowy. W wyniku prowadzonych prac możliwe było wyznaczenie dokładnego modelu parametrycznego dla zadanej serii danych (Rys. 5.8, a), z błędem średniokwadratowym na poziomie 5,2%. Weryfikacja modelu dla innych warunków pracy udowadniała, że otrzymane modele mają charakter lokalny (Rys. 5.8, b), przykładowo dla przedstawionych danych testowych błąd średniokwadratowy wynosił 32,49%. Z tego względu, w kolejnym podejściu, próbowano wyznaczyć zestaw modeli dla różnych warunków pracy urządzenia z algorytmem przejścia pomiędzy nimi (model rozmyty). 67
68 P in P out P pin Model parametryczny Q out Rys. 5.7 Struktura poszukiwanego modelu urządzenia wspomagania pracy serca a) b) przepływ (l/min) czas (s) Q out pomiar Q out model przepływ (l/min) 6 Q 4 out pomiar Q out model czas (s) Rys. 5.8 Przebiegi sygnału przepływu wylotowego urządzenia wspomagania zmierzonego i zamodelowanego z wykorzystaniem identyfikacji parametrycznej. Model ARMAX, estymator GLS, rząd 3. a) dane identyfikacyjne modelu, SDP = 15 mmhg, MSE 5,2%, b) dane testowe dla modelu, SDP = 1 mmhg, MSE 32,49%. Pozostałe parametry sterowania zgodnie z Tabela 4.2, odpowiednio serie 3 i Model oparty na wnioskowaniu rozmytym Jednym z podejść do wyznaczenia modelu przepływu wylotowego krwi dla urządzenia wspomagania pracy serca były prace prowadzone przez prof. K. Janiszowskiego, dotyczące zastosowania identyfikacji opartej na wnioskowaniu rozmytym [97]. Najlepsze rezultaty otrzymano w przypadku zastosowania dwóch zmiennych rozmywających. Dla każdej ze zmiennych dokonano podziału zakresu zmienności na trzy podobszary (Rys. 5.9). Rys. 5.9 Funkcje rozmywające dla zmiennej rozmywającej. a) ΔP różnica pomiędzy średnią wartością ciśnienia na wylocie i wlocie do komory krwistej urządzenia, b) wartość przepływu Q out [98] 68
69 Pierwszą z zastosowanych zmiennych rozmywających była informacja o różnicy pomiędzy średnią wartością ciśnienia na wylocie i wlocie do komory krwistej urządzenia (ΔP). Drugą informacja o stanie otwarcia zastawki, zdefiniowana na podstawie wartości przepływu wylotowego (Q out ). Tak wyznaczony model pozwolił na uzyskanie dokładnych wyników modelowania dla szerokiego zakresu zmienności warunków pracy urządzenia (Rys. 5.1). a) b) Rys. 5.1 Przykładowe, zmierzone i modelowane za pomocą modelu rozmytego przebiegi wartości wypływu z komory POLVAD. a) ΔP = 1 mmhg, b) ΔP = 175 mmhg [97] Dla poprawnego działania modelu, niezbędna jest jednak wiedza o stanie domknięcia zastawki. Ze względu na fakt, że wartości przepływów są, w założeniu celów modelowania, wartością niemierzoną, konieczne byłoby wprowadzenie alternatywnego sygnału, umożliwiającego określenie stanu domknięcia zastawki np. z dedykowanego układu optycznego. Bez informacji o wartości przepływu, nie udało się uzyskać satysfakcjonujących rezultatów przy wykorzystaniu modelowania rozmytego Model oparty na sieci neuronowej W ramach pracy magisterskiej [99], opracowane zostały neuronowe modele urządzenia wspomagania pracy serca POLVAD-MEV. Badania były prowadzone na podstawie wyników z eksperymentu nr 1 (rozdział 4.1). Struktury utworzonych sieci były projektowane w oparciu o wszystkie znane wielkości wejściowe (P out, P in, P pin, SDP, DDP), które powinny mieć wpływ na wielkość modelowaną. Zaimplementowany w programie Statistica Neural Networks algorytm doboru cech sieci pozwalał jednak na automatyczne wyznaczenie i odrzucenie tych wielkości, które nie miały znaczącego wpływu, na jakość tworzonej sieci. Wynikowo wejściami sieci były najczęściej zestawy składające się z wartości ciśnienia obciążenia na wlocie i wylocie z komory (P in, P out ), ciśnienie w drenie pneumatycznym (P pin ) oraz zadane ciśnienie w zbiorniku zasilania systoli (SDP). W początkowym etapie prac, na podstawie wyników serii pomiarowych dla pracy zestawu wspomagania pod obciążeniem stałym (rozdział 4.1, Tabela 4.3), utworzono cztery osobne sieci, odtwarzające wartość przepływu wylotowego (Q out ) w zależności od 69
70 występujących warunków napełnienia komory krwistej urządzenia. Dokonano w tym celu osobnego trenowania sieci dla przypadku całkowitego wyrzutu i napełnienia, niepełnego wyrzutu i napełnienia oraz sytuacji mieszanych, kiedy występował tylko jeden stan skrajny. Poszczególne modele wykazywały się dobrymi właściwościami predykcyjnymi w swojej grupie warunków pracy, jednak nie sprawdzały się dla przypadków plików testowych z innych grup. Próbowano również wyznaczyć sieć o dwóch wyjściach, modelujących przebieg wartości przepływu zarówno wlotowego, jak i wylotowego. Ustalono, że podejście takie daje bardzo słabą jakość predykcji dla obu sygnałów. Utworzenie osobnych sieci dla każdego z sygnałów wyjściowych było dużo korzystniejsze. Kolejnym etapem prac była próba wyznaczenia jednej sieci neuronowej dla wszystkich warunków napełnienia komory krwistej urządzenia. Utworzony model wykazywał lepsze właściwości dla szerokiego zakresu zmian warunków pracy w porównaniu z modelami cząstkowymi dla danych z innych grup niż grupa ucząca. Jednak nadal uzyskiwane błędy były wysokie, szczególnie w przypadku niewielkiej różnicy pomiędzy maksymalną wartością ciśnienia sterującego a wartością ciśnienia obciążenia wyjściowego. Podjęto również próby wykonania modelu neuronowego odtwarzającego przepływ wylotowy z urządzenia (Q out ) na podstawie serii pomiarowych dla modelowania niewydolności pracy serca (rozdział 4.1, Tabela 4.2). Uzyskane wyniki potwierdziły, że można uzyskać satysfakcjonujące rezultaty dla danego punktu pracy urządzenia. Jednak zmiana istotnych parametrów sterowania, jak stopień wypełnienia sygnału sterującego (%SYS) czy ilości cykli pracy na minutę (AHR) skutkuje znacznym pogorszeniem jakości predykcji. Wykorzystanie wyłącznie serii pomiarowych wykonanych dla przypadku symulacji niewydolności układu krążenia nie pozwala na ocenę uniwersalności wykonanego modelu dla innych przypadków stanu pacjenta Model o parametrach skupionych Wcześniejsze badania nad modelem urządzenia wspomagania nie przyniosły zadowalającego rozwiązania. Między innymi z tego względu postanowiono przeprowadzić eksperyment identyfikacyjny nr 2 (rozdział 4.2), w którym daną rejestrowaną był również sygnał sterujący zaworu liniowego jednostki sterującej. Dzięki temu otrzymano informację o momentach występowania zmian faz zasilania. Na podstawie uzyskanych wyników próbowano wyznaczyć model bazując na opisie zawartym w pracy [76]. Opis ten zakłada, że różnica ciśnień pomiędzy ciśnieniem w komorze pneumatycznej (P pn ) urządzenia 7
71 a ciśnieniem w tętnicy, do której dołączony jest wylot urządzenia (P out ) może być wyznaczona, jako: P pn (t) P out (t) = R vo (t)q out (t) + L dq out(t), (5.7) dt gdzie: P pn (t) ciśnienie w komorze pneumatycznej urządzenia, P out (t) ciśnienie w tętnicy, do której dołączony jest wylot urządzenia (aorta), Q out (t) przepływ wylotowy z urządzenia wspomagania, R vo (t) L bezwładność płynu w przewodzie wylotowym. zmienny w czasie opór zastawki wylotowej, Na podstawie powyższego równania możliwe jest wyznaczenie wartości przepływu w kaniuli wylotowej na podstawie znajomości wartości ciśnienia na wyjściu urządzenia, w komorze powietrznej i zmiennej w czasie rezystancji zastawki (Rys. 5.12) poprzez rozwiązanie równania różniczkowego: dq out (t) dt = 1 L [P pn(t) P out (t) R vo (t)q out (t)] (5.8) W opisie zawartym w pracy [76], rezystancja zastawki R v (t) została opisana jako funkcja czasu i granicznych wartości rezystancji. Model ten zakłada stałą, wysoką wartość oporu zastawki w pozycji zamkniętej (R c ), dobraną w taki sposób, aby odwzorować wartość przepływów wstecznych przez zastawkę. W pozycji otwartej wartość rezystancji jest bliska zeru (R ). W chwilach czasowych związanych z otwieraniem i zamykaniem zastawek następuje liniowa zmiana wartości rezystancji pomiędzy wartościami skrajnymi. Czas rozpoczęcia zamykania bądź otwierania zastawki, jak również jego długość dobrana była adekwatnie do konkretnego przypadku. W zaadoptowanym rozwiązaniu postanowiono wyznaczać wartość rezystancji na podstawie sygnału sterującego i danych doświadczalnych (Rys. 5.11). ster f(ster) P pn P out R vo (t) Model analityczny Q out Rys Schemat koncepcyjny modelu o parametrach skupionych. P pn ciśnienie w komorze pneumatycznej urządzenia, P out - ciśnienie aorcie, Q out - przepływ wylotowy z urządzenia wspomagania, R vo (t) - zmienny w czasie opór zastawki wylotowej, ster sygnał sterujący zaworu liniowego jednostki sterującej. Na podstawie danych eksperymentalnych wyznaczono wartość opóźnienia otwierania i zamykania zastawki względem sygnału sterującego zaworem liniowym (ster), czas otwierania i zamykania zastawki, wartość oporu w pozycji otwartej (R ) i zamkniętej (R c ) jak 71
72 Rvo (mmhg*s/ml) Rvo (mmhg*s/ml) również wartość bezwładności (L). Wartości wyznaczonych parametrów przedstawiono w tabeli 5.1. W eksperymencie nr 2 nie był prowadzony pomiar ciśnienia w komorze pneumatycznej urządzenia. Dlatego w równaniu (5.8) wykorzystano wartość ciśnienia w komorze krwistej, która z punktu widzenia poprawności rezultatu modelowania powinna dawać lepsze wyniki. Tabela 5.1 Wartość parametrów funkcji zmiennej w czasie oporności zastawki oraz modelu urządzenia. parametr opóźnienie względem sygnału ster czas otwarcia zastawki czas zamykania zastawki opór zastawki otwartej symbol τ (s) t (s) t c (s) R o mmhg s ml opór zastawki zamkniętej R c mmhg s ml bezwładność cieczy w kaniuli L mmhg s2 ml wartość W wyniku przeprowadzonych symulacji dla przykładowych danych dla wspomagania w układzie przedsionkowo-aortalnym uzyskano wyniki przedstawione na rysunku (Rys. 5.12, a). W późniejszych badaniach, po przeprowadzeniu eksperymentu identyfikacyjnego dla urządzenia wspomagającego pracującego w układzie koniuszek serca aorta, powrócono do przedstawionego modelu w celu sprawdzenia poprawności jego działania dla tego przypadku (Rys. 5.12, b). a) b) Przepływ (l/min) 5-5 Q out model Q out pomiar 5-5 Przepływ (l/min) 5-5 Q out model Q out pomiar 5-5 R vo Czas (s) R vo Czas (s) Rys Przebiegi czasowe zmierzonej (Q out pomiar) i zamodelowanej (Q out model) wartości przepływu wylotowego z pulsacyjnego urządzenia wspomagania pracy serca oraz funkcji oporności zastawki wylotowej (R vo ). a) dane dla wspomagania przedsionkowego (SDP = 25 mmhg, DDP = -75 mmhg, %SYS = 4, AHR = 6), b) dane dla wspomagania w układzie koniuszek serca aorta (SDP = 25 mmhg, DDP = -5 mmhg, %SYS = 4, AHR = 6). Otrzymane, zamodelowane wartości przepływu krwi w kaniuli wylotowej dla wspomagania w układzie przedsionkowym są w wysokim stopniu zbieżne z wartością mierzoną. Dla powyższych przypadków obliczony został współczynnik determinacji, który 72
73 jest miarą jakości dopasowania modelu wyznaczaną jako kwadrat korelacji między wartością przewidywaną a rzeczywistą. Wyniósł on dla obu przypadków.95, co odpowiada bardzo dobremu dopasowaniu. Podkreślić należy, że otrzymane współczynniki podane są dla modelu o identycznych parametrach. Oznacza to, że estymuje on dobrze wartość modelowaną przy zmianie miejsca dołączenia urządzenia względem układu krążenia. Niemniej jednak, w obu przypadkach przedstawionych na rysunku 5.12, kaniula wylotowa pracowała na podobne obciążenie, czyli ciśnienie panujące w aorcie, a parametry sterowania były bardzo zbliżone. Przy zmianie parametrów sterowania, bez zmiany parametrów modelu, uzyskiwano znacznie niższe wartości współczynnika determinacji, na poziomie Oznacza to, że model jest w znacznym stopniu modelem lokalnym a zmiana warunków pracy wiąże się z koniecznością ponownego doboru wartości parametrów modelu Posumowanie Przy użyciu opisanych w niniejszym rozdziale metod nie udało się wyznaczyć wiernego modelu przepływu krwi w urządzeniu wspomagania pracy serca dla rożnych warunków pracy. Przebadane modele odtwarzały wartość modelowaną albo mało dokładnie albo tylko w lokalnym zakresie warunków pracy urządzenia (Tabela 5.2). Problemy występowały pomimo wykorzystania jako danych wejściowych, informacji o ciśnieniach obciążenia urządzenia czy ciśnieniach w samym urządzeniu. Informacje te nie są dostępne pomiarowo w warunkach klinicznych, dlatego nie powinny być używane w docelowym modelu. Podobna dokładność modelu dla szerokiego zakresu punktów pracy otrzymana została dla modelu bazującego na równaniach analitycznych oraz dla modelu opartego na logice rozmytej. Ze względu na brak możliwości uzyskania informacji o stanie otwarcia zastawki, w dalszej części pracy skoncentrowano się na analitycznym podejściu do problemu. Jego celem było wyznaczenie równań umożliwiających estymację wartości przepływu krwi na podstawie standardowych danych pomiarowych jednostki sterującej. Rozważane było również wykorzystanie sygnałów, których dodanie do klinicznej wersji urządzenia jest medycznie dopuszczalne (przepływ powietrza w drenie, ciśnienie w komorze powietrznej urządzenia). Z analizy problemu wynika, że jedyną możliwością wykonania tego typu modelu jest bazowanie na sygnale pomiarowym, który w sposób pośredni odzwierciedla zmiany przepływu krwi. Zmiany te są zależne od zmian parametrów zasilania oraz stanu wydolności układu krążenia. Oznacza to, że niezbędna jest informacja o przebiegu fizycznej wielkości, związanej z warunkami zasilania urządzenia, która pozwoli na oszacowanie wartości przepływu krwi przez urządzenie wspomagające (Rys. 5.13). 73
74 Tabela 5.2 Zestawienie opracowanych modeli urządzenia bazujących na wszystkich dostępnych danych pomiarowych. model Dane z eksp. nr Dwuelastancyjny 1 Analityczny 1 Parametryczny 1 Rozmyty 1 Neuronowy 1 O parametrach skupionych 2, 3 Wejścia modelu Ciśnienie przedsionkowe Ciśnienie aortalne Ciśnienie przedsionkowe Ciśnienie aortalne Ciśnienie zasilania Ciśnienie przedsionkowe Ciśnienie aortalne Ciśnienie zasilania Ciśnienie przedsionkowe Ciśnienie aortalne Ciśnienie zasilania Przepływ wlotowy Ciśnienie przedsionkowe Ciśnienie aortalne Ciśnienie zasilania Ciśnienie w komorze krwistej Ciśnienie aortalne Sygnał sterujący Cechy modelu średnio dokładny lokalny średnio dokładny globalny dobra dokładność lokalny dobra dokładność globalny niezbędna informacja o stanie otwarcia zastawki dobra dokładność lokalny dobra dokładność lokalny P in P out warunki zasilania (jednostka sterująca) P z Q pn urządzenie wspomagające VAD P pn Q in Q out warunki obciążenia (układ krążenia) α β Model VAD Q bl_m Rys Schemat koncepcji budowy modelu urządzenia wspomagania pracy serca bazującego wyłącznie na sygnałach pomiarowych dostępnych klinicznie. α poszukiwana, uzupełniająca zmienna pomiarowa odzwierciedlająca wpływ zmiany obciążenia na wartość przepływu, β - zmienne pomiarowe dostępne w jednostce sterującej. P z ciśnienie sterujące, Q pn przepływ powietrza zasilającego w drenie pneumatycznym, P pn ciśnienie w komorze pneumatycznej urządzenia, P in, P out - ciśnienie obciążenia na wlocie i wylocie urządzenia, Q in, Q out - przepływ wlotowy i wylotowy z urządzenia wspomagania, Q bl_m modelowana wartość przepływu przez komorę krwistą urządzenia. 74
75 Bazując na ogólnej wiedzy o urządzeniu wspomagającym, zauważono, że model tego typu (Rys. 5.13) pozwoli wyłącznie na oszacowanie wartości przepływu krwi w komorze krwistej urządzenia a nie umożliwi wyznaczenia osobno wartości przepływu wlotowego i wylotowego z urządzenia. Wynika to między innymi z faktu występowania dwóch zastawek mechanicznych w urządzeniu, których efekty działania są trudne do zamodelowania. Związane jest to z ich nieliniowością, występowaniem zjawiska odbicia zastawki od pierścienia oraz zależnością przepływów, tak w kierunku przewodzenia, jak i wstecznych od nieznanej wartości obciążenia urządzenia. Informacja niesiona przez zakładaną zmienną pomiarową pochodzić będzie z części pneumatycznej urządzenia oraz jednostki sterującej i może, co najwyżej, nieść w sobie informację o sumarycznej ilości cieczy, która została przepompowana przez urządzenie. Z tego względu skoncentrowano się na wyznaczeniu modelu wartości przepływu przez komorę krwistą urządzenia, czyli różnicy pomiędzy przepływem wylotowym i wlotowym urządzenia (5.9): Q bl (t) = Q out (t) Q in (t), (5.9) gdzie: Q bl przepływ przez komorę krwistą urządzenia, Q out przepływ w kaniuli wylotowej urządzenia, Q in przepływ w kaniuli dolotowej urządzenia. Na podstawie zebranych danych pomiarowych zaobserwowano, że zmiana warunków pracy urządzenia ma wpływ na przebieg zmian: ciśnienia w komorze powietrznej urządzenia, wartości przepływu powietrza w drenie oraz ciśnienia sterującego w drenie pneumatycznym. Z tego względu rozpoczęto prace nad wyznaczeniem modeli bazujących na tych zmiennych pomiarowych. Wyniki tych prac przedstawiono w kolejnych rozdziałach. 75
76 5.2. Model przepływu krwi bazujący na danych z jednostki sterującej i części pneumatycznej urządzenia wspomagającego Jednym z głównych problemów przy próbie estymacji wartości przepływu krwi w urządzeniu wspomagania pracy serca, jest fakt, że w warunkach wspomagania klinicznego nie ma możliwości pozyskania danych pomiarowych dotyczących stanu wydolności pacjenta a tym samym wartości obciążenia urządzenia wspomagającego. Natomiast wartość tego obciążenia ma realny wpływ na wartość przepływu krwi w urządzeniu, którą staramy się wyznaczyć przy pomocy modelu. Jednakże możliwy jest pomiar przepływu powietrza w pneumatycznym drenie zasilającym oraz, w przypadku komór pozaustrojowych, czyli urządzeń wspomagających, które znajdują się na zewnątrz ciała pacjenta (niewszczepialnych), pomiar ciśnienia panującego w komorze powietrznej urządzenia. Celem prowadzonych prac było wyznaczenie modelu, umożliwiającego estymację wartości przepływu krwi w urządzeniu wspomagania pracy serca. Jego oszacowanie powinno być realizowane na podstawie danych pomiarowych dostarczanych z jednostki sterującej oraz z części pneumatycznej samego urządzenia wspomagającego. Założeniem do wyznaczenia modelu bazującego na danych z części pneumatycznej urządzenia, było przekonanie, że zmiana wartości obciążeń, powodująca zmianę wielkości przepływu krwi będzie miała odzwierciedlenie w zmianie wartości przepływu powietrza w drenie zasilającym oraz ciśnienia w komorze powietrznej urządzenia wspomagającego. Z tego względu postanowiono prowadzić prace nad wyznaczeniem modelu przepływu krwi w urządzeniu (Q bl_m ) bazującego wyłącznie na pomiarze wartości przepływu powietrza w drenie zasilającym oraz sygnału sterującego zaworu liniowego odpowiedzialnego za formowanie fali ciśnienia zasilania (Rys. 5.14, model nr 1). Gdyby wyznaczony model przepływu krwi miał niedostateczną dokładność, rozważano możliwość wykorzystania danych pomiarowych z ciśnieniomierza umieszczonego w komorze pneumatycznej (Rys. 5.14, model nr 2). Q pn ster Model (1) Q bl_m Q pn Model ster (2) P pn Q bl_m Rys Struktura modelu bazującego na danych z przepływomierza powietrznego. Model 1 struktura modelu przepływu krwi w urządzeniu, bazującego wyłącznie na sygnale z przepływomierza pneumatycznego i sygnale sterującym. Model 2 model rozszerzony o ciśnienie w komorze powietrznej urządzenia wspomagania pracy serca. Podstawą rozważania modelu była obserwacja, że przebieg mierzony wartości przepływu powietrza w drenie (Q pn ) ma zbliżony charakter do mierzonej wartości przepływu krwi w komorze (Q bl ) co pokazane jest na rysunku Dla sprawdzonych różnych warunków 76
77 pracy komory współczynnik determinacji sygnału wyniósł średnio.74 (Tabela 5.4), co odpowiada zadowalającemu dopasowaniu. Rozpoczęto więc prace nad umożliwieniem wyznaczenia modelu przepływu krwi w komorze (Q bl ) na podstawie pomiaru przepływu powietrza w drenie zasilającym. W tym celu zaadoptowana została metoda opisu zastawek komory przedstawiona w pracy [76], gdzie rezystancja zastawek została opisana jako funkcja czasu i granicznych wartości rezystancji. Model ten zakłada stałą, wysoką wartość oporu zastawki R c w pozycji zamkniętej, dobraną w taki sposób, aby odwzorować wartość przepływów wstecznych przez zastawkę. W pozycji otwartej wartość rezystancji jest bliska zeru (R ). W chwilach czasowych związanych z otwieraniem i zamykaniem zastawek następuje liniowa zmiana wartości rezystancji pomiędzy wartościami skrajnymi. W rozważanym przypadku opis rezystancyjny zastawki zastąpiony został funkcją przepuszczalności K. Oznacza to, że charakter przebiegu pozostał ten sam, jednak wysoka wartość funkcji, zbliżona do jedności, występuje dla otwartej pozycji zastawki natomiast jej niska wartość, zbliżona do zera, gdy zastawka jest zamknięta (Rys. 5.16). 2 Q bl Przepływ (l/min) a1 a2 a6 a7 Q pn Czas (s) Rys Przebieg mierzonej wartości przepływu krwi w komorze (Q bl ) oraz przepływu powietrza w drenie zasilającym (Q pn ) dla przypadków pomiarowych a1, a2, a6 i a7 (Tabela 4.5). Wartość funkcji K in K out ster Czas (s) Rys Zależność czasowa funkcji przepuszczalności dla zastawki wlotowej (Κ in ) i wylotowej (Κ out ) wyznaczana na podstawie sygnału sterującego zaworem liniowym jednostki sterującej (ster). Wartość sygnału sterującego została znormalizowana do jedności. Wysoka wartość sygnału sterującego oznacza fazę wyrzutu krwi z komory. 77
78 W celu uzyskania uniwersalnego opisu dla różnych przypadków sterowania, funkcja przepuszczalności zastawek została wyznaczona na podstawie sygnału sterującego jednostki sterującej (ster). Czasy otwierania i zamykania zastawek oraz wartości opóźnień względem sygnału zasilania zostały wyznaczone eksperymentalnie na podstawie danych pomiarowych. Parametry wyznaczonych funkcji przedstawiono w tabeli 5.3. Tabela 5.3 Parametry funkcji przepuszczalności zastawek parametr opóźnienie względem sygnału Ster czas otwarcia zastawki czas zamykania zastawki min/max przepuszczalność zastawki wlotowej min/max przepuszczalność zastawki wylotowej symbol τ (s) t (s) t c (s) Κ in min Κ in max Κ out min Κ out max wartość Wartość przepływu wlotowego(q in_m ) i wylotowego (Q out_m ) opisano zależnościami: Q in_m (t) = Q pn (t) Κ in (t), (5.1) Q out_m (t) = Q pn (t) Κ out (t), (5.11) a modelowana wartość przepływu krwi przez komorę (Q bl_m ) wynosi: Q bl_m (t) = Q out_m (t) Q in_m (t), (5.12) gdzie: Q in_m, Q out_m modelowany przepływ w kaniuli wlotowej i wylotowej urządzenia wspomagającego, Q pn wartość przepływu powietrza w drenie zasilającym, Κ in, Κ out funkcja przepuszczalności zastawki wlotowej i wylotowej, Q bl_m modelowana wartość przepływu krwi w komorze. 2 Q bl Q bl_m Przepływ (l/min) a1 a2 a6 a Czas (s) Rys Przebieg wartości modelowanej (Q bl_m ) i zmierzonej (Q bl ) przepływu krwi przez komorę urządzenia wspomagającego dla przypadków pomiarowych a1, a2, a6 i a7 (Tabela 4.5). 78
79 Otrzymany w ten sposób model przepływu krwi pozwolił na wierniejsze odwzorowanie wartości przepływu (Rys. 5.17) a współczynnik determinacji dla rożnych przypadków pomiarowych wyniósł średnio.81, co odpowiada dobremu dopasowaniu. W dalszych badaniach poszukiwano metody, która umożliwiłaby uwzględnienia dynamiki zmian przepływu bazując wyłącznie na pomiarze wartości przepływu powietrza w drenie (Q pn ). W urządzeniu wspomagania pompowana jest krew o określonej masie. Dlatego zmiana jej prędkości wiąże się ze zjawiskami bezwładnościowymi zależnymi od prędkości zmian wartości przepływu. Przetestowano możliwość uzupełnienia modelu o czynnik powiązany z wartością pochodnej wartości przepływu powietrza zasilającego w drenie (5.13): Q bl_mdq (t) = Q out_m (t) Q in_m (t) M dq pn(t), (5.13) gdzie współczynnik M został wyznaczony eksperymentalnie na poziomie M =.13 [s]. W modelu tym korzystne było zastosowanie filtracji sygnału pochodnej przepływu powietrza w drenie, co wprowadza określone opóźnienie do modelu. Szacunkowa wartość tego opóźnienia wynosi τ =.47s. Otrzymany, w powyższy sposób (równanie 5.13), model przepływu krwi pozwolił na dalszą poprawę jakości odwzorowania wartości przepływu (Rys. 5.18) a współczynnik determinacji dla rożnych przypadków pomiarowych wyniósł średnio.88, co odpowiada dobremu dopasowaniu modelu. dt Przepływ (l/min) a1 a2 a6 a7 Q bl Q bl_mdq Czas (s) Rys Przebieg wartości modelowanej (Q bl_mdq ) i zmierzonej (Q bl ) przepływu krwi przez komorę urządzenia wspomagającego dla przypadków pomiarowych a1, a2, a6 i a7 (Tabela 4.5). Dalsze próby poprawienia uzyskiwanych rezultatów na podstawie informacji o wartości przepływu powietrza zasilającego nie przyniosły poprawy uzyskiwanych współczynników determinacji. Z tego względu postanowiono zbadać możliwość wyznaczenia opisu modelu, 79
80 w którym wartością wejściową byłby również sygnał pomiarowy ciśnienia pneumatycznego w komorze powietrznej urządzenia wspomagającego (model 2, Rys. 5.14, b). Dla tego przypadku zaproponowano równanie, w którym uwzględniona została podatność komory powietrznej urządzenia wspomagającego: Q bl_mdp (t) = Q out_m (t) Q in_m (t) C dp pn(t), (5.14) gdzie wartość podatności C została wyznaczona na podstawie danych doświadczalnych na poziomie C =.2 [ l s mmhg min ]. Również w tym przypadku wprowadzono filtrowanie sygnału pochodnej, skutkujące powstaniem opóźnienia τ =.47s. dt 2 Q bl Q bl_mdp Przepływ (l/min) a1 a2 a6 a Czas (s) Rys Przebieg wartości modelowanej (Q bl_mdp ) i zmierzonej (Q bl ) przepływu krwi przez komorę urządzenia wspomagającego. Model opisany równaniem (5.14) został przetestowany dla 2 różnych przypadków pracy urządzenia wspomagającego (dane a1-a2, Tabela 4.5), tzn. dla różnych wartości parametrów sterujących i modelowanych stanów wydolności układu krążenia. Przykładowe wyniki przedstawiono na rysunku Dla tego modelu średnia wartość współczynnika determinacji wyniosła.92, co odpowiada bardzo dobremu dopasowaniu. Jego wadą jest konieczność wykorzystania mierzonej wartości ciśnienia panującego w komorze pneumatycznej urządzenia wspomagania. Pomiar ten był realizowany w warunkach prowadzonego eksperymentu jednak do tej pory nie jest wykonywany w warunkach wspomagania klinicznego. Dodatkowo jego ewentualne wprowadzenie jest możliwe wyłącznie w przypadku wspomagania pozaustrojowego. Dla wszystkich przedstawionych modeli (równania (5.12), (5.13) i (5.14)) badanych dla wszystkich przypadków pomiarowych, parametry funkcji przepuszczalności zastawek (Κ in, Κ out ) nie były zmienne (Tabela 5.3). Oznacza to, że modele cechują się podobną jakością 8
81 odwzorowania wielkości przepływu dla różnych punktów pracy urządzenia wspomagającego. W tabeli 5.4 przedstawiono zestawienie wartości współczynnika determinacji otrzymanego dla poszczególnych modeli przepływu krwi dla dwudziestu różnych warunków pracy. Wartości współczynnika determinacji z tabeli 5.4 zostały wyznaczone przy pomocy skryptu oprogramowania Matlab. Wartość średnia współczynnika jest średnią arytmetyczną ze wszystkich przebadanych przypadków. Odchylenie standardowe oszacowane zostało zgodnie z zależnością: σ = N i=1 (X X ) 2 N, (5.15) gdzie: σ - odchylenie standardowe, X - średnia wartość z wszystkich przypadków, X - wartość dla danego przypadku pomiarowego, N - liczba przypadków pomiarowych. Tabela 5.4 Wartość współczynnika determinacji (R 2 ) dla poszczególnych modeli i danych pomiarowych Model Nr pomiaru Q pn Q bl_m Q b_mdq Q b_mdp R 2 σ (odchylenie standardowe)
82 cisnienie (mmhg) Podsumowanie W wyniku analizy wyników symulacji (Rys ) dla poszczególnych modeli (równania (5.12), (5.13) i (5.14)) można stwierdzić, że: - otrzymane przebiegi charakteryzują się wysoką zgodnością wartości mierzonej (Q bl ) i wartości modelowanych przepływu krwi (Q bl_m, Q bl_mdq, Q bl_mdp ) dla okresów wyrzutu i napełniania komory, - zgodność przebiegów jest zbliżona dla wszystkich badanych przypadków pomiarowych bez konieczności zmian parametrów modelu, - w przypadku wystąpienia pełnego wyrzutu lub napełnienia komory krwistej urządzenia (osiągnięcie nasycenia, brak ruchu membrany) model mniej dokładnie odwzorowuje wartość przepływu w porównaniu do okresów napełniania i opróżniania. - zgodność modelowanej wartości z daną pomiarową jest najniższa w momentach zmian faz zasilania, co odpowiada medianom czasowym otwierania i zamykania zastawek, - najwyższy współczynnik determinacji, równoważny bardzo dobremu odwzorowaniu, osiągany jest dla modelu Q b_mdp (5.14), lecz wymagana jest wówczas znajomość wartości ciśnienia pneumatycznego w części powietrznej komory, - bazując wyłącznie na pomiarze wartości przepływu powietrza w drenie oraz sygnale sterującym możliwa jest osiągnięcie dobrego dopasowania modelu przepływu krwi w urządzeniu (Q b_mdq ). 2 Q bl III III Q bl_mdp P z 15 przepływ (l/min) I II czas (s) -5 Rys. 5.2 Przebieg mierzonej (Q bl ) i modelowanej (Q bl_mdp ) wartości przepływu krwi dla dwóch różnych przypadków pracy. I przypadek wystąpienia pełnego wyrzuty, II przypadek wystąpienia całkowitego napełnienia, III momenty zmiany faz zasilania urządzenia wspomagającego dla przypadków pomiarowych a6 i a7 (Tabela 4.5). 82
83 5.3. Model przepływu krwi bazujący na danych z jednostki sterującej Celem przedstawionych prac było wyznaczenie modelu, umożliwiającego estymację wartości przepływu krwi w pulsacyjnym urządzeniu wspomagania pracy serca na podstawie danych pomiarowych dostarczanych wyłącznie z jednostki sterującej. Niezbędne badania wykonano na urządzeniu wspomagającym dołączonym do hybrydowego symulatora układu krążenia w konfiguracji koniuszek serca aorta zgodnie z opisem zawartym w rozdziale 4.3. Poglądowy schemat zadania badawczego przedstawiono na rysunku Na podstawie parametrów zadanych w jednostce sterującej ustawiane są wartości ciśnień zasilania systoli i diastoli oraz wyznaczany jest sygnał sterujący zaworem liniowym. Zawór łączy naprzemiennie dren pneumatyczny urządzenia POLVAD-MEV z odpowiednim zbiornikiem zasilającym. Pod wpływem wytworzonej fali ciśnienia następuje ruch membrany urządzenia wspomagającego i odpowiednio napełnianie i wyrzut z komory krwistej urządzenia. Jednostka sterująca POLVAD-MEV SDP zbiornik ciśnienia zasilania systoli (P z+ ) zestaw parametrów sterowania AHR %SYS generator sygnału sterującego (ster) zawór liniowy DDP zbiornik ciśnienia zasilania diastoli (P z- ) ciśnienie zasilania (P z ) wielkości mierzalne ciśnienie systoli ciśnienie diastoli sygnał sterujący ciśnienie zasilania Hybrydowy symulator układu krążenia (pacjent) VAD przepływ krwi (Q b ) Model komora aorta modelowana wielkość przepływ krwi Rys Schemat zespołu wspomagania pracy serca w połączeniu z hybrydowym symulatorem układu krążenia. Wyznaczany model miał bazować na wielkościach mierzalnych w jednostce sterującej, czyli ciśnieniu systoli i diastoli (P z+, P z- ), sygnale sterującym (ster) i ciśnieniu na wyjściu zaworu liniowego (ciśnienie zasilania, P z ). Wyjściem modelu powinna być wartość przepływu krwi (Q b ) zdefiniowana, jako różnica przepływu wylotowego (Q out ) i wlotowego urządzenia (Q in ). W trakcie pracy urządzenia wspomagającego, wartość przepływu wytworzonego przez zespół wspomagania pracy serca jest zależna od ciśnień panujących 83
84 w punktach wszczepienia urządzenia (ciśnienie w komorze serca i aorcie). Ciśnienia te w warunkach wspomagania klinicznego są niedostępne pomiarowo. Ze względu na brak bezpośredniej informacji dotyczącej wartości obciążenia urządzenia, opracowanie modelu przepływu krwi bazującego wyłącznie na danych z jednostki sterującej było zadaniem problematycznym. W ramach badań identyfikacyjnych urządzenia VAD przeprowadzono testy dla różnych przypadków obciążenia jednostki sterującej (Rys. 5.22). Zbierane były między innymi dane dotyczące pracy jednostki dla zasymulowanego stanu prawidłowej fizjologii układu krążenia, dla niewydolności lewej komory serca (patologia) oraz dla przypadku, w którym urządzenie wspomagające było odłączone od jednostki sterującej POLPDU-51 a wyjście przyłączeniowe drenu powietrznego było zablokowane (bieg jałowy, brak przepływu). Przypadki pomiarowe (różne obciążenia jednostki sterującej): brak przepływu POLPDU-51 SDP = 2 DEL = 15 DDP = -5 %SYS = 4 AHR = 6 patologia POLPDU-51 SDP = 2 DEL = 15 DDP = -5 %SYS = 4 AHR = 6 fizjologia POLPDU-51 SDP = 2 DEL = 15 DDP = -5 %SYS = 4 AHR = 6 VAD Pacjent 1 (silna niewydolność lewej komory) VAD Pacjent 2 (stan fizjologiczny normalny) Rys Schemat przestawiający sytuacje pomiarowe dla przypadków nazwanych: brak przepływu, niewydolność oraz fizjologia. a) Ciśnienie sterujące (mmhg) brak przepływu patologia fizjologia P 1 P b) Przepływ krwi (l/min) brak przepływu patologia fizjologia Q b1 Q b Czas (s) Czas (s) Rys Zmierzone przebiegi ciśnienia sterującego (a) i przepływu krwi (b) dla trzech przypadków pomiarowych: braku przepływu, patologii i fizjologii 84
85 Na rysunku 5.23 przedstawiono wartość ciśnienia i przepływu krwi w komorze urządzenia wspomagającego dla trzech przypadków pomiarowych: braku przepływu, patologii, fizjologii i tych samych parametrów sterowania jednostki sterującej. Oznacza to, że na wartość przepływu miały wpływ wyłącznie warunki obciążenia urządzenia wspomagającego. Jak wspomniano, w pierwszym przypadku urządzenie wspomagania było odłączone a przyłącze drenu pneumatycznego jednostki sterującej było zablokowane. Osiągane w tym przypadku ciśnienie na wyjściu zaworu liniowego nazwane zostało na potrzeby niniejszej pracy ciśnieniem bazowym zasilania. Ze względu na brak pracy urządzenia, wartość przepływu krwi była w tym przypadku równa zeru. Jak widać na rysunku 5.23, w czasie pracy urządzenia wspomagania, ciśnienie na wyjściu zaworu jest, co do wartości bezwzględnej, niższe od ciśnienia bazowego. Podstawą prac nad wyznaczeniem modelu przepływu było przypuszczenie, że można oszacować wartość wytworzonego przez urządzenie przepływu krwi na podstawie różnicy pomiędzy zmierzonym ciśnieniem zasilającym a ciśnieniem bazowym zasilania (Rys. 5.24). Ciśnienie bazowe zasilania (nieznane w warunkach wspomagania pacjenta) Ciśnienie zmierzone zasilania Model przepływu krwi estymowany przepływ krwi Rys Schemat koncepcji struktury modelu do estymacji wartości przepływu krwi Podejście takie wymagało uzyskania informacji o wartości ciśnienia bazowego dla aktualnych parametrów pracy jednostki sterującej. Technicznie możliwe jest przeprowadzenie eksperymentu pomiarowego dla przypadku odłączonego urządzenia wspomagania i wybranych parametrów pracy jednostki sterującej w celu zebrania odpowiednich danych. Jakkolwiek zebranie takich informacji dla wszystkich możliwych kombinacji parametrów pracy jednostki byłoby bardzo trudne. Przewidzieć można również problemy z synchronizacją czasową zebranych w ten sposób danych historycznych z aktualnymi danymi pomiarowymi. W sytuacji zatkania drenu, ciśnienie zasilania za zaworem rozdzielającym zależy od ciśnienia panującego w zbiorniku ciśnienia wysokiego, podciśnienia, sygnału sterującego oraz charakterystyki dynamicznej zaworu rozdzielającego. Z tego względu zaproponowano złożoną strukturę modelu (Rys. 5.25) składającego się z modelu głównego (model przepływu krwi) i modelu wartości pomocniczej (model zaworu liniowego). 85
86 ster P z+ P z- Model zaworu liniowego (1) estymowana wartość ciśnienia bazowego zasilania (P z_m ) Model przepływu krwi (2) estymowany przepływ krwi (Q b_m ) P z Rys Struktura modelu bazującego na danych z jednostki sterującej. Model 1 model wartości ciśnienia bazowego zasilania, model 2 model wartości przepływu krwi w warunkach pracy urządzenia wspomagania. P z+, P z- ciśnienia w zbiornikach zasilających, ster sygnał sterujący, P z_m modelowany sygnał ciśnienia bazowego zasilania dla przypadku braku przepływu, P z mierzony sygnał ciśnienia sterującego w czasie pracy komory, Q b_m modelowany sygnał przepływu krwi. W zaproponowanej strukturze, model zaworu liniowego (model 1, Rys. 5.25) odpowiada za wyznaczenie wartości ciśnienia bazowego zasilania. Informacjami wejściowymi są: zmierzona wartość ciśnienia w zbiorniku ciśnienia zasilania systoli (wysokiego, P z+ ) i diastoli (niskiego, P z- ) oraz sygnał sterujący zaworem liniowym (ster). Na ich podstawie wyznaczana jest wartość bazowego ciśnienia sterującego (P z_m ), czyli wartość ciśnienia za zaworem liniowym w przypadku braku przepływu w drenie pneumatycznym. Jak wspomniano wcześniej, w przypadku pracy urządzenia przebieg ciśnienia zasilania różni się od przebiegu bazowego. Dlatego drugim elementem modelu złożonego jest model przepływu krwi w komorze (model 2, Rys. 5.25) wyznaczanego na podstawie różnicy pomiędzy wartością zmierzonego ciśnienia zasilania (ciśnienia w warunkach pracy urządzenia, P z ) oraz zamodelowanego ciśnienia zasilania w przypadku braku przepływu w drenie (P z_m ). Ponieważ wartość modelowanego ciśnienia bazowego sterowania ma służyć jako dana wejściowa do kolejnego modelu, dokładność estymacji miała w tym przypadku kluczowe znaczenie dla dokładności modelu przepływu krwi Model zaworu liniowego W celu wyznaczenia modelu zaworu liniowego wykorzystane zostały dane pomiarowe z badań prowadzonych dla przypadku biegu jałowego jednostki sterującej, czyli braku przepływu. Tabela 4.5, kolumna Pomiary dla biegu jałowego, przedstawia zestawienie przebadanych przypadków pomiarowych dla różnych parametrów sterowania. W celu wyznaczenia modelu wykorzystywane były dane z dziesięciu różnych przypadków sterowania o nazwach b1 9, b15 i b18. Parametr sterowania DEL, mówiący o opóźnieniu wyrzutu z urządzenia wspomagania względem skurczu komory pacjenta jest nieistotny w przypadku braku przepływu z jednostki sterującej. Również nie ma w tym przypadku znaczenia zmiana symulowanego stanu pacjenta. Dlatego niektóre przypadki pomiarowe, różne dla dołączonego urządzenia pomiarowego, były analogiczne względem siebie dla biegu jałowego. W takim 86
87 przypadku nie były one wykonywane powtórnie. Sytuacje tę oznaczono w tabeli poprzez przypisanie tej samej nazwy dla sytuacji analogicznych. Pierwszym podejściem do wyznaczenia modelu zaworu liniowego była próba wyznaczenia modelu metodami identyfikacji obiektów dynamicznych z wykorzystaniem narzędzia System Identyfication Toolbox pakietu obliczeniowego Matlab. Drugim wykorzystanym podejściem było opracowanie modelu analitycznego, bazującego na zależnościach matematycznych. W obu przypadkach poszukiwany był model odtwarzający wartość ciśnienia bazowego zasilania na podstawie informacji dostępnych w jednostce sterującej (model 1, Rys. 5.25). A. Modele bazujące na identyfikacji obiektu W metodzie bazującej na identyfikacji obiektu, do wyznaczenia modelu zaworu liniowego wykorzystano narzędzie System Identification Toolbox pakietu obliczeniowego Matlab (rozdział 4.4.3), umożliwiające wyznaczanie modeli matematycznych układów dynamicznych na podstawie danych pomiarowych sygnałów wejściowych i wyjściowych. W celu wyznaczenia modelu zaworu liniowego, w pierwszej kolejności poszukiwany był model transmitancyjny. Oznacza to, że relacje między sygnałami wejść i wyjść systemu opisane są w postaci transmitancji cząstkowych, tzn. wyjście modelu jest sumą iloczynów wejść do modelu i odpowiednich transmitancji G (Rys. 5.26). u1 G u1 u2 G u2 + y1 u3 G u3 Rys Schemat modelu transmitancyjnego MISO. W pakiecie Matlab wyznaczane są transmitancje operatorowe z ciągłą reprezentacją czasu i opóźnieniami: Y(s) = nums(s) den(s) e sτ U(s) + E(s), (5.16) gdzie: Y(s), U(s) i E(s) - transformaty Laplace a sygnałów wyjścia, wejścia oraz szumu, num(s) mianownik transmitancji, den(s) mianownik transmitancji, τ opóźnienie transportowe. 87
88 Możliwe jest także wyznaczenie modeli z czasem dyskretnym opartych na transmitancji Z: y(t) = num(z 1 ) u(t τ) + e(t) den(z 1 ) num(z 1 ) = b + b 1 z 1 + b 2 z 2 +. (5.17) den(z 1 ) = 1 + a 1 z 1 + a 2 z 2 + Do wyznaczenia modeli wykorzystano dwa zestawy danych. Jako dane identyfikacyjne użyte zostały pliki b1 9, (Tabela 4.5), a jako dane walidacyjne zestawy 15 i 18. Wielkościami wejściowymi modelu były odpowiednio: u1 ciśnienie zasilania systoli (P z+ ), u2 ciśnienie zasilania diastoli (P z- ), u3 sygnał sterujący (ster). Wielkością wyjściową y1 był sygnał ciśnienia za zaworem liniowym (P z ) w przypadku braku przepływu w drenie. Model z czasem ciągłym wyliczony automatycznie przez pakiet obliczeniowy umożliwił uzyskanie dopasowania do danych estymacyjnych na poziomie 73.26%. W wyniku modyfikacji manualnej parametrów modelu, takich jak rząd licznika i mianownika oraz opóźnienia, udało się uzyskać jakość odtwarzania na poziomie 8.67%. Model z czasem dyskretnym, wyliczony na parametrach dobranych automatycznie przez program, umożliwił uzyskanie dopasowania do danych estymacyjnych na poziomie 73.26%. Po ręcznej kalibracji parametrów modelu udało się uzyskać jakość odtwarzania na poziomie 8.54%. Zestawienie parametrów wejściowych procesu identyfikacji dla wyznaczonych modeli przedstawia Tabela 5.5. Tabela 5.5 Zestawienie parametrów wejściowych procesu identyfikacji dla wyznaczonych modeli Dziedzin a czasowa Tryb identyfikacji Rząd licznika Rząd Nastawione opóźnienia sygnałów wejściowych u1 u2 u3 Symbol modelu mianownika Dopasowanie ciągła dyskretna auto 1 2 auto auto auto Ϭ % manual 2 3 auto auto auto Ϭ % auto 1 2 auto auto auto Ϭ % manual Ϭ %. 88
89 Przykładowo, dla modelu Ϭ 2, transmitancje poszczególnych wejść wynosiły: G u1 =.1874s s.2545 s s s G u2 =.9588s s s s s+.87 (5.18) (5.19) G u3 = 1396s e 5 s 3481 s s s+4.768e 7 (5.2) Na rysunku 5.27A przedstawiono przykładowy widok przebiegów wartości mierzonej i modelowanej bazowego ciśnienia zasilania dla modelu o najwyższej uzyskanej jakości odtwarzania (Tabela 5.5, Ϭ 2 ). Jak można zaobserwować, odtwarzany sygnał charakteryzuje się znaczną rozbieżnością względem wartości modelowanej. W kolejnych badaniach poszukiwano modelu zaworu w dostępnych w oprogramowaniu postaciach: modelu zmiennych stanu (State-space), modelu procesu (Process Model), modelu parametrycznego (Polynomial) oraz modelu nieliniowego. W wyniku prowadzonych badań nie udało się uzyskać satysfakcjonujących wyników. Przykładowo, najlepszy uzyskany model zmiennych stanu o współczynniku dopasowania 97.1%, po eksporcie do środowiska Simulink dawał rezultaty ukazane na rysunku 5.27B a współczynnik determinacji dla tego przypadku wynosił zaledwie Próby wyznaczenia modelu w oparciu o logikę rozmytą oraz opartego na sieciach neuronowych również nie przyniosły oczekiwanych rezultatów. Ze względu na konieczność uzyskania modelu zaworu liniowego o bardzo wysokim współczynniku dopasowania, podjęto próbę wyznaczenia modelu analitycznego, opartego na zależnościach fizycznych, równaniach bilansowych i wiedzy ogólnej o obiekcie. A B Rys A przykładowy widok (dla modelu o symbolu Ϭ 2 ) przebiegów czasowych mierzonej (czarny) i modelowanej (niebieski) wartości ciśnienia za zaworem liniowym otrzymanych za pomocą narzędzia System Identyfication Toolbox pakietu obliczeniowego Matlab. B przebiegi czasowe mierzonej (czarny) i modelowanej (czerwony) wartości ciśnienia za zaworem liniowym uzyskane po eksporcie modelu do środowiska Simulink. 89
Opracował: Arkadiusz Podgórski
 Opracował: Arkadiusz Podgórski Serce to pompa ssąco-tłocząca, połoŝona w klatce piersiowej. Z zewnątrz otoczone jest workiem zwanym osierdziem. Serce jest zbudowane z tkanki mięśniowej porzecznie prąŝkowanej
Opracował: Arkadiusz Podgórski Serce to pompa ssąco-tłocząca, połoŝona w klatce piersiowej. Z zewnątrz otoczone jest workiem zwanym osierdziem. Serce jest zbudowane z tkanki mięśniowej porzecznie prąŝkowanej
(total artificial heart overview 10 min) Implanty i Sztuczne Narządy Piotr Jasiński
 https://www.youtube.com/watch?v=bv0ydt3rqli (total artificial heart overview 10 min) Implanty i Sztuczne Narządy Piotr Jasiński 1 2 Serce Czynność serca objawia się zgodnymi i na przemian występującymi
https://www.youtube.com/watch?v=bv0ydt3rqli (total artificial heart overview 10 min) Implanty i Sztuczne Narządy Piotr Jasiński 1 2 Serce Czynność serca objawia się zgodnymi i na przemian występującymi
układu krążenia Paweł Piwowarczyk
 Monitorowanie układu krążenia Paweł Piwowarczyk Monitorowanie Badanie przedmiotowe EKG Pomiar ciśnienia tętniczego Pomiar ciśnienia w tętnicy płucnej Pomiar ośrodkowego ciśnienia żylnego Echokardiografia
Monitorowanie układu krążenia Paweł Piwowarczyk Monitorowanie Badanie przedmiotowe EKG Pomiar ciśnienia tętniczego Pomiar ciśnienia w tętnicy płucnej Pomiar ośrodkowego ciśnienia żylnego Echokardiografia
Anatomia i fizjologia układu krążenia. Łukasz Krzych
 Anatomia i fizjologia układu krążenia Łukasz Krzych Wytyczne CMKP Budowa serca RTG Unaczynienie serca OBSZARY UNACZYNIENIA Układ naczyniowy Układ dąży do zachowania ośrodkowego ciśnienia tętniczego
Anatomia i fizjologia układu krążenia Łukasz Krzych Wytyczne CMKP Budowa serca RTG Unaczynienie serca OBSZARY UNACZYNIENIA Układ naczyniowy Układ dąży do zachowania ośrodkowego ciśnienia tętniczego
MODEL FUNKCJONOWANIA UKŁADU KRĄŻENIA [ BAP_2014969.doc ]
![MODEL FUNKCJONOWANIA UKŁADU KRĄŻENIA [ BAP_2014969.doc ] MODEL FUNKCJONOWANIA UKŁADU KRĄŻENIA [ BAP_2014969.doc ]](/thumbs/27/11438308.jpg) MODEL FUNKCJONOWANIA UKŁADU KRĄŻENIA [ ] Użytkowanie Jak napełnić model układu krążenia? 1. Model ułożyć poziomo, płasko na stole. 2. Odłączyć niebieskie rurki od układu krążenia, łączenie znajduje się
MODEL FUNKCJONOWANIA UKŁADU KRĄŻENIA [ ] Użytkowanie Jak napełnić model układu krążenia? 1. Model ułożyć poziomo, płasko na stole. 2. Odłączyć niebieskie rurki od układu krążenia, łączenie znajduje się
PL B1. Akustyczne urządzenie do pomiaru chwilowej objętości krwi w komorze wspomagania serca
 PL 221894 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 221894 (13) B1 (21) Numer zgłoszenia: 394074 (51) Int.Cl. A61M 1/10 (2006.01) G01F 23/22 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
PL 221894 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 221894 (13) B1 (21) Numer zgłoszenia: 394074 (51) Int.Cl. A61M 1/10 (2006.01) G01F 23/22 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
Zestawy pompowe PRZEZNACZENIE ZASTOSOWANIE OBSZAR UŻYTKOWANIA KONCEPCJA BUDOWY ZALETY
 PRZEZNACZENIE Zestawy pompowe typu z przetwornicą częstotliwości, przeznaczone są do tłoczenia wody czystej nieagresywnej chemicznie o ph=6-8. Wykorzystywane do podwyższania ciśnienia w instalacjach. Zasilane
PRZEZNACZENIE Zestawy pompowe typu z przetwornicą częstotliwości, przeznaczone są do tłoczenia wody czystej nieagresywnej chemicznie o ph=6-8. Wykorzystywane do podwyższania ciśnienia w instalacjach. Zasilane
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI
 Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Modelowanie pracy sztucznej komory serca oraz układu krążenia człowieka
 Modelowanie pracy sztucznej komory serca oraz układu krążenia człowieka Alicja Siewnicka, Bartłomiej Fajdek, Krzysztof Janiszowski Zakład Urządzeń Wykonawczych Automatyki i Robotyki, Instytut Automatyki
Modelowanie pracy sztucznej komory serca oraz układu krążenia człowieka Alicja Siewnicka, Bartłomiej Fajdek, Krzysztof Janiszowski Zakład Urządzeń Wykonawczych Automatyki i Robotyki, Instytut Automatyki
dr inż. Piotr Pawełko / Przed przystąpieniem do realizacji ćwiczenia patrz punkt 6!!!
 Laboratorium nr2 Temat: Sterowanie pośrednie siłownikami jednostronnego i dwustronnego działania. 1. Wstęp Sterowanie pośrednie stosuje się do sterowania elementami wykonawczymi (siłownikami, silnikami)
Laboratorium nr2 Temat: Sterowanie pośrednie siłownikami jednostronnego i dwustronnego działania. 1. Wstęp Sterowanie pośrednie stosuje się do sterowania elementami wykonawczymi (siłownikami, silnikami)
Ćwiczenie 9. Podstawy fizjologii wysiłku fizycznego
 Ćwiczenie 9 Podstawy fizjologii wysiłku fizycznego Zagadnienia teoretyczne 1. Kryteria oceny wydolności fizycznej organizmu. 2. Bezpośredni pomiar pochłoniętego tlenu - spirometr Krogha. 3. Pułap tlenowy
Ćwiczenie 9 Podstawy fizjologii wysiłku fizycznego Zagadnienia teoretyczne 1. Kryteria oceny wydolności fizycznej organizmu. 2. Bezpośredni pomiar pochłoniętego tlenu - spirometr Krogha. 3. Pułap tlenowy
Fizjologia Układu Krążenia 3. seminarium
 Fizjologia Układu Krążenia 3. seminarium Cykl sercowy: Skurcz izowolumetryczny: szczyt załamka R - początek skurczu komory skurcz Cardiac zwiększa ciśnienie w Cycle Lewej komorze powyżej ciśnienia w lewym
Fizjologia Układu Krążenia 3. seminarium Cykl sercowy: Skurcz izowolumetryczny: szczyt załamka R - początek skurczu komory skurcz Cardiac zwiększa ciśnienie w Cycle Lewej komorze powyżej ciśnienia w lewym
Algorytmy optymalizacji systemu ICT wspomagające zarządzanie siecią wodociągową
 Katowice GPW 2014 Algorytmy optymalizacji systemu ICT wspomagające zarządzanie siecią wodociągową Jan Studziński 1 1. Wstęp Cel projektu Usprawnienie zarządzania siecią wodociągową za pomocą nowoczesnych
Katowice GPW 2014 Algorytmy optymalizacji systemu ICT wspomagające zarządzanie siecią wodociągową Jan Studziński 1 1. Wstęp Cel projektu Usprawnienie zarządzania siecią wodociągową za pomocą nowoczesnych
Zajęcia laboratoryjne
 Zajęcia laboratoryjne Napęd Hydrauliczny Instrukcja do ćwiczenia nr 1 Charakterystyka zasilacza hydraulicznego Opracowanie: R. Cieślicki, Z. Kudźma, P. Osiński, J. Rutański, M. Stosiak Wrocław 2016 Spis
Zajęcia laboratoryjne Napęd Hydrauliczny Instrukcja do ćwiczenia nr 1 Charakterystyka zasilacza hydraulicznego Opracowanie: R. Cieślicki, Z. Kudźma, P. Osiński, J. Rutański, M. Stosiak Wrocław 2016 Spis
09 - Dobór siłownika i zaworu. - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika
 - Dobór siłownika i zaworu - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika OPÓR PRZEPŁYWU W ZAWORZE Objętościowy współczynnik przepływu Qn Przepływ oblicza się jako stosunek
- Dobór siłownika i zaworu - Opór przepływu w przewodzie - Dobór rozmiaru zaworu - Dobór rozmiaru siłownika OPÓR PRZEPŁYWU W ZAWORZE Objętościowy współczynnik przepływu Qn Przepływ oblicza się jako stosunek
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
PL 187505 B1 (12) OPIS PATENTOWY (19) PL (11) 187505 (13) B1. (21) Numer zgłoszenia: 324415. (51) IntCl7 A61F 5/34
 RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej (12) OPIS PATENTOWY (19) PL (11) 187505 (21) Numer zgłoszenia: 324415 (22) Data zgłoszenia: 22.01.1998 (13) B1 (51) IntCl7 A61F 5/34 (54)Urządzenie
RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej (12) OPIS PATENTOWY (19) PL (11) 187505 (21) Numer zgłoszenia: 324415 (22) Data zgłoszenia: 22.01.1998 (13) B1 (51) IntCl7 A61F 5/34 (54)Urządzenie
ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ
 ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ 1. Cel i zakres ćwiczenia Celem ćwiczenia jest opanowanie umiejętności dokonywania pomiarów parametrów roboczych układu pompowego. Zapoznanie z budową
ĆWICZENIE WYZNACZANIE CHARAKTERYSTYK POMPY WIROWEJ 1. Cel i zakres ćwiczenia Celem ćwiczenia jest opanowanie umiejętności dokonywania pomiarów parametrów roboczych układu pompowego. Zapoznanie z budową
Pomiar ciśnienia krwi metodą osłuchową Korotkowa
 Ćw. M 11 Pomiar ciśnienia krwi metodą osłuchową Korotkowa Zagadnienia: Oddziaływania międzycząsteczkowe. Siły Van der Waalsa. Zjawisko lepkości. Równanie Newtona dla płynięcia cieczy. Współczynniki lepkości;
Ćw. M 11 Pomiar ciśnienia krwi metodą osłuchową Korotkowa Zagadnienia: Oddziaływania międzycząsteczkowe. Siły Van der Waalsa. Zjawisko lepkości. Równanie Newtona dla płynięcia cieczy. Współczynniki lepkości;
Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny
 Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny Sterowanie układem hydraulicznym z proporcjonalnym zaworem przelewowym Opracowanie: Z. Kudźma, P. Osiński, M. Stosiak 1 Proporcjonalne elementy
Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny Sterowanie układem hydraulicznym z proporcjonalnym zaworem przelewowym Opracowanie: Z. Kudźma, P. Osiński, M. Stosiak 1 Proporcjonalne elementy
Tester funkcji TBH-400. Technika pomiarowo-kontrolna dla medycyny i przemysłu
 Tester funkcji TBH-400 Urządzenie do symulacji termometrów medycznych, urządzeń do pomiaru rzutu serca, inwazyjnych i nieinwazyjnych urządzeń do pomiaru ciśnienia krwi temperatura 0 70 C generacja sygnałów
Tester funkcji TBH-400 Urządzenie do symulacji termometrów medycznych, urządzeń do pomiaru rzutu serca, inwazyjnych i nieinwazyjnych urządzeń do pomiaru ciśnienia krwi temperatura 0 70 C generacja sygnałów
Doświadczenia w eksploatacji gazomierzy ultradźwiękowych
 Doświadczenia w eksploatacji gazomierzy ultradźwiękowych Daniel Wysokiński Mateusz Turkowski Rogów 18-20 września 2013 Doświadczenia w eksploatacji gazomierzy ultradźwiękowych 1 Gazomierze ultradźwiękowe
Doświadczenia w eksploatacji gazomierzy ultradźwiękowych Daniel Wysokiński Mateusz Turkowski Rogów 18-20 września 2013 Doświadczenia w eksploatacji gazomierzy ultradźwiękowych 1 Gazomierze ultradźwiękowe
Instrukcja do ćwiczeń laboratoryjnych. Sterowanie odbiornikiem hydraulicznym z rozdzielaczem typu Load-sensing
 Instrukcja do ćwiczeń laboratoryjnych Sterowanie odbiornikiem hydraulicznym z rozdzielaczem typu Load-sensing Wstęp teoretyczny Poprzednie ćwiczenia poświęcone były sterowaniom dławieniowym. Do realizacji
Instrukcja do ćwiczeń laboratoryjnych Sterowanie odbiornikiem hydraulicznym z rozdzielaczem typu Load-sensing Wstęp teoretyczny Poprzednie ćwiczenia poświęcone były sterowaniom dławieniowym. Do realizacji
BiPAP Vision. z PAV (Proportional Assist Ventilation)
 BiPAP Vision z PAV (Proportional Assist Ventilation) P A V nowa generacja nieinwazyjnej wentylacji PAV nowy tryb wentylacji asystującej - różnica w koncepcji - wspomaganie ciśnieniowe proporcjonalne do
BiPAP Vision z PAV (Proportional Assist Ventilation) P A V nowa generacja nieinwazyjnej wentylacji PAV nowy tryb wentylacji asystującej - różnica w koncepcji - wspomaganie ciśnieniowe proporcjonalne do
WYKŁAD 11 POMPY I UKŁADY POMPOWE
 WYKŁAD 11 POMPY I UKŁADY POMPOWE Historia Czerpak do wody używany w Egipcie ok. 1500 r.p.n.e. Historia Nawadnianie pól w Chinach Historia Koło wodne używane w Rzymie Ogólna klasyfikacja pomp POMPY POMPY
WYKŁAD 11 POMPY I UKŁADY POMPOWE Historia Czerpak do wody używany w Egipcie ok. 1500 r.p.n.e. Historia Nawadnianie pól w Chinach Historia Koło wodne używane w Rzymie Ogólna klasyfikacja pomp POMPY POMPY
Układ krążenia krwi. Bogdan Walkowiak. Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka. 2014-11-18 Biofizyka 1
 Wykład 7 Układ krążenia krwi Bogdan Walkowiak Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka 2014-11-18 Biofizyka 1 Układ krążenia krwi Source: INTERNET 2014-11-18 Biofizyka 2 Co
Wykład 7 Układ krążenia krwi Bogdan Walkowiak Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka 2014-11-18 Biofizyka 1 Układ krążenia krwi Source: INTERNET 2014-11-18 Biofizyka 2 Co
Zastosowanie symulacji komputerowej do badania właściwości hydraulicznych sieci wodociągowej
 Zastosowanie symulacji komputerowej do badania właściwości hydraulicznych sieci wodociągowej prof. dr hab. inż. Andrzej J. OSIADACZ Politechnika Warszawska Wydział Inżynierii Środowiska dr hab. inż. Maciej
Zastosowanie symulacji komputerowej do badania właściwości hydraulicznych sieci wodociągowej prof. dr hab. inż. Andrzej J. OSIADACZ Politechnika Warszawska Wydział Inżynierii Środowiska dr hab. inż. Maciej
Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych
 Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych Politechnika Warszawska Zakład Systemów Ciepłowniczych i Gazowniczych Prof. dr hab. inż. Andrzej J. Osiadacz Dr hab. inż. Maciej
Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych Politechnika Warszawska Zakład Systemów Ciepłowniczych i Gazowniczych Prof. dr hab. inż. Andrzej J. Osiadacz Dr hab. inż. Maciej
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
biologia w gimnazjum UKŁAD KRWIONOŚNY CZŁOWIEKA
 biologia w gimnazjum 2 UKŁAD KRWIONOŚNY CZŁOWIEKA SKŁAD KRWI OSOCZE Jest płynną częścią krwi i stanowi 55% jej objętości. Jest podstawowym środowiskiem dla elementów morfotycznych. Zawiera 91% wody, 8%
biologia w gimnazjum 2 UKŁAD KRWIONOŚNY CZŁOWIEKA SKŁAD KRWI OSOCZE Jest płynną częścią krwi i stanowi 55% jej objętości. Jest podstawowym środowiskiem dla elementów morfotycznych. Zawiera 91% wody, 8%
Wprowadzenie. - Napęd pneumatyczny. - Sterowanie pneumatyczne
 Wprowadzenie Pneumatyka - dziedzina nauki i techniki zajmująca się prawami rządzącymi przepływem sprężonego powietrza; w powszechnym rozumieniu także technika napędu i sterowania pneumatycznego. Zastosowanie
Wprowadzenie Pneumatyka - dziedzina nauki i techniki zajmująca się prawami rządzącymi przepływem sprężonego powietrza; w powszechnym rozumieniu także technika napędu i sterowania pneumatycznego. Zastosowanie
Instrukcja obsługi SPEED CONTROL. Electro-pneumatic Speed control system Elektropneumatyczny Regulator Wydajności Pompy
 SPEED CONTROL Electro-pneumatic Speed control system Elektropneumatyczny Regulator Wydajności Pompy Informacje ogólne Sterownik Warren Rupp SPEED CONTROL może być stosowany do sterowania wydajnością pomp
SPEED CONTROL Electro-pneumatic Speed control system Elektropneumatyczny Regulator Wydajności Pompy Informacje ogólne Sterownik Warren Rupp SPEED CONTROL może być stosowany do sterowania wydajnością pomp
Wielkością i kształtem przypomina dłoń zaciśniętą w pięść. Położone jest w klatce piersiowej tuż za mostkiem. Otoczone jest mocnym, łącznotkankowym
 Wielkością i kształtem przypomina dłoń zaciśniętą w pięść. Położone jest w klatce piersiowej tuż za mostkiem. Otoczone jest mocnym, łącznotkankowym workiem zwanym osierdziem. Wewnętrzna powierzchnia osierdzia
Wielkością i kształtem przypomina dłoń zaciśniętą w pięść. Położone jest w klatce piersiowej tuż za mostkiem. Otoczone jest mocnym, łącznotkankowym workiem zwanym osierdziem. Wewnętrzna powierzchnia osierdzia
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA
 Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Laboratorium Elektronicznej Aparatury Medycznej I
 Laboratorium Elektronicznej Aparatury Medycznej I Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Katedra Inżynierii Biomedycznej Dr inż. Elżbieta Szul-Pietrzak ĆWICZENIE NR 4 APARATURA
Laboratorium Elektronicznej Aparatury Medycznej I Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Katedra Inżynierii Biomedycznej Dr inż. Elżbieta Szul-Pietrzak ĆWICZENIE NR 4 APARATURA
Elżbieta Łoniewska-Paleczny. Oddział Anestezjologii i Intensywnej Terapii Szpital Wojewódzki w Bielsku-Białej
 Elżbieta Łoniewska-Paleczny Oddział Anestezjologii i Intensywnej Terapii Szpital Wojewódzki w Bielsku-Białej Ryzyko powikłań związanych z zastosowaniem metody nie może przewyższać korzyści z uzyskanych
Elżbieta Łoniewska-Paleczny Oddział Anestezjologii i Intensywnej Terapii Szpital Wojewódzki w Bielsku-Białej Ryzyko powikłań związanych z zastosowaniem metody nie może przewyższać korzyści z uzyskanych
Fizjologia czlowieka seminarium + laboratorium. M.Eng. Michal Adam Michalowski
 Fizjologia czlowieka seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
Fizjologia czlowieka seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
Płyny newtonowskie (1.1.1) RYS. 1.1
 Miniskrypt: Płyny newtonowskie Analizujemy cienką warstwę płynu zawartą pomiędzy dwoma równoległymi płaszczyznami, które są odległe o siebie o Y (rys. 1.1). W warunkach ustalonych następuje ścinanie w
Miniskrypt: Płyny newtonowskie Analizujemy cienką warstwę płynu zawartą pomiędzy dwoma równoległymi płaszczyznami, które są odległe o siebie o Y (rys. 1.1). W warunkach ustalonych następuje ścinanie w
POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY
 POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY AUTOMATYKA CHŁODNICZA TEMAT: Racje techniczne wykorzystania rurki kapilarnej lub dyszy w małych urządzeniach chłodniczych i sprężarkowych pompach ciepła Mateusz
POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY AUTOMATYKA CHŁODNICZA TEMAT: Racje techniczne wykorzystania rurki kapilarnej lub dyszy w małych urządzeniach chłodniczych i sprężarkowych pompach ciepła Mateusz
Ostra niewydolność serca
 Ostra niewydolność serca Prof. dr hab. Jacek Gajek, FESC Uniwersytet Medyczny we Wrocławiu Niewydolność serca Niewydolność rzutu minutowego dla pokrycia zapotrzebowania na tlen tkanek i narządów organizmu.
Ostra niewydolność serca Prof. dr hab. Jacek Gajek, FESC Uniwersytet Medyczny we Wrocławiu Niewydolność serca Niewydolność rzutu minutowego dla pokrycia zapotrzebowania na tlen tkanek i narządów organizmu.
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI ĆWICZENIE NR 7 BADANIE POMPY II
 INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 7 BADANIE POMPY II 2 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i działaniem
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki płynów ĆWICZENIE NR 7 BADANIE POMPY II 2 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i działaniem
BTL CARDIOPOINT CPET SYSTEM ERGOSPIROMETRYCZNY
 BTL CARDIOPOINT CPET SYSTEM ERGOSPIROMETRYCZNY BADANIE ERGOSPIROMETRYCZNE Dokładność pomiaru, zaawansowane funkcje diagnostyczne oraz komfort obsługi sprawiają, że system BTL CardioPoint CPET doskonale
BTL CARDIOPOINT CPET SYSTEM ERGOSPIROMETRYCZNY BADANIE ERGOSPIROMETRYCZNE Dokładność pomiaru, zaawansowane funkcje diagnostyczne oraz komfort obsługi sprawiają, że system BTL CardioPoint CPET doskonale
Szanowni Studenci, Szanowne Studentki,
 Szanowni Studenci, Szanowne Studentki, Pracownia Sztucznego Serca zaprasza chętne osoby na miesięczne lub dłuższe praktyki studenckie. Proponujemy Wam realizację ciekawych projektów, których opisy znajdują
Szanowni Studenci, Szanowne Studentki, Pracownia Sztucznego Serca zaprasza chętne osoby na miesięczne lub dłuższe praktyki studenckie. Proponujemy Wam realizację ciekawych projektów, których opisy znajdują
Ćwiczenie 1. Badanie aktuatora elektrohydraulicznego. Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium. Instrukcja laboratoryjna
 Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium Ćwiczenie 1 Badanie aktuatora elektrohydraulicznego Instrukcja laboratoryjna Opracował : mgr inż. Arkadiusz Winnicki Warszawa 2010 Badanie
Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium Ćwiczenie 1 Badanie aktuatora elektrohydraulicznego Instrukcja laboratoryjna Opracował : mgr inż. Arkadiusz Winnicki Warszawa 2010 Badanie
Choroba wieńcowa i zawał serca.
 Choroba wieńcowa i zawał serca. Dr Dariusz Andrzej Tomczak Specjalista II stopnia chorób wewnętrznych Choroby serca i naczyń 1 O czym będziemy mówić? Budowa układu wieńcowego Funkcje układu wieńcowego.
Choroba wieńcowa i zawał serca. Dr Dariusz Andrzej Tomczak Specjalista II stopnia chorób wewnętrznych Choroby serca i naczyń 1 O czym będziemy mówić? Budowa układu wieńcowego Funkcje układu wieńcowego.
PRACA PRZEJŚCIOWA SYMULACYJNA. Zadania projektowe
 Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA PRACA PRZEJŚCIOWA SYMULACYJNA Zadania projektowe dr inż. Roland PAWLICZEK Praca przejściowa symulacyjna 1 Układ pracy 1. Strona tytułowa
Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA PRACA PRZEJŚCIOWA SYMULACYJNA Zadania projektowe dr inż. Roland PAWLICZEK Praca przejściowa symulacyjna 1 Układ pracy 1. Strona tytułowa
STEROWANIE CIŚNIENIEM BEZWZGLĘDNYM W APARACIE UDOJOWYM DLA KRÓW
 Inżynieria Rolnicza 7(95)/2007 STEROWANIE CIŚNIENIEM BEZWZGLĘDNYM W APARACIE UDOJOWYM DLA KRÓW Henryk Juszka, Stanisław Lis, Marcin Tomasik Katedra Energetyki Rolniczej, Akademia Rolnicza w Krakowie Streszczenie.
Inżynieria Rolnicza 7(95)/2007 STEROWANIE CIŚNIENIEM BEZWZGLĘDNYM W APARACIE UDOJOWYM DLA KRÓW Henryk Juszka, Stanisław Lis, Marcin Tomasik Katedra Energetyki Rolniczej, Akademia Rolnicza w Krakowie Streszczenie.
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji
 Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Temat: Układy pneumatyczno - hydrauliczne
 Copyright by: Krzysztof Serafin. Brzesko 2007 Na podstawie skryptu 1220 AGH Temat: Układy pneumatyczno - hydrauliczne 1. Siłownik z zabudowanym blokiem sterującym Ten ruch wahadłowy tłoka siłownika jest
Copyright by: Krzysztof Serafin. Brzesko 2007 Na podstawie skryptu 1220 AGH Temat: Układy pneumatyczno - hydrauliczne 1. Siłownik z zabudowanym blokiem sterującym Ten ruch wahadłowy tłoka siłownika jest
PODSTAWY AUTOMATYKI IV. URZĄDZENIA GRZEJNE W UKŁADACH AUTOMATYCZNEJ REGULACJI
 PODSTAWY AUTOMATYKI IV. URZĄDZENIA GRZEJNE W UKŁADACH AUTOMATYCZNEJ REGULACJI Ćwiczenie nr 4 BADANIE TERMOSTATYCZNYCH GŁOWIC GRZEJNIKOWYCH Rzeszów 2001 2 1. WPROWADZENIE Termostatyczne zawory grzejnikowe
PODSTAWY AUTOMATYKI IV. URZĄDZENIA GRZEJNE W UKŁADACH AUTOMATYCZNEJ REGULACJI Ćwiczenie nr 4 BADANIE TERMOSTATYCZNYCH GŁOWIC GRZEJNIKOWYCH Rzeszów 2001 2 1. WPROWADZENIE Termostatyczne zawory grzejnikowe
Sterowanie układem zawieszenia magnetycznego
 Politechnika Śląska w Gliwicach Wydział: Automatyki, Elektroniki i Informatyki Kierunek: Automatyka i Robotyka Specjalność: Komputerowe systemy sterowania Sterowanie układem zawieszenia magnetycznego Maciej
Politechnika Śląska w Gliwicach Wydział: Automatyki, Elektroniki i Informatyki Kierunek: Automatyka i Robotyka Specjalność: Komputerowe systemy sterowania Sterowanie układem zawieszenia magnetycznego Maciej
Fizjologia człowieka
 Akademia Wychowania Fizycznego i Sportu w Gdańsku Katedra: Promocji Zdrowia Zakład: Biomedycznych Podstaw Zdrowia Fizjologia człowieka Osoby prowadzące przedmiot: Prof. nadzw. dr hab. Zbigniew Jastrzębski
Akademia Wychowania Fizycznego i Sportu w Gdańsku Katedra: Promocji Zdrowia Zakład: Biomedycznych Podstaw Zdrowia Fizjologia człowieka Osoby prowadzące przedmiot: Prof. nadzw. dr hab. Zbigniew Jastrzębski
KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK
 Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Metoda zaburz-obserwuj oraz metoda wspinania
 Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
4. SPRZĘGŁA HYDRAULICZNE
 4. SPRZĘGŁA HYDRAULICZNE WYTYCZNE PROJEKTOWE www.immergas.com.pl 26 SPRZĘGŁA HYDRAULICZNE 4. SPRZĘGŁO HYDRAULICZNE - ZASADA DZIAŁANIA, METODA DOBORU NOWOCZESNE SYSTEMY GRZEWCZE Przekazywana moc Czynnik
4. SPRZĘGŁA HYDRAULICZNE WYTYCZNE PROJEKTOWE www.immergas.com.pl 26 SPRZĘGŁA HYDRAULICZNE 4. SPRZĘGŁO HYDRAULICZNE - ZASADA DZIAŁANIA, METODA DOBORU NOWOCZESNE SYSTEMY GRZEWCZE Przekazywana moc Czynnik
PRACA RÓWNOLEGŁA PRĄDNIC SYNCHRONICZNYCH WZBUDZANYCH MAGNESAMI TRWAŁYMI
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 66 Politechniki Wrocławskiej Nr 66 Studia i Materiały Nr 32 2012 Zdzisław KRZEMIEŃ* prądnice synchroniczne, magnesy trwałe PRACA RÓWNOLEGŁA
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 66 Politechniki Wrocławskiej Nr 66 Studia i Materiały Nr 32 2012 Zdzisław KRZEMIEŃ* prądnice synchroniczne, magnesy trwałe PRACA RÓWNOLEGŁA
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Podstawy użytkowania i pomiarów za pomocą MULTIMETRU
 Podstawy użytkowania i pomiarów za pomocą MULTIMETRU Spis treści Informacje podstawowe...2 Pomiar napięcia...3 Pomiar prądu...5 Pomiar rezystancji...6 Pomiar pojemności...6 Wartość skuteczna i średnia...7
Podstawy użytkowania i pomiarów za pomocą MULTIMETRU Spis treści Informacje podstawowe...2 Pomiar napięcia...3 Pomiar prądu...5 Pomiar rezystancji...6 Pomiar pojemności...6 Wartość skuteczna i średnia...7
MONITOROWANIE OSÓB ZAGROŻONYCH KARDIOLOGICZNIE W ŻYCIU CODZIENNYM DOŚWIADCZENIA INSTYTUTU TECHNIKI I APARATURY MEDYCZNEJ W ZABRZU ADAM GACEK
 MONITOROWANIE OSÓB ZAGROŻONYCH KARDIOLOGICZNIE W ŻYCIU CODZIENNYM DOŚWIADCZENIA INSTYTUTU TECHNIKI I APARATURY MEDYCZNEJ W ZABRZU ADAM GACEK POLSKO BRYTYJSKIE FORUM NOWOCZESNEJ OCHRONY ZDROWIA ZABRZE 27-28.03.2015
MONITOROWANIE OSÓB ZAGROŻONYCH KARDIOLOGICZNIE W ŻYCIU CODZIENNYM DOŚWIADCZENIA INSTYTUTU TECHNIKI I APARATURY MEDYCZNEJ W ZABRZU ADAM GACEK POLSKO BRYTYJSKIE FORUM NOWOCZESNEJ OCHRONY ZDROWIA ZABRZE 27-28.03.2015
Ćwiczenie Nr 2. Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów
 Ćwiczenie Nr 2 Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów 1. Wprowadzenie Sterowanie prędkością tłoczyska siłownika lub wału silnika hydraulicznego
Ćwiczenie Nr 2 Temat: Zaprojektowanie i praktyczna realizacja prostych hydraulicznych układów sterujących i napędów 1. Wprowadzenie Sterowanie prędkością tłoczyska siłownika lub wału silnika hydraulicznego
AUTOMATYKA I STEROWANIE W CHŁODNICTWIE, KLIMATYZACJI I OGRZEWNICTWIE L4 STEROWANIE KOLUMNĄ REKTYFIKACYJNĄ
 ĆWICZENIE LABORATORYJNE AUTOMATYKA I STEROWANIE W CHŁODNICTWIE, KLIMATYZACJI I OGRZEWNICTWIE L4 STEROWANIE KOLUMNĄ REKTYFIKACYJNĄ Wersja: 2013-09-30-1- 4.1. Cel ćwiczenia okresowej. Celem ćwiczenia jest
ĆWICZENIE LABORATORYJNE AUTOMATYKA I STEROWANIE W CHŁODNICTWIE, KLIMATYZACJI I OGRZEWNICTWIE L4 STEROWANIE KOLUMNĄ REKTYFIKACYJNĄ Wersja: 2013-09-30-1- 4.1. Cel ćwiczenia okresowej. Celem ćwiczenia jest
Ćwiczenia laboratoryjne z przedmiotu : Napędy Elektryczne, Hydrauliczne i Pneumatyczne
 Laboratorium nr1 Temat: Sterowanie bezpośrednie siłownikami jednostronnego i dwustronnego działania. 1. Wstęp Sterowanie bezpośrednie pracą aktuatora pneumatycznego (siłownika lub silnika) stosuje się
Laboratorium nr1 Temat: Sterowanie bezpośrednie siłownikami jednostronnego i dwustronnego działania. 1. Wstęp Sterowanie bezpośrednie pracą aktuatora pneumatycznego (siłownika lub silnika) stosuje się
Regulacja wydajności układów sprężarkowych. Sprężarki tłokowe
 Regulacja wydajności układów sprężarkowych. Sprężarki tłokowe Rozbudowane instalacje chłodnicze stawiają przed nami sporo wymagań. Zapotrzebowanie cieplne układów nie jest stałe i wciąż się zmienia. Załączanie
Regulacja wydajności układów sprężarkowych. Sprężarki tłokowe Rozbudowane instalacje chłodnicze stawiają przed nami sporo wymagań. Zapotrzebowanie cieplne układów nie jest stałe i wciąż się zmienia. Załączanie
Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa
 MECHANIK 7/2014 Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa WYZNACZENIE CHARAKTERYSTYK EKSPLOATACYJNYCH SIŁOWNI TURBINOWEJ Z REAKTOREM WYSOKOTEMPERATUROWYM W ZMIENNYCH
MECHANIK 7/2014 Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa WYZNACZENIE CHARAKTERYSTYK EKSPLOATACYJNYCH SIŁOWNI TURBINOWEJ Z REAKTOREM WYSOKOTEMPERATUROWYM W ZMIENNYCH
SPIS TREŚCI Obliczenia zwężek znormalizowanych Pomiary w warunkach wykraczających poza warunki stosowania znormalizowanych
 SPIS TREŚCI Spis ważniejszych oznaczeń... 11 Wstęp... 17 1. Wiadomości ogólne o metrologii przepływów... 21 1.1. Wielkości fizyczne występujące w metrologii przepływów, nazewnictwo... 21 1.2. Podstawowe
SPIS TREŚCI Spis ważniejszych oznaczeń... 11 Wstęp... 17 1. Wiadomości ogólne o metrologii przepływów... 21 1.1. Wielkości fizyczne występujące w metrologii przepływów, nazewnictwo... 21 1.2. Podstawowe
PL 203461 B1. Politechnika Warszawska,Warszawa,PL 15.12.2003 BUP 25/03. Mateusz Turkowski,Warszawa,PL Tadeusz Strzałkowski,Warszawa,PL
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 203461 (13) B1 (21) Numer zgłoszenia: 354438 (51) Int.Cl. G01F 1/32 (2006.01) G01P 5/01 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 203461 (13) B1 (21) Numer zgłoszenia: 354438 (51) Int.Cl. G01F 1/32 (2006.01) G01P 5/01 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data
Transformacja wiedzy w budowie i eksploatacji maszyn
 Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
Ćwiczenie: "Silnik indukcyjny"
 Ćwiczenie: "Silnik indukcyjny" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia: Zasada
Ćwiczenie: "Silnik indukcyjny" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia: Zasada
Badanie zależności temperatury wrzenia wody od ciśnienia
 Ćwiczenie C2 Badanie zależności temperatury wrzenia wody od ciśnienia C2.1. Cel ćwiczenia Celem ćwiczenia jest pomiar zależności temperatury wrzenia wody od ciśnienia (poniżej ciśnienia atmosferycznego),
Ćwiczenie C2 Badanie zależności temperatury wrzenia wody od ciśnienia C2.1. Cel ćwiczenia Celem ćwiczenia jest pomiar zależności temperatury wrzenia wody od ciśnienia (poniżej ciśnienia atmosferycznego),
Laboratorium. Hydrostatyczne Układy Napędowe
 Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
MECHANIKA PŁYNÓW LABORATORIUM
 MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
Pomiar zadymienia spalin
 Pomiar zadymienia spalin Zajęcia laboratoryjne w pracowni badao silników spalinowych Katedra Mechatroniki Wydział Nauk Technicznych UWM Opiekun Naukowy : mgr Maciej Mikulski Pomiar zadymienia spalin Zadymienie
Pomiar zadymienia spalin Zajęcia laboratoryjne w pracowni badao silników spalinowych Katedra Mechatroniki Wydział Nauk Technicznych UWM Opiekun Naukowy : mgr Maciej Mikulski Pomiar zadymienia spalin Zadymienie
WYZNACZANIE OPTYMALIZOWANYCH PROCEDUR DIAGNOSTYCZNO-OBSŁUGOWYCH
 ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTRONICZNYCH INSTYTUT SYSTEMÓW ELEKTRONICZNYCH WYDZIAŁ ELEKTRONIKI WOJSKOWA AKADEMIA TECHNICZNA ---------------------------------------------------------------------------------------------------------------
ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTRONICZNYCH INSTYTUT SYSTEMÓW ELEKTRONICZNYCH WYDZIAŁ ELEKTRONIKI WOJSKOWA AKADEMIA TECHNICZNA ---------------------------------------------------------------------------------------------------------------
BADANIA LABORATORYJNE ZMODERNIZOWANEGO REGULATORA PRZEPŁYWU 2FRM-16 STOSOWANEGO W PRZEMYŚLE
 Szybkobieżne Pojazdy Gąsienicowe (25) nr 1/2010 Paweł GLEŃ BADANIA LABORATORYJNE ZMODERNIZOWANEGO REGULATORA PRZEPŁYWU 2FRM-16 STOSOWANEGO W PRZEMYŚLE Streszczenie. W pracy przedstawiono wyniki badań doświadczalnych,
Szybkobieżne Pojazdy Gąsienicowe (25) nr 1/2010 Paweł GLEŃ BADANIA LABORATORYJNE ZMODERNIZOWANEGO REGULATORA PRZEPŁYWU 2FRM-16 STOSOWANEGO W PRZEMYŚLE Streszczenie. W pracy przedstawiono wyniki badań doświadczalnych,
PL B1. POLITECHNIKA ŚLĄSKA, Gliwice, PL BUP 20/10
 PL 213989 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 213989 (13) B1 (21) Numer zgłoszenia: 387578 (51) Int.Cl. E03F 5/22 (2006.01) F04B 23/12 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
PL 213989 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 213989 (13) B1 (21) Numer zgłoszenia: 387578 (51) Int.Cl. E03F 5/22 (2006.01) F04B 23/12 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
Fizjologia układu krążenia
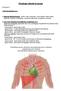 Fizjologia układu krążenia Ćwiczenie II. l. Badanie fizykalne serca a/ oglądanie klatki piersiowej - punkty i linie orientacyjne, ocena kształtu, budowy klatki piersiowej /symetria, wysklepienie, ruchomość
Fizjologia układu krążenia Ćwiczenie II. l. Badanie fizykalne serca a/ oglądanie klatki piersiowej - punkty i linie orientacyjne, ocena kształtu, budowy klatki piersiowej /symetria, wysklepienie, ruchomość
Zawór redukcyjny. Części składowe
 Zawór redukcyjny 1500 6. Zawór sterujący 8. Optyczny wskaźnik położenia opcja: elektryczny wskaźnik położenia, ogranicznik - dla wody pitnej (inne media na zapytanie). - Redukcja ciśnienia w sieci wodociągowej.
Zawór redukcyjny 1500 6. Zawór sterujący 8. Optyczny wskaźnik położenia opcja: elektryczny wskaźnik położenia, ogranicznik - dla wody pitnej (inne media na zapytanie). - Redukcja ciśnienia w sieci wodociągowej.
Sterowniki Programowalne (SP)
 Sterowniki Programowalne (SP) Wybrane aspekty procesu tworzenia oprogramowania dla sterownika PLC Podstawy języka funkcjonalnych schematów blokowych (FBD) Politechnika Gdańska Wydział Elektrotechniki i
Sterowniki Programowalne (SP) Wybrane aspekty procesu tworzenia oprogramowania dla sterownika PLC Podstawy języka funkcjonalnych schematów blokowych (FBD) Politechnika Gdańska Wydział Elektrotechniki i
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7
 Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Układ krążenia część 2. Osłuchiwanie serca.
 Układ krążenia część 2 Osłuchiwanie serca. Osłuchiwanie serca Osłuchiwanie serca miejsce osłuchiwania Miejsca osłuchiwania : Zastawka dwudzielna - V międzyżebrze palec przyśrodkowo od lewej linii środkowo-
Układ krążenia część 2 Osłuchiwanie serca. Osłuchiwanie serca Osłuchiwanie serca miejsce osłuchiwania Miejsca osłuchiwania : Zastawka dwudzielna - V międzyżebrze palec przyśrodkowo od lewej linii środkowo-
Dział programu: Funkcjonowanie człowieka Hasło programowe: Krążenie
 Konspekt lekcji I klasa gimnazjum Autorka: Bogumiła Bąk Dział programu: Funkcjonowanie człowieka Hasło programowe: Krążenie Temat: Na czym polega współpraca małego i dużego obiegu krwi? Dział programu:
Konspekt lekcji I klasa gimnazjum Autorka: Bogumiła Bąk Dział programu: Funkcjonowanie człowieka Hasło programowe: Krążenie Temat: Na czym polega współpraca małego i dużego obiegu krwi? Dział programu:
Dlaczego pompa powinna być "inteligentna"?
 Dlaczego pompa powinna być "inteligentna"? W ciepłowniczych i ziębniczych układach pompowych przetłaczanie cieczy ma na celu transport ciepła, a nie, jak w pozostałych układach, transport masy. Dobrym
Dlaczego pompa powinna być "inteligentna"? W ciepłowniczych i ziębniczych układach pompowych przetłaczanie cieczy ma na celu transport ciepła, a nie, jak w pozostałych układach, transport masy. Dobrym
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Przygotowanie zadania sterowania do analizy i syntezy zestawienie schematu blokowego
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Przygotowanie zadania sterowania do analizy i syntezy zestawienie schematu blokowego
Szanowni Studenci, Szanowne Studentki,
 Szanowni Studenci, Szanowne Studentki, Pracownia Sztucznego Serca zaprasza chętne osoby (po III roku studiów inżynierskich) na miesięczne lub dłuższe praktyki studenckie. Proponujemy Wam realizację ciekawych
Szanowni Studenci, Szanowne Studentki, Pracownia Sztucznego Serca zaprasza chętne osoby (po III roku studiów inżynierskich) na miesięczne lub dłuższe praktyki studenckie. Proponujemy Wam realizację ciekawych
Biologiczne mechanizmy zachowania - fizjologia. zajecia 8 :
 Biologiczne mechanizmy zachowania - fizjologia zajecia 8 : 19.11.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ I gr 08:30 10:00 II gr 10:15 11:45 III gr 12:00 13:30
Biologiczne mechanizmy zachowania - fizjologia zajecia 8 : 19.11.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ I gr 08:30 10:00 II gr 10:15 11:45 III gr 12:00 13:30
OCENA PRZYCZYN I KONSEKWENCJI WYSTĘPOWANIA TĘTNIAKA TĘTNICY PŁUCNEJ U PACJENTÓW Z NADCIŚNIENIEM PŁUCNYM
 OCENA PRZYCZYN I KONSEKWENCJI WYSTĘPOWANIA TĘTNIAKA TĘTNICY PŁUCNEJ U PACJENTÓW Z NADCIŚNIENIEM PŁUCNYM Marcin Kurzyna, Instytut Gruźlicy i Chorób Płuc w Warszawie Grzegorz Harańczyk, StatSoft Polska Choroby
OCENA PRZYCZYN I KONSEKWENCJI WYSTĘPOWANIA TĘTNIAKA TĘTNICY PŁUCNEJ U PACJENTÓW Z NADCIŚNIENIEM PŁUCNYM Marcin Kurzyna, Instytut Gruźlicy i Chorób Płuc w Warszawie Grzegorz Harańczyk, StatSoft Polska Choroby
Lekcja 6. Rodzaje sprężarek. Parametry siłowników
 Lekcja 6. Rodzaje sprężarek. Parametry siłowników Sprężarki wyporowe (tłokowe) Sprężarka, w której sprężanie odbywa sięcyklicznie w zarżniętej przestrzeni zwanej komorąsprężania. Na skutek działania napędu
Lekcja 6. Rodzaje sprężarek. Parametry siłowników Sprężarki wyporowe (tłokowe) Sprężarka, w której sprężanie odbywa sięcyklicznie w zarżniętej przestrzeni zwanej komorąsprężania. Na skutek działania napędu
WZBOGACANIE BIOGAZU W METAN W KASKADZIE MODUŁÓW MEMBRANOWYCH
 biogaz, wzbogacanie biogazu separacja membranowa Andrzej G. CHMIELEWSKI *, Marian HARASIMOWICZ *, Jacek PALIGE *, Agata URBANIAK **, Otton ROUBINEK *, Katarzyna WAWRYNIUK *, Michał ZALEWSKI * WZBOGACANIE
biogaz, wzbogacanie biogazu separacja membranowa Andrzej G. CHMIELEWSKI *, Marian HARASIMOWICZ *, Jacek PALIGE *, Agata URBANIAK **, Otton ROUBINEK *, Katarzyna WAWRYNIUK *, Michał ZALEWSKI * WZBOGACANIE
Laboratorium LAB3. Moduł pomp ciepła, kolektorów słonecznych i hybrydowych układów grzewczych
 Laboratorium LAB3 Moduł pomp ciepła, kolektorów słonecznych i hybrydowych układów grzewczych Pomiary identyfikacyjne pól prędkości przepływów przez wymienniki, ze szczególnym uwzględnieniem wymienników
Laboratorium LAB3 Moduł pomp ciepła, kolektorów słonecznych i hybrydowych układów grzewczych Pomiary identyfikacyjne pól prędkości przepływów przez wymienniki, ze szczególnym uwzględnieniem wymienników
Laboratorium MATLA. Ćwiczenie 2. Programowanie. Skrypty i funkcje. Instrukcje sterujące.
 Laboratorium MATLA Ćwiczenie 2. Programowanie. Skrypty i funkcje. Instrukcje sterujące. Opracowali: - dr inż. Beata Leśniak-Plewińska Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii Biomedycznej
Laboratorium MATLA Ćwiczenie 2. Programowanie. Skrypty i funkcje. Instrukcje sterujące. Opracowali: - dr inż. Beata Leśniak-Plewińska Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii Biomedycznej
Opiekun pracy: Dr n. med. Waldemar Machała
 Marcin Pachucki Anna Durka Monitorowanie rzutu serca CO za pomocą metod mało inwazyjnych: czujnika FloTrac TM i monitora Vigileo TM przedstawienie metody, opis przypadku. Opiekun pracy: Dr n. med. Waldemar
Marcin Pachucki Anna Durka Monitorowanie rzutu serca CO za pomocą metod mało inwazyjnych: czujnika FloTrac TM i monitora Vigileo TM przedstawienie metody, opis przypadku. Opiekun pracy: Dr n. med. Waldemar
Seria Jubileuszowa. Rozwiązania informatyczne. Sprężarki śrubowe Airpol PRM z przetwornicą częstotliwości. oszczędność energii. ochrona środowiska
 Sprężarki śrubowe Airpol PRM z przetwornicą częstotliwości Seria Jubileuszowa Każda sprężarka śrubowa z przetwornicą częstotliwości posiada regulację obrotów w zakresie od 50 do 100%. Jeżeli zużycie powietrza
Sprężarki śrubowe Airpol PRM z przetwornicą częstotliwości Seria Jubileuszowa Każda sprężarka śrubowa z przetwornicą częstotliwości posiada regulację obrotów w zakresie od 50 do 100%. Jeżeli zużycie powietrza
Sterowanie pracą reaktora chemicznego
 Sterowanie pracą reaktora chemicznego Celem ćwiczenia jest opracowanie na sterowniku programowalnym programu realizującego jednopętlowy układ regulacji a następnie dobór nastaw regulatora zapewniających
Sterowanie pracą reaktora chemicznego Celem ćwiczenia jest opracowanie na sterowniku programowalnym programu realizującego jednopętlowy układ regulacji a następnie dobór nastaw regulatora zapewniających
Simulink MATLAB Przegląd obiektów i przykłady zastosowań
 Simulink MATLAB Przegląd obiektów i przykłady zastosowań M. Berndt-Schreiber 1 Simulink MATLAB SIMULINK jest rozszerzeniem pakietu MATLAB; przy pomocy graficznego środowiska pozwala konstruować diagramy
Simulink MATLAB Przegląd obiektów i przykłady zastosowań M. Berndt-Schreiber 1 Simulink MATLAB SIMULINK jest rozszerzeniem pakietu MATLAB; przy pomocy graficznego środowiska pozwala konstruować diagramy
Sterowanie napędów maszyn i robotów
 Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO
 Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
Inwazyjne monitorowanie hemodynamiczne u pacjentów w do operacji torakochirurgicznych z wysokim ążeniowych
 Marcin Pachucki Inwazyjne monitorowanie hemodynamiczne u pacjentów w do operacji torakochirurgicznych z wysokim ryzykiem powikłań krąż ążeniowych Opiekun ITS: drr n. med. Waldemar Machała Studenckie Koło
Marcin Pachucki Inwazyjne monitorowanie hemodynamiczne u pacjentów w do operacji torakochirurgicznych z wysokim ryzykiem powikłań krąż ążeniowych Opiekun ITS: drr n. med. Waldemar Machała Studenckie Koło
Audyt energetyczny sprężonego powietrza
 Do rąk: Adres 1: Adres 2: Miejscowość: Kod pocztowy: Telefon: email: Strona internetowa: Wasz przedstawiciel handlowy Nazwisko: Wojciech Krzyżak, Marcin Fiut Firma: AIR MASTER S.C. Adres 1: ul. Magazynowa
Do rąk: Adres 1: Adres 2: Miejscowość: Kod pocztowy: Telefon: email: Strona internetowa: Wasz przedstawiciel handlowy Nazwisko: Wojciech Krzyżak, Marcin Fiut Firma: AIR MASTER S.C. Adres 1: ul. Magazynowa
