Projektowanie elementów sprężonych metodą Magnela
|
|
|
- Jan Jasiński
- 8 lat temu
- Przeglądów:
Transkrypt
1 ROJEKT OSTY BETONOWE ojetoanie elementó spężonh metodą anela. odsta teoetne metod anela.. ojetoanie peoju popeneo dźiaó statnie naalnh W pojetoaniu peoju beli spężonej można odębnić t podstaoe ppadi: a) d mia eometne peoju są nane a posuiana jest siła i mimośód sił spężająej b) d mia eometne peoju są oeślone unji jeo soośi i posuiana jest soość peoju oa siła i mimośód sił spężająej ) d piesm etapie posuiane są eh peoju uoólnioneo (moment beładnośi soość pole peoju lędne położenie śoda iężośi) oa siła i mimośód sił spężająej a duim etapie mia eometne peoju spełniająe eh peoju uoólnioneo. inż. Ksto Ślediesi (.slediesi@pollub.pl)
2 ROJEKT OSTY BETONOWE Najęśiej spotan jest ppade pies. Dot on pede sstim pojetoania mostó płtoh i snoh aóno peaboanh ja i onanh in-situ. oostałe da podejśia oblienioe stosuje się łónie p pojetoaniu ielopęsłoh mostó beloh peaboanh.. T stadia obiążenia Nieależnie od baneo ppadu oblieniah należ ulędnić t stadia obiążenia: Stadium budo obejmująe pede sstim stadium poątoe (spężenie) a taże stadium tanspotu montażu itp. Stadium beużtoe obejmująe oes po aońeniu budo tóm stępują tlo obiążenia stałe Stadium użtoe obejmująe ppade estemalnh obiążeń asie esploataji. W stadium poątom siła spężająa ma najięsa atość a stadiah beużtom użtom pjmuje się że diała już tała siła spężająa mniejsona o stat doaźne i eoloine. Dla stadium poątoeo obiążeniem będie ięża łasn elementu: G Dla stadium beużtoeo obiążenie stałe ośnie o ięża betonu dodan po spężeniu oa ięża elementó posażenia: G+ G W stadium użtom opó iężau stałeo na ustój będie diałało obiążenie użtoe: G+ G+Q 3. Założenia metod Dla nanh miaó peoju popeneo można nać sstie haatesti eometne: - pole peoju - moment beładnośi - położenie śoda iężośi i - saźni inania W W ( W v ; W ) v -anie denia łaśieo W W ( W ; W ) inż. Ksto Ślediesi (.slediesi@pollub.pl)
3 ROJEKT OSTY BETONOWE inż. Ksto Ślediesi 3 o pjęiu sił spężająej i mimośodu spężająeo można nać napężenia sajnh łónah peoju: - stadium poątom d - stadium beużtom d - stadium użtom q d q Dla napężeń pjmuje się następująe atośi anine: i masmalna dopusalna atość napężeń danm stadium i minimalna dopusalna atość napężeń danm stadium. UWG!! W oblieniah pjmujem i e naiem - tó onaa oiąanie. Watośi iąane są e stanem aninm nośnośi spężstej iąu m sił enętne naa się dla obiążeń oblienioh podstaiają: d d Watośi są natomiast iąane e stanem aninm użtoalnośi tóm sił enętne naa się dla obiążeń haatestnh podstaiają: - dla mostó dooh: 5 t - dla mostó olejoh: 5 t - dla sstih odajó mostó onanh sementó:.
4 ROJEKT OSTY BETONOWE inż. Ksto Ślediesi 4 4. Wauni na napężenia sajnh łónah peoju Dla pieseo ppadu oblienioeo tóm posuianmi bł siła spężająa i jej mimośód naam te atośi pestałają pożse o otmują: - stadium poątom W ) ( W ) ( - stadium beużtom W W - stadium użtom q W q W die: - spółnni stat eoloinh.
5 ROJEKT OSTY BETONOWE W płasim uładie spółędnh półpłasna oaniająą ją postą. obsaem oiąań ażdej nieónośi jest Rs.. Obsa dopusalnh oiąań ielośi sił spężająej i mimośodu sił spężająej. Roiąaniem metod anela jest spóln obsa seśiu półpłasn (s. ) tó należ oanić dodatomi aunami. inż. Ksto Ślediesi (.slediesi@pollub.pl) 5
6 ROJEKT OSTY BETONOWE 4.. Waune onstujn Ze lędu na onieność apenienia stali spężająej odpoiedniej otulin należ pożs obsa dodatoo oanić auniem onstujnm: a p min max UWG!! doboe max. dopusalneo mimośodu abli spężająeo max należ pamiętać że oblieniah posłuujem się położeniem ięna padoeo. ięna eiste stępują taże poniżej ięna padoeo. 4.. Waune bepieeństa asoania oment sują ołuje sajnh łónah napężenia oiąająe. o pjęiu uposoneo linioeo oładu napężeń oiąająh estemalną atośią tm aunu ónoai na napężenia nomalne dla sajneo łóna oiąająeo otmuje się: tm W tm W die: jest spółnniiem uplastnienia le pjmoanm 7 ale E jest ón o pestałeniah uładie spółędnh otmujem olejną półpłasnę a oaniająą ją postą: s q tm W inż. Ksto Ślediesi (.slediesi@pollub.pl) 6
7 ROJEKT OSTY BETONOWE 4.3. Waune bepieeństa na nisenie peoju Znisenie peoju spężoneo może bć spoodoane epaniem nośnośi ste oiąanej lub epaniem nośnośi ste śisanej betonu. jmuje się że nisenie nastąpi po asoaniu. Roład sił pedstaion jest na sunu p następująh ałożeniah: - ónomien oład napężeń steie śisanej odpoiada tmałośi betonu - pominieie betonu steie oiąanej - napężenia stali spężająej i bojenioej steie oiąanej odpoiadają tmałośi na oiąanie - napężenia stali bojenioej steie śisanej osiąają tmałość na śisanie. Dla ppadu nisenia e lędu na stal aunu ónoai sił peoju: - sum momentó lędem padoej ste śisanej betonu: - sum utó sił: h a x h a x x R p p p p s s a p p s s p p pominięiu bojenia łeo oa stali spężająej steie śisanej otmujem: S R p p p i p p die: - spółnni spółpa ięna betonem ( dla stunobetonu 75 p bau spółpa) S p - moment statn peoju stali spężająej lędem śoda iężośi ste śisanej betonu inż. Ksto Ślediesi (.slediesi@pollub.pl) 7
8 ROJEKT OSTY BETONOWE S s - moment statn peoju stali bojenioej lędem śoda iężośi ste śisanej betonu. Niespełnienie mou bepieeństa na nisenie e lędu na stal nie maa ani ięsenia peoju betonoeo ani sił spężająej- sta ięsć peój stali spężająej bądź łej. Nie ma atem płu na dobó sił spężająej i mimośodu sił spężająej. Dla ppadu nisenia e lędu na beton sum momentó lędem śoda iężośi oiąanej stali spężająej p pominięiu bojenia łeo i bau stali spężająej steie śisanej otmujem: R S S - moment statn śisanej ste betonu lędem śoda iężośi oiąanej stali spężająej. O ile ppadu nisenia e lędu na stal soość ste śisanej naa się aunu sum utó sił to ppadu nisenia e lędu na beton mam do nienia aniną soośią ste śisanej. Ulędniają to jaiso ó na nośność e lędu na beton można po ilu uposeniah pedstaić następująej postai: i R S S S S p - moment statn użteneo peoju betonoeo lędem śoda iężośi oiąanej stali spężająej. ostatenie: (atość można pbliżeniu pjąć 75). R o ulędnieniu aunu bepieeństa s 3 otmujem: R q s q min o naniesieniu na es sstih pożsh aunó (stan nośnośi spężstej aune bepieeństa na asoanie i na nisenie oa aune onstujn) usuje się ostatenie pole poalająe dobać mimośód i siłę spężająą. ostatenm spadeniu aunó stanu anineo nośnośi spężstej stadium poątom elementó ablobetonoh należ pjąć peój netto (po potąeniu otoó) natomiast dla elementó stunobetonoh dla sstih stadió oa dla elementó ablobetonoh po ainietoaniu anałó ( stadium beużtom i użtom) należ pjąć peój spoadon tj. ulędnieniem stali spężająej i bojenia. inż. Ksto Ślediesi (.slediesi@pollub.pl) 8
9 ROJEKT OSTY BETONOWE 5. lotm pojetoania Dla ustaloneo peoju elementu spężoneo elu apojetoania sił spężająej i mimośodu sił spężająej należ:. Oblić estemalne moment inająe: od obiążeń haatestnh od obiążeń oblienioh.. jąć atośi: tmałośi oblienioh () tmałośi haatestnh () tmałośi haatestnh spółnnia stat eoloinh lobalnh spółnnió bepieeństa s s s3 minimalnej otulin padoeo ięna i stali bojenioej spółnnia uplastnienia spółnnia spółodstałalnośi. 3. Wnać haatesti eometne peoju: ole peoju ołożenie śoda iężośi moment beładnośi saźnii inania W W Ganie denia łaśieo. 4. Wnać obsa seśiu półpłasn podstaiają odpoiednio moment od obiążeń haatestnh () i oblienioh dla ażdej a pa ( ). 5. Wnać półpłasnę ulędniająą aune na asoanie (podstaiają moment od obiążeni haatestnh). 6. Wnać półpłasnę ulędniająą aune bepieeństa na nisenie e lędu na beton (podstaiają moment od obiążeń oblienioh). 7. Nanieść półpłasnę oaniająą minimalną otulinę betonu. 8. Dobać siłę spężająą i mimośód sił spężająej dopusalneo obsau (le dąż się do pjęia masmalneo mimośodu p minimalnej atośi sił spężająej). pjąć mimośód padoej sił spężająej ( min max ) p odtać odpoiadająą pjętemu mimośodoi atość siła po statah oblić siłę spężająą (odotność odtanej es atośi) oblić poątoą siłę spężająą. 9. Oblić potebną poiehnię stali spężająej i libę abli peoju omieseniem spełniająm auni onstujne.. jąć bojenie onstujne e stali łej. inż. Ksto Ślediesi (.slediesi@pollub.pl) 9 p pjąć odaj abli.55 p
1) Cechy geometryczne: bez współpracy przekroju belki (rys. 3.9) i szyny Pole przekroju:
.. Pład licbo Ocenić nośność i stność beli podsunicoej jednopęsłoej o peoju popecnm monosmetcnm spaanm blach: pas gón 00 x 0 pas doln 00 x 0 śodni 0 x 5 sna 50 x 0 połącona pasem gónm ołącnie. Długość
Pręty silnie zakrzywione 1
Pęt silnie akwione. DEFIICJ Pętem silnie akwionm nawam pęt, któego oś jest płaską kwą, a stosunek wmiau pekoju popecnego (leżącego w płascźnie kwin) do pomienia kwin osi ciężkości () pęta spełnia waunek.
Rys. 1. Przekrój konstrukcji wzmacnianej. Pole przekroju zbrojenia głównego: A s = A s1 = 2476 mm 2 Odległość zbrojenia głównego: od włókien dolnych
Spis treśi 1. DANE OGÓNE 3 1.1. OPIS KONSTUKCJI WZACNIANEJ 3 1.. DANE WYJŚCIOWE 3 1.3. CECHY ATEIAŁOWE 3. NOŚNOŚĆ KONSTUKCJI PZED WZOCNIENIE 4 3. ZAKES WZOCNIENIA 5 4. WZOCNIENIE KONSTUKCJI 5 4.1. PZYJĘCIE
Ł Ą Ę Ń ć Ź ź ĘŚ ÓŁ Ę Ę ń ń ź Ę ń Ż ć ć ń ń ń Ę ń Ę ń ń Ę ń Ę ń ń ć ć ń Ę Ą Ś ń Ę Ą Ł ź ć Ś ć ć ć Ź Ł Ś ć ć ć ć ć Ł ć ć ź ń ń ń ń ń ń ń ź ź ć ń ć ć ć ź Ł ń Ę ÓŁ ń ź ź ź ń ć ć ć ń ń ń Ą ń ń ń ń ń Ś Ę
Ą Ą ć Ó Ó Ó Ś Ź Ź Ó ż Ź Ź Ś Ś ż Ę ĘŚ ń ń ć Ś Ą Ę ż ć Ś ć ć Ć Ó Ó ć ć Ó ć Ó ć ć ń ć Ą Ó Ó Ó Ą Ć ń ń Ź Ó ń ć Ó ć ć ć ń ż ć ć Ć Ć ć ż ć Ź Ó ć ć ć ć Ó ć ĘŚ ń ń ż ć Ś ć Ą Ó ń ć ć Ś ć Ę Ć Ę Ó Ó ń ż ź Ó Ó Ś ń
Ó ź ę ę ś Ą Ą Ę Ę Ł ę ę ź Ę ę ę ś ś Ł ę ś ś ę Ą ź ę ś ś ś ś ę ś ę ę ź ę ę ś ę ś ę ę ś Ś ś ę ę ś ś ę ę ę ś ę ę ę ę ś ę ź Ł Ą Ę Ł ę ś ź ść ś ę ę ę ę ę ę ś ś ś ę ę ś ę ę ś ę ź Ć ŚĆ ć ś ś ć ę ś ś ę ś ś ź ś
Temat III Założenia analizy i obliczeń zginanych konstrukcji żelbetowych.
Temat III Założenia analizy i oblizeń zginanyh konstrukji żelbetowyh. 1. Eektywna rozpiętość belek i płyt. omenty podporowe l e l n a 1 a Jeżeli belka lub płyta jest monolityznie połązona z podporami,
Rozciąganie i ściskanie prętów projektowanie 3
Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
TEORIA SPRĘŻYSTOŚCI 10
W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,
Lp Opis obciążenia Obc. char. kn/m 2 f
0,10 0,30 L = 0,50 0,10 H=0,40 OBLICZENIA 6 OBLICZENIA DO PROJEKTU BUDOWLANEGO PRZEBUDOWY SCHODÓW ZEWNĘTRZNYCH, DRZWI WEJŚCIOWYCH SZT. 2 I ZADASZENIA WEJŚCIA GŁÓWNEGO DO BUDYNKU NR 3 JW. 5338 przy ul.
Rozwiązywanie ram płaskich wyznaczanie reakcji i wykresów sił przekrojowych 7
ozwiązwanie ram płaskich wznaczanie reakcji i wkresów sił przekrojowch 7 Obciążenie ram płaskiej, podobnie jak w przpadku beek rozdział 6, mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe
ń ę ń ę ń ę ń ę ę ę ę ę ź ń ź Ś ę Ł ń ę ę ń ę ń ę ę ę ę ę ę ź ę ę Ż ę ŚĆ ę Ż ń ń ę ń ę ę ę ę ę ź ę ę Ś Ś Ś Ś ź ę ń ę ę Ź ń Ś Ś ę ń ę ę ę ę ę ź ń ŚĆ Ś ń ń ń Ą ń ę ę ŚĆ ę Ż ę ń ę ę ę ę ę ź ń Ś Ś ź Ś Ł ę
Obciążenia. Wartość Jednostka Mnożnik [m] oblicz. [kn/m] 1 ciężar [kn/m 2 ]
![Obciążenia. Wartość Jednostka Mnożnik [m] oblicz. [kn/m] 1 ciężar [kn/m 2 ]](/thumbs/48/24910872.jpg "Obciążenia. Wartość Jednostka Mnożnik [m] oblicz. [kn/m] 1 ciężar [kn/m 2 ]")
Projekt: pomnik Wałowa Strona 1 1. obciążenia -pomnik Obciążenia Zestaw 1 nr Rodzaj obciążenia 1 obciążenie wiatrem 2 ciężar pomnika 3 ciężąr cokołu fi 80 Wartość Jednostka Mnożnik [m] obciążenie charakter.
ŁOŻYSKA KULKOWE WZDŁUŻNE JEDNO I DWUKIERUNKOWE
KULKOWE WZDŁUŻNE JEDNO I DWUKIERUNKOWE KULKOWE WZDŁUŻNE JEDNO I DWUKIERUNKOWE Ze względu na konstrukcję, łożyska kulkowe wzdłużne są podzielone na jedno i dwukierunkowe. Łożyska wzdłużne jednokierunkowe
ć Ó ć Ź ć ć ć ć ć ć Ś Ą ć ź Ź ć Ź Ź ć ć ć Ą Ź ĄĄ ć ź ć ć ć ć ć ć Ą ź Ó ć ć ć ć ć ć ć Ą ć ź ć ć ć Ś Ą ź ć Ó ć ć ć Ł ć ć Ą ć ć Ą Ó ć ć ć ć ź ć ć ć ć ć ć Ść ć ć Ó ć Ę ć ć ÓĄ Ś ć ć ć Ą ć ć Ź ź Ś ć Ź ć ć ć
Atom wodoru. -13.6eV. Seria Lymana. od 91 nm to 122 nm. n = 2, 3,... Seria Paschena n = 4, 5,... n = 5, 6,... Seria Bracketta.
Atom wodou -3.6eV Seia Lmana n 2, 3,... od 9 nm to 22 nm Seia Paschena n 4, 5,... Seia Backetta n 5, 6,... Ogólnie: n 2, 2, 3; n (n 2 + ), (n 2 + 2),... Atom wodou We współędnch sfecnch: metoda odielania
KONSTRUKCJE BETONOWE PROJEKT ŻELBETOWEJ HALI SŁUPOWO-RYGLOWEJ
KONSTRUKCJE BETONOWE PROJEKT ŻELBETOWEJ HALI PRZEMYSŁOWEJ O KONSTRUKCJI SŁUPOWO-RYGLOWEJ SŁUP - PROJEKTOWANIE ZAŁOŻENIA Słup: szerokość b wysokość h długość L ZAŁOŻENIA Słup: wartości obliczeniowe moment
Wewnętrzny stan bryły
Stany graniczne Wewnętrzny stan bryły Bryła (konstrukcja) jest w równowadze, jeżeli oddziaływania zewnętrzne i reakcje się równoważą. P α q P P Jednak drugim warunkiem równowagi jest przeniesienie przez
Rozwiązywanie belek prostych i przegubowych wyznaczanie reakcji i wykresów sił przekrojowych 6
ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch 6 Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs. 6.. s. 6. rzed przstąpieniem
PRAWA ZACHOWANIA Prawa zachowania najbardziej fundamentalne prawa:
PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
( ) O k k k. A k. P k. r k. M O r 1. -P n W. P 1 P k. Rys. 3.21. Redukcja dowolnego przestrzennego układu sił
3.7.. Reducja dowolego uładu sił do sił i par sił Dowolm uładem sił będiem awać uład sił o liiach diałaia dowolie romiescoch w prestrei. tm pucie ajmiem się sprowadeiem (reducją) taiego uładu sił do ajprostsej
τ R2 := 0.32MPa τ b1_max := 3.75MPa E b1 := 30.0GPa τ b2_max := 4.43MPa E b2 := 34.6GPa
10.6 WYMIAROWANE PRZEKROJÓW 10.6.1. DANE DO WMIAROWANIA Beton istniejącej konstrukcji betonowej klasy B5 dla którego: - wytrzymałość obliczeniowa na ściskanie (wg. PN-91/S-1004 dla betonu B5) - wytrzymałość
OBLICZENIE ZARYSOWANIA
SPRAWDZENIE SG UŻYTKOWALNOŚCI (ZARYSOWANIA I UGIĘCIA) METODAMI DOKŁADNYMI, OMÓWIENIE PROCEDURY OBLICZANIA SZEROKOŚCI RYS ORAZ STRZAŁKI UGIĘCIA PRZYKŁAD OBLICZENIOWY. ZAJĘCIA 9 PODSTAWY PROJEKTOWANIA KONSTRUKCJI
GEOMETRIA ANALITYCZNA W PRZESTRZENI
GEOMETRIA ANALITYCZNA W PRZESTRZENI Współęde postoąte De są t osie OX OY OZ wjemie postopdłe peijąe się w puie O. Oiem pewie odie jo jedostow i om pe współęde putów odpowiedih osih. DEFINICJA Postoątm
Projekt z konstrukcji żelbetowych.
ŁUKASZ URYCH 1 Projekt z konstrukcji żelbetowych. Wymiary elwmentów: Element h b Strop h f := 0.1m Żebro h z := 0.4m b z := 0.m Podciąg h p := 0.55m b p := 0.3m Rozplanowanie: Element Rozpiętość Żebro
e = 1/3xH = 1,96/3 = 0,65 m Dla B20 i stali St0S h = 15 cm h 0 = 12 cm 958 1,00 0,12 F a = 0,0029x100x12 = 3,48 cm 2
OBLICZENIA STATYCZNE POZ.1.1 ŚCIANA PODŁUŻNA BASENU. Projektuje się baseny żelbetowe z betonu B20 zbrojone stalą St0S. Grubość ściany 12 cm. Z = 0,5x10,00x1,96 2 x1,1 = 21,13 kn e = 1/3xH = 1,96/3 = 0,65
Wykład 4. Zasada zachowania energii. Siły zachowawcze i niezachowawcze
Wład 4 Zasada achowania enegii Sił achowawce i nieachowawce Wsstie istniejące sił możem podielić na sił achowawce i sił nie achowawce. Siła jest achowawca jeżeli paca tóą wonuję ta siła nad puntem mateialnm
- ---Ą
Ą ż ą ą ą Ą ó ą ł ą ł Ąą ż ś Ę ÓŁ Ę Ó ŁĄ ŁŚĆ ł ż ł ż ó ł Ó Ć Ą Ł ŁÓ ŁŚ Ą ż Ó ŁÓ Ę ś ś ł ż ł Ą ęś Ą ń ź ć ą ą ę ń ż ąń ę ę ć óź ŁĄ ą ł ę ę ł ę ń Ą Ęł ą Ł ł ł ż ó ą ł ęę ĘĘ ęć ó ą ń ł ą Ą ęś ł ś ÓŁ Ą ę ę
1/k Obliczenia statyczne.
/k Obliczenia statyczne. 48,0 8,7 94, 94, 94, A 0,0,4 4,9 4,9 4,9 78,7 798, B,0 0 7, 8,8 00,0 680,0 00,0 9,0 DANE: Szkic wiązaa A 0,0,4 48,0 8,7 94, 94, 94, 4,9 4,9 4,9 78,7 798, 00,0 680,0 00,0 9,0 B,0
1.11. RÓWNANIE RÓŻNICZKOWE OSI UGIĘTEJ
.. RÓWNANIE RÓŻNICZKOWE OSI UGIĘTEJ od płem obciążenia prostolinioa oś podłużna belki staje się krzolinioa. Zakrzioną oś belki nazam linią ugięcia (osią ugiętą), przemieszczenie pionoe ( x) tej osi nazam
Hufce 2.3. Podanie do wiadomości wyników wyborów
C h o r ą g i e w D o l n o l ą s k a Z H P W r o c ł a w, 3 1 g r u d z i e 2 0 1 5 r. Z w i ą z e k H a r c e r s t w a P o l s k i e g o K o m e n d a n t C h o r ą g w i D o l n o 6 l ą s k i e j Z
EKSPERTYZA TECHNICZNA-KONSTRUKCYJNA stanu konstrukcji i elementów budynku
EKSPERTYZA TECHNICZNA-KONSTRUKCYJNA stanu konstrukcji i elementów budynku TEMAT MODERNIZACJA POMIESZCZENIA RTG INWESTOR JEDNOSTKA PROJEKTOWA SAMODZIELNY PUBLICZNY ZESPÓŁ OPIEKI ZDROWOTNEJ 32-100 PROSZOWICE,
3. 4 n a k r ę t k i M k o r p u s m i s a n a w o d ę m i s a n a w ę g i e l 6. 4 n o g i
M G 5 0 4 W Ę D Z A R K A M G 5 0 4 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z E Ń S T W A S z a n o w n i P a s t w o, D z i ę k u j e m y z a z a k u p p r o d u k t u M a s t e r G r i l l
Ż ć Ó Ś Ó ć Ę Ó Ś ź Ż Ż Ó Ż ź Ó ÓŚ Ć Ó ź Ó ź Ó Ź ć Ę Ó Ś Ż Ó Ó Ń Ą ź ź Ź Ś Ą Ą Ś Ą Ś ć ć ź ź Ó Ó Ę Ź Ą Ź Ę ĘŚ ć ź Ę Ę ź Ę ć Ś Ś Ę Ż Ż ć Ść ć ć Ń Ż Ś ć Ż Ż Ż Ż Ż Ó Ą Ę Ę Ę Ą Ż Ż Ż Ź Ż ć Ś Ż Ż Ż Ż Ż ć Ś
ó ą ę ó ó Ż ć ó ó ó ę Ó ó ą ć ę ó ą ę ż Ó Ń ą ą ę ó Ę ó Ą ć ę ó ą ą ę ó
Ą ę ć Ą ą ą ą ż ż ó ą ż ć ą ą ć ż ć ó ó ą ó ą ń ą ę ą ę ż ń ą ó ą ą ą ą ą ą ą ó ż Ś ę ą ę ą ą ż ĘŚ ż ń ę ę ą ó ż ą Ą Ź ń Ó ą ą ó ą ę ó ą ę ó ó Ż ć ó ó ó ę Ó ó ą ć ę ó ą ę ż Ó Ń ą ą ę ó Ę ó Ą ć ę ó ą ą
ń Ę Ę Ę Ę ń ń Ś ź Ę ś ś Ę Ś Ą Ę Ę Ę Ę Ż Ę Ę ść Ą Ł Ę Ć ć Ś Ę Ę ś Ę Ż Ś Ę Ę ń Ż Ę Ć ź ć Ł ś Ę ś Ż ś Ś ś Ę ć Ł ś Ż ŚĆ Ę ń ŚĆ ść ś ś ń ś Ś ś ś Ęś Ę ć ś ść ń ń Ć ś Ą ń ć Ą Ś ń ś ś ć ć ś źć ć ź ś ń Ę ś Ę ć
G:\WYKLAD IIIBC 2001\FIN2001\Ruch falowy2001.doc. Drgania i fale II rok Fizyki BC
3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ruh falow: Fala rohodąe się w presreni aburenie lub odsałenie (pole). - impuls lub drgania. Jeśli rohodi się prędośią o po asie : ( r)
ń ń ć ń Ź ć ń ć Ź ń Ź ź ć Ę ć Ź ć ź ń ń ź
ń ń Ę Ó Ń Ł ń Ł Ó Ł Ść ń ć Ś Ó ń ń ń ń Ź ć ć ń ń ć ń Ź ć ń ć Ź ń Ź ź ć Ę ć Ź ć ź ń ń ź ć ć ń ń ń ń ń ć ć ń Ź ń Ź ń ń ź ń Ł ć ź ź ź ź ń ć Ź ć ń ń ń ń ź ń ć ń ń ń ń ń ć ń ń ń ć ź ń ć ź Ź ń ń Ę ź Ć ź ć ć
WYCIĄG Z OBLICZEŃ STATYCZNO - WYTRZYMAŁOŚCIOWYCH
WYCIĄG Z OBLICZEŃ STATYCZNO - WYTRZYMAŁOŚCIOWYCH Betonowe mury oporowe w km 296+806-297,707 1. PODSTAWA OBLICZEŃ [1] - PN-85/S-10030 Obiekty mostowe. Obciążenia. [2] - PN-91/S-10042 Obiekty mostowe. Konstrukcje
Nośność przekroju pala żelbetowego 400x400mm wg PN-EN 1992 (EC2) Beton C40/50, stal zbrojeniowa f yk =500MPa, 12#12mm
Nośność przekroju pala żelbetowego 400400mm wg PN-EN 199 (EC) Beton C40/50, stal zbrojeniowa =500MPa, 1#1mm 5000 Czyste śiskanie bez wybozenia (4476kN, 0kNm) Śiskanie mimośrodowe =d 1 (3007kN, 08kNm) Siła
Opracowanie: Emilia Inczewska 1
Dla żelbetowej belki wykonanej z betonu klasy C20/25 ( αcc=1,0), o schemacie statycznym i obciążeniu jak na rysunku poniżej: należy wykonać: 1. Wykres momentów- z pominięciem ciężaru własnego belki- dla
Ó Ż ź Ó Ą Ż Ó ń ń ć ć ĘŚ Ś ŚĆ Ę ć ć ć ć Ś Ź ń ź ŚĆ ń Ś ź ć ć Ó ć ć ź ć ć ć ń ń Ł ć ź ć ń Ś ć ć ć Ł Ę Ś Ł Ę Ł ć ń ć Ś ź Ć Ś Ś ć ź Ó ź ć ć Ś ń ź Ś ź Ó Ś Ó Ś Ś ń Ś Ś ć ć ń ć ć Ż Ś ć ń ń Ł Ł ń ć ź ć ć Ó ć
Ruch kulisty bryły. Kinematyka
Ruch kulist bł. Kinematka Ruchem kulistm nawam uch, w casie któego jeden punktów bł jest stale nieuchom. Ruch kulist jest obotem dookoła chwilowej osi obotu (oś ta mienia swoje położenie w casie). a) b)
Ś ś Ł ń ń ś ś Ś ś Ę ę ś ę ś ĘŚ ś Ęś ę ĘŚĆ ĘŚ Ęś ĘŚ ĘŚ ę ĘŚĆ ĘŚĆ ĘŚĆ ĘŚĆ Ęś ĘŚĆ ĘŚ ĘŚĆ ń ĘŚĆ ĘŚ ĘŚĆ ę ĘŚ ś Ęś ń ś ś ś ę ź ę ś ę ś Ź ń ę ń ś ń ń ę ń ń ń ń Ę ś ń ęś ń ń ń ę ń Ż ś ń ń ę ń ś ń ń ń ę ś ń ś Ż
Ą ć ę ż ż Ż ć ć Ż ć ń ę ę Ż ń ż ęż ę ę Ę ż ż ĘŚ ę Ż Ż Ż Ż Ż Ż Ż Ż ż ż ń ę ęż ęż Ó ęź Ą ń ę Ś Ż ć ę Ą ę ż ę ż ć ę ę Ż ę ż ż ę ń ń ę Ą ż ę Ł Ą ę ż ę Ą ę ę Ę Ą ę ę ęć ż Ę ęż ż ę Ą Ę ę ę Ą ę ę Ą Ą Ż ć ć Ń
WłAśCIWOśCI ZASTOSOWANIE. Technical data sheet BSD - WIESZAK BELKI SPECJALNY
Wieszaki belki BSD przeznaczone są do elementów o większym przekroju. Produkt standardowy umożliwia montaż w połączeniu drewnodrewno przy pomocy\ gwoździ CNA lub wkrętów CSA. Aprobata techniczna dopuszcza
TYP X. Podstawa słupa krzyżowa Stal węglowa ocynkowana ogniowo TYP X - 01 USZTYWNIONY INNOWACYJNY DWIE WERSJE WSZECHSTRONNY ZASTOSOWANIE
TYP X Podstawa słupa krzyżowa Stal węglowa ocynkowana ogniowo USZTYWNIONY Wytrzymały na moment zginający dzięki wpuszczeniu metalowego elementu oporowego w nacięcia trzpienia słupa ZASTOSOWANIE Do połączeń
Sterowanie obiektu wysokiego rzędu z wykorzystaniem regulatora redukcyjnego
Pomiay Automatya Robotya 7-8/00 Steoanie obietu ysoiego zędu z yozystaniem egulatoa eduyjnego Kzysztof Opzędieiz W pay pzedstaiono popozyję syntezy egulatoa eduyjnego obietu ysoiego zędu, opisanego tansmitanją
Wektor położenia. Zajęcia uzupełniające. Mgr Kamila Rudź, Podstawy Fizyki. http://kepler.am.gdynia.pl/~karudz
Kartezjański układ współrzędnych: Wersory osi: e x x i e y y j e z z k r - wektor o współrzędnych [ x 0, y 0, z 0 ] Wektor położenia: r t =[ x t, y t,z t ] każda współrzędna zmienia się w czasie. r t =
Ż Ę ź Ó
ź ź Ę Ą Ż Ę ź Ó Ź Ó ź Ę ź Ę Ę Ą Ź Ą Ń Ź Ź Ź Ź ź Ą ź Ę Ą Ć ź ź ź Ę ź Ź ź ź Ę Ł ź Ź Ź Ź ź ź Ź Ź ź ź Ą Ł Ó Ó Ą Ą Ś Ę Ę Ą Ą Ś Ś Ł Ę Ę ź ź Ó Ą Ą Ą Ł Ą Ę Ź Ę ź ź Ę Ą Ź Ź ź Ł Ą Ł Ą ź Ą ź Ł Ą Ó ĘŚ Ą Ę Ę ź Ź Ę
ń Ó Ń ś ń ś ń Ó ę ą Ż ę ą ę Ż ó Ę ą ą ę ś Ę ó Ż ę Ó
ć ń ó ą ś ą ą ż ó ó ą ż ó ś ą ś ą ś ć ż ść ó ó ą ó ą ń ą ę ą ę ż ń ą ó ś ą ą ą ń ó ą ą ą ś ą ó ż ś ęż ęś ś ń ą ęś ś ą ą ś ż ś Ę ę ń Ż ą ż ń ą ą ą ę ą ę ń Ó Ń ś ń ś ń Ó ę ą Ż ę ą ę Ż ó Ę ą ą ę ś Ę ó Ż ę
SCENARIUSZ ZAJĘĆ KOŁA NAUKOWEGO z MATEMATYKI. prowadzonego w ramach projektu Uczeń OnLine
rojekt Uczeń online współfinansowany ze środków Unii Europejskiej w ramach Europejskiego unduszu Społecznego SCENARIUSZ ZAJĘĆ KOŁA NAUKOWEGO z MATEMATYKI 1. Autor: Anna Wołoszyn prowadzonego w ramach projektu
DANE OGÓLNE PROJEKTU
1. Metryka projektu Projekt:, Pozycja: Posadowienie hali Projektant:, Komentarz: Data ostatniej aktualizacji danych: 2016-07-04 Poziom odniesienia: P 0 = +0,00 m npm. DANE OGÓLNE PROJEKTU 15 10 1 5 6 7
LISTA OBECNOŚCI EGZAMINY USTNE JĘZYK WŁOSKI B2/C1 9.03.2015 R. PWP Kształcenie zawodowe na neofilologiach KUL na potrzeby rynku pracy
JĘZYK WŁOSKI B2/C1 9.03.2015 R. 8 14.00-14.50 9 14.30-15.20 10 15.00-15.50 JĘZYK WŁOSKI B2/C1 10.03.2015 R. 8 14.00-14.50 9 14.30-15.20 10 15.00-15.50 JĘZYK WŁOSKI B2/C1 14.03.2015 R. 1 8.30-9.20 2 9.00-9.50
Malowanki wiejskie. OB OKI / agodne ręce lata. œ œ œ # œ œ. œ œ œ # œœ œ œ. œ œ œ œ. j œ œ œ # œ œ œ. j œ. & œ # œ œ œ œ œœ. œ & œ i. œ i I. œ # œ.
Maloanki ieskie na sopan lu mezzo-sopan z fotepianem Rok postania: 1990 aykonanie: aszaska siedzia ZAiKS-u, 1991 OB OKI / agodne ęe lata Muzyka: ezy Baue S oa: Kazimiea I akoizóna iano q = a (uato) I i
Zginanie belek o przekroju prostokątnym i dwuteowym naprężenia normalne i styczne, projektowanie 8
Zinanie belek o przekroju prostokątnm i dwuteowm naprężenia normalne i stczne, projektowanie 8 Na rs. 8.1 przedstawiono belkę obciążoną momentami zinającmi w płaszczźnie x. oment nąceo dla tak obciążonej
GTR W SP A19 ŁĄCZNIKI Z PODKŁADKĄ DO MOCOWANIA PŁYT WARSTWOWYCH
GTR W SP A19 ŁĄCZNIKI Z PODKŁADKĄ DO MOCOWANIA PŁYT WARSTWOWYCH OPIS PRODUKTU Łączniki samogwintujące (dwugwintowe) ze stali węglowej utwardzanej powierzchniowo, z punktem wiercącym do drewna, gwintem
Ł Ż Ó Ź ĘŚ Ą Ń Ł Ą Ł ĘŚ Ę Ł Ż Ż Ż Ń Ł Ó Ą Ż Ś ć Ś ć ć Ź Ś ć ć Ó ż Ó Ó Ź Ó Ś ŚÓ ż Ś ć ć Ś Ś ż Ó Ć Ś Ś ŚÓ Ś ć ć Ś Ś Ś ć ć Ś Ę Ś Ó Ś Ó Ś Ż Ś Ść ź Ś ć Ó Ś Ć Ó Ś Ść Ó ć Ę ć Ś Ś Ę Ó Ó Ź Ź Ó ż ć ć ć ć ć ć ż ć
Projekt belki zespolonej
Pomoce dydaktyczne: - norma PN-EN 1994-1-1 Projektowanie zespolonych konstrukcji stalowo-betonowych. Reguły ogólne i reguły dla budynków. - norma PN-EN 199-1-1 Projektowanie konstrukcji z betonu. Reguły
ż ń Ś Ó ó Ą Ą ó ż Ó ż ć Ś ż ć ó ó ó ń ń ń ó Ę Ś ó Ś Ś ń ó ĘŚ ż Ę Ś ó ż Ś ż ż ń ż ń ó ż ń Ń ń ń Ą ń ó ó ń ć Ń ć ó Ę ż ó ó ó ż ń Ą ó ó ż ń ń ó ż ó ż ó ó Ś ó ó ó ć ć ż Ę ń ó Ń Ń ń ż ż ĘŚ ń óź ż ż ń ó ń ó
Ę Ś ę ł ł ęł ś ę ń ł ń ść ń ę ś ś ś ł ś ę ł ć ń ę ł ś ń ę ś ć ł ś ś ć ł ń ń Ę ł ę ł ę ś ę ś ł ść ś ł ł ę ę ć ś ć ł ł Ść ść ł ść Ę ę ć ł ć ł ś ł ł ć ł ł ś ł ść ł ś ń ń ń ń ę ę ś ć ł ś ę ń ę ś ś ę ł ł ś
Ćwiczenie nr 2. obliczeniowa wytrzymałość betonu na ściskanie = (3.15)
Ćwiczenie nr 2 Temat: Wymiarowanie zbrojenia ze względu na moment zginający. 1. Cechy betonu i stali Beton zwykły C../.. wpisujemy zadaną w karcie projektowej klasę betonu charakterystyczna wytrzymałość
Rozwiązywanie belek prostych i przegubowych wyznaczanie reakcji i wykresów sił przekrojowych 4-5
ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch - Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs... s.. rzed przstąpieniem
Przykład: Nośność podstawy słupa ściskanego osiowo. Dane. Sprawdzenie wytrzymałości betonu na ściskanie. α cc = 1,0.
Dokument Ref: Str. 1 z 4 Example: Column base onnetion under axial ompression śiskanego osiowo Dot. Euroodu EN 1993-1-8 Wykonał Ivor RYAN Data Jan 006 Sprawdził Alain BUREAU Data Jan 006 Przykład: Nośność
Ó ń ń ń ŚĆ ń Ą ń ź Ć ć ń ć ź ĘŚ Ó Ł Ą ń ŚĆ ź ć Ść ć Ś ć ź ź ń ź ŚĆ ń ź ć ć ć Ó ń Ę ń ć ń ć ć ń ń ń ń ć ć ń ź ć ć ń ń ć ń ń ć Ą ć ć ń ź ń ń ź Ź ć Ó Ł Ę Ł ć ń ń ć ć ć ń ć Ę ć ć ń ć Ć ć ć ć Ś ć ń ć ć ź ń
Jolanta i Tymoteusz Klaudia i Sylwester
O F E R T A W E S E L N A O F E R U J E M YA A W y k w i n t n e m e n u z b o g a c t w e m d a P g L [ w n y c h o r a z z i m n y c h p r z e k H s e k A P r o f e s j o n a l n H o b s L u g g k e
Praktyczne aspekty wymiarowania belek żelbetowych podwójnie zbrojonych w świetle PN-EN
Budownictwo i Architektura 12(4) (2013) 219-224 Praktyczne aspekty wymiarowania belek żelbetowych podwójnie zbrojonych w świetle PN-EN 1992-1-1 Politechnika Lubelska, Wydział Budownictwa i Architektury,
Wyniki wymiarowania elementu żelbetowego wg PN-B-03264:2002
Wyniki ymiaroania elementu żelbetoego g PN-B-0364:00 RM_Zelb v. 6.3 Cechy przekroju: zadanie Żelbet, pręt nr, przekrój: x a=,5 m, x b=3,75 m Wymiary przekroju [cm]: h=78,8, b =35,0, b e=00,0, h =0,0, skosy:
mr1 Klasa betonu Klasa stali Otulina [cm] 4.00 Średnica prętów zbrojeniowych ściany φ 1 [mm] 12.0 Średnica prętów zbrojeniowych podstawy φ 2
![mr1 Klasa betonu Klasa stali Otulina [cm] 4.00 Średnica prętów zbrojeniowych ściany φ 1 [mm] 12.0 Średnica prętów zbrojeniowych podstawy φ 2](/thumbs/39/19116172.jpg "mr1 Klasa betonu Klasa stali Otulina [cm] 4.00 Średnica prętów zbrojeniowych ściany φ 1 [mm] 12.0 Średnica prętów zbrojeniowych podstawy φ 2")
4. mur oporowy Geometria mr1 Wysokość ściany H [m] 2.50 Szerokość ściany B [m] 2.00 Długość ściany L [m] 10.00 Grubość górna ściany B 5 [m] 0.20 Grubość dolna ściany B 2 [m] 0.24 Minimalna głębokość posadowienia
7/S5. Klapy przeciwpożarowe FD40. www.klimaoprema.pl
7/S5 Klapy przeciwpożarowe FD40 386 www.klimaoprema.pl 7/S5 v 2.5 (en) Klapy przeciwpożarowe FD40 www.klimaoprema.pl 387 Klapy - FD40 Klapy przeciwpożarowe, typ FD 40 Instalowane w przegrodach miedzy strefami
Schöck Isokorb typu K-Eck
1. Warstwa (składający się z dwóch części: 1 warstwy i 2 warstwy) Spis treści Strona Ułożenie elementów/wskazówki 62 Tabele nośności 63-64 Ułożenie zbrojenia Schöck Isokorb typu K20-Eck-CV30 65 Ułożenie
Parametry geotechniczne gruntów ustalono na podstawie Metody B Piasek średni Stopień zagęszczenia gruntu niespoistego: I D = 0,7.
.11 Fundamenty.11.1 Określenie parametrów geotechnicznych podłoża Rys.93. Schemat obliczeniowy dla ławy Parametry geotechniczne gruntów ustalono na podstawie Metody B Piasek średni Stopień zagęszczenia
ń ń ś ń ę ę Ś ę Ż ę ę ś ń ę ż ń ęś ę ż ń ń Ą Ę ś ś ś ż Ż ś Ś ś ę ś Ś
ę ę Ą Ą ń Ó ś ś ś ń ń Ż ń Ą Ż śó ŚĆ ś ę ę ś ś ś Ż ś ść ń Ż Ś ń ń ś ń ę ę Ś ę Ż ę ę ś ń ę ż ń ęś ę ż ń ń Ą Ę ś ś ś ż Ż ś Ś ś ę ś Ś ę ę ś ń Ż Ż Ż ę ś ć Ą Ż Ż ś Ś Ą Ż ś Ś Ą Ż ś ś ś Ę Ą ę ń ś ę ż Ż ć Ś ń ę
Schöck Isokorb typu V
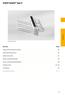Schöck Isokorb typu Schöck Isokorb typu Spis treści Strona Przykłady ułożenia elementów i przekroje 100 Tabele nośności/rzuty poziome 101 Przykłady zastosowania 102 Zbrojenie na budowie/wskazówki 103 Rozstaw
BIURO ARCHITEKTONICZNO - KONSERWATORSKIE A R C H I T E K C I G Z O W S K I & G Z O W S K I s.c.
Studia magisterskie ENERGETYKA. Jan A. Szantyr. Wybrane zagadnienia z mechaniki płynów. Ćwiczenia 2. Wyznaczanie reakcji hydrodynamicznych I
Studia magisteskie ENERGETYK Jan. Szanty Wybane zagadnienia z mehaniki płynów Ćwizenia Wyznazanie eakji hydodynamiznyh I Pzykład 1 Z dyszy o śedniah =80 [mm] i d=0 [mm] wypływa woda ze śednią pędkośią
OPIS PRODUKTU ZASTOSOWANIE SPOSÓB MONTAŻU DOSTĘPNOŚĆ ZGODNOŚĆ. TRANSPORT i PRZECHOWYWANIE ALFA FR BOARD A TDS EW
OPIS PRODUKTU Płyta ogniochronna ALFA FR BOARD A składa się z płyty z wełny mineralnej o gęstości 150kg/m 3 i grubości 60mm pokrytej jednostronnie powłoką z farby ablacyjnej ALFA FR COAT A o grubości warstwy
KARTA TECHNICZNA PRODUKTU WCF-EASF/WCF-EASF-E/WCF-EASF-C
Sekcja 1. OPIS PRODUKTU KOTWA INIEKCYJNA METAKRYLANOWA WCF-EASF/WCF-EASF-E/WCF-EASF-C Metakrylanowa dwuskładnikowa 1:10 kotwa iniekcyjna bez styrenu. Dedykowana dla profesjonalistów do odpowiedzialnych