Optymalizacja efektywności hamowania odzyskowego w transporcie szynowym przez sterowanie czasem przyjazdu na stację
|
|
|
- Sylwia Jabłońska
- 6 lat temu
- Przeglądów:
Transkrypt
1 PROLEMY KOLEJNICTWA RAILWAY REPORT Zeszy 18 (wrzesień 18) ISSN (druk) ISSN (on-line) 61 Opymlizcj efekywności hmowni odzyskowego w rnsporcie szynowym przez serownie czsem przyjzdu n scję Michł URANIAK 1 Ew KARDAS-CINAL Sreszczenie Arykuł nwiązuje do poprzednich prc uorów w kórych przedswiono model orgnizcji ruchu kooperujących pociągów z uwzględnieniem opymlizcji wykorzysni energii zwrcnej do sieci jezdnej. W przedswionym rykule zmodyfikowno model zmienijąc główną zmienną serującą mjącą wpływ n efekywne wykorzysnie energii z czsu odjzdu n czs przyjzdu pociągu n scję lu przysnek. Opymlizcj jes dokonywn przez serownie czsem przyjzdu n scję w dopuszczlnym (rozkłdowym) jego zkresie i przy zchowniu rozkłdowego czsu odjzdu z wykorzysniem meody równego podziłu (isekcji) do osiągnięci opymlnego rozwiązni. Zmodyfikowną meodę opymlizcji zimplemenowno w uorskim modelu orgnizcji ruchu kolejowego. Uwzględniono w nim opymlne wykorzysnie energii odzysknej podczs hmowni elekrodynmicznego przy zsosowniu sregii przesyłu energii do sieci jezdnej zkłdjąc koopercję pry pociągów cłkowią wielkość energii możliwej do odzyskni orz czs posoju n scji. Słow kluczowe: rnspor szynowy hmownie odzyskowe opymlizcj rekupercji energii orgnizcj ruchu 1. Wsęp Porze opymlizcji efekywności hmowni odzyskowego w rnsporcie szynowym jes wynikiem isniejących prolemów rnsporowych j. konieczności ogrniczeni koszów przewozu przy jednoczesnym zchowniu dopuszczlnych sndrdów ogrniczeni emisji znieczyszczeń przy zchowniu wymgnej łdowności orz wzroście zporzeowni n usługi rnsporowe. Poz rcjonlizcją prcujących pociągów [1] konieczne jes wprowdzenie nowoczesnych orz ekologicznych echnologii zgodnych z dokumenmi pulikownymi przez insyucje krjowe orz Unię Europejską [19]. Jednym ze sposoów n ogrniczenie pooru energii w rnsporcie kolejowym ym smym zmniejszenie koszów (w ym środowiskowych) jes zsosownie echnologii rekupercji w celu odzyskni części prądu w czsie hmowni elekrodynmicznego. Odzyskn w en sposó energi może yć ponownie uży i w efekcie może pomóc poprwić ilns energii nie ylko pojedynczego przejzdu le kże cłego sysemu rnsporu szynowego. Spośród różnych sposoów wykorzysni energii pochodzącej z hmowni odzyskowego możn wyróżnić nsępujące meody [8 3 4]: 1) wykorzysnie energii ezpośrednio w pociągch do porze nierkcyjnych j. oświeleni klimyzcji ) przechowywnie jej w scjonrnych lu pokłdowych mgzynch energii nsępnie użycie w czsie zwiększonego zporzeowni [3 14]. 3) przekznie odzysknej energii do krjowej sieci energeycznej [1 13 5] 4) przekznie odzysknej energii do sieci rkcyjnej co umożliwi ezpośrednie jej użycie przez inny pojzd w fzie przyspieszni [ ] lu urzymnie prwidłowego poziomu npięci w sieci. Kżd z wymienionych meod m swoje wdy i zley [8 3] nleży jednk zuwżyć że ylko ezpośrednie wykorzysnie odzysknej energii pomijjące proces mgzynowni lu zminy prądu z DC n AC (syucj konieczn w polskim sysemie zsilni) nie wymg ponoszeni dodkowych koszów infrsrukurlnych. Zrówno użycie energii z hmowni odzyskowego do celów nierkcyjnych 1 Mgr inż. dokorn Poliechniki Wrszwskiej Wydził Trnsporu; sysen Poliechnik Gdńsk Wydził Inżynierii Lądowej i Środowisk; e-mil: michl.urnik@pg.edu.pl. Dr h. inż. prof. PW; Poliechnik Wrszwsk Wydził Trnsporu.
2 6 Urnik M. Krds-Cinl E. pojzdu jk i zwrcnie odzysknej energii do sieci jezdnej w wrunkch energeycznej koopercji kilku pojzdów możn nzwć meodmi ezkoszowymi. Użycie odzysknej energii do nierkcyjnych porze pociągu nie wymg dodkowej ingerencji w proces echniczny lu orgnizcyjny. Zwrócenie odzysknej energii z powroem do sieci jezdnej i wykorzysnie jej przez inne pociągi zleży od koordyncji rozkłdu jzdy pociągów orz nężeni ruchu.. Model koopercji pociągów z uwzględnieniem rekupercji energii Opisny model zkłd że przy dnym i oowiązującym rozkłdzie jzdy ędzie możliwe przekznie energii z rekupercji hmującego pociągu (pojzd ) przez sieć jezdną do innego pojzdu kóry wyjeżdż ze scji (pojzd A). Doprowdzi o do ogrniczeni zporzeowni n energię przekzywną z podscji rkcyjnej w czsie rozruchu (rys. 1). Ilość odzysknej orz użyej w en sposó energii ędzie zleżeć od czsu odjzdu pociągu w zkresie dopuszczlnym przez rozkłd. Odzysk orz wykorzysnie energii z hmowni elekrodynmicznego wymg współprcy co njmniej pry pojzdów i jes możliwe przede wszyskim n scjch lu przysnkch gdzie wysępuje njwiększe nężenie i powrzlność procesów rozruchu i hmowni pociągów [9 1]. Idelną syucją yłoy gdyy przyspiesznie orz hmownie pry kooperujących pojzdów poruszjących się w przeciwnych kierunkch miło miejsce n kżdej scji lu przysnku dnej linii kolejowej (rys. ). W prkyce o złożenie jes niesey rdzo wymgjące i możn je wprowdzić jedynie w perfekcyjnie funkcjonujących sysemch mer (gdzie nie wysępują nwe minimlne opóźnieni). Z ego powodu proponowny model zkłd możliwość energeycznej koopercji jedynie n pojedynczych scjch orz przysnkch. Podswy modelowni jzdy pojzdów szynowych opisno już między innymi w prcch J. Podoskiego i innych uorów [17 18] niemniej modele oliczeniowe są sle modyfikowne orz doprcowywne przez różnych nukowców w zleżności od ndrzędnego celu kóry m yć osiągnięy. Model eoreycznego przejzdu w głównej mierze sprowdz się do rozwiązni równni ruchu pojzdu kolejowego (równnie Newon) gdzie pociąg jes rkowny jko punk merilny o msie m. Możn je sformułowć w nsępujący sposó [ 1 4]: dv km u RsvRg( x) d dx v () d (1) Rys. 1. Wykorzysnie odzysknej energii serownie czsem przyjzdu pociągu; oprcownie włsne n podswie [ 1 4] gdzie: sił u() dziłjąc n pojzd jes siłą rozruchu u = F() lu siłą hmowni u = F() w zleżności od fzy ruchu zś współczynnik k uwzględni momeny ezwłdności ms wirujących. Celem ych oliczeń jes uslenie prmerów przejzdu pociągu (np. nężeni prądu pornego z sieci rkcyjnej zporzeowni n moc w celu zrelizowni przejzdu id.) w zleżności od czsu orz odległości pokonnej przy dnej chrkerysyce rkcyjnej pojzdu orz znnych prmerch geomerycznych rsy. Opory ruchu R s (v) są głównie związne z siłmi erodynmicznymi i oddziływnimi koło szyn. Rys.. Schem idelnej koordyncji n linich podmiejskich lu mer między hmującymi i ruszjącymi pociągmi; oprcownie włsne n podswie [1]
3 Opymlizcj efekywności hmowni odzyskowego w rnsporcie szynowym przez serownie czsem przyjzdu Ich zleżność od prędkości jzdy v jes zzwyczj opisywn funkcją kwdrową [7 1]: s R v k k v k v () 1 gdzie: współczynniki k k 1 k są słymi związnymi z konsrukcją oru: jego msą orz prmermi opisującymi oddziływnie koł z szyną. Opory ruchu R g (x) = mgp(x) nomis w prosy sposó zleżą o d pochyleni p(x) linii kolejowej kóre zmieni się wrz z kulnym położeniem x wzdłuż oru. Pochylenie o jes zdefiniowne jko p = Δh / l gdzie Δh jes różnicą wysokości pomiędzy dwom punkmi oru odległymi od sieie o l i jes zzwyczj wyrżne w promilch. Wówczs wyrżenie przyjmuje posć: R g (x) = mgp(x) / 1. Pondo jeżeli w chwili moc poiern przez pojzdy w fzie rozruchu wynosi P () nomis moc generown podczs hmowni elekrodynmicznego jes oznczon jko P r (s) o dl dnych przeiegów prędkości pojzdów A i : v = v () i v = v () wielkości P = F()v () i P r (s) = φ(s)()v () możn wyznczyć ezpośrednio z równni ruchu [4]: 1 1 P mv( ) mv( ) Eloss / 1 1 Pr s ( s) mv() mv( ) Elo ss / (3) gdzie: Δ jes krókim odcinkiem czsu zś φ(s) jes prmerem o wrościch z przedziłu [ 1] kóry określ efekywność rnsferu energii w zleżności od odległości s pomiędzy kooperującymi pojzdmi. W przedswionym w prcch [ 1 4] modelu opymlizcji minimlizowny jes jedynie rzeczywisy poór energii w czsie przejzdu kóry przyjmuje formę: E p = E E r (4) gdzie: E = E + E jes sumą energii rkcyjnych zużyych przez pojzdy A i zś E r jes wykorzysną częścią energii odzysknej podczs hmowni pojzdu wyrżoną przez: T E min{ P P s }d. (5) r Dl kżdego z ych pojzdów energi zuży w rkcie przejzdu w przedzile czsu [T] wyrż się przez cłkę z mocy związnej z siłą rkcyjną: T T u u En mx u v d v d (n = ). r (6) Specyfikę procesu opymlizcji uwzględnijącą zleżności pomiędzy różnymi wrinmi czsów odjzdów ze scji z możliwością koopercji hmujących i przyspieszjących pojzdów szynowych przedswiono n rysunku 3. W rozwżnych rzech przypdkch pociąg A jes w fzie rozruchu nomis pociąg jes w fzie hmowni. Czs rozpoczęci i czs zkończeni hmowni ( orz 1 ) pociągu są kie sme we wszyskich rzech przypdkch nomis zmieni się czs rozpoczęci rozruchu pociągu A. Może yć on opóźniny ż do grnicznego gr umożliwijącego plnowy przyjzd n kolejną scję. W wyniku zmin czsu odjzdu zmieni się wykorzysnie przez pociąg A energii odzysknej Rys. 3. Wykorzysnie odzysknej energii serownie czsem odjzdu pociągu; oprcownie włsne n podswie [ 1 4]
4 64 Urnik M. Krds-Cinl E. podczs hmowni pociągu co przedswiją rzy zleżności [ 1 4]: w przypdku 1: w przypdku : r 1 Er P r s d (7) 1 d r d (8) w przypdku 3: E P P s r 1 d P r sd. (9) E P Po wykonniu nlizy chrkeru zminy wykorzysni energii rekupercji E r w zleżności od czsu odjzdu (rośnie w przypdkch 1 i lu mleje w przypdkch i 3) możn swierdzić że może yć on opisn funkcją unimodlną. Nsępnie nleży zuwżyć że zgodnie z nsępującymi relcjmi przedswionymi w prcch [ 1 4]: de d de d de d p p p gdy gdy g ** ** ** dy (1) rzeczywise zużycie energii rkcyjnej E p w pierwszym epie mleje nsępnie rośnie wrz ze zwiększeniem opóźnieni czsu odjzdu pociągu ze scji. Ozncz o że minimlne rzeczywise zużycie energii rkcyjnej E p wysępuje dl czsu odjzdu = ** i możn je wyznczyć korzysjąc z meody równego podziłu (isekcji) [4 5] rozwiązując równnie nieliniowe w posci: de /d. (11) p Algorym ego rozwiązni poleg n złożeniu njwcześniejszego i możliwie njpóźniejszego czsu odjzdu pociągu ze scji orz wyznczeniu grdienu rzeczywisego zużyci energii rkcyjnej dl ych dwóch czsów odjzdów. W przypdku gdy oie orzymne wrości są dodnie nleży swierdzić że njwcześniejszy możliwy czs odjzdu ze scji jes rozwiązniem opymlnym. W kżdym innym przypdku wyzncz się opymlną wrość zwężjąc sopniowo przedził czsów odjzdu i nlogicznie szukjąc opymlnego rozwiązni meodą isekcji zsosowną do funkcji dep / d w kórym o grdieny ędą wrościmi dodnimi [4]. 3. Modyfikcj modelu N wsępie nleży przyjąć że sieć rkcyjn jes zsiln prądem o słym npięciu (np. 3 kv DC kóre jes ypowym npięciem zsilni n polskich linich kolejowych) sn oru orz infrsrukury umożliwi wykorzysnie echnologii hmowni rekupercyjnego z przesyłem odzysknej energii do sieci jezdnej [11]. W przedswionym modelu w odróżnieniu od modelu wyjściowego zproponowno zmienną serującą przejzdem eoreycznym w posci czsu zkończeni hmowni ( ). Wrość jes równoznczn z rzeczywisym czsem przyjzdu pocią- KH gu n scję lu przysnek czyli KH T. Syucję RP ę ilusruje rysunek 4. Rys. 4. Wykorzysnie odzysknej energii serownie czsem przyjzdu pociągu; [oprcownie włsne]
5 Opymlizcj efekywności hmowni odzyskowego w rnsporcie szynowym przez serownie czsem przyjzdu Jes o syucj gdy czsy rozpoczęci i zkończeni rozruchu przez pojzd A są wrościmi słymi A A ( PR cons. orz KR cons. ) co z ym idzie chrkerysyk prowdzeni pojzdu A nie uleg zminie w zkresie rozruchu i wymgnej do jego przeprowdzeni energii. Przesunięciu podlegją nomis czsy rozpoczęci i zkończeni hmowni pociągu ( orz PH ) przy czym njwcześniejszy KH momen zkończeni hmowni pociągu nie może nsąpić wcześniej niż czs rozpoczęci rozruchu pociągu A ( A KH )njpóźniejszy zś czs rozpoczęci PR hmowni pojzdu nie może nsąpić później niż momen zkończeni rozruchu pojzdu A ( A PH ). KR Nleży przy ym również pmięć że rzeczywisy czs przyjzdu pociągu n scję T musi zwierć RP się w przedzile między njwcześniejszym i njpóźniejszym czsem przyjzdu dnego pociągu n scję dopuszczlnym przez służowy rozkłd jzdy: TRP TPP ; TWP. Dlsze podswowe złożeni modelu przejzdu eoreycznego (1) (3) pozoswiono niezmienione. Niemniej wiedząc że sieć rkcyjn jes zsiln prądem o słym npięciu moc prądu słego wyrż się iloczynem npięci U i nężeni prądu I: P() = ηui() (1) gdzie: η o sprwność silnik (η E ) lu sprwność hmowni rekupercyjnego (η ) I() poierne lu generowne nężenie prądu. Wówczs orzymuje się: 1 1 EUI A mv( ) mv( ) Eloss / 1 1 UI s( s) mv() mv( ) Eloss / (13) gdzie: energi niezędn do pokonni oporu ruchu wyrżn jes przez []: Eloss Rs ( v ) Rg ( x ) x Eloss Rs ( v ) Rg ( x ) x (14) gdzie: Δx = v Δ i Δx = v Δ są długościmi odcinków oru kóre przeyły odpowiednio: pojzd A ędący w fzie rozruchu i pojzd ędący w fzie hmowni. Nężenie poiernego / indukownego prądu I możn nomis wyznczyć znjąc siłę porzeną n pokonnie oporów ruchu F() kulną prędkość pojzdu v() orz sprwność silnik / silnik prądnicy η: () I F() v. (15) U Siłę pociągową F() dl fzy rozruchu pociągu możn określić z zleżności [17 18]: F A1 = k m A. (16) dl przyspieszni przy słej sile gdzie A o mksymlne przyspieszenie rozruchu nomis dl przyspieszeni ze słą mocą mksymlną sił równ się: F A PE E (17) v () gdzie: P E o moc wszyskich silników pojzdu v A () o chrkerysyk prędkość oliczn z wrunku F A1 = F A. Podonie siłę rkcyjną F() możn wyznczyć dl pociągu hmującego: A F 1 = k m (18) F PE E (19) v () gdzie: o mksymlne opóźnienie hmowni v () o prędkość chrkerysyczn odpowidjąc F 1 = F. Poniewż njwiększe zporzeownie n moc i energię elekryczną wysępuje podczs prowdzeni rozruchu e porzey możn zmniejszyć przez odpowiednie wykorzysnie energii pochodzącej z hmowni odzyskowego innego pociągu. Zporzeownie n energię elekryczną w kim przypdku ędzie równe ilnsowi energii porzenej n wykonnie rozruchu i możliwej do wykorzysni części energii odzysknej z hmowni [ ]. W proponownym podejściu serowni czsem przyjzdu nie m konieczności dodkowej opymlizcji cłego przejzdu w celu osiągnięci sosunkowo wymiernych korzyści w ilnsie energeycznym jedynie frgmenu doyczącego hmowni i rozruchu. Z ego powodu jko główną skłdową funkcji celu zproponowno: E P EE min () RW gdzie: E P jes rzeczywisą wrością energii zużyą podczs rozruchu pojzdu A E jes wielkością energii porzeną n wykonnie rozruchu nomis E RW jes energią odzyskną podczs hmowni elekrodynmicznego pojzdu i wykorzysną w procesie koopercji ou pociągów. Pmięjąc o zleżności (1)
6 66 Urnik M. Krds-Cinl E. poszczególne wrości energii możn wyznczyć nsępująco: TKR E U I() d (1) TKH TPR E U min{ I I s } d () RW A TPR gdzie: I A () o prąd poierny przez pociąg przyspieszjący (A) I (s) o prąd generowny przez pociąg hmujący (). Swierdzono również że isnieją inne kryeri kóre powinny yć uwzględnione przy opymlizcji wielokryerilnej dlego przyjęo: TKH ERO U I() d mx (3) TPH gdzie: E RO jes cłkowią odzyskną energią podczs hmowni rekupercyjnego pojzdu możliwą do wykorzysni również w inny sposó niż ezpośredni przesył do sieci jezdnej (np. dodkowe zsoniki energii) orz: T T T min (4) P O RP gdzie: T P ozncz czs posoju kóry powinien yć możliwie minimlny ze względu n możliwości przepusowe scji T O jes rozkłdowym czsem odjzdu pociągu nomis T RP jes jego rzeczywisym czsem przyjzdu. iorąc pod uwgę przedswione rozwżni orzymuje się glolną funkcję celu posci: FT ( T ) we we wt min (5) O RP 1 P RO 3 P gdzie: w 1 w w 3 są wgmi poszczególnych funkcji skłdowych odzwierciedljącymi ich wżność w zleżności od swinych celów. Funkcj jes minimlizow n zem funkcje cząskowe kóre również są minimlizowne zpisuje się ze znkiem dodnim (E P T P ) nomis mksymlizowną funkcję cząskową (E RO ) zpisuje się ze znkiem ujemnym. Korzysjąc z przedswionego modelu zopymlizowno wielkość odzysknej orz wykorzysnej przy koopercji pociągów energii dl scji kolejowej Gdńsk Żink AWFiS n linii kolejowej nr 5 Gdńsk Główny Rumi (l. 1). W wyniku opymlizcji z wykorzysniem lgorymu świelik wykzno że w ciągu doy podczs hmowni rekupercyjnego isnieje możliwość odzyskni energii elekrycznej o wrości E RO = 9744 kwh z czego E RW = 6544 kwh może zosć wykorzysn w procesie energeycznej koopercji pociągów. W przypdku cłkowiego zporzeowni pociągów n energię rkcyjną n nlizownym odcinku (Gdńsk Oliw Gdńsk Żink AWFiS Sopo Wyścigi) wynoszącemu E P = 161 kwh energi wykorzysn ezpośrednio w procesie energeycznej koopercji pociągów snowi pond 4% cłkowiego zporzeowni. Ozncz o że rzeczywise zporzeownie n energię rkcyjną wynosi 9666 kwh. Wynik en jes zliżony do wielkości energii możliwej do wykorzysni przy uwzględnieniu energeycznej koopercji pociągów określonej w prcch [] lu [6]. Tlic 1 Wyniki opymlizcji z pomocą lgorymu świelik dl przysnku pociągu Gdńsk Żink AWF E P [kwh] E RO [kwh] E RW [kwh] Sum: [Oprcownie włsne] 4. Wnioski Podsumowując nleży swierdzić że isnieją już pewne modele i sposoy opymlizcji wykorzysni energii pochodzącej z rekupercji z wykorzysniem przesyłu do sieci jezdnej orz wzjemnej koopercji kilku pojzdów np. przez serownie czsem odjzdu pociągu. Nleży jednk zznczyć że ndl isnieje wiele niezdnych możliwości zwiększeni efekywności hmowni odzyskowego jk choćy jego opymlizcj z wykorzysniem rezerwy czsu przejzdu uwzględnionej w rozkłdzie jzdy przez serownie czsem przyjzdu. Meody e choć podone różnią się sposoem prowdzeni pojzdu i poorem energii. W pierwszym przypdku (serownie czsem odjzdu) wrz z jego sopniowym opóźnieniem zwiększ się energi konieczn n pokonnie kolejnego odcink międzyscyjnego związn między innymi z koniecznością uzyskni większych prędkości. W drugim przypdku nomis (serownie czsem przyjz-
7 Opymlizcj efekywności hmowni odzyskowego w rnsporcie szynowym przez serownie czsem przyjzdu du n scję) wrz z opóźnieniem przyjzdu spd zporzeownie n energię np. dzięki wydłużeniu jzdy ez pooru prądu rozwijniu niższych prędkości czy mksymlnemu opóźnieniu hmowni. Znne modele w dlszym ciągu możn modyfikowć i rozwijć dososowując je do swinych wymgń isniejących (zmienijących się) wrunków i porze np. przez doprecyzownie zpisu wprowdzjąc możliwość edycji podswowych dnych lu rezygnując z części oliczeń zsępując je innymi zleżnościmi poencjlnie skrcjąc ym smym cły proces oliczeń i nlizy. W konekście opymlizcji rze podkreślić że orgnizcji ruchu pociągów (czy innych sysemów rnsporu szynowego) nie możn modyfikowć wyłącznie pod względem opymlizcji zużyci energii czy efekywności rekupercji. Ze względu n ndrzędne kryeri kie jk określony czs przejzdu czs posoju zdolności przepusowe linii kolejowych i scji le przede wszyskim wymgni od srony popyu możliw jes reorgnizcj ruchu ylko w wąskim zkresie. Znlzło o odzwierciedlenie zrówno w złożenich modelu TRP TPP ; TWP jk i w minimlizownej glolnej funkcji celu. Zsosownie zproponownego modelu zkłdjącego wykorzysnie energii z rekupercji przy uwzględnieniu energeycznej koopercji pociągów wrz z opymlizcją przejzdu wskzło że w przypdku nlizy wykonnej dl pojedynczej scji isnieje możliwość zoszczędzeni nwe do 4% energii rkcyjnej. Lierur 1. A ENVILINE ERS rkcyjny ukłd odzyskiwni energii Rynek Infrsrukury hp://www. rynekinfrsrukury.pl/widomosci/enviline-ers- -rkcyjny-ukld-odzyskiwni-energii hml [dosęp ].. Açikş S. Söylemez M.T.: Prmeers ffecing rking energy recuperion re in DC ril rnsi Join Ril Conference 7 s rrero R. Tckoen X. vn Mirelo J.: Sionry or onord energy sorge sysems for energy consumpion reducion in mero nework Proceedings of he Insiuion of Mechnicl Engineers Pr F: Journl of Ril nd Rpid Trnsi 1 nr 4 pp urden R.L. Fires J.D.: The isecion lgorihm. PWS Pulishers oson Corliss G.: Which roo does he isecion lgorihm find? SIAM 1977 /19 p Czuch J. Krwowski K. Mizn M. Pzdro P.: Efekywność odzysku energii hmowni elekrodynmicznego w komunikcji miejskiej Przegląd Elekroechniczny 1/4 s De Mrinis V. Gllo M.: Models nd mehods o opimize rin speed profiles wih nd wihou energy recovery sysems: suurn es cse. Procedi Socil nd ehviorl Sciences 13 Vol. 87 pp Gonzlez-Gil A. Plcin R. y P. Powell J.P.: Energy-efficien urn ril sysems: sregies for n opiml mnge-men of regenerive rking Energy Trnspor Reserch Aren Pryż Jcyn M. Urnik M.: Orgnizcj ruchu pociągów w oręie scji oszczędność energii Prce Nukowe Poliechniki Wrszwskiej Trnspor z. 115/17 Wrszw Oficyn Wydwnicz Poliechniki Wrszwskiej s Jcyn M. Urnik M.: Wyrne zgdnieni opymlizcji orgnizcji ruchu kolejowego w celu minimlizcji koszów zużyci energii Prce Nukowe Poliechniki Wrszwskiej Trnspor z. 19 Oficyn Wydwnicz Poliechniki Wrszwskiej Wrszw 16 s Krkosińsk-rzozowsk N. Urnik M.: riery sosowni echnologii odzysku energii w rnsporcie szynowym Prce Nukowe Poliechniki Wrszwskiej Trnspor z. 115/17 Wrszw Oficyn Wydwnicz Poliechniki Wrszwskiej s Kwśnikowski J.: Elemeny eorii ruchu i rcjonlizcji prowdzeni pociągów Wydwnicwo Nukowe Insyuu Technologii Eksplocji PI Rdom Oreg J.M. Iiondo H.: Kineic energy recovery on rilwy sysems wih feedck o he grid WCRR 11 Lille Frncj. 14. Pwełczyk M.: Rozwój sysemów wykorzysujących kumulcję energii w rnsporcie szynowym TTS Technik Trnsporu Szynowego 11 nr 1/11 s Pzdro P.: Koncepcj ruchowej opymlizcji efekywności hmowni odzyskowego. TTS Technik Trnsporu Szynowego Eksplocj 3 nr 1 /3 s Pen Alcrz M. e.l.: Opiml underground imele design sed on power flow mximizing he use of regenerive-rking Energy Proceedings of he Insiuion of Mechnicl Engineers Pr F: Journl of Ril nd Rpid Trnsi 1 nr 6 pp Podoski J. Msłek J. Kcprzk J.: Zsdy rkcji elekrycznej Wydwnicwo Komunikcji i Łączności Wrszw Podoski J.: Zsdy rkcji elekrycznej Wydwnicwo Komunikcji i Łączności Wrszw Rodmp o Single Europen Trnspor Are Towrds compeiive nd resource efficien rnspor sysem: hp://eur-lex.europ.eu/leglconen/pl/txt/pdf/?uri=celex:511dc14 4&from=EN [dosępny r.].
8 68 Urnik M. Krds-Cinl E.. Su S. Tng T. Roers C.: A Cooperive Trin Conrol Model for Energy Sving. IEEE Trnscions on Inelligen Trnsporion Sysems om: 16 wydnie: s Su S. To T. Wng Y.: Evluion of Sregies o Reducing Trcion Energy Consumpion of Mero Sysems Using n Opiml Trin Conrol Simulion Model Energies 16 9() nr 15.. Tomczyk M. Pcholczyk M. Krwowski K.: Comprehensive modelling of he cos effecivness of rilwy line elecrificion Zeszyy Nukowe Wydziłu Elekroechniki i Auomyki Poliechniki Gdńskiej Gdńsk 16 nr 51 s Urnik M. Jcyn M. Krds-Cinl E.: Meody wykorzysni rekupercji w rnsporcie szynowym TTS Technik Trnsporu Szynowego 16 1(73) s Urnik M. Krds-Cinl E.: Modelownie reorgnizcji ruchu w rnsporcie szynowym zwiększjącej efekywne wykorzysnie energii z hmowni odzyskowego Prce Nukowe Poliechniki Wrszwskiej Trnspor z. 118 Wrszw 17 s Wrin Y. Lnselle R. Thiounn M.: Acive sudsion 9-y Świowy Kongres do. dń Kolejowych WCRR 11 Lille Frncj.
Autor: Zbigniew Tuzimek Opracowanie wersji elektronicznej: Tomasz Wdowiak
 DNIE UKŁDÓW LOKD UTOMTYCZNYCH uor: Zigniew Tuzimek Oprcownie wersji elekronicznej: Tomsz Wdowik 1. Cel i zkres ćwiczeni Celem ćwiczeni jes zpoznnie sudenów z udową orz dziłniem zezpieczeń i lokd sosownych
DNIE UKŁDÓW LOKD UTOMTYCZNYCH uor: Zigniew Tuzimek Oprcownie wersji elekronicznej: Tomsz Wdowik 1. Cel i zkres ćwiczeni Celem ćwiczeni jes zpoznnie sudenów z udową orz dziłniem zezpieczeń i lokd sosownych
Stanisław RADKOWSKI. Politechnika Warszawska, Instytut Podstaw Budowy Maszyn,
 WYKORZYSTANIE STACJONARNYCH STACJI MONITORINGU W WYKRYWANIU USZKODZEŃ POJAZDÓW Snisłw RADKOWSKI Poliechnik Wszwsk, Insyu Podsw Budowy Mszyn, ul. Nbu 84, 0-54 Wszw 0 660 86, e-mil: s@sim.pw.edu.pl Scj monioingu
WYKORZYSTANIE STACJONARNYCH STACJI MONITORINGU W WYKRYWANIU USZKODZEŃ POJAZDÓW Snisłw RADKOWSKI Poliechnik Wszwsk, Insyu Podsw Budowy Mszyn, ul. Nbu 84, 0-54 Wszw 0 660 86, e-mil: s@sim.pw.edu.pl Scj monioingu
Fizyka 1- Mechanika. Wykład 2 12.X Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów
 Fizyk 1- Mechnik Wykłd 1.X.17 Zygmun Szefliński Środowiskowe Lbororium Ciężkich Jonów szef@fuw.edu.pl hp://www.fuw.edu.pl/~szef/ Pojęci podswowe Punk merilny Ciło, kórego rozmiry możn w dnym zgdnieniu
Fizyk 1- Mechnik Wykłd 1.X.17 Zygmun Szefliński Środowiskowe Lbororium Ciężkich Jonów szef@fuw.edu.pl hp://www.fuw.edu.pl/~szef/ Pojęci podswowe Punk merilny Ciło, kórego rozmiry możn w dnym zgdnieniu
PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH
 SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
MECHANIKA. Podstawy kinematyki Zasady dynamiki. Zasada zachowania pędu Zasada zachowania energii Ruch harmoniczny i falowy
 MECHANIKA Podswy kineyki Zsdy dyniki Siły Równnie ruchu Ukłdy inercjlne i nieinercjlne Zsd zchowni pędu Zsd zchowni energii Ruch hroniczny i flowy ruch rejesrowne w czsie w sposób ciągły ziny położeni
MECHANIKA Podswy kineyki Zsdy dyniki Siły Równnie ruchu Ukłdy inercjlne i nieinercjlne Zsd zchowni pędu Zsd zchowni energii Ruch hroniczny i flowy ruch rejesrowne w czsie w sposób ciągły ziny położeni
Komisja Egzaminacyjna dla Aktuariuszy LII Egzamin dla Aktuariuszy z 15 marca 2010 r. Część I Matematyka finansowa
 Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych
 Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
RÓWNANIA TRYGONOMETRYCZNE Z PARAMETREM
 ÓWNANIA TYGONOMETYCZNE Z PAAMETEM Do grupy zgdnień eycznyc, w kóryc wysępuje pojęcie preru, nleżą równni rygonoeryczne. ozprywnie równń rygonoerycznyc z prere swrz ożliwość powórzeni i urwleni ożsości
ÓWNANIA TYGONOMETYCZNE Z PAAMETEM Do grupy zgdnień eycznyc, w kóryc wysępuje pojęcie preru, nleżą równni rygonoeryczne. ozprywnie równń rygonoerycznyc z prere swrz ożliwość powórzeni i urwleni ożsości
MODELOWANIE REORGANIZACJI RUCHU W TRANSPORCIE SZYNOWYM ZWIĘKSZAJĄCEJ EFEKTYWNE WYKORZYSTANIE ENERGII Z HAMOWANIA ODZYSKOWEGO
 PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 118 Tnso 217 Michł Unik Poliechnik Gdńsk Wydził Inżynieii Lądowej i Śodowisk Poliechnik Wszwsk Wydził Tnsou Ew Kds-Cinl Poliechnik Wszwsk Wydził Tnsou MODELOWANIE
PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 118 Tnso 217 Michł Unik Poliechnik Gdńsk Wydził Inżynieii Lądowej i Śodowisk Poliechnik Wszwsk Wydził Tnsou Ew Kds-Cinl Poliechnik Wszwsk Wydził Tnsou MODELOWANIE
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
CAŁKOWANIE NUMERYCZNE
 Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew Pbisek Adm Wostko Wprowdzenie
Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew Pbisek Adm Wostko Wprowdzenie
PODSTAWY BAZ DANYCH Wykład 3 2. Pojęcie Relacyjnej Bazy Danych
 PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
MODELOWANIE I STABILNOŚĆ RYNKU
 Wcłw Gierulski 1) Bogusłw Rdziszewski ) MODEOWANIE I STABINOŚĆ RYNKU STRESZCZENIE W prcy rozwż się kilk różnych modeli rynku i sposoby zchowni ceny bieżącej względem ceny równowgi. Szczególną uwgę zwrócono
Wcłw Gierulski 1) Bogusłw Rdziszewski ) MODEOWANIE I STABINOŚĆ RYNKU STRESZCZENIE W prcy rozwż się kilk różnych modeli rynku i sposoby zchowni ceny bieżącej względem ceny równowgi. Szczególną uwgę zwrócono
Metoda sił jest sposobem rozwiązywania układów statycznie niewyznaczalnych, czyli układów o nadliczbowych więzach (zewnętrznych i wewnętrznych).
 Metod sił jest sposoem rozwiązywni ukłdów sttycznie niewyznczlnych, czyli ukłdów o ndliczowych więzch (zewnętrznych i wewnętrznych). Sprowdz się on do rozwiązni ukłdu sttycznie wyznczlnego (ukłd potwowy
Metod sił jest sposoem rozwiązywni ukłdów sttycznie niewyznczlnych, czyli ukłdów o ndliczowych więzch (zewnętrznych i wewnętrznych). Sprowdz się on do rozwiązni ukłdu sttycznie wyznczlnego (ukłd potwowy
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
POMIARY MAŁYCH CZĘSTOTLIWOŚCI W OBECNOŚCI ZAKŁÓCEŃ
 Meriły konferencji nukowo-echnicznej PPM 0 Poliechnik Lubelsk Kedr Auomyki i Merologii POMIARY MAŁYCH CZĘSTOTLIWOŚCI W OBECNOŚCI ZAKŁÓCEŃ W prcy porusz się problemykę pomiru młych częsoliwości w obecności
Meriły konferencji nukowo-echnicznej PPM 0 Poliechnik Lubelsk Kedr Auomyki i Merologii POMIARY MAŁYCH CZĘSTOTLIWOŚCI W OBECNOŚCI ZAKŁÓCEŃ W prcy porusz się problemykę pomiru młych częsoliwości w obecności
KONKURS MATEMATYCZNY. Model odpowiedzi i schematy punktowania
 KONKURS MATEMATYCZNY dl uczniów gimnzjów orz oddziłów gimnzjlnych województw mzowieckiego w roku szkolnym 2018/2019 Model odpowiedzi i schemty punktowni Z kżde poprwne i pełne rozwiąznie, inne niż przewidzine
KONKURS MATEMATYCZNY dl uczniów gimnzjów orz oddziłów gimnzjlnych województw mzowieckiego w roku szkolnym 2018/2019 Model odpowiedzi i schemty punktowni Z kżde poprwne i pełne rozwiąznie, inne niż przewidzine
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
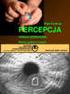 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
ROZPORZĄDZENIE MINISTRA INFRASTRUKTURY 1) z dnia 16 grudnia 2004 r.
 Typ/orgn wydjący Rozporządzenie/Minister Infrstruktury Tytuł w sprwie szczegółowych wrunków i trybu wydwni zezwoleń n przejzdy pojzdów nienormtywnych Skrócony opis pojzdy nienormtywne Dt wydni 16 grudni
Typ/orgn wydjący Rozporządzenie/Minister Infrstruktury Tytuł w sprwie szczegółowych wrunków i trybu wydwni zezwoleń n przejzdy pojzdów nienormtywnych Skrócony opis pojzdy nienormtywne Dt wydni 16 grudni
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
CAŁKOWANIE NUMERYCZNE
 Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I rok kdemicki 01/013 Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew
Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I rok kdemicki 01/013 Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie 9. BADANIE UKŁADÓW ZASILANIA I STEROWANIA STANOWISKO I. Badanie modelu linii zasilającej prądu przemiennego
 ortorium elektrotechniki Ćwiczenie 9. BADAIE UKŁADÓ ZASIAIA I STEOAIA STAOISKO I. Bdnie modelu linii zsiljącej prądu przemiennego Ukłd zowy (ez połączeń wrintowych) 30 V~ A A A 3 3 3 A 3 A 6 V 9 0 I A
ortorium elektrotechniki Ćwiczenie 9. BADAIE UKŁADÓ ZASIAIA I STEOAIA STAOISKO I. Bdnie modelu linii zsiljącej prądu przemiennego Ukłd zowy (ez połączeń wrintowych) 30 V~ A A A 3 3 3 A 3 A 6 V 9 0 I A
Wymagania na ocenę dopuszczającą z matematyki klasa II Matematyka - Babiański, Chańko-Nowa Era nr prog. DKOS 4015-99/02
 Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Równania i nierówności kwadratowe z jedną niewiadomą
 50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
2. PODSTAWY STATYKI NA PŁASZCZYŹNIE
 M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 2014/2015 Zadania dla grupy elektronicznej na zawody II stopnia
 EOELEKTA Ogólnopolsk Olimpid Wiedzy Elektrycznej i Elektronicznej ok szkolny 204/205 Zdni dl grupy elektronicznej n zwody stopni Zdnie Dl diody półprzewodnikowej, której przeieg chrkterystyki prądowo-npięciowej
EOELEKTA Ogólnopolsk Olimpid Wiedzy Elektrycznej i Elektronicznej ok szkolny 204/205 Zdni dl grupy elektronicznej n zwody stopni Zdnie Dl diody półprzewodnikowej, której przeieg chrkterystyki prądowo-npięciowej
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych
 Klucz odpowiedzi do zdń zmkniętych i schemt ocenini zdń otwrtych Klucz odpowiedzi do zdń zmkniętych 4 5 6 7 8 9 0 4 5 6 7 8 9 0 D D D Schemt ocenini zdń otwrtych Zdnie (pkt) Rozwiąż nierówność x + x+ 0
Klucz odpowiedzi do zdń zmkniętych i schemt ocenini zdń otwrtych Klucz odpowiedzi do zdń zmkniętych 4 5 6 7 8 9 0 4 5 6 7 8 9 0 D D D Schemt ocenini zdń otwrtych Zdnie (pkt) Rozwiąż nierówność x + x+ 0
Pasek narzędziowy Symbolic [View Toolbars Math Symbolic] Pasek narzędziowy Modifier [Symbolic Modifiers]
![Pasek narzędziowy Symbolic [View Toolbars Math Symbolic] Pasek narzędziowy Modifier [Symbolic Modifiers] Pasek narzędziowy Symbolic [View Toolbars Math Symbolic] Pasek narzędziowy Modifier [Symbolic Modifiers]](/thumbs/93/114308530.jpg) Psek nrzędziowy Symolic [View Toolrs Mth Symolic] Psek nrzędziowy Modifier [Symolic Modifiers] Słow kluczowe możn wprowdzić z pomocą psk nrzędziowego [Symolic] lu ezpośrednio z klwitury. Wprowdznie z klwitury
Psek nrzędziowy Symolic [View Toolrs Mth Symolic] Psek nrzędziowy Modifier [Symolic Modifiers] Słow kluczowe możn wprowdzić z pomocą psk nrzędziowego [Symolic] lu ezpośrednio z klwitury. Wprowdznie z klwitury
Projektowanie układów sterowana. dr inż. Anna Czemplik (C-3/317a) Katedra Automatyki, Mechatroniki i Systemów Sterowania
 Projekownie kłdów serown dr inż. Ann zeplik -/7 edr Aoyki, Mechroniki i Syseów Serowni hp://www.k.pwr.ed.pl/ Wyszkiwrk zjęci, konslcje hp://nn.czeplik.sff.iir.pwr.wroc.pl -> rsy -> Projekownie kłdów serowni
Projekownie kłdów serown dr inż. Ann zeplik -/7 edr Aoyki, Mechroniki i Syseów Serowni hp://www.k.pwr.ed.pl/ Wyszkiwrk zjęci, konslcje hp://nn.czeplik.sff.iir.pwr.wroc.pl -> rsy -> Projekownie kłdów serowni
Wymagania kl. 2. Uczeń:
 Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Rozwiązywanie zadań z dynamicznego ruchu płaskiego część I 9
 ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Kodowanie liczb. Kodowanie stałopozycyjne liczb całkowitych. Niech liczba całkowita a ma w systemie dwójkowym postać: Kod prosty
 Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 2014/2015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A2, A3, A4, A6, A7)
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II TAK
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
MECHANIKA BUDOWLI 5 UWZGLĘDNIENIE WPŁYWU TEMPERATURY, OSIADANIA PODPÓR I BŁĘDÓW MONTAŻOWYCH W RÓWNANIU PRACY WIRTUALNEJ.
 WYKŁ DY Z ECHNIKI BUDOWLI WPŁYW TEPERTURY I BŁĄDÓW, SPOSÓB WERESZCZEGIN- OHR OBLICZNI CŁEK O Kopcz, m Łoowski, Wojciec Pwłowski, icł Płokowik, Krzszof Tmper Konsucje nukowe: prof. r. JERZY RKOWSKI Poznń
WYKŁ DY Z ECHNIKI BUDOWLI WPŁYW TEPERTURY I BŁĄDÓW, SPOSÓB WERESZCZEGIN- OHR OBLICZNI CŁEK O Kopcz, m Łoowski, Wojciec Pwłowski, icł Płokowik, Krzszof Tmper Konsucje nukowe: prof. r. JERZY RKOWSKI Poznń
Wymagania edukacyjne z matematyki FUNKCJE dopuszczającą dostateczną dobrą bardzo dobrą
 Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II LO
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO
 MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
LOW FREQUENCY MEASUREMENTS IN THE PRESENCE OF NOISE
 Podswowe Problemy Merologii PPM 0 Usroń, 7-9 mj 00 r. POMIARY MAŁYCH CZĘSTOTLIWOŚCI W OBECNOŚCI ZAKŁÓCEŃ LOW FREQUENCY MEASUREMENTS IN THE PRESENCE OF NOISE dr inż. Eligiusz Pwłowski POLITECHNIKA LUBELSKA
Podswowe Problemy Merologii PPM 0 Usroń, 7-9 mj 00 r. POMIARY MAŁYCH CZĘSTOTLIWOŚCI W OBECNOŚCI ZAKŁÓCEŃ LOW FREQUENCY MEASUREMENTS IN THE PRESENCE OF NOISE dr inż. Eligiusz Pwłowski POLITECHNIKA LUBELSKA
Przetworniki Elektromaszynowe st. n. st. sem. V (zima) 2018/2019
 Kolokwium główne Wrint A Przetworniki lektromszynowe st. n. st. sem. V (zim 018/019 Trnsormtor Trnsormtor trójzowy m nstępujące dne znmionowe: S 00 kva 50 Hz HV / LV 15 ±x5% / 0,4 kv poł. Dyn Pondto widomo,
Kolokwium główne Wrint A Przetworniki lektromszynowe st. n. st. sem. V (zim 018/019 Trnsormtor Trnsormtor trójzowy m nstępujące dne znmionowe: S 00 kva 50 Hz HV / LV 15 ±x5% / 0,4 kv poł. Dyn Pondto widomo,
4. RACHUNEK WEKTOROWY
 4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
O PEWNYCH MODELACH DECYZJI FINANSOWYCH
 DECYZJE nr 1 czerwiec 2004 37 O PEWNYCH MODELACH DECYZJI FINANSOWYCH Krzysztof Jjug Akdemi Ekonomiczn we Wrocłwiu Wprowdzenie modele teorii finnsów Teori finnsów, zwn również ekonomią finnsową, jest jednym
DECYZJE nr 1 czerwiec 2004 37 O PEWNYCH MODELACH DECYZJI FINANSOWYCH Krzysztof Jjug Akdemi Ekonomiczn we Wrocłwiu Wprowdzenie modele teorii finnsów Teori finnsów, zwn również ekonomią finnsową, jest jednym
VI. Rachunek całkowy. 1. Całka nieoznaczona
 VI. Rchunek cłkowy. Cłk nieoznczon Niech F : I R i f : I R będą funkcjmi określonymi n pewnym przedzile I R. Definicj. Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I, gdy F (x) = f(x) dl x
VI. Rchunek cłkowy. Cłk nieoznczon Niech F : I R i f : I R będą funkcjmi określonymi n pewnym przedzile I R. Definicj. Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I, gdy F (x) = f(x) dl x
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Dla danego czynnika termodynamicznego i dla określonej przemiany ciepło właściwe w ogólności zależy od dwóch niezależnych
 Ciepło włśiwe Nieh zynnik ermodynmizny m sn określony przez emperurę orz iśnienie p. Dl dowolnej elemenrnej przeminy zzynjąej się od ego snu możemy npisć dq [J/kg] ( Równnie ( wiąże pohłninie lub oddwnie
Ciepło włśiwe Nieh zynnik ermodynmizny m sn określony przez emperurę orz iśnienie p. Dl dowolnej elemenrnej przeminy zzynjąej się od ego snu możemy npisć dq [J/kg] ( Równnie ( wiąże pohłninie lub oddwnie
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
f(x)dx (1.7) b f(x)dx = F (x) = F (b) F (a) (1.2)
 Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
ANALIZA PRACY SYSTEMU ENERGETYCZNO-NAPĘDOWEGO STATKU TYPU OFFSHORE Z WYKORZYSTANIEM METODY DRZEW USZKODZEŃ
 MGR INŻ. LSZK CHYBOWSKI Politchnik Szczcińsk Wydził Mchniczny Studium Doktorncki ANALIZA PRACY SYSTMU NRGTYCZNO-NAPĘDOWGO STATKU TYPU OFFSHOR Z WYKORZYSTANIM MTODY DRZW USZKODZŃ STRSZCZNI W mtril przdstwiono
MGR INŻ. LSZK CHYBOWSKI Politchnik Szczcińsk Wydził Mchniczny Studium Doktorncki ANALIZA PRACY SYSTMU NRGTYCZNO-NAPĘDOWGO STATKU TYPU OFFSHOR Z WYKORZYSTANIM MTODY DRZW USZKODZŃ STRSZCZNI W mtril przdstwiono
Matematyka finansowa 10.03.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część I
 Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
ZASTOSOWANIE RÓWNANIA NASGRO DO OPISU KRZYWYCH PROPAGACYJI PĘKNIĘĆ ZMĘCZENIOWYCH
 Sylwester KŁYSZ *, **, nn BIEŃ **, Pweł SZBRCKI ** ** Instytut Techniczny ojsk Lotniczych, rszw * Uniwersytet rmińsko-mzurski, Olsztyn ZSTOSONIE RÓNNI NSGRO DO OPISU KRZYYCH PROPGCYJI PĘKNIĘĆ ZMĘCZENIOYCH
Sylwester KŁYSZ *, **, nn BIEŃ **, Pweł SZBRCKI ** ** Instytut Techniczny ojsk Lotniczych, rszw * Uniwersytet rmińsko-mzurski, Olsztyn ZSTOSONIE RÓNNI NSGRO DO OPISU KRZYYCH PROPGCYJI PĘKNIĘĆ ZMĘCZENIOYCH
Materiały szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA. Serwis internetowy BEZPIECZNIEJ CIOP-PIB
 Mteriły szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA Serwis internetowy BEZPIECZNIEJ CIOP-PIB 1. Wprowdzenie Drgnimi nzywne są procesy, w których chrkterystyczne dl nich wielkości fizyczne
Mteriły szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA Serwis internetowy BEZPIECZNIEJ CIOP-PIB 1. Wprowdzenie Drgnimi nzywne są procesy, w których chrkterystyczne dl nich wielkości fizyczne
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
σ - ułamka granicy plastyczności R e lub granicy proporcjonalności R c.
 Rozdził VII Hipoezy wyężeniowe Merił konsrukcji w zeżności od wrunków obciążeni może się znjdowć w różnych snch nprężeń. począku procesu, przy sosunkowo niedużych obciążenich będą o sny sprężyse, nomis
Rozdził VII Hipoezy wyężeniowe Merił konsrukcji w zeżności od wrunków obciążeni może się znjdowć w różnych snch nprężeń. począku procesu, przy sosunkowo niedużych obciążenich będą o sny sprężyse, nomis
Planowanie złożonych przedsięwzięć wieloczynnościowych (Project Management - zarządzanie projektami)
 D Miszczyńsk, M.Miszczyński KBO UŁ, Bdni opercyjne, metod PERT 1 Plnownie złożonych przedsięwzięć wieloczynnościowych (Project Mngement - zrządznie projektmi) Anlizujemy złożone przedsięwzięci wieloczynnościowe.
D Miszczyńsk, M.Miszczyński KBO UŁ, Bdni opercyjne, metod PERT 1 Plnownie złożonych przedsięwzięć wieloczynnościowych (Project Mngement - zrządznie projektmi) Anlizujemy złożone przedsięwzięci wieloczynnościowe.
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część I Matematyka finansowa
 Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
MXZ INVERTER SERIA. Jedna jednostka zewnętrzna może obsługiwać do 8 pomieszczeń. Ograniczenie poboru prądu. Efektywność energetyczna: klasa A
 INVERTER SERIA MXZ Typoszereg MXZ gwrntuje cicy, wysokowydjny i elstyczny system, spełnijący wszystkie wymgni w zkresie klimtyzcji powietrz. 6 MXZ-2C30VA MXZ-2C40VA MXZ-2C52VA MXZ-3C54VA MXZ-3C68VA MXZ-4C71VA
INVERTER SERIA MXZ Typoszereg MXZ gwrntuje cicy, wysokowydjny i elstyczny system, spełnijący wszystkie wymgni w zkresie klimtyzcji powietrz. 6 MXZ-2C30VA MXZ-2C40VA MXZ-2C52VA MXZ-3C54VA MXZ-3C68VA MXZ-4C71VA
Zbiory wyznaczone przez funkcje zdaniowe
 pojęci zbioru i elementu RCHUNEK ZIORÓW zbiór zwier element element nleży do zbioru jest elementem zbioru ( X zbiór wszystkich przedmiotów indywidulnych, których dotyczy dn nuk zbiór pełny (uniwerslny
pojęci zbioru i elementu RCHUNEK ZIORÓW zbiór zwier element element nleży do zbioru jest elementem zbioru ( X zbiór wszystkich przedmiotów indywidulnych, których dotyczy dn nuk zbiór pełny (uniwerslny
BADANIE ZALEŻNOŚCI PRZENIKALNOŚCI MAGNETYCZNEJ
 ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
Oznaczenia: K wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające
 Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Przeguby precyzyjne KTR z łożyskowaniem ślizgowym lub igiełkowym
 Przeguy precyzyjne KTR z łożyskowniem ślizgowym lu igiełkowym Przeguy KTR, to pod względem technicznym, wysokojkościowe elementy do łączeni dwóch włów, o dopuszczlnej wielkości kąt prcy dl pojedynczego
Przeguy precyzyjne KTR z łożyskowniem ślizgowym lu igiełkowym Przeguy KTR, to pod względem technicznym, wysokojkościowe elementy do łączeni dwóch włów, o dopuszczlnej wielkości kąt prcy dl pojedynczego
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM
 ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
Wymagania edukacyjne z matematyki
 Wymgni edukcyjne z mtemtyki LICEUM OGÓLNOKSZTAŁCĄCE Kls II Poniżej przedstwiony zostł podził wymgń edukcyjnych n poszczególne oceny. Wiedz i umiejętności konieczne do opnowni (K) to zgdnieni, które są
Wymgni edukcyjne z mtemtyki LICEUM OGÓLNOKSZTAŁCĄCE Kls II Poniżej przedstwiony zostł podził wymgń edukcyjnych n poszczególne oceny. Wiedz i umiejętności konieczne do opnowni (K) to zgdnieni, które są
Część 2 7. METODA MIESZANA 1 7. METODA MIESZANA
 Część 2 7. METODA MIESZANA 7. 7. METODA MIESZANA Metod mieszn poleg n jednoczesnym wykorzystniu metody sił i metody przemieszczeń przy rozwiązywniu ukłdów sttycznie niewyznczlnych. Nwiązuje on do twierdzeni
Część 2 7. METODA MIESZANA 7. 7. METODA MIESZANA Metod mieszn poleg n jednoczesnym wykorzystniu metody sił i metody przemieszczeń przy rozwiązywniu ukłdów sttycznie niewyznczlnych. Nwiązuje on do twierdzeni
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
zestaw DO ĆWICZEŃ z matematyki
 zestaw DO ĆWICZEŃ z mtemtyki poziom rozszerzony rozumownie i rgumentcj krty prcy ZESTAW I Zdnie 1. Wykż, że odcinek łączący środki dwóch dowolnych oków trójkąt jest równoległy do trzeciego oku i jest równy
zestaw DO ĆWICZEŃ z mtemtyki poziom rozszerzony rozumownie i rgumentcj krty prcy ZESTAW I Zdnie 1. Wykż, że odcinek łączący środki dwóch dowolnych oków trójkąt jest równoległy do trzeciego oku i jest równy
Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor
![Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor](/thumbs/64/52076488.jpg) Wektor N fizce w szkole średniej spotkcie się z dwom tpmi wielkości fizcznch. Jedne z nich, np. ms, tempertur, łdunek elektrczn są opiswne przez jedną liczę; te nzwm wielkościmi sklrnmi, w skrócie - sklrmi.
Wektor N fizce w szkole średniej spotkcie się z dwom tpmi wielkości fizcznch. Jedne z nich, np. ms, tempertur, łdunek elektrczn są opiswne przez jedną liczę; te nzwm wielkościmi sklrnmi, w skrócie - sklrmi.
Matematyka stosowana i metody numeryczne
 Ew Pbisek Adm Wostko Piotr Pluciński Mtemtyk stosown i metody numeryczne Konspekt z wykłdu 0 Cłkownie numeryczne Wzory cłkowni numerycznego pozwlją n obliczenie przybliżonej wrtości cłki: I(f) = f(x) dx
Ew Pbisek Adm Wostko Piotr Pluciński Mtemtyk stosown i metody numeryczne Konspekt z wykłdu 0 Cłkownie numeryczne Wzory cłkowni numerycznego pozwlją n obliczenie przybliżonej wrtości cłki: I(f) = f(x) dx
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka. Poziom rozszerzony. Listopad Wskazówki do rozwiązania zadania =
 Vdemecum GIELDAMATURALNA.PL ODBIERZ KOD DOSTĘPU* Mtemtyk - Twój indywidulny klucz do wiedzy! *Kod n końcu klucz odpowiedzi KRYTERIA OCENIANIA ODPOWIEDZI Prón Mtur z OPERONEM Operon 00% MATURA 07 VA D EMECUM
Vdemecum GIELDAMATURALNA.PL ODBIERZ KOD DOSTĘPU* Mtemtyk - Twój indywidulny klucz do wiedzy! *Kod n końcu klucz odpowiedzi KRYTERIA OCENIANIA ODPOWIEDZI Prón Mtur z OPERONEM Operon 00% MATURA 07 VA D EMECUM
Legenda. Optymalizacja wielopoziomowa Inne typy bramek logicznych System funkcjonalnie pełny
 Dr Glin Criow Legend Optymlizcj wielopoziomow Inne typy brmek logicznych System funkcjonlnie pełny Optymlizcj ukłdów wielopoziomowych Ukłdy wielopoziomowe ukłdy zwierjące więcej niż dw poziomy logiczne.
Dr Glin Criow Legend Optymlizcj wielopoziomow Inne typy brmek logicznych System funkcjonlnie pełny Optymlizcj ukłdów wielopoziomowych Ukłdy wielopoziomowe ukłdy zwierjące więcej niż dw poziomy logiczne.
DZIAŁANIE III.6 ROZWÓJ MIKRO- I MAŁYCH PRZEDSIĘBIORSTW
 DZIAŁANIE III.6 ROZWÓJ MIKRO- I MAŁYCH PRZEDSIĘBIORSTW 1 Nzw progrmu opercyjnego Regionlny Progrm Opercyjny Województw Łódzkiego n lt 2007-2013. 2 Numer i nzw osi priorytetowej Oś priorytetow III: Gospodrk,
DZIAŁANIE III.6 ROZWÓJ MIKRO- I MAŁYCH PRZEDSIĘBIORSTW 1 Nzw progrmu opercyjnego Regionlny Progrm Opercyjny Województw Łódzkiego n lt 2007-2013. 2 Numer i nzw osi priorytetowej Oś priorytetow III: Gospodrk,
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Oscylator harmoniczny tłumiony drgania wymuszone
 Oscylor hroniczny łuiony rgni wyuszone x / Γ x e x Oscylor swoony łuiony Γ x Jeśli Γ
Oscylor hroniczny łuiony rgni wyuszone x / Γ x e x Oscylor swoony łuiony Γ x Jeśli Γ
JĘZYKI FORMALNE I AUTOMATY SKOŃCZONE
 ZBIÓR ZADAŃ do WYKŁADU prof. Tdeusz Krsińskiego JĘZYKI FORMALNE I AUTOMATY SKOŃCZONE rozdził 2. Automty skończone i języki regulrne Wyrżeni i języki regulrne Zdnie 2.1. Wypisz wszystkie słow nleżące do
ZBIÓR ZADAŃ do WYKŁADU prof. Tdeusz Krsińskiego JĘZYKI FORMALNE I AUTOMATY SKOŃCZONE rozdził 2. Automty skończone i języki regulrne Wyrżeni i języki regulrne Zdnie 2.1. Wypisz wszystkie słow nleżące do
Ekoenergetyka Matematyka 1. Wykład 15. CAŁKI OZNACZONE. Egzaminy I termin poniedziałek :00 Aula B sala 12B Wydział Informatyki
 Ekoenergetyk Mtemtyk 1. Wykłd 15. CAŁKI OZNACZONE Egzminy I termin poniedziłek 31.01 14:00 Aul B sl 12B Wydził Informtyki Definicj (podził odcink) II termin poprwkowy czwrtek 9.02 14:00 WE-030 Podziłem
Ekoenergetyk Mtemtyk 1. Wykłd 15. CAŁKI OZNACZONE Egzminy I termin poniedziłek 31.01 14:00 Aul B sl 12B Wydził Informtyki Definicj (podził odcink) II termin poprwkowy czwrtek 9.02 14:00 WE-030 Podziłem
4.5 Deterministyczne i zupełne automaty Moore a i Mealy ego
 4.5 Deterministyczne i zupełne utomty Moore i Mely ego Automty Moore i Mely ego ędziemy rozwżć tylko w rsji deterministycznej i zupełnej. W definicjch tych utomtów nie pojwi się pojęcie ów końcowych, z
4.5 Deterministyczne i zupełne utomty Moore i Mely ego Automty Moore i Mely ego ędziemy rozwżć tylko w rsji deterministycznej i zupełnej. W definicjch tych utomtów nie pojwi się pojęcie ów końcowych, z
Algebra macierzowa. Akademia Morska w Gdyni Katedra Automatyki Okrętowej Teoria sterowania. Mirosław Tomera 1. ELEMENTARNA TEORIA MACIERZOWA
 kdemi Morsk w Gdyni Ktedr utomtyki Okrętowej Teori sterowni lger mcierzow Mirosłw Tomer. ELEMENTRN TEORI MCIERZOW W nowoczesnej teorii sterowni rdzo często istnieje potrze zstosowni notcji mcierzowej uprszczjącej
kdemi Morsk w Gdyni Ktedr utomtyki Okrętowej Teori sterowni lger mcierzow Mirosłw Tomer. ELEMENTRN TEORI MCIERZOW W nowoczesnej teorii sterowni rdzo często istnieje potrze zstosowni notcji mcierzowej uprszczjącej
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 2015/2016
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
Wspomaganie obliczeń za pomocą programu MathCad
 Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Karta oceny merytorycznej wniosku o dofinansowanie projektu konkursowego PO KL 1
 Złącznik 3 Krt oceny merytorycznej wniosku o dofinnsownie konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA WNIOSEK:. NUMER KONKURSU 2/POKL/8.1.1/2010 TYTUŁ PROJEKTU:... SUMA KONTROLNA
Złącznik 3 Krt oceny merytorycznej wniosku o dofinnsownie konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA WNIOSEK:. NUMER KONKURSU 2/POKL/8.1.1/2010 TYTUŁ PROJEKTU:... SUMA KONTROLNA
Całki niewłaściwe. Rozdział Wprowadzenie Całki niewłaściwe I rodzaju
 Rozdził 3 Cłki niewłściwe 3. Wprowdzenie Omwine w poprzednim rozdzile cłki oznczone są cłkmi funkcji ciągłych n przedzile domkniętym, więc funkcji ogrniczonych n przedzile skończonym. Wiele zgdnień prktycznych
Rozdził 3 Cłki niewłściwe 3. Wprowdzenie Omwine w poprzednim rozdzile cłki oznczone są cłkmi funkcji ciągłych n przedzile domkniętym, więc funkcji ogrniczonych n przedzile skończonym. Wiele zgdnień prktycznych
MATURA 2014 z WSiP. Zasady oceniania zadań
 MATURA z WSiP Mtemtyk Poziom podstwowy Zsdy ocenini zdń Copyright by Wydwnictw Szkolne i Pedgogiczne sp. z o.o., Wrszw Krtotek testu Numer zdni 6 7 8 9 6 7 8 9 Uczeń: Sprwdzn umiejętność (z numerem stndrdu)
MATURA z WSiP Mtemtyk Poziom podstwowy Zsdy ocenini zdń Copyright by Wydwnictw Szkolne i Pedgogiczne sp. z o.o., Wrszw Krtotek testu Numer zdni 6 7 8 9 6 7 8 9 Uczeń: Sprwdzn umiejętność (z numerem stndrdu)
O RELACJACH MIĘDZY GRUPĄ OBROTÓW, A GRUPĄ PERMUTACJI
 ZESZYTY NAUKOWE 7-45 Zenon GNIAZDOWSKI O RELACJACH MIĘDZY GRUPĄ OBROTÓW, A GRUPĄ PERMUTACJI Streszczenie W prcy omówiono grupę permutcji osi krtezjńskiego ukłdu odniesieni reprezentowną przez mcierze permutcji,
ZESZYTY NAUKOWE 7-45 Zenon GNIAZDOWSKI O RELACJACH MIĘDZY GRUPĄ OBROTÓW, A GRUPĄ PERMUTACJI Streszczenie W prcy omówiono grupę permutcji osi krtezjńskiego ukłdu odniesieni reprezentowną przez mcierze permutcji,
Wymagania na poszczególne oceny z matematyki w Zespole Szkół im. St. Staszica w Pile. Kl. I poziom podstawowy
 Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
POROZUMIENIE. zawarte w dniu 16 maja 2014 r. w Warszawie, zwane dalej Porozumieniem, pomiędzy:
 POROZUMIENIE w sprwie przeprowdzeni pilotżu systemu komunikcji dl osób niedosłyszących (pętle indukcyjne przenośne) w jednostkch obsługujących użytkowników publicznie dostępnych usług telefonicznych orz
POROZUMIENIE w sprwie przeprowdzeni pilotżu systemu komunikcji dl osób niedosłyszących (pętle indukcyjne przenośne) w jednostkch obsługujących użytkowników publicznie dostępnych usług telefonicznych orz
KSZTAŁTOWANIE ŁUKOWO-KOŁOWEJ LINII ZĘBÓW W UZĘBIENIU CZOŁOWYM NA FREZARCE CNC
 KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 8 nr Archiwum Technologii Mszyn i Automtyzcji 008 PIOTR FRĄCKOWIAK KSZTAŁTOWANIE ŁUKOWO-KOŁOWEJ LINII ZĘBÓW W UZĘBIENIU CZOŁOWYM NA FREZARCE CNC W rtykule
KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 8 nr Archiwum Technologii Mszyn i Automtyzcji 008 PIOTR FRĄCKOWIAK KSZTAŁTOWANIE ŁUKOWO-KOŁOWEJ LINII ZĘBÓW W UZĘBIENIU CZOŁOWYM NA FREZARCE CNC W rtykule
Laura Opalska. Klasa 1. Gimnazjum nr 1 z Oddziałami Integracyjnym i Sportowymi im. Bł. Salomei w Skale
 Trójkąt Pscl od kuchni Kls 1 Gimnzjum nr 1 z Oddziłmi Integrcyjnym i Sportowymi im. Bł. Slomei w Skle ul. Ks.St.Połetk 32 32-043 Skł Gimnzjum nr 1 z Oddziłmi Integrcyjnymi i Sportowymi im. Bł. Slomei w
Trójkąt Pscl od kuchni Kls 1 Gimnzjum nr 1 z Oddziłmi Integrcyjnym i Sportowymi im. Bł. Slomei w Skle ul. Ks.St.Połetk 32 32-043 Skł Gimnzjum nr 1 z Oddziłmi Integrcyjnymi i Sportowymi im. Bł. Slomei w
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE Ib ZAKRES PODSTAWOWY
 . LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje liczbę do odpowiedniego zbioru liczb stosuje cechy podzielności
. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje liczbę do odpowiedniego zbioru liczb stosuje cechy podzielności
T-08 Sprawozdanie o przewozach morską i przybrzeżną flotą transportową
 GŁÓWNY URZĄD STATYSTYCZNY, l. Niepodległości 208, 00-925 Wrszw www.stt.gov.pl Nzw i dres jednostki sprwozdwczej T-08 Sprwozdnie o przewozch morską i przyrzeżną flotą trnsportową Portl sprwozdwczy GUS www.stt.gov.pl
GŁÓWNY URZĄD STATYSTYCZNY, l. Niepodległości 208, 00-925 Wrszw www.stt.gov.pl Nzw i dres jednostki sprwozdwczej T-08 Sprwozdnie o przewozch morską i przyrzeżną flotą trnsportową Portl sprwozdwczy GUS www.stt.gov.pl
WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH
 Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
