Inżynieria Finansowa: 6. Wycena martyngałowa, dynamiczna replikacja i model dwumianowy
|
|
|
- Sławomir Jabłoński
- 6 lat temu
- Przeglądów:
Transkrypt
1 Inżynieria Finansowa: 6. Wycena martyngałowa, dynamiczna replikacja i model dwumianowy Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Kwiecień 2017 r. Warszawa, Szkoła Główna Handlowa
2 Wycena pochodnych: ułatwiona Stworzenie statycznego portfela replikującego służącego do określenia ceny pewnego instrumentu wymaga: Istnienia odpowiedniej ilości płynnych aktywów bazowych Liniowej zależności pomiędzy ceną instrumentu replikowanego i aktywów użytych do replikacji Jeśli cena instrumentu pochodnego zmienia się liniowo wraz ze zmianą ceny aktywu bazowego możliwa jest statyczna replikacja, gdyż wartość portfela replikującego zmienia się proporcjonalnie do zmian cen bazowego
3 Wycena pochodnych: utrudniona Kiedy: Istnieje odpowiednia ilość płynnych aktywów bazowych, ale Zależności pomiędzy ceną instrumentu replikowanego i aktywów bazowych (używanych do replikacji) jest nieliniowa zmiany cen obydwu nie są stabilnie proporcjonalne Konieczna jest dynamiczna replikacja.
4 Przykład: zabezpieczenie pozycji opcyjnej Wystawiliśmy opcję kupna 100 akcji o terminie zapadalności 1Y, K=105, przy cenie bieżącej S0=100. Stopa procentowa wynosi 5%. Chcemy zabezpieczyć ryzyko, jakie generuje pozycja opcyjna (koszt tego zabezpieczenia powie nam jednocześnie ile opcja powinna kosztować). Rozważmy trzy strategie zabezpieczenia: 1. Kupujemy 100 akcji już dziś za pożyczone pieniądze 2. Brak zakupu jakichkolwiek akcji 3. Kupujemy 50 akcji już dziś za pożyczone pieniądze (np. szacujemy, że istnieje 50% szans na wykonanie kontraktu) Przy trzech scenariuszach zmiany cen: 1. Cena wzrośnie do Cena pozostanie bez zmian 3. Cena spadnie do 80
5 Przykład: zabezpieczenie pozycji opcyjnej Wyniki z poszczególnych strategii są następujące: 1. π T = max S T K, 0 + S T K e rτ S t π T = max S T K, π T = max S T K, S T K e rτ S t % 0% 50% S T = ,5 S T = ,5 S T = ,5 Wniosek: żadna ze strategii nas nie zabezpieczyła (zabezpieczenie oznaczałoby, że niezależnie od scenariusza nasz wynik pozostaje taki sam i wynosi 0)
6 Dynamiczna replikacja Portfel replikujący: Dokładnie odzwierciedla końcowe wypłaty z wycenianego instrumentu Nie wymaga wypłat ani wpłat pieniędzy Zwykle ma zmienną strukturę na przestrzeni czasu Ta metoda wymaga określenia charakteru współzależności pomiędzy cenami instrumentu wycenianego (replikowanego) i aktywu bazowego Model (drzewo) dwumianowe Równania różniczkowe cząstkowe Stochastyczne równania różniczkowe
7 Jednookresowy model dwumianowy - schemat p S T,U = S t0 U S t0 1 p S T,D = S t0 D t0 T
8 Jednookresowy model dwumianowy - założenia Rozpatrujemy tylko dwa punkty w czasie: t0 (w skrócie 0) oraz T Dwa aktywa na rynku: pozbawiona ryzyka obligacja zerokuponowa B(0,T), która jest także utożsamiana z rachunkiem bankowym i daje deterministyczny dochód B 0, T = DF 0, T = 1/(1 + Lr) = e rτ gdzie τ = (0, T) Aktywo obarczone ryzykiem, którego wartość (cena) w chwili obecnej jest znana: S 0 nie przynosi dochodu w okresie [0,T] i ma losową wartość (cenę) w T: gdzie 0 < D < U S T = ቊ S 0U z prawdopodobieństwem "p" S 0 D z prawdopodobieństwem "1 p"
9 Jednookresowy model dwumianowy - założenia Wartość ryzykownego aktywu w momencie T możemy także zapisać jako: S T = S 0 Z gdzie Z jest zmienną losową: Z = ቄ U D z prawdopodobieństwem "p" z prawdopodobieństwem "1 p" Wartość europejskiego instrument pochodnego X wystawionego na aktywo S w terminie zapadalności jest zmienną losową opisanego pewną funkcją φ: X T = φ(s T ) Np. dla opcji kupna ta funkcja ma postać: X T = φ(s T ) = max S T K, 0 = max S 0 Z K, 0
10 Model dwumianowy - przykład U = = D = = 30 Bieżąca cena obligacji wolnej od ryzyka: B 0, T = Cena obligacji w terminie zapadalności (pewna): B T = 1 B 0, T = 1/(1 + r) zatem stopa wolna od ryzyka: r = 3.6% Jak jest oczekiwana stopa zwrotu z ryzykownego aktywu?
11 Przykład c.d. 0.7 S T = 35.1 U = = 41 B(T) = 1 S 0 = 35.1 B(0, T) = E P S T = = 37.7 stąd: p = 35.1 < e Cena S 0 jest niższa niż bieżąca wartość oczekiwana wypłat e r E P S T : Jaka jest oczekiwana stopa zwrotu z akcji? S T = 35.1 D = = 30 B(T) = 1 E P R S = p S 0U S p S 0D = S R S = 1 + r = 7.4% = = 1.074
12 Cena = wartość oczekiwana wypłat? Zgromadziliśmy 10 mln PLN majątku: W t =10 mln Czego spodziewamy się w przyszłości? P W t+1 = 0 = 1% P W t+1 = W t = 98% P W t+1 = 2W t = 1% Stany natury i przypisane im prawdopodobieństwa 1% 98% 1% Wypłaty
13 Cena = wartość oczekiwana wypłat? Oferuje się nam instrumenty U i D, gdzie U wypłaca 10 mln w pozytywnym scenariuszu, a D 10 mln w negatywnym. Stany natury i przypisane im prawdopodobieństwa 1% 98% 1% Wypłaty D Pytanie: Czy za instrument U i D bylibyśmy skłonni zapłacić tyle samo? U
14 WZÓR wyceny aktywów Cena p i = E(mx i ) Oczekiwania (prawdopodobieństwo) Czynnik dyskontujący Wypłaty Asset prices should equal expected discounted cashflows John Cochrane, JoF (2011) Co jest ważne? Wypłaty x Mechanizmy oczekiwań E Czynnik dyskontujący m (zależny od preferencji stochastic discount factor, zwany zależnie od okoliczności także state-price density, pricing kernel)
15 Przykład Przestrzeń stanów S=(załamanie gospodarcze, kryzys, stagnacja, wzrost, silny wzrost) π S = (2%, 10%, 20%, 50%, 18%) x 1 obligacja bez ryzyka x 2 obligacja korporacyjna o ratingu A x 3 akcja x 4 ubezpieczenie x 5 venture capital X = x 1s1 x 1s5 = x 5s1 x 5s
16 Wycena - przykład Preferencje Co jest dla nas ważne (zwykle z punktu widzenia majątku/konsumpcji)? S=(załamanie gospodarcze, kryzys, stagnacja, wzrost, silny wzrost) M S = Ceny p x 1 = E mx 1 = π s m s x 1s = = = = p X = s
17 Przykład c.d. Ceny cd. Ile kosztowałyby papiery, gdyby patrzeć tylko na wartość oczekiwaną? Jak obie ceny mają się do siebie? p x 1 = E x 1 = π s x 1s = = = 1 p X = p X p X = = (1 + r) Ich relacja określa oczekiwaną stopę zwrotu z aktywu, która stanowi kompensację za ryzyko s
18 Równoważne spojrzenia na równanie wyceny Stochastyczny czynnik dyskontujący p(x) = E(mx) Ceny przestrzeni stanów (Arrow-Debreu) p(x) = pc s x s Miara martyngałowa (equivalent martingale measure, risk-neutral valuation) p(x) = 1 1+r f E Q (x) gdzie π Q s = R f pc s
19 Ceny przestrzeni stanów (AD) Niech S będzie zmienną losową opisującą przyszłe stany natury, a s ich realizacjami Instrument Arrow-Debreu wypłaca 1 jeśli wystąpi stan s i 0 w przeciwnym wypadku. Cena takiego instrumenty to pc(s). Ile kosztuje instrument, który wypłaca x(s)? Zdefiniujmy pc s = m s π(s) 1, wtedy p(x) = π s m s x s = pc s x(s) Cena aktywu jest sumą cen składających się na niego instrumentów A-D. Inżynieria finansowa wydobywa ceny AD z cen rynkowych.
20 Ceny przestrzeni stanów (AD) A gdybyśmy chcieli stworzyć aktywa, które wypłacają 1 w pewnym stanie i 0 w pozostałych? Portfel je opisujący byłby macierzą jednostkową XX 1 = I = Ile by te aktywa kosztowały? p = X q q = X 1 p q = Ceny q są iloczynem prawdopodobieństw każdego ze stanów i przypisywanej mu wagi. p(x) = pc s x s = π s m(s) x s Mając je możemy wycenić dowolny papier
21 Wycena arbitrażowa Ile kosztowałoby aktywo dające poniższe wypłaty? x 6 = Zwrócimy uwagę, że składa się ona z 4 instrumentów A-D dla pierwszego stanu, 1 dla drugiego i 0.5 dla trzeciego. Mając ceny A-D q = przykładamy je do składu dowolnego portfela p(x 6 ) = i otrzymujemy cenę tegoż portfela p(x 6 ) = W jakich warunkach możemy w jednoznaczny sposób uzyskać ceny A-D?
22 Kompletny rynek Rynek jest kompletny jeśli za pomocą odpowiedniego portfela inwestycyjnego można otrzymać dowolną wypłatę we wszystkich stanach Warunek konieczny i wystarczający: rz(m) = S (tzn. J S) X = Jeśli rynek jest kompletny możemy jednoznacznie odtworzyć ceny A-D. Portfel je opisujący byłby macierzą jednostkową XX 1 = I = Jeśli nie jest kompletny, nie można odwrócić macierzy, a równanie opisujące ceny A-D ma wiele rozwiązań (jest nieoznaczone): wiele kombinacji cen A-D daje ceny rynkowe
23 Risk-neutral valuation Zdefiniujmy q s jako: q s = R f m s π s = R f pc s = pc s /E(m) q s spełnia aksjomaty prawdopodobieństwa: Jest wszędzie dodatnie, mniejsze (równe) 1 i sumuje się do 1 Zapiszmy równanie dla ceny jeszcze raz: p x = pc s x s = 1 q s x s = EQ x R f R f Cena równa się zdyskontowanej wartości oczekiwanej (liczonej wg nowej miary prawdopodobieństwa) Nazywa się ją także ekwiwalentną miarą martyngałową, gdyż deflując ceny ryzykownych aktywów ceną obligacji : p x = E Q x 1 + r f
24 Risk-neutral valuation - intuicja Ceny A-D (EMM) Risk-neutral measure Wypłata Cena = Prawdopodobieństwo Użyteczność, czynnik dyskontujący Źródło: Opracowanie własne 8
25 Model dwumianowy i risk-neutral pricing - przykład? 35.1 U = = ? 35.1 D = = 30 Czy możemy znaleźć takie wartości prawdopodobieństwa dla których cena bieżąca będzie równa zdyskontowanej wartości oczekiwanej przyszłych cen? S 0 = 1 R f E Q X T Te nowe prawdopodobieństwa zawierałyby łączny wpływ obiektywnego prawdopodobieństwa i premii za ryzyka różnych stanów.
26 Model dwumianowy - rozwiązanie Szukamy takich q U, D by: S 0 = 1 R f E Q S T = 1 R f (q U S 0 U + q D S 0 D) Uprościmy zapis q U = q U pamiętając, że q U = 1 q D 35.1 = (qu (1 q U ) ) Dzielimy obie strony przez S 0, mnożymy przez 1 + r f : 1 + r f = q U U + (1 q U ) D q U = 1 + r f D U D = = 0.58 q D = r f D U D = U 1 + r f U D = = 0.42
27 Dwa prawdopodobieństwa zmiana miary Jak te wartości miały się do obiektywnych prawdopodobieństw? q U = 0.58 podczas gdy p U = 0.7 q D = 0.42 podczas gdy p D = 0.3 Dzięki zmianie miary, tak by nowe prawdopodobieństwo uwzględniało zarówno prawdopodobieństwo zajścia, jak i wagę poszczególnych zdarzeń aktywa możemy wyceniać w formie wartości oczekiwanej. E Q X T 1 + r f = E P mx T
28 Model dwumianowy inne spojrzenie Nasz rynek możemy przedstawić jako (wiersze to aktywa, kolumny to wypłaty w poszczególnych stanach): = pc D pc U (Rynek jest kompletny, bo liczba stanów równa się liczbie niezależnych aktywów i można odwrócić macierz portfela) pc D pc U = pc D pc U = Jak ceny AD wiążą się z prawdopodobieństwami R-N? q s = R f pc s q D q U = = pc D pc U R f =
29 Wycena instrumentu pochodnego Chcemy wycenić roczną opcję z kursem wykonania K=35.1 Ile powinna kosztować? S 0 = 35.1 B 0, T = S T = 35.1 U = = 41 B(T) = 1 C T = max S T K, 0 = 5. 9 C 0 (K = 35. 1, T) S T = 35.1 D = = 30 B(T) = 1 C T = max S T K, 0 = 0
30 Wycena risk-neutral (EMM) Każdy instrument możemy wycenić stosując prawdopodobieństwa martyngałowe (risk-neutral): X 0 = 1 R f E Q X T C 0 = 1 R f q U C T (U) + q D C T (D) C 0 = qu q D 0 Jak wcześniej policzyliśmy q U = 0.58 a q D = 0.42 C 0 = = 3.3 Przy okazji: jaka jest oczekiwana stopa zwrotu z opcji E P C T? E P C T /C 0 = = r = 25.2% 3.3
31 Risk-neutral valuation - intuicja Aktywo 1 Aktywo 2 (np. risk-free) P up Q = p up m up S T,U = S t0 U P up Q = p up m up B T,U = 1 S t0 B t0 Q P down = p down m down S T,D = S t0 D Q P down = p down m down B T,D = 1 Prawdopodobieństwo Użyteczność, czynnik dyskontujący Źródło: Opracowanie własne 8
32 Risk-neutral valuation - intuicja Aktywo 1 Aktywo 2 (np. risk-free) P up Q = p up m up S T,U = S t0 U P up Q = p up m up B T,U = 1 S t0 B t0 Q P down = p down m down S T,D = S t0 D Q P down = p down m down B T,D = 1 Zupełny rynek: liczba stanów = liczbie niezależnych instrumentów, można jednoznacznie wyznaczyć ceny A-D i miarę martyngałową. Nasz rynek: dwa stany, dwa instrumenty Dwa równania, dwie niewiadome = jedno rozwiązanie = R f P up Q Q P down 8
33 Model dwumianowy - warunek braku arbitrażu Jeśli zachodzi: 1 + r f = q U U + q D D To spełnione jest również: D < 1 + r f < U A na rynku nie jest możliwy arbitraż.
34 Portfel - definicja Portfel rynkowy h definiujemy jako parę: h = (x, y) gdzie x jest kwotą zainwestowaną w obligację, a y ilość ryzykownego aktywu; x, y (, + ) Przykład: Portfel h=(-50,50): pożyczamy 50 i kupujemy 50 akcji Portfel h=(10,-50): sprzedajemy 50 akcji i składamy depozyt Wartość portfela w czasie t0: V 0 h = x + ys 0 Wartość portfela w czasie T jest zmienną losową zależną od Z: V T h = x(1 + Lr) + ys 0 Z L to operator przenoszący roczną stopę na czas trwania kontraktu
35 Portfel arbitrażowy To portfel rynkowy h(x,y) spełniający trzy warunki: Koszt jego utworzenia wynosi 0: V 0 h = 0 Na pewno nie przyniesie strat: P(V T h 0) = 1 Być może przyniesie zysk: P(V T h > 0) > 0
36 Brak arbitrażu - dowód Konstruujemy portfel ( y S 0 to ilość akcji w portfelu, czyli ich wartość to y) V 0 h( y, y S 0 ) = 0 W terminie zapadalności jego wartość wyniesie: V T h = y (U 1 + r f ) y (D 1 + r f ) w stanie"u" w stanie"d" Jeśli 1 + r f D U V T h = y (U 1 + r f ) 0 y (D 1 + r f ) 0 w stanie"u" w stanie"d" Czyli mamy arbitraż. (jeśli D U 1 + r f konstruujemy odwrotny portfel)
37 Wycena na bazie replikacji-przykład Rozpatrzmy portfel składający się z: Δ jednostek aktywu bazowego S 0 sprzedanego instrumentu pochodnego X T po cenie Π 0 (X T ) (opcji kupna K=35.1) Wartość portfela w terminie zapadalności wynosi: V T h = S 0U φ(s 0 U) S 0 D φ(s 0 D) w stanie"u" w stanie "D" V T h = ቄ 30 0 w stanie"u" w stanie "D" Chcemy by portfel był pozbawiony ryzyka, tj. by jego wartość była taka sama niezależnie od stanu rynku: S 0 U φ(s 0 U) = S 0 D φ(s 0 D) = 30
38 Wycena na bazie replikacji - przykład c.d. Rozwiążmy z uwagi na Δ: = φ(s 0U) φ(s 0 D) S 0 (U D) = = 0.53 Przy ilości Δ zakupionego aktywu bazowego zmiany ceny obydwu składników portfela wzajemnie się znoszą Koszt utworzenia portfela w czasie 0 wynosi: V 0 h = S 0 Π 0 (X T ) Jako pozbawiony ryzyka (bo jego wartość jest taka sama niezależnie od stanu natury w przyszłości) musi dawać dochód równy obligacji B(0,T): 1 + Lr f V 0 h = V T h 1 + Lr f S 0 π X 0 = S 0 U φ(s 0 U) = S 0 D φ(s 0 D)
39 Wycena na bazie replikacji - przykład c.d. Rozwiązujemy równanie z uwagi na Π X 0 : 1 + Lr f S 0 Π 0 (X T ) = S 0 U φ(s 0 U) = S 0 D φ(s 0 D) Π 0 (X T ) = S r f (S 0 U φ(s 0 U)) Używając naszego przykładu liczbowego: Π 0 (X T ) = ( ) = 3.3 czyli tyle samo ile stosując wycenę risk-neutral!
40 Wycena na bazie replikacji - założenia Cenę instrumentu pochodnego Π t (X) powinna być równa kosztowi jego replikacji, dokonywanej w oparciu o aktywa bazowe: Π t X = V t h gdzie h = x, y, x jest kwotą zainwestowaną w obligację, a y ilością ryzykownego aktywu, czyli V 0 h = x + S 0 y Instrument pochodny jest osiągalny jeśli: P(V T h = Π T X ) = 1 Portfel h(x) nazywamy replikującym, a h zabezpieczającym Aby instrument był osiągalny konieczne jest by: V T h = φ(s 0U) φ(s 0 D) w stanie"u" w stanie "D"
41 Wycena na bazie replikacji - założenia Z warunku: V T h = φ(s 0U) φ(s 0 D) w stanie"u" w stanie "D" oraz V T h = 1 + Lr f x + S 0 Zy wynika, że (przyrównujemy wypłat w obydwu stanach (Rów. 1) z wartością portfela (Rów. 2)): 1 + Lr f x + S 0 Uy = φ(s 0 U) 1 + Lr f x + S 0 Dy = φ(s 0 D) Rozwiązując układ równań otrzymujemy: x = 1 Uφ(S 0 D) Dφ(S 0 U) = Lr f (U D) y = φ(s 0U) φ(s 0 D) = = S 0 (U D)
42 Wycena na bazie replikacji inne spojrzenie Nasz rynek możemy przedstawić jako: = pc D pc U Gdzie wiersze odpowiadają poszczególnym aktywów, a kolumny stanom. Zapisujemy każdy aktyw jak zbiór instrumentów AD Jeśli mamy sprzedać obligacji za 15.1, to ile ich mamy sprzedać? = Tworzymy portfel przy kupując i sprzedając odpowiednie ilości x i y: = = 3.3
43 Replikacja a risk-neutral Jak jest relacja pomiędzy dwiema metodami? Zacznijmy od replikacji: Π 0 X = x + S 0 y = 1 Uφ(S 0 D) Dφ(S 0 U) φ(s 0 U) φ(s 0 D) + S 1 + Lr f (U D) 0 S 0 (U D) Mnożymy drugi wyraz przez 1 + Lr f i porządkujemy zmienne φ(s 0 D): = Lr f D φ(s 1 + Lr f U D 0 U) + U 1 + Lr f U D φ(s 0 D) = Lr f q U φ(s 0 U) + q D φ(s 0 D) = Lr f E Q (φ(s T )) = 1 R f E Q X T
44 Dwa spojrzenia Przy założeniu kompletności rynku inżynieria finansowa sprowadza się do: Wydobywania z cen aktywów na rynku cen AD i używaniu ich do wyceny dowolnego instrumentu, którego wypłaty w różnych stanach możemy określić (risk-neutral valuation) lub do tworzenia portfela, którego skład (pod względem instrumentów AD) dokładnie odzwierciedla skład replikowanego instrumentu (replikacja) Koncepcyjnie wydają się różne, ale (przy założeniu zupełnego rynku) dają ten sam rezultat.
45 Wycena martyngałowa Co musimy znać, by wyznaczyć miarę martyngałową? Cenę bieżącą i cenę (wypłatę) w przyszłych stanach. Innymi słowy musimy znać charakterystykę procesu, który opisuje zmiany ceny. Jeśli przyjmiemy złe założenia co do powyższego procesu, to wycena będzie niepoprawna i może prowadzić do arbitrażu. Czego nie musimy znać? Prawdopodobieństwa wystąpienia poszczególnych stanów.
Moduł 1: Opcje wprowadzenie i przypomnienie
 Piotr Bańbuła Katedra Ekonomii Ilościowej Szkoła Główna Handlowa w Warszawie Styczeń 2018 Materiał e-learningowy w formie 2 modułów z dodatkowym zestawem pytań dotyczącym całego wykładu, mającym stanowić
Piotr Bańbuła Katedra Ekonomii Ilościowej Szkoła Główna Handlowa w Warszawie Styczeń 2018 Materiał e-learningowy w formie 2 modułów z dodatkowym zestawem pytań dotyczącym całego wykładu, mającym stanowić
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Inżynieria Finansowa: 5. Opcje
 Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE wiecień 2017 r. Warszawa, Szkoła Główna Handlowa Amounts outstanding of assets and derivatives Derivatives Derivatives Note:
Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE wiecień 2017 r. Warszawa, Szkoła Główna Handlowa Amounts outstanding of assets and derivatives Derivatives Derivatives Note:
Zatem, jest wartością portfela (wealth) w chwili,. j=1
 Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Matematyka finansowa 20.06.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż
 Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż Piotr Bańbuła pbanbu@sgh.waw.pl Katedra Rynków i Instytucji Finansowych, KES 5 marca 2014 r. Warszawa, Szkoła Główna Handlowa
Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż Piotr Bańbuła pbanbu@sgh.waw.pl Katedra Rynków i Instytucji Finansowych, KES 5 marca 2014 r. Warszawa, Szkoła Główna Handlowa
Matematyka finansowa 8.12.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 30.09.2013 r. Komisja Egzaminacyjna dla Aktuariuszy. LXV Egzamin dla Aktuariuszy z 30 września 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 15.12.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Opcje - wprowadzenie. Mała powtórka: instrumenty liniowe. Anna Chmielewska, SGH,
 Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Inżynieria Finansowa: 5. Opcje
 Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE Listopad 2014 r. Warszawa, Szkoła Główna Handlowa Opcje - typy Opcja jest asymetrycznym instrumentem. Opcja (standardowa, prosta,
Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE Listopad 2014 r. Warszawa, Szkoła Główna Handlowa Opcje - typy Opcja jest asymetrycznym instrumentem. Opcja (standardowa, prosta,
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja
 Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę terminową
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę terminową
Forward Rate Agreement
 Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Opcje (2) delta hedging strategie opcyjne
 Opcje (2) delta hedging strategie opcyjne 1 Co robi market-maker wystawiający opcje? Najchętniej zawiera transakcję przeciwstawną. Ale jeśli nie może, to ją replikuje. Dealer wystawił opcję call, więc
Opcje (2) delta hedging strategie opcyjne 1 Co robi market-maker wystawiający opcje? Najchętniej zawiera transakcję przeciwstawną. Ale jeśli nie może, to ją replikuje. Dealer wystawił opcję call, więc
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
R NKI K I F I F N N NSOW OPCJE
 RYNKI FINANSOWE OPCJE Wymagania dotyczące opcji Standard opcji Interpretacja nazw Sposoby ustalania ostatecznej ceny rozliczeniowej dla opcji na GPW OPCJE - definicja Kontrakt finansowy, w którym kupujący
RYNKI FINANSOWE OPCJE Wymagania dotyczące opcji Standard opcji Interpretacja nazw Sposoby ustalania ostatecznej ceny rozliczeniowej dla opcji na GPW OPCJE - definicja Kontrakt finansowy, w którym kupujący
Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym. Opcje Strategie opcyjne
 Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym Opcje Strategie opcyjne 1 Współczynniki greckie Współczynniki greckie określają o ile zmieni się kurs opcji w wyniku zmiany wartości poszczególnych
Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym Opcje Strategie opcyjne 1 Współczynniki greckie Współczynniki greckie określają o ile zmieni się kurs opcji w wyniku zmiany wartości poszczególnych
Wycena opcji. Dr inż. Bożena Mielczarek
 Wycena opcji Dr inż. Bożena Mielczarek Stock Price Wahania ceny akcji Cena jednostki podlega niewielkim wahaniom dziennym (miesięcznym) wykazując jednak stały trend wznoszący. Cena może się doraźnie obniżać,
Wycena opcji Dr inż. Bożena Mielczarek Stock Price Wahania ceny akcji Cena jednostki podlega niewielkim wahaniom dziennym (miesięcznym) wykazując jednak stały trend wznoszący. Cena może się doraźnie obniżać,
3.1 Analiza zysków i strat
 3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż
 Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż Piotr Bańbuła pbanbu@sgh.waw.pl Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zajęcia
Inżynieria Finansowa: 1. Wprowadzenie: zasady wyceny, spekulacja, arbitraż Piotr Bańbuła pbanbu@sgh.waw.pl Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zajęcia
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Komisja Egzaminacyjna dla Aktuariuszy. XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja
 Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę
Artykuł przedstawia w zarysie problematykę inŝynierii finansowej, wyjaśniając podstawowe pojęcia, takie jak:
 InŜynieria finansowa Prof. Leszek S. Zaremba Autor jest wykładowcą w POU WyŜsza Szkoła Zarządzania / Polish Open University wprowadza do programu nauczania wykład poświęcony inŝynierii finansowej, przeznaczony
InŜynieria finansowa Prof. Leszek S. Zaremba Autor jest wykładowcą w POU WyŜsza Szkoła Zarządzania / Polish Open University wprowadza do programu nauczania wykład poświęcony inŝynierii finansowej, przeznaczony
istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe
 Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Matematyka finansowa 26.05.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Matematyka finansowa 15.06.2015 r. Komisja Egzaminacyjna dla Aktuariuszy. LXXI Egzamin dla Aktuariuszy z 15 czerwca 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Opcje. istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii).
 Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Takie, w których funkcja wypłaty jest liniowa (np. forward, futures,
Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Takie, w których funkcja wypłaty jest liniowa (np. forward, futures,
Inżynieria Finansowa: 4. FRA i IRS
 Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
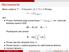 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Inżynieria Finansowa - Egzamin - 28 stycznia Rozwiązania zadań Wersja z dnia 1 marca 2005, z drobnymi poprawkami
 Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Pożyczki papierów i krótka sprzedaż w działalności inwestycyjnej
 Giełda Papierów Wartościowych w Warszawie S.A. Pożyczki papierów i krótka sprzedaż w działalności inwestycyjnej Krzysztof Mejszutowicz Dział Instrumentów Finansowych Dlaczego krótka sprzedaż jest niezbędna
Giełda Papierów Wartościowych w Warszawie S.A. Pożyczki papierów i krótka sprzedaż w działalności inwestycyjnej Krzysztof Mejszutowicz Dział Instrumentów Finansowych Dlaczego krótka sprzedaż jest niezbędna
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Strategie inwestycyjne na rynku kapitałowym Inwestowanie na rynku dr Piotr Stobiecki Uniwersytet Ekonomiczny w Poznaniu 13 października 2011 r. PLAN WYKŁADU I. Wprowadzenie
Akademia Młodego Ekonomisty Strategie inwestycyjne na rynku kapitałowym Inwestowanie na rynku dr Piotr Stobiecki Uniwersytet Ekonomiczny w Poznaniu 13 października 2011 r. PLAN WYKŁADU I. Wprowadzenie
Inwestor musi wybrać następujące parametry: instrument bazowy, rodzaj opcji (kupna lub sprzedaży, kurs wykonania i termin wygaśnięcia.
 Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
3.1 Analiza zysków i strat
 3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty podniesione.
3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty podniesione.
Czas dyskretny. 1 Modele o jednym okresie. 1.1 Model dwumianowy
 Część I Czas dyskretny Kursy otwarcia czy zamknięcia pojawiaja się w kolejnych ustalonych momentach czasu. Jeśli pominiemy dni wolne od handlu otrzymamy ciag kolejnych momentów pojawiania się notowań (0,
Część I Czas dyskretny Kursy otwarcia czy zamknięcia pojawiaja się w kolejnych ustalonych momentach czasu. Jeśli pominiemy dni wolne od handlu otrzymamy ciag kolejnych momentów pojawiania się notowań (0,
WERSJA TESTU A. Komisja Egzaminacyjna dla Aktuariuszy. XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. RozwaŜmy
Komisja Egzaminacyjna dla Aktuariuszy XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. RozwaŜmy
7.2. Rozwiąż problem z zadania 7.1 stosując Twierdzenie 7.16.
 Rozdział 7 Funkcje użyteczności 7 Rozważ model dwumianowy z cenami akcji S0 R { S S = U = S0 + U z prawdopodobieństwem p S D = S0 + D z prawdopodobieństwem p oraz walorem wolnym od ryzyka A0 = A = + r
Rozdział 7 Funkcje użyteczności 7 Rozważ model dwumianowy z cenami akcji S0 R { S S = U = S0 + U z prawdopodobieństwem p S D = S0 + D z prawdopodobieństwem p oraz walorem wolnym od ryzyka A0 = A = + r
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Inżynieria Finansowa: 4. FRA i Swapy
 Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
2010 W. W. Norton & Company, Inc. Wybór Międzyokresowy
 2010 W. W. Norton & Company, Inc. Wybór Międzyokresowy Wybór Międzyokresowy Dochód często jest otrzymywany w stałych kwotach, np. miesięczna pensja. Jaki jest podział dochodu na kolejne miesiące? (oszczędności
2010 W. W. Norton & Company, Inc. Wybór Międzyokresowy Wybór Międzyokresowy Dochód często jest otrzymywany w stałych kwotach, np. miesięczna pensja. Jaki jest podział dochodu na kolejne miesiące? (oszczędności
Opcje giełdowe. Wprowadzenie teoretyczne oraz zasady obrotu
 Opcje giełdowe Wprowadzenie teoretyczne oraz zasady obrotu NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny (kontrakt opcyjny), Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach
Opcje giełdowe Wprowadzenie teoretyczne oraz zasady obrotu NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny (kontrakt opcyjny), Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
STOPA DYSKONTOWA 1+ =
 Piotr Cegielski, MAI, MRICS, CCIM STOPA DYSKONTOWA (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 10 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Piotr Cegielski, MAI, MRICS, CCIM STOPA DYSKONTOWA (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 10 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa
 Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa Rozpisywanie przepływów gotówkowych, zabezpieczanie, spekulacja: 1. Za 9 miesięcy musisz zapłacić za wycieczkę 1500 EUR. Posiadasz konto
Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa Rozpisywanie przepływów gotówkowych, zabezpieczanie, spekulacja: 1. Za 9 miesięcy musisz zapłacić za wycieczkę 1500 EUR. Posiadasz konto
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
4.5. Obligacja o zmiennym oprocentowaniu
 .5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
.5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
1) jednostka posiada wystarczające środki aby zakupić walutę w dniu podpisania kontraktu
 Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
OGŁOSZENIE O ZMIANIE STATUTU SEZAM IX FUNDUSZU INWESTYCYJNEGO ZAMKNIĘTEGO AKTYWÓW NIEPUBLICZNYCH Z DNIA 16 STYCZNIA 2014 R.
 OGŁOSZENIE O ZMIANIE STATUTU SEZAM IX FUNDUSZU INWESTYCYJNEGO ZAMKNIĘTEGO AKTYWÓW NIEPUBLICZNYCH Z DNIA 16 STYCZNIA 2014 R. Niniejszym, SKARBIEC Towarzystwo Funduszy Inwestycyjnych S.A., na podstawie art.
OGŁOSZENIE O ZMIANIE STATUTU SEZAM IX FUNDUSZU INWESTYCYJNEGO ZAMKNIĘTEGO AKTYWÓW NIEPUBLICZNYCH Z DNIA 16 STYCZNIA 2014 R. Niniejszym, SKARBIEC Towarzystwo Funduszy Inwestycyjnych S.A., na podstawie art.
Zagadnienia przygotowujące do egzaminu z wykładu Inżynieria Finansowa w semestrze zimowym 2013/2014
 Zagadnienia przygotowujące do egzaminu z wykładu Inżynieria Finansowa w semestrze zimowym 2013/2014 Jakie warunki musi spełniać strategia inwestycyjna, by z teoretycznego punktu widzenia móc nazwać ją
Zagadnienia przygotowujące do egzaminu z wykładu Inżynieria Finansowa w semestrze zimowym 2013/2014 Jakie warunki musi spełniać strategia inwestycyjna, by z teoretycznego punktu widzenia móc nazwać ją
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures
 10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
- w art. 8 ust. 3 Statutu otrzymuje nowe, następujące brzmienie:
 KBC Towarzystwo Funduszy Inwestycyjnych S.A. działające, jako organ KBC Alfa Specjalistycznego Funduszu Inwestycyjnego Otwartego, uprzejmie informuje o dokonaniu zmian statutu dotyczących polityki inwestycyjnej
KBC Towarzystwo Funduszy Inwestycyjnych S.A. działające, jako organ KBC Alfa Specjalistycznego Funduszu Inwestycyjnego Otwartego, uprzejmie informuje o dokonaniu zmian statutu dotyczących polityki inwestycyjnej
Lokalna odwracalność odwzorowań, odwzorowania uwikłane
 Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Teoria opcji 2018/19. Instytut Matematyki Uniwersytet Gdański. (IM UG) Teoria opcji 1 / 49
 Teoria opcji Instytut Matematyki Uniwersytet Gdański 2018/19 (IM UG) Teoria opcji 1 / 49 Sprawy organizacyjne Kontakt i strona E-mail: mwrzosek@mat.ug.edu.pl Konsultacje: środa, 12 14, p.323 Materiały:
Teoria opcji Instytut Matematyki Uniwersytet Gdański 2018/19 (IM UG) Teoria opcji 1 / 49 Sprawy organizacyjne Kontakt i strona E-mail: mwrzosek@mat.ug.edu.pl Konsultacje: środa, 12 14, p.323 Materiały:
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty dla
Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty dla
STOPA ZWROTU NIEUBEZPIECZONY PARYTET STÓP PROCENTOWYCH
 STOPA ZWROTU 1 Stopy zwrotu z aktywów denominowanych w złotówkach i walucie zagranicznej mówią nam jak ich wartości zmieniają się w ciągu pewnego okresu czasu. Inną informacją, której potrzebujemy by móc
STOPA ZWROTU 1 Stopy zwrotu z aktywów denominowanych w złotówkach i walucie zagranicznej mówią nam jak ich wartości zmieniają się w ciągu pewnego okresu czasu. Inną informacją, której potrzebujemy by móc
OGŁOSZENIE O ZMIANIE STATUTU MCI.BioVentures Funduszu Inwestycyjnego Zamkniętego z dnia 31 lipca 2013 r.
 OGŁOSZENIE O ZMIANIE STATUTU MCI.BioVentures Funduszu Inwestycyjnego Zamkniętego z dnia 31 lipca 2013 r. Niniejszym, MCI Capital Towarzystwo Funduszy Inwestycyjnych S.A. z siedzibą w Warszawie, ogłasza
OGŁOSZENIE O ZMIANIE STATUTU MCI.BioVentures Funduszu Inwestycyjnego Zamkniętego z dnia 31 lipca 2013 r. Niniejszym, MCI Capital Towarzystwo Funduszy Inwestycyjnych S.A. z siedzibą w Warszawie, ogłasza
 Wykład 8 Rynek akcji nisza inwestorów indywidualnych Rynek akcji Jeden z filarów rynku kapitałowego (ok 24% wartości i ok 90% PK globalnie) Źródło: http://www.marketwatch.com (dn. 2015-02-12) SGH, Rynki
Wykład 8 Rynek akcji nisza inwestorów indywidualnych Rynek akcji Jeden z filarów rynku kapitałowego (ok 24% wartości i ok 90% PK globalnie) Źródło: http://www.marketwatch.com (dn. 2015-02-12) SGH, Rynki
OGŁOSZENIE Z DNIA 05 lipca 2016 r. O ZMIANIE STATUTU UNIFUNDUSZE SPECJALISTYCZNEGO FUNDUSZU INWESTYCYJNEGO OTWARTEGO
 OGŁOSZENIE Z DNIA 05 lipca 2016 r. O ZMIANIE STATUTU UNIFUNDUSZE SPECJALISTYCZNEGO FUNDUSZU INWESTYCYJNEGO OTWARTEGO Niniejszym, Union Investment Towarzystwo Funduszy Inwestycyjnych S.A. ogłasza o zmianie
OGŁOSZENIE Z DNIA 05 lipca 2016 r. O ZMIANIE STATUTU UNIFUNDUSZE SPECJALISTYCZNEGO FUNDUSZU INWESTYCYJNEGO OTWARTEGO Niniejszym, Union Investment Towarzystwo Funduszy Inwestycyjnych S.A. ogłasza o zmianie
Wersja 1.1 16.10.2013r.
 Metodologia SPAN Obliczenia depozytów dla portfeli kontraktów terminowych na stawki referencyjne WIBOR i kontraktów terminowych na obligacje skarbowe z rozliczeniem pieniężnym Wersja 1.1 16.10.2013r. Spis
Metodologia SPAN Obliczenia depozytów dla portfeli kontraktów terminowych na stawki referencyjne WIBOR i kontraktów terminowych na obligacje skarbowe z rozliczeniem pieniężnym Wersja 1.1 16.10.2013r. Spis
Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995.
 Bibliografia Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995. Elton E.J., Gruber M.J., Nowoczesna teoria portfelowa i analiza papierów wartościowych,
Bibliografia Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995. Elton E.J., Gruber M.J., Nowoczesna teoria portfelowa i analiza papierów wartościowych,
Załącznik do dokumentu zawierającego kluczowe informacje DODATKOWE UBEZPIECZENIE Z FUNDUSZEM W RAMACH:
 Załącznik do dokumentu zawierającego kluczowe informacje DODATKOWE UBEZPIECZENIE Z FUNDUSZEM W RAMACH: GRUPOWEGO UBEZPIECZENIA NA ŻYCIE WARTA EKSTRABIZNES GRUPOWEGO UBEZPIECZENIA NA ŻYCIE WARTA EKSTRABIZNES
Załącznik do dokumentu zawierającego kluczowe informacje DODATKOWE UBEZPIECZENIE Z FUNDUSZEM W RAMACH: GRUPOWEGO UBEZPIECZENIA NA ŻYCIE WARTA EKSTRABIZNES GRUPOWEGO UBEZPIECZENIA NA ŻYCIE WARTA EKSTRABIZNES
Finanse behawioralne. Finanse 110630-1165
 behawioralne Plan wykładu klasyczne a behawioralne Kiedy są przydatne narzędzia finansów behawioralnych? Przykłady modeli finansów behawioralnych klasyczne a behawioralne klasyczne opierają się dwóch założeniach:
behawioralne Plan wykładu klasyczne a behawioralne Kiedy są przydatne narzędzia finansów behawioralnych? Przykłady modeli finansów behawioralnych klasyczne a behawioralne klasyczne opierają się dwóch założeniach:
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
TRANSAKCJE KASOWE. Sekcja I (produkty inwestycyjne)
 Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
Ekonomiczny Uniwersytet Dziecięcy. Młody inwestor na giełdzie Strategie inwestycyjne Grzegorz Kowerda EKONOMICZNY UNIWERSYTET DZIECIĘCY
 Ekonomiczny Uniwersytet Dziecięcy Młody inwestor na giełdzie Strategie inwestycyjne Grzegorz Kowerda Uniwersytet w Białymstoku 8 maja 2014 r. Początki giełdy przodek współczesnych giełd to rynek (jarmark,
Ekonomiczny Uniwersytet Dziecięcy Młody inwestor na giełdzie Strategie inwestycyjne Grzegorz Kowerda Uniwersytet w Białymstoku 8 maja 2014 r. Początki giełdy przodek współczesnych giełd to rynek (jarmark,
Opcje giełdowe i zabezpieczenie inwestycji. Filip Duszczyk Dział Rynku Terminowego
 Opcje giełdowe i zabezpieczenie inwestycji Filip Duszczyk Dział Rynku Terminowego Agenda: Analiza Portfela współczynnik Beta (β) Opcje giełdowe wprowadzenie Podstawowe strategie opcyjne Strategia Protective
Opcje giełdowe i zabezpieczenie inwestycji Filip Duszczyk Dział Rynku Terminowego Agenda: Analiza Portfela współczynnik Beta (β) Opcje giełdowe wprowadzenie Podstawowe strategie opcyjne Strategia Protective
INWESTYCJE Instrumenty finansowe, ryzyko SPIS TREŚCI
 INWESTYCJE Instrumenty finansowe, ryzyko Jajuga Krzysztof, Jajuga Teresa SPIS TREŚCI Przedmowa Wprowadzenie - badania w zakresie inwestycji i finansów Literatura Rozdział 1. Rynki i instrumenty finansowe
INWESTYCJE Instrumenty finansowe, ryzyko Jajuga Krzysztof, Jajuga Teresa SPIS TREŚCI Przedmowa Wprowadzenie - badania w zakresie inwestycji i finansów Literatura Rozdział 1. Rynki i instrumenty finansowe
Struktura terminowa rynku obligacji
 Krzywa dochodowości pomaga w inwestowaniu w obligacje Struktura terminowa rynku obligacji Wskazuje, które obligacje są atrakcyjne a których unikać Obrazuje aktualną sytuację na rynku długu i zmiany w czasie
Krzywa dochodowości pomaga w inwestowaniu w obligacje Struktura terminowa rynku obligacji Wskazuje, które obligacje są atrakcyjne a których unikać Obrazuje aktualną sytuację na rynku długu i zmiany w czasie
II ETAP EGZAMINU EGZAMIN PISEMNY
 II ETAP EGZAMINU NA DORADCĘ INWESTYCYJNEGO EGZAMIN PISEMNY 20 maja 2012 r. Warszawa Treść i koncepcja pytań zawartych w teście są przedmiotem praw autorskich i nie mogą być publikowane lub w inny sposób
II ETAP EGZAMINU NA DORADCĘ INWESTYCYJNEGO EGZAMIN PISEMNY 20 maja 2012 r. Warszawa Treść i koncepcja pytań zawartych w teście są przedmiotem praw autorskich i nie mogą być publikowane lub w inny sposób
Zarządzanie portfelem inwestycyjnym
 Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska Strategie opcyjne Opcje egzotyczne 2 Współczynniki greckie Współczynniki greckie określają, o ile zmieni się kurs opcji w wyniku zmiany wartości
Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska Strategie opcyjne Opcje egzotyczne 2 Współczynniki greckie Współczynniki greckie określają, o ile zmieni się kurs opcji w wyniku zmiany wartości
Papiery wartościowe o stałym dochodzie
 Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
OGŁOSZENIE O ZMIANACH STATUTU SFIO AGRO Kapitał na Rozwój
 Warszawa, 31 lipca 2013 r. OGŁOSZENIE O ZMIANACH STATUTU SFIO AGRO Kapitał na Rozwój Niniejszym Towarzystwo Funduszy Inwestycyjnych AGRO Spółka Akcyjna z siedzibą w Warszawie ogłasza poniższe zmiany statutu
Warszawa, 31 lipca 2013 r. OGŁOSZENIE O ZMIANACH STATUTU SFIO AGRO Kapitał na Rozwój Niniejszym Towarzystwo Funduszy Inwestycyjnych AGRO Spółka Akcyjna z siedzibą w Warszawie ogłasza poniższe zmiany statutu
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Ryzyko stopy procentowej
 Ryzyko stopy procentowej Inwestycje i teoria portfela Strona 1 z 37 1. Ryzyko inwestowania w obligacje inwestycja w obligacje jest obarczona ryzykiem trzy podstawowe rodzaje ryzyka związane z inwestowaniem
Ryzyko stopy procentowej Inwestycje i teoria portfela Strona 1 z 37 1. Ryzyko inwestowania w obligacje inwestycja w obligacje jest obarczona ryzykiem trzy podstawowe rodzaje ryzyka związane z inwestowaniem
9 Funkcje Użyteczności
 9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 Model wyceny aktywów kapitałowych Najczęściej stosowana metoda zakłada wykorzystanie danych historycznych do wskazania korelacji między stopa zwrotu z danej inwestycji a portfelem rynkowym.
Ćwiczenia ZPI 1 Model wyceny aktywów kapitałowych Najczęściej stosowana metoda zakłada wykorzystanie danych historycznych do wskazania korelacji między stopa zwrotu z danej inwestycji a portfelem rynkowym.
Marcin Bartkowiak Krzysztof Echaust INSTRUMENTY POCHODNE WPROWADZENIE DO INŻYNIERII FINANSOWEJ
 Marcin Bartkowiak Krzysztof Echaust INSTRUMENTY POCHODNE WPROWADZENIE DO INŻYNIERII FINANSOWEJ Spis treści Przedmowa... 7 1. Rynek instrumentów pochodnych... 9 1.1. Instrumenty pochodne... 9 1.2. Rynek
Marcin Bartkowiak Krzysztof Echaust INSTRUMENTY POCHODNE WPROWADZENIE DO INŻYNIERII FINANSOWEJ Spis treści Przedmowa... 7 1. Rynek instrumentów pochodnych... 9 1.1. Instrumenty pochodne... 9 1.2. Rynek
1. Charakterystyka obligacji. 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji.
 mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
Strategie inwestowania w opcje. Filip Duszczyk Dział Rynku Terminowego
 Strategie inwestowania w opcje Filip Duszczyk Dział Rynku Terminowego Agenda: Opcje giełdowe Zabezpieczenie portfela Spekulacja Strategie opcyjne 2 Opcje giełdowe 3 Co to jest opcja? OPCJA JAK POLISA Zabezpieczenie
Strategie inwestowania w opcje Filip Duszczyk Dział Rynku Terminowego Agenda: Opcje giełdowe Zabezpieczenie portfela Spekulacja Strategie opcyjne 2 Opcje giełdowe 3 Co to jest opcja? OPCJA JAK POLISA Zabezpieczenie
Uniwersytet Ekonomiczny we Wrocławiu Wydział Ekonomii, Zarządzania i Turystyki Katedra Ekonometrii i Informatyki
 Wydział Ekonomii, Zarządzania i Turystyki Katedra Ekonometrii i Informatyki http://keii.ue.wroc.pl Analiza ryzyka transakcji wykład ćwiczenia Literatura Literatura podstawowa: 1. Kaczmarek T. (2005), Ryzyko
Wydział Ekonomii, Zarządzania i Turystyki Katedra Ekonometrii i Informatyki http://keii.ue.wroc.pl Analiza ryzyka transakcji wykład ćwiczenia Literatura Literatura podstawowa: 1. Kaczmarek T. (2005), Ryzyko
dr hab. Renata Karkowska
 dr hab. Renata Karkowska Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu.
dr hab. Renata Karkowska Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu.
OPCJE MIESIĘCZNE NA INDEKS WIG20
 OPCJE MIESIĘCZNE NA INDEKS WIG20 1 TROCHĘ HISTORII 1973 Fisher Black i Myron Scholes opracowują precyzyjną metodę obliczania wartości opcji słynny MODEL BLACK/SCHOLES 2 TROCHĘ HISTORII 26 kwietnia 1973
OPCJE MIESIĘCZNE NA INDEKS WIG20 1 TROCHĘ HISTORII 1973 Fisher Black i Myron Scholes opracowują precyzyjną metodę obliczania wartości opcji słynny MODEL BLACK/SCHOLES 2 TROCHĘ HISTORII 26 kwietnia 1973
8. Papiery wartościowe: obligacje
 8. Papiery wartościowe: obligacje Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w 8. Krakowie) Papiery wartościowe: obligacje
8. Papiery wartościowe: obligacje Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w 8. Krakowie) Papiery wartościowe: obligacje
Własności wyznacznika
 Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Najchętniej odwraca pozycję. Ale jeśli nie może, to replikuje transakcję przeciwstawną. strategie opcyjne
 Opcje (2) delta hedging strategie opcyjne 1 Co robi market-maker maker wystawiający opcje? Najchętniej odwraca pozycję Ale jeśli nie może, to replikuje transakcję przeciwstawną SGH, Rynki Finansowe, Materiały
Opcje (2) delta hedging strategie opcyjne 1 Co robi market-maker maker wystawiający opcje? Najchętniej odwraca pozycję Ale jeśli nie może, to replikuje transakcję przeciwstawną SGH, Rynki Finansowe, Materiały
UBEZPIECZENIA NA ŻYCIE
 UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH
 Mariusz Próchniak Katedra Ekonomii II, SGH PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH Ekonomia menedżerska 1 2 Wartość przyszła (FV future value) r roczna stopa procentowa B kwota pieniędzy, którą
Mariusz Próchniak Katedra Ekonomii II, SGH PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH Ekonomia menedżerska 1 2 Wartość przyszła (FV future value) r roczna stopa procentowa B kwota pieniędzy, którą
