Rotacje i drgania czasteczek
|
|
|
- Bernard Karpiński
- 6 lat temu
- Przeglądów:
Transkrypt
1 Rotacje i drgania czasteczek wieloatomowych Gdy znamy powierzchnie energii potencjalnej V( R 1, R 2,..., R N ) to możemy obliczyć poziomy energetyczne czasteczki. Poziomy te sa w ogólności efektem: rotacji moleku ly jako ca lości drgań o ma lej amplitudzie rotacji wewn etrznej - swobodnej lub hamowanej tunelowania drgań o dużej amplitudzie (drgań van der Waalsa) Przejścia pomiedzy tymi poziomami obserwujemy w spektroskopii: podczerwień wibracje terahertz (submillimeter) rotacje, drgania o dużej amplitudzie) mikrofalowa rotacje, tunelowanie Przejścia te zachodza pomiedzy wartościami w lasnymi Hamiltonianu dla ruchu jader: Ĥ = 1 N 1 R 2 m i + V( R 1, R 2,..., R N ) i gdzie m i to masa jadra i. Zak ladamy tu przybliżenie Borna-Oppenheimera.
2 Rotacje i drgania czasteczek dwieloatomowych, c.d. Dla czasteczek wieloatomowych nie da sie ściśle odseparować rotacji i wibracji Jest to możliwe tylko w przybliżeniu (czesto bardzo dobrym) dla tzw. czasteczek sztywnych takich jak: woda ditlenek w egla metan etylen benzen Rotacje opisujemy wtedy jako rotacje cia la sztywnego (baka odpowiedniego typu). Wibracje opisujemy jako drgania a ma lej amplitudzie wokól rotujacych po lożeń równowagi. Energie ca lkowita przybliżamy wtedy przez sume energii rotacji i wibracji Dla czasteczek niesztywnych (floppy molecules), takich jak: dwumetyloacetylen propan amoniak etanol dimer wody przybliżenie takie nie dzia la i każdy przypadek trzeba rozważać oddzielnie. Teoria ruchu jader takich moleku l jeszcze sie rozwija i nie bedziemy sie nia tu zajmować ponieważ: Brak jest komercjyjnych programów umożliwjaj acych obliczenie widma rowibracyjnego takich moleku l.
3 Rotacje czasteczek wieloatomowych Klasycznie rotacje bry ly sztywnej opisujemy przez podanie wektora predkości katowej ω takiego, że predkość v i i-tej czastki (jadra atomowego) dana jest wzorem: v i = ω R i Moment pedu bry ly dany jest wówczas wzorem N N L = R i (m i v i ) = m i R i ( ω R i ) = II ω, gdzie II jest macierza (tensora) momentu bezw ladności: i m i (Yi 2 + Zi 2) i m i X i Y i i m i X i, Z i II = i m i Y i X i i m i (Xi 2 + Z2 i ) i m i Y i Z i i m i Z i X i i m i Z i Y i i m i (Xi 2 + Y i 2) Macierz II jest symetryczna, np. II XY =II Y X. W uk ldzie wspó lrzednych zwiazanych z rotujac a moleku ly II nie zależy od czasu. II można w tym uk ladzie wspó lrzednych zdiagonalizować.
4 Rotacje czasteczek wieloatomowych, c.d. Jak każda macierz symetryczna macierz II można zdiagonalizować. W nowym uk ladzie wspó lrzednych, też na sta le zwiazanym z moleku l a, macierz ta ma postać: I A 0 0 II = 0 I B I C gdzie I A, I B, i I C sa to tzw. g lówne momenty bezw ladności czasteczki. Wektory w lasne A, B, i C, odpowiadajace wartościom w lasnym I A, I B, i I C wyznaczaja nam tzw. osie g lowne baka (czasteczki). Jeśli moleku la ma symetrie to A, B, i C sa osiami symetrii moleku ly. G lówne momenty bezw ladności dane sa wzorami: I A = i m i (B 2 i + C2 i ) I B = i m i (A 2 i + C2 i ) I C = i m i (A 2 i + B2 i ) gdzie A i, B i i C i to sa odleg lości i-tego jadra od odpowiedniej osi g lównej. Jeśli moleku la ma symetrie to wektory A, B, C leża na osiach symetrii.
5 Rotacje czasteczek wieloatomowych, c.d. Jeśli w uk ladzie osig lównych macierz II jest diagonalna to wektor momentu p edu L = II ω ma w tej bazie postać: L A = I A ω A, L B = I B ω B, L C = I C ω C, Można też latwo pokazać, że energia kinetyczna rotacji ma postać E rot = 1 N m i v i v i = 1 N m i v i ( ω R i ) = 1 N m i ω ( R i v i ) = ω L W uk ladzie osi g lównych ω L = ω A L A + ω B L B + ω C L C, stad E rot = 1 2 I A ω 2 A I B ω 2 B I C ω 2 C lub E rot = 1 L 2 A + 1 2I B L 2 B + 1 2I C L 2 C Aby otrzymać Hamiltonian uk ladu wsz edzie dopisujemy daszki Ĥ rot = 1 ˆL 2 A + 1 2I B ˆL 2 B + 1 2I C ˆL 2 C
6 Rotacje czasteczek wieloatomowych, c.d. Wartości w lasne i funkcje w lasne Ĥ rot zależa istotnie od wartości g lównych momentów bezw ladności. Mamy 4 typy baków: baki sferyczne, I A = I B = I C (metan, sześciofluorek uranu) baki symetryczne wyd lużone (prolate), I A < I B = I C (amoniak, CH 3 Cl) baki symetryczne sp laszczone (oblate), I A = I B < I C (benzen, SO 3, CHCl 3 ) baki asymetryczne I A I B I C (woda, etylen, naftalen) Dla baka symetrycznego sp laszczonego mamy I A = I B wiec można napisać: Ĥ rot = 1 ˆL 2 A + 1 2I B ˆL 2 B + 1 2I C ˆL 2 C = 1 ˆL 2 A + 1 ˆL 2 B + 1 ˆL 2 C + 1 2I C ˆL 2 C 1 czyli Ĥ rot = 1 ˆL 2 + ( 1 1 ) 2I C ˆL 2 C ˆL 2 C Ponieważ wartości w lasne ˆL 2 i ˆL C to J(J + 1) 2 i M wiec wartości w lasne Ĥ rot sa nastepuj ace (w jednostkach atomowych = 1) E JK = 1 ( 1 J(J + 1) + 1 ) K 2 2I C
7 Rotacje czasteczek wieloatomowych, c.d. Dla baka wyd lużonego otrzymujemy taki sam wzór tylko najmniejszy i najwieklszy moment bezw ladności I A i I C sa zamienione: E JK = 1 ( 1 J(J + 1) + 1 ) K 2 2I C 2I C Dla baka symetrycznego degeneracja poziomu E JK wynosi 2(2J + 1), 2 ze wzgledu na K i 2J + 1 ze wzgledu na M. Dla baka sferycznego I A =I B =I C wiec: E J = 1 J(J + 1) Degeneracja w tym przypadku wynosi (2J + 1) 2. Dla baka asymetrycznego (woda, etylen) nie znamy analitycznego wzoru na poziomy rotacyjne. Degeneracja ze wzgl du na K jest tu zniesiona. K przestaje być dobra liczba kwantowa. Czasteczki liniowe w stanach Π,, etc. tez sa bakami symetrycznymi wyd lużonymi z K = Λ gdzie Λ = 1 dla stanów Π, Λ = 2 dla stanów, etc. Ich energia rotacji dana jest zatem wzorem E JΛ = 1 [J(J + 1) Λ 2 ] + 1 Λ 2 2I C gdzie I C =µre 2 a Λ2 /( ) jest sta la wliczana do enerii elektronowej.
8 Schemat poziomów rotacyjnych baka symetrycznego
9 Schemat poziomów rotacyjnych baka asymetrycznego
10 Wibracje czasteczek wieloatomowych Rozważmy N jader atomowych. Po lożenie każdego z nich bedziemy mierzyc przez wspó lrzedne kartezjańskie x i, y i i z i określajace wychylenie i-tego jadra z jego ustalonego w przestrzni po lożenia równowagi. Hamiltonian wibracyjny uk ladu ma postać: Ĥ vib = 1 2m i 2 u 2 i + V (u 1, u 2,..., u 3N ) gdzie u i,,...,3n oznaczaja kolektywnie wszystkie wspó lrzedne kartezjańskie x 1, y 1, z 1, x 2, y 2, z 2,... a masy sa tak dobrane, że m 1 =m 2 =m 3, m 4 = m 5 =m 6,... Potencja l V (u 1, u 2,..., u 3N ) rozwijamy w szereg Taylora wokó l u 1 =u 2 =u 3 = 0 ( ) V V (u 1, u 2,..., u 3N ) = V 0 + u i + 1 ( 2 ) V u i u j + u i 2 u i u j Pierwsze pochodne znikaja w minimum, trzecie zaniedbujemy (przybliżenie harmoniczne). Sta l a V 0 wliczamy do energii elektronowej, stad: Ĥ vib = 1 2m i 2 u 2 i j=1 j=1 V ij u i u j gdzie V ij to macierz drugich pochodnych w minimum, czyli macierz Hessjanu.
11 Wibracje czasteczek wieloatomowych, c.d. Aby znaleźć wartości w lasne tego Hamiltonianu trzeba wprowadzić tzw. wspó lrz edne masowe: w i = m i u i W tych wspó lrz ednych Hamiltonian ma postać: Ĥ vib = w 2 i j=1 V ij mi m j w i w j Macierz V ij / m i m j jest symetryczna wiec można ja zdiagonalizować przy pomocy macierzy U ij i wprowadzić wspó lrzedne normalne q k : q k = U ik w i w i = k=1 U ik q k We wspó lrzednych normalnych Hamiltonian ma postać ( Ĥ vib = ) 2 2 λ k q 2 k k=1 gdzie λ k to wartości w lasne macierzy V ij / m i m j. Energie w lasne Ĥ vib to: ( E v1,v 2,... = ω k v k + 1 ) gdzie ω k = λ k 2 k=1 q 2 k
12 Translacje, rotacje i drgania czasteczki trójatomowej
13 Drgania czasteczki wody
14 Tunelowanie rezonansowe w widmie wibracyjnym amoniaku
15 Rezonans Fermiego wzbudzeń wibracyjnch ω 1 = 1333 cm 1 i 2 ω 2 = 1338 cm 1 w czasteczce CO 2
16 Wp lyw si ly Coriolisa na drgania czasteczki CO 2
i elektronów w czasteczkach (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra 2M b a i b; m -masa elektronu e 2 r ij
 Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Uklady modelowe III - rotator, atom wodoru
 Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
Oddzia lywania miedzycz. jony molekularne lub atomy. edzy A i B:
 Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Uk lady modelowe II - oscylator
 Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Struktura elektronowa czasteczek. przybliżenie Borna-Oppenheimera. równania Schrödingera dla elektronów przy ustalonym po lożeniu jader
 Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Algorytm określania symetrii czasteczek
 O czym to b Podzi 21 września 2007 O czym to b O czym to b Podzi 1 2 3 O czym to b Podzi W lasności symetrii hamiltonianu: zmniejszenie z lożoności obliczeń i wymagań pami eciowych, utrzymanie tożsamościowych
O czym to b Podzi 21 września 2007 O czym to b O czym to b Podzi 1 2 3 O czym to b Podzi W lasności symetrii hamiltonianu: zmniejszenie z lożoności obliczeń i wymagań pami eciowych, utrzymanie tożsamościowych
w jednowymiarowym pudle potencja lu
 Do wyk ladu II czastka w pudle potencja lu oscylator harmoniczny rotator sztywny Ścis le rozwiazania równania Schrödingera: atom wodoru i jon wodoropodobny) Czastka w jednowymiarowym pudle potencja lu
Do wyk ladu II czastka w pudle potencja lu oscylator harmoniczny rotator sztywny Ścis le rozwiazania równania Schrödingera: atom wodoru i jon wodoropodobny) Czastka w jednowymiarowym pudle potencja lu
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego
 Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE.
 1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
Symbol termu: edu (sumy ca lkowitego orbitalnego momentu edu i ca lkowitego spinu) Przyk lad: 2 P 3. kwantowa
 Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
JEDNOSTKI ATOMOWE =1, m e =1, e=1, ; 1 E 2 h = 4, J. Energia atomu wodoru lub jonu wodoropodobnego w jednostkach atomowych:
 do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
Zastosowanie Robotów. Ćwiczenie 6. Mariusz Janusz-Bielecki. laboratorium
 Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Czastka swobodna Bariera potencja lu Pud lo jednowymiarowe FEMO Pud la wielowymiarowe. Wyk lad 3. Uk lady modelowe I
 Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Spis treści. Przedmowa redaktora do wydania czwartego 11
 Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Przestrzenie wektorowe, liniowa niezależność wektorów, bazy przestrzeni wektorowych
 Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE
 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń
 Wyk lad 6 Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń Uk lady modelowe czastka swobodna czastka na barierze potencja lu czastka w pudle oscylator harmoniczny oscylator Morse
Wyk lad 6 Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń Uk lady modelowe czastka swobodna czastka na barierze potencja lu czastka w pudle oscylator harmoniczny oscylator Morse
VII.1 Pojęcia podstawowe.
 II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE
 1 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE 2 Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
1 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE 2 Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
Po lożenie punktu w przestrzenie w chwili czasowej t może być opisane jako wektor x(t), reprezentujacy
 1. Bry la sztywna Symulacja komputerowa ruchu bry ly sztywnej jest ważnym zagadnieniem podczas modelowania i weryfikacji różnych systemów fizycznych. Mówiac bry la sztywna, mamy na myśli bry l e, która
1. Bry la sztywna Symulacja komputerowa ruchu bry ly sztywnej jest ważnym zagadnieniem podczas modelowania i weryfikacji różnych systemów fizycznych. Mówiac bry la sztywna, mamy na myśli bry l e, która
Hierarchia baz gaussowskich (5)
 Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
Projekt pracy magisterskiej
 Symulacja widma dichroizmu ko lowego (1R,2R)-1,2-bis(1,8 -naftalimido)cykloheksanu przy użyciu rozszerzonego modelu dimerowego Promotor prof. dr hab. Marek Pawlikowski 2 grudnia 2009 Plan prezentacji 1
Symulacja widma dichroizmu ko lowego (1R,2R)-1,2-bis(1,8 -naftalimido)cykloheksanu przy użyciu rozszerzonego modelu dimerowego Promotor prof. dr hab. Marek Pawlikowski 2 grudnia 2009 Plan prezentacji 1
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wyk lad 11 1 Wektory i wartości w lasne
 Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Stany atomu wieloelektronowego o określonej energii. być przypisywane elektrony w tym stanie atomu.
 Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab.
 WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Zadania. kwiecień 2009. Ćwiczenia IV. w laściwe dla rotatora sztywnego hetoronuklearnej moleku ly. Rozwiazanie E JM = 2 J(J + 1).
 kwiecień 9 Ćwiczenia IV Zadania Zadanie Obliczyć kanoniczna sum e statystyczna funkcj e podzia lu, energi e swobodna i ciep lo w laściwe dla rotatora sztywnego hetoronuklearnej moleku ly Rozwiazanie :
kwiecień 9 Ćwiczenia IV Zadania Zadanie Obliczyć kanoniczna sum e statystyczna funkcj e podzia lu, energi e swobodna i ciep lo w laściwe dla rotatora sztywnego hetoronuklearnej moleku ly Rozwiazanie :
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej. Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać:
 Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
Chemia kwantowa. Pytania egzaminacyjne. 2010/2011: 1. Przesłanki doświadczalne mechaniki kwantowej.
 1 Chemia kwantowa. Pytania egzaminacyjne. 21/211: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny - interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest licza
1 Chemia kwantowa. Pytania egzaminacyjne. 21/211: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny - interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest licza
Modelowanie molekularne
 Ck08 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 10 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody
Ck08 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 10 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3
 WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
Bryła sztywna. Wstęp do Fizyki I (B+C) Wykład XXI:
 Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XXI: Porównanie ruchu obrotowego z ruchem postępowym Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Równania Eulera Bak swobodny Porównanie
Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XXI: Porównanie ruchu obrotowego z ruchem postępowym Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Równania Eulera Bak swobodny Porównanie
Postulaty mechaniki kwantowej
 Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Model uogólniony jądra atomowego
 Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Normy wektorów i macierzy
 Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych
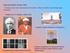 WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
Teoria funkcjona lu g Density Functional Theory (DFT)
 Teoria funkcjona lu g estości Density Functional Theory (DFT) Cz eść slajdów tego wyk ladu pochodzi z wyk ladu wyg loszonego przez dra Lukasza Rajchela w Interdyscyplinarnym Centrum Modelowania Matematycznego
Teoria funkcjona lu g estości Density Functional Theory (DFT) Cz eść slajdów tego wyk ladu pochodzi z wyk ladu wyg loszonego przez dra Lukasza Rajchela w Interdyscyplinarnym Centrum Modelowania Matematycznego
Transformacja Lorentza - Wyprowadzenie
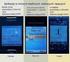 Transformacja Lorentza - Wyprowadzenie Rozważmy obserwatorów zwiazanych z różnymi inercjalnymi uk ladami odniesienia, S i S. Odpowiednie osie uk ladów S i S sa równoleg le, przy czym uk lad S porusza sie
Transformacja Lorentza - Wyprowadzenie Rozważmy obserwatorów zwiazanych z różnymi inercjalnymi uk ladami odniesienia, S i S. Odpowiednie osie uk ladów S i S sa równoleg le, przy czym uk lad S porusza sie
Wyk lad 14 Formy kwadratowe I
 Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Bąk wirujący wokół pionowej osi jest w równowadze. Momenty działających sił są równe zero (zarówno względem środka masy S jak i punktu podparcia O).
 Bryła sztywna (2) Bąk Równowaga Rozważmy bąk podparty wirujący do okoła pionowej osi. Z zasady zachowania mementu pędu wynika, że jeśli zapewnimy znikanie momentów sił to kierunek momentu pędu pozostanie
Bryła sztywna (2) Bąk Równowaga Rozważmy bąk podparty wirujący do okoła pionowej osi. Z zasady zachowania mementu pędu wynika, że jeśli zapewnimy znikanie momentów sił to kierunek momentu pędu pozostanie
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Wyk lad 10 Przestrzeń przekszta lceń liniowych
 Wyk lad 10 Przestrzeń przekszta lceń liniowych 1 Określenie przestrzeni przekszta lceń liniowych Niech V i W bed a przestrzeniami liniowymi Oznaczmy przez L(V ; W ) zbór wszystkich przekszta lceń liniowych
Wyk lad 10 Przestrzeń przekszta lceń liniowych 1 Określenie przestrzeni przekszta lceń liniowych Niech V i W bed a przestrzeniami liniowymi Oznaczmy przez L(V ; W ) zbór wszystkich przekszta lceń liniowych
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
Pierwsze kolokwium z Matematyki I 4. listopada 2013 r. J. de Lucas
 Pierwsze kolokwium z Matematyki I 4. listopada 03 r. J. de Lucas Uwagi organizacyjne: Każde zadanie rozwi azujemy na osobnej kartce, opatrzonej imieniem i nazwiskiem w lasnym oraz osoby prowadz acej ćwiczenia,
Pierwsze kolokwium z Matematyki I 4. listopada 03 r. J. de Lucas Uwagi organizacyjne: Każde zadanie rozwi azujemy na osobnej kartce, opatrzonej imieniem i nazwiskiem w lasnym oraz osoby prowadz acej ćwiczenia,
SPEKTROSKOPIA ROTACYJNA
 SPEKTROSKOPIA ROTACYJNA Co to jest spektroskopia mikrofalowa Obejmuje obszar częstości od 3GHz do 300GHz czyli od 0.1 do 10 cm -1 Wykrywa przejścia pomiędzy skwantowanymi poziomami energetycznymi obracającej
SPEKTROSKOPIA ROTACYJNA Co to jest spektroskopia mikrofalowa Obejmuje obszar częstości od 3GHz do 300GHz czyli od 0.1 do 10 cm -1 Wykrywa przejścia pomiędzy skwantowanymi poziomami energetycznymi obracającej
TEORIA FUNKCJONA LÓW. (Density Functional Theory - DFT) Monika Musia l
 TEORIA FUNKCJONA LÓW GȨSTOŚCI (Density Functional Theory - DFT) Monika Musia l PRZEDMIOT BADAŃ Uk lad N elektronów + K j ader atomowych Przybliżenie Borna-Oppenheimera Zamiast funkcji falowej Ψ(r 1,σ 1,r
TEORIA FUNKCJONA LÓW GȨSTOŚCI (Density Functional Theory - DFT) Monika Musia l PRZEDMIOT BADAŃ Uk lad N elektronów + K j ader atomowych Przybliżenie Borna-Oppenheimera Zamiast funkcji falowej Ψ(r 1,σ 1,r
WNIOSKOWANIE W MODELU REGRESJI LINIOWEJ
 WNIOSKOWANIE W MODELU REGRESJI LINIOWEJ Dana jest populacja generalna, w której dwuwymiarowa cecha (zmienna losowa) (X, Y ) ma pewien dwuwymiarowy rozk lad. Miara korelacji liniowej dla zmiennych (X, Y
WNIOSKOWANIE W MODELU REGRESJI LINIOWEJ Dana jest populacja generalna, w której dwuwymiarowa cecha (zmienna losowa) (X, Y ) ma pewien dwuwymiarowy rozk lad. Miara korelacji liniowej dla zmiennych (X, Y
Rozdzia l 11. Przestrzenie Euklidesowe Definicja, iloczyn skalarny i norma. iloczynem skalarnym.
 Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Podczerwień bliska: cm -1 (0,7-2,5 µm) Podczerwień właściwa: cm -1 (2,5-14,3 µm) Podczerwień daleka: cm -1 (14,3-50 µm)
 SPEKTROSKOPIA W PODCZERWIENI Podczerwień bliska: 14300-4000 cm -1 (0,7-2,5 µm) Podczerwień właściwa: 4000-700 cm -1 (2,5-14,3 µm) Podczerwień daleka: 700-200 cm -1 (14,3-50 µm) WIELKOŚCI CHARAKTERYZUJĄCE
SPEKTROSKOPIA W PODCZERWIENI Podczerwień bliska: 14300-4000 cm -1 (0,7-2,5 µm) Podczerwień właściwa: 4000-700 cm -1 (2,5-14,3 µm) Podczerwień daleka: 700-200 cm -1 (14,3-50 µm) WIELKOŚCI CHARAKTERYZUJĄCE
2008/2009. Seweryn Kowalski IVp IF pok.424
 2008/2009 seweryn.kowalski@us.edu.pl Seweryn Kowalski IVp IF pok.424 Model powłokowy Moment kwadrupolowy w jednocząstkowym modelu powłokowym: Dla pojedynczego protonu znajdującego się na orbicie j (m j
2008/2009 seweryn.kowalski@us.edu.pl Seweryn Kowalski IVp IF pok.424 Model powłokowy Moment kwadrupolowy w jednocząstkowym modelu powłokowym: Dla pojedynczego protonu znajdującego się na orbicie j (m j
Mechanika. Wykład 7. Paweł Staszel
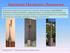 Mechanika Wykład 7 Paweł Staszel 1 Dynamika bryły sztywnej Bryłą (ciałem) sztywnym nazywamy zbiór cząstek zachowujących stałe odległości między sobą. Pomijamy więc zjawiska związane z powstawaniem odkształceń
Mechanika Wykład 7 Paweł Staszel 1 Dynamika bryły sztywnej Bryłą (ciałem) sztywnym nazywamy zbiór cząstek zachowujących stałe odległości między sobą. Pomijamy więc zjawiska związane z powstawaniem odkształceń
Kondensacja Bosego-Einsteina
 Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym
 Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Niezb. ednik matematyczny. Niezb. ednik matematyczny
 Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Kondensat Bosego-Einsteina okiem teoretyka
 Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Bryła sztywna. Fizyka I (B+C) Wykład XXII: Porównanie ruchu obrotowego z ruchem postępowym. Bak Precesja Żyroskop
 Bryła sztywna Wykład XXII: Fizyka I (B+C) Porównanie ruchu obrotowego z ruchem postępowym Bak Precesja Żyroskop Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Porównanie Punkt
Bryła sztywna Wykład XXII: Fizyka I (B+C) Porównanie ruchu obrotowego z ruchem postępowym Bak Precesja Żyroskop Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Porównanie Punkt
Rozkłady wielu zmiennych
 Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Teoria funkcjona lu g
 Notatki do wyk ladu XI Teoria funkcjona lu g estości Density Functional Theory - DFT Czy znajomość funkcji falowej jest niezb edna? Ψ(1,, 3,..., N) dla uk ladu N-elektronowego zależy od 4N zmiennych (dla
Notatki do wyk ladu XI Teoria funkcjona lu g estości Density Functional Theory - DFT Czy znajomość funkcji falowej jest niezb edna? Ψ(1,, 3,..., N) dla uk ladu N-elektronowego zależy od 4N zmiennych (dla
Wyk lad 11 Przekszta lcenia liniowe a macierze
 Wyk lad 11 Przekszta lcenia liniowe a macierze 1 Izomorfizm przestrzeni L(V ; W ) i M m n (R) Twierdzenie 111 Niech V i W bed a przestrzeniami liniowymi o bazach uporzadkowanych (α 1,, α n ) i (β 1,, β
Wyk lad 11 Przekszta lcenia liniowe a macierze 1 Izomorfizm przestrzeni L(V ; W ) i M m n (R) Twierdzenie 111 Niech V i W bed a przestrzeniami liniowymi o bazach uporzadkowanych (α 1,, α n ) i (β 1,, β
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera
 Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Uniwersytet Śląski w Katowicach str. 1 Wydział Matematyki, Fizyki i Chemii
 Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Notatki do wyk ladu IV (z 27.10.2014)
 Dla orbitalnego momentu p edu (L): Notatki do wyk ladu IV (z 7.10.014) ˆL ψ nlm = l(l + 1) ψ nlm (1) ˆL z ψ nlm = m ψ nlm () l + 1 możliwych wartości rzutu L z na wyróżniony kierunek w przestrzeni (l -liczba
Dla orbitalnego momentu p edu (L): Notatki do wyk ladu IV (z 7.10.014) ˆL ψ nlm = l(l + 1) ψ nlm (1) ˆL z ψ nlm = m ψ nlm () l + 1 możliwych wartości rzutu L z na wyróżniony kierunek w przestrzeni (l -liczba
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Procesy Stochastyczne - Zestaw 1
 Procesy Stochastyczne - Zestaw 1 Zadanie 1 Niech ξ i η bed a niezależnymi zmiennymi losowymi o rozk ladach N (0, 1). Niech X = ξ +η i Y = ξ η. Znaleźć rozk lad (X, Y ) i rozk lad warunkowy L X ( Y ). Zadanie
Procesy Stochastyczne - Zestaw 1 Zadanie 1 Niech ξ i η bed a niezależnymi zmiennymi losowymi o rozk ladach N (0, 1). Niech X = ξ +η i Y = ξ η. Znaleźć rozk lad (X, Y ) i rozk lad warunkowy L X ( Y ). Zadanie
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA. Ćwiczenia. http://zcht.mfc.us.edu.pl/ mm
 CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
u nk = n c nn u n 0 wyznacza siȩ empirycznie (elementy przejść) lub próbuje oszacować w obliczeniach typu ab initio Rachunek zaburzeń Löwdina
 Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane) to ich wzajemny wp lyw musi być uwzglȩdniony wariacyjnie - w I rzȩdzie RZ dla stanow zdegenerowanych
Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane) to ich wzajemny wp lyw musi być uwzglȩdniony wariacyjnie - w I rzȩdzie RZ dla stanow zdegenerowanych
1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej?
 Tematy opisowe 1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej? 2. Omów pomiar potencjału na granicy faz elektroda/roztwór elektrolitu. Podaj przykład, omów skale potencjału i elektrody
Tematy opisowe 1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej? 2. Omów pomiar potencjału na granicy faz elektroda/roztwór elektrolitu. Podaj przykład, omów skale potencjału i elektrody
Wersja testu D 14 września 2011 r. 1. Czy prawda jest, że a) x Z y Z y 2 = 2 ; b) x Z y Z x 2 = 1 ; c) x Z y Z x 2 = 2 ; d) x Z y Z y 2 = 1?
 1. Czy prawda jest, że a) x Z y Z y 2 = 2 ; b) x Z y Z x 2 = 1 ; c) x Z y Z x 2 = 2 ; d) x Z y Z y 2 = 1? 2. Czy prawda jest, że a) 5 8 1 jest podzielne przez 4 ; b) 5 7 1 jest podzielne przez 4 ; c) 3
1. Czy prawda jest, że a) x Z y Z y 2 = 2 ; b) x Z y Z x 2 = 1 ; c) x Z y Z x 2 = 2 ; d) x Z y Z y 2 = 1? 2. Czy prawda jest, że a) 5 8 1 jest podzielne przez 4 ; b) 5 7 1 jest podzielne przez 4 ; c) 3
Podstawy robotyki wykład VI. Dynamika manipulatora
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 1: Wahadło fizyczne. opis ruchu drgającego a w szczególności drgań wahadła fizycznego
 Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Statystyka w analizie i planowaniu eksperymentu
 23 kwietnia 2014 Korelacja - wspó lczynnik korelacji 1 Gdy badamy różnego rodzaju rodzaju zjawiska (np. przyrodnicze) możemy stwierdzić, że na każde z nich ma wp lyw dzia lanie innych czynników; Korelacja
23 kwietnia 2014 Korelacja - wspó lczynnik korelacji 1 Gdy badamy różnego rodzaju rodzaju zjawiska (np. przyrodnicze) możemy stwierdzić, że na każde z nich ma wp lyw dzia lanie innych czynników; Korelacja
w = w i ξ i. (1) i=1 w 1 w 2 :
 S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
1. Przesłanki doświadczalne mechaniki kwantowej.
 1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
Ciepło właściwe. Autorzy: Zbigniew Kąkol Bartek Wiendlocha
 Ciepło właściwe Autorzy: Zbigniew Kąkol Bartek Wiendlocha 01 Ciepło właściwe Autorzy: Zbigniew Kąkol, Bartek Wiendlocha W module zapoznamy się z jednym z kluczowych pojęć termodynamiki - ciepłem właściwym.
Ciepło właściwe Autorzy: Zbigniew Kąkol Bartek Wiendlocha 01 Ciepło właściwe Autorzy: Zbigniew Kąkol, Bartek Wiendlocha W module zapoznamy się z jednym z kluczowych pojęć termodynamiki - ciepłem właściwym.
SPEKTROSKOPIA RAMANA. Laboratorium Laserowej Spektroskopii Molekularnej PŁ
 SPEKTROSKOPIA RAMANA Laboratorium Laserowej Spektroskopii Molekularnej PŁ WIDMO OSCYLACYJNE Zręby atomowe w molekule wykonują oscylacje wokół położenia równowagi. Ruch ten można rozłożyć na 3n-6 w przypadku
SPEKTROSKOPIA RAMANA Laboratorium Laserowej Spektroskopii Molekularnej PŁ WIDMO OSCYLACYJNE Zręby atomowe w molekule wykonują oscylacje wokół położenia równowagi. Ruch ten można rozłożyć na 3n-6 w przypadku
P (x, y) + Q(x, y)y = 0. g lym w obszrze G R n+1. Funkcje. zania uk ladu (1) o wykresie przebiegaja
 19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
Diagnostyka plazmy - spektroskopia molekularna. Ewa Pawelec wykład dla pracowni specjalistycznej
 Diagnostyka plazmy - spektroskopia molekularna Ewa Pawelec wykład dla pracowni specjalistycznej Plazma Różne rodzaje plazmy: http://www.ipp.cas.cz/mi/index.html http://www.pro-fusiononline.com/welding/plasma.htm
Diagnostyka plazmy - spektroskopia molekularna Ewa Pawelec wykład dla pracowni specjalistycznej Plazma Różne rodzaje plazmy: http://www.ipp.cas.cz/mi/index.html http://www.pro-fusiononline.com/welding/plasma.htm
Zagadnienie Keplera F 12 F 21
 Zagadnienie Keplera To zagadnienie bedzie potraktowane bardzo skrótowo i planuje podanie w tym miejscu jedynie podstawowych informacji. Zagadnienie Keplera jest dyskutowane w każdym podreczniku mechaniki.
Zagadnienie Keplera To zagadnienie bedzie potraktowane bardzo skrótowo i planuje podanie w tym miejscu jedynie podstawowych informacji. Zagadnienie Keplera jest dyskutowane w każdym podreczniku mechaniki.
Metody obliczeniowe chemii teoretycznej
 Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Zadania. kwiecień 2009. Ćwiczenia III. Zadanie 1. Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B.
 kwiecień 009 Ćwiczenia III Zadania Zadanie 1 Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B Udowodnić że jeżeli ln Ω A (E A < ln Ω B(E B E A E B to energia przep lynie z uk
kwiecień 009 Ćwiczenia III Zadania Zadanie 1 Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B Udowodnić że jeżeli ln Ω A (E A < ln Ω B(E B E A E B to energia przep lynie z uk
stosunek przyrostu funkcji y do odpowiadajacego dy dx = lim y wielkości fizycznej x, y = f(x), to pochodna dy v = ds edkości wzgl edem czasu, a = dv
 Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
Symetria w obliczeniach molekularnych
 Zak lad Metod Obliczeniowych Chemii UJ 15 marca 2005 1 2 Możliwości przyspieszenia obliczeń 3 GAMESS 2004 4 Zastosowania symetrii Zmniejszenie zapotrzebowania na zasoby (procesor, pami eć, dysk) Utrzymanie
Zak lad Metod Obliczeniowych Chemii UJ 15 marca 2005 1 2 Możliwości przyspieszenia obliczeń 3 GAMESS 2004 4 Zastosowania symetrii Zmniejszenie zapotrzebowania na zasoby (procesor, pami eć, dysk) Utrzymanie
Wyznaczanie temperatury gazu z wykorzystaniem widm emisyjnych molekuł dwuatomowych
 Wyznaczanie temperatury gazu z wykorzystaniem widm emisyjnych molekuł dwuatomowych Opracował: Hubert Lange Aby przygotować się do ćwiczenia należy przeczytać i zrozumieć materiał w książce:. adlej, pektroskopia
Wyznaczanie temperatury gazu z wykorzystaniem widm emisyjnych molekuł dwuatomowych Opracował: Hubert Lange Aby przygotować się do ćwiczenia należy przeczytać i zrozumieć materiał w książce:. adlej, pektroskopia
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
ZASADY ZALICZENIA PRZEDMIOTU MBS
 ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
Optyczna spektroskopia oscylacyjna. w badaniach powierzchni
 Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Indeks odwzorowania zmiennej zespolonej wzgl. krzywej zamknietej
 Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
