Od obligacji do swapcji. Ile to kosztuje?
|
|
|
- Miłosz Ciesielski
- 6 lat temu
- Przeglądów:
Transkrypt
1
2 Od obligacji do swapcji Ile to kosztuje?
3 Względny udział w rynku instrumentów pochodnych
4 Jaka jest cena pieniadza? Zwyczajowo jest to procent kapitału jaki podlega obrotowi. Taka definicja nie jest wygodna. Wygodniej jest odnieść ten procent do jednostkowego kapitału. Wtedy mówimy o stopie procentowej.
5 Jak poprawnie zdefiniować stopę procentowa Rozważmy pożyczkę kapitału N. Opłata za tę pożyczkę zależeć powinna nie tylko od wielości kapitału N, ale także od czasu na jaki pożyczamy te pieniadze. Opłata ta powinna zależeć także od tego czy pożyczamy dziś, czy też dziś chcemy się umówić na pożyczkę, która zaciagniemy za miesiac. Stóp procentowych może więc być wiele. Jedna zasada obowiazuje powszechnie: stopę procentowa podaje się zawsze jako stopę odniesiona do jednego roku. Jeśli kapitał N pożyczamy na okres inny niż 1 rok, to musimy znać regułę według której stopę roczna przelicza się na okresy o innej długości.
6 Obligacje Zaczniemy od definicji abstrakcyjnej obligacji (zero-kuponowej). Obligacja zero-kuponowa o czasie zapadalności T jest to papier wartościowy, który gwarantuje właścicielowi wypłatę jednostki waluty w chwili T. Cena w chwili t T obligacji o czasie zapadalności T oznaczana jest symbolem P(t, T ). Z definicji tej wynika, że P(T, T ) = 1. Założenie, że pieniadze można przechowywać bez ponoszenia dodatkowych kosztów, prowadzi do wniosku, że P(t, T ) 1 dla każdego t T (w normalnych warunkach P(t, T ) < 1 dla t < T, co oznacza, że obligacje zero-kuponowe sa sprzedawane z dyskontem). Przyjmujac jako instrument podstawowy obligacje zero-kuponowe możemy zdefiniować kilka stóp procentowych.
7 Stopy procentowe definicje Stopa terminowa (forward interest rate) w chwili t na okres [S, T ] nazywamy iloraz R(t; S, T ) = ln P(t, T ) ln P(t, S). T S Dysponujac stopa terminowa możemy zdefiniować stopę natychmiastowa (spot interest rate) na okres [S, T ] R(S, T ) = R(S; S, T ), a także chwilowa stopę terminowa (instantaneous forward rate) f (t, T ) = lim S T R(t; S, T ) = T ln P(t, T ), i chwilowa stopę natychmiastowa (instantaneous spot rate) r(t) = f (t, t).
8 Obligacje abstrakcyjne wyjaśnienie Obligacje te nazwaliśmy abstrakcyjnymi, ponieważ chcemy mieć takie obligacje dla każdego T T, gdzie T jest horyzontem inwestycyjnym. Ponadto chcemy, aby były to obligacje o gładkiej zależności ceny od czasu zapadalności (aby istniały odpowiednie pochodne). Takich obligacji nie ma na rynku! Ale korzystajac z tych obligacji można zdefiniować ważny obiekt krzywa dyskontowa. Pokażemy później jak krzywa dyskontowa można zbudować korzystajac z instrumentów dostępnych na rynku finansowym. Ponieważ z krzywej dyskontowej potrafimy odczytać część zdefiniowanych wcześniej stóp procentowych, możemy mówić o tych stopach także na rzeczywistym rynku.
9 Krzywa dyskontowa Krzywa dyskontowa to funkcja T P(t, T ). Oznacza to, że dla każdej chwili czasu t mamy inna krzywa dyskontowa.
10 Krzywa stóp forward Ponieważ f (t, T ) = T ln P(t, T ), to z gładkiej krzywej dyskontowej można wyliczyć stopy forward. Rysunek ilustruje 3 podstawowe kształty krzywej stóp forward: opadajac a, wznoszac a i garbata.
11 Krzywa dyskontowa na rzeczywistym rynku Krzywa dyskontowa możemy zbudować tylko na dziś, bo tylko dziś znamy ceny obligacji. Krzywej dyskontowej na przyszłe daty nie możemy zbudować, bo nie ma danych. Na rynku sa dostępne obligacje rzadowe. To nie sa zwykle obligacje zero-kuponowe, ale to nie jest poważnym problemem. Ważniejszy jest fakt, czy codziennie mamy podawane ceny tych obligacji. Ceny sprzedaży tych obligacji przez rzad znamy tylko w nielicznych dniach (rzady zwykle sprzedaja obligacje co jakiś czas: raz w tygodniu, raz w miesiacu,... ). Istnieje rynek wtórny tych obligacji (OTC), ale jest to rynek chimeryczny. Niektóre obligacje sa przedmiotem transakcji na tym rynku często, ale inne bardzo rzadko. W efekcie krzywa dyskontowa musielibyśmy tworzyć z bardzo małej liczby punktów (czasem nie wiedzac, które ceny sa wiarygodne).
12 Krzywa dyskontowa międzybankowa Bardziej wiarygodna krzywa dyskontowa dostaniemy wykorzystujac instrumenty na rynku międzybankowym. Stopa LIBOR L(t, T, T + δ) na okres δ oznacza stopę procentowa terminowa widziana z chwili czasu t dla depozytu założonego w chwili T i rozwiazanego po okresie δ, tj. L(t, T, T + δ) = R(t; T, T + δ). Stopa f (t, T ) jest zwiazana ze stopa LIBOR zwiazkiem ( T +δ ) δl(t, T, T + δ) = exp f (t, u)du 1. T Wynika stad także zwiazek z krzywa dyskontowa L(t, T, T + δ) = P(t, T ) P(t, T + δ). δp(t, T + δ) Zwykle czas t jest dobrze znany i stosuje się uproszczony zapis stóp LIBOR L(T, T + δ).
13 Tworzenie krzywej dyskontowej z danych LIBOR Załóżmy, że mamy dane o stopach LIBOR6M dla pewnych dat zapadalności. Aby stworzyć z tych danych krzywa dyskontowa należy aproksymować wartości pośrednie. Jak?
14 Aproksymacja liniowa?
15 Aproksymacja wielomianowa?
16 Aproksymacja krzywa Nelsona-Siegela?
17 Dobra krzywa dyskontowa Dobra krzywa dyskontowa musi: nie prowadzić do arbitrażu, 1 w szczególności musi być ściśle malejaca, musi być wystarczajaco gładka aby można obliczyć z niej stopę forward, stopy forward wynikajace z krzywej musza być realistyczne. 1 Arbitrażem nazywamy taka strategię inwestycyjna, która startujac z zerowego kapitału, nie doprowadzi do bankructwa (ujemnego kapitału) a z dodatnim prawdopodobieństwem przyniesie zysk, czyli dodatni kapitał.
18 Cena obligacji (kuponowej) Obligacja kuponowa o stałym oprocentowaniu r o nominale N i czasie zapadalności T n nazywamy papier wartościowy, który w w ustalonych momentach czasu T 1 < T 2 < < T n wypłaca właścicielowi kupony w wysokości rn a w chwili T n także nominał N. Znajac krzywa dyskontowa P(t, T ) na moment czasu t można obliczyć cenę takiej obligacji w chwili t: P(t) = n P(t, T i )rn + P(t, T n )N. i=1
19 Kontrakty wymiany procentowej SWAP (IRS) Kontrakt wymiany procentowej (IRS) składa się z dwóch strumieni pieniężnych, tzw. nóg kontraktu. Strona kontraktu IRS otrzymuje/płaci płatności występujace na jednej nodze kontraktu w zamian za co płaci drugiej stronie/otrzymuje od drugiej strony kontraktu płatności drugiej nogi. Wyróżniamy dwa rodzaje nóg kontraktów wymiany procentowej: nogę stała (ang. fixed leg) odsetki sa liczone według stałej stopy, nogę zmienna (ang. floating leg) odsetki sa liczone według zmiennej stopy. Z każda noga kontraktu zwiazana jest struktura dyskretnych dat T j (tenor), j = 0,..., m. Daty T 0,..., T m 1 sa datami ustalania wielkości przepływów (reset dates), daty T 1,..., T m sa datami przepływów (settlement dates) a m nazywa się długościa trwania kontraktu.
20 Noga stała kontraktu IRS Noga stała kontraktu to strumień płatności C(T i ) następujacych w chwilach T i, i = 1,..., M (T M jest terminem zapadalności kontraktu), na który składaja się odsetki wyliczone według ustalonej w kontrakcie stałej stopy κ C(T i ) = κ i N i, gdzie i = (T i T i 1 ) jest długościa okresu odsetkowego obliczona według właściwej dla stopy kontraktu konwencji a N i jest nominałem, od którego w okresie odsetkowym [T i 1, T i ) liczone sa odsetki. Ostatnia płatność musi także uwzględniać płatność nominału. Stad C(T M ) = N + κ M N M.
21 Noga zmienna kontraktu IRS Noga zmienna kontraktu to strumień płatności Ĉ(ˆT i ) następujacych w chwilach ˆT i, i = 1,..., J (ˆT J = T M jest terminem zapadalności kontraktu), 2 na który składaja się odsetki wyliczone według zmiennej przyszłej stopy rynkowej LIBOR L (ˆT i 1, ˆT i ) powiększonej o marżę m Ĉ(ˆT i ) = (L (ˆT i 1, ˆT i ) + m) ˆ i ˆNi, gdzie ˆ i = (ˆT i ˆT i 1 ) jest długościa okresu odsetkowego dla nogi zmiennej a ˆN i jest nominałem, od którego w okresie odsetkowym [ˆT i 1, ˆT i ) liczone sa odsetki. Dodatkowo Ĉ(ˆT J ) powiększamy o spłatę nominału N. 2 Okresy odsetkowe dla nogi stałej i zmiennej mog a być różne; ważne jest tylko aby oba strumienie płatności kończyły się w tym samym momencie.
22 Losowe stopy LIBOR Przy wycenie nogi zmiennej kontraktu SWAP wprowadziliśmy stopę LIBOR L (T, S). Stopa ta jest stopa procentowa jaka będzie obowiazywała w okresie [T, S). W chwili t < T jest to zmienna losowa. Aby przeprowadzać obliczenia dla tej stopy podobnie jak dla deterministycznej stopy LIBOR L(t, T, S) wprowadźmy losowy czynnik dyskontowy D(T, S). Wielkość D(T, S) jest wartościa w chwili T instrumentu, który w chwili S płaci jednostkę waluty. Wtedy L D(T, T ) D(T, S) (T, S) = (T, S)D(T, S), gdzie (T, S) jest długościa okresu [T, S) liczona według właściwej konwencji. Zauważmy, że w momencie T stopa L (T, S) jest znana i równa L(T, T, S).
23 Cena kontraktu SWAP Dla uproszczenia przyjmijmy, że terminy płatności nogi stałej i zmiennej sa jednakowe a nominał jest stały i równy N. Przyjmijmy także, że marża m = 0 (to nie jest istotne założenie, bo m 0 można sprowadzić do przypadku m = 0 modyfikujac stała stopę κ). FS 0 (κ) =PV float (0) PV fixed (0) M =NP(0, T 0 ) NP(0, T M ) Nκ P(0, T i ) i Wartość nogi stałej i=1 PV fixed (0) = M M P(0, T i )C(T i ) = κn P(0, T i ) i + P(0, T M )N. i=1 i=1
24 Cena kontraktu SWAP c.d. Wartość nogi zmiennej Z definicji PV float (0) = = N M P(0, T i )Ĉ(T i) i=1 M P(0, T i )L (T i 1, T i ) i + P(0, T M )N. i=1 L (T, S) = D(T, T ) D(T, S) (T, S)D(T, S), więc P(0, T i )L 1 (T i 1, T i ) i = P(0, T i )( D(T i 1,T i ) 1) = P(0, T i 1 ) P(0, T i ). 1 Ponieważ D(T, S) D(T,S) = 1, więc posiadanie 1 D(T,S) jednostek pieniężnych w chwili S jest równoważne posiadaniu 1 jednostki 1 w chwili T. Stad D(T i 1,T i ) jednostek (losowych) w chwili T i jest równoważne 1 jednostce w chwili T i 1, a to jest równoważne P(0, T i 1 ) jednostkom w chwili 0.
25 Poprawna wycena SWAP Model rynku finansowego: istnieje na rynku miara martyngałowa spot P, wartości czynników dyskontowych D(t, T ) zdyskontowane wartościa rachunku bankowego B T sa martyngałami względem P, stopy LIBOR L(T i 1, T i ) utożsamiamy ze stopami LIBOR D(t,T ) D(t,S) forward F(T i 1, T i 1, T i ), gdzie F(t, T, S) = (T,S)D(t,S), stopy LIBOR forward F(t, T i 1, T i ) sa martyngałami względem miary P Ti. Na takim rynku FS t (κ) = E P [ M i=1 B t ( F(t, Ti 1, T i ) κ ) ] Ft i, B Ti gdzie B t oznacza wartość rachunku bankowego w chwili t.
26 Stopa swapowa Stopa swapowa (przyszła) nazywamy taka stopę κ, przy której wartość kontraktu SWAP w chwili t T 0 wynosi zero ( M ) 1. κ(t, T 0, T M ) = (P(t, T 0 ) P(t, T M ) P(t, T i ) i Jeśli znamy stopę swapowa, to cenę kontraktu SWAP na dowolna inna stała stopę można łatwo obliczyć ze wzoru FS t (κ) = FS t (κ) FS t (κ(t, T 0, T M )) M = (κ(t, T 0, T M ) κ) P(t, T i ) i. i=1 i=1
27 Krzywa dyskontowa raz jeszcze Stopy LIBOR, które służyły nam do konstrukcji krzywej dyskontowej znane sa jedynie dla czasów do 2 lat. Dla dłuższych okresów zapadalności, aby zbudować krzywa dyskontowa (międzybankowa) dysponujemy stopami swapowymi. Jak zobaczyliśmy to ostatnio, stopa swapowa, to stopa po której dyskontujemy wszystkie przepływy finansowe w kontrakcie SWAP, aby dostać zerowa wartość kontraktu. Załóżmy dla uproszczenia, że płatności w kontrakcie SWAP następuja raz w roku. Jeśli znamy czynniki dyskontowe do 2 lat oraz znamy stopę swapowa w kontrakcie na 3 lata, to możemy wyznaczyć czynnik dyskontowy na 3 lata. Następnie na 4 lata, 5 lat itd.
28 Krzywa dyskontowa raz jeszcze c.d. To postępowanie załamuje się w dwóch przypadkach: 1) nie mamy stóp swapowych podawanych w kolejnych latach (bo kontrakty o pewnej długości nie sa standardowo kwotowane) 2) płatności sa częstsze niż raz w roku a stopy swapowe sa podawane tylko dla pełnych lat. Najczęściej (dla większości walut) oba te przypadki zachodza jednocześnie. Co wtedy? Musimy przyjać jakaś regułę aproksymacji czynników dyskontowych a następnie rozwiazywać zadanie samouzgodnienia czynników dyskontowych. To jest skomplikowane numerycznie (pierwiastki nieliniowego równania) i nie ma twierdzenia, które gwarantuje istnienie jednoznacznego rozwiazania.
29 Capy i floory Kontrakt cap na stopę procentowa jest kontraktem opcyjnym o ustalonej strukturze czasowej (tenor) 0 < T 0 < T 1 < < T n, w którym wystawca opcji zobowiazuje się zapłacić posiadaczowi opcji w każdym terminie T i, i = 1,..., n, różnicę między bazowa stopa LIBOR ustalona w momencie T i 1 a stopa referencyjna K, jeśli stopa bazowa przekracza stopę referencyjna. Płatność jest odniesiona do wartości nominalnej kontraktu (płaci się procent od wartości nominalnej). Kontrakt floor to analogiczny kontrakt, w którym płacona jest różnica między stopa referencyjna a stopa bazowa, jeśli stopa bazowa jest niższa niż stopa referencyjna. W standardowym kontrakcie stopa bazowa LIBOR to stopa L (T i 1, T i ). Cap można traktować jako sumę pojedynczych opcji (capletów) płatnych w momentach T i. Analogicznie floor składa się z sumy floorletów.
30 Wzór Blacka Cena capletu o terminie zapadalności T i 1 i stopie referencyjnej K na okres [T i 1, T i ] dana jest wzorem Blacka gdzie Cpl B (0, T i 1, T i, K ) = P(0, T i )(T i T i 1 )C B (F i (0), K, v i ), C B (F i (0), K, v i ) = F i (0)Φ(d 1 ) K Φ(d 2 ), d 1 = ln(f i/k ) + vi 2 /2, d 2 = ln(f i/k ) vi 2 /2, v i v i F i = F(0, T i 1, T i ) jest stopa forward na okres [T i 1, T i ] a v 2 i = T i 1 ν 2 T i 1. ν Ti 1 w ostatnim wzorze jest rynkowa volatility capletu o terminie zapadalności T i 1, która z volatility stóp forward zwiazana jest zależnościa ν 2 T i 1 = 1 T i 1 Ti 1 0 σ 2 i (t)dt.
31 Skad wzór Blacka? Wzór Blacka wynika z przyjętego ad hoc założenia, że dynamika stopy LIBOR forward F(t, T, S) opisywana jest geometrycznym ruchem Browna (bez dryfu) względem pewnej miary Q df(t, T, S) = F(t, T, S)σdW t, gdzie W t jest jednowymiarowym standardowym ruchem Browna względem Q a σ jest dodatnia deterministyczna funkcja σ(t). Przy tych założeniach wzór Blacka jest szczególna postacia wzoru Blacka-Scholesa. Istnienie takiej miary i dynamiki można wykazać przy pewnych technicznych założeniach w modelu Heatha, Jarrowa i Mortona (HJM) dynamiki stopy forward f (t, T ). Ale istnienie odpowiednich miar oraz ewolucji stóp LIBOR forward dla wszystkich capletów wchodzacych w skład capa stało się możliwe dopiero dzięki pracom Musieli i Rutkowskiego.
32 Wykorzystanie wzoru Blacka do wyceny capów Typowa tabela kwotowań volatility capów.
33 Wykorzystanie wzoru Blacka do wyceny capów c.d. Volatility kwotowane na rynku nie sa wartościami volatility capletów, ale wielkościa, która przy wycenie capa jako sumy capletów ma tę sama wartość we wzorze Blacka dla wszystkich capletów, czyli zgodnie z konwencja rynkowa cena capa o terminie zapadalności T j dana jest wzorem j i=1 (T i T i 1 )P(0, T i )C B ( Fi (0), k, T i 1 ν cap T j ). Aby odzyskać volatility poszczególnych capletów musimy rozwiazać równanie, w którym powyższe wyrażenie przyrównamy do j i=1 ( (T i T i 1 )P(0, T i )C B Fi (0), k, T i 1 ν caplet ) T i 1 i rozwiażemy ze względu na ν caplet T i 1.
34 Wykorzystanie wzoru Blacka do wyceny capów c.d. Rozwiazanie takie jest mało skomplikowane jeśli mamy kwotowane volatility capów dla wszystkich kolejnych maturity, np. dla capów na LIBOR6M mamy kwotowanie co 6M. Wtedy obliczyć możemy wartości ν caplet T i 1 robiac rekurencję po j startujac od j = 1 aż do najdłuższej maturity. Kiedy volatility jest kwotowane nie dla wszystkich maturity możemy postapić dwojako: 1 dokonać interpolacji brakujacych wartości volatility i zastosować standardowa procedurę rekurencyjnego obliczania volatility capletów; 2 przyjać, że volatility capletów dla brakujacych kwotowań jest taka sama jak dla kolejnego dostępnego kwotowania; wtedy należy rozwiazać nieco trudniejsze zadanie algebraiczne polegajace na odwróceniu wzoru Blacka dla kilku różnych czasów zapadalności jednocześnie.
35 Wykorzystanie wzoru Blacka do wyceny capów c.d. Zadanie odwracania wzoru Blacka posiada zwykle poprawne rozwiazanie. Poprawność polega na tym, że otrzymane rozwiazanie jest dodatnie. Ale istnienie dodatniego rozwiazania nie jest oczywiste. W końcu szukamy miejsca zerowego skomplikowanej nieliniowej funkcji ( A + v 2 /2 ) f (v) = AΦ Φ v ( A v 2 /2 Doświadczenia numeryczne pokazuja, że przy braku niektórych kwotowań, poprawne rozwiazanie łatwiej jest otrzymać korzystajac wyłacznie z wartości kwotowanych na rynku niż dokonujac interpolacji brakujacych wielkości. v ).
36 Swapcje Swapcja z czasem wykonania T i cena referencyjna κ jest kontraktem opcyjnym, w którym właściciel opcji ma prawo wejść w chwili T = T 0 w kontrakt SWAP o ustalonej strukturze czasowej (tenor) T 0 < T 1 < < T n ze stopa referencyjna κ. W praktyce występuja dwa rodzaje opcji: payer swaption, gdy właściciel opcji ma prawo wejść w kontrakt payer swap, czyli kontrakt, w którym dostaje nogę stała kontraktu a płaci nogę zmienna, receiver swaption, gdy właściciel opcji ma prawo wejść w kontrakt receiver swap, czyli kontrakt, w którym płaci nogę stała kontraktu a dostaje nogę zmienna. Przy wycenie tych opcji przyjmuje się, że nominał kontraktu SWAP N = 1.
37 Wzór Blacka dla swapcji Cena swapcji o terminie zapadalności T 0 i stopie referencyjnej κ na kontrakt SWAP o strukturze czasowej T 0 < T 1 < < T n dana jest wzorem Blacka PS(0) = n ( P(0, T i ) i κ(0, T0, T n )Φ(h 1 ) κφ(h 2 ) ), i=1 gdzie h 1 = ln(κ(0, T 0, T n )/κ) + v 2 /2 v, h 2 = ln(κ(0, T 0, T n )/κ) v 2 /2, v κ(0, T 0, T n ) jest stopa swapowa kontraktu SWAP (stopa przy której wartość tego kontraktu jest zero) a v jest pewna stała zależna od tenora kontraktu SWAP (volatility stóp swapowych).
38 Wykorzystanie wzoru Blacka do wyceny swapcji To jest dużo trudniejsze zadanie niż dla capów. Tablica rynkowych kwotowań volatility swapcji Wartości w pierwszej kolumnie to czas życia swapcji (swaption maturity). Wartości w pierwszym wierszu to czasy życia kontraktów SWAP, na które wystawiona jest swapcja.
39 Wykorzystanie wzoru Blacka do wyceny swapcji c.d. Tablica jak a musimy z kwotowań rynkowych stworzyć. Element S m,n tej tablicy to volatility stopy LIBOR forward na moment T n 1 na okres [T m 1, T m ).
40 Brak zgodności modelu rynku capów i swapcji Nie może istnieć model w którym jednocześnie sa log-normalne stopy LIBOR forward, które pozwalaja wyprowadzić wzór Blacka dla capletów oraz stopy swapowe, które pozwalaja wyprowadzić wzór Blacka dla swapcji. Ten problem czeka na rozwiazanie!
41
Inżynieria Finansowa: 4. FRA i Swapy
 Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
4.5. Obligacja o zmiennym oprocentowaniu
 .5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
.5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową
 Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową Tomasz Romanowski Opis wycenianych instrumentów Caplet / Floorlet Jest to pojedyncza opcja kupna/sprzedaży stopy rynkowej L(T,
Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową Tomasz Romanowski Opis wycenianych instrumentów Caplet / Floorlet Jest to pojedyncza opcja kupna/sprzedaży stopy rynkowej L(T,
Inżynieria Finansowa: 4. FRA i IRS
 Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS
 Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
Inżynieria Finansowa - Egzamin - 28 stycznia Rozwiązania zadań Wersja z dnia 1 marca 2005, z drobnymi poprawkami
 Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Papiery wartościowe o stałym dochodzie
 Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS
 Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS Struktura kontraktu OIS Wycena kontraktu OIS 2 Struktura kontraktu
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS Struktura kontraktu OIS Wycena kontraktu OIS 2 Struktura kontraktu
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Inżynieria finansowa Wykład II Stopy Procentowe
 Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
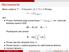 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo
 Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Dokument przedstawia zaimplementowane w systemie KDPW_CCP formuły wyceny instrumentów
Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Dokument przedstawia zaimplementowane w systemie KDPW_CCP formuły wyceny instrumentów
Instrumenty pochodne Instrumenty wbudowane
 www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
Obligacje, Swapy, FRAsy i Bob Citron
 Obligacje, Swapy, FRAsy i Bob Citron Andrzej Kulik andrzej.kulik@pioneer.com.pl +22 321 4106/ 609 691 729 1 Plan Przypomnienie informacji o rynku długu Rodzaje obligacji Ryzyko obligacji yield curve Duration
Obligacje, Swapy, FRAsy i Bob Citron Andrzej Kulik andrzej.kulik@pioneer.com.pl +22 321 4106/ 609 691 729 1 Plan Przypomnienie informacji o rynku długu Rodzaje obligacji Ryzyko obligacji yield curve Duration
Analiza instrumentów pochodnych
 Analiza instrumentów pochodnych Dr Wioletta Nowak Wykład 2-3 Kontrakt forward na przyszłą stopę procentową Kontrakty futures na długoterminowe instrumenty procentowe Swapy procentowe Przykład 1 Inwestor
Analiza instrumentów pochodnych Dr Wioletta Nowak Wykład 2-3 Kontrakt forward na przyszłą stopę procentową Kontrakty futures na długoterminowe instrumenty procentowe Swapy procentowe Przykład 1 Inwestor
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Dokumentacja Wycena papierów wartościowych o stałym oprocentowaniu
 Dokumentacja Wycena papierów wartościowych o stałym oprocentowaniu Piotr Szawlis Wstęp Wycena papierów wartościowych ze wzorów analitycznych jest najprostszym możliwym zadaniem obliczeniowym. W poniższym
Dokumentacja Wycena papierów wartościowych o stałym oprocentowaniu Piotr Szawlis Wstęp Wycena papierów wartościowych ze wzorów analitycznych jest najprostszym możliwym zadaniem obliczeniowym. W poniższym
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
Wykład XII. Instrumenty pochodne stopy procentowej
 Inżynieria Finansowa - Wykład XII 1 Wykład XII Instrumenty pochodne stopy procentowej Proste instrumenty pochodne stopy procentowej Instrumenty pochodne, których wypłaty zależą od struktury stóp procentowych,
Inżynieria Finansowa - Wykład XII 1 Wykład XII Instrumenty pochodne stopy procentowej Proste instrumenty pochodne stopy procentowej Instrumenty pochodne, których wypłaty zależą od struktury stóp procentowych,
ZARZĄDZANIE RYZYKIEM STOPY PROCENTOWEJ. dr Grzegorz Kotliński; Katedra Bankowości AE w Poznaniu
 ZARZĄDZANIE RYZYKIEM STOPY PROCENTOWEJ 1 DEFINICJA RYZYKA STOPY PROCENTOWEJ Ryzyko stopy procentowej to niebezpieczeństwo negatywnego wpływu zmian rynkowej stopy procentowej na sytuację finansową banku
ZARZĄDZANIE RYZYKIEM STOPY PROCENTOWEJ 1 DEFINICJA RYZYKA STOPY PROCENTOWEJ Ryzyko stopy procentowej to niebezpieczeństwo negatywnego wpływu zmian rynkowej stopy procentowej na sytuację finansową banku
1. Charakterystyka obligacji. 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji.
 mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC
 Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Załącznik przedstawia
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Załącznik przedstawia
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem. Temat wykładu: Wycena kontraktów swap
 Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
- zabezpieczanie za pomocą opcji
 Ryzyko stopy procentowej - zabezpieczanie za pomocą opcji Caplets and Floorlets Opcje opiewające na wysokość terminowej stopy procentowej Alternatywa dla FRA Caplet N x M @ i% - kupno daje prawo płacić
Ryzyko stopy procentowej - zabezpieczanie za pomocą opcji Caplets and Floorlets Opcje opiewające na wysokość terminowej stopy procentowej Alternatywa dla FRA Caplet N x M @ i% - kupno daje prawo płacić
Forward Rate Agreement
 Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE
 TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
Matematyka finansowa - lista zagadnień teoretycznych
 Matematyka finansowa - lista zagadnień teoretycznych Ostatnie zadanie na egzaminie będzie się składać z jednego bardziej skomplikowanego lub dwóch prostych pytań teoretycznych. Pytanie takie będzie dotyczyło
Matematyka finansowa - lista zagadnień teoretycznych Ostatnie zadanie na egzaminie będzie się składać z jednego bardziej skomplikowanego lub dwóch prostych pytań teoretycznych. Pytanie takie będzie dotyczyło
OPISY PRODUKTÓW. Rabobank Polska S.A.
 OPISY PRODUKTÓW Rabobank Polska S.A. Warszawa, marzec 2010 Wymiana walut (Foreign Exchange) Wymiana walut jest umową pomiędzy bankiem a klientem, w której strony zobowiązują się wymienić w ustalonym dniu
OPISY PRODUKTÓW Rabobank Polska S.A. Warszawa, marzec 2010 Wymiana walut (Foreign Exchange) Wymiana walut jest umową pomiędzy bankiem a klientem, w której strony zobowiązują się wymienić w ustalonym dniu
8. Papiery wartościowe: obligacje
 8. Papiery wartościowe: obligacje Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w 8. Krakowie) Papiery wartościowe: obligacje
8. Papiery wartościowe: obligacje Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w 8. Krakowie) Papiery wartościowe: obligacje
Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA
 Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA Wydział Matematyki Informatyki i Mechaniki UW 18 października 2011 Zadanie 3.1 W dniu 18 października 2004 Bank X kwotował: 3M PLN Depo -
Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA Wydział Matematyki Informatyki i Mechaniki UW 18 października 2011 Zadanie 3.1 W dniu 18 października 2004 Bank X kwotował: 3M PLN Depo -
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych
 Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo Tabela zmian Wersja dokumentu Wprowadzone
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo Tabela zmian Wersja dokumentu Wprowadzone
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy. XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Inżynieria finansowa Ćwiczenia II Stopy Procentowe
 Inżynieria finansowa Ćwiczenia II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 Zadanie 2.1 Oprocentowanie 3M pożyczki wynosi 5.00% (ACT/365). Natomiast, 3M bon skarbowy
Inżynieria finansowa Ćwiczenia II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 Zadanie 2.1 Oprocentowanie 3M pożyczki wynosi 5.00% (ACT/365). Natomiast, 3M bon skarbowy
Inwestycje finansowe. Wycena obligacji. Stopa zwrotu z akcji. Ryzyko.
 Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
Bank określa w Komunikacie waluty oraz kwoty, dla których przeprowadza transakcje. Rozdział 2. Zasady zawierania Transakcji
 REGULAMIN TRANSAKCJI ZAMIANY STÓP PROCENTOWYCH IRS ORAZ WALUTOWEJ TRANSAKCJI ZAMIANY STÓP PROCENTOWYCH CIRS W POWSZECHNEJ KASIE OSZCZĘDNOŚCI BANKU POLSKIM SPÓŁCE AKCYJNEJ Rozdział 1. Postanowienia ogólne
REGULAMIN TRANSAKCJI ZAMIANY STÓP PROCENTOWYCH IRS ORAZ WALUTOWEJ TRANSAKCJI ZAMIANY STÓP PROCENTOWYCH CIRS W POWSZECHNEJ KASIE OSZCZĘDNOŚCI BANKU POLSKIM SPÓŁCE AKCYJNEJ Rozdział 1. Postanowienia ogólne
Inwestowanie w obligacje
 Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
Obligacje o stałym oprocentowaniu (fixed-interest bonds)
 Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
 NOTA 6 - INSTRUMENTY POCHODNE BPH Fundusz Inwestycyjny Otwarty Parasolowy BPH Subfundusz Obligacji 2 na dzień 31.12.2012 Typ zajętej pozycji Rodzaj instrumentu pochodnego Cel otwarcia pozycji Wartość otwartej
NOTA 6 - INSTRUMENTY POCHODNE BPH Fundusz Inwestycyjny Otwarty Parasolowy BPH Subfundusz Obligacji 2 na dzień 31.12.2012 Typ zajętej pozycji Rodzaj instrumentu pochodnego Cel otwarcia pozycji Wartość otwartej
Dr hab. Renata Karkowska, ćwiczenia Zarządzanie ryzykiem 1
 1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
Obligacje o stałym oprocentowaniu (fixed- interest bonds) Najprostsze z nich to
 Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
STOPA PROCENTOWA I STOPA ZWROTU
 Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Spis treści. Przedmowa 11
 Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino
 Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Wstęp. Część pierwsza. Rynek walutowy i pieniężny. Rozdział 1. Geneza rynku walutowego i pieniężnego
 Wstęp Część pierwsza. Rynek walutowy i pieniężny Rozdział 1. Geneza rynku walutowego i pieniężnego Rynki natychmiastowe Rynek pieniężny Transakcje na rynku pieniężnym Rynek walutowy Geneza rynku walutowego
Wstęp Część pierwsza. Rynek walutowy i pieniężny Rozdział 1. Geneza rynku walutowego i pieniężnego Rynki natychmiastowe Rynek pieniężny Transakcje na rynku pieniężnym Rynek walutowy Geneza rynku walutowego
IRS Interest Rate Swap. Transakcja wymiany płatności odsetkowych
 IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 IRS - Interest Rate Swap (1) Umowa (transakcja) pomiędzy dwoma podmiotami, w której strony zobowiązują się do cyklicznej wymiany, w ustalonym
IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 IRS - Interest Rate Swap (1) Umowa (transakcja) pomiędzy dwoma podmiotami, w której strony zobowiązują się do cyklicznej wymiany, w ustalonym
Regulamin Transakcji Swap Procentowy
 Regulamin Transakcji Swap Procentowy 1. 1. Regulamin Transakcji Swap Procentowy zwany dalej Regulaminem SP określa szczegółowe zasady i tryb zawierania oraz rozliczania Transakcji Swap Procentowy na podstawie
Regulamin Transakcji Swap Procentowy 1. 1. Regulamin Transakcji Swap Procentowy zwany dalej Regulaminem SP określa szczegółowe zasady i tryb zawierania oraz rozliczania Transakcji Swap Procentowy na podstawie
Powtórzenie. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
System finansowy gospodarki. Zajęcia nr 6 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 2
 Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 8
 Ćwiczenia 8 Opcja jest to umowa między nabywcą (posiadaczem) a sprzedawcą (wystawcą), dająca nabywcy prawo do kupna (opcja kupna) lub sprzedaży (opcja sprzedaży) instrumentu bazowego przed lub w ustalonym
Ćwiczenia 8 Opcja jest to umowa między nabywcą (posiadaczem) a sprzedawcą (wystawcą), dająca nabywcy prawo do kupna (opcja kupna) lub sprzedaży (opcja sprzedaży) instrumentu bazowego przed lub w ustalonym
Zajęcia 1. Pojęcia: - Kapitalizacja powiększenie kapitału o odsetki, które zostały przez ten kapitał wygenerowane
 Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
IRS Interest Rate Swap. Transakcja wymiany płatności odsetkowych
 IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH
 Mariusz Próchniak Katedra Ekonomii II, SGH PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH Ekonomia menedżerska 1 2 Wartość przyszła (FV future value) r roczna stopa procentowa B kwota pieniędzy, którą
Mariusz Próchniak Katedra Ekonomii II, SGH PLANOWANIE I OCENA PRZEDSIĘWZIĘĆ INWESTYCYJNYCH Ekonomia menedżerska 1 2 Wartość przyszła (FV future value) r roczna stopa procentowa B kwota pieniędzy, którą
Regulamin Transakcji Swap Procentowy
 Regulamin Transakcji Swap Procentowy 1. Niniejszy Regulamin Transakcji Swap Procentowy, zwany dalej Regulaminem SP, określa szczegółowe zasady i tryb zawierania oraz rozliczania Transakcji Swap Procentowy
Regulamin Transakcji Swap Procentowy 1. Niniejszy Regulamin Transakcji Swap Procentowy, zwany dalej Regulaminem SP, określa szczegółowe zasady i tryb zawierania oraz rozliczania Transakcji Swap Procentowy
płatności odsetkowych
 IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
1) jednostka posiada wystarczające środki aby zakupić walutę w dniu podpisania kontraktu
 Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC
 Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeń Transakcji (obrót niezorganizowany)
Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeń Transakcji (obrót niezorganizowany)
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej
 5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt)
 II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
Instrumenty pochodne - Zadania
 Jerzy A. Dzieża Instrumenty pochodne - Zadania 27 marca 2011 roku Rozdział 1 Wprowadzenie 1.1. Zadania 1. Spekulant zajął krótką pozycję w kontrakcie forward USD/PLN zapadającym za 2 miesiące o nominale
Jerzy A. Dzieża Instrumenty pochodne - Zadania 27 marca 2011 roku Rozdział 1 Wprowadzenie 1.1. Zadania 1. Spekulant zajął krótką pozycję w kontrakcie forward USD/PLN zapadającym za 2 miesiące o nominale
Matematyka finansowa 8.12.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
SWAPY. Autorzy: Paweł Czyż Sebastian Krajewski
 SWAPY Autorzy: Paweł Czyż Sebastian Krajewski Plan prezentacji Swap - definicja Rodzaje swapów Przykłady swapów Zastosowanie swapów 2/29 Swap Swap umowa pomiędzy dwoma podmiotami na wymianę przyszłych
SWAPY Autorzy: Paweł Czyż Sebastian Krajewski Plan prezentacji Swap - definicja Rodzaje swapów Przykłady swapów Zastosowanie swapów 2/29 Swap Swap umowa pomiędzy dwoma podmiotami na wymianę przyszłych
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171)
 Przedmiot: MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171) Prowadzący wykład: dr Krzysztof Samotij, e-mail: krzysztof.samotij@pwr.edu.pl Czas i miejsce wykładu: poniedziałki (wg definicji J.M. Rektora) g. 9:15-11:00,
Przedmiot: MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171) Prowadzący wykład: dr Krzysztof Samotij, e-mail: krzysztof.samotij@pwr.edu.pl Czas i miejsce wykładu: poniedziałki (wg definicji J.M. Rektora) g. 9:15-11:00,
Różnorodność swapów i ich zastosowań, przyczyny popularności swapów w porównaniu z pozostałymi grupami instrumentów pochodnych
 Różnorodność swapów i ich zastosowań, przyczyny popularności swapów w porównaniu z pozostałymi grupami instrumentów pochodnych Monika Michalak Klaudia Michrowska Swap polega na zawarciu dwóch umów natychmiastowej
Różnorodność swapów i ich zastosowań, przyczyny popularności swapów w porównaniu z pozostałymi grupami instrumentów pochodnych Monika Michalak Klaudia Michrowska Swap polega na zawarciu dwóch umów natychmiastowej
Forward kontrakt terminowy o charakterze rzeczywistym (z dostawą instrumentu bazowego).
 Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
3b. Mierniki oceny inwestycji finansowych
 3b. Mierniki oceny inwestycji finansowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 3b. wmierniki Krakowie) oceny inwestycji
3b. Mierniki oceny inwestycji finansowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 3b. wmierniki Krakowie) oceny inwestycji
MIĘDZYNARODOWE FINANSE PRZEDSIĘBIORSTW. Anna Chmielewska, SGH Warunki zaliczenia
 MIĘDZYNARODOWE FINANSE PRZEDSIĘBIORSTW Anna Chmielewska Warunki zaliczenia 40 pkt praca samodzielna (szczegóły na kolejnym wykładzie) 60 pkt egzamin (forma testowa) 14 punktów obecności W przypadku braku
MIĘDZYNARODOWE FINANSE PRZEDSIĘBIORSTW Anna Chmielewska Warunki zaliczenia 40 pkt praca samodzielna (szczegóły na kolejnym wykładzie) 60 pkt egzamin (forma testowa) 14 punktów obecności W przypadku braku
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures
 10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
IRS Interest Rate Swap. Transakcja wymiany płatności odsetkowych
 IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
IRS Interest Rate Swap Transakcja wymiany płatności odsetkowych 1 Kontrakt IRS Kupujący IRS Odsetki wg ustalonej stopy stałej Odsetki według rzeczywistej stopy zmiennej Sprzedający IRS Strumienie płatności
System finansowy gospodarki. Zajęcia nr 5 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych
 Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Struktura terminowa rynku obligacji
 Krzywa dochodowości pomaga w inwestowaniu w obligacje Struktura terminowa rynku obligacji Wskazuje, które obligacje są atrakcyjne a których unikać Obrazuje aktualną sytuację na rynku długu i zmiany w czasie
Krzywa dochodowości pomaga w inwestowaniu w obligacje Struktura terminowa rynku obligacji Wskazuje, które obligacje są atrakcyjne a których unikać Obrazuje aktualną sytuację na rynku długu i zmiany w czasie
Rynek kapitałowopieniężny. Wykład 1 Istota i podział rynku finansowego
 Rynek kapitałowopieniężny Wykład 1 Istota i podział rynku finansowego Uczestnicy rynku finansowego Gospodarstwa domowe Przedsiębiorstwa Jednostki administracji państwowej i lokalnej Podmioty zagraniczne
Rynek kapitałowopieniężny Wykład 1 Istota i podział rynku finansowego Uczestnicy rynku finansowego Gospodarstwa domowe Przedsiębiorstwa Jednostki administracji państwowej i lokalnej Podmioty zagraniczne
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Egzamin XXVII dla Aktuariuszy z 12 października 2002 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC
 Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeo Transakcji (obrót niezorganizowany)
Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeo Transakcji (obrót niezorganizowany)
Zatem, jest wartością portfela (wealth) w chwili,. j=1
 Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Prof. nadzw. dr hab. Marcin Jędrzejczyk
 Prof. nadzw. dr hab. Marcin Jędrzejczyk 1. Zakup akcji, udziałów w obcych podmiotach gospodarczych według cen nabycia. 2. Zakup akcji i innych długoterminowych papierów wartościowych, traktowanych jako
Prof. nadzw. dr hab. Marcin Jędrzejczyk 1. Zakup akcji, udziałów w obcych podmiotach gospodarczych według cen nabycia. 2. Zakup akcji i innych długoterminowych papierów wartościowych, traktowanych jako
Elementy matematyki finansowej w programie Maxima
 Maxima-03_windows.wxm 1 / 8 Elementy matematyki finansowej w programie Maxima 1 Wartość pieniądza w czasie Umiejętność przenoszenia kwot pieniędzy w czasie, a więc obliczanie ich wartości na dany moment,
Maxima-03_windows.wxm 1 / 8 Elementy matematyki finansowej w programie Maxima 1 Wartość pieniądza w czasie Umiejętność przenoszenia kwot pieniędzy w czasie, a więc obliczanie ich wartości na dany moment,
II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014. Zadanie 2
 II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014 Zadanie 2 1/ Analizowane są dwie spółki Alfa i Gamma. Spółka Alfa finansuje swoją działalność nie korzystając z długu, natomiast spółka Gamma finansuje
II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014 Zadanie 2 1/ Analizowane są dwie spółki Alfa i Gamma. Spółka Alfa finansuje swoją działalność nie korzystając z długu, natomiast spółka Gamma finansuje
OGÓLNE RENTY ŻYCIOWE
 OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
dr hab. Marcin Jędrzejczyk
 dr hab. Marcin Jędrzejczyk Przez inwestycje należy rozumieć aktywa nabyte w celu osiągnięcia korzyści ekonomicznych, wynikających z przyrostu wartości tych zasobów, uzyskania z nich przychodów w postaci
dr hab. Marcin Jędrzejczyk Przez inwestycje należy rozumieć aktywa nabyte w celu osiągnięcia korzyści ekonomicznych, wynikających z przyrostu wartości tych zasobów, uzyskania z nich przychodów w postaci
identyfikator transakcji nadany przez KDPW_CCP identyfikator transakcji nadany przez platformę konfirmacji
 1. Daily Variation: Current MTM Baseline MTM/Settled MTM Daily Variation/Settlement PAI/PAA Type bieżąca wycena transakcji wyrażona w walucie transakcji wycena transakcji na poprzedni dzień roboczy wyrażona
1. Daily Variation: Current MTM Baseline MTM/Settled MTM Daily Variation/Settlement PAI/PAA Type bieżąca wycena transakcji wyrażona w walucie transakcji wycena transakcji na poprzedni dzień roboczy wyrażona
Matematyka finansowa 20.06.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Ekonomika Transportu Morskiego wykład 08ns
 Ekonomika Transportu Morskiego wykład 08ns dr Adam Salomon, Katedra Transportu i Logistyki Wydział Nawigacyjny, Akademia Morska w Gdyni Wykład 8ns : tematyka 1. Oprocentowanie, dyskontowanie, współczynnik
Ekonomika Transportu Morskiego wykład 08ns dr Adam Salomon, Katedra Transportu i Logistyki Wydział Nawigacyjny, Akademia Morska w Gdyni Wykład 8ns : tematyka 1. Oprocentowanie, dyskontowanie, współczynnik
Matematyka bankowa 2
 1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
