Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz.i
|
|
|
- Stefan Kwiecień
- 6 lat temu
- Przeglądów:
Transkrypt
1 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz.i Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 214 hazardu Warszawa / 45
2 Elementarny model rynku 1 Obligacje zero-kuponowe o deterministycznej chwilowej stopie procentowej (r(u), u ) sa jedynymi aktywami w które możemy inwestować. ( ) T B(t, T ) = exp r(u)du = B(t) B(T ), gdzie t ( t ) B t = exp r(u)du jest wartościa rachunku oszczędnościowego w momencie t. 2 Moment default u jest dodatnia zmienna losowa na (Ω, G, Q). F(t) := Q(τ t) = t f (u)du hazardu Warszawa / 45
3 Elementarny model rynku Założenie A : Zakładamy, że F(t) < 1 dla każdego t >. 1 Wypłaty 1 {T <τ} nie da się dokładnie zabezpieczyć na takim rynku. 2 Wzór wyceny arbitrażowej jest więc postulowany. 3 W praktyce rozkład τ przy Q- mierze martyngałowej jest wyznaczany na podstawie cen rynkowych instrumentów na rynku. hazardu Warszawa / 45
4 Funkcja Hazardu i jej własności Definicja Funkcja hazardu momentu losowego τ nazywamy funkcję Γ(t) = ln(1 F(t)) Funkcja Γ : R + R + ma następujace własności 1 niemalejaca, 2 Γ() = oraz 3 lim Γ(t) = +. t hazardu Warszawa / 45
5 Funkcja Hazardu i jej intensywność Lemat Załóżmy że F jest absolutnie ciagła względem miary Lebesgue a o gęstości f. Wtedy funkcja hazardu Γ jest absolutnie ciagła tzn. Γ t = t γ(u)du, gdzie γ(t) = f (u) 1 F(u) t R +. Definicja Funkcję γ nazywamy funkcja intensywności momentu τ (intensity lub hazard rate) hazardu Warszawa / 45
6 Intensywność 1 Mamy wzór 2 Interpretacja Q(τ > t) = 1 F(t) = e Γ(t) = e t γ(u)du, γ(t) = lim Q(t < τ t + h τ > t). h h 1 3 Niech τ będzie momentem pierwszego skoku procesu Poissona N z deterministyczna funkcja intensywności (λ(t), t ). Wtedy N t t λ(u)du jest FN -martyngałem. 4 Przez zastopowanie także 1 {τ t} t τ λ(u)du jest F N -martyngałem. hazardu Warszawa / 45
7 Rozgrzewka 1 Niech H będzie procesem indykatora defaultu tzn H t := 1 {t τ}, 2 Przez H oznaczamy naturalna filtrację dla H tzn. H t = σ{{s τ} : s t} 3 H jest najmniejsza filtracja względem której τ jest momentem stopu. 4 Kluczowa obserwacja: Dla X L 1 (Q) mamy E(X H t )1 {τ>t} = E(X τ > t)1 {τ>t} = E(X1 {τ>t}) Q(τ > t) 1 {τ>t} hazardu Warszawa / 45
8 Stały odzysk w terminie wykupu Obligacja (L = 1) bez kuponów (DZC -Defaultable-Zero-Coupon Bond) o terminie wykupu T i odzyskiwanej wartości δ płaconej w T jest reprezentowana przez dwa przepływy. Płatności jednostki pieniężnej L = 1 w T jeżeli {τ > T } Płatność δ [, 1] jednostek pieniężnych dokonywana w T jeżeli {τ T } Cena takiej obligacji jest (formalnie) wartościa oczekiwana przy Q D δ ( ) (, T ) = B(, T )E Q 1{T <τ} + δ1 {τ T } Z tego otrzymujemy D δ (, T ) = B(, T ) }{{} (1 δ)b(, T )F(T ). }{{} Obligacja skarbowa Oczekiwana strata przy Q hazardu Warszawa / 45
9 Wycena dla t [, T ) Na zbiorze {t τ} mamy pewna płatność δ w T której wartość w t wynosi δb(t, T ) Na zbiorze {t < τ} mamy pewna wartość D δ (t, T ), Mamy więc D δ (t, T ) = 1 {t τ} δb(t, T ) + 1 {t<τ} Dδ (t, T ) gdzie D δ (t, T ) dla t [, T ] jest tzw. wartościa przed defaultem Z kluczowej uwagi mamy D δ (t, T ) = E Q (B(t, T )(1 {T <τ} + δ1 {τ T } ) t < τ). hazardu Warszawa / 45
10 Policzmy D δ (t, T ): D δ (t, T ) = B(t, T ) (1 (1 δ)q(τ T t < τ)) ( = B(t, T ) 1 (1 δ) Q(t < τ T ) ) Q(t < τ) ( ) G(t) G(T ) = B(t, T ) 1 (1 δ), G(t) gdzie G(t) = 1 F(t) jest funkcja przeżycia (survival function). Zdefiniujmy dla t [, T ] funkcję ( B γ (t, T ) := B(t, T ) G(T ) G(t) = exp T t r(u) + γ(u)du ). hazardu Warszawa / 45
11 Wtedy wartość przed defaultem można zapisać D δ (t, T ) = B γ (t, T ) + δ (B(t, T ) B γ (t, T )). W szczególności dla δ = (obligacja bez odzysku - zero recovery) mamy D (t, T ) = B γ (t, T ) i dlatego D (t, T ) = 1 {t<τ} D (t, T ) = 1 {t<τ} B γ (t, T ) D δ jest nieciagła w τ, ponieważ na zbiorze {τ T } mamy D δ (τ, T ) D δ (τ, T ) = δb(τ, T ) D δ (τ, T ) = (δ 1)B γ (t, T ) < hazardu Warszawa / 45
12 Reprezentacja ceny Zauważmy, że wartość przed defaultem ma strukturę D δ (t, T ) = B(t, T )(1 LGD DP) gdzie LGD (loss-given-default) i DP (default probability) sa zdefiniowane wzorami LGD := 1 δ, DP := Q(t < τ T ) Q(t < τ) = Q(τ T t < τ) hazardu Warszawa / 45
13 Spready kredytowe Załóżmy że γ(t) = const wtedy mamy S(t, T ) := 1 B(t, T ) ln T t D δ (t, T ) = γ 1 ( ) T t ln 1 + δ(e γ(t t) 1). Krótko terminowy spread jest lim S(t, T ) = γ(1 δ) > gdy γ > i δ < 1. T t Zadanie Czy spready sa dodatnie dla każdego t [, T ]? hazardu Warszawa / 45
14 Spready kredytowe Gdy γ nie jest stała to w przypadku δ = mamy D (t, T ) = B γ (t, T ) = exp( T t ˆr(u)du) gdzie ˆr = r + γ - to tzw. stopa procentowa uwzględniajaca ryzyko kredytowe(deafult-risk-adjusted interest rate). Wtedy S(t, T ) := 1 B(t, T ) ln T t D (t, T ) = 1 T t T Widzimy, że ˆr > r jeżeli γ > co odpowiada jeżeli P(τ T t < τ) >. D (t, T ) < B(t, T ). t γ(u)du > gdy γ >. hazardu Warszawa / 45
15 Ogólny odzysk w terminie wykupu Załóżmy, że płatność w terminie wykupu jest deterministyczna funkcja o momentu τ oznaczana δ : R + R. Wtedy wartość w chwili takiej obligacji jest dana wzorem lub dokładniej D δ (, T ) = B(, T )E Q ( 1{T <τ} + δ(τ)1 {τ T } ), D δ (, T ) = B(, T ) ( G(T ) + T δ(s)f (s)ds Jak poprzednio cena ex-dividend dla t [, T ) jest dana wzorem D δ (t, T ) = B(t, T )E Q ( 1{T <τ} + δ(τ)1 {τ T } H t ) ). hazardu Warszawa / 45
16 Lemat Cena obligacji dla t [, T ) jest dana D δ (t, T ) = 1 Dδ {t<τ} (t, T ) + 1 {t τ} δ(τ)b(t, T ) gdzie wartość przed defaultem D δ (t, T ) jest dana D δ ( (t, T ) := B(t, T )E Q 1{T <τ} + δ(τ)1 {τ T } t < τ ) = B γ (t, T ) + B γ (t, T ) T t δ(u)γ(u)e T u γ(v)dv du. Dynamika procesu ( D δ (t, T ), t [, T ]) jest d D δ (t, T ) = (r(t) + γ(t)) D δ (t, T )dt B(t, T )γ(t)δ(t)dt. Dowód. Na ćwiczeniach : skorzystać z db γ (t, T ) = (r(t) + γ(t))b γ (t, T )dt. hazardu Warszawa / 45
17 Wypłata zastępcza (odzysk) w momencie defaultu Posiadacz otrzymuje jednostkę pieniężna w chwili T jeżeli default jeszcze (do chwili T) nie nastapił, Lub płatność δ(τ) jednostek pieniężnych w momencie τ jeżeli τ T, gdzie δ jest funkcja deterministyczna. Cena w chwili takiej obligacji jest równa D δ (, T ) = E Q ( B(, T )1{T <τ} + B(, τ)δ(τ)1 {τ T } ) = B(, T )Q(T < τ) + T B(, u)δ(u)df(u) T = G(T )B(, T ) + B(, u)δ(u)f (u)du hazardu Warszawa / 45
18 Lemat Cena obligacji dla t [, T ) jest dana D δ (t, T ) = 1 Dδ {t<τ} (t, T ) gdzie wartość przed defaultem D δ (t, T ) jest dana D δ ( (t, T ) := B(t, T )E Q 1{T <τ} + B(t, τ)δ(τ)1 {τ T } t < τ ) = B γ (t, T ) + T t B γ (t, u)δ(u)γ(u)du. Dynamika procesu ( D δ (t, T ), t [, T ]) jest d D δ (t, T ) = (r(t) + γ(t)) D δ (t, T )dt γ(t)δ(t)dt. Dowód. Na ćwiczeniach hazardu Warszawa / 45
19 Konwencje odzysku/wypłaty zastępczej W praktyce spotyka się następujace konwencje odzysku Fractional recovery of Par Value - obligacja płaci stała kwotę δ w momencie τ. Wartość przed defaultem pokrywa się z wartościa przed defaultem dla obligacji z odzyskiem w momencie wykupu z funkcja δb 1 (t, T ) Fractional recovery of Treasury Value - obligacja płaci δ(t) = δb(t, T ) w momencie defaultu. Wartość przed defaultem jest wtedy taka sama jak dla obligacji ze stałym odzyskiem w momencie wykupu T. D δ (t, T ) = e T t (r(u)+γ(u))du + δb(t, T ) G(t) = D (t, T ) + δb(t, T ) T t T t γ(u)e u γ(v)dv du γ(u)e u t γ(v)dv du hazardu Warszawa / 45
20 Częściowy odzysk wartości rynkowej Fractional recovery of Market Value - obligacja płaci w momencie defaultu odzysk równy δ(t) D δ (t, T ), gdzie δ jest deterministyczna funkcja. Wartość przed defaultem ma wtedy dynamikę d D δ (t, T ) = (r(t) + γ(t)(1 δ(t))) D δ (t, T )dt, Dδ (T, T ) = 1 z czego otrzymujemy dla każdego t [, T ] ( ) T D δ (t, T ) = exp r(u) + γ(u)(1 δ(u)))du t hazardu Warszawa / 45
21 Warunkowe wartości oczekiwane zwiazane z H 1 Niech H będzie procesem indykatora defaultu tzn H t := 1 {t τ}, 2 Przez H oznaczamy naturalna filtrację dla H tzn. 3 Własności filtracji H H t = σ{h s : s t}, H = σ{h s : s R + }, H.1 : H t = σ{{s τ} : s t}, H.2 : H t = σ{σ(τ) {τ t}}, H.3 : H t = σ(τ t) {τ > t}, H.4 : H t = H t+, H.5 : H = σ(τ), H.6 : Dla każdego A H mamy A {τ t} H t. hazardu Warszawa / 45
22 Lemat-KLUCZ Lemat Niech Y z.l. G-mierzalna. Wtedy mamy 1 {τ t} E Q (Y H t ) = E Q (Y 1 {τ t} H ) = 1 {τ t} E Q (Y τ), oraz 1 {τ>t} E Q (Y H t ) = 1 {τ>t} E(Y 1 {τ>t} ) Q(τ > t). hazardu Warszawa / 45
23 Kluczowe wnioski Wniosek Niech Y z.l. G-mierzalna. Wtedy mamy E Q (Y H t ) = 1 {τ t} E Q (Y τ) + 1 {τ>t} E(Y 1 {τ>t} ) Q(τ > t). Wniosek Jeżeli Y jest H t mierzalna Y = 1 {τ t} E Q (Y τ) + 1 {τ>t} E(Y 1 {τ>t} ) Q(τ > t). hazardu Warszawa / 45
24 Kluczowe wnioski Wniosek Niech Y z.l. H -mierzalna tzn. Y = h(τ) dla pewnej funkcji borelowskiej h : R + R. Wtedy: Jeżeli funkcja hazardu Γ jest ciagła to mamy E Q (Y H t ) = 1 {τ t} h(τ) + 1 {τ>t} h(u)e Γ(t) Γ(u) dγ(u). Jeżeli τ ma funkcję intensywności γ to E Q (Y H t ) = 1 {τ t} h(τ) + 1 {τ>t} W szczególności dla s > t mamy Q(τ > s H t ) = 1 {τ>t} e s t γ(v)dv t t h(u)γ(u)e u t γ(v)dv du. hazardu s γ(v)dv Warszawa / 45
25 Martyngały zwiazane z momentem defaultu τ Lemat Procesy dane wzorami sa H-martyngałami. L t = (1 H t )e Γ(t), t, df(u) M t = H t (,t τ] 1 F(u ), t, hazardu Warszawa / 45
26 Martyngały zwiazane z momentem defaultu τ Wniosek Załóżmy że funkcja hazardu Γ jest ciagła. Wtedy jest H-martyngałem. Ponadto L t = 1 M t = H t Γ(t τ), t (,t] L u dm u Jeżeli τ ma intensywność to mamy t τ M t = H t γ(u)du = H t t (1 H u )γ(u)du hazardu Warszawa / 45
27 Wzór na całkowanie przez części Lemat Niech g i h będa funkcjami cadlag. Jeżeli g i h maja skończone wachanie na [, t] to wtedy mamy g(t)h(t) = g()h() + g(u )dh(u) + h(u)dg(u) = g()h() + = g()h() + (,t] (,t] (,t] + u t g(u) h(u) g(u)dh(u) + (,t] g(u )dh(u) + (,t] (,t] h(u )dg(u) h(u )dg(u) hazardu Warszawa / 45
28 Dynamiki cen DZC Załóżmy że τ ma funkcję intensywności γ. Wtedy DZC z wypłata zastępcza δ(τ) w momencie defaultu τ ma dynamikę dd δ (t, T ) = (r(t)d δ (t, T ) δ(t)γ(t)(1 H t ))dt D δ (t, T )dm t gdzie M jest H-martyngałem danym wzorem M t = H t t τ γ(u)du = H t t (1 H u )γ(u)du. Widzimy że proces D δ (t, T )B 1 (t) nie jest H-martyngałem. Analogicznie DZC z wypłata zastępcza δ(τ) w momencie wykupu obligacji ma dynamikę dd δ (t, T ) = r(t)d δ (t, T )dt + (δ(t)b(t, T ) D δ (t, T ))dm t hazardu Warszawa / 45
29 Twierdzenie o reprezentacji martyngałowej Theorem Niech h będzię funkcja borelowska E( h(τ) ) = h(u) df(u) <. Wtedy H-martyngał M h zdefinowany wzorem Mt h = E(h(τ) H t ), t ma reprezentację M h t = E(h(τ)) + t τ (h(u) g(u))dm u, t, gdzie g(u) := u h(s)dg(s) G(u) = E(h(τ) τ > u) hazardu Warszawa / 45
30 Twierdzenie o reprezentacji Ponadto g jest ciagł a funkcja i zachodzi g(u) = M h u na zbiorze {τ > u} Stad możemy zapisać martyngał M h nastepujaco M h t = E(h(τ)) + t τ Wniosek Każdy H-martyngał X ma reprezentację (h(u) M h u )dm u, t, t X t = X + ξ u dm u, t, gdzie ξ jest procesem H-prognozowalnym. hazardu Warszawa / 45
31 Zamiana miary Niech P będzie miara probabilistyczna na (Ω, H ) taka, że P < Q Wtedy istnieje η H taka że P(A) = ηdq, A dp dq = η, Ponieważ η = h(τ) to τ ma (wszędzie zdefiniowana) funkcję hazardu jeżeli P(τ > t) = h(u)df (u) >, t. (t, ) Zakładamy że warunek powyżej jest spełniony! Niech F(t) := P(τ t), Γ(t) := ln(1 F(t)), t. hazardu Warszawa / 45
32 Zamiana miary - Twierdzenie Girsanova Lemat Załóżmy, że F jest ciagła. Wtedy F jest ciagła oraz mamy t Γ(t) = ĥ(u)dγ(u), gdzie ĥ(u) = h(t) g(t), g(t) = eγ(t) (t, ) h(u)df(u). Stad proces M dany wzorami t τ M t = H t ĥ(u)dγ(u) = M t jest H martyngałem przy P. t τ (ĥ(u) 1)dΓ(u) hazardu Warszawa / 45
33 Zamiana miary Można pójść w druga stronę, tzn. jeżeli dla pewnej funkcji ĥ funkcja t Γ(t) := ĥ(u)dγ(u), jest funkcja ciagł a taka, że lim Γ(t) = + t to można znaleźć miarę P < Q taka że Γ jest funkcja hazardu τ przy mierze P. Forma tego twierdzenia może nie być wygodna w zastosowaniach. Bardziej przydatna może być postać twierdzenia Girsanova w języku procesu gęstości i eksponenty stochastycznej. hazardu Warszawa / 45
34 Zamiana miary - proces gęstości RN jako eksponenta stochastyczna Niech η t := dp dq H t = E Q (h(τ) H t ) Theorem Niech F bedzie ciagł a funkcja, E oznacza eksponentę stochastyczna. Wtedy t η t = 1 + η u (ĥ(u) 1)dM u, t, lub równoważnie η t = E t ( (, ](ĥ(u) 1)dM u ), t. hazardu Warszawa / 45
35 Zamiana miary - eksponenta stochastyczna Niech κ mierzalna funkcja taka że κ 1, oraz Wtedy t κ(u)dγ(u) <, t, ( ) η t := E t κ(u)dm u, t. (, ] jest nieujemnym H-martyngałem przy mierze Q. Czy można wykorzystać η do konstrukcji miary P < Q takiej że t Γ(t) = (1 + κ(u))dγ(u), t. TAK! Ale tylko jeżeli dodatkowo mamy (1 + κ(u))dγ(u) = hazardu Warszawa / 45
36 Zamiana miary - eksponenta stochastyczna Wtedy η t = E Q (η H t ), gdzie η := lim η t. t Można wtedy wprowadzić miarę probabilistyczna P < Q kładac dp dq := η, Wtedy funkcja hazardu przy P jest dobrze zdefinowana i ma postać t Γ(t) = (1 + κ(u))dγ(u), t. Stad procesy M t = M t t τ κ(u)dγ(u) = H t sa H-martyngałami przy mierze P. t τ (1 + κ(u))dγ(u) hazardu Warszawa / 45
37 Niezupełność Elementarnego Modelu W elementarnym modelu rynku możemy inwestować w obligacje bez ryzyka o deterministycznej stopie procentowej. Zdyskontowane ceny sa stałymi, stad zbiór Q równoważnych miar martyngałowych jest zbiorem miar równoważnych mierze rzeczywistej. Dlatego istnieje nieskończenie wiele miar martyngałowych i mamy doczynienia z rynkiem niezupełnym. Dla dowolnej Q Q, niech F Q (t) := Q(τ t) Przedział cen bezarbitrażowych. Dla DZC o stałym odzysku płaconym w momencie wykupu jest Przedział cen jest równy {E Q (B(, T )(1 {T <τ} + δ1 τ T )); Q Q} (δb(, T ), B(, T )) hazardu Warszawa / 45
38 Równoważne miary martyngałowe/wyceniajace Brak arbitrażu jest zazwyczaj interpretowany jako istnienie równoważej miary martyngałowej. Jeżeli DZC sa instrumentami dostępnymi na rynku to ich ceny sa dane przez rynek. Miara martyngałowa wybrana przez rynek jest taka miara Q, że na zbiorze {t < τ} D(t, T ) = B(t, T )E Q (1 {T <τ} + δ1 τ T t < τ) Można więc rozkład τ przy Q wyciagn ać z cen rynkowych DZC hazardu Warszawa / 45
39 Obligacje bez odzysku Jeżeli DZC bez odzysku sa handlowane na rynku po cenach D(t, T ) to należa one do przedziału (, B(, T )) Zdyskonotwane ceny B(, t)d(t, T ) sa Q martyngałami i ich ceny spełniaja D(t, T )B(, t) = E Q (B(, T )1 {T <τ} H t ) = 1 {t<τ} e T t γ Q (s)ds B(, T ) gdzie γ Q (s) = f Q(s) 1 F Q (s). Stad intensywność przy mierze Q można by otrzymać z cen DZC za pomoca wzoru r(t) + γ Q (t) = T ln D(t, T ) T =t hazardu Warszawa / 45
40 Obligacje bez odzysku W praktyce jednak kalibruje się względem zmieniajacego się T w chwili t = B(, T ) D(, T ) F Q (T ) = B(, T ) Jeżeli δ i ceny DZC o różnych maturity sa znane, to F Q (T ) = B(, T ) D(, T ) B(, T )(1 δ) Rozkład τ przy Q jest więc znany! hazardu Warszawa / 45
41 Obligacje z odzyskiem w momencie defaultu Niech T D oznacza pochodna DZC względem maturity cen w chwili zero D(, T ) Mamy T D(, T ) = g(t )B(, T ) G(T )B(, T )r(t ) δ(t )g(t )B(, T ), gdzie g(t) = G (t). Stad, rozwiazuj ac to równanie różniczkowe otrzymujemy [ t Q(τ > y) = G(t) = (t) 1+ gdzie ( t (t) = exp ] 1 T D(, s) B(, s)(1 δ(s)) ( (s)) 1 ds ) r(u) 1 δ(u) du hazardu Warszawa / 45
42 Cena ex-dividend wypłat narażonych na ryzyko Ogólna wypłata narażona na ryzyko kredytowe (X, X, A, Z, τ) składa się z: Przyrzeczona wypłata X - zobowiazanie do spłacenia w momencie wykupu T < T Przyrzeczone dywidendy A - zobowiazania (kupony) płacone w sposób cigły lub dyskretny. Wypłata zastępcza X wypłacana w T jeżeli default nastapił przed lub w momencie wykupu T. Proces wypłaty zastępczęj (odzysku) Z - wypłata zastępcza wypłacana w momencie defaultu. Momen defaultu τ. hazardu Warszawa / 45
43 Proces dywidend i ceny ex-dividend Definicja Procesem dywidend D wypłaty narażonej na ryzyko kredytowe (X, A, X, Z, τ) o terminie wykupu T definujemy dla każdego t R + wzorem D t = XT d 1 [T, [(t) + (1 H u )da u + Z u dh u, (,t] (,t] gdzie X d T := X1 {τ<t } + X1 {τ T }. Definicja Dla każdego t [[, T ]] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu 1 dd u F t. (t,t ] hazardu Warszawa / 45
44 Dynamiki cen kontraktów na przetrwanie: (X,,,, τ) Założenie A : Zakładamy, że rynek wybrał miarę martyngałowa Q. Założenie B : Zakładamy, że chwilowa stopa procentowa r jest stała. Niech (X,,,, τ) będzie kontratem na dożycie/przetrwanie (survival claim) chwili T. Wypłata w T jest postaci 1 {T <τ} X Cena w chwili t jest dana wzorem Y t = e rt E Q (1 {T <τ} e rt X H t ) Dynamika cen jest natomiast dana wzorem dy t = ry t dt Y t dm t hazardu Warszawa / 45
45 Dynamiki cen wypłat zastępczych: (,,, Z, τ) Niech (,,, Z, τ) będzie wypłata zastępcza (recovery claim). Wypłata w τ jest równa Z (τ)1 {τ T } Cena ex-dividend w chwili t jest dana wzorem S t = e rt E Q (1 {t<τ T } e rτ Z (τ) H t ) Dynamika cen ex-dividend jest natomiast dana wzorem ds t = (1 H t )(rs t Z t )dt S t dm t Cena skumulownaych dividend w chwili t jest dana wzorem oraz Y t = e rt E Q (1 {τ T } e rτ Z (τ) H t ) ( ) Z (t) dy t = ry t dt + B(t) Y t dm t hazardu Warszawa / 45
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
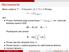 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU
 Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008
 Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014
 Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
Wykład 2 Zmienne losowe i ich rozkłady
 Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
4 Kilka klas procesów
 Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Wzory matematyka finansowa
 Wzory matematyka finansowa MaciejRomaniuk 29 września 29 K(t) funkcjaopisującaakumulacjęwchwiliczasut,k() kapitał,i stopazyskuwchwilit: i= K(t) K() (1) K() K kapitał,i stałastopaprocentowadlaustalonegookresuczasut,
Wzory matematyka finansowa MaciejRomaniuk 29 września 29 K(t) funkcjaopisującaakumulacjęwchwiliczasut,k() kapitał,i stopazyskuwchwilit: i= K(t) K() (1) K() K kapitał,i stałastopaprocentowadlaustalonegookresuczasut,
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Papiery wartościowe o stałym dochodzie
 Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Wykład 11: Martyngały: definicja, twierdzenia o zbieżności
 RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
Teoria ze Wstępu do analizy stochastycznej
 eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga
 RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik. Historia
 1 Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik Całka stochastyczna ( t ) H s dx s = H X. t Historia K. Itô (1944) konstrukcja całki stochastycznej
1 Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik Całka stochastyczna ( t ) H s dx s = H X. t Historia K. Itô (1944) konstrukcja całki stochastycznej
Prawdopodobieństwo i statystyka
 Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
21 maja, Mocna własność Markowa procesu Wienera. Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Parametr Λ w populacji ubezpieczonych ma rozkład dany na półosi dodatniej gęstością: 3 f
 Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A
 Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Zadania ze Wstępu do Analizy Stochastycznej 1. = 0 p.n.
 Zadania ze Wstępu do Analizy Stochastycznej 1 1. Znajdź rozkład zmiennej 5W 1 W 3 + W 7. 2. Dla jakich parametrów a i b, zmienne aw 1 W 2 oraz W 3 + bw 5 są niezależne? 3. Znajdź rozkład wektora losowego
Zadania ze Wstępu do Analizy Stochastycznej 1 1. Znajdź rozkład zmiennej 5W 1 W 3 + W 7. 2. Dla jakich parametrów a i b, zmienne aw 1 W 2 oraz W 3 + bw 5 są niezależne? 3. Znajdź rozkład wektora losowego
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω)
 PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami:
 Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Zadania z Procesów Stochastycznych 1
 Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
1. Ubezpieczenia życiowe
 1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Zatem, jest wartością portfela (wealth) w chwili,. j=1
 Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Zadanie 1. są niezależne i mają rozkład z atomami: ( ),
 Zadanie. Zmienne losowe są niezależne i mają rozkład z atomami: ( ) ( ) i gęstością: ( ) na przedziale ( ). Wobec tego ( ) wynosi: (A) 0.2295 (B) 0.2403 (C) 0.2457 (D) 0.25 (E) 0.269 Zadanie 2. Niech:
Zadanie. Zmienne losowe są niezależne i mają rozkład z atomami: ( ) ( ) i gęstością: ( ) na przedziale ( ). Wobec tego ( ) wynosi: (A) 0.2295 (B) 0.2403 (C) 0.2457 (D) 0.25 (E) 0.269 Zadanie 2. Niech:
Prawdopodobieństwo i statystyka
 Wykład V: Zmienne losowe i ich wartości oczekiwane 25 października 2017 Definicja zmiennej losowej Definicja Zmienne losowa to charakterystyka liczbowa wyniku eksperymentu losowego. Zmienne losowa na przestrzeni
Wykład V: Zmienne losowe i ich wartości oczekiwane 25 października 2017 Definicja zmiennej losowej Definicja Zmienne losowa to charakterystyka liczbowa wyniku eksperymentu losowego. Zmienne losowa na przestrzeni
Matematyka finansowa 05.12.2005 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 100 minut 1 1.
Wykład 3 Jednowymiarowe zmienne losowe
 Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Statystyka i eksploracja danych
 Wykład II: i charakterystyki ich rozkładów 24 lutego 2014 Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa,
Wykład II: i charakterystyki ich rozkładów 24 lutego 2014 Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa,
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Inżynieria finansowa Wykład II Stopy Procentowe
 Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej
 5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
Rozdział 1. Wektory losowe. 1.1 Wektor losowy i jego rozkład
 Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
}, gdzie a = t (n) )(f(t(n) k. ) f(t(n) k 1 ) 1+δ = 0,
 Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 4: UBEZPIECZENIA NA ŻYCIE Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 4: UBEZPIECZENIA NA ŻYCIE Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub
2. P (E) = 1. β B. TSIM W3: Sygnały stochastyczne 1/27
 SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
Modelowanie krzywej dochodowości
 Modelowanie krzywej dochodowości Marek Świętoń (2002) Terminowa struktura dochodowości skarbowych papierów wartościowych w Polsce w latach 1998-2001 Materiały i Studia nr 150. Modelowanie Rynków Finansowych
Modelowanie krzywej dochodowości Marek Świętoń (2002) Terminowa struktura dochodowości skarbowych papierów wartościowych w Polsce w latach 1998-2001 Materiały i Studia nr 150. Modelowanie Rynków Finansowych
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu.
 Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS
 Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 3: WYZNACZANIE ROZKŁADU CZASU PRZYSZŁEGO ŻYCIA 1 Hipoteza jednorodnej populacji Rozważmy pewną populację osób w różnym wieku i załóżmy, że każda z tych osób
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 3: WYZNACZANIE ROZKŁADU CZASU PRZYSZŁEGO ŻYCIA 1 Hipoteza jednorodnej populacji Rozważmy pewną populację osób w różnym wieku i załóżmy, że każda z tych osób
Strategie zabezpieczaj ce
 04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
Matematyka finansowa 20.06.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Tablice trwania życia
 ROZDZIAŁ 3 Tablice trwania życia 1 Przyszły czas życia Osobę, która ukończyła x lat życia, będziemy nazywać x-latkiem i oznaczać symbolem x Jej przyszły czas życia, tzn od chwili x do chwili śmierci, będziemy
ROZDZIAŁ 3 Tablice trwania życia 1 Przyszły czas życia Osobę, która ukończyła x lat życia, będziemy nazywać x-latkiem i oznaczać symbolem x Jej przyszły czas życia, tzn od chwili x do chwili śmierci, będziemy
Prawdopodobieństwo i statystyka
 Wykład IV: 27 października 2014 Współczynnik korelacji Brak korelacji a niezależność Definicja współczynnika korelacji Współczynnikiem korelacji całkowalnych z kwadratem zmiennych losowych X i Y nazywamy
Wykład IV: 27 października 2014 Współczynnik korelacji Brak korelacji a niezależność Definicja współczynnika korelacji Współczynnikiem korelacji całkowalnych z kwadratem zmiennych losowych X i Y nazywamy
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
W3 - Niezawodność elementu nienaprawialnego
 W3 - Niezawodność elementu nienaprawialnego Henryk Maciejewski Jacek Jarnicki Jarosław Sugier www.zsk.iiar.pwr.edu.pl Niezawodność elementu nienaprawialnego 1. Model niezawodności elementu nienaprawialnego
W3 - Niezawodność elementu nienaprawialnego Henryk Maciejewski Jacek Jarnicki Jarosław Sugier www.zsk.iiar.pwr.edu.pl Niezawodność elementu nienaprawialnego 1. Model niezawodności elementu nienaprawialnego
Zadanie 1. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k =
 Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
O procesie Wienera. O procesie Wienera. Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Proces Wienera. Ruch Browna. Ułamkowe ruchy Browna
 Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Czy opcje walutowe mogą być toksyczne?
 Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
W2 Podstawy rachunku prawdopodobieństwa (przypomnienie)
 W2 Podstawy rachunku prawdopodobieństwa (przypomnienie) Henryk Maciejewski Jacek Jarnicki Marek Woda www.zsk.iiar.pwr.edu.pl Rachunek prawdopodobieństwa - przypomnienie 1. Zdarzenia 2. Prawdopodobieństwo
W2 Podstawy rachunku prawdopodobieństwa (przypomnienie) Henryk Maciejewski Jacek Jarnicki Marek Woda www.zsk.iiar.pwr.edu.pl Rachunek prawdopodobieństwa - przypomnienie 1. Zdarzenia 2. Prawdopodobieństwo
Matematyka finansowa 15.06.2015 r. Komisja Egzaminacyjna dla Aktuariuszy. LXXI Egzamin dla Aktuariuszy z 15 czerwca 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Komisja Egzaminacyjna dla Aktuariuszy. XXXIX Egzamin dla Aktuariuszy z 5 czerwca 2006 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH
 REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
Spis treści. Przedmowa 11
 Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Przykład 1 W przypadku jednokrotnego rzutu kostką przestrzeń zdarzeń elementarnych
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Zadanie 1. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną:
 Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
4.5. Obligacja o zmiennym oprocentowaniu
 .5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
.5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych
 Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
Zmienne losowe ciągłe i ich rozkłady
 Statystyka i opracowanie danych W3 Zmienne losowe ciągłe i ich rozkłady Dr Anna ADRIAN Paw B5, pok47 adan@agh.edu.pl Plan wykładu Rozkład Poissona. Zmienna losowa ciągła Dystrybuanta i funkcja gęstości
Statystyka i opracowanie danych W3 Zmienne losowe ciągłe i ich rozkłady Dr Anna ADRIAN Paw B5, pok47 adan@agh.edu.pl Plan wykładu Rozkład Poissona. Zmienna losowa ciągła Dystrybuanta i funkcja gęstości
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Wokół nierówności Dooba
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Tomasz Tkocz Nr albumu: 24957 Wokół nierówności Dooba Praca licencjacka na kierunku MATEMATYKA w ramach Międzywydziałowych Indywidualnych
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Tomasz Tkocz Nr albumu: 24957 Wokół nierówności Dooba Praca licencjacka na kierunku MATEMATYKA w ramach Międzywydziałowych Indywidualnych
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures
 10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
Zadania z Rachunku Prawdopodobieństwa III - 1
 Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Prawa wielkich liczb, centralne twierdzenia graniczne
 , centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
, centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sp. ze stałymi kosztami za transakcje
 Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Proces rezerwy w czasie dyskretnym z losową stopą procentową i losową składką
 z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
III. ZMIENNE LOSOWE JEDNOWYMIAROWE
 III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3
 Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Zmienna losowa i jej
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Zmienna losowa i jej
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Literatura. Leitner R., Zacharski J., Zarys matematyki wyŝszej dla studentów, cz. III.
 Literatura Krysicki W., Bartos J., Dyczka W., Królikowska K, Wasilewski M., Rachunek Prawdopodobieństwa i Statystyka Matematyczna w Zadaniach, cz. I. Leitner R., Zacharski J., Zarys matematyki wyŝszej
Literatura Krysicki W., Bartos J., Dyczka W., Królikowska K, Wasilewski M., Rachunek Prawdopodobieństwa i Statystyka Matematyczna w Zadaniach, cz. I. Leitner R., Zacharski J., Zarys matematyki wyŝszej
Procesy stochastyczne 2.
 Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Matematyka finansowa 30.09.2013 r. Komisja Egzaminacyjna dla Aktuariuszy. LXV Egzamin dla Aktuariuszy z 30 września 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
