Dyskretna teoria Morse a
|
|
|
- Wanda Czech
- 6 lat temu
- Przeglądów:
Transkrypt
1 Dyskretna teoria Morse a Toruńska Letnia Szkoła Matematyki 2011 Michał Kukieła Uniwersytet Mikołaja Kopernika w Toruniu θ R θ
2 Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n R - funkcja gładka.
3 Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n R - funkcja gładka. Punkt x M n nazwiemy krytycznym, o ile f x i (x) = 0 dla i = 1,...,n.
4 Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n R - funkcja gładka. Punkt x M n nazwiemy krytycznym, o ile f x i (x) = 0 dla i = 1,...,n. Punkt krytyczny x M n jest niezdegenerowany, o ile macierz Hessego jest nieosobliwa. [ 2 ] f (x) x i x j i,j=1,...,n
5 Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n R - funkcja gładka. Punkt x M n nazwiemy krytycznym, o ile f x i (x) = 0 dla i = 1,...,n. Punkt krytyczny x M n jest niezdegenerowany, o ile macierz Hessego jest nieosobliwa. [ 2 ] f (x) x i x j i,j=1,...,n Funkcję f nazywamy funkcja Morse a, o ile wszystkie jej punkty krytyczne sa niezdegenerowane.
6 Klasyczna teoria Morse a Oznaczmy: M a = {x M n : f(x) a} dla a R.
7 Klasyczna teoria Morse a Oznaczmy: M a = {x M n : f(x) a} dla a R.
8 Klasyczna teoria Morse a Twierdzenie: Niech f 1 ([a,b]) nie zawiera punktów krytycznych. Wówczas: M a jest dyfeomorficzne z M b (oraz M a jest retraktem deformacyjnym M b ), f 1 (a) jest dyfeomorficzne z f 1 (b), f 1 ([a,b]) jest dyfeomorficzne z f 1 (a) [a,b].
9 Klasyczna teoria Morse a Twierdzenie: Niech f 1 ([a,b]) nie zawiera punktów krytycznych. Wówczas: M a jest dyfeomorficzne z M b (oraz M a jest retraktem deformacyjnym M b ), f 1 (a) jest dyfeomorficzne z f 1 (b), f 1 ([a,b]) jest dyfeomorficzne z f 1 (a) [a,b].
10 Klasyczna teoria Morse a Indeksem punktu x M krytycznego funkcji f nazywamy maksymalny wymiar przestrzeni liniowej, na której forma kwadratowa wyznaczona przez macierz Hessego jest ujemnie określona.
11 Klasyczna teoria Morse a Indeksem punktu x M krytycznego funkcji f nazywamy maksymalny wymiar przestrzeni liniowej, na której forma kwadratowa wyznaczona przez macierz Hessego jest ujemnie określona. Twierdzenie: Niech x będzie jedynym punktem krytycznym funkcji f należacym do f 1 ([a,b]), gdzie a = f(x) ǫ, b = f(x) + ǫ. Wówczas przestrzeń M b jest homotopijnie równoważna przestrzeni M a g D i, gdzie g : D i M a, zaś i oznacza indeks punktu x.
12 Klasyczna teoria Morse a Indeksem punktu x M krytycznego funkcji f nazywamy maksymalny wymiar przestrzeni liniowej, na której forma kwadratowa wyznaczona przez macierz Hessego jest ujemnie określona. Twierdzenie: Niech x będzie jedynym punktem krytycznym funkcji f należacym do f 1 ([a,b]), gdzie a = f(x) ǫ, b = f(x) + ǫ. Wówczas przestrzeń M b jest homotopijnie równoważna przestrzeni M a g D i, gdzie g : D i M a, zaś i oznacza indeks punktu x.
13 Klasyczna teoria Morse a Indeksem punktu x M krytycznego funkcji f nazywamy maksymalny wymiar przestrzeni liniowej, na której forma kwadratowa wyznaczona przez macierz Hessego jest ujemnie określona. Twierdzenie: Niech x będzie jedynym punktem krytycznym funkcji f należacym do f 1 ([a,b]), gdzie a = f(x) ǫ, b = f(x) + ǫ. Wówczas przestrzeń M b jest homotopijnie równoważna przestrzeni M a g D i, gdzie g : D i M a, zaś i oznacza indeks punktu x.
14 Klasyczna teoria Morse a Dowolna funkcję Morse a można zaburzyć tak, aby na zbiorze punktów krytycznych była różnowartościowa. Mamy zatem: Twierdzenie: Jeśli funkcja Morse a f na rozmaitości M n posiada c i punktów krytycznych indeksu i, to M n jest homotopijnie równoważna CW-kompleksowi posiadajacemu dokładnie c i komórek wymiaru i.
15 Klasyczna teoria Morse a Dowolna funkcję Morse a można zaburzyć tak, aby na zbiorze punktów krytycznych była różnowartościowa. Mamy zatem: Twierdzenie: Jeśli funkcja Morse a f na rozmaitości M n posiada c i punktów krytycznych indeksu i, to M n jest homotopijnie równoważna CW-kompleksowi posiadajacemu dokładnie c i komórek wymiaru i. Wniosek (Nierówności Morse a): Niech b i oznacza i-ta liczbę Bettiego M n, zaś c i liczbę punktów krytycznych indeksu i. Wówczas: c k c k 1 + c k 2... ± c 0 c k c k 1 + c k 2... ± c 0 dla wszystkich k N; c i b i dla wszystkich i N; χ(m n ) = i N ( 1)i b i = i N ( 1)i c i.
16 Dyskretne funkcje Morse a Niech X będzie regularnym CW-kompleksem. Funkcję f : X R ze zbioru komórek X w R nazywamy dyskretna funkcja Morse a na X, o ile dla każdej komórki σ X zbiory u f (σ) = {τ > σ : dim(τ) = dim(σ) + 1,f(τ) f(σ)} d f (σ) = {µ < σ : dim(µ) = dim(σ) 1,f(µ) f(σ)} maja co najwyżej po jednym elemencie.
17 Dyskretne funkcje Morse a Niech X będzie regularnym CW-kompleksem. Funkcję f : X R ze zbioru komórek X w R nazywamy dyskretna funkcja Morse a na X, o ile dla każdej komórki σ X zbiory u f (σ) = {τ > σ : dim(τ) = dim(σ) + 1,f(τ) f(σ)} d f (σ) = {µ < σ : dim(µ) = dim(σ) 1,f(µ) f(σ)} maja co najwyżej po jednym elemencie. Komórkę σ X nazywamy krytyczn a, o ile u f (σ) =, d f (σ) =. Indeks komórki krytycznej σ jest równy dim(σ).
18 Dyskretne funkcje Morse a Niech X będzie regularnym CW-kompleksem. Funkcję f : X R ze zbioru komórek X w R nazywamy dyskretna funkcja Morse a na X, o ile dla każdej komórki σ X zbiory u f (σ) = {τ > σ : dim(τ) = dim(σ) + 1,f(τ) f(σ)} d f (σ) = {µ < σ : dim(µ) = dim(σ) 1,f(µ) f(σ)} maja co najwyżej po jednym elemencie. Komórkę σ X nazywamy krytyczn a, o ile u f (σ) =, d f (σ) =. Indeks komórki krytycznej σ jest równy dim(σ).
19 Dyskretna teoria Morse a Oznaczmy: X a = f(σ) a τ σ τ dla a R.
20 Dyskretna teoria Morse a Oznaczmy: X a = f(σ) a τ σ τ dla a R. Jeśli σ,τ X sa komórkami takimi, że σ < τ oraz σ δ dla każdej komórki δ τ, to X {τ,σ} jest retraktem deformacyjnym X. Mamy wówczas zgniecenie elementarne X ց e X {τ,σ}. Ciag zgnieceń elementarnych X ց e X 1 ց e X 2... ց e X n nazywamy zgnieceniem i piszemy X ց X n.
21 Dyskretna teoria Morse a Oznaczmy: X a = f(σ) a τ σ τ dla a R. Jeśli σ,τ X sa komórkami takimi, że σ < τ oraz σ δ dla każdej komórki δ τ, to X {τ,σ} jest retraktem deformacyjnym X. Mamy wówczas zgniecenie elementarne X ց e X {τ,σ}. Ciag zgnieceń elementarnych X ց e X 1 ց e X 2... ց e X n nazywamy zgnieceniem i piszemy X ց X n. Twierdzenie: Jeśli f 1 ([a,b]) nie zawiera komórek krytycznych, to CW kompleksy X a i X b sa homotopijnie równoważne. Co więcej, X b zgniata się do X a.
22 Dyskretna teoria Morse a Oznaczmy: X a = f(σ) a τ σ τ dla a R. Jeśli σ,τ X sa komórkami takimi, że σ < τ oraz σ δ dla każdej komórki δ τ, to X {τ,σ} jest retraktem deformacyjnym X. Mamy wówczas zgniecenie elementarne X ց e X {τ,σ}. Ciag zgnieceń elementarnych X ց e X 1 ց e X 2... ց e X n nazywamy zgnieceniem i piszemy X ց X n. Twierdzenie: Jeśli f 1 ([a,b]) nie zawiera komórek krytycznych, to CW kompleksy X a i X b sa homotopijnie równoważne. Co więcej, X b zgniata się do X a. Twierdzenie: Jeśli σ jest jedyna komórka krytyczna należac a do f 1 ([a,b]), to CW kompleks X b jest homotopijnie równoważny CW kompleksowi powstałemu z X a poprzez doklejenie komórki wymiaru dim(σ).
23 Dyskretna teoria Morse a Twierdzenie: Regularny CW kompleks X z dyskretna funkcja Morse a f jest homotopijnie równoważny CW kompleksowi posiadajacemu po jednej komórce i-wymiarowej na każda komórkę krytyczna o indeksie i.
24 Dyskretna teoria Morse a Twierdzenie: Regularny CW kompleks X z dyskretna funkcja Morse a f jest homotopijnie równoważny CW kompleksowi posiadajacemu po jednej komórce i-wymiarowej na każda komórkę krytyczna o indeksie i. Wniosek (Nierówności Morse a): Niech b i oznacza i-ta liczbę Bettiego X, zaś c i liczbę komórek krytycznych indeksu i. Wówczas: c k c k 1 + c k 2... ± c 0 c k c k 1 + c k 2... ± c 0 dla wszystkich k N; c i b i dla wszystkich i N; χ(x) = i N ( 1)i b i = i N ( 1)i c i.
25 Skojarzenia Morse a
26 Skojarzenia Morse a
27 Skojarzenia Morse a
28 Skojarzenia Morse a Twierdzenie: Skojarzenie na diagramie Hassego częściowego porzadku zawierania ścian CW kompleksu X odpowiada pewnej dyskretnej funkcji Morse a na X wtedy i tylko wtedy, gdy digraf uzyskany przez odwórcenie strzałek należacych do tego skojarzenia nie zawiera cykli.
29 Przykład - zgniatalność Przypuśćmy, że X ց Y, tzn. mamy ci ag: X = X 0 ց e X 1... ց e X n = Y, gdzie X i+1 = X i {σ i < τ i }.
30 Przykład - zgniatalność Przypuśćmy, że X ց Y, tzn. mamy ciag: X = X 0 ց e X 1... ց e X n = Y, gdzie X i+1 = X i {σ i < τ i }. W diagramie Hassego X odwracamy strzałki prowadzace z σ i do τ i (tworza one skojarzenie). Nietrudno zauważyć, że jest to skojarzenie acykliczne.
31 Przykład - zgniatalność Przypuśćmy, że X ց Y, tzn. mamy ciag: X = X 0 ց e X 1... ց e X n = Y, gdzie X i+1 = X i {σ i < τ i }. W diagramie Hassego X odwracamy strzałki prowadzace z σ i do τ i (tworza one skojarzenie). Nietrudno zauważyć, że jest to skojarzenie acykliczne. Wniosek: Jeśli X ց Y, to na X istnieje dyskretna funkcja Morse a, której zbiorem komórek krytycznych jest Y.
32 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki),
33 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki), wersje algebraiczne,
34 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki), wersje algebraiczne, wersja ekwiwariantna,
35 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki), wersje algebraiczne, wersja ekwiwariantna, dyskretna teoria Morse a na kompleksach nieskończonych,
36 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki), wersje algebraiczne, wersja ekwiwariantna, dyskretna teoria Morse a na kompleksach nieskończonych, dyskretna teoria Morse a-wittena, Morse a-novikova,
37 Uogólnienia Wiele by można opowiadać: dyskretne pola wektorowe i przepływy gradientowe, dyskretne homologie Morse a, optymalizacja dyskretnych funkcji Morse a, kompleksy dyskretnych funkcji Morse a... Uogólnienia: szersza klasa przestrzeni (CW kompleksy nieregularne, częściowe porzadki), wersje algebraiczne, wersja ekwiwariantna, dyskretna teoria Morse a na kompleksach nieskończonych, dyskretna teoria Morse a-wittena, Morse a-novikova, ogólniej: dyskretna geometria różniczkowa.
38 Zastosowania Zastosowania: kombinatoryka topologiczna,
39 Zastosowania Zastosowania: kombinatoryka topologiczna, topologia kombinatoryczna,
40 Zastosowania Zastosowania: kombinatoryka topologiczna, topologia kombinatoryczna, analiza obrazów,
41 Zastosowania Zastosowania: kombinatoryka topologiczna, topologia kombinatoryczna, analiza obrazów, fizyka,
42 Zastosowania Zastosowania: kombinatoryka topologiczna, topologia kombinatoryczna, analiza obrazów, fizyka, matematyka ciagła?
43 Która teoria jest lepsza? Interesuje nas rozkład na jak najmniejsza liczbę komórek. Przypuśćmy, że mamy dana rozmaitość gładka i jej triangulację. Która teoria da mniejszy rozkład na komórki?
44 Która teoria jest lepsza? Interesuje nas rozkład na jak najmniejsza liczbę komórek. Przypuśćmy, że mamy dana rozmaitość gładka i jej triangulację. Która teoria da mniejszy rozkład na komórki? Funkcja Morse a (dyskretna lub gładka) jest perfekcyjna, o ile c i = b i dla wszystkich i N.
45 Która teoria jest lepsza? Interesuje nas rozkład na jak najmniejsza liczbę komórek. Przypuśćmy, że mamy dana rozmaitość gładka i jej triangulację. Która teoria da mniejszy rozkład na komórki? Funkcja Morse a (dyskretna lub gładka) jest perfekcyjna, o ile c i = b i dla wszystkich i N. Na sferze S n istnieje perfekcyjna gładka funkcja Morse a. Jednak dla wszystkich n 3 i k 0 istnieje triangulacja S n, na której każda dyskretna funkcja Morse a ma co najmniej k krytycznych komórek 1-wymiarowych.
46 Która teoria jest lepsza? Interesuje nas rozkład na jak najmniejsza liczbę komórek. Przypuśćmy, że mamy dana rozmaitość gładka i jej triangulację. Która teoria da mniejszy rozkład na komórki? Funkcja Morse a (dyskretna lub gładka) jest perfekcyjna, o ile c i = b i dla wszystkich i N. Na sferze S n istnieje perfekcyjna gładka funkcja Morse a. Jednak dla wszystkich n 3 i k 0 istnieje triangulacja S n, na której każda dyskretna funkcja Morse a ma co najmniej k krytycznych komórek 1-wymiarowych. Teoria dyskretna wypada blado. Co gdy pozwolimy na dowolność w wyborze triangulacji?
47 Która teoria jest lepsza? Twierdzenie(B. Benedetti, 2010): Niech M n będzie rozmaitościa z ustalona PL triangulacja oraz funkcja Morse a posiadajaca c i punktów krytycznych indeksu i. Wówczas istnieje k takie, że na k-tym podziale barycentrycznym triangulacji M n istnieje dyskretna funkcja Morse a o c i komórkach krytycznych wymiaru i.
48 Która teoria jest lepsza? Twierdzenie(B. Benedetti, 2010): Niech M n będzie rozmaitościa z ustalona PL triangulacja oraz funkcja Morse a posiadajaca c i punktów krytycznych indeksu i. Wówczas istnieje k takie, że na k-tym podziale barycentrycznym triangulacji M n istnieje dyskretna funkcja Morse a o c i komórkach krytycznych wymiaru i. Twierdzenie(J.H.C. Whitehead, 1939): Jeśli pewna PL triangulacja M n jest zgniatalna do punktu, to M n jest homeomorficzna z kula.
49 Która teoria jest lepsza? Twierdzenie(B. Benedetti, 2010): Niech M n będzie rozmaitościa z ustalona PL triangulacja oraz funkcja Morse a posiadajaca c i punktów krytycznych indeksu i. Wówczas istnieje k takie, że na k-tym podziale barycentrycznym triangulacji M n istnieje dyskretna funkcja Morse a o c i komórkach krytycznych wymiaru i. Twierdzenie(J.H.C. Whitehead, 1939): Jeśli pewna PL triangulacja M n jest zgniatalna do punktu, to M n jest homeomorficzna z kula. Twierdzenie(K. Adiprasito, B. Benedetti, 2011): Dla każdego n 5 istnieje rozmaitość M n, która nie jest homeomorficzna z kula, ale posiada triangulację zgniatalna do punktu. (Oczywiście, triangulacja ta nie jest PL).
50 Która teoria jest lepsza? Twierdzenie(B. Benedetti, 2010): Niech M n będzie rozmaitościa z ustalona PL triangulacja oraz funkcja Morse a posiadajaca c i punktów krytycznych indeksu i. Wówczas istnieje k takie, że na k-tym podziale barycentrycznym triangulacji M n istnieje dyskretna funkcja Morse a o c i komórkach krytycznych wymiaru i. Twierdzenie(J.H.C. Whitehead, 1939): Jeśli pewna PL triangulacja M n jest zgniatalna do punktu, to M n jest homeomorficzna z kula. Twierdzenie(K. Adiprasito, B. Benedetti, 2011): Dla każdego n 5 istnieje rozmaitość M n, która nie jest homeomorficzna z kula, ale posiada triangulację zgniatalna do punktu. (Oczywiście, triangulacja ta nie jest PL). Wniosek: Teoria dyskretna jest lepsza!
51 Bibliografia K. Adiprasito, B. Benedetti, Metric geometry and collapsibility, arxiv: v1. B. Benedetti, Discrete Morse theory is as perfect as Morse theory, arxiv: v2. J. Milnor, Morse Theory, Princeton University Press, R. Forman, Morse theory for cell complexes, Advances in Mathematics 134 (1998), V. Prasolov, Elements of combinatorial and differential topology, Graduate Studies in Mathematics 74,
N (f, K, (V, φ), (U, ψ), ɛ) := {g : M N g(k) V ; D k (ψgφ 1 ) D k (ψfφ 1 ) < ɛ, k = 0,..., r}
 1. Przestrzenie funkcji: otwartość. Będziemy się poruszać wyłącznie po rozmaitościach różniczkowych, czyli klasy co najmniej C 1. Zakładamy parazwartość, ośrodkowość, drugi aksjomat przeliczalności, normalność,
1. Przestrzenie funkcji: otwartość. Będziemy się poruszać wyłącznie po rozmaitościach różniczkowych, czyli klasy co najmniej C 1. Zakładamy parazwartość, ośrodkowość, drugi aksjomat przeliczalności, normalność,
Charakterystyka Eulera Sławomir Cynk
 Charakterystyka Eulera Sławomir Cynk 22 listopada 2001 roku Leonard Euler ur. 15 kwietnia 1707 w Bazylei (Szwajcaria) zm. 18 września 1783 w St. Petersburgu (Rosja). Wzór Eulera Twierdzenie 1. Dla dowolnego
Charakterystyka Eulera Sławomir Cynk 22 listopada 2001 roku Leonard Euler ur. 15 kwietnia 1707 w Bazylei (Szwajcaria) zm. 18 września 1783 w St. Petersburgu (Rosja). Wzór Eulera Twierdzenie 1. Dla dowolnego
Topologia Algebraiczna 2 Zadania egzaminacyjne
 Topologia Algebraiczna 2 Zadania egzaminacyjne Agnieszka Bojanowska, Stefan Jackowski 9 czerwca 2013 1 Kompleksy łańcuchowe Zad. 1. Niech I będzie odcinkiem w kategorii kompleksów łańcuchowych, czyli kompleksem
Topologia Algebraiczna 2 Zadania egzaminacyjne Agnieszka Bojanowska, Stefan Jackowski 9 czerwca 2013 1 Kompleksy łańcuchowe Zad. 1. Niech I będzie odcinkiem w kategorii kompleksów łańcuchowych, czyli kompleksem
Typy homotopijne kompleksów niezwartych i punkty stałe ich niezwartych odwzorowań
 UNIWERSYTET MIKOŁAJA KOPERNIKA WYDZIAŁ MATEMATYKI I INFORMATYKI Michał Jerzy Kukieła Typy homotopijne kompleksów niezwartych i punkty stałe ich niezwartych odwzorowań Promotor: prof. dr hab. Marek Golasiński
UNIWERSYTET MIKOŁAJA KOPERNIKA WYDZIAŁ MATEMATYKI I INFORMATYKI Michał Jerzy Kukieła Typy homotopijne kompleksów niezwartych i punkty stałe ich niezwartych odwzorowań Promotor: prof. dr hab. Marek Golasiński
Topologia Algebraiczna - Pomocnik studenta. 7. Klasyfikacja homotopijna odwzorowań
 Topologia Algebraiczna - Pomocnik studenta. 7. Klasyfikacja homotopijna odwzorowań Agnieszka Bojanowska Stefan Jackowski 31 stycznia 2011 1 Odwzorowania w sfery Wykażemy, że klasa homotopii odwzorowania
Topologia Algebraiczna - Pomocnik studenta. 7. Klasyfikacja homotopijna odwzorowań Agnieszka Bojanowska Stefan Jackowski 31 stycznia 2011 1 Odwzorowania w sfery Wykażemy, że klasa homotopii odwzorowania
Fale biegnące w równaniach reakcji-dyfuzji
 Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Topologia Algebraiczna - Pomocnik studenta 50 zadań na Egzamin z Topologii Algebraicznej I Semestr zimowy roku akademickiego 2010/2011
 Topologia Algebraiczna - Pomocnik studenta 50 zadań na Egzamin z Topologii Algebraicznej I Semestr zimowy roku akademickiego 2010/2011 Agnieszka Bojanowska Stefan Jackowski 10 lutego 2011 1 Kategorie i
Topologia Algebraiczna - Pomocnik studenta 50 zadań na Egzamin z Topologii Algebraicznej I Semestr zimowy roku akademickiego 2010/2011 Agnieszka Bojanowska Stefan Jackowski 10 lutego 2011 1 Kategorie i
Zadania z Algebry Studia Doktoranckie Instytutu Matematyki Uniwersytetu Śląskiego 1
 Zadania z Algebry Studia Doktoranckie Instytutu Matematyki Uniwersytetu Śląskiego 1 1. (a) Udowodnić, że jeśli grupa ilorazowa G/Z(G) jest cykliczna, to grupa G jest abelowa (Z(G) oznacza centrum grupy
Zadania z Algebry Studia Doktoranckie Instytutu Matematyki Uniwersytetu Śląskiego 1 1. (a) Udowodnić, że jeśli grupa ilorazowa G/Z(G) jest cykliczna, to grupa G jest abelowa (Z(G) oznacza centrum grupy
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka finansowa Rocznik: 2014/2015 Język wykładowy: Polski Semestr
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka finansowa Rocznik: 2014/2015 Język wykładowy: Polski Semestr
O ROZMAITOŚCIACH TORYCZNYCH
 O ROZMAITOŚCIACH TORYCZNYCH NA PODSTAWIE REFERATU NGUYEN QUANG LOCA Przez cały referat K oznaczać będzie ustalone ciało algebraicznie domknięte. 1. Przez cały referat N oznaczać będzie ustaloną kratę izomorficzną
O ROZMAITOŚCIACH TORYCZNYCH NA PODSTAWIE REFERATU NGUYEN QUANG LOCA Przez cały referat K oznaczać będzie ustalone ciało algebraicznie domknięte. 1. Przez cały referat N oznaczać będzie ustaloną kratę izomorficzną
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka w informatyce Rocznik: 2013/2014 Język wykładowy: Polski
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka w informatyce Rocznik: 2013/2014 Język wykładowy: Polski
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2013/2014 Język wykładowy: Polski
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2013/2014 Język wykładowy: Polski
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka finansowa Rocznik: 2013/2014 Język wykładowy: Polski Semestr
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka finansowa Rocznik: 2013/2014 Język wykładowy: Polski Semestr
Rozwłóknienie Milnora i twierdzenie Picarda-Lefschetza
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Aleksander Doan Nr albumu: 290720 Rozwłóknienie Milnora i twierdzenie Picarda-Lefschetza Praca licencjacka na kierunku MATEMATYKA Praca
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Aleksander Doan Nr albumu: 290720 Rozwłóknienie Milnora i twierdzenie Picarda-Lefschetza Praca licencjacka na kierunku MATEMATYKA Praca
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH
 ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH Punkty okresowe, zbiory graniczne, sprzężenia Zadanie 1. Pokazać, że trajektoria (w przód) punktu x w przestrzeni metrycznej X pod działaniem ciągłego
ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH Punkty okresowe, zbiory graniczne, sprzężenia Zadanie 1. Pokazać, że trajektoria (w przód) punktu x w przestrzeni metrycznej X pod działaniem ciągłego
15. Macierze. Definicja Macierzy. Definicja Delty Kroneckera. Definicja Macierzy Kwadratowej. Definicja Macierzy Jednostkowej
 15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych.
 5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych. Przeprowadzimy obecnie skróconą klasyfikację skończonych grup prostych. 5.1.
5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych. Przeprowadzimy obecnie skróconą klasyfikację skończonych grup prostych. 5.1.
3 Abstrakcyjne kompleksy symplicjalne.
 3 Abstrakcyjne kompleksy symplicjalne. Uwaga 3.1. Niech J będzie dowolnym zbiorem indeksów, niech R J = {(x α ) α J J α x α R} będzie produktem kartezjańskim J kopii R, niech E J = {(x α ) α J R J x α
3 Abstrakcyjne kompleksy symplicjalne. Uwaga 3.1. Niech J będzie dowolnym zbiorem indeksów, niech R J = {(x α ) α J J α x α R} będzie produktem kartezjańskim J kopii R, niech E J = {(x α ) α J R J x α
Zadania z Algebry liniowej 3 semestr zimowy 2008/2009
 Zadania z Algebry liniowej 3 semestr zimowy 2008/2009 1. Niech V będzie przestrzenią wektorową nad ciałem K i niech 0 K oraz θ V będą elementem zerowym ciała K i wektorem zerowym przestrzeni V. Posługując
Zadania z Algebry liniowej 3 semestr zimowy 2008/2009 1. Niech V będzie przestrzenią wektorową nad ciałem K i niech 0 K oraz θ V będą elementem zerowym ciała K i wektorem zerowym przestrzeni V. Posługując
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u
 Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
n=0 Dla zbioru Cantora prawdziwe są wersje lematu 3.6 oraz lematu 3.8 przy założeniu α = :
 4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
B jest liniowo niezależny V = lin (B) 1. Układ pusty jest bazą przestrzeni trywialnej {θ}. a i v i = i I. b i v i, (a i b i ) v i = θ.
 8 Baza i wymiar Definicja 8.1. Bazą przestrzeni liniowej nazywamy liniowo niezależny układ jej wektorów, który generuję tę przestrzeń. Innymi słowy, układ B = (v i ) i I wektorów z przestrzeni V jest bazą
8 Baza i wymiar Definicja 8.1. Bazą przestrzeni liniowej nazywamy liniowo niezależny układ jej wektorów, który generuję tę przestrzeń. Innymi słowy, układ B = (v i ) i I wektorów z przestrzeni V jest bazą
Wykład 5. Ker(f) = {v V ; f(v) = 0}
 Wykład 5 Niech f : V W będzie przekształceniem liniowym przestrzeni wektorowych Wtedy jądrem przekształcenia nazywamy zbiór tych elementów z V, których obrazem jest wektor zerowy w przestrzeni W Jądro
Wykład 5 Niech f : V W będzie przekształceniem liniowym przestrzeni wektorowych Wtedy jądrem przekształcenia nazywamy zbiór tych elementów z V, których obrazem jest wektor zerowy w przestrzeni W Jądro
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
TEORIA wiązań Magdalena Pawłowska Gr. 10B2
 TEORIA wiązań Magdalena Pawłowska Gr. 10B2 Techniki kombinatoryczne rozróżniania węzłów i splotów ØLiczba skrzyżowań, ØLiczba mostów, ØKolorowanie, ØIndeks zaczepienia, ØSzkic elementów arytmetyki węzłów.
TEORIA wiązań Magdalena Pawłowska Gr. 10B2 Techniki kombinatoryczne rozróżniania węzłów i splotów ØLiczba skrzyżowań, ØLiczba mostów, ØKolorowanie, ØIndeks zaczepienia, ØSzkic elementów arytmetyki węzłów.
Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii
 Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii Agnieszka Bojanowska Stefan Jackowski 24 listopada 2010 1 Podstawowe pojęcia Bedziemy uzywać następujących pojęć i przykładów dotyczących
Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii Agnieszka Bojanowska Stefan Jackowski 24 listopada 2010 1 Podstawowe pojęcia Bedziemy uzywać następujących pojęć i przykładów dotyczących
Projekt matematyczny
 Projekt matematyczny Tomasz Kochanek Uniwersytet Śląski Instytut Matematyki Katowice VI Święto Liczby π 15 marca 2012 r. Tomasz Kochanek (Uniwersytet Śląski) Projekt matematyczny 1 / 32 Wielkie twierdzenie
Projekt matematyczny Tomasz Kochanek Uniwersytet Śląski Instytut Matematyki Katowice VI Święto Liczby π 15 marca 2012 r. Tomasz Kochanek (Uniwersytet Śląski) Projekt matematyczny 1 / 32 Wielkie twierdzenie
Procesy stochastyczne
 Wykład I: Istnienie procesów stochastycznych 21 lutego 2017 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane
Wykład I: Istnienie procesów stochastycznych 21 lutego 2017 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane
MODEL RACHUNKU OPERATORÓW DLA RÓŻ NICY WSTECZNEJ PRZY PODSTAWACH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
Wyznaczniki. Algebra. Aleksander Denisiuk
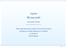 Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Geometria Różniczkowa II wykład piąty
 Geometria Różniczkowa II wykład piąty Wykład piąty poświęcony będzie pojęciu całkowalności dystrybucji oraz fundamentalnemu dal tego zagadnienia twierdzeniu Frobeniusa. Przy okazji postanowiłam sprawdzić
Geometria Różniczkowa II wykład piąty Wykład piąty poświęcony będzie pojęciu całkowalności dystrybucji oraz fundamentalnemu dal tego zagadnienia twierdzeniu Frobeniusa. Przy okazji postanowiłam sprawdzić
Zadania z Algebry liniowej 4 Semestr letni 2009
 Zadania z Algebry liniowej 4 Semestr letni 2009 Ostatnie zmiany 23.05.2009 r. 1. Niech F będzie podciałem ciała K i niech n N. Pokazać, że niepusty liniowo niezależny podzbiór S przestrzeni F n jest także
Zadania z Algebry liniowej 4 Semestr letni 2009 Ostatnie zmiany 23.05.2009 r. 1. Niech F będzie podciałem ciała K i niech n N. Pokazać, że niepusty liniowo niezależny podzbiór S przestrzeni F n jest także
FUNKCJE LICZBOWE. Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y.
 FUNKCJE LICZBOWE Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y. Innymi słowy f X Y = {(x, y) : x X oraz y Y }, o ile (x, y) f oraz (x, z) f pociąga
FUNKCJE LICZBOWE Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y. Innymi słowy f X Y = {(x, y) : x X oraz y Y }, o ile (x, y) f oraz (x, z) f pociąga
1 Macierz odwrotna metoda operacji elementarnych
 W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
Procesy stochastyczne
 Wykład I: Istnienie procesów stochastycznych 2 marca 2015 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane są
Wykład I: Istnienie procesów stochastycznych 2 marca 2015 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane są
Ciągłość i topologia. Rozdział Ciągłość funkcji wg. Cauchy
 Rozdział 1 Ciągłość i topologia Nadanie precyzyjnego sensu intiucyjnemu pojęciu ciągłości jest jednym z głównych tematów dziedziny matematyki, zwanej topologią. Definicja funkcji ciągłej znana z podstawowego
Rozdział 1 Ciągłość i topologia Nadanie precyzyjnego sensu intiucyjnemu pojęciu ciągłości jest jednym z głównych tematów dziedziny matematyki, zwanej topologią. Definicja funkcji ciągłej znana z podstawowego
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU
 Zał. nr do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim MATEMATYKA DYSKRETNA Nazwa w języku angielskim DISCRETE MATHEMATICS Kierunek studiów (jeśli dotyczy): Matematyka
Zał. nr do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim MATEMATYKA DYSKRETNA Nazwa w języku angielskim DISCRETE MATHEMATICS Kierunek studiów (jeśli dotyczy): Matematyka
Grzegorz Bobiński. Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe
 Grzegorz Bobiński Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika w Toruniu 2012 Spis treści Notacja 1 1 Podstawowe pojęcia
Grzegorz Bobiński Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika w Toruniu 2012 Spis treści Notacja 1 1 Podstawowe pojęcia
Niezmienniki wielomianowe: wielomian Aleksandra, wielomian Jonesa. Justyna Ostrowska 10 B2
 Niezmienniki wielomianowe: wielomian Aleksandra, wielomian Jonesa Justyna Ostrowska 10 B2 Przed rokiem 1920, było tylko kilka prac dotyczących węzłów, głównie autorstwa K. F Gaussa oraz Maxa Dehn a Teoria
Niezmienniki wielomianowe: wielomian Aleksandra, wielomian Jonesa Justyna Ostrowska 10 B2 Przed rokiem 1920, było tylko kilka prac dotyczących węzłów, głównie autorstwa K. F Gaussa oraz Maxa Dehn a Teoria
Zadania o transferze
 Maria Donten, 5.12.2007 Zadania o transferze 1. Oznaczenia, założenia i przypomnienia Przez M i M będziemy oznaczać rozmaitości gładkie, przy czym M nakrywa M. Przyjmujemy, że gładkie odwzorowanie p :
Maria Donten, 5.12.2007 Zadania o transferze 1. Oznaczenia, założenia i przypomnienia Przez M i M będziemy oznaczać rozmaitości gładkie, przy czym M nakrywa M. Przyjmujemy, że gładkie odwzorowanie p :
Grupa klas odwzorowań powierzchni
 Grupa klas odwzorowań powierzchni Błażej Szepietowski Uniwersytet Gdański Horyzonty matematyki 2014 Błażej Szepietowski (UG) Grupa klas odwzorowań Horyzonty matematyki 2014 1 / 36 Grupa klas odwzorowań
Grupa klas odwzorowań powierzchni Błażej Szepietowski Uniwersytet Gdański Horyzonty matematyki 2014 Błażej Szepietowski (UG) Grupa klas odwzorowań Horyzonty matematyki 2014 1 / 36 Grupa klas odwzorowań
Podstawowe pojęcia. Co w matematyce możemy nazwać. węzłem, a co. splotem?
 Magdalena Czarna Podstawowe pojęcia Co w matematyce możemy nazwać węzłem, a co splotem? Podstawowe pojęcia Węzeł to krzywa zamknięta (splątany okrąg) w przestrzeni 3-wymiarowej. W związku z tym węzłem
Magdalena Czarna Podstawowe pojęcia Co w matematyce możemy nazwać węzłem, a co splotem? Podstawowe pojęcia Węzeł to krzywa zamknięta (splątany okrąg) w przestrzeni 3-wymiarowej. W związku z tym węzłem
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
Eliza Wajch, Geometria z Topologią, wykład 1, 2012/2013
 Eliza Wajch Wykłady i ćwiczenia z geometrii analitycznej z elementami topologii w UPH w Siedlcach w semestrze zimowym roku akad. 2012/2013. Literatura podstawowa: 1. K. Kuratowski, A. Mostowski: Teoria
Eliza Wajch Wykłady i ćwiczenia z geometrii analitycznej z elementami topologii w UPH w Siedlcach w semestrze zimowym roku akad. 2012/2013. Literatura podstawowa: 1. K. Kuratowski, A. Mostowski: Teoria
Zbiory wypukłe i stożki
 Katedra Matematyki i Ekonomii Matematycznej 28 kwietnia 2016 Hiperpłaszczyzna i półprzestrzeń Definicja Niech a R n, a 0, b R. Zbiór H(a, b) = {x R n : (a x) = b} nazywamy hiperpłaszczyzną, zbiory {x R
Katedra Matematyki i Ekonomii Matematycznej 28 kwietnia 2016 Hiperpłaszczyzna i półprzestrzeń Definicja Niech a R n, a 0, b R. Zbiór H(a, b) = {x R n : (a x) = b} nazywamy hiperpłaszczyzną, zbiory {x R
φ(x 1,..., x n ) = a i x 2 i +
 Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Numeryczne metody optymalizacji Optymalizacja w kierunku. informacje dodatkowe
 Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany
 Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Załóżmy, że wiemy co to są liczby naturalne... Język (I-go rzędu): V, { F n : n IN
Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Załóżmy, że wiemy co to są liczby naturalne... Język (I-go rzędu): V, { F n : n IN
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J.
 Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J. Szmański: Matematyka dyskretna dla informatyków, UAM, 2008 Uzupełniająca:
Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J. Szmański: Matematyka dyskretna dla informatyków, UAM, 2008 Uzupełniająca:
Algebry skończonego typu i formy kwadratowe
 Algebry skończonego typu i formy kwadratowe na podstawie referatu Justyny Kosakowskiej 26 kwietnia oraz 10 i 17 maja 2001 Referat został opracowany w oparciu o prace Klausa Bongartza Criterion for finite
Algebry skończonego typu i formy kwadratowe na podstawie referatu Justyny Kosakowskiej 26 kwietnia oraz 10 i 17 maja 2001 Referat został opracowany w oparciu o prace Klausa Bongartza Criterion for finite
Funkcje analityczne. Wykład 2. Płaszczyzna zespolona. Paweł Mleczko. Funkcje analityczne (rok akademicki 2017/2018)
 Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
Spektrum pierścienia i topologia Zariskiego
 Uniwersytet Warmińsko Mazurski w Olsztynie Wydział Matematyki i Informatyki Kierunek: Matematyka Anna Michałek Spektrum pierścienia i topologia Zariskiego Praca magisterska wykonana w zakładzie Algebry
Uniwersytet Warmińsko Mazurski w Olsztynie Wydział Matematyki i Informatyki Kierunek: Matematyka Anna Michałek Spektrum pierścienia i topologia Zariskiego Praca magisterska wykonana w zakładzie Algebry
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Struktury niewygładzalne Zdzisław POGODA, Kraków
 Jest to zapis odczytu wygłoszonego na XXXIV Szkole Matematyki Poglądowej NIE w matematyce i okolicach, styczeń 2005. Rys.1 Struktury niewygładzalne Zdzisław POGODA, Kraków Podstawowym zadaniem topologii
Jest to zapis odczytu wygłoszonego na XXXIV Szkole Matematyki Poglądowej NIE w matematyce i okolicach, styczeń 2005. Rys.1 Struktury niewygładzalne Zdzisław POGODA, Kraków Podstawowym zadaniem topologii
Całki powierzchniowe w R n
 Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Zbiory liczbowe widziane oczami topologa
 Zbiory liczbowe widziane oczami topologa Aleksander Błaszczyk Instytut Matematyki Uniwersytetu Ślaskiego Brenna, 25 wrzesień 2018 Aleksander Błaszczyk (UŚ) Zbiory liczbowe widziane oczami topologa Brenna,
Zbiory liczbowe widziane oczami topologa Aleksander Błaszczyk Instytut Matematyki Uniwersytetu Ślaskiego Brenna, 25 wrzesień 2018 Aleksander Błaszczyk (UŚ) Zbiory liczbowe widziane oczami topologa Brenna,
Analiza II.2*, lato komentarze do ćwiczeń
 Analiza.2*, lato 2018 - komentarze do ćwiczeń Marcin Kotowski 5 czerwca 2019 1 11 2019, zadanie 2 z serii domowej 1 Pokażemy, że jeśli f nie jest stała, to całka: f(x f(y B B x y dx dy jest nieskończona.
Analiza.2*, lato 2018 - komentarze do ćwiczeń Marcin Kotowski 5 czerwca 2019 1 11 2019, zadanie 2 z serii domowej 1 Pokażemy, że jeśli f nie jest stała, to całka: f(x f(y B B x y dx dy jest nieskończona.
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów.
 5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
Zmienne losowe. Powtórzenie. Dariusz Uciński. Wykład 1. Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski
 Powtórzenie Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 1 Podręcznik podstawowy Jacek Koronacki, Jan Mielniczuk: Statystyka dla studentów kierunków technicznych i przyrodnicznych,
Powtórzenie Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 1 Podręcznik podstawowy Jacek Koronacki, Jan Mielniczuk: Statystyka dla studentów kierunków technicznych i przyrodnicznych,
1 Macierze i wyznaczniki
 1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
TwierdzeniePoincaré 1 Bendixsona 2
 Twierdzenie Poincaré Bendixsona 1 TwierdzeniePoincaré 1 Bendixsona 2 1 TwierdzeniePoincaré Bendixsona W bieżącym podrozdziale zakładamy, że U jest otwartym podzbiorem płaszczyzny R 2 if:u R 2 jestpolemwektorowymklasyc
Twierdzenie Poincaré Bendixsona 1 TwierdzeniePoincaré 1 Bendixsona 2 1 TwierdzeniePoincaré Bendixsona W bieżącym podrozdziale zakładamy, że U jest otwartym podzbiorem płaszczyzny R 2 if:u R 2 jestpolemwektorowymklasyc
MATEMATYKA I SEMESTR ALK (PwZ) 1. Sumy i sumy podwójne : Σ i ΣΣ
 MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
Metody optymalizacji. notatki dla studentów matematyki semestr zimowy 2015/2016
 Metody optymalizacji notatki dla studentów matematyki semestr zimowy 2015/2016 Aktualizacja: 11 stycznia 2016 Spis treści Spis treści 2 1 Wprowadzenie do optymalizacji 1 11 Podstawowe definicje i własności
Metody optymalizacji notatki dla studentów matematyki semestr zimowy 2015/2016 Aktualizacja: 11 stycznia 2016 Spis treści Spis treści 2 1 Wprowadzenie do optymalizacji 1 11 Podstawowe definicje i własności
13 Układy równań liniowych
 13 Układy równań liniowych Definicja 13.1 Niech m, n N. Układem równań liniowych nad ciałem F m równaniach i n niewiadomych x 1, x 2,..., x n nazywamy koniunkcję równań postaci a 11 x 1 + a 12 x 2 +...
13 Układy równań liniowych Definicja 13.1 Niech m, n N. Układem równań liniowych nad ciałem F m równaniach i n niewiadomych x 1, x 2,..., x n nazywamy koniunkcję równań postaci a 11 x 1 + a 12 x 2 +...
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Julia Radwan-Pragłowska gr. 10B2. Elementy teorii węzłów
 Julia Radwan-Pragłowska gr. 10B2 Elementy teorii węzłów Plan prezentacji 1. Wprowadzenie Niezmiennik Wielomian Wielomian wielomian węzła Warkocz Grupa warkocza Wielomian Laurenta 2. Niezmienniki homologiczne
Julia Radwan-Pragłowska gr. 10B2 Elementy teorii węzłów Plan prezentacji 1. Wprowadzenie Niezmiennik Wielomian Wielomian wielomian węzła Warkocz Grupa warkocza Wielomian Laurenta 2. Niezmienniki homologiczne
MATEMATYKA DYSKRETNA
 MATEMATYKA DYSKRETNA Wykład I Dr inż. Jolanta Błaszczuk Instytut Matematyki Politechnika Częstochowska Kontakt Dr inż. Jolanta Błaszczuk Instytut Matematyki Częstochowa, ul. Dąbrowskiego 73, pok. 184 tel.:
MATEMATYKA DYSKRETNA Wykład I Dr inż. Jolanta Błaszczuk Instytut Matematyki Politechnika Częstochowska Kontakt Dr inż. Jolanta Błaszczuk Instytut Matematyki Częstochowa, ul. Dąbrowskiego 73, pok. 184 tel.:
Trzeci problem milenijny: hipoteza Poincarégo
 ROCZNIKI POLSKIEGO TOWARZYSTWA MATEMATYCZNEGO Seria II: WIADOMOŚCI MATEMATYCZNE XXXVIII(2002) Roman Duda(Wrocław) Trzeci problem milenijny: hipoteza Poincarégo 1. Wstęp. Topologia jest dyscypliną niejednolitą
ROCZNIKI POLSKIEGO TOWARZYSTWA MATEMATYCZNEGO Seria II: WIADOMOŚCI MATEMATYCZNE XXXVIII(2002) Roman Duda(Wrocław) Trzeci problem milenijny: hipoteza Poincarégo 1. Wstęp. Topologia jest dyscypliną niejednolitą
Lokalna odwracalność odwzorowań, odwzorowania uwikłane
 Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Rozdział 6. Ciągłość. 6.1 Granica funkcji
 Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
2. Definicja pochodnej w R n
 2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim PODSTAWY GEOMETRII RÓŻNICZKOWEJ Nazwa w języku angielskim INTRODUCTION TO DIFFERENTIAL GEOMETRY Kierunek
Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim PODSTAWY GEOMETRII RÓŻNICZKOWEJ Nazwa w języku angielskim INTRODUCTION TO DIFFERENTIAL GEOMETRY Kierunek
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy
 Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Matematyka dyskretna
 Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x 1, x 2,...}, to mówimy, że jest to zmienna dyskretna.
 Wykład 4 Rozkłady i ich dystrybuanty Dwa typy zmiennych losowych Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x, x 2,...}, to mówimy, że jest to zmienna dyskretna.
Wykład 4 Rozkłady i ich dystrybuanty Dwa typy zmiennych losowych Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x, x 2,...}, to mówimy, że jest to zmienna dyskretna.
Wielomiany dodatnie na zwartych zbiorach semialgebraicznych
 Uniwersytet Śląski w Katowicach Wydział Matematyki, Fizyki i Chemii Kierunek matematyka Praca dyplomowa magisterska Wielomiany dodatnie na zwartych zbiorach semialgebraicznych Promotor: dr Paweł Gładki
Uniwersytet Śląski w Katowicach Wydział Matematyki, Fizyki i Chemii Kierunek matematyka Praca dyplomowa magisterska Wielomiany dodatnie na zwartych zbiorach semialgebraicznych Promotor: dr Paweł Gładki
14. Przestrzenie liniowe
 14. 14.1 Sformułować definicję przestrzeni liniowej. Podać przykłady. Przestrzenią liniową nad ciałem F nazywamy czwórkę uporządkowaną (V, F,+, ), gdzie V jest zbiorem niepustym, F jest ciałem, + jest
14. 14.1 Sformułować definicję przestrzeni liniowej. Podać przykłady. Przestrzenią liniową nad ciałem F nazywamy czwórkę uporządkowaną (V, F,+, ), gdzie V jest zbiorem niepustym, F jest ciałem, + jest
Wykład 9. Matematyka 3, semestr zimowy 2011/ listopada 2011
 Wykład 9. Matematyka 3, semestr zimowy 2011/2012 4 listopada 2011 W trakcie poprzedniego wykładu zdefiniowaliśmy pojęcie k-kowektora na przestrzeni wektorowej. Wprowadziliśmy także iloczyn zewnętrzny wielokowektorów
Wykład 9. Matematyka 3, semestr zimowy 2011/2012 4 listopada 2011 W trakcie poprzedniego wykładu zdefiniowaliśmy pojęcie k-kowektora na przestrzeni wektorowej. Wprowadziliśmy także iloczyn zewnętrzny wielokowektorów
Ekoenergetyka Matematyka 1. Wykład 3.
 Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Treść wykładu. Układy równań i ich macierze. Rząd macierzy. Twierdzenie Kroneckera-Capellego.
 . Metoda eliminacji. Treść wykładu i ich macierze... . Metoda eliminacji. Ogólna postać układu Układ m równań liniowych o n niewiadomych x 1, x 2,..., x n : a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21
. Metoda eliminacji. Treść wykładu i ich macierze... . Metoda eliminacji. Ogólna postać układu Układ m równań liniowych o n niewiadomych x 1, x 2,..., x n : a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21
Postać Jordana macierzy
 Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Ciągłość funkcji. Seminarium dyplomowe powtórzenie wiadomości. Jan Kowalski. 22 maja Uniwersytet Mikołaja Kopernika w Toruniu
 Seminarium dyplomowe powtórzenie wiadomości Uniwersytet Mikołaja Kopernika w Toruniu 22 maja 2013 1 Podstawowe definicje i fakty 2 funkcji w punkcie Definicja Niech f będzie funkcją określoną na zbiorze
Seminarium dyplomowe powtórzenie wiadomości Uniwersytet Mikołaja Kopernika w Toruniu 22 maja 2013 1 Podstawowe definicje i fakty 2 funkcji w punkcie Definicja Niech f będzie funkcją określoną na zbiorze
Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki.
 3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
Równania liniowe. Rozdział Przekształcenia liniowe. Niech X oraz Y będą dwiema niepustymi przestrzeniami wektorowymi nad ciałem
 Rozdział 6 Równania liniowe 6 Przekształcenia liniowe Niech X oraz Y będą dwiema niepustymi przestrzeniami wektorowymi nad ciałem F Definicja 6 Funkcję f : X Y spełniającą warunki: a) dla dowolnych x,
Rozdział 6 Równania liniowe 6 Przekształcenia liniowe Niech X oraz Y będą dwiema niepustymi przestrzeniami wektorowymi nad ciałem F Definicja 6 Funkcję f : X Y spełniającą warunki: a) dla dowolnych x,
Rachunek prawdopodobieństwa i statystyka
 Rachunek prawdopodobieństwa i statystyka Przestrzeń probabilistyczna Niech Ω będzie dowolnym zbiorem, zwanym przestrzenią zdarzeń elementarnych. Elementy ω tej przestrzeni nazywamy zdarzeniami elementarnymi.
Rachunek prawdopodobieństwa i statystyka Przestrzeń probabilistyczna Niech Ω będzie dowolnym zbiorem, zwanym przestrzenią zdarzeń elementarnych. Elementy ω tej przestrzeni nazywamy zdarzeniami elementarnymi.
1 Zbiory. 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =.
 1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
WYKŁADY Z MATEMATYKI DLA STUDENTÓW UCZELNI EKONOMICZNYCH
 WYKŁADY Z MATEMATYKI DLA STUDENTÓW UCZELNI EKONOMICZNYCH Pod redakcją Anny Piweckiej Staryszak Autorzy poszczególnych rozdziałów Anna Piwecka Staryszak: 2-13; 14.1-14.6; 15.1-15.4; 16.1-16.3; 17.1-17.6;
WYKŁADY Z MATEMATYKI DLA STUDENTÓW UCZELNI EKONOMICZNYCH Pod redakcją Anny Piweckiej Staryszak Autorzy poszczególnych rozdziałów Anna Piwecka Staryszak: 2-13; 14.1-14.6; 15.1-15.4; 16.1-16.3; 17.1-17.6;
4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne
 Równania w postaci Leibniza 4 1 4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne 4.1 Równania różniczkowe w postaci Leibniza Załóżmy, że P : D R i Q: D R są funkcjami ciągłymi określonymi
Równania w postaci Leibniza 4 1 4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne 4.1 Równania różniczkowe w postaci Leibniza Załóżmy, że P : D R i Q: D R są funkcjami ciągłymi określonymi
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Przestrzeń unitarna. Jacek Kłopotowski. 23 października Katedra Matematyki i Ekonomii Matematycznej SGH
 Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Zaawansowane metody numeryczne
 Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Klasyfikacja przestrzeni soczewkowych
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Bartosz Wcisło Nr albumu: 276697 Klasyfikacja przestrzeni soczewkowych Praca licencjacka na kierunku MATEMATYKA Praca wykonana pod kierunkiem
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Bartosz Wcisło Nr albumu: 276697 Klasyfikacja przestrzeni soczewkowych Praca licencjacka na kierunku MATEMATYKA Praca wykonana pod kierunkiem
5.6 Klasyczne wersje Twierdzenia Stokes a
 Ostatecznie f = 1 r 2 f ) r 2 r r + ctg ϑ f r 2 ϑ + 1 2 f r 2 ϑ + 1 2 2 f r 2 sin 2 ϑ ϕ 2 56 Klasyczne wersje Twierdzenia Stokes a Odpowiedniość między polami wektorowymi i jednoformami lub n 1)-formami
Ostatecznie f = 1 r 2 f ) r 2 r r + ctg ϑ f r 2 ϑ + 1 2 f r 2 ϑ + 1 2 2 f r 2 sin 2 ϑ ϕ 2 56 Klasyczne wersje Twierdzenia Stokes a Odpowiedniość między polami wektorowymi i jednoformami lub n 1)-formami
