Teoria sygna³ów. Wstêp. Wydanie II poprawione i uzupe³nione
|
|
|
- Sebastian Kot
- 7 lat temu
- Przeglądów:
Transkrypt
1 IDZ DO PRZYK ADOWY ROZDZIA KATALOG KSI EK ZAMÓW DRUKOWANY KATALOG Wydawnicwo Helion ul Chopina Gliwice el (32) helion@helionpl TWÓJ KOSZYK CENNIK I INFORMACJE ZAMÓW INFORMACJE ONOWOŒCIACH ZAMÓW CENNIK CZYTELNIA SPIS TREŒCI KATALOG ONLINE DODAJ DO KOSZYKA FRAGMENTY KSI EK ONLINE Teoria sygna³ów Wsêp Wydanie II poprawione i uzupe³nione Auorzy: Jacek Izydorczyk, Grzegorz P³onka, Grzegorz Tyma ISBN: Forma: B5, sron: 34 Kompendium wiedzy na ema sygna³ów i meod ich przewarzania Modulacja sygna³ów Transformay Fouriera i Laplace a Filry analogowe i cyfrowe Teoria sygna³ów o jedna z fundamenalnych dziedzin wiedzy echnicznej Jej znajomoœæ jes niezbêdna nie ylko projekanom urz¹dzeñ elekronicznych, ale równie auomaykom, informaykom, elekroechnikom i specjalisom od elekomunikacji Rozwój echniki cyfrowej zrewolucjonizowa³ meody przewarzania sygna³ów, lecz podsawy ych mechanizmów s¹ niezmienne nadal wykorzysywane s¹ ransformay Fouriera i Laplace a, klasyczne algorymy modulacji oraz regu³y projekowania urz¹dzeñ Ksi¹ ka Teoria sygna³ów Wsêp Wydanie II o kolejne wydanie publikacji poœwiêconej sygna³om i ich przewarzaniu Zawiera zbiór najwa niejszych informacji zwi¹zanych z przeksza³caniem i modulowaniem sygna³ów meodami analogowymi i cyfrowymi oraz projekowaniem filrów akywnych i pasywnych Ka dy jej rozdzia³ sanowi osobny wyk³ad uzupe³niony przyk³adami i zadaniami do samodzielnego rozwi¹zania, kóry mo na przeczyaæ bez odwo³ywania siê do pozosa³ych wyk³adów Szeregi i ransformay Fouriera Modulacja sygna³ów Przeksza³cenie Laplace a Projekowanie filrów analogowych Sygna³y dyskrene i cyfrowe Modulacja impulsowa Dyskrena ransformaa Fouriera Liniowe uk³ady cyfrowe Projekowanie filrów cyfrowych Opanuj podsawy echnologii cyfrowej
2 Spis reści Rozdział Szereg Fouriera 9 Wsęp 9 2 Definicja rozwinięcia w szereg Fouriera 3 Warunki Dirichlea 6 4 Wybrane własności szeregów Fouriera 8 5 San usalony w obwodach liniowych z wymuszeniami okresowymi 2 6 Przykłady zasosowań szeregów Fouriera 22 7 Lieraura 26 8 Zadania 26 Rozdział 2 Transformacja Fouriera 3 2 Definicja przekszałcenia Fouriera 3 22 Warunki Dirichlea isnienia ransformay Fouriera Wybrane własności przekszałcenia Fouriera Gęsość widmowa sygnału na wyjściu układu liniowego Przykłady Lieraura 48 Rozdział 3 Modulacja 49 3 Wsęp Modulacja w paśmie podsawowym 5 33 Modulacja sygnału sinusoidalnego 5 33 Modulacja ampliudowa Przemiana częsoliwości Modulacja kąowa Modulacja kwadraurowa Lieraura Zadania 66
3 6 Spis reści Rozdział 4 Przekszałcenie Laplace a 67 4 Przekszałcenie Laplace a Odwrona ransformacja Laplace a Wzór Riemanna-Mellina Funkcje wymierne, residua i rozkład na ułamki prose Własności przekszałcenia Laplace a 8 43 Liniowość ransformay Transformaa pochodnej sygnału L -ransformowalnego Transformaa całki sygnału L -ransformowalnego Granica sygnału w zerze Pochodna ransformay sygnału L -ransformowalnego Opóźnienie sygnału L -ransformowalnego Przesunięcie argumenu obrazu L -ransformowalnego Transformaa sygnału okresowego Transformaa splou sygnałów L -ransformowalnych Zasosowanie przekszałcenia Laplace a Równania różniczkowe zwyczajne Równania różniczkowe cząskowe Równania całkowe 9 45 Transmiancja 9 45 Odpowiedź impulsowa układu Badanie sabilności układu Transmiancja operaorowa a ransmiancja symboliczna 46 Lieraura 2 47 Zadania 2 Rozdział 5 Filry analogowe 5 5 Filr idealny 5 52 Aproksymacja charakerysyki ampliudowej filru idealnego 8 52 Filr Buerworha Aproksymacja Czebyszewa Przekszałcenia częsoliwości Syneza pasywnych filrów LC o charakerysyce Buerworha i Czebyszewa Obwód łańcuchowy owary na końcu Obciążony obwód łańcuchowy Wzory dla synezy filrów Buerworha symeryczny obwód łańcuchowy Wzory dla synezy filrów Buerworha Wzory dla synezy filrów Czebyszewa Przekszałcenia częsoliwości raz jeszcze Kilka słów o projekowaniu filrów pasywnych Syneza filrów akywnych RC Idealny wzmacniacz operacyjny Kaskadowy filr akywny Równoległy filr akywny Transmiancje rzędu drugiego Układy z wielokronym sprzężeniem zwronym 6 55 Charakerysyka opóźnienia grupowego Opóźnienie grupowe filru o sałych skupionych 64
4 Spis reści Wyrównywanie charakerysyki fazowej filru Meandry przyczynowości Lieraura Zadania 73 Rozdział 6 Modulacja impulsowa, sygnały dyskrene i cyfrowe 75 6 Transformaa Fouriera dysrybucji dela Diraca 75 6 Transformay Fouriera funkcji rygonomerycznych Transformaa Fouriera skoku jednoskowego Transformaa Fouriera całki sygnału Transformaa Fouriera szeregu impulsów Diraca Transformaa Fouriera funkcji okresowej 8 66 Reguła sumacyjna Poissona Sygnał o ograniczonym paśmie częsoliwości i sygnał o ograniczonym czasie rwania Nierówność Schwarza Własności sygnałów o ograniczonym czasie rwania Własności sygnałów o ograniczonym paśmie częsoliwości Sygnał dyskreny Modulacja impulsowa sygnał dyskreny Widmo sygnału dyskrenego Odwarzanie sygnału analogowego na podsawie sygnału dyskrenego Twierdzenie Koelnikowa-Shannona-Nyquisa Wpływ kszału sygnałów próbkujących na widmo sygnału zmodulowanego Decymacja i inerpolacja Dowód wierdzenia o próbkowaniu bez eorii dysrybucji Próbkowanie sygnałów pasmowych obwiednia sygnału 2 64 Sygnał cyfrowy Sałoprzecinkowy, binarny forma zapisu liczb Zmiennoprzecinkowy, binarny forma zapisu liczb Podział kanału w dziedzinie czasu (TDM ime division muliplexing) Szumy kwanowania Przewarzanie Σ Wzór Shannona Lieraura Zadania 225 Rozdział 7 Dyskrena ransformacja Fouriera Dyskrena ransformacja Fouriera Sygnał dyskreny o skończonym czasie rwania i jego widmo Dyskrena ransformacja Fouriera Własności DFT Szybki algorym obliczania dyskrenej ransformay Fouriera (FFT) Algorym FFT z podziałem w dziedzinie czasu Algorym FFT z podziałem w dziedzinie częsoliwości O dodawaniu i mnożeniu liczb przez kompuery Przykłady zasosowań DFT poza cyfrowym przewarzaniem sygnałów Algorym świergoowy 252
5 74 Lieraura Zadania 255 Rozdział 8 Transformacja Z Wsęp Definicja ransformacji Z Transformacja odwrona Transformacja Z sygnału przyczynowego Transformacja sygnału sabilnego Własności ransformacji Z Związek z ransformacją Fouriera Lieraura Zadania 268 Rozdział 9 Liniowe układy dyskrene Wsęp Równania różnicowe i równania sanu Odpowiedź impulsowa Transmiancja Przyczynowość i sabilność układów cyfrowych a obszar zbieżności ransmiancji Charakerysyka częsoliwościowa a zera i bieguny ransmiancji Lieraura Zadania 278 Rozdział Filry cyfrowe 279 Filry SOI 28 Meoda okien czasowych 28 2 Filry NOI Projekowanie filrów NOI Lieraura 292 Skorowidz 293
6 Transformacja Fouriera Grzegorz Tyma 2 2 Definicja przekszałcenia Fouriera Spróbujmy znaleźć wzory na ransformację Fouriera sygnałów aperiodycznych, korzysając z wyników orzymanych dla szeregów Fouriera Pomysł jes nasępujący: niech analizowany sygnał aperiodyczny zosanie na chwilę zamieniony na okresowy przez jego powielenie z okresem T Dla akiego sygnału porafimy znaleźć rozwinięcie Nasępnie sprawdzimy, jak będą się zachowywały współczynniki rozwinięcia w przypadku, gdy z okresem będziemy zdążać do nieskończoności Zabieg en spowoduje, iż nasz szucznie powielony, okresowy przebieg znów zamieni się w sygnał aperiodyczny Rozparzmy przypadek sygnału okresowego, kórego rozwinięcie zosało znalezione w przykładzie 8, w rozdziale poświęconym szeregom Fouriera Sygnał en, o okresie T, może być opisany wzorem x() = {, gdy < T,, gdy T < < T /2 (2) Znalezione współczynniki rozwinięcia mają posać Zdefiniujmy nową wielkość w posaci c k = 2sin(kω T ), gdzie ω = kω T T (22) T c k = 2sin(ωT ) ω (23) ω=kω i nazwijmy funkcję sojącą po prawej sronie równości obwiednią Współczynniki rozwinięcia mogą być rakowane jako próbki obwiedni pobierane w równych odsępach
7 32 2 Transformacja Fouriera (rysunek 2) Dla usalonej warości T obwiednia jes niezależna od T Wraz ze wzrosem T maleją odsępy pomiędzy pobieranymi próbkami obwiedni W granicznym przypadku, gdy T dąży do nieskończoności, sygnał okresowy saje się sygnałem aperiodycznym, a próbki T c k worzą obwiednię a) T 4 T Tc k 2 b) T 8T Tc k 4 Rysunek 2 Obwiednia T c k i próbki pobierane z niej z okresem próbkowania (a) T = 4T i (b) T = 8T Oznaczmy szucznie uworzony sygnał okresowy przez x () (rysunek 22) Możemy dla niego napisać znane wzory rozwinięcia w szereg Fouriera: c k = T x () = k= T /2 T /2 c k e jkω, x ()e jkω d, (24a) (24b) gdzie ω = /T Sygnał okresowy x () powsał przez powielenie z okresem T sygnału x(), zaem x () = x() dla < T /2, ponado x() = poza ym przedziałem Korzysając z ych informacji możemy poprzedni wzór zapisać w posaci c k = T T /2 T /2 x()e jkω d = T x( ) x()e jkω d (25) T x ( ) T T T T T Rysunek 22 Sygnał aperiodyczny x() i szucznie uworzony sygnał okresowy x ()
8 22 Warunki Dirichlea isnienia ransformay Fouriera 33 Zaem obwiednię X (jω) z T c k można przedsawić jako X (jω) = Współczynniki rozwinięcia wyliczamy: Korzysając z ego, orzymujemy x () = k= x()e jω d (26) c k = T X (jkω ) (27) T X (jkω )e jkω = k= X (jkω )e jkω ω (28) Gdy okres T dąży do nieskończoności, o x () dąży do x(), a ω dąży do zera W efekcie w osanim wzorze x() zasąpi x (), a po prawej sronie suma zosanie zasąpiona całką x() = X (jω)e jω dω (29) Osaecznie orzymaliśmy parę wzorów na prose i odwrone przekszałcenie Fouriera: X (jω) = x() = x()e jω d, X (jω)e jω dω Funkcja po ransformacji może być zapisana we współrzędnych biegunowych: (2a) (2b) X (jω) = X (jω) e jarg[x (jω)] (2) Moduł X (ω) = X (jω) nosi nazwę gęsości widmowej ampliudy, naomias faza ϕ(ω) = arg [ X (jω) ] nazywana jes gęsością widmową fazy (częso zamiennie mówi się o widmie ampliudowym i fazowym) Podane zosaną eraz warunki, jakie musi spełniać funkcja x(), aby można było znaleźć jej ransformaę Fouriera 22 Warunki Dirichlea isnienia ransformay Fouriera Podobnie jak dla sygnałów okresowych podaje się rzy warunki, zwane warunkami Dirichlea, na isnienie ransformacji Fouriera funkcji x() Warunek Funkcja x() jes bezwzględnie całkowalna, zn x() d < (22) Warunek 2 Funkcja x() ma skończoną liczbę maksimów i minimów w dowolnym skończonym przedziale
9 34 2 Transformacja Fouriera Warunek 3 Funkcja x() ma skończoną liczbę punków nieciągłości w dowolnym skończonym przedziale Ponado warości funkcji w ych punkach muszą być ograniczone W kolejnym podrozdziale przedsawiono wybrane własności przekszałcenia Fouriera 23 Wybrane własności przekszałcenia Fouriera Liniowość Jeżeli x() ˆ= X (jω) oraz y() ˆ= Y (jω), (23a) o a x() + b y() ˆ= a X (jω) + b Y (jω) (23b) Dowód wierdzenia o liniowości przekszałcenia Fouriera jes ławy i wynika wpros ze wzoru na prose przekszałcenie Fouriera Przesunięcie w czasie Jeżeli x() ˆ= X (jω), o x( ) ˆ= e jω X (jω) Udowodnijmy o Wiemy, iż Wprowadzając przesunięcie w czasie, orzymujemy x() = X (jω)e jω dω (24) x( ) = X (jω)e jω( ) dω = e jω X (jω)e jω dω (25) Dosajemy zaem F { x( ) } = e jω X (jω) (26) Waro zauważyć, że przesunięcie oryginału powoduje zmianę jedynie gęsości widmowej fazy, naomias bez zmiany pozosaje gęsość widmowa ampliudy Przesunięcie w dziedzinie częsoliwości Jeżeli x() ˆ= X (jω), o e jω x() ˆ= X [j(ω ω )] Udowodnijmy o Wiemy, iż x() = X (jω)e jω dω (27) Wprowadzając przesunięcie w częsoliwości, orzymujemy F { X [j(ω ω )] } = X [j(ω ω )]e jω dω = = ejω X (v)e jv dv = e jω x() (28)
10 23 Wybrane własności przekszałcenia Fouriera 35 Różniczkowanie i całkowanie oryginału Zróżniczkujmy wzór x() = X (jω)ejω dω po czasie; w efekcie orzymamy dx() d ˆ= jωx (jω) (29) Twierdzenie powyższe jes prawdziwe, gdy funkcja x() jes bezwzględnie całkowalna w przedziale (,+ ), ciągła i dąży do zera dla ± oraz ma prawie wszędzie pochodną ẋ(), kóra jes bezwzględnie całkowalna w przedziale (, + ) Niesey wzór na ransformaę Fouriera całki nie jes ak prosy, jak w przypadku ransformay Laplace a: x(ζ)dζ ˆ= X (jω) + π X ()δ(ω) (22) jω Aby go udowodnić, rzeba zauważyć, że sygnał x(ζ)dζ jes sploem sygnału x() z jedynką Heaviside a { dla, () = (22) dla <, i zasosować wierdzenie o ransformacie Fouriera splou sygnałów Skalowanie w czasie i częsoliwości (podobieńswo) Jeżeli x() ˆ= X (jω), o dla dowolnej sałej a > zachodzi x(a) ˆ= a X ( jω a ) (222) Dowód: F [x(a)] = x(a)e jω d = x(τ)e j ω a τ dτ a = a X ( jω a ) (223) Twierdzenie o ransformacie splou Jeżeli x() ˆ= X (jω) oraz y() ˆ= Y (jω), (224a) o Udowodnijmy o: { } F x( τ)y(τ) dτ = x( τ)y(τ)dτ ˆ= X (jω)y (jω) = ] x( τ)y(τ) dτ y(τ) [ [ e jω d = x( τ)e jω d ] dτ (224b) (225) Więcej o ransformacie Fouriera jedynki Heaviside a napisano w podrozdziale 62 na sronie 76
11 36 2 Transformacja Fouriera Wprowadzając nową zmienną całkowania u = τ, mamy d = du oraz = u +τ, wobec ego { } [ ] F x( τ)y(τ)dτ = y(τ) x(u)e jω(u+τ) d dτ = (226) = y(τ)e jωτ dτ x(u)e jωu du = X (jω)y (jω) Wzór Parsevala Jeżeli o Spróbujmy o wykazać: x() 2 d = x() ˆ= X (jω), x() 2 d = Zmieniając kolejność całkowania, orzymujemy x() 2 d = [ X (jω) = (227a) X (jω) 2 dω (227b) [ ] x() x ()d = x() X (jω)e jω dω d (228) ] x()e jω d X (jω) X (jω)dω = dω = X (jω) 2 dω Wzór Parsevala posiada inerpreację fizyczną Warość całki x() 2 d może być rakowana jako energia zamieniona na ciepło na oporniku Ω przy przepływie prądu i = x() w nieskończenie wielkim przedziale czasowym Zgodnie ze wzorem Parsevala całka z kwadrau gęsości widmowej ampliudy również przedsawia energię Dlaego mówi się o rozkładzie energii w funkcji pulsacji, a wielkość X (jω) 2 /() nazywana jes gęsością widmową energii 2 Symeria dualna Podobieńswo wzorów na prose i odwrone przekszałcenie Fouriera pociąga za sobą dualność oryginałów i ich obrazów Zilusrujmy o przykładem Znajdźmy obraz dla sygnału czasowego będącego pojedynczym impulsem prosokąnym, a nasępnie znajdźmy oryginał dla pojedynczego impulsu prosokąnego w dziedzinie częsoliwości: x () = { dla < T, dla T < x 2 () = sin(ω ) π ˆ= X (jω) = 2sin(ωT ) ω { dla ω < ω, ˆ= X 2 (jω) = dla ω < ω (229a) (229b) 2 Jeżeli całkowanie we wzorze (227b) odbywa się względem częsoliwości f wyrażonej w hercach, a nie względem pulsacji ω wyrażonej w radianach na sekundę, o pomija się współczynnik /()
12 23 Wybrane własności przekszałcenia Fouriera 37 Odpowiednie pary (oryginał i ransformaa) przedsawiono na rysunku 23 Ławo zauważyć symerię, jaka wysępuje w ych dwóch przekszałceniach Będzie ona wysępowała akże w przypadku innych funkcji Jeżeli ylko weźmiemy jedną funkcję i policzymy jej ransformaę, a nasępnie oryginał porakujemy jako obraz i zasosujemy do niego odwrone przekszałcenie, o orzymane w en sposób obraz i oryginał będą do siebie podobne Możemy o zapisać w nasępującej posaci: x() ˆ= X (jω) X () ˆ= x( ω) (23) x ( ) X ( j) 2T /T T T x ( ) 2 / X ( j) 2 / Rysunek 23 Podobieńswo oryginałów i obrazów Sprzężenie i symeria Jeżeli o x() ˆ= X (jω), x () ˆ= X ( jω) (23a) (23b) Można o w prosy sposób udowodnić Obliczając warość sprzężoną X (jω), orzymujemy [ X (jω) = x()e d] jω = x ()e jω d (232) Zamieniając ω na ω, uzyskujemy X ( jω) = x ()e jω d = F { x () } (233) Jeśli x() jes rzeczywise i x () = x(), o na podsawie dwóch poprzednich wzorów ławo pokazać, że X ( jω) = X (jω) oraz X ( jω) = X (jω) (234) Jeżeli przedsawimy X (jω) w posaci X (jω) = Re{X (jω)} + jim{x (jω)}, (235)
13 38 2 Transformacja Fouriera o korzysając ze wzoru (234) orzymujemy nasępujące zależności (cały czas zakładamy, że x() jes rzeczywise): Re{X (jω)} = Re{X ( jω)}, Im{X (jω)} = Im{X ( jω)} (236) Ze wzorów ych wynika akże, że gęsość widmowa ampliudy jes funkcją parzysą, a gęsość widmowa fazy funkcją nieparzysą Wynik en można akże orzymać w inny sposób Jeśli zapiszemy e jω = cos(ω) jsin(ω), o ransformaa Fouriera sygnału x() może być zapisana w posaci gdzie F {x()} = X (jω) = X (jω) jx 2 (jω), (237) X (jω) = X 2 (jω) = x()cos(ω)d, x()sin(ω)d (238) Widać, że funkcja X (jω) jes parzysa, zaś X 2 (jω) nieparzysa względem ω Zaem ławo pokazać, iż gęsość widmowa ampliudy jes funkcją parzysą, a gęsość widmowa fazy funkcją nieparzysą względem ω W abeli 2 zebrano niekóre własności ransformay Fouriera Naomias w abeli 22 znalazły się wybrane pary ransforma Wyliczenia poszczególnych ransforma Czyelnik może znaleźć w podrozdziale zawierającym przykłady Tabela 2 Własności ransformay Fouriera Własność Sygnał aperiodyczny x(), y() Transformaa Fouriera X (jω), Y (jω) Liniowość a x() + b y() a X (jω) + b Y (jω) Przesunięcie w czasie x( ) e jω X (jω) Przesunięcie w częsoliwości e jω x() X [j(ω ω )] Różniczkowanie oryginału Całkowanie oryginału Skalowanie w czasie i częsoliwości (podobieńswo) Splo Wzór Parsevala dx() jω X (jω) d X (jω) x(ζ) dζ jω + π X ()δ(ω) ( ) jω x(a), a > a X a x( τ) y(τ)dτ X (jω)y (jω) x() 2 d = X (jω) 2 dω
14 24 Gęsość widmowa sygnału na wyjściu układu liniowego 39 Tabela 22 Wybrane pary ransforma Oryginał c k e jkω k= e jω Obraz c k δ(ω kω ) k= δ(ω ω ) cos(ω ) π[δ(ω + ω ) + δ(ω ω )] sin(ω ) jπ[δ(ω + ω ) δ(ω ω )] x() = δ(ω) δ() () jω + πδ(ω) δ( ) e jω sin(ω ) ω e ω2 2 e ω 2 ω ω 2 + ω2 { π/ω dla ω < ω, X (jω) = dla ω > ω ) π ( ω exp ω2 4ω 2 24 Gęsość widmowa sygnału na wyjściu układu liniowego Przedsawiając własności przekszałcenia Fouriera, pokazano, że splo dwóch sygnałów równy jes iloczynowi ransforma Fouriera ych sygnałów Korzysając z ej własności, możemy podać związek pomiędzy ransformaą Fouriera X (jω) sygnału na wejściu układu liniowego a ransformaą Fouriera Y (jω) sygnału wyjściowego Dany jes on zależnością Y (jω) = K (jω) X (jω), (239) gdzie K (jω) = K (jω) e jarg[k (jω)] jes charakerysyką częsoliwościową obwodu Związki pomiędzy gęsościami widmowymi ampliudy i fazy sygnału wejściowego i wyjściowego dane są wzorami Y (jω) = K (jω) X (jω), (24a) arg[y (jω)] = arg[k (jω)] + arg[x (jω)] (24b) 25 Przykłady Przykład 2 Znajdź ransformaę Fouriera dely Diraca
15 4 2 Transformacja Fouriera Rozwiązanie Korzysając z definicji prosego przekszałcenia Fouriera, orzymujemy F {δ()} = δ()e jω d = Przykład 22 Znajdź ransformaę Fouriera sygnału jednoskowego () = {, gdy < <,, gdy > > Rozwiązanie Niesey, w przypadku ej funkcji nie możemy skorzysać z wierdzenia o obrazie pochodnej, gdyż nie spełnia ona założeń Wykorzysamy naomias wierdzenie o obrazie całki Skok jednoskowy może być przedsawiony jako całka z dely Diraca, j () = δ(ζ)dζ W efekcie orzymujemy F {x()} = jω + πδ(ω) Przykład 23 Znajdź oryginał X (jω) = δ(ω) Rozwiązanie Korzysając z definicji odwronego przekszałcenia Fouriera, orzymujemy x() = δ(ω)e jω dω = Dzięki emu wynikowi możemy zapisać, jak wygląda ransformaa Fouriera warości sałej: F {} = δ(ω) Przykład 24 Znajdź ransformaę Fouriera sygnału okresowego x() mającego rozwinięcie w wykładniczy szereg Fouriera Rozwiązanie Sygnał x() posiada rozwinięcie w szereg Fouriera, zaem x() = k= c k e jkω Znajdźmy ransformaę Fouriera ego sygnału Skorzysamy w ym przypadku z wierdzenia o przesunięciu obrazu 3 : F {x()} = F { c k e jkω } = c k δ(ω kω ) k= k= 3 Chodzi u o przesunięcie obrazu funkcji w dziedzinie częsoliwości
16 25 Przykłady 4 Przykład 25 Znajdź ransformaę Fouriera funkcji x() = cos(ω ) Rozwiązanie Zapiszmy funkcję x(), korzysając ze wzorów Eulera: x() = cos(ω ) = e jω +e jω 2 Korzysając eraz z wierdzenia o przesunięciu obrazu i wzoru na ransformaę warości sałej, orzymujemy końcowy wzór: F {cos(ω )} = πδ(ω + ω ) + πδ(ω ω ) W ym miejscu waro przeanalizować, jak wygląda gęsość widmowa funkcji ypu y() = x()cos(ω ), w przypadku gdy znamy obraz funkcji x() Ławo pokazać, korzysając z wierdzenia o przesunięciu obrazu, że jeżeli F {x()} = X (jω), o { x() F {y()} = F 2 e jω + x() } 2 ejω = 2 X [j(ω + ω )] + 2 X [j(ω ω )] Więcej informacji na en ema można znaleźć w rozdziale poświęconym modulacji Przykład 26 Znajdź ransformaę Fouriera funkcji x() = sin(ω ) Rozwiązanie Zapiszmy funkcję x() w innej posaci: x() = sin(ω ) = ejω e jω 2j Korzysając eraz z wierdzenia o przesunięciu obrazu i wzoru na ransformaę warości sałej, orzymujemy końcowy wzór: F {sin(ω )} = πjδ(ω + ω ) πjδ(ω ω ) Przykład 27 Znajdź oryginał dla X (jω) danego wzorem X (jω) = π ω [(ω + ω ) (ω ω )] Rozwiązanie Korzysając z definicji odwronego przekszałcenia Fouriera, orzymujemy x() = ω πe jω dω = e jω ω ω ω 2jω = 2jsin(ω ) = sin(ω ) ω 2jω ω Zaem x() = sin(ω ) ω
17 42 2 Transformacja Fouriera Przykład 28 Znajdź ransformaę Fouriera sygnału przedsawionego na rysunku 24 x( ) A a b b a Rysunek 24 Sygnał x() z przykładu 28 Rozwiązanie Można oczywiście znaleźć obraz zadanej funkcji, korzysając ze wzoru definiującego o przekszałcenie Spróbujmy jednak uławić sobie rochę dojście do rozwiązania, wykorzysując wierdzenie o obrazie zróżniczkowanej funkcji Zróżniczkujmy dwukronie funkcję x() Zabieg en zosał zilusrowany na rysunkach 25 i 26 Druga pochodna składa się z czerech impulsów Diraca W prosy sposób możemy znaleźć obraz drugiej pochodnej F {ẍ()} = A a b F { δ( + a) δ( + b) δ( b) + δ( a) } = A a b (ejωa e jωb e jωb +e jωa ) = A [cos(ωa) cos(ωb)] a b A/( a b) x ( ) a b b a A/( a b) Rysunek 25 Pierwsza pochodna sygnału x() z przykładu 28 A/( a b) x ( ) A/( a b) a b b a A/( a b) A/( a b) Rysunek 26 Druga pochodna sygnału x() z przykładu 28 Pamięając, że orzymujemy F {ẍ()} = (jω) 2 F {x()}, F {x()} = A ω 2 [cos(ωa) cos(ωb)] a b
18 25 Przykłady 43 Przykład 29 Znajdź ransformaę Fouriera sygnału x() przedsawionego na rysunku 27 x( ) A Rysunek 27 Sygnał x() z przykładu 29 Rozwiązanie Zróżniczkujmy dwukronie funkcję x() Zabieg en zosał zilusrowany na rysunku 28 Druga pochodna składa się z rzech impulsów Diraca W prosy sposób możemy znaleźć obraz drugiej pochodnej: F {ẍ()} = A ε F { δ( + ε) 2δ() + δ( ε) } = A ε (ejωε 2 + e jωε ) = 2A ε [cos(ωε) ] = 4A ε sin2 ( ωε 2 ) A/ x ( ) x ( ) A/ A/ A/ 2 A/ Rysunek 28 Pierwsza i druga pochodna sygnału x() z przykładu 29 Pamięając, że orzymujemy F {ẍ()} = (jω) 2 F {x()}, F {x()} = ( ω )[ 2 4A ( )] ωε ε sin2 = 4A 2 εω 2 sin2 ( ωε 2 ) Przykład 2 Oblicz oryginalny sygnał x(), kórego widmo przedsawione jes na rysunku 29 Rozwiązanie Korzysając z definicji odwronego przekszałcenia Fouriera, możemy zapisać x() = = 2A X (jω)e jω dω = π A 2A (2A + ω)ejω dω + 2A π A 2A (2A ω)ejω dω
19 44 2 Transformacja Fouriera X ( j ) / A 2A 2A Rysunek 29 Widmo sygnału x() z przykładu 2 Obliczmy warość pierwszej całki: I = 4A 2 = 4A 2 oraz drugiej: I 2 = 4A 2 = 4A 2 2A (2A + ω)e jω dω = {[ 2A j ejω 2A ] + 2A (2A ω)e jω dω = {[ 2A j ejω W efekcie orzymujemy ] 2A [ ] ω [ ] } j ejω + 2A 2 ejω = [ 2A 2A 4A 2 j + ] 2 ( e j2a ) [ ω + j e jω ] 2A [ 2 ejω ] 2A } = [ 2A 4A 2 ] j 2 (ej2a ) Zaem x() = I + I 2 = 4(A) 2 ( e ja + e ja ) = [ cos(2a)] = 2(A) 2 = 2(A) 2 [sin2 (A) + cos 2 (A) cos 2 (A) + sin 2 (A)] [ ] x() = sin2 (A) sin(a) 2 (A) 2 = A Przykład 2 Określić pulsację graniczną idealnego filru dolnoprzepusowego o wzmocnieniu w paśmie przepuszczania równym 2, jeżeli wiadomo, że po pobudzeniu sygnałem x() = 5sin2 (5) (5) 2 energia sygnału na wejściu i wyjściu filru jes aka sama Rozwiązanie Na rysunku 2 przedsawiono gęsość widmową sygnału na wejściu filru X (ω), wyjściu Y (ω) oraz charakerysykę częsoliwościową filru K (ω) Obliczmy energię sygnału na wejściu filru Zgodnie ze wzorem Parsevala możemy zapisać E x = + x() 2 d = + X (ω) 2 dω
20 25 Przykłady 45 K( ) X ( ) 2 Y ( ) 2 g g g g Rysunek 2 Gęsości widmowe X (ω) i Y (ω) oraz charakerysyka częsoliwościowa filru K (ω) W naszym przypadku E x = = π [ ( π + ω ( + ω )] 2 dω + ) 2 dω = π[ω + ω2 Energia sygnału na wyjściu filru dana jes wzorem E y = [ ( 2 + ω )] 2 dω = 4π[ω + ω2 ω g Zgodnie z warunkami zadania E x = E y, zaem ω g ω2 g Rozwiązując o równanie, orzymujemy ω 3 g [ ( π ω )] 2 dω = ω 3 ] ω 3 ] 6 6 = 2 3 = π3 3 ( = 4π ω g ω2 g ω g 3 + ω 3 g 3 6 ω g 9,4rad/s Przykład 22 Znajdź ransformaę Fouriera sygnału x() = e a, a > Rozwiązanie Zgodnie z definicją prosego przekszałcenia Fouriera możemy zapisać X (jω) = Zaem X (jω) = a jω e(a jω) e a e jω d = a + jω e (a+jω) e a e jω d + e a e jω d ) = a jω + a + jω = 2a a 2 + ω 2 Przykład 23 Wyznacz gęsość widmową impulsu prosokąnego przedsawionego na rysunku 2: f () = A[( + ε) ( ε)]
21 46 2 Transformacja Fouriera f ( ) A A ( ) f ( ) A ( ) Rysunek 2 Sygnał f () z przykładu 23 oraz jego pierwsza pochodna Rozwiązanie Korzysając z wierdzenia o ransformacie funkcji przesunięej w czasie, znajdujemy ransformaę Fouriera f (): F { f ()} = A[F {δ( + ε)} F {δ( ε)}] = A(e jωε e jωε ) Równocześnie na podsawie wierdzenia o ransformacie pochodnej funkcji czasowej mamy F { f ()} = jωf (ω) Wobec ego W efekcie orzymujemy jωf (ω) = A(e jωε e jωε ) F (ω) = 2A(ejωε e jωε ) 2jω = 2A ω sin(ωε) Przykład 24 Sygnał x() = (π) sin() podano na dwa połączone kaskadowo filry, kórych charakerysyki ampliudowe przedsawiono na rysunku 22, przy czym filry e nie obciążają się wzajemnie Oblicz energię sygnału y() na wyjściu układu K ( ) A K ( ) B Rysunek 22 Charakerysyki ampliudowe filrów z przykładu 24 Rozwiązanie Na rysunku 23 przedsawiono gęsości widmowe sygnałów na wejściu i wyjściu układu Korzysając ze wzoru Parsevala oraz uwzględniając symerię gęsości widmowej sygnału na wyjściu układu, możemy obliczyć szukaną energię: E y = 8 4 ( ) ω 2 2 dω = 8 2 ( ) ω 2 dω = π 2
22 25 Przykłady 47 X ( ) Y ( ) Rysunek 23 Gęsości widmowe sygnałów wejściowego i wyjściowego w przykładzie 24 Przykład 25 Sygnał x() = A cos(ω) sin(ω ), ω gdzie Ω = 3 rad/s, ω = rad/s, A = 2, podano na wejście idealnego filru górnoprzepusowego o wzmocnieniu w paśmie przepuszczania równym 2 Oblicz i narysuj gęsość widmową sygnału x() Wyznacz pulsację graniczną filru, jeżeli wiadomo, że energia sygnału y() na wyjściu filru sanowi 25% energii sygnału wejściowego Rozwiązanie Gęsość widmową sygnału x() przedsawiono na rysunku 24 Wyznaczono ją jako gęsość widmową sygnału cos(ω), zmodulowanego sygnałem Sa(ω ) 4 Analiycznie może być ona zapisana w posaci X (jω) = π[(ω + 4) (ω + 2) + (ω 2) (ω 4)] X ( ) 2 Sa( ) Rysunek 24 Gęsość widmowa sygnału x() z przykładu 25 Energię sygnału x(), zgodnie ze wzorem Parsevala, możemy obliczyć: E x = 2 4 (π) 2 dω + Naomias energia sygnału y() wynosi 4 Sa(ω ) = (ω ) sin(ω ) E y = π (π) 2 dω = π 4 2 ω g () 2 dω = 4π(4 ω g ) (π) 2 dω = 2π
23 48 2 Transformacja Fouriera Zgodnie z warunkami zadania E y =,25E x, zaem 4π(4 ω g ) =,25 2π Rozwiązując o równanie, orzymujemy ω g = 387,5rad/s 26 Lieraura [] M Krakowski, Elekroechnika eoreyczna, Pańswowe Wydawnicwo Naukowe, Warszawa 99 [2] A V Oppenheim, R W Schafer, Cyfrowe przewarzanie sygnałów, Wydawnicwa Komunikacji i Łączności, Warszawa 979 [3] A V Oppenheim, A S Willisky, Signals & Sysems, Prenice Hall Inc, Upper Saddle River, New Jersey 997 [4] A Wojnar, Teoria sygnałów, Wydawnicwa Naukowo-Techniczne, Warszawa 98
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład VII Przekształcenie Fouriera.
 7. Całka Fouriera w posaci rzeczywisej. Wykład VII Przekszałcenie Fouriera. Doychczas rozparywaliśmy szeregi Fouriera funkcji w ograniczonym przedziale [ l, l] lub [ ] Teraz pokażemy analogicznie przedsawienie
7. Całka Fouriera w posaci rzeczywisej. Wykład VII Przekszałcenie Fouriera. Doychczas rozparywaliśmy szeregi Fouriera funkcji w ograniczonym przedziale [ l, l] lub [ ] Teraz pokażemy analogicznie przedsawienie
Szeregi Fouriera. Powyższe współczynniki można wyznaczyć analitycznie z następujących zależności:
 Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Wykład 5 Elementy teorii układów liniowych stacjonarnych odpowiedź na dowolne wymuszenie
 Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
POMIAR PARAMETRÓW SYGNAŁOW NAPIĘCIOWYCH METODĄ PRÓKOWANIA I CYFROWEGO PRZETWARZANIA SYGNAŁU
 Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Podstawowe człony dynamiczne
 Podsawowe człony dynamiczne charakerysyki czasowe. Człon proporcjonalny = 2. Człony całkujący idealny 3. Człon inercyjny = = + 4. Człony całkujący rzeczywisy () = + 5. Człon różniczkujący rzeczywisy ()
Podsawowe człony dynamiczne charakerysyki czasowe. Człon proporcjonalny = 2. Człony całkujący idealny 3. Człon inercyjny = = + 4. Człony całkujący rzeczywisy () = + 5. Człon różniczkujący rzeczywisy ()
ĆWICZENIE 4 Badanie stanów nieustalonych w obwodach RL, RC i RLC przy wymuszeniu stałym
 ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Temat 6. ( ) ( ) ( ) k. Szeregi Fouriera. Własności szeregów Fouriera. θ możemy traktować jako funkcje ω, których dziedziną jest dyskretny zbiór
 ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
1. Rezonans w obwodach elektrycznych 2. Filtry częstotliwościowe 3. Sprzężenia magnetyczne 4. Sygnały odkształcone
 Wyład 6 - wersja srócona. ezonans w obwodach elerycznych. Filry częsoliwościowe. Sprzężenia magneyczne 4. Sygnały odszałcone AMD ezonans w obwodach elerycznych Zależności impedancji dwójnia C od pulsacji
Wyład 6 - wersja srócona. ezonans w obwodach elerycznych. Filry częsoliwościowe. Sprzężenia magneyczne 4. Sygnały odszałcone AMD ezonans w obwodach elerycznych Zależności impedancji dwójnia C od pulsacji
[ ] [ ] [ ] [ ] 1. Sygnały i systemy dyskretne (LTI, SLS) y[n] x[n] 1.1. Systemy LTI. liniowy system dyskretny
![[ ] [ ] [ ] [ ] 1. Sygnały i systemy dyskretne (LTI, SLS) y[n] x[n] 1.1. Systemy LTI. liniowy system dyskretny [ ] [ ] [ ] [ ] 1. Sygnały i systemy dyskretne (LTI, SLS) y[n] x[n] 1.1. Systemy LTI. liniowy system dyskretny](/thumbs/63/49833403.jpg) Cyfrowe rzewarzanie sygnałów --. Sygnały i sysemy dyskrene (LTI, SLS).. Sysemy LTI Pojęcie sysemy LTI oznacza liniowe sysemy niezmienne w czasie (ang. Linear Time - Invarian ). W lieraurze olskiej częściej
Cyfrowe rzewarzanie sygnałów --. Sygnały i sysemy dyskrene (LTI, SLS).. Sysemy LTI Pojęcie sysemy LTI oznacza liniowe sysemy niezmienne w czasie (ang. Linear Time - Invarian ). W lieraurze olskiej częściej
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
ANALIZA HARMONICZNA RZECZYWISTYCH PRZEBIEGÓW DRGAŃ
 Ćwiczenie 8 ANALIZA HARMONICZNA RZECZYWISTYCH PRZEBIEGÓW DRGAŃ. Cel ćwiczenia Analiza złożonego przebiegu drgań maszyny i wyznaczenie częsoliwości składowych harmonicznych ego przebiegu.. Wprowadzenie
Ćwiczenie 8 ANALIZA HARMONICZNA RZECZYWISTYCH PRZEBIEGÓW DRGAŃ. Cel ćwiczenia Analiza złożonego przebiegu drgań maszyny i wyznaczenie częsoliwości składowych harmonicznych ego przebiegu.. Wprowadzenie
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Rys.1. Podstawowa klasyfikacja sygnałów
 Kaedra Podsaw Sysemów echnicznych - Podsawy merologii - Ćwiczenie 1. Podsawowe rodzaje i ocena sygnałów Srona: 1 1. CEL ĆWICZENIA Celem ćwiczenia jes zapoznanie się z podsawowymi rodzajami sygnałów, ich
Kaedra Podsaw Sysemów echnicznych - Podsawy merologii - Ćwiczenie 1. Podsawowe rodzaje i ocena sygnałów Srona: 1 1. CEL ĆWICZENIA Celem ćwiczenia jes zapoznanie się z podsawowymi rodzajami sygnałów, ich
Gr.A, Zad.1. Gr.A, Zad.2 U CC R C1 R C2. U wy T 1 T 2. U we T 3 T 4 U EE
 Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Podstawowe wyidealizowane elementy obwodu elektrycznego Rezystor ( ) = ( ) ( ) ( ) ( ) ( ) ( ) ( τ ) i t i t u ( ) u t u t i ( ) i t. dowolny.
 Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
Wykład 4 Metoda Klasyczna część III
 Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Przekształcenie Laplace a. Definicja i własności, transformaty podstawowych sygnałów
 Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Analityczne reprezentacje sygnałów ciągłych
 Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
ZASTOSOWANIE WZMACNIACZY OPERACYJNYCH DO LINIOWEGO PRZEKSZTAŁCANIA SYGNAŁÓW. Politechnika Wrocławska
 Poliechnika Wrocławska Insyu elekomunikacji, eleinformayki i Akusyki Zakład kładów Elekronicznych Insrukcja do ćwiczenia laboraoryjnego ZASOSOWANIE WZMACNIACZY OPEACYJNYCH DO LINIOWEGO PZEKSZAŁCANIA SYGNAŁÓW
Poliechnika Wrocławska Insyu elekomunikacji, eleinformayki i Akusyki Zakład kładów Elekronicznych Insrukcja do ćwiczenia laboraoryjnego ZASOSOWANIE WZMACNIACZY OPEACYJNYCH DO LINIOWEGO PZEKSZAŁCANIA SYGNAŁÓW
Wojciech Grąziewicz. Skrypt dla studentów politechnik. Centrum Nauczania Matematyki i Kształcenia na Odległość
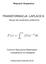 Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
imei 1. Cel ćwiczenia 2. Zagadnienia do przygotowania 3. Program ćwiczenia
 CYFROWE PRZEWARZANIE SYGNAŁÓW Laboraorium Inżynieria Biomedyczna sudia sacjonarne pierwszego sopnia ema: Wyznaczanie podsawowych paramerów okresowych sygnałów deerminisycznych imei Insyu Merologii Elekroniki
CYFROWE PRZEWARZANIE SYGNAŁÓW Laboraorium Inżynieria Biomedyczna sudia sacjonarne pierwszego sopnia ema: Wyznaczanie podsawowych paramerów okresowych sygnałów deerminisycznych imei Insyu Merologii Elekroniki
2. Cyfrowe reprezentacje sygnału fonicznego
 3. Cyrowe reprezenacje sygnału onicznego Treść niniejszego rozdziału zosała opracowana przy założeniu, że Czyelnik jes zaznajomiony z podsawami eorii sygnałów dyskrenych. Podsawowe zagadnienia, związane
3. Cyrowe reprezenacje sygnału onicznego Treść niniejszego rozdziału zosała opracowana przy założeniu, że Czyelnik jes zaznajomiony z podsawami eorii sygnałów dyskrenych. Podsawowe zagadnienia, związane
WSTĘP DO ELEKTRONIKI
 WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Regulatory. Zadania regulatorów. Regulator
 Regulaory Regulaor Urządzenie, kórego podsawowym zadaniem jes na podsawie sygnału uchybu (odchyłki regulacji) ukszałowanie sygnału serującego umożliwiającego uzyskanie pożądanego przebiegu wielkości regulowanej
Regulaory Regulaor Urządzenie, kórego podsawowym zadaniem jes na podsawie sygnału uchybu (odchyłki regulacji) ukszałowanie sygnału serującego umożliwiającego uzyskanie pożądanego przebiegu wielkości regulowanej
Sygnały zmienne w czasie
 Sygnały zmienne w czasie a) b) c) A = A = a A = f(+) d) e) A d = A = A sinω / -A -A ys.. odzaje sygnałów: a)sały, b)zmienny, c)okresowy, d)przemienny, e)sinusoidalny Sygnały zmienne okresowe i ich charakerysyczne
Sygnały zmienne w czasie a) b) c) A = A = a A = f(+) d) e) A d = A = A sinω / -A -A ys.. odzaje sygnałów: a)sały, b)zmienny, c)okresowy, d)przemienny, e)sinusoidalny Sygnały zmienne okresowe i ich charakerysyczne
Przetwarzanie analogowocyfrowe
 Przewarzanie analogowocyfrowe Z. Serweciński 05-03-2011 Przewarzanie u analogowego na cyfrowy Proces przewarzania u analogowego (ciągłego) na cyfrowy składa się z rzech podsawowych operacji: 1. Próbkowanie
Przewarzanie analogowocyfrowe Z. Serweciński 05-03-2011 Przewarzanie u analogowego na cyfrowy Proces przewarzania u analogowego (ciągłego) na cyfrowy składa się z rzech podsawowych operacji: 1. Próbkowanie
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
POLITECHNIKA BIAŁOSTOCKA
 DODATEK A POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI ĆWICZENIE NR 1 CHARAKTERYSTYKI CZASOWE I CZĘSTOTLIWOŚCIOWE PROSTYCH UKŁADÓW DYNAMICZNYCH PRACOWNIA SPECJALISTYCZNA
DODATEK A POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI ĆWICZENIE NR 1 CHARAKTERYSTYKI CZASOWE I CZĘSTOTLIWOŚCIOWE PROSTYCH UKŁADÓW DYNAMICZNYCH PRACOWNIA SPECJALISTYCZNA
TRANSFORMATA FOURIERA
 TRANSFORMATA FOURIERA. Wzór całkowy Fouriera Wzór ten wykorzystujemy do analizy funkcji nieokresowych; funkcje te mogą opisywać np.przebiegi eleektryczne. Najpierw sformułujmy tzw. warunki Dirichleta.
TRANSFORMATA FOURIERA. Wzór całkowy Fouriera Wzór ten wykorzystujemy do analizy funkcji nieokresowych; funkcje te mogą opisywać np.przebiegi eleektryczne. Najpierw sformułujmy tzw. warunki Dirichleta.
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LABORATORIUM PODSTAW ELEKTRONIKI PROSTOWNIKI
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM PODSTAW ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 5 PROSTOWNIKI DO UŻYTKU
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM PODSTAW ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 5 PROSTOWNIKI DO UŻYTKU
LABORATORIUM SYGNAŁÓW I SYSTEMÓW. Ćwiczenie 1
 POLIECHNIKA WARSZAWSKA INSYU RADIOELEKRONIKI ZAKŁAD RADIOKOMUNIKACJI LABORAORIUM SYGNAŁÓW I SYSEMÓW Ćwiczenie ema: MODELE CZĘSOLIWOŚCIOWE SYGNAŁÓW Opracowała: mgr inż. Kajeana Snope Warszawa Cel ćwiczenia
POLIECHNIKA WARSZAWSKA INSYU RADIOELEKRONIKI ZAKŁAD RADIOKOMUNIKACJI LABORAORIUM SYGNAŁÓW I SYSEMÓW Ćwiczenie ema: MODELE CZĘSOLIWOŚCIOWE SYGNAŁÓW Opracowała: mgr inż. Kajeana Snope Warszawa Cel ćwiczenia
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Ćw. S-II.2 CHARAKTERYSTYKI SKOKOWE ELEMENTÓW AUTOMATYKI
 Dr inż. Michał Chłędowski PODSAWY AUOMAYKI I ROBOYKI LABORAORIUM Ćw. S-II. CHARAKERYSYKI SKOKOWE ELEMENÓW AUOMAYKI Cel ćwiczenia Celem ćwiczenia jes zapoznanie się z pojęciem charakerysyki skokowej h(),
Dr inż. Michał Chłędowski PODSAWY AUOMAYKI I ROBOYKI LABORAORIUM Ćw. S-II. CHARAKERYSYKI SKOKOWE ELEMENÓW AUOMAYKI Cel ćwiczenia Celem ćwiczenia jes zapoznanie się z pojęciem charakerysyki skokowej h(),
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH
 POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
Przeksztacenie Laplace a. Krzysztof Patan
 Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
Dobór przekroju żyły powrotnej w kablach elektroenergetycznych
 Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
Pobieranie próby. Rozkład χ 2
 Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
Silniki cieplne i rekurencje
 6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
Cyfrowe przetwarzanie sygnału przetwornika obrotowo-impulsowego
 Cyfrowe przewarzanie sygnału przewornika obroowo-impulsowego Eligiusz PAWŁOWSKI Poliechnika Lubelska, Kaedra Auomayki i Merologii ul. Nadbysrzycka 38 A, 20-68 Lublin, email: elekp@elekron.pol.lublin.pl
Cyfrowe przewarzanie sygnału przewornika obroowo-impulsowego Eligiusz PAWŁOWSKI Poliechnika Lubelska, Kaedra Auomayki i Merologii ul. Nadbysrzycka 38 A, 20-68 Lublin, email: elekp@elekron.pol.lublin.pl
PAlab_4 Wyznaczanie charakterystyk częstotliwościowych
 PAlab_4 Wyznaczanie charakerysyk częsoliwościowych Ćwiczenie ma na celu przedsawienie prakycznych meod wyznaczania charakerysyk częsoliwościowych elemenów dynamicznych. 1. Wprowadzenie Jedną z podsawowych
PAlab_4 Wyznaczanie charakerysyk częsoliwościowych Ćwiczenie ma na celu przedsawienie prakycznych meod wyznaczania charakerysyk częsoliwościowych elemenów dynamicznych. 1. Wprowadzenie Jedną z podsawowych
LOKALNA ANALIZA CZĘSTOTLIWOŚCIOWA SYGNAŁÓW. 1. Definicja 2. Okna 3. Transformacja Gabora. Spis treści
 LOKALNA ANALIZA CZĘSOLIWOŚCIOWA SYGNAŁÓW. Deinicja. Okna 3. ransormacja Gabora Spis reści Analiza czasoo-częsoliościoa sygnału moy Ampliuda.. andrzej 35_m.av -. 3 4 5 6 7 8 9 D 4. 3.5 D 3. DW D3 D4.5..5
LOKALNA ANALIZA CZĘSOLIWOŚCIOWA SYGNAŁÓW. Deinicja. Okna 3. ransormacja Gabora Spis reści Analiza czasoo-częsoliościoa sygnału moy Ampliuda.. andrzej 35_m.av -. 3 4 5 6 7 8 9 D 4. 3.5 D 3. DW D3 D4.5..5
Lista nr Znaleźć rozwiązania ogólne następujących równań różniczkowych: a) y = y t,
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
Analiza właściwości dynamicznych wybranych podstawowych członów automatyki niecałkowitych rzędów
 Mirosław uf, Arur Nowocień, Daniel Pieruszczak Analiza właściwości dynamicznych wybranych podsawowych członów auomayki niecałkowiych rzędów JE: 97 DO: 10.4136/aes.018.443 Daa zgłoszenia: 19.11.018 Daa
Mirosław uf, Arur Nowocień, Daniel Pieruszczak Analiza właściwości dynamicznych wybranych podsawowych członów auomayki niecałkowiych rzędów JE: 97 DO: 10.4136/aes.018.443 Daa zgłoszenia: 19.11.018 Daa
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap szkolny 5 listopada 2013 Czas 90 minut
 Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem próbkowania t takim, że T = t N 1 t
 4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
Wyznaczanie charakterystyk częstotliwościowych
 Wyznaczanie charakerysyk częsoliwościowych Ćwiczenie ma na celu przedsawienie prakycznych meod wyznaczania charakerysyk częsoliwościowych elemenów dynamicznych. 1. Wprowadzenie Jedną z podsawowych meod
Wyznaczanie charakerysyk częsoliwościowych Ćwiczenie ma na celu przedsawienie prakycznych meod wyznaczania charakerysyk częsoliwościowych elemenów dynamicznych. 1. Wprowadzenie Jedną z podsawowych meod
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
Szeregi Fouriera (6 rozwiązanych zadań +dodatek)
 PWR I Załad eorii Obwodów Szeregi ouriera (6 rozwiązanych zadań +dodae) Opracował Dr Czesław Michali Zad Znaleźć ores nasępujących sygnałów: a) y 3cos(ω ) + 5cos(7ω ) + cos(5ω ), b) y cos(ω ) + 5cos(ω
PWR I Załad eorii Obwodów Szeregi ouriera (6 rozwiązanych zadań +dodae) Opracował Dr Czesław Michali Zad Znaleźć ores nasępujących sygnałów: a) y 3cos(ω ) + 5cos(7ω ) + cos(5ω ), b) y cos(ω ) + 5cos(ω
Ćwiczenie. Analiza widmowa sygnałów
 Program Rozwojowy Poliechniki Warszawskiej, Zadanie 36 Przygoowanie i modernizacja programów sudiów oraz maeriałów dydakycznych na Wydziale Elekrycznym Laboraorium kwizycja, przewarzanie i przesyłanie
Program Rozwojowy Poliechniki Warszawskiej, Zadanie 36 Przygoowanie i modernizacja programów sudiów oraz maeriałów dydakycznych na Wydziale Elekrycznym Laboraorium kwizycja, przewarzanie i przesyłanie
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Ćwiczenie E-5 UKŁADY PROSTUJĄCE
 KŁADY PROSJĄCE I. Cel ćwiczenia: pomiar podsawowych paramerów prosownika jedno- i dwupołówkowego oraz najprosszych filrów. II. Przyrządy: płyka monaŝowa, wolomierz magneoelekryczny, wolomierz elekrodynamiczny
KŁADY PROSJĄCE I. Cel ćwiczenia: pomiar podsawowych paramerów prosownika jedno- i dwupołówkowego oraz najprosszych filrów. II. Przyrządy: płyka monaŝowa, wolomierz magneoelekryczny, wolomierz elekrodynamiczny
Wykład 4: Transformata Laplace a
 Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTTUTU TECHNIKI CIEPLNEJ WDZIAŁ INŻNIERII ŚRODOWISKA I ENERGETKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORJNA Tema ćwiczenia: WZNACZANIE WSPÓŁCZNNIKA PRZEWODZENIA CIEPŁA CIAŁ STAŁCH METODĄ STANU UPORZĄDKOWANEGO
INSTTUTU TECHNIKI CIEPLNEJ WDZIAŁ INŻNIERII ŚRODOWISKA I ENERGETKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORJNA Tema ćwiczenia: WZNACZANIE WSPÓŁCZNNIKA PRZEWODZENIA CIEPŁA CIAŁ STAŁCH METODĄ STANU UPORZĄDKOWANEGO
zestaw laboratoryjny (generator przebiegu prostokątnego + zasilacz + częstościomierz), oscyloskop 2-kanałowy z pamięcią, komputer z drukarką,
 - Ćwiczenie 4. el ćwiczenia Zapoznanie się z budową i działaniem przerzunika asabilnego (muliwibraora) wykonanego w echnice dyskrenej oraz TTL a akże zapoznanie się z działaniem przerzunika T (zwanego
- Ćwiczenie 4. el ćwiczenia Zapoznanie się z budową i działaniem przerzunika asabilnego (muliwibraora) wykonanego w echnice dyskrenej oraz TTL a akże zapoznanie się z działaniem przerzunika T (zwanego
Drgania elektromagnetyczne obwodu LCR
 Ćwiczenie 61 Drgania elekromagneyczne obwodu LCR Cel ćwiczenia Obserwacja drgań łumionych i przebiegów aperiodycznych w obwodzie LCR. Pomiar i inerpreacja paramerów opisujących obserwowane przebiegi napięcia
Ćwiczenie 61 Drgania elekromagneyczne obwodu LCR Cel ćwiczenia Obserwacja drgań łumionych i przebiegów aperiodycznych w obwodzie LCR. Pomiar i inerpreacja paramerów opisujących obserwowane przebiegi napięcia
Matematyczne Metody Fizyki II
 Matematyczne Metody Fizyki II Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 7 M. Przybycień (WFiIS AGH) Matematyczne Metody Fizyki II Wykład 7 1 / 11 Reprezentacja
Matematyczne Metody Fizyki II Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 7 M. Przybycień (WFiIS AGH) Matematyczne Metody Fizyki II Wykład 7 1 / 11 Reprezentacja
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
Katedra Systemów Przetwarzania Sygnałów SZEREGI FOURIERA
 Ćwiczenie Zmodyfiowano 7..5 Prawa auorsie zasrzeżone: Kaedra Sysemów Przewarzania Sygnałów PWr SZEREGI OURIERA Celem ćwiczenia jes zapoznanie się z analizą i synezą sygnałów oresowych w dziedzinie częsoliwości.
Ćwiczenie Zmodyfiowano 7..5 Prawa auorsie zasrzeżone: Kaedra Sysemów Przewarzania Sygnałów PWr SZEREGI OURIERA Celem ćwiczenia jes zapoznanie się z analizą i synezą sygnałów oresowych w dziedzinie częsoliwości.
VII. ZAGADNIENIA DYNAMIKI
 Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
ĆWICZENIE 2. Autor pierwotnej i nowej wersji; mgr inż. Leszek Widomski
 ĆWICZENIE Auor pierwonej i nowej wersji; mgr inż. Leszek Widomski UKŁADY LINIOWE Celem ćwiczenia jes poznanie właściwości i meod opisu linioch układów elekrycznych i elekronicznych przenoszących sygnały.
ĆWICZENIE Auor pierwonej i nowej wersji; mgr inż. Leszek Widomski UKŁADY LINIOWE Celem ćwiczenia jes poznanie właściwości i meod opisu linioch układów elekrycznych i elekronicznych przenoszących sygnały.
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
WNIOSKOWANIE STATYSTYCZNE
 Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wykład X. ε, ε, ε = ε oznaczają współrzędne tensora odkształcenia, u i w są współrzędnymi wektora WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ
 Wykład X ROZWIĄZANIE RÓWNAŃ RÓŻNICZKOWYC Z WYKORZYSTANIEM TRANSFORMACJI LAPLACE A i FOURIERA CIĄG DALSZY. Konsolidacja półprzesrzeni konsolidujące pod działaniem ruchomego obciążenia skupionego. Rozważmy
Wykład X ROZWIĄZANIE RÓWNAŃ RÓŻNICZKOWYC Z WYKORZYSTANIEM TRANSFORMACJI LAPLACE A i FOURIERA CIĄG DALSZY. Konsolidacja półprzesrzeni konsolidujące pod działaniem ruchomego obciążenia skupionego. Rozważmy
XXXIV Olimpiada Wiedzy Elektrycznej i Elektronicznej Kraków 31 marca 2011. Test dla grupy elektronicznej
 XXXIV Olimpiada Wiedzy lekrycznej i lekronicznej Kraków marca Tes dla grupy elekronicznej.ezysancja zasępcza widziana z zacisków B wynosi:,,4,6,8 B. W poniższym układzie do wyznaczenia prądu w rezysancji
XXXIV Olimpiada Wiedzy lekrycznej i lekronicznej Kraków marca Tes dla grupy elekronicznej.ezysancja zasępcza widziana z zacisków B wynosi:,,4,6,8 B. W poniższym układzie do wyznaczenia prądu w rezysancji
POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH. Cel ćwiczenia. Program ćwiczenia
 Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
4. Modulacje kątowe: FM i PM. Układy demodulacji częstotliwości.
 EiT Vsemesr AE Układy radioelekroniczne Modulacje kąowe 1/26 4. Modulacje kąowe: FM i PM. Układy demodulacji częsoliwości. 4.1. Modulacje kąowe wprowadzenie. Cecha charakerysyczna: na wykresie wskazowym
EiT Vsemesr AE Układy radioelekroniczne Modulacje kąowe 1/26 4. Modulacje kąowe: FM i PM. Układy demodulacji częsoliwości. 4.1. Modulacje kąowe wprowadzenie. Cecha charakerysyczna: na wykresie wskazowym
2. Próbkowanie Sygnały okresowe (16). Trygonometryczny szereg Fouriera (17). Częstotliwość Nyquista (20).
 SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
Przetworniki analogowo-cyfrowe.
 POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIEII ŚODOWISKA I ENEGETYKI INSTYTUT MASZYN I UZĄDZEŃ ENEGETYCZNYCH LABOATOIUM ELEKTYCZNE Przeworniki analogowo-cyfrowe. (E 11) Opracował: Dr inż. Włodzimierz OGULEWICZ
POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIEII ŚODOWISKA I ENEGETYKI INSTYTUT MASZYN I UZĄDZEŃ ENEGETYCZNYCH LABOATOIUM ELEKTYCZNE Przeworniki analogowo-cyfrowe. (E 11) Opracował: Dr inż. Włodzimierz OGULEWICZ
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1
 ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ĆWICZENIE NR 43 U R I (1)
 ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZENIE 7. Splot liniowy i kołowy sygnałów
 Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZEIE 7 Splot liniowy i kołowy sygnałów 1. Cel ćwiczenia Operacja splotu jest jedną z najczęściej wykonywanych operacji na sygnale. Każde przejście
Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZEIE 7 Splot liniowy i kołowy sygnałów 1. Cel ćwiczenia Operacja splotu jest jedną z najczęściej wykonywanych operacji na sygnale. Każde przejście
IMPLEMENTACJA WYBRANYCH METOD ANALIZY STANÓW NIEUSTALONYCH W ŚRODOWISKU MATHCAD
 Pior Jankowski Akademia Morska w Gdyni IMPLEMENTACJA WYBRANYCH METOD ANALIZY STANÓW NIEUSTALONYCH W ŚRODOWISKU MATHCAD W arykule przedsawiono możliwości (oraz ograniczenia) środowiska Mahcad do analizy
Pior Jankowski Akademia Morska w Gdyni IMPLEMENTACJA WYBRANYCH METOD ANALIZY STANÓW NIEUSTALONYCH W ŚRODOWISKU MATHCAD W arykule przedsawiono możliwości (oraz ograniczenia) środowiska Mahcad do analizy
ANALIZA ODPOWIEDZI UKŁADÓW KONSTRUKCYJNYCH NA WYMUSZENIE W POSTACI SIŁY O DOWOLNYM PRZEBIEGU CZASOWYM
 Budownicwo Mariusz Poński ANALIZA ODPOWIEDZI UKŁADÓW KONSTRUKCYJNYCH NA WYMUSZENIE W POSTACI SIŁY O DOWOLNYM PRZEBIEGU CZASOWYM Wprowadzenie Coraz większe ograniczenia czasowe podczas wykonywania projeków
Budownicwo Mariusz Poński ANALIZA ODPOWIEDZI UKŁADÓW KONSTRUKCYJNYCH NA WYMUSZENIE W POSTACI SIŁY O DOWOLNYM PRZEBIEGU CZASOWYM Wprowadzenie Coraz większe ograniczenia czasowe podczas wykonywania projeków
Laseryimpulsowe-cotojest?
 Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
Przetwarzanie sygnałów z czasem ciągłym
 Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Andrzej Wyszkowski. GRAFIKA KOMPUTEROWA W ANALIZIE LINIOWYCH UKŁADÓW REGULACJI Zastosowania programu Mathcad
 Andrzej Wyszkowski GRAFIKA KOMPUTEROWA W ANALIZIE LINIOWYCH UKŁADÓW REGULACJI Zasosowania programu Mahcad Andrzej Wyszkowski GRAFIKA KOMPUTEROWA W ANALIZIE LINIOWYCH UKŁADÓW REGULACJI Zasosowania programu
Andrzej Wyszkowski GRAFIKA KOMPUTEROWA W ANALIZIE LINIOWYCH UKŁADÓW REGULACJI Zasosowania programu Mahcad Andrzej Wyszkowski GRAFIKA KOMPUTEROWA W ANALIZIE LINIOWYCH UKŁADÓW REGULACJI Zasosowania programu
Układy RLC oraz układ czasowy 555
 Układy L oraz układ czasowy 555 Sonda oscyloskopowa s Kabel Obwód wejsciowy oscyloskopu wes wes s k we we Konspek do ćwiczeń laboraoryjnych z przedmiou TEHNIKA YFOWA SPIS TEŚI. Układ różniczkujący... 3.
Układy L oraz układ czasowy 555 Sonda oscyloskopowa s Kabel Obwód wejsciowy oscyloskopu wes wes s k we we Konspek do ćwiczeń laboraoryjnych z przedmiou TEHNIKA YFOWA SPIS TEŚI. Układ różniczkujący... 3.
Filtracja. Krzysztof Patan
 Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
2. Wprowadzenie. Obiekt
 POLITECHNIKA WARSZAWSKA Insyu Elekroenergeyki, Zakład Elekrowni i Gospodarki Elekroenergeycznej Bezpieczeńswo elekroenergeyczne i niezawodność zasilania laoraorium opracował: prof. dr ha. inż. Józef Paska,
POLITECHNIKA WARSZAWSKA Insyu Elekroenergeyki, Zakład Elekrowni i Gospodarki Elekroenergeycznej Bezpieczeńswo elekroenergeyczne i niezawodność zasilania laoraorium opracował: prof. dr ha. inż. Józef Paska,
Przekształcenie Z. Krzysztof Patan
 Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH
 Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
