Fig. 1. Interferometr A. A. Michelsona.
|
|
|
- Jadwiga Sadowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Efek Sagnaa dr Janusz. Kępka Wsęp. Jednym z najbardziej reklamowanyh eksperymenów był i jes eksperymen lbera brahama Mihelsona zapoząkowany w 88, i nasępnie powarzany po roku 880 we współpray z Ewardem Williamsem Morleyem. Celem ego eksperymenu było wykryie ruhu absolunego Ziemi. Obenie, eksperymen en znany jes pod ogólną nazwą eksperymenu Mihelsona-Morleya. Eksperymen en przeprowadzany był za pomoą inerferomeru.. Mihelsona (Fig..). Fig.. Inerferomer.. Mihelsona. Inerferomer.. Mihelsona (Fig. ) składa się z monohromayznego źródła świała S, półprzepuszzalnej płyki P, oraz dwóh zwieriadeł i, usawionyh w równyh odległośiah P P l od miejsa padania wiązki świała na płykę P. Na usawioną pod kąem 5 o płykę P pada wiązka świała ze źródła S, kóra ulega rozszzepieniu na dwie wiązki biegnąe wzajemnie prosopadle do zwieriadeł i. Po odbiiu się od i, wiązki e wraają do płyki P, gdzie ponownie ulegają rozszzepieniu, i zęść wraa do źródła S, a pozosała zęść biegnie razem do eleskopu T. Na drodze PT obydwie wiązki inerferują ze sobą, a obraz inerferenyjny oglądany jes w głównej płaszzyźnie ogniskowej eleskopu T. Gdyby inerferomer był absolunie nieruhomy w hipoeyznym eerze, zyli w układzie absolunie absolunym -spae, o drogi przebye przez świało w obydwu ramionah inerferomeru byłyby sobie dokładnie równe. W akim przypadku, dowolny obró inerferomeru nie zmienia długośi dróg przebyyh przez świało w obydwu ramionah inerferomeru. Tym samym nie zmienia się obraz inerferenyjny w eleskopie T. Załóżmy eraz, że inerferomer porusza się ruhem ranslayjnym w hipoeyznym eerze. Ławo zauważyć, że w ogólnośi w zasie ruhu ranslayjnego inerferomeru w -spae, drogi przebywane przez świało w obydwu ramionah inerferomeru nie są sobie równe... Mihelson przyjął, że jeżeli inerferomer będzie obraany względem środka płyki P, o nasąpi zmiana długośi dróg w obydwu ramionah inerferomeru, o z kolei spowoduje zmianę położenia prążków inerferenyjnyh. W en sposób, będzie można wykryć ruh orbialny Ziemi. Jednak, powarzane przez kilka dziesiąek la ego rodzaju eksperymeny, w różnyh porah roku i w różnyh miejsah na kuli ziemskiej, zawsze dawały wynik negaywny: brak zmiany położenia prążków inerferenyjnyh. Powyższe może oznazać ylko dwie różne syuaje:
2 . Ziemia jes absolunie nieruhoma w Kosmosie, zn. nie isnieje ruh wirowy wokół własnej osi, ani eż ruh po orbiie okołosłoneznej (byłby o dowód na prawdziwość eorii geoenryznej).. Eksperymen jes wadliwie przeprowadzany. Przyjęo warian rzei: eksperymen jes wzorowo poprawnie przeprowadzony. Naomias nie jes możliwe wykryie ruhu absolunego, ponieważ nie isnieje eer, zyli nie isnieje przesrzeń kosmizna (si!), w kórej najławiej rozhodzi się świało. Jeżeli jednak przyjmiemy, że eer isnieje, o jes on ałkowiie unoszony przez Ziemię, zyli przesrzeń kosmizna jes ałkowiie unoszona przez Ziemię i dlaego ni nie widać (w inerferomerze, ozywiśie). Obenie, Janusz. Kępka w swej książe uh absoluny i względny (Warszawa, 999) wykazał, że w zasie eksperymenu rzezywiśie nasępuje zmiana długośi dróg świała w obydwu ramionah inerferomeru Mihelsona, ale zmiany są ego rodzaju, że zmiany dróg o and fro w każdym z ramion wzajemnie kompensują się. Z ego właśnie względu nie jes możliwe uzyskanie zmiany położenia prążków inerferenyjnyh. Oznaza o, że inerferomer Mihelsona nie jes właśiwym przyrządem do przeprowadzania ego rodzaju eksperymenów. Eksperymen Sagnaa W roku 93 uzony franuski Georges Sagna (869-98) wykazał doświadzalnie za pomoą zmodyfikowanego inerferomeru Mihelsona (Fig..), że możliwe jes wykryie ruhu Ziemi w hipoeyznym eerze (Georges Sagna, Compes endus 57, 93). Fig.. Inerferomer Sagnaa. W inerferomerze Mihelsona dwie wiązki oraz świała przebywają dwie drogi w różnyh, wzajemnie prosopadłyh ramionah inerferomeru. Naomias w inerferomerze Sagnaa dwie wiązki świała oraz biegną po ej samej krzywej zamknięej, ale we wzajemnie przeiwnyh kierunkah. Można o wpros odwzorować jako ruh po okręgu w dwu przeiwnyh kierunkah. ozparzmy bieg wiązek świała w inerferomerze Sagnaa. Paradoks Zenona z Elei Oznazmy ałkowią długość drogi PP PP w inerferomerze jako. Odległość świało przebywa z prędkośią w zasie :. Załóżmy, że inerferomer obraany jes w lewo ze sałą prędkośią kąową ons. Względem impulsu świała biegnąego od płyki P w kierunku zgodnym z kierunkiem obrou inerferomeru, płyka P uieka przed ym impulsem. Znalezienie odległośi jaką impuls świała przebędzie, aby wróić do płyki P, jes równoważne znalezieniu rozwiązania słynnego
3 3 paradoksu Zenona z Elei: zy hilles dogoni żółwia (poząkowa odległość między nimi wynosi, hilles biegnie z prędkośią, a żółw z prędkośią ): gdzie: W powyższym: prędkość liniowa dowolnego punku na okręgu o promieniu (Fig. ); prędkość świała. Ponieważ:, o z powyższego znajdujemy: Podobnie znajdujemy zas po jakim impuls dobiegnie do płyki P: W podobny sposób znajdujemy dla impulsu świała biegnąego w kierunku przeiwnym do kierunku obrou inerferomeru (w ym przypadku, hilles i żółw biegną naprzeiwko siebie): oraz Z powyższego, znajdujemy: () oraz ) ( () ϕ (3) a akże: ϕ () Z powyższyh rozważań wpros wynika, że w zasie obrou inerferomeru ) ( 0 powsaje różnia dróg (Eq. ) przebywanyh przez świało w kierunkah przeiwnyh. Z elemenarnej opyki wiadomo, że fale o jednakowyh okresah wzmaniają się najsilniej, gdy różnia dróg jes równa ałkowiej wielokronośi długośi fali λ : λ k, gdzie: k 0,,,..., n. Fale maksymalnie osłabiają się, jeśli różnia dróg wynosi nieparzysą lizbę połówek długośi fali: ) (k λ Powyższe zwane jes ogólnie inerferenją ruhu falowego. Jeżeli inerferomer nie jes obraany ) ( 0, o z zależnośi od () do (), mamy: 0, 0 oraz 0 i możemy obserwować sabilny obraz inerferenyjny. Wiązki świała oraz inerferują w równyh fazah na drodze PT (Fig. ).
4 W zasie obrou przyrządu, pojawia się różnia dróg ( ) 0, a przebyyh przez świało w dwu przeiwnyh kierunkah w inerferomerze. Z ego względu nasąpi zmiana obrazu inerferenyjnego (zmiana położenia oraz naężenia prążków inerferenyjnyh). Zmiana a spowodowana jes ym, że wiązki świała oraz spoykają się w różnyh fazah na drodze PT. Powyższe wykorzysywane jes obenie do budowy preyzyjnyh przyrządów, zwanyh żyroskopami. Przyrządy e pozwalają wykryć obró przyrządu o 0,000 sopnia na godzinę (Eq. ). Efek Dopplera Zauważmy, że płyka P w inerferomerze spełnia podwójną rolę: źródła S świała dla wiązek świała oraz biegnąyh od płyki P w kierunku zwieriadeł oraz ; obserwaora O dla obydwu wiązek oraz gdy wiązki e przebywają w inerferomerze odpowiednie drogi w kierunkah wzajemnie przeiwnyh i biegną do płyki P. Zauważmy eż, że prędkość S źródła drgań S oraz prędkość O obserwaora O są sobie dokładnie równe oraz równe prędkośi dowolnego punku na obwodzie okręgu o promieniu inerferomeru: S O. Z powyższyh względów, wysępuje podwójny efek Dopplera dla poruszająego się źródła S drgań oraz obserwaora O. Ogólny opis podwójnego efeku Dopplera podany jes w książe: Janusz. Kępka uh absoluny i względny, Warszawa 999. Jeżeli obserwaor O wyprzedza źródło S, o w opisywanym wyżej przypadku odnosi się do wiązki świała, o spełnione są warunki: O fd ν S λ ( S ) gdzie: ν zęsoliwość generowanej fali w danym ośrodku, gdy źródło drgań jes nieruhome. λ długość fali generowanej w danym ośrodku przez nieruhome źródło drgań. Powyżej wskazaliśmy, że spełniony jes warunek: S O. Wobe ego, z powyższej zależnośi znajdujemy, że: f D ν (5) < λ Podobnie mamy dla przypadku, gdy źródło S wyprzedza obserwaora O: O fd ν S λ ( S ) oraz: f D ν (6) > λ Z powyższego wpros wynika, że w eksperymenie Sagnaa nie wysępuje zmiana zęsoliwośi inerferująyh wiązek świała oraz. Dyskusja. Przede wszyskim zauważmy, że pozyywny wynik eksperymenu Sagnaa zosał uzyskany za pomoą lekko zmodyfikowanego inerferomeru.. Mihelsona! Przed rokiem 933, uzony amerykański Dayon C. Miller przeprowadził eksperymeny za pomoą zmodyfikowanego inerferomeru Mihelsona w en sposób, że ramiona ego inerferomeru były wyraźnie wzajemnie sobie nierówne. Uzyskał wynik pozyywny (D.C. Miller, eiews of Modern Physis, 5, 03, 933).
5 Powyższe wpros oznaza, że (nie modyfikowany) inerferomer Mihelsona nie nadaje się do ego rodzaju eksperymenów. Jednak w 007 r. Janusz. Kępka ( uh absoluny i względny, Warszawa 007) wskazał, że możliwe jes uzyskanie pozyywnego wyniku za pomoą inerferomeru Mihelsona, jeżeli jedno z ramion ego inerferomeru zahowa sały kierunek w przesrzeni (lokalny układ odniesienia). Można o uzyskać za pomoą obrou przyrządu względem ylko jednego z jego ramion. Warunek en nie był spełniony w eksperymenah wykonywanyh przez Mihelsona, Morleya i innyh. W zw. lieraurze przedmiou, eksperymeny G. Sagnaa oraz D.C. Millera były i są sarannie przemilzane, lub znazenie ih jes maksymalnie zaniżane. Naomias wyolbrzymiane jes znazenie eksperymenu.. Mihelsona, kóry o eksperymen (ponoć) sanowił podsawę szzególnej i ogólnej, a nawe szzególnie ogólnej eorii względnośi niejakiego lbera Einseina. Esperymeny G. Sagnaa oraz D.C. Millera z opyki oraz wześniejszy (85 r.) eksperymen z wahadłem Fouaul (Jean ernard éon, , fizyk franuski), wpros dowodzą, że zw. eorie względnośi lbera Einseina są rażąo niezgodne z doświadzeniem. Wobe ego, niekórzy wierdzą, że: The Sagna effe (in auum) is onsisen wih saionary eher heories (suh as he orenz eher heory) as well as wih Einsein's heory of relaiiy. I is generally aken o be inonsisen wih emission heories of ligh, aording o whih he speed of ligh depends on he speed of he soure. ("hp://en.wikipedia.org/wiki/georges_sagna") Tak wię, wg Wikipedii, efek Sagnaa powierdza, że eer spozywa i jednoześnie fruwa. azem z eorią względnośi Einseina, ozywiśie. Poważnie? nie jes ak, że: albo albo? oo kolejne oszuswa w wydaniu Wikipedii. Oóż, nieprawdą jes, że H..orenz (853-98) jes wórą eorii eeru (sprężysy ośrodek rozhodzenia się fal świelnyh > bezwzględny układ odniesienia). Znaznie wześniej Holender Chrisian Huygens (69-695), wierdził, że świało polega na rozhodzeniu się fal w eerze sprężysej subsanji zapełniająej ały wszehświa ( Traka o świele, 690). Ponado, nieprawdą jes, że według eorii emisji świała prędkość świała zależy od prędkośi źródła świała. ył aki pomysł, ale nayhmias z niego zrezygnowano, ponieważ nie jes o słuszne dla ruhu falowego (świało ma wszyskie ehy ruhu falowego, jes o fala poprzezna). Naomias, według lbera Einseina prędkość świała jes dokładnie aka sama względem dowolnie poruszająego się (akże nieruhomego, sojąego, leżąego i nawe wisząego) obserwaora. Opisany wyżej efek Sagnaa wpros z doświadzenia dowodzi, że nie jes o prawdziwe. To lber Einsein nie ma raji? To jes niedopuszzalne! Wobe ego, relaywiśi z Wikipedii (i nie ylko) wierdzą, że efek Sagnaa jes zgodny z eorią względnośi lbera Einseina! I w en oo prosy sposób eoria względnośi lbera Einseina jes zgodna z doświadzeniem. Pyanie: ko u jes idioą, a ko oszusem? Pardon! Pyać nie wolno? Uwagi końowe Przy pomoy inerferomeru Sagnaa można wykryć zmianę kierunku ruhu układu obserwaora, np. ruh wirowy zy orbialny Ziemi. Jednak za pomoą ego przyrządu nie można wykryć ruhu ranslayjnego prosoliniowego obserwaora. Jednak aką możliwość deekji ruhu absolunego Ziemi, wskazano wyżej. Eksperymen jes dosyć rudny do wykonania ze względów ehniznyh. Jednak, ego rodzaju eksperymen można znakomiie uprośić wykorzysują ruh wirowy Ziemi, właśnie. Uwaga: akże w książe Janusza. Kępki uh absoluny i względny, Warszawa 007, podany jes pełny dowód sposobu wylizenia prędkośi ranslayjnej Słońa w Kosmosie (ok km/s), ylko na podsawie znajomośi prędkośi orbialnej Ziemi w perihelium oraz w aphelium, lub odległośi od Słońa Ziemi w perihelium oraz w aphelium. dr Janusz. Kępka Warszawa, 009 5
VII.5. Eksperyment Michelsona-Morleya.
 Janusz. Kępka Ruch absoluny i względny VII.5. Eksperymen Michelsona-Morleya. Zauważmy że pomiar ruchu absolunego jakiegokolwiek obieku maerialnego z założenia musi odnosić się do prędkości fali świelnej
Janusz. Kępka Ruch absoluny i względny VII.5. Eksperymen Michelsona-Morleya. Zauważmy że pomiar ruchu absolunego jakiegokolwiek obieku maerialnego z założenia musi odnosić się do prędkości fali świelnej
Szkoła z przyszłością. szkolenie współfinansowane przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
II.1. Zagadnienia wstępne.
 II.1. Zagadnienia wsępne. Arysoeles ze Sagiry wyraźnie łączy ruch z czasem: A jes niemożliwe, żeby zaczął się albo usał ruch, gdyż jak powiedzieliśmy ruch jes wieczny, a ak samo i czas, bo czas jes albo
II.1. Zagadnienia wsępne. Arysoeles ze Sagiry wyraźnie łączy ruch z czasem: A jes niemożliwe, żeby zaczął się albo usał ruch, gdyż jak powiedzieliśmy ruch jes wieczny, a ak samo i czas, bo czas jes albo
Mechanika relatywistyczna
 Mehanika relatywistyzna Konepja eteru Eter kosmizny miał być speyfiznym ośrodkiem, wypełniająym ałą przestrzeń, który miał być nośnikiem fal świetlnyh (później w ogóle pola elektromagnetyznego). W XIX
Mehanika relatywistyzna Konepja eteru Eter kosmizny miał być speyfiznym ośrodkiem, wypełniająym ałą przestrzeń, który miał być nośnikiem fal świetlnyh (później w ogóle pola elektromagnetyznego). W XIX
I.1. Paradoksy Zenona z Elei.
 I.1. Paradoksy Zenona z Eei. Janusz B. Kępka Ruch absouny i wzgędny Arysoees ze Sagiry w swej FIZYCE mówi o paradoksach Zenona z Eei (fiozof grecki, ok.490 430 p.n.e.): Isnieją czery argumeny Zenona doyczące
I.1. Paradoksy Zenona z Eei. Janusz B. Kępka Ruch absouny i wzgędny Arysoees ze Sagiry w swej FIZYCE mówi o paradoksach Zenona z Eei (fiozof grecki, ok.490 430 p.n.e.): Isnieją czery argumeny Zenona doyczące
7. Szczególna teoria względności. Wybór i opracowanie zadań : Barbara Kościelska Więcej zadań z tej tematyki znajduje się w II części skryptu.
 7 Szzególna eoria względnośi Wybór i opraowanie zadań 7-79: Barbara Kośielska Więej zadań z ej emayki znajduje się w II zęśi skrypu 7 Czy można znaleźć aki układ odniesienia w kórym Chrzes Polski i Biwa
7 Szzególna eoria względnośi Wybór i opraowanie zadań 7-79: Barbara Kośielska Więej zadań z ej emayki znajduje się w II zęśi skrypu 7 Czy można znaleźć aki układ odniesienia w kórym Chrzes Polski i Biwa
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Transformacja Galileusza ( )
 Tansfomaja Galileusza (564-64) z z y y Zasada względnośi Galileusza: pawa mehaniki są jednakowe we wszyskih inejalnyh układah odniesienia. F F a a Uwaga: newonowskie dodawanie pędkośi: u u S S, S S Poblem
Tansfomaja Galileusza (564-64) z z y y Zasada względnośi Galileusza: pawa mehaniki są jednakowe we wszyskih inejalnyh układah odniesienia. F F a a Uwaga: newonowskie dodawanie pędkośi: u u S S, S S Poblem
Oryginalna metoda wyprowadzania transformacji dla kinematyk z uniwersalnym układem odniesienia
 Oryginalna meoda wyprowadzania ransformaji dla kinemayk z uniwersalnym układem odniesienia Roman Szosek Poliehnika Rzeszowska Kaedra Meod Ilośiowyh Rzeszów Polska rszosek@prz.edu.pl Sreszzenie: Arykuł
Oryginalna meoda wyprowadzania ransformaji dla kinemayk z uniwersalnym układem odniesienia Roman Szosek Poliehnika Rzeszowska Kaedra Meod Ilośiowyh Rzeszów Polska rszosek@prz.edu.pl Sreszzenie: Arykuł
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
Transformacja Galileusza ( )
 Tansfomaja Galileusza (564-64) z z y y Zasada względnośi Galileusza: pawa mehaniki są jednakowe we wszyskih inejalnyh układah odniesienia. F F a a Uwaga: newonowskie dodawanie pędkośi: u u S S, S S Poblem
Tansfomaja Galileusza (564-64) z z y y Zasada względnośi Galileusza: pawa mehaniki są jednakowe we wszyskih inejalnyh układah odniesienia. F F a a Uwaga: newonowskie dodawanie pędkośi: u u S S, S S Poblem
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Podwaliny szczególnej teorii względności
 W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
Laseryimpulsowe-cotojest?
 Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak 2 Plan wykładu Zakłócenia w modelu DAD/DAS: Wzros produkcji poencjalnej; Zakłócenie podażowe o sile
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak 2 Plan wykładu Zakłócenia w modelu DAD/DAS: Wzros produkcji poencjalnej; Zakłócenie podażowe o sile
Przemieszczeniem ciała nazywamy zmianę jego położenia
 1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
5. Równania Maxwella. 5.1 Równania Maxwella 5.2 Transformacja pól 5.3 Fala elektromagnetyczna
 5 Równania Maxwella 5 Równania Maxwella 5 Transformaja pól 53 ala eleromagnezna 86 5 Równania Maxwella Wśród poazanh uprzednio równań Maxwella znajduje się prawo Ampere a j Jedna można pozać, że posać
5 Równania Maxwella 5 Równania Maxwella 5 Transformaja pól 53 ala eleromagnezna 86 5 Równania Maxwella Wśród poazanh uprzednio równań Maxwella znajduje się prawo Ampere a j Jedna można pozać, że posać
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Energia w ruchu harmonicznym
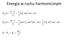 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Wykład 3: Kinematyka - względność ruchów. dr inż. Zbigniew Szklarski
 Wykład 3: Kinemayka - względność ruhów dr inż. Zbigniew Szklarski szkla@agh.edu.pl hp://layer.ui.agh.edu.pl/z.szklarski/ Wzgledność ruhów Każdy ruh opisujemy względem jakiegoś układu odniesienia W hwili
Wykład 3: Kinemayka - względność ruhów dr inż. Zbigniew Szklarski szkla@agh.edu.pl hp://layer.ui.agh.edu.pl/z.szklarski/ Wzgledność ruhów Każdy ruh opisujemy względem jakiegoś układu odniesienia W hwili
Elementy mechaniki relatywistycznej
 Podstawy Proesów i Konstrukji Inżynierskih Elementy mehaniki relatywistyznej 1 Czym zajmuje się teoria względnośi? Teoria względnośi to pomiary zdarzeń ustalenia, gdzie i kiedy one zahodzą, a także jaka
Podstawy Proesów i Konstrukji Inżynierskih Elementy mehaniki relatywistyznej 1 Czym zajmuje się teoria względnośi? Teoria względnośi to pomiary zdarzeń ustalenia, gdzie i kiedy one zahodzą, a także jaka
I. KINEMATYKA I DYNAMIKA
 piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
9.6. Promieniowanie rentgenowskie. Dyfrakcja promieniowania rentgenowskiego (prawo Bragga).
 9. Optyka 9.6. Promieniowanie rentgenowskie. yfrakja promieniowania rentgenowskiego (prawo Bragga). Shemat budowy lampy rentgenowskiej. Przyspieszone do dużej prędkośi elektrony uderzają w antykatodę zmniejszają
9. Optyka 9.6. Promieniowanie rentgenowskie. yfrakja promieniowania rentgenowskiego (prawo Bragga). Shemat budowy lampy rentgenowskiej. Przyspieszone do dużej prędkośi elektrony uderzają w antykatodę zmniejszają
Politechnika Częstochowska Wydział Inżynierii Mechanicznej i Informatyki. Sprawozdanie #2 z przedmiotu: Prognozowanie w systemach multimedialnych
 Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Kombinowanie prognoz. - dlaczego należy kombinować prognozy? - obejmowanie prognoz. - podstawowe metody kombinowania prognoz
 Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Wykład 4: Względność ruchów. dr inż. Zbigniew Szklarski
 Wykład 4: Względność ruhów dr inż. Zbigniew Szklarski szkla@agh.edu.pl hp://layer.ui.agh.edu.pl/z.szklarski/ Wzgledność ruhów Każdy ruh opisujemy względem jakiegoś układu odniesienia W hwili 0 rusza samohód
Wykład 4: Względność ruhów dr inż. Zbigniew Szklarski szkla@agh.edu.pl hp://layer.ui.agh.edu.pl/z.szklarski/ Wzgledność ruhów Każdy ruh opisujemy względem jakiegoś układu odniesienia W hwili 0 rusza samohód
2.6.3 Interferencja fal.
 RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
ANEMOMETRIA LASEROWA
 1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap szkolny 5 listopada 2013 Czas 90 minut
 Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Promieniowanie synchrotronowe i jego zastosowania
 Universias Jagellonica Cracoviensis Promieniowanie synchroronowe i jego zasosowania Wykład II J.J. Kołodziej Pokój: G--11, IFUJ Łojasiewicza 11 Tel.+1 664 4838 jj.kolodziej@uj.edu.pl Wykłady na WFAiS,
Universias Jagellonica Cracoviensis Promieniowanie synchroronowe i jego zasosowania Wykład II J.J. Kołodziej Pokój: G--11, IFUJ Łojasiewicza 11 Tel.+1 664 4838 jj.kolodziej@uj.edu.pl Wykłady na WFAiS,
Zaznacz prawdziwą odpowiedź: Fale elektromagnetyczne do rozchodzenia się... ośrodka materialnego A. B.
 Imię i nazwisko Pytanie 1/ Zaznacz właściwą odpowiedź: Fale elektromagnetyczne są falami poprzecznymi podłużnymi Pytanie 2/ Zaznacz prawdziwą odpowiedź: Fale elektromagnetyczne do rozchodzenia się... ośrodka
Imię i nazwisko Pytanie 1/ Zaznacz właściwą odpowiedź: Fale elektromagnetyczne są falami poprzecznymi podłużnymi Pytanie 2/ Zaznacz prawdziwą odpowiedź: Fale elektromagnetyczne do rozchodzenia się... ośrodka
BADANIE INTERFERENCJI MIKROFAL PRZY UŻYCIU INTERFEROMETRU MICHELSONA
 ZDNIE 11 BDNIE INTERFERENCJI MIKROFL PRZY UŻYCIU INTERFEROMETRU MICHELSON 1. UKŁD DOŚWIDCZLNY nadajnik mikrofal odbiornik mikrofal 2 reflektory płytka półprzepuszczalna prowadnice do ustawienia reflektorów
ZDNIE 11 BDNIE INTERFERENCJI MIKROFL PRZY UŻYCIU INTERFEROMETRU MICHELSON 1. UKŁD DOŚWIDCZLNY nadajnik mikrofal odbiornik mikrofal 2 reflektory płytka półprzepuszczalna prowadnice do ustawienia reflektorów
zestaw laboratoryjny (generator przebiegu prostokątnego + zasilacz + częstościomierz), oscyloskop 2-kanałowy z pamięcią, komputer z drukarką,
 - Ćwiczenie 4. el ćwiczenia Zapoznanie się z budową i działaniem przerzunika asabilnego (muliwibraora) wykonanego w echnice dyskrenej oraz TTL a akże zapoznanie się z działaniem przerzunika T (zwanego
- Ćwiczenie 4. el ćwiczenia Zapoznanie się z budową i działaniem przerzunika asabilnego (muliwibraora) wykonanego w echnice dyskrenej oraz TTL a akże zapoznanie się z działaniem przerzunika T (zwanego
K gęstość widmowa (spektralna) energii: 12 Classical theory (5000 K) 10 Rozbieżność w obszarze krótkich fal (katastrofa w nadfiolecie)
 Opyka kwanowa wprowadzenie Króka (pre-)hisoria foonu (9-93) Począki modelu foonowego Własności świała i jego oddziaływania z maerią, niedające się opisać w ramach fizyki klasycznej Deekcja pojedynczych
Opyka kwanowa wprowadzenie Króka (pre-)hisoria foonu (9-93) Począki modelu foonowego Własności świała i jego oddziaływania z maerią, niedające się opisać w ramach fizyki klasycznej Deekcja pojedynczych
PRACOWNIA ELEKTRONIKI
 PRACOWNIA ELEKTRONIKI Tema ćwiczenia: BADANIE MULTIWIBRATORA UNIWERSYTET KAZIMIERZA WIELKIEGO W BYDGOSZCZY INSTYTUT TECHNIKI. 2. 3. Imię i Nazwisko 4. Daa wykonania Daa oddania Ocena Kierunek Rok sudiów
PRACOWNIA ELEKTRONIKI Tema ćwiczenia: BADANIE MULTIWIBRATORA UNIWERSYTET KAZIMIERZA WIELKIEGO W BYDGOSZCZY INSTYTUT TECHNIKI. 2. 3. Imię i Nazwisko 4. Daa wykonania Daa oddania Ocena Kierunek Rok sudiów
Prawo odbicia światła. dr inż. Romuald Kędzierski
 Prawo odbicia światła dr inż. Romuald Kędzierski Odbicie fal - przypomnienie Kąt padania: Jest to kąt pomiędzy tzw. promieniem fali padającej (wskazującym kierunek i zwrot jej propagacji), a prostą prostopadłą
Prawo odbicia światła dr inż. Romuald Kędzierski Odbicie fal - przypomnienie Kąt padania: Jest to kąt pomiędzy tzw. promieniem fali padającej (wskazującym kierunek i zwrot jej propagacji), a prostą prostopadłą
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
IV.5. Promieniowanie Czerenkowa.
 Jansz B. Kępka Rh absoltny i względny IV.5. Promieniowanie Czerenkowa. Fizyk rosyjski Pawieł A. Czerenkow podjął badania (1934 r.) nad znanym słabym świeeniem niebiesko-białym wydzielanym przez silne preparaty
Jansz B. Kępka Rh absoltny i względny IV.5. Promieniowanie Czerenkowa. Fizyk rosyjski Pawieł A. Czerenkow podjął badania (1934 r.) nad znanym słabym świeeniem niebiesko-białym wydzielanym przez silne preparaty
Sprawujesz osobistą opiekę nad dzieckiem? Przeczytaj koniecznie!
 Sprawujesz osobisą opiekę nad dzieckiem? Przeczyaj koniecznie! Czy z yułu sprawowania osobisej opieki nad dzieckiem podlegasz ubezpieczeniom społecznym i zdrowonemu Od 1 września 2013 r. osoba sprawująca
Sprawujesz osobisą opiekę nad dzieckiem? Przeczyaj koniecznie! Czy z yułu sprawowania osobisej opieki nad dzieckiem podlegasz ubezpieczeniom społecznym i zdrowonemu Od 1 września 2013 r. osoba sprawująca
z graniczną technologią
 STUDIA OECOOMICA POSAIESIA 23, vol., no. (25) Uniwersye Ekonomiczny w Poznaniu, Wydział Informayki i Gospodarki Elekronicznej, Kaedra Ekonomii Maemaycznej emil.panek@ue.poznan.pl iesacjonarny model von
STUDIA OECOOMICA POSAIESIA 23, vol., no. (25) Uniwersye Ekonomiczny w Poznaniu, Wydział Informayki i Gospodarki Elekronicznej, Kaedra Ekonomii Maemaycznej emil.panek@ue.poznan.pl iesacjonarny model von
Wstęp do szczególnej teorii względności.
 Wsęp do szzególne eorii względnośi. o o nam szzególna eoria względnośi?? Drogi Uzni! omiaą aspeky nakowe akie ak na przykład fale elekromagneyzne, ząski elemenarne, asrofizyka, mehanika kwanowa, fizyka
Wsęp do szzególne eorii względnośi. o o nam szzególna eoria względnośi?? Drogi Uzni! omiaą aspeky nakowe akie ak na przykład fale elekromagneyzne, ząski elemenarne, asrofizyka, mehanika kwanowa, fizyka
Matematyka A, kolokwium, 15 maja 2013 rozwia. ciem rozwia
 Maemayka A kolokwium maja rozwia zania Należy przeczyać CA LE zadanie PRZED rozpocze ciem rozwia zywania go!. Niech M. p. Dowieść że dla każdej pary liczb ca lkowiych a b isnieje aka para liczb wymiernych
Maemayka A kolokwium maja rozwia zania Należy przeczyać CA LE zadanie PRZED rozpocze ciem rozwia zywania go!. Niech M. p. Dowieść że dla każdej pary liczb ca lkowiych a b isnieje aka para liczb wymiernych
Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu.
 Efekt Dopplera Cel ćwiczenia Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu. Wstęp Fale dźwiękowe Na czym
Efekt Dopplera Cel ćwiczenia Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu. Wstęp Fale dźwiękowe Na czym
Elementy optyki. Odbicie i załamanie fal Zasada Huygensa Zasada Fermata Interferencja Dyfrakcja Siatka dyfrakcyjna
 Elementy optyki Odbiie i załamanie fal Zasada Huygensa Zasada Fermata Interferenja Dyfrakja Siatka dyfrakyjna 1 Odbiie i załamanie fal elektromagnetyznyh na graniah dwóh ośrodków Normalna do powierzhni
Elementy optyki Odbiie i załamanie fal Zasada Huygensa Zasada Fermata Interferenja Dyfrakja Siatka dyfrakyjna 1 Odbiie i załamanie fal elektromagnetyznyh na graniah dwóh ośrodków Normalna do powierzhni
Rozdział 4 Instrukcje sekwencyjne
 Rozdział 4 Insrukcje sekwencyjne Lisa insrukcji sekwencyjnych FBs-PLC przedsawionych w niniejszym rozdziale znajduje się w rozdziale 3.. Zasady kodowania przy zasosowaniu ych insrukcji opisane są w rozdziale
Rozdział 4 Insrukcje sekwencyjne Lisa insrukcji sekwencyjnych FBs-PLC przedsawionych w niniejszym rozdziale znajduje się w rozdziale 3.. Zasady kodowania przy zasosowaniu ych insrukcji opisane są w rozdziale
Część I. MECHANIKA. Wykład KINEMATYKA PUNKTU MATERIALNEGO. Ruch jednowymiarowy Ruch na płaszczyźnie i w przestrzeni.
 Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Ronda, skrzyżowania i inne trudne zjawiska (3 pytania) 1. Korzystając z pasa rozpędowego
 Ronda, skrzyżowania i inne trudne zjawiska (3 pytania) 1. Korzystają z pasa rozpędowego a. można jadą nim wyprzedza ć samohody jadą e po naszej lewej stronie (Nie. Pas rozpędowy nie służy do wyprzedzania
Ronda, skrzyżowania i inne trudne zjawiska (3 pytania) 1. Korzystają z pasa rozpędowego a. można jadą nim wyprzedza ć samohody jadą e po naszej lewej stronie (Nie. Pas rozpędowy nie służy do wyprzedzania
Synteza i analiza stanu polaryzacji światła metodą ogólnego prawa Malusa
 nsrukcja robocza do ćwiczenia 4 Syneza i analiza sanu polaryzacji świała meodą ogólnego prawa Malusa. Układ pomiarowy Układ pomiarowy składa się z polarymeru, zasilacza sabilizowanego ZS-52, wolomierza
nsrukcja robocza do ćwiczenia 4 Syneza i analiza sanu polaryzacji świała meodą ogólnego prawa Malusa. Układ pomiarowy Układ pomiarowy składa się z polarymeru, zasilacza sabilizowanego ZS-52, wolomierza
Gr.A, Zad.1. Gr.A, Zad.2 U CC R C1 R C2. U wy T 1 T 2. U we T 3 T 4 U EE
 Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Kinematyka relatywistyczna
 Kinematyka relatywistyczna Fizyka I (B+C) Wykład VIII: Paradoks bliźniat Relatywistyczny efekt Dopplera Przypomnienie Transformacja Lorenza dla różnicy współrzędnych dwóch wybranych zdarzeń A i B: t x
Kinematyka relatywistyczna Fizyka I (B+C) Wykład VIII: Paradoks bliźniat Relatywistyczny efekt Dopplera Przypomnienie Transformacja Lorenza dla różnicy współrzędnych dwóch wybranych zdarzeń A i B: t x
Powstanie i rola Szczególnej Teorii Względności (STW)
 Powsanie i rola Szzególnej Teorii Względnośi (STW Co znał Einsein przed 905 rokiem? Równania Maxwella, Problem eeru (doświadzenie Mihelsona Morleya?, Aberaje świała, Wlezenia eeru Fresnela, Znał praę orenza
Powsanie i rola Szzególnej Teorii Względnośi (STW Co znał Einsein przed 905 rokiem? Równania Maxwella, Problem eeru (doświadzenie Mihelsona Morleya?, Aberaje świała, Wlezenia eeru Fresnela, Znał praę orenza
Przemysław Klęsk. Słowa kluczowe: analiza składowych głównych, rozmaitości algebraiczne
 Przemysław Klęsk O ALGORYTMIE PRINCIPAL MANIFOLDS OPARTYM NA PCA SŁUŻACYM DO ZNAJDOWANIA DZIEDZIN JAKO ROZMAITOŚCI ALGEBRAICZNYCH NA PODSTAWIE ZBIORU DANYCH, PROPOZYCJA MIAR JAKOŚCI ROZMAITOŚCI Sreszczenie
Przemysław Klęsk O ALGORYTMIE PRINCIPAL MANIFOLDS OPARTYM NA PCA SŁUŻACYM DO ZNAJDOWANIA DZIEDZIN JAKO ROZMAITOŚCI ALGEBRAICZNYCH NA PODSTAWIE ZBIORU DANYCH, PROPOZYCJA MIAR JAKOŚCI ROZMAITOŚCI Sreszczenie
Rozkład i Wymagania KLASA III
 Rozkład i Wymagania KLASA III 10. Prąd Lp. Tema lekcji Wymagania konieczne 87 Prąd w mealach. Napięcie elekryczne opisuje przepływ w przewodnikach, jako ruch elekronów swobodnych posługuje się inuicyjnie
Rozkład i Wymagania KLASA III 10. Prąd Lp. Tema lekcji Wymagania konieczne 87 Prąd w mealach. Napięcie elekryczne opisuje przepływ w przewodnikach, jako ruch elekronów swobodnych posługuje się inuicyjnie
Dendrochronologia Tworzenie chronologii
 Dendrochronologia Dendrochronologia jes nauką wykorzysującą słoje przyrosu rocznego drzew do określania wieku (daowania) obieków drewnianych (budynki, przedmioy). Analizy różnych paramerów słojów przyrosu
Dendrochronologia Dendrochronologia jes nauką wykorzysującą słoje przyrosu rocznego drzew do określania wieku (daowania) obieków drewnianych (budynki, przedmioy). Analizy różnych paramerów słojów przyrosu
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Fale mechaniczne i akustyczne
 Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczytaj koniecznie!
 Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczyaj koniecznie! Jeseś osobą prowadzącą pozarolniczą działalność, jeśli: prowadzisz pozarolniczą działalność gospodarczą na podsawie przepisów
Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczyaj koniecznie! Jeseś osobą prowadzącą pozarolniczą działalność, jeśli: prowadzisz pozarolniczą działalność gospodarczą na podsawie przepisów
Zarządzanie Projektami. Wykład 3 Techniki sieciowe (część 1)
 Zarządzanie Projekami Wykład 3 Techniki sieciowe (część ) Przedsięwzięcie wieloczynnościowe Przedsięwzięcie wieloczynnościowe skończona liczba wzajemnie ze sobą powiązanych czynności (eapów). Powiązania
Zarządzanie Projekami Wykład 3 Techniki sieciowe (część ) Przedsięwzięcie wieloczynnościowe Przedsięwzięcie wieloczynnościowe skończona liczba wzajemnie ze sobą powiązanych czynności (eapów). Powiązania
Postęp techniczny. Model lidera-naśladowcy. Dr hab. Joanna Siwińska-Gorzelak
 Posęp echniczny. Model lidera-naśladowcy Dr hab. Joanna Siwińska-Gorzelak Założenia Rozparujemy dwa kraje; kraj 1 jes bardziej zaawansowany echnologicznie (lider); kraj 2 jes mniej zaawansowany i nie worzy
Posęp echniczny. Model lidera-naśladowcy Dr hab. Joanna Siwińska-Gorzelak Założenia Rozparujemy dwa kraje; kraj 1 jes bardziej zaawansowany echnologicznie (lider); kraj 2 jes mniej zaawansowany i nie worzy
RUCH HARMONICZNY. sin. (r.j.o) sin
 RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
O prędkościach nadświetlnych
 FOTON 94, Jesień 006 17 O prędkośiah nadświetlnyh Leszek M. Sokołowski Obserwatorium Astronomizne UJ Poskarżył się pewien nauzyiel fizyki, że w szkolnym wykładzie szzególnej teorii względnośi (STW) obowiązuje
FOTON 94, Jesień 006 17 O prędkośiah nadświetlnyh Leszek M. Sokołowski Obserwatorium Astronomizne UJ Poskarżył się pewien nauzyiel fizyki, że w szkolnym wykładzie szzególnej teorii względnośi (STW) obowiązuje
Wyznaczanie zależności współczynnika załamania światła od długości fali światła
 Ćwiczenie O3 Wyznaczanie zależności współczynnika załamania światła od długości fali światła O3.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie zależności współczynnika załamania światła od długości fali
Ćwiczenie O3 Wyznaczanie zależności współczynnika załamania światła od długości fali światła O3.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie zależności współczynnika załamania światła od długości fali
4.2. Obliczanie przewodów grzejnych metodą dopuszczalnego obciążenia powierzchniowego
 4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
Z przedstawionych poniżej stwierdzeń dotyczących wartości pędów wybierz poprawne. Otocz kółkiem jedną z odpowiedzi (A, B, C, D lub E).
 Zadanie 1. (0 3) Podczas gry w badmintona zawodniczka uderzyła lotkę na wysokości 2 m, nadając jej poziomą prędkość o wartości 5. Lotka upadła w pewnej odległości od zawodniczki. Jest to odległość o jedną
Zadanie 1. (0 3) Podczas gry w badmintona zawodniczka uderzyła lotkę na wysokości 2 m, nadając jej poziomą prędkość o wartości 5. Lotka upadła w pewnej odległości od zawodniczki. Jest to odległość o jedną
Ćwiczenie: "Zagadnienia optyki"
 Ćwiczenie: "Zagadnienia optyki" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia: 1.
Ćwiczenie: "Zagadnienia optyki" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia: 1.
TRANFORMACJA GALILEUSZA I LORENTZA
 TRANFORMACJA GALILEUSZA I LORENTZA Wykład 4 2012/2013, zima 1 Założenia mechaniki klasycznej 1. Przestrzeń jest euklidesowa 2. Przestrzeń jest izotropowa 3. Prawa ruchu Newtona są słuszne w układzie inercjalnym
TRANFORMACJA GALILEUSZA I LORENTZA Wykład 4 2012/2013, zima 1 Założenia mechaniki klasycznej 1. Przestrzeń jest euklidesowa 2. Przestrzeń jest izotropowa 3. Prawa ruchu Newtona są słuszne w układzie inercjalnym
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
WYKORZYSTANIE TESTU OSTERBERGA DO STATYCZNYCH OBCIĄŻEŃ PRÓBNYCH PALI
 Prof. dr hab.inż. Zygmun MEYER Poliechnika zczecińska, Kaedra Geoechniki Dr inż. Mariusz KOWALÓW, adres e-mail m.kowalow@gco-consul.com Geoechnical Consuling Office zczecin WYKORZYAIE EU OERERGA DO AYCZYCH
Prof. dr hab.inż. Zygmun MEYER Poliechnika zczecińska, Kaedra Geoechniki Dr inż. Mariusz KOWALÓW, adres e-mail m.kowalow@gco-consul.com Geoechnical Consuling Office zczecin WYKORZYAIE EU OERERGA DO AYCZYCH
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
 Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
ĆWICZENIE 2. BADANIE WAHADEŁ SPRZĘŻONYCH.
 ĆWICZENIE BADANIE WAHADEŁ SPRZĘŻONYCH Wahadło sprzężone Weźmy pod uwagę układ złożony z dwóch wahadeł o długościach połączonych sprężyną o współczynniku kierującym k Rys Na wahadło działa siła będąca składową
ĆWICZENIE BADANIE WAHADEŁ SPRZĘŻONYCH Wahadło sprzężone Weźmy pod uwagę układ złożony z dwóch wahadeł o długościach połączonych sprężyną o współczynniku kierującym k Rys Na wahadło działa siła będąca składową
Silniki cieplne i rekurencje
 6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
ZARZĄDZANIE KOSZTAMI UTRZYMANIA GOTÓWKI W ODDZIAŁACH BANKU KOMERCYJNEGO
 ZARZĄDZANIE KOSZTAMI UTRZYMANIA GOTÓWKI W ODDZIAŁACH BANKU KOMERCYJNEGO Sreszczenie Michał Barnicki Poliechnika Śląska, Wydział Oranizacji i Zarządzania Monika Odlanicka-Poczobu Poliechnika Śląska, Wydział
ZARZĄDZANIE KOSZTAMI UTRZYMANIA GOTÓWKI W ODDZIAŁACH BANKU KOMERCYJNEGO Sreszczenie Michał Barnicki Poliechnika Śląska, Wydział Oranizacji i Zarządzania Monika Odlanicka-Poczobu Poliechnika Śląska, Wydział
Krzywe stożkowe. 1 Powinowactwo prostokątne. 2 Elipsa. Niech l będzie ustaloną prostą i k ustaloną liczbą dodatnią.
 Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Wykład 3 POLITYKA PIENIĘŻNA POLITYKA FISKALNA
 Makroekonomia II Wykład 3 POLITKA PIENIĘŻNA POLITKA FISKALNA PLAN POLITKA PIENIĘŻNA. Podaż pieniądza. Sysem rezerwy ułamkowej i podaż pieniądza.2 Insrumeny poliyki pieniężnej 2. Popy na pieniądz 3. Prowadzenie
Makroekonomia II Wykład 3 POLITKA PIENIĘŻNA POLITKA FISKALNA PLAN POLITKA PIENIĘŻNA. Podaż pieniądza. Sysem rezerwy ułamkowej i podaż pieniądza.2 Insrumeny poliyki pieniężnej 2. Popy na pieniądz 3. Prowadzenie
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
 Ł Ź Ź Ł Ź Ę Ś Ę Ę Ś Ą Ę Ś Ą Ć Ć ć Ę Ą Ł Ś ć ń ć Ł ć Ź ć Ę Ą Ą Ź ź ź ć ć ć ć ć ń ń ć ć ń Ó ź Ę Ą ć ć ć Ź ć Ź ć ć ń ń ć ń Ó ć Ą ń ć Ę Ą Ą ń ń ń ń ć ń ć ć Ź ć ń Ź ń ń Ć ń ń ń Ę Ą Ś Ą ń ć ń ć ź ń Ę Ś Ą Ąć
Ł Ź Ź Ł Ź Ę Ś Ę Ę Ś Ą Ę Ś Ą Ć Ć ć Ę Ą Ł Ś ć ń ć Ł ć Ź ć Ę Ą Ą Ź ź ź ć ć ć ć ć ń ń ć ć ń Ó ź Ę Ą ć ć ć Ź ć Ź ć ć ń ń ć ń Ó ć Ą ń ć Ę Ą Ą ń ń ń ń ć ń ć ć Ź ć ń Ź ń ń Ć ń ń ń Ę Ą Ś Ą ń ć ń ć ź ń Ę Ś Ą Ąć
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Pojęcia podstawowe Punkt materialny Ciało, którego rozmiary można w danym zagadnieniu zaniedbać. Zazwyczaj przyjmujemy, że punkt materialny powinien być dostatecznie mały. Nie jest
Kinematyka: opis ruchu Pojęcia podstawowe Punkt materialny Ciało, którego rozmiary można w danym zagadnieniu zaniedbać. Zazwyczaj przyjmujemy, że punkt materialny powinien być dostatecznie mały. Nie jest
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 5 Temat: Interferometr Michelsona 7.. Cel i zakres ćwiczenia 7 INTERFEROMETR MICHELSONA Celem ćwiczenia jest zapoznanie się z budową i
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 5 Temat: Interferometr Michelsona 7.. Cel i zakres ćwiczenia 7 INTERFEROMETR MICHELSONA Celem ćwiczenia jest zapoznanie się z budową i
Wymagania na poszczególne oceny przy realizacji programu i podręcznika Zrozumieć fizykę
 Klasa III 10. Prąd elekryczny Tema według 10.1. Prąd elekryczny w mealach. Napięcie elekryczne 10.. Źródła prądu. Obwód elekryczny Wymagania na poszczególne oceny przy realizacji i podręcznika Zrozumieć
Klasa III 10. Prąd elekryczny Tema według 10.1. Prąd elekryczny w mealach. Napięcie elekryczne 10.. Źródła prądu. Obwód elekryczny Wymagania na poszczególne oceny przy realizacji i podręcznika Zrozumieć
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak E i E E i r r 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa Oczekiwania Reguła poliyki monearnej
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak E i E E i r r 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa Oczekiwania Reguła poliyki monearnej
Optyka stanowi dział fizyki, który zajmuje się światłem (także promieniowaniem niewidzialnym dla ludzkiego oka).
 Optyka geometryczna Optyka stanowi dział fizyki, który zajmuje się światłem (także promieniowaniem niewidzialnym dla ludzkiego oka). Założeniem optyki geometrycznej jest, że światło rozchodzi się jako
Optyka geometryczna Optyka stanowi dział fizyki, który zajmuje się światłem (także promieniowaniem niewidzialnym dla ludzkiego oka). Założeniem optyki geometrycznej jest, że światło rozchodzi się jako
WPŁYW PODATNOŚCI GŁÓWKI SZYNY NA ROZKŁAD PRZEMIESZCZEŃ WZDŁUŻNYCH PRZY HAMOWANIU POCIĄGU 1
 A R C H I W U M I N S T Y T U T U I N Ż Y N I E R I I L Ą D O W E J Nr 5 ARCHIVES OF INSTITUTE OF CIVIL ENGINEERING 017 WPŁYW PODATNOŚCI GŁÓWKI SZYNY NA ROZKŁAD PRZEMIESZCZEŃ WZDŁUŻNYCH PRZY HAMOWANIU
A R C H I W U M I N S T Y T U T U I N Ż Y N I E R I I L Ą D O W E J Nr 5 ARCHIVES OF INSTITUTE OF CIVIL ENGINEERING 017 WPŁYW PODATNOŚCI GŁÓWKI SZYNY NA ROZKŁAD PRZEMIESZCZEŃ WZDŁUŻNYCH PRZY HAMOWANIU
Przekaźniki czasowe ATI opóźnienie załączania Czas Napięcie sterowania Styki Numer katalogowy
 W celu realizowania prosych układów opóźniających można wykorzysać przekaźniki czasowe dedykowane do poszczególnych aplikacji. Kompakowa obudowa - moduł 22,5 mm, monaż na szynie DIN, sygnalizacja sanu
W celu realizowania prosych układów opóźniających można wykorzysać przekaźniki czasowe dedykowane do poszczególnych aplikacji. Kompakowa obudowa - moduł 22,5 mm, monaż na szynie DIN, sygnalizacja sanu
Zostałeś delegowany do pracy za granicą w UE, EOG lub Szwajcarii? Sprawdź, gdzie jesteś ubezpieczony
 Zosałeś delegowany do pracy za granicą w UE, EOG lub Szwajcarii? Sprawdź, gdzie jeseś ubezpieczony Każde z pańsw członkowskich Unii Europejskiej (UE), Europejskiego Obszaru Gospodarczego (EOG) oraz Szwajcaria
Zosałeś delegowany do pracy za granicą w UE, EOG lub Szwajcarii? Sprawdź, gdzie jeseś ubezpieczony Każde z pańsw członkowskich Unii Europejskiej (UE), Europejskiego Obszaru Gospodarczego (EOG) oraz Szwajcaria
Tabela doboru przekaźników czasowych MTR17
 M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
00013 Mechanika nieba A
 1 00013 Mechanika nieba A Dane osobowe właściciela arkusza 00013 Mechanika nieba A Czas pracy 90/150 minut Instrukcja dla zdającego 1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 10 stron. Ewentualny
1 00013 Mechanika nieba A Dane osobowe właściciela arkusza 00013 Mechanika nieba A Czas pracy 90/150 minut Instrukcja dla zdającego 1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 10 stron. Ewentualny
Zasady względności w fizyce
 Zasady względności w fizyce Mechanika nierelatywistyczna: Transformacja Galileusza: Siły: Zasada względności Galileusza: Równania mechaniki Newtona, określające zmianę stanu ruchu układów mechanicznych,
Zasady względności w fizyce Mechanika nierelatywistyczna: Transformacja Galileusza: Siły: Zasada względności Galileusza: Równania mechaniki Newtona, określające zmianę stanu ruchu układów mechanicznych,
W tym module rozpoczniemy poznawanie właściwości fal powstających w ośrodkach sprężystych (takich jak fale dźwiękowe),
 Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
Prawa optyki geometrycznej
 Optyka Podstawowe pojęcia Światłem nazywamy fale elektromagnetyczne, o długościach, na które reaguje oko ludzkie, tzn. 380-780 nm. O falowych własnościach światła świadczą takie zjawiska, jak ugięcie (dyfrakcja)
Optyka Podstawowe pojęcia Światłem nazywamy fale elektromagnetyczne, o długościach, na które reaguje oko ludzkie, tzn. 380-780 nm. O falowych własnościach światła świadczą takie zjawiska, jak ugięcie (dyfrakcja)
ELEMENTY SZCZEGÓLNEJ TEORII WZGLĘDNOŚCI. I. Zasada względności: Wszystkie prawa przyrody są takie same we wszystkich
 ELEMENTY SZCZEGÓLNEJ TEORII WZGLĘDNOŚCI Postulaty Einsteina (95 r) I Zasada względnośi: Wszystkie prawa przyrody są takie same we wszystkih inerjalnyh układah odniesienia lub : Równania wyrażająe prawa
ELEMENTY SZCZEGÓLNEJ TEORII WZGLĘDNOŚCI Postulaty Einsteina (95 r) I Zasada względnośi: Wszystkie prawa przyrody są takie same we wszystkih inerjalnyh układah odniesienia lub : Równania wyrażająe prawa
