Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study Bogumił Miller
|
|
|
- Ryszard Karpiński
- 8 lat temu
- Przeglądów:
Transkrypt
1 INSTYTUT MATEMATYKI UNIWERSYTET HUMANISTYCZNO-PRZYRODNICZY Jana Kochanowskiego w Kielcach ul. Świętokrzyska Kielce tel fax imat@ujk.kielce.pl Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study Bogumił Miller tel.: bogumilmiller@interia.eu O p r a c o w a n i e f i n a n s o w a n e z e ś r o d k ó w p r o j e k t u s y s t e m o w e g o Z a m a w i a n i e k s z t a ł c e n i a n a k i e r u n k a c h t e c h n i c z n y c h, m a t e m a t y c z n y c h i p r z y r o d n i c z y c h p i l o t a ż r e a l i z o w a n e g o w r a m a c h P o d d z i a ł a n i a Z w i ę k s z e n i e l i c z b y a b s o l w e n t ó w k i e r u n k ó w o k l u c z o w y m z n a c z e n i u d l a g o s p o d a r k i o p a r t e j n a w i e d z y Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 0
2 Wstęp Przedsiębiorstwo, tuż po określeniu prognoz popytu rynkowego na wytwarzane produkty, gotowe jest do realizacji planu produkcji. Jego stworzenie z długodystansowym wyprzedzeniem jest bardzo istotne z punktu widzenia minimalizacji strat oraz optymalizacji działalności. Jak dowodzi praktyka, produkcja oparta o planowanie krótkoterminowe rzadko kiedy pozwala na generowanie zysków natomiast w długim okresie potrafi nawet przynosić straty. Analogicznie produkcja w chaosie doprowadza do natychmiastowej utraty odbiorców i strat o znaczeniu strategicznym. ProPack jest przedsiębiorstwem działającym na rynku z dość dużym już stażem. Posiada wyrobione struktury zarządzania oraz sposoby działalności formowane przez lata. Długoterminowe umowy ze stałymi odbiorcami przez długi okres pozwalały na swobodne funkcjonowanie firmy na granicy zyskowności czy to w okresie niedoboru czerpiąc z ogromnego kapitału zgromadzonego w okresie wcześniejszym. W momencie jednak podpisania w 2009 roku umowy z przedstawicielem franczyzowej sieci pizzerii konieczne były silne zmiany. Wymogi stawiane firmie zaczęły przerastać możliwości systemu zarządzania czy to produkcją czy też strukturami logistycznymi. Czynnikami nowymi były: korzystanie z outsourcingu zamówienia składane z dnia na dzień konieczność stworzenia magazynów buforowych założenie dynamicznej płynności dostaw surowców oraz odbioru produktu ogromna sieć odbiorców rozłożona na sześciodniowy tydzień pracy Spośród wielu produktów, do outsourcingu przeznaczono opakowania na pizzę. Jego koszt z racji dużych zamówień oraz prostego projektu był znacznie niższy. Jednym z warunków obniżenia kosztu jednostkowego było odgórne określenie wielkości produkcji na dany miesiąc w umowie rocznej co zostało zadeklarowane po uprzednim przeprowadzeniu prognozy. Spodziewany popyt wygląda następująco: Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 1
3 maj-10 cze-10 lip-10 sie-10 wrz-10 paź-10 lis-10 gru-10 sty-11 lut-11 mar-11 kwi-11 Tabela 5. Prognozy wykonane Okres maj-10 cze-10 lip-10 sie-10 wrz-10 paź-10 lis-10 gru-10 sty-11 lut-11 mar-11 kwi-11 Metoda średniej ruchomej (k=3) 83,77 79,92 81,46 81,72 81,03 81,40 81,39 81,27 81,36 81,34 81,32 81,35 Metoda średniej ruchomej ważonej 78,17 75,67 78,05 76,35 77,35 77,04 77,50 77,20 76,39 80,10 77,77 78,50 Metoda Holta 79,28 79,28 79,28 79,28 79,28 79,28 79,28 79,28 79,28 79,28 79,28 79,28 Metoda ARMA 83,00 85,67 73,81 87,12 79,79 85,03 85,52 80,05 84,21 81,09 84,70 85,79 Metoda Browna 85,15 80,30 82,69 81,51 82,09 81,81 81,95 81,88 81,91 81,89 81,90 81,90 AMALGAMAT 81,86 79,87 79,49 80,86 79,98 80,69 80,87 80,00 80,46 80,72 80,79 81,09 Źródło: Opracowanie własne Wykres 2. Zestawienie prognoz a realizacja 88,00 86,00 84,00 82,00 80,00 78,00 76,00 74,00 72,00 Metoda średniej ruchomej (k=3) Metoda średniej ruchomej ważonej Metoda Holta Metoda ARMA Metoda Browna AMALGAMAT REALIZACJA Źródło: Opracowanie własne Konieczne było stworzenie systemu wspierającego zarządzanie, w pełni automatycznego i zdolnego do podejmowania natychmiastowych decyzji z określeniem prawdopodobnych wyników działań. Każde potężne narzędzie (Navision, Subiect czy aktualnie działająca Symfonia) okazywały się zbyt mało elastyczne a przez to niemożliwe do dostosowania do specyficznego profilu działalności firmy. Dział handlowy jednak podobnie jak dział księgowości posiadały już w pełni skonfigurowane i dostosowane moduły Symfonii z których rezygnacja byłaby niewygodna i kosztowna. Wymogiem więc stało się stworzenie systemu dedykowanego na tyle jednak elastycznego aby była możliwość ciągłej i prostej jego modyfikacji jak również doprowadzenie do zgodności z już istniejącą instalacją Symfonii. Dodatkowymi czynnikami była cena stworzenia programu, koszty dostosowywania do bieżących zmian, koszt implementacji dla pracowników (szkolenia) oraz koszty odnawiania licencji. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 2
4 Decyzje te były podejmowane równolegle z modyfikacją struktury zatrudnienia. Przeprowadzono wewnętrzny egzamin kompetencyjny z wykorzystaniem centrum certyfikacji jako obiektywnej jednostki sprawdzającej. Okazało się, iż zatrudnienie powinno wzrosnąć o 20% z racji wzrostu ilości dokumentacji oraz liczby założeń kompetencyjnych. Zmiany w zatrudnieniu, zgodnie z wynikami testu, powinny były sięgnąć około 30% kadry zarządzającej (kadra produkcyjna nie brała udziału w testach z racji braku zmian w technologii produkcji). Mnogość decyzji została jednak zakwestionowana przez zarząd wprowadzono więc ich kolejkowanie. Etapy zmian plasowały się następująco: 1. zmiany w systemie zatrudnienia 2. wykonanie projektu zmian 3. modyfikacja zarządzania produkcją 4. modyfikacja systemu logistycznego Pierwszy etap zakładał stworzenie grupy pracowników o małej rotacji w przyszłości jednak o dość dużych predyspozycjach do wprowadzania innowacyjności. Podpisano umowę z lokalnym uniwersytetem (wydział informatyki oraz ekonomii) oraz politechniką (wydział zarządzania i inżynierii produkcji) o zorganizowaniu systemu praktyk połączonego z grą o staż. Każdy student miał za zadanie wykonanie projektu oraz zaproponowanie innowacji zgodnej z jego profilem oraz zainteresowaniami. Aby do gry przystąpili wyłącznie najlepsi przeprowadzono podobny egzamin jak ten, dla wewnętrznych pracowników. Okres dostosowania trwał 5 miesięcy. Wybrana została nowa kadra o strukturze 50% doświadczonych pracowników oraz 50% nowych. System wewnętrznych szkoleń przeprowadzonych z nowymi pracownikami pozwolił na stworzenie umów o staż i pracę w systemie lojalnościowym co zapewniło firmie zwrot z inwestycji w nową kadrę. Ponieważ Symfonia, która powinna pozostać jako program księgowy i handlowy w firmie, wspierał oprogramowanie VBA jak również opierał się na bazie danych SQL podjęto decyzję o rozwoju oprogramowania w oparciu o ten właśnie język oraz zakupiony już pakiet MS Excel minimalizując dzięki temu koszty zakupu nowych i drogich systemów. Baza danych wymagała minimalnych zmian natomiast pakiet MS Office już był zainstalowany i obeznany każdemu pracownikowi. Rozszerzenie było jedynie funkcjonalną nakładką spełniającą funkcje programów dedykowanych. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 3
5 Kolejnym etapem było stworzenie projektu zmian. Wymagał tego rozmach modyfikacji oraz brak możliwości jakichkolwiek przesunięć w czasie. Podjęto decyzję o zastosowaniu systemu zarządzania projektami PERT / CPM oparty na teorii grafów. Powodem takiej decyzji była prostota algorytmu tej metody oraz szybkość projektowania w przeciwieństwie do powszechnie stosowanej metody CPM / SPM doskonałej przy dużej powtarzalności silnie rozbudowanych i zróżnicowanych projektów. Ponadto, zmiany pozbawione były jakichkolwiek kosztów wybrany projekt opracowali zatrudnieni informatycy w czasie godzin pracy prawa autorskie automatycznie przeszły na własność firmy. Kolejne etapy postępowania można przedstawić następująco: a. oszacowanie listy czynności subiektywne b. określenie czasów trwania czynności (min, max, prob) subiektywne c. określenie czasów trwania projektu, wariancji i odchylenia standardowego (1) gdzie: a czas najkrótszy czynności m czas najbardziej prawdopodobny czynności b czas najdłuższy czynności (2) gdzie: a czas najkrótszy czynności b czas najdłuższy czynności gdzie: wariancja czasu czynności (3) Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 4
6 d. określenie prawdopodobieństw realizacji (4) gdzie: t oczekiwany czas realizacji projektu czas realizacji projektu dla ścieżki krytycznej Pierwszym krokiem było wygenerowanie listy czynności której układ wyglądał następująco: Tabela 1. Lista czynności modelu PERT Czynność Poprzedzana przez określenie potrzeb działu zarządzania produkcją oraz logistyki - propozycje różnych systemów informatycznych - wybór odpowiedniego systemu wykonanie systemu modyfikacje i parametryzacja strefy zarządzania produkcją modyfikacje i parametryzacja strefy zarządzania magazynem modyfikacje i parametryzacja strefy zarządzania transportem implementacja na stacjach klienckich implementacja serwera bazy danych oraz backupu system szkoleń pracowniczych testowanie poprawności działania systemu Źródło: Opracowanie własne na podstawie Trzaskalik T. Wprowadzenie do badań operacyjnych z komputerem A B C C E C D F G Określenie czasu realizacji czynności z racji braku doświadczenia zostało opracowane przy współudziale nowo zatrudnionych informatyków oraz kadry pomocniczej. Każda czynność została określona jako czas minimalny, maksymalny oraz najbardziej prawdopodobny do jej wykonania (w tygodniach). Plan reprezentuje poniższa tabela. Tabela 2. Czas trwania poszczególnych zadań Czynność optymistyczny Czas trwania (w tygodniach) D F H I J prawdopodobny pesymistyczny A. określenie potrzeb działu zarządzania produkcją oraz logistyki B. propozycje różnych systemów informatycznych C. wybór odpowiedniego systemu Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 5
7 D. wykonanie systemu E. modyfikacje i parametryzacja strefy zarządzania produkcją F. modyfikacje i parametryzacja strefy zarządzania magazynem G. modyfikacje i parametryzacja strefy zarządzania transportem H. implementacja na stacjach klienckich I. implementacja serwera bazy danych oraz backupu J. system szkoleń pracowniczych K. testowanie poprawności działania systemu Źródło: Opracowanie własne na podstawie Trzaskalik T. Wprowadzenie do badań operacyjnych z komputerem Graficznie optymalizacja wykonania projektu prezentuje się następująco: Rysunek 1. Graf metody ścieżki krytycznej 1 A P 1 2 D F I P 2 \\\ 9 J K B C 3 4 E G H 7 8 Źródło: Opracowanie własne \\ Ścieżka krytyczna opisuje najkrótszy czas realizacji projektu (pogrubienia na powyższym grafie). Wykres 1. Czas realizacji a prawdopodobieństwo Źródło: Opracowanie własne Czas realizacji Prawdopodobieństwo % 16 80% 14 60% 12 40% 10 20% 0% Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 6
8 Jak można zauważyć, krytycznymi zadaniami są: propozycje różnych systemów informatycznych wybór odpowiedniego systemu modyfikacje i parametryzacja strefy zarządzania transportem implementacja na stacjach klienckich system szkoleń pracowniczych testowanie poprawności działania systemu Projekt z prawdopodobieństwem 90% będzie przeprowadzony w ciągu 11,8 tygodni. Wykres 1 przedstawia (na pod wykresie prawdopodobieństwo) żółtym kolorem przebieg czasu realizacji projektu z zadanym prawdopodobieństwem. Linie pomocnicze (kolor niebieski) oznaczają możliwe odchylenia od wskazanego czasu rozumiane jako odchylenie standardowe od wartości średniej. Z prawdopodobieństwem 90%, projekt nie zostanie ukończony w czasie krótszym niż 12,7 tygodnia. Wyniki analizy okazały się dla firmy doskonałą wiadomością, gdyż początek projektu założono na drugi miesiąc zmian kadrowych podczas którego podjęto decyzję o przyjęciu bądź odrzuceniu poszczególnych studentów zainteresowanych pracą. Dwunasto tygodniowy okres realizacji pozwoli zakończyć projekt w momencie końca punktu założonego przez zarząd jako deadline zmian. Zestawienie obliczeń przedstawia poniższa tabela. Tabela 3. Metoda PERT Czynność Zdarzenie początkowe Zdarzenie końcowe a m b t 0 sig^2 A ,833 0,028 B ,167 0,250 C ,333 0,111 D ,167 0,250 E ,167 0,250 F ,000 0,444 G ,167 0,028 H ,167 0,028 I ,167 0,250 J ,167 0,028 K ,833 0,028 Czynność czas ES EF LS LF rezerwa trwania A B C D E F G H Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 7
9 I J K Czynność czy krytyczna t 0 na ścieżce krytycznej sig^2 na ścieżce krytycznej poprzedzane przez A 0,000 0,000 - B tak 2,167 0,250 - C tak 1,333 0,111 A B D 0,000 0,000 C E 0,000 0,000 C F 0,000 0,000 E G tak 2,167 0,028 C H tak 1,167 0,028 D F G I 0,000 0,000 D F J tak 2,167 0,028 H K tak 2,833 0,028 I J Czas oczekiwany realizacji projektu: 11,833 Wariancja realizacji projektu: 0,472 Odchylenie standardowe: 0,687 Czas realizacji z zadanym prawdopodobieństwem: Prawdopodobieństwo zadane: 10% 20% 30% 40% Czas realizacji: 10,953 11,255 11,473 11,659 Prawdopodobieństwo zadane: 50% 60% 70% 80% Czas realizacji: 11,833 12,007 12,194 12,412 Prawdopodobieństwo zadane: 90% 100% Czas realizacji: 12,714 17,441 Prawdopodobieństwo realizacji w zadanym czasie: Czas zadany: Prawdopodobieństwo: 0,00% 0,00% 0,38% 11,26% Czas zadany: Prawdopodobieństwo: 59,58% 95,52% 99,92% 100,00% Czas zadany: Prawdopodobieństwo: 100,00% 100,00% Źródło: Opracowanie własne Tak dokładny plan projektu dał szansę na optymalizację czasowo kosztową i pozwolił na wprowadzenie projektu w zamierzonym terminie 12,5 tygodnia. Poszczególne zmiany dotyczyły systemu podejmowania decyzji zwanego potocznie business inteligence. System ten pozwolił na implikację wiedzy eksperckiej do systemu automatycznej reakcji na zachodzące czynniki a przez to możliwość podejmowania natychmiastowych i skutecznych decyzji. Implementowane w systemie zmiany również miały podstawy pochodzące bezpośrednio z teorii optymalizacji. System magazynowy dla magazynów produktu gotowego miał początkowo zostać stworzony w oparciu Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 8
10 o optymalizację dynamiczną. Metoda ta jednak okazała się zbyt mało elastyczna i jednocześnie zbyt skomplikowana do ciągłej modyfikacji. Zdecydowano ostatecznie o stworzeniu magazynów buforowych obsługiwanych metodą LIFO (straty z długiego okresu magazynowania okazały się niższe od tych generowanych przez ciągłe przemieszczanie produktu gotowego) mających na celu obsługę odchyleń wartości zrealizowanej od prognozowanej (zapisanej w umowie outsourcingu). Magazyn buforowy powinien być systematycznie zapełniony a ewentualne zapotrzebowanie ponad zakup zewnętrzny powinno być obsługiwane właśnie z buforów. System produkcji uzupełniający wspomniany magazyn powinien być zorganizowany metodą Just-In-Time. Magazyny surowca również nie zostały objęte metodami probabilistycznymi a jedynie deterministyczną metodą mieszaną EOQ oraz ABC/XYZ. Z zastosowania czystej metody EOQ zrezygnowano ponieważ odbiór zamówionego produktu nie występuje w relatywnie krótkim czasie od zamówionego surowca natomiast koszt operacyjny jednostkowego zamówienia nie koniecznie jest stały. Metodą badania statystycznego, uwzględniając również wiele czynników zewnętrznych, ustalony został minimalny poziom zapasów zwany sygnalnym. W momencie uzyskania założonego poziomu zapasów model generuje sygnał wystawienia zamówienia w celu uzupełnienia magazynu o daną wielkość. Ilość każdorazowego zamówienia jest uwarunkowana czynnikami popytowymi. Dla metody EOQ priorytetem jest generowanie takich zamówień, które pozwolą realizować najniższe koszty. Plusami użycia metody ABC / XYZ jest podział surowca na grupy zapotrzebowania oraz silny bezpośredni nadzór nad stanami faktycznymi oraz fluktuacjami. W systemie zaimplementowana została metoda rozumiana pod postacią następujących zależności: (5) gdzie: k s koszty stałe D oczekiwany popyt k m koszty zmienne Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 9
11 (6) gdzie: k s koszty stałe D oczekiwany popyt k m koszty zmienne Zapas w celu minimalizacji kosztu magazynu zdefiniowany jest loco magazyn dostawcy. Metodyka optymalizacji zapasu surowców opracowana za pomocą powyższego systemu na okres prognozy maj 2010 kwiecień 2011 przedstawia się następująco: Tabela 4. Optymalizacja stanów magazynowych Numer dobra (typ tektury; liczba 10-maj 10-cze 10-lip 10-sie 10-wrz 10-paź warstw; grubość; ile barwionych stron) tektura falista 3wE2k tektura falista 3wB1k tektura falista 3wB1k tektura falista 3wB2k tektura falista 3wC1k tektura falista 5wBC1k tektura falista 5wBE2k tektura falista 5wCE1k tektura falista 5wCE2k tektura lita 800-2k Numer dobra (typ tektury; liczba warstw; grubość; ile barwionych stron) 10-lis 10-gru 11-sty 11-lut 11-mar 11-kwi tektura falista 3wE2k tektura falista 3wB1k tektura falista 3wB1k tektura falista 3wB2k tektura falista 3wC1k tektura falista 5wBC1k tektura falista 5wBE2k tektura falista 5wCE1k tektura falista 5wCE2k tektura lita 800-2k Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 10
12 Numer dobra (typ tektury; liczba warstw; grubość; ile barwionych stron) Popyt Koszt Wartość zużycia (popyt x koszt) Wartość (%) - narastająco ABC Zmienność popytu (szt.) XYZ tektura falista 3wE2k 765 2, ,1 0,43% C 0,99% X tektura falista 3wB1k , ,7 1,43% C 1,46% X tektura falista 3wB1k , ,82% A 2,06% X tektura falista 3wB2k , ,3 42,30% B 2,21% X tektura falista 3wC1k 450 4, ,72% C 1,41% Y tektura falista 5wBC1k 590 2, ,09% C 4,72% Y tektura falista 5wBE2k , ,3 44,32% C 6,48% Y tektura falista 5wCE1k , ,76% A 0,18% Y tektura falista 5wCE2k , ,47% C 1,72% Z tektura lita 800-2k , ,00% A 7,32% Z ,4 Numer dobra (typ tektury; liczba warstw; grubość; ile barwionych stron) Zapas sygnalny Optymalna wielkość zamówienia Czas utrzymania zapasu (dni) Koszty całkowite tektura falista 3wE2k ,0 tektura falista 3wB1k ,8 tektura falista 3wB1k ,3 tektura falista 3wB2k ,9 tektura falista 3wC1k ,7 tektura falista 5wBC1k ,0 tektura falista 5wBE2k ,1 tektura falista 5wCE1k ,0 tektura falista 5wCE2k ,5 tektura lita 800-2k ,8 Rodzaj kosztu Wartość Jednostka kosztu Koszt organizacji zamówień 500 PLN Koszt utrzymania 0,05 PLN / szt. powierzchni magazynowej Koszt kapitału 10% % Koszt ubytków 4% % Koszt ubezpieczenia 5% % Cykl planowania 300 dni Opóźnienia w transporcie 7 dni Założenia dostawy "loco magazyn dostawcy" Źródło: Opracowanie własne 34116,1 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 11
13 W celu optymalizacji transportu postanowiono wykorzystać jeden z sukcesywnie rozwijanych algorytmów algorytm komiwojażera a dokładnie symetryczną jego postać (STSP). Symetria polegać ma na tym, iż droga pomiędzy dwoma punktami i powrotna jest dokładnie taka sama. W teorii stanowi ono zagadnienie z teorii grafów, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym. Cykl Hamiltona to taki cykl w grafie, gdzie każdy wierzchołek grafu przemierzany jest jednokrotnie (z wyłączeniem wierzchołka startowego). Celem staje się znalezienie cyklu o minimalnej sumie wag krawędzi. Reasumując rozważania teoretyczne, optymalizacyjny problem komiwajażera jest problemem NP - trudnym co ogólnie można rozumieć jako problem dla którego występuje problem NP - zupełny i jest do niego redukowalny wielomianową transformacją Turinga. Algorytm komiwojażera został rozwiązany metodą algorytmu mieszanego (będącego częściową implementacją rozwiązań algorytmu Little a). Część kodu źródłowego odpowiedzialnego za działanie algorytmu przedstawione jest w załączniku A Algortym STSP. Profil działalności przedsiębiorstwa niejednokrotnie dotyczy umów chwilowych oraz zamówień jednorazowych. Znacznie utrudnia to zarządzanie systemem produkcji oraz zmusza decydentów do tworzenia indywidualnych kalkulacji. W trakcie implementacji systemu przedsiębiorstwo stanęło do przetargu dotyczącego produkcji bardzo dużej liczby pudełek dla jednej z największych na polskim rynku firm produkującej artykuły gospodarstwa domowego. Przetarg dotyczył 5 serii produkcyjnych a miał wybrać tego realizatora, który zadeklaruje najniższy koszt przy zachowaniu zobowiązania do likwidacji szkód spowodowanych wybrakowanymi opakowaniami oraz do uznawania reklamacji na produkty. Decyzja była o tyle trudna, iż opakowania były różnego kształtu i wagi a tektura charakteryzuje się silnym zróżnicowaniem dotyczącym wytrzymałości w zależności od użytego jej typu i przeznaczenia. Obliczenia cząstkowe zostały wykonane przez dział technologiczny a w celu określenie struktury produkcji został wykorzystany prototypowy system podejmowania decyzji w oparciu o drzewo probabilistyczne. Metoda ta na etapie projektowania systemu zdystansowała inne metody podejmowania decyzji w warunkach niepewności (jak kryterium Hurwicza czy Savage a) swoją prostotą, przejrzystością oraz możliwością użycia gotowej w pełni konfigurowalnej wersji zawartej w Wszystkie wartości dotyczyły tys. PLN. Poniższe drzewo decyzyjne zostało tworzone jako iloczyn prawdopodobieństw zajścia określonych zdarzeń przy zastosowaniu odpowiedniego rodzaju tektury generując realne koszty wykonania produkcji zgodnie z założeniami przetargu. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 12
14 Rysunek 2. Precision Tree Źródło: Opracowanie własne Łatwo zauważyć, iż proponowana struktura surowcowa do kalkulacji przetargowej to 100% trójwarstwowej tektury falistej jednostronnie barwionej (B). Warto nadmienić, iż z tak zaproponowanym kosztem, przetarg został przez firmę wygrany a kolejny uczestnik zaproponował cenę niższą o jedynie 3,7%. Wygraną w przetargu uratowała więc dokładność obliczeń i umiejętność balansowania na krawędzi zyskowności z umiejętnym aparatem probabilistycznym. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 13
15 Zastosowano następujące wzory dotyczące budowy struktury zależności gałęzi: wartość przypadku: (7) wartość gałęzi: (8) wartość drzewa: (9) gdzie: p prawdopodobieństwo zajścia zdarzenia v wartość kosztu lub zysku przypadku opt(ev j ) optymalna (min lub max) z wartości decyzyjnych Wygrana w przetargu wymagała jednak wyboru najlepszego z dostawców tektury. Ponieważ rynek papieru jest dość mocno hermetyczny a proponujące surowiec firmy charakteryzują zasady daleko odbiegające od typowo rynkowych wybór jest wyjątkowo trudny i złożony. W systemie wykonanym w celu optymalizacji produkcji stworzono moduł wyboru wielokryterialnego opartego o metodę AHP z wagowaniem systemem DEMATEL który znajdzie właśnie w tym przypadku szczególnie istotne zastosowanie. Działanie w metodzie AHP można przedstawić w trzech krokach: I. Budowa macierzy porównań parami II. Wyznaczanie rankingów indywidualnych III. Wyznaczenie rankingu wielokryteriowego W każdej z macierzy A (i) porównywane są obiekty osobno w ramach każdego kryterium. W osobnej macierzy porównywane są również same kryteria między sobą. W porównaniach używana jest, zaproponowana przez Saaty ego, skala dziewięciostopniowa o wartościach numerycznych 1 do 9. Każda z macierzy powinna spełniać następujące warunki: (10) (11) (12) gdzie: a wartości macierzy porównań parami Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 14
16 Kolejnym krokiem jest badanie spójności ocen decydenta. Jest ono na tyle istotne, iż proces generowania macierzy porównań parami jest dość subiektywny przez co łatwo o utratę spójności w ciągach porównań. W tym celu obliczany jest wskaźnik CR wg następującego wzoru: (13) gdzie: CI indeks spójności RI indeks losowy (stablicowany w tabeli 5) Indeks spójności w powyższym wzorze wyliczany jest jako: (14) gdzie: (14a) Tabela 5. Indeksy losowe RI Saaty ego n r i 3 0,52 4 0,89 5 1,11 6 1,25 7 1,35 8 1,4 9 1, , , , , ,57 Źródło: Saaty T. L. (1994), s. 84 (14b) Drugi etap w metodzie AHP to wyznaczanie rankingów indywidualnych. Wyznacza się je dla każdej macierzy porównań parami początkowo normując kolumnami jej elementy w następujący sposób: Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 15
17 (15) Następnie, wg wzoru 16, należy obliczyć indywidualne indeksy preferencji tworzące ranking indywidualny (określający pozycję obiektu wg danego kryterium lub samego kryterium wg pozostałych kryteriów): (16) Ostatnim etapem metody AHP jest ranking wielokryteriowy. Uzyskuje się go obliczając wielokryteriowy indeks preferencji określający pozycję obiektu w rankingu wielokryteriowym: (17) Wagi dotyczące poszczególnych kryteriów w metodzie AHP można wybrać arbitralnie lub posłużyć się jedną z zaproponowanych metod (m. in. przez Saaty ego). Zarząd jednak przychylił się do propozycji analityka sugerującego użycie metody DEMATEL. Głównym argumentem było przeznaczenie systemu jako w pełni automatyzującego podejmowanie decyzji. Metoda ta pozwala kompleksowo ujmować wpływ znaczących uwarunkowań rozpatrywanego zagadnienia. Dzięki analizie DEMATEL możliwe jest określenie najistotniejszych czynników warunkujących wybór kontrahenta, dzięki czemu decyzje podejmowane w celu określenia płynności i jakości produkcji będą cechowały się większą efektywnością i skutecznością. Podstawę metody stanowi teoria grafów zastosowanie grafu o ukierunkowanej postaci dzięki czemu jest możliwe czytelne ujmowanie wpływu. Miarą siły zależności zachodzącej pomiędzy czynnikami jest ocena a, skojarzona z łukiem łączącym wierzchołki grafu, odpowiadające czynnikom i oraz j. Dyskretna skala ocen (od całkowitego braku wpływu, aż po maksymalny wpływ) obejmuje stopnie od zera do czterech, gdzie: 0 brak wpływu 1 minimalny wpływ 2 przeciętny wpływ 3 istotny wpływ 4 bardzo silny wpływ Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 16
18 Oceny wpływu dokonuje sie w ramach każdej z par rozpatrywanych n czynników. Tożsamościowej relacji wpływu czynnika odpowiada ocena zerowa a ii = 0. Kolejnym krokiem jest zbudowanie kwadratowej macierzy bezpośredniego wpływu czynników A. Dla wspomnianych wartości wylicza się wartości maksymalne, ich odwrotności a następnie minimum z wyliczonych wartości odwrotnych wg następujących wzorów: (18a) (18b) (18c) (18d) (18e) Następnie na podstawie macierzy A można wyznaczyć jej znormalizowaną postać N, dzieląc wyrazy każdego wiersza A przez sumę jego minimalnych elementów. Kolejnym krokiem jest wyznaczenie macierzy całkowitego wpływu czynników T. Jej strukturę i modyfikacje reprezentuje poniższy wzór: (19) Elementy macierzy T ujmują oprócz wpływu bezpośredniego także wpływ pośredni czynników, wynikający z ich niejawnych powiązań. Siłę wyłącznie niejawnych powiązań obrazuje wynik działania: (20) Na podstawie powyższej macierzy można sklasyfikować czynniki zarówno względem analizowanego zjawiska jak i znaczenie w odniesieniu do pozostałych czynników. Służą temu odpowiednio syntetyczne miary s+ i oraz s- i, oparte na wartościach sum wierszy (r i ) i kolumn (c i ) macierzy T, odpowiadających i temu czynnikowi: (21a) (21b) Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 17
19 Wartość miary znaczenia i tego czynnika z uwagi na rozpatrywane zagadnienie opisuje suma: (21c) Wartość s+,i pozwala zidentyfikować czynniki neutralne z uwagi na zagadnienie (im większa wartość sumy tym wyższy stopień znaczenia czynnika). Wartość miary znaczenia czynnika względem pozostałych opisuje różnica: (21d) Wartość s - i stanowi podstawę wyodrębnienia 3 grup czynników: przeważających nad pozostałymi czynnikami (s - i > 0) neutralnych względem innych czynników (s - i = 0) zdominowanych przez pozostałe czynniki (s - i < 0) Im większa jest wartość bezwzględna miary tym większa różnica znaczenia pomiędzy i tym czynnikiem a pozostałymi czynnikami. Obliczone wskaźniki s+ zostały, jak już zostało wspomniane, ujęte jako wagi modelu AHP. Powyższe założenia teoretyczne zostały wprowadzone do systemu z drobnymi modyfikacjami nie dotyczącymi jednak struktury matematycznej a jedynie algorytmiczną wygodę i wynikowość (bez uwzględniania pośrednich punktów obliczeń). Strukturę zależności między czynnikowych dla DEMATEL przedstawia tabela 6. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 18
20 T (macierz łącznego wpływu) Tabela 6. Obliczenia DEMATEL Z Jakość surowca Różnorodność surowca Cena sur. Szybkość realizacji zamówienia Cena realizacji zamów. Opinia innych kontrah. Opinia z dotychczasowej współpracy Czas pobytu na rynku Płynność finansowa Jakość surowca Różnorodność surowca Cena surowca Szybkość realizacji zamówienia Cena realizacji zamówienia Opinia innych kontrahentów Opinia z dotychczasowej współpracy Czas pobytu na rynku Płynność finansowa X (macierz znormalizowana) =S*Z Jakość surow. Różnor. surowca Cena sur. Szybkość realizacji zamówienia Cena realizacji zamów. Opinia innych kontrah. Opinia z dotychczasowej współpracy Czas pobytu na rynku Płynność finansowa Jakość surowca 0 0,050 0,200 0,100 0,200 0,200 0,100 0,000 0,050 Różnorodność surowca 0, ,050 0,000 0,000 0,000 0,200 0,150 0,150 Cena surowca 0,000 0, ,000 0,000 0,000 0,200 0,150 0,200 Szybkość realizacji zamówienia 0,000 0,200 0, ,150 0,150 0,050 0,050 0,100 Cena realizacji zamówienia 0,000 0,150 0,100 0, ,200 0,150 0,050 0,150 Opinia innych kontrahentów 0,000 0,100 0,050 0,000 0, ,200 0,100 0,150 Opinia z dotychczasowej współpracy 0,000 0,000 0,050 0,000 0,000 0, ,000 0,100 Czas pobytu na rynku 0,000 0,050 0,000 0,000 0,000 0,000 0, ,100 Płynność finansowa 0,000 0,100 0,000 0,000 0,000 0,000 0,050 0,000 0 r (wpływa) d (skutek) 0,000 0,192 0,285 0,127 0,274 0,274 0,311 0,119 0,274 1,856 0,000 0,032 0,063 0,000 0,000 0,000 0,229 0,164 0,207 0,696 0,000 0,085 0,016 0,000 0,000 0,000 0,233 0,165 0,256 0,754 0,000 0,298 0,208 0,019 0,191 0,191 0,233 0,156 0,284 1,581 0,000 0,250 0,161 0,106 0,062 0,228 0,309 0,143 0,319 1,578 0,000 0,182 0,101 0,021 0,212 0,046 0,313 0,159 0,286 1,320 0,000 0,015 0,052 0,000 0,000 0,000 0,019 0,010 0,115 0,211 0,000 0,062 0,004 0,000 0,000 0,000 0,019 0,010 0,113 0,208 0,000 0,104 0,009 0,000 0,000 0,000 0,074 0,017 0,026 0,230 0,000 1,220 0,900 0,274 0,739 0,739 1,740 0,942 1,880 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 19
21 s+r s-r Jakość surowca 1,856 1,856 Różnorodność surowca 1,915-0,524 Cena surowca 1,654-0,146 Szybkość realizacji zamówienia 1,855 1,307 Cena realizacji zamówienia 2,317 0,840 Opinia innych kontrahentów 2,059 0,582 Opinia z dotychczasowej współpracy 1,951-1,529 Czas pobytu na rynku 1,150-0,735 Płynność finansowa 2,110-1,650 Źródło: Opracowanie własne Wykres 2. Graficzna reprezentacja metody DEMATEL (indeksów preferencji) 2,50 2,00 1,50 1,00 0,50 0,00-0,50-1,00-1,50-2,00 1,856 ; 1,856 1,855 ; 1,307 2,317 ; 0,840 2,059 ; 0, ,654 ; -0, ,915 ; -0,524 1,150 ; -0,735 1,951 ; -1,529 2,110 ; -1,650 Źródło: Opracowanie własne Z użyciem wyliczonych metodą DEMATEL wag stworzono porównanie wielokryterialne metodą AHP dla wspomnianych firm wg zadanych kategorii. Okazało się, iż najlepsze firmy to Wiwo, Cylex oraz Pale. Pełny ranking preferencji przedstawia tabela 7. Ranking taki jednak pozwala na dogłębną analizę dotyczącą poszczególnych kryteriów. W związku z tym, wybór pierwszej firmy z brzegu byłby nieuzasadniony. Kolejnym ważnym kryterium jest jakość surowca dla którego z wskazanych firm najlepsza okazuje się Pale (6 pozycja w rankingu indywidualnym). Decydujące znaczenie ma jednak cena a ta dla wspomnianej Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 20
22 firmy plasuje ją na ostatniej pozycji rankingu indywidualnego. Ostateczną decyzją, umowa Zostanie podpisana dla 30% dostaw z firmą Cylex oraz 70% dostaw z firmą Wiwo. Wszelkie obliczenia dotyczące metody AHP znajdują się w załączniku B Metoda AHP. Tabela 7. Indeks wielokryteriowy AHP Lp. Obiekty Indeksy 1. Wiwo 0, Cylex 0, Pale 0, Tekturopak 0, Eurobox 0, Bart 0, Tektura Wrocław 0, Smurfit 0, Eko-Tektura 0, Interpapier 0, Alken 0, Apis 0, Werner Kenkel 0, Papiery Kielce 0, Technopol 0, MegaPack 0, Aquila 0, Scopak 0, Mbox 0, Packprofil 0, Inter pak 0,0286 Źródło: Opracowanie własne Podsumowując wprowadzone zmiany i modyfikacje wynik finansowy firmy znacząco wzrósł. Zmianę przyniosła zarówno ekspansja na rynku jak również poprawa jakości produkcji poprzez minimalizację strat i zbędnych kosztów. Ekspansja dotyczyła zwiększonej precyzji obliczeń oraz mniejszego marginesu bezpieczeństwa zakładanego przy przetargach. Analiza prawdopodobieństw pozwala na minimalizację strat związaną z zastosowaniem niewłaściwego surowca do określonego produktu końcowego jak również w analizach stochastycznych dotyczących prognoz rynkowych gwarantuje zwiększoną szansę na przewidzenie zmian cen surowca oraz popytu na wprowadzany produkt. Teoria gier (podejmowanie decyzji w warunkach niepewności) traktowana niejednokrotnie jako typowa przygoda z matematyką również znajduje nieocenione zastosowanie w przewidywaniu posunięć konkurencji i przygotowywaniu strategii obronnych. W opisywanym przedsiębiorstwie moduł gier wieloosobowych jest obecnie implementowany natomiast zakończenie projektu szacowane jest na połowę roku Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 21
23 Opisywane metody porównań wielokryterialnych dają szansę na pełną kontrolę nad podejmowanymi przez podwładnych decyzjami dotyczącymi wyboru surowca, dostawcy lub innych środków produkcji a przez swoją unifikację zapewniają o identycznej wadze czynników wpływających na podejmowane decyzje. Nie do przecenienia jest również istotność wprowadzenie algorytmu komiwojażera. Ten system oparty na teorii grafów nadal posiada wiele wad przede wszystkim jest systemem wolnym w działaniu (przy dużej ilości punktów) jak również przybliża do drogi najkrótszej niejednokrotnie nie podając jej dokładnej wartości. Zasadą jednak była kontrola czy to obliczeń i roszczeń wynajętych firm transportowych czy też kontrola własnych kierowców. Pewne formy samowoli powodowały silne obciążenia dla budżetu firmy które w krótkim okresie wydawały się być niskie jednak w skali roku dawały sumę pozwalającą pokryć choćby premie pracowników. W polskich przedsiębiorstwach w przeciwieństwie do tych z kapitałem zagranicznym nie przywiązuje się dużej wagi do optymalizacji działań. Koszty wprowadzenia modyfikacji są początkowo dość wysokie szczególnie w odniesieniu do możliwych do uzyskania w początkowym okresie zysków jednak analizowanie strat ponoszonych z decyzji o niskiej precyzji nie powinno odbywać się w skali lokalnej lecz jako roczne uogólnienia. Wprawdzie koszty działań poprawiających metodykę zarządzania produkcją i logistyką są początkowo wysokie jednak w odpowiednio zaprojektowanym systemie nie ponosi się jego amortyzacji a wartość elastycznego oprogramowania rośnie wykładniczo w stosunku do nakładów związanych z przekazywaniem do niego nowych metod opartych na doświadczeniu zarządu. Praca staję się dokładniejsza, pomijany jest błąd czynnika ludzkiego a dla pracowników pozostawione jest więcej czasu pozwalającego na pracę twórczą i rozwój nowych pomysłów. Systemy business inteligence mają przecież na celu nie wyeliminowanie kadry ludzkiej a przeniesienie jej zainteresowania na stronę nowych ścieżek rozwoju firmy samemu zajmując się pracą odtwórczą i powtarzalną. Decyzje nadal muszą być wspierane przez zarząd jednak dzięki szybkości i mnogości informacji będą one szybsze i skuteczniejsze. Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 22
24 Bibliografia: 1. Trzaskalik T., Wprowadzenie do badań operacyjnych z komputerem, PWE, Warszawa Kukuła K., Badania operacyjne w przykładach i zadaniach, PWN, Warszawa Ignasiak E., Badania operacyjne, PWE, Warszawa Miszczyńska D., Miszczyński M., Wybrane metody badań operacyjnych, WSEH, Skierniewice, Gajda J., Jadczak R., Badania operacyjne w praktyce", Wydawnictwo Uniwersytetu Łódzkiego, Łódź Gąsiorowska E., Decyzje zakupowe na rynku małych przedsiębiorstw, DIFIN, Warszawa Krawczyk S., Metody ilościowe w planowaniu (działalności przedsiębiorstwa), C.H. Beck, Warszawa Praca zbiorowa, DEMATEL, Katedra Badań Operacyjnych w Zarządzaniu Wydział Zarządzania i Inżynierii Produkcji Politechniki Opolskiej, Opole 2008 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 23
25 Spis wzorów: Nr wzoru Strona Opis Źródło (punkt w bibliografii) 1 4 Czas trwania projektu 1, Wariancja czasu trwania projektu 1, Odchylenie czasu trwania projektu 1, Prawdopodobieństwo realizacji projektu w zadanym czasie 1, Ekonomiczna wartość zapasu 6, Optymalna częstotliwość dostaw 6, Wartość przypadku 2, Wartość gałęzi decyzji 2, Wartość drzewa decyzyjnego 2, Warunki struktury macierzy porównań parami Warunek struktury parametrów macierzy porównań parami Warunek spójności ocen decydenta Współczynnik spójności Indeks spójności Normowanie macierzy porównań parami Indywidualny indeks preferencji Wielokryteriowy indeks preferencji Normalizacja macierzy bezpośredniego wpływu Macierz całkowitego wpływu czynników Określenie siły niejawnych powiązań Określenie pozycji rankingu 8 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 24
26 Załącznik A Algortym STSP p = 33 nazwanajlepsze = nazwamax1 wielkoscnajlepsze = max2 pozycjanajlepszenazwa = ("a" & 33) pozycjanajlepszewielkosc = ("b" & 33) najlepsze = Range("b31") For p = 33 To 61 If Range("a" & p) = "" And Range("a" & p + 1) <> "" Then Range("b" & p) = max1 Range("a" & p) = nazwamax1 Dim spr3 As Variant spr3 = Range("a" & p - 1) spr1 = Range("a" & p + 1) spr2 = nazwamax1 Sheets(a).Activate For z = 3 To 30 If Range("b" & z) = spr1 Then rspr1 = z Next Dim op As Integer Dim rspr3 As Variant For op = 3 To 30 If Range("b" & op) = spr3 Then rspr3 = op Next If Range("c2") = spr2 Then rspr2 = "c" ElseIf Range("d2") = spr2 Then rspr2 = "d" ElseIf Range("e2") = spr2 Then rspr2 = "e" ElseIf Range("f2") = spr2 Then rspr2 = "f" ElseIf Range("g2") = spr2 Then rspr2 = "g" ElseIf Range("h2") = spr2 Then rspr2 = "h" ElseIf Range("i2") = spr2 Then rspr2 = "i" ElseIf Range("j2") = spr2 Then rspr2 = "j" ElseIf Range("k2") = spr2 Then rspr2 = "k" ElseIf Range("l2") = spr2 Then rspr2 = "l" ElseIf Range("m2") = spr2 Then Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 25
27 rspr2 = "m" ElseIf Range("n2") = spr2 Then rspr2 = "n" ElseIf Range("o2") = spr2 Then rspr2 = "o" ElseIf Range("p2") = spr2 Then rspr2 = "p" ElseIf Range("q2") = spr2 Then rspr2 = "q" ElseIf Range("r2") = spr2 Then rspr2 = "r" ElseIf Range("s2") = spr2 Then rspr2 = "s" ElseIf Range("t2") = spr2 Then rspr2 = "t" ElseIf Range("u2") = spr2 Then rspr2 = "u" ElseIf Range("v2") = spr2 Then rspr2 = "v" ElseIf Range("w2") = spr2 Then rspr2 = "w" ElseIf Range("x2") = spr2 Then rspr2 = "x" ElseIf Range("y2") = spr2 Then rspr2 = "y" ElseIf Range("z2") = spr2 Then rspr2 = "z" elka = Range(rspr2 & rspr1) elka2 = Range(rspr2 & rspr3) Sheets("roboczy").Activate 'powrót do właściwego arkusza Range("b" & p) = elka2 Range("b" & p + 1) = elka 'wpisanie odległości If Range("b31") < najlepsze Then najlepsze = Range("b31") nazwanajlepsze = nazwamax1 wielkoscnajlepsze = max1 pozycjanajlepszenazwa = ("a" & p) pozycjanajlepszewielkosc = ("b" & p) Range("a" & p) = "" Range("b" & p) = "" Next Range(pozycjanajlepszenazwa) = nazwanajlepsze Range(pozycjanajlepszewielkosc) = wielkoscnajlepsze Dim sk As Variant Dim sla As Variant For sk = 32 To 63 Step 2 If Range("a" & sk) <> "" Then Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 26
28 If Range("a" & sk + 1) = "" Then Else sla = sk + 1 Rows(sla).Select Selection.Insert Shift:=xlDown Next Next For wsk = 32 To 80 Step 2 If Range("a" & wsk) = "" Then ostatki = wsk Next For q = 32 To ostatki Step 2 jedno = Range("a" & q) drugie = Range("a" & q + 2) Sheets(a).Activate For row = 3 To 30 If Range("b" & row) = jedno Then rspr1 = row Next If Range("c2") = drugie Then rspr2 = "c" ElseIf Range("d2") = drugie Then rspr2 = "d" ElseIf Range("e2") = drugie Then rspr2 = "e" ElseIf Range("f2") = drugie Then rspr2 = "f" ElseIf Range("g2") = drugie Then rspr2 = "g" ElseIf Range("h2") = drugie Then rspr2 = "h" ElseIf Range("i2") = drugie Then rspr2 = "i" ElseIf Range("j2") = drugie Then rspr2 = "j" ElseIf Range("k2") = drugie Then rspr2 = "k" ElseIf Range("l2") = drugie Then rspr2 = "l" ElseIf Range("m2") = drugie Then rspr2 = "m" ElseIf Range("n2") = drugie Then rspr2 = "n" ElseIf Range("o2") = drugie Then rspr2 = "o" ElseIf Range("p2") = drugie Then Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 27
29 rspr2 = "p" ElseIf Range("q2") = drugie Then rspr2 = "q" ElseIf Range("r2") = drugie Then rspr2 = "r" ElseIf Range("s2") = drugie Then rspr2 = "s" ElseIf Range("t2") = drugie Then rspr2 = "t" ElseIf Range("u2") = drugie Then rspr2 = "u" ElseIf Range("v2") = drugie Then rspr2 = "v" ElseIf Range("w2") = drugie Then rspr2 = "w" ElseIf Range("x2") = drugie Then rspr2 = "x" ElseIf Range("y2") = drugie Then rspr2 = "y" ElseIf Range("z2") = drugie Then rspr2 = "z" anka = Range(rspr2 & rspr1) Sheets("roboczy").Activate Range("b" & q + 2) = anka Next If trasa.dzien = 1 Then If trasa.p1 = True Then i1 = trasa.pw1 If trasa.p2 = True Then i2 = trasa.pw2 If trasa.p3 = True Then i3 = trasa.pw3 If trasa.p4 = True Then i4 = trasa.pw4 If trasa.p5 = True Then i5 = trasa.pw5 If trasa.p6 = True Then i6 = trasa.pw6 If trasa.p7 = True Then i7 = trasa.pw7 If trasa.p8 = True Then i8 = trasa.pw8 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 28
30 If trasa.p9 = True Then i9 = trasa.pw9 If trasa.p10 = True Then i10 = trasa.pw10 If trasa.p11 = True Then i11 = trasa.pw11 waga = i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + i11 ElseIf trasa.dzien = 2 Then i1 = trasa.ww1 i2 = trasa.ww2 i3 = trasa.ww3 i4 = trasa.ww4 i5 = trasa.ww5 i6 = trasa.ww6 i7 = trasa.ww7 i8 = trasa.ww8 i9 = trasa.ww9 i10 = trasa.ww10 i11 = trasa.ww11 i12 = trasa.ww12 i13 = trasa.ww13 i14 = trasa.ww14 i15 = trasa.ww15 i16 = trasa.ww16 i17 = trasa.ww17 i18 = trasa.ww18 waga = i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + i11 + i12 + i13 + i14 + i15 + i16 + i17 + i18 ElseIf trasa.dzien = 3 Then i1 = trasa.sw1 i2 = trasa.sw2 i3 = trasa.sw3 i4 = trasa.sw4 i5 = trasa.sw5 i6 = trasa.sw6 i7 = trasa.sw7 i8 = trasa.sw8 i9 = trasa.sw9 i10 = trasa.sw10 i11 = trasa.sw11 i12 = trasa.sw12 i13 = trasa.sw13 i14 = trasa.sw14 i15 = trasa.sw15 i16 = trasa.sw16 i17 = trasa.sw17 waga = i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + i11 + i12 + i13 + i14 + i15 + i16 + i17 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 29
31 ElseIf trasa.dzien = 4 Then i1 = trasa.cw1 i2 = trasa.cw2 i3 = trasa.cw3 i4 = trasa.cw4 i5 = trasa.cw5 i6 = trasa.cw6 i7 = trasa.cw7 i8 = trasa.cw8 i9 = trasa.cw9 i10 = trasa.cw10 i11 = trasa.cw11 i12 = trasa.cw12 waga = i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + i11 + i12 ElseIf trasa.dzien = 5 Then i1 = trasa.piw1 i2 = trasa.piw2 i3 = trasa.piw3 i4 = trasa.piw4 i5 = trasa.piw5 i6 = trasa.piw6 i7 = trasa.piw7 i8 = trasa.piw8 i9 = trasa.piw9 i10 = trasa.piw10 i11 = trasa.piw11 i12 = trasa.piw12 i13 = trasa.piw13 waga = i1 + i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + i11 + i12 + i13 ElseIf trasa.dzien = 6 Then i1 = trasa.sow1 i2 = trasa.sow2 waga = i1 + i2 If waga > Then Dim waga2 As Variant waga2 = waga If waga2 > Then Dim waga3 As Variant waga3 = waga If waga3 > 6000 Then Dim waga4 As Variant If waga4 > 600 Then raport.samochod.caption = "Wszystkie dostępne + firma zewn." ElseIf waga > Then raport.samochod.caption = "Mercedes Transporter (I)" ElseIf waga > 6000 Then Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 30
32 raport.samochod.caption = "Fiat Ducato (II)" ElseIf waga > 600 Then raport.samochod.caption = "Ford Transport (III)" Else raport.samochod.caption = "Citroen C4 (IV)" If Range("a70") <> "" Then raport.a20 = "20.) " & Range("a70") If Range("a68") <> "" Then raport.a19 = "19.) " & Range("a68") If Range("a66") <> "" Then raport.a18 = "18.) " & Range("a66") If Range("a64") <> "" Then raport.a17 = "17.) " & Range("a64") If Range("a62") <> "" Then raport.a16 = "16.) " & Range("a62") If Range("a60") <> "" Then raport.a15 = "15.) " & Range("a60") If Range("a58") <> "" Then raport.a14 = "14.) " & Range("a58") If Range("a56") <> "" Then raport.a13 = "13.) " & Range("a56") If Range("a54") <> "" Then raport.a12 = "12.) " & Range("a54") If Range("a52") <> "" Then raport.a11 = "11.) " & Range("a52") If Range("a50") <> "" Then raport.a10 = "10.) " & Range("a50") If Range("a48") <> "" Then raport.a9 = "9.) " & Range("a48") If Range("a46") <> "" Then raport.a8 = "8.) " & Range("a46") If Range("a44") <> "" Then raport.a7 = "7.) " & Range("a44") If Range("a42") <> "" Then raport.a6 = "6.) " & Range("a42") Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 31
33 If Range("a40") <> "" Then raport.a5 = "5.) " & Range("a40") If Range("a38") <> "" Then raport.a4 = "4.) " & Range("a38") If Range("a36") <> "" Then raport.a3 = "3.) " & Range("a36") If Range("a34") <> "" Then raport.a2 = "2.) " & Range("a34") If Range("a32") <> "" Then raport.a1 = "1.) " & Range("a32") Range("a80").FormulaLocal = "=ile.niepustych(a32:a72)" raport.razem = "Trasa ma " & Range("a80") & " węzłów." Application.ScreenUpdating = True raport.show Sheets("roboczy").Select ActiveWindow.SelectedSheets.Delete Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 32
34 Załącznik B Metoda AHP Jakość Różnorodność Cena Szybkość Cena realizacji Opinia innych Opinia z dot. Czas pobytu Płynność surowca surowca surowca realizacji zamów. zamówienia kontrahentów współpracy na rynku finansowa kierunek max max min min min max max max max waga 1, , , , , , , , , Wiwo 0, , ,125 3,875 12,075 10, ,2 1, ,85 Pale 1, ,774 13,2 7,9 16,9 14,4 19,58 5, ,86 Smurfit 1, ,502 12,5 7,5 14, ,8775 1, MegaPack 1, ,1 13,2 7,525 15,9 12,8 14,37 0, ,4 Tektura Wrocław 1, ,972 12,9 7,8 15,5 12,7 16,175 4, ,2 Aquila 1, ,575 12,5 7,25 15,4 12,2 14,35 4, ,2 Bart 1, ,924 12,8 7,95 15,8 12,35 22,1 1, ,8 Papiery Kielce 1, ,05 12,8 7,9 16,9 12,8 21,1 2, ,6 Alken 1, ,898 12,6 8,2 15,9 12,45 18,7675 3, ,4 Eurobox 1, ,55 11,4 7,2 14,5 11,05 4,135 0, ,4 Packprofil 1, ,748 10,6 7,35 15,5 11,4 3, , ,8 Scopak 1, ,525 12,2 7,15 15,2 12,25 9,55 0, ,6 Mbox 1, ,172 11,6 7,4 14,6 10,95 2, , ,6 Interpapier 1, ,5 11,8 7, ,65 4,18 1, ,6 Werner Kenkel 1,4 12,722 11,7 7,5 15,1 11,35 6,375 1, ,4 Tekturopak 1, ,95 11,5 6, ,1 3,2275 0, ,4 Apis 1, ,074 11,7 7,9 15,1 11,95 7,355 0, ,4 Cylex 1, ,5 10,7 7,05 14,6 10,95 5,0025 0, ,4 Eko-Tektura 1, ,104 10,9 7, ,5 4,94 0, ,4 Technopol 1, ,9 11,1 6,95 14,9 11,1 2,73 0, ,6 Inter pak 1, ,124 11,1 7,55 16,4 12,2 9, , ,4 Bogumił Miller Zastosowanie metod optymalizacji i wyboru wielokryterialnego w procesie produkcyjnym case study 33
Inżynieria oprogramowania. Część 8: Metoda szacowania ryzyka - PERT
 UNIWERSYTET RZESZOWSKI KATEDRA INFORMATYKI Opracował: mgr inż. Przemysław Pardel v1.01 2010 Inżynieria oprogramowania Część 8: Metoda szacowania ryzyka - PERT ZAGADNIENIA DO ZREALIZOWANIA (3H) PERT...
UNIWERSYTET RZESZOWSKI KATEDRA INFORMATYKI Opracował: mgr inż. Przemysław Pardel v1.01 2010 Inżynieria oprogramowania Część 8: Metoda szacowania ryzyka - PERT ZAGADNIENIA DO ZREALIZOWANIA (3H) PERT...
Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz.
 14.12.2005 r. Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz. 2 3.2. Implementacja w Excelu (VBA for
14.12.2005 r. Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz. 2 3.2. Implementacja w Excelu (VBA for
Rozdział 7 ZARZĄDZANIE PROJEKTAMI
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 7 ZARZĄDZANIE PROJEKTAMI 7.2. Ćwiczenia komputerowe Ćwiczenie 7.1 Wykorzystując
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 7 ZARZĄDZANIE PROJEKTAMI 7.2. Ćwiczenia komputerowe Ćwiczenie 7.1 Wykorzystując
Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów. Dawid Doliński
 Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów Dawid Doliński Dlaczego MonZa? Korzyści z wdrożenia» zmniejszenie wartości zapasów o 40 %*» podniesienie poziomu obsługi
Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów Dawid Doliński Dlaczego MonZa? Korzyści z wdrożenia» zmniejszenie wartości zapasów o 40 %*» podniesienie poziomu obsługi
Istnieje możliwość prezentacji systemu informatycznego MonZa w siedzibie Państwa firmy.
 system informatyczny wspomagający monitorowanie i planowanie zapasów w przedsiębiorstwie System informatyczny MonZa do wspomagania decyzji managerskich w obszarze zarządzania zapasami jest odpowiedzią
system informatyczny wspomagający monitorowanie i planowanie zapasów w przedsiębiorstwie System informatyczny MonZa do wspomagania decyzji managerskich w obszarze zarządzania zapasami jest odpowiedzią
Harmonogramowanie przedsięwzięć
 Harmonogramowanie przedsięwzięć Mariusz Kaleta Instytut Automatyki i Informatyki Stosowanej Politechnika Warszawska luty 2014, Warszawa Politechnika Warszawska Harmonogramowanie przedsięwzięć 1 / 25 Wstęp
Harmonogramowanie przedsięwzięć Mariusz Kaleta Instytut Automatyki i Informatyki Stosowanej Politechnika Warszawska luty 2014, Warszawa Politechnika Warszawska Harmonogramowanie przedsięwzięć 1 / 25 Wstęp
Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych
 dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
Dr Andrzej Podleśny Poznań, dnia r. MODUŁ KSZTAŁCENIA (SYLABUS)
 Dr Andrzej Podleśny Poznań, dnia 1.10.2017 r. MODUŁ KSZTAŁCENIA (SYLABUS) dla przedmiotu Informatyka w zarządzaniu na kierunku Zarządzanie i prawo w biznesie I. Informacje ogólne 1. Nazwa modułu : Informatyka
Dr Andrzej Podleśny Poznań, dnia 1.10.2017 r. MODUŁ KSZTAŁCENIA (SYLABUS) dla przedmiotu Informatyka w zarządzaniu na kierunku Zarządzanie i prawo w biznesie I. Informacje ogólne 1. Nazwa modułu : Informatyka
ANALIZA HIERARCHICZNA PROBLEMU W SZACOWANIU RYZYKA PROJEKTU INFORMATYCZNEGO METODĄ PUNKTOWĄ. Joanna Bryndza
 ANALIZA HIERARCHICZNA PROBLEMU W SZACOWANIU RYZYKA PROJEKTU INFORMATYCZNEGO METODĄ PUNKTOWĄ Joanna Bryndza Wprowadzenie Jednym z kluczowych problemów w szacowaniu poziomu ryzyka przedsięwzięcia informatycznego
ANALIZA HIERARCHICZNA PROBLEMU W SZACOWANIU RYZYKA PROJEKTU INFORMATYCZNEGO METODĄ PUNKTOWĄ Joanna Bryndza Wprowadzenie Jednym z kluczowych problemów w szacowaniu poziomu ryzyka przedsięwzięcia informatycznego
Z-LOG-120I Badania Operacyjne Operations Research
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-LOG-10I Badania Operacyjne Operations Research A. USYTUOWANIE MODUŁU W
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-LOG-10I Badania Operacyjne Operations Research A. USYTUOWANIE MODUŁU W
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI
 DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
BADANIA OPERACYJNE i teoria optymalizacji. Prowadzący: dr Tomasz Pisula Katedra Metod Ilościowych
 BADANIA OPERACYJNE i teoria optymalizacji Prowadzący: dr Tomasz Pisula Katedra Metod Ilościowych e-mail: tpisula@prz.edu.pl 1 Literatura podstawowa wykorzystywana podczas zajęć wykładowych: 1. Gajda J.,
BADANIA OPERACYJNE i teoria optymalizacji Prowadzący: dr Tomasz Pisula Katedra Metod Ilościowych e-mail: tpisula@prz.edu.pl 1 Literatura podstawowa wykorzystywana podczas zajęć wykładowych: 1. Gajda J.,
Controlling operacyjny i strategiczny
 Controlling operacyjny i strategiczny dr Piotr Modzelewski Katedra Bankowości, Finansów i Rachunkowości Wydziału Nauk Ekonomicznych Uniwersytetu Warszawskiego Plan zajęć 1, 2. Wprowadzenie do zagadnień
Controlling operacyjny i strategiczny dr Piotr Modzelewski Katedra Bankowości, Finansów i Rachunkowości Wydziału Nauk Ekonomicznych Uniwersytetu Warszawskiego Plan zajęć 1, 2. Wprowadzenie do zagadnień
t i L i T i
 Planowanie oparte na budowaniu modelu struktury przedsięwzięcia za pomocą grafu nazywa sie planowaniem sieciowym. Stosuje się do planowania i kontroli realizacji założonych przedsięwzięć gospodarczych,
Planowanie oparte na budowaniu modelu struktury przedsięwzięcia za pomocą grafu nazywa sie planowaniem sieciowym. Stosuje się do planowania i kontroli realizacji założonych przedsięwzięć gospodarczych,
Badania operacyjne Operation research. Transport I stopień (I stopień / II stopień) Ogólnoakademicki (ogólno akademicki / praktyczny)
 Załącznik nr 7 do Zarządzenia Rektora nr../12 z dnia.... 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Badania
Załącznik nr 7 do Zarządzenia Rektora nr../12 z dnia.... 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Badania
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Zarządzanie projektami. Tadeusz Trzaskalik
 Zarządzanie projektami Tadeusz Trzaskalik 7.1. Wprowadzenie Słowa kluczowe Projekt Sieć czynności zynność bezpośrednio poprzedzająca Zdarzenie, zdarzenie początkowe, zdarzenie końcowe Właściwa numeracja
Zarządzanie projektami Tadeusz Trzaskalik 7.1. Wprowadzenie Słowa kluczowe Projekt Sieć czynności zynność bezpośrednio poprzedzająca Zdarzenie, zdarzenie początkowe, zdarzenie końcowe Właściwa numeracja
Diagnostyka ekonomiczna w systemach automatycznego zarządzania przedsiębiorstwem. dr Jarosław Olejniczak
 Diagnostyka ekonomiczna w systemach automatycznego zarządzania przedsiębiorstwem dr Jarosław Olejniczak Agenda Diagnostyka, diagnostyka techniczna i diagnostyka ekonomiczna; Obszary diagnostyki ekonomicznej,
Diagnostyka ekonomiczna w systemach automatycznego zarządzania przedsiębiorstwem dr Jarosław Olejniczak Agenda Diagnostyka, diagnostyka techniczna i diagnostyka ekonomiczna; Obszary diagnostyki ekonomicznej,
PRZEWODNIK PO PRZEDMIOCIE. stacjonarne. II stopnia. ogólnoakademicki. podstawowy WYKŁAD ĆWICZENIA LABORATORIUM PROJEKT SEMINARIUM
 Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Badania Operacyjne Ćwiczenia nr 5 (Materiały)
 ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
Z-ZIP2-1067złd Gospodarka magazynowa Warehouse management. Specjalnościowy Obowiązkowy Polski Semestr drugi
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2015/2016 Z-ZIP2-1067złd Gospodarka magazynowa Warehouse management A. USYTUOWANIE
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2015/2016 Z-ZIP2-1067złd Gospodarka magazynowa Warehouse management A. USYTUOWANIE
PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI MARCIN FOLTYŃSKI
 PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI WŁAŚCIWIE PO CO ZAPASY?! Zasadniczą przyczyną utrzymywania zapasów jest występowanie nieciągłości w przepływach materiałów i towarów. MIEJSCA UTRZYMYWANIA ZAPASÓW
PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI WŁAŚCIWIE PO CO ZAPASY?! Zasadniczą przyczyną utrzymywania zapasów jest występowanie nieciągłości w przepływach materiałów i towarów. MIEJSCA UTRZYMYWANIA ZAPASÓW
Planowanie przedsięwzięć
 K.Pieńkosz Badania Operacyjne Planowanie przedsięwzięć 1 Planowanie przedsięwzięć Model przedsięwzięcia lista operacji relacje poprzedzania operacji modele operacji funkcja celu planowania K.Pieńkosz Badania
K.Pieńkosz Badania Operacyjne Planowanie przedsięwzięć 1 Planowanie przedsięwzięć Model przedsięwzięcia lista operacji relacje poprzedzania operacji modele operacji funkcja celu planowania K.Pieńkosz Badania
Standardy oceny biznesplanów
 Załącznik nr 8 do Regulaminu przyznawania wsparcia finansowego na rozwój przedsiębiorczości Standardy oceny biznesplanów L.p. Kryterium Punktacja Uzasadnienie punktacji I.1 Celowość przedsięwzięcia 0-5
Załącznik nr 8 do Regulaminu przyznawania wsparcia finansowego na rozwój przedsiębiorczości Standardy oceny biznesplanów L.p. Kryterium Punktacja Uzasadnienie punktacji I.1 Celowość przedsięwzięcia 0-5
Wyznaczanie optymalnej trasy problem komiwojażera
 Wyznaczanie optymalnej trasy problem komiwojażera Optymalizacja w podejmowaniu decyzji Opracowała: mgr inż. Natalia Malinowska Wrocław, dn. 28.03.2017 Wydział Elektroniki Politechnika Wrocławska Plan prezentacji
Wyznaczanie optymalnej trasy problem komiwojażera Optymalizacja w podejmowaniu decyzji Opracowała: mgr inż. Natalia Malinowska Wrocław, dn. 28.03.2017 Wydział Elektroniki Politechnika Wrocławska Plan prezentacji
Działanie algorytmu oparte jest na minimalizacji funkcji celu jako suma funkcji kosztu ( ) oraz funkcji heurystycznej ( ).
 Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
BADANIA OPERACYJNE. dr Adam Sojda Pokój A405
 BADANIA OPERACYJNE dr Adam Sojda adam.sojda@polsl.pl http://dydaktyka.polsl.pl/roz6/asojda/default.aspx Pokój A405 Przedsięwzięcie - zorganizowanie działanie ludzkie zmierzające do osiągnięcia określonego
BADANIA OPERACYJNE dr Adam Sojda adam.sojda@polsl.pl http://dydaktyka.polsl.pl/roz6/asojda/default.aspx Pokój A405 Przedsięwzięcie - zorganizowanie działanie ludzkie zmierzające do osiągnięcia określonego
Z-ZIP-120z Badania Operacyjne Operations Research. Stacjonarne Wszystkie Katedra Matematyki dr Monika Skóra
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Z-ZIP-120z Badania Operacyjne Operations Research A. USYTUOWANIE MODUŁU
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Z-ZIP-120z Badania Operacyjne Operations Research A. USYTUOWANIE MODUŁU
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH
 MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH 1. Przedmiot nie wymaga przedmiotów poprzedzających 2. Treść przedmiotu Proces i cykl decyzyjny. Rola modelowania matematycznego w procesach decyzyjnych.
MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH 1. Przedmiot nie wymaga przedmiotów poprzedzających 2. Treść przedmiotu Proces i cykl decyzyjny. Rola modelowania matematycznego w procesach decyzyjnych.
PRZEWODNIK PO PRZEDMIOCIE
 Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Politechnika Częstochowska, Wydział Zarządzania PRZEWODNIK PO PRZEDMIOCIE Nazwa przedmiotu Kierunek Forma studiów Poziom kwalifikacji Rok Semestr Jednostka prowadząca Osoba sporządzająca Profil Rodzaj
Badania operacyjne i teorie optymalizacji
 Badania operacyjne i teorie optymalizacji dr Zbigniew Karwacki Wydział Ekonomiczno-Socjologiczny Katedra Badań Operacyjnych Centrum Informatyczno-Ekonometryczne pok. E-137 Środa, 16.30-18.00 zakarwacki@uni.lodz.pl
Badania operacyjne i teorie optymalizacji dr Zbigniew Karwacki Wydział Ekonomiczno-Socjologiczny Katedra Badań Operacyjnych Centrum Informatyczno-Ekonometryczne pok. E-137 Środa, 16.30-18.00 zakarwacki@uni.lodz.pl
LOGISTYKA. Zapas: definicja. Zapasy: podział
 LOGISTYKA Zapasy Zapas: definicja Zapas to określona ilość dóbr znajdująca się w rozpatrywanym systemie logistycznym, bieżąco nie wykorzystywana, a przeznaczona do późniejszego przetworzenia lub sprzedaży.
LOGISTYKA Zapasy Zapas: definicja Zapas to określona ilość dóbr znajdująca się w rozpatrywanym systemie logistycznym, bieżąco nie wykorzystywana, a przeznaczona do późniejszego przetworzenia lub sprzedaży.
Przykład: budowa placu zabaw (metoda ścieżki krytycznej)
 Przykład: budowa placu zabaw (metoda ścieżki krytycznej) Firma budowlana Z&Z podjęła się zadania wystawienia placu zabaw dla dzieci w terminie nie przekraczającym 20 dni. Listę czynności do wykonania zawiera
Przykład: budowa placu zabaw (metoda ścieżki krytycznej) Firma budowlana Z&Z podjęła się zadania wystawienia placu zabaw dla dzieci w terminie nie przekraczającym 20 dni. Listę czynności do wykonania zawiera
PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem
 1 PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem DANE I INFORMACJE 2 Planowanie przepływów jest ciągłym procesem podejmowania decyzji, które decydują o efektywnym
1 PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem DANE I INFORMACJE 2 Planowanie przepływów jest ciągłym procesem podejmowania decyzji, które decydują o efektywnym
PROGRAM OPTYMALIZACJI PLANU PRODUKCJI
 Strona 1 PROGRAM OPTYMALIZACJI PLANU PRODUKCJI Program autorski opracowany przez Sławomir Dąbrowski ul. SIENKIEWICZA 3 m. 18 26-220 STĄPORKÓW tel: 691-961-051 email: petra.art@onet.eu, sla.dabrowscy@onet.eu
Strona 1 PROGRAM OPTYMALIZACJI PLANU PRODUKCJI Program autorski opracowany przez Sławomir Dąbrowski ul. SIENKIEWICZA 3 m. 18 26-220 STĄPORKÓW tel: 691-961-051 email: petra.art@onet.eu, sla.dabrowscy@onet.eu
Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia)
 Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia) Zgodnie z Zarządzeniem Rektora ZPSB w sprawie Regulaminu Procedur Dyplomowych, na egzaminie dyplomowym (licencjackim)
Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia) Zgodnie z Zarządzeniem Rektora ZPSB w sprawie Regulaminu Procedur Dyplomowych, na egzaminie dyplomowym (licencjackim)
Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change
 Raport 4/2015 Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change autor: Michał Osmoła INIME Instytut nauk informatycznych i matematycznych
Raport 4/2015 Optymalizacja parametrów w strategiach inwestycyjnych dla event-driven tradingu dla odczytu Australia Employment Change autor: Michał Osmoła INIME Instytut nauk informatycznych i matematycznych
Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia)
 Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia) Zgodnie z Zarządzeniem Rektora ZPSB w sprawie Regulaminu Procedur Dyplomowych, na egzaminie dyplomowym (licencjackim)
Zestawy zagadnień na egzamin dyplomowy (licencjacki) dla kierunku EKONOMIA (studia I stopnia) Zgodnie z Zarządzeniem Rektora ZPSB w sprawie Regulaminu Procedur Dyplomowych, na egzaminie dyplomowym (licencjackim)
Badania Operacyjne Ćwiczenia nr 6 (Materiały)
 Otwarte zagadnienie transportowe Jeżeli łączna podaż dostawców jest większa niż łączne zapotrzebowanie odbiorców to mamy do czynienia z otwartym zagadnieniem transportowym. Warunki dla dostawców (i-ty
Otwarte zagadnienie transportowe Jeżeli łączna podaż dostawców jest większa niż łączne zapotrzebowanie odbiorców to mamy do czynienia z otwartym zagadnieniem transportowym. Warunki dla dostawców (i-ty
PROGNOZOWANIE I SYMULACJE EXCEL 1 AUTOR: MARTYNA MALAK PROGNOZOWANIE I SYMULACJE EXCEL 1 AUTOR: MARTYNA MALAK
 1 PROGNOZOWANIE I SYMULACJE 2 http://www.outcome-seo.pl/excel1.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodatek Solver jest dostępny w menu Narzędzia. Jeżeli Solver nie jest
1 PROGNOZOWANIE I SYMULACJE 2 http://www.outcome-seo.pl/excel1.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodatek Solver jest dostępny w menu Narzędzia. Jeżeli Solver nie jest
Optymalizacja zapasów magazynowych przykład optymalizacji
 Optymalizacja zapasów magazynowych przykład optymalizacji www.strattek.pl Strona 1 Spis 1. Korzyści z optymalizacji zapasów magazynowych 3 2. W jaki sposób przeprowadzamy optymalizację? 3 3. Przykład optymalizacji
Optymalizacja zapasów magazynowych przykład optymalizacji www.strattek.pl Strona 1 Spis 1. Korzyści z optymalizacji zapasów magazynowych 3 2. W jaki sposób przeprowadzamy optymalizację? 3 3. Przykład optymalizacji
Opis przedmiotu. Karta przedmiotu - Badania operacyjne Katalog ECTS Politechniki Warszawskiej
 Kod przedmiotu TR.SIK306 Nazwa przedmiotu Badania operacyjne Wersja przedmiotu 2015/16 A. Usytuowanie przedmiotu w systemie studiów Poziom kształcenia Studia I stopnia Forma i tryb prowadzenia studiów
Kod przedmiotu TR.SIK306 Nazwa przedmiotu Badania operacyjne Wersja przedmiotu 2015/16 A. Usytuowanie przedmiotu w systemie studiów Poziom kształcenia Studia I stopnia Forma i tryb prowadzenia studiów
Opis przedmiotu: Badania operacyjne
 Opis : Badania operacyjne Kod Nazwa Wersja TR.SIK306 Badania operacyjne 2013/14 A. Usytuowanie w systemie studiów Poziom Kształcenia Stopień Rodzaj Kierunek studiów Profil studiów Specjalność Jednostka
Opis : Badania operacyjne Kod Nazwa Wersja TR.SIK306 Badania operacyjne 2013/14 A. Usytuowanie w systemie studiów Poziom Kształcenia Stopień Rodzaj Kierunek studiów Profil studiów Specjalność Jednostka
Opis przedmiotu. Karta przedmiotu - Badania operacyjne Katalog ECTS Politechniki Warszawskiej
 Kod przedmiotu TR.NIK405 Nazwa przedmiotu Badania operacyjne Wersja przedmiotu 2015/2016 A. Usytuowanie przedmiotu w systemie studiów Poziom kształcenia Studia I stopnia Forma i tryb prowadzenia studiów
Kod przedmiotu TR.NIK405 Nazwa przedmiotu Badania operacyjne Wersja przedmiotu 2015/2016 A. Usytuowanie przedmiotu w systemie studiów Poziom kształcenia Studia I stopnia Forma i tryb prowadzenia studiów
Spis treści. Przedmowa
 Spis treści Przedmowa 1.1. Magazyn i magazynowanie 1.1.1. Magazyn i magazynowanie - podstawowe wiadomości 1.1.2. Funkcje i zadania magazynów 1.1.3. Rodzaje magazynów 1.1.4. Rodzaje zapasów 1.1.5. Warunki
Spis treści Przedmowa 1.1. Magazyn i magazynowanie 1.1.1. Magazyn i magazynowanie - podstawowe wiadomości 1.1.2. Funkcje i zadania magazynów 1.1.3. Rodzaje magazynów 1.1.4. Rodzaje zapasów 1.1.5. Warunki
A.Miszkiewicz, Wroclaw University of Economic
 A.Miszkiewicz, Wroclaw University of Economic Krótkoterminowe planowanie finansowe na podstawie przedsiębiorstwa z branży z branży firm centralnych (head offices) i holdingów z wyłączeniem holdingów finansowych.
A.Miszkiewicz, Wroclaw University of Economic Krótkoterminowe planowanie finansowe na podstawie przedsiębiorstwa z branży z branży firm centralnych (head offices) i holdingów z wyłączeniem holdingów finansowych.
Rachunek prawdopodobieństwa WZ-ST1-AG--16/17Z-RACH. Liczba godzin stacjonarne: Wykłady: 15 Ćwiczenia: 30. niestacjonarne: Wykłady: 9 Ćwiczenia: 18
 Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Analityka gospodarcza I. Informacje podstawowe Nazwa przedmiotu Rachunek prawdopodobieństwa Nazwa przedmiotu w j. ang. Język prowadzenia przedmiotu
Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Analityka gospodarcza I. Informacje podstawowe Nazwa przedmiotu Rachunek prawdopodobieństwa Nazwa przedmiotu w j. ang. Język prowadzenia przedmiotu
Poziom przedmiotu: II stopnia. Liczba godzin/tydzień: 2W, 2L, 1C PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Matematyka Rodzaj przedmiotu: przedmiot obowiązkowy dla specjalności matematyka finansowa i ubezpieczeniowa Rodzaj zajęć: wykład, laboratorium Metody optymalizacji w ekonomii
Nazwa przedmiotu: Kierunek: Matematyka Rodzaj przedmiotu: przedmiot obowiązkowy dla specjalności matematyka finansowa i ubezpieczeniowa Rodzaj zajęć: wykład, laboratorium Metody optymalizacji w ekonomii
Barometr Finansów Banków (BaFiB) propozycja badania koniunktury w sektorze bankowym
 Jacek Batóg Uniwersytet Szczeciński Barometr Finansów Banków (BaFiB) propozycja badania koniunktury w sektorze bankowym Jednym z ważniejszych elementów każdej gospodarki jest system bankowy. Znaczenie
Jacek Batóg Uniwersytet Szczeciński Barometr Finansów Banków (BaFiB) propozycja badania koniunktury w sektorze bankowym Jednym z ważniejszych elementów każdej gospodarki jest system bankowy. Znaczenie
Z-ZIP-1004 Matematyka dyskretna Discrete mathematics. Stacjonarne Wszystkie Katedra Matematyki Dr hab. Artur Maciąg, prof. PŚk
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod Nazwa Nazwa w języku angielskim Obowiązuje od roku akademickiego 2012/13 Z-ZIP-1004 Matematyka dyskretna Discrete mathematics A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
KARTA MODUŁU / KARTA PRZEDMIOTU Kod Nazwa Nazwa w języku angielskim Obowiązuje od roku akademickiego 2012/13 Z-ZIP-1004 Matematyka dyskretna Discrete mathematics A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
Ćwiczenia laboratoryjne - 4. Projektowanie i harmonogramowanie produkcji metoda CPM-COST. Logistyka w Hutnictwie Ćw. L. 4
 Ćwiczenia laboratoryjne - 4 Projektowanie i harmonogramowanie produkcji metoda CPM-COST Ćw. L. 4 Metody analizy sieciowej 1) Deterministyczne czasy trwania czynności są określane jednoznacznie (jedna liczba)
Ćwiczenia laboratoryjne - 4 Projektowanie i harmonogramowanie produkcji metoda CPM-COST Ćw. L. 4 Metody analizy sieciowej 1) Deterministyczne czasy trwania czynności są określane jednoznacznie (jedna liczba)
Zarządzanie płynnością finansową przedsiębiorstwa
 Zarządzanie płynnością finansową przedsiębiorstwa Cz. 4 Zarządzanie zapasami Składniki zapasów Konieczność utrzymywania zapasów Koszty zapasów 1. Koszty utrzymania zapasów - kapitałowe, - magazynowania,
Zarządzanie płynnością finansową przedsiębiorstwa Cz. 4 Zarządzanie zapasami Składniki zapasów Konieczność utrzymywania zapasów Koszty zapasów 1. Koszty utrzymania zapasów - kapitałowe, - magazynowania,
5. WARUNKI REALIZACJI ZADAŃ LOGISTYCZNYCH
 5. WARUNKI REALIZACJI ZADAŃ LOGISTYCZNYCH Praktyka działania udowadnia, że funkcjonowanie organizacji w sektorze publicznym, jak i poza nim, oparte jest o jej zasoby. Logistyka organizacji wykorzystuje
5. WARUNKI REALIZACJI ZADAŃ LOGISTYCZNYCH Praktyka działania udowadnia, że funkcjonowanie organizacji w sektorze publicznym, jak i poza nim, oparte jest o jej zasoby. Logistyka organizacji wykorzystuje
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
1. Opakowania wielokrotnego użytku: 2. Logistyczny łańcuch opakowań zawiera między innymi następujące elementy: 3. Które zdanie jest prawdziwe?
 1. Opakowania wielokrotnego użytku: A. Są to zwykle opakowania jednostkowe nieulegające zniszczeniu po jednokrotnym użyciu (opróżnieniu), które podlegają dalszemu skupowi. B. Do opakowań wielokrotnego
1. Opakowania wielokrotnego użytku: A. Są to zwykle opakowania jednostkowe nieulegające zniszczeniu po jednokrotnym użyciu (opróżnieniu), które podlegają dalszemu skupowi. B. Do opakowań wielokrotnego
Sterowanie wielkością zamówienia w Excelu - cz. 3
 Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Nazwa przedmiotu. I. Informacje podstawowe. Wydział: Wydział Zarządzania Kierunek: Rachunkowość i Controlling. Nazwa przedmiotu w j. ang.
 Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Rachunkowość i Controlling I. Informacje podstawowe Nazwa przedmiotu Programy komputerowe w rachunkowości Nazwa przedmiotu w j. ang. Język prowadzenia
Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Rachunkowość i Controlling I. Informacje podstawowe Nazwa przedmiotu Programy komputerowe w rachunkowości Nazwa przedmiotu w j. ang. Język prowadzenia
Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02
 Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Metoda analizy hierarchii Saaty ego Ważnym problemem podejmowania decyzji optymalizowanej jest często występująca hierarchiczność zagadnień.
 Metoda analizy hierarchii Saaty ego Ważnym problemem podejmowania decyzji optymalizowanej jest często występująca hierarchiczność zagadnień. Istnieje wiele heurystycznych podejść do rozwiązania tego problemu,
Metoda analizy hierarchii Saaty ego Ważnym problemem podejmowania decyzji optymalizowanej jest często występująca hierarchiczność zagadnień. Istnieje wiele heurystycznych podejść do rozwiązania tego problemu,
Wstęp do teorii niepewności pomiaru. Danuta J. Michczyńska Adam Michczyński
 Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
Metody niedyskontowe. Metody dyskontowe
 Metody oceny projektów inwestycyjnych TEORIA DECYZJE DŁUGOOKRESOWE Budżetowanie kapitałów to proces, który ma za zadanie określenie potrzeb inwestycyjnych przedsiębiorstwa. Jest to proces identyfikacji
Metody oceny projektów inwestycyjnych TEORIA DECYZJE DŁUGOOKRESOWE Budżetowanie kapitałów to proces, który ma za zadanie określenie potrzeb inwestycyjnych przedsiębiorstwa. Jest to proces identyfikacji
Zaawansowane planowanie i harmonogramowanie produkcji. Wrocław r.
 Zaawansowane planowanie i harmonogramowanie produkcji. Wrocław 18.11.2009 r. SIMPLE.APS Zlecenie produkcyjne: pochodzące z zewnętrznych systemów ERP dane o zleceniach produkcyjnych posiadających przypisane
Zaawansowane planowanie i harmonogramowanie produkcji. Wrocław 18.11.2009 r. SIMPLE.APS Zlecenie produkcyjne: pochodzące z zewnętrznych systemów ERP dane o zleceniach produkcyjnych posiadających przypisane
Identyfikacja towarów i wyrobów
 Identyfikacja towarów i wyrobów Identyfikacja towarów i wyrobów w firmie produkcyjnej jest kluczowa pod kątem profesjonalnej obsługi Klienta. Firma chcąc zapewnić wysoką jakość swoich wyrobów musi być
Identyfikacja towarów i wyrobów Identyfikacja towarów i wyrobów w firmie produkcyjnej jest kluczowa pod kątem profesjonalnej obsługi Klienta. Firma chcąc zapewnić wysoką jakość swoich wyrobów musi być
Poziom Obsługi Klienta
 Poziom Obsługi Klienta Zadanie 1. Na podstawie przedstawionego poniżej profilu popytu na telefony komórkowe marki X w salonie firmowym jednego z operatorów sieci telefonii komórkowej, obserwowanego w czasie
Poziom Obsługi Klienta Zadanie 1. Na podstawie przedstawionego poniżej profilu popytu na telefony komórkowe marki X w salonie firmowym jednego z operatorów sieci telefonii komórkowej, obserwowanego w czasie
Proces i narzędzia analizy potencjału wybranych obszarów rynku farmaceutycznego
 Proces i narzędzia analizy potencjału wybranych obszarów rynku farmaceutycznego Przyglądając się rynkowi farmaceutycznemu w Polsce możemy zauważyć, że jest to jedna z lepiej zwymiarowanych i opisanych
Proces i narzędzia analizy potencjału wybranych obszarów rynku farmaceutycznego Przyglądając się rynkowi farmaceutycznemu w Polsce możemy zauważyć, że jest to jedna z lepiej zwymiarowanych i opisanych
POLITYKA ZARZĄDZANIA RYZYKIEM
 POLITYKA ZARZĄDZANIA RYZYKIEM ROZDZIAŁ I Postanowienia ogólne 1.1.Ilekroć w dokumencie jest mowa o: 1) ryzyku należy przez to rozumieć możliwość zaistnienia zdarzenia, które będzie miało wpływ na realizację
POLITYKA ZARZĄDZANIA RYZYKIEM ROZDZIAŁ I Postanowienia ogólne 1.1.Ilekroć w dokumencie jest mowa o: 1) ryzyku należy przez to rozumieć możliwość zaistnienia zdarzenia, które będzie miało wpływ na realizację
2. Ogólne narzędzia controllingowe
 Kluge et al.: Arbeitsmaterial Controlling w zintegrowanych systemach zarzadzania 1 Prof. dr hab. Paul-Dieter Kluge Dr inż. Krzysztof Witkowski Mgr. inż. Paweł Orzeszko Controlling w zintegrowanych systemach
Kluge et al.: Arbeitsmaterial Controlling w zintegrowanych systemach zarzadzania 1 Prof. dr hab. Paul-Dieter Kluge Dr inż. Krzysztof Witkowski Mgr. inż. Paweł Orzeszko Controlling w zintegrowanych systemach
Wykład z modelowania matematycznego. Zagadnienie transportowe.
 Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY WSPOMAGANIA DECYZJI. Kod przedmiotu: Ecs 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY WSPOMAGANIA DECYZJI. Kod przedmiotu: Ecs 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
K.Pieńkosz Badania Operacyjne Wprowadzenie 1. Badania Operacyjne. dr inż. Krzysztof Pieńkosz
 K.Pieńkosz Wprowadzenie 1 dr inż. Krzysztof Pieńkosz Instytut Automatyki i Informatyki Stosowanej Politechniki Warszawskiej pok. 560 A tel.: 234-78-64 e-mail: K.Pienkosz@ia.pw.edu.pl K.Pieńkosz Wprowadzenie
K.Pieńkosz Wprowadzenie 1 dr inż. Krzysztof Pieńkosz Instytut Automatyki i Informatyki Stosowanej Politechniki Warszawskiej pok. 560 A tel.: 234-78-64 e-mail: K.Pienkosz@ia.pw.edu.pl K.Pieńkosz Wprowadzenie
Planowanie przyszłorocznej sprzedaży na podstawie danych przedsiębiorstwa z branży usług kurierskich.
 Iwona Reszetar Uniwersytet Ekonomiczny we Wrocławiu Planowanie przyszłorocznej sprzedaży na podstawie danych przedsiębiorstwa z branży usług kurierskich. Dokument roboczy Working paper Wrocław 2013 Wstęp
Iwona Reszetar Uniwersytet Ekonomiczny we Wrocławiu Planowanie przyszłorocznej sprzedaży na podstawie danych przedsiębiorstwa z branży usług kurierskich. Dokument roboczy Working paper Wrocław 2013 Wstęp
Rys Wykres kosztów skrócenia pojedynczej czynności. k 2. Δk 2. k 1 pp. Δk 1 T M T B T A
 Ostatnim elementem przykładu jest określenie związku pomiędzy czasem trwania robót na planowanym obiekcie a kosztem jego wykonania. Związek ten określa wzrost kosztów wykonania realizacji całego przedsięwzięcia
Ostatnim elementem przykładu jest określenie związku pomiędzy czasem trwania robót na planowanym obiekcie a kosztem jego wykonania. Związek ten określa wzrost kosztów wykonania realizacji całego przedsięwzięcia
Dlaczego należy uwzględniać zarówno wynik maturalny jak i wskaźnik EWD?
 EWD co to jest? Metoda EWD to zestaw technik statystycznych pozwalających oszacować wkład szkoły w końcowe wyniki egzaminacyjne. Wkład ten nazywamy właśnie edukacyjną wartością dodaną. EWD jest egzaminacyjnym
EWD co to jest? Metoda EWD to zestaw technik statystycznych pozwalających oszacować wkład szkoły w końcowe wyniki egzaminacyjne. Wkład ten nazywamy właśnie edukacyjną wartością dodaną. EWD jest egzaminacyjnym
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
Teoria gier. prof. UŚ dr hab. Mariusz Boryczka. Wykład 4 - Gry o sumie zero. Instytut Informatyki Uniwersytetu Śląskiego
 Instytut Informatyki Uniwersytetu Śląskiego Wykład 4 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Instytut Informatyki Uniwersytetu Śląskiego Wykład 4 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Gospodarka zapasami. Studia stacjonarne Semestr letni 2011/2012. Wykład
 Gospodarka zapasami Studia stacjonarne Semestr letni 2011/2012 Wykład 1 9.02.2012 Program wykładów: Przedmiot Gospodarka zapasami obejmuje następujące zagadnienia: Podstawowe pojęcia w zarządzaniu zapasami
Gospodarka zapasami Studia stacjonarne Semestr letni 2011/2012 Wykład 1 9.02.2012 Program wykładów: Przedmiot Gospodarka zapasami obejmuje następujące zagadnienia: Podstawowe pojęcia w zarządzaniu zapasami
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
K A R T A P R Z E D M I O T U
 K A R T A P R Z E D M I O T U AKADEMIA MARYNARKI WOJENNEJ WYDZIAŁ DOWODZENIA I OPERACJI MORSKICH I. CHARAKTERYSTYKA PRZEDMIOTU Nazwa przedmiotu: Zarządzanie systemami logistycznymi Kod: Gua Kierunek studiów:
K A R T A P R Z E D M I O T U AKADEMIA MARYNARKI WOJENNEJ WYDZIAŁ DOWODZENIA I OPERACJI MORSKICH I. CHARAKTERYSTYKA PRZEDMIOTU Nazwa przedmiotu: Zarządzanie systemami logistycznymi Kod: Gua Kierunek studiów:
Zarządzanie projektami
 Dr Adam Kucharski Spis treści Podstawowe pojęcia Metoda CPM 3 3 Przykład analizy metodą CPM 5 Podstawowe pojęcia Przedsięwzięcia złożone z wielu czynności spotykane są na każdym kroku. Jako przykład może
Dr Adam Kucharski Spis treści Podstawowe pojęcia Metoda CPM 3 3 Przykład analizy metodą CPM 5 Podstawowe pojęcia Przedsięwzięcia złożone z wielu czynności spotykane są na każdym kroku. Jako przykład może
...Gospodarka Materiałowa
 1 Gospodarka Materiałowa 3 Obsługa dokumentów magazynowych 4 Ewidencja stanów magazynowych i ich wycena 4 Inwentaryzacja 4 Definiowanie indeksów i wyrobów 5 Zaopatrzenie magazynowe 5 Kontrola jakości 5
1 Gospodarka Materiałowa 3 Obsługa dokumentów magazynowych 4 Ewidencja stanów magazynowych i ich wycena 4 Inwentaryzacja 4 Definiowanie indeksów i wyrobów 5 Zaopatrzenie magazynowe 5 Kontrola jakości 5
Zadania przykładowe na egzamin. przygotował: Rafał Walkowiak
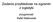 Zadania przykładowe na egzamin z logistyki przygotował: Rafał Walkowiak Punkt zamawiania Proszę określić punkt dokonywania zamawiania jeżeli: zapas bezpieczeństwa wynosi 10 sztuk, czas realizacji zamówienia
Zadania przykładowe na egzamin z logistyki przygotował: Rafał Walkowiak Punkt zamawiania Proszę określić punkt dokonywania zamawiania jeżeli: zapas bezpieczeństwa wynosi 10 sztuk, czas realizacji zamówienia
LOGISTYKA DYSTRYBUCJI II ćwiczenia 3 WYBÓR DOSTAWCY USŁUG WIELOKRYTERIALNE MODELE DECYZYJNE. AUTOR: dr inż. ROMAN DOMAŃSKI WYBÓR DOSTAWCY USŁUG
 1 LOGISTYKA DYSTRYBUCJI II ćwiczenia 3 WIELOKRYTERIALNE MODELE DECYZYJNE AUTOR: dr inż. ROMAN DOMAŃSKI METODY OCENY I WYBORU DOSTAWCÓW 2 Wybór odpowiedniego dostawcy jest gwarantem niezawodności realizowanych
1 LOGISTYKA DYSTRYBUCJI II ćwiczenia 3 WIELOKRYTERIALNE MODELE DECYZYJNE AUTOR: dr inż. ROMAN DOMAŃSKI METODY OCENY I WYBORU DOSTAWCÓW 2 Wybór odpowiedniego dostawcy jest gwarantem niezawodności realizowanych
OPTYMALIZACJA PRZEPŁYWU MATERIAŁU W PRODUKCJI TURBIN W ROLLS-ROYCE DEUTSCHLAND LTD & CO KG
 Andrew Page Rolls-Royce Deutschland Ltd & Co KG Bernd Hentschel Technische Fachhochschule Wildau Gudrun Lindstedt Projektlogistik GmbH OPTYMALIZACJA PRZEPŁYWU MATERIAŁU W PRODUKCJI TURBIN W ROLLS-ROYCE
Andrew Page Rolls-Royce Deutschland Ltd & Co KG Bernd Hentschel Technische Fachhochschule Wildau Gudrun Lindstedt Projektlogistik GmbH OPTYMALIZACJA PRZEPŁYWU MATERIAŁU W PRODUKCJI TURBIN W ROLLS-ROYCE
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Podniesienie poziomu wiedzy studentów z zagadnień dotyczących analizy i syntezy algorytmów z uwzględnieniem efektywności
Nazwa przedmiotu: I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Podniesienie poziomu wiedzy studentów z zagadnień dotyczących analizy i syntezy algorytmów z uwzględnieniem efektywności
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Z-LOG-1004 Matematyka dyskretna Discrete mathematics. Przedmiot podstawowy Wybieralny polski Semestr III
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Z-LOG-1004 Matematyka dyskretna Discrete mathematics A. USYTUOWANIE MODUŁU
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Z-LOG-1004 Matematyka dyskretna Discrete mathematics A. USYTUOWANIE MODUŁU
sprawozdawczego oraz dostarczenie informacji o funkcjonowaniu spółki. Natomiast wadą jest wymóg wyważonego doboru wskaźników, których podstawą jest
 ANALIZA WSKAŹNIKOWA Analiza danych finansowych za pomocą analizy wskaźnikowej wykorzystuje różne techniki badawcze, podkreślając porównawczą oraz względną wagę prezentowanych danych, które mają ocenić
ANALIZA WSKAŹNIKOWA Analiza danych finansowych za pomocą analizy wskaźnikowej wykorzystuje różne techniki badawcze, podkreślając porównawczą oraz względną wagę prezentowanych danych, które mają ocenić
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych. Badania operacyjne. Dr inż.
 Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
1. Eliminuje się ze zbioru potencjalnych zmiennych te zmienne dla których korelacja ze zmienną objaśnianą jest mniejsza od krytycznej:
 Metoda analizy macierzy współczynników korelacji Idea metody sprowadza się do wyboru takich zmiennych objaśniających, które są silnie skorelowane ze zmienną objaśnianą i równocześnie słabo skorelowane
Metoda analizy macierzy współczynników korelacji Idea metody sprowadza się do wyboru takich zmiennych objaśniających, które są silnie skorelowane ze zmienną objaśnianą i równocześnie słabo skorelowane
Analiza finansowa przedsiębiorstw z punktu widzenia współpracującego z analizowanym przedsiębiorstwem
 Agnieszka Mikołajczyk Uniwersytet Ekonomiczny we Wrocławiu Analiza finansowa przedsiębiorstw z punktu widzenia współpracującego z analizowanym przedsiębiorstwem Słowa kluczowe: rentowność, zadłużenie,
Agnieszka Mikołajczyk Uniwersytet Ekonomiczny we Wrocławiu Analiza finansowa przedsiębiorstw z punktu widzenia współpracującego z analizowanym przedsiębiorstwem Słowa kluczowe: rentowność, zadłużenie,
Zarządzanie logistyką w przedsiębiorstwie
 Zarządzanie logistyką w przedsiębiorstwie Cele szkolenia Zasadniczym celem szkolenia jest rozpracowanie struktury organizacyjnej odpowiedzialnej za organizację procesów zaopatrzeniowo - dystrybucyjnych,
Zarządzanie logistyką w przedsiębiorstwie Cele szkolenia Zasadniczym celem szkolenia jest rozpracowanie struktury organizacyjnej odpowiedzialnej za organizację procesów zaopatrzeniowo - dystrybucyjnych,
TSM TIME SLOT MANAGEMENT
 TSM TIME SLOT MANAGEMENT System zarządzania zamówieniami i oknami czasowymi dostaw Spis treści O Firmie Nam zaufali Możliwości rozwiązań О produkcie Bezpieczeństwo i dostęp do informacji Problemy produkcyjne
TSM TIME SLOT MANAGEMENT System zarządzania zamówieniami i oknami czasowymi dostaw Spis treści O Firmie Nam zaufali Możliwości rozwiązań О produkcie Bezpieczeństwo i dostęp do informacji Problemy produkcyjne
Teoria gier. dr Przemysław Juszczuk. Wykład 2 - Gry o sumie zero. Instytut Informatyki Uniwersytetu Śląskiego
 Instytut Informatyki Uniwersytetu Śląskiego Wykład 2 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Instytut Informatyki Uniwersytetu Śląskiego Wykład 2 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Krótkoterminowe planowanie finansowe na przykładzie przedsiębiorstw z branży wydawniczej
 Uniwersytet Ekonomiczny we Wrocławiu Krótkoterminowe planowanie finansowe na przykładzie przedsiębiorstw z branży wydawniczej Karolina Piątkowska Wrocław 2013 Spis treści: Wstęp... 3 I. Opis teoretyczny
Uniwersytet Ekonomiczny we Wrocławiu Krótkoterminowe planowanie finansowe na przykładzie przedsiębiorstw z branży wydawniczej Karolina Piątkowska Wrocław 2013 Spis treści: Wstęp... 3 I. Opis teoretyczny
Ujawnienia informacji związanych z adekwatnością kapitałową ERSTE Securities Polska S.A. według stanu na dzień 31.12.2011 r.
 Ujawnienia informacji związanych z adekwatnością kapitałową ERSTE Securities Polska S.A. według stanu na dzień 31.12.2011 r. Niniejsze Sprawozdanie stanowi wykonanie Polityki Informacyjnej Domu Maklerskiego
Ujawnienia informacji związanych z adekwatnością kapitałową ERSTE Securities Polska S.A. według stanu na dzień 31.12.2011 r. Niniejsze Sprawozdanie stanowi wykonanie Polityki Informacyjnej Domu Maklerskiego
 Zapraszamy do współpracy FACULTY OF ENGINEERING MANAGEMENT www.fem.put.poznan.pl Agnieszka Stachowiak agnieszka.stachowiak@put.poznan.pl Pokój 312 (obok czytelni) Dyżury: strona wydziałowa Materiały dydaktyczne:
Zapraszamy do współpracy FACULTY OF ENGINEERING MANAGEMENT www.fem.put.poznan.pl Agnieszka Stachowiak agnieszka.stachowiak@put.poznan.pl Pokój 312 (obok czytelni) Dyżury: strona wydziałowa Materiały dydaktyczne:
ECONOMIC ORDER QUANTITY (EOQ)
 Systemy Logistyczne Wojsk nr 41/2014 MODEL EKONOMICZNEJ WIELKOŚCI ZAMÓWIENIA (EOQ) ECONOMIC ORDER QUANTITY (EOQ) Małgorzata GRZELAK Jarosław ZIÓŁKOWSKI Wojskowa Akademia Techniczna Wydział Logistyki Instytut
Systemy Logistyczne Wojsk nr 41/2014 MODEL EKONOMICZNEJ WIELKOŚCI ZAMÓWIENIA (EOQ) ECONOMIC ORDER QUANTITY (EOQ) Małgorzata GRZELAK Jarosław ZIÓŁKOWSKI Wojskowa Akademia Techniczna Wydział Logistyki Instytut
Plan wykładu. Przykład. Przykład 3/19/2011. Przykład zagadnienia transportowego. Optymalizacja w procesach biznesowych Wykład 2 DECYZJA?
 /9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
/9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
