2.2 Model odsetek prostych 9
|
|
|
- Julia Kowalik
- 8 lat temu
- Przeglądów:
Transkrypt
1 2.2 Model odsetek prostych 9 Uwaga Komentarza wymaga znaczenie stopy bazowej. Z definicji wynika, że i T = FV PV, co wcale nie oznacza, że wartość indeksu i PV T zależy od wartości pocz atkowej PV.Wskaźnik i T liczbowo przedstawia dwa aspekty MOP: czas trwaniazjawiskaorazjegodynamikȩ. Miar a dynamiki zjawiska zmiany wartości kapita lu w czasie jest iloraz K(t o +Δt) K(t o ), Δt gdzie 0 t o <T, Δt >0 i t o +Δt T.Zauważmy, że z za lożenia (2.1) iwzoru (2.2), dla danego MOP dynamika ta jest zawsze sta la i wynosi q = FV PV T. W takim razie, jeśli dla takiego MOP zmieni a siȩ warunki brzegowe na PV i to zawsze FV PV FV PV = = i PV T. PV FV, Uwaga MOP odpowiada klasyczna transakcja, któr a najprościej jest opisać w uk ladzie bilateralnym. Dane s a dwa podmioty A i B, zktórych podmiot A dysponuje nadwyżk a finansow a reprezentuje podaż, podmiot B reprezentuje popyt. Podmioty te zawieraj a umowȩ: na określony czas (liczony w ilościach dni) podmiot A pożycza podmiotowi B kapita l w wysokości PV,który musi być zwrócony na koniec. Miar a poniesionego kosztu przez podmiot B s a odsetki naliczone jednorazowo od pożyczonego kapita lu za czas trwania transakcji. Dla podmiotu A odsetki te s a zyskiem z transakcji. Przyk lad Wspólnota mieszkaniowa lokuje z l na lokacie rocznej w banku, której oprocentowanie w skali roku wynosi 5%. Ile wspólnota otrzyma po up lywie roku? Mamy tutaj obraz sytuacji opisanej w uwadze powyżej. Z za lożenia T = (liczba dni roku), i T =0, 05, PV = Zysk z lokaty, to odsetki I T za okres T,dlategoPV + I T stanowi kwotȩ jak a otrzyma wspólnota po roku, czyli FV = PV + I T = , 05 = W praktyce wygodniej jest pos lugiwać siȩ standardow a d lugości a okresu T jak a jest (patrz przyk lad wyżej). Ponieważ wtedy na ogó l T <,należy przed lużyć funkcjȩ t K(t) z przedzia lu [0,T] na przedzia l [0,] (patrz rys. 3). Oczywiście dalej dostaniemy funkcjȩ liniow a. Po podstawieniu t = do wzoru (2.5) otrzymamy K() =PVi T T + PV. (2.9) 9
2 10 Matematyka finansowa i bankowa Oznaczaj ac we wzorze (2.9), R = i T T, czyli i T = R T, (2.10) dostaniemy zasadȩ dopasowania stopy bazowej do stopy rocznej R zwanej teżstop a p.a. (z lac. per annum). K PV T t Rysunek 2.3: ilustracja przed lużenia funkcji t K(t) Przyk lad Wspólnota stoi przed wyborem: czy ulokować 5000 z l na pó l roku wed lug stopy rocznej 7%, czy4000 z l na rok wed lug stopy rocznej 9%. Ztreści przyk ladu możemy siȩ domyślać, że wspólnota nie dysponuje duż a nadwyżk a finansow a i dlatego rozważa różne okresy deponowania swoich środków, bior ac 10
3 2.2 Model odsetek prostych 11 pod uwagȩ ryzyko zwi azane ze zjawiskiem utraty p lynności. Zauważmy, że warianty brane pod uwagȩ s a nieporównywalne. Zgodnie bowiem z zasad a datowania kapita lu nie można ze sob a porównywać wartości przysz lych datowanych różnie. W takim razie wariant pierwszy należy prolongować doca lego roku. Niech I T, gdzie T = oznaczaj a odsetki dla wariantu pierwszego za okres T, I 2 1 odsetki zuwzglȩdnieniem przed lużenia tej transakcji, a wiȩc należne po up lywie roku. Wtedy, z zasady dopasowania stopy, dlastopyi T =0, 07 /2 =0, 035 dostaniemy I 1 = 5000 i T i T = 350. Tymczasem odsetki I 2 należne również po roku z transakcji drugiej wynios a I 2 = , 09 = 360. ponieważ I 2 >I 1,wiȩc przy nie uwzglȩdnianiu ryzyka zwi azanego z być może utrat a p lynności, wariant drugi jest korzystniejszy. Analiza przedstawiona w powyższym przyk ladzie prowadzi nas do nastȩpuj acego wniosku Wniosek Przypuśćmy, że MOP z parametrami: T,PV,i T zosta l prolongowany do okresu nt dla pewnej liczby naturalnej n>1. Oznaczmy przez FV n wartość przysz l a po up lywie czasu nt.wtedy FV n = PV + I 1 + I I n, (2.11) gdzie I j oznaczaj a odsetki liczone od wartości pocz atkowej PV za okres T. Zauważmy, że ponieważ odsetki I j s a należne dopiero po up lywie nt dni, datowane s a jednakowo i dlatego można je dodaj ac kumulować. W takim razie, z (2.11) dostaniemy FV n = PV + PVi T PVi T = PV + PVni T = PV(1 + ni T ). (2.12) Na koniec zauważmy, że do takiego samego wyniku możemy dojść przed lużaj ac funkcjȩ t K(t) do przedzia lu [0,nT], takjaktozrobiliśmy w przypadku zasady dostosowania stopy. Istotnie, ze wzoru (2.3), po podstawieniu t = nt dostaniemy FV n = K(nT )=PVi T nt T + PV = PV(1 + ni T ). Procedura opisana w ostatnim wniosku ma znaczenie czysto teoretyczne, jak pokazaliśmy to w powyższym przyk ladzie. W praktyce spotykamy siȩ zezja- wiskiem w pewnym sensie odwrotnym. Dok ladniej, w pierwszej fazie trwania transakcji z parametrami: T,i T,PV, po up lywie T 1 dni, 0 <T 1 <Tzaczȩ la obowi azywać nowastopar 1 podana jako stopa p.a. Po up lywie kolejnych T 2 11
4 12 Matematyka finansowa i bankowa dni, T 1 + T 2 <T zaczȩ la obowi azywać stopa p.a. R 2. Wreszcie, po up lywie kolejnych T n 1 dni, T 1 + T T n 1 <T,dokońca przez T n dni obowi azywa la stopa p.a. R n 1 (patrz rys. 4)). Wyliczymy w zaistnia lej sytuacji przys luguj ace odsetki w ramach MOP. it R1 R2 Rn-1 x x x x x x 0 i1 T1 i2 T1+T2 i3 T1+T2+T3 T1+ +Tn-1 in T=T1+ +Tn Rysunek 2.4: ilustracja zjawiska zmiany stopy bazowej w MOP W tym celu podzielmy oryginalny przedzia l czasowy [0,T] chwilami: T 1,T 1 + T 2,...,T = T 1 + T T n.dlakażdego z tak powsta lych podokresów niech i j oznacza obowi azuj ac a w nim stopȩ. Dostaniemy kolejno: T 1 i 1 = i T T,i T 2 2 = R 1,...,i T n n = R n 1. Wtedy odsetki I j naliczone za kolejne podokresy od wartości pocz atkowej wed lug stopy i j wynios a I j = PVi j. Ponieważ należne bȩd a dopiero po up lywie T dni, jako jednakowo datowane bȩdzie je można skumulować do wartości I T. Dlatego I T = I 1 + I I n = PV(i 1 + i i n ). Przyk lad Wdniu17marcaw laściciele lokali we wspólnocie Alternatywy 4 zobowi azali zarz adcȩ doulokowaniawolnychśrodków stanowi acych rezerwy z op lat bież acych w laścicieli w wysokości 8000 z l na rocznej lokacie terminowej oprocentowanej na 8%. Zarz adca nastȩpnego dnia wykona l dyspozycje w banku zgodn a zuchwa l aw laścicieli. Po up lywie 90 dni od za lożenia lokaty bank powiadomi l zarz adcȩ o zmianie stopy p.a. na 7%. Niestety, 10 grudnia tego samego roku nast api la awaria instalacji elektrycznej, zmuszaj aca wspólnotȩ do natychmiastowej likwidacji lokaty celem pokrycia kosztów remontu. Bank w takiej sytuacji nalicza odsetki wed lug MOP. Obliczyć wysokość odsetek należnych wspólnocie. Przyj ać, że rok ten ma 365 dni. Zaczynamy od konstrukcji przedzia lu czasowego i kolejnych podokresów (patrz rys. 5). Pocz atkiem przedzia lu jest dzień 18 marca. Wydarzeniem, które wyróżnia pierwszy podokres jest zmiana oprocentowania i liczy on 90 dni. Kończy siȩ zatem 25 czerwca. Kolejny podokres trwa od 26 czerwca do 10 grudnia i spowodowany jest zerwaniem umowy o lokatȩ. Okres ten trwa 168 dni. W okresach tych 12
5 2.2 Model odsetek prostych 13 obowi azuj a stopy bazowe, gdzie 90 i 1 =0, =0, 019, i 2 =0, =0, St ad I T = I 1 + I 2,gdzieT = 258 oraz I 1 = PVi 1 = , 019 = 152, 00, I 2 = PVi 2 = , 032 = 257, 75, czyli I T = 409, i1 90 i2 258 x x x 18 marca 25 czerwca 10 grudnia Rysunek 2.5: ilustracja do przyk ladu
6 14 Matematyka finansowa i bankowa 2.3 Model odsetek z lożonych Weźmy klasyczny przypadek MOP z parametrami: T,i T,PV,FV. Okres [0,T] podtraktujmy jako kolejny j ty podokres przedzia lu czasowego [0,nT]dla n>1 z parametrami: i T,PV j,fv j,gdziefv j = PV j+1, czyli wartość przysz la j tego podokresu jest wartości a teraźniejsz a podokresu nastȩpnego j + 1 (patrz rysunek 6). Wtedy na mocy MOP Wtakimrazie FV j = PV j (1 + i T ), dla j =1, 2,...,n. (2.13) FV 2 = PV 2 (1 + i T )=FV 1 (1 + i T )=PV(1 + i T )(1 + i T )=PV(1 + i T ) 2. I ogólnie, dla każdego 1 j n FV j = PV(1 + i T ) j. (2.14) W szczególności FV n = PV(1 + i T ) n. (2.15) Zjawisko oparte na powyższych za lożeniach i opisane wzorami (2.13) (2.15) nazywamy modelem odsetek z lożonych (MOZ). Natomiast równość FV j = PV j+1 nazywamy kapitalizacj a odsetek, bowiem odsetki naliczone na koniec okresu w wysokości PV j i T powiȩkszaj a kapita l PV j staj ac siȩ sk ladow a kolejnego kapita lu pocz atkowego PV j+1.mówimy też, że odsetki skapitalizowa ly siȩ. PV=PV1 FV1=PV2 FV2=PV3 FVn 0 x T x 2T nt Rysunek 2.6: ilustracja do MOZ Przyk lad Wspólnota mieszkaniowa lokuje na trzy lata 5000 z l na koncie bankowym oprocentowanym w skali roku na 6%. Zak ladaj ac MOZ z kapitalizacj a pó lroczn a wyznaczyćwartość depozytu na koniec umowy. Zza lożenia mamy do czynienia z n = 6 krotn a kapitalizacj a, ze stop a bazow a i T =0, 06 /2 =0, 03. W takim razie, z (2.15) dostaniemy FV 6 = 5000 (1 + 0, 03) 6 = 5970, 26. Gdybyśmy zdecydowali siȩ tylko na dwukrotne prolongowanie rocznej lokaty, to zgodnie z MOP FV 6 = 5000 ( , 06) = 5900,
7 2.3 Model odsetek z lożonych 15 I ogólnie, ponieważ dla każdej liczby naturalnej n 2 i liczby rzeczywistej a 0 zachodzi nierówność Bernoulliego (1 + a) n > 1+na, widzimy, że MOZ z lożony z n krotnej kapitalizacji z lożonej jest wydajniejszy od MOP realizuj acego dla tych samych podokresów zjawisko prolongaty, czyli PV(1 + i T ) n >PV(1 + ni T ). Wróćmy do powyższego przyk ladu i wyznaczmy wartości naliczonych odsetek na koniec kolejnych podokresów (patrz rys. 7). I1 I2 I3 I4 I5 I6 x x x x x PV PV1=FV PV2=FV1 PV3=FV2 PV4=FV3 PV5=FV4 6T=FV5 Rysunek 2.7: ilustracja do przyk ladu ZMOP,przyuwzglȩdnieniu zjawiska kapitalizacji dostaniemy kolejno: I 1 = PVi T = , 03 = 150, I 2 = PV 1 i T = FVi T =(PV + I 1 )i T = , 03 = 154, 50, I 3 = PV 2 i T = FV 1 i T =(PV 1 + I 2 )i T = 5304, 5 0, 03 = 159, 14, I 4 = PV 3 i T = FV 2 i T =(PV 2 + I 3 )i T = 5463, 64 0, 03 = 163, 91, I 5 = PV 4 i T = FV 3 i T =(PV 3 + I 4 )i T = 5627, 55 0, 03 = 168, 83, I 6 = PV 5 i T = FV 4 i T =(PV 4 + I 5 )i T = 5796, 38 0, 03 = 173, 89. I ostatecznie FV 5 = PV 5 + I 6 = 5796, , 89 = 5970, 27. W sytuacji ogólnej, ponieważ FV j = PV j + I j oraz PV j = FV j 1,dostaniemy FV j = PV j + I j = FV j 1 + I j, (2.16) sk ad ze wzoru (2.15) otrzymamy I j = FV j FV j 1 = PV(1 + i T ) j PV(1 + i T ) j 1 = PVi T (1 + i T ) j 1. (2.17) Z drugiej strony możemy mówić oodsetkachi sk takich, że FV n = PV + I sk, czyli I sk = I T. (2.18) 15
8 16 Matematyka finansowa i bankowa Wtedy ze wzoru (2.15) I sk = PV((1 + i T ) n 1). (2.19) Odsetki te (nie mylić zodsetkamii j ) nazwiemy dalej odsetkami skumulowanymi. Ich rolȩ wyjaśnia kolejny przyk lad Przyk lad Wspólnota mieszkaniowa podejmuje decyzjȩ o wp lacie do banku na trzy lata kwoty z l stanowi acej środki funduszu remontowego. Obowi azuj aca w tym okresie stopa roczna wynosi 8%, odsetki kapitalizowane s a w cyklu rocznym. O ile powiȩkszy siȩ z lożony kapita l na koniec umowy? O jak a wartość przyrosn a odsetki po pierwszym, po drugim oraz po trzecim roku trwania lokaty? Kapita l powiȩkszy siȩ o odsetki skumulowane. Obliczymy je zgodnie z formu l a (2.19), co daje I sk = PV((1 + i T ) n 1) = (1, ) = 5194, 24. Po pierwszym roku lokaty wartość odsetek wyniesie zgodnie ze wzorem (2.17) Po drugim roku Po trzecim, ostatnim roku I 1 = PVi T = , 08 = 1600, 00. I 2 = PVi T (1 + i T ) = , 08 1, 08 = 1728, 00. I 3 = PVi T (1 + i T ) 2 = , 08 1, = 1866, 24. Zauważmy, że I 1 + I 2 + I 3 = 5194, 24 = I sk. Ostatni wynik wymaga komentarza. Z jednej strony pope lniamy b l ad, lami ac zapis zasady porównywania kapita lu, próbuj ac dodawać do siebie kapita l różnie datowany. Z drugiej strony na przytoczonym przyk ladzie zauważamy pewn a prawid lowość. Odniesiemy siȩ najpierw do drugiej kwestii. W tym celu weźmy pod uwagȩ wartości kolejnych odsetek: I 1,I 2,...,I n. Spośród nich wybierzmy s asiednie I j,i j+1 ikorzystaj ac z (2.17) podzielmy je przez siebie I j+1 I j = PVi T (1 + i T ) j PVi T (1 + i T ) j 1. Po uproszeniu dostaniemy I j+1 I j =1+i T, 16
9 2.3 Model odsetek z lożonych 17 co oznacza, że każdy taki iloraz jest jednakowy. W matematyce mówimy wtedy, że I 1,I 2,...,I n s a kolejnymi wyrazami ci agu geometrycznego o ilorazie równym 1+i T. Ponadto wiadomo, że wtedy I 1 + I I n = I 1 1 (1 + i T ) n 1 (1 + i T ), (2.20) co po uproszeniu i skorzystaniu ze wzoru na I sk daje I 1 + I I n = PVi T (1 + i T ) n 1 i T = PV((1 + i T ) n 1) = I sk. (2.21) Zatem w MOZ zawsze odsetki skumulowane równe s a sumie odsetek naliczonych za kolejne okresy kapitalizacji. Usprawidliwieniem możliwości dodawania do siebie tych odsetek jest fakt, że ich należność zapada dopiero na koniec kapitalizacji i w tym sensie s a jednakowo datowane. Możemy teraz zdefiniować kolejn astopȩ i ef, gdzie na mocy (2.21), i ef = I sk PV = I T PV =(1+i T ) n 1, (2.22) któr a nazywamy stop a efektywn a wmozzaokresnt. Zauważmy, że dla tej stopy FV n = PV + PVi ef. (2.23) Ponadto, z nierówności Bernoulliego, dla tej stopy mamy nierówność, której wersjȩ już widzieliśmy przy porównaniu obu modeli odsetkowych i ef >ni T, o ile n 2. (2.24) Przyk lad Wspólnota mieszkaniowa otrzyma la dwie propozycje ulokowania wolnych środków: z l na 18 miesiȩcy z kapitalizacj a kwartaln a w.g. stopy p.a. równej 7%; z l na 18 miesiȩcy z kapitalizacj a pó lroczn a w.g. stopy p.a. R. Dla jakiej wartości R wariant pierwszy bȩdzie korzystniejszy? Ponieważ 6T 1 =3T 2,gdzieT 1 i T 2 oznaczaj a okresy kapitalizacji dla tych wariantów, wykorzystamy pojȩcie stopy efektywnej. Dla wariantu pierwszego mamy: i T1 =0, 07 1/4 =0, 0175, 17
10 18 Matematyka finansowa i bankowa wiȩc I sk1 = I 6T1 = PV 1 ((1 + i T1 ) 6 1) = (1, ) = 1097, 02. Dlatego i ef1 = I sk 1 = 0, PV 1 Wartość stopyr musi być taka, aby i ef1 >i ef2, bowiem obie stopy efektywne obejmuj a ten sam okres. Oznacza to, że 0, 1097 > Po przekszta lceniu otrzymamy idlategor<0, 0706, czyli R<7, 06%. ( 1+ R 2 ) 3 1, bowiem it2 = R R 2 < 3 1, 1097 = 1, 0353 Dla MOZ z parametrami: PV,i T,n porównamy teraz wartość stopy efektywnej ze stop a roczn a. Zaczniemy od przyk ladu liczbowego, wykorzystuj ac do tego celu dane z przyk ladu powyższego: R =0, 07, i ef =0, Problem polega na tym, że stopy te odnosz a siȩ do różnych okresów dlatego nie można ich porównywać. W takim razie należy wartość stopy efektywnej zrelatywizować do okresu. W tym celu do jej obliczenia należy wzi ać takien o,że n o T =, ( ) co w naszym przypadku oznacza, że n o =4. WtedyPV (1 + i T ) no 1 opisuje zysk z MOZ za okres roku. Oznaczmy tȩ stopȩ przez i o, czyli i o =(1+i T ) no 1=1, = 0, >R. Rozważmy teraz sytuacjȩ ogóln a. Wtedy i T Za lóżmy, że n o T = = R T i i ef =(1+i T ) n 1. dla pewnej liczby naturalnej n o, co oznacza, że T<iwci agu kapitalizacja przebiega ca lkowit a ilość razy.wtedy i o = ( 1+R T ) no ( 1= 1+ R ) no 1. n o Znierówności Bernoulliego mamy teraz i o >R, o ile n o 2. Możemy wiȩc sformu lować nastȩpuj acy wniosek 18
11 2.3 Model odsetek z lożonych 19 Wniosek Niech dla MOZ, T<iwci agu kapitalizacja odbywa siȩ n o razy, czyli n o T =. Jeśli n o =1,toi o = R = i T. W przeciwnym razie mamy zawsze R<i o. Stopȩ i o dalej bȩdziemy nazywali efektywn a stop a nominaln a. Poznaliśmy w ten sposób cztery rodzaje stóp procentowych: stopȩ bazow a i T,stopȩp.a. R, stopȩ efektywn a i ef istopȩ efektywn a nominaln a i o.wnastȩpnym rozdziale poznamy kolejn a, pi at a stopȩ stopȩ dyskontow a. 19
Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010
 R. Rȩbowski 1 WPROWADZENIE Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010 1 Wprowadzenie Powszechnie uważa siȩ, że metoda simplex, jako uniwersalny algorytm pozwalaj acyznaleźć rozwi azanie optymalne
R. Rȩbowski 1 WPROWADZENIE Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010 1 Wprowadzenie Powszechnie uważa siȩ, że metoda simplex, jako uniwersalny algorytm pozwalaj acyznaleźć rozwi azanie optymalne
Czym jest ciąg? a 1, a 2, lub. (a n ), n = 1,2,
 Ciągi liczbowe Czym jest ciąg? Ciąg liczbowy, to funkcja o argumentach naturalnych, której wartościami są liczby rzeczywiste. Wartość ciągu dla liczby naturalnej n oznaczamy symbolem a n i nazywamy n-tym
Ciągi liczbowe Czym jest ciąg? Ciąg liczbowy, to funkcja o argumentach naturalnych, której wartościami są liczby rzeczywiste. Wartość ciągu dla liczby naturalnej n oznaczamy symbolem a n i nazywamy n-tym
Finanse i Rachunkowość studia stacjonarne Wprowadzenie do Matematyki Finansowej 1 (treść wykładów z 14 i 21 stycznia 2015)
 dr inż. Ryszard Rębowski 1 SFORMUŁOWANIE GŁÓWNEGO PROBLEMU Finanse i Rachunkowość studia stacjonarne Wprowadzenie do Matematyki Finansowej 1 (treść wykładów z 14 i 21 stycznia 2015) 1 Sformułowanie głównego
dr inż. Ryszard Rębowski 1 SFORMUŁOWANIE GŁÓWNEGO PROBLEMU Finanse i Rachunkowość studia stacjonarne Wprowadzenie do Matematyki Finansowej 1 (treść wykładów z 14 i 21 stycznia 2015) 1 Sformułowanie głównego
Zastosowania matematyki
 Zastosowania matematyki Monika Bartkiewicz 1 / 143 Dyskonto-przypomnienie Obliczanie kapitaªu pocz tkowego P v na podstawie znanej warto±ci kapitaªu ko«cowego F v nazywa si dyskontowaniem kapitaªu F v.
Zastosowania matematyki Monika Bartkiewicz 1 / 143 Dyskonto-przypomnienie Obliczanie kapitaªu pocz tkowego P v na podstawie znanej warto±ci kapitaªu ko«cowego F v nazywa si dyskontowaniem kapitaªu F v.
3.3 Budżet nieruchomości. aktualnej ceny przeciȩtnego, nie odbiegaj acego standardem lokalu;
 3.3 Budżet nieruchomości 47 aktualnej ceny przeciȩtnego, nie odbiegaj acego standardem lokalu; danych o charakterze demograficznym celem ustalenia liczby potencjalnych nabywców, najemców; tendencji na
3.3 Budżet nieruchomości 47 aktualnej ceny przeciȩtnego, nie odbiegaj acego standardem lokalu; danych o charakterze demograficznym celem ustalenia liczby potencjalnych nabywców, najemców; tendencji na
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Teoria miary WPPT IIr. semestr zimowy 2009 Wyk lady 6 i 7. Mierzalność w sensie Carathéodory ego Miara Lebesgue a na prostej
 Teoria miary WPPT IIr. semestr zimowy 2009 Wyk lady 6 i 7. Mierzalność w sensie Carathéodory ego Miara Lebesgue a na prostej 27-28/10/09 ZBIORY MIERZALNE WZGLȨDEM MIARY ZEWNȨTRZNEJ Niech µ bȩdzie miar
Teoria miary WPPT IIr. semestr zimowy 2009 Wyk lady 6 i 7. Mierzalność w sensie Carathéodory ego Miara Lebesgue a na prostej 27-28/10/09 ZBIORY MIERZALNE WZGLȨDEM MIARY ZEWNȨTRZNEJ Niech µ bȩdzie miar
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice
 Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Zajęcia 1. Pojęcia: - Kapitalizacja powiększenie kapitału o odsetki, które zostały przez ten kapitał wygenerowane
 Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
3.4 Podstawy analizy finansowo ekonomicznej nieruchomości
 52 Ekonomiczne podstawy zarz adzania nieruchomościami Lp. Pozycja 2010 2011 2012 Koszty 9.3 RAZEM(9.1+9.2) 10. Koszty razem(8.6+9.3) 11. Przychody razem (z przeniesienia) 12. Fundusz remontowy na k. roku
52 Ekonomiczne podstawy zarz adzania nieruchomościami Lp. Pozycja 2010 2011 2012 Koszty 9.3 RAZEM(9.1+9.2) 10. Koszty razem(8.6+9.3) 11. Przychody razem (z przeniesienia) 12. Fundusz remontowy na k. roku
Niech X bȩdzie dowolnym zbiorem. Dobry porz adek to relacja P X X (bȩdziemy pisać x y zamiast x, y P ) o w lasnościach:
 Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Rozdzia l 3. Elementy algebry uniwersalnej
 Rozdzia l 3. Elementy algebry uniwersalnej 1. Podalgebry, homomorfizmy Definicja. Niech = B A oraz o bȩdzie n-argumentow a operacj a na zbiorze A. Mówimy, że zbiór B jest zamkniȩty na operacjȩ o, gdy dla
Rozdzia l 3. Elementy algebry uniwersalnej 1. Podalgebry, homomorfizmy Definicja. Niech = B A oraz o bȩdzie n-argumentow a operacj a na zbiorze A. Mówimy, że zbiór B jest zamkniȩty na operacjȩ o, gdy dla
2a. Przeciętna stopa zwrotu
 2a. Przeciętna stopa zwrotu Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2a. Przeciętna stopa zwrotu Matematyka
2a. Przeciętna stopa zwrotu Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2a. Przeciętna stopa zwrotu Matematyka
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Jednorazowa sk ladka netto w przypadku stochastycznej stopy procentowej. Ubezpieczenie na ca le życie z n-letnim okresem odroczenia.
 Jednorazowa sk ladka netto w przypadku stochastycznej stopy procentowej Ubezpieczenie na ca le życie z n-letnim okresem odroczenia Wartość obecna wyp laty Y = Zatem JSN = = Kx +1 0, K x = 0, 1,..., n 1,
Jednorazowa sk ladka netto w przypadku stochastycznej stopy procentowej Ubezpieczenie na ca le życie z n-letnim okresem odroczenia Wartość obecna wyp laty Y = Zatem JSN = = Kx +1 0, K x = 0, 1,..., n 1,
Zajęcia 8 - Równoważność warunków oprocentowania
 Zajęcia 8 - Równoważność warunków oprocentowania Zadanie 1 Mając roczną stopę oprocentowania prostego 18% wyznaczyć równoważną stopę: 1. miesięczną. 2. tygodniową. 3. 2-letnią. Uzasadnić wyniki. Czy czas
Zajęcia 8 - Równoważność warunków oprocentowania Zadanie 1 Mając roczną stopę oprocentowania prostego 18% wyznaczyć równoważną stopę: 1. miesięczną. 2. tygodniową. 3. 2-letnią. Uzasadnić wyniki. Czy czas
Rozdzia l 10. Najważniejsze normalne logiki modalne
 Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
INDEKS FINANSISTY. Monika Skrzydłowska. PWSZ w Chełmie. wrzesień Projekt dofinansowała Fundacja mbanku
 INDEKS FINANSISTY Monika Skrzydłowska PWSZ w Chełmie wrzesień 2017 Projekt dofinansowała Fundacja mbanku Monika Skrzydłowska (PWSZ w Chełmie) INDEKS FINANSISTY wrzesień 2017 1 / 40 Spis treści 1 Wprowadzenie
INDEKS FINANSISTY Monika Skrzydłowska PWSZ w Chełmie wrzesień 2017 Projekt dofinansowała Fundacja mbanku Monika Skrzydłowska (PWSZ w Chełmie) INDEKS FINANSISTY wrzesień 2017 1 / 40 Spis treści 1 Wprowadzenie
ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 3 Tablice trwania życia 2
 Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 3 Tablice trwania życia 2 1 Przypomnienie Jesteśmy już w stanie wyznaczyć tp x = l x+t l x, gdzie l x, l x+t, to liczebności kohorty odpowiednio
Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 3 Tablice trwania życia 2 1 Przypomnienie Jesteśmy już w stanie wyznaczyć tp x = l x+t l x, gdzie l x, l x+t, to liczebności kohorty odpowiednio
ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne.
 Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne. 1 Przypomnienie Umowa ubezpieczenia zawiera informacje o: Przedmiocie ubezpieczenia Czasie
Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne. 1 Przypomnienie Umowa ubezpieczenia zawiera informacje o: Przedmiocie ubezpieczenia Czasie
4. Strumienie płatności: okresowe wkłady oszczędnościowe
 4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1
 1 STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1 Klasyczny Rachunek Prawdopodobieństwa. 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany. Posiadamy
1 STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1 Klasyczny Rachunek Prawdopodobieństwa. 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany. Posiadamy
1940, 17 = K 4 = K 2 (1, 05)(1 + x 200 )3. Stąd, po wstawieniu K 2 dostaję:
 Poniższe rozwiązania są jedynie przykładowe. Każde z tych zadań da się rozwiązać na wiele sposobów, ale te na pewno są dobre (i prawdopodobnie najprostsze). Komentarze (poza odpowiedziami) są zbędne -
Poniższe rozwiązania są jedynie przykładowe. Każde z tych zadań da się rozwiązać na wiele sposobów, ale te na pewno są dobre (i prawdopodobnie najprostsze). Komentarze (poza odpowiedziami) są zbędne -
Geometria odwzorowań inżynierskich perspektywa wnȩtrza 06C
 Scriptiones Geometrica Volumen I (2014), No. 6C, 1 8. Geometria odwzorowań inżynierskich perspektywa wnȩtrza 06C Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa czo lowa wnȩtrza Rys. 6C-01:
Scriptiones Geometrica Volumen I (2014), No. 6C, 1 8. Geometria odwzorowań inżynierskich perspektywa wnȩtrza 06C Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa czo lowa wnȩtrza Rys. 6C-01:
Po wprowadzeniu zmiennych uzupe lniaj acych otrzymamy równoważny mu problem w postaci kanonicznej:
 ROZDZIA L Metoda sympleksowa Motto: Matematyka nie może wype lnić życia ale jej nieznajomość już niejednemu je wype lni la H Steinhaus Tablica sympleksowa Rozważmy ZPL w postaci klasycznej maksymalizować
ROZDZIA L Metoda sympleksowa Motto: Matematyka nie może wype lnić życia ale jej nieznajomość już niejednemu je wype lni la H Steinhaus Tablica sympleksowa Rozważmy ZPL w postaci klasycznej maksymalizować
z n n=1 S n nazywamy sum a szeregu. Szereg, który nie jest zbieżny, nazywamy rozbieżnym. n=1
 3 Szeregi zespolone 3. Szeregi liczbowe Mówimy, że szereg o wyrazach zespolonych jest zbieżny, jeżeli ci ag jego sum czȩściowych {S n }, gdzie S n = z + z +... + jest zbieżny do granicy w laściwej. Granicȩ
3 Szeregi zespolone 3. Szeregi liczbowe Mówimy, że szereg o wyrazach zespolonych jest zbieżny, jeżeli ci ag jego sum czȩściowych {S n }, gdzie S n = z + z +... + jest zbieżny do granicy w laściwej. Granicȩ
STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA
 1 STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany.
1 STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany.
LOGIKA ALGORYTMICZNA
 LOGIKA ALGORYTMICZNA 0.0. Relacje. Iloczyn kartezjański: A B := (a, b) : a A i b B} (zak ladamy, że (x, y) i (u, v) s a równe wtedy i tylko wtedy gdy x = u i y = v); A n := (x 1,..., x n ) : x i A}; R
LOGIKA ALGORYTMICZNA 0.0. Relacje. Iloczyn kartezjański: A B := (a, b) : a A i b B} (zak ladamy, że (x, y) i (u, v) s a równe wtedy i tylko wtedy gdy x = u i y = v); A n := (x 1,..., x n ) : x i A}; R
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ANALIZA II 15 marca 2014 Semestr letni. Ćwiczenie 1. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la?
 Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Matematyka bankowa 2
 1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
Rozdzia l 6. Wstȩp do statystyki matematycznej. 6.1 Cecha populacji generalnej
 Rozdzia l 6 Wstȩp do statystyki matematycznej 6.1 Cecha populacji generalnej W rozdziale tym zaprezentujemy metodȩ probabilistycznego opisu zaobserwowanego zjawiska. W takim razie (patrz rozdzia l 2.4)zjawiskotobȩdziemy
Rozdzia l 6 Wstȩp do statystyki matematycznej 6.1 Cecha populacji generalnej W rozdziale tym zaprezentujemy metodȩ probabilistycznego opisu zaobserwowanego zjawiska. W takim razie (patrz rozdzia l 2.4)zjawiskotobȩdziemy
w = w i ξ i. (1) i=1 w 1 w 2 :
 S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu)
 WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu) PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we wzorach oznaczamy
WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu) PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we wzorach oznaczamy
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE
 WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Matematyka finansowa dla liderów Matematyka finansowa wokół nas dr Agnieszka Bem Uniwersytet Ekonomiczny we Wrocławiu 20 listopada 2017 r. Wartość pieniądzaw czasie Wartość
Akademia Młodego Ekonomisty Matematyka finansowa dla liderów Matematyka finansowa wokół nas dr Agnieszka Bem Uniwersytet Ekonomiczny we Wrocławiu 20 listopada 2017 r. Wartość pieniądzaw czasie Wartość
na p laszczyźnie kartezjaṅskiej prowadzimy prost a o rȯwnaniu s 1. (1.1) s 0 + t 1 t 0
 Chapter 1 Interpolacja 1.1 Interpolacja liniowa Zacznijmy opis pojȩcia inter-polacji od prostego przyk ladu. Przyk lad 1.1 Oblicz ile kilometrȯw przejecha l samochȯd po 3 godzinach jazdy, jeżeli po jednej
Chapter 1 Interpolacja 1.1 Interpolacja liniowa Zacznijmy opis pojȩcia inter-polacji od prostego przyk ladu. Przyk lad 1.1 Oblicz ile kilometrȯw przejecha l samochȯd po 3 godzinach jazdy, jeżeli po jednej
Zagadnienie Dualne Zadania Programowania Liniowego. Seminarium Szkoleniowe Edyta Mrówka
 Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
176 Wstȩp do statystyki matematycznej = 0, 346. uczelni zdaje wszystkie egzaminy w pierwszym terminie.
 176 Wtȩp do tatytyki matematycznej trści wynika że H o : p 1 przeciwko hipotezie H 3 1: p< 1. Aby zweryfikować tȩ 3 hipotezȩ zatujemy tet dla frekwencji. Wtedy z ob 45 1 150 3 1 3 2 3 150 0 346. Tymczaem
176 Wtȩp do tatytyki matematycznej trści wynika że H o : p 1 przeciwko hipotezie H 3 1: p< 1. Aby zweryfikować tȩ 3 hipotezȩ zatujemy tet dla frekwencji. Wtedy z ob 45 1 150 3 1 3 2 3 150 0 346. Tymczaem
MATEMATYKA DYSKRETNA - wyk lad 1 dr inż Krzysztof Bryś. Wprowadzenie
 1 MATEMATYKA DYSKRETNA - wyk lad 1 dr inż Krzysztof Bryś Wprowadzenie Istniej a dwa różne kryteria mówi ace, które narzȩdzia matematyczne należy zaliczyć do matematyki dyskretnej. Pierwsze definiuje matematykȩ
1 MATEMATYKA DYSKRETNA - wyk lad 1 dr inż Krzysztof Bryś Wprowadzenie Istniej a dwa różne kryteria mówi ace, które narzȩdzia matematyczne należy zaliczyć do matematyki dyskretnej. Pierwsze definiuje matematykȩ
System finansowy gospodarki. Zajęcia nr 6 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
Matematyka bankowa 1 1 wykład
 Matematyka bankowa 1 1 wykład Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Matematyka bankowa 1 1 wykład Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Normy wektorów i macierzy
 Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 5 Kalkulacja sk ladki netto I
 Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 5 Kalkulacja sk ladki netto I 1 Kodeks cywilny Tytu l XXVII, Umowa ubezpieczenia Dzia l I. Przepisy ogólne Dzia l II. Ubezpieczenia majatkowe
Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 5 Kalkulacja sk ladki netto I 1 Kodeks cywilny Tytu l XXVII, Umowa ubezpieczenia Dzia l I. Przepisy ogólne Dzia l II. Ubezpieczenia majatkowe
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady
 Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1
 TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1 Podstawowym pojęciem dotyczącym transakcji arbitrażowych jest wartość teoretyczna kontraktu FV. Na powyższym diagramie przedstawiono wykres oraz wzór,
TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1 Podstawowym pojęciem dotyczącym transakcji arbitrażowych jest wartość teoretyczna kontraktu FV. Na powyższym diagramie przedstawiono wykres oraz wzór,
OSOBNO ANALITYCZNYCH
 Uniwersytet Jagielloński Instytut Matematyki Zbigniew B locki ZBIORY OSOBLIWOŚCI FUNKCJI OSOBNO ANALITYCZNYCH Praca magisterska Promotor: Prof. dr hab. Józef Siciak Kraków 99 .Wstȩp. Jeśli Ω jest zbiorem
Uniwersytet Jagielloński Instytut Matematyki Zbigniew B locki ZBIORY OSOBLIWOŚCI FUNKCJI OSOBNO ANALITYCZNYCH Praca magisterska Promotor: Prof. dr hab. Józef Siciak Kraków 99 .Wstȩp. Jeśli Ω jest zbiorem
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Geometria odwzorowań inżynierskich Zadania 06
 Scriptiones Geometrica Volumen I (2014), No. Z6, 1 9. Geometria odwzorowań inżynierskich Zadania 06 Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Przenikanie siȩ figur (bry l) w rzutach Monge a
Scriptiones Geometrica Volumen I (2014), No. Z6, 1 9. Geometria odwzorowań inżynierskich Zadania 06 Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Przenikanie siȩ figur (bry l) w rzutach Monge a
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza. Oś liczbowa. Liczba 1, to nie jest liczba pierwsza
 1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 3 Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza 2 1 0 1 2 3 x Oś liczbowa. Liczba 1, to nie jest liczba pierwsza MATEMATYKA
1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 3 Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza 2 1 0 1 2 3 x Oś liczbowa. Liczba 1, to nie jest liczba pierwsza MATEMATYKA
Wyk lad 12. (ii) najstarszy wspó lczynnik wielomianu f jest elementem odwracalnym w P. Dowód. Niech st(f) = n i niech a bedzie
 1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
System finansowy gospodarki. Zajęcia nr 5 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
Cztery lokaty Zadanie Którą lokatę wybrać?
 Marian Maciocha Cztery lokaty Zadanie Którą lokatę wybrać? Chcemy ulokować 1000 zł na cztery miesiące i mamy do wyboru cztery propozycje: Propozycja 1: Lokata z oprocentowaniem 4% w skali roku. Odsetki
Marian Maciocha Cztery lokaty Zadanie Którą lokatę wybrać? Chcemy ulokować 1000 zł na cztery miesiące i mamy do wyboru cztery propozycje: Propozycja 1: Lokata z oprocentowaniem 4% w skali roku. Odsetki
POCHODNA KIERUNKOWA. DEFINICJA Jeśli istnieje granica lim. to granica ta nazywa siȩ pochodn a kierunkow a funkcji f(m) w kierunku osi l i oznaczamy
 POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
Rozdzia l 8. Pojȩcie liczby porz adkowej
 Rozdzia l 8. Pojȩcie liczby porz adkowej 1. Liczby naturalne a liczby porz adkowe Oto cztery pierwsze liczby naturalne zapisane wed lug różnych czterech notacji w porz adku od najmniejszej do najwiȩkszej:,
Rozdzia l 8. Pojȩcie liczby porz adkowej 1. Liczby naturalne a liczby porz adkowe Oto cztery pierwsze liczby naturalne zapisane wed lug różnych czterech notacji w porz adku od najmniejszej do najwiȩkszej:,
Temat 1: Wartość pieniądza w czasie
 Temat 1: Wartość pieniądza w czasie Inwestycja jest w istocie bieżącym wyrzeczeniem się dla przyszłych korzyści. Ale teraźniejszość jest względnie dobrze znana, natomiast przyszłość to zawsze tajemnica.
Temat 1: Wartość pieniądza w czasie Inwestycja jest w istocie bieżącym wyrzeczeniem się dla przyszłych korzyści. Ale teraźniejszość jest względnie dobrze znana, natomiast przyszłość to zawsze tajemnica.
Statystyka w analizie i planowaniu eksperymentu
 31 marca 2014 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
31 marca 2014 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
Wyk lad 14 Formy kwadratowe I
 Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
TABELA OPROCENTOWANIA DEPOZYTÓW W BANKU SPÓŁDZIELCZYM W NOWYM DWORZE MAZOWIECKIM
 Załącznik nr 1 do Uchwały Nr 40/2016 Zarządu Banku Spółdzielczego w Nowym Dworze Maz. z dnia 06.04.2016 r. TABELA OPROCENTOWANIA DEPOZYTÓW W BANKU SPÓŁDZIELCZYM W NOWYM DWORZE MAZOWIECKIM Tabela 1. Rachunki
Załącznik nr 1 do Uchwały Nr 40/2016 Zarządu Banku Spółdzielczego w Nowym Dworze Maz. z dnia 06.04.2016 r. TABELA OPROCENTOWANIA DEPOZYTÓW W BANKU SPÓŁDZIELCZYM W NOWYM DWORZE MAZOWIECKIM Tabela 1. Rachunki
0.1 Sposȯb rozk ladu liczb na czynniki pierwsze
 1 Temat 5: Liczby pierwsze Zacznijmy od definicji liczb pierwszych Definition 0.1 Liczbȩ naturaln a p > 1 nazywamy liczb a pierwsz a, jeżeli ma dok ladnie dwa dzielniki, to jest liczbȩ 1 i sam a siebie
1 Temat 5: Liczby pierwsze Zacznijmy od definicji liczb pierwszych Definition 0.1 Liczbȩ naturaln a p > 1 nazywamy liczb a pierwsz a, jeżeli ma dok ladnie dwa dzielniki, to jest liczbȩ 1 i sam a siebie
5. Strumienie płatności: renty
 5. Strumienie płatności: renty Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5. Strumienie płatności: renty Matematyka
5. Strumienie płatności: renty Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5. Strumienie płatności: renty Matematyka
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Matematyka finansowa wokół nas Michał Trzęsiok Uniwersytet Ekonomiczny w Katowicach 6 listopada 2017 r. Czym jest pieniądz? Pieniądz - dobro, które jest powszechnie akceptowane
Akademia Młodego Ekonomisty Matematyka finansowa wokół nas Michał Trzęsiok Uniwersytet Ekonomiczny w Katowicach 6 listopada 2017 r. Czym jest pieniądz? Pieniądz - dobro, które jest powszechnie akceptowane
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Statystyka w analizie i planowaniu eksperymentu
 29 marca 2011 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
29 marca 2011 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA. Ćwiczenia. http://zcht.mfc.us.edu.pl/ mm
 CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 2
 Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV
 DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV Stopa procentowa Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w jakiejkolwiek
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV Stopa procentowa Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w jakiejkolwiek
Matematyka A, klasówka, 24 maja zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le. rozwia
 Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Suma i przeciȩcie podprzestrzeń, suma prosta, przestrzeń ilorazowa Javier de Lucas
 Suma i przeciȩcie podprzestrzeń suma prosta przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1 W zależności od wartości parametru p podaj wymiar przestrzeni W = v 1 v v 3 gdzie p 0 v 1 = 1 + p 3 v = 5 3
Suma i przeciȩcie podprzestrzeń suma prosta przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1 W zależności od wartości parametru p podaj wymiar przestrzeni W = v 1 v v 3 gdzie p 0 v 1 = 1 + p 3 v = 5 3
Rozdzia l 9. Zbiory liczb porz adkowych. Liczby porz adkowe izolowane i graniczne
 Rozdzia l 9. Zbiory liczb porz adkowych. Liczby porz adkowe izolowane i graniczne 1. Kresy wzglȩdem dowolnego zbioru liczb porz adkowych Poświȩcimy teraz uwagȩ przede wszystkich kratowym w lasnościom klasy
Rozdzia l 9. Zbiory liczb porz adkowych. Liczby porz adkowe izolowane i graniczne 1. Kresy wzglȩdem dowolnego zbioru liczb porz adkowych Poświȩcimy teraz uwagȩ przede wszystkich kratowym w lasnościom klasy
Sprawdzian 4- lokaty i kredyty
 Sprawdzian 4- lokaty i kredyty Przykładowetypowe) zadania ZADANIE. Pan X wpłacił 000 zł do banku na czteroletni a lokatę oprocentowana w wysokości 8% rocznie. Odsetki dopisywane były do kapitału w końcu
Sprawdzian 4- lokaty i kredyty Przykładowetypowe) zadania ZADANIE. Pan X wpłacił 000 zł do banku na czteroletni a lokatę oprocentowana w wysokości 8% rocznie. Odsetki dopisywane były do kapitału w końcu
2b. Inflacja. Grzegorz Kosiorowski. Uniwersytet Ekonomiczny w Krakowie. Matematyka finansowa
 2b. Inflacja Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2b. Inflacja Matematyka finansowa 1 / 22 1 Motywacje i
2b. Inflacja Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2b. Inflacja Matematyka finansowa 1 / 22 1 Motywacje i
166 Wstȩp do statystyki matematycznej
 166 Wstȩp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwi azać nasz zasadniczy problem zwi azany z identyfikacj a cechy populacji generalnej
166 Wstȩp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwi azać nasz zasadniczy problem zwi azany z identyfikacj a cechy populacji generalnej
Arytmetyka. Działania na liczbach, potęga, pierwiastek, logarytm
 Arytmetyka Działania na liczbach, potęga, pierwiastek, logarytm Zbiory liczbowe Zbiór liczb naturalnych N = {1,2,3,4, }. Zbiór liczb całkowitych Z = {, 3, 2, 1,0,1,2,3, }. Zbiory liczbowe Zbiór liczb wymiernych
Arytmetyka Działania na liczbach, potęga, pierwiastek, logarytm Zbiory liczbowe Zbiór liczb naturalnych N = {1,2,3,4, }. Zbiór liczb całkowitych Z = {, 3, 2, 1,0,1,2,3, }. Zbiory liczbowe Zbiór liczb wymiernych
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym
 Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 2 Tablice trwania życia
 Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 2 Tablice trwania życia 1 Cele (na dzisiaj): Zrozumieć w jaki sposób można wyznaczyć przysz ly czas życia osoby w wieku x. Zrozumieć parametry
Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 2 Tablice trwania życia 1 Cele (na dzisiaj): Zrozumieć w jaki sposób można wyznaczyć przysz ly czas życia osoby w wieku x. Zrozumieć parametry
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym
 Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania
 Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera
 Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
Obligacje. nazywamy papier warto sciowy maj acy, po_zyczki przez instytucj e, obligacj e, u jej nabywcy.
 Obligacje De nicja Obligacj nazywamy papier warto sciowy maj acy, charakter wierzycielski. Obligacj jest zaci agni, eciem, po_zyczki przez instytucj e, sprzedaj ac, obligacj e, u jej nabywcy. Sprzedaj
Obligacje De nicja Obligacj nazywamy papier warto sciowy maj acy, charakter wierzycielski. Obligacj jest zaci agni, eciem, po_zyczki przez instytucj e, sprzedaj ac, obligacj e, u jej nabywcy. Sprzedaj
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady część II
 Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina.
 Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia 2015 r.)
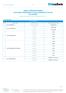 Duma Przedsiębiorcy 1/8 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia ) 1. Oprocentowanie LOKATY TERMINOWE L.p. Nazwa Lokaty umowny Oprocentowanie
Duma Przedsiębiorcy 1/8 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia ) 1. Oprocentowanie LOKATY TERMINOWE L.p. Nazwa Lokaty umowny Oprocentowanie
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE
 Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE Zmianą wartości pieniądza w czasie zajmują się FINANSE. Finanse to nie to samo co rachunkowość. Rachunkowość to opowiadanie JAK BYŁO i JAK JEST Finanse zajmują
Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE Zmianą wartości pieniądza w czasie zajmują się FINANSE. Finanse to nie to samo co rachunkowość. Rachunkowość to opowiadanie JAK BYŁO i JAK JEST Finanse zajmują
Pierwiastki arytmetyczne n a
 Chapter 1 Pierwiastki arytmetyczne n a Operacja wyci aganie pierwiastka stopnia n z liczby a jest odwrotn a operacj a do potȩgowania, jeżeli operacja odwrotna jest wykonalna w liczbach rzeczywistych. Zacznijmy
Chapter 1 Pierwiastki arytmetyczne n a Operacja wyci aganie pierwiastka stopnia n z liczby a jest odwrotn a operacj a do potȩgowania, jeżeli operacja odwrotna jest wykonalna w liczbach rzeczywistych. Zacznijmy
Polscy Giganci BIS. Forma prawna Agent: Ubezpieczyciel: Euro Bank S.A. Okres Odpowiedzialności: Wiek: Zwrot kapitału: 18-77 lat
 produkt strukturyzowany Polscy Giganci BIS Forma prawna Agent: Ubezpieczyciel: indywidualne ubezpieczenie na życie i dożycie Euro Bank S.A. Towarzystwo Ubezpieczeń na Życie Europa S.A. Okres Odpowiedzialności:
produkt strukturyzowany Polscy Giganci BIS Forma prawna Agent: Ubezpieczyciel: indywidualne ubezpieczenie na życie i dożycie Euro Bank S.A. Towarzystwo Ubezpieczeń na Życie Europa S.A. Okres Odpowiedzialności:
Matematyka finansowa 26.05.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
ZADANIE 1. NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI
 ZADANIE 1 Na budowę domu możesz zaciagn ać pożyczkę w wysokości 63450 e. Do wyboru sa dwa warianty spłaty: I w każdym miesiacu spłacasz równe raty, każda w wysokości 2% pożyczonej kwoty. II pierwsza rata
ZADANIE 1 Na budowę domu możesz zaciagn ać pożyczkę w wysokości 63450 e. Do wyboru sa dwa warianty spłaty: I w każdym miesiacu spłacasz równe raty, każda w wysokości 2% pożyczonej kwoty. II pierwsza rata
Geometria odwzorowań inżynierskich. 1. Perspektywa odbić w zwierciad lach p laskich 06F
 Scriptiones Geometrica Volumen I (2014), No. 6F, 1 10. Geometria odwzorowań inżynierskich Perspektywa odbić w zwierciad lach p laskich 06F Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa
Scriptiones Geometrica Volumen I (2014), No. 6F, 1 10. Geometria odwzorowań inżynierskich Perspektywa odbić w zwierciad lach p laskich 06F Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Matematyka Finansowa dla liderów dr Aneta Kaczyńska Uniwersytet Ekonomiczny w Poznaniu 30 listopada 2017 r. Dr Tomaszie Projektami EKONOMICZNY UNIWERSYTET DZIECIĘCY Copywrite
Akademia Młodego Ekonomisty Matematyka Finansowa dla liderów dr Aneta Kaczyńska Uniwersytet Ekonomiczny w Poznaniu 30 listopada 2017 r. Dr Tomaszie Projektami EKONOMICZNY UNIWERSYTET DZIECIĘCY Copywrite
Funkcje wielu zmiennych
 Funkcje wielu zmiennych 8 Pochodna kierunkowa funkcji Definicja Niech funkcja f określona bȩdzie w otoczeniu punktu P 0 = (x 0, y 0 ) oraz niech v = [v x, v y ] bȩdzie wektorem. Pochodn a kierunkow a funkcji
Funkcje wielu zmiennych 8 Pochodna kierunkowa funkcji Definicja Niech funkcja f określona bȩdzie w otoczeniu punktu P 0 = (x 0, y 0 ) oraz niech v = [v x, v y ] bȩdzie wektorem. Pochodn a kierunkow a funkcji
STOPA PROCENTOWA I STOPA ZWROTU
 Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Wyk lad 6 Podprzestrzenie przestrzeni liniowych
 Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
Inwestowanie w obligacje
 Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
MATEMATYKA REPREZENTACJA LICZB W KOMPUTERZE
 1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 B l ad bezwzglȩdny zaokr aglenia liczby ɛ = fl() B l ad wzglȩdny zaokr aglenia liczby 0 δ = fl() B l ad procentowy zaokr aglenia liczby 0
1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 B l ad bezwzglȩdny zaokr aglenia liczby ɛ = fl() B l ad wzglȩdny zaokr aglenia liczby 0 δ = fl() B l ad procentowy zaokr aglenia liczby 0
